Finger-String Interaction Analysis in Guitar Playing With Optical Motion Capture

1. Introduction

The interaction between a musician and a musical instrument determines the characteristics of the sound produced. Understanding such interaction is a field with growing interest, driven in recent years by technological advances that have allowed the emergence of more accurate yet less expensive measuring devices. The ability to measure the actions that control a musical instrument (i.e., instrument control parameters) has applications in many areas of knowledge, such as acoustics (Schoonderwaldt et al., 2008), music pedagogy (Visentin et al., 2008), sound synthesis (Erkut et al., 2000; Maestre et al., 2010; Pérez-Carrillo et al., 2012), augmented performances (Wanderley and Depalle, 2004; Bevilacqua et al., 2011), or performance transcription (Zhang and Wang, 2009).

In the classical guitar, this interaction occurs with the left hand (fingering) and right hand (plucking). Fingering mainly determines the tone (pitch), while plucking determines the qualities of the sound. Guitar control parameters can also be divided into excitation gestures that introduce energy into the system, and modification gestures that relate to changes applied to the guitar after playing a note (Cadoz and Wanderley, 2000). In this work we are focusing mainly on the former type (excitation gestures).

Although plucking can be considered an instantaneous event, it is actually a process with three main phases (Townsend, 1996): (a) a preparation stage during which the player places his/her finger above the string; (b) a pressure stage during which the string is taken away from its resting position; (c) and a release stage during which the string slides over the fingertip and then it is left to oscillate freely. The excitation gestures determine the initial conditions with which the string is released at the end of the interaction with the finger.

The parameters of the excitation gesture that have the greatest influence on the sound are (Scherrer, 2013): the plucked string; the fingering (which fret); the plucking force, which is related to the string displacement; the position in which the string is pulled (distance to the bridge); the direction in which the string is released at the end of the plucking interaction; and whether the interaction occurs with the nail or flesh.

The methods used for the acquisition of control parameters in music performances fall into three main categories (Miranda and Wanderley., 2006): direct acquisition, which focuses on the actual realization of the gesture, is performed using sensors to measure various physical quantities, such as distance, speed, or pressure; indirect acquisition (Wanderley and Depalle, 2004; Pérez-Carrillo and Wanderley, 2015), which considers the consequence of the gesture, that is, the resulting sound, as the source of information about the gesture. It is based on the analysis of the audio signal; and physiological acquisition, which analyzes the causes of the gesture by measuring muscle (or even brain) activity.

In guitar playing, we mostly find reports on direct and indirect methods or combinations or both. Indirect methods are mainly related to the detection of pitch, and together with the tuning of the strings, provide a good estimate of the plucked string and the pressed fret. It is also common to find methods that can calculate the plucking position on the string, that is, the distance to the guitar bridge (Traube and Smith, 2000; Traube and Depalle, 2003; Penttinen and Välimäki, 2004). More advanced methods are capable of detecting left and right hand techniques (Reboursière et al., 2012), expression styles (Abesser and Lukashevich, 2012) and even more complex features such as the plucking direction (Scherrer and Depalle, 2012) that is retrieved by combination of sound analysis informed with physical models. The audio recording devices used range from microphones that measure sound pressure to pickups that measure mechanical vibration of guitar plates, and also opto-electronic sensors (Lee et al., 2007).

The use of sensors allows to extract more parameters with greater precision. Some methods use capacitive sensors placed on the fret board (Guaus and Arcos, 2010) or video cameras (Burns and Wanderley, 2006). However, the most reliable methods are based on a 3D representation of the motion. They are mainly based on mechanical (Collins et al., 2010), inertial (Linden et al., 2009), electro-magnetic (EMF, Maestre et al., 2007; Pérez-Carrillo, 2009), or optical systems. With the exception of optical systems, these methods remain too intrusive to measure the fine movement of the fingers.

Regarding optical systems, they are becoming more popular, since they are generally low or non-intrusive. A low-cost video camera was mounted on the head of the guitar by Burns and Wanderley (2006) to capture the position of left-hand fingertips with respect to the grid of strings and frets, being able to identify chords without the use of markers on the hands. Although very practical for some applications, such a system cannot capture fine movements in the fingers due to the low sampling rate, the difficulty of current computer vision algorithms to recognize fingertips, and it is limited to the tracking of fingertips in the left hand. Heijink and Meulenbroek (2002) used an active optical motion capture system with infrared light emitting diodes placed on the hands and guitar to track the motion of the left- hand fingertips.

Chadefaux et al. (2012) used high-speed video cameras to manually extract features during the plucking of harp strings. Colored dots were painted on the fingertips and a small marker was attached to the string. The marker had a corner to measure the string rotation. This advanced method provides very high resolution and accuracy in analyzing the finger-string interaction. However, it needs an extremely controlled setup. We discarded such an approach due to the complexity of obtaining 3D coordinates and also due to the unfeasability of measuring all the joints of the fingers.

Norton (2008) was also interested in analyzing fine motion of the fingers and compared several motion capture systems to track the 3D position of most hand joints (e.g., passive cameras, active cameras, or gloves). The main experiment was based on an active system based on cameras that detect light-emitting diodes. The author faced very similar problems to ours and reports the difficulty of dealing with marker occlusion, especially those at the finger nails. Norton focuses on the methodology and does not provide details on feature computation or on the statistics of marker dropouts and the approach to deal with dropouts is linear interpolation of 3D positions. In addition, he reported complications due to the reflection of the LEDs in the body of the guitar, which forced him to fix black felt on the plate of the guitar. Another difference is that he does not measure the position of the strings, and therefore, it is not possible to compute finger-string interaction features.

The most similar work regarding objectives (analysis of finger-string interaction) and methodology (motion capture based on high-speed passive markers) is by Perez-Carrillo et al. (2016). An acknowledged obstacle in that work is that of marker occlusion, especially in the fingertips of the right hand during the process of plucking, where the string-finger interaction occurs. The reported percentage of correctly identified markers on the fingertips during plucking is very low (around 60%), meaning that it looses the track of half of the plucks. In addition, the plucking gesture was considered as an instantaneous event that happens at note-onsets and therefore, it cannot extract information about the different stages during the plucking process.

The presented method is able to track 3D motion of each joint in both hands along with the position of the guitar strings. This allows to track the finger-string interaction with high accuracy and time resolution, and to calculate a comprehensive set of interaction features that are directly related to the characteristics of the sound produced. The method is based on high-speed cameras that track the position of reflective (passive) markers. This method is intrusive to some extent (markers are placed on the joints of the hand) and it requires a careful and controlled setup (maker protocol and camera placement). However, according to the participants, it still allows to perform in conditions very close to those in a practice environment.

Beyond the methodology for data acquisition, the main contribution of this research is a hand model that is able to reconstruct the position of occluded markers on the finger tips. This approach allows observing and analyzing the trajectories of the fingertips during the plucks, gaining spatial-temporal accuracy during the finger-string interaction, as well as a more robust and accurate feature estimation algorithm.

In section 2 we present the materials and equipment used to acquire the motion and audio data. In section 3 we describe the Guitar Body Model used to track the position of the strings and in section 4 we present the Hand Model, which is used to track the hands and recover lost markers. Later, in section 5, we disclose the analysis of the plucking process and we give details about the computation of the finger-string interaction features. Finally, conclusions are drawn in section 6.

2. Materials and Methods

2.1. Overview

The objective of this work is to analyze and characterize the interaction between the finger and the string during the process of plucking. Therefore, we need to know the position of the (plucked) string and the motion trajectory of the (plucking) finger during a time window around the note onset. To achieve this, we combine audio with Motion Capture (MoCap) analysis. From the audio we can obtain note onsets and pitch. Note onsets will determine the plucking times and the pitch will help determine the string. From the MoCap we obtain the 3D position of the strings and finger joints. The position of the strings can be easily estimated through the definition of a Rigid Body (section 3) and the major concern is how to correctly track the motion of the hands since the small markers placed on them can be very easily occluded, specially during the plucks. For this reason, we define a hand model that is capable of reconstructing lost markers in the hand (section 4). Once all the markers are correctly reconstructed and identified, we proceed to analyze the trajectories of the fingertips (section 5.1) and finally, a large set of guitar excitation features is computed (section 5.2). The complete procedure is represented in Figure 1.

FIGURE 1

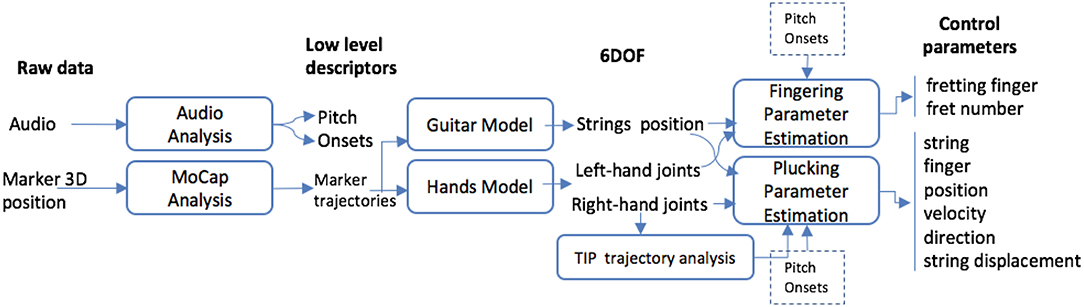
Figure 1. General Schema for the calculation of excitation gestures in guitar performances. From the audio signal we extract the pitch and the onsets, which determine the plucking instants and help in the detection of the string and fret. From the trajectories of 3D markers as provided by the MoCap system, we can obtain the position of the strings and fingers, by applying a guitar and a hand model respectively. Then, we analyze the fingertip (TIP) trajectories around the note onset times and we compute a comprehensive set of string excitation features.

2.2. Database Corpus

The methods and algorithms presented are based on a dataset of multimodal recordings of guitar performances that contain synchronized audio and motion data streams. The corpus of the database is composed of ten monophonic fragments from exercises number V, VI, VII, VIII, XI, and XVII of Etudes Faciles by Leos Brouwer ¹. Each fragment averaged about a minute and was performed by two guitarists. In total, the collection contains around 1.500 plucks (i.e., notes). For model training we use 150 frame windows centered in the note onsets, making a total of about 225.000 data frames.

The recording sessions opened with an information sheet outlining the topic and purpose of the study and instructing respondents that they were providing informed consent. Ethical approval for the study, including consenting procedures, was granted by the Conservatoires UK Research Ethics Committee following the guidelines of the British Psychological Society.

2.3. Equipment and Setup

Audio and Motion streams were recorded on two different computers and synchronized by means of a world clock generator that controls the sampling instants of the capture devices and sends a 25 Hz SMPTE signal that is saved as timestamps with the data. Audio to motion alignment consists simply of aligning the SMPTE timestamps.

2.3.1. Audio Recording and Analysis

Audio was recorded using a piezoelectric contact transducer (a Schaller Oyster S/P) that measures the vibration of the top plate of the guitar. Sampling frequency was set to 48 kHz and quantization to 16−bits. The piezo cutoff frequency is around 15 kHz, which is enough for our analysis. The captured signal is better adapted for audio analysis than that of a microphone, since it is not affected by room acoustics or sound radiation. The audio stream is segmented into notes by onset detection (Duxbury et al., 2003) and pitch tracking was performed based on the auto-correlation function (de Cheveigné and Kawahara, 2002).

2.3.2. MoCap Analysis

Motion capture was performed with a Qualysis ² system. This system uses high-speed video cameras that emit infrared light and detect the 3D coordinates of reflective markers by triangulation (i.e., each marker must be identified by at least three cameras placed in different planes). The sampling frequency of the cameras is 240 Hz and determines the sampling rate of our data. From the 3D coordinates of the markers, the Qualysis software tracks the trajectory over time of each marker and assigns a label to each trajectory (i.e., trajectory identification). In our configuration, we used twelve cameras and they were installed very carefully around the guitarist to maximize the correct detection of markers and the identification of their trajectories as well as to minimize the manual cleaning of the data, that is, assign the appropriate labels to incorrectly identified and non-identified trajectories.

Statistics of correct marker detection are shown in Table 1. We can observe how markers on the strings and on most of the finger joints have a 99% rate of correct detection. However, the rate for the fingertips (TIP) decreases dramatically, especially in the right hand during plucking instants, where the finger-string interaction takes place and, therefore, the most important instants in this study. To overcome this issue, we propose a hand model that is capable of reconstructing the position of lost markers (section 4).

TABLE 1

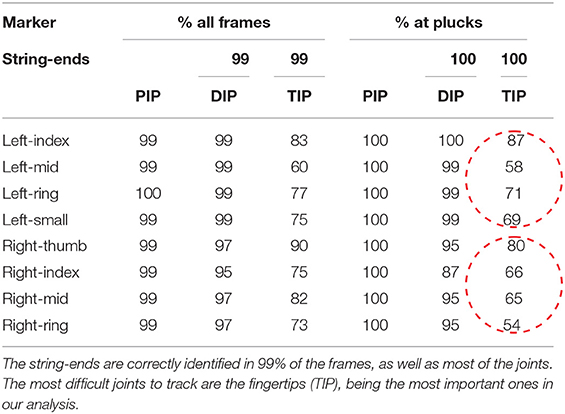
Table 1. Marker detection rates. PIP, DIP, and TIP refer to the last three finger joints as shown later in section 4.1.

The 3D marker trajectories retrieved with the Qualisys system undergo a pre-processing stage consisting of small-gap filling and smoothing. We perform linear interpolation to gaps of a maximum size of 25 frames (around 100 ms) and smoothing is performed by 20-points moving average. An example of the Smoothing and Gap Filling (S.GF) process is shown in Figure 2 for a maker trajectory corresponding to the index fingertip.

FIGURE 2

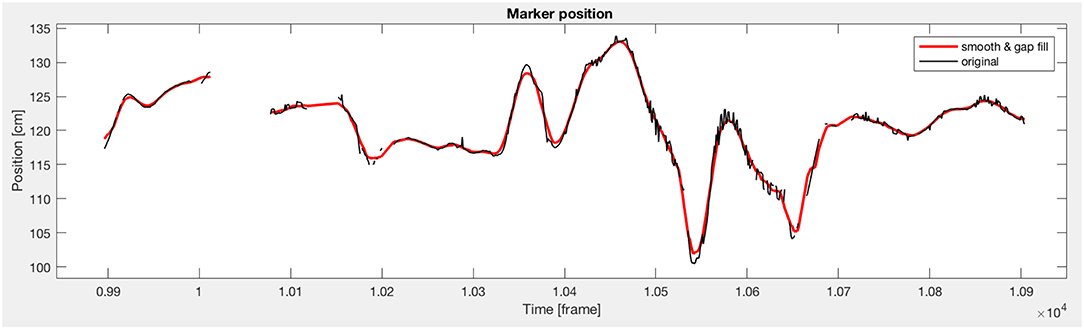
Figure 2. Smoothing and small gap filling corresponding to the x-coordinate of the right index fingertip. Small gaps of maximum 100 ms are filled by linear interpolation and trajectories are smoothed in order to clean the data from jitter and other noise.

3. Guitar Rigid Body

The position of the strings is determined by the definition of a guitar Rigid Body (RB). A RB is a rigid structure of six degrees-of-freedom (6DOF) defined by the position of a set of markers and associated with a local system of coordinates (SoC). This allows to track the 3D position and orientation of the RB with respect to the global SoC. The position of the markers is constant, relative to the local SoC and their global coordinates can be obtained by a simple rotation and translation from the local to the global SoC. The guitar RB is built by placing markers at each string-end as well as reference markers attached to the guitar body. The markers at the string-ends cannot remain attached during a performance as it would be very intrusive, so they are defined as virtual markers. Virtual markers are only used for calibration to define the SoC structure. During the actual tracking, virtual markers are reconstructed from the reference markers.

Special care has to be taken when placing the reference markers to the guitar body as the plates are reflective to light, causing interference with the markers. In order to avoid these unwanted reflections, the markers are placed on the edge of the guitar body and outside the guitar plates by means of antennas (extensions attached to the body). Five reference markers were used and they were placed as shown in Figure 3 (green markers). The tracking of the position of the strings following this procedure achieves almost 100% of correctly reconstructed frames.

FIGURE 3

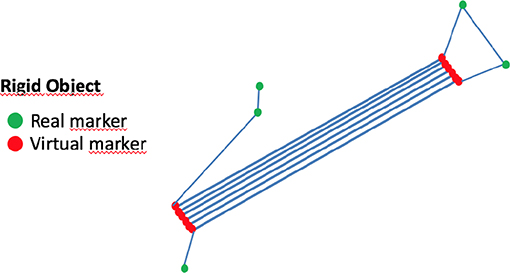
Figure 3. Rigid Body model for the guitar. The green dots are the auxiliary markers of the guitar, and are used to track the motion of the guitar as a rigid object. The red dots represent the virtual markers at the strings-ends, and are only present during the calibration of the model. During the performance, their position is reconstructed form the auxiliary ones.

4. Hand Model

4.1. Marker Placement Protocol

Hand motion is tracked by placing reflective markers on the joints of the hands and fingers, as shown in Figure 4. These joints involve four bones for each finger: metacarpal, proximal phalanx, middle phalanx, and distal phalanx. The joint between the metacarpal and proximal phalanx is named the metacarpophalangeal joint (MCP). The joint between the proximal phalanx and the middle phalanx is called the proximal interphalangeal joint (PIP), and the joint between the middle phalanx and the distal phalanx is called the distal interphalangeal joint (DIP). The exception is the thumb, which does not have a middle phalanx and therefore it does not have a DIP joint.

FIGURE 4

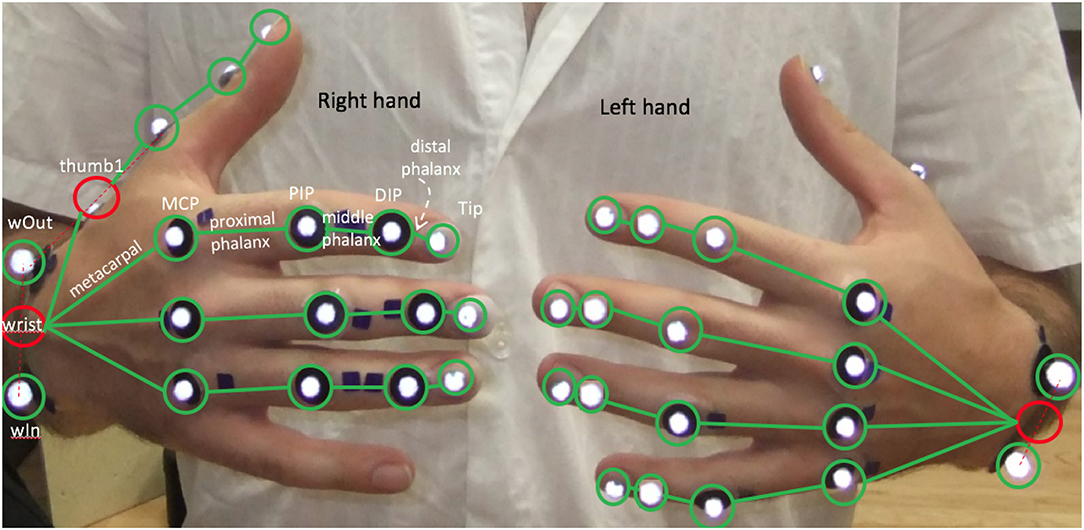
Figure 4. Placement of hand markers. The red circles indicate the position of the virtual markers that do not exist physically (their position is computed from the position of the real ones). Virtual marker wrist is the middle point between wIn to wOut and thumb₁ is at 1/3 of the line that goes from wOut to the MCP joint of the thumb.

The right hand has markers on every finger expect for the little finger, and the left hand has markers in every finger except for the thumb, since those are the fingers used in traditional guitar playing. The red circles indicate the position of the virtual markers, whose position is computed from the position of the real ones. The position of the virtual marker wrist is defined at the midpoint between the line $\overline{w_{out}-w_{in}}$, and the position of the virtual marker thumb₁ is defined at 1/3 of the length of the line $\overline{MC{P}_{thumb}-w_{out}}$.

Although markers are very small and light, placing them on the nails is intrusive to some extent and may affect the musical performance. The participants agreed that the markers were not really interfering physically, but the feeling of having them on their nails made them play with less confidence. The good news is that, even if the way of performing is altered, the relationship between control parameters and the sound produced remains the same.

4.2. Finger Model

The main problem during hand tracking is that of marker occlusion and it occurs mainly in the fingertips and more specifically during the plucks, which are precisely the instants that we intend to analyze. We need hand model that can reconstruct the position of lost makers at the fingertips. We propose a model that considers the fingers as planes and translates 3D marker positions into 2D angles on the planes. Marker recovery in the angle domain is much more straightforward as there is a high correlation among joint angles of the same finger.

The procedure for modeling the hands is shown in Figure 5. The MoCap system provides the 3D trajectories of the markers (0), which is followed by an automatic process of cleaning (2), i.e., smoothing and small-gap filling as explained in section 2.3.2. Then, we find the plane that represents each finger (3), computed as the plane that minimizes the distances to its markers. We immediately translate the general 3D coordinates into 2D coordinates in the plane (4) and translate 2D coordinates into joint angles in the plane (5). After a second process of cleaning and outlier removal (6), the missing angles (θ₂ and θ₃) are reconstructed from models trained with ground truth data (7). The process is finally reversed to get the reconstructed 3D positions of the markers. In addition, a process of correcting the position of the markers to match the center of rotation (CoR) of the joints is applied to the 2D local coordinates (4).

FIGURE 5

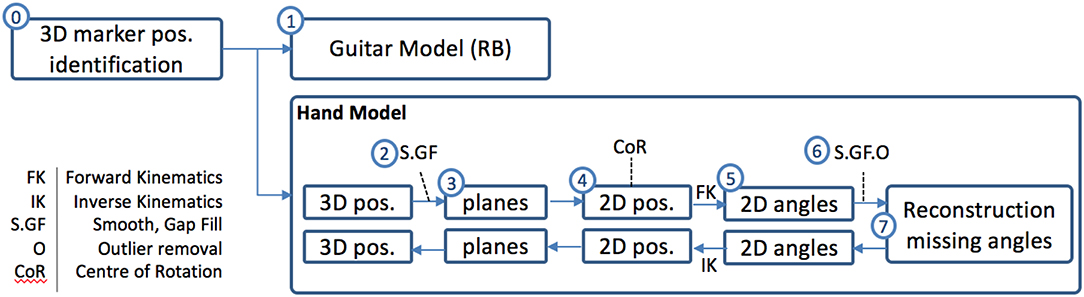
Figure 5. Procedure to model the hands. 3D marker trajectories are provided by the MoCap system. After pre-processing the data (2) 3D marker coordinates are translated into 2D finger plane coordinates (3). Then, the CoR is corrected (4) and 2D coordinates are translated to angles. Later, missing angles are reconstructed (7) and finally the process is reversed (except the CoR correction) to obtain the 3D coordinates of the joints.

4.2.1. Define Finger Planes (3)

Each of the fingers is represented as a plane (Figure 6). The plane of a finger is estimated from the position of its five joints as the plane with minimum distance to them. In order to estimate the best fitting plane, we need at least three correctly identified markers, which is a reasonable condition since the first joints of each finger, the wrist, MCP and PIP are correctly identified in 99% of the frames.

FIGURE 6

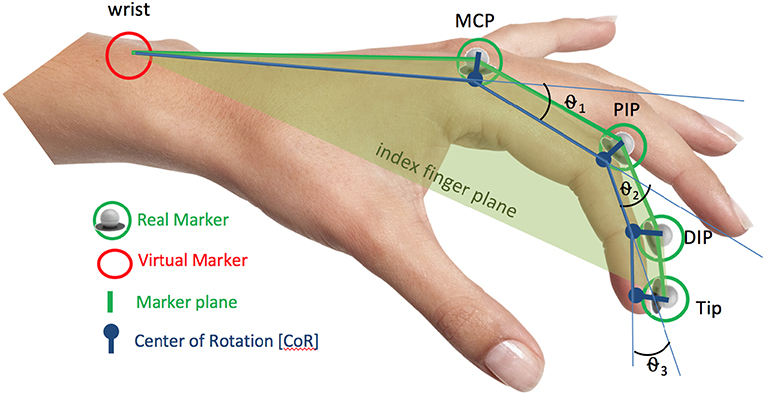
Figure 6. Representation of the plane for the index finger (translucent green) obtained from the position of the joints and bones. CoR correction is depicted in blue as well as the angles θ₁, θ₂, θ₃.

The planes are obtained by Singular Value Decomposition (svd) of matrix A, i.e., USV = svd(A). Where A = [XYZ] and X, Y, and Z are column vectors representing the 3D coordinates of the finger joints after having subtracted out the centroid (i.e., the column means). The normal vector of the best-fitting plane is the third column vector of the right singular matrix (matrix V). Intuitively, the vectors in matrix V are a set of orthonormal eigenvectors, ordered by the spacial direction in which data has more variance. Therefore, the first two vectors represent the base for the plane and the third vector is the vector normal to the plane.

4.2.2. Convert to 2D Local Positions (4)

The next step is to project the finger joints on to their own plane to get 2D local coordinates (local to the plane). To compute local coordinates, we must first define coordinate system of the finger plane. Let x-axis be the unit vector that goes from the MCP joint to the virtual marker wrist and the y-axis is computed as the cross-product y_axis = x_axis × z_axis, where z_axis is the plane normal vector. Following this procedure, we can also get rotation and translation matrices for each plane that we will need later for the reconstruction of the 3D position of the markers.

The projection of any point p = (p_x, p_y, p_z) onto a plane (the projection with closest distance) is computed based on the dot product. Given a plane determined by point A and the plane normal vector $\overrightarrow{n}$, the projection is obtained as $p_{proj}=p-((p-A)·\overrightarrow{n})\times \overrightarrow{n}$.

4.2.3. Center of Rotation Correction

The next step is to correct the position of the markers to match the Centers of Rotation (CoR) of the joints or, in the case of the fingertips, the part of the finger flesh that makes contact with the string (Figure 6). This step is very important especially to correct the position of the fingertips as shown in Figure 7. This figure presents 2D projections of several trajectories of the thumb-tip during the plucking process. It can be observed how marker positions are shifted upwards and to the left with respect to the actual plucked string. The computation of the CoR allows for the correction of this displacement. For simplicity, CoR's are assumed to be at 0.5 cm distance to the actual marker positions, toward the center of the plane and at the half of the inter-bone angle (Figure 6). This distance was arbitrarily set as an average estimate of the finger width (the approximate distance from center of the markers to the actual joint rotation center).

FIGURE 7

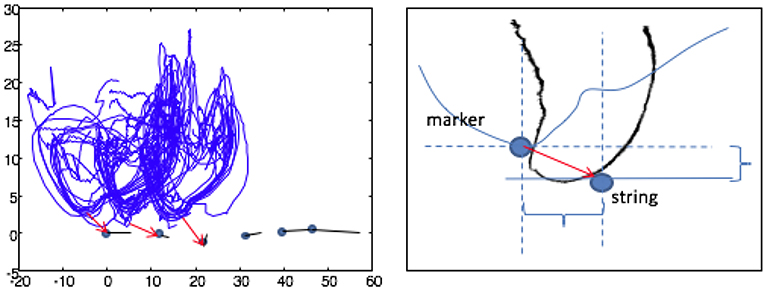
Figure 7. Finger vs. Marker Position. On the left we can observe several trajectories of the thumb-tip during the process of plucking and the corresponding plucked strings (with red arrows). We can clearly see how the trajectories are shifted upwards and to the left with respect to the plucked string. The reason is that the position of the marker is on the nail and, therefore, shifted with respect to the part of the finger that comes into contact with the string.

4.2.4. Translation Into 2D Inter-Bone Angles (5)

Once we have an estimation of the local coordinates of the CoR, we compute the angles between the bones (θ₁, θ₂, and θ₃ as depicted in Figure 6). From this step, we need to store the length of the bone segments in order to reconstruct later the 2D-plane positions from angles (forward kinematics). The length of the bones are calculated as the average length of all frames.

4.2.5. Missing Angle Reconstruction (7)

This step consists of reconstructing the missing angles due to marker occlusion. From Table 1, we know that MCP and PIP joints are correctly identified in 99% of the frames, but DIP and Tip may be lost during the plucking process. This means that θ₁ has a 99% of correct identification rate but θ₂ and θ₃ only about 60%. The good news is that the three angles are highly correlated and a specific finger posture has always a very similar combination of angles. This allows for the estimation of missing θ₂ and θ₃ from θ₁ by training machine learning algorithms.

Our approach was to train Non-linear Autoregressive Networks with Exogenous Inputs (NARX) in Matlab ³, a kind of Neural Network with recursive connections and tapped delays that considers previous inputs and outputs. The recursive connection is a link from the output layer directly to the input. The reason for choosing NARX networks was because such architectures are very well adapted to time series prediction. First, they can handle information of several previous inputs and also, they have a recursive input, which adds very important contextual information to the network. In addition, NARX networks do not need large amounts of data when trained as other architectures such as LSTM networks.

We trained two networks per finger, the first one, Net₁, has as input θ₁ and as output θ₂. The second network, Net₂, has as inputs θ₁ and θ₂ and predicts θ₃. The internal structure of such networks is depicted in Figure 8. The parameters of the selected networks were the following: 10 frames of input delays, 10 feedback delays, and hidden layer size of 10 neurons. The optimization method was Levenberg-Marquardt with Mean Squared Error (MSE) as the cost function. The weights of the neural connections returned a MSE of about 4 × 10⁻⁴ after about 12 epochs. The size of the dataset was of about 225.000 frames, corresponding to 150 plucks. From these, 30 plucks were allocated for testing and no validation set was used due to the small size (in plucks) of the dataset. The evaluation results were obtained by performing a 10-fold cross-validation.

FIGURE 8

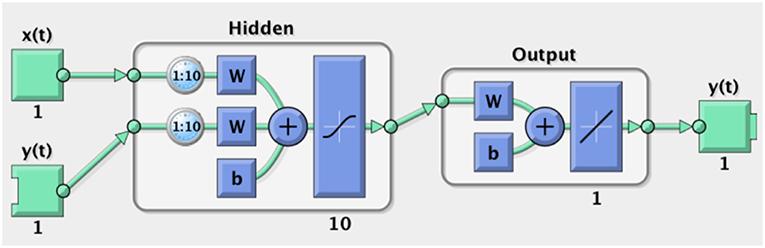
Figure 8. Architecture of NARX Net₁ that predicts θ₂ from θ₁. It has 10 tapped input delays (i.e., it takes the inputs of the last 10 frames) 10 tapped recursive connections that route the output (y(t)) directly into the input. It has a hidden layer with 10 neurons and a Sigmoid activation function. Net₂ is very similar, except that it takes an extra tapped delay input (θ₂) and the output is θ₃.

4.2.6. Inverse Kinematics and 3D Reconstruction

Once the missing angles are recovered, we preform the reverse process to get the reconstructed 3D position of the missing markers. First we apply inverse kinematics to get the 2D local positions of the joints from the angles and finally, 2D positions are converted into 3D coordinates using plane information (the normal vector and the coordinates of the common wrist joint). The only process that is not reversed is the displacement of the CoR so that we recover the estimated position of the joints instead of the markers.

The improvement of correct TIP marker detection with respect to the baseline rates reported in Table 1 when this algorithm is applied is very satisfactory. As the algorithm outputs an estimation for every TIP marker, the theoretic marker detection percentage is of 100%. However, there is an average error in the estimation of less than 3 mm (obtained from the MSE error in angle space and later 3D geometric data reconstruction).

5. Finger-String Interaction

5.1. Plucking Process Analysis

Once we have recovered the position of the occluded joints, we can visualize and analyze the 3D trajectories and the interaction between the finger and the string during the pluck. The plucking action is not an instantaneous event, but a process that involves several phases (Scherrer, 2013). It starts with the finger getting in contact with the string (preparation phase), then the finger pushes the string (pressure phase), and finally the finger releases the string (release phase). The note onset occurs after the release of the string. The precise instants when these events occur can be determined by observation of the motion data.

In Figure 9 we can see a representative example of the thumb-TIP trajectories in a short window of 150 frames (0.625 s) around the note onset, and a series of subfigures that show different parameters during the pluck. The note onset is represented in each plot as a red cross along with a vertical dashed line in red. Plucking trajectories of other fingertips look very similar, except that they occur in the opposite direction in the x-axis. In Figure 9B the guitar strings are depicted along with the reference coordinate system: axis ŷ is a unit vector in the direction of the sixth string (lowest pitch). A temporary vector $\widehat{x}$ is defined as the unitary vector that goes from the sixth string notch on the bridge to the first string notch on the fret. $\widehat{x}$ and ŷ define the strings plane. Axis ẑ is the cross product $ẑ=\widehat{x}\times ŷ$ and finally the $\widehat{x}$ axis is corrected (at this point, $\widehat{x}$ may not be completely orthogonal to ŷ) by computing the cross product $\widehat{x}=ŷ\times ẑ$.

FIGURE 9

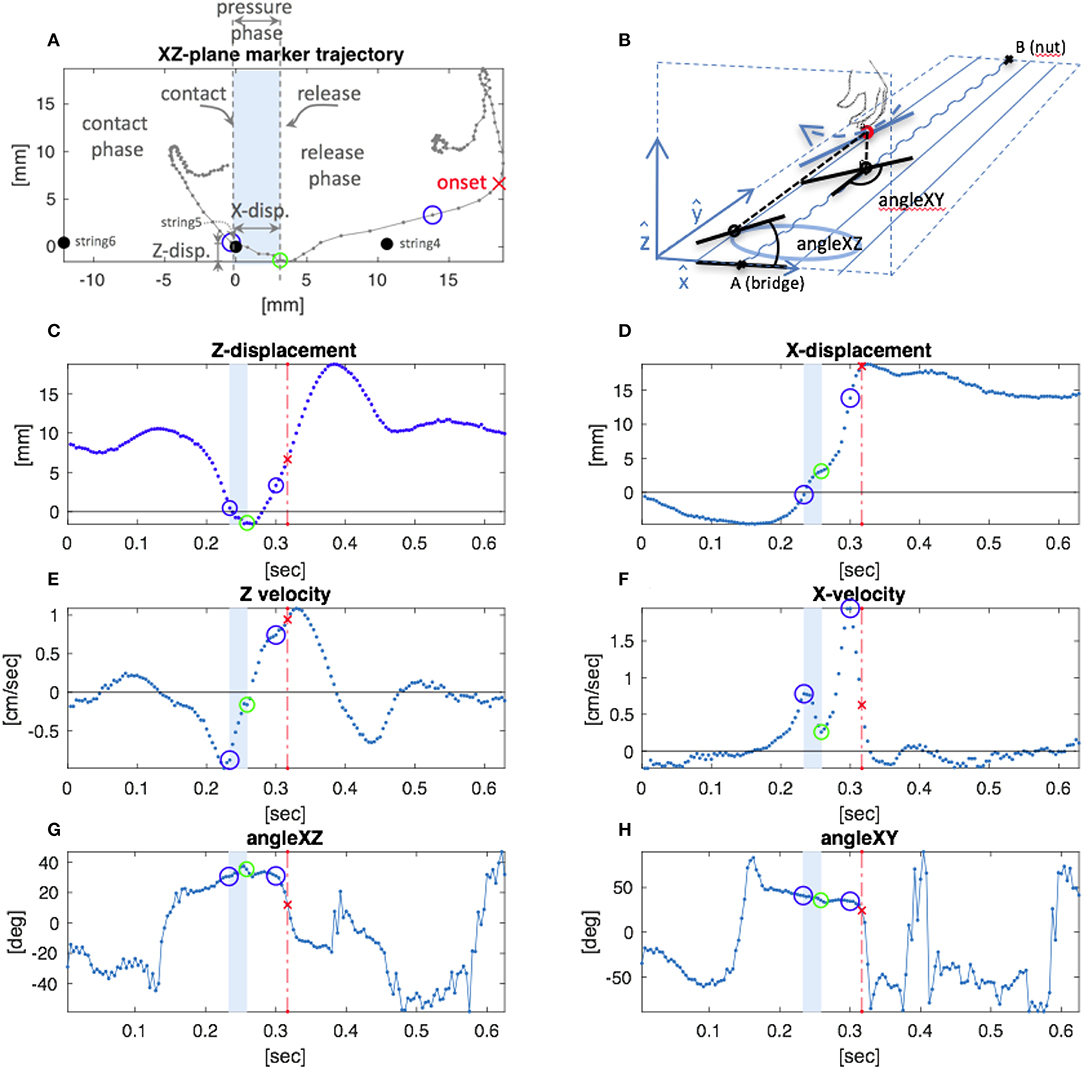
Figure 9. Trajectory and features of the right hand thumb-TIP during a pluck. In (B) there is a representation of the pluck with the hand and the strings and indications regarding the reference coordinate axis. In (A) we can observe the trajectory of the TIP projected into plane XZ. The blue dots represent the strings. We can observe how the TIP comes in contact with the string, the string displacement and the release. In (C,D) the displacement in time along the X and Z axes is plotted; in (E,F) the directional velocity along Z and X axes; and in (G,H) the angles of the pluck. The shape of V_x is very informative. A typical pluck has two peaks in v_X, the first peak corresponds to the contact instant and the valley between both represents the release time.

Figure 9A shows the TIP trajectory projected into the XZ plane. From this projection, the displacement in the z-axis (Figure 9C) and x-axis (Figure 9D) are computed, as well as their respective derivatives, i.e., the velocity in the X (v_X) and Z (v_Z) directions (Figures 9E,F). Additionally, the plucking direction (angles) at the contact and release instants are also computed (Figures 9G,H).

Velocity in the X direction (v_X, Figure 9F) resulted to be specially relevant in our analysis. This feature presents two peaks right before the onset of the note, which are directly related to the different phases of the pluck. The instants where the peaks occur are located in each plot as small blue circles, and the valley between both peaks as a green circle. During the pluck preparation phase, the finger starts moving toward the string (left slope of the first peak) until it gets in contact (first peak). Then, the velocity of the finger starts to decrease until the tension of the string is greater than the kinematic energy of the finger, when the string is released (valley between the main peaks). After the finger is released there is a second peak and later, it takes place the note onset (in red). With this information, we can estimate the contact and release instants.

5.2. Excitation Features

There is a myriad of gesture features that can be extracted using the presented MoCap method. The most important for us are the parameters that directly affect the qualities of the sound. From Townsend (1996) and Scherrer (2013), we know that these parameters are (a) the plucking position, (b) the plucking direction (c) the plucking force; and (d) the nature of the pluck (nail or flesh). Except for the latter, all these parameters can be estimated after applying the models of the guitar (section 3) and hands (section 4) and after determining the instants of contact and release (section 5.1).

Previous to the computation of these parameters, there is the need for the estimation of the basic controls, that is, string, fret, and plucking finger. Basic controls are computed following previous work of Perez-Carrillo et al. (2016) with the main improvements that we have greater spacial resolution (reconstruction of occluded markers and CoR correction) and temporal resolution (estimation of the instants of plucking) thanks to our hand model:

• Plucked string. It is estimated as the most likely string to be plucked during a short window around the note onset. The likelihood that a string is being played (l_S) is determined as a function of the pitch and the distances of the strings to the left and right hand fingers, d_L and d_R. The pitch restricts the possible string candidates and the left hand distance to the frets will determine almost uniquely the string among those candidates. Finally, the right hand TIPs distance to the strings will confirm the string.

• Pressed fret. Once the string is known, obtaining the fret is straight-forward based on the pitch and the tuning of the strings.

• Plucking finger. It is the finger whose TIP is closest to the estimated string.

After the estimation of these basic parameters, we can proceed to the computation of the excitation parameters that take place during the pluck. More details on the computation of the position, velocity, and direction can be found in Perez-Carrillo et al. (2016):

• Plucking position. This feature refers to the distance from the bridge of the guitar to the excitation point on the string. It is obtained by projecting the TIP of the finger on the string (Figure 9B).

• Plucking direction. This feature refers to the angle at which the string is released. As can be observed in Figure 9B, we can compute two angles, one in the X-Z plane, the other in the X-Y plane. The angle $\widehat{XZ}$ is almost negligible being the angle $\widehat{XY}$ the one that has an important influence on the sound. Also, we can compute the angles at the contact and release instants (Figures 9G,H), although only the release angle is relevant in the production of the sound.

• Plucking velocity. This feature is computed as the derivative of the displacement of the TIP. We can compute different velocities: the speed is the derivative of the displacement of the marker in 3D and then we can compute the directional velocities for each dimension. The most relevant movements occurs along the X_axis(v_X) and its contour is used to determine the exact points of contact and release (section 5.1). Contours of v_X and v_Z can be observed in Figures 9E,F).

• Plucking force and string displacement. The strength of the plucking force is related to the displacement of the string before release and, therefore, to the intensity of the sound pressure (Cuzzucoli and Lombardo, 1997). The presented method cannot measure the plucking force, but it is able to estimate the string displacement by assuming that the string moves with the finger from the contact until the release instants. This displacement is an Euclidean distance computed from the 3D positions of the TIP. In Figure 9A we can observe the displacement in the XZ plane and in Figures 9C,D we plot the displacement over time along the X and Z axis respectively.

Additional parameters can be extracted using our method, such as the fretting finger, the duration of plucking phases, the shape of the TIPs trajectories during the plucks or acceleration profiles among others. However, they are not included in this report as they do not directly affect the qualities of the sound.

6. Conclusion

This work presents a method to analyze the finger-string interaction in guitar playing and the extraction of a comprehensive set of string excitation gestures. The method is based on motion capture and audio analysis. Motion is measured through high-speed cameras that detect the position of reflective markers attached to the guitar and hands of the performer, and audio is recorded using a vibration transducer attached to the top plate of the guitar. Audio analysis is performed to obtain the onset and pitch of the notes. Onsets are used to find a window around which the process of plucking occurs and pitch is used along with Euclidean distances to estimate the plucked string, the fret and the plucking finger. Motion data is processed to recover occluded markers and to correct the position of the Center-of-Rotation of the joints. The positions of the strings are reconstructed by applying a Rigid Body Model and the position of the hand joints by applying a Hand Model that takes into account the correlation among joint angles. Once the strings and hands are correctly identified and located, we proceed to the computation of excitation gestures based on Euclidean Geometry. The computed excitation features are directly related to the characteristics of the sound produced and include the plucking position, velocity, direction and force (or, in fact, its related magnitude, the string displacement during the pluck).

The major contributions in this work are the hand model and the analysis of the trajectories of the fingertips during the plucking instants. The hand model considers the fingers as planes and translates 3D joints position into 2D local coordinates at the finger planes. Then, 2D coordinates are converted into 2D joint angles because angles in the same finger are highly correlated. A recursive Neural Network is trained to model these correlations and used to recover the missing angles due to occluded markers. Then, inverse kinematics are applied to translate the angles back into 3D joint positions. In addition, the model can correct the position of the markers to fit the Centers-of-Rotation of the joints. After this process of joint recovery and correction, we proceed to the analysis of the trajectories of the fingertips in a window around the note onset and we find patterns in the velocity of the trajectories that allow to accurately determine the instants when the finger contacts the string and also when the string is released. These instants demarcate the different phases of the plucking gesture (i.e., contact, pressure, and release) and allow to extract a handful of features, especially those considered as the most important in shaping the quality of the sound.

Evaluation of the method against a validation data set, shows a very low MSE Error, meaning that the accuracy of the marker recovery is very high. The method allows for the correct tracking of plucking in monophonic melodies without overlapping notes. In the future, based on a more robust pitch detection algorithm, we will attempt to extend the work to polyphonic scores with no restriction on note overlapping. We also plan to use the presented method to analyze and compare different performers and playing styles.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Funding

This work has been sponsored by the European Union Horizon 2020 research and innovation program under grant agreement No. 688269 (TELMI project) and Beatriu de Pinos grant 2010 BP-A 00209 by the Catalan Research Agency (AGAUR).

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The reviewer GV declared to the handling editor that they are currently organizing a Research Topic with the author, and confirms the absence of any other collaboration.

Footnotes

1. ^https://www.scribd.com/doc/275517165/187736084-6786545-Leo-Brouwer-20-Estudios-Sencillos-pdf

2. ^http://www.qualisys.com/

3. ^https://www.mathworks.com/help/deeplearning/ug/design-time-series-narx-feedback-neural-networks.html

References

Abesser, G. S. J., and Lukashevich, H. (2012). “Feature-based extraction of plucking and expression styles of the electric bass,” in Proceedings of the ICCASP Conference (Kyoto).

Google Scholar

Bevilacqua, F., Schnell, N., Rasamimanana, N., Zamborlin, B., and Guédy, F. (2011). “Online gesture analysis and control of audio processing,” in Musical Robots and Interactive Multimodal Systems, volume 74 of Springer Tracts in Advanced Robotics, eds J. Solis and K. Ng (Berlin; Heidelberg: Springer), 127–142.

Google Scholar

Burns, A.-M., and Wanderley, M. M. (2006). “Visual methods for the retrieval of guitarist fingering,” in Proceedings of NIME (Paris: IRCAM), 196–199.

Google Scholar

Cadoz, C., and Wanderley, M. (2000). “Chapter: Gesture-music,” in Trends in Gestural Control of Music, eds M. M. Wanderley and M. Battier (Editions Ircam edition), 71–93.

Google Scholar

Chadefaux, D., Carrou, J.-L. L., Fabre, B., and Daudet, L. (2012). Experimentally based description of harp plucking. J. Acoust. Soc. Am. 131, 844–855. doi: 10.1121/1.3651246

CrossRef Full Text | Google Scholar

Collins, N., Kiefer, C., Patoli, Z., and White, M. (2010). “Musical exoskeletons: experiments with a motion capture suit,” in New Interfaces for Musical Expression (Sydney).

Google Scholar

Cuzzucoli, G., and Lombardo, V. (1997). “Physical model of the plucking process in the classical guitar,” in Proceedings of the International Computer Music Conference, International Computer Music Association and Program of Psychoacoustics of the Aristotle University of Thessaloniki (Thessaloniki: Aristotle University of Thessaloniki), 172–179.

Google Scholar

de Cheveigné, A., and Kawahara, H. (2002). YIN, a fundamental frequency estimator for speech and music. J. Acoust. Soc. Am. 111, 1917–1930. doi: 10.1121/1.1458024

CrossRef Full Text | Google Scholar

Duxbury, C., Bello, J. P., Davies, M., and Sandler, M. (2003). “Complex domain onset detection for musical signals,” in Proc. DAFx (London: Queen Mary University).

Google Scholar

Erkut, C., Välimäki, V., Karjalainen, M., and Laurson, M. (2000).Erkut, C., Välimäki, V., Karjalainen, M., and Laurson, M. (2000). “Extraction of physical and expressive parameters for model-based sound synthesis of the classical guitar,” in Audio Engineering Society Convention 108.

Google Scholar

Guaus, E., and Arcos, J. L. (2010). “Analyzing left hand fingering in guitar playing,” in Proc. of SMC (Barcelona: Universitat Pompeu Fabra).

Google Scholar

Heijink, H., and Meulenbroek, R. (2002). On the complexity of classical guitar playing: functional adaptations to task constraints. J. Motor Behav. 34, 339–351. doi: 10.1080/00222890209601952

CrossRef Full Text | Google Scholar

Lee, N., Chaigne, A. III, Smith, J., and Arcas, K. (2007). “Measuring and understanding the gypsy guitar,” in Proceedings of the International Symposium on Musical Acoustics (Barcelona).

Google Scholar

Maestre, E., Blaauw, M., Bonada, J., Guaus, E., and Pérez, A. (2010). “Statistical modeling of bowing control applied to sound synthesis,” in IEEE Transactions on Audio, Speech and Language Processing. Special Issue on Virtual Analog Audio Effects and Musical Instruments.

Google Scholar

Maestre, E., Bonada, J., Blaauw, M., Pérez, A., and Guaus, E. (2007). Acquisition of Violin Instrumental Gestures Using a Commercial EMF Device. Copenhagen: International Conference on Music Computing.

Google Scholar

Miranda, E. R., and Wanderley, M. M. (2006). New Digital Musical Instruments: Control and Interaction Beyond the Keyboard. A-R Editions, Inc.

Google Scholar

Norton, J. (2008). Motion capture to build a foundation for a computer-controlled instrument by study of classical guitar performance (Ph.D. thesis). Department of Music, Stanford University, Stanford, CA, United States.

Google Scholar

Penttinen, H., and Välimäki, V. (2004). A time-domain approach to estimating the plucking point of guitar tones obtained with an under-saddle pickup. Appl. Acoust. 65, 1207–1220. doi: 10.1016/j.apacoust.2004.04.008

CrossRef Full Text | Google Scholar

Pérez-Carrillo, A. (2009). Enhancing Spectral Synthesis Techniques with Performance Gestures using the Violin as a Case Study (Ph.D. thesis). Universitat Pompeu Fabra, Barcelona, Spain.

Google Scholar

Perez-Carrillo, A., Arcos, J.-L., and Wanderley, M. (2016). Estimation of Guitar Fingering and Plucking Controls Based on Multimodal Analysis of Motion, Audio and Musical Score. Cham: Springer International Publishing, 71–87.

Google Scholar

Pérez-Carrillo, A., Bonada, J., Maestre, E., Guaus, E., and Blaauw, M. (2012). Performance control driven violin timbre model based on neural networks. IEEE Trans. Audio Speech Lang. Process. 20, 1007–1021. doi: 10.1109/TASL.2011.2170970

CrossRef Full Text | Google Scholar

Pérez-Carrillo, A., and Wanderley, M. (2015). Indirect acquisition of violin instrumental controls from audio signal with hidden markov models. IEEE ACM Trans. Audio Speech Lang. Process. 23, 932–940. doi: 10.1109/TASLP.2015.2410140

CrossRef Full Text | Google Scholar

Reboursière, L., Lähdeoja, O., Drugman, T., Dupont, S., Picard-Limpens, C., and Riche, N. (2012). “Left and right-hand guitar playing techniques detection,” in NIME (Ann Arbor, MI: University of Michigan).

Google Scholar

Scherrer, B. (2013). Physically-informed indirect acquisition of instrumental gestures on the classical guitar: Extracting the angle of release (Ph.D. thesis). McGill University, Montréal, QC, Canada.

Google Scholar

Scherrer, B., and Depalle, P. (2012). “Extracting the angle of release from guitar tones: preliminary results,” in Proceedings of Acoustics (Nantes).

Google Scholar

Schoonderwaldt, E., Guettler, K., and Askenfelt, A. (2008). An empirical investigation of bow-force limits in the Schelleng diagram. AAA 94, 604–622. doi: 10.3813/AAA.918070

CrossRef Full Text | Google Scholar

Townsend, B. (1996). The Guitarists's Complete Technique Kit. Mel Bay Publications Inc.

Google Scholar

Traube, C., and Depalle, P. (2003). “Deriving the plucking point location along a guitar string from a least-square estimation of a comb filter delay,” in IEEE Canadian Conference on Electrical and Computer Engineering, Vol. 3 (Montreal, QC), 2001–2004.

Google Scholar

Traube, C., and Smith, J. O. (2000). “Estimating the plucking point on a guitar string,” in Proceedings of COST-G6 conference on Digital Audio Effects (Verona).

Google Scholar

van der Linden, J., Schoonderwaldt, E., and Bird, J. (2009). “Towards a realtime system for teaching novices correct violin bowing technique,” in IEEE International Workshop on Haptic Audio visual Environments and Games (Lecco), 81–86.

Google Scholar

Visentin, P., Shan, G., and Wasiak, E. B. (2008). Informing music teaching and learning using movement analysis technology. Int. J. Music Educ. 26, 73–87. doi: 10.1177/0255761407085651

CrossRef Full Text | Google Scholar

Wanderley, M. M., and Depalle, P. (2004). “Gestural control of sound synthesis,” in Proceedings of the IEEE, 632–644.

Google Scholar

Zhang, B., and Wang, Y. (2009). Automatic Music Transcription Using Audio-Visual Fusion for Violin Practice in Home Environment. Technical Report TRA7/09, Shool of Computing, National University of Singapore.

Google Scholar