Spine and Individual Vertebrae Segmentation in Computed Tomography Images Using Geometric Flows and Shape Priors

The surgical treatment of injuries to the spine often requires the placement of pedicle screws. To prevent damage to nearby blood vessels and nerves, the individual vertebrae and their surrounding tissue must be precisely localized. To aid surgical planning in this context we present a clinically applicable geometric flow based method to segment the human spinal column from computed tomography (CT) scans. We first apply anisotropic diffusion and flux computation to mitigate the effects of region inhomogeneities and partial volume effects at vertebral boundaries in such data. The first pipeline of our segmentation approach uses a region-based geometric flow, requires only a single manually identified seed point to initiate, and runs efficiently on a multi-core central processing unit (CPU). A shape-prior formulation is employed in a separate second pipeline to segment individual vertebrae, using both region and boundary based terms to augment the initial segmentation. We validate our method on four different clinical databases, each of which has a distinct intensity distribution. Our approach obviates the need for manual segmentation, significantly reduces inter- and intra-observer differences, runs in times compatible with use in a clinical workflow, achieves Dice scores that are comparable to the state of the art, and yields precise vertebral surfaces that are well within the acceptable 2 mm mark for surgical interventions.

1 Introduction

Surgical treatment is required for many spine-related conditions including spinal tumours, herniated discs, scoliosis, spinal stenosis, injuries to the cranio-cervical junction and osteoporosis. These surgical procedures often require the placement of pedicle screws and rods to provide better mechanical stability when adjacent vertebrae must be fused. A mal-positioned screw can have severe neurological (Mac-Thiong et al., 2013), vascular or mechanical ramifications. Screw diameter errors or slight deviations in orientation can cause medial and inferior cortical perforation leading to nerve damage. Pedicle wall fractures associated with cortical perforations decrease screw fixation strength. Length errors can also be critical; a screw that is too long may injure the vessels anteriorly and a screw that is too short can be associated with weaker fixation. Unfortunately, when using free-hand techniques, screw malpositioning is relatively common, with rates ranging widely in the literature from 0 to over 50% (Laine et al., 1997; Xu et al., 1998; Kuklo et al., 2005; Di Silvestre et al., 2007; Kim et al., 2008; Upendra et al., 2008; Şarlak et al., 2009; Cui et al., 2012) with more common error rates of 20–30% reported in (Castro et al., 1996; Schulze et al., 1998; Haberland et al., 2000; Laine et al., 2000; Koller et al., 2008). Image-guided surgical navigation provide tools to track the patient’s anatomy and surgical instruments to ensure the accurate placement of these screws, while minimizing potential complications or damage to nearby blood vessels, nerves or tissues due to screw malpositioning (Goulet, 2010; Drouin et al., 2017).

The first step in image-guided spinal surgery is the segmentation of the vertebral column from a patient’s CT images to build 3D surface models to be used by the surgical navigation system. The success of downstream tasks such as the registration of pre-operative scans to a patient’s anatomy, depends on the accuracy of the segmented vertebral models. Manual segmentation is time consuming and subject to errors that can cause inter- and intra-observer variability. Furthermore, the 20–30 min required to manually segment vertebrae makes this step difficult to justify for a busy surgeon. Automatic segmentation of the spine is challenging since it is a complex structure, with vertebrae changing in shape from the top to the bottom of the spine, and with there being additional variations between subjects. There might be gaps in the vertebral boundaries due to partial volume effects, insufficient bone density or fractures. The intensity distribution inside the trabecular bone and outside the cortical bone can also be inhomogeneous. In addition, the CT images may be acquired on different scanners, with different parameters, causing additional variability. Figure 1A provides qualitative examples of some of the challenges faced in spine segmentation due to these reasons.

FIGURE 1

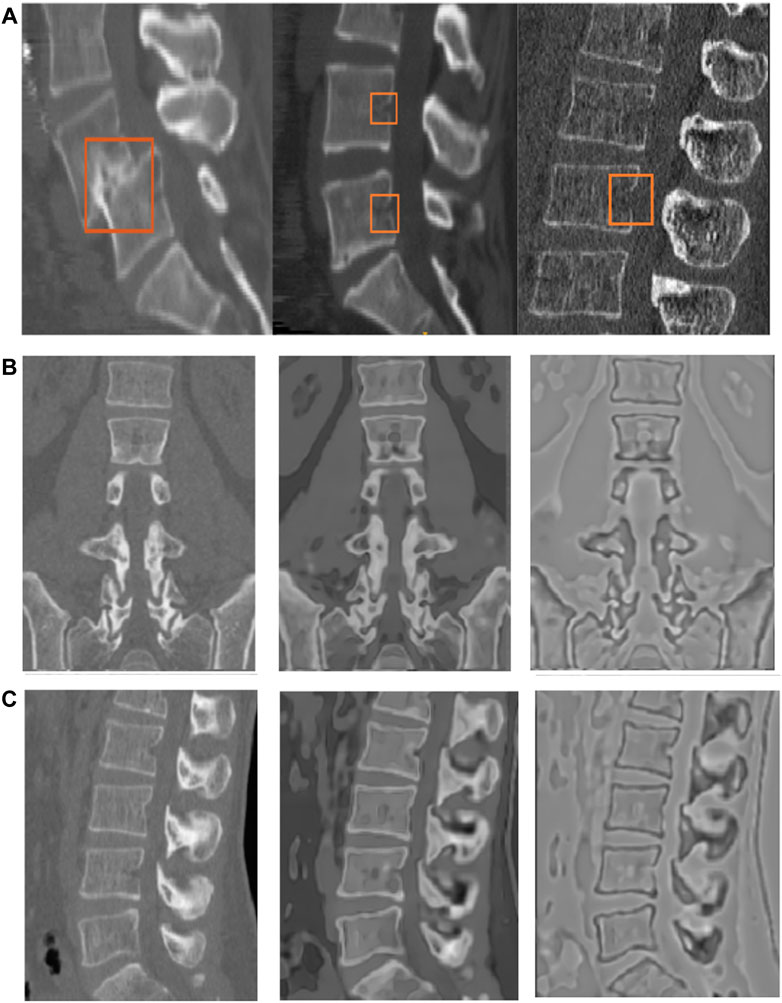
FIGURE 1. (A) Examples of challenges in spine segmentation. The image on the extreme left shows an anterior-posterior subluxation of the L4 and L5 vertebrae. The image in the middle shows gaps on the vertebral boundary, which may be physiological due to vessel injection at this location. The image on the right has missing boundaries as well, and a different intensity distribution due to the use of a different scanner and acquisition protocol. (B and C) Coronal and sagittal slices of the original image (left column), edge-enhanced image (middle column) and flux-map (rightmost column). The application of the edge-enhancing diffusion process, as explained in Section 2.2.1, on the original image (left column) results in the edge-enhanced image (middle column). The contrast between the vertebral cortical bone surface and its nearby regions (rightmost image) is enhanced due to the flux computation step, as explained in Section 2.2.2.

The limited availability of ground truth segmentations has lead to the development of algorithms that are specialized for specific datasets. In principle the segmentation method should not be limited by the field-of-view of the image scans and it should be able to segment vertebrae which are partially visible, if necessary. Given the fact that the CT images are often obtained using different protocols, the method should also be applicable to different image intensity distributions. We begin with a review of related work on vertebrae segmentation from CT images and highlight some of its present drawbacks.

CT Vertebrae Segmentation

CT vertebrae segmentation approaches can be broadly classified into the following categories: thresholding based techniques, active contours and level-sets, graph-cuts, deformable shape-based models, machine learning methods with handcrafted features, and deep learning methods.

Thresholding based methods are used to separate regions based on their raw intensity values. A fully automatic 3D segmentation method using adaptive thresholding was proposed in (Zhang et al., 2010). An initial segmentation is followed by automatic flood-filling and is then refined by an iterative and adaptive thresholding step, exploiting local connectivity and intensity statistics. An interactive segmentation tool was developed by Kaminsky et al. (2004), combining different techniques including logical and morphological operators, filtering, region growing, affine, and rigid transformations. Whereas such methods may work in practice, they rely on heuristics to select an appropriate range of threshold values. They might fail in cases where there is no clear demarcation between the foreground and the background intensity values.

Active contours or surfaces evolve a deformable model to extract the region of interest in two-dimensional (2D) image or a three-dimensional (3D) volume. Such techniques have often been used to segment vertebra. As an example, Tan et al. (2008) uses a cascade of active contours, to segment vertebrae by exploiting image information at multiple scales. Each level-set follows the geodesic active contour (GAC) formulation (Caselles et al., 1995) differing only in the criteria used for the gradient term. An edge and region-based level-set (ERBLS) with an Otsu adaptive threshold automatic initialization method was proposed by Huang (2013), which reconstructs 3D vertebral models from 2D axial segmented slices. This method was not directly applied to 3D volumes but rather was used to segment each individual 2D slice. Lim et al. (2013) combined a Willmore force term, a boundary energy functional, and a kernel density estimation based shape-prior within a level-set framework to produce good segmentations of the lumbar region in 3D. A related method was proposed by Kim and Kim (2009) using 3D deformable fences (3DDF) to separate adjacent vertebrae, but this approach required heuristic thresholds and an alternation between 2D and 3D segmentations of vertebrae, discs and the spinal cord.

The variation in vertebral shape complexity and pixel intensities in CT data can be captured from a training dataset of ground truth segmented volumes, to create an appearance model. Klinder et al. (2009) described a pipeline for one of the earliest appearance-based models to segment vertebrae in previously aligned CT data, automatically detecting, identifying, and segmenting vertebrae. Ibragimov et al. (2015) and Korez et al. (2015a) have combined alignment and detection with a shape-constrained model to segment vertebrae. The detection is based on interpolation theory, consisting of an alignment step between a 3D mean shape mesh and each vertebra using an objective function, followed by a mesh deformation step. A part-based active shape model (ASM) decomposition and conditional shape model based segmentation procedure was proposed by Pereañez et al. (2015), to better resolve fine details that are not segmented by standard shape models. Ibragimov et al. (2014a) used a landmark based shape representation using concepts from the theory of transport, and combined it with a landmark detection algorithm to segment vertebrae in 3D. Forsberg (2015) proposed an atlas-based registration method, while Stern et al. (2011) used a parameterized 3D model to segment vertebral bodies. A statistical multi-vertebrae shape and pose model was developed by Rasoulian et al. (2013). This method depends heavily on a training set to segment the entire lumbar region, and assumes that the shape and pose of different vertebrae are highly correlated. Castro-Mateos et al. (2015) introduced a statistical inter-space model, which uses a multi-object structure to learn the statistical distribution of relationships between neighboring regions to segment the vertebral column. Kadoury and Paragios (2010) used a training set of prior mesh models to develop a low dimensional manifold embedding which establishes patterns of global shape variations, followed by the capture of appearance. At inference time, a higher-order Markov Random Field (MRF) is used to measure the similarity between data and shape. A graph-cuts formulation, which integrates a linear combination of Gaussians (LCG), a Markov Gibbs Random Field (MGRF), and a distance probabilistic model obtained from a 3D shape-prior, was developed by Aslan et al. (2010) to model shape and appearance variations. A disadvantage of the above appearance and shape-based methods is that they require the manual identification of multiple landmark points, which can be laborious.

A machine learning method by Chu et al. (2015) automatically localizes and segments 3D vertebral bodies by using a random forest regressor, and a Hidden Markov Model (HMM). As part of a detection pipeline, Kelm et al. (2013) developed a segmentation approach based on iterative marginal space learning, incorporating pose prior information. Wang et al. (2015) used a multi-kernel multi-dimensional support vector regressor to segment multiple structures, i.e., axial and sagittal vertebral slices and discs, in multiple imaging modalities. A disadvantage of such algorithms is that they require training data and thus cannot be easily adopted in clinical settings, where such data may be scarce.

In recent years deep learning approaches have become very popular for CT spine segmentation (Korez et al., 2016; Korez et al., 2017; Sekuboyina et al., 2017; Janssens et al., 2018; Lessmann et al., 2019; Khandelwal and Yushkevich, 2020; Sekuboyina et al., 2020). Vertebrae are segmented in succession using a convolutional neural network (ConvNet) based approach by Lessmann et al. (2019). The network is augmented with a memory component which acts as a prior, and is used to iteratively constrain the search for the next vertebra to be segmented. Korez et al. (2016) have designed a 3D ConvNet architecture which is used to learn the appearance of the vertebral bodies of MR images to generate 3D spatial probability maps, which guide a deformable model toward their boundaries. Janssens et al. (2018) used a cascade of fully convolutional networks (FCNs) to localize the bounding-box around the lumbar region as an initialization, together with a segmentation network to label pixels as either belonging to the foreground or the background.

A vertebrae detection and segmentation challenge, VerSe: “A Vertebrae Labelling and Segmentation Benchmark for Multi-detector CT Images” (Löffler et al., 2020; Sekuboyina et al., 2020), consisting of a variety of fields of view, thoraco-lumbar and cervico-thoraco-lumbar scans, a mix of sagittal and isotropic reformatting, and cases with vertebral fractures, metallic implants, and foreign materials, was introduced in 2019. A total of eleven groups, using deep learning, participated in the competition and benchmarked their segmentation algorithms on a test set of 80 images using a training set of 80 images. A disadvantage of deep learning methods is that the results of the segmentations obtained by them are not directly interpretable in that the learned network weights may not have a clear biological meaning to a clinician or a radiologist. This can be an obstacle to their acceptance in the clinic. Deep learning methods also depend on a large number of annotated training images and the learned models may not easily generalize to handle different data distributions.

Contributions of This Paper

In this paper we propose two independent pipelines to segment the entire spine, as well as each individual vertebra on standard dose imaging. The first pipeline uses geometric flows within a level-set framework to segment the entire spine as a single surface object. The second pipeline incorporates knowledge of vertebral geometry (shape) with information gained from the distributions of the image intensities in their vicinity to segment individual vertebrae. Such approaches are not only more intuitive and practical than previous patch-based and complex shape based methods, but also prove to be accurate and precise. We show that it is possible to achieve close to state-of-the-art results for spine segmentation from CT images, as well as for segmentations of individual vertebrae, with a limited number of labelled vertebrae to build the shape prior. In both cases the computation time on multi-core CPUs is acceptable for use in clinical settings.

Our approach uses an anisotropic diffusion and flux integral based geometric flow to pre-process the CT images, which helps mitigate some of the challenges in spine segmentation due to poor image quality. By having the clinician place one or more seeds on the spine, which takes only a few seconds, we obviate the need to automatically detect inter-vertebral discs or other structures to segment the spine. We demonstrate the clinical relevance of the method by validating it on three publicly available databases and on one in-house database. The entire procedure takes only 15 min, making it easy to fit in the clinical workflow. We highlight additional advantages of our approach, in comparison to the methods reviewed above, in Section 4.

2 Materials and Methods

2.1 Databases

Four sets of vertebral data were used to test our proposed algorithm.

2.1.1 Database 1: Healthy Cases (Lumbar Vertebrae)

A publicly available database from Ibragimov et al. (2014b) of 50 vertebrae was extracted from 10 axially reconstructed CT images of the lumbar region of the spine, with in-plane voxel size between 0.282 and 0.791 mm, and slice thickness between 0.725 and 1.530 mm. The lumbar vertebrae (L1-L5) were manually segmented to obtain a binary mask for each vertebra.

2.1.2 Database 2: CSI MICCAI Challenge Database (Thoracular-Lumbar Vertebrae)

The Department of Radiological Sciences, University of California, Irvine, School of Medicine acquired data on the Philips or Siemens multidetector CT scanners (Yao et al., 2012). The datasets of spine CT were acquired during daily clinical routine work in a trauma center from 10 adults ranging in age from 16 to 35 years, without intravenous contrast. The in-plane resolution is between 0.3125 and 0.3613 mm and the slice thickness is 1 mm. In each scan, all 12 thoracic and 5 lumbar vertebrae, totalling, 120 thoracic and 50 lumbar vertebrae across 10 subjects, have been manually segmented and are provided as groundtruth references.

2.1.3 Database 3: Pathology Cases (Lumbar Vertebrae)

The Montréal Neurological Institute (MNI) provided CT images of the lumbar region of 30 patients. The images were acquired using a Picker International PQ6000 scanner. Manual voxel-based segmentations of the L4 vertebra were provided for each image. The in-plane resolution is 512 × 512 voxels with a voxel size of 0.352 × 0.352 mm². The number of slices ranges from 55 to 200, with a slice thickness of 1.0–2.0 mm. The labels were assigned by a person familiar with the anatomy and were then checked and revised by a neurosurgeon. The non low-dose images were acquired with 130 kVp tube potential and 175A tube current with one image acquired with 225A tube current. The patients consist of 22 females and 5 males, 48–79 years in age, with a median age of 67. A manual voxel-based segmentation of the L4 vertebra was provided for each image. We note that we are missing age and sex information for three subjects out of the cohort of thirty.

2.1.4 Database 4: VerSe Dataset: Segmentation Benchmark for Multi-Detector CT Images

We use the open source VerSe Database (Sekuboyina et al., 2020) collected from multiple multi-detector CT scanners. The dataset resembles a typical clinical distribution in terms of field-of-view (FoV), scan setting, and findings in emergency as well as in oncological and neurosurgical conditions. It consists of a variety of field of FOVs, including thoraco-lumbar and cervico-thoraco-lumbar scans, a mix of sagittal and isotropic reformatting, and cases with vertebral fractures, metallic implants, and foreign materials. The database provides manual segmentations of cervical, thoracic and lumbar regions, where available, across the different scans. Our method is not designed to work on low-dose CT images and images with implants. Therefore, to have a selection criterion for our method, we compute Signal-to-Noise ratio (SNR), defined to be the ratio of the average signal value to the standard deviation of the signal (Rowlands, 2017), for each image. We then selected images with SNR in the top 50th percentile from the training, validation, and test sets. This leaves us with a set of 43 medium-to-high dose CT images with which to evaluate our method.

2.2 Pre-processing of CT Volumes

We first normalized the intensity values to fall within a specified range. We capped the values above the 95th percentile to be 1 and the values below the 5th percentile to be 0. The rest of the Hounsfield Units were then scaled proportionately to fall between 0 and 1. One subject (Subject number 06 in Database 2) was found to have an intensity distribution that was quite different from the representative distribution, i.e., the Hounsfield Units did not follow the chosen 5th and 95th percentile thresholds. Therefore, we removed this subject from further analysis.

2.2.1 Non-linear Anisotropic Diffusion Filtering

In most previous methods a Gaussian filter is used to smooth the image to have well defined image gradients, and to avoid intensity singularities. This often leads to an unnecessary loss in detail, for example, a Gaussian filter might substantially blur the edges of the vertebrae. Some of the earliest filtering methods are based on the anisotropic edge preserving diffusion method proposed by Perona and Malik (1990). In our approach we also propose to use anisotropic diffusion-based filters to smooth the CT images. We make use of the coherence and edge-enhancing diffusion filters of Weickert and Scharr (2002), based on diffusion and structure tensors. These filters have the advantage that they make the vertebral edges sharper, while producing smooth homogeneous regions inside and outside the vertebrae, as they adapt to the underlying image structure (Frangakis and Hegerl, 2001). They have been used for CT bone enhancement in Descoteaux et al. (2005). In particular, we use the method proposed by Kroon and Slump (2009), Kroon et al. (2010), which is described in the Supplementary Appendix.

2.2.2 Flux-Maximizing Feature Map (Flux-Map)

We derive a flux map from the diffused volume to enhance image contrast near the vertebral surface. Flux maximizing geometric flows were first proposed by Vasilevskiy and Siddiqi (2002) and later Law and Chung (2009) developed an efficient algorithm with linear running time. We exploit the result by Vasilevskiy and Siddiqi (2002) to enhance the contrast of the vertebral edges. Instead of evolving the flows as done in the two aforementioned articles, we obtain the flux magnitude at every voxel of the edge-enhanced diffused image and generate a flux-based feature image (henceforth called the flux-map), based on the fast implementation by Law and Chung (2009).

The main result in Vasilevskiy and Siddiqi (2002) is that the direction in which the inward flux of the vector field $\mathrm{V}$ (which is taken as the normalized gradient of the image) through the curve C is increasing most rapidly is given by $\frac{\partial \mathrm{C}}{\partial t}=div\left(\mathrm{V}\right)\mathcal{N}$. In other words, the gradient flow which maximizes the rate of increase of the total inward flux is obtained by moving each point of the curve in the direction of the inward normal by an amount proportional to the divergence of the vector field.

Figures 1B,C shows some qualitative examples which highlight the differences between the images before and after running the non-linear anisotropic diffusion scheme on the normalized vertebrae scans and the obtained flux-map. The most notable advantages of this scheme include the closing of many of the fragmented edges, and the denoising of inhomogeneous regions. The edges also appear to be sharper than before. Qualitatively, the edge-enhanced flux-map looks almost piece-wise constant.

2.3 Segmentation Methodology

We now describe our proposed segmentation pipelines. In pipeline one, a number of vertebrae are segmented together as a single spine object, with no training data required, but with manual identification of at least one seed in a vertebrae. In a separate second pipeline, a shape prior is coupled with a flow to segment individual vertebrae. For this part some ground truth data is required to build the shape-prior.

2.3.1 Pipeline 1: Region-Based Segmentation of the Spine

Once a flux-map is obtained, the user is required to initialize the surface evolution process by placing an initial seed on the cortical bone of the vertebrae. A single seed is sufficient to initialize the surface evolution. However, the user could choose to place multiple seeds at several such locations, which could then evolve simultaneously to speed up the segmentation. We then run a region-based flow implemented using a sparse field method (Whitaker, 1998) for stable numerical updates. Such a flow uses feature measurements to devise a partition of a volume into regions for which there are similar feature statistics. In our case, we simply use the flux-map intensities, since our goal is to extract the exterior surface of the vertebral cortical bone of the spine. This surface has a distinct intensity distribution from that of the vertebral body and the region just outside the spine in the flux-map. Whereas a variety of region-based geometric flows can be used (Cremers and Soatto, 2003; Rousson et al., 2003; Rousson and Cremers, 2005; Bresson et al., 2006; Brox and Weickert, 2006; Cremers et al., 2006; Cremers et al., 2006; Rathi et al., 2006; Cremers et al., 2007; Dambreville et al., 2007; Michailovich et al., 2007; Sandhu et al., 2008; Chung and Vese, 2009; Salah et al., 2009; Li et al., 2010; Zhang et al., 2015), the results presented in this paper are based on the flow of Chan and Vese (2001). Here, an evolving surface C (embedded as the zero level-set of a higher dimensional function ϕ) in an image domain $\text{Ω}$ has a bi-partition defined by $inside\left(C\right)$ and $outside\left(C\right)$, respectively, with each having approximately piece-wise constant intensities. Let an object of interest be represented by intensity value $u_0^i$ and the background with an intensity value $u_0^o$. Thus, we have $u_0=u_0^i$ inside the object and $u_0=u_0^o$ outside the object. Let $c_1$ and $c_2$ be the mean intensity values inside and outside the propagating interface. The objective is then to minimize an energy functional $F\left(c_1,c_2,\mathrm{C}\right)$, i.e., to compute $\underset{c_1,c_2,C}{Inf}F\left(c_1,c_2,\mathrm{C}\right)$. The associated evolution equation for ϕ is given by

$\frac{\partial \varphi }{\partial t}=\delta \left(\varphi \right)\left[\mu \nabla .\frac{\nabla \varphi }{\left|\nabla \varphi \right|}-v-{\lambda }_1{\left(u_0-c_1\right)}^2+{\lambda }_2{\left(u_0-c_2\right)}^2\right],(1)$

where, ${\lambda }_1$ and ${\lambda }_2$ are the weights for the inside and outside terms, and μ and v are the weighting terms for the length of the curve C and the area of the region bounded by the curve C, as given in (Chan and Vese (2001). The two mean intensities represent the two partitions, and this model is thus suited to problems where there is piece-wise constant intensity within a region. Here, we set ${\lambda }_1$, ${\lambda }_2$, μ, v equal to 1.

Figure 2 shows the surface extraction process in 3D on the flux-map. See Figure 3 for the complete segmentation process. We start with placing a seed on the vertebral body. Next, the surface of the spine is extracted using the region-based flow on the flux-map. The extracted surface contains some holes due to a lack of signal at portions of the boundary. It is possible to obtain a complete segmentation of each vertebrae by employing the well established geodesic active contour (Caselles et al., 1995; Kichenassamy et al., 1996; Marquez-Neila et al., 2013) to “shrink-wrap” from the outside, starting with a bounding-box. For this, an automatically placed bounding-box is used to initialize the flow. The inward flow shrinks the bounding-box towards the vertebral region and thus wraps around the desired surface whose zero level-set gives the final segmentation of the spine. This fills the interior of each of the vertebrae present in the image, with the added advantage of closing small gaps present on the surface of the spine.

FIGURE 2

FIGURE 2. (Left to right and top to bottom) The surface segmentation process for Database 1, using the region based flow on the flux-map, as explained in Section 3.2. Samples of the entire evolution are shown, from initialization to the final extracted surface. Here we initialize the flow with multiple seeds to illustrate their simultaneous evolution. In our experiments using Pipeline 1 we typically used two or three seeds placed within the vertebral surface, in the middle of the FoV. Note: The adjoining sacrum and hips are manually removed using the methods in Yushkevich et al. (2006). In the text we explain how the subjects with larger holes on the extracted surface are handled.

FIGURE 3

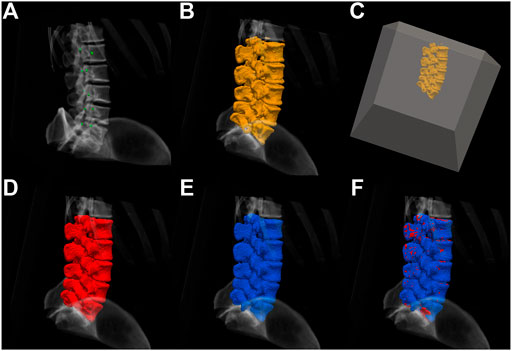
FIGURE 3. (A) The initialization by placing seeds, (B) the extracted surface using the region-based flow on the flux-map, and (C) an automatically-placed bounding-box placed around the extracted surface, which starts the process of shrink-wrapping around the middle segmentation, thus closing small holes in the surface. (D) The resulting spine segmentation, which now contains a vertebral volume, (E) a ground truth segmentation image obtained by manual segmentation, and (F) the obtained segmentation overlaid on the ground truth. The process is detailed in Section 2.3.1.

2.3.2 Pipeline 2: Shape-Prior Based Flows for Individual Vertebra Segmentation

In order to combat signal loss or partial volume effects, prior knowledge about the desired object shape can be useful. Complex anatomical structures, such as the spine, provide a suitable test case, because they are largely rigid objects with a fixed part structure. Images with occlusions or missing parts of the desired objects could also benefit from shape-priors. In the present article we use shape-priors to segment L4 lumbar vertebrae in a challenging database containing pathology cases, as presented and discussed in Sections 3 and 4. This involves a shape modelling pipeline, where generic shape characteristics are learnt from a training set, and a constrained segmentation pipeline using an energy functional minimization algorithm, which optimizes the required model parameters. Shape-based segmentation methods were popularized by Cootes et al. (1995) in their landmark based active shape models (ASMs) formulation. Leventon et al. (2000) were amongst the first to combine the edge and curvature information in a geodesic active contour evolution with the shape model, using a maximum a posteriori approach.

Figure 4A shows a training set of groundtruth binary volumes for the L4 vertebra. These images are aligned with respect to the same origin and the signed distance function (SDF) is then computed for every shape in the training set. After applying Principal Component Analysis (PCA) on these training images, we obtain different eigenmodes $\left\{{\text{Φ}}_1,{\text{Φ}}_2,{\text{Φ}}_3,\dots \dots ,{\text{Φ}}_n\right\}$ which can be permuted to get different eigenshapes which capture variations in shape and pose of the vertebral anatomy. Figure 4B depicts the obtained eigenshapes, the shape variations.

FIGURE 4

FIGURE 4. (A) Sample gold standard volumes comprising the training set of groundtruth segmentations of L4 vertebra, with subtle differences in shape. This is a representative database, with variations in the vertebral processes and in the thickness of the vertebral bodies. (B) Shape Variations. The first four eigenshapes are depicted with the first and second negative and positive shape variations obtained by $\overline{\varphi }\pm {\sigma }_i{\lambda }_i{\varphi }_i$. Each row depicts one eigenshape. Left to right: in each row, one can see how the eigenshape changes. There is a visible change in the structure of the vertebral processes. Top to bottom: there are clear visible differences amongst the different eigenshapes, especially in the vertebral processes.

The PCA based shape model described above is built offline. This model has to be integrated within a level-set framework to obtain a constrained segmentation. Usually edge and region-based terms are used in conjunction with the shape model to optimize the parameters to obtain a final segmentation. We employ the technique proposed by Tsai et al. (2003), which iteratively minimizes an energy functional using gradient descent to optimize the pose p and shape w parameters. The gradient of the region-based energy functional ($E_{CV}$) defined by Chan and Vese (2001) with respect to the parameters p and w, is given by the following two equations:

${\nabla }_{\mathrm{w}}{E}_{CV}=-2\left(\mu \nabla \mathrm{w}{S}_u+v\nabla \mathrm{w}{S}_v\right),+\left({\mu }^2\nabla \mathrm{w}{A}_u\right)+v^2\nabla \mathrm{w}{A}_v)(2)$

${\nabla }_{\mathrm{p}}{E}_{CV}=-2\left(\mu \nabla \mathrm{p}{S}_u+v\nabla \mathrm{p}{S}_v\right)+\left({\mu }^2\nabla \mathrm{p}{A}_u\right)+v^2\nabla \mathrm{p}{A}_v)(3)$

where $R^u$ and $R^v$ are the regions inside and outside the evolving front respectively. μ and v represent the mean intensities in the two regions. S and A represent the sum of intensities and the area for a given region, respectively. The parameters $\mathrm{w}$ and $\mathrm{p}$ are updated using gradient descent at every iteration. At the end of an iteration, a new shape is computed as:

$\varphi \left[\mathrm{w},\mathrm{p}\right]\left(x,y,z\right)=\overline{\text{Φ}}\left(\tilde{x},\tilde{y},\tilde{z}\right)+{\displaystyle \sum }_{i=1}^k{w}_i{\varphi }_i\left(\tilde{x},\tilde{y},\tilde{z}\right)(4)$

where,

$\left(\begin{array}{c}\tilde{x}\\ \tilde{y}\\ \tilde{z}\\ 1\end{array}\right)=T\left[\mathrm{p}\right]\left(\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right)$

and $T\left[\mathrm{p}\right]$ is the transformation matrix. The zero level-set of ϕ represents the evolving surface and upon convergence the final segmentation. This algorithm is initialized by placing the mean shape, obtained from the training set, near the vertebra which is to be segmented. Figure 5 illustrates our segmentation approach using a flowchart.

FIGURE 5

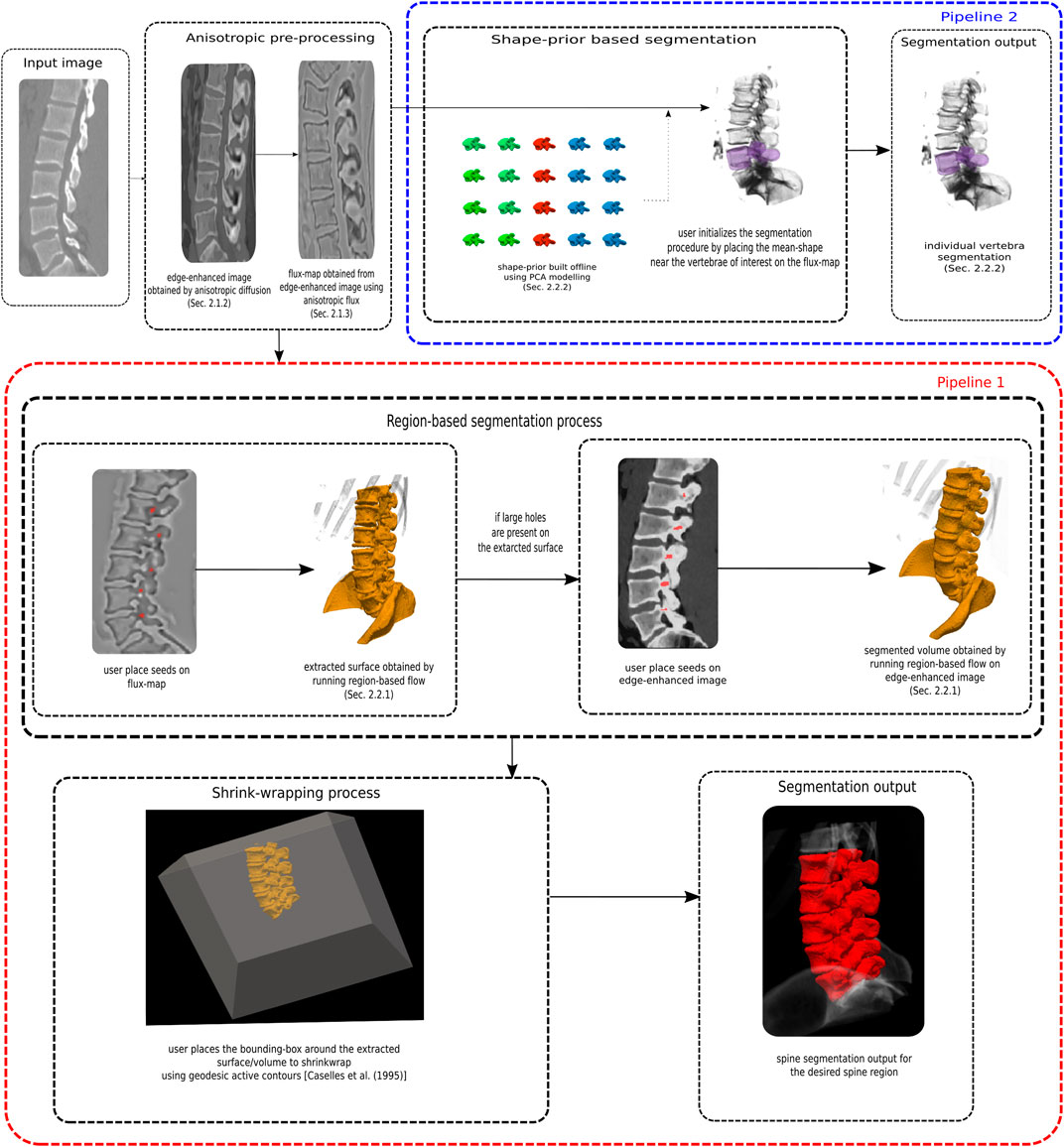
FIGURE 5. A flowchart summarizing the two segmentation pipelines. In pipeline one, a number of vertebrae are segmented together as a single spine object, with no training data required, but with manual identification of seed in a vertebrae. In a separate second pipeline, a shape prior is coupled with a flow to segment individual vertebrae. For this part some ground truth data is required to build the shape-prior.

2.4 Segmentation Evaluation Metrics

We use the toolboxes by Taha and Hanbury (2015) and Maier et al. (2019) to produce the comparison metrics for evaluating our segmentation results. We report volume and surface based metrics using the Dice score, Average Symmetric Surface Distance (ASSD), Average Surface Distance (ASD), and Hausdorff Distance 95th percentile (HD95). We report these surface based distances because they are known to be less sensitive to outliers. These metrics are described in further detail in the Supplementary Appendix.

3 Results

3.1 Pipeline 1: Region-Based Segmentation of the Spine

We have evaluated our first pipeline, discussed in Section 2.3.1, on Databases 1, 2, and 4.

3.1.1 Database 1

On Database 1, the application of our region-based flow segmentation method on the edge-enhanced flux-maps yielded an average Dice score of 92.36 $\pm$ 1.34$\text{\%}$. This is comparable to the results of Chu et al. (2015) and Ibragimov et al. (2014), but is not as good as those of Lessmann et al. (2019). The average symmetric surface distance is at 1.14 $\pm$ 0.29 mm, which is better than that of Rasoulian et al. (2013). The average surface distance is 0.99 $\pm$ 0.88 mm, which is comparable to that of the two other techniques, indicating that there is very little bias in the extracted surface position. This is very close to the 2 mm clinical accuracy threshold reported in Cleary (2000). The 95th percentile Hausdorff distance is at 2.90 $\pm$ 1.38 mm, indicating that 95% of the surface extracted is within 2.90 mm of the gold standard surface. Table 1 summarizes the results of using different metrics for this database. Figure 6 shows box plots for the four different metrics used for evaluation across all the subjects in each database.

TABLE 1

TABLE 1. Spine segmentation results reported for Database 1.

FIGURE 6

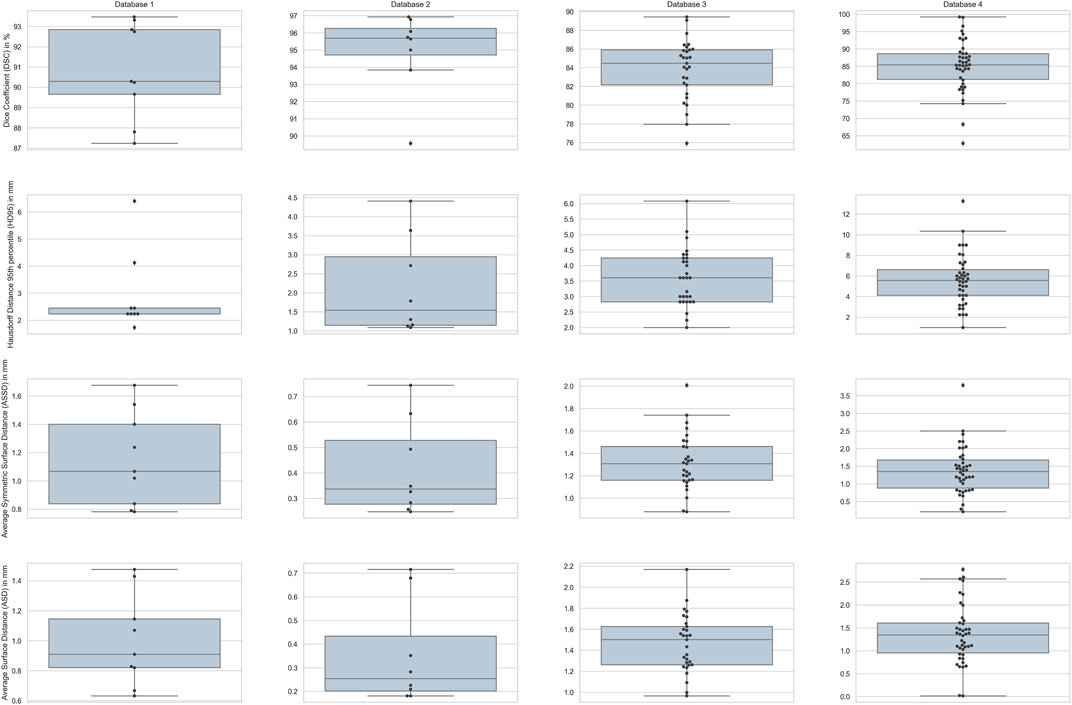
FIGURE 6. Box-plots for the four different metrics used for evaluation across all the subjects in each database. Columns show the plots for the four databases with rows depicting the four metrics.

3.1.2 Database 2

We have divided the vertebral region into two groups to report results: the lumbar and thoracic regions, for two reasons. First, this helps with CPU and memory constraints, since the image volume is large. Second, thoracic and lumbar vertebrae have different shapes and varying surrounding properties such as tissue contrast and intensity distributions. Thus, separating the different vertebral regions can help in assessing the quality of the segmentations. Table 2 shows the segmentation results for the thoracic and lumbar regions, and reports the metrics averaged over the entire thoracic and lumbar regions for the CSI database. We report an average Dice score of 94.97 $\pm$ 2.22$\text{\%}$, which is comparable to the results of Lessmann et al. (2019) and is better than the methods of (Hammernik et al., 2015) and (Korez et al., 2015b), with the average symmetric surface distance at 0.41 $\pm$ 0.17 mm. The 95th percentile Hausdorff distance is 2.15 $\pm$ 1.20 mm, while the average surface distance is 0.35 $\pm$ 0.20 mm.

TABLE 2

TABLE 2. Spine segmentation results reported for Database 2: CSI database.

3.1.3 Database 4

We evaluate our method on 43 subjects from the VerSe database (see Section 2.1.4). We report a mean Dice score of 84.90 $\pm$ 7.53$\text{\%}$, ASSD: 1.39 $\pm$ 0.65 mm, ASD: 1.37 $\pm$ 0.64 mm, and HD95: 5.64 $\pm$ 2.38 mm. We refer the reader to the Challenge paper by Sekuboyina et al. (2020) for the tabulated results (Table 3) from the eleven participating groups. The best performing methods have a mean Dice score performance on the public dataset of: Payer C. (90.90 $\text{\%}$), Chen M. (93.01$\text{\%}$), Lessmann N. (85.08$\text{\%}$), Hu Y. (84.07$\text{\%}$), Sekuboyina A. (83.06$\text{\%}$), Jiang T. (82.70$\text{\%}$), Dong Y. (76.74$\text{\%}$), Wang X. (71.88$\text{\%}$), Amiranashvili T. (67.02$\text{\%}$), and Brown K. (62.69$\text{\%}$). We note that our results are not directly comparable to those of the methods proposed by the participating teams. Those teams evaluated their methods on the full test set, which included challenging cases, whereas in our evaluation we excluded the low dose cases using our SNR selection criterion. At the same time, for our method the results are reported on a combination of images from the training, validation and test sets, since our method does not have a training phase. For the participating teams the reported results are on images from the test set only.

TABLE 3

TABLE 3. Spine segmentation results reported for Database 3.

3.2 Pipeline 2: Shape-Prior Based Flows for Individual Vertebra Segmentation

We use a six-fold cross-validation approach. We build the shape-prior with 25 vertebrae and evaluate the method on the remaining five. This procedure is then repeated for the six different folds. When applied to Database 3, pipeline 2 yields an average Dice score of 83.84 $\pm$ 3.10$\text{\%}$, and an average symmetric surface distance at 1.31 $\pm$ 0.24 mm. The 95th percentile Hausdorff distance is 3.59 $\pm$ 0.90 mm.

4 Discussion

We now discuss our segmentation results and compare them to those of other approaches in the literature. Our geometric flow based approach traverses the outer cortical bone of the vertebral column to segment its surface, while also delineating the spinal cord and the inter-vertebral discs. Pipeline 1 of the approach relies on minimal user input to identify seed points, is simple to implement, and can be applied to the segmentation of any vertebral region of the spine or alternatively any visible spinal region in a given volume. This is of direct clinical relevance since the 3D model of the spine can be used for surgical planning and downstream tasks. The proposed segmentation procedure is very fast, even when implemented on a CPU. On an Intel(R) Xeon(R) CPU running at 3.50 GHz with 12 cores, the edge-enhancing pre-processing step takes around 4 min, and it takes another 15 s to compute the flux-map. These pre-processing steps are carried out offline. The surface extraction takes about 5 min while the shrink-wrapping procedure takes another 5–10 min on average, for the entire lumbar region in 3D.

4.1 Pipeline 1: Region-Based Segmentation of the Spine

4.1.1 Database 1

The results in Table 1 demonstrate that our approach is comparable to the other methods in terms of Dice coefficient and surface based metrics. We point out that the Dice coefficient on its own is not a sufficient measure for translation to what is clinically acceptable for spine surgery, and for the latter the surface based distance measures are important. The box plot in Figure 6 show our ASD errors to peak at about 1mm, and to be well below the clinically accepted threshold of 2 mm across all surface voxels.

With regard to surface-evolution approaches, Lim et al. (2013) use an edge-mounted Willmore flow with a kernelized shape-prior based level-set method for lumbar vertebrae segmentation, while Tan et al. (2008) use a series of geodesic active contours (GAC) to segment the vertebral body. Lim et al. (2013) show that for 2D slices the GAC and Chan-Vese based methods fail to segment the CT vertebrae. This is in contrast to our approach, likely because of the filtering method we have used in pre-processing the volumes. Our one-click initialization (a few voxel suffices) is also substantially less cumbersome than the doughnut shaped initialization used by Lim et al. (2013). Our method outperforms this approach, which reports a Dice score of 89.32 $\pm$ 1.70$\text{\%}$ and a Hausdorff distance of 14.03 $\pm$ 1.40 mm, for the lumbar region.

Our approach is simpler in comparison to methods (Rasoulian et al., 2013; Ibragimov et al., 2014a; Korez et al., 2015a; Castro-Mateos et al., 2015; Pereañez et al., 2015) as it does not require constrained optimization. For example, Pereañez et al. (2015) segment the vertebral body and the processes separately and independently, while we do not require such a restriction. Rasoulian et al. (2013) make an assumption that there is a strong correlation between the shapes and poses of different vertebrae, within the same patient, an assumption that we avoid. We outperform the approach of Rasoulian et al. (2013) (the datasets used in Rasoulian et al. (2013) and Lim et al. (2013) are not publicly available but involve the CT lumbar region) on the comparable metric of HD95 with 2.90 $\pm$ 1.38 mm vs. 3.80 $\pm$ 1.61 mm on Database 1. We report comparable segmentation results in terms of Dice coefficients and Hausdorff distances to the methods of Korez et al. (2015); Ibragimov et al. (2014).

A recent competitive method based on deep learning, is that of Lessmann et al. (2019). Here the different vertebrae are iteratively segmented using a memory network, exploiting information from the already segmented vertebrae. This approach, which is automatic, yields an impressive Dice score of 96.50 $\pm$ 0.8$\text{\%}$. However, this requires keeping track of nearby segmented vertebrae. In this formulation the images were cropped to the region which contains the vertebrae to be segmented, to restrict the field of view. In contrast, in our approach we segment the full spine or a desired individual vertebra, relying on seed points from the user. Our ASSD of 1.14 + 0.29 mm is well within the acceptable surface error of 2 mm for facet joint injection procedures (Gill et al., 2012). A possible reason that our method reports slightly worse Dice score on Database 1 than Lessmann et al. (2019) might be that of mis-segmentations at the intersection of the processes of adjacent vertebrae because the method in pipeline 1 does not segment each vertebrae individually.

4.1.2 Database 2

For the segmentation of the thoracic vertebrae, where there is a loss of signal at the boundaries, we apply our region-based flow directly on the edge-enhanced image rather than the flux-map. This leads to better segmentation of the vertebrae and their processes, but with a few holes present inside the vertebral bodies due to inhomogeneities in the signal. After this, we run the shrink-wrapping step to obtain complete vertebral segmentations, while filling small holes in the vertebral bodies if present.

Figure 7 shows 2D slices of the segmented spine overlaid on the ground truth for the two Databases 1 and 2. Figure 8 depicts the segmented spine overlaid on the ground truth volume. In the thoracic region, the ribs get segmented too as they are attached to the vertebrae. The middle figure shows the zoomed in thoracic region. Using ITK-SNAP (Yushkevich et al., 2006; Yushkevich et al., 2019), we manually crop the ribs, the coccyx and the sacrum bones for the purpose of computing the evaluation metrics, with the result of the cropping overlaid on the ground truth in the rightmost figure.

FIGURE 7

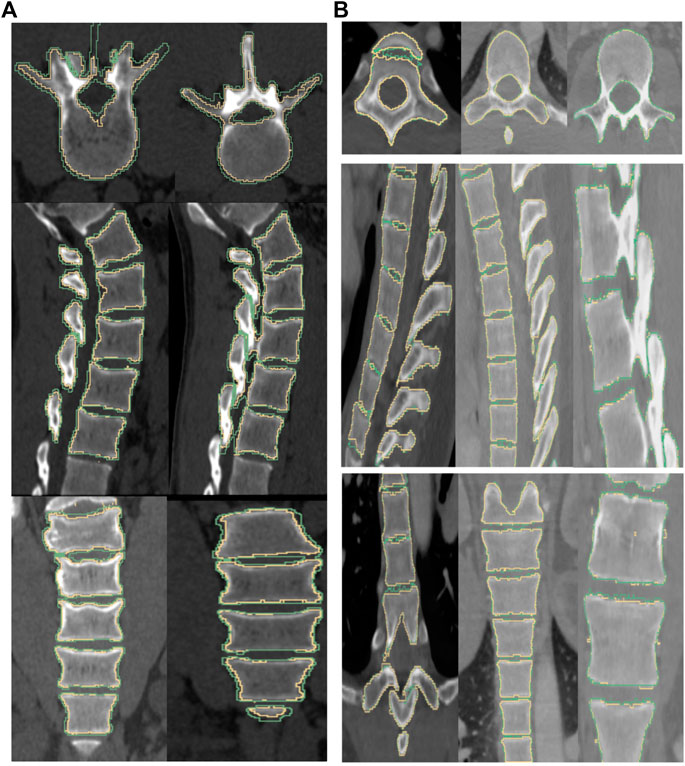
FIGURE 7. The boundary of the segmentation (yellow) and groundtruth (green) overlaid on top of the image for a subject from Database 1 (left column) and Database 2 (right column). (From top to bottom) axial, sagittal and coronal views. Note: We noticed that some of the manually labelled segmentations provided in the CSI Database had errors, especially in the thoracic regions, and this could adversely affect the quality metrics.

FIGURE 8

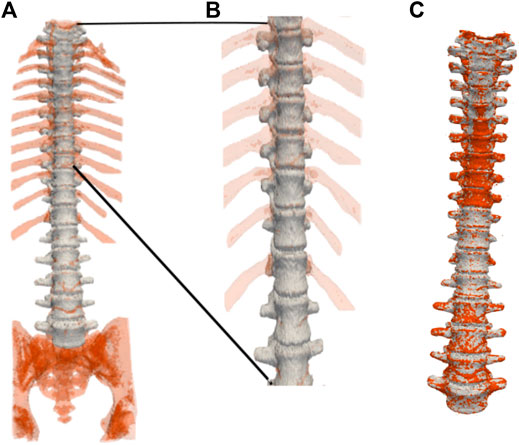
FIGURE 8. Three-dimensional spine segmentation rendering. (A): Shown in light grey is the vertebrae region that is common to both, the ground truth and the segmentation obtained by our method. The extra regions segmented such as the ribs, the coccyx and the sacrum, and other voxels in the spinal column, are shown in red. (B): A zoomed-in image of the upper thoracic region. (C): The segmented spine (shown in red) overlaid on top of the ground truth (shown in light grey) after cropping-out the regions manually using ITK-SNAP. Manual cropping of the extraneous regions such as the ribs, the coccyx and the sacrum after segmentation could be regarded as selecting a region of interest (ROI) before an input image is fed into an automated segmentation method (Lessmann et al., 2019; Sekuboyina et al., 2020). For example, in Lessmann et al. (2019), images are cropped to restrict the field of view of the vertebrae that were not included in the reference segmentation in order to avoid training the network with vertebra voxels incorrectly labeled as background voxels. In contrast, we feed in the entire image, consisting of the entire FoV, to our algorithm, which then produces the desired segmentation of the spine. Our flow-based segmentation approach is designed to also segment the ribs, and the sacrum when available. Therefore, in order to compute volume and surface-based quantitative measurements of the vertebral segmentations for which the ground truth segmentations are available, we crop out the regions such as the ribs, and the sacrum using ITK-SNAP.

Table 2 reports results separately for the thoracic and lumbar regions. Our segmentation results are quite similar for these two regions. Our method performs better than that of Hammernik et al. (2015), for the lumbar and the thoracic regions, and thus the entire spine as well. The approaches outlined in the thesis of Hammernik (2015) and the CSI workshop article (Hammernik et al., 2015) are similar in spirit to ours, since they are geometric flow based. In contrast to our method, Hammernik et al. (2015) use the “Rudin-Osher-Fatemi” (Rudin et al., 1992) model for denoising, and they then minimize a variational energy functional in a convex optimization framework. The energy functional consists of a structure tensor based geodesic active contour term, a mean-shape model and a bone prior map.

Our approach outperforms the non deep-learning methods in terms of both volume overlap and surface distance errors, as demonstrated in Table 2. The box plot in Figure 6 shows the voxel wise ASD errors to be very small, typically well below 1mm, meeting the clinically acceptable threshold of 2 mm. The Dice score of 94.94 $\pm$ 2.22$\text{\%}$ reported by our method is very close to the current state of the art Dice score of 96.30 $\pm$ 1.3$\text{\%}$ of Lessmann et al. (2019), an approach which relies on the availability of large image databases for training. The other methods rely on training data and can thus only segment the vertebrae for which the ground truth segmentations are available. In fact, deep learning based methods typically require days to train, e.g., Lessmann et al. (2019) report that they trained their network for 4–5 days on Nvidia Titan X GPUs with 12 gigabytes of memory. But, deep learning methods are quite fast at the time of inference, because they require a simple forward pass through the network. In contrast, with no requirement for training our pipeline 1 approach, from pre-processing to shrink-wrapping, takes around 15 min per lumbar region on a CPU, as discussed earlier.

4.1.3 Database 4

Figure 9 shows qualitative examples for seven subjects, where our approach performs well. We provide segmentation results on a variety of image distributions across different vendors spanning the different vertebral regions for both healthy and pathological cases. The resampling of the original volumes to an isotropic grid might lead to inaccuracy in the groundtruth labels which in turn would contribute to some of the discrepancies (Figure 9). The main limitations of our formulation are that the flow does not segment vertebrae with surgical implants, and fails to work in low-dose (high noise) images, with partially visible vertebrae. Our results are not directly comparable to those reported in Sekuboyina et al. (2020), since our method was only applied to a subset of the dataset, as explained in Section 2.1.4.

FIGURE 9

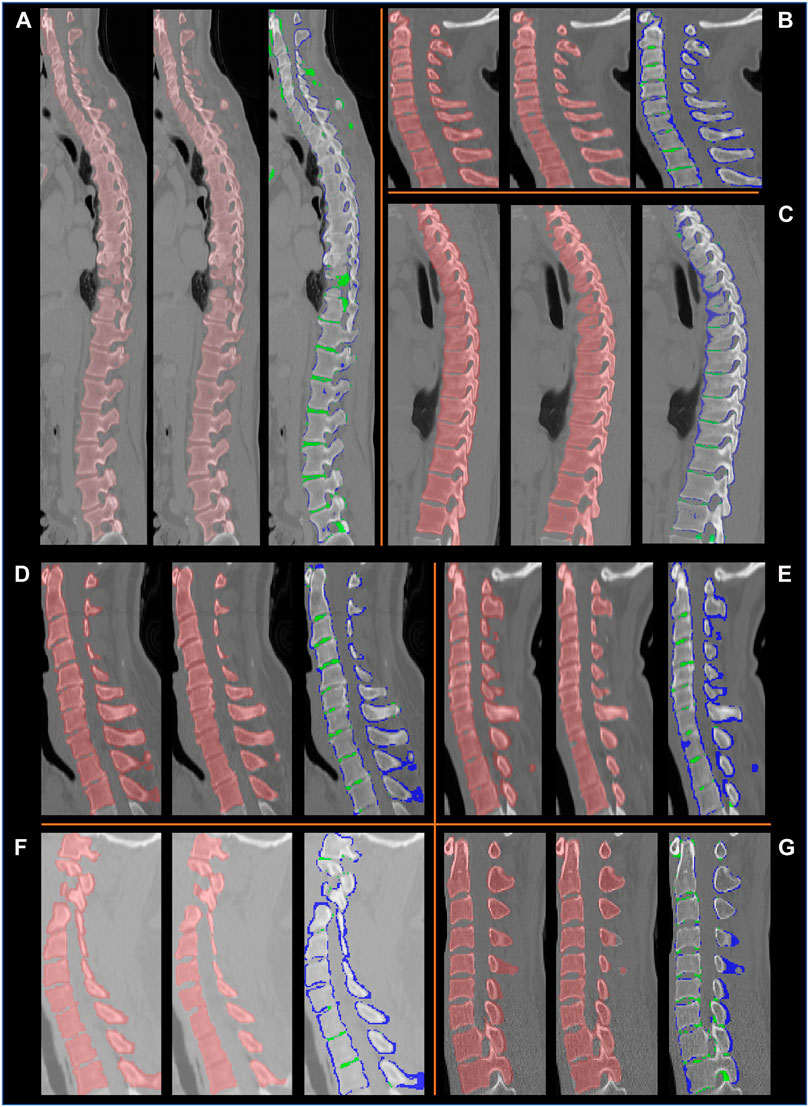
FIGURE 9. Example segmentation results on the VerSe database, shown in the sagittal plane for eight subjects (A–G). For each subject, a set of three images are presented: left: the ground truth labels; middle: the segmentation by our method, right: the difference between our segmentation and the ground truth labels. In the latter the voxels in blue are in the ground truth labels but not in our segmentation, and the voxels in green are segmented by our method but are not present in the ground truth labels. We observe that the ground truth labels (blue) can be outside the vertebral boundaries. Our method correctly delineates the vertebrae, except at some intervertebral discs.

4.2 Pipeline 2: Shape-Prior Based Flows for Individual Vertebra Segmentation

We evaluate the shape-prior based segmentation method, discussed in Section 2.3.2, on Database 3. To motivate the need to use a shape prior, we first present some results of the region based segmentation pipeline 1 on this challenging database of patients with trauma, Database 3. A 2D slice obtained by the surface extraction method is shown in Figure 10A (left) and the filled volume is shown in Figure 10A (right). The segmentations are accurate, as the flow evolves along the vertebral boundary, but it is hard to demarcate each individual vertebrae separately because several vertebrae are either fused, dislocated or are fractured severely. Thus, we hypothesized that a shape-prior based segmentation method applied to each individual vertebra can help eliminate this problem, as illustrated in Figure 10B. The algorithm is initialized with the mean-shape of the training population, placed near the region of interest. This PCA based shape-prior level-set method is not only fast, but also requires very little effort to set up. The PCA modelling step takes around a minute to complete for a set of 25 vertebrae. This step is carried out offline, before the actual segmentation step. It takes a couple of minutes to segment an individual vertebra, which is the online step. A possible disadvantage of the shape-prior based method proposed in the present article is that it might get trapped in a local minimum.

FIGURE 10

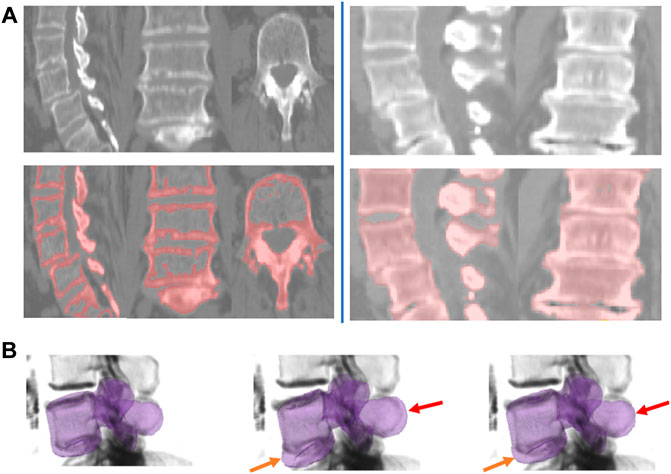
FIGURE 10. Shape-prior based segmentation in pipeline 2. (A) Region-based segmentation Pipeline 1 applied to two example subjects from Database 3 with the pathology cases. Left: Sample slices shown for the region-based surface extraction on the flux-map for Database 3. Right: Sample slices shown for the shrink-wrapping process for Database 3. (B) Intermediate steps for the shape-prior based segmentation process for a subject from Database 3. Left column: shape-prior initialization. The middle and rightmost columns shows how the vertebral body and the spinous process are pulled-in (shown by orange and red arrows respectively) and evolve to segment the individual vertebra.

We outperform the method of Stephansen (2012), based on active shape and appearance models, both in terms of Dice score and surface distance errors. Although the ASD errors are larger than those for databases without pathology, the box plot in Figure 6 shows them to still be well under the clinically accepted threshold of 2 mm. Table 3 provides a comparison between the results of our method and those of Stephansen (2012). Hammernik et al. (2015) use an energy functional that incorporates a mean-shape and bone priors. A potential weakness of this approach is that it relies on only the mean-shape of the training population. We overcome this challenge by modelling the variations in shape and pose. Additionally, we use the more adaptive edge-enhancing method by Weickert and Scharr (2002) along with flux integral of Vasilevskiy and Siddiqi (2002) to pre-process the volumes, instead of the total variation norm based (Rudin et al., 1992) method.

Conclusion

In summary, we have proposed two pipelines to segment the spine in CT images, which employs geometric flows. Our use of anisotropic diffusion filtering combined with flux maximizing flows is new in this context, to the best of our knowledge. We have validated our region-based surface extraction approach and the subsequent shrink-wrapping step on three publicly available databases. The shape-prior based method to segment individual vertebrae has been evaluated on a database containing pathological cases. We do not require tracking or segmentation of nearby structures in the spinal column, which reduces computational burden. We have shown that our method achieves accurate and precise vertebral segmentations, with surface distance errors that are well below the clinically acceptable threshold of 2 mm. Our method works across different CT data distributions, because it exploits information directly from the normalized CT images, using the geometry of their isophotes. This novel semi-automatic technique will obviate the need for time-consuming manual segmentations and eliminate errors due to inter- and intra-observer variability. The shape-based initialization technique constrains the segmented surfaces to plausible locations, thus avoiding local segmentation errors. In future we hope to integrate our segmentation pipelines into a pre-operative surgical planning platform, and improve the flow-based method to segment vertebrae in low-dose and surgical implant images. This would allow for better navigation, and would facilitate downstream tasks.

Data Availability Statement

Publicly available datasets were analyzed in this study. This data can be found here: (1) http://lit.fe.uni-lj.si/tools.php?lang=eng. (2) http://spineweb.digitalimaginggroup.ca/spineweb/index.php?n=Main.Datasets. (3) https://github.com/anjany/verse.

Ethics Statement

The studies involving human participants were reviewed and approved by Montreal Neurological Institute (MNI) Research Ethics Board, Montreal Neurological Institute and Hospital 3801 Rue University, Montréal, QC H3A 2B4. The patients/participants provided their written informed consent to participate in this study.

Author Contributions

PK: conceptualization, methodology, software, writing. DC: conceptualization, writing. KS: conceptualization, methodology, writing.

Funding

This research was supported by funding from the Natural Sciences and Engineering Research Council of Canada (NSERC), Fonds de Recherche du Que´bec Nature et technologies (FRQNT), and the Canadian Institutes of Health Research (CIHR).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This article is based on work reported in the master’s thesis of the first author, PK Khandelwal (2019). We are grateful to the developers of several open-source software repositories we have used, including: ITK-SNAP (Yushkevich et al., 2006; Yushkevich et al., 2019) for placement of seeds, cropping, and for conversion between different file formats; Paraview (Ayachit, 2015), 3DSlicer (Kikinis et al., 2014), and the Seaborn library (Waskom, 2021) for visualization; MedPy (Maier et al., 2019) and EvaluateSegmentation (Taha and Hanbury, 2015) for computing performance metrics; and FreeSurfer (Dale et al., 1999) for registration of the volumes to a common space; and Inkscape (Bah, 2011) for image editing and for figure design.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fcomp.2021.592296/full#supplementary-material

Supplementary Videos | Several movies illustrating our geometric flow based segmentation of the spine are provided as supplementary data. A brief explanation of the contents of each movie is below.

Supplementary Video 1 | Movie1. mp4 shows the surface extraction of the spine, using the Chan-Vese flow, as explained in Section 2.3.1.

Supplementary Video 2 | Movie2. mp4 shows the positive eigenshapes. The mean vertebra is shown in red and the first ten positive eigenshapes are shown in green (Section 2.3.2).

Supplementary Video 3 | Movie3. mp4 shows the negative eigenshapes. The mean vertebra is shown in red and the first ten negative eigenshapes are shown in blue (Section 2.3.2).

Supplementary Video 4 | Movie4. mp4 illustrates the segmentation of individual vertebra, using the shape prior based method (Section 2.3.2).

References

Aslan, M. S., Ali, A., Farag, A. A., Rara, H., Arnold, B., and Xiang, P. (2010). “3d Vertebral Body Segmentation Using Shape Based Graph Cuts,” in 2010 20th International Conference on Pattern Recognition, Istanbul, Turkey, August 23–26, 2010, 3951–3954.

CrossRef Full Text | Google Scholar

Ayachit, U. (2015). The ParaView Guide: A Parallel Visualization Application (USA: Kitware, Inc.).

Bah, T. (2011). Inkscape: Guide to a Vector Drawing Program (Upper Saddle River, NJ, USA: Prentice Hall Press).4th edn.

Bresson, X., Vandergheynst, P., and Thiran, J.-P. (2006). A Variational Model for Object Segmentation Using Boundary Information and Shape Prior Driven by the mumford-shah Functional. Int. J. Comput. Vis. 68, 145–162. doi:10.1007/s11263-006-6658-x

CrossRef Full Text | Google Scholar

Brox, T., and Weickert, J. (2006). Level Set Segmentation with Multiple Regions. IEEE Trans. Image Process. 15, 3213–3218. doi:10.1109/tip.2006.877481

PubMed Abstract | CrossRef Full Text | Google Scholar

Caselles, V., Kimmel, R., and Sapiro, G. (1995). “Geodesic Active Contours,” in Proceedings of IEEE International Conference on Computer Vision, Cambridge, MA, June 20–23, 1995, 694–699.

Google Scholar

Castro, W. H. M., Halm, H., Jerosch, J., Malms, J., Steinbeck, J., and Blasius, S. (1996). Accuracy of Pedicle Screw Placement in Lumbar Vertebrae. Spine 21, 1320–1324. doi:10.1097/00007632-199606010-00008

PubMed Abstract | CrossRef Full Text | Google Scholar

Castro-Mateos, I., Pozo, J. M., Pereañez, M., Lekadir, K., Lazary, A., and Frangi, A. F. (2015). Statistical Interspace Models (SIMs): Application to Robust 3d Spine Segmentation. IEEE Trans. Med. Imaging 34, 1663–1675. doi:10.1109/tmi.2015.2443912

PubMed Abstract | CrossRef Full Text | Google Scholar

Chan, T. F., and Vese, L. A. (2001). Active Contours without Edges. IEEE Trans. Image Process. 10, 266–277. doi:10.1109/83.902291

PubMed Abstract | CrossRef Full Text | Google Scholar

Chu, C., Belavỳ, D. L., Armbrecht, G., Bansmann, M., Felsenberg, D., and Zheng, G. (2015). Fully Automatic Localization and Segmentation of 3d Vertebral Bodies from Ct/mr Images via a Learning-Based Method. PloS one 10, 1–22. doi:10.1371/journal.pone.0143327

CrossRef Full Text | Google Scholar

Chung, G., and Vese, L. A. (2009). Image Segmentation Using a Multilayer Level-Set Approach. Comput. Vis. Sci. 12, 267–285. doi:10.1007/s00791-008-0113-1

CrossRef Full Text | Google Scholar

Chunming Li, C., Chenyang Xu, C., Changfeng Gui, C., and Fox, M. D. (2010). Distance Regularized Level Set Evolution and its Application to Image Segmentation. IEEE Trans. Image Process. 19, 3243–3254. doi:10.1109/tip.2010.2069690

PubMed Abstract | CrossRef Full Text | Google Scholar

Cleary, K. (2000). Final Report of the Technical Requirements for Image-Guided Spine Procedures Workshop. Computer Aided Surg. 5, 180–215. doi:10.3109/10929080009148889

PubMed Abstract | CrossRef Full Text | Google Scholar

Cootes, T. F., Taylor, C. J., Cooper, D. H., and Graham, J. (1995). Active Shape Models-Their Training and Application. Computer Vis. Image Understanding 61, 38–59. doi:10.1006/cviu.1995.1004

CrossRef Full Text | Google Scholar

Cremers, D., Osher, S. J., and Soatto, S. (2006). Kernel Density Estimation and Intrinsic Alignment for Shape Priors in Level Set Segmentation. Int. J. Comput. Vis. 69, 335–351. doi:10.1007/s11263-006-7533-5

CrossRef Full Text | Google Scholar

Cremers, D., Rousson, M., and Deriche, R. (2007). A Review of Statistical Approaches to Level Set Segmentation: Integrating Color, Texture, Motion and Shape. Int. J. Comput. Vis. 72, 195–215. doi:10.1007/s11263-006-8711-1

CrossRef Full Text | Google Scholar

Cremers, D., and Soatto, S. (2003). “A Pseudo-distance for Shape Priors in Level Set Segmentation,” in 2nd IEEE workshop on variational, geometric and level set methods in computer vision (Citeseer), Nice, France, October 11–12, 2003, 15 26–32.

Google Scholar

Cui, G., Watanabe, K., Hosogane, N., Tsuji, T., Ishii, K., Nakamura, M., et al. (2012). Morphologic Evaluation of the Thoracic Vertebrae for Safe Free-Hand Pedicle Screw Placement in Adolescent Idiopathic Scoliosis: a Ct-Based Anatomical Study. Surg. Radiol. Anat. 34, 209–216. doi:10.1007/s00276-011-0849-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Dale, A. M., Fischl, B., and Sereno, M. I. (1999). Cortical Surface-Based Analysis. NeuroImage 9, 179–194. doi:10.1006/nimg.1998.0395

PubMed Abstract | CrossRef Full Text | Google Scholar

Dambreville, S., Tannenbaum, A., Yezzi, A., and Niethammer, M. (2007). “A Variational Framework Combining Level-Sets and Thresholding,” in Proc. BMVC. 53.

CrossRef Full Text | Google Scholar

Descoteaux, M., Audette, M., Chinzei, K., and Siddiqi, K. (2005). “Bone Enhancement Filtering: Application to Sinus Bone Segmentation and Simulation of Pituitary Surgery,” in International Conference on Medical Image Computing and Computer-Assisted Intervention, Palm Springs, CA, October 26–29, 2005 (Springer), 9–16. doi:10.1007/11566465_2

CrossRef Full Text | Google Scholar

Di Silvestre, M., Parisini, P., Lolli, F., and Bakaloudis, G. (2007). Complications of Thoracic Pedicle Screws in Scoliosis Treatment. Spine 32, 1655–1661. doi:10.1097/brs.0b013e318074d604

PubMed Abstract | CrossRef Full Text | Google Scholar

Drouin, S., Kochanowska, A., Kersten-Oertel, M., Gerard, I. J., Zelmann, R., De Nigris, D., et al. (2017). Ibis: an or Ready Open-Source Platform for Image-Guided Neurosurgery. Int. J. CARS 12, 363–378. doi:10.1007/s11548-016-1478-0

CrossRef Full Text | Google Scholar

Forsberg, D. (2015). “Atlas-Based Registration for Accurate Segmentation of Thoracic and Lumbar Vertebrae in CT Data,” Atlas-Based Registration for Accurate Segmentation of Thoracic and Lumbar Vertebrae in CT Data (Cham: Springer International Publishing), 49–59. chap. skip. doi:10.1007/978-3-319-14148-0_5

CrossRef Full Text | Google Scholar

Frangakis, A. S., and Hegerl, R. (2001). Noise Reduction in Electron Tomographic Reconstructions Using Nonlinear Anisotropic Diffusion. J. Struct. Biol. 135, 239–250. doi:10.1006/jsbi.2001.4406

PubMed Abstract | CrossRef Full Text | Google Scholar

Gill, S., Abolmaesumi, P., Fichtinger, G., Boisvert, J., Pichora, D., Borshneck, D., et al. (2012). Biomechanically Constrained Groupwise Ultrasound to Ct Registration of the Lumbar Spine. Med. Image Anal. 16, 662–674. Computer Assisted Interventions. doi:10.1016/j.media.2010.07.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Goulet, B. (2010). Lumbar-sacral Pedicle Screw Insertion with Preoperative CT-based Navigation (Montréal, QC: McGill University). Ph.D. thesis.

Haberland, N., Ebmeier, K., Grunewald, J. P., Hliscs, R., and Kalff, R.-L. (2000). Incorporation of Intraoperative Computerized Tomography in a Newly Developed Spinal Navigation Technique. Computer Aided Surg. 5, 18–27. doi:10.3109/10929080009148868

CrossRef Full Text | Google Scholar

Hammernik, K. (2015). Convex Framework for 2D & 3D Image Segmentation Using Shape Constraints (Graz, Austria: Graz University of Technology). Ph.D. thesis.

Hammernik, K., Ebner, T., Stern, D., Urschler, M., and Pock, T. (2015). “Vertebrae Segmentation in 3d Ct Images Based on a Variational Framework,” in Recent Advances in Computational Methods and Clinical Applications for Spine Imaging (Boston, MA: Springer), 227–233. doi:10.1007/978-3-319-14148-0_20

CrossRef Full Text | Google Scholar

Huang, J., Jian, F., Wu, H., and Li, H. (2013). An Improved Level Set Method for Vertebra Ct Image Segmentation. BioMedical Eng. OnLine 12, 48. doi:10.1186/1475-925x-12-48

PubMed Abstract | CrossRef Full Text | Google Scholar

Ibragimov, B., Korez, R., Likar, B., Pernuš, F., and Vrtovec, T. (2015). “Interpolation-Based Detection of Lumbar Vertebrae in CT Spine Images,” Interpolation-Based Detection of Lumbar Vertebrae in CT Spine Images (Cham: Springer International Publishing), 73–84. doi:10.1007/978-3-319-14148-0_7

CrossRef Full Text | Google Scholar

Ibragimov, B., Likar, B., Pernuš, F., and Vrtovec, T. (2014b). “Segmentation of Vertebrae from 3d Spine Images by Applying Concepts from Transportation and Game Theories,”. Computational Methods and Clinical Applications for Spine Imaging. Editors J. Yao, T. Klinder, and S. Li (Boston, MA: Springer International Publishing), 3–14. doi:10.1007/978-3-319-07269-2_1

CrossRef Full Text | Google Scholar

Ibragimov, B., Likar, B., Pernuš, F., and Vrtovec, T. (2014a). Shape Representation for Efficient Landmark-Based Segmentation in 3-d. IEEE Trans. Med. Imaging 33, 861–874. doi:10.1109/tmi.2013.2296976

PubMed Abstract | CrossRef Full Text | Google Scholar

Janssens, R., Zeng, G., and Zheng, G. (2018). “Fully Automatic Segmentation of Lumbar Vertebrae from Ct Images Using Cascaded 3d Fully Convolutional Networks,” in 2018 IEEE 15th International Symposium on Biomedical Imaging (ISBI 2018), Washington, DC, April 4–7, 2018, 893–897.

CrossRef Full Text | Google Scholar

Kadoury, S., and Paragios, N. (2010). “Nonlinear Embedding towards Articulated Spine Shape Inference Using Higher-Order Mrfs,”. Medical Image Computing and Computer-Assisted Intervention – MICCAI 2010. Editors T. Jiang, N. Navab, J. P. W. Pluim, and M. A. Viergever (Berlin, Heidelberg: Springer Berlin Heidelberg), 579–586. doi:10.1007/978-3-642-15711-0_72

CrossRef Full Text | Google Scholar

Kaminsky, J., Klinge, P., Rodt, T., Bokemeyer, M., Luedemann, W., and Samii, M. (2004). Specially Adapted Interactive Tools for an Improved 3d-Segmentation of the Spine. Comput. Med. Imaging Graphics 28, 119–127. doi:10.1016/j.compmedimag.2003.12.001

CrossRef Full Text | Google Scholar

Khandelwal, P. (2019). Spine Segmentation in Computed Tomography Images Using Geometric Flows and Shape PriorsMaster’s Thesis (Canada: McGill University).

Khandelwal, P., and Yushkevich, P. (2020). “Domain Generalizer: A Few-Shot Meta Learning Framework for Domain Generalization in Medical Imaging,”. Domain Adaptation and Representation Transfer, and Distributed and Collaborative Learning. Editors S. Albarqouni, S. Bakas, K. Kamnitsas, M. J. Cardoso, B. Landman, W. Li, F. Milletari, N. Rieke, H. Roth, D. Xu, and Z. Xu (Cham: Springer International Publishing), 73–84. doi:10.1007/978-3-030-60548-3_8

CrossRef Full Text | Google Scholar

Kichenassamy, S., Kumar, A., Olver, P., Tannenbaum, A., and Yezzi, A. (1996). Conformal Curvature Flows: from Phase Transitions to Active Vision. Arch. Rational Mech. Anal. 134, 275–301. doi:10.1007/bf00379537

CrossRef Full Text | Google Scholar

Kikinis, R., Pieper, S. D., and Vosburgh, K. G. (2014). “3D Slicer: A Platform for Subject-specific Image Analysis, Visualization, and Clinical Support,” 3D Slicer: A Platform for Subject-specific Image Analysis, Visualization, and Clinical Support (New York, NY: Springer New York), 277–289. doi:10.1007/978-1-4614-7657-3_19

CrossRef Full Text | Google Scholar

Kim, Y.-W., Lenke, L. G., Kim, Y. J., Bridwell, K. H., Kim, Y. B., Watanabe, K., et al. (2008). Free-Hand Pedicle Screw Placement during Revision Spinal Surgery. Spine 33, 1141–1148. doi:10.1097/brs.0b013e31816f28a1

PubMed Abstract | CrossRef Full Text | Google Scholar

Kim, Y., and Kim, D. (2009). A Fully Automatic Vertebra Segmentation Method Using 3d Deformable Fences. Comput. Med. Imaging Graphics 33, 343–352. doi:10.1016/j.compmedimag.2009.02.006

CrossRef Full Text | Google Scholar

Klinder, T., Ostermann, J., Ehm, M., Franz, A., Kneser, R., and Lorenz, C. (2009). Automated Model-Based Vertebra Detection, Identification, and Segmentation in Ct Images. Med. Image Anal. 13, 471–482. doi:10.1016/j.media.2009.02.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Koller, H., Acosta, F., Tauber, M., Fox, M., Martin, H., Forstner, R., et al. (2008). Cervical Anterior Transpedicular Screw Fixation (ATPS)-Part II. Accuracy of Manual Insertion and Pull-Out Strength of ATPS. Eur. Spine J. 17, 539–555. doi:10.1007/s00586-007-0573-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Korez, R., Ibragimov, B., Likar, B., Pernuš, F., and Vrtovec, T. (2015a). A Framework for Automated Spine and Vertebrae Interpolation-Based Detection and Model-Based Segmentation. IEEE Trans. Med. Imaging 34, 1649–1662. doi:10.1109/tmi.2015.2389334

PubMed Abstract | CrossRef Full Text | Google Scholar

Korez, R., Ibragimov, B., Likar, B., Pernuš, F., and Vrtovec, T. (2015b). “An Improved Shape-Constrained Deformable Model for Segmentation of Vertebrae from CT Lumbar Spine Images,” An Improved Shape-Constrained Deformable Model for Segmentation of Vertebrae from CT Lumbar Spine Images (Boston, MA: Springer International Publishing), 85–94. doi:10.1007/978-3-319-14148-0_8

CrossRef Full Text | Google Scholar

Korez, R., Likar, B., Pernuš, F., and Vrtovec, T. (2016). “Model-based Segmentation of Vertebral Bodies from Mr Images with 3d Cnns,”. Medical Image Computing and Computer-Assisted Intervention – MICCAI 2016. Editors S. Ourselin, L. Joskowicz, M. R. Sabuncu, G. Unal, and W. Wells (Athens, Greece: Springer International Publishing), 433–441. doi:10.1007/978-3-319-46723-8_50

CrossRef Full Text | Google Scholar

Korez, R., Likar, B., Pernuš, F., and Vrtovec, T. (2017). “Segmentation of Pathological Spines in Ct Images Using a Two-Way Cnn and a Collision-Based Model,” in International Workshop on Computational Methods and Clinical Applications in Musculoskeletal Imaging, Quebec City, QC, 10 September (Springer), 95–107.

Google Scholar

Kroon, D.-J., Slump, C. H., and Maal, T. J. J. (2010). “Optimized Anisotropic Rotational Invariant Diffusion Scheme on Cone-Beam Ct,” in International Conference on Medical Image Computing and Computer-Assisted Intervention, Beijing, China, September 20–24, 2010 (Springer), 221–228. doi:10.1007/978-3-642-15711-0_28

CrossRef Full Text | Google Scholar

Kroon, D., and Slump, C. H. (2009). “Coherence Filtering to Enhance the Mandibular Canal in Cone-Beam Ct Data,” in IEEE-EMBS Benelux Chapter Symposium, 11, 40–41.

Google Scholar

Kuklo, T. R., Lenke, L. G., O’Brien, M. F., Lehman, R. A., Polly, D. W., and Schroeder, T. M. (2005). Accuracy and Efficacy of Thoracic Pedicle Screws in Curves More Than 90°. Spine 30, 222–226. doi:10.1097/01.brs.0000150482.26918.d8

PubMed Abstract | CrossRef Full Text | Google Scholar

Laine, T., Lund, T., Ylikoski, M., Lohikoski, J., and Schlenzka, D. (2000). Accuracy of Pedicle Screw Insertion with and without Computer Assistance: a Randomised Controlled Clinical Study in 100 Consecutive Patients. Eur. Spine J. 9, 235–240. doi:10.1007/s005860000146

PubMed Abstract | CrossRef Full Text | Google Scholar

Laine, T., Schlenzka, D., Mäkitalo, K., Tallroth, K., Nolte, L.-P., and Visarius, H. (1997). Improved Accuracy of Pedicle Screw Insertion with Computer-Assisted Surgery. Spine 22, 1254–1258. doi:10.1097/00007632-199706010-00018

PubMed Abstract | CrossRef Full Text | Google Scholar

Law, M., and Chung, A. (2009). Efficient Implementation for Spherical Flux Computation and its Application to Vascular Segmentation. IEEE Trans. Image Process. 18, 596–612. doi:10.1109/tip.2008.2010073

PubMed Abstract | CrossRef Full Text | Google Scholar

Lessmann, N., van Ginneken, B., de Jong, P. A., and Išgum, I. (2019). Iterative Fully Convolutional Neural Networks for Automatic Vertebra Segmentation and Identification. Med. Image Anal. 53, 142–155. doi:10.1016/j.media.2019.02.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Leventon, M. E., Grimson, W. E. L., and Faugeras, O. (2000). “Statistical Shape Influence in Geodesic Active Contours,” in Proceedings IEEE Conference on Computer Vision and Pattern Recognition. CVPR 2000 (Cat. No.PR00662), Hilton Head, SC, June 13–15, 2000, 316–323.1

Google Scholar

Lim, P. H., Bagci, U., and Bai, L. (2013). Introducing Willmore Flow into Level Set Segmentation of Spinal Vertebrae. IEEE Trans. Biomed. Eng. 60, 115–122. doi:10.1109/tbme.2012.2225833

PubMed Abstract | CrossRef Full Text | Google Scholar

Löffler, M. T., Sekuboyina, A., Jacob, A., Grau, A.-L., Scharr, A., El Husseini, M., et al. (2020). A Vertebral Segmentation Dataset with Fracture Grading. Radiol. Artif. Intelligence 2, e190138. doi:10.1148/ryai.2020190138

CrossRef Full Text | Google Scholar

Mac-Thiong, J.-M., Parent, S., Poitras, B., Joncas, J., and Hubert, L. (2013). Neurological Outcome and Management of Pedicle Screws Misplaced Totally within the Spinal Canal. Spine 38, 229–237. doi:10.1097/brs.0b013e31826980a9

PubMed Abstract | CrossRef Full Text | Google Scholar

Maier, O., Rothberg, A., Raamana, P. R., Bèges, R., Isensee, F., Ahern, M., et al. (2019). Loli/medpy: Medpy. 0.4.0. [Dataset].

Marquez-Neila, P., Baumela, L., and Alvarez, L. (2013). A Morphological Approach to Curvature-Based Evolution of Curves and Surfaces. IEEE Trans. Pattern Anal. Machine Intelligence 36, 2–17.

Google Scholar

Michael Kelm, B., Wels, M., Kevin Zhou, S., Seifert, S., Suehling, M., Zheng, Y., et al. (2013). Spine Detection in Ct and Mr Using Iterated Marginal Space Learning. Med. Image Anal. 17, 1283–1292. doi:10.1016/j.media.2012.09.007

PubMed Abstract | CrossRef Full Text | Google Scholar

Michailovich, O., Rathi, Y., and Tannenbaum, A. (2007). Image Segmentation Using Active Contours Driven by the Bhattacharyya Gradient Flow. IEEE Trans. Image Process. 16, 2787–2801. doi:10.1109/tip.2007.908073

PubMed Abstract | CrossRef Full Text | Google Scholar

Pereañez, M., Lekadir, K., Hoogendoorn, C., Castro-Mateos, I., and Frangi, A. (2015). “Detailed Vertebral Segmentation Using Part-Based Decomposition and Conditional Shape Models,” Detailed Vertebral Segmentation Using Part-Based Decomposition and Conditional Shape Models (Cham: Springer International Publishing), 95–103. doi:10.1007/978-3-319-14148-0_9

CrossRef Full Text | Google Scholar

Perona, P., and Malik, J. (1990). Scale-space and Edge Detection Using Anisotropic Diffusion. IEEE Trans. Pattern Anal. Machine Intell. 12, 629–639. doi:10.1109/34.56205

CrossRef Full Text | Google Scholar

Rasoulian, A., Rohling, R., and Abolmaesumi, P. (2013). Lumbar Spine Segmentation Using a Statistical Multi-Vertebrae Anatomical Shape+pose Model. IEEE Trans. Med. Imaging 32, 1890–1900. doi:10.1109/tmi.2013.2268424

PubMed Abstract | CrossRef Full Text | Google Scholar

Rathi, Y., Michailovich, O., Malcolm, J., and Tannenbaum, A. (2006). Seeing the Unseen: Segmenting with Distributions. Int. Conf. Signal Image Process. 534, 1–5. doi:10.1117/12.769010

Google Scholar

Rousson, M., Brox, T., and Deriche, R. (2003). “Active Unsupervised Texture Segmentation on a Diffusion Based Feature Space,” in 2003 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 2003. Proceedings (Madison, Wisconsin: IEEE). 2. II–699.

Google Scholar

Rousson, M., and Cremers, D. (2005). “Efficient Kernel Density Estimation of Shape and Intensity Priors for Level Set Segmentation,” International Conference on Medical Image Computing and Computer-Assisted Intervention (Palm Springs, CA: Springer), 757–764. doi:10.1007/11566489_93

CrossRef Full Text | Google Scholar

Rowlands, A. (2017). Physics of Digital Photography (Bristol, United Kingdom: IOP Publishing).

Rudin, L. I., Osher, S., and Fatemi, E. (1992). Nonlinear Total Variation Based Noise Removal Algorithms. Physica D: Nonlinear Phenomena 60, 259–268. doi:10.1016/0167-2789(92)90242-f

CrossRef Full Text | Google Scholar

Salah, M. B., Mitiche, A., and Ayed, I. B. (2009). Effective Level Set Image Segmentation with a Kernel Induced Data Term. IEEE Trans. Image Process. 19, 220–232. doi:10.1109/tip.2009.2032940

CrossRef Full Text | Google Scholar

Sandhu, R., Georgiou, T., and Tannenbaum, A. (2008). A New Distribution Metric for Image Segmentation. Med. Imaging 2008: Image Process. Int. Soc. Opt. Photon. 6914, 6914. doi:10.1117/12.769010

CrossRef Full Text | Google Scholar

Sarlak, A. Y., Tosun, B., Atmaca, H., Sarisoy, H. T., and Buluç, L. (2009). Evaluation of Thoracic Pedicle Screw Placement in Adolescent Idiopathic Scoliosis. Eur. Spine J. 18, 1892–1897. doi:10.1007/s00586-009-1065-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Schulze, C. J., Munzinger, E., and Weber, U. (1998). Clinical Relevance of Accuracy of Pedicle Screw Placement. Spine 23, 2215–2220. doi:10.1097/00007632-199810150-00014

PubMed Abstract | CrossRef Full Text | Google Scholar

Sekuboyina, A., Bayat, A., Husseini, M. E., Löffler, M., Rempfler, M., Kukačka, J., et al. (2020). Verse: A Vertebrae Labelling and Segmentation Benchmark. arXiv preprint arXiv:2001.09193.

Google Scholar

Sekuboyina, A., Kukačka, J., Kirschke, J. S., Menze, B. H., and Valentinitsch, A. (2017). “Attention-driven Deep Learning for Pathological Spine Segmentation,” in International Workshop on Computational Methods and Clinical Applications in Musculoskeletal Imaging, Quebec City, QC, September 10, 2017 (Springer), 108–119.

Google Scholar

Stephansen, U. L. (2012). Level-set Appearance Modeling for Segmentation of Anatomical Structures in 3-d Medical Images. McGill University. Technical Report.

Google Scholar

Stern, D., Likar, B., Pernuš, F., and Vrtovec, T. (2011). Parametric Modelling and Segmentation of Vertebral Bodies in 3d Ct and Mr Spine Images. Phys. Med. Biol. 56 (23), 7505–7522. doi:10.1088/0031-9155/56/23/011

PubMed Abstract | CrossRef Full Text | Google Scholar

Taha, A. A., and Hanbury, A. (2015). Metrics for Evaluating 3D Medical Image Segmentation: Analysis, Selection, and Tool. BMC Med. Imaging 15, 29. doi:10.1186/s12880-015-0068-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Tan, S., Jianhua Yao, J., Ward, M. M., Yao, L., and Summers, R. M. (2008). Computer Aided Evaluation of Ankylosing Spondylitis Using High-Resolution Ct. IEEE Trans. Med. Imaging 27, 1252–1267. doi:10.1109/tmi.2008.920612

PubMed Abstract | CrossRef Full Text | Google Scholar

Tsai, A., Yezzi, A., Wells, W., Tempany, C., Tucker, D., Fan, A., et al. (2003). A Shape-Based Approach to the Segmentation of Medical Imagery Using Level Sets. IEEE Trans. Med. Imaging 22 (2), 137–154. doi:10.1109/tmi.2002.808355

PubMed Abstract | CrossRef Full Text | Google Scholar

Upendra, B. N., Meena, D., Chowdhury, B., Ahmad, A., and Jayaswal, A. (2008). Outcome-based Classification for Assessment of Thoracic Pedicular Screw Placement. Spine 33, 384–390. doi:10.1097/brs.0b013e3181646ba1

PubMed Abstract | CrossRef Full Text | Google Scholar

Vasilevskiy, A., and Siddiqi, K. (2002). Flux Maximizing Geometric Flows. IEEE Trans. Pattern Anal. Machine Intell. 24, 1565–1578. doi:10.1109/tpami.2002.1114849

CrossRef Full Text | Google Scholar

Wang, Z., Zhen, X., Tay, K., Osman, S., Romano, W., and Li, S. (2015). Regression Segmentation for $M^{3}$ Spinal Images. IEEE Trans. Med. Imaging 34, 1640–1648. doi:10.1109/tmi.2014.2365746

PubMed Abstract | CrossRef Full Text | Google Scholar

Waskom, M. L. (2021). Seaborn: Statistical Data Visualization. J. Open Source Software 6 (60), 3021.

Weickert, J., and Scharr, H. (2002). A Scheme for Coherence-Enhancing Diffusion Filtering with Optimized Rotation Invariance. J. Vis. Commun. Image Representation 13, 103–118. doi:10.1006/jvci.2001.0495

CrossRef Full Text | Google Scholar

Whitaker, R. T. (1998). A Level-Set Approach to 3d Reconstruction from Range Data. Int. J. Computer Vis. 29, 203–231. doi:10.1023/a:1008036829907

CrossRef Full Text | Google Scholar

Xu, R., Ebraheim, N. A., Ou, Y., and Yeasting, R. A. (1998). Anatomic Considerations of Pedicle Screw Placement in the Thoracic Spine. Spine 23, 1065–1068. doi:10.1097/00007632-199805010-00021

PubMed Abstract | CrossRef Full Text | Google Scholar

Yao, J., Burns, J. E., Munoz, H., and Summers, R. M. (2012). “Detection of Vertebral Body Fractures Based on Cortical Shell Unwrapping,” International Conference on Medical Image Computing and Computer-Assisted Intervention (Nice, France: Springer), 509–516. doi:10.1007/978-3-642-33454-2_63

CrossRef Full Text | Google Scholar

Yushkevich, P. A., Pashchinskiy, A., Oguz, I., Mohan, S., Schmitt, J. E., Stein, J. M., et al. (2019). User-guided Segmentation of Multi-Modality Medical Imaging Datasets with Itk-Snap. Neuroinform 17, 83–102. doi:10.1007/s12021-018-9385-x

CrossRef Full Text | Google Scholar

Yushkevich, P. A., Piven, J., Hazlett, H. C., Smith, R. G., Ho, S., Gee, J. C., et al. (2006). User-guided 3D Active Contour Segmentation of Anatomical Structures: Significantly Improved Efficiency and Reliability. Neuroimage 31, 1116–1128. doi:10.1016/j.neuroimage.2006.01.015

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, J., Yan, C.-H., Chui, C.-K., and Ong, S.-H. (2010). Fast Segmentation of Bone in Ct Images Using 3d Adaptive Thresholding. Comput. Biol. Med. 40, 231–236. doi:10.1016/j.compbiomed.2009.11.020

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, K., Zhang, L., Lam, K. M., and Zhang, D. (2016). A Level Set Approach to Image Segmentation with Intensity Inhomogeneity. IEEE Trans. Cybern 46, 546–557. doi:10.1109/TCYB.2015.2409119

PubMed Abstract | CrossRef Full Text | Google Scholar