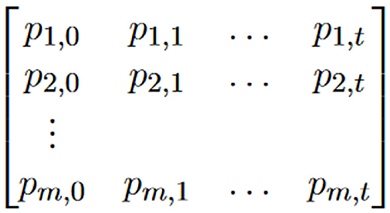- Department of Computer Engineering, Çankaya University, Ankara, Türkiye
A password hashing algorithm is a cryptographic method that transforms passwords into a secure and irreversible format. It is used not only for authentication purposes but also for key derivation mechanisms. The primary purpose of password hashing is to enhance the security of user credentials by preventing the exposure of plaintext passwords in the event of a data breach. As a key derivation function, password hashing aims to derive secret keys from a master key, password, or passphrase using a pseudorandom function. This review focuses on the design and analysis of time-memory trade-off (TMTO) attacks on recent password hashing algorithms. This review presents a comprehensive survey of TMTO attacks and recent studies on password hashing for authentication by examining the literature. The study provides valuable insights and strategies for safely navigating transitions, emphasizing the importance of a systematic approach and thorough testing to mitigate risk. The purpose of this paper is to provide guidance to developers and administrators on how to update cryptographic practices in response to evolving security standards and threats.
1 Introduction
In the field of information security, password hashing plays a central role and serves two main purposes: to obfuscate passwords in databases and to act as a password-based key derivation function (KDF). Unfortunately, passwords chosen by users are usually short and lack sufficient entropy (Shannon, 1951; Burr et al., 2013). As a result, these systems are often compromised by adversaries who then use generic attacks due to the relatively low entropy of passwords. Generic attacks treat the password hash function as a black box entity and are not interested in the inner workings of the method. Examples of such attacks include exhaustive search, dictionary tables, and time-memory trade-off techniques. Since the effectiveness of these attacks depends on both time and memory requirements, security experts strive to make such attacks infeasible by increasing the resource overhead. In password hashing, there are also important attacks such as side-channels; especially when password hashing is used for authentication, we may not be concerned about such attacks.
One way to protect against common types of attacks is to hash passwords with salt. This approach achieves a dual purpose: first, it prevents the identification of identical passwords across different users and services, and second, it increases the memory requirements, thereby extending the time required for an attacker's efforts (Ghoshal and Tessaro, 2023). However, in order to increase the cost of password checking for potential attackers, there's been a trend to use faster hash functions in multiple iterations of calculations. Since the simple use of secure hash functions is not sufficient either, specialized password hashing schemes (PHS) are proposed, such as PBKDF2 (Kaliski, 2000), Bcrypt (Provos and Mazieres, 1999), and Scrypt (Percival, 2009).
Advances in specialized hardware devices and parallel computing have made password cracking computationally practical. Attacks using ASICs, FPGAs, and GPUs now have a significant advantage in revealing user information by testing large numbers of potential passwords simultaneously (Dürmuth et al., 2012; Abbas et al., 2014; Malvoni et al., 2014). For example, PBKDF2 is vulnerable to GPU attacks because it uses a relatively small amount of RAM, allowing efficient implementation on GPUs (Ruddick and Yan, 2016a).
Then Bcrypt was introduced in 1999 to provide protection against GPU/ASIC/FPGA attacks, but the memory usage is still fixed. In 2009, Scrypt was introduced, which requires a significant amount of memory (RAM), making it unsuitable for fast parallel processing on GPU or ASIC hardware. The computational process relies on memory, with memory access being the limiting factor in the computations; it allows tuning of both time-based and memory-based security parameters. However, it has been criticized for allowing a time-memory trade-off, as faster access to RAM can speed up the computation.1 Another problem with the scrypt is its complicated nature; it calls a number of subroutines, and the reasoning behind its design has not been fully justified. As of August 2016, it is officially standardized in RFC 7914.
The Password Hashing Competition was launched in 2013 with the aim of discovering new password hashing methods to improve the current state-of-the-art (Peslyak, 2014). Argon2 (Biryukov et al., 2015) was the winner of the competition in July 2015, with special recognition given to Catena (Forler et al., 2013), Lyra2 (Simplicio et al., 2015), yescrypt (Peslyak, 2014), and Makwa (Pornin, 2015). The Balloon is also a memory-hard password-hashing function (Boneh et al., 2016). The authors also show that scrypt and Argon2i are memory-hard password-hashing functions in the random-oracle model, and prove that they are secure against dictionary attacks.
The focus of this review is to analyze the structure and evaluation of generic attacks targeted at modern password hashing algorithms. This review provides a comprehensive survey of Time-Memory Trade-Off (TMTO) attacks and recent advancements in password hashing for authentication by examining existing literature. The study offers valuable insights and methodologies for securely managing transitions in hashing schemes. It emphasizes the importance of a systematic approach and extensive testing to minimize risks associated with these transitions. The following sections are organized as follows: Section 2 provides essential background knowledge and reviews relevant existing work. Section 3 analyzes recent password hashing schemes, and Section 4 assesses default hashing schemes through a memory-time analysis. Section 5 analyzes the issue from a practical standpoint, and presents the conclusions.
2 TMTO attacks
Generic attacks treat the encryption function as a black box without going into details of its structure. Their focus is not on unraveling the complexities of the encryption function. Common examples of attacks include methods such as exhaustive search, lookup table methods, and time-memory trade-offs.
2.1 Exhaustive search attacks
Exhaustive search attacks represent an approach to uncover a pre-image of a one-way function (Knudsen et al., 2011). This attack strategy involves systematically testing all potential keys to identify the correct one. In the context of a PHS, a malicious actor who gains unauthorized access to a server and acquires a file containing hashed passwords can employ an exhaustive search attack to uncover certain user passwords by trying all possible password combinations based on two parameters: the password length and the character set. Although a brute-force attempt across the entire password space is certain to retrieve the password, it is often impractical due to limitations in time and memory.
2.2 Lookup table attacks
A lookup table replaces the real-time calculation process by creating a simple table that includes all possible results and their corresponding inputs. This approach offers an alternative way to reverse a one-way function, but it requires extensive memory resources. An attacker can directly look up the hash in the table to find a match.
Dictionary attacks systematically test all possible character combinations on a specific set of frequently used passwords, words, or phrases.2 Unlike lookup table attacks, which only target specific passwords, dictionary attacks are more comprehensive and can be more effective. It is important to use strong, unique passwords to protect against these types of attacks since the attacker uses a predefined dictionary of words and their variations to guess the correct password. Pre-defined mangling rules using probabilistic context-free grammars (Weir et al., 2009) may be recommended as a precaution. However, Kelley et al. (2012) have shown that one billion guesses are enough to crack 40.3% of passwords with at least eight characters. Bošnjak et al. (2018) demonstrate the ability to crack most user-created passwords using simple and predictable patterns in a Slovenian university's online grading system.
2.3 Hellman's attack
Time Memory Trade-Off (TMTO) attack is a strategy that combines exhaustive search and lookup table methods, proposed by Hellman (1980). The objective of this approach is to execute an attack with lower memory complexity compared to a lookup table and lower online time complexity compared to exhaustive searching. In essence, the attack can be summarized as follows:
Consider a one-way function f : {0, 1}n → {0, 1}n. For the sake of simplicity, this function is considered as a hash function, we assume that both x and f(x) are chosen from the same set:
• The attacker creates a table of size M and can generate tables within a given (offline) time, P.
• Given a target point c0 ∈ X, using the prepared table, the attacker searches for x ∈ X such that f(x) = c0 within a specified time, T, among the values stored in the table.
There are primarily two phases involved in TMTO: the offline (precomputation) phase and the online phase. In the first phase, referred to as the Precomputation/Offline Phase, a table is generated similar to the lookup table method, but only a subset of the table data is retained. In the second phase, the Online Phase, when presented with a specific point, the preimage is sought within the previously calculated table. The pre-computation time, denoted as P, remains comparable to exhaustive searching. The compromise lies between M and T, where M signifies memory complexity, and T represents online time complexity.
The construction of a Hellman table typically follows two main phases (precomputation and online phases). The precomputation phase has two steps; precomputation and storage. The Online phase has one step; retrieval.
Precomputation steps: Starting from a set of plaintext, pi,0, 1 ≤ i ≤ m, the cryptanalyst recursively computes (t times) the corresponding value using the relevant cryptographic hash function
where 1 ≤ j ≤ t. The cryptanalyst chooses parameters m and t to find an equilibrium between time and memory considerations in the analysis. In each entry of a table, Hellman recognizes to use a reduction function that maps hash values back to the potential plaintext space.
Storage steps: a sorted table is constructed based on available memory constraints and sorted; the pairs of plaintext, pi,0 and resulting hash values, pi,t as the result of this phase. Retrieval step: during the online phase, the attacker can use the precomputed table to look up hash values and find corresponding plaintexts. If a hash value of the attacker's plaintext is in the table, either the searched value or it has more than one inverse; it is referred to as a false alarm.
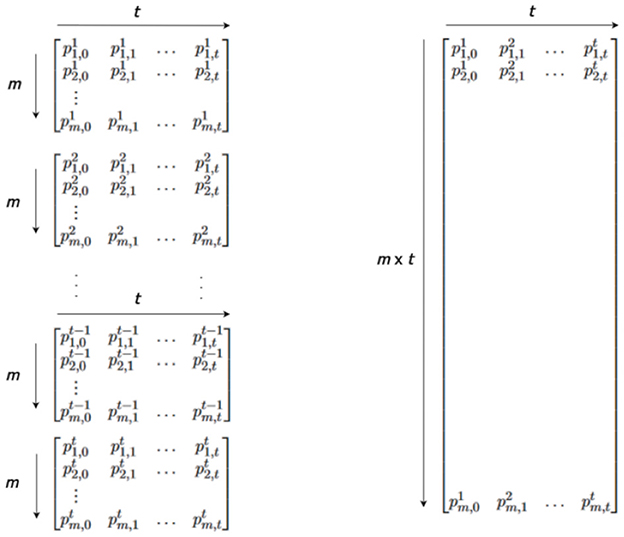
When utilizing the Hellman tables method, the relevant parameters include the chain length (t), the number of chains (m), and the number of tables (r). As in Figure 1, there are r tables with different reduction functions. Memory complexity represents the memory needed for storing pre-computed data, expressed as M = 2 * m * r * m0, where M is the memory amount, and m0 is the memory required for storing start and end points (usually omitted). Time complexity, crucial for successful attacks, is compared to exhaustive key searches and is divided into precomputation and online time complexities in time-memory trade-offs. The worst-case time required in the online phase is T = t * r * t0, where T is the time complexity, and t0 is the time needed to evaluate the function (generally omitted). False alarms are not taken into account. The time complexity in the precomputation phase is given by P = m * t * r, but it is typically excluded from the overall attack complexity. For a N bit cryptosystem, TMTO recovers each key T = N2/3 operational with M = N2/3 words of memory (average values) after a precomputation which requires P = N operations. Hellman recommends employing various tables (l ≈ t) with distinct masking functions to reduce the occurrence of repetitions. Different masking functions will exhibit diverse cycle structures for random mapping (Sönmez Turan et al., 2008; Saran, 2009).
Cryptanalytic Time Memory Data Tradeoffs (TMDTO) is a variant that accepts D inversion problems and has to be successful in at least one of them. The presence of multiple data enhances the efficiency of the attack (Babbage, 1995). Golić (1997) examines this scenario and refers to it as “one out of many keys.” Multiple data TMTO has also been studied in several papers (Biryukov and Shamir, 2000; Hong and Sarkar, 2005a; Dunkelman and Keller, 2008). This situation typically occurs in stream ciphers, where it is adequate to reverse the function that links an internal state to the produced output. Biryukov (2005) also considers a chosen plaintext scenario where a single message is encrypted with many keys, and the resulting ciphertexts are accessible to the attacker. It is shown that most of block cipher modes of operations are vulnerable to TMDTO (Hong and Sarkar, 2005b). There are two main improvements of TMTO method; Distinguished Method and Rainbow Method.
2.4 Distinguished method
In 1982, Rivest suggested using distinguished points as endpoints to minimize the frequency of memory accesses, particularly when dealing with large tables that incur high memory access costs (accessing data on disk can be significantly slower compared to the evaluation of the function f). Instead of generating a fixed chain length, the iteration of the chain continues until an endpoint meeting specific criteria is identified. He suggested using distinguished points to reduce the number of disk accesses to about . This concept has been extensively investigated in Quisquater and Delescaille (1990), Borst (2001), Standaert et al. (2003), and Mentens et al. (2006).
Distinguished points (DP) refer to specific range points that meet defined criteria, like having all last d bits set to zero. These points reduce memory access during the online phase, as a search is conducted only when the end point (or its iterations) constitutes a distinguished point.
Notably, a chain may enter an infinite loop without distinguished points, and may not produce a DPi as in Figure 2. Only endpoints that encounter a DP in fewer than t iterations are preserved, while others are discarded. Chains are created until a distinguished point is encountered. The chain is discarded if a DP is not reached within tmax iterations. Additionally, if the chain length is below a threshold, for instance, tmin, it is also discarded. In cases where the same DP appears in different chains, the tuple with the maximum chain length is retained (since merged chains share the same endpoint) (Borst et al., 1998; Borst, 2001). Storing the length of each precomputation chain in the DP table can address this issue; however, this enlarges the size of the precomputation table. During the online phase, when presented with an initial message digest, keys will be generated iteratively until a distinguished point is encountered. Only at that point will a memory lookup be performed. This significantly decreases the overall number of memory lookups. The Perfect Table, as described in Borst et al. (1998), represents a modification of the distinguished points (DP) table. In this variant, certain redundancies in the precomputed tables are eliminated and substituted with nonoverlapping data obtained through supplementary precomputation. In the precomputation stage, chain collisions are resolved by retaining only the longest chain among those that merge. Additional chains are created until a total of m non-merging DP chains are gathered. The resultant perfect DP matrix ensures there are no overlapping points. The online phase of the perfect DP tradeoff remains unchanged compared to the non-perfect version.
The advantages of distinguished points are outlined in Oechslin (2003) as follows:
• Reduced table lookups: the tables are searched during the online phase when only a distinguished point (DP) is encountered. This results in a reduction of table lookups by a factor of 2d.
• Loop freeness: if no distinguished point is encountered within tmax iterations, the chain is considered to contain a cycle potentially and is subsequently discarded. This ensures that the tables are free from loops.
• Merge freeness: in perfect DP tables, chains with identical endpoints are discarded. As a result, merges are avoided without incurring additional costs, especially since the tables are sorted.
2.5 Rainbow tables
A variant time/memory tradeoff scheme was suggested by Oechslin (2003). Instead of creating r tables with distinct reduction functions, Oechslin suggests the creation of new tables known as rainbow tables. These tables employ a consecutive reduction function for each column in the chain, with a total of t reduction functions as Figure 3. It claims to save a factor 2 in the worst-case time complexity compared to Hellman's original scheme. The overall number of computations is expressed as , compared to rt in the conventional method.
The advantages of rainbow tables are outlined in Oechslin (2003) as follows:
• Collision handling: if two chains collide, they only merge if the collision occurs in the same column. If the collision happens at different columns, they continue with varying reduction functions and do not merge. Merges, which would lead to identical endpoints, are discarded in Perfect Rainbow Tables. It's important to note that discarding identical endpoints in Rainbow tables could increase precomputation compared to distinguished points. This is because, in DP tables, there are t tables, but in rainbow tables, identical points accumulate within one table, potentially resulting in extensive precomputation.
• Loop freeness: rainbow tables inherently avoid loops since each column employs different reduction functions.
• Constant chain length: rainbow chains maintain a constant length, contributing to a reduction in false alarms.
Creating tables without merges reduces table coverage. However, opting for merge-free tables presents a trade-off, as it raises precomputation time (Avoine et al., 2005). Ideally, perfect tables are those where merges are infrequent. Rainbow and DP tables share the characteristic of having identical endpoints in merging chains. The process involves generating more chains initially and subsequently discarding chains with matching endpoints. This disposal of chains contributes to an increase in precomputation time. Avoine et al. proposed using checkpoints to rule out false alarms using little additional memory (on some intermediate points of a chain) without regenerating the pre-computed chain for rainbow tables. In the online phase, the attacker recreates the pre-computed chain only if there is a match in both the ending point and the checkpoints.
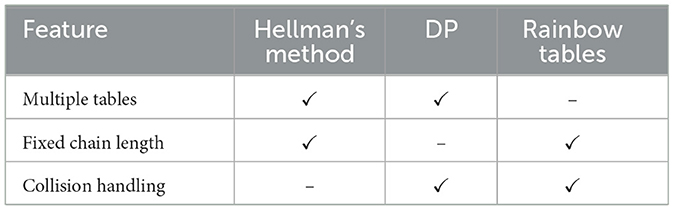
In recent years, Avoine et al. have proposed two new methods: distributed filtration-computation and stepped rainbows. In the first, Avoine et al. (2021) introduce a distributed method and filter the results to optimize the precomputation phase of generating rainbow tables. Distribution process spreads the precomputation workload across multiple computing units and filtration process involves identifying and eliminating unnecessary or redundant computations where they demonstrate a significant reduction in precomputation time, reportedly up to six times faster in tested scenarios. In the following, Avoine et al. (2023) use a process of recycling discarded values where they utilize values that are typically discarded in traditional rainbow table construction in order to reduce substantial workload in both precomputation and attack phases. The comparison of these types of trade off algorithms may be listed as in Table 1.
Note that the DP table doesn't have fixed chain length, on the other hand, the Perfect DP table is designed with the objective of achieving chain lengths that are either fixed or exhibit a more consistent distribution.
3 Password hashing algorithms
Password hashing is a crucial aspect of authentication systems designed to generate a cryptographic key from a password. These algorithms find widespread use in various security and authentication applications, enhancing user credentials' security. In this section, the password is considered as the input of a one-way function (password hashing function), and the password hash is identified as the image (output) of the function.
User registration: When a user creates an account or updates their password, the authentication system generates (a random) value called a salt. Using a unique salt for each user and combining it with the user's password is recommended. Employing deterministic or easily predictable salts can subject the system to undermine the security advantages associated with the randomness of salts.
Hashing process and storing: The system combines the user's password and the salt and then utilizes a cryptographic hash function (such as SHA, PBKDF2, bcrypt) on the resulting string. The outcome of this procedure is the hashed password—a string of characters with a fixed length that seems random. The system stores the fixed-length hashed password and its associated salt in its database without keeping the original password. In a data breach, hashed passwords provide a greater resistance to attacks compared to the storage of plaintext passwords.
Authentication: When a user attempts to log in, the system retrieves the stored salt associated with that user and combines it with the entered password, then hashes this combination and compares it to the stored hashed password. The user is granted access if the generated hash matches the stored hash.
Recent schemes incorporate techniques like multiple iterations of the hash function to enhance security further, making it computationally expensive and time-consuming for attackers to use TMTO attacks.
3.1 PBKDF2
Password-based key derivation function (PBKDF) is a cryptographic algorithm designed to derive a cryptographic key from a password. PBKDF2 employs a pseudorandom function, like a hash-based message authentication code (HMAC), on the provided password or passphrase along with a salt value. This process is iterated numerous times to generate a derived key, serving as a cryptographic key for subsequent operations as seen in Figure 4. The number of iterations, N, used in PBKDF is typically a parameter that can be adjusted based on the desired level of security and the computational resources available.
It is also used to derive cryptographic keys from passwords for secure communication in protocols like SRP (Secure Remote Password) or SSL/TLS handshake. It also has a wide range of usability in file /disk encryption systems TrueCrypt3/VeraCrypt4 where a user's password needs to be transformed into an encryption key. PBKDF2 is still widely used in many security-related systems such as WPA/WPA2 encryption process (IEEE Std 802.11-2007, 2007), Linux Unified Key Setup (LUKS1),5 OpenOffice, and many others.
PBKDF2 (Moriarty et al., 2017) can be implemented with a very small amount of RAM for temporary intermediate values, making it preferable in small devices to memory-hard password hashing options (Weatherley, 2023). In some applications such as Bitwarden,6 a popular password manager, email addresses are proposed to be used as salt since each user has a unique email address, even if they use the same password. The attacker would need to attack each hash individually, significantly increasing the time and resources required where precomputed tables of hashed passwords are used to crack passwords.
PBKDF2 is designed to resist TMTO attacks due to iterative hashing, salt usage, tunable work factor, and some memory requirements. In Ruddick and Yan (2016b), the authors focus on accelerating attacks on PBKDF2 using GPUs. The efficiency of attack is not only due to parallel hardware architectures but also through effective algorithmic optimizations. The paper's implications are crucial for understanding PBKDF2's vulnerability in security systems like Microsoft .NET framework and WiFi Protected Access (WPA2). The choice of the hash function in PBKDF2 impacts its security (Li et al., 2015; Visconti et al., 2015; Kodwani et al., 2021). Visconti et al. (2019) investigate the expenses related to breaching PBKDF2's defenses, considering elements like the complexity of passwords, the cost of electricity, and the efficiency of different hardware setups. It further examines how system configurations, such as 32-bit versus 64-bit systems and the choice of cryptographic backends, can influence the number of iterations required in PBKDF2, affecting its overall security efficiency. Using multiple FPGAs, they managed to process 250,000 passwords per second at 2,000 iterations (Abbas et al., 2014), and another study achieved a rate of 356,352 passwords per second with 1,000 iterations (Dürmuth et al., 2012).
When the standard7 was written in the 2000s, the recommended minimum iteration count was 1,000. However, the parameter is intended to be increased over time as CPU speeds increase. National Institute of Standards and Technology (NIST) (2010) suggests that it is a good practice to select the iteration count as large as possible. As of 2023, OWASP8 recommends 600,000 iterations for PBKDF2-HMAC-SHA256 and 210,000 iterations for PBKDF2-HMAC-SHA512, 1,300,000 iterations for PBKDF2 with SHA-1.
3.2 bcrypt and scrypt
bcrypt9 is a password hashing function developed by Provos and Mazieres (1999), based on the Blowfish cipher. It incorporates a salt to defend against rainbow table attacks. It is adaptive, meaning its iteration count can be increased over time to maintain resistance against TMTO attacks, even as computational power increases. bcrypt is notable for its “expensive key setup” phase, which makes it slower and thus more secure against generic attacks. The bcrypt algorithm serves as the standard password hashing method for OpenBSD and default as of PHP 5.5.0,10 and it was previously the primary choice for several Linux distributions, including SUSE Linux. Its vulnerability to Time-Memory Trade-Off attacks is partly due to its lower memory requirements in contrast to its computational demands. Attackers might leverage increased processing power to offset this lower memory usage, which can heighten bcrypt's susceptibility to these attacks. This contrasts with algorithms that need substantial memory resources, where simply boosting computational power is a less effective strategy.
scrypt, created by Colin Percival in 2009, is a password-based key derivation function that requires large amounts of memory to thwart large-scale custom hardware attacks. It is published by IETF as RFC 7914 (Percival and Josefsson, 2016). Its high memory requirement makes hardware implementations costly, limiting the parallelism an attacker can use. Scrypt's algorithm generates a significant vector of pseudorandom bit strings, accessed pseudo-randomly, and combined to produce the derived key. This process demands significant memory if all elements are stored simultaneously, creating a trade-off between time and memory usage. However, scrypt is also criticized for its ability to adjust the trade-off between time and memory since its flexibility allows for constant memory consumption while varying the computation required.11 Scrypt has been adopted in several cryptocurrencies as a proof-of-work algorithm.
3.3 Argon2
Argon2, developed by Alex Biryukov, Daniel Dinu, and Dmitry Khovratovich, crowned as the winner of the Password Hashing Competition in 2015 (Biryukov et al., 2016). It is a key derivation function with three versions: Argon2d, Argon2i, and Argon2id. Argon2d is resistant to GPU cracking attacks, Argon2i is optimized against side-channel attacks, and Argon2id is a hybrid of both, recommended for general use. It's notable for its customizable parameters controlling execution time, memory requirements, and parallelism, which makes it adaptable and secure against various attack methods, including time-memory trade-off attacks.
3.4 Balloon
Balloon is a memory-hard key derivation function that was developed by Boneh et al. (2016). It is intended to use a substantial amount of memory in addition to CPU resources. In other words, it is resistant to attacks that leverage hardware-based optimizations, such as those that use GPUs or customized hardware, which generally have lower memory and bandwidth capacities than general-purpose CPUs. The hashing algorithm is known for its established memory-hardness characteristics that protect it from time-memory trade-off (TMTO) attacks. A password-independent access pattern is used to achieve this security feature, meaning that the order in which memory accesses (reads and writes) occur throughout the hashing process is independent of the password. Rather, it is dependent upon the results of previous hashing steps. After initializing a buffer with a mix of the password, salt, and other inputs, the algorithm repeatedly mixes the contents of this buffer in a complex way. This aspect of the algorithm is designed to enhance its resistance to side-channel attacks.
4 Analysis of rainbow tables efficacy in password hashing schemes
A typical password hash is usually a sequence of at least 128 bits. PBKDF2 depends on the underlying hash function being used, for bcrypt it typically produces 184 bits (23 bytes), for scrypt it is configurable, usually 256 bits, for Argon2 it is configurable, usually 256 bits, for Balloon configurable may vary depending on implementation. Note that the total number of 10-character alphanumeric passwords is about 6210. That's about 259.54. A hash function H(x) derived from a password x will, in most cases, uniquely identify x on its own. However, human-generated passwords are not evenly distributed over the entire possible password space. Attackers typically focus on a smaller, more manageable subset of passwords, called |P|, which is part of the total set of possible passwords. The size of this subset is determined by the attacker's available computational resources for precomputation and is generally targeted to include the most commonly used passwords since the set of password hashes |H| is much larger than the considered password set |P|. Since TMTOs use reduction functions R:H → P, and the online phase algorithm works with the colored iteration functions Hk = Rk ∘ H:P → P for k − th table (Hong and Moon, 2013). Rainbow table with k different reduction functions to compute the chains is only applicable to password hashing schemes that do not consider salt as an input with a password.
Chang et al. examine Argon2i, Catena, and Rig, which participated in the Password Hashing Competition. The authors give a generic algorithm for traversing the directed acyclic graph (DAG) that allows for variation in memory, and compute the increased algorithmic runtime (recomputation penalties) for various trade-off options (varying memory and time). They highlight the shortcomings of Argon2i in achieving its stated memory hardness goals. The research provides valuable perspectives on the resilience and efficiency of password hashing schemes considering different time and memory resource allocation scenarios (Chang et al., 2019).
The prevailing belief is that adding salt can counteract preprocessing attacks. Indeed, recent research has examined the security of random oracles when additional information is available, and to some extent confirmed the benefits of using salts (Unruh, 2007; Coretti et al., 2018). However, these studies have limitations, especially in the context of password hashing, since they tend to focus on securing only one password. On the other hand, Bellare et al. (2012) emphasize that multi-instance security metrics should be considered when analyzing the security of password hashing. This is crucial to ensure that the complexity of cracking passwords escalates with the number of passwords targeted (Farshim and Tessaro, 2021).
Some systems store passwords in the database using honeywords or fake passwords associated with each user's account to prevent attacks12 using graphical-processing unit (GPU). Their approach involves a specialized secure server called a “honeychecker,” which identifies the legitimate password from a set of honeywords. This system triggers an immediate alert if a honeyword is used, enhancing security measures against unauthorized access. However, there are two problems with these systems: the typo safety problem and the storage overhead problem. In Genç et al. (2018), the authors introduce an enhanced honeywords system that is generating typo-safe honeywords and managing old passwords which may be a solution to the active attacks problem.
5 Discussion
Password Hashes Schemes (PHS) are used in a variety of areas, including but not limited to web applications and database applications. PHS are also used in network access protocols, cloud services, and any system where user authentication is critical. This section examines the complexities and inherent risks associated with switching from one password-hashing algorithm to another. Compatibility issues, security/performance implications, and potential vulnerabilities introduced during the migration process are among the many challenges facing developers. Migrating to a new password hashing scheme can introduce several potential vulnerabilities, especially if not managed properly. Special attention should be paid to the impact of these challenges on user data integrity and application security during system maintenance. Poor password management practices are exploited by attackers who expose user credentials, harming both users and vendors. Here's a list of some key issues to consider:
5.1 Security/performance implications
Selecting appropriate algorithms and regularly updating them is crucial, but it can also present challenges. Developers must choose a hash function that is currently considered secure, such as SHA-3 or Argon2, instead of weaker ones like MD5 or SHA-1, which have known vulnerabilities. It is important to stay informed about the latest developments in cryptographic practices and update algorithms. However, in resource-constrained environments, such as those with limited computing power, memory, or energy efficiency, there may be a trade-off between security and performance. For instance, PBKDF2 is less memory-intensive compared to bcrypt or Argon2. However, Argon2 is designed to be resistant to a wide range of attacks, although it can be more demanding in terms of resources compared to PBKDF2 and bcrypt. Furthermore, algorithms have parameters that require optimization. For example, optimizing parameters in Argon2 is essential to achieve a balance between resource utilization and overall performance. This process involves selecting the optimal variant of Argon2, determining the appropriate lengths of salt and tag, and adjusting the parameters of time, memory, and parallelism. This optimization aims to use resources efficiently while maintaining performance within acceptable limits.
5.2 Compatibility issues
In the realm of information technology and cybersecurity, compatibility refers to the ability of different systems, software, or components to operate smoothly with each other without problems. This includes the smooth integration and operation of both software and hardware components, compliance with common protocols or standards, and the effective exchange and accurate interpretation of data. When migrating to a new standard in PHS, many compatibility issues can arise. For example, to use the Argon2id hashing algorithm in PHP, the PHP installation must include Argon2 support. If the current PHP setup lacks this integration, this requirement may pose a challenge. To address this issue, one may need to recompile PHP with Argon2 support or seek out a hosting solution that offers a PHP build with Argon2 support. Such adjustments can require additional configuration effort, especially in scenarios where developers have limited control over the PHP environment (see text footnote10). Moreover, Argon2 may produce longer hashes, necessitating changes in database schema to accommodate larger hash values.
5.3 Migration process
Transitioning from a less secure and less demanding algorithm such as MD5 to a more secure yet more resource-intensive one like bcrypt can greatly affect the system's performance, particularly in environments with a high frequency of authentication requests. Handling an excessive number of passwords simultaneously on the server could lead to performance issues similar to those experienced during a Distributed Denial of Service (DDoS) attack. As direct access to plaintext passwords is not possible, a common strategy is to re-hash passwords when users log in next. However, this approach requires all users to log in again, which may not be practical or user-friendly. Furthermore, extensive testing is necessary to ensure that the new hashing system functions properly with all components of the system.
The ongoing research in this domain continues to balance the computational and memory resources, optimizing the success rate of these cryptographic attacks. Comparative analyses have shown the resilience of popular hashing algorithms such as PBKDF2, bcrypt, Argon2, and Balloon against TMTO attacks. The results suggest that Argon2 and Balloon are more resilient due to their memory-intensive properties. PBKDF2 is inefficient; it requires high iteration counts to be secure. In other words, it's slow for the defender and fast for the attacker.13
Author contributions
AS: Conceptualization, Formal analysis, Investigation, Methodology, Project administration, Resources, Visualization, Writing—original draft, Writing—review & editing.
Funding
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Footnotes
1. ^https://www.drupal.org/node/1201444#comment-4675994
2. ^https://cryptokait.com/2020/09/02/taking-password-cracking-to-the-next-level/
3. ^TrueCrypt—Free Open-Source On-the-fly Encryption: http://www.truecrypt.org.
4. ^VeraCrypt—Free Open-Source On-the-fly Encryption based on TrueCrypt https://www.veracrypt.fr/.
5. ^https://en.wikipedia.org/wiki/Linux_Unified_Key_Setup
6. ^https://www.ghacks.net/2023/02/02/bitwarden-to-increase-its-server-side-iterations-to-600000-heres-how-to-set-it-manually/
7. ^PKCS #5 v2.0, also published as Internet Engineering Task Force's RFC 2898.
8. ^OWASP- Password Storage Cheat Sheet https://cheatsheetseries.owasp.org/cheatsheets/Password_Storage_Cheat_Sheet.html.
9. ^https://en.wikipedia.org/wiki/Bcrypt
10. ^https://php.net/manual/en/function.password-hash.php
11. ^https://mail.tarsnap.com/scrypt/msg00029.html
References
Abbas, A., Voss, R., Wienbrandt, L., and Schimmler, M. (2014). “An efficient implementation of PBKDF2 with RIPEMD-160 on multiple FPGAs,” in Proceedings of the 20th IEEE International Conference on Parallel and Distributed Systems (ICPADS) (Hsinchu), 454–461. doi: 10.1109/PADSW.2014.7097841
Avoine, G., Carpent, X., and Leblanc-Albarel, D. (2021). “Precomputation for rainbow tables has never been so fast,” in Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), Volume 12973, eds E. Bertino, H. Shulman, and M. Waidner (Cham: Springer). 215–234. doi: 10.1007/978-3-030-88428-4_11
Avoine, G., Carpent, X., and Leblanc-Albarel, D. (2023). “Stairway to rainbow,” in Proceedings of the 2023 ACM Asia Conference on Computer and Communications Security (New York, NY: ACM), 286–299. doi: 10.1145/3579856.3582825
Avoine, G., Junod, P., and Oechslin, P. (2005). “Time-memory trade-offs: False alarm detection using checkpoints,” in Progress in Cryptology - INDOCRYPT 2005, eds S. Maitra, C. E. Veni Madhavan, and R. Venkatesan (Berlin: Springer Berlin Heidelberg), 183–196. doi: 10.1007/11596219_15
Babbage, S. (1995). “Improved “exhaustive search” attacks on stream ciphers,” in European Convention on Security and Detection (Brighton: IEEE), 161–166. doi: 10.1049/cp:19950490
Bellare, M., Ristenpart, T., and Tessaro, S. (2012). “Multi-instance security and its application to password-based cryptography,” in Annual Cryptology Conference (Cham: Springer), 312–329. doi: 10.1007/978-3-642-32009-5_19
Biryukov, A. (2005). Some Thoughts on Time-Memory-data Tradeoffs. Cryptology ePrint Archive, Paper 2005/207. Available online at: https://eprint.iacr.org/2005/207 (accessed February 19, 2024).
Biryukov, A., Dinu, D., and Khovratovich, D. (2015). Argon2 (version 1, 2.). Technical Report. Luxembourg: University of Luxembourg.
Biryukov, A., Dinu, D., and Khovratovich, D. (2016). “Argon2: new generation of memory-hard functions for password hashing and other applications,” in 2016 IEEE European Symposium on Security and Privacy (EuroS&P) (Saarbruecken: IEEE), 292–302. doi: 10.1109/EuroSP.2016.31
Biryukov, A., and Shamir, A. (2000). “Cryptanalytic time/memory/data tradeoffs for stream ciphers,” in Advances in Cryptology – ASIACRYPT 2000, ed. T. Okamoto (Berlin: Springer Berlin Heidelberg), 1–13. doi: 10.1007/3-540-44448-3_1
Boneh, D., Corrigan-Gibbs, H., and Schechter, S. (2016). Balloon Hashing: A Memory-Hard Function Providing Provable Protection Against Sequential Attacks. Technical Report 2016/027, Cryptology ePrint Archive. Berlin. doi: 10.1007/978-3-662-53887-6_8
Borst, J. (2001). Block Ciphers: Design, Analysis and Side-channel Analysis [PhD thesis]. Belgium: Dept. Elektrotechniek, Katholieke Universiteit Leuven.
Borst, J., Preneel, B., and Vandewalle, J. (1998). “On the time-memory tradeoff between exhaustive key search and table precomputation,” in Symposium on Information Theory in the Benelux (Delft: Technische Universiteit Delft), 111–118.
Bošnjak, L., Sreš, J., and Brumen, B. (2018). “Brute-force and dictionary attack on hashed real-world passwords,” in 2018 41st International Convention on Information and Communication Technology, Electronics and Microelectronics (Mipro) (Opatija: IEEE), 1161–1166. doi: 10.23919/MIPRO.2018.8400211
Burr, W., Dodson, D., Newton, E., Perlner, R., Polk, W., Gupta, S., et al. (2013). SP 800-63-2. Electronic Authentication Guideline. Technical Report. Gaithersburg, MD: The U.S. National Institute of Standards and Technology. doi: 10.6028/NIST.SP.800-63-2
Chang, D., Jati, A., Mishra, S., and Sanadhya, S. K. (2019). Cryptanalytic time-memory trade-off for password hashing schemes. Int. J. Inf. Secur. 18, 163–180. doi: 10.1007/s10207-018-0405-5
Coretti, S., Dodis, Y., Guo, S., and Steinberger, J. (2018). “Random oracles and non-uniformity,” in Annual International Conference on the Theory and Applications of Cryptographic Techniques (Berlin: Springer), 227–258. doi: 10.1007/978-3-319-78381-9_9
Dunkelman, O., and Keller, N. (2008). Treatment of the Initial Value in Time-Memory-Data Tradeoff Attacks on Stream Ciphers. Cryptology ePrint Archive, Paper 2008/311. Available online at: https://eprint.iacr.org/2008/311 (accessed February 19, 2024).
Dürmuth, M., Güneysu, T., Kasper, M., Paar, C., Yalcin, T., and Zimmermann, R. (2012). “Evaluation of standardized password-based key derivation against parallel processing platforms,” in Computer Security-ESORICS 2012, 17th European Symposium on Research in Computer Security, Pisa, Italy, September 10-12, 2012. Proceedings 17 (Cham: Springer), 716–733. doi: 10.1007/978-3-642-33167-1_41
Farshim, P., and Tessaro, S. (2021). “Password hashing and preprocessing,” in Annual International Conference on the Theory and Applications of Cryptographic Techniques (Cham: Springer), 64–91. doi: 10.1007/978-3-030-77886-6_3
Forler, C., Lucks, S., and Wenzel, J. (2013). Catena: A Memory-Consuming Password-Scrambling Framework. Technical Report 2013/525, Cryptology ePrint Archive. Available online at: http://eprint.iacr.org/ (accessed February 19, 2024).
Genç, Z. A., Kardaş, S., and Kiraz, M. S. (2018). “Examination of a new defense mechanism: honeywords,” in Information Security Theory and Practice, eds G. P. Hancke, and E. Damiani (Cham: Springer International Publishing), 130–139. doi: 10.1007/978-3-319-93524-9_8
Ghoshal, A., and Tessaro, S. (2023). The Query-Complexity of Preprocessing Attacks. Technical report. Santa Barbara, CA. doi: 10.1007/978-3-031-38545-2_16
Golić, J. D. (1997). “Cryptanalysis of alleged a5 stream cipher,” in Advances in Cryptology – EUROCRYPT '97, ed. W. Fumy (Berlin: Springer Berlin Heidelberg), 239–255. doi: 10.1007/3-540-69053-0_17
Hellman, M. (1980). A cryptanalytic time-memory trade-off. IEEE Trans. Inf. Theory 26, 401–406. doi: 10.1109/TIT.1980.1056220
Hong, J., and Moon, S. (2013). A comparison of cryptanalytic tradeoff algorithms. J. Cryptol. 26, 559–637. doi: 10.1007/s00145-012-9128-3
Hong, J., and Sarkar, P. (2005a). “New applications of time memory data tradeoffs,” in Advances in Cryptology - ASIACRYPT 2005, ed. B. Roy (Berlin: Springer Berlin Heidelberg), 353–372. doi: 10.1007/11593447_19
Hong, J., and Sarkar, P. (2005b). Rediscovery of Time Memory Tradeoffs. Cryptology ePrint Archive, Paper 2005/090. Available online at: https://eprint.iacr.org/2005/090 (accessed February 19, 2024).
IEEE Std 802.11-2007 (2007). IEEE Standard for Information Technology Telecommunications and Information Exchange Between Systems Local, and Metropolitan Area Networks-Specific Requirements Part 11: (IEEE Std 802.11-2007 (Revision of IEEE Std 802.11-1999)), Vol. 12. Wireless LAN medium access control (mac) and physical layer (phy) specifications, CI-1184. Available online at: https://standards.ieee.org/ieee/802.11/3605/ (accessed February 19, 2024).
Kaliski, B. (2000). RFC 2898—PKCS #5: Password-based Cryptography Specification Version 2.0. Technical report. Fremont, CA: IETF. doi: 10.17487/rfc2898
Kelley, P. G., Komanduri, S., Mazurek, M. L., Shay, R., Vidas, T., Bauer, L., et al. (2012). “Guess again (and again and again): measuring password strength by simulating password-cracking algorithms,” in 2012 IEEE Symposium on Security and Privacy (San Francisco, CA: IEEE), 523–537. doi: 10.1109/SP.2012.38
Knudsen, L. R., Robshaw, M. J., Knudsen, L. R., and Robshaw, M. J. (2011). “Brute force attacks,” in The Block Cipher Companion, eds L. R. Knudsen, and M. J. B. Robshaw (Berlin: Springer), 95–108. doi: 10.1007/978-3-642-17342-4_5
Kodwani, G., Arora, S., and Atrey, P. K. (2021). “On security of key derivation functions in password-based cryptography,” in 2021 IEEE International Conference on Cyber Security and Resilience (CSR) (Rhodes: IEEE), 109–114. doi: 10.1109/CSR51186.2021.9527961
Li, X., Zhao, C., Pan, K., Lin, S., Chen, X., Chen, B., et al. (2015). On the security analysis of pbkdf2 in openoffice. J. Softw. 10, 116–126. doi: 10.17706/jsw.10.2.116-126
Malvoni, K., Designer, S., and Knezovic, J. (2014). “Are your passwords safe: energy-efficient bcrypt cracking with low-cost parallel hardware,” in Proceedings of the 8th USENIX Workshop on Offensive Technologies (WOOT'14) (San Diego, CA), 10.
Mentens, N., Batina, L., Preneel, B., and Verbauwhede, I. (2006). “Time-memory trade-off attack on fpga platforms: unix password cracking,” in Reconfigurable Computing: Architectures and Applications, eds K. Bertels, J. M. P. Cardoso, and S. Vassiliadis (Berlin: Springer Berlin Heidelberg), 323–334. doi: 10.1007/11802839_41
Moriarty, K., Kaliski, B., and Rusch, A. (2017). PKCS #5: Password-based Cryptography Specification Version 2.1. RFC Editor. Available online at: https://www.rfc-editor.org/info/rfc8018
National Institute of Standards and Technology (NIST) (2010). Recommendation for Password-based Key Derivation. Special Publication 800-132. Gaithersburg, MD: National Institute of Standards and Technology.
Oechslin, P. (2003). “Making a faster cryptanalytic time-memory trade-off,” in Advances in Cryptology - CRYPTO 2003, ed. D. Boneh (Berlin: Springer Berlin Heidelberg), 617–630. doi: 10.1007/978-3-540-45146-4_36
Percival, C. (2009). “Stronger key derivation via sequential memory-hard functions,” in Proceedings of the BSD Conference (Ottawa, ON), 81–92.
Percival, C., and Josefsson, S. (2016). The Scrypt Password-based Key Derivation Function. RFC Editor. Available online at: https://www.rfc-editor.org/info/rfc7914
Peslyak, A. (2014). yescrypt “Password Hashing Scalable Beyond Bcrypt and Scrypt.” Technical report. Bedford, MA: Openwall, Inc.
Pornin, T. (2015). The MAKWA Password Hashing Function (2015). Technical report. Available online at: https://www.bolet.org/makwa/makwa-spec-20150422.pdf. (accessed February 19, 2024).
Provos, N., and Mazieres, D. (1999). “Future-adaptable password scheme,” in Proceedings of the USENIX Annual Technical Conference (Monterey, CA), 81–92.
Quisquater, J.-J., and Delescaille, J.-P. (1990). “How easy is collision search? Application to des,” in Advances in Cryptology – EUROCRYPT '89, eds J. -J. Quisquater, and J. Vandewalle (Berlin: Springer Berlin Heidelberg), 429–434. doi: 10.1007/3-540-46885-4_43
Ruddick, A., and Yan, J. (2016a). “Acceleration attacks on PBKDF2: or, what is inside the black-box of oclHashcat?” in 10th USENIX Workshop on Offensive Technologies (Austin, TX).
Ruddick, A., and Yan, J. (2016b). “Acceleration attacks on PBKDF2: or, what is inside the Black-Box of oclHashcat?” in 10th USENIX Workshop on Offensive Technologies (WOOT 16) (Austin, TX: USENIX Association).
Saran, N. (2009). Time Memory Trade off Attack on Symmetric Ciphers [PhD thesis]. Ankara: Dept. Cryptography, Middle East Technical University.
Shannon, C. (1951). Prediction and entropy of printed English. Bell. Syst. Tech. J. 30, 50–64. doi: 10.1002/j.1538-7305.1951.tb01366.x
Simplicio Jr, M., Almeida, L., Andrade, E., dos Santos, P., and Barreto, P. (2015). Lyra2: Password Hashing Scheme with Improved Security against Time-Memory Trade-offs. Technical Report 2015/136, Cryptology ePrint Archive. Available online at: https://eprint.iacr.org/2015/136.pdf (accessed February 19, 2024).
Sönmez Turan, M., Çalık, Ç., Saran, N. B., and Doğanaksoy, A. (2008). “New distinguishers based on random mappings against stream ciphers,” in Sequences and Their Applications-SETA 2008: 5th International Conference Lexington, KY, USA, September 14-18, 2008 Proceedings 5 (Berin: Springer), 30–41. doi: 10.1007/978-3-540-85912-3_3
Standaert, F.-X., Rouvroy, G., Quisquater, J.-J., and Legat, J.-D. (2003). “A time-memory tradeo. using distinguished points: new analysis and FPGA results,” in Cryptographic Hardware and Embedded Systems - CHES 2002, eds B. S. Kaliski, Ç. K. Koç, and C. Paar (Berlin: Springer Berlin Heidelberg), 593–609. doi: 10.1007/3-540-36400-5_43
Unruh, D. (2007). “Random oracles and auxiliary input,” in Advances in Cryptology-CRYPTO 2007, 27th Annual International Cryptology Conference, Santa Barbara, CA, USA, August 19-23, 2007. Proceedings 27 (Berlin: Springer), 205–223. doi: 10.1007/978-3-540-74143-5_12
Visconti, A., Bossi, S., Ragab, H., and Calò, A. (2015). “On the weaknesses of pbkdf2,” in Cryptology and Network Security: 14th International Conference, CANS 2015, Marrakesh, Morocco, December 10-12, 2015. Proceedings 14 (Berlin: Springer), 119–126. doi: 10.1007/978-3-319-26823-1_9
Visconti, A., Mosnáček, O., Brož, M., and Matyáš, V. (2019). Examining pbkdf2 security margin—case study of Luks. J. Inf. Sec. Appl. 46, 296–306. doi: 10.1016/j.jisa.2019.03.016
Weatherley, R. (2023). “Additional modes for ascon version 1.1,” in Paper presented at the Lightweight Cryptography Workshop 2023. Available online at: https://eprint.iacr.org/2023/391 (accessed February 19, 2024).
Keywords: time-memory trade-offs (TMTOs), password hashing schemes (PHS), PBKDF2, dictionary attacks, rainbow tables
Citation: Saran AN (2024) On time-memory trade-offs for password hashing schemes. Front. Comput. Sci. 6:1368362. doi: 10.3389/fcomp.2024.1368362
Received: 10 January 2024; Accepted: 13 February 2024;
Published: 29 February 2024.
Edited by:
Muhammad Adnan Khan, Gachon University, Republic of KoreaReviewed by:
Aleksandra Mileva, Goce Delcev University, North MacedoniaCopyright © 2024 Saran. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ayse Nurdan Saran, YnV6QGNhbmtheWEuZWR1LnRy
 Ayse Nurdan Saran
Ayse Nurdan Saran