Efficient lightweight cryptographic solutions for enhancing data security in healthcare systems based on IoT

The growing integration of the Internet of Things (IoT) within healthcare systems has notably enhanced patient monitoring and data collection processes. Nonetheless, IoT devices exhibit significant susceptibility to cyber threats, primarily attributed to their constrained computational capabilities and their exposure to network-based attacks. Conventional encryption techniques, including advanced encryption standard (AES) and rivest–shamir–adleman (RSA), frequently fall short for IoT applications because of their significant processing demands. Consequently, creating lightweight cryptographic solutions is crucial for guaranteeing secure and efficient data transmission in healthcare environments that utilise IoT technology. This study presents three efficient cryptographic methods: (1) a hybrid encryption algorithm that incorporates a Fibonacci sequence and a 6D hyper-chaotic system to improve confusion and diffusion; (2) hybrid lightweight encryption that utilizes logistic parity-based chaotic maps for secure data transformation; and (3) combined transformation and expansion (CTE)-based lightweight cryptography that employs dynamic chaotic systems for strong encryption. The proposed models are assessed through various security metrics, including Unified Averaged Change Intensity (UACI), Number of Pixel Change Rate (NPCR), and Cross-Entropy. The findings from the experiments demonstrate that the suggested encryption techniques surpass traditional methods regarding both efficiency and resilience in encryption. The Fibonacci Q-matrix and logistic-parity-based chaotic maps exhibit significant resilience against differential and brute-force attacks. The UACI and NPCR values indicate that the encryption techniques produce ciphertexts that are highly random and difficult to anticipate, all while requiring minimal additional computational resources. This study introduces innovative lightweight cryptographic algorithms aimed at enhancing security in IoT-based healthcare systems. The proposed models demonstrate excellent encryption performance, minimal computational complexity, and robust resistance to attacks, rendering them well-suited for resource-limited IoT settings. Future efforts will concentrate on enhancing this technique for real-time application within extensive healthcare systems.

1 Introduction

The Internet of Things (IoT) is a transformative technology that links various physical items to collect and transmit data over the Internet. The fast expansion of IoT systems anticipates that 126 million smart devices will connect to the Internet by 2030, highlighting the need to tackle difficulties such as short battery life, limited memory, and restricted connection range inherent in IoT deployment (Wang et al., 2021). The substantial progress in enhanced connectivity and real-time data insights has resulted in a broad infrastructure encompassing several industries, including healthcare, transportation, smart homes, and environmental monitoring. The architecture has several levels, including cloud services, Internet-connected gateways, and edge devices, each defined by distinct security criteria. IoT devices are very susceptible to cyberattacks and energy depletion, rendering them more sensitive to energy and security hazards. Creating safe and energy-efficient systems is essential for the continuous growth and advancement of IoT systems (Khan et al., 2022). The convergence of transformative technologies, including blockchain, the Internet of Things (IoT), and artificial intelligence, is reshaping various sectors. Applications such as IoT-based health monitoring systems illustrate their potential to revolutionise real-time healthcare delivery (Sandner et al., 2020; Valsalan et al., 2020).

The increasing use of digital communication and multimedia technologies has stimulated research on secure and effective image encryption and authentication systems. Recent research has established frameworks integrating advanced mathematical models and computational techniques to tackle resilience, efficiency, and scalability (Guo et al., 2024). An optical image encryption and authentication scheme utilizing computational ghost imaging (CGI) enhances security and efficiency in image processing applications (Guo et al., 2024). Quaternion-based watermarking and multi-image encryption (Gong and Luo, 2023) have enhanced resilience to geometric distortion and attacks. Extensive surveys, such as SaberiKamarposhti et al. (2024), identify deficiencies in current approaches and inform future research. Innovative methods employing spatial and frequency domain transformations (Chen et al., 2021) and non-linear dynamics (Hu et al., 2024) illustrate the possibilities of multidisciplinary integration. These research initiatives aim to develop robust, adaptable, and high-performance image security systems to meet evolving requirements.

The implementation of IoT across diverse sectors employs networked devices to oversee and regulate several facets of daily life, hence improving sustainability and efficiency. The intelligent environmental monitoring system employs IoT devices to collect temperature, humidity, and air quality data, enabling precise environmental management. Smart homes employ IoT devices to regulate heating, lighting, and security systems, whereas smart buildings aim to optimize operating efficiency and reduce energy consumption. Integrating IoT with intelligent platforms and communication systems facilitates interaction with both real and virtual things, providing dynamic capabilities that may be seamlessly integrated into current technologies. The primary notion of IoT integrates AI-driven automation, sophisticated analytics, and intelligent manufacturing apparatus to enhance economic efficiency for humanity.

In healthcare, IoT facilitates the continuous monitoring of health indicators, illness development, and treatment efficacy, assisting healthcare practitioners in making informed decisions and enhancing patient outcomes. Remote monitoring of patient health streamlines the healthcare process by decreasing the frequency of hospital visits. It is essential to enhance the privacy, validity, and integrity of the data transferred and stored by IoT devices. Securing IoT devices necessitates deploying extensive security programs, including routine updates and strong encryption methods (Karunarathne et al., 2021). Traditional encryption techniques are susceptible to attacks due to manipulating pixel arrangements and value alterations. In this context, cryptographic algorithms serve as a protective measure for the efficient transmission and storage of data between devices. Due to the limitations of IoT devices regarding power, memory, and energy resources, conventional cryptographic methods are excessively burdensome, necessitating the implementation of lightweight cryptographic solutions.

Lightweight cryptography (LWC) is engineered to sustain minimal power and computational demands in resource-limited settings, guaranteeing secure data transfer among devices against unauthorized access and other cyber threats. In healthcare systems, secure data transfer is essential due to the vulnerability of wireless communication to eavesdropping and assaults (Chaudhary and Chatterjee, 2020). LWC safeguards the confidentiality and security of patient and healthcare provider data. The expansion of IoT necessitates the development and implementation of LWC to safeguard sensitive health information and guarantee the reliable functioning of healthcare equipment. This study presents LWC algorithms for efficient and intelligent data transfer in healthcare.

The important contribution of the study is:

• To devise effective cryptography methods for IoT healthcare devices.

• To formulate and implement novel lightweight cryptographic algorithms based on chaos theory, with the objective of improving encryption efficiency and minimizing processing complexity by utilizing chaotic maps, hyper-chaotic systems, and Fibonacci Q-matrices. These strategies enhance the encryption process by utilizing low-complexity algorithms and dynamic key generation, guaranteeing strong data security with little computing burden.

• To execute the hybrid lightweight encryption algorithm employing the logistic-parity-based chaotic map, which serves as its foundational element. This map produces pseudo-random sequences derived from beginning circumstances, guaranteeing increased sensitivity and unpredictability. Its lightweight computational architecture renders it appropriate for resource-limited IoT devices, while its chaotic characteristics augment encryption resilience against prevalent assaults by including dynamic and non-linear changes in the encryption procedure.

• To develop a 6D hyper-chaotic system utilizing a Fibonacci Q-matrix, wherein the hyper-chaotic system denotes a dynamic system characterized by multiple positive Lyapunov exponents, hence guaranteeing heightened sensitivity to begin circumstances and intricate behavior suitable for cryptographic applications. The Fibonacci Q-matrix, originating from Fibonacci sequences, facilitates organized yet adaptable key creation, hence augmenting the unpredictability and security of the encryption process.

• To assess the efficacy of the suggested lightweight cryptography methods utilizing UACI, NPCR, and cross-entropy metrics.

The subsequent sections of the article are organized as follows: Section 2 examines the current literature, identifying areas that require more research. Section 3 comprehensively delineates the process. Section 4 comprehensively examines the results obtained from the suggested technique. Section 5 summarizes the research results, encompassing the principal findings and insights derived from the study.

2 Literature review

Raziq et al. (2024) proposed a hybrid lightweight cryptographic algorithm based on encryption and decryption algorithms such as advanced encryption standard, elliptical curve cryptography, and secure efficient encryption algorithms by considering sensor nodes and gateway nodes. The model utilized a powerful public key encryption process for generating session keys to protect wireless body area networks. The model improved network threats and minimized delay and overhead issues, possessing limitations in the authenticity between user and nodes. Olayah et al. (2024) utilized gray wolf optimization and hyperelliptic curve cryptography and improved the quality of service in IoT networks and key management. By integrating a quantum neural network to predict and prevent bogus data entries, the model achieved 97.9% data confidentiality with a minimized delay of 0.37 s.

Qaid and Ebrahim (2023) introduced lightweight encryption using DNA sequences to improve IoT communication security. A secure key was generated by employing the inherent randomness of the DNA sequence. The encryption technique utilized the transposition and substitution approaches. The results indicated robust encryption by better key size, distortion preparation, and encryption time. Das et al. (2023) proposed a lightweight authentication scheme to maintain the device privacy through temporary identity updates after each session by ensuring reliable authentication without storing sensitive data on device memory utilizing physically unclonable functions (PUFs). Evaluations showed that the model outperformed existing methods.

Mahajan and Junnarkar (2023) employed a blockchain-based secure medical image processing incorporating elliptic curve cryptography combined with elliptic curve Diffie–Hellman and elliptic curve digital signature algorithm. The architecture includes different layers to secure data while maintaining privacy. Experiments revealed higher computational efficiency with reduced mean square error. Alluhaidan and Prabu (2023) proposed an efficient and secure method that used a symmetrical encryption key block by minimizing the processing cycles while maintaining safety. The model involved the generation of subkeys through a genetic algorithm using a modified Feistel architecture as a custom proxy network. The ciphers reduced power consumption by 15.75% compared to previous ciphers, and the challenges included vulnerability to advanced attacks.

Mahlake et al. (2023) explored lightweight security algorithm employing a hybrid approach, integrating the security protocol for sensor networks with secure IoT encryption, and enhancing data security and key generation efficiency while reducing power consumption. The results indicated a packet drop ratio ranging from 90 to 99%, with challenges including computational and network performance during encryption and key expansion. Al-Azzawi and Al-Dabbagh (2024) focused on the implementation of a 32-bit processor utilizing Type-2 Generalized Feistel Networks with a partial permutation layer, demonstrating strong security characteristics. The performance evaluation on real IoT devices highlights superior encryption and decryption speeds.

Das and Namasudra (2023) proposed an authentication scheme for preserving the privacy of network devices. The model is established with the lightweight cryptographic primitives such as hash operation, concatenation, and XOR operations for preventing unauthorized devices to access healthcare systems. Hosny et al. (2021) investigated smart irrigation systems using cryptographic algorithms, incorporating Secure Hash Algorithm (SHA-256), Elliptic Curve Cryptography (ECC), and Rivest Cipher (RC4). The ECC method encrypts the RC4 key, and the output is converted to SHA-256 for hashing. The SHA-256 method encodes the RC4 cipher text for data integrity.

Jebri et al. (2021) aimed to enhance the secure data transmission of IoT devices, including the anonymity of link directions and dynamic virtual identity, to solve the issues of tractability. The results showed that the execution time is sufficient using Raspberry cards and the MIRACL library. Hasan et al. (2021) suggested two permutation algorithms to enhance medical image security. This encryption method outperformed traditional models in terms of security and execution time.

A novel image encryption method by Hua et al. (2019) uses a cosine-transform-based chaotic system to merge chaotic dynamics with the frequency domain. The approach generates high-dimensional chaotic sequences using a unique cosine transform, improving encryption confusion and diffusion. The system is highly sensitive to beginning conditions, preventing brute force and differential attacks. The proposed method is computationally efficient and suited for real-time encryption. This study shows that mathematical transforms and chaotic systems can be used to create improved image encryption methods.

To safeguard digital data, image encryption has investigated chaotic systems and hybrid approaches. Wu et al. (2018) introduced a 2D Hénon-Sine map employing DNA encoding for picture encryption. The approach is contingent upon initial conditions and robust against assaults. Li et al. (2017) proposed a chaotic tent map encryption technique that is both straightforward and resilient owing to its unpredictability. Niyat et al. (2017) enhanced diffusion and confusion in a hybrid hyper-chaotic system utilizing cellular automata for color image encryption. Integrating spatial and value-domain modifications, Enayatifar et al. (2017) devised a synchronous permutation-diffusion image encryption method that enhanced security. The abovementioned studies demonstrate that chaotic and hybrid methodologies can enhance the security and efficiency of image encryption.

The study by Zou et al. (2025) introduces a watermarking model that combines hierarchical residual fusion with multi-scale convolution to enhance resilience and invisibility. The method is proficient at integrating watermarks into multimedia, guaranteeing substantial resistance to diverse assaults. The study by Zhou et al. (2023) introduces a quaternion-based encryption method utilizing discrete fractional Chebyshev moment transform and cross-coupling procedures. It offers improved security and efficiency for the simultaneous encryption of several pictures, tackling significant issues in multi-image cryptosystems.

3 Materials and methods

Ensuring integrity, confidentiality, and authenticity of sensitive patient data is crucial in maintaining trust in healthcare systems. The rapid growth of IoT demands the necessity of scalable cryptographic algorithms. Moreover, robust, lightweight cryptography is essential to protect against various security challenges. So, this study proposes lightweight cryptographic algorithms used for secure data transmission in IoT healthcare devices. Medical images are utilized to design and develop lightweight cryptographic algorithms. The medical images used as input encompass a range of diagnostic modalities, such as ECG, MRI, EEG, and X-ray. Supplementary Figure S1 depicts examples of these medical images.

3.1 Hybrid encryption algorithm using Fibonacci sequence and chaotic map

The non-linear and dynamic behavior of chaotic functions results in unpredictable responses, enhanced by hyper-chaotic functions, with their more complex dynamical behavior than lower-dimensional chaotic functions. For a system to be classified as hyper-chaotic, it must possess at least four dimensions. The proposed encryption system employs a six-dimensional (6D) hyper-chaotic system, leveraging its advanced complexity to significantly enhance the security of the encryption process. This increased dimensionality contributes to the robustness of the encryption, making it exceedingly tough for unauthorized entities to predict or decipher the encrypted data.

The proposed algorithm for encrypting grayscale images utilizes a 6D hyper-chaotic system and a Fibonacci Q-matrix, executed in two primary steps. First, the 6D hyper-chaotic system scrambles the pixel positions of the original image to create confusion. To achieve this, three sequences from the hyper-chaotic system are randomly selected to determine the new pixel positions, ensuring a high degree of randomness and security. Second, the diffusion process utilizes the Fibonacci Q-matrix, which further enhances security by altering the pixel values. This diffusion process is done to the sub-blocks of the image that have already undergone confusion, ensuring that both the positions and values of pixels are significantly transformed, thus securing the image against unauthorized access and analysis. The 6D-chaotic system is defined by the following Equations 1–6.

$\begin{array}{ll}\dot{x_1}=a\left(x_2-x_1\right)+x_4-x_5-x_6& (1)\end{array}$

$\begin{array}{ll}\dot{x_2}=c{x}_1-x_2-x_1{x}_3& (2)\end{array}$

$\begin{array}{ll}\dot{x_3}=-b{x}_3+x_1{x}_2& (3)\end{array}$

$\begin{array}{ll}\dot{x_4}=d{x}_4+x_2{x}_3& (4)\end{array}$

$\begin{array}{ll}\dot{x_5}=e{x}_6+x_3{x}_2& (5)\end{array}$

$\begin{array}{ll}\dot{x_6}=r{x}_1& (6)\end{array}$

where a, c, b, d, e, and r are constants, and x₁, x₂, x₃, x₄, x₅, and x₆, are state variables. Here, we considered the values of constants as a = 10, c = 28, b = 8/3, d = −1, e = 8, and r = 3.

Mathematically, the Fibonacci sequence usually starts with 0 and 1, and each succeeding number is the sum of the preceding two. Fibonacci numbers, an element of the Fibonacci sequence, are denoted by $F_n$ . The sequence typically begins with 0, or in some cases, it may start with 1 or occasionally start with 1 and 2. An example of a Fibonacci sequence that starts with 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, and 144 is given in Supplementary Figure S2, where the side length of the successive number is tiled into squares.

The element of the Fibonacci sequence, $F_n$ , is given by Equation 7

$\begin{array}{ll}{F}_n=F_{n-1}+F_{n-2},n\ge 1& (7)\end{array}$

The Fibonacci Q-matrix is described by Equation 8

$Q=\left[\begin{array}{cc}1& 1\\ 1& 0\end{array}\right]\text{ (8)}$

The nth power of Fibonacci Q-matrix is constructed by Equation 9

$Q^n=\left[\begin{array}{cc}{F}_{n+1}& F_n\\ F_n& F_{n-1}\end{array}\right]\text{ (9)}$

The inverse Q-matrix is defined by Equation 10

$Q^{-n}=\left[\begin{array}{cc}{F}_{n-1}& -F_n\\ -F_n& F_{n+1}\end{array}\right]\text{ (10)}$

The encryption algorithm incorporates a 6D hyper-chaotic system and a Fibonacci Q-matrix to enhance image security using a two-step process: confusion and diffusion, as given in Supplementary Figure S11, achieving rapid diffusion of scrambled images efficiently. The encryption performance and safety are greatly enhanced by the 6D hyper-chaotic system, exhibiting intricate high-dynamic behaviors and is characterized by two positive Lyapunov exponents. The pixel arrangement and values are modified in the encryption stage. Initially, the confusion step utilizes the hyper-chaotic system to rearrange pixel positions based on three selected sequences $x_1,x_3,x_5$ , which are derived from iterating the system after calculating the initial conditions from the plain image. This sorted vector determines the new pixel positions, effectively scrambling the image and obfuscating the original image. In the diffusion process, the scrambled image is partitioned into 2 × 2 blocks, with each block undergoing diffusion using the Fibonacci Q-matrix, modifying pixel values to further secure the image. This entire process, involving two rounds of confusion and diffusion, results in the final encrypted image.

In the decryption process, C, the encrypted image is separated into 2 × 2 blocks, and each block undergoes diffusion using the $Q^{10}$ equation as described in Equation 11, and the scrambled image D is converted into a vector W.

$\left[\begin{array}{cc}{D}_{i,j}^{\prime }& D_{i,j+1}^{\prime }\\ D_{i+1,j}^{\prime }& D_{i+1,j+1}^{\prime }\end{array}\right]=\left[\begin{array}{cc}{C}_{i,j}& C_{i,j+1}\\ C_{i+1,j}& C_{i+1,j+1}\end{array}\right]\left[\begin{array}{cc}34& -55\\ -55& 89\end{array}\right]mod256\text{ (11)}$

After applying the vector S to revert each pixel to its initial position, converting this vector back into a matrix results in the decrypted image following two decryption rounds, as described in Equation 12.

$\begin{array}{ll}ER\left(S_i\right)=W_i,i=1:MN\text{.}& (12)\end{array}$

3.2 Hybrid lightweight encryption algorithm using logistic-parity-based chaotic map

The proposed hybrid LWC algorithm utilized the concatenation of logistic map and parity map to encrypt grayscale images. It is defined as a non-linear combination of two separate 1D chaotic maps acting as initial seed maps. This configuration allows for complex interactions between the maps, enhancing their chaotic behavior and computational versatility, as depicted in Supplementary Figure S3. The logistic map is a classic representation of a dynamic system that shows chaotic behavior. A system that exhibits chaotic behavior exhibits high sensitivity toward initial conditions, which leads to unpredictable long-term behavior, even though the system dynamics are deterministic and guided by simple rules. In the case of a logistic map, chaos arises when the growth parameter increases beyond a certain threshold. The population (or whatever quantity is being modeled) possesses stable behavior at low growth rate values, which typically converges to a fixed point or oscillates between a finite set of values.

The logistic map is the modest dynamic equation displaying intricate chaotic dynamics, as formulated in Equation 13.

$\begin{array}{ll}{X}_{n+1}=\mathcal{L}\left(r,X_n\right)=r{X}_n\left(1-X_n\right)& (13)\end{array}$

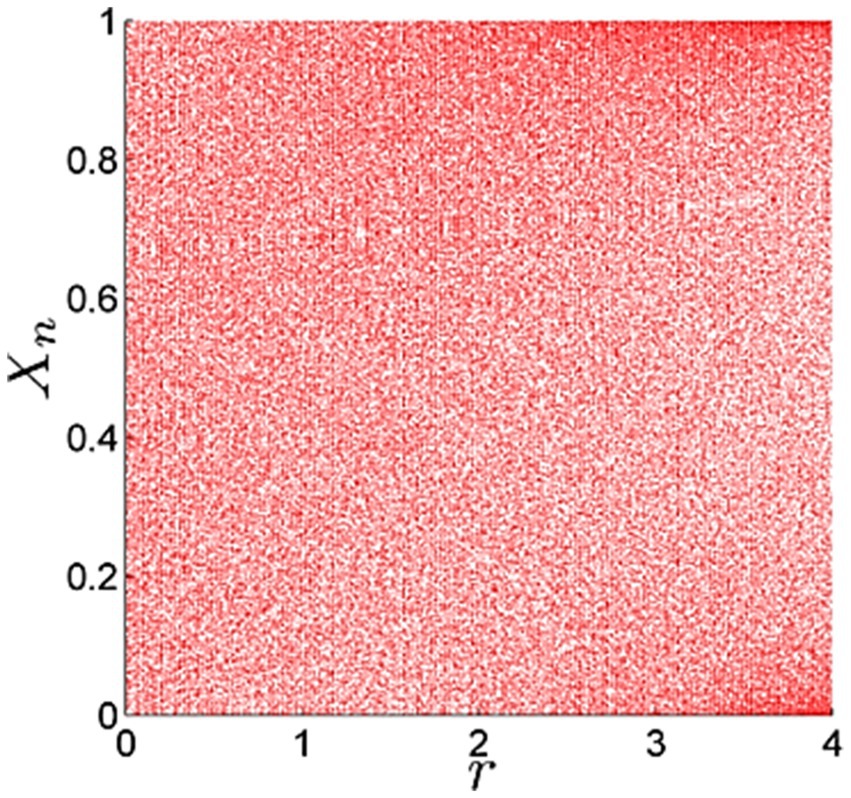
where r lies in the interval of [0 4], and $X_n$ denotes the resulting chaotic sequence. The attractor for the values of the parameter r is shown by the bifurcation diagram, as given in Supplementary Figure S4.

The logistic map’s constrained chaotic range within [3.57; 4], coupled with its non-uniform distribution within the [0, 1] interval, imposes limitations on its practical applications. So, the logistic map must be concatenated with other maps to improve the performance. The parity map is another 1D dynamical system that exhibits chaotic behavior. The map is created by considering odd and even values of the parameters. The behavior of the parity map can be quite complex depending on the value of the growth rate (u). At low values of u, the map may exhibit stable behavior, converging to fixed points or periodic orbits. As u increases, the parity map can undergo period-doubling bifurcations, leading to chaotic behavior. A parity map can be mathematically defined by Equation 14

$X_{n+1\text{ (14)}}=\mathcal{T}\left(u,X_n\right)=\{\begin{array}{c}u{X}_n/2X_i<0.5\\ u\left(1-X_n\right)/2X_i\ge 0.5\end{array}$

where parameter u is an element of [0; 4]. The bifurcation diagram of the parity map is given in Supplementary Figure S5.

In logistic parity maps, the hybrid mapping system utilizes logistic and parity maps as seed maps, called the logistic-parity system (LPS). The combined parameter settings for each seed map aim to streamline the intricate complexity outlined in Equation 15.

$\begin{array}{l}{X}_{n+1}=A_{\mathcal{L}\mathcal{T}}\left(r,X_n\right)=\left(\mathcal{L}\left(r,X_n\right)+\mathcal{T}\left(\left(4-r\right),X_n\right)\right)mod1\\ =\{\begin{array}{c}\begin{array}{l}\left(r{X}_n\left(1-X_n\right)+\left(4-r\right)X_n/2\right)mod1\\ X_i<0.5\end{array}\\ \begin{array}{l}\left(r{X}_n\left(1-X_n\right)+\left(4-r\right)\left(1-X_n\right)/2\right)mod1\\ X_i\ge 0.5\end{array}\end{array}\end{array}\text{ (15)}$

Here, parameter r is an element of [0:4]. The expansive chaotic range observed in the bifurcation diagram of the logistic-parity map, spanning between [0:4], far exceeds the chaotic intervals typically seen in either the logistic or parity maps (see Figure 1).

Figure 1

Figure 1. Bifurcation diagram of logistic-parity map.

To ensure robust image encryption, the proposed model employs a complex structure with four rounds, each comprising five distinct procedural steps outlined in Figure 2.

Figure 2

Figure 2. Encryption block diagram.

In the first step, a random pixel is inserted with a randomized element at the start of every row in the original image, adding variability and unpredictability to the dataset, as in Equation 16,

$I\left(i,j\right)=\{\begin{array}{c}\mathrm{Rand}\left(i\right)\mathrm{if}j=1\\ O\left(i,j-1\right)\mathrm{otherwise}\end{array}\text{ (16)}$

In this context, O represents $M\times N$ sized input image, while $I\left(i,j\right)$ represents a processed image with size $M\times \left(N+1\right)$ and $\mathrm{Rand}\left(i\right)$ is a random function that produces random numbers. The second step involves separating each row into a one-dimensional data matrix, isolating the rows for individual processing as in Equation 17,

$\begin{array}{ll}{R}_i\left(j\right)=I\left(i,j\right)& (17)\end{array}$

where $R_i$ is the ith ID row matrix with a length of $\left(N+1\right)$ . Next, in the substitution step, the data values within each 1D matrix are altered to further confuse the original image data as in Equation 18,

$B_i\left(j\right)=\{\begin{array}{c}{R}_i\left(j\right)\mathrm{}\mathrm{if}j=1\\ B_i\left(j-1\right)\oplus R_i\left(j\right)\oplus \left(\begin{array}{l}⌊S_k\left(i,j\right)\times {10}^{10}⌋\\ mod256\end{array}\right)\mathrm{}\mathrm{otherwise}\end{array}\text{ (18)}$

where $S_k\left(i,j\right)$ represents arbitrary sequence for k = 1, 2, 3, 4 encryption, as created by the anticipated logistic-parity map, as in Equation 19

$S_k\left(i,j\right)=\{\begin{array}{c}{S}_1\left(0,0\right)\mathrm{f}\mathrm{o}\mathrm{r}i=0,j=0,k=1\\ S_2\left(M,0\right)\mathrm{f}\mathrm{o}\mathrm{r}i=0,j=0,k=3\\ \begin{array}{c}{S}_{K-1}\left(N,0\right)\mathrm{f}\mathrm{o}\mathrm{r}i=0,j=0,k=2,4\\ \begin{array}{c}{A}_{\mathcal{L}\mathcal{T}}\left(r_0,S_k\left(i-1,0\right)\right)\mathrm{f}\mathrm{o}\mathrm{r}i>1,j=0\\ A_{\mathcal{L}\mathcal{T}}\left(r_k,S_k\left(i,j-1\right)\right)\mathrm{f}\mathrm{o}\mathrm{r}i>1,j>0\end{array}\end{array}\end{array}\text{ (19)}$

Following substitution, during the row combination step, the adjusted 1D matrices are reintegrated into a cohesive two-dimensional data structure, ensuring that each matrix retains its initial row alignment as in Equation 20,

$\begin{array}{ll}C\left(i,j\right)=B_i\left(j+1\right)& (20)\end{array}$

where 2D image matrix with dimension $M\times N$ and $j>N$ is C. Finally, image rotation makes the 2D matrix rotate 90 degrees counterclockwise to add another layer of complexity, as in Equation 21

$\begin{array}{ll}E\left(i,j\right)=C\left(j,N-i+1\right)& (21)\end{array}$

The final encrypted image is obtained after repeating these five steps across four rounds that are highly secure due to the multiple layers of transformations and randomness applied throughout the process. Now, the decryption process is done with an encrypted image, as depicted in Supplementary Figure S6.

Decryption involves reversing the encryption process to recover the original data or message. Initially, the encrypted image undergoes rotation, reversing the 90-degree clockwise rotation done in encryption. Then, it is separate into individual rows to transform the image into a 1D data matrix for each row. Following separation, inverse ID substitution is done, where the data values in each 1D matrix are reverted to their original values before encryption. It can be given as Equation 22.

$\begin{array}{ll}{R}_i\left(j\right)=B_i\left(j-1\right)\oplus B_i\left(j\right)\oplus \left(⌊S_k\left(i,j\right)\times {10}^{10}⌋mod256\right)& (22)\end{array}$

Now, 1D matrices are recombined into 2D data matrices by restoring the image. Finally, to obtain the image in its original dimension, random pixels that are added during the encryption process are removed. Similar to encryption, decryption is also performed in four rounds to accurately retrieve the original image.

3.3 Lightweight cryptographic algorithms using CTE and dynamic chaotic system

Chaos theory explores systems characterized by unpredictable and highly sensitive behaviors to initial states, often termed deterministic chaos. The phenomenon, referred to as the butterfly effect, indicates that even a minor variance in the initial situations leads to highly conflicting results, making long-term predictions generally infeasible. In the proposed model, the initial approach involved employing a 4D dynamic chaos-based system characterized by two positive Lyapunov exponents, which measure how quickly trajectories diverge from each other over time. It can be represented by the Equation 23.

$\begin{array}{ll}\lambda =\underset{n\to \infty }{lim}\frac{1}{n}{\displaystyle \sum }_{n=0}^{N-1}ln\left|\frac{\mathrm{d}f\left(x_n,u\right)}{\mathrm{d}x}\right|& (23)\end{array}$

The workflow of the proposed model is given by Supplementary Figure S7.

The security of the model is enhanced by introducing medical image information as the initial parameters of the dynamic chaos system. Supplementary Figure S8 represents a dynamic, chaotic system. The pixels are then transformed and expanded using a dynamic chaos sequence. There are matrices generated by dynamic chaos sequences. Particularly, an index matrix specifies which pixels will expand and transformed, while second mask matrix determines the manner of pixel expansion. This approach utilizes a novel dynamic, chaotic system to produce chaotic sequences for encryption, providing a robust and secure method for encrypting medical images. It can be given as Equation 24

$\begin{array}{c}\begin{array}{c}x=a\left(y-x\right)+w\\ y=bx-xz+w\end{array}\\ z=xy-z-w\\ w=-c\left(x+y\right)\end{array}\text{ (24)}$

where constants a, b, and c are positive, while x, y, z, and w are the state variables in the system.

Generating initial values for the dynamic chaotic system is crucial and is employed by dividing the input image K into 32 blocks, which is represented as $K=\left\{k_1,,k_2,,k_3,,\dots ,,k_{32}\right\}$ . The four intermediate parameters $d_1$ , $d_2$ , $d_3$ , and $d_4$ are calculated using $b_1,b_2,b_3$ , and $b_4$ . User-defined parameters that function as security keys can be defined by the user for enhanced system security, as in Equation 25.

$\{\begin{array}{c}{d}_1=b_1+\frac{1}{256}\left(k_1\oplus k_2\oplus \cdots \oplus k_8\right)\\ d_2=b_2+\frac{1}{256}\left(k_9\oplus k_{10}\oplus \cdots \oplus k_{16}\right)\\ \begin{array}{c}{d}_3=b_3+\frac{1}{256}\left(k_{17}\oplus k_{18}\oplus \cdots \oplus k_{24}\right)\\ d_4=b_4+\frac{1}{256}\left(k_{25}\oplus k_{26}\oplus \cdots \oplus k_{32}\right)\end{array}\end{array}\text{ (25)}$

From these intermediate parameters, the initial values of a dynamic chaotic system, $x_0$ , $y_0$ , $z_0$ , and $w_0$ , are expressed in terms of $d_1$ , $d_2$ , $d_3$ , and $d_4$ , as in Equation 26.

$\{\begin{array}{c}{x}_0=\frac{mod\left(\left(d_1+d_2+d_3\right)\times {10}^8,256\right)}{255}\\ y_0=\frac{mod\left(\left(d_2+d_3+d_4\right)\times {10}^8,256\right)}{255}\\ \begin{array}{c}{z}_0=\frac{mod\left(\left(d_1+d_2+d_3+d_4\right)\times {10}^8,256\right)}{255}\\ w_0=\frac{mod\left(\mathrm{mean}\left(d_1+d_2+d_3+d_4\right)\times {10}^8,256\right)}{255}\end{array}\end{array}\text{ (26)}$

Using these initial values, the 4D dynamic chaotic system iterates and creates sequences of adequate length to ensure effective encryption procedures. The four state values obtained in $j\mathrm{t}\mathrm{h}$ iteration are expressed as in Equation 27.

$\begin{array}{ll}{S}^j=\left\{x_j,y_j,z_j,w_j\right\}& (27)\end{array}$

A dynamic chaotic sequence S is obtained after the termination of iteration, as in Equation 28

$\begin{array}{c}S=\left\{s^1,s^2,s^3,\dots .s^N\right\}\\ =\left\{x_1,y_1,z_1,w_1,\dots \dots ,x_N,y_N,z_N,w_N\right\}\\ =\left\{s_1,s_2,s_3,s_4,\dots \dots .,s_{4N-3},s_{4N-2},s_{4N-1},s_{4N}\right\}\end{array}\text{ (28)}$

The proposed CTE scheme relies on incorporating two distinct auxiliary matrices crucial to its operation. The schematic illustration is shown in Supplementary Figure S9. The first matrix determines which pixels must be processed, while the other is used for expansion.

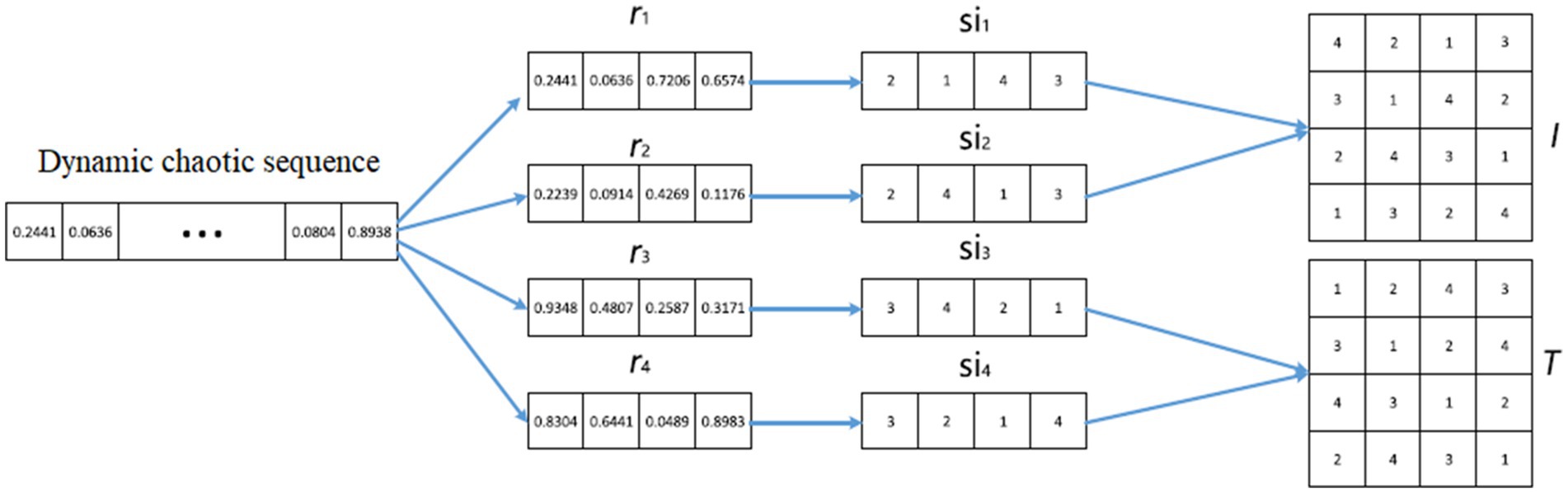
Consider an image having height h and weight w, with h × w dimension, and four random sequences $r_1,r_2,r_3$ , and $r_4$ obtained from S and used for generating two index matrices, I and T as in Equation 29.

$\begin{array}{c}I\left(i,j\right)=s{i}_1\left(mod\left(i+s{i}_2\left(j\right)-1,w\right)+1\right)\\ T\left(i,j\right)=s{i}_3\left(mod\left(i+s{i}_4\left(j\right)-1,w\right)+1\right)\end{array}\text{ (29)}$

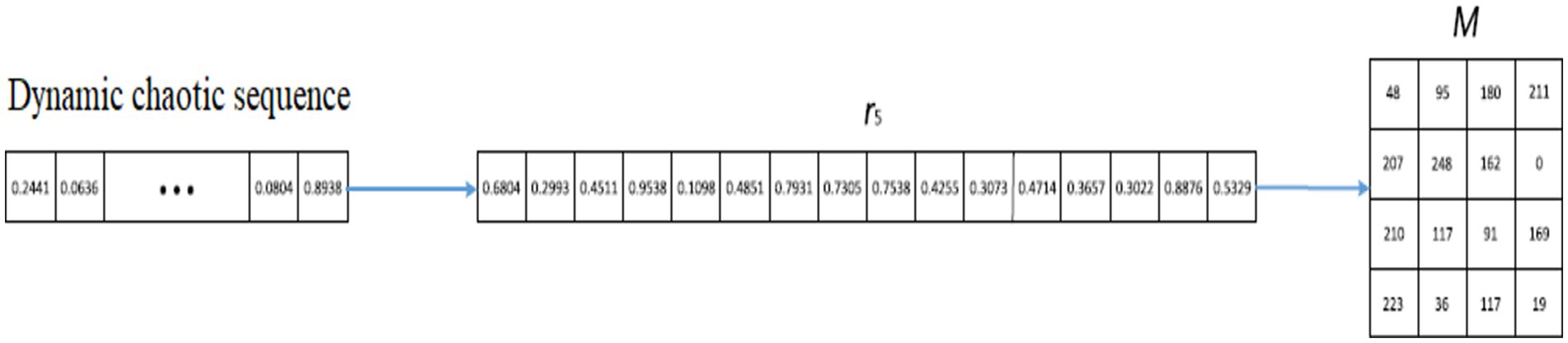
The generation of index matrices and mask matrices is shown in Figures 3, 4, respectively. The mask matrix (M) is computed in accordance with the expansion procedure as in Equation 30.

$\begin{array}{ll}M=\mathrm{reshape}\left(mod\left(\left(r_5-r_5\right)\times 2^{32}\right),256\right),\left[h,w\right])& (30)\end{array}$

Figure 3

Figure 3. Generation of T and I.

Figure 4

Figure 4. Generation of M.

Encryption transforms a plain image into a cipher image, while decryption reverts it to its original plain form. To encrypt or decrypt data using cryptographic algorithms, a key, which is a particular character sequence, is essential. Supplementary Figure S10 represents the proposed CTE for decryption and encryption.

Given the index matrices I and T, the mask matrix M, a single-channel plain image P, and a user-defined key F, the cipher image C can be constructed as in Equation 31.

$C_{I_{i,j},j\text{ (31)}}=\{\begin{array}{c}mod\left(M_{i,j}\oplus P_{T_{j,I_{i,j}},I_{i,j}}+P_{I_{h,w},w}\right),F),\mathrm{if}i=1,j=1\\ mod\left(M_{i,j}\oplus P_{T_{j,I_{i,j}},I_{i,j}}+C_{I_{i-1,w},w}\right),F),\mathrm{if}i\ne 1,j=1\\ mod\left(M_{i,j}\oplus P_{T_{j,I_{i,j}},I_{i,j}}+C_{I_{i,j-1},j-1}\right),F),\mathrm{if}j\ne 1\end{array}$

The decrypted image D can be obtained from T, M, I, F, and C as expressed below Equation 32:

$D_{T_{j,I_{i,j}},I_{i,j}\text{ (32)}}=\{\begin{array}{c}mod\left(M_{i,j}\oplus C_{{I_{i,j}}_{,},j}+C_{I_{h,w},w}\right),F),\mathrm{if}i=1,j=1\\ mod\left(M_{i,j}\oplus C_{{I_{i,j}}_{,},j}+C_{I_{i-1,w},w}\right),F),\mathrm{if}i\ne 1,j=1\\ mod\left(M_{i,j}\oplus C_{{I_{i,j}}_{,},j}+C_{I_{i,j-1},j-1}\right),F),\mathrm{if}j\ne 1\end{array}$

3.4 Hardware and software

The system is equipped with an Intel Core i7-6850K processor with 12 cores running at 3.60 GHz and is featured with an NVIDIA GeForce GTX 1080 Ti GPU, which has 2,760 CUDA cores and 4 MB of memory. The implementation platform for the lightweight cryptographic algorithms is MATLAB.

4 Results and discussion

4.1 Performance evaluation

The effectiveness of the suggested lightweight cryptographic algorithms is assessed through metrics such as unified averaged changed intensity (UACI), number of pixel changing rate (NPCR), and cross-entropy. NPCR is employed to assess the robustness of image encryption techniques and ciphers. It is intended to measure the variation in pixel values between the encrypted image and the original. Mathematically, NPCR is expressed in terms of a bipolar array D as in Equation 33.

$\begin{array}{c}D\left(i,j\right)=\{\begin{array}{c}0,\mathrm{if}{C}^1\left(i,j\right)=C^2\left(i,j\right)\\ 1,\mathrm{if}{C}^1\left(i,j\right)\ne C^2\left(i,j\right)\end{array}\\ \mathrm{NPCR}:N\left(c^1,c^2\right)={\displaystyle \sum }_{i,j}\frac{D\left(i,j\right)}{T}\times 100\%\end{array}\text{ (33)}$

where $c^1$ is the original image, $c^2$ is the cipher image, and T is the total number of pixels. UACI quantifies the average change in intensity between the cipher image and the original image. Mathematically it is expressed as in Equation 34.

$\begin{array}{ll}\mathrm{UACI}:u\left(C^1,C^2\right)={\displaystyle \sum }_{i,j}\frac{\left|C^1\left(i,j\right)-C^2\left(i,j\right)\right|}{F.T}\times 100\%& (34)\end{array}$

where F represents the maximum pixel value supported. The cross-entropy metric efficiently measures the randomness and uncertainty between the original and encrypted images, providing a quantitative assessment of encryption strength. The cross-entropy is expressed as in Equation 35.

$\begin{array}{ll}H\left(C^1,c^2\right)=-{\displaystyle \sum }_x{C}^1\left(x\right)log{C}^2\left(x\right)& (35)\end{array}$

The evaluation of the cipher image and the original image’s performance for the suggested hybrid encryption algorithm using the Fibonacci sequence and chaotic map is given in Table 1.

Table 1

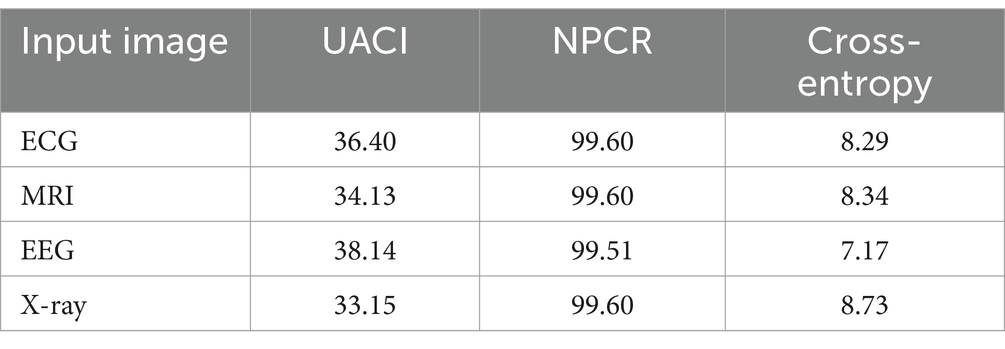
Table 1. Analysis of original image vs. encrypted images for hybrid encryption algorithm using Fibonacci sequence and chaotic map.

Table 1 reveals that the UACI and NPCR values are exceptionally high, highlighting the significant change between the original medical image and its encrypted counterpart. This indicates that the encryption process has successfully ensured a high level of dissimilarity between the two images. The finiteness of the cross-entropy indicates a high level of structural dissimilarity between the encrypted and original images. The performance analysis of encrypted and original images for the proposed hybrid lightweight encryption algorithm using logistic-parity-based chaotic map is tabulated in Table 2.

Table 2

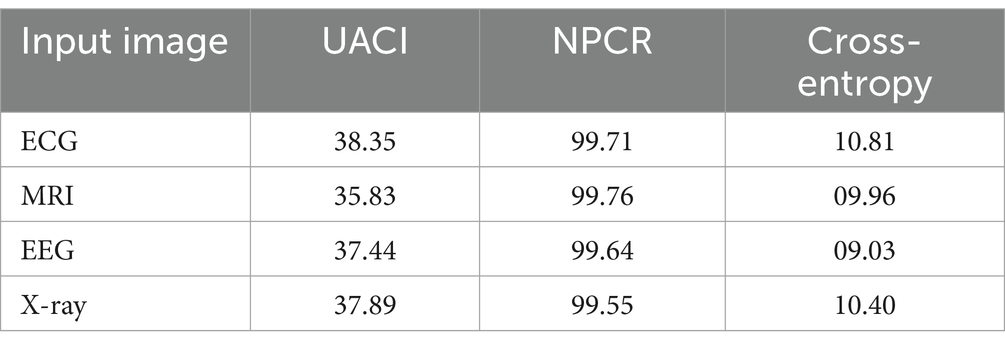
Table 2. Analysis of original image vs. encrypted images for hybrid lightweight encryption algorithm using logistic-parity-based chaotic map.

From Table 2, the high NPCR value indicates that even minor changes in the original image result in substantial variations in the encrypted image. The high UACI value suggests that the encryption process uniformly affects the intensity of pixel changes for the original medical images. The finite cross-entropy value denotes that the pixel distribution is unpredictable. The performance of proposed lightweight cryptographic algorithms using CTE and the dynamic chaotic system is analyzed and tabulated in Table 3.

Table 3

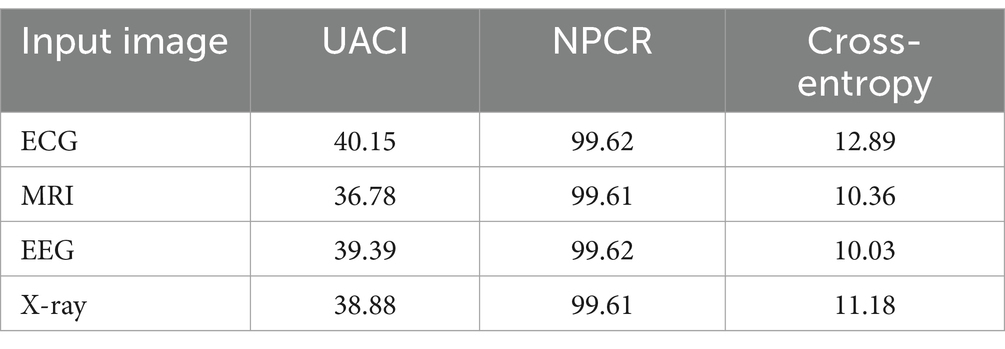
Table 3. Analysis of original image vs. encrypted images for lightweight cryptographic algorithms using CTE and dynamic chaotic system.

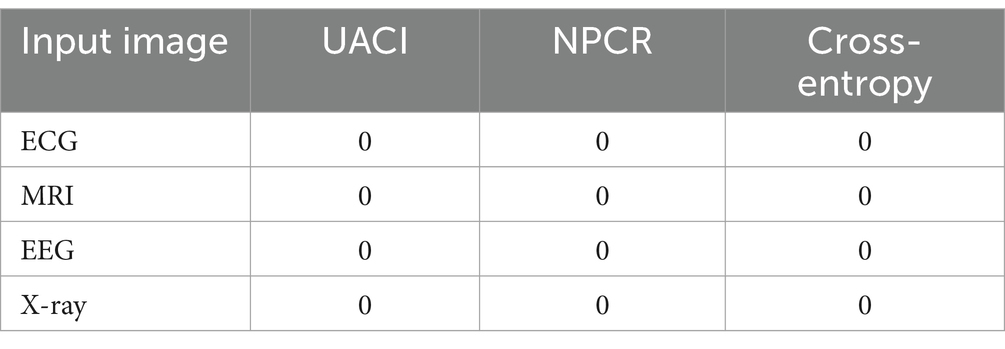
Table 3 examines the performance of the proposed lightweight algorithm with high NPCR and substantial UACI and cross-entropy value undergoes significant changes, ensuring robust protection against cyberattacks or unauthorized access. The performance evaluation of the decrypted image and original image is given in Table 4.

Table 4

Table 4. Performance analysis of original image vs. decrypted images.

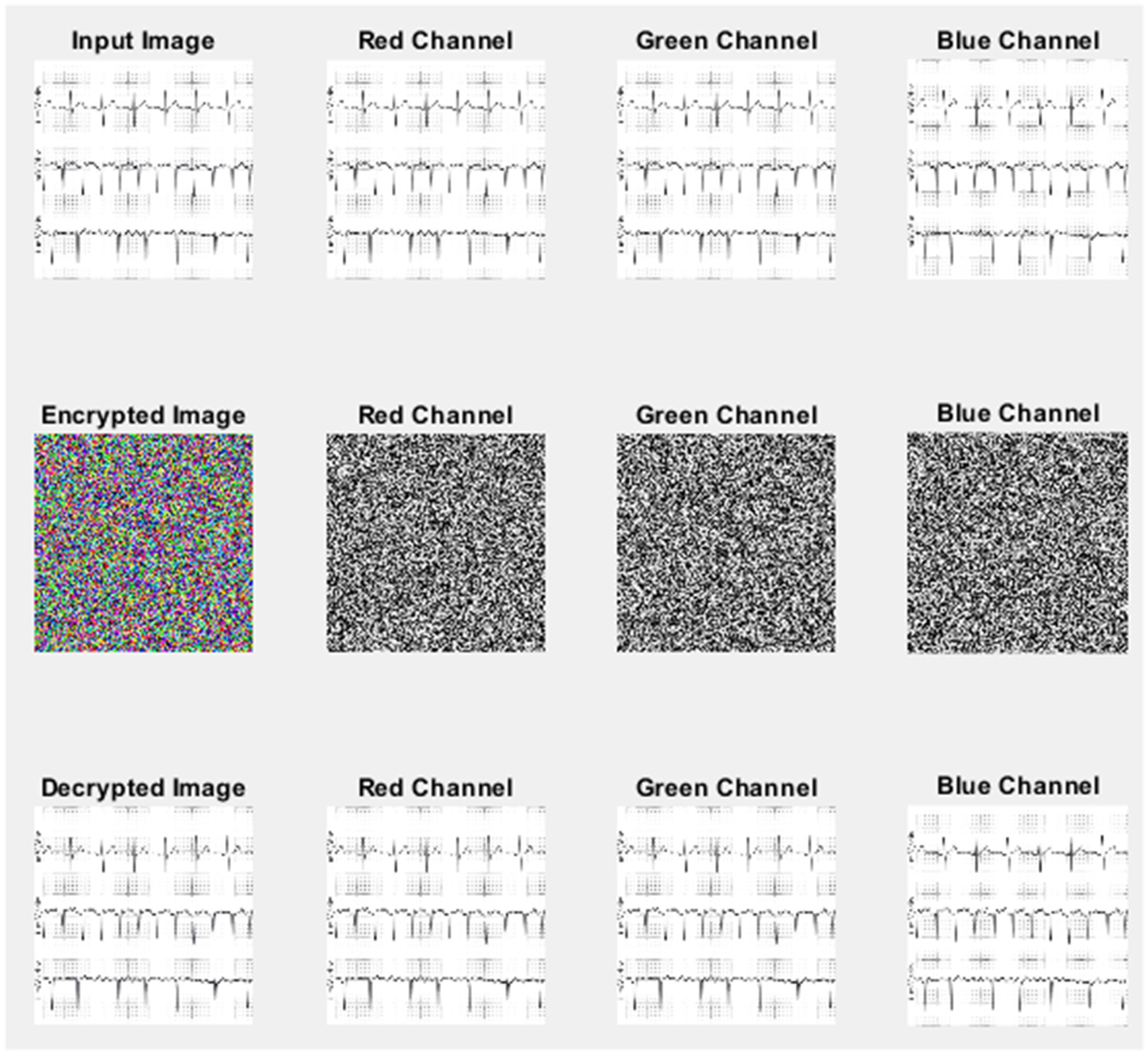
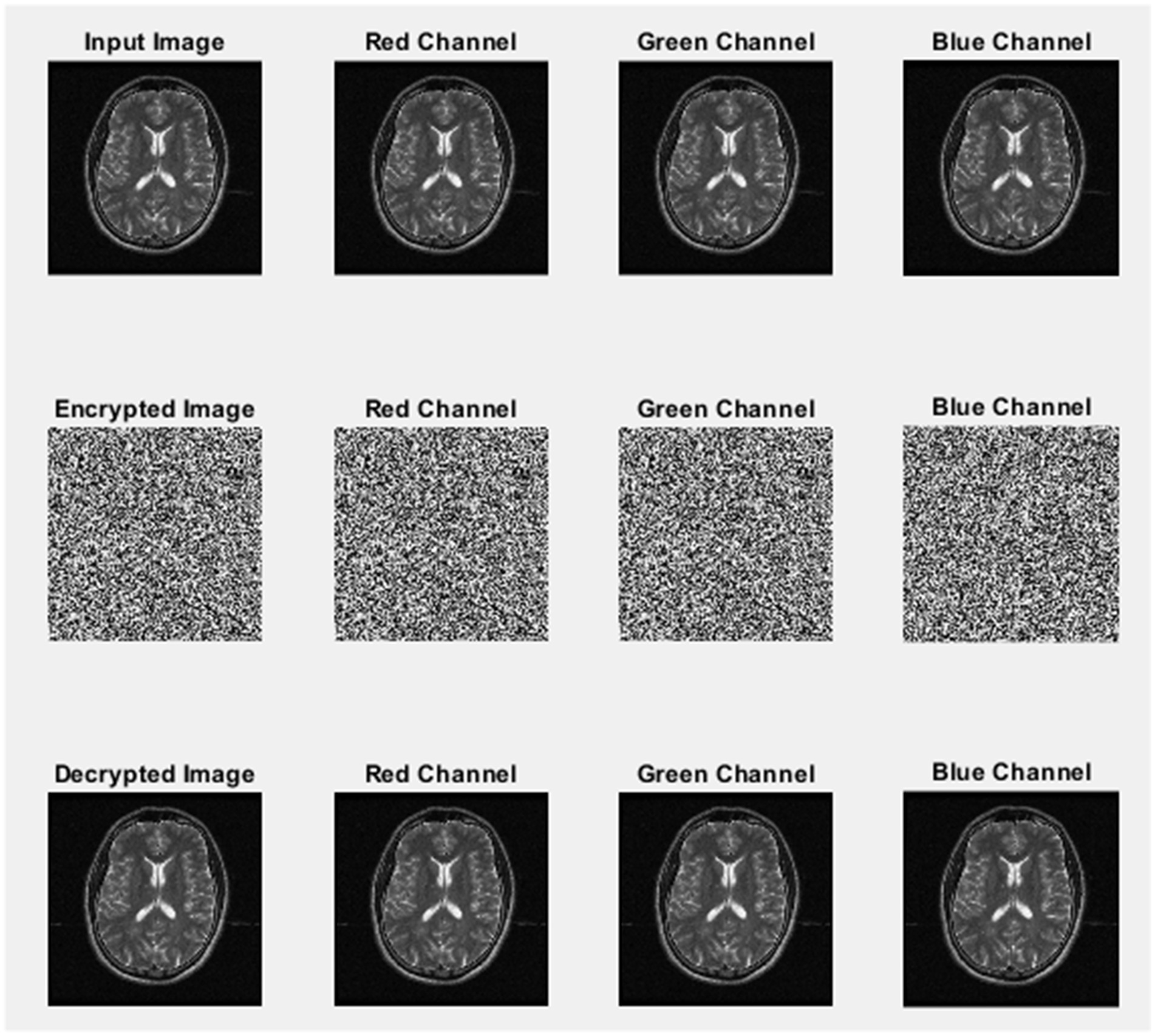
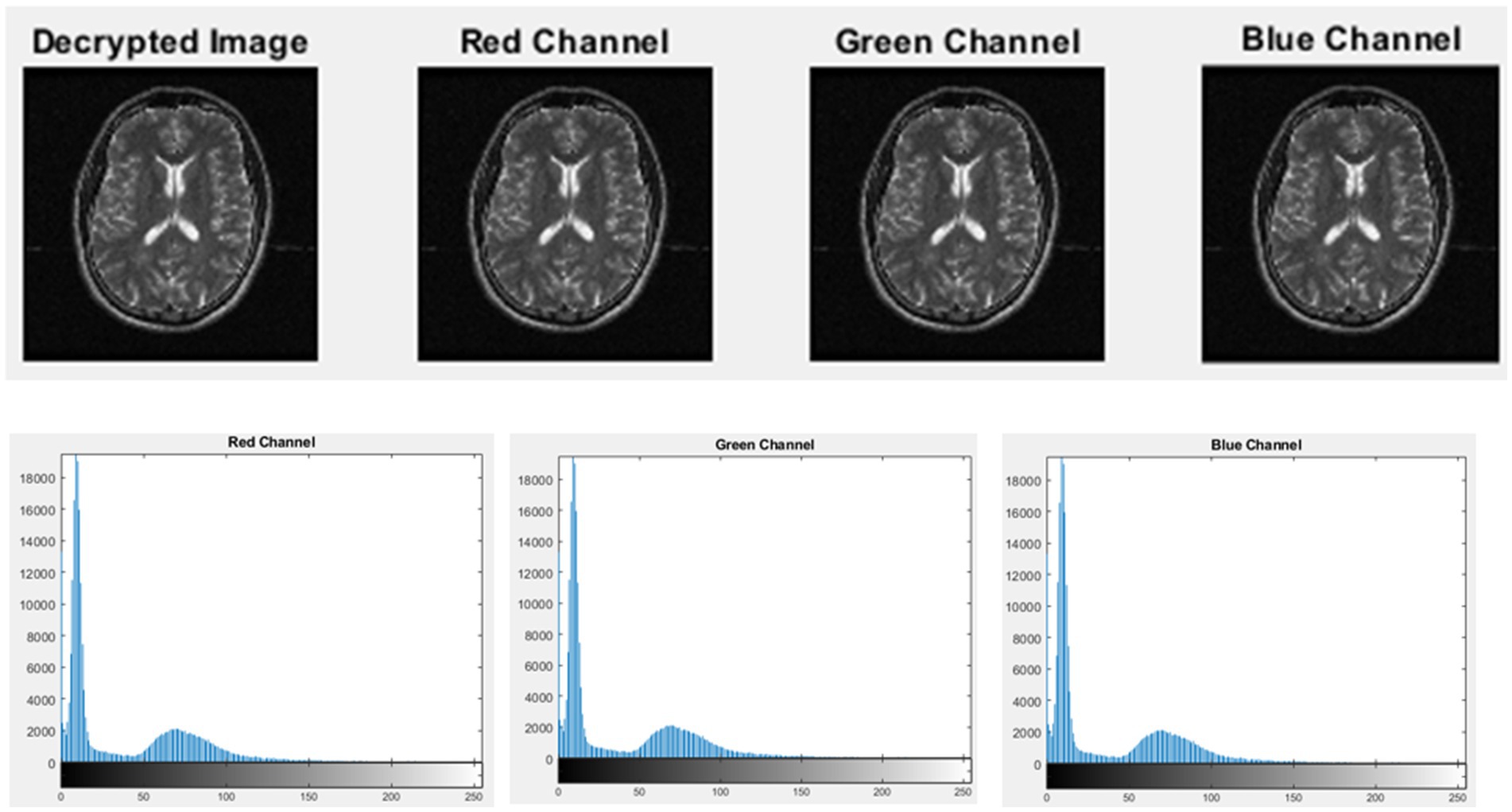
From Table 4, the null values for UACI, NPCR, and cross-entropy indicate a high degree of similarity between the original and decrypted images. The encryption and decryption processes become more reliable by using different channels. This guarantees that the image is securely transformed and precisely restored by protecting the integrity and confidentiality of data. The encryption and decryption processes of ECG, EEG, MRI, and X-ray medical images using the Fibonacci sequence and chaotic map are illustrated in Figures 5–8, respectively.

Figure 5

Figure 5. Encryption and decryption processes in ECG image.

Figure 6

Figure 6. Encryption and decryption processes in EEG image.

Figure 7

Figure 7. Encryption and decryption processes in MRI image.

Figure 8

Figure 8. Encryption and decryption processes in X-ray image.

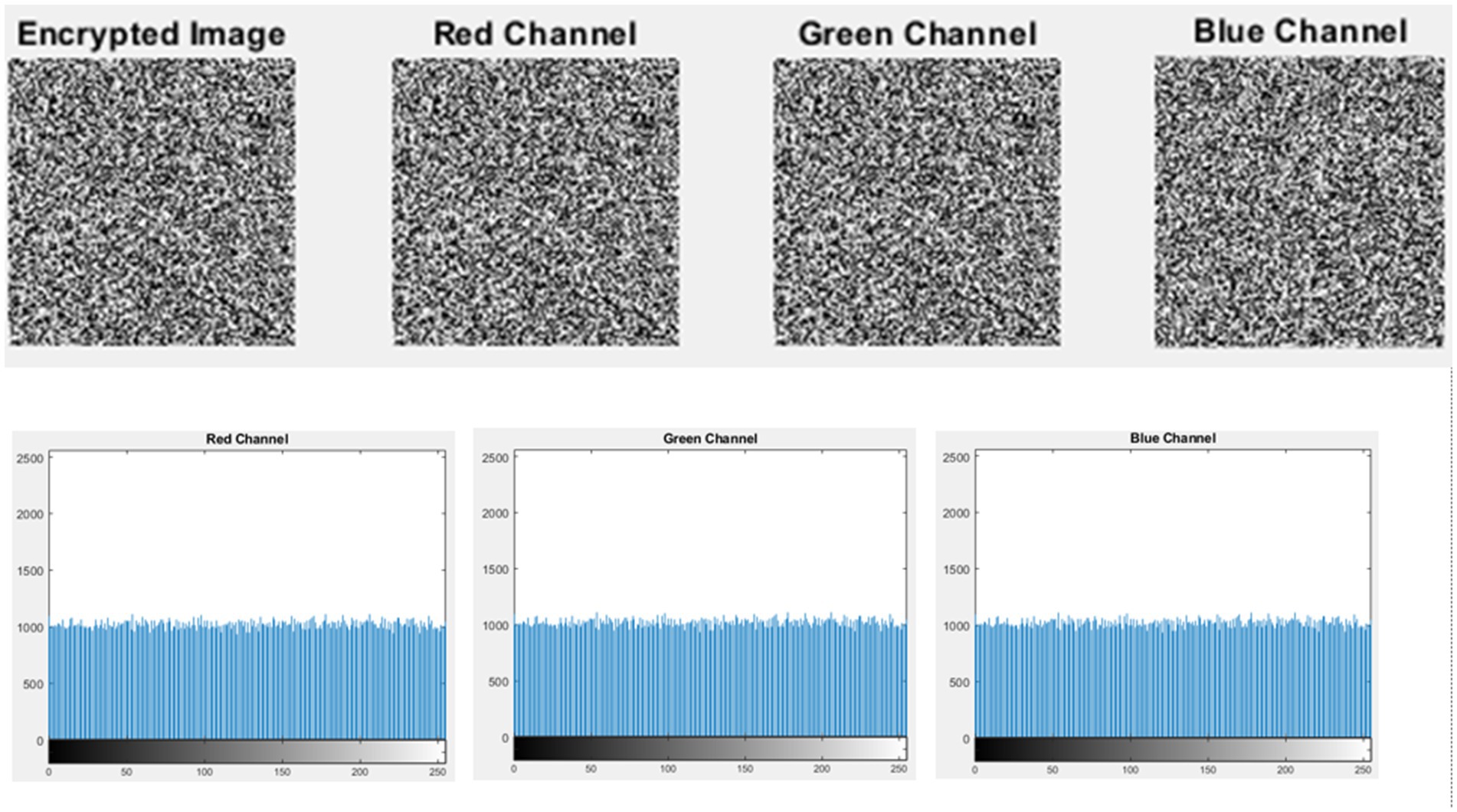
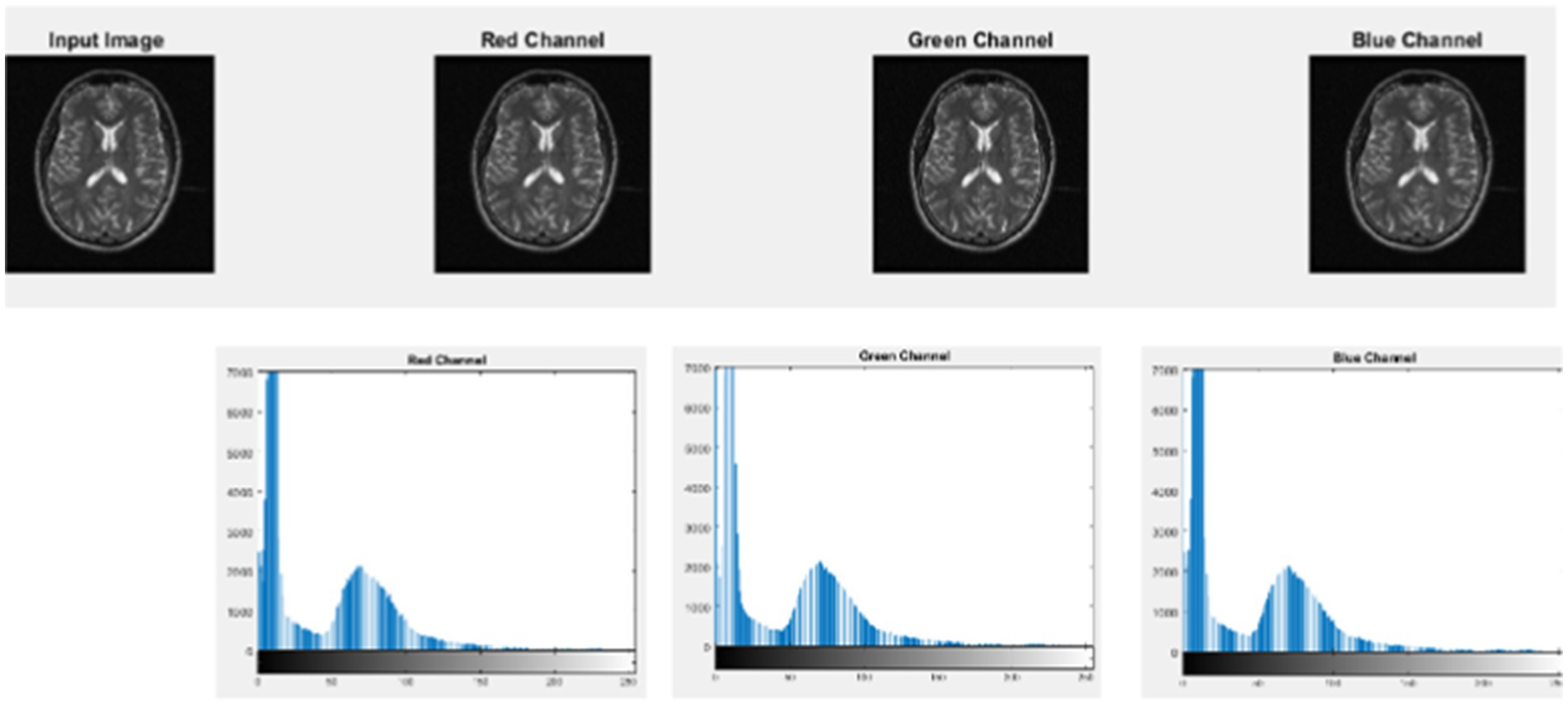
Figures 9–11 illustrate the histogram analysis of the input image, encrypted image channel, and decrypted image channel.

Figure 9

Figure 9. Histogram of original image.

Figure 10

Figure 10. Histogram analysis of encrypted image channels.

Figure 11

Figure 11. Histogram of decrypted image channels.

The encryption and decryption processes using the logistic-parity-based chaotic map are illustrated in Figure 12.

Figure 12

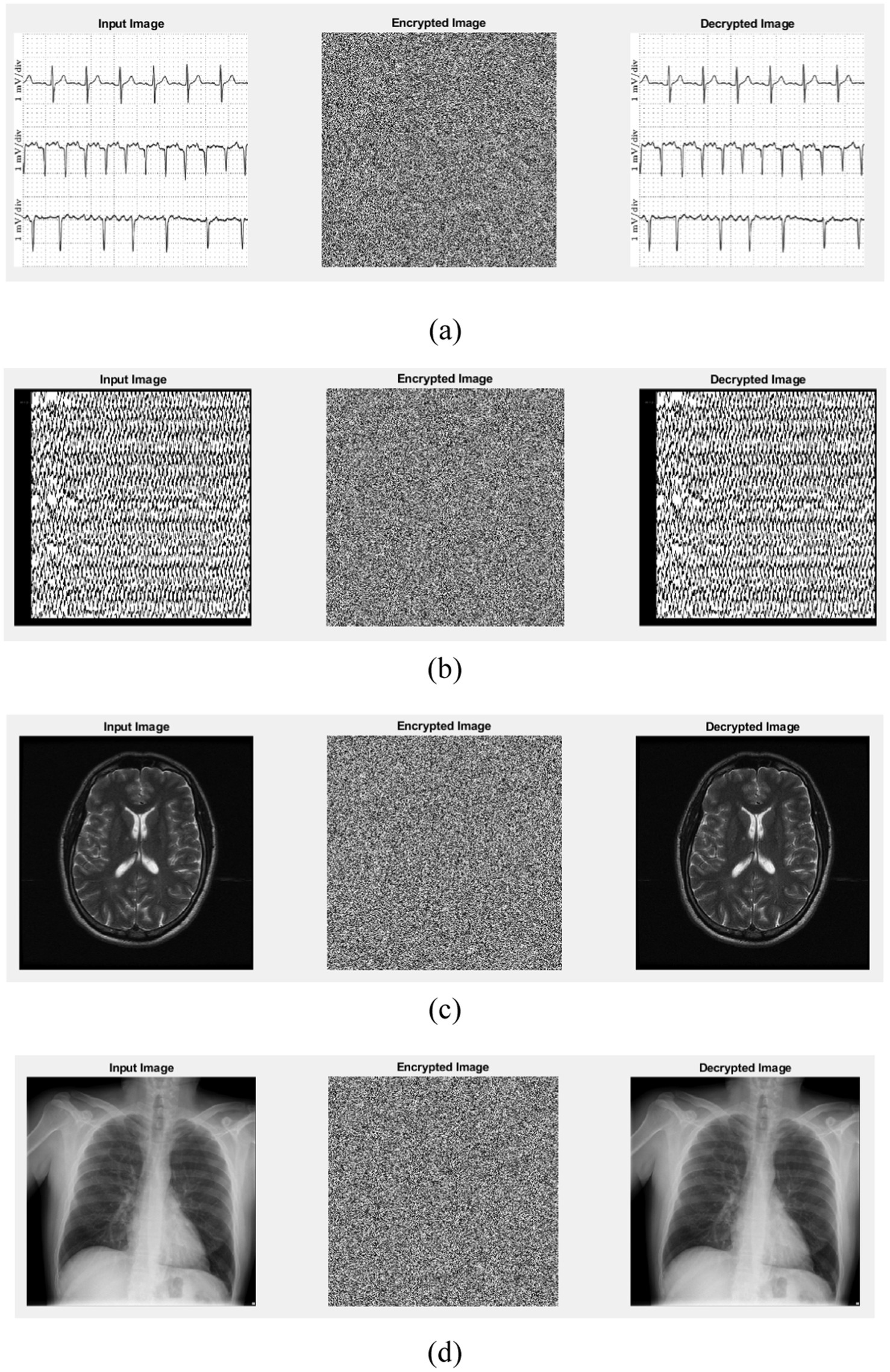
Figure 12. Encryption and decryption processes using the logistic-parity-based chaotic map: (a) ECG, (b) EEG, (c) MRI, and (d) X-ray.

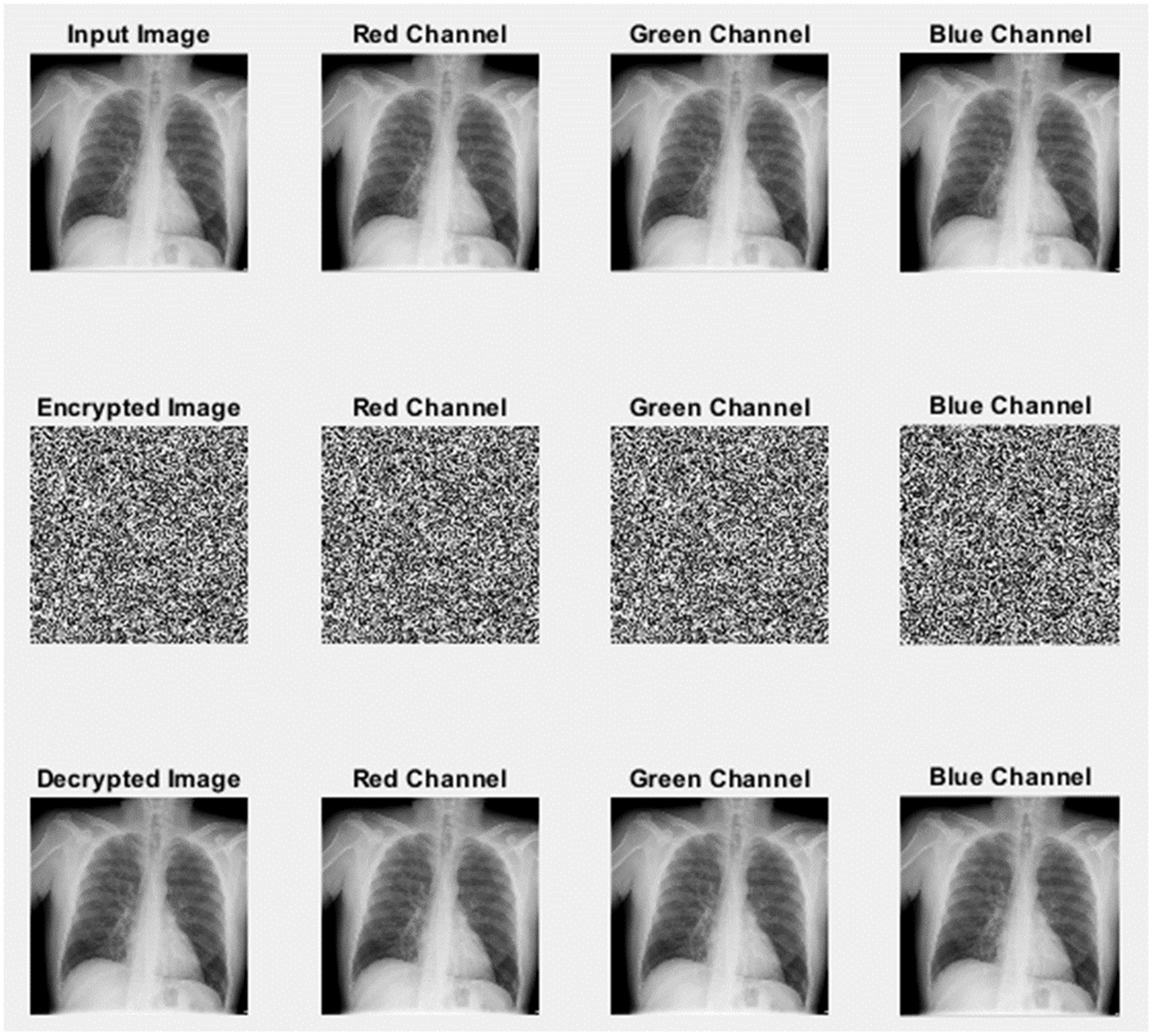
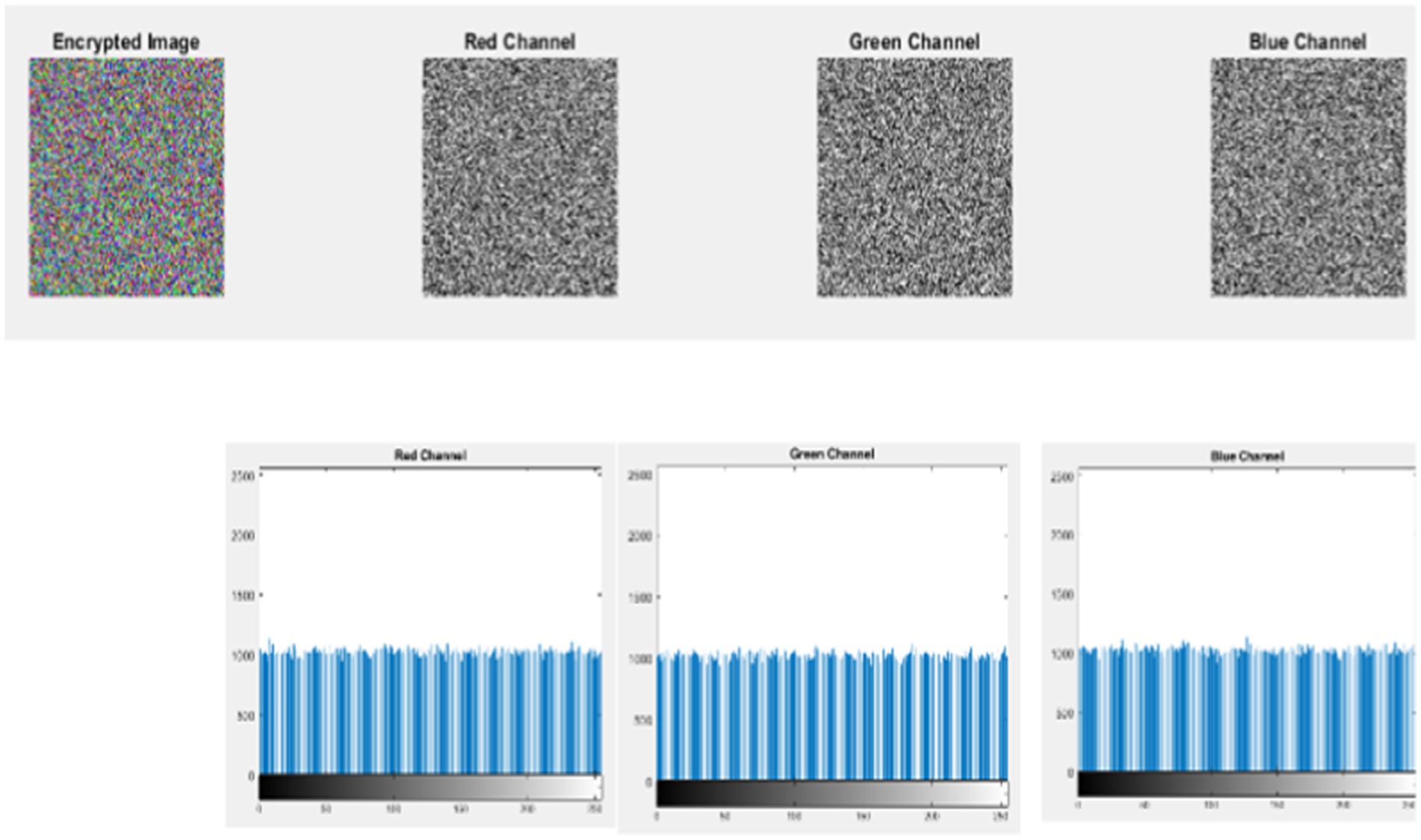
The histogram of the input X-ray image, encrypted image, and decrypted image using the logistic-parity-based chaotic map is illustrated in Figure 13.

Figure 13

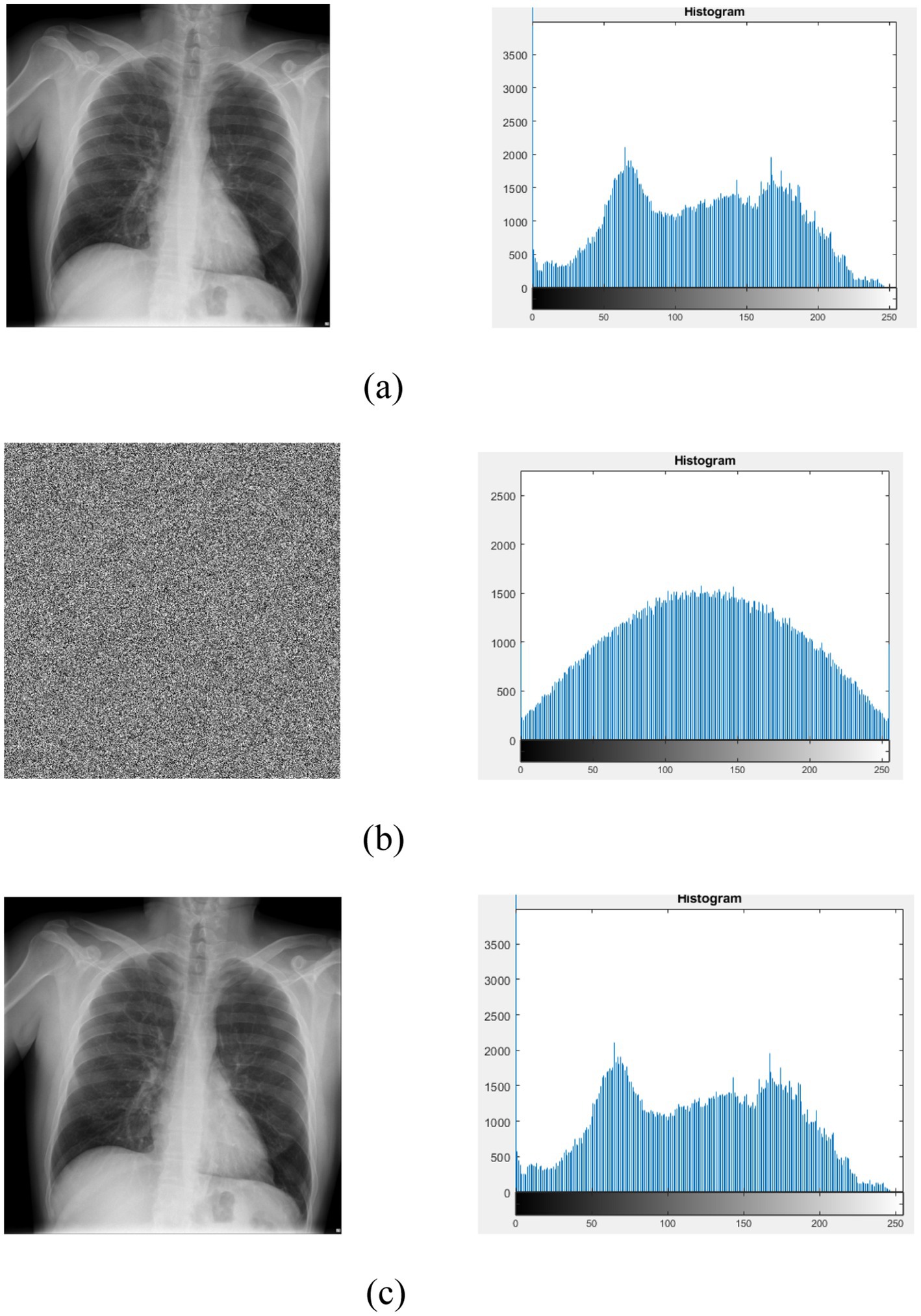
Figure 13. Histogram of input, encrypted, and decrypted X-ray image. (a) Input image with corresponding histogram analysis. (b) Encrypted image with corresponding histogram analysis. (c) Decrypted image with corresponding histogram analysis.

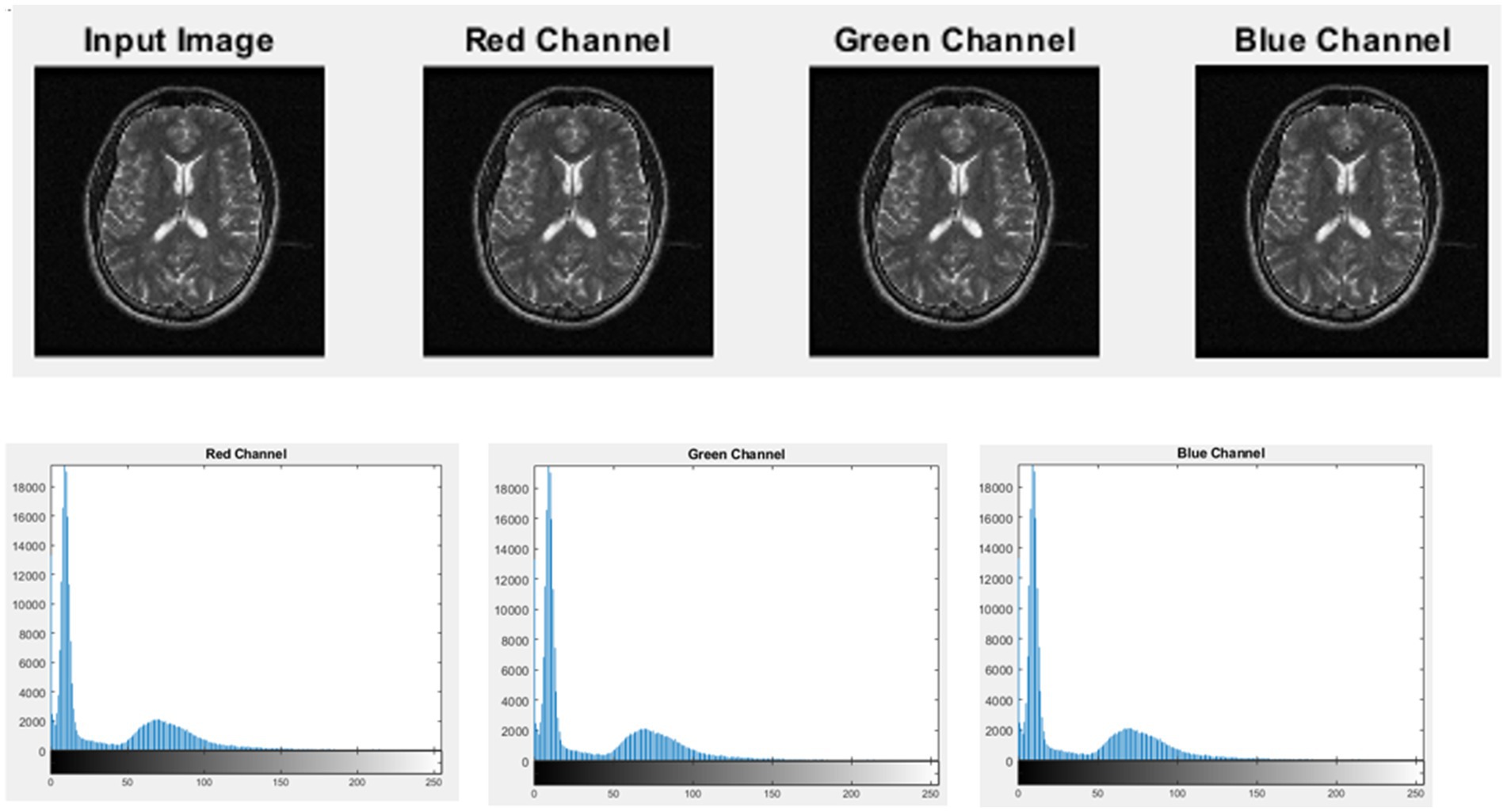
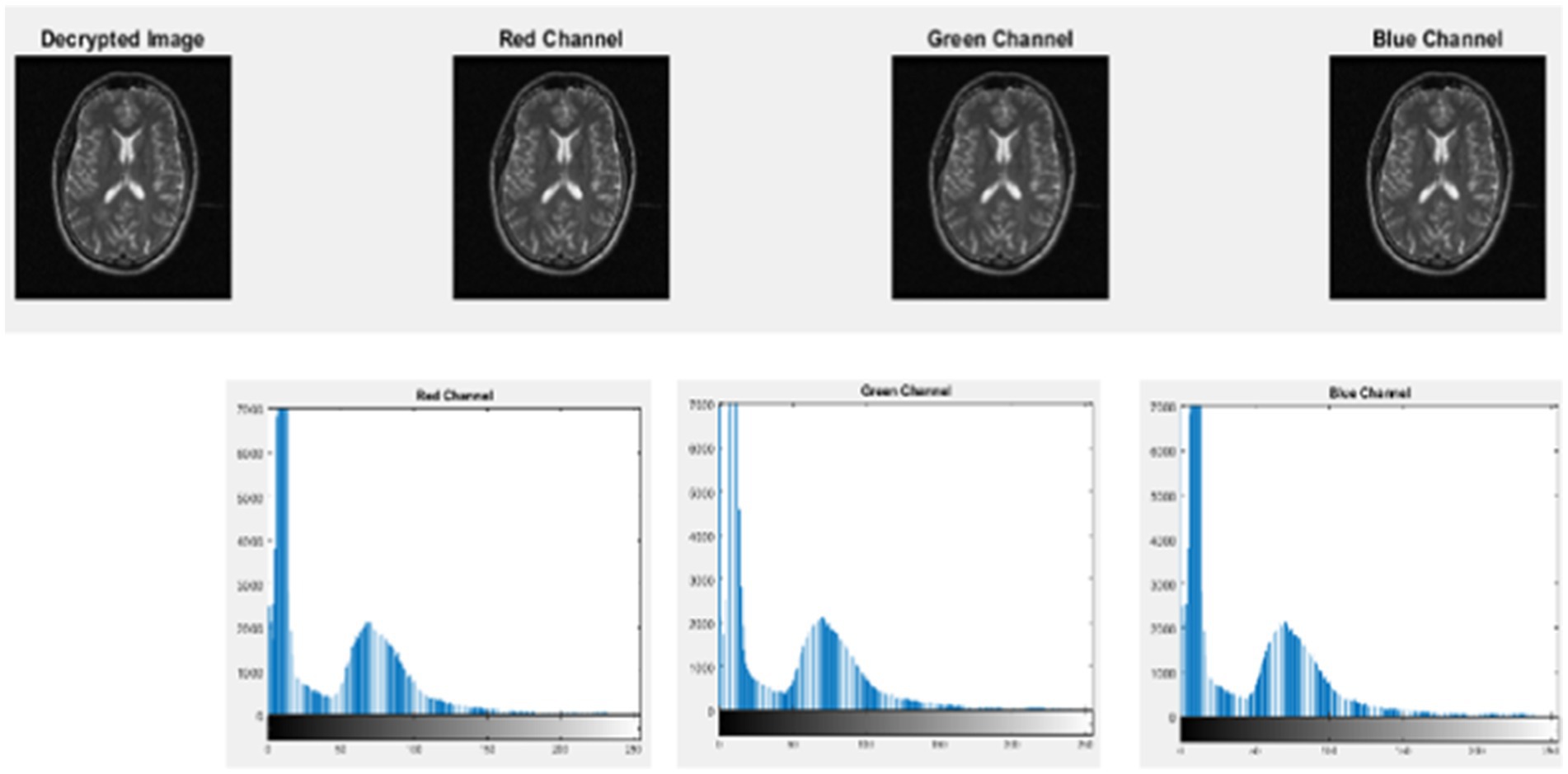
The histograms of the input image’s channel, the encrypted image’s channel, and the decrypted images of MRI medical image using CTE and dynamic chaotic system channel provide visual representations of their respective intensity distributions and are illustrated in Figures 13–16.

Figure 14

Figure 14. Histogram of input MRI image channel.

Figure 15

Figure 15. Histogram of encrypted MRI image channel.

Figure 16

Figure 16. Histogram of decrypted MRI image channel.

4.2 Performance comparison

Table 5 illustrates the performance comparison of the suggested algorithms with conventional methods in terms of evaluation metrics.

Table 5

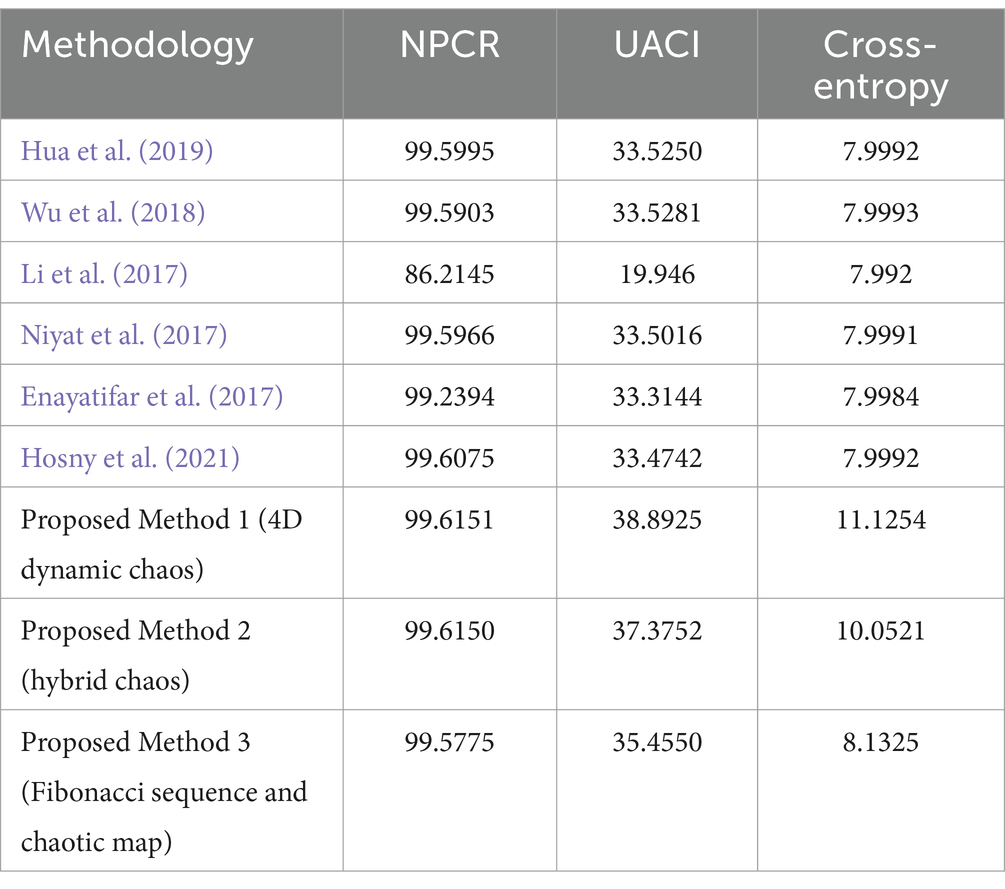
Table 5. Performance comparison of proposed lightweight cryptographic algorithms with existing methods.

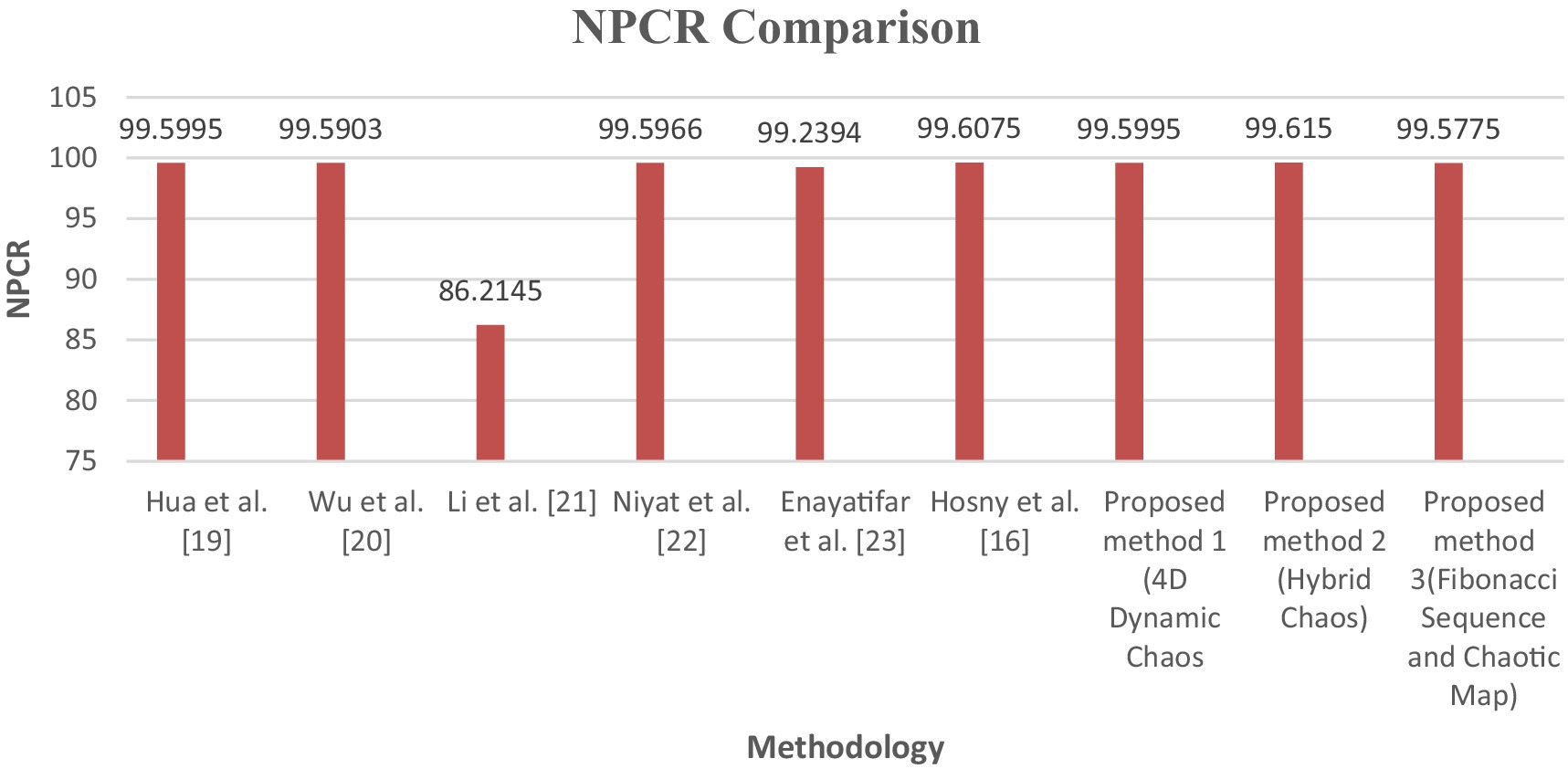
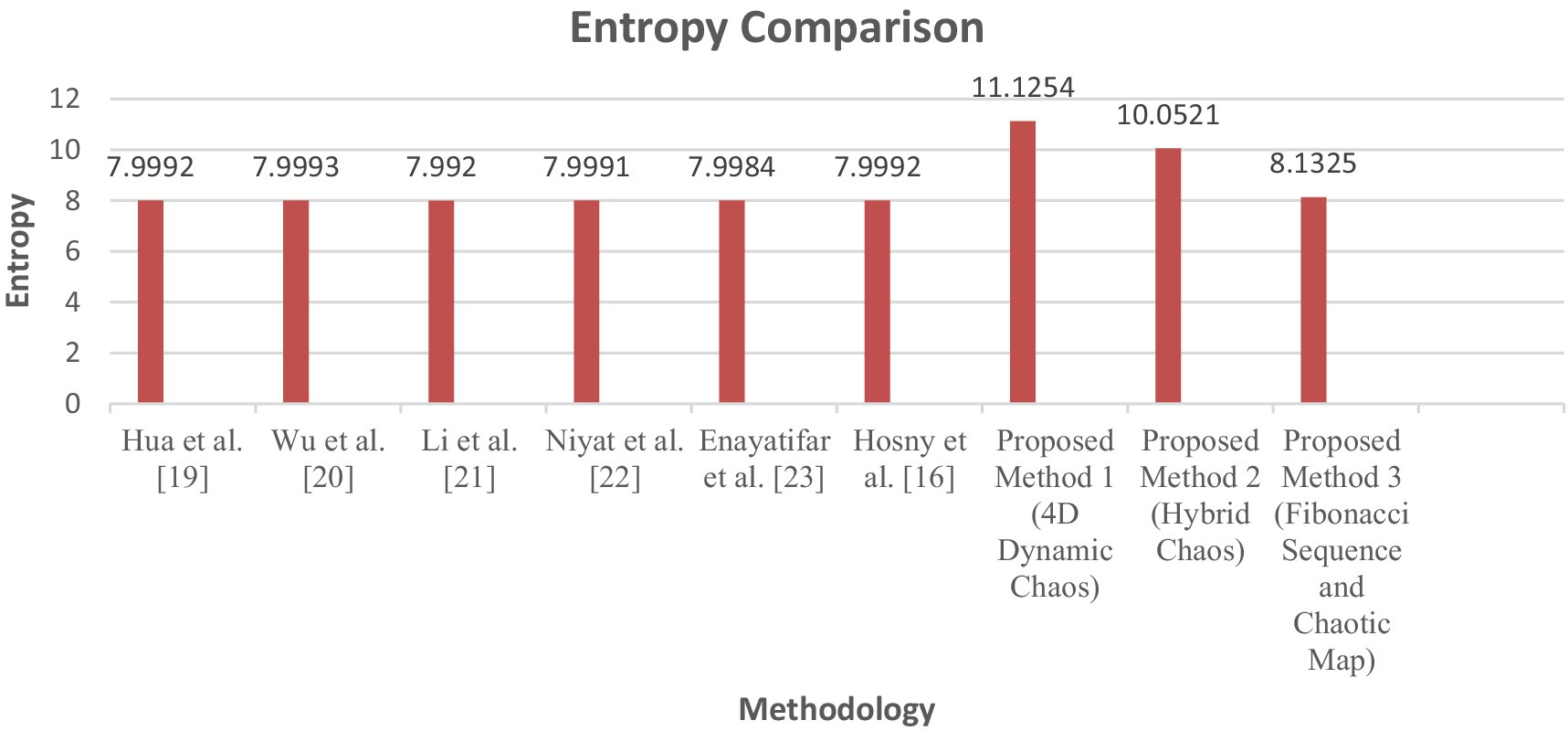
From Table 5, it is clear that the proposed lightweight cryptographic algorithms demonstrated enhanced security, outperforming existing methodologies in aspects of image encryption. The graphical representation of performance comparison in terms of evaluation metrics is given in Figures 17–19.

Figure 17

Figure 17. Graphical representation of NPCR comparison.

Figure 18

Figure 18. Graphical representation of UACI comparison.

Figure 19

Figure 19. Graphical representation of entropy comparison.

The proposed methods (Method 1 and Method 2) showed the highest NPCR at 99.6151 and 99.6150, respectively, indicating superior security against pixel change attacks. Method 3 also performed well with an NPCR of 99.5775, surpassing most existing techniques.

The proposed Method 1 and Method 2 excelled with UACI values of 38.8925 and 37.3752, respectively, demonstrating superior capability in pixel intensity change. Method 3 also outperformed existing methods with an UACI of 35.455.

Cross-entropy value of 8.1325 for proposed Method 3 (Fibonacci sequence and chaotic map) shows better unpredictability than existing techniques (7.992–7.9993). This improvement shows that Method 3 delivers encrypted outputs that are more secure and less predictable than prior solutions.

Proposed Method 1 (4D dynamic chaos) and Method 2 (hybrid chaos) greatly outperform Method 3. Method 1, with an entropy value of 11.1254, was the most random and secure. Method 2 fared well with an entropy value of 10.0521, demonstrating security and efficiency. These numbers show that the suggested approaches produce more unpredictable and secure encrypted pictures than existing methods. Method 3 performs well in pixel change rate and intensity diffusion with UACI and NPCR values of 35.4550 and 99.5775%, respectively. Overall performance is lower than Methods 1 and 2, which produce higher UACI values (38.8925% for Method 1 and 37.3752% for Method 2), demonstrating their greater encryption strength. Maximum randomization and encryption make Method 1 the best choice for high-security medical IoT applications.

For moderately constrained situations, Method 2 balances security and resource efficiency. Method 3 has better cross-entropy than Methods 1 and 2 but is less secure. It works best for modest security and resource-constrained applications. In conclusion, Method 1 and Method 2 improve data security and unpredictability beyond existing cryptographic algorithms.

4.3 Security analysis

This section will provide a systematic evaluation of the security of the proposed cryptographic system, focusing on its resilience against common attack strategies, including brute force attacks, differential attacks, and statistical/entropy-based attacks. The analysis utilizes essential cryptographic metrics to illustrate the system’s resilience and offers insights into its appropriateness for practical, real-world applications, including IoT environments.

4.3.1 Brute force attacks

Brute force assaults try all keys until the right one is located. The key space size and algorithm computational complexity define the proposed cryptographic scheme’s brute force resistance.

• Key space: Each dimension of the cryptographic model’s 6D hyper-chaotic system complicates the key space. Each chaotic map (logistic-parity map, Fibonacci Q-matrix) increases non-linearity and beginning condition sensitivity, improving system security. This creates an increasingly vast key space that makes brute force attacks computationally impossible. Even with high-efficiency parallel processing, the key space increases too fast for present computational resources.

• Cryptographic validation: NPCR and UACI values exceed 99.6 and 38%, respectively. These data show that even little plaintext modifications produce significantly different cipher texts, giving attackers no useful hints. The chaotic encryption prevents brute force attackers from using incomplete matches to find the key.

• Computational complexity: The exponential growth in key space complexity and significant initial condition sensitivity make brute force assaults impracticable under realistic time limitations. Even with contemporary processing power, brute force assaults are inefficient in IoT systems due to resource constraints.

4.3.2 Differential attacks

Differential attacks seek to identify correlations between plaintext and cipher text by examining the impact of minor alterations in the plaintext on the resulting encrypted output.

• Pixel sensitivity analysis: The NPCR and UACI metrics consistently demonstrate values exceeding 99.6 and 38%, respectively. This demonstrates that even slight modifications in the plaintext result in significant and unpredictable changes in the cipher text, effectively countering differential attacks. The elevated pixel sensitivity guarantees that attackers cannot deduce relationships between the input and output images.

• The proposed system utilizes a hybrid approach that integrates various chaotic maps, specifically the logistic-parity and Fibonacci Q-matrix, to improve both confusion and diffusion mechanisms.

• The 6D hyper-chaotic system facilitates confusion by scrambling pixel positions according to chaotic sequences. This guarantees that neighboring pixels in the plaintext are unpredictably altered.

• Diffusion transpires via the Fibonacci Q-matrix, modifying pixel values such that alterations disseminate throughout the entire image, thereby preventing any direct correlation between the original image and its encrypted version.

• The interplay of confusion and diffusion makes differential attacks ineffective due to the absence of a direct or predictable mapping from plaintext to cipher text.

4.3.3 Attacks based on statistical analysis and entropy

Statistical and entropy-based attacks utilize patterns in pixel intensity distributions within encrypted images to reveal information regarding the original image. The proposed system demonstrates significant resilience to these attacks, attributed to its randomization features and uniform distribution of pixel values.

• The histogram analysis of encrypted images reveals a uniform distribution of pixel intensities, suggesting that all pixel values possess equal probability. This uniformity inhibits attackers from conducting statistical analysis to identify patterns in the encrypted image.

• Entropy metrics: The entropy of the encrypted image, assessed through cross-entropy, attains values up to 11.1254, notably surpassing the threshold typically observed in conventional encryption methods, which is approximately 7.999. High entropy values suggest that the encrypted image exhibits significant randomness, lacking discernible structure or predictable patterns, thereby rendering statistical analysis impractical.

4.3.4 Pragmatic aspects and implementation in real-world scenarios

The proposed cryptographic system aims to be both lightweight and efficient, making it suitable for implementation in resource-constrained environments such as IoT devices, where computational power and memory are often limited.

• The encryption and decryption processes have been validated through implementation on standard hardware, demonstrating that the proposed system operates efficiently without introducing significant overhead, making it suitable for real-time applications in IoT scenarios.

• Resistance to specific attacks: While this study did not carry out explicit simulations for brute force or differential attacks, the cryptographic metrics reported (NPCR, UACI, and entropy) offer compelling theoretical support for the robustness of the proposed system. Future studies may involve comprehensive simulations of brute force time estimates and differential attack propagation to enhance the empirical evidence of the system’s resilience.

This study shows that the cryptographic system is secure against brute force, differential, and statistical/entropy attacks. The proposed system is secure and efficient because of its wide key space, high entropy, and excellent confusion and diffusion mechanisms. It is promising for safe picture encryption, especially in IoT contexts that require lightweight cryptographic solutions.

5 Comparison and recommendations

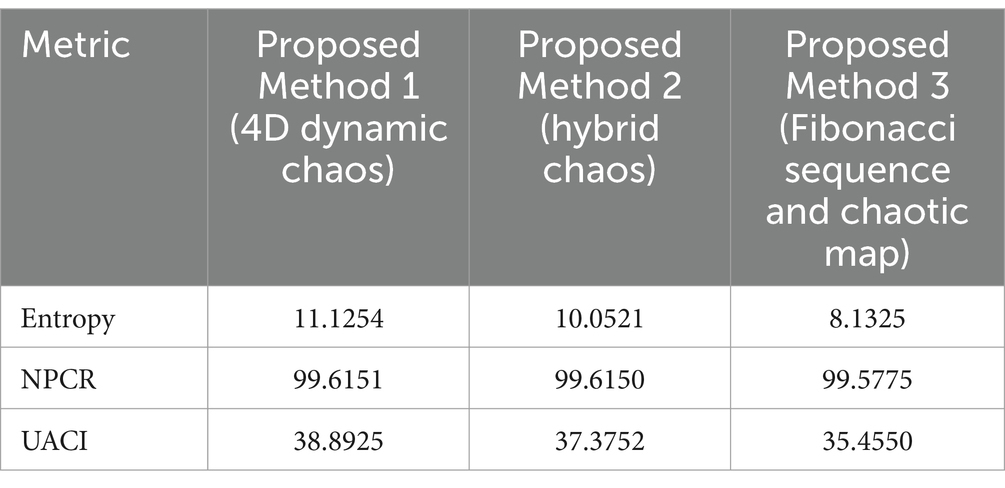
5.1 Entropy

• Proposed Method 1 (4D dynamic chaos): 11.1254—high randomness and secure.

• Proposed Method 2 (hybrid chaos): 10.0521—good randomness, but less than Method 1.

• Proposed Method 3 (Fibonacci sequence and chaotic map): 8.1325—low randomness, vulnerable to analysis.

5.2 NPCR

• Proposed Method 1: 99.59995%—excellent diffusion.

• Proposed Method 2: 99.615%—slightly better than Method 1.

• Proposed Method 3: 99.5775%—strong but slightly less effective than others.

5.3 UACI

• Proposed Method 1: 38.8925%—effective distribution of intensity changes.

• Proposed Method 2: 37.3752%—strong performance.

• Proposed Method 3: 35.4550%—weaker performance.

5.4 Interpretation

• Entropy: Higher entropy indicates better randomness and security in the encrypted image. Method 1 exhibits the highest entropy, suggesting it produces a highly randomized output. Method 2 is good but lower than Method 1, while Method 3 has significantly low entropy, indicating predictability (see Table 6).

Table 6

Table 6. Comparison of proposed algorithm methods.

All three approaches excel in this aspect, with Method 2 somewhat surpassing the others, suggesting that little alterations in the plain text considerably impact the encrypted picture.

• NPCR: NPCR values close to 100% suggest strong diffusion. All three methods perform excellently in this regard, with Method 2 slightly outperforming the others, indicating that small changes in the plaintext affect the encrypted image significantly.

• UACI: UACI values indicate how well changes in the plaintext result in changes in pixel intensity. Method 1 has the highest UACI, indicating an effective distribution of pixel intensity changes, followed closely by Method 2. Method 3 shows a lower UACI, suggesting weaker performance.

5.5 Lightweight complexity analysis

5.5.1 Proposed Method 1 (4D dynamic chaos)

Lightweight complexity: moderate to high. This method employs dynamic chaos with four dimensions, which can involve complex calculations. While it may require more resources than simpler methods, it is effective for high-security applications. Security performance: high entropy (11.1254), strong NPCR (99.6151%), and excellent UACI (38.8925%) indicate this method’s robustness in encryption.

5.5.2 Proposed Method 2 (hybrid chaos)

Lightweight complexity: moderate. It balances the complexity of chaos theory with practical encryption needs. The hybrid approach can optimize resource use while maintaining a good security profile. Security performance: slightly lower entropy (10.0521) than Method 1, but with very close NPCR (99.6150%) and UACI (37.3752%) values, indicating a solid performance that still prioritizes security.

5.5.3 Proposed Method 3 (Fibonacci sequence and chaotic map)

Lightweight complexity: low. This method relies on the Fibonacci sequence, making it computationally less intensive. However, this simplicity can compromise security. Security performance: very low entropy (8.1325), indicating poor randomness and predictability. Despite achieving a decent NPCR (99.5775%) and UACI (35.4550%), the overall security is compromised due to the lack of randomness.

6 Conclusion

In the realm of secure data transmission for medical IoT applications, it is essential to tackle the intertwined issues of security and computational efficiency. The swift advancement of IoT technology requires strong security protocols to safeguard sensitive information against possible breaches. Conventional encryption techniques, although secure, frequently entail significant computational demands that are inappropriate for the resource-limited contexts characteristic of IoT devices. This study introduces lightweight cryptographic algorithms tailored for healthcare IoT applications. The proposed algorithms utilize advanced techniques, including a 6D hyper-chaotic system with a Fibonacci Q-matrix, a logistic-parity-based chaotic map, and combined transformation and expansion with a dynamic chaotic system to attain a balance between security and performance. The evaluation metrics, namely, NPCR, UACI, and cross-entropy, illustrate the efficacy of these algorithms in preserving high-security levels while reducing computational complexity. Among the proposed methods, Method 1 (4D dynamic chaos) stands out as the most effective option for encrypted image security, demonstrating superior entropy along with robust NPCR and UACI values. This indicates a strong ability to generate random outputs and efficiently mitigate pixel intensity variations, rendering it suitable for high-security applications. Method 2 (hybrid chaos) presents a viable alternative, offering an effective balance between security and resource efficiency, thus making it appropriate for applications with moderate resource limitations. In contrast, Method 3 (Fibonacci sequence and chaotic map) is straightforward to implement and demands minimal computational resources; however, it is unsuitable for secure applications because of its markedly low entropy and inadequate randomness. This trade-off underscores the necessity of choosing the suitable encryption method according to the application’s specific requirements. In conclusion, the suggested methods for ensuring secure data transmission in medical IoT applications are as follows: optimal for security: Proposed Method 1 (4D dynamic chaos), optimal for balanced performance: Proposed Method 2 (hybrid chaos), and optimal for lightweight implementation: Proposed Method 3 (Fibonacci sequence and chaotic map), although it is advised against its application in security-sensitive contexts due to identified deficiencies in randomness and distribution.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

AR: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Writing – original draft, Writing – review & editing. RK: Supervision, Validation, Visualization, Writing – review & editing.

Funding

The author(s) declare that no financial support was received for the research and/or publication of this article.

Acknowledgments

The author AR wishes to convey their heartfelt appreciation to all who aided the study. They express their sincere gratitude to their supervisor, family, coworkers and fellow researchers for their support and understanding during the challenging stages of the study.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The authors declare that no Gen AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fcomp.2025.1522184/full#supplementary-material

SUPPLEMENTARY FIGURE S1 | Input medical images.

SUPPLEMENTARY FIGURE S2 | Illustration of Fibonacci sequence.

SUPPLEMENTARY FIGURE S3 | Modified logistic map.

SUPPLEMENTARY FIGURE S4 | Bifurcation diagram of logistic map.

SUPPLEMENTARY FIGURE S5 | Bifurcation diagram of parity map.

SUPPLEMENTARY FIGURE S6 | Decryption block diagram.

SUPPLEMENTARY FIGURE S7 | Block diagram of CTE and dynamic chaotic system.

SUPPLEMENTARY FIGURE S8 | Dynamic chaotic system.

SUPPLEMENTARY FIGURE S9 | Block diagram of combined transformation and expansion.

SUPPLEMENTARY FIGURE S10 | Encryption and decryption processes in CTE.

References

Al-Azzawi, R. M. A., and Al-Dabbagh, S. S. M. (2024). Securing data in IoT-RFID-based systems using lightweight cryptography algorithm. Advances in intelligent computing techniques and applications. eds. F. Saeed, F. Mohammed, and Y. Fazea (Cham: Springer.) 211, 26–38.

Google Scholar

Alluhaidan, A. S. D., and Prabu, P. (2023). End-to-end encryption in resource-constrained IoT device. IEEE Access 11, 70040–70051. doi: 10.1109/ACCESS.2023.3292829

Crossref Full Text | Google Scholar

Chaudhary, R. R. K., and Chatterjee, K. (2020). An efficient lightweight cryptographic technique for IoT based E-healthcare system. 2020 7th International Conference on Signal Processing and Integrated Networks (SPIN). 991–995.

Google Scholar

Chen, H., Liu, Z., Tanougast, C., Liu, F., and Blondel, W. (2021). Optical cryptosystem scheme for hyperspectral image based on random spiral transform in gyrator domains. Opt. Lasers Eng. 137:106375. doi: 10.1016/j.optlaseng.2020.106375

Crossref Full Text | Google Scholar

Das, S., and Namasudra, S. (2023). Lightweight and efficient privacy-preserving mutual authentication scheme to secure internet of things-based smart healthcare. Trans. Emerg. Telecommun. Technol. 34:e4716. doi: 10.1002/ett.4716

Crossref Full Text | Google Scholar

Das, S., Namasudra, S., Deb, S., Ger, P. M., and Crespo, R. G. (2023). Securing IoT-based smart healthcare systems by using advanced lightweight privacy-preserving authentication scheme. IEEE Internet Things J. 10, 18486–18494. doi: 10.1109/JIOT.2023.3283347

Crossref Full Text | Google Scholar

Enayatifar, R., Abdullah, A. H., Isnin, I. F., Altameem, A., and Lee, M. (2017). Image encryption using a synchronous permutation-diffusion technique. Opt. Lasers Eng. 90, 146–154. doi: 10.1016/j.optlaseng.2016.10.006

Crossref Full Text | Google Scholar

Gong, L. H., and Luo, H. X. (2023). Dual color images watermarking scheme with geometric correction based on quaternion FrOOFMMs and LS-SVR. Opt. Laser Technol. 167:109665. doi: 10.1016/j.optlastec.2023.109665

Crossref Full Text | Google Scholar

Guo, Z., Chen, S. H., Zhou, L., and Gong, L. H. (2024). Optical image encryption and authentication scheme with computational ghost imaging. Appl. Math. Model. 131, 49–66. doi: 10.1016/j.apm.2024.04.012

Crossref Full Text | Google Scholar

Hasan, M. K., Islam, S., Sulaiman, R., Khan, S., Hashim, A. H. A., Habib, S., et al. (2021). Lightweight encryption technique to enhance medical image security on internet of medical things applications. IEEE Access 9, 47731–47742. doi: 10.1109/ACCESS.2021.3061710

Crossref Full Text | Google Scholar

Hosny, K. M., Kamal, S. T., Darwish, M. M., and Papakostas, G. A. (2021). New image encryption algorithm using hyperchaotic system and Fibonacci Q-matrix. Electronics 10:1066. doi: 10.3390/electronics10091066

Crossref Full Text | Google Scholar

Hu, L., Chen, M., Wang, M., and Zhou, N. (2024). A multi-image encryption scheme based on block compressive sensing and nonlinear bifurcation diffusion. Chaos Solitons Fractals 188:115521. doi: 10.1016/j.chaos.2024.115521

Crossref Full Text | Google Scholar

Hua, Z., Zhou, Y., and Huang, H. (2019). Cosine-transform-based chaotic system for image encryption. Inf. Sci. 480, 403–419. doi: 10.1016/j.ins.2018.12.048

Crossref Full Text | Google Scholar

Jebri, S., Ben Amor, A., Abid, M., and Bouallegue, A. (2021). Enhanced lightweight algorithm to secure data transmission in IoT systems. Wirel. Pers. Commun. 116, 2321–2344. doi: 10.1007/s11277-020-07792-3

Crossref Full Text | Google Scholar

Karunarathne, S. M., Saxena, N., and Khan, M. K. (2021). Security and privacy in IoT smart healthcare. IEEE Internet Comput. 25, 37–48. doi: 10.1109/MIC.2021.3051675

Crossref Full Text | Google Scholar

Khan, A. A., Laghari, A. A., Shaikh, Z. A., Dacko-Pikiewicz, Z., and Kot, S. (2022). Internet of Things (IoT) security with blockchain technology: a state-of-the-art review. IEEE Access 10, 122679–122695. doi: 10.1109/ACCESS.2022.3223370

Crossref Full Text | Google Scholar

Li, C., Luo, G., Qin, K., and Li, C. (2017). An image encryption scheme based on chaotic tent map. Nonlinear Dyn. 87, 127–133. doi: 10.1007/s11071-016-3030-8

Crossref Full Text | Google Scholar

Mahajan, H. B., and Junnarkar, A. A. (2023). Smart healthcare system using integrated and lightweight ECC with private blockchain for multimedia medical data processing. Multimed. Tools Appl. 82, 44335–44358. doi: 10.1007/s11042-023-15204-4

PubMed Abstract | Crossref Full Text | Google Scholar

Mahlake, N., Mathonsi, T. E., Du Plessis, D., and Muchenje, T. (2023). A lightweight encryption algorithm to enhance wireless sensor network security on the internet of things. J. Commun. 18, 47–57. doi: 10.12720/jcm.18.1.47-57

PubMed Abstract | Crossref Full Text | Google Scholar

Niyat, A. Y., Moattar, M. H., and Torshiz, M. N. (2017). Color image encryption based on hybrid hyper-chaotic system and cellular automata. Opt. Lasers Eng. 90, 225–237. doi: 10.1016/j.optlaseng.2016.10.019

Crossref Full Text | Google Scholar

Olayah, F., Yami, M. A., Abosaq, H. A., Abdelrahman Ali, Y. A., Siddiqui, M. A., Irshad, R. R., et al. (2024). An efficient lightweight crypto security module for protecting data transmission through IOT based electronic sensors. J. Nanoelectron. Optoelectron. 19, 646–657. doi: 10.1166/jno.2024.3609

Crossref Full Text | Google Scholar

Qaid, G. R., and Ebrahim, N. S. (2023). A lightweight cryptographic algorithm based on DNA computing for IoT devices. Secur. Commun. Netw. 2023, 1–12. doi: 10.1155/2023/9967129

PubMed Abstract | Crossref Full Text | Google Scholar

Raziq, A., Qureshi, K. N., Yar, A., Ghafoor, K. Z., and Jeon, G. (2024). Lightweight hybrid cryptography algorithm for wireless body area sensor networks using cipher technique. Comput. Assist. Methods Eng. Sci. 31, 213–240. doi: 10.24423/cames.2024.594

Crossref Full Text | Google Scholar

SaberiKamarposhti, M., Ghorbani, A., and Yadollahi, M. (2024). A comprehensive survey on image encryption: taxonomy, challenges, and future directions. Chaos Solitons Fractals 178:114361. doi: 10.1016/j.chaos.2023.114361

Crossref Full Text | Google Scholar

Sandner, P., Gross, J., and Richter, R. (2020). Convergence of blockchain, IoT, and AI. Front. Blockchain 3:522600. doi: 10.3389/fbloc.2020.522600

Crossref Full Text | Google Scholar

Valsalan, P., Ahmed, T., and Ali, H. (2020). IoT based health monitoring system. J. Crit. Rev. doi : doi: 10.31838/jcr.07.04.137

Crossref Full Text | Google Scholar

Wang, J., Lim, M. K., Wang, C., and Tseng, M. L. (2021). The evolution of the Internet of Things (IoT) over the past 20 years. Comput. Ind. Eng. 155:107174. doi: 10.1016/j.cie.2021.107174

Crossref Full Text | Google Scholar

Wu, J., Liao, X., and Yang, B. (2018). Image encryption using 2D Hénon-Sine map and DNA approach. Signal Process. 153, 11–23. doi: 10.1016/j.sigpro.2018.06.008

Crossref Full Text | Google Scholar

Zhou, N. R., Tong, L. J., and Zou, W. P. (2023). Multi-image encryption scheme with quaternion discrete fractional Tchebyshev moment transform and cross-coupling operation. Signal Process. 211:109107. doi: 10.1016/j.sigpro.2023.109107

Crossref Full Text | Google Scholar

Zou, J. Z., Chen, M. X., and Gong, L. H. (2025). Invisible and robust watermarking model based on hierarchical residual fusion multi-scale convolution. Neurocomputing 614:128834. doi: 10.1016/j.neucom.2024.128834

Crossref Full Text | Google Scholar