- School of Computing and Communications, Lancaster University, Lancaster, United Kingdom
Classical models of computation are useful for understanding computability in the small; however, they fall short when it comes to analyzing large-scale, complex computations. To address this gap, theoretical computer science has witnessed the emergence of several formalisms that attempt to raise the level of abstraction with the aim of describing not only a single computing device but interactions among a collection of them. In this paper, we unify such formalisms under a common framework, which we refer to as Models of High-Level Computation. Our aim is to offer an accessible overview of these models.
1 Introduction
Classical models of computation formally emerged during the first half of the century 20th, as an attempt to capture the very essence of computation in the form of information processing. Under the Church-Turing thesis, these models have been successful to describe any possible effective procedure construed as a (monolithic) algorithmic process. Although they can be used to describe complex computations, classical models fail to provide expressive means to do so, apart from not being suitable to accept information streams at computation-time. Describing complex computations has become essential nowadays since the scale and complexity of computing systems is exponentially increasing (especially in the realm of distributed computing). Accordingly, plenty of Models of High-Level Computation (MHCs) have been proposed over the last half century so as to capture the essence of complex computations. In this paper, we describe the meaning, key properties and representative paradigms of MHCs, and identify promising directions for future research in advancing their theory and application.
The rest of the paper is structured as follows. Section 2 describes the general notion of MHCs. Section 3 sketches the design of a simple MHC with the aim of discussing the key elementary properties of such models. Section 4 presents a preliminary classification of MHCs by considering three major paradigms. Section 5 outlines the conclusions and future directions of the research area this paper introduces.
2 What is a model of high-level computation?
Before describing what an MHC is, let us consider an e-commerce web application composed of several microservices running on different machines, each with its own state and behavior (e.g., user authentication or payment processing). Modeling this application as a single Turing machine (i.e., as a low-level computing device) would require encoding all possible states and communication interleavings into one massive transition table, which may be both impractical and intractable, especially as the number of microservices and interactions increase. To make things worse, this application would require not only reasoning about control flow but also about data flow to formally determine the order in which (distributed) computing devices (i.e., microservices) are activated and how data is exchanged among them, respectively. As classical, single-device models of computation primarily focus on control flow, they are unsuitable to adequately describe or analyse our web application and modern computing systems in general. Rather than thinking about computation in the small, what we need is a formal approach to compositionally construct global complex behavior from local simple computations. This is where MHCs come into play.
An MHC raises the level of abstraction of its classical, low-level counterpart (e.g., Turing Machines) by providing a birds-eye-view of multiple computing devices rather than focusing on a single one (see Box 1).1 As individual devices are treated as modular black boxes, their internal details are irrelevant. What matters is how to glue together multiple (low- or even high-level) computations in order to form more complex ones. Thus, an MHC induces modularity and describes how computing devices interact with the aim of processing information that may be initially encoded, that can continuously be produced by an exogenous entity or any combination thereof.2 That is, an MHC can be open or closed.3
Box 1. What is an MHC?
Rather than describing how a single computing device produces an output from a given input, an MHC gives a birds-eye-view on multiple interacting computing devices. For this, an MHC provides formal rules to determine the moment in which a each participant device should compute and how devices must interact.
By the above, it is evident that an MHC needs to intrisically separate computation from interaction. Therefore, a so-called composition mechanism needs to be used. A composition mechanism particularly specifies how computing devices interact from a high-level perspective. An interaction always defines control flow either implicitly or explicitly. It is explicit when there is a clear construct specifying the order of invocation of computing devices, and implicit otherwise. Apart from control, an interaction can optionally define implicit or explicit data flow to establish a data exchange scheme among computing devices.4
Typically, computing devices facilitate composition by providing interfaces that serve as endpoints to entry or exit some internal computational structure. Enabling these endpoints is what allows treating computing devices as high-level, modular black boxes which can be composed algebraically or non-algebraically (see Box 2). Only algebraic composition enables compositionality, a necessary property to ensure closure by the provision of higher-order operators that receive a number of computing devices and produce a composite one which can, in turn, be used as an operand to construct even more complex computing devices (see Figure 1).
Box 2. Key properties of an MHC.
An MHC (i) can be open or closed, (ii) induces modularity by black-boxing computing devices (with clear interfaces), (iii) separates computation from interaction, (iv) always defines explicit or implicit control flow, (v) optionally defines explicit or implicit data flow, and (vi) enables interaction among computing devices via a composition mechanism (which can be algebraic or non-algebraic).

Figure 1. Conceptual representation of an algebraic composition operator that takes M computing devices and produces a composite one. Each device operand can be either composite or non-composite.
Evidently, algebraic composition relies on well-defined operators, together with algebraic laws (e.g., associativity), to formally combine computing devices; thereby, ensuring that the structure of any composite is deterministic (i.e., predictable) and can be reasoned about formally. Algebraic composition supports high modularity and reuse, since computations are designed to be composable according to predefined rules. Any algebraic composite is itself a valid (high-level) computation that preserves properties from the operands and can be further composed into more complex computing devices. Non-algebraic (ad-hoc) composition does not guarantee this preservation property or predictability because computations need to be glued together manually without any formal basis, leading to unforeseen incompatibilities and no guarantees that composites are valid, modular or reusable.5
3 Designing a simple MHC
For the sake of argument, even if not computationally powerful, in this section we design a simple MHC to demonstrate the key properties discussed in Section 2. For this, we consider computing devices in the form of Nondeterministic Finite Automata (NFAs) as well as composition operators for concatenating (⊕) and parallelising (⊗) — see Definition 1. The behavior of ⊕ and ⊗ is directly derivable from the respective proofs of closure under concatenation and union of regular languages (Sipser, 2013), as shown by Definitions 2 and 3.
Definition 1 (NFA). Let 𝔸 be the universe of NFAs. A NFA N ∈ 𝔸 is a tuple (Σ, S, s, δ, F) where Σ is a finite set of input symbols which always contains the empty string ϵ, S is a finite set of states, s ∈ S is called an initial state, is a transition function and F ⊆ S is an empty or nonempty set of final states. We say that N accepts a string w = x1x2 … xn over Σ if there is a sequence satisfying the following conditions:
1. p0 = s,
2. pi + 1 ∈ δ(pi, xi+1) for i = 0, …, n − 1 and
3. pn ∈ F.
Definition 2 (Concatenative NFA). The concatenation operator ⊕:𝔸 × 𝔸 → 𝔸 is a binary function that receives two NFAS, N1 = (Σ1, S1, s1, δ1, F1) and N2 = (Σ2, S2, s2, δ2, F2), and produces a concatenative NFA N1 ⊕ N2 = (Σ0, S0, s0, δ0, F0) where Σ0 = Σ1 ∪ Σ2, S0 = S1 ∪ S2, s0 is the initial state s1 of N1, F0 = F2 and:
for any state s ∈ S0 and any symbol x ∈ Σ0.
Definition 3 (Parallel NFA). The parallelising operator ⊗:𝔸 × 𝔸 → 𝔸 is a binary function that receives two NFAS, N1 = (Σ1, S1, s1, δ1, F1) and N2 = (Σ2, S2, s2, δ2, F2), and produces a parallel NFA N1 ⊗ N2 = (Σ0, S0, s0, δ0, F0) where Σ0 = Σ1 ∪ Σ2, S0 = S1 ∪ S2 ∪ {s0}, F0 = F1 ∪ F2 and:
for any state s ∈ S0 and any symbol x ∈ Σ0.
After defining the algebraic composition operators for our MHC, let us now consider the NFA N1 depicted in Figure 2a which recognizes the language L1 = {w} where w is a string over {a, b} containing the symbol “b” at the third position (from right to left) such as abaabaa (Sipser, 2013). Also, consider the NFA N2 depicted in Figure 2b which recognizes the language for m > 0 and n ≥ 0.
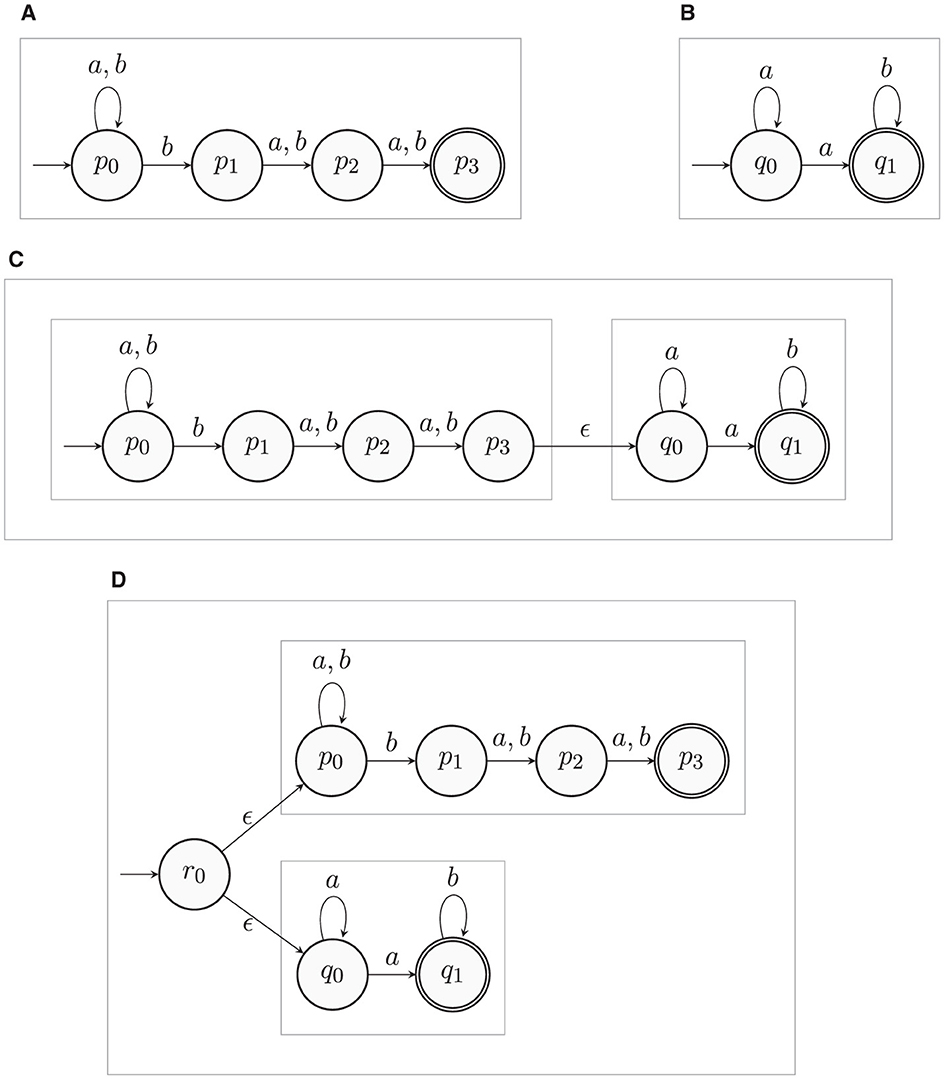
Figure 2. The NFAs displayed in (a) and (b) serve as building blocks to construct more complex NFAs such as (c) and (d). We use an enclosing box to denote that the internal details of an automaton are abstracted away. Only initial and final states are visible from a high-level perspective. That is, both (a) and (b) are treated as black boxes. (a) NFA N1. (b) NFA N2. (c) Concatenative NFA N1 ⊕ N2 (as per Definition 2). (d) Parallel NFA N1 ⊗ N2 (as per Definition 3).
Treating N1 and N2 as high-level computations (by just considering their respective initial and final states), enable us to compose them into more complex automata (i.e., high-level computations) via the operators described in Definitions 2 and 3. Particularly, N1 and N2 can be composed into the concatenative NFA N1 ⊕ N2 to accept strings in the language {wambn}. The structure of such a composite is depicted in Figure 2c. Figure 2d shows that N1 and N2 can also be composed into the parallel NFA N1 ⊗ N2 to recognizing the language L1 ∪ L2. As it is well-known that regular languages are closed under concatenation and union, both N1 ⊕ N2 and N1 ⊗ N2 can in turn be inductively composed into more complex NFAs using the same composition operators. That is, our MHC satisfies closure. It also satisfies the closed-world property since it is well-known that every (classical) NFA does not admit external data streams while computing.
Control flow between composed NFAs is implicitly defined in the added state transitions of a composite NFA. For instance, the transition δ(p3, ϵ) = {q0} of N1 ⊕ N2 serves to implicitly pass control from N1 to N2, whereas the transition δ(r0, ϵ) = {p0, q0} of N1 ⊗ N2 defines implicit control for the simultaneous activation of N1 and N2.
Although explicit data flow is not directly supported by our MHC, it is important to analyse how data is processed within a composite automaton. In the case of a concatenative NFA, an input string is esentially computed in two different chunks. In a parallel NFA, there is no data partitioning but each composed NFA computes the whole input independently. For instance, if aabaaaab needs to be processed by N1 ⊗ N2 then both N1 and N2 would compute and reject on aabaaaab simultaneously. Injecting the same input into N1 ⊕ N2 would lead to N1 passing control to N2 just after implicitly determining that aabaa is in L1. After receiving control, N2 would just compute and accept on aab. If we were to extend our MHC with the notion of explicit data flows (e.g., by introducing direct message passing), N1 ⊕ N2 could sequentially pass aab from N1 to N2. By the same token, we could also enable data replication within N1 ⊗ N2 to make sure both N1 and N2 receive a copy of the whole input before computing.
Returning to the motivating scenario introduced in Section 2, we could use our composition operators to incrementally define the global behavior of our e-commerce application. For example, the ⊕ operator can be used to sequentially compose the behavior of microservices for order processing and customer notification, in that order. Similarly, ⊗ can be employed to construct a composite microservice for parallel inventory checks across multiple third-party suppliers. This composite can, in turn, be sequentially composed with another microservice to display the inventory results. This bottom-up composition process can be continued until forming a complex, large-scale e-commerce system. In this example, we opt to explicitly deal with microservices since they are increasingly being used as (composable) units of computation in modern distributed systems. With our state-oriented MHC, although limited in computational power, we can mirror how microservice-based applications are designed and composed in practice (i.e., in a bottom-up manner). State-oriented MHCs are not the only way of defining high-level computations as we shall see in the next section.
4 What classes of MHCs do currently exist?
In this section, we classify MHCs into three different classes: state-oriented, data-oriented and control-oriented. For each of them, we provide a brief description and present a few examples.
State-oriented MHCs are built upon traditional Finite State Machines (FSMs) to enable the description of complex computing systems. The most representative models in this class are the so-called Communicating Finite State Machines (CFSMs) (Brand and Zafiropulo, 1983) and Hierarchical Finite State Machines (HFSMs) (Harel, 1987).6 CFSMs introduce “send” and “receive” operations in their semantics to enable concurrent interactions among distinct FSMs via (unbounded) First-In-First-Out (FIFO) channels. The overall behavior of a system is described through traces of configurations each of which is a tuple of both the state of the FSMs involved and the content of FIFO channels. Extensions of CFSMs include open CFSMs (Barbanera et al., 2019) and parameterised CFSMs (Bollig, 2014). The other subclass of state-oriented MHCs is that of HFSMs which allow the specification of nested FSMs in the form of so-called superstates. Due to their simplicity to modeling complex high-level computations, HFSMs have influenced the design of several industry-oriented formalisms such as the UML Superstructure specification which, in turn, has become the de facto standard for modeling complex software systems. In Section 3, we designed a simple MHC which can be classified as a HFSM. Other examples pertaining to this class are Hierarchical Featured State Machines (Fragal et al., 2019) and scope-dependent HFSMs (La Torre et al., 2008).
Data-oriented MHCs originated in late sixtees as an attempt to model concurrent computations in the form of direct message passing among a collection of interacting computing devices (usually referred to as actors). In these models, control flow is not explicit but implicit in the collaborative exchange of data. Here, data-driven computations are typically expressed as directed graphs in which nodes and edges denote data processing actors and explicit communication channels for directionally exchanging data streams, respectively (Dennis, 1974).7 Perhaps the most representative MHCs pertaining to this class are Kahn Process Networks (KPNs) (Kahn, 1974) and the Actor Model (Hewitt, 1977). On the one hand, KPNs define denotational semantics for modeling (high-level) concurrent actors that communicate through FIFO queues. Although operational semantics have been proposed to explicitly describe the flow of data values (Dennis, 1974), it has been showed that such a semantics coincide with the original denotational notion of KPNs (Lee and Matsikoudis, 2009). The operational idea is that there is a static network of actors in which every actor consumes input tokens, perfoms some computation on those tokens and produces output tokens that can potentially be consumed by other actors. The Actor Model does not operate on a static network of data processing actors, but it allows actors to dynamically create other actors, send messages to other actors and decide how to handle data. Other data-oriented MHCs that have been proposed over time (many of them variants of KPNs) include Synchronous Data Flow (SDF) (Lee and Messerschmitt, 1987), dataflow process networks (Lee and Parks, 1995), reactive process networks (Geilen and Basten, 2004) and synchronous blocks (Edwards and Lee, 2003). Interestingly, there are some MHCs [e.g., Reo (Arbab, 2004)] which do not allow direct data passing among computing devices, but data exchanges are “coordinated exogenously” via well-defined algebraic dataflow structures.8
Control-oriented MHCs enable the specification of explicit order in which individual computing devices need to be invoked so that interacting devices behave as passive units of computation. Examples of MHCs belonging to this class are exogenous connectors for encapsulated components (Lau et al., 2006), Behavior Trees (Colledanchise and Ögren, 2018) and workflow control flow models (Russell et al., 2016). Particularly, exogenous connectors allow the formation of hierarchical control flow structures that define (exogenous) coordination for the invocation of different computing devices. A few extensions of this model have been proposed over time (e.g., Lau and Ornaghi, 2009; Rana et al., 2022; Arellanes et al., 2023). Behavior trees are similar to exogenous connectors in the sense that hierarchical control flow structures are formed. The difference lies in the operational semantics of control flow coordination. Over time, several extensions and enhacements of Behavior Trees have been proposed (see Iovino et al., 2022), mainly to modeling modular Robot behavior. Apart from exogenous connectors and Behavior Trees, we also have workflow control flow models which define formal rules to govern the computation of workflows. Here, control flow specifies the order in which workflow activities are activated. A workflow activity is a fundamental unit of computation which can either be indivisible or contain other activities. Specific examples of workflow control flow models include Workflow Nets (Van der Aalst, 1998), formal BPEL process models (Ouyang et al., 2007), YAWL (Van der Aalst and ter Hofstede, 2005), among others.9
It is important to note that the three classes of MHCs we just considered are not exhaustive but indicative of the vast range of MHCs that have been proposed over time in the need of describing complex computations. For instance, we did not consider MHCs that combine state- and data-oriented features (e.g., SDF with HFSMs), typically within the Ptolemy framework (Tripakis et al., 2013). Similarly, we did not consider process calculi (Baeten et al., 2009) which are KPN-influenced models that borrow properties from both data- and control-oriented MHCs, in order to enable the description of inter-process communication through well-defined algebraic laws for equational reasoning. In the last years, there has been an increasing tendency to move toward describing high-level processes via algebras over operads of wiring diagrams (Yau, 2018) which provide formal constructs to reasoning about functional and concurrent computations in an intuitive yet rigorous manner, typically in the language of symmetric monoidal categories wherein morphisms express high-level computations that can graphically be depicted as string diagrams (Piedeleu and Zanasi, 2025).10 We believe that such category-theoretic operadic models are collectively forging the foundations of promising compositionality-enabling MHCs. Examples within this paradigm include tape diagrams (Bonchi et al., 2025), the many-worlds calculus (Chardonnet et al., 2025), the calculus of signal flows (Bonchi et al., 2017), the resource calculus (Bonchi et al., 2019) and the zx-calculus (Coecke and Duncan, 2011). Although not operadic in nature, other formalisms deserving attention are so-called component models (Lau and Di Cola, 2017) since many of them form MHCs themselves. For instance, Reo (Arbab, 2004) and exogenous connectors (Lau et al., 2006) are component models that yield data- and control-oriented MHCs, respectively, as mentioned previously.
5 Conclusions and future directions
In this paper, we introduced a new class of models of computation referred to as MHCs. Contrary to their low-level counterpart, the purpose of an MHC is to define interactions among diverse computing devices through a certain composition mechanism, so that interaction results from composition (not the other way round). As interactions occur outside the internal structure of each composed computing device, an MHC separates computation from interaction and induces modularity by treating computing devices as black bloxes. Composition can be done either algebraically or non-algebraically in order to specify (explicit/implicit) control flow and, optionally, (explicit/implicit) data flow.
In Section 3, we presented a closed MHC for facilitating the interaction of NFAs through an algebraic composition mechanism that defines implicit control flow and implicit data flow. Through this example, we demonstrated the modularity property that permeates the notion of MHCs. Although our examplary MHC satisfies closure over NFAs, there are other MHCs that do not necessarily compose state machines so as to deal with the well-known state explosion problem, e.g., (Arbab, 2004; Lau et al., 2006). There even are MHCs that provide mechanisms to sequentially compose Turing Machines (Goldin et al., 2004). In Section 4, we classified MHCs into three major classes: state-oriented, data-oriented and control-oriented. Although our review is introductory only, it can serve as a starting point to devise a more complete classification scheme (or even a whole taxonomy). For a more detailed analysis and comparison between MHC classes, one can examine limitations in terms of the properties presented in Section 2 and beyond such as determinism vs. non-determinism or algebraic vs. non-algebraic.
We believe that algebraically composing computing devices is of paramount importance to tame the complexity of interactions, especially as the size of computing devices becomes larger and larger. Algebraic composition can also be beneficial to compositionally verify certain properties such as termination and reachability. Nevertheless, there are number of directions that need to be addressed before unleashing the full potential of MHCs, including (compositional) concurrency for unrestricted synchronization among computing devices at different granularity levels (as the most pressing challenge). Specifying, analyzing and verifying concurrent behaviors in a compositional manner can mitigate state explosion through modular reasoning. Another potential direction is concerned with the classification of expressive power (especially of open MHCs) to rigorously compare classes of problems that can be solved while determining trade-offs between computational power and computational tractability. Equivalence proofs with respect to existing models of computation are also needed to establish computational universality while clarifying (or extending) computability boundaries. In this sense, high-level complexity (i.e., computational complexity of “algorithms over algorithms") is also important for analyzing how time, space and communication costs scale with the number of computing devices. These four directions are concerned with the theoretical analysis of MHCs. For their practical adoption, we envision novel programming languages built on top on the notion of MHCs, tool support development and learning curve analysis, just to name a few directions.
Moving up the ladder of abstraction from low- to high-level computations resembles the paradigm shift from low- to high-level programming languages. It is also analogous to the change of perspective from concrete mathematical structures to high-level ones (as in Category Theory). The paradigm shift we present in this paper clearly indicates that raising the level of abstraction is inevitably fundamental to deal with the intrinsic complexity that surround us. Accordingly, we envision that MHCs will play a crucial role in specifying complex, large-scale computing systems (or systems of systems) across various domains in the coming years. We invite the theoretical computing community to continue exploring and expanding the promising and intriguing frontiers of what we call Models of High-Level Computation.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material. Further inquiries can be directed to the corresponding author.
Author contributions
DA: Conceptualization, Formal analysis, Investigation, Methodology, Writing – original draft, Writing – review & editing.
Funding
The author(s) declare that financial support was received for the research and/or publication of this article. The author acknowledges that the publication fees for this article were covered by Lancaster University through its institutional agreement with Frontiers.
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Generative AI statement
The author(s) declare that no Gen AI was used in the creation of this manuscript.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Footnotes
1. ^We should not confuse high-level with higher-order computations (Longley and Normann, 2015). Higher-order computability is a well-established field in theoretical computer science, whose aim is to study computations that receive and produce other computations.
2. ^By exogenous, we mean an entity that is out of the scope of the interacting computing devices, e.g., a human operator.
3. ^Classical, low-level models of computation are inherently closed because they have a fixed input before computing (e.g., on a tape) so outputs can only be read after termination. Open models of computation contrast with this behavior by allowing the processing of data streams from the external world while computing. An example is a workflow process that pauses a data pipeline and waits for a human operator's input before proceeding, just as in the original Turing c-machines (Turing, 1937).
4. ^For example, Reo (Arbab, 2004) defines explicit data flows (via timed connectors) and implicit control flow, whereas process calculi (Baeten et al., 2009) typically define explicit control flow (e.g., via message passing) and implicit data flow.
5. ^The original Actor Model (Hewitt, 1977) is a concrete example of a non-algebraic MHC, whereas Reo (Arbab, 2004) is an example of the counterpart, which allows the algebraic construction of high-level computations in the form of data flow circuits. The next section presents another example of an algebraic MHC.
6. ^Note that there also is a hybrid variant called Communicating Hierarchical State Machines (Alur et al., 1999).
7. ^Some data-oriented MHCs [e.g., Token Flows (Buck and Lee, 1993)] introduce special actors to enable control constructs such as branching.
8. ^Data-oriented MHCs are increasingly finding applications in domains that require the processing of data streams in some predefined order such as the Internet of Things. For this, various tools built upon dataflow models have emerged over time [e.g., Node-Red (Hagino and O'Leary, 2021)].
9. ^A workflow engine is an abstract machine able to receive a workflow control flow model M and a workflow specification S, before computing the activities in S according to the rules imposed by M. Workflow engines are particularly useful in the real-world for business process automation (Reijers, 2021).
10. ^String diagrams have their roots in the Penrose graphical notation for tensor networks (Penrose, 1971).
References
Alur, R., Kannan, S., and Yannakakis, M. (1999). “Communicating hierarchical state machines,” in Automata, Languages and Programming, Lecture Notes in Computer Science, eds. J. Wiedermann, P. van Emde Boas, and M. Nielsen (Berlin: Springer), 169–178. doi: 10.1007/3-540-48523-6_14
Arbab, F. (2004). Reo: a channel-based coordination model for component composition. Math. Struct. Comput. Sci. 14, 329–366. doi: 10.1017/S0960129504004153
Arellanes, D., Lau, K.-K., and Sakellariou, R. (2023). Decentralized data flows for the functional scalability of service-oriented IoT systems. Comput. J. 66, 1477–1506. doi: 10.1093/comjnl/bxac023
Baeten, J. C. M., Basten, T., and Reniers, M. A. (2009). “Process algebra: equational theories of communicating processes,” in Cambridge Tracts in Theoretical Computer Science (Cambridge: Cambridge University Press). doi: 10.1017/CBO9781139195003
Barbanera, F., de'Liguoro, U., and Hennicker, R. (2019). Connecting open systems of communicating finite state machines. J. Logical and Algebr. Methods Program. 109, 1–34. doi: 10.1016/j.jlamp.2019.07.004
Bollig, B. (2014). “Logic for communicating automata with parameterized topology,” in Proceedings of the Joint Meeting of the 23rd EACSL Annual Conference on Computer Science Logic (CSL) and the 29th Annual ACM/IEEE Symposium on Logic in Computer Science (LICS) (New York, NY: ACM), 1–10. doi: 10.1145/2603088.2603093
Bonchi, F., Di Giorgio, A., and Di Lavore, E. (2025). “A diagrammatic algebra for program logics,” in Foundations of Software Science and Computation Structures, eds. P. A. Abdulla, and D. Kesner (Cham: Springer), 308–330. doi: 10.1007/978-3-031-90897-2_15
Bonchi, F., Holland, J., Piedeleu, R., Sobociński, P., and Zanasi, F. (2019). Diagrammatic algebra: from linear to concurrent systems. Proc. ACM Program. Lang. 3(POPL), 1–28. doi: 10.1145/3290338
Bonchi, F., Sobociński, P., and Zanasi, F. (2017). The calculus of signal flow diagrams I: linear relations on streams. Inf. Comput. 252, 2–29. doi: 10.1016/j.ic.2016.03.002
Brand, D., and Zafiropulo, P. (1983). On communicating finite-state machines. J. ACM 30, 323–342. doi: 10.1145/322374.322380
Buck, J., and Lee, E. (1993). Scheduling dynamic dataflow graphs with bounded memory using the token flow model. IEEE Int. Conf. Acoust. Speech Signal Process. 1, 429–432. doi: 10.1109/ICASSP.1993.319147
Chardonnet, K., Visme, M. d., Valiron, B., and Vilmart, R. (2025). The many-worlds calculus. Logical in Comput. Sci. 21, 13:1–13:44. doi: 10.46298/lmcs-21(2:13)2025
Coecke, B., and Duncan, R. (2011). Interacting quantum observables: categorical algebra and diagrammatics. New J. Phys. 13, 1–85. doi: 10.1088/1367-2630/13/4/043016
Colledanchise, M., and Ögren, P. (2018). Behavior Trees in Robotics and AI: An Introduction, 1st Edn. Boca Raton, FL: CRC Press. doi: 10.1201/9780429489105
Dennis, J. B. (1974). “First version of a data flow procedure language,” in Proceedings of Symposium on Programming, ed. B. Robinet (Paris), 362–376. doi: 10.1007/3-540-06859-7_145
Edwards, S. A., and Lee, E. A. (2003). The semantics and execution of a synchronous block-diagram language. Sci. Comput. Program. 48, 21–42. doi: 10.1016/S0167-6423(02)00096-5
Fragal, V. H., Simao, A., and Mousavi, M. R. (2019). Hierarchical featured state machines. Sci. Comput. Program. 171, 67–88. doi: 10.1016/j.scico.2018.10.001
Geilen, M., and Basten, T. (2004). “Reactive process networks,” in Proceedings of the 4th ACM International Conference on Embedded Software (New York, NY: ACM), 137–146. doi: 10.1145/1017753.1017778
Goldin, D. Q., Smolka, S. A., Attie, P. C., and Sonderegger, E. L. (2004). Turing machines, transition systems, and interaction. Information and Computation, 194, 101–128. doi: 10.1016/j.ic.2004.07.002
Hagino, T., and O'Leary, N. (2021). Practical Node-RED Programming: Learn Powerful Visual Programming Techniques And Best Practices for the Web and IoT. Birmingham: Packt Publishing.
Harel, D. (1987). Statecharts: a visual formalism for complex systems. Sci. Comput. Program. 8, 231–274. doi: 10.1016/0167-6423(87)90035-9
Hewitt, C. (1977). Viewing control structures as patterns of passing messages. Artif. Intell. 8, 323–364. doi: 10.1016/0004-3702(77)90033-9
Iovino, M., Scukins, E., Styrud, J., Ögren, P., and Smith, C. (2022). A survey of Behavior Trees in robotics and AI. Robot. Auton. Syst. 154:104096. doi: 10.1016/j.robot.2022.104096
Kahn, G. (1974). The Semantics of a Simple Language for Parallel Programming. Amsterdam: North-Holland Publishing Co.
La Torre, S., Napoli, M., Parente, M., and Parlato, G. (2008). Verification of scope-dependent hierarchical state machines. Inf. Comput. 206, 1161–1177. doi: 10.1016/j.ic.2008.03.017
Lau, K.-K., and Di Cola, S. (2017). An Introduction to Component-Based Software Development, 1st Edn. Singapore: World Scientific. doi: 10.1142/10486
Lau, K.-K., and Ornaghi, M. (2009). “Control encapsulation: a calculus for exogenous composition of software components,” in Component-Based Software Engineering, Lecture Notes in Computer Science, eds. G. A. Lewis, I Poernomo., and C. Hofmeister (Berlin: Springer), 121–139. doi: 10.1007/978-3-642-02414-6_8
Lau, K.-K., Ornaghi, M., and Wang, Z. (2006). “A software component model and its preliminary formalisation,” in Formal Methods for Components and Objects, Lecture Notes in Computer Science, eds. F. S. de Boer, M. M. Bonsangue, S. Graf, and W.-P. de Roever (Berlin, Heidelberg: Springer), 1–21. doi: 10.1007/11804192_1
Lee, E., and Messerschmitt, D. (1987). Synchronous data flow. Proceedings of the IEEE, 75, 1235–1245. doi: 10.1109/PROC.1987.13876
Lee, E., and Parks, T. (1995). Dataflow process networks. Proc. IEEE 83, 773–801. doi: 10.1109/5.381846
Lee, E. A., and Matsikoudis, E. (2009). “The semantics of dataflow with firing,” in “From Semantics to Computer Science: Essays in Honour of Gilles Kahn, eds. G. Plotkin, G. Huet, J.-J. Lévy, and Y. Bertot (Cambridge: Cambridge University Press), 71–94. doi: 10.1017/CBO9780511770524.005
Longley, J., and Normann, D. (2015). Higher-Order Computability, 1st Edn. Berlin: Springer. doi: 10.1007/978-3-662-47992-6
Ouyang, C., Verbeek, E., van der Aalst, W. M. P., Breutel, S., Dumas, M., and ter Hofstede, A. H. M. (2007). Formal semantics and analysis of control flow in WS-BPEL. Sci. Comput. Program. 67, 162–198. doi: 10.1016/j.scico.2007.03.002
Penrose, R. (1971). “Applications of negative dimensional tensors,” in Combinatorial Mathematics and its Applications, ed. D. Welsh (New York, NY: Academic Press), 221–244.
Piedeleu, R., and Zanasi, F. (2025). An Introduction to String Diagrams for Computer Scientists. Elements in Applied Category Theory, 1st Edn. Cambridge, MA: Cambridge University Press. doi: 10.1017/9781009625715
Rana, T., Maqbool, A., Rana, T. A., Mirza, A., Iqbal, Z., Khan, M. A., et al. (2022). Achieving stepwise construction of cyber physical systems in EX-MAN component model. J. King Saud Univ. Comput. Inf. Sci. 34(10, Part B), 10319–10338. doi: 10.1016/j.jksuci.2022.10.024
Reijers, H. A. (2021). Business process management: the evolution of a discipline. Comput. Ind. 126, 1–5. doi: 10.1016/j.compind.2021.103404
Russell, N., van der Aalst, W. M. P., and ter Hofstede, A. H. M. (2016). Workflow Patterns: The Definitive Guide. Cambridge, MA: The MIT Press. doi: 10.7551/mitpress/8085.001.0001
Sipser, M. (2013). Introduction to the Theory of Computation, 3rd Edn. Boston, MA: Cengage Learning.
Tripakis, S., Stergiou, C., Shaver, C., and Lee, E. A. (2013). A modular formal semantics for Ptolemy. Math. Struct. Comput. Sci. 23, 834–881. doi: 10.1017/S0960129512000278
Turing, A. M. (1937). On computable numbers, with an application to the entscheidungs problem. Proc. London Math. Soc. s2–42, 230–265. doi: 10.1112/plms/s2-42.1.230
Van der Aalst, W. M. P. (1998). The application of petri-nets to workflow management. J. Circuits Syst. Comput. 8, 21–66. doi: 10.1142/S0218126698000043
Van der Aalst, W. M. P., and ter Hofstede, A. H. M. (2005). YAWL: yet another workflow language. Inf. Syst. 30, 245–275. doi: 10.1016/j.is.2004.02.002
Keywords: models of computation, computability theory, high-level computation, compositionality, algebraic composition
Citation: Arellanes D (2025) Models of high-level computation. Front. Comput. Sci. 7:1564048. doi: 10.3389/fcomp.2025.1564048
Received: 21 January 2025; Accepted: 10 June 2025;
Published: 09 July 2025.
Edited by:
Huai Liu, Swinburne University of Technology, AustraliaReviewed by:
Mengjiao Guo, Swinburne University of Technology, AustraliaCopyright © 2025 Arellanes. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Damian Arellanes, ZGFtaWFuLmFyZWxsYW5lc0BsYW5jYXN0ZXIuYWMudWs=
 Damian Arellanes
Damian Arellanes