An application layer with protocol-based java smart contract verification

Smart contracts are software that runs in blockchain and expresses the rules of an agreement between parties. An incorrect smart contract might allow blockchain users to violate its rules and even jeopardize its expected security. Smart contracts cannot be easily replaced to patch a bug since the nature of contracts requires them to be immutable. More problems occur when a smart contract is written in a general-purpose language, such as Java, whose executions, in a blockchain, could hang the network, break consensus or violate data encapsulation. To limit these problems, there exist automatic static analyzers that find bugs before smart contracts are installed in the blockchain. This so-called off-chain verification is optional because programmers are not forced to use it. This paper presents a general framework for the verification of smart contracts, instead, that is part of the protocol of the nodes and applies when the code of the smart contracts gets installed. It is a mandatory entry filter that bans code that does not abide by the verification rules. Consequently, such rules become part of the consensus rules of the blockchain. Therefore, an improvement in the verification protocol entails a consensus update of the network. This paper describes an implementation of a smart contracts application layer with protocol-based verification for smart contracts written in the Takamaka subset of Java, that filters only those smart contracts whose execution in blockchain is not dangerous. This application layer runs on top of a consensus engine such as Tendermint and its derivatives Ignite and CometBFT (proof of stake), or Mokamint (proof of space). This paper provides examples of actual implementations of verification rules that check if the smart contracts satisfy some constraints required by the Takamaka language. This paper shows that protocol-based verification works and reports how consensus updates are implemented. It shows actual experiments as well as limits to its use, mainly related to the fact that protocol-based verification must be fast and its complexity must never explode, or otherwise, it would compromise the performance of the blockchain network.

1 Introduction

Blockchain is a distributed ledger that replicates data in a peer-to-peer network of nodes. Transactions are ledger updates digitally signed by the account requiring their execution. The nodes of the network collect broadcasted transactions into a growing cryptographically-linked chain of blocks. A set of consensus rules specifies constraints on the way the blockchain grows, which normally amounts to expected security guarantees for the state of the blockchain: money cannot be spent twice, and, in general, the evolution of the state must be consistent with the semantics of the transactions. Once consensus is achieved, it is hard, or impossible, to withdraw transactions from the blockchain. In this sense, blockchains are immutable data structures.

Smart contracts specify rules and effects of transactions and can be either built-in, as a fixed module of the blockchain software, or given as code dynamically deployed inside the same blockchain. In the second case, users who deploy the code identify themselves by signing a code install transaction request. The typical applications of smart contracts are related to finance and cryptocurrencies, tokens, coordination of purchases, electronic elections, and law. The critical nature of such applications and the fact that smart contracts cannot be replaced after being installed require a high level of code quality. That is, smart contracts are expected to be flawless, as much as possible, and to not harm the network.

Smart contracts can be written in a variety of programming languages, either specific for them or general-purpose. Most such languages are Turing-complete, with the notable exception of Bitcoin's. Not surprisingly, Turing-completeness for smart contracts introduces the risk of many kinds of bugs (Atzei et al., 2017; Popper, 2016). An extensive review for the specific case of Ethereum is in Antonopoulos and Wood (2018) and includes the reentrancy issue, arithmetic under/overflows, incorrect use of low-level calls, weak encapsulation, ineffective randomization, logical bugs in the code of contracts, fund locking, wrong identification of the transaction originator. Such vulnerabilities have actually been exploited in practice. Because of this, there exist many analyzers that verify smart contracts before they get installed in the blockchain (Hejazi and Lashkari, 2025; Kushwaha et al., 2022; Ressi et al., 2024). Furthermore, there are companies that provide code audit services, using both automatic tools and human investigation (Certik, 2025; OpenZeppelin, 2025; Consensys Diligence, 2025). A limit of these tools and procedures is that they are optional and external to the blockchain (hence off-chain): the latter does not actively protect itself against the deployment of incorrect or dangerous code. Moreover, they mostly apply to Solidity rather than to general-purpose languages used for writing smart contracts.

This paper makes the following contributions:

• It defines protocol-based code verification, where the nodes of the blockchain verify the code being deployed. That is, the same network, internally, runs a mandatory code verification step and rejects code that does not pass it. As a consequence, protocol-based verification is a defensive, proactive technique that guarantees that all code executed in the blockchain has been successfully verified.

• It describes an actual implementation of a blockchain with protocol-based verification for filtering smart contracts written in the Takamaka subset of Java (Spoto, 2019). This implementation is a software layer called Hotmoka, which runs as an application on top of Tendermint (Kwon, 2014) (also its derivatives such as Ignite¹ and CometBFT²), a third-party tool for implementing blockchains based on Byzantine fault tolerance and proof of stake. Hotmoka is a runtime for smart contracts written in the Takamaka subset of Java that users can install dynamically, as in Solidity over Ethereum. Hotmoka also runs on top of Mokamint,³ a similar tool based on a proof of space consensus. Hotmoka includes 21 verification checks that mostly verify the correct use of Takamaka's primitives and code annotations and the use of a deterministic subset of Java. That is, such checks filter the smart contracts installed in blockchain to avoid those that would crash the blockchain peers, hang their execution, make consensus impossible or violate data encapsulation. Therefore, they are relevant security checks, although we acknowledge that they are relatively simple. As shown later (Section 7) the goal is to have quick checks that do not delay the creation of the blocks, since the blockchain peers must perform such checks during the same creation of the new blocks. In general, our technique is best suited for the safe use of general-purpose languages (such as Java, in our case) for writing smart contracts for a permissionless blockchain, instead of using a new specific language such as Solidity.

• It describes the coordination of an update to the verification protocol of a blockchain and a lazy re-verification approach that copes with the evolution of the code verification rules. Namely, protocol-based verification is run as part of code installation transactions. Hence, its rules are part of the network consensus rules, and their evolution requires a network update. Moreover, code previously successfully verified with old verification rules might fail to pass the new verification rules.

This paper is organized as follows.

Section 2 provides the background of this paper. Section 3 presents related work. Section 4 describes the Takamaka subset of Java for smart contracts and its Hotmoka runtime. Section 5 defines a general architecture for protocol-based code verification. Section 6 describes our implementation of protocol-based verification, over Tendermint and Mokamint, and shows two examples of protocol-based checks. Section 7 reports experiments with our implementation and describes how readers and reviewers can validate them. Section 8 shows how the blockchain can cope with the evolution of code verification rules. Section 9 concludes the paper and discusses limitations.

This paper is an extended version of Olivieri et al. (2021). The main differences with that conference paper are: a more extended related work section; an extended description of Takamaka and Hotmoka; a second example of verification rule implementation; the description of the implementation of the verification module update; the implementation over Mokamint, not just over Tendermint, which gives more relevance to the results; a simplification of the execution of the experiments; a global revision and extension of the article.

2 Background

Bitcoin (Nakamoto, 2008; Antonopoulos, 2017) was the first popular blockchain implementation. It is a peer-to-peer electronic cash system that stores and transmits value in a currency called bitcoin, by using a Proof of Work (PoW) consensus algorithm: each block contains a proof that some heavy work has been performed to create the block, which makes double-spending attacks expensive. A Turing-incomplete low-level Script language specifies the effects of Bitcoin's transactions. Script can be seen as a limited scripting language for smart contracts.

Ethereum (Buterin, 2013; Antonopoulos and Wood, 2018) later introduced a Turing-complete bytecode for executing actual fully-fledged smart contracts, with the goal of developing decentralized applications. Ethereum smart contracts can be programmed in various high-level languages, with Solidity being the most popular one, but all run on the Ethereum virtual machine. Ethereum used PoW previously to switch to Proof of Stake (PoS). Solidity embeds some features specific to the development of smart contracts, such as a notion of gas, charged for code execution, that allows to meter the amount of code execution and avoids the risk of non-termination; and a strict deterministic execution.

PoS is a consensus algorithm with reduced resource consumption (Sedlmeir et al., 2020). It limits the right to propose a next block to a small set of nodes called validators. This set can be static or dynamic, exclusive or delegatable: in any case, this limitation allows the network to scale better and avoid the computational cost of PoW. Network participants that want to become validators freeze a certain amount of stake, which acts as an economic incentive that dissuades from validating or creating fraudulent transactions. If the validator does its job correctly, it will be remunerated for every confirmed transaction. If, instead, the network detects a fraudulent transaction, the culprit loses part of its stake and possibly the right to act as a validator. The Tendermint protocol (Kwon, 2014) provides a generic and customizable infrastructure for networking and consensus through PoS, with a pseudo-random election of the validator for the next block. This protocol tolerates up to $\frac{1}{3}$ of misbehaving validators. The Tendermint's architecture is shown in Figure 1 and consists of three software layers:

• Networking: discovers and connects nodes (peers) with each other, propagates requests for transactions, propagates blocks to and from the peers.

• Consensus: approves or rejects the blocks received from the peers, adding them to the blockchain if they are approved.

• Application: specifies which transaction requests are valid, how their responses are computed and how the application's state consequently evolves.

Figure 1

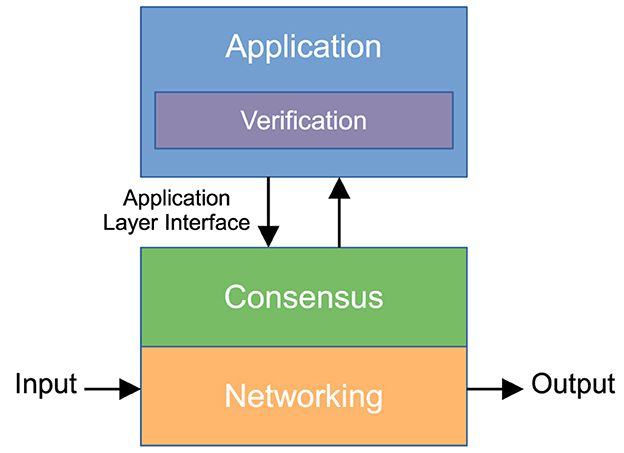
Figure 1. High-level architecture of an application running on a generic blockchain engine and performing protocol-based verification. This is the architecture of both Tendermint and of Mokamint.

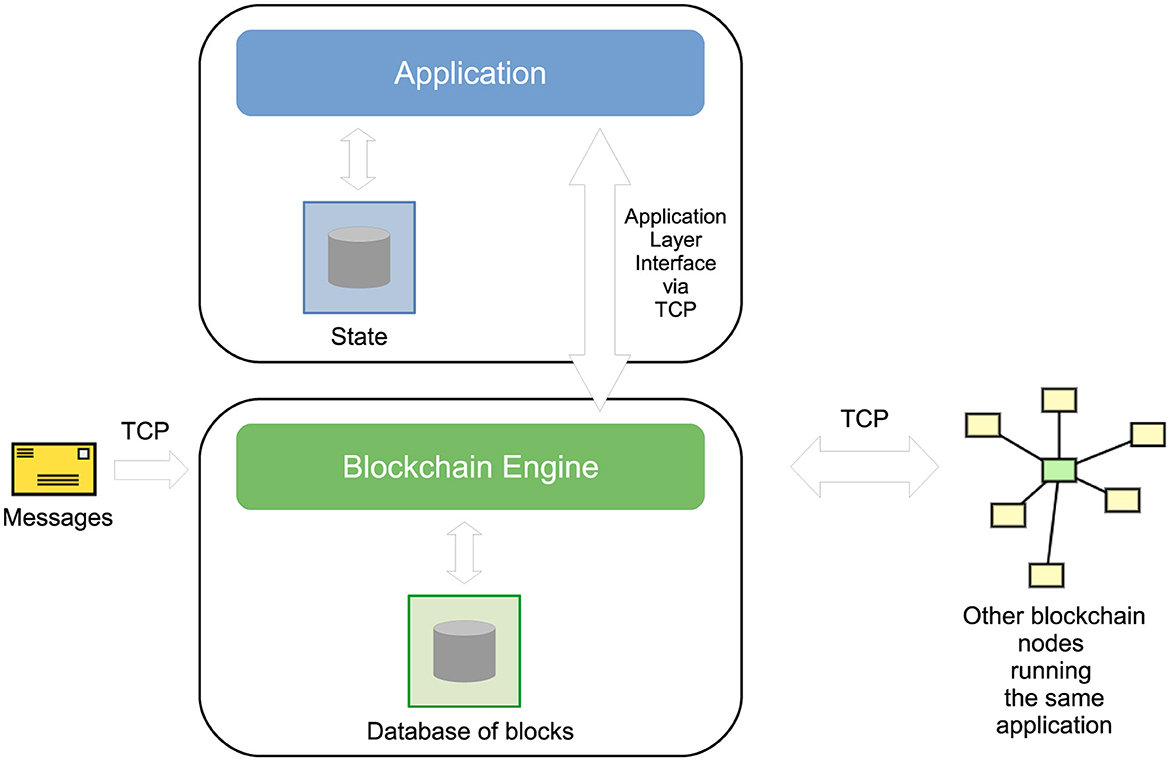
Tendermint is a generic blockchain engine since it is not a monolithic software application for a specific set of blockchain transactions (like Bitcoin or Ethereum and most of all other blockchains), but it leaves the notion of transaction unspecified: programmers can develop an application layer that runs on top of Tendermint (Figure 1) and specifies which transactions exist and which is their semantics. This application layer can be written in any programming language and can even be an actual software layer that executes Turing-complete smart contracts, as it will be in our case, as long as it connects with the blockchain engine through its Application BlockChain Interface (ABCI). The blockchain engine replicates the application state on each machine of the network.

Proof of Stake (PoS) is often criticized for being based on a restricted club of validators that should be trusted because they are rich and, by acting as validators, become even richer. But another problem is that, to start a new network, it is difficult to convince independent entities to run, maintain and update the validators node since the cryptocurrency of a new network has initially no economic value. Therefore, another alternative has been developed, called proof of space (PoSp) (Ateniese et al., 2014; Dziembowski et al., 2015; Abusalah et al., 2017), where miners must dedicate a large amount of disk memory in order to be able to propose a new block. The idea is that the proposal of a new block requires to solve a challenge whose solution can be computed easily in terms of computational power but requires one to allocate a large amount of disk space. Moreover, the quality of the solution determines if the block will be preferred to other blocks proposed concurrently by other miners, and this quality is proportional to the amount of disk memory committed to the task. The energy consumption of PoSp is negligeable, and no special hardware helps for mining; currently, the technology is both cheap and democratic. Moreover, PoSp allows one to capitalize on unused memory, for free, while PoW always has an inherent electricity cost. There are a few implementations of PoSp networks that can execute Turing-complete smart contracts, namely, Chia⁴ and Signum.⁵ Mokamint is a generic engine for running applications over the PoSp protocol of Signum, as formalized in Spoto (2025). Therefore, Mokamint is the equivalent of Tendermint but for PoSp, and its architecture is identical to that of Tendermint (see Figure 1): the only difference is that the Mokamint's consensus layer is based on PoSp. The same ABCI of Mokamint is almost identical to that of Tendermint.

3 Related work

Smart contract verification is challenging and most of the available solutions are for Ethereum-based blockchains, mainly for economic reasons: Ethereum-based blockchains currently lock the highest amount of economic value.⁶ Static analysis techniques can detect issues without executing the code before the contract gets deployed and becomes immutable. Specifically, these techniques examine the syntax, structure, and in some cases also the semantics of the contract at different stages of development. An intuitive example of static analysis is the compiler. For instance, in Ethereum smart contracts, the Solidity compiler (e.g., solc) performs basic checks on syntax and grammar. It issues alerts during the compilation process, ensuring that the source code is well-formed before being translated into EVM bytecode. It applies a static analysis because the checked code is the high-level source code (typically, Solidity), and it is static because the executable code (that is, the EVM bytecode) has not been generated yet. However, since the compiler focuses primarily on code correctness rather than on performing security checks, additional tools are necessary for more comprehensive verification. In the early stages of software development, linters may help maintain coding standards and best practices by identifying code smells, minor bugs, and stylistic inconsistencies. Popular solutions for Ethereum include Ethlint (formerly Solium) (Dua, 2025) and Solhint (Protofire, 2025). Beyond linters, also advanced static analysis tools can be applied for deeper code investigation, to detect complex security vulnerabilities and logic errors. Compared to linters, they offer more detailed and precise results by analyzing the semantics of the instructions, though they may require significant computational resources and extended processing time. Notable examples are Oyente (Loi et al., 2016), SmartCheck (Tikhomirov et al., 2018), Slither (Feist et al., 2019), eThor (Schneidewind et al., 2020), Echidna (Grieco et al., 2020), EtherSolve (Pasqua et al., 2023), and EVMLiSA (Arceri et al., 2024). Advanced tools are also delivered as a service, such as https://mythx.io. Furthermore, there are companies that provide code audit services by using both automatic tools and human investigation. However, a limit of these off-chain tools and procedures is that they are optional: users are not required to analyze their code before it gets deployed in the blockchain.

To the best of our knowledge, this paper defines and implements the first protocol-based code verification for smart contracts that allows the same blockchain to reject the code that does not pass a set of verification rules. From this point of view, the technique is related to continuous integration, that builds and deploys code only if it passes all compilation and testing requirements. The main difference is that smart contracts cannot be replaced or debugged once installed in blockchain.

Some blockchains, such as Ethereum, apply a notion of transparency (Oliva et al., 2020), that lets one store in blockchain the source code of the smart contracts to guarantee that it actually compiles into their bytecode. But this is only an optional technique that ensures that bytecode and source code match and no code verification is applied.

The specific technique for updating the consensus rules of a network, after a change in the verification rules (Section 8), is orthogonal to our work. In Cosmos, the government module supports such an update, with (dis-)incentives to minimize misconduct within the participants. Polkadot delegates updates to periodic referendums among stakeholders. Algorand (Chen and Micali, 2019) triggers an update if a large majority of block proposers declare to be ready for that.

4 Takamaka and Hotmoka

This section introduces the Takamaka smart contract language and its Hotmoka runtime. The goal of this section is to provide knowledge about the specific language that we analyze, with examples that clarify the difference with Solidity (use of a general-purpose language, use of generic types, access to the keys of a map, checked casts). These examples show correct uses of Takamaka, so that subsequent static analyses become clear. Moreover, the voting example in this section is also used to coordinate the update of the verification module (Section 8).

Solidity is probably the most used programming language for smart contracts. Despite its success, it has limits that make its use complex and error-prone. The first problem is that it lacks support for runtime type introspection and dynamic dispatch: types used in the code can be violated at runtime since casts cannot be checked. Objects cannot even be checked at runtime for their actual type (no instanceof operator exists in Solidity). Lack of runtime type checks and certain safety features have contributed to bugs and vulnerabilities in many Solidity smart contracts (Antonopoulos and Wood, 2018). Moreover, Solidity does not feature modern programming patterns such as generic types. Smart contracts use maps extensively but, in Solidity, these are not real data structures and miss basic functionalities, such as the ability to iterate over their set of keys and values.

On the contrary, modern programming languages such as Java provide strong types, generic types and complex data structures (including actual and flexible maps). However, they miss some features that are specific to smart contracts: Java does not allow one to access the caller of a method, nor to sign method calls; Java does not natively include a gas mechanism to limit resource consumption, a feature that smart contract platforms typically use to enforce predictable execution and prevent infinite loops. Finally, Java is not deterministic, which is a problem in blockchain, whose consensus requires to reach the same state in all nodes of the network, impossible in the case of non-determinism.

For this reason, Java (and other general-purpose languages) has been used for writing blockchain code, statically installed in the blockchain at deployment time or only in the context of permissioned blockchains. But a free dynamic deployment model in a permissionless blockchain, in the style of Solidity, has never been possible with Java and other general-purpose languages, since they allow many dangerous executions in blockchain and contain a large library that allows programmers to perform actions that, in blockchain, are both meaningless and dangerous, such as file access, reflection and non-deterministic object finalization.

The goal of the Takamaka project was exactly to enable the use of Java as a smart contract language, analogous to how Solidity is used in Ethereum. The use of a well-known programming language such as Java leverages expertise and existing mature development tools. The application layer of Takamaka is a state machine (the application in Figure 2) that executes transactions from request to response. Requests can specify the addition of a jar in the permanent state of the application, or the execution of a constructor, or of an instance or static method of code previously installed in the state. Responses include the effects of the transaction as a set of field updates. Updates can be computed since the jar of the Java code is instrumented before being installed in the blockchain, with extra code that keeps track of the affected fields of objects (Spoto, 2019). Determinism is ensured by a static analysis that ensures that only a deterministic subset of Java is used, restricted to a minimal deterministic and non-dangerous API of the Java library. The state machine (runtime) of Takamaka is called Hotmoka⁷ and is implemented itself in Java. It runs on a standard Java virtual machine. The state is kept in a Merkle-Patricia trie that implements a map from the hash of requests to their corresponding response. This trie is kept in the Xodus transactional database by JetBrains.⁸

Figure 2

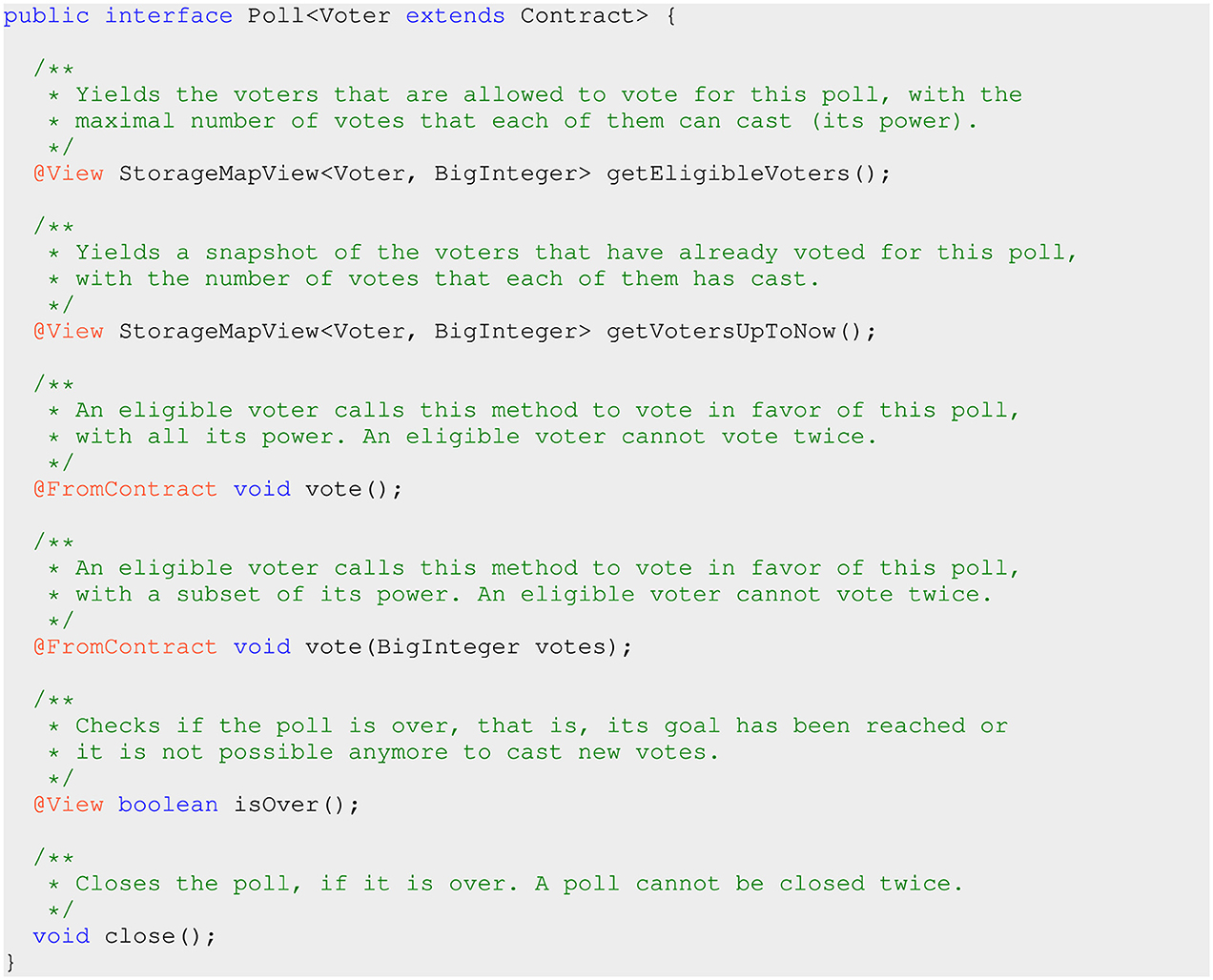
Figure 2. The interface of a poll smart contract. The complete code is available at: https://github.com/Hotmoka/io-takamaka-code/blob/main/io-takamaka-code/src/main/java/io/takamaka/code/dao/Poll.java.

An important difference between Takamaka and Solidity is that smart contracts are deployed in Solidity, together with their compiled code: every deployed instance of the contract carries its own copy of the code. In Takamaka, instead, the standard Java approach is used: the code of the smart contract is installed in the database of the blockchain, once and for all; later, smart contracts are instantiated from that single code instance by calling their respective constructors. Because of this, this paper refers to the installation of the code of a smart contract and to the subsequent instantiation of specific smart contract instances, rather than to the deployment of a smart contract, which is the usual terminology in Solidity. This difference is important for the scalability of our technique, as Section 7 will show later.

Another significant difference is that externally-owned accounts are just a special case of smart contracts in Takamaka, while they are different concepts in Solidity. Namely, in Takamaka, an externally-owned account is a smart contract that embeds a public key and that has the right to originate a transaction, as long as that transaction is signed with the matching private key. Externally-owned accounts, in Takamaka, have an actual type (a class), that extends Contract and can be redefined and specialized.⁹ It follows that externally-owned accounts are objects in Takamaka (in the sense of object-oriented programming) and that two distinct objects might even contain the same public key and therefore be controllable with the same, corresponding private key. It is even possible to rotate the key of an externally-owned account, and still keep the identity of that object. None of this is possible in Solidity. As in Solidity, also in Takamaka both smart contracts and externally-owned accounts have a balance.

In Takamaka, bytecode instrumentation is also used to add features that are needed for smart contracts but that are not available in standard Java: for instance, in Takamaka the caller of a method can be identified as caller(); cryptocurrency can be used to pay for code execution; the latter is metered through gas and stops if gas expires. Instrumentation is run by each node when smart contracts get installed (Spoto, 2019); the correct use of caller() and payments are enforced by a set of static analyses (see Section 6). All such analyses are implemented at the protocol level, as mandatory steps for the installation of new smart contracts and could be improved/expanded in the future, as this paper will show. A specific Takamaka library includes typical data structures used in smart contracts, such as very flexible maps. Takamaka has been proven to be able to implement non-trivial smart contracts for tokens and data snapshots (Crosara et al., 2023) and to support smart contracts with generic types (Spoto et al., 2023).

Let us see an example of a Takamaka smart contract for the implementation of a poll. Its interface is given in Figure 2. It is a generic interface parametric w.r.t. the type Voter of the voters allowed to vote. A poll is similar to the vote of the shareholders of a company. Each of them has a power, that is, a maximal number of votes that it can cast. This information is returned by method getEligibleVoters(). Note that this method returns a map from each eligible voter to its power. Maps are real data structures in Takamaka. Therefore, clients can find the keys and the values of a map and iterate over them. Shareholders vote by calling one of the vote() methods: they cannot vote twice, or otherwise, these methods will throw an exception. The votes cast up to now are returned by getVotersUpToNow(). Method isOver() checks if the poll is over (that is, if a majority of the votes have been cast or all voters have voted). Method close() closes the poll if it is over and runs an action if a majority has been reached. This method cannot be called twice.

Figure 2 shows the use of specific Takamaka annotations: these are a Java mechanism for adding metadata information to source and compiled code. They are irrelevant for the code executor but can be used by code analysis and instrumentation tools. Namely, @FromContract states that a method or constructor can only be called from the code of a contract, which, as said before, in Takamaka includes externally-owned accounts as well. Such annotation allows the programmer to refer to the caller of the method as caller(). This is important, for instance, for the vote() methods, which need to be sure of the actual intent of the caller to cast its vote. This explains why the generic type Voter is bound to be a Contract: Voter extends Contract. If a method or constructor is annotated as @FromContract, then it can be additionally annotated with @Payable, which states that the caller can send cryptocurrency when calling the method or constructor. The fact that @Payable only works together with @FromContract is to guarantee that the caller is a contract and, therefore, that it has a balance to pay with. Moreover, @Payable only works in contracts, to guarantee that the callee has a balance and can receive cryptocurrency.

The annotation @View states that a method has no side-effect and, consequently, can be run without modifying the state of the blockchain. This allows to call @View methods without paying for their execution since they do not give rise to transactions stored in blockchain but simply read its persistent state.

A possible concrete implementation of a poll is given in Figure 3. It is a class that implements the Poll interface and extends Storage. The latter is a class of Takamaka's runtime whose instances can be created, kept and shared in blockchain: without extends Storage, instances of class Poll could only be used as temporary objects in methods. A Contract is a Storage with a balance. SimplePoll is not a Contract since it does not need a balance, and indeed none of its methods receive cryptocurrency at call-time (none is @Payable).

Figure 3

Figure 3. An implementation of the Poll interface from Figure 2. The complete code is available at: https://github.com/Hotmoka/io-takamaka-code/blob/main/io-takamaka-code/src/main/java/io/takamaka/code/dao/SimplePoll.java.

The constructor of SimplePoll receives a map that states who the voters are and how many votes each of them can cast. This is not necessarily a modifiable map but just a map view: it is possible to read its mappings but not necessarily to modify them. The constructor iterates on the voters to compute the sum of all votes that can be cast. As said before, this iteration would be impossible in Solidity. The addition of two Java's BigIntegers is not performed through their add() method, which would be rejected by the static verifier of Takamaka's code since its complexity is not constant; hence, its gas consumption is not constant either. Instead, the support class BigIntegerSupport is used, which charges a variable amount of gas, depending on the size of the BigIntegers. The constructor terminates by computing an immutable snapshot of the (currently empty) map of votes cast that will be returned to clients by the getVotersUpToNow() method. The constructor receives a second argument action, that implements the local class Action and that it stores in the poll. This action will be used later, to run its run() method if the poll reaches its goal.

The vote() methods modify the votersUpToNow map. Since these are @FromContract methods, they are allowed to refer to the caller() contract, the one that signed the transaction for calling the method. Method vote() delegates to vote(BigInteger votes) by passing the total amount of votes that the caller can cast. The latter method checks if the caller is allowed to cast votes votes. That is, if the caller is actually a potential voter, if it did not already vote, if votes is non-negative and if votes is not larger than the maximal amount of votes that the caller can cast (see the auxiliary method checkIfCanVote()). Note the use of containsKey() inside it, which would be impossible in Solidity. Moreover, note that vote() recreates the snapshotOfVotersUpToNow, since the votes have changed.

Method close() checks if the poll has been closed already. Otherwise, it checks if the poll is over (a majority has been reached or all voters have cast their vote). If a majority has been reached (goalReached()) the action gets run, that was provided to the constructor of the poll.

Hotmoka is the runtime that instruments the bytecode of Takamaka smart contracts, interprets their annotations and runs their constructors and methods inside database transactions. Instrumentation is needed since annotations such as @FromContract and the access to the caller() are not available in Java, hence they must be provided by code instrumentation. A full description of Hotmoka is beyond the scope of this paper, therefore no more details are provided here. The interested reader can find more information in Spoto (2019). Here, we just say that the state of all smart contracts installed in blockchain, and their bytecode, is stored inside a persistent database. The bytecode instrumentation allows Hotmoka to infer the set of fields of objects modified by a transaction. This set is stored in the database, as the result of a transaction. The database implements a Merkle-Patricia trie, exactly as in Ethereum. Therefore, it is possible to revert to previous states. This is important if Hotmoka runs on top of a consensus engine that requires history changes, such as Mokamint.

5 Protocol-based code verification

This section presents protocol-based code verification in the context of a generic blockchain engine, such as Tendermint or Mokamint. This allows one to understand where it runs and which software architecture can be used to support its execution.

Figure 4 shows a more detailed picture of a generic blockchain engine and of an application connected through its application layer interface, such as ABCI. It shows that the engine keeps the blocks of the blockchain in its own database, that does not need to be the same used to hold the application's state. The latter holds, for instance, the code of the smart contracts installed in blockchain and the value of their state variables. The engine needs only the hash of the application state, for consensus, to ensure that all nodes have reached the same application state.

Figure 4

Figure 4. A generic blockchain engine and an application, with their respective databases.

One can define the application state as a map σ from the hash of the requests that the blockchain has executed to the responses that have been computed for them. Therefore, the responses are contained in the application state; instead, the requests are not contained in the application state: only their hash is used and mapped into the corresponding response. Since the state is a map, it can be implemented as a Merkle-Patricia trie from hashes of requests to responses. The full requests are contained in the database of blocks of the engine since they are needed to replay the transactions in all nodes of the network.

Protocol-based code verification requires a code verification module (Figure 1). This is part of the application layer since it contributes to the execution of the application-specific requests to install code (for instance, smart contracts) in blockchain. Assume that a request, whose hash is request_h, reaches the blockchain, requiring to install, in blockchain, the code of some smart contracts, reported inside request.

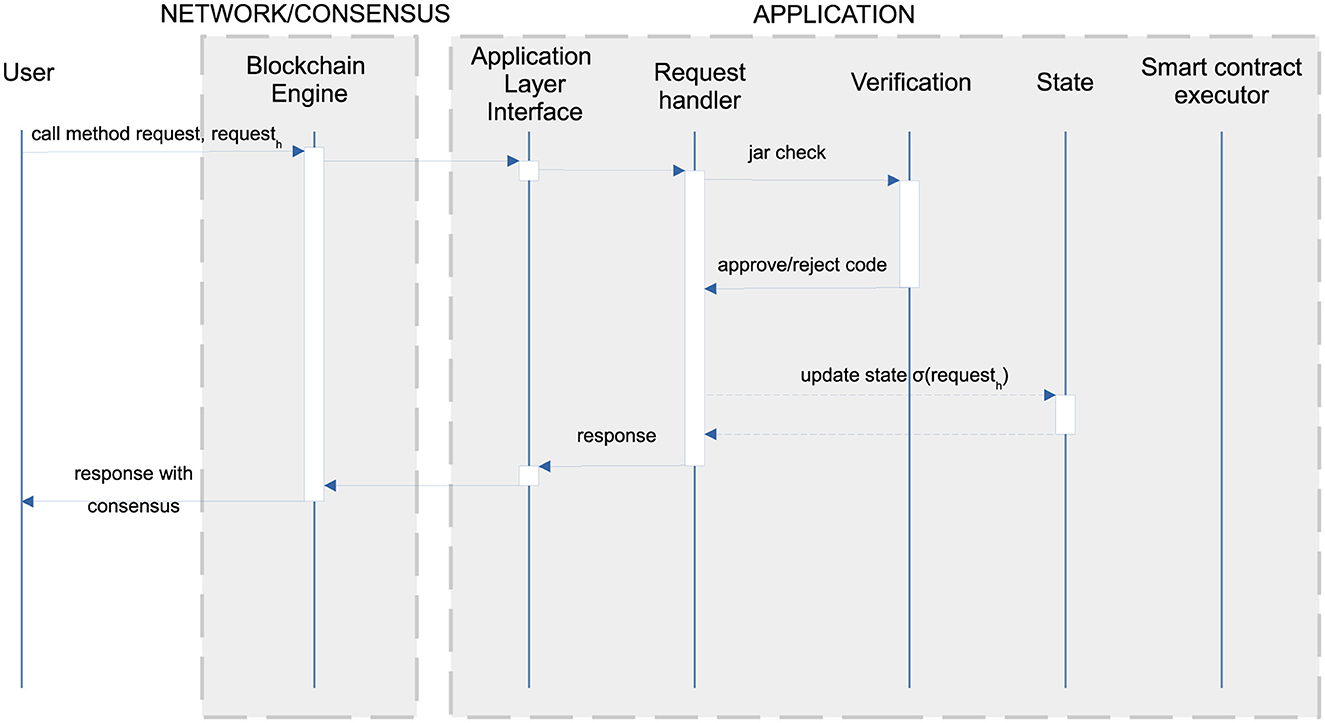
Figure 5 shows the sequence diagram for the execution of request. Namely, the generic blockchain engine routes request through networking and consensus up to the application, which uses its verification module to either approve or reject the code. If approved, the application packs the installed code in a response and updates its state σ with a new binding: σ(request_h) = response. The hash request_h is an immutable, machine-independent reference to this code, used later to instantiate and execute smart contracts. If the code is rejected, instead, the application state is expanded with a failure response; this kind of response does not contain any installed code since failure prevented the installation of any code in blockchain.

Figure 5

Figure 5. Sequence diagram for code verification and installation in blockchain.

Figure 6 reports an example of application state evolution. It reports the requests in full for readability, but we stress that only the hash of the requests is kept in the application state. Figure 6a shows the application state after the execution of a code installation request for which verification succeeds. In this example, the code is Java bytecode because it is the target of the compilation of Takamaka, packaged into a jar, i.e., a zipped container of Java bytecode. The response contains the instrumented jar. In terms of Java, the hash of the request can be used as the classpath of subsequent code executions. Figure 6b reports, instead, a request whose code fails to verify. The response does not include any instrumented code to install in the blockchain. This shows that the verification rules are part of the consensus rules that determine which code installation request is valid and which must be rejected instead (Figures 6a, b). Hence, they must be the same in every node of the network and must be deterministic.

Figure 6

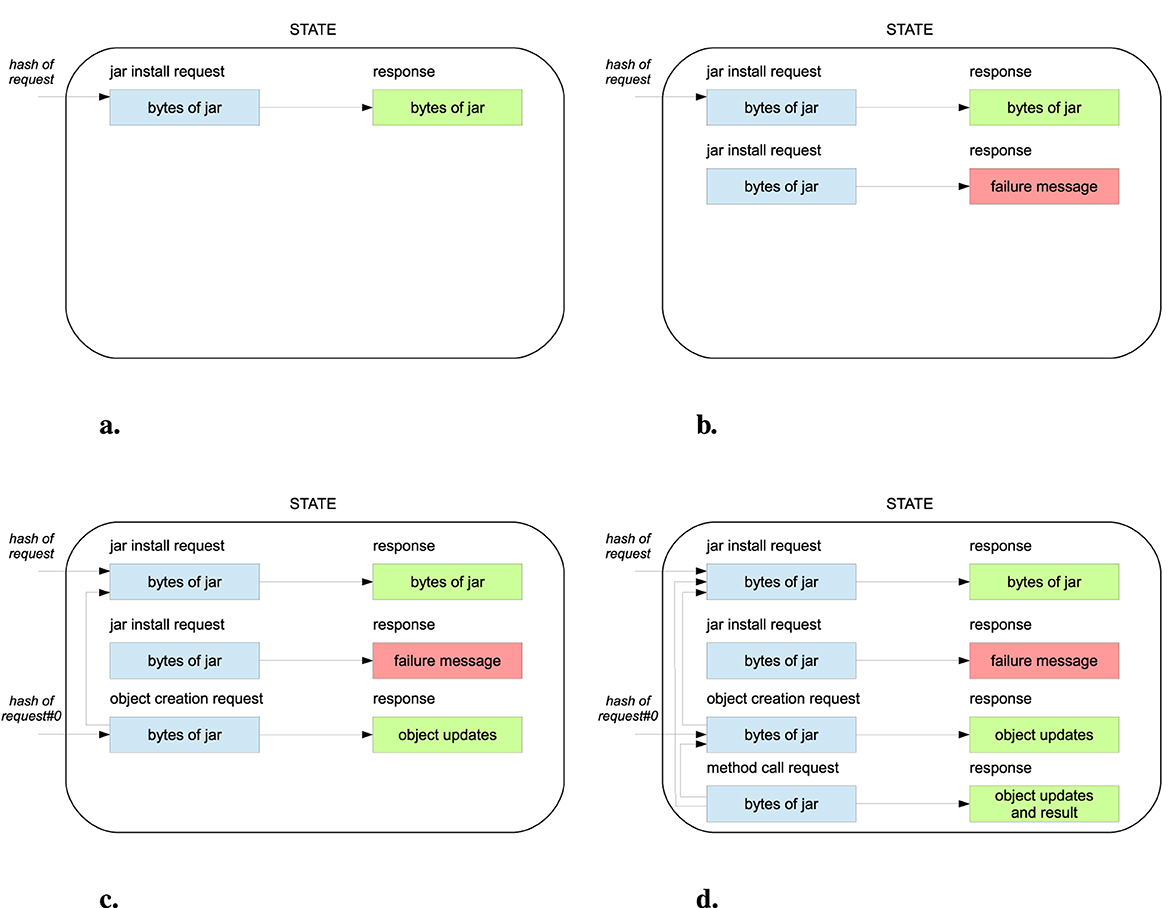
Figure 6. The evolution of the application state during a sequence of requests. (a) Successful verification. (b) Failed verification. (c) Instantiation of a smart contract. (d) Call a method of a contract instance.

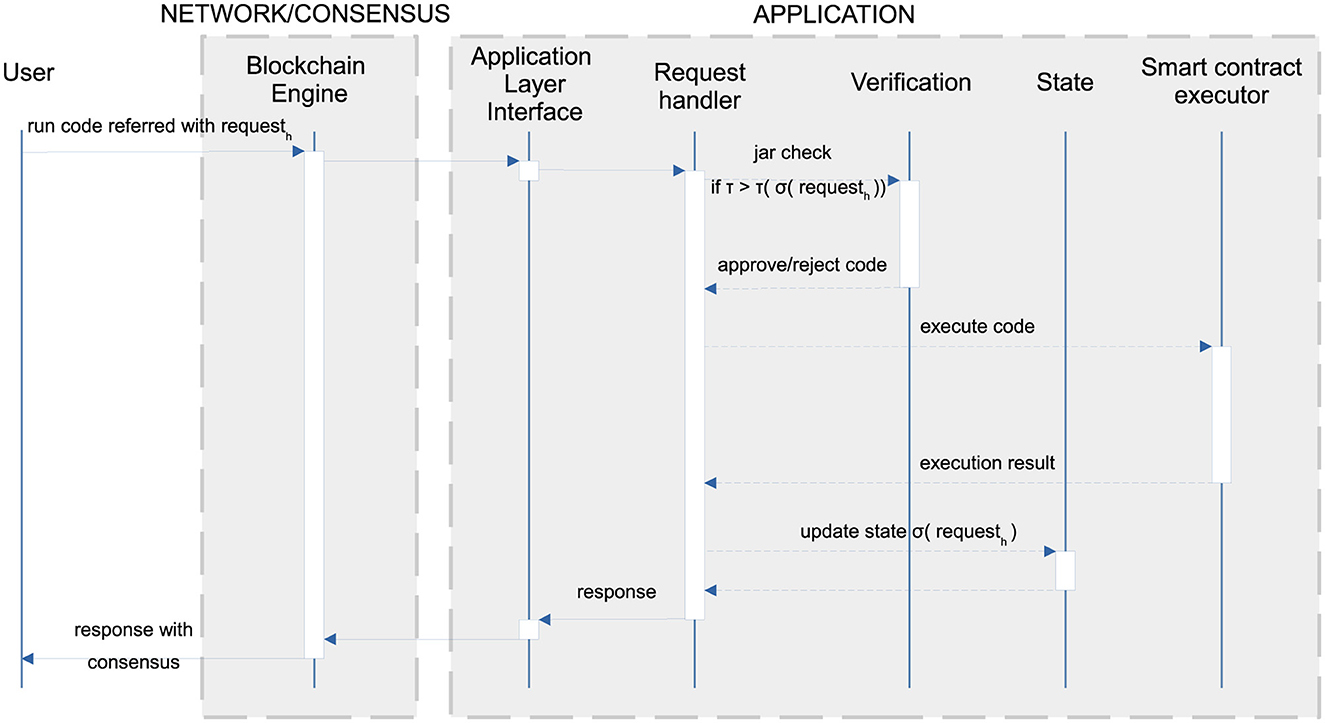
Protocol-based verification performs code verification statically, only once, when the code is installed in the blockchain. For instance, Figure 6c shows a subsequent request that asks to instantiate a smart contract whose code has been installed by the request in Figure 6a. The request in Figure 6c uses the hash of the request in Figure 6a as its classpath and contains the parameters for calling the constructor of the smart contract. The execution of the request runs that constructor without code verification: the latter has already been performed in Figure 6a. The immutable reference hash of request#0 is used later to refer to the new smart contract: the index #0 is used in the implementation of Takamaka to refer to the first object created during the execution of a request. In general, a request can instantiate many objects, depending on the code that it executes (for simplicity, this example assumes that only one has been instantiated). The state of the new smart contract is reported in the response as a set of updates, that is, instance fields modified during the execution of the request, including those of the smart contract instance hash of request#0 that has been created in blockchain. Finally, Figure 6d shows the execution of a request asking to call a method on the instance of the smart contract hash of request#0. This last request refers to both the classpath and the target instance smart contract. Its execution, in general, modifies some instance fields of some objects in the blockchain that are reported as updates in its response. This last request does not verify the code either since it is not a code installation request.

The fact that code verification is run only once, at code installation time, is important for efficiency since the installation of new code in the blockchain is a relatively rare event in comparison to the instantiation of new smart contracts and the execution of their methods. This is particularly the case for Hotmoka, where the code of a smart contract is installed once and then recycled for all instances of the smart contract that get subsequently created. This is different from Ethereum, where each instance of the smart contract reinstalls the code, although it is identical to that of the other instances. Therefore, Hotmoka installs (and verifies) the code of a smart contract only once, independently from how many instances of that smart contract will be created later. This is at the basis of the efficiency results that will be described in Section 7.

The rules of protocol-based verification are part of the consensus rules of the blockchain, since they determine if the response of a request to install code in blockchain is successful or fails. Therefore, they determine the evolution of the state of the application layer and its hash, which is reported in the blocks of the underlying blockchain engine and used for consensus. This means that all nodes must use the same verification rules, or otherwise, the network nodes will never agree on a common state: nodes that use different rules will automatically exclude each other.

6 Implementation

We have implemented protocol-based verification inside the Hotmoka runtime for executing smart contracts written in the Takamaka subset of Java. Hotmoka is an application with an interface to the ABCI. Hence, it can therefore run on top of both Tendermint and Mokamint (Figure 4). Hence, our protocol-based verification is currently available for both PoS and PoSp blockchains.

The verification module is implemented as a sequence of checks performed on methods and classes. Since a request to install new code in blockchain contains the compiled bytecode only, such checks run at Java bytecode level, by using the BCEL library for Java bytecode manipulation.¹⁰ The source code is simply not available in blockchain. Currently, Takamaka's protocol-based verification performs 21 checks on every jar that gets installed in blockchain. They must all pass, or otherwise the jar will be rejected. Figure 7 describes some of them.

Figure 7

Figure 7. Some of the 21 protocol-based verifications currently performed by Hotmoka on Takamaka smart contracts, when they get installed in blockchain.

The checks in Figure 7 filter out smart contracts whose installation would compromize the security and the functionality of the blockchain. As already discussed in the introduction, they are specific of a general-purpose language that must be used for writing smart contracts. For instance, the correct type for the storage fields is already enforced by the compiler of Solidity, while a specific check is needed for Java, that was not devised for smart contracts, originally. Determinism comes out-of-the-box in Solidity, that was designed for being deterministic, while that is not true in general-purpose languages. The rule that enforces a white-listed API is needed in Java also to avoid library calls to the file system, for instance, that are not useful for smart contracts and dangerous in blockchain, while Solidity has almost no library support and the little that exists is meant for smart contracts. Note that this same rule forbids calls to Java reflection, that is, to low-level calls that might bypass most security checks, and correspond to the dangerous delegatecall() of Solidity.

The rest of this section shows, in detail, the implementation of the last two checks from Figure 7.

6.1 Correct context for caller()

This check verifies that the method caller() is used in the right context. That method corresponds to msg.sender in Solidity: it allows programmers to get a reference to the contract that called a method or constructor X. Namely, the method caller() can be used inside the code of X only if X satisfies two constraints:

1. X is annotated as @FromContract(class), for some class;

2. the invocation of caller() occurs on this.

The rationale of constraint 1 is that @FromContract(class) guarantees that X can only be called from a contract (hence, also from an externally-owned account, in Takamaka) of type class, or subclass.¹¹ Therefore, the caller actually exists. For instance, methods vote() in Figure 3 can use caller() since they are annotated as @FromContract. Instead, the use of caller() would be illegal in the constructor of SimplePoll, since it is not annotated as @FromContract: that constructor could be called from any piece of code, not necessarily from a contract.

As another example, the following contract stores its creator in field owner. The use of caller() is correct here, since it occurs inside a @FromContract constructor, and is a typical pattern in smart contracts, to identify the creator contract of another contract:

 

public class C1 extends Contract {

  private C1 owner;

  public @FromContract(C1.class) C1() {

    owner = (C1) caller(); // ok

  }

}

 

Instead, it is incorrect to invoke caller() in a method or constructor not annotated as @FromContract, since its caller is not necessarily a contract and caller() would be meaningless in that case:

 

public class C2 extends Contract {

  public void m() {

    ... = caller(); // error at installation time

  }

}

 

The reason for constraint 2 is that this.caller() allows a method or constructor to access its caller during its current execution, which is sensible and useful, while other calls not on this would let one access the caller of the last invoked method or constructor of other contracts, with possible logical inconsistencies and privacy issues. For the same reason, the use of tx.origin is normally an antipattern in Solidity [see Tx.origin Authentication in (Antonopoulos and Wood 2018)]. Constraint 2 holds in every use of caller() in Figure 3, as well as in classes C1 and C2 above, while it is violated for instance below:

 

public class C3 extends Contract {

  private C3 owner;

  public @FromContract(C3.class) C3() {

   owner = (C3) caller(); // ok

  }

  public @FromContract void m() {

   ... owner.caller() ...; // error at deployment-time

  }

}

 

Figure 8 reports our implementation of a check that verifies if a method satisfies constraints 1 and 2 above. The code has been simplified for readability. Full understanding of the code in Figure 8 requires knowledge about Java bytecode and BCEL, which is outside the scope of this paper. Nevertheless, it is possible to understand its structure at the pseudocode level: the constructor of the check scans the Java bytecode instructions of the method, filters those that call a the method caller() of a Takamaka's storage object and checks two conditions for each of them (with the two nested if's inside the more external if): the method must be annotated as FromContract (constraint 1 above), and the invocation must be immediately preceded by a bytecode instruction that pushes this on the stack, as the receiver of the call to caller() (constraint 2 above). If any of the if's is satisfied, an issue is generated. The presence of an issue is enough to reject, later, the installation of the code in blockchain.

Figure 8

Figure 8. Pseudocode of the protocol-based check for the correct use of caller() in a given method. The actual full Java code is available at: https://github.com/Hotmoka/hotmoka/blob/master/io-hotmoka-verification/src/main/java/io/hotmoka/verification/internal/checksOnMethods/CallerIsUsedOnThisAndInFromContractCheck.java.

6.2 Correct fields in storage classes

As said above, storage objects, in Takamaka, are those that can be stored in blockchain and therefore get duplicated in each node that holds a copy of the blockchain. Therefore, they cannot hold machine-dependent fields, or otherwise consensus would be lost. In particular, they cannot hold RAM memory addresses, since these would be different in each node of the blockchain, that runs the code in its own JVM. Because of this requirement, the classes C that define storage objects, in Takamaka, are allowed to define fields only if such fields hold storage objects themselves: since storage objects are represented by machine-independent hashes, they can be shared without any risk of losing consensus. But this would not be flexible enough. Namely, Takamaka allows such classes C to define also fields of primitive (often called basic) type (the eight Java types boolean, char, byte, short, int, long, float, and double). These have a fixed, machine-independent representation in Java. Hence, they are represented identically in each node of the blockchain. Furthermore, Takamaka allows C to define fields whose type is BigInteger, that is a Java way to perform infinite arithmetic and replaces Solidity's uint256; or String, that is paramount in every programming language. Both BigInteger and String can be represented as machine-independent byte arrays and stored in blockchain.

Figure 9 reports a simplified code of the implementation of this protocol-based check. The constructor of the check scans the fields of the class under verification and checks if their type is allowed in Takamaka. Otherwise, an issue is generated. As described above, the pseudocode checks if the type of the field is a storage type itself (that is, it is not an array and it extends Storage); or a primitive type of Java; or BigInteger or String. If this check passes, then the strongly-typed guarantee of Java bytecode allows one to run the code without checking what is actually written into the fields, since it can only be one of these types, statically checked once and for all at code installation time.

Figure 9

Figure 9. Pseudocode of the protocol-based check for the correct type of the fields of a given storage class. The actual full Java code is available at: https://github.com/Hotmoka/hotmoka/blob/master/io-hotmoka-verification/src/main/java/io/hotmoka/verification/internal/checksOnClass/StorageClassesHaveFieldsOfStorageTypeCheck.java.

For extra flexibility, Takamaka allows fields to have Object type and to have an interface type (see Figure 9). The reason for this is that interfaces are largely used in modern programming languages and they would be strongly missed in Takamaka. For instance, StorageMapView in Figure 3 is an interface and field snapshotOfVotersUpToNow has an interface type. If interfaces would be banned in Takamaka, then the smart contract in Figure 3 would be rejected by the protocol-based verification of Takamaka. The reason for allowing Object, instead, is that generic types, in Java, are compiled by erasure into Java bytecode (Naftalin and Wadler, 2006), that is, replaced by Object and checked at run time through casts added by the compiler. If storage classes would ban fields of type Object then, for instance, it would become impossible to write generic storage classes such as StorageMap in Figure 3, since that class uses two generic type parameters that are compiled in bytecode through fields of type Object. Therefore, StorageMap (and, by transitivity, the SimplePoll class itself) would be rejected by the protocol-based verification of Takamaka.

This justifies why Object and interfaces are allowed in Figure 9. As a consequence, code instrumentation of Takamaka smart contracts adds checks to all write operations to fields of type Object or interface, to verify that, at run time, only values of storage type or BigIntegers or Strings are stored into such fields (primitive types are not subtypes of Object or interfaces in Java, thus there is no need to check for them). That is, only for fields of type Object or of interface type, the check has been moved from static to dynamic.

7 Experiments

This section reports experiments with protocol-based verification. The goal is twofold:

1. to show that its implementation is possible (Section 7.1);

2. to show that its cost can be extremely low, so that it does not increase the actual execution time of the transactions in blockchain (Section 7.2).

The evaluation metric, in the second case, is the extra time required for the protocol-based verification, in comparison with the same blockchain without protocol-based verification. This will of course depend on the complexity of the analyses that one wants to perform. Therefore, the context of this paper are the 21 analyses for Takamaka, in part reported in Figure 7.

7.1 Implementation

We have implemented our protocol-based verification for the Takamaka subset of Java, inside its Hotmoka runtime that works as a Tendermint and as a Mokamint application. Therefore, it is an actual blockchain, based on PoS (Tendermint) or PoSp (Mokamint) consensus, that can be programmed with smart contracts written in Java. We have created testcases that start a blockchain and request to install in blockchain the examples from Section 6. We have also created a test that installs a smart contract that runs many transactions, to check the scalability of the technique and evaluate the effect of turning protocol-based verification on and off. Readers who want to run the experiments and inspect the results need a Linux machine with Java version 21 or later, and the standard development tools Git and Maven. In order to run tests against a Tendermint blockchain, that software (version 0.34.15) must be downloaded from https://github.com/tendermint/tendermint/releases/tag/v0.34.15 and added to the command-line path.

The source code of Hotmoka can be downloaded with

 

    git clone https://github.com/Hotmoka/hotmoka.git

 

That repository also contains the code of the 21 checks of protocol-based verification (including those in Figures 8, 9). After download, one can enter the new hotmoka directory:

 

    cd hotmoka

 

and compile the project with

 

    mvn clean install

 

After a successful compilation, enter the test subproject:

 

    cd io-hotmoka-tests

 

The first JUnit testcase that we show starts a blockchain of a single node, connects to the node and requests a transaction that installs a jar containing class C1 from Section 6:

 

    mvn test -Dtest=io.hotmoka.tests.SSVMT2025_C1

             -Dverbose=true -DnodeType=tendermint

 

The result is successful, since C1 passes all verification checks:

 

    Test io.hotmoka.tests.SSVMT2025_C1:

      the jar has been installed in the node without

                                         exception

   

 

It is possible to run the test on a PoSp blockchain as well, by turning on a Mokamint node instead of a Tendermint node (Mokamint's start-up will be slower, since it initializes a big disk file for its proof of space consensus):

 

    mvn test -Dtest=io.hotmoka.tests.SSVMT2025_C1

             -Dverbose=true -DnodeType=mokamint

 

The result will be the same.

The subsequent experiment tries to install C2 instead:

 

    mvn test -Dtest=io.hotmoka.tests.SSVMT2025_C2

             -Dverbose=true -DnodeType=mokamint

 

This attempt will fail since protocol-based verification fails for C2, as expected:

 

    Test io.hotmoka.tests.SSVMT2025_C2:

      the installation of the jar threw exception:

      io.hotmoka.verification.VerificationException:

      io/hotmoka/examples/ssvmt2025/c2/C2.java:10:

        caller() can only be used inside a @FromContract

               method or constructor

    

 

The third experiment tries to install C3 in blockchain, which does not pass the protocol-based verification, as expected:

 

    mvn test -Dtest=io.hotmoka.tests.SSVMT2025_C3

             -Dverbose=true -DnodeType=mokamint

 

    Test io.hotmoka.tests.SSVMT2025_C3:

      the installation of the jar threw exception:

      io.hotmoka.verification.VerificationException:

      io/hotmoka/examples/ssvmt2025/c3/C3.java:16:

        caller() can only be called on ‘‘this''

 

7.2 Scalability

In order to evaluate the scalability of our technique, we have created a JUnit testcase that installs in blockchain a smart contract that creates and funds 500 externally-owned accounts. The test subsequently performs 1, 000 random transfers of cryptocurrency among the accounts and finally determines which, at the end, is the richest among them (which one has the highest balance). The whole process is repeated ten times. The testcase can be run with:

 

    mvn test -Dtest=io.hotmoka.tests.SSVMT2025

             -Dverbose=true -DnodeType=tendermint

 

We prefer to use Tendermint above because the execution time information is stable: Tendermint has a fixed block creation rate, while the PoSp of Mokamint can have significant random fluctuations around an average block creation rate. The result of the execution of the testcase is something like:

 

  1/10, the richest is bf8ed9dd...5efed998b78eb7#2f8

  2/10, the richest is f3382128...9f7961f04e9d7e#77a

  3/10, the richest is 2d8438af...af6e501216339a#1e08

  4/10, the richest is 869b1973...ad04698cff35a9#1da

  5/10, the richest is e47bc238...d6a922828428b8#184b

  6/10, the richest is 37c4b4c6...008fa79db22096#10c7

  7/10, the richest is 233c59e4...007b58930368cc#88a

  8/10, the richest is 11334c64...08cf5ca24305bb#10c7

  9/10, the richest is 55b2cbbe...d55943a4022f89#c74

  10/10, the richest is 7f5740c...9c80096b760743#116c

  10000 money transfers, 10011 transactions in 88445 ms

                                             [113 tx/s]

 

The execution time of this testcase is 88.445 seconds and it does not change from machine to machine: it is determined by the block creation rate of Tendermint and by the fact that a limited number of transactions can fit in a block, since a transaction for an account must wait for the completion of the previous transaction for the same account or otherwise the transaction nonce would be incorrect and the newer transaction would be rejected. This is a typical limitation of all blockchains, starting from Ethereum. In total (including code installation and account creation) the test runs 10, 011 transactions, that is, it performs around 113 transactions per second. Let us turn code verification off now¹²:

 

  1/10, the richest is bf8ed9dd...5efed998b78eb7#1e87

  2/10, the richest is f3382128...9f7961f04e9d7e#92f

  3/10, the richest is 2d8438af...af6e501216339a#f65

  4/10, the richest is 869b1973...ad04698cff35a9#1bd2

  5/10, the richest is e47bc238...d6a922828428b8#2877

  6/10, the richest is 37c4b4c6...008fa79db22096#f3

  7/10, the richest is 233c59e4...007b58930368cc#ea8

  8/10, the richest is 11334c64...08cf5ca24305bb#15fb

  9/10, the richest is 55b2cbbe...d55943a4022f89#df1

  10/10, the richest is 7f5740c...9c80096b760743#c5f

  10000 money transfers, 10011 transactions in 88356 ms

                                             [113 tx/s]

 

As shown above, by turning protocol-based verification off, the same testcase runs in almost the same time, with the same number of transactions per second. That is, there is no evidence that protocol-based code verification affects the execution time of the test (Figure 10). This is not surprising:

• protocol-based code verification is performed only once, in the unique transaction that installs the smart contract's code (see Section 4). The other 10, 010 transactions run without any code verification, since they are not code installation transactions but rather object creation transactions or method execution transactions for money transfer.

• The code of the installed smart contract is just a few lines of code, hence its verification is very quick.

• The 21 code verifications that Takamaka performs are relatively simple and run quite fast.

Figure 10

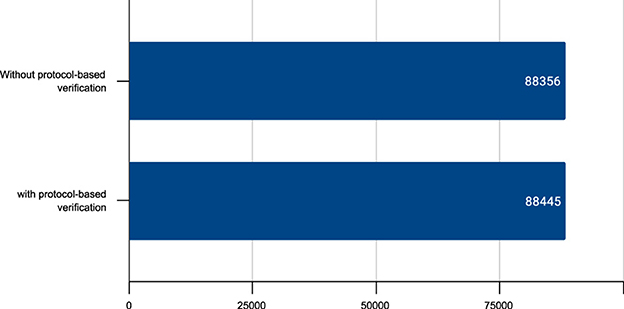
Figure 10. Comparison of the execution time (in milliseconds) of the test smart contract with and without protocol-based verification.

This last experiment shows that protocol-based verification, if limited to simple analyses, does not affect the execution time of a blockchain application. The latter is, instead, largely dependent on the block creation rate of the blockchain and on the ability of the application (in our example, of the testcase) to pack as many independent transactions as possible into the same block. Which is completely unrelated with protocol-based verification. This does not mean that protocol-based verification does not cost anything, but only that its cost disappears inside the much larger amount of time during which a blockchain sits idle, waiting for the next block to be minted. In particular, we have measured the cost of each of the 21 static analyses performed by our tool. We computed this measure twice: once for the installation of the jar containing the Takamaka run-time library (which occurs only once at blockchain start-up time) (Figure 11) and once for the installation of the jar containing our test smart contract used above (which occurs only once, the first time that that smart contract is installed in blockchain) (Figure 12). In the former case, the most expensive analysis requires less than 250 milliseconds. In the latter case, it requires less than 2.5 milliseconds. Such time disappears inside the default 4 seconds block rate of Tendermint: the analyses are performed while the blockchain sits idle waiting to mint the next block.

Figure 11

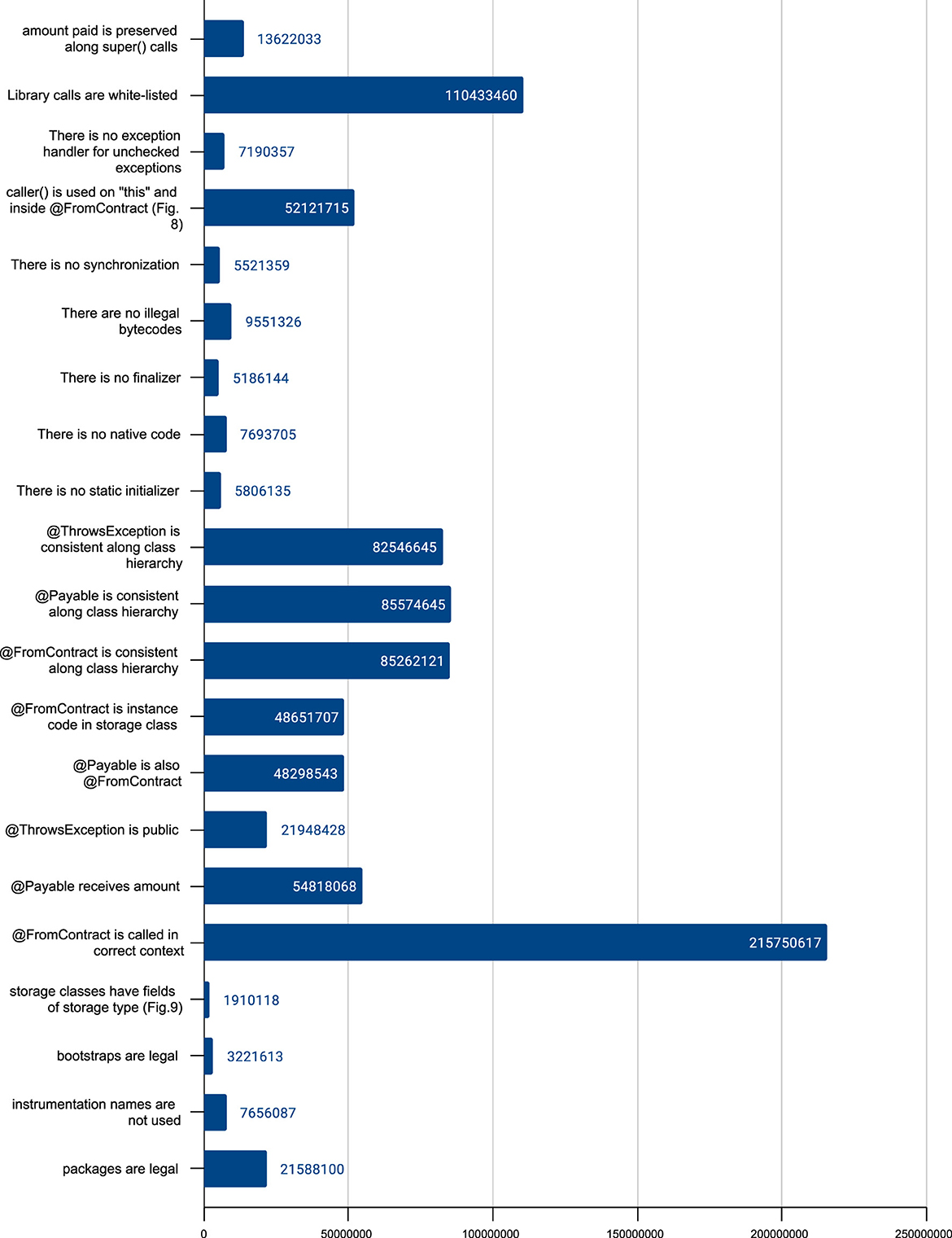
Figure 11. The time (in nanoseconds) for the execution of each of the 21 static analyses performed by our tool, on the jar file containing the run-time of Takamaka.

Figure 12

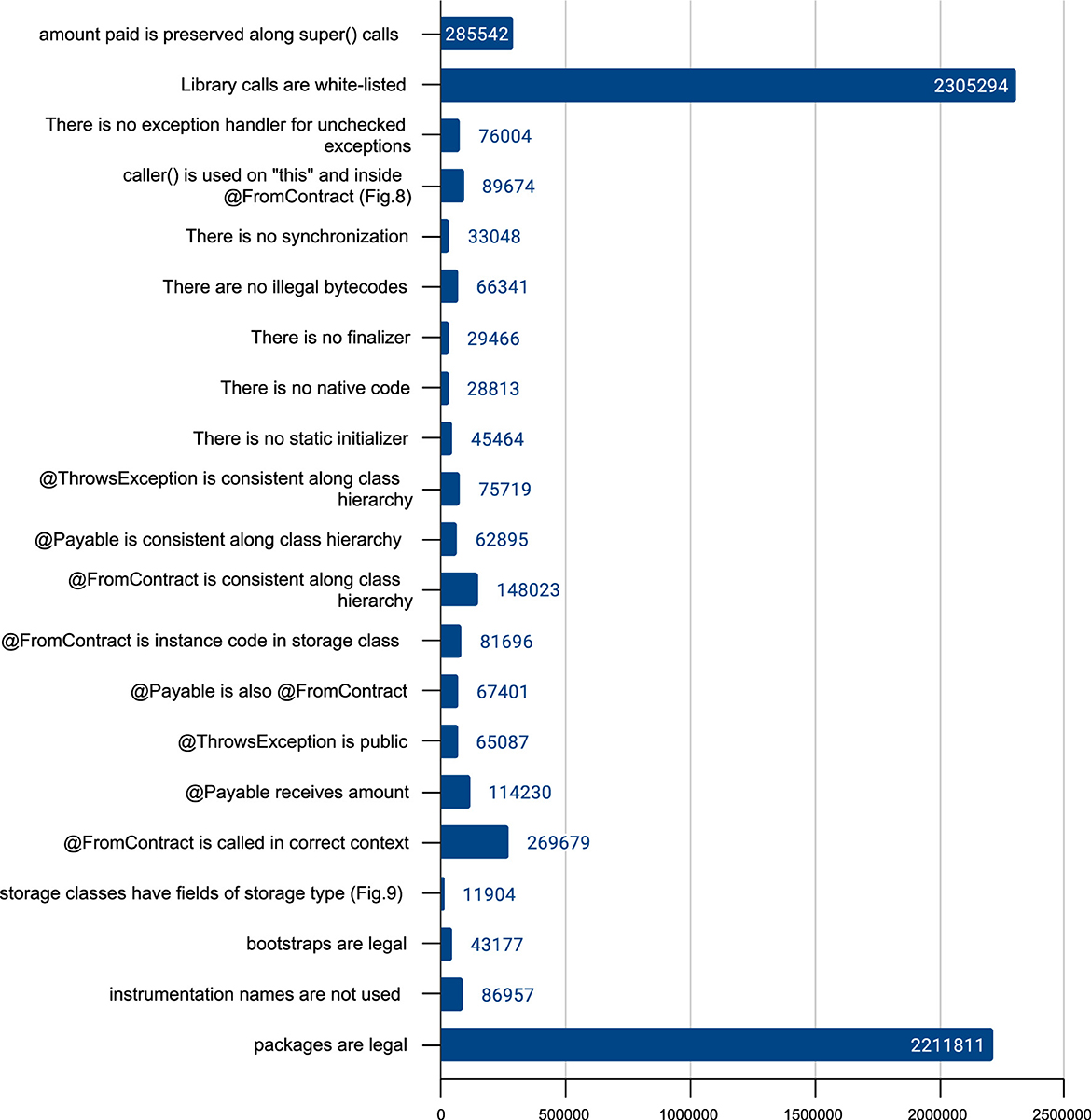
Figure 12. The time (in nanoseconds) for the execution of each of the 21 static analyses performed by our tool, on the jar file containing the test smart contract used in Section 7.2.

As an example of a limitation of our technique, consider the check for numerical overflows and underflows. The standard approach is to use some abstract domain for numerical approximations, such as polyhedra (Bagnara et al., 2008), to bound the possible values of the numerical variables. This becomes more complicated when variables are not just local variables but also fields of objects, whose number is not statically bound. Experience with such analyses shows that they immediately become very expensive, in time and memory, and do not allow to easily and deterministically bound the resources needed for their execution. The results are currently suboptimal, at least for the analysis of Java, as our experience with the Julia static analyzer has shown in the past. Such analyses are currently out of reach for a protocol-based verification technique.

We conclude by observing that the above 113 transactions per second is not the maximal throughput of Hotmoka. The latter can well process thousands of transactions per second, as long as they are independent, that is, if they do not origin from the same externally-owned account. Otherwise, the nonces of the transactions would be inconsistent and some of such transactions would end up being rejected by the blockchain.

8 Evolution of code verification

This section shows how to deal with updates to the verification module of a blockchain that applies protocol-based code verification. There are many reasons for an update: the verification module might need to be updated in order to include new verification rules or to improve the precision of the already existing rules or even to patch some bugs in the module itself. When a new version is deployed, it becomes necessary to update all nodes to that version (or at least all validators), or otherwise consensus might be lost. A change in the verification rules, if deployed on a subset of the network only, entails that the updated nodes might accept a request that the non-updated nodes might reject instead, or vice versa. Moreover, there must be a way to coordinate the moment when the update must be considered activated.

8.1 Coordinating an update to the verification module

In order to decide if and when to update to a newer version of the verification module, Hotmoka uses a technique purely based on a set of smart contracts installed in blockchain at deployment time. Namely:

• A Hotmoka blockchain publishes a non-replaceable smart contract, called the manifest of the blockchain, that knows about the current set of validators; these might coincide with the consensus validators if PoS is used, or might just be a set of accounts allowed to vote on system updates, according to some governance agreement of the network.

• The manifest also publishes a non-replaceable Versions smart contract that keeps track of the current version of the verification module; this smart contract allows each validator to start a poll among all validators, whose final action is to increase the verification version.

The typical scenario for passing from version τ of the verification module to version τ + 1 of the same module is the following:

1. Version τ + 1 of the verification module is advertized on social channels, for instance web pages, social networks, or blogs of the blockchain communities, suggesting all nodes to update the the latest Hotmoka software that provides version τ + 1 of the verification module.

2. During the update, the verification version of the blockchain, contained in the Versions smart contract, remains τ and therefore the new updated nodes still keep working according to the rules of version τ.

3. Eventually, a validator account decides that it is time to bump the verification version to τ + 1 and starts a poll among all validators, that allows them to vote in favor of the switch to version τ + 1.

4. The poll is an object of class SimplePoll (Figure 3) whose Voters are the validators of the blockchain; their power might be equal among them, or it might coincide with their stakes (in PoS) or it might be based on another governance-specific algorithm.

5. If the poll reaches its goal (that is, if enough validators voted in favor) then some validator can call method close() of the poll (Figure 3), that will run an action that increases the verification version in Versions to τ + 1.

6. From that moment, the updated nodes will see version τ + 1 in the Versions smart contract and will use version τ + 1 of their verification module to verify new code to install in the blockchain.

It is also possible to use a poll with a maximal duration, that allows validators to vote only inside a given time window. An implementation of such a poll is available in the library of Takamaka, but it is not discussed here further.

Figure 13 reports the simplified code of the Versions smart contract. This smart contract is typically created and installed when the blockchain starts, together with the creation of the manifest. It is a class generic w.r.t. the type of the validators of the blockchain. Its creation requires to specify the manifest of the node and the current verification version. When a validator wants to propose a poll about the switch to version τ + 1 of the verification module, it calls method newIncreasePoll, that creates a poll among the validators of the blockchain, recovered from the manifest of the blockchain. That poll, if it reaches its goal, will trigger an action that increases the verification version contained in the Versions object.

Figure 13

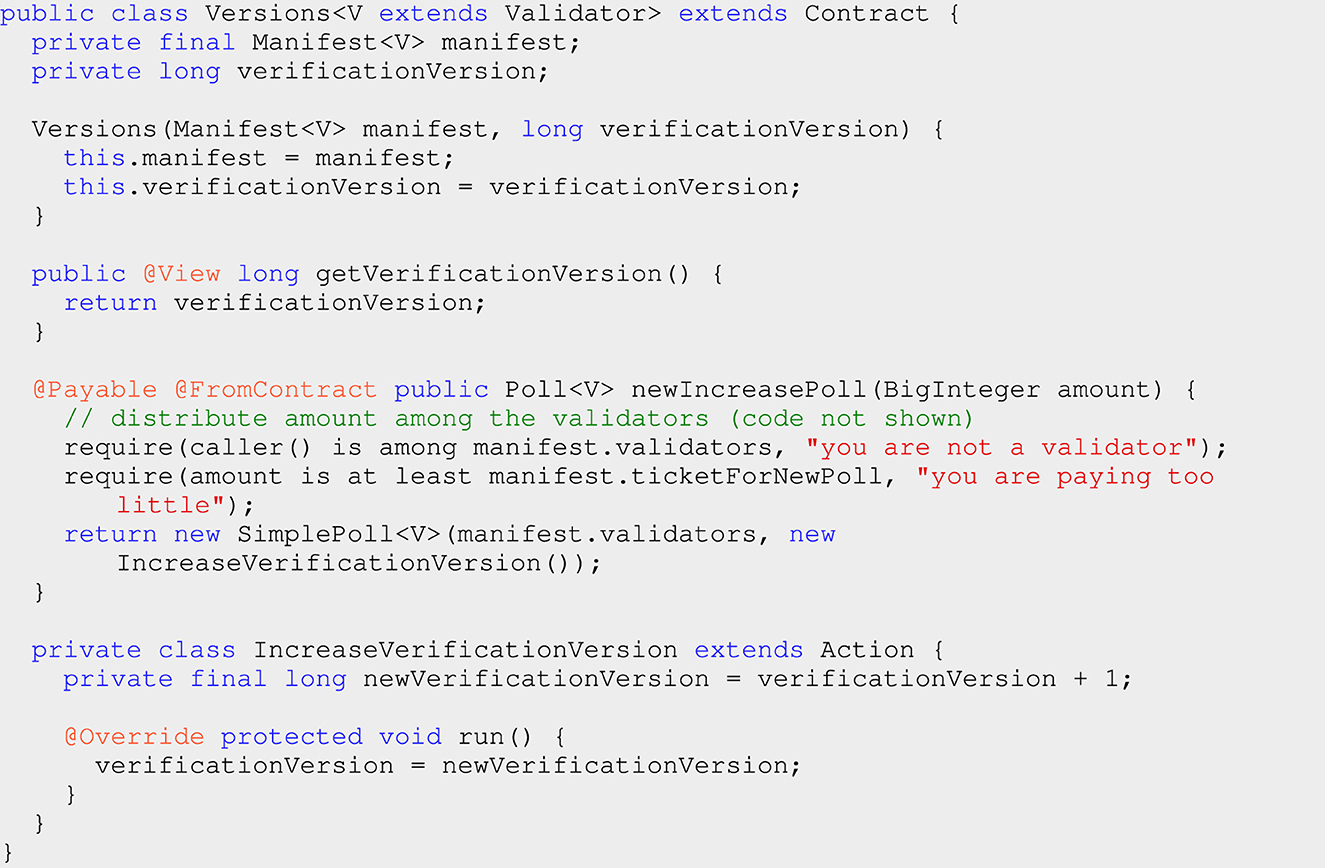
Figure 13. The smart contract that keeps track of the current verification version and of its updates. The complete code is available at https://github.com/Hotmoka/io-takamaka-code/blob/main/io-takamaka-code/src/main/java/io/takamaka/code/governance/Versions.java.

Method newIncreasePoll is @Payable, that is, its caller must pay to call it. There is a minimal ticketForNewPoll that must be paid, as specified in the manifest, in order to discourage the creation of too many cheap polls, that would just add noise. This amount gets distributed to all validators, as a remuneration for their effort to vote. In any case, only validators are allowed to start a version update poll.

It is interesting to observe, in Figure 13, that the newVerificationVersion is computed at the time of creating the action, that is, at the time of creating the new poll inside method newIncreasePoll(). Namely, it is not computed later, when the run() method of the action runs. This avoids the risk of starting n > 1 polls to increase the current verification versions to τ + 1, possibly under request of distinct validators, without waiting for their closure, and end up increasing the verification version to τ + n instead of τ + 1. With the code in Figure 13, all such polls would end up increasing the verification version to the same value τ + 1, repeatedly, which is what is expected.

8.2 Deadling with code verified with legacy verification rules

When the verification version in the Versions smart contract gets updated, the smart contracts existing in blockchain at that moment will still pass the old (legacy) verification rules, but not necessarily the new rules implemented by the new verification module. Hence, there must be a mechanism that enforces that the execution of some code in blockchain occurs only if that code passes the current verification rules. Conceptually, this means that an update of the verification module triggers a re-verification of all code previously successfully installed in blockchain. In practice, this cannot be performed, since it would be extremely expensive and would hang the nodes for a long time. Hotmoka's solution, that we are going to describe, is to lazily re-verify the code on-demand, when it is asked to run. This amortizes the cost of re-verification. Moreover, only 0.05% of all contracts installed in Ethereum are involved in 80% of the transactions. Hence, a lazy approach avoids the re-verification of code that might actually never run again (Oliva et al., 2020).

In order to implement this lazy re-verification approach, Hotmoka expands the information in the response of a successful code installation request (Figure 6). Namely, together with the installed code, response is enriched with a numerical tag τ(response), i.e., the version of the verification module that has been used to verify the code inside response. The sequence diagram in Figure 14 shows the workflow for lazy code re-verification. Assume that a request arrives, that requires to run code referred with the hash request_h of a previous, successful code installation request (as in Figures 6c, d). The node finds out that σ(request_h) = response has a verification tag τ(response) and compares it with the current version τ of the verification module. There are two possibilities:

1. τ = τ(response): the code was verified with the current version of the verification module, it does not need re-verification and can be run immediately;

2. τ > τ(response): the code was verified with an old version of the verification module; it must be re-verified before being run.

Figure 14

Figure 14. Sequence diagram for lazy code re-verification.

In the second case, the node verifies the code again, using the current version τ of the verification module. This is possible since response includes that code (Figure 6a). A new response response′ will be computed (it could be a successful response, having τ as verification module version, or a failed response) and the application state is updated as $\sigma ({request}_h)={response}^{\prime }$. The use of request_h in future requests will not re-verify the code anymore, at least not until a yet newer version of the verification module is installed. Note that the update of the response is possible since it occurs in the state, not in the blockchain, whose blocks are immutable.

It is important to note that response′ might state that reverification failed, because the old code passed the previous verification rules but not the new ones. In that case, the execution of the code will fail, since its classpath is not valid anymore. This means that a smart contract might work today, but might stop working tomorrow, if updated verification rules reject its code. In theory, the converse is also possible: the same contract might be reactivated after tomorrow, if another change in the verification rules replaces a failed response with a successful response. However, Hotmoka currently forbids this second scenario, since it might be surprising to most users.

9 Conclusion

To the best of our knowledge, this paper presents the first protocol-based verification of blockchain code. The technique is fully implemented inside the Hotmoka runtime for executing smart contracts written in the Takamaka subset of Java. Experiments show that the addition of a code verification layer to the nodes of a blockchain network does not affect its efficiency (Section 7). However, this is true also because the static analyses performed by the verification module of Hotmoka are still quite simple and largely related to checking the correct use of the annotations and primitives of the Takamaka language (Figure 7). The cost of verification might explode, instead, if more complicated static analyses would be considered in the future, such as those already existing for Java.

In comparison with off-chain static analysis, the following considerations are relevant:

• An off-chain static analyzer can afford a large execution time, while a protocol-based static analysis must be quick or otherwise it might not terminate in time for the creation of the next block or it might not work timely on the least powerful nodes of the network.

• An off-chain static analyzer might even afford to diverge and never provide an answer, while, at the protocol level, that would mean that the whole blockchain network would hang, a disaster that must be avoided.

• An off-chain static analyzer may contain bugs that lead to an undesirable but not disastrous crash; instead, protocol-based analysis should not crash or otherwise all (or most) nodes of the network might stop working.

• An off-chain static analyzer can afford non-deterministic results, typically due to optimizations such as parallel executions or time-outs; the same cannot be accepted for protocol-based static analysis, since non-deterministic results make it impossible for the network to reach a consensus.

Such considerations imply that protocol-based and off-chain static analyses could actually coexist since they address different goals: the former checks the correct use of the language primitives that, if violated, would introduce security holes in the blockchain network itself; while the latter verifies more complicated, global properties of the code, that would not introduce security risks to the network but might be of paramount importance to the programmer. That is, protocol-based verification must be understood as a mandatory, defensive verification technique for the blockchain, rather than as a replacement of the off-chain verification that is useful for the programmer.

The issue of reverification of legacy code after an update of the verification module has not been studied much up to now. In Section 8.2, it is said that it should trigger the re-verification of code already in blockchain. But this might not be the best choice, since it might disable some smart contracts already in blockchain and lock their funds for ever. Moreover, a large number of users could oppose a change of the verification rules that affects some highly popular contracts. Future work will investigate linguistic primitives and programming patterns that allow funds to be unlocked or specify that some contract should not be re-verified after an update of the verification module.

Protocol-based verification has been developed to support the safe use of general-purpose languages in a permissionless blockchain. As such, its applicability is much larger than the case of Java, and spans all general-purpose languages used so far for writing smart contracts (Golang, Python, and Rust, for instance). Its application to Solidity remains limited, since Solidity was meant for writing smart contracts, from its very inception, therefore most of our checks are already performed by the Solidity compiler. Nevertheless, it is possible, in principle, to modify the Ethereum Virtual Machine and trigger code verification of every Solidity smart contract deployed in Ethereum. This would be perfectly possible for simple checks (for instance, for the use of msg.sender instead of tx.origin or for unexpected and non-standard uses of delegatecall()) while we remain skeptical about protocol-based verification of more complicated security issues, such as overflows, underflows and reentrancy, whose computational cost is quite higher. For reentrancy, a more syntactical approach, such as making the default payment method final, as done in Takamaka, catches most attacks in a much simpler way than a static analysis.

Data availability statement

Publicly available datasets were analyzed in this study. This data can be found here: https://github.com/Hotmoka/hotmoka.

Author contributions

LO: Data curation, Validation, Writing – original draft, Writing – review & editing. FS: Conceptualization, Data curation, Software, Supervision, Writing – original draft, Writing – review & editing. FT: Data curation, Validation, Writing – original draft, Writing – review & editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work partially supported by SERICS (PE00000014 -CUP H73C2200089001) and iNEST (ECS00000043 -CUP H43C22000540006) projects funded by PNRR NextGeneration EU.

Conflict of interest

FT was employed by Equixly Srl.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Gen AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

1. ^https://docs.ignite.com/welcome (Accessed June, 2025).

2. ^https://docs.cometbft.com/v1.0/ (Accessed June, 2025).

3. ^https://github.com/Mokamint-chain/mokamint

4. ^https://www.chia.net

5. ^https://wiki.signum.network

6. ^Total value locked in the blockchains: ~50% Ethereum (main-net),~8% Solana, ~6% Bitcoin, ~6% BSC (Ethereum-based), ~5%Tron (Ethereum-based), ~25% others [https://defillama.com/chains, Accessed March, 2025].

7. ^https://github.com/Hotmoka/hotmoka

8. ^https://github.com/JetBrains/xodus

9. ^See https://github.com/Hotmoka/io-takamaka-code/blob/main/io-takamaka-code/src/main/java/io/takamaka/code/lang/ExternallyOwnedAccount.java.

10. ^https://commons.apache.org/proper/commons-bcel

11. ^If class is not specified, then Takamaka assumes the default class Contract for it.

12. ^This option is available for testing, but a real Hotmoka blockchain would never be installed without code verification and code verification cannot be turned off after a blockchain has been started.

References

Abusalah, H., Alwen, J., Cohen, B., Khilko, D., Pietrzak, K., and Reyzin, L. (2017). “Beyond hellman's time-memory trade-offs with applications to proofs of space,” in Proceedings of Advances in Cryptology, the 23rd International Conference on the Theory and Applications of Cryptology and Information Security (ASIACRYPT'17), part II, eds. T. Takagi, and T. Peyrin (Hong Kong, China: Springer), 357–379. doi: 10.1007/978-3-319-70697-9_13

Crossref Full Text | Google Scholar

Antonopoulos, A. M. (2017). Mastering Bitcoin: Unlocking Digital Cryptocurrencies. New York: O'Reilly, 2nd edition.

Google Scholar

Antonopoulos, A. M., and Wood, G. (2018). Mastering Ethereum: Building Smart Contracts and Dapps. New York: O'Reilly.

Google Scholar

Arceri, V., Merenda, S. M., Dolcetti, G., Negrini, L., Olivieri, L., and Zaffanella, E. (2024). “Towards a sound construction of EVM bytecode control-flow graphs,” in Proceedings of the 26th ACM International Workshop on Formal Techniques for Java-like Programs, FTfJP 2024 (New York, NY, USA: Association for Computing Machinery), 11–16. doi: 10.1145/3678721.3686227

Crossref Full Text | Google Scholar

Ateniese, G., Bonacina, I., Faonio, A., and Galesi, N. (2014). “Proofs of space: when space is of the essence,” in Proceedings of the 9th International Conference on Security and Cryptography for Networks (SCN'14), eds. M. Abdalla, and R. De Prisco (Amalfi, Italy: Springer), 538–557. doi: 10.1007/978-3-319-10879-7_31

Crossref Full Text | Google Scholar

Atzei, N., Bartoletti, M., and Cimoli, T. (2017). “A survey of attacks on ethereum smart contracts (SoK),” in 6th International Conference on Principles of Security and Trust (POST'17) (Uppsala, Sweden: Springer), 164–186. doi: 10.1007/978-3-662-54455-6_8

Crossref Full Text | Google Scholar

Bagnara, R., Hill, P. M., and Zaffanella, E. (2008). The parma polyhedra library: toward a complete set of numerical abstractions for the analysis and verification of hardware and software systems. Sci. Comput. Progr. 72, 3–21. doi: 10.1016/j.scico.2007.08.001

Crossref Full Text | Google Scholar

Buterin, V. (2013). Ethereum Whitepaper. Available online at: https://ethereum.org/en/whitepaper/ (Accessed March 9, 2025).

Google Scholar

Certik (2025). Certik. Available online at: https://www.certik.com/ (Accessed August, 2025).

Google Scholar

Chen, J., and Micali, S. (2019). Algorand: a secure and efficient distributed ledger. Theor. Comput. Sci. 777, 155–183. doi: 10.1016/j.tcs.2019.02.001

Crossref Full Text | Google Scholar

Consensys Diligence (2025). Blockchain Security &Ethereum Smart Contract Audits. Available online at: https://diligence.consensys.io/ (Accessed August, 2025).

Google Scholar

Crosara, M., Olivieri, L., Spoto, F., and Tagliaferro, F. (2023). Fungible and non-fungible tokens with snapshots in java. Cluster Comput. 26, 2701–2718. doi: 10.1007/s10586-022-03756-3

Crossref Full Text | Google Scholar

Dua, R. (2025). Ethlint – Documentation. Available online at: https://ethlint.readthedocs.io/en/latest/ (Accessed March 2025).

Google Scholar

Dziembowski, S., Faust, S., Kolmogorov, V., and Pietrzak, K. (2015). “Proofs of space,” in Proceedings of Advances in Cryptology (CRYPTO 2015) - 35th Annual Cryptology Conference, part II, eds. R. Gennaro, and M. Robshaw (Santa Barbara, CA, USA: Springer), 585–605. doi: 10.1007/978-3-662-48000-7_29

Crossref Full Text | Google Scholar

Feist, J., Grieco, G., and Groce, A. (2019). “Slither: a static analysis framework for smart contracts,” in 2nd International Workshop on Emerging Trends in Software Engineering for Blockchain (WETSEB@ICSE'19) (Montreal, QC, Canada: IEEE/ACM), 8–15. doi: 10.1109/WETSEB.2019.00008

Crossref Full Text | Google Scholar

Grieco, G., Song, W., Cygan, A., Feist, J., and Groce, A. (2020). “Echidna: effective, usable, and fast fuzzing for smart contracts,” in 29th ACM SIGSOFT International Symposium on Software Testing and Analysis (ISSTA'20) (USA: ACM), 557–560. doi: 10.1145/3395363.3404366

Crossref Full Text | Google Scholar

Hejazi, N., and Lashkari, A. H. (2025). A comprehensive survey of smart contracts vulnerability detection tools: techniques and methodologies. J. Netw. Comput. Applic. 237:104142. doi: 10.1016/j.jnca.2025.104142

Crossref Full Text | Google Scholar

Kushwaha, S. S., Joshi, S., Singh, D., Kaur, M., and Lee, H.-N. (2022). Ethereum smart contract analysis tools: a systematic review. IEEE Access 10, 57037–57062. doi: 10.1109/ACCESS.2022.3169902

Crossref Full Text | Google Scholar

Kwon, J. (2014). Tendermint: Consensus without Mining. Available online at: https://www.weusecoins.com/assets/pdf/library/Tendermint%20Consensus%20without%20Mining.pdf (Accessed August 26, 2024).

Google Scholar

Loi, L., Duc-Hiep, C., Hrishi, O., Prateek, S., and Aquinas, H. (2016). “Making smart contracts smarter,” in Weippl, E. R., Katzenbeisser, S., Kruegel, C., Myers, A. C., and Halevi, S., editors, Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, Vienna, Austria, October 24-28, 2016 (ACM), 254–269. doi: 10.1145/2976749.2978309

Crossref Full Text | Google Scholar

Naftalin, M., and Wadler, P. (2006). Java Generics and Collections: Speed Up the Java Development Process. New York: O'Reilly.

Google Scholar

Nakamoto, S. (2008). Bitcoin: A Peer-to-Peer Electronic Cash System. Available at https://bitcoin.org/bitcoin.pdf (Accessed August 24, 2025).

PubMed Abstract | Google Scholar

Oliva, G. A., Hassan, A. E., and Jiang, Z. M. (2020). An exploratory study of smart contracts in the ethereum blockchain platform. Empir. Softw. Eng. 25, 1864–1904. doi: 10.1007/s10664-019-09796-5

Crossref Full Text | Google Scholar

Olivieri, L., Spoto, F., and Tagliaferro, F. (2021). “On-chain smart contract verification over tendermint,” in Financial Cryptography and Data Security. FC 2021 International Workshops, eds. M. Bernhard, A. Bracciali, L. Gudgeon, T. Haines, A. Klages-Mundt, S. Matsuo, et al. (Berlin, Heidelberg: Springer), 333–347. doi: 10.1007/978-3-662-63958-0_28

Crossref Full Text | Google Scholar

OpenZeppelin (2025). The OpenZeppelin Security Audit. Available online at: https://www.openzeppelin.com/security-audits (Accessed August 2025).

Google Scholar

Pasqua, M., Benini, A., Contro, F., Crosara, M., Dalla Preda, M., and Ceccato, M. (2023). Enhancing ethereum smart-contracts static analysis by computing a precise control-flow graph of ethereum bytecode. J. Syst. Softw. 200:111653. doi: 10.1016/j.jss.2023.111653

Crossref Full Text | Google Scholar

Popper, N. (2016). A Hacking of More than $50 Million Dashes Hopes in the World of Virtual Currency. The New York Times, 2016-06-18.

Google Scholar

Protofire (2025). Solhint - Official Website. Available online at: https://protofire.io/projects/solhint (Accessed March 2025).

Google Scholar

Ressi, D., Spanò, A., Benetollo, L., Piazza, C., Bugliesi, M., and Rossi, S. (2024). Vulnerability detection in ethereum smart contracts via machine learning: a qualitative analysis. arXiv preprint arXiv:2407.18639.

Google Scholar

Schneidewind, C., Grishchenko, I., Scherer, M., and Maffei, M. (2020). “eThor: practical and provably sound static analysis of ethereum smart contracts,” in Proceedings of the 2020 ACM SIGSAC Conference on Computer and Communications Security, CCS '20 (New York, NY, USA: Association for Computing Machinery), 621–640. doi: 10.1145/3372297.3417250

Crossref Full Text | Google Scholar

Sedlmeir, J., Buhl, H. U., Fridgen, G., and Keller, R. (2020). The energy consumption of blockchain technology: beyond myth. Bus. Inf. Syst. Eng. 62, 599–608. doi: 10.1007/s12599-020-00656-x

Crossref Full Text | Google Scholar

Spoto, F. (2019). “A java framework for smart contracts,” in 3rd Workshop on Trusted Smart Contracts (WTSC'19) (St. Kitts and Nevis: Springer), 122–137. doi: 10.1007/978-3-030-43725-1_10

Crossref Full Text | Google Scholar

Spoto, F. (2025). “A formalization of signum's consensus,” in 9th Workshop on Trusted Smart Contracts (WTSC'25), Lecture Notes in Computer Science, Miyakojima, Japan (Springer).

Google Scholar

Spoto, F., Migliorini, S., Gambini, M., and Benini, A. (2023). On the use of generic types for smart contracts. Cluster Comput. 26, 2099–2113. doi: 10.1007/s10586-022-03688-y

Crossref Full Text | Google Scholar

Tikhomirov, S., Voskresenskaya, E., Ivanitskiy, I., Takhaviev, R., Marchenko, E., and Alexandrov, Y. (2018). “SmartCheck: static analysis of ethereum smart contracts,” in 2018 IEEE/ACM 1st International Workshop on Emerging Trends in Software Engineering for Blockchain (WETSEB), 9–16. doi: 10.1145/3194113.3194115

Crossref Full Text | Google Scholar