- Institute for Biomechanics, ETH Zürich, Zürich, Switzerland
How mechanical forces influence the regeneration of bone remains an open question. Their effect has been demonstrated experimentally, which has allowed mathematical theories of mechanically driven tissue differentiation to be developed. Many simulations driven by these theories have been presented, however, validation of these models has remained difficult due to the number of independent parameters considered. An overview of these theories and models is presented along with a review of experimental studies and the factors they consider. Finally limitations of current experimental data and how this influences modeling are discussed and potential solutions are proposed.
Introduction
Bone’s capability of “perfect” regeneration is unique, unlike other tissues it is capable of recovering its form without permanent scars. However not all fractures heal spontaneously, it has been found that 20 per 100,000 people per year will have delayed healing or a non-union, where the fractured bone fails to fuse (1). It is known that mechanical forces can influence the pathways through which healing occurs; several studies have shown that changes in the mechanical environment can modulate the time taken to heal, change the proportions of different tissue type as well as gene expression patterns of cells in the healing bone (2, 3). The exact mechanism through which mechanical stimuli are sensed and incorporated in the healing process is not fully understood and still remains an open question. Answering this question will lead to improved treatment methods for bone fracture repair, reducing the amount of time patients are hospitalized. To this end, we have compiled a summary of literature on the topic examining the experimental studies and numerical theories.
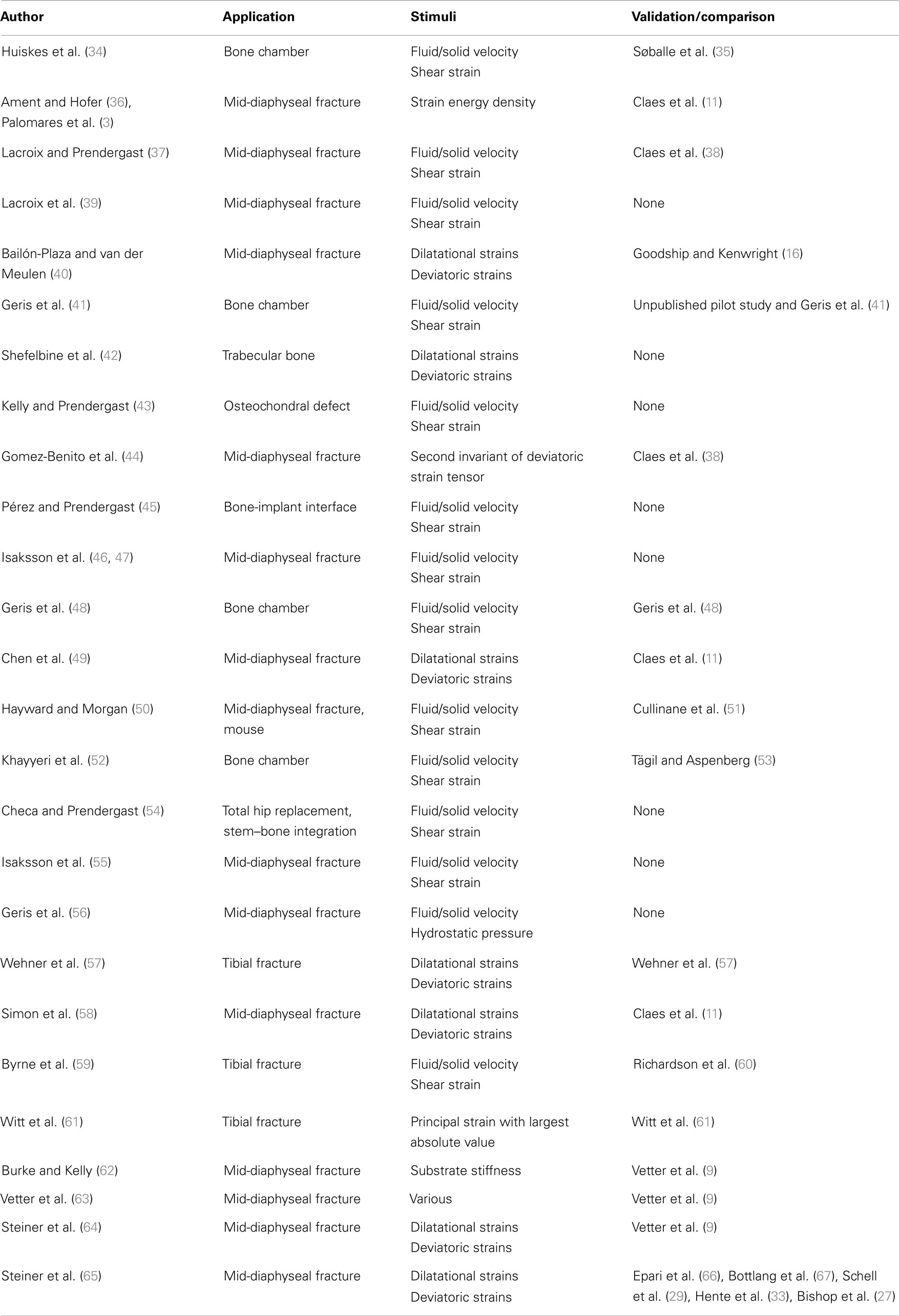
Depending on the stability of the bone fragments the healing can progress down two paths, rigidly fixed fragments with only a small fracture gap can heal through primary bone healing, where the bone remodeling units, responsible for the adaption of the cortical bone, bridge the gap; secondary fracture healing occurs when relative motion occurs between the bone fragments, causing a callus to form. Secondary fracture healing can be divided into three overlapping stages as described in Figure 1, the reactive, reparative, and remodeling phases. Immediately post-fracture there is an inflammatory response, termed the reactive phase, in which blood vessels, which have ruptured fill the injured area with blood forming clot called the fracture hematoma. The fracture hematoma is infiltrated by fibroblasts and small blood vessels, becoming granulation tissue. The initial callus is thus a mixture of hematoma, fibrous tissues, and infiltrating blood vessels. The reparative phase begins once bone and cartilage form, the bone is initially formed through intramembranous ossification initiating on the existing cortical bone and progressing with time toward the plane of the fracture, while the cartilage forms in regions of low oxygen tension (4, 5). Once the blood supply is sufficient enough, cartilage is calcified and converted into woven bone through endochondral ossification. The stability of a fracture influences the amount of intramembranous and endochondral ossification, with more cartilage being formed in less stable fractures and thus more endochondral ossification (6). Bony bridging, the union of the hard callus from either side of the fracture, occurs making the structure extremely stable. The remodeling phase begins during the reparative stage, with the bone structure being adapted back to its original load bearing form. The cortical bone is also remodeled with the cortical bone adjacent to the fracture becoming woven bone, likely as the vasculature within this bone is damaged during the fracture, causing hypoxia (7–9). Hypoxia has been shown to up regulate the formation, size, and activity of osteoclasts, the cells responsible for the resorption of bone (10). The remodeling phase concludes with the callus being completely remodeled into the shape of the original bone, recovering the original strength, and functionality. The events are driven through intercellular signaling, levels of oxygen tension and the mechanical environment directing mesenchymal stems cells to differentiate into osteoblasts, chondrocytes, or fibroblasts each of these cells being responsible for the production of particular tissues (7). In this review, we concentrate explicitly on the mechanical factors influencing bone regeneration, what has been experimentally observed as well as theories and models, which have been developed to explain this.
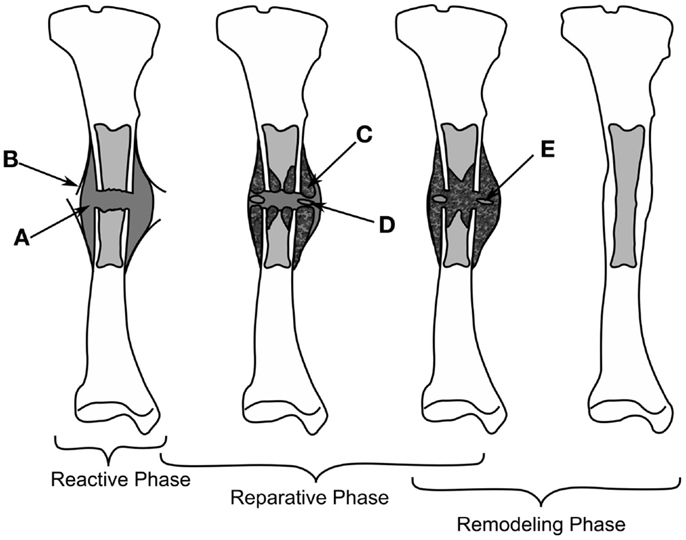
Figure 1. The healing of a tibial fracture. A hematoma (A) forms during the reactive phase, beneath the injured periosteum (B). During the reparative phase woven bone (C) forms through intramembranous ossification along with cartilage (C), which is eventually ossified (E), bony bridging occurs and finally the callus is remodeled into cortical bone.
Experimental Studies
Mechanical loads are applied at the organ level and propagate to a level where cells can sense them, which in turn results in changes at the tissue level. Many studies have investigated applying different forces to fractured bones in vivo and quantifying the tissue produced or the mechanical competence of the bone. Loads applied to bone cause non-homogenous strains throughout the healing tissue, resulting in a variety of tissues forming. Experimentally, these strains cannot be quantified in vivo preventing the direct development of mechanobiological rules, however, the result of organ level loading is important for validating fracture healing models, as an accurate rule set should predict the outcomes of such studies. Experimental studies investigating the effect of inter-fragmentary movement (IFM) and fixator stability/stiffness are essentially referring to how loading effects fracture healing outcome. IFM is ambiguously used to describe either axial tension/compression of the bone defect, shear movement in the plane of the defect, relative axial rotation of the fragments, or a bending. Here, we will distinguish between these different modes using the following terms: inter-fragmentary compression (IFC), inter-fragmentary tension (IFT), inter-fragmentary bending (IFB), and inter-fragmentary shear (IFS). The different loading modes are illustrated in Figures 2A–E with the exception of IFT, which is just the opposite of IFC. The cases of shear movement and rotation both create a non-uniform shear loading within the tissue, therefore we combine both of these loading states as IFS.
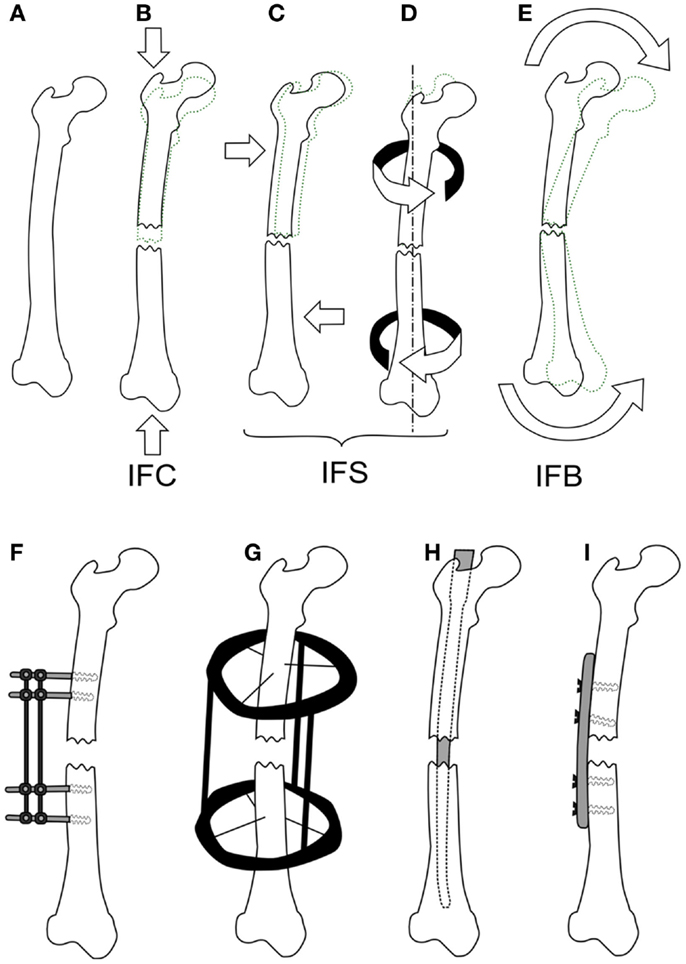
Figure 2. The different loading modes for a fracture, shown on a femur (A). IFC causes in a narrowing of the fracture gap (B), IFS is a shear movement (C) across the gap plane, or a relative torsional movement around the axis of the bone (D), and IFB is a bending movement (E) centered around the fracture. Fixation methods for fractures are shown in (F,G), external fixator (F), the ring fixator (G), intramedullary nailing (H), and plating (I).
To study the effect of each mode of movement demands the precise control and measurement of bone fragment movement requiring the use of some form of fixation. There are two categories of fixation used in biomechanical research, external and internal fixation, which can be seen in Figures 2F–I. External fixation is commonly used in large animal studies often with modifications to the fixator or to the surgical technique so as to change the stability of the fixator, or be instrumented to measure the fragment displacements (11). In contrast, internal fixators are simpler in design and technique. An intramedullary nail for example is guided by the medullary cavity and can be a single piece, which has made them much more commonly used in small animal studies (12–15). The fixation method has a large effect on the loads, which can be applied, external fixation allows for controlled movements or fixed forces, whereas, internal fixation typically limits the load to an applied force. The fragile nature of the soft tissue means that constant loading throughout a study is not always possible, thus some studies will define a maximum load and displacement. For example, Goodship and Kenwright (16) apply a 33% inter-fragmentary strain or a 360 N load, as initially such a load would induce strains in the hematoma that inhibited healing, whereas, once bony bridging occurs, this level of strain would damage the new bone.
There exists no standard methodology for loading during fracture healing. Studies can either use active loading like Goodship and Kenwright (16) passively allow a limited amount of movement as done by Claes et al. (11) or use a fixator structure or orientation with a different stiffness as done by Klein et al. (17) and Schell et al. (18). While it is often possible to compare initial loading of the callus, the loading is altered as the tissue distribution changes. This can lead to diverging results making comparisons between how bone heals in relation to loading difficult between studies. We attempt to provide a summary of how different organ level loadings affect the healing outcome and were possible highlight variations in fixation and loading between studies.
Inter-Fragmentary Compression and Inter-Fragmentary Tension
There are a substantial number of studies, which have investigated the effects of IFC on bone healing, several are summarized within Table 1. It is widely accepted that a certain amount of IFC has a positive effect on the healing process, which was first shown by Goodship and Kenwright (16). The timing of the load is also critical with Gardner et al. (12) showing that immediate application of loading post-surgery resulted in reduced healing potential compared to those applied 4 days after. They also demonstrated that too high an IFC force can be detrimental to healing. However, as they used an intramedullary nail and applied a force rather than a displacement, it is difficult to compare the results. Rate dependence with respect to the application of IFC has been identified by Goodship et al. (19) showing that for the same number of cycles a strain rate of 40 mm/s showed superior healing compared to 2 and 400 mm/s. High frequency low amplitude IFC was investigated by Goodship et al. (20) demonstrating an increase in the callus stiffness.
Table 1. Experimental studies considering the effects of inter-fragmentary compression on fracture healing.
Inter-fragmentary tension is movement applied in the opposite direction to compression, causing an increase in gap size. Cheal et al. (25) showed that high tensile loads lead to reduced healing with even cortical resorption occurring, while lower tensile loads lead to callus formation.
Inter-Fragmentary Shear
How IFS affects the bone regeneration process remains controversial, with studies showing that it can inhibit healing and others showing that it can have a positive effect. Several studies in this area are summarized in Table 2, with Bishop et al. (27) and Park et al. (28) showing neutral or positive effects and the others showing negative outcomes. These differences are likely due to the loading conditions. Park et al. (28) studied rabbits in which the femur was fractured instead of the more common method of cutting a discrete unit of bone out with a saw, i.e., osteotomy. They compared compression and shear loading showing an increase in periosteal cartilage formation and a significantly stiffer callus after 4 weeks. It is possible that traumatic injury will solicit a different biological response, which osteotomies do not cause. In addition, fracture planes will not have been as uniform and perhaps will have influenced the tissue loading.
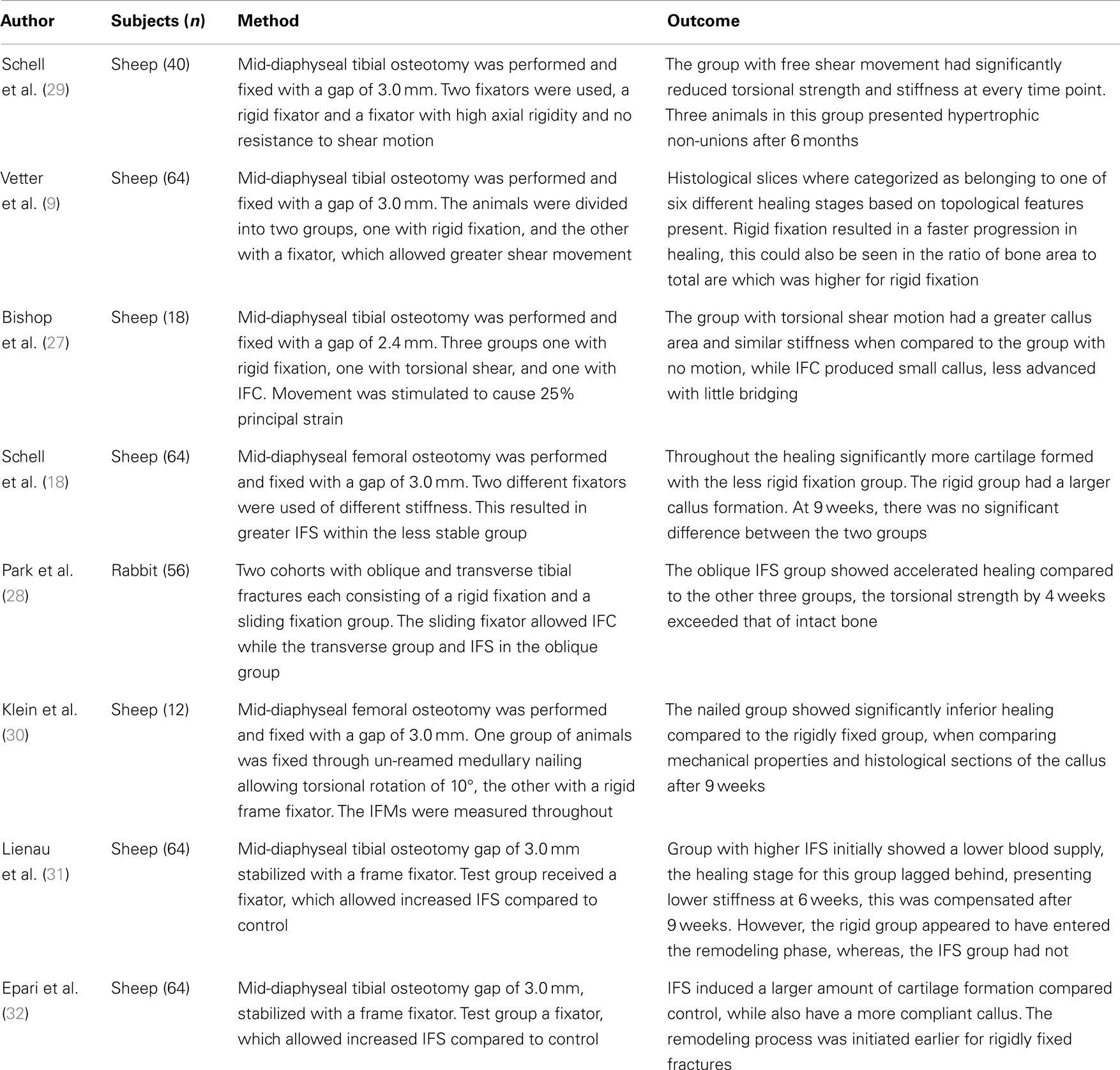
Table 2. Experimental studies considering the effects of inter-fragmentary shear on fracture healing.
Bishop et al. (27), for example, applied torsion using a custom designed fixator aiming to produce a principal strain of 25% between the fragments and compared it to equivalent principal strain produced though IFC, he reports torsion having stimulated intercortical mineralization. The complex loading condition presented through shear loading confounds such a comparison, as the pure shear loading produced an equal maximum and minimum principal strains of ±25%, whereas as compression produces a single negative principle strain of −25%. Thus the gap tissue stored twice the amount of elastic energy in the case of IFS as IFC. Additionally, the rotation of 7.2° with a cortical radius of 10 mm and a gap of 2.4 mm would have induced principal strains of 52%, not the 25% stated within the paper. Bishop et al. (27) assumed their torsional fixator to be completely rigid axially with no IFC, in comparison Schell et al. (18) measure both the IFS and IFC for their flexible fixator, when considering just the IFS they calculated a principal strain of ±26%, while including it they received +18.5% and −33%, respectively. It is possible that compliance of the fixator and physiological loading created a beneficial amount of IFC, which was not considered by Bishop et al. (27) in their study. The conclusion which can be drawn is that pure shear motion applied to the whole organ is not pure shear within the healing tissue. It seems inappropriate to compare tissue strain between loading cases using a single value from the strain tensor, a solution would be through using a scalar valued function such as strain energy density (SED), or a combination of deviatoric and volumetric strain.
Inter-Fragmentary Bending
The case of IFB has not be sufficiently investigated to form a conclusion, the two studies, which consider this are summarized in Table 3. What has been shown is that asymmetric bending, results in asymmetric callus formation. Healing appears to be inhibited on the tensile side of the callus and promoted on the compressive side (33). This is in agreement with studies looking at axial compression and tension individually as shown before. Cyclic bending appears to cause bone healing to take a different pathway. It has been shown that cyclic bending induces changes in gene expression, where genes responsible for bone morphogenetic proteins are down regulated while genes responsible for cartilage production are up regulated. More cartilage within the callus was observed compared to the unloaded case indicating that the balance of tissue production during the reparative phase was altered (3). The increased level of cartilage indicates that the stimulated callus is not as vascularized as the fixed callus, and the healing will progress along the endochondral ossification pathway rather than through endochondral ossification.

Table 3. Experimental studies considering the effects of inter-fragmentary bending on fracture healing.
Theories and Models
In this section, different theories for tissue differentiation are described followed by an overview of the simulations, which have been performed using them (summary of these data can be found in Table 4). Experimental evidence demonstrates that mechanical forces can direct the healing process, i.e., tissue differentiation is mechanobiologically regulated. There are several theories as to which mechanical quantities are the stimuli for differentiation such as SED, deviatoric and volumetric strain, or relative fluid flow between cells and the matrix. Due to the complicated geometries, which occur in fracture healing it is not possible to analytically apply these theories. Instead they are applied as components of simulations, we concentrate here on mechanically driven simulations, which typically consist of five parts summarized in Figure 3; the geometries of bone, defect and callus; the boundary conditions; finite element analysis used to determine the mechanical signal in the callus; the tissue differentiation rules, through which a new callus geometry is created; and finally most simulations consider an additional “biological aspect,” which adds a temporal scale and directs spatially where the ossification occurs. A simulation will go through several iterations changing the tissues composing the callus until a state of equilibrium is reached.
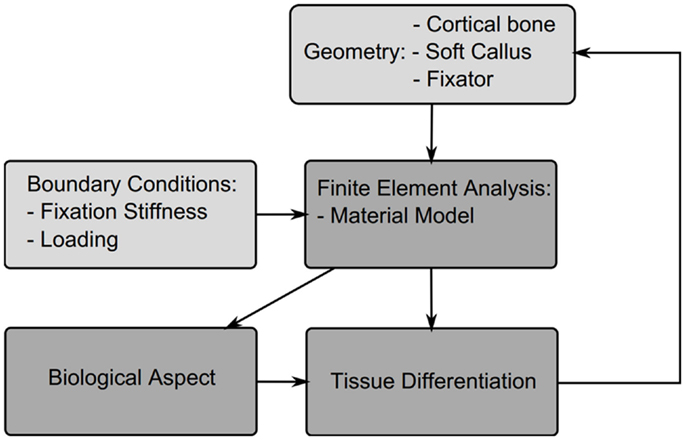
Figure 3. Structure of a typical fracture healing simulation. Initially a model is created consisting of the cortical bone fragments, soft callus, and the fixator. Material properties and boundary conditions are then applied to the model based on the tissue distribution and fixator properties, a finite element analysis is performed to determine the mechanicals stimuli, this then is used to drive cell proliferation and tissue differentiation, which updates the tissue distribution and thus new mechanical properties for the next iteration.
The callus geometries are typically assumed to be constant and ellipsoidal, so simulations of fracture healing start at the reparative phase once the soft callus has formed. The only exception to this is the model of Gomez-Benito et al. (44) who presented a model, which allows the callus boundaries to evolve over time. Boundary conditions are based upon the loading described by the experimental study the authors aim to replicate.
Tissue Differentiation Theories
In 1960, Pauwels first proposed that tissue differentiation within a fracture callus was governed by mechanical stimuli. He theorized that cartilage formed as a result of local hydrostatic pressure causing mesenchymal stem cells to become chondroblasts, whereas, bone and fibrous tissues resulted from shear strains causing mesenchymal stem cells to differentiate into osteoblasts and fibroblasts, respectively (68). Perren and Cordey (69) defined the upper limits of mechanical stimulation of fracture healing. Their inter-fragmentary strain theory states that the tissue within the fracture gap must be capable of withstanding the strain produced by the IFM. They then suggested that rigid fixation of fractures should result in the healing process commencing at a later stage. This was later contradicted by the study of Goodship and Kenwright (16) that showed that a certain level of micro-movement accelerated aspects of the healing process. However, their inter-fragmentary strain theory certainly governs what tissues can exist and is particularly important in cases where tension is dominant.
The theory of Pauwels (68) was numerically investigated by Carter et al. (70). As a fracture callus is an internal three dimensional structure, it was not possible to study the strain in vivo. Using a finite element model of an idealized fracture geometry with soft callus they investigated what they called the osteogenic index, a relationship between hydrostatic pressure and octahedral shear stress.
Where I is the osteogenic index, c is the number of load cases, n is the number of loading cycles, Si is the cyclic octahedral shear stress, Di is the cyclic hydrostatic pressure, and k is a scaling factor relating the two. They also recognized that the load applied to a fracture would not be constant, but vary between different load cases. The osteogenic index was therefore a summation of the mechanical signals at these different load cases. The proposed theory also considered a distinction between tissues with poor and good bloody supply, with good blood supply being capable of forming all tissue types, but requiring significant hydrostatic pressure to form cartilage, whereas, tissue with poor blood supply formed either connective tissue of cartilage (70).
Prendergast and Huiskes (71) studied how the osteogenic index differed between the use of linear-elastic or poro-elastic material properties for the healing tissues. The aqueous nature of biological tissues, particularly soft tissues, means that representing them as a mixture of fluid and solid phases describes the tissue behavior more accurately than linear-elastic models. Using the experiments of Søballe et al. (35), where a loadable bone chamber was implanted in the femoral condyle of canines and the tissues, which formed under different loadings quantified cross-sectionally over a number of weeks, Prendergast and Huiskes (71) were able to determine that the poro-elastic model predicted the osteogenic index more appropriately when compared to tissue distributions in the experiment. They expanded on this work by developing a new theory, that the relative velocity between fluid, solid, and shear strain, rather than hydrostatic pressure and shear strain where the stimuli for tissue differentiation as described by Figure 4A (72).
where γ is the deviatoric shear strain, ν is the solid/fluid velocity, and a and b are empirically derived constants varying for each tissue type.
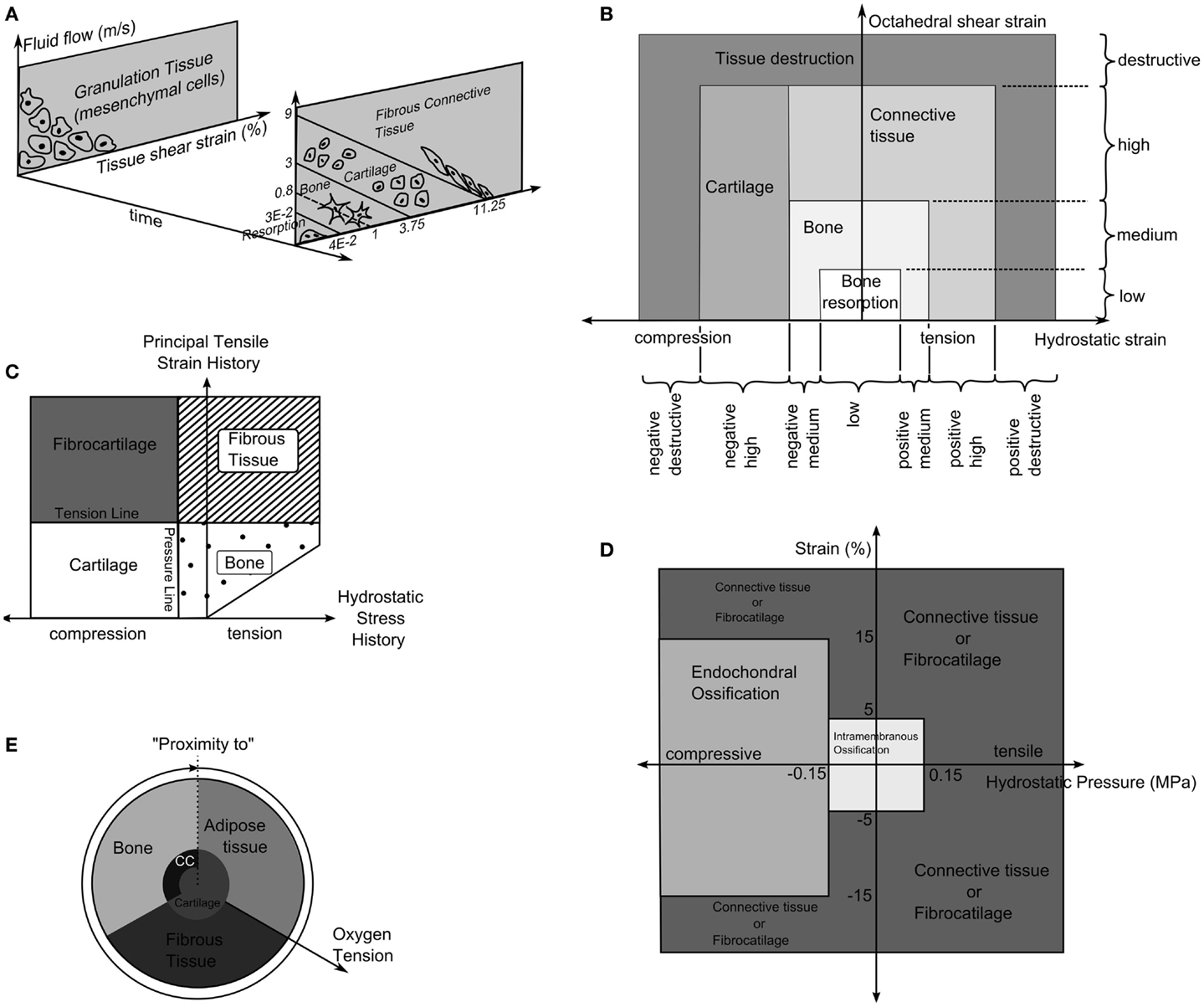
Figure 4. (A) The tissue differentiation rules based on fluid flow relative to solid phase and shear strain. Reprinted from Lacroix and Prendergast (37) with permission from Elsevier. (B) Tissue differentiation based on hydrostatic and octahedral shear strain. Reprinted from Shefelbine et al. (42) with permission from Elsevier. (C) The tissue differentiation rules with pressure line and tension line. Reprinted from Carter et al. (73) with permission from Lippincott Williams and Wilkins. (D) The tissue differentiation rules using hydrostatic pressure and strain. Reprinted from L. Claes and Heigele (4) with permission from Elsevier. (E) The tissue differentiation rule based on substrate stiffness and oxygen tension. Reprinted from Burke and Kelly (62) with permission from PLoS ONE.
The relationship was defined as a summation of maximal distortional strain and relative velocity between fluid and solid (34). It is important to reiterate that this theory was developed from experiments using a bone chamber, which has a simple geometry known a priori that can be easily represented in finite element simulations with the applied loads being known. In contrast, the boundaries of the callus are not known exactly and the loading is an approximation of the physiological condition.
Carter et al. (73) proposed that tissue differentiation was determined through tensile principal strain and hydrostatic pressure as shown in Figure 4C. High principal tensile strains result in fibrous tissue when pressure is low and fibrocartilage when pressure is high, whereas, low principal tensile strains results in bone and cartilage when pressure is low or high, respectively.
The theory of Pauwels (68) was revisited by Claes et al. (38) who in a large interdisciplinary study compared the tissue distribution of healing tibial fractures in an animal study and equivalent finite element study. They attempted to determine the values of hydrostatic pressure and axial strains, which caused differing tissue differentiation. They determined that bellow a hydrostatic pressure of 0.15 MPa and strain <5% stimulate intramembranous ossification, compressive hydrostatic pressure >0.15 MPa and strain <15% stimulated endochondral ossification and that pressure and strain outside of these regions resulted in fibrous tissue or cartilage, as shown in Figure 4D. Claes and Heigele (4) then proposed ossification only occurs on an existing bony surface. While they did not develop a simulation, they created FE models, which represented the healing callus at different stages and correlated the stress and strain from these models with histological sections from an animal study, which was performed in parallel.
Ament and Hofer (36) presented a simulation using a fuzzy logic controller with nine linguistic rules, which defined how levels of SED and the concentration of bone in neighboring elements to control the differentiation of elements into three tissue types, cartilage, bone, and fibrous connective tissue. The SED could be within four different levels; low, physiological, increased, and pathological. These were independent of the tissue type, as SED is relatively invariant to tissue type. Results were compared with the experiments of Claes et al. (11) and showed strong similarities in the reduction of IFM over time.
Fuzzy logic was again used by Shefelbine et al. (42), modeling trabecular regeneration. Their model was based on the proposed relationship of Claes and Heigele (4). However, they modified the tissue differentiation theory replacing the hydrostatic pressure criteria with an equivalent volumetric strain. Thus, the mechanical stimuli became volumetric strain and octahedral shear strain, described in Figure 4B. This model had 21 linguistic rules to describe how tissue differentiated; it considered three tissue types, bone, cartilage, and fibrous tissue. In addition, vascularization was also modeled using fuzzy rules. The simulation required the strains in a particular element to reach a certain range before tissue within the element began differentiating, for bone to form the elements must also have sufficient vascularity while cartilage formed independently of vascularity. The vasculature was also driven mechanically only advancing to elements within an acceptable strain level. The model was implemented as a three dimensional linear-elastic simulation. While this model can capture the events of bone regeneration, Steiner et al. (65) conducted a parameter study of fixator stiffness, which encompassed values used several in vivo studies and achieved comparable outcomes, it is a linguistic representation of observed phenomenon. Thus it is entirely phenomenological and does not encompass any underlying mechanism in physical or chemical terms. This raises issues with regards scaling, should the resolution of the model or length of the iteration change, as there is no governing equation.
Biological Aspects
The majority of simulations included an additional level often described as the biological aspect. As Claes and Heigele (4) observed the front of healing bone follows a path, starting at the original cortical faces and advancing toward the fracture gap. The inclusion of biological aspects in the form of cell, revascularization, nutrient supply, or oxygen tension, allows ossification to follow such a path. These biological elements are typically modeled as diffusive processes (39), random walks (45, 74), or through logical association of neighboring elements (36, 42). While cell proliferation and revascularization are vital aspects of fracture healing, the interplay between mechanical forces and these processes are not fully understood, in addition there is limited experimental data available so the validation of such model becomes much more difficult.
How the biologic aspect influences the course of fracture healing can vary, Lacroix et al. (39) considered cells diffusing within the callus and scaled the tissue stiffness according to cell destiny within an element. An issue exists with this approach, as the maturity of the tissue is determined purely by the cell number within and the tissue phenotype by the mechanical stimuli this allows mature cartilage to switch directly to mature bone. Kelly and Prendergast (43) similarly applied a scaling, but considered multiple cell phenotypes and so multiple tissues within a single element removing this issue. Shefelbine et al. (42) considered nutrient supply to be the critical biological factor in bone development, and so bone could only form in areas with good vascularization. This was again used by Wehner et al. (57) and Simon et al. (58). Chen et al. (49) added an additional level to this considering nutrient diffusion from the developing vasculature.
Burke and Kelly (62) proposed a theory in which tissue differentiation is indirectly driven by mechanical forces. Revascularization is allowed on in elements where the deviatoric strain is below a level of 6%. The blood vessels were assumed to diffuse into the tissue.
Where V is the vascularity, γ is the deviatoric strain, and Ω is the computational domain with all elements where this strain was <6%. The oxygen is then assumed to diffuse from the vasculature without any dependence on the local mechanical environment.
Here O2 is the oxygen concentration, D is the diffusion coefficient of oxygen in the tissue, Q is the oxygen consumption rate of cells in the tissue, and n represents the number of cells in the element and nmax the maximum cell density. The tissues then differentiated based on the oxygen tension and the stiffness of neighboring elements as described in Figure 4E.
Several models exist which consider purely biological factors in fracture healing, Bailon-Plaza and Van Der Meulen (75) first proposed a model for bone regeneration, which included diffusion of stem cells, and various growth factors, but no mechanical feedback. Geris et al. (76) applied this model to simulate the healing of tibial fractures in mice, finding that the model could predict the course of healing, but was sensitive to initial levels of growth factor production. Geris et al. (56) investigated if mechanical regulation of angiogenesis and growth factor production could improve this model and account for load induced non-unions, and concluded that mechanical feedback for both angiogenesis and osteogenesis was required to correctly predict unions and non-unions. Later changes to this model have excluded mechanics and focused on more detailed representations of angiogenesis (77, 78).
These theories consider cell density in homogenous tissue elements and apply rules for motion, differentiation, and proliferation to the cell population based upon tissue level stimuli. In vivo, the structure of tissues within callus is microscopically heterogeneous, thus mechanical stimuli at the tissue level are not easily translated to the cellular level. While at the tissue level, strains and perfusion of interstitial fluid (ISF) in the callus can be accurately determined, the stimulation they cause at the cellular level will be different for each cell within a tissue element due to the heterogeneity. This has not yet been quantified in vivo, however, fluid dynamic studies of perfusion bioreactors can lend insights as to the heterogeneity of mechanical stimuli when fluid is perfused through a structure at physiological rates. Zermatten et al. (79) used high resolution micro computed tomography (micro-CT) images of bone tissue engineering scaffolds. Fluid dynamic simulations of medium perfusion showed the wall shear stress within a scaffold had a wide range of values. It has been known for some time that in vitro osteoblastic differentiation and bone formation are augmented with ISF flow (80), however, application of this biological information in silico will require more detailed models of the tissue structure.
The features all these biological aspects share are the boundary conditions, considering the periosteum of the cortical fragments and the surrounding tissue at the source of cells, nutrients, or vascular tissue. The propagation of these are mainly all diffusive processes, though for ease of implementation and to reduce computational power required implementations have varied, the random walk used by Pérez and Prendergast (45) and fuzzy logic of Shefelbine et al. (42) allowed diffusive behavior without the computational cost of solving the diffusion equation numerically.
Comparison of Model Performance
Validation of models has remained a significant problem, looking at Table 4 approximately half of the studies have no experimental reference. The study of Claes et al. (11) has frequently been used as a comparison due to clear experimental method and inclusion of IFC values longitudinally as well as histological slices obtained cross-sectionally. However, while the IFC data are available no quantitative comparison has be made between simulations and the results, instead visually comparing general trends and histological slices has predominated. In Figure 5, we see simulation results from (A) Burke and Kelly (62), (B) Lacroix and Prendergast (37), and (C) Steiner et al. (65) these all consist of a uniform cortical bone and callus geometry, which is made up of non-uniform finite elements, in the case of Burke and Kelly (62) and Lacroix and Prendergast (37) they are two dimensional axisymmetric simulations and in Steiner et al. (65) three dimensional. Figure 5D is a histological section from an in vivo study by Claes and Heigele (4); we see the callus is non-uniform and asymmetric. This mismatch between the asymmetric callus in the histological images and uniformly simulated calluses complicates direct comparison, additionally axisymmetric boundary conditions implies the simulation should match every quadrant of the histological slice, which is clearly impossible, when using three dimensional models like Steiner et al. (65) one must also find the correct slice of the model to compare to the histology. Vetter et al. (63) compared the use of volumetric strain, deviatoric strain, greatest-shear strain, and principal strain as stimuli for tissue differentiation. Through carrying out a parametric study they found that all of these could accurately predict bone healing within a range of thresholds. They used quantitative metrics to assess the accuracy, comparing averaged histological sections from Vetter et al. (9) with simulated images. This allowed the comparison of volume fraction and number of co-located pixels. However, this work was in two dimensions and thus did not consider IFS or IFB. The data of Vetter et al. (9) were later used a visual comparison by Burke and Kelly (62), who showed their simulations appeared to agree well with the results, however, no quantitative comparison was used.
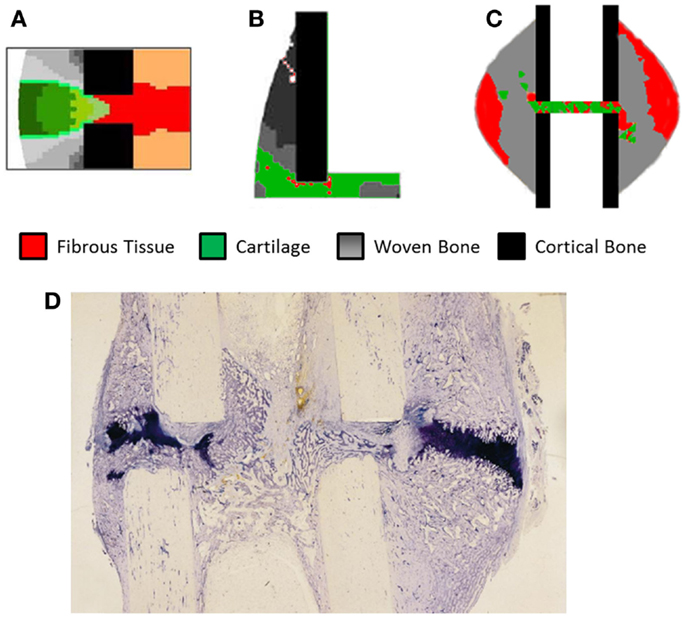
Figure 5. The results of fracture healing simulations, (A) Burke and Kelly (62) reprinted with permission from PLoS ONE. (B) Lacroix and Prendergast (37) reprinted with permission from Elsevier. (C) Steiner et al. (65) reprinted with permission from PLoS ONE. (D) Histological section of healing ovine tibia, new woven bone is lightly stained, while cartilage is darkly stained. Reprinted with permission from Elsevier.
There are several studies comparing the performance of the different tissue differentiation theories. Isaksson et al. (81) and Epari et al. (82) both compared the models of Prendergast and Huiskes (71) and Claes and Heigele (4). Both used three dimensional models with poro-elastic element properties, however, different results were presented for similar load cases. Isaksson et al. (81) found that under 7.2° of torsion only the model of Prendergast and Huiskes (71) correctly predicted healing. While Epari et al. (82) found that for 10° of torsion both models predicted fracture healing. The differences can possibly be explained through differences in material properties, with Isaksson et al. (81) using an elastic modulus for the granulation tissue an order of magnitude larger than Epari et al. (82). However, the mechanical properties for all of the tissues included by Epari et al. (82) are not listed, making a complete comparison not possible. One further erroneous element is the formation of unconnected bone in both studies when using the Claes and Heigele (4) differentiation theory. This theory explicitly states that ossification occurs in the soft tissue contacting the surface of existing bone, and that the rest of the callus is fibrous tissue unless a pressure of −0.15 MPa is present and then it becomes cartilage. The formation of unconnected bone can only imply that both implementations did not consider this aspect of the differentiation rules, and applied the surface ossification rules throughout the callus. To complicate this further Klein et al. (30) and Bishop et al. (27) found contradictory results for healing under torsional loading. The theory of Shefelbine et al. (42) is essentially an equivalent theory to Claes and Heigele (4) except it uses deviatoric and dilatational stress and strain rather than stress. This model has been used by Steiner et al. (64), Wehner et al. (57), and Simon et al. (58). Steiner et al. (64) demonstrated that with the correct threshold values the model could predict union for the cases of IFC and IRF, but non-union for IFS.
Isaksson et al. (83) again compared the theories of Claes and Heigele (4) and Prendergast and Huiskes (71), as well as Carter et al. (73). They found the theories predicted extremely similar temporal and spatial patterns in healing. In addition, they compared the volumetric components (relative fluid solid velocity and pore pressure) of the theories with the distortional components, finding that deviatoric strain alone could also predict similar tissue formations, whereas, volumetric components such as pore pressure and fluid velocity could not predict healing by themselves. This is however contradicted by Isaksson et al. (81) who found that the tissue formation predicted by deviatoric strain alone did not match in vivo data.
Hayward and Morgan (50) implemented a model using Prendergast and Huiskes (71) theory of tissue differentiation. They used three dimensional models based on micro-CT images of a mouse femur. The model correctly predicted a mechanically induced non-union and larger volume of cartilage formed due to the loading, but was not completely accurate in the patterns of tissue formation, predicting an excess of bone formation within the gap. Checa et al. (84) investigated if the Prendergast and Huiskes (71) theory could be directly applied different species, specifically rats and sheep. They reported that differences in healing between the species observed in vivo cannot be purely attributed to differences in loading and animal size, but also the thresholds for formation are different between, for sheep a larger mechanical stimuli was capable of forming bone, which in the case of the rat would result in cartilage. Given that Hayward and Morgan (50) did not scale these parameters for mice, this is a limitation of their study, which was not considered.
Another form of validation is possible; instead of using results directly from fracture healing one can compare how algorithms perform when modeling a bone chamber. Geris et al. (48) compared the differentiation rules of Prendergast and Huiskes (71), Carter et al. (73), and Claes and Heigele (4) against tissue formation in a bone chamber. They concluded that the models only partially matched experimental findings, with models predicting cartilage formation, which was not observed experimentally. The implementation of Prendergast and Huiskes (71) algorithm did not consider bone resorption, which is found in the implementation of Lacroix and Prendergast (37). As the other algorithms do not include resorption this modification is understandable to enable comparison between them, however, it would be interesting to see if its inclusion increased or decreased the accuracy.
Outlook
Mechanical forces and bone regeneration are intrinsically linked. While there has been a vast amount of research on this topic, experimental comparison between studies is extremely difficult. The greatest difficulty comes from non-standard experimental setups, specifically, different defect sizes and use of modified and non-standard fixators. While great efforts have been made to characterize the movements and stiffness of devices, without knowing the true bone geometry and exact tissue composition it is difficult to determine the precise strains tissues are experiencing. These factors play a part in the validation of simulations using this data, as differences in geometry between simulation and experiments should cause different mechanical stimuli.
Validation of models with experimental data is crucial for all simulation work, and is the distinguishing factor between simulation and animation. What is clear is that in the field of bone regeneration, comparing the results of in silico studies with in vivo studies is not trivial. It is impossible to measure every factor simultaneously, yet models for fracture healing have become increasingly complicated. More factors are considered such as cellular events, revascularization, and even protein secretion. While validation of such models is not impossible it requires large cross-sectional studies, which have yet to be performed. To compound this, current models of bone regeneration all consider tissues as homogenous continuum, while woven bone is a macroscopically porous structure. The theories of Carter et al. (73), Claes and Heigele (4), and Prendergast et al. (72) are based on comparing the results of continuum finite element analyzes with histological data, and correlating the areas where bone has formed with the local mechanical environment. The histological data were the result of cross-sectional studies, so while they could observe the formation of woven bone, they could not see how individual structures evolved. One solution to this problem lies in in vivo micro-CT. Micro-CT uses two dimensional X-ray images of a sample taken from multiple directions to reconstruct a three dimensional image of the sample. The application of in vivo micro-CT means time-lapsed longitudinal studies can be performed, where the same animals can be imaged at several time points. These images can then be compared, highlighting the changes in the regenerating tissue. When combined with a well-defined loading regime an equivalent finite element analysis can be performed using the micro-CT images as a basis. The results of which can be compared to the changes in tissue observed in vivo, allowing the validation or falsification of current theories for tissue differentiation.
The development and maturation of the callus (reactive and reparative phase) is a single aspect of fracture healing, eventually the bone must remodel to its original form, while Lacroix and Prendergast (37) include this, it has never been shown that this is the correct mechanism. Schell et al. (8) have shown that early in the healing process osteoclasts are present, and that cortical bone closest to the defect gets remodeled into woven bone, then back to cortical. With in vivo micro-CT based studies this remodeling can be quantified. With quantitative data remodeling theories can be corroborated. Such a study could provide a window into the relationship between cortical remodeling and trabecular remodeling and what causes the differentiation between the two.
Subject specific simulations are a necessity, allowing direct comparison between simulations and experimental results on a sample by sample basis. Currently, no study has performed an animal specific simulation and determined if the simulation produces results without a significant difference to the in vivo results. This will remove the any error associated with averaging experimental results so they can be compared to simulations using idealized geometry. Additionally simulations using realistic geometry and loading conditions will allow the effects of the non-uniform bone geometry and strain distribution within the callus to be quantified. In Figure 5D, we can see clearly how asymmetric the callus is, and that on the left side of the bone cartilage has formed within the osteotomy gap whereas on the right side of the image the cartilage is bridging the larger hard callus. The asymmetry of the bone, callus, and loading cannot be captured in axisymmetric models and only partially using idealized models of the geometry. This geometric information will be the product of studies using in vivo micro-CT. What parameters should be compared between such models is an open question, which must be addressed first. Work already presented in the field of bone remodeling and adaptation (85) provides a basis for what can be measured, and models for bone remodeling such as Schulte et al. (86) may also be incorporated in simulations, representing the remodeling phase.
Conclusion
This review has presented how the mechanical models and experiments of fracture healing have developed since Pauwels (68) first proposed his theory. The differences between the types of data produced by simulations and experimental studies remains an obstacle for advancing the field. Existing rules without exception have all been derived from two dimensional continuum finite element models, though associating the simulated mechanical stimuli to tissue growth seen in histological section from cross-sectional a study. As more detailed, quantitative and longitudinal data are being gathered experimentally these rules must be re-examined, their accuracy assessed using longitudinal time-lapsed data. With simulations there is a need for simulations to move away from simplified representations of the geometry with continuum material properties, toward real bone microstructural geometries measured through micro-CT, so as to allow direct and quantitative comparison of their predicted tissue distribution directly to the results of in vivo studies, rather than a visual comparison with single histological slices.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors gratefully acknowledge financial support from the European Union (BIODESIGN FP7-NMP-2012-262948).
References
1. Mills LA, Simpson AHRW. The relative incidence of fracture non-union in the Scottish population (5.17 million): a 5-year epidemiological study. BMJ Open (2013) 3:e002276. doi: 10.1136/bmjopen-2012-002276
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
2. Carter DR. Mechanical loading history and skeletal biology. J Biomech (1987) 20(11):1095–109. doi:10.1016/0021-9290(87)90027-3
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
3. Palomares KTS, Gleason RE, Mason ZD, Cullinane DM, Einhorn TA, Gerstenfeld LC, et al. Mechanical stimulation alters tissue differentiation and molecular expression during bone healing. J Orthop Res (2009) 27(9):1123–32. doi:10.1002/jor.20863
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
4. Claes L, Heigele C. Magnitudes of local stress and strain along bony surfaces predict the course and type of fracture healing. J Biomech (1999) 32(3):255–66. doi:10.1016/S0021-9290(98)00153-5
5. Taylor DK, Meganck JA, Terkhorn S, Rajani R, Naik A, O’Keefe RJ, et al. Thrombospondin-2 influences the proportion of cartilage and bone during fracture healing. J Bone Miner Res (2009) 24(6):1043–54. doi:10.1359/jbmr.090101
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
6. Thompson Z, Miclau T, Hu D, Helms JA. A model for intramembranous ossification during fracture healing. J Orthop Res (2002) 20(5):1091–8. doi:10.1016/S0736-0266(02)00017-7
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
7. Einhorn TA. The cell and molecular biology of fracture healing. Clin Orthop Relat Res (1998) 355:S7–21. doi:10.1097/00003086-199810001-00003
8. Schell H, Lienau J, Epari DR, Seebeck P, Exner C, Muchow S, et al. Osteoclastic activity begins early and increases over the course of bone healing. Bone (2006) 38(4):547–54. doi:10.1016/j.bone.2005.09.018
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
9. Vetter A, Epari DR, Seidel R, Schell H, Fratzl P, Duda GN, et al. Temporal tissue patterns in bone healing of sheep. J Orthop Res (2010) 28(11):1440–7. doi:10.1002/jor.21175
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
10. Utting JC, Flanagan AM, Brandao-Burch A, Orriss IR, Arnett TR. Hypoxia stimulates osteoclast formation from human peripheral blood. Cell Biochem Funct (2010) 28(5):374–80. doi:10.1002/cbf.1660
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
11. Claes L, Augat P, Suger G, Wilke H-J. Influence of size and stability of the osteotomy gap on the success of fracture healing. J Orthop Res (1997) 15(4):577–84. doi:10.1002/jor.1100150414
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
12. Gardner MJ, van der Meulen MC, Demetrakopoulos D, Wright TM, Myers ER, Bostrom MP. In vivo cyclic axial compression affects bone healing in the mouse tibia. J Orthop Res (2006) 24(8):1679–86. doi:10.1002/jor.20230
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
13. Gardner MJ, Putnam SM, Wong A, Streubel PN, Kotiya A, Silva MJ. Differential fracture healing resulting from fixation stiffness variability: a mouse model. J Orthop Sci (2011) 16(3):298–303. doi:10.1007/s00776-011-0051-5
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
14. Garcia P, Holstein JH, Maier S, Schaumlöffel H, Al-Marrawi F, Hannig M, et al. Development of a reliable non-union model in mice. J Surg Res (2008) 147(1):84–91. doi:10.1016/j.jss.2007.09.013
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
15. Holstein JH, Matthys R, Histing T, Becker SC, Fiedler M, Garcia P, et al. Development of a stable closed femoral fracture model in mice. J Surg Res (2009) 153(1):71–5. doi:10.1016/j.jss.2008.02.042
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
16. Goodship A, Kenwright J. The influence of induced micromovement upon the healing of experimental tibial fractures. J Bone Joint Surg Br (1985) 67(4):650–5.
17. Klein P, Schell H, Streitparth F, Heller M, Kassi J-P, Kandziora F, et al. The initial phase of fracture healing is specifically sensitive to mechanical conditions. J Orthop Res (2003) 21(4):662–9. doi:10.1016/S0736-0266(02)00259-0
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
18. Schell H, Epari D, Kassi J, Bragulla H, Bail H, Duda G. The course of bone healing is influenced by the initial shear fixation stability. J Orthop Res (2005) 23(5):1022–8. doi:10.1016/j.orthres.2005.03.005
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
19. Goodship AE, Cunningham JL, Kenwright J. Strain rate and timing of stimulation in mechanical modulation of fracture healing. Clin Orthop Relat Res (1998) 355:S105–15. doi:10.1097/00003086-199810001-00012
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
20. Goodship AE, Lawes TJ, Rubin CT. Low-magnitude high-frequency mechanical signals accelerate and augment endochondral bone repair: preliminary evidence of efficacy. J Orthop Res (2009) 27(7):922–30. doi:10.1002/jor.20824
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
21. Kenwright J, Goodship A, Kelly D, Newman J, Harris J, Richardson J, et al. Effect of controlled axial micromovement on healing of tibial fractures. Lancet (1986) 328(8517):1185–7. doi:10.1016/S0140-6736(86)92196-3
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
22. Kenwright J, Richardson J, Cunningham J, White S, Goodship A, Adams M, et al. Axial movement and tibial fractures. A controlled randomised trial of treatment. J Bone Joint Surg Br (1991) 73(4):654–9.
23. Claes L, Eckert-Hübner K, Augat P. The effect of mechanical stability on local vascularization and tissue differentiation in callus healing. J Orthop Res (2002) 20(5):1099–105. doi:10.1016/S0736-0266(02)00044-X
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
24. Claes L, Eckert-Hübner K, Augat P. The fracture gap size influences the local vascularization and tissue differentiation in callus healing. Langenbecks Arch Surg (2003) 388(5):316–22. doi:10.1007/s00423-003-0396-0
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
25. Cheal E, Mansmann K, DiGioia A III, Hayes W, Perren S. Role of interfragmentary strain in fracture healing: ovine model of a healing osteotomy. J Orthop Res (1991) 9(1):131–42. doi:10.1002/jor.1100090116
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
26. Mark H, Nilsson A, Nannmark U, Rydevik B. Effects of fracture fixation stability on ossification in healing fractures. Clin Orthop Relat Res (2004) 419:245–50. doi:10.1097/00003086-200402000-00040
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
27. Bishop N, Van Rhijn M, Tami I, Corveleijn R, Schneider E, Ito K. Shear does not necessarily inhibit bone healing. Clin Orthop Relat Res (2006) 443:307–14. doi:10.1097/01.blo.0000191272.34786.09
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
28. Park S-H, O’CONNOR K, McKellop H, Sarmiento A. The influence of active shear or compressive motion on fracture-healing*. J Bone Joint Surg Am (1998) 80(6):868–78.
29. Schell H, Thompson MS, Bail HJ, Hoffmann J-E, Schill A, Duda GN, et al. Mechanical induction of critically delayed bone healing in sheep: radiological and biomechanical results. J Biomech (2008) 41(14):3066–72. doi:10.1016/j.jbiomech.2008.06.038
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
30. Klein P, Opitz M, Schell H, Taylor W, Heller M, Kassi J-P, et al. Comparison of unreamed nailing and external fixation of tibial diastases – mechanical conditions during healing and biological outcome. J Orthop Res (2004) 22(5):1072–8. doi:10.1016/j.orthres.2004.02.006
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
31. Lienau J, Schell H, Duda GN, Seebeck P, Muchow S, Bail HJ. Initial vascularization and tissue differentiation are influenced by fixation stability. J Orthop Res (2005) 23(3):639–45. doi:10.1016/j.orthres.2004.09.006
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
32. Epari DR, Schell H, Bail HJ, Duda GN. Instability prolongs the chondral phase during bone healing in sheep. Bone (2006) 38(6):864–70. doi:10.1016/j.bone.2005.10.023
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
33. Hente R, Füchtmeier B, Schlegel U, Ernstberger A, Perren S. The influence of cyclic compression and distraction on the healing of experimental tibial fractures. J Orthop Res (2004) 22(4):709–15. doi:10.1016/j.orthres.2003.11.007
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
34. Huiskes R, Van Driel W, Prendergast P, Søballe K. A biomechanical regulatory model for periprosthetic fibrous-tissue differentiation. J Mater Sci Mater Med (1997) 8(12):785–8.
35. Søballe K, Hansen ES, B-Rasmussen H, Jørgensen PH, Bünger C. Tissue ingrowth into titanium and hydroxyapatite-coated implants during stable and unstable mechanical conditions. J Orthop Res (1992) 10(2):285–99. doi:10.1002/jor.1100100216
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
36. Ament C, Hofer E. A fuzzy logic model of fracture healing. J Biomech (2000) 33(8):961–8. doi:10.1016/S0021-9290(00)00049-X
37. Lacroix D, Prendergast P. A mechano-regulation model for tissue differentiation during fracture healing: analysis of gap size and loading. J Biomech (2002) 35(9):1163–71. doi:10.1016/S0021-9290(02)00086-6
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
38. Claes LE, Heigele CA, Neidlinger-Wilke C, Kaspar D, Seidl W, Margevicius KJ, et al. Effects of mechanical factors on the fracture healing process. Clin Orthop Relat Res (1998) 355:S132–47. doi:10.1097/00003086-199810001-00015
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
39. Lacroix D, Prendergast P, Li G, Marsh D. Biomechanical model to simulate tissue differentiation and bone regeneration: application to fracture healing. Med Biol Eng Comput (2002) 40(1):14–21. doi:10.1007/BF02347690
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
40. Bailón-Plaza A, van der Meulen MC. Beneficial effects of moderate, early loading and adverse effects of delayed or excessive loading on bone healing. J Biomech (2003) 36(8):1069–77. doi:10.1016/S0021-9290(03)00117-9
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
41. Geris L, Andreykiv A, Oosterwyck HV, Sloten JV, Keulen F, van Duyck J, et al. Numerical simulation of tissue differentiation around loaded titanium implants in a bone chamber. J Biomech (2004) 37(5):763–9. doi:10.1016/j.jbiomech.2003.09.026
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
42. Shefelbine SJ, Augat P, Claes L, Simon U. Trabecular bone fracture healing simulation with finite element analysis and fuzzy logic. J Biomech (2005) 38(12):2440–50. doi:10.1016/j.jbiomech.2004.10.019
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
43. Kelly D, Prendergast PJ. Mechano-regulation of stem cell differentiation and tissue regeneration in osteochondral defects. J Biomech (2005) 38(7):1413–22. doi:10.1016/j.jbiomech.2004.06.026
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
44. Gomez-Benito M, Garcia-Aznar J, Kuiper J, Doblaré M. Influence of fracture gap size on the pattern of long bone healing: a computational study. J Theor Biol (2005) 235(1):105–19. doi:10.1016/j.jtbi.2004.12.023
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
45. Pérez M, Prendergast P. Random-walk models of cell dispersal included in mechanobiological simulations of tissue differentiation. J Biomech (2007) 40(10):2244–53. doi:10.1016/j.jbiomech.2006.10.020
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
46. Isaksson H, van Donkelaar CC, Huiskes R, Yao J, Ito K. Determining the most important cellular characteristics for fracture healing using design of experiments methods. J Theor Biol (2008) 255(1):26–39. doi:10.1016/j.jtbi.2008.07.037
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
47. Isaksson H, van Donkelaar CC, Huiskes R, Ito K. A mechano-regulatory bone-healing model incorporating cell-phenotype specific activity. J Theor Biol (2008) 252(2):230–46. doi:10.1016/j.jtbi.2008.01.030
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
48. Geris L, Vandamme K, Naert I, Vander Sloten J, Duyck J, Van Oosterwyck H. Application of mechanoregulatory models to simulate peri-implant tissue formation in an in vivo bone chamber. J Biomech (2008) 41(1):145–54. doi:10.1016/j.jbiomech.2007.07.008
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
49. Chen G, Niemeyer F, Wehner T, Simon U, Schuetz M, Pearcy M, et al. Simulation of the nutrient supply in fracture healing. J Biomech (2009) 42(15):2575–83. doi:10.1016/j.jbiomech.2009.07.010
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
50. Hayward LNM, Morgan EF. Assessment of a mechano-regulation theory of skeletal tissue differentiation in an in vivo model of mechanically induced cartilage formation. Biomech Model Mechanobiol (2009) 8(6):447–55. doi:10.1007/s10237-009-0148-3
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
51. Cullinane DM, Fredrick A, Eisenberg SR, Pacicca D, Elman MV, Lee C, et al. Induction of a neoarthrosis by precisely controlled motion in an experimental mid-femoral defect. J Orthop Res (2002) 20(3):579–86. doi:10.1016/S0736-0266(01)00131-0
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
52. Khayyeri H, Checa S, Tägil M, Prendergast PJ. Corroboration of mechanobiological simulations of tissue differentiation in an in vivo bone chamber using a lattice-modeling approach. J Orthop Res (2009) 27(12):1659–66. doi:10.1002/jor.20926
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
53. Tägil M, Aspenberg P. Cartilage induction by controlled mechanical stimulation in vivo. J Orthop Res (1999) 17(2):200–4. doi:10.1002/jor.1100170208
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
54. Checa S, Prendergast PJ. A mechanobiological model for tissue differentiation that includes angiogenesis: a lattice-based modeling approach. Ann Biomed Eng (2009) 37(1):129–45. doi:10.1007/s10439-008-9594-9
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
55. Isaksson H, Van Donkelaar CC, Ito K. Sensitivity of tissue differentiation and bone healing predictions to tissue properties. J Biomech (2009) 42(5):555–64. doi:10.1016/j.jbiomech.2009.01.001
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
56. Geris L, Vander Sloten J, Van Oosterwyck H. Connecting biology and mechanics in fracture healing: an integrated mathematical modeling framework for the study of nonunions. Biomech Model Mechanobiol (2010) 9(6):713–24. doi:10.1007/s10237-010-0208-8
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
57. Wehner T, Claes L, Niemeyer F, Nolte D, Simon U. Influence of the fixation stability on the healing time – a numerical study of a patient-specific fracture healing process. Clin Biomech (2010) 25(6):606–12. doi:10.1016/j.clinbiomech.2010.03.003
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
58. Simon U, Augat P, Utz M, Claes L. A numerical model of the fracture healing process that describes tissue development and revascularisation. Comput Methods Biomech Biomed Engin (2011) 14(01):79–93. doi:10.1080/10255842.2010.499865
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
59. Byrne DP, Lacroix D, Prendergast PJ. Simulation of fracture healing in the tibia: mechanoregulation of cell activity using a lattice modeling approach. J Orthop Res (2011) 29(10):1496–503. doi:10.1002/jor.21362
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
60. Richardson J, Cunningham J, Goodship A, O’connor B, Kenwright J. Measuring stiffness can define healing of tibial fractures. J Bone Joint Surg Br (1994) 76(3):389–94.
61. Witt F, Petersen A, Seidel R, Vetter A, Weinkamer R, Duda GN. Combined in vivo/in silico study of mechanobiological mechanisms during endochondral ossification in bone healing. Ann Biomed Eng (2011) 39(10):2531–41. doi:10.1007/s10439-011-0338-x
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
62. Burke DP, Kelly DJ. Substrate stiffness and oxygen as regulators of stem cell differentiation during skeletal tissue regeneration: a mechanobiological model. PLoS One (2012) 7(7):e40737. doi:10.1371/journal.pone.0040737
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
63. Vetter A, Witt F, Sander O, Duda G, Weinkamer R. The spatio-temporal arrangement of different tissues during bone healing as a result of simple mechanobiological rules. Biomech Model Mechanobiol (2012) 11(1-2):147–60. doi:10.1007/s10237-011-0299-x
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
64. Steiner M, Claes L, Ignatius A, Niemeyer F, Simon U, Wehner T. Prediction of fracture healing under axial loading, shear loading and bending is possible using distortional and dilatational strains as determining mechanical stimuli. J R Soc Interface (2013) 10:20130389. doi:10.1098/rsif.2013.0389
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
65. Steiner M, Claes L, Ignatius A, Simon U, Wehner T. Numerical simulation of callus healing for optimization of fracture fixation stiffness. PLoS One (2014) 9(7):e101370. doi:10.1371/journal.pone.0101370
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
66. Epari DR, Kassi J-P, Schell H, Duda GN. Timely fracture-healing requires optimization of axial fixation stability. J Bone Joint Surg Am (2007) 89(7):1575–85. doi:10.2106/JBJS.F.00247
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
67. Bottlang M, Lesser M, Koerber J, Doornink J, von Rechenberg B, Augat P, et al. Far cortical locking can improve healing of fractures stabilized with locking plates. J Bone Joint Surg Am (2010) 92(7):1652–60. doi:10.2106/JBJS.I.01111
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
68. Pauwels F. Eine neue Theorie über den Einfluß mechanischer Reize auf die Differenzierung der Stützgewebe. Zeitschrift für Anatomie und Entwicklungsgeschichte (1960) 121(6):478–515. doi:10.1007/BF00523401
69. Perren SM, Cordey J. The concept of interfragmentary strain. In: Uhthoff HK, Stahl E, editors. Current Concepts of Internal Fixation of Fractures. New York, NY: Springer (1980). p. 63–77.
70. Carter D, Blenman P, Beaupre G. Correlations between mechanical stress history and tissue differentiation in initial fracture healing. J Orthop Res (1988) 6(5):736–48. doi:10.1002/jor.1100060517
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
71. Prendergast P, Huiskes R. Finite element analysis of fibrous tissue morphogenesis: a study of the osteogenic index using a biphasic approach. Mech Comp Mater (1996) 32(2):209–18. doi:10.1007/BF02254782
72. Prendergast P, Huiskes R, Søballe K. Biophysical stimuli on cells during tissue differentiation at implant interfaces. J Biomech (1997) 30(6):539–48. doi:10.1016/S0021-9290(96)00140-6
73. Carter DR, Beaupré GS, Giori NJ, Helms JA. Mechanobiology of skeletal regeneration. Clin Orthop Relat Res (1998) 355:S41–55. doi:10.1097/00003086-199810001-00006
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
74. Byrne DP, Lacroix D, Planell JA, Kelly DJ, Prendergast PJ. Simulation of tissue differentiation in a scaffold as a function of porosity, Young’s modulus and dissolution rate: application of mechanobiological models in tissue engineering. Biomaterials (2007) 28(36):5544–54. doi:10.1016/j.biomaterials.2007.09.003
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
75. Bailon-Plaza A, Van Der Meulen MC. A mathematical framework to study the effects of growth factor influences on fracture healing. J Theor Biol (2001) 212(2):191–209. doi:10.1006/jtbi.2001.2372
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
76. Geris L, Gerisch A, Maes C, Carmeliet G, Weiner R, Vander Sloten J, et al. Mathematical modeling of fracture healing in mice: comparison between experimental data and numerical simulation results. Med Biol Eng Comput (2006) 44(4):280–9. doi:10.1007/s11517-006-0040-6
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
77. Peiffer V, Gerisch A, Vandepitte D, Van Oosterwyck H, Geris L. A hybrid bioregulatory model of angiogenesis during bone fracture healing. Biomech Model Mechanobiol (2011) 10(3):383–95. doi:10.1007/s10237-010-0241-7
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
78. Carlier A, Geris L, Bentley K, Carmeliet G, Carmeliet P, Van Oosterwyck H. MOSAIC: a multiscale model of osteogenesis and sprouting angiogenesis with lateral inhibition of endothelial cells. PLoS Comput Biol (2012) 8(10):e1002724. doi:10.1371/journal.pcbi.1002724
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
79. Zermatten E, Vetsch JR, Ruffoni D, Hofmann S, Müller R, Steinfeld A. Micro-computed tomography based computational fluid dynamics for the determination of shear stresses in scaffolds within a perfusion bioreactor. Ann Biomed Eng (2014) 42(5):1085–94. doi:10.1007/s10439-014-0981-0
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
80. Hillsley M, Frangos J. Review: bone tissue engineering: the role of interstitial fluid flow. Biotechnol Bioeng (1994) 43(7):573–81. doi:10.1002/bit.260430706
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
81. Isaksson H, van Donkelaar CC, Huiskes R, Ito K. Corroboration of mechanoregulatory algorithms for tissue differentiation during fracture healing: comparison with in vivo results. J Orthop Res (2006) 24(5):898–907. doi:10.1002/jor.20118
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
82. Epari DR, Taylor WR, Heller MO, Duda GN. Mechanical conditions in the initial phase of bone healing. Clin Biomech (2006) 21(6):646–55. doi:10.1016/j.clinbiomech.2006.01.003
83. Isaksson H, Wilson W, van Donkelaar CC, Huiskes R, Ito K. Comparison of biophysical stimuli for mechano-regulation of tissue differentiation during fracture healing. J Biomech (2006) 39(8):1507–16. doi:10.1016/j.jbiomech.2005.01.037
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
84. Checa S, Prendergast PJ, Duda GN. Inter-species investigation of the mechano-regulation of bone healing: comparison of secondary bone healing in sheep and rat. J Biomech (2011) 44(7):1237–45. doi:10.1016/j.jbiomech.2011.02.074
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
85. Levchuk A, Zwahlen A, Weigt C, Lambers FM, Badilatti SD, Schulte FA, et al. The Clinical Biomechanics Award 2012 – presented by the European Society of Biomechanics: large scale simulations of trabecular bone adaptation to loading and treatment. Clin Biomech (2014) 29(4):355–62. doi:10.1016/j.clinbiomech.2013.12.019
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
86. Schulte FA, Zwahlen A, Lambers FM, Kuhn G, Ruffoni D, Betts D, et al. Strain-adaptive in silico modeling of bone adaptation: a computer simulation validated by in vivo micro-computed tomography data. Bone (2013) 52(1):485–92. doi:10.1016/j.bone.2012.09.008
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Keywords: bone regeneration, fracture healing, mechanobiology, simulation
Citation: Betts DC and Müller R (2014) Mechanical regulation of bone regeneration: theories, models, and experiments. Front. Endocrinol. 5:211. doi: 10.3389/fendo.2014.00211
Received: 17 October 2014; Paper pending published: 05 November 2014;
Accepted: 23 November 2014; Published online: 10 December 2014.
Edited by:
Jonathan H. Tobias, University of Bristol, UKReviewed by:
Jan Josef Stepan, Charles University, Czech RepublicSarah Taylor, Stanford University, USA
Copyright: © 2014 Betts and Müller. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ralph Müller, Institute for Biomechanics, ETH Zurich, Vladimir-Prelog-Weg 3, Zurich 8093, Switzerland e-mail:cmFtQGV0aHouY2g=
 Duncan Colin Betts
Duncan Colin Betts Ralph Müller
Ralph Müller