- 1School of Economics and Management, China University of Geosciences, Beijing, China
- 2Beijing University of Chemical Technology Institute for Carbon-Neutrality of Chinese Industries, Beijing, China
- 3Key Laboratory of Carrying Capacity Assessments for Resources and Environment, Ministry of Natural Resources of the People’s Republic of China, Beijing, China
- 4School of Economics and Management, Beijing University of Chemical Technology, Beijing, China
The carbon quota allocation scheme serves as the fundamental backbone for ensuring the smooth and sustainable operation of the carbon market. Despite numerous prior studies, ongoing debates persist regarding the impact of historical emissions, both positive and negative, on carbon quota allocation. Utilizing the four indicators of historical emissions (both positive and negative), egalitarianism, payment capability, and emission efficiency, this paper employs the entropy method to develop 22 distinct carbon quota allocation plans tailored for China’s provincial regions in the year 2030. Subsequently, utilizing the shadow price method, the study calculates the emission reduction costs of each province under each allocation scheme, thereby evaluating the carbon quota plans from the perspective of emission reduction costs. Finally, a comparative analysis is conducted to assess the impact of both positive and negative historical emissions on the carbon quota allocation scheme, and the paper identifies the carbon quota allocation approach that minimizes the overall emission reduction cost for China. The findings suggest that: 1) allocating more allowances to provinces with higher historical emissions can effectively reduce emission reduction costs for each province; 2) the most cost-effective option for carbon quota allocation is a scheme that takes into account both egalitarian and historical emission criteria; 3) in order to further decrease the overall cost of emissions reduction, it is crucial to achieve comprehensive coverage of the carbon market and facilitate inter-provincial carbon quota trading.
1 Introduction
Climate change has become a pressing concern for all nations across the globe. In response to this challenge, countries are presenting their carbon neutrality plans. China, too, announced its ambition in September 2020 to reach a “carbon peak” by 2030 and achieve “carbon neutrality” by 2060, reflecting its commitment as a global leader. Carbon markets will play a pivotal role in attaining these objectives, and China has been proactive in this domain, commencing regional carbon trials in 2011. In 2021, the national carbon emission trading market was officially launched, marking steady progress in China’s carbon market development. Consequently, the influence of carbon markets must be taken into account when striving to achieve the dual carbon targets.
Currently, the allocation of carbon quotas occurs primarily in two stages: from the central government to provincial levels and subsequently from provinces to enterprises. The distribution of carbon quotas from the central government to provinces significantly impacts the cost of emission reduction in each province. The reduction costs of provinces are determined by various indicators such as GDP, energy consumption, employment, fixed capital stock, and carbon emissions. The imposition of carbon quota constraints will significantly alter these indicators in each province. Therefore, under different carbon quota allocation schemes, the reduction costs of provinces vary significantly. The reduction cost determines the financial burden each province must bear to fulfill carbon quota constraints. Consequently, a carbon quota allocation scheme that minimizes the reduction cost for provinces naturally attracts greater attention. Among the factors involved in the formulation of carbon quota allocation schemes, historical emissions are the most controversial. Some argue that historical emissions are the responsibility of emitters and thus provinces with higher historical emissions should receive fewer carbon quotas. Others, adhering to the “grandfather law” principle, maintain that provinces with greater historical emissions should be allocated more carbon quotas. It requires further investigation to determine which viewpoint is more conducive to reducing the cost of emission reduction in each province.
Based on the above analysis, this article utilizes four indicators: historical emissions (positive and negative), egalitarianism, payment ability, and emission efficiency, to develop 22 carbon quota allocation scenarios for China’s provinces in 2030 using the entropy method. Subsequently, the shadow price method is employed to calculate the reduction costs of each province under various allocation scenarios, evaluating each carbon quota plan from the perspective of reduction costs. Finally, a comparative analysis is conducted to assess the impact of both positive and negative historical emissions on the carbon quota allocation scheme, and the paper identifies the carbon quota allocation approach that minimizes the overall emission reduction cost for China.
2 Literature review
During the period from the first Conference of the Parties to the United Nations Climate Change Conference to the signing of the Kyoto Protocol, various countries proposed a total of 16 carbon quota allocation schemes. Among these schemes, indicators such as historical emissions, emission intensity, population, and GDP represented fundamental principles of fairness, equality, and efficiency in CO2 emission reduction allocation from different perspectives. Consequently, they were widely used as the design basis for provincial carbon quota allocation schemes by most researchers. Among these indicators, historical emissions have garnered significant attention from scholars. There exist two contrasting views regarding historical emissions. Some scholars contend that historical carbon emissions have inflicted considerable harm on the environment, and the emitters should be accountable for their actions. Therefore, provinces with higher historical emissions should be allocated fewer carbon allowances (Pan, 2014a; Wei et al., 2014; Meng, 2018; Wang et al., 2018; Kong, 2019). However, other scholars maintain that the principle of the “grandfather law” should serve as the foundation for allocation. According to this view, provinces with larger historical emissions should be awarded a greater carbon quota (Zhou et al., 2023; Ye et al., 2019; Schmidt and Heitzig, 2014; Zhou, 2013; Shi et al., 2012; Goulder et al., 1999; Wang and Chen, 2016). Furthermore, carbon emission intensity, population, and GDP are crucial indicators in the design of carbon quota schemes. The carbon intensity indicator takes into account the cost-effectiveness of emission reduction efforts. Provinces with higher emissions per unit of GDP would be allocated a lower carbon quota, as this is considered a more efficient approach (Wang et al., 2011). Population has also been a key area of scholarly investigation, with the genesis of the scheme traced back to Britain. The right to emit encompasses both the right to survival and the right to development. It is generally acknowledged that universal access to carbon emission rights should be safeguarded, and the allocation of these rights should aim to secure equal per capita emissions across all regions in the future (Janssen, 1995; Rose, 2004; Zhou, 2013; Feng, 2015; Liu, 2016; Liu, 2016; Zhou and Wang, 2016; Zhou, 2021). The distribution of GDP serves as a reflection of regional economic disparities. Typically, regions or industries with a higher proportion of GDP tend to emit greater amounts of carbon dioxide while also benefiting more significantly from carbon emissions. Consequently, they should shoulder a heavier responsibility in reducing emissions (Janssen, 1995; Rose, 2004; Zhou, 2013; Liu, 2016; Zhou and Wang, 2016).
In the evaluation of carbon allocation methods, current research primarily focuses on assessing fairness and efficiency. The effectiveness of implementation hinges heavily on the equitable nature of the distribution scheme. The majority of existing literature pertaining to carbon quotas incorporates discussions surrounding the equity of distribution schemes (Zhou and Wang, 2016). Fairness can be categorized into two distinct types: subjective and objective. Subjective fairness concerns the evaluation of participants’ individual perceptions of whether a given situation is deemed fair or unfair. Objective fairness, on the other hand, involves the establishment of an objective criterion or methodology for assessing fairness. While the objective approach is generally considered more practical, the definition of fairness remains a subject of ongoing debate. Regarding the evaluation of subjective fairness, predecessors have primarily conducted empirical analyses, questionnaire surveys, and fairness measurements that rely on participants’ subjective consciousness to assess the fairness of carbon markets (Hammar, 2007; Liao, 2015; Howard, 2016; Soumis, 2016). And after the completion of carbon allocation, a direct comparison of results is conducted to analyze the equity of each method (Liao, 2015; Liu, 2016). Objective fairness analysis is primarily conducted through the construction of evaluation indices, such as Theil and Gini indices (Pan, 2014a; Feng, 2015). This index evaluation method involves selecting certain parameters, such as population and GDP, and comparing their shares to the carbon quota to determine the index size for each region, thereby ensuring fairness.
In summary, although numerous studies have been conducted on carbon quota allocation schemes, there remains controversy regarding the positive and negative impacts of historical emissions in such allocations. Some studies have evaluated the allocation schemes, primarily from the perspectives of fairness and efficiency. However, in reality, the emission reduction costs incurred by various provinces and regions under the carbon quota allocation scheme are their primary concern. Therefore, this article studies the positive and negative impacts of historical emissions in carbon quota allocation from the perspective of emission reduction costs.
3 Methods and data
3.1 Research methods
3.1.1 Design of carbon quota allocation scheme
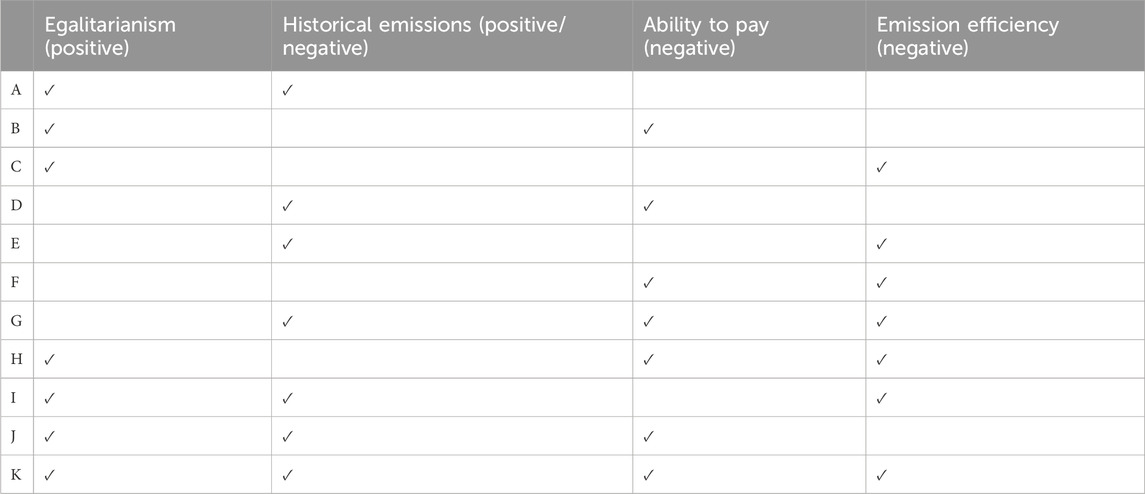
Based on the principles of egalitarianism, historical emissions, ability to pay, and emission efficiency, we selected four indicators: population, carbon emissions over the past decade, per capita GDP, and carbon emission intensity. The core of egalitarianism is the equal right to carbon emission, implying that provinces with larger populations should be allotted larger carbon quotas commensurate with their size (Dong et al., 2024; Chen et al., 2022; Fang et al., 2019). Regarding historical emissions, there are two opposing viewpoints. One school of thought maintains that the higher the level of historical emissions, the greater the responsibility for carbon emission reduction, justifying the allocation of fewer carbon allowances (Wei et al., 2013; Pan, 2014b; Meng, 2018; Wang et al., 2018; Kong, 2019); while another advocates for grandfathering, whereby a larger quantity of historical emissions warrants an increase in carbon allowances (Zhou et al., 2023; Ye et al., 2019; Schmidt and Heitzig, 2014; Zhou, 2013; Shi et al., 2012; Goulder et al., 1999). The economic strength of each province is reflected in its ability to pay, which determines the extent to which emissions can be reduced. Therefore, provinces with stronger financial capabilities are entitled to smaller carbon emission quotas (Gan et al., 2022; He et al., 2021). Emission intensity denotes the amount of carbon emissions produced per unit of GDP. The higher the carbon intensity of GDP, the more emissions should be reduced and the smaller the carbon quota becomes (He and Bin, 2021; Ji et al., 2017).
These indicators are combined to design 11 different carbon quota schemes. Then, taking into account the contentiousness of prior literature regarding the positive and negative impacts of historical emissions on carbon quota allocation, this paper has developed a total of 22 schemes–11 for each category—based on the original 11 carbon quota allocation schemes. The particulars are presented in Table 1.
To differentiate between the positive and negative attributes of historical emissions, we have designated the 11 schemes with negative attributes as series 1, denoted by
3.1.2 Entropy method
Research has revealed that scholars utilize diverse methods for allocating carbon quotas, encompassing techniques such as the entropy method, ZSG-DEA method, scenario analysis, subjective weight + entropy weight approach, and fuzzy optimization model, among others (Mu, 2016; Wang et al., 2016; Yang, 2017; Zhao, 2017). The entropy method, among various other techniques, relies solely on objective data, thereby eliminating subjective biases in the weight assignment process. Consequently, it is frequently employed by scholars to allocate carbon emission reduction targets across diverse industries (Guo et al., 2023; Cheng et al., 2022; Tian et al., 2022). The procedures and algorithms of the entropy weight method for determining index weights are outlined below (Cui et al., 2021).
Firstly, the evaluation indicators for each province are selected based on four perspectives: egalitarianism, historical emissions, ability to pay, and emission efficiency. These indicators include population, historical emissions, per capita GDP, and emission intensity. The decision matrix X is then constructed using information entropy, as shown in Equation (1).
Where Xij represents the jth index value of the ith province (where
Then, each index of the same province needs to be normalized, as shown in Equations (2) and (3).
The jth characteristic ratio in the ith province is computed as Equation (4):
After normalizing the data, the decision matrix is transformed from X to P, as shown in Equation (5).
According to the entropy method, the weight entropy value of index j (ej) can be obtained through the Equation (6).
The weight of indicator j is then determined, as shown in Equation (7).
Comprehensive evaluation value of carbon emission rights of province i, as shown in Equation (8):
Allocation coefficient of carbon emission reduction for province i, as shown in Equation (9):
3.1.3 Shadow price method
The shadow price is defined as the incremental cost incurred by increasing production of a product by one unit, to achieve optimal resource allocation at a given level (Zhang et al., 2024). In recent years, the issue of carbon emissions has garnered increasing attention from experts and scholars. The shadow price method has also been invoked to the issue of CO2 emissions, to calculate the shadow price of CO2 (Boussemart et al., 2017; Wang et al., 2022). The shadow price of carbon dioxide refers to the reduction in output resulting from a one-unit decrease in carbon dioxide emissions, which is equivalent to the cost of reducing such emissions (Shen et al., 2023; Zhang et al., 2014).
The directional distance function is currently the prevailing model for computing the shadow price of CO2. The directional distance function is defined as the Equation (10):
Where y is the desired output and b is the undesired output, which respectively represent economic benefits and carbon dioxide emissions in the study of this paper.
R represents the maximum revenue when the production possibility is satisfied as Equation (11):
Where p is the price of desired output and q is the price of undesired output. Let
Take the ratio of the two, we can get the Equation (13):
The shadow price of carbon dioxide is represented by the Equation (14):
The directional distance function can be decomposed into three approaches: nonparametric data envelopment analysis (DEA), parametric stochastic frontier analysis (SFA), and parametric linear programming (LP). The most commonly utilized nonparametric modeling approach is the data envelopment analysis (DEA) model, which offers the advantage of not requiring a specific form of the distance function to be specified. However, the DEA model cannot ensure the “existence” of shadow prices and the computed shadow prices are not necessarily unique. The parametric SFA approach employs an econometric model to estimate the distance function, which enables the investigation of the impact of random shocks and technical inefficiency factors on the environmental output frontier while ensuring differentiability throughout. The econometric model, however, cannot predefine production technology constraints. Therefore, post-evaluation is necessary to determine whether the shadow price satisfies relevant constraints. The parametric LP model requires the construction of a second-order flexible, continuously differentiable function in advance to approximate the real but unknown production frontier. Subsequently, the parameters of the function are estimated based on data and shadow prices are obtained. The LP model is currently the most extensively employed method as it ensures the existence and uniqueness of shadow prices while also allowing for flexible constraint settings (Lee et al., 2002; Wei et al., 2014; Boussemart et al., 2017).
The parametric LP model can be classified into translog and quadratic functions based on different parameter forms. The translog function typically assumes that desirable and undesirable outputs are equivalent, meaning that output efficiency and shadow prices are determined through simultaneous expansion or contraction. As a result, it fails to meet the requirements of environmental regulation. The quadratic function not only resolves the translog function issue, but also satisfies the transfer property, quadratic differentiability, and directional distance function flexibility. Theoretical studies have demonstrated that the quadratic function outperforms the translog functional form across various conditions (Vardanyan, 2006; Fare, 2010). To conclude, the quadratic function of the parametric LP model has been selected in this paper to compute the shadow price. The specific model functions are presented as Equation (15):
To determine the shadow price, it is necessary to estimate the parameters in Eq. 14 with precision. In this paper, linear programming is employed to determine the optimal parameters. We assume that each province as close to the production frontier as possible and minimize the sum of quadratic production functions for all provinces as our linear programming objective function, as shown in Equation (16).
The significance of each constraint is delineated as follows: Constraint 1 ensures that each DMU is positioned on or within the production technology frontier, thereby satisfying the non-negativity constraint of the directional distance function; Constraints 2 and 3 are designed to ensure the monotonicity of desirable and undesirable outputs with respect to the distance function, guaranteeing their monotonically decreasing and increasing. That is to say, under unchanged conditions, an increase in desirable output will result in a decrease in the distance function value, while an increase in undesirable output will lead to an increase in the distance function. Similarly, Constraint 4 ensures the input is monotonically increasing; Constraints 5 and 6 represent the transformation properties and symmetry of the directional distance function, respectively.
After formulating the model, we utilize Matlab to solve the linear program and derive the parameters.
3.2 Data processing
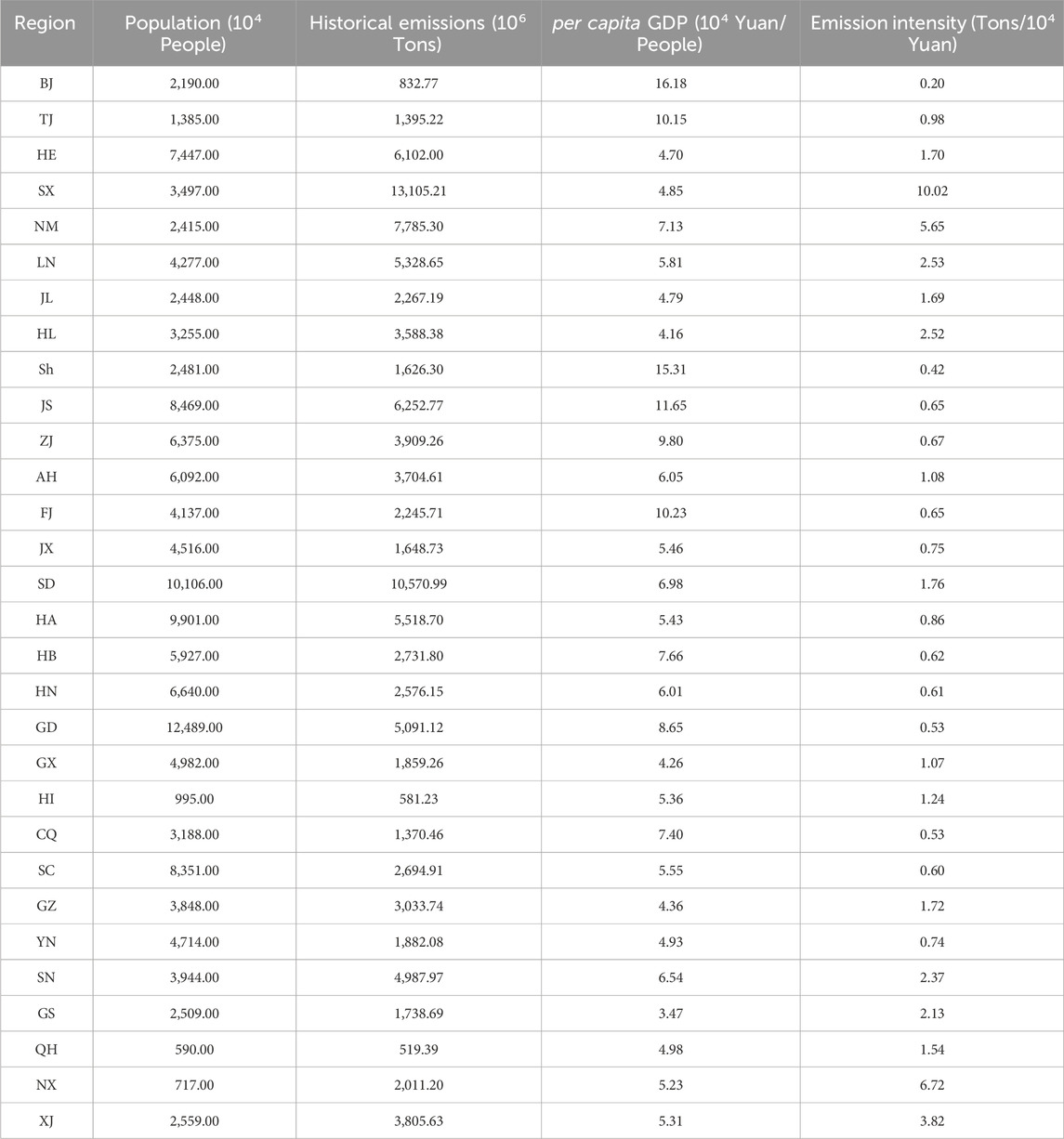
In the calculation of the entropy method, this paper selects four indicators—population, historical emissions, per capita GDP, and emission intensity—to determine the allocation of carbon quotas among provinces. On 30 December 2016, the China State Council released the National Population Development Plan (2016–2030) (China State Council, 2016), which projected China’s total population to reach approximately 1.45 billion by 2030. This paper adopts this projected number as the estimated total population. Additionally, the research gathers data on the total population of all provinces and regions from 2011 to 2020, sourced from the National Bureau of Statistics, and subsequently calculates the average proportion of each province’s population within the national total during this timeframe. The average ratio serves as an indicator of each province’s population share in the total national population projected for 2030, enabling an estimation of each province’s population in that year. For historical emissions, the cumulative emissions from 2010 to 2019 are chosen, and the data utilized in this study are sourced from the China Carbon Accounting Database (Guan et al., 2021). The GDP growth rate for each province during the 14th Five-Year Plan period is derived from their respective 14th Five-Year Plans. The GDP growth rate of each province in the 15th Five-Year Plan has been adjusted by a downward revision of 20% based on the 14th Five-Year Plan, to estimate the GDP of each province for the year 2030. Emission intensity is calculated as the ratio of carbon emissions to the GDP of each province and region in 2019. The detailed data are shown in Table 2.
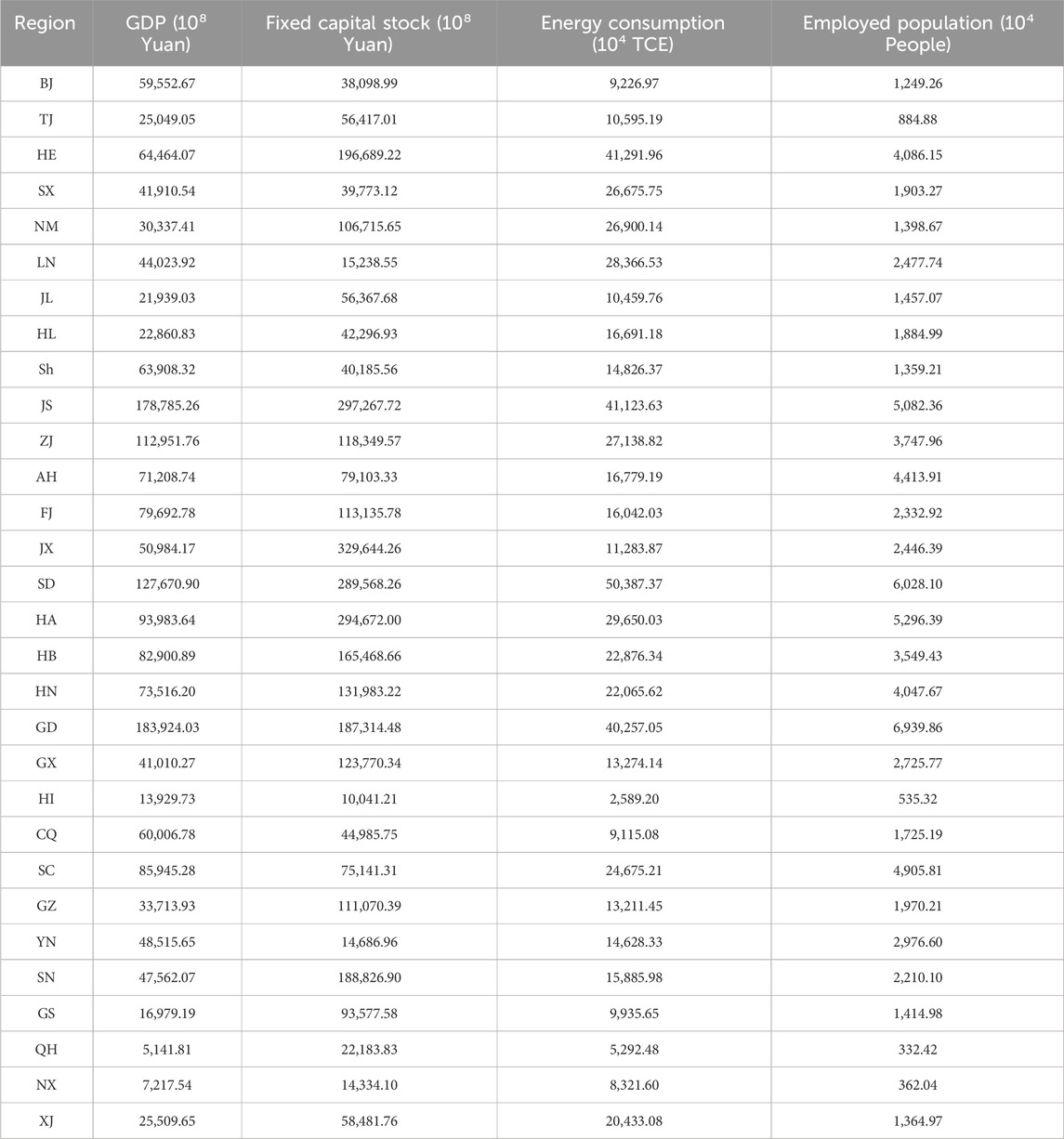
In the shadow price method calculation, this paper selects fixed capital stock, energy consumption, employed population, GDP, and carbon dioxide emissions as the indicators for computation. The GDP for 2030 has been previously mentioned in the aforementioned section. Data of fixed capital stock in 2030 Based on the previous research (Shan, 2008), the fixed asset investment, price deflator, and price index of fixed asset investment from 2007 to 2019 are collected from the statistical yearbooks of all provinces and regions to calculate the fixed asset stock from 2007 to 2019. The average growth rate of fixed assets in each province and region during the aforementioned years is computed, serving as the growth rate for fixed asset stock in each province and region from 2020 to 2030. Subsequently, the fixed capital stock in 2030 can be determined. The projected energy consumption data for 2030 is based on the Energy Production and Consumption Revolution Strategy (2016–2030) (National Development and Reform Commission, 2017), which stipulates that the total energy consumption in 2030 should be limited to 6 billion tce, a value adopted in this paper as well. The proportion of energy consumption for each province is calculated as the average ratio of its energy consumption to the total energy consumption from 2011 to 2020, based on data extracted from statistical yearbooks of respective provinces. The employed population data for 2030 is derived from the population-to-employment ratio of each province and region in that year. Among them, the population data has been previously expounded upon in the preceding section. The employing-population ratio is calculated as the average of the employing-population ratios for each province and region from 2011 to 2020, using data sourced from the statistical yearbooks of said provinces and regions. The total carbon dioxide emissions are derived from the Action Plan for Carbon Peak before 2030, which proposes a 65% reduction in carbon emission intensity by 2030 compared to that of 2005. The total carbon emissions in 2030 are calculated by 2030 GDP and carbon emission intensity. The emissions proportion in each province is not determined through data collection alone, but rather from the calculation results of the previous entropy weight method. By multiplying the total national carbon emissions in 2030 by the carbon quota proportion of each province, we can estimate the carbon emissions of each province in that year. Carbon dioxide emissions, which belong to the calculation results of entropy method, are not displayed here in this article. Only the four data of GDP, fixed capital stock, energy consumption, and employment are shown. Detailed data are shown in Table 3.
4 Results and analysis
This paper’s calculation process comprises two principal segments. In the first segment, the entropy weight method is employed to allocate carbon quotas across various provinces and regions. Subsequently, the second segment utilizes the shadow price method to estimate the emission reduction cost of each province and region under distinct allocation scenarios, drawing upon the emissions data obtained from the first segment. Initially, the first segment is analyzed.
4.1 Allocation of carbon quotas among provinces under various allocation schemes
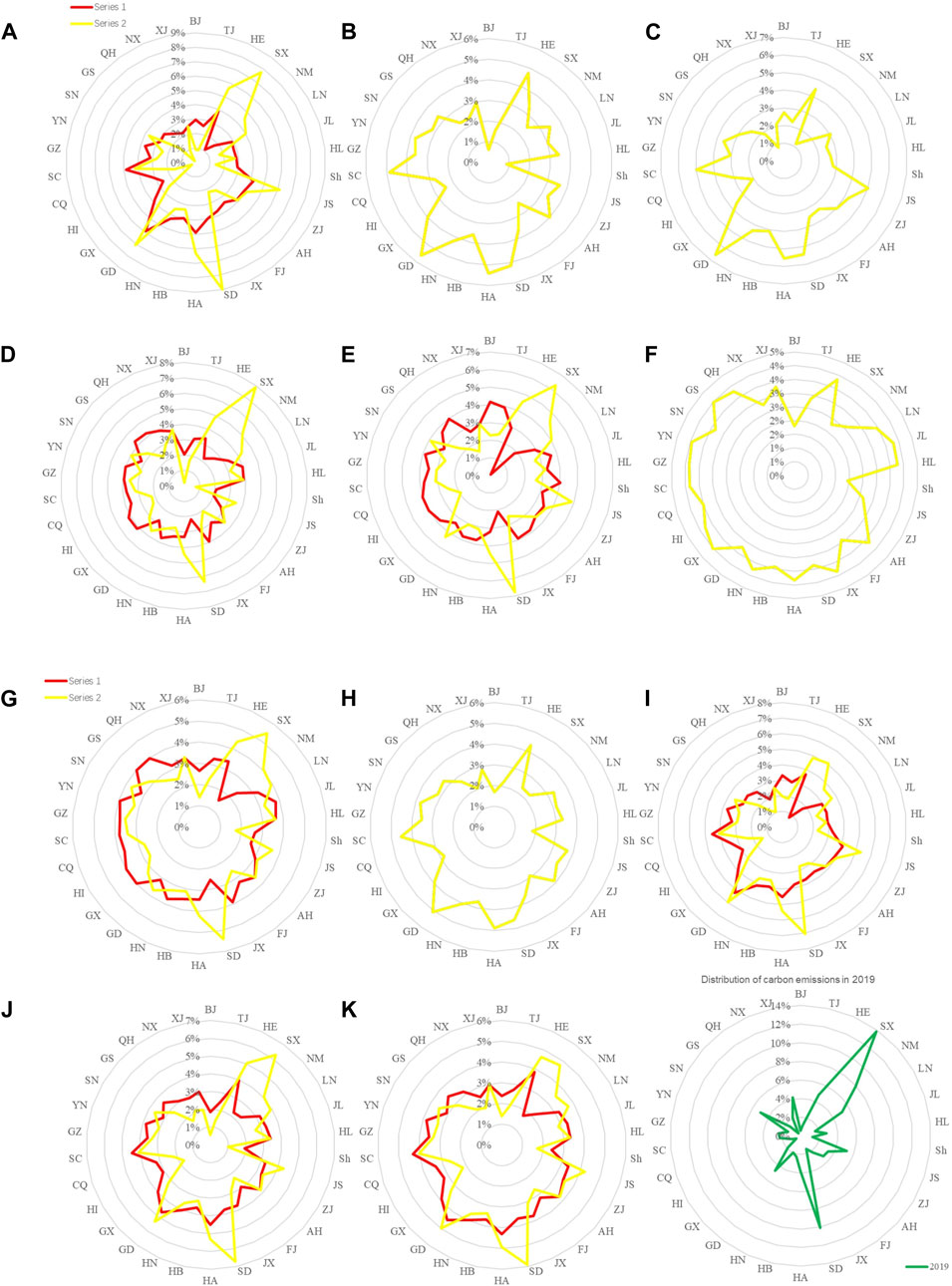
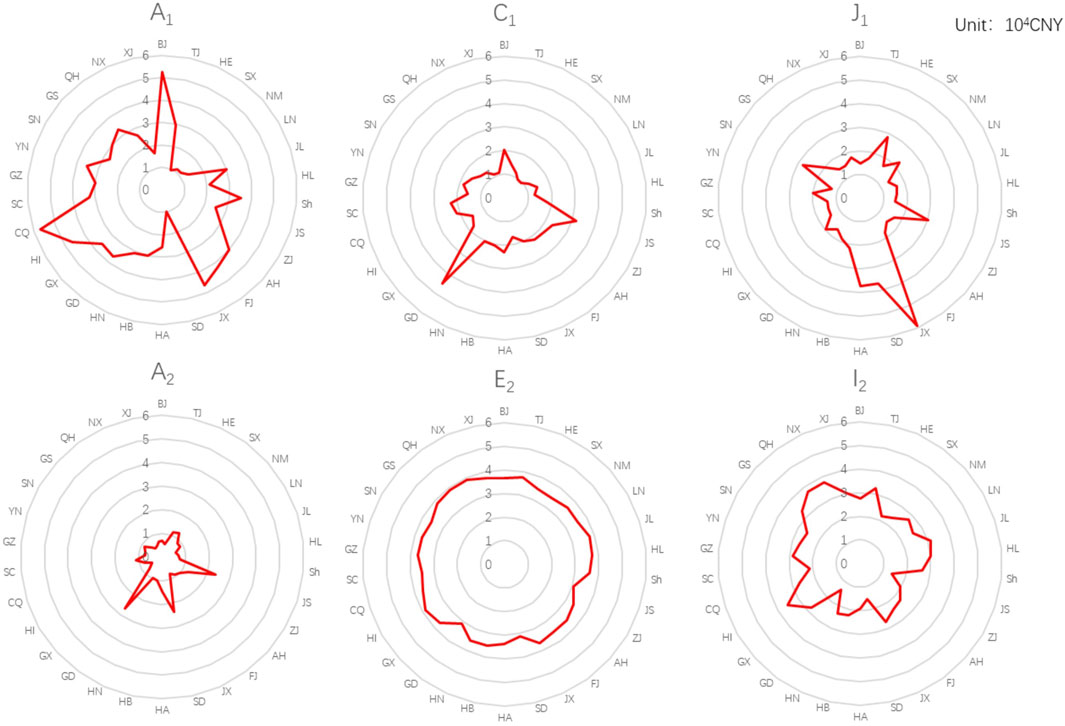
There are significant variations in carbon allocation among different provinces in China under diverse allocation schemes, as illustrated in Figure 1.
Within Scheme series 1, Guangdong, Henan, and Sichuan stand out as the provinces with the most significant proportion of carbon quotas, whereas Ningxia, Inner Mongolia, and Shanxi receive the least allocation. Notably, Guangdong holds the largest carbon quota in schemes A1, C1, G1, H1, I1, and J1, and also ranks prominently in other schemes. Henan and Sichuan follow close behind, occupying a relatively large proportion of carbon quotas in various schemes of Series 1. The allocation of a substantial carbon quota to Guangdong is primarily driven by its population size and emission intensity. Since both these metrics rank among the highest in China, Guangdong is able to secure a significant amount of carbon quota. While the GDP per capita and cumulative emissions of Guangdong Province also play a moderate role in the allocation of carbon quotas, their impact is relatively weaker compared to the other two factors. In Henan province, the primary factors determining carbon quota allocation are emission intensity, GDP per capita, and population. In Sichuan province, the key factors are emission intensity, cumulative emissions, and GDP per capita. On the other hand, in Ningxia province, the lower carbon quota allocation is primarily attributed to population size and emission intensity. Similarly, in Inner Mongolia and Shanxi provinces, the main influencing factors include population size, emission intensity levels, and cumulative emissions. Due to the differences in data selection and index selection, the research results cannot be completely consistent with the previous studies in terms of carbon quota allocation. However, the allocation of carbon quotas among provinces is very similar to that of the previous studies. In the previous studies, the research results with historical emissions as negative indicators are similar to the results of Series 1 in this paper. The provinces with high proportion of carbon quota allocation include Shandong, Henan, Guangdong, Sichuan and other places (Tian et al., 2022; Chen et al., 2022).
The difference between Series 2 and Series 1 lies in the treatment of historical emissions as a positive or negative indicator, resulting in disparities in carbon quota allocation outcomes within schemes that incorporate historical emissions metrics. These schemes include A, D, E, I, J, and K. Examine the variations in carbon quota allocation between Series 2 and Series 1 for these schemes. When historical emissions are treated as a positive indicator instead of a negative one, there are some changes in the carbon quota allocation among different provinces. In Series 2, the carbon quotas of provinces with higher historical emissions have increased, while those of provinces with lower historical emissions have decreased. Provinces such as Shandong, Shanxi, and Inner Mongolia have seen the largest increases in carbon quotas, while Qinghai, Hainan, and Beijing have seen the largest decreases. Therefore, in Series 2, Shandong, Guangdong, and Henan are the provinces with the largest proportion of carbon quotas, while Shanghai, Ningxia, and Beijing are the regions with the lowest carbon quotas. Similarly, the research findings are similar to those in previous studies where historical emissions were treated as a positive indicator (Liu, 2016).
4.2 Results and analysis of shadow prices
The shadow price denotes the expense of decreasing one unit of carbon dioxide, and a higher shadow price indicates a greater cost associated with reducing carbon dioxide. The shadow prices for each province and region have been computed under each allocation scheme, and the results have been thoroughly analyzed. It is evident that in the majority of schemes, the shadow price of carbon quota in certain provinces is exceedingly high. This indicates that, under these allocation schemes, the cost of emission reduction in these provinces will be significantly high. Such allocation outcomes are clearly disconnected from the actual demand and lack feasibility. Therefore, we eliminate these schemes from further consideration and focus our analysis on the remaining ones.
After rigorous screening, the outcomes of the remaining schemes are presented in Table 4; Figure 2. Firstly, a comparison between the results of Scheme A1 and A2 reveals that the shadow price of carbon quota in most provinces is lower under Scheme A2 than under Scheme A1. Similarly, the comparative results for other schemes within Series 1 and 2 yield largely consistent outcomes. This demonstrates that under the allocation criteria favoring greater historical emissions and higher carbon allowances, the cost of emission reduction is reduced. A1 and A2 are selected as representative examples for analysis. The primary difference in calculating the shadow prices of A1 and A2 lies in the allocation of carbon quotas. This difference arises from the varying approaches towards historical emissions in the two schemes. As per the previous section’s findings on carbon quota allocation, Scheme A1 adheres to the principle of assigning fewer carbon quotas to provinces with higher historical emissions. Consequently, the carbon quota disparities among provinces in Scheme A1 are narrower. The criterion of Scheme A2 is that provinces with higher historical emissions receive more carbon quotas, resulting in a carbon quota allocation that is more aligned with the actual distribution of carbon emissions. Conversely, the distribution outcomes of Scheme A1 overlook the disparities in the economic and social environments among provinces. This disconnect between the actual situation in some provinces and their emission reduction tasks leads to a sharp increase in the cost of emission reduction. Scheme A2, however, achieves a better balance between the actual situation and the emission reduction tasks of each province, resulting in a lower emission reduction cost compared to Scheme A1.
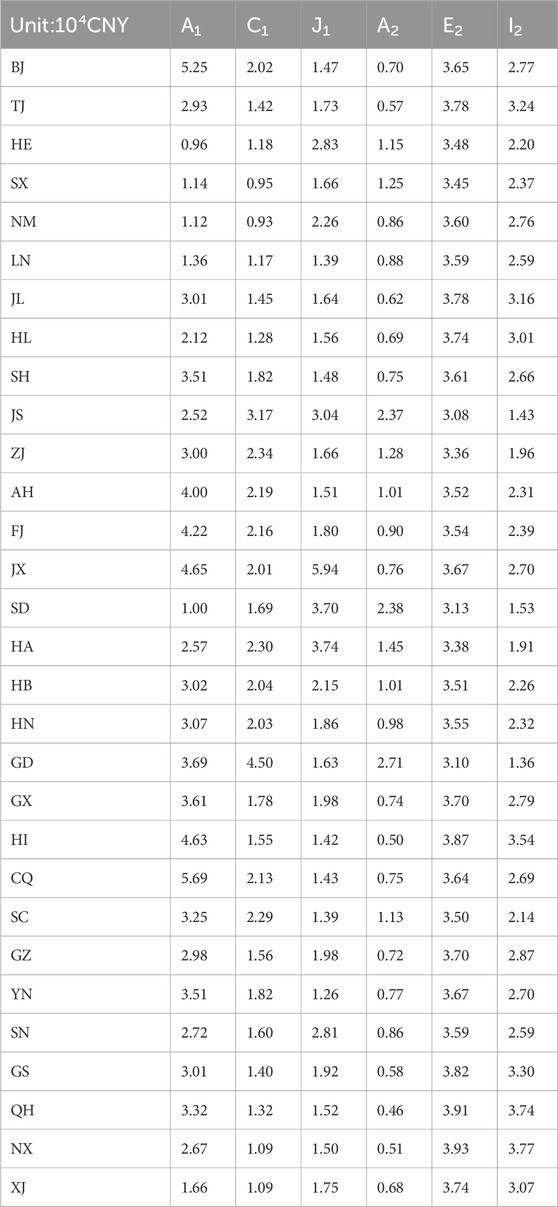
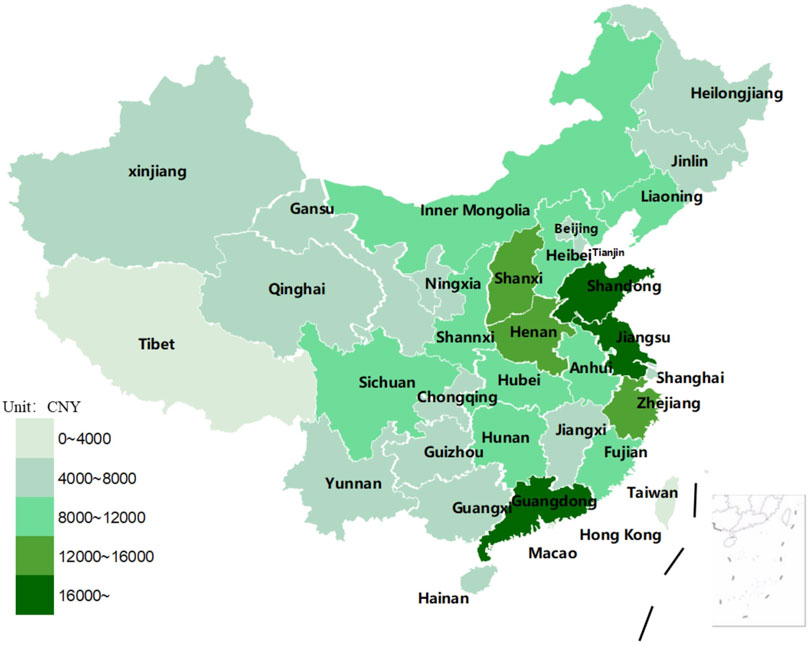
The paper examines various schemes within a reasonable range of shadow prices and reveals that the average shadow price in Jiangxi, Guangdong, and Chongqing is the highest among all provinces and regions, indicating relatively high emission reduction costs. The average shadow price in each province of scheme A2 is CNY 10006/ton, which is the most cost-effective option among all schemes. Figure 3 illustrates the shadow prices for each province under A2.
Figure 3 reveals that the regions exhibiting higher shadow prices are predominantly concentrated in central and eastern China. Shandong, Jiangsu, and Guangdong are the three regions with the highest shadow prices, exceeding CNY 16,000. The three second-level regions, namely, Shanxi, Henan, and Zhejiang, exhibit shadow prices ranging from CNY 12,000 to 16,000. The third level area is centered around the first and second tier cities, indicating a trend of encirclement. The shadow prices of provinces in western China generally rank in the fourth and fifth level, indicating a relatively low level compared to other regions. In Scheme A2, the shadow prices of Shandong, Jiangsu, Guangdong, Shanxi, Henan, Zhejiang, and other regions exceed the average level. If the emission reduction task is completed according to the allocation of carbon quota, the emission reduction cost is huge. Therefore, these provinces can purchase carbon allowances in the carbon market, while other regions with low emission reduction costs can overachieve carbon emission reduction and sell the excess carbon allowances through the carbon market.
5 Conclusion and suggestions
5.1 Conclusion
Utilizing the four indicators of historical emissions (both positive and negative), egalitarianism, payment capability, and emission efficiency, this paper employs the entropy method to develop 22 distinct carbon quota allocation plans tailored for China’s provincial regions in the year 2030. Subsequently, utilizing the shadow price method, the study calculates the emission reduction costs of each province under each allocation scheme, thereby evaluating the carbon quota plans from the perspective of emission reduction costs. Finally, a comparative analysis is conducted to assess the impact of both positive and negative historical emissions on the carbon quota allocation scheme, and the paper identifies the carbon quota allocation approach that minimizes the overall emission reduction cost for China. The conclusions are as follows:
1. The shadow price of the schemes with negative historical emissions is significantly higher than that of the schemes with positive historical emissions. This shows that in terms of the factor of historical carbon emissions, the carbon quota allocation scheme based on the principle that the more carbon emissions are, the more carbon quotas are, can significantly reduce the shadow price of carbon emissions in each province. Therefore, from the perspective of reducing the emission cost of each province, the principle of allocating more emissions allowances to provinces with higher emissions has greater advantages.
2. After conducting an analysis and comparison of the shadow prices associated with 22 different carbon allocation schemes, it has been determined that the carbon quota allocation scheme which is based on egalitarian principles and historical emissions results in lower shadow prices for each province when compared to other schemes. The results indicate that the carbon quota allocation scheme which is based on egalitarian principles and historical emissions offers the lowest emission reduction cost for each province, making it a more favorable option for achieving the emission reduction target.
3. The carbon quota shadow price gap between provinces is significant in each scheme. To minimize the overall cost of emission reduction, it is imperative to establish a nationwide carbon market that facilitates inter-provincial trading of carbon allowances.
5.2 Suggestions
Based on the analysis of carbon emissions shadow prices in all provinces and regions under 22 different carbon quota allocation schemes for 2030, this paper proposes the following recommendations:
1. Provincial carbon quota allocation is a crucial stage in the process of carbon quota allocation, as it determines whether the carbon market can effectively fulfill its role in reducing emissions. The allocation of carbon quotas is significantly influenced by historical emissions. To minimize the cost of emission reduction, it is recommended that the government allocate more carbon quotas to provinces with higher historical emissions.
2. The cost of emissions reduction is a primary concern for provinces when implementing emission reduction measures. For those who aim to reduce emissions, the lower the cost of emission reduction, the greater their motivation for reducing emissions. Therefore, to minimize the cost of emission reduction across all provinces and regions, it is recommended that the government allocate carbon quotas based on principles of egalitarianism and historical emissions.
3. The shadow prices exhibit significant variations across different provinces. The trading of carbon quota among provinces is an effective means to balance the distribution of carbon quota and reduce the overall cost of emissions reduction. Currently, the carbon market has yet to achieve full coverage across all provinces and industries, necessitating further expansion of its scope to encompass all regions in China. Meanwhile, it is imperative to enhance the carbon quota trading mechanism within the carbon market to facilitate inter-provincial transactions.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding authors.
Ethics statement
Ethical review and approval was not required for the study on human participants in accordance with the local legislation and institutional requirements. Written informed consent from the [patients/ participants OR patients/participants legal guardian/next of kin] was not required to participate in this study in accordance with the national legislation and the institutional requirements.
Author contributions
CL: Conceptualization, Formal Analysis, Methodology, Data curation, Investigation, Project administration, Software, Visualization, Writing–original draft. YL: Conceptualization, Formal Analysis, Funding acquisition, Resources, Supervision, Writing–review and editing. WC: Data curation, Methodology, Supervision, Validation, Visualization, Writing–review and editing. YJ: Funding acquisition, Project administration, Resources, Supervision, Validation, Visualization, Writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the National Natural Science Foundation of China (No. 72104116) and the Fundamental Research Funds for the Central Universities (ZY2339).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Boussemart, J. P., Leleu, H., and Shen, Z. (2017). Worldwide carbon shadow prices during 1990–2011. Energy Policy 109, 288–296. doi:10.1016/j.enpol.2017.07.012
Chen, B., Zhang, H., Li, W., Du, H., Huang, H., Wu, Y., et al. (2022). Research on provincial carbon quota allocation under the background of carbon neutralization. Energy Rep. 8, 903–915. doi:10.1016/j.egyr.2022.02.023
Chen, Y., and Lin, S. (2015). Decomposition and allocation of energy-related carbon dioxide emission allowance over provinces of China. Nat. Hazards 76, 1893–1909. doi:10.1007/s11069-014-1576-7
Cheng, Y., Gu, B., Tan, X., Yan, H., and Sheng, Y. (2022). Allocation of provincial carbon emission allowances under China's 2030 carbon peak target: a dynamic multi-criteria decision analysis method. Sci. Total Environ. 837, 155798. doi:10.1016/j.scitotenv.2022.155798
China State Council (2016). National population development plan (2016−2030). (in Chinese) Available at: http://www.gov.cn/zhengce/content/2017-01/25/content_5163309.htm.
Cui, X., Zhao, T., and Wang, J. (2021). Allocation of carbon emission quotas in China’s provincial power sector based on entropy method and ZSG-DEA. J. Clean. Prod. 284, 124683. doi:10.1016/j.jclepro.2020.124683
Dong, H., and Yang, J. (2024). Study on regional carbon quota allocation at provincial level in China from the perspective of carbon peak. J. Environ. Manag. 351, 119720. doi:10.1016/j.jenvman.2023.119720
Fang, K., Zhang, Q., Long, Y., Yoshida, Y., Sun, L., Zhang, H., et al. (2019). How can China achieve its Intended Nationally Determined Contributions by 2030? A multi-criteria allocation of China’s carbon emission allowance. Appl. Energy 241, 380–389. doi:10.1016/j.apenergy.2019.03.055
Färe, R., Martins-Filho, C., and Vardanyan, M. (2010). On functional form representation of multi-output production technologies. J. Prod. Analysis 33, 81–96. doi:10.1007/s11123-009-0164-4
Feng, C., Chu, F., Ding, J., Bi, G., and Liang, L. (2015). Carbon Emissions Abatement (CEA) allocation and compensation schemes based on DEA. Omega 53, 78–89. doi:10.1016/j.omega.2014.12.005
Gan, L., Ren, H., Cai, W., Wu, K., Liu, Y., and Liu, Y. (2022). Allocation of carbon emission quotas for China's provincial public buildings based on principles of equity and efficiency. Build. Environ. 216, 108994. doi:10.1016/j.buildenv.2022.108994
Goulder, L. H., Parry, I. W., Williams Iii, R. C., and Burtraw, D. (1999). The cost-effectiveness of alternative instruments for environmental protection in a second-best setting. J. Public Econ. 72 (3), 329–360. doi:10.1016/s0047-2727(98)00109-1
Guan, Y., Shan, Y., Huang, Q., Chen, H., Wang, D., and Hubacek, K. (2021). Assessment to China's recent emission pattern shifts. Earth Future 9 (11). doi:10.1029/2021ef002241
Guo, A., Yang, J., and Zhong, F. (2023). Carbon emission quotas and a reduction incentive scheme integrating carbon sinks for China's provinces: an equity perspective. Sustain. Prod. Consum. 41, 213–227. doi:10.1016/j.spc.2023.08.014
Hammar, H., and Jagers, S. C. (2007). What is a fair CO2 tax increase? On fair emission reductions in the transport sector. Ecol. Econ. 61 (2-3), 377–387. doi:10.1016/j.ecolecon.2006.03.004
He, W., and Zhang, B. (2021). A comparative analysis of Chinese provincial carbon dioxide emissions allowances allocation schemes in 2030: an egalitarian perspective. Sci. Total Environ. 765, 142705. doi:10.1016/j.scitotenv.2020.142705
He, W., Zhang, B., Li, Y., and Chen, H. (2021). A performance analysis framework for carbon emission quota allocation schemes in China: perspectives from economics and energy conservation. J. Environ. Manag. 296, 113165. doi:10.1016/j.jenvman.2021.113165
Howard, R. J., Tallontire, A. M., Stringer, L. C., and Marchant, R. A. (2016). Which “fairness”. whom, why? Empir. analysis plural notions fairness Fairtrade Carbon Proj. using Q Methodol. Environ. Sci. Policy 56, 100–109. doi:10.1016/j.envsci.2015.11.009
Janssen, M., and Rotmans, J. (1995). Allocation of fossil CO2 emission rights quantifying cultural perspectives. Ecol. Econ. 13 (1), 65–79. doi:10.1016/0921-8009(94)00058-4
Ji, J., Zhang, Z., and Yang, L. (2017). Comparisons of initial carbon allowance allocation rules in an O2O retail supply chain with the cap-and-trade regulation. Int. J. Prod. Econ. 187, 68–84. doi:10.1016/j.ijpe.2017.02.011
Kong, Y., Zhao, T., Yuan, R., and Chen, C. (2019). Allocation of carbon emission quotas in Chinese provinces based on equality and efficiency principles. J. Clean. Prod. 211, 222–232. doi:10.1016/j.jclepro.2018.11.178
Lee, J. D., Park, J. B., and Kim, T. Y. (2002). Estimation of the shadow prices of pollutants with production/environment inefficiency taken into account: a nonparametric directional distance function approach. J. Environ. Manag. 64 (4), 365–375. doi:10.1006/jema.2001.0480
Liao, Z., Zhu, X., and Shi, J. (2015). Case study on initial allocation of Shanghai carbon emission trading based on Shapley value. J. Clean. Prod. 103, 338–344. doi:10.1016/j.jclepro.2014.06.045
Lining, W. A. N. G., and Wenying, C. H. E. N. (2015). CO2 emission allowances for typical allocation regimes and their equality assessments. J. Tsinghua Univ. Sci. Technol. 55 (6), 672–677. doi:10.16511/j.cnki.qhdxxb.2015.06.012
Liu, X. (2016). The carbon emissions quota allocation research of Chinese provinces based on the justice and envelopment. Syst. Eng. 4 (2), 64–69.
Meng, M., Wang, L., and Chen, Q. (2018). Quota allocation for carbon emissions in China’s electric power industry based upon the fairness principle. Energies 11 (9), 2256. doi:10.3390/en11092256
Mu, H., Li, L., Li, N., Xue, Z., and Li, L. (2016). Allocation of carbon emission permits among industrial sectors in Liaoning province. Energy Procedia 104, 449–455. doi:10.1016/j.egypro.2016.12.076
National Development and Reform Commission (2017). Energy production and consumption revolution strategy (2016−2030). (in Chinese) Available at: https://www.ndrc.gov.cn/xxgk/zcfb/tz/201704/W020190905516411660681.pdf.
Pan, X., Teng, F., Ha, Y., and Wang, G. (2014b). Equitable access to sustainable development: based on the comparative study of carbon emission rights allocation schemes. Appl. Energy 130, 632–640. doi:10.1016/j.apenergy.2014.03.072
Pan, X., Teng, F., and Wang, G. (2014a). Sharing emission space at an equitable basis: allocation scheme based on the equal cumulative emission per capita principle. Appl. Energy 113, 1810–1818. doi:10.1016/j.apenergy.2013.07.021
Rose, A., and Zhang, Z. X. (2004). Interregional burden-sharing of greenhouse gas mitigation in the United States. Mitig. Adapt. Strategies Glob. Change 9 (4), 477–500. doi:10.1023/b:miti.0000038850.72913.8e
Schmidt, R. C., and Heitzig, J. (2014). Carbon leakage: grandfathering as an incentive device to avert firm relocation. J. Environ. Econ. Manag. 67 (2), 209–223. doi:10.1016/j.jeem.2013.12.004
Shan, H. J. (2008). Reestimating the capital stock of China: 1952–2006. Quantitative Tech. Econ. 10 (1), 17–31. (in Chinese).
Shen, Z., Bai, G., and Deng, H. (2023). Environmental performance in agricultural supply chain: evidence from the major grain crops in China. Environ. Dev. Sustain., 1–20. doi:10.1007/s10668-023-03059-6
Shi, M. J., Wang, Y., Zhang, Z. Y., and Zhou, X. (2012). Regional carbon footprint and interregional transfer of carbon emissions in China. Acta Geogr. Sin. 67 (10), 1327–1338. (in Chinese).
Soumis, F., and Zaccour, G. (2016). Measuring unfairness feeling in allocation problems. Omega 65, 138–147. doi:10.1016/j.omega.2016.01.005
Tian, M., Hu, Y. J., Wang, H., and Li, C. (2022). Regional allowance allocation in China based on equity and efficiency towards achieving the carbon neutrality target: a composite indicator approach. J. Clean. Prod. 342, 130914. doi:10.1016/j.jclepro.2022.130914
Vardanyan, M., and Noh, D. W. (2006). Approximating pollution abatement costs via alternative specifications of a multi-output production technology: a case of the US electric utility industry. J. Environ. Manag. 80 (2), 177–190. doi:10.1016/j.jenvman.2005.09.005
Wang, F., and Ge, X. (2022). Inter-provincial responsibility allocation of carbon emission in China to coordinate regional development. Environ. Sci. Pollut. Res. 29 (5), 7025–7041. doi:10.1007/s11356-021-16097-2
Wang, H., Liu, H., He, X., and Zeng, W. (2016). Allocation of carbon emissions right based on the intergenerational equity. China Environ. Sci. 36 (6), 1895–1904. (in Chinese).
Wang, J., Cai, B., Cao, D., Zhou, Y., and Liu, L. C. (2011). Scenario study on regional allocation of CO2 emissions allowance in China. Acta Sci. Circumstantiae 31 (4), 680–685. (in Chinese). doi:10.13671/j.hjkxxb.2011.04.012
Wang, W., and Kong, X. (2022). Analysis on China’s provincial carbon quota allocation based on the 2030 carbon peak goal. Quantitative Tech. Econ. 39 (7), 113–132. (in Chinese). doi:10.13653/j.cnki.jqte.2022.07.002
Wang, Y., Cheng, Y., Yang, G., and Dong, Y. (2018). Provincial decomposition of China's carbon emission rights under the constraint of 2020 and 2030 carbon intensity targets. China Environ. Sci. 38 (8), 3180–3188. doi:10.19674/j.cnki.issn1000-6923.2018.0339
Wang, Z., Song, Y., and Shen, Z. (2022). Global sustainability of carbon shadow pricing: the distance between observed and optimal abatement costs. Energy Econ. 110, 106038. doi:10.1016/j.eneco.2022.106038
Wei, C., Löschel, A., and Liu, B. (2013). An empirical analysis of the CO2 shadow price in Chinese thermal power enterprises. Energy Econ. 40, 22–31. doi:10.1016/j.eneco.2013.05.018
Wei, Y. M., Wang, L., Liao, H., Wang, K., Murty, T., and Yan, J. (2014). Responsibility accounting in carbon allocation: a global perspective. Appl. Energy 130, 122–133. doi:10.1016/j.apenergy.2014.05.025
Xian-Chun, T. A. N., Miao-Miao, N. I. U., Bai-He, G. U., Yong-Long, C. H. E. N. G., and Kai-Wei, Z. H. U. (2023). Evaluation of China’s provincial carbon quota allocation scheme from the perspective of high-quality development. Adv. Clim. Change Res. 19 (1), 74.
Yang, B., Liu, C., Su, Y., and Jing, X. (2017). The allocation of carbon intensity reduction target by 2020 among industrial sectors in China. Sustainability 9 (1), 148. doi:10.3390/su9010148
Ye, F., Fang, X. L., Li, L. X., Li, Y. N., and Chang, C. T. (2019). Allocation of carbon dioxide emission quotas based on the energy-economy-environment perspective: evidence from Guangdong Province. Sci. Total Environ. 669, 657–667. doi:10.1016/j.scitotenv.2019.03.058
Zhang, X., Xu, Q., Zhang, F., Guo, Z., and Rao, R. (2014). Exploring shadow prices of carbon emissions at provincial levels in China. Ecol. Indic. 46, 407–414. doi:10.1016/j.ecolind.2014.07.007
Zhang, Y., Zhuo, J., Baležentis, T., and Shen, Z. (2024). Measuring the carbon shadow price of agricultural production: a regional-level nonparametric approach. Environ. Sci. Pollut. Res. 31, 17226–17238. doi:10.1007/s11356-024-32274-5
Zhao, R., Min, N., Geng, Y., and He, Y. (2017). Allocation of carbon emissions among industries/sectors: an emissions intensity reduction constrained approach. J. Clean. Prod. 142, 3083–3094. doi:10.1016/j.jclepro.2016.10.159
Zhou, H., Ping, W., Wang, Y., Wang, Y., and Liu, K. (2021). China’s initial allocation of interprovincial carbon emission rights considering historical carbon transfers: program design and efficiency evaluation. Ecol. Indic. 121, 106918. doi:10.1016/j.ecolind.2020.106918
Zhou, P., and Wang, M. (2016). Carbon dioxide emissions allocation: a review. Ecol. Econ. 125, 47–59. doi:10.1016/j.ecolecon.2016.03.001
Zhou, P., Zhang, L., Zhou, D. Q., and Xia, W. J. (2013). Modeling economic performance of interprovincial CO2 emission reduction quota trading in China. Appl. Energy 112, 1518–1528. doi:10.1016/j.apenergy.2013.04.013
Keywords: carbon quota allocation policy, evaluation of quota allocation scheme, abatement costs, shadow price, historical emission
Citation: Liu C, Lei Y, Chen W and Jiang Y (2024) Study on China’s 2030 provincial carbon quota allocation scheme considering the positive and negative effects of historical emissions. Front. Environ. Sci. 12:1349200. doi: 10.3389/fenvs.2024.1349200
Received: 04 December 2023; Accepted: 20 March 2024;
Published: 28 March 2024.
Edited by:
Zhangqi Zhong, Guangdong University of Foreign Studies, ChinaReviewed by:
Pibin Guo, North University of China, ChinaXiaofeng Zhong, Guangdong University of Foreign Studies, China
Copyright © 2024 Liu, Lei, Chen and Jiang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yalin Lei, leiyalin@cugb.edu.cn; Wenhui Chen, chenwenhui@buct.edu.cn
 Chuanwang Liu1,2
Chuanwang Liu1,2 Yalin Lei
Yalin Lei Wenhui Chen
Wenhui Chen