- 1 Centre for Immunology and Infection, Department of Biology and Hull York Medical School, York, UK
- 2 Department of Computer Science, University of York, York, UK
- 3 Department of Electronics, University of York, York, UK
- 4 Instituto de Medicina Molecular, Faculdade de Medicina de Lisboa, Edifício Egas Moniz, Lisboa, Portugal
The use of genetic tools, imaging technologies and ex vivo culture systems has provided significant insights into the role of tissue inducer cells and associated signaling pathways in the formation and function of lymphoid organs. Despite advances in experimental technologies, the molecular and cellular process orchestrating the formation of a complex three-dimensional tissue is difficult to dissect using current approaches. Therefore, a robust set of simulation tools have been developed to model the processes involved in lymphoid tissue development. Specifically, the role of different tissue inducer cell populations in the dynamic formation of Peyer’s patches has been examined. Utilizing approaches from systems engineering, an unbiased model of lymphoid tissue inducer cell function has been developed that permits the development of emerging behaviors that are statistically not different from that observed in vivo. These results provide the confidence to utilize statistical methods to explore how the simulator predicts cellular behavior and outcomes under different physiological conditions. Such methods, known as sensitivity analysis techniques, can provide insight into when a component part of the system (such as a particular cell type, adhesion molecule, or chemokine) begins to have an influence on observed behavior, and quantifies the effect a component part has on the end result: the formation of lymphoid tissue. Through use of such a principled approach in the design, calibration, and analysis of a computer simulation, a robust in silico tool can be developed which can both further the understanding of a biological system being explored, and act as a tool for the generation of hypotheses which can be tested utilizing experimental approaches.
Introduction
The analysis of mice deficient for key transcription factors (ID2, RORγt), cytokines (IL-7), chemokines (CXCL13, CCL19/21), TNF superfamily members (LTβ, RANK), RET, adhesion molecules, and associated signaling pathways has led to an understanding of the detailed cellular and molecular elements that play a key role in secondary lymphoid tissue development. However, a reductionist approach focusing on the role of individual cells types and molecules is limited in the insight it can provide into how this tissue develops, because it is the complex temporal interactions between cells and signaling molecules that dictates the end result: the formation of the organ.
To further understand the underlying mechanisms in such systems, mathematical and computational biology is becoming increasingly prevalent. Such approaches permit the development of models which aim to provide an interpretation of the underlying biological data upon which they are constructed (Guo and Tay, 2005), and to act as a tool for exploration and development of new hypotheses which may lead to testable outcomes that can be examined using traditional experimental approaches (Andrews et al., 2008). The application of such modeling techniques has permitted the exploration of a range of complex biological systems, including T cell signaling cascades (Chakraborty and Das, 2010), autoimmune disease pathology (Read et al., 2009), investigating cell migration within germinal centers (Figge et al., 2008), emergence of immune memory (Lagreca et al., 2001; Jacob et al., 2004), and system dynamics under HIV-1 infection (Sieburg et al., 1990; Stafford et al., 2000). However, the approach has yet to be adopted in the exploration of immune system development.
Work in this paper examines the application of a structured methodology that integrates traditional in vivo and ex vivo experimental techniques such as gene knockouts, real-time imaging, gene expression data sets, and functional ex vivo culture systems, in the creation of a model that encompasses the dynamics of a complex system being studied (Figure 1A). The objective is to demonstrate that a structured process is required in the design of any computer simulation of a biological process if confidence is to be retained in the use of that simulation as a scientific tool. We then demonstrate how statistical tools that analyze output from the constructed simulator can be used to predict changes in cellular behavior under different physiological conditions. These lead to predictions being made that may be tested within the laboratory. As Figure 1A demonstrates, this leads to the generation of an iterative process, where the biological understanding heavily influences the development of the model and simulator, from which results may influence laboratory investigations, which may in turn produce results which inform later iterations of model development.
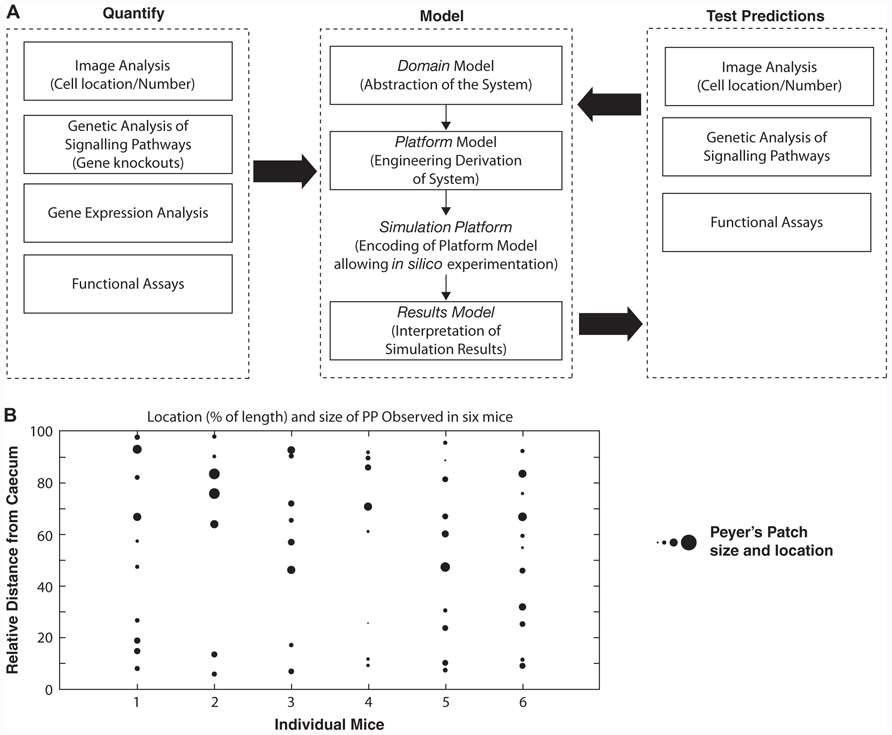
FIGURE 1. (A) Schematic of the modeling process. Data obtained using experimental biological approaches was used to develop a series of models: Domain Model – explicitly capturing an abstraction of the biological system; Platform Model – detailing how the biological system is implemented as a computer simulation; Simulation Platform – coding the platform model; Results Model – interpretation of simulation results and relationship to biological system. Through use of in silico experimental results model new models and new hypothesis can be developed. (B) To determine if the size and number of PP that form in mice is stochastic, the relative size and location of PP from six adult mice was determined.
Any exploration of a biological system, whether this uses traditional experimental or computational methods, will be open to a degree of skepticism as the understanding of each underlying detail is incomplete. This is addressed through the making of assumptions, justified by available evidence. Thus, the exploration is focusing on an abstraction of the real system. The abstraction captured in any computer simulation will be greater than that examined using traditional laboratory approaches, as it is intractable to capture all current understanding in a model. It is critical that this is taken into consideration when judging how relevant any results are to the biological system under study. For this reason, it is important that a rigorous process is adopted in the design of any simulation, where all assumptions and abstractions are documented and justified for scrutiny alongside simulation results, and the link between the underlying biological system and how this is encoded is fully appreciated by both immunologists and the modeler. The methodology involved in developing the model and simulation in our case study utilizes the principled approach of the CoSMoS (Complex Systems Modeling and Simulation Infrastructure) process (Andrews et al., 2010), which can be used to create and validate simulations of complex systems. In this process, the biological system being explored is termed the domain of interest. Understanding of the functional elements in the system is captured in a series of models: domain, platform, simulation, and results. The domain model encapsulates the current scientific understanding for each biological entity within the model. The platform model specifies how the domain model will be implemented as a computer simulation. The simulation model is executable software constructed from the specification in the platform model. The results model is a mapping detailing how the output from the simulation relates back to the biology. The construction of each model is an important step in the process, with the aim of ensuring that confidence is retained in the model as a representation of the system, and that results from the simulation relate back to the biological system and can be justified.
As a demonstration of how this approach can be applied, the role lymphoid tissue inducer and initiator cell populations (LTi/LTin) have in the development of Peyer’s patches (PP) was examined. PPs have an essential role in the initiation of adaptive immune responses to infection within the gastrointestinal tract, and are comprised of an organized structure of B cell follicles containing follicular dendritic cells (FDC), T cell zone and associated fibroblastic reticular cells (FRC), surrounded by a mucosal epithelium (Jung et al., 2010). Antigens are transported by specialized epithelial cells, M cells, to dendritic cells in the FRC, which triggers an adaptive immune response. Pre-natal studies show that an average of 60 PP develop in the human fetal gut (Cornes, 1965), and 8–12 in the mouse (Figure 1B), distributed along the gut length with a large variation in the location, number, and size of PP between different genetically identical mice, indicating a stochastic nature to the process.
Peyer’s patches form through a clustering of hematopoietic and stromal cells on the anti-mesenteric side of the small intestine (Randall et al., 2008). The properties of the key cellular and molecular components involved in the development process are well understood (van de Pavert and Mebius, 2010). In the mouse, migration of hematopoietic LTin and LTi cells into the mid-gut occurs from embryonic day 14.5. LTin cells express the tyrosine kinase receptor RET and initiate the process of PP induction through an adhesion-dependent chemokine-independent process, ultimately leading to lymphoid tissue organizer (LTo) cell maturation (Fukuyama and Kiyono, 2007; Veiga-Fernandes et al., 2007; Patel et al., 2012). Upon LTo triggering, LTi cells interact with Vcam + LTo cells through LTb/LTβ receptor inducing the production of IL-7, and chemokines CXCL13, CCL19, and CCL21 (Adachi et al., 1997; Luther et al., 2003). LTi cells express the corresponding receptors for these chemokines (CXCR5 and CCR7; Adachi et al., 1997), thus further hematopoietic cells are attracted to the region through chemotaxis, and retained by adhesion molecules. This promotes further cellular interaction, which increases the concentration of IL-7, chemokines, and localized expression of adhesion molecules in the forming cluster. This is a self-sustaining process, up to a point at E18.5 where, for reasons not currently understood, further clustering of PPs ceases to occur (Randall et al., 2008).
In the development of any simulator, it is essential that the questions it will be used to address are defined prior to its construction, as this directly affects the choice of modeling strategy. Recent ex vivo experimental work has focused on the initial 12 h of PP development, which has revealed that the behavior of LTin/LTi cells within 50μm of a RET ligand-expressing ARTN soaked micro-sphere is statistically different to that of cells further away (Patel et al., 2012). The cellular behavior observed in the ex vivo culture system is thought to emerge from interactions between LTin/LTi cells and the LTo cells. In conjunction with the experimental approaches, our model captures the cellular dynamics up to this time-point, in the hope of generating hypotheses on why, for each cell, this emergent behavior becomes apparent. Thus, it is not possible to use a traditional ordinary differential equation (ODE) modeling strategy, as our focus is at an individual rather than the population level (Guo and Tay, 2005). In such cases a multi-agent models is necessary. In this approach, each biological entity exists as an autonomous object, referred to as an agent, with associated states and within a specified spatial environment (Forrest and Beauchemin, 2007). These agents interact with others in the environment through a set of rules that in turn change the agent’s state. At this level, it is possible to observe entity behavior or structural formation that emerges through interactions between agents.
As we are seeking to understand the behavior of each cell individually, our demonstration of this methodology focuses on the creation of a multi-agent simulation. Our purpose is to explore how cellular interactions have led to the emergent behavior observed. This allows us to create a model at a higher level of abstraction, removing the need to explicitly model each individual component involved in the interaction and each underlying mechanism. As Germain et al. (2011) note, the focus shifts from an examination of each individual component part to that of the higher order behavior and how this emerges from components which lack the capability to do this alone. This permits an understanding of how small perturbations in individual system components affect the end outcome of the process (Germain et al., 2011).
With the application of the CoSMoS process (Andrews et al., 2010), we demonstrate how the set of models is generated and the underlying biology captured through the use of Unified Modeling Language (UML) diagrams. We then describe how the simulator created from these models has been calibrated to reproduce emergent behaviors that are statistically similar to those observed ex vivo (Patel et al., 2012), providing a level of confidence that the simulator is an adequate representation of the real system. The latter part of this study demonstrates how the simulator can be used to explore the complex system under examination. Using the PP simulator, we show how the capacity of the model to replicate previously published gene knockout and over expression experimental results can be rigorously tested. Using statistical analysis techniques, including sensitivity analysis techniques, changes in observed behavior when the model is run under different conditions was used to determine the relative role of different parameters involved in PP development. Specifically, we focused on the role chemoattractant molecules have in influencing cellular behavior and tissue organogenesis, and the time-point at which these molecules become influential. Use of these methodologies permits quantification of the capacity of simulation to determine changes in cellular behaviors and emergent behaviors when quantitative changes are applied to each system component, allowing in silico experimentation with the aim of informing future laboratory experimentation.
Materials and Methods
Model Development
To develop a computer simulation of lymphoid tissue formation, an agent-based approach to complex systems modeling was utilized, and through the application of the CoSMoS process a series of models created (Andrews et al., 2010).
Domain Model
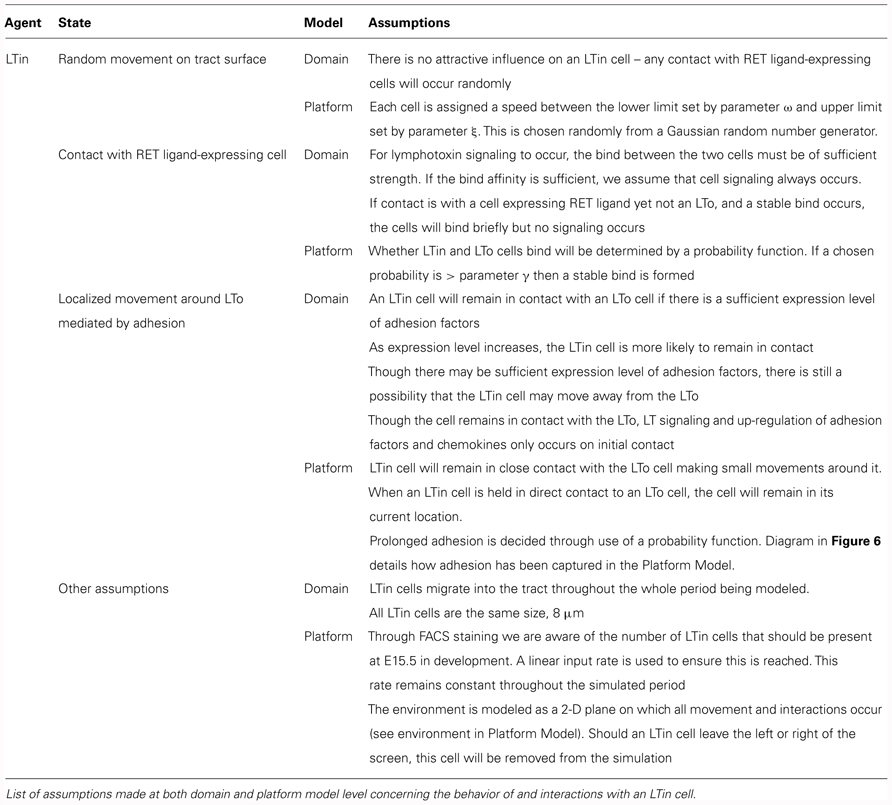
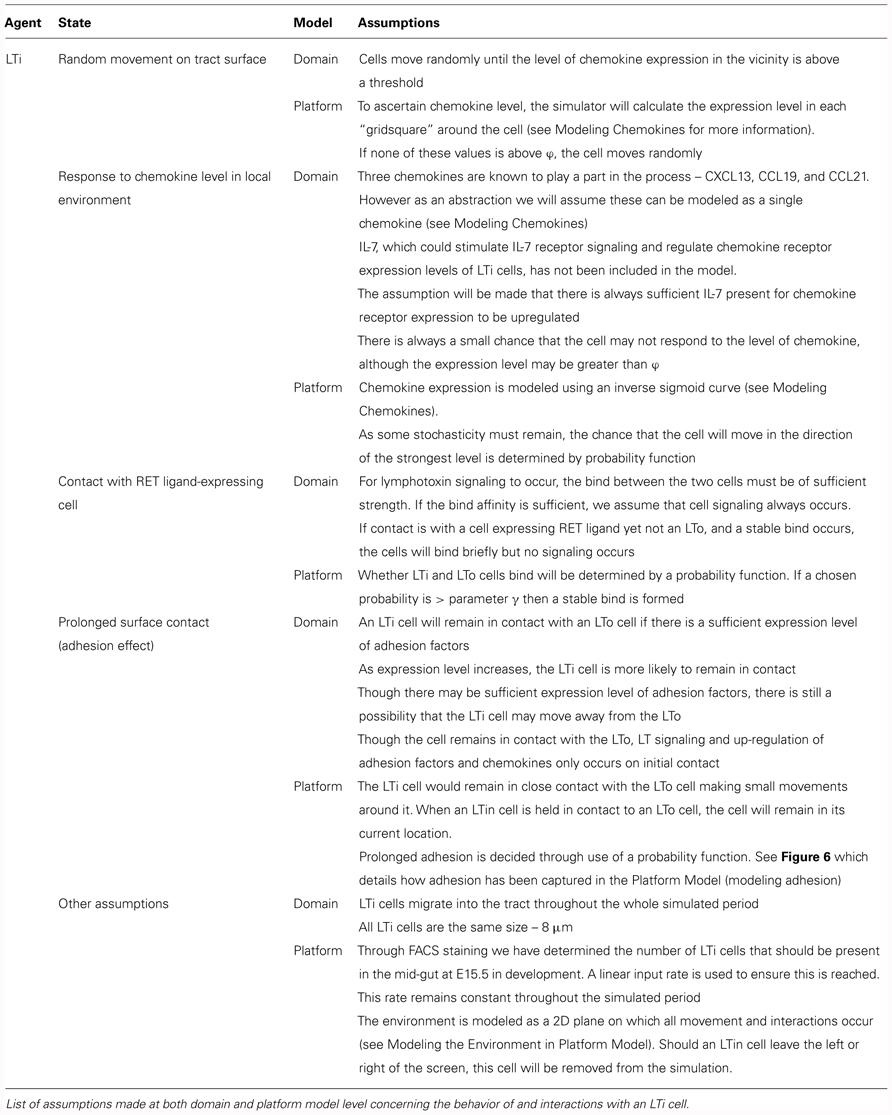
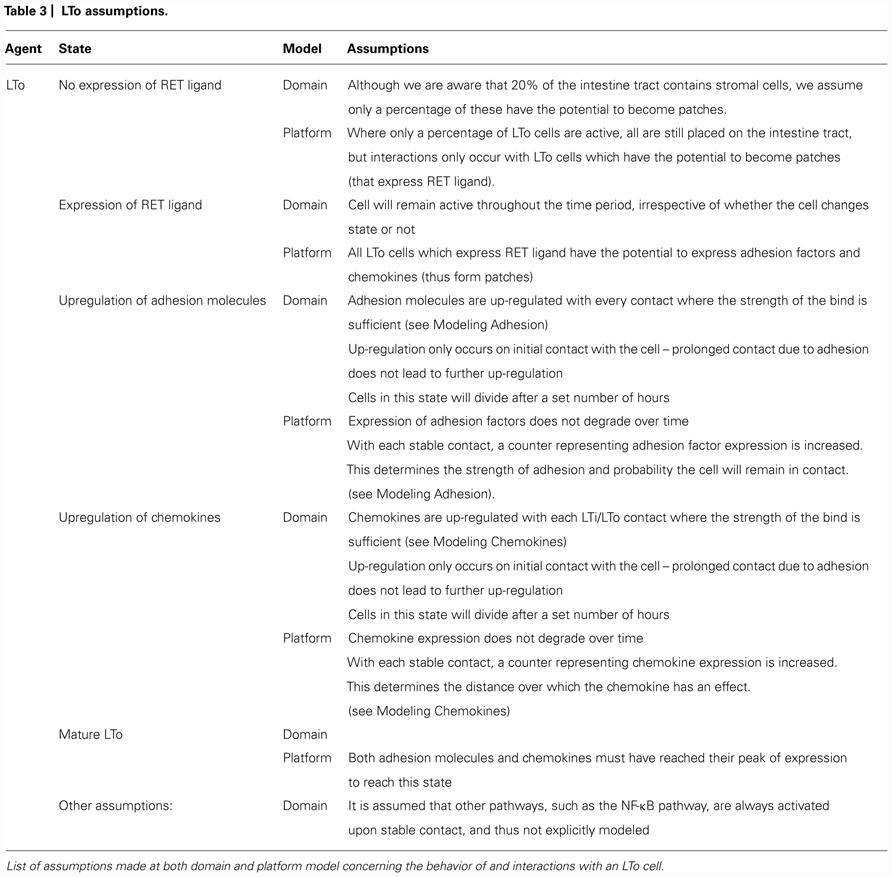
The domain model (Figure 2) focuses on modeling the biological system by encapsulating current scientific understanding of cellular behavior. Thus, this is a purely biological model, ensuring isolation between the understanding of the system to be captured, and how this translates into computer code. This is important as at this point the details of how the simulation is to be implemented are not of concern, and may distract from the specific modeling of the biological system. The domain features the component parts of the system which will be included in the in silico model including the cell types, the factors which influence cell behavior (e.g., chemokines, adhesion factors) and a description of the environment in which interactions take place (e.g., the fetal intestinal tract). Any abstractions and necessary assumptions made are clearly documented for later scrutiny (Tables 1–3).
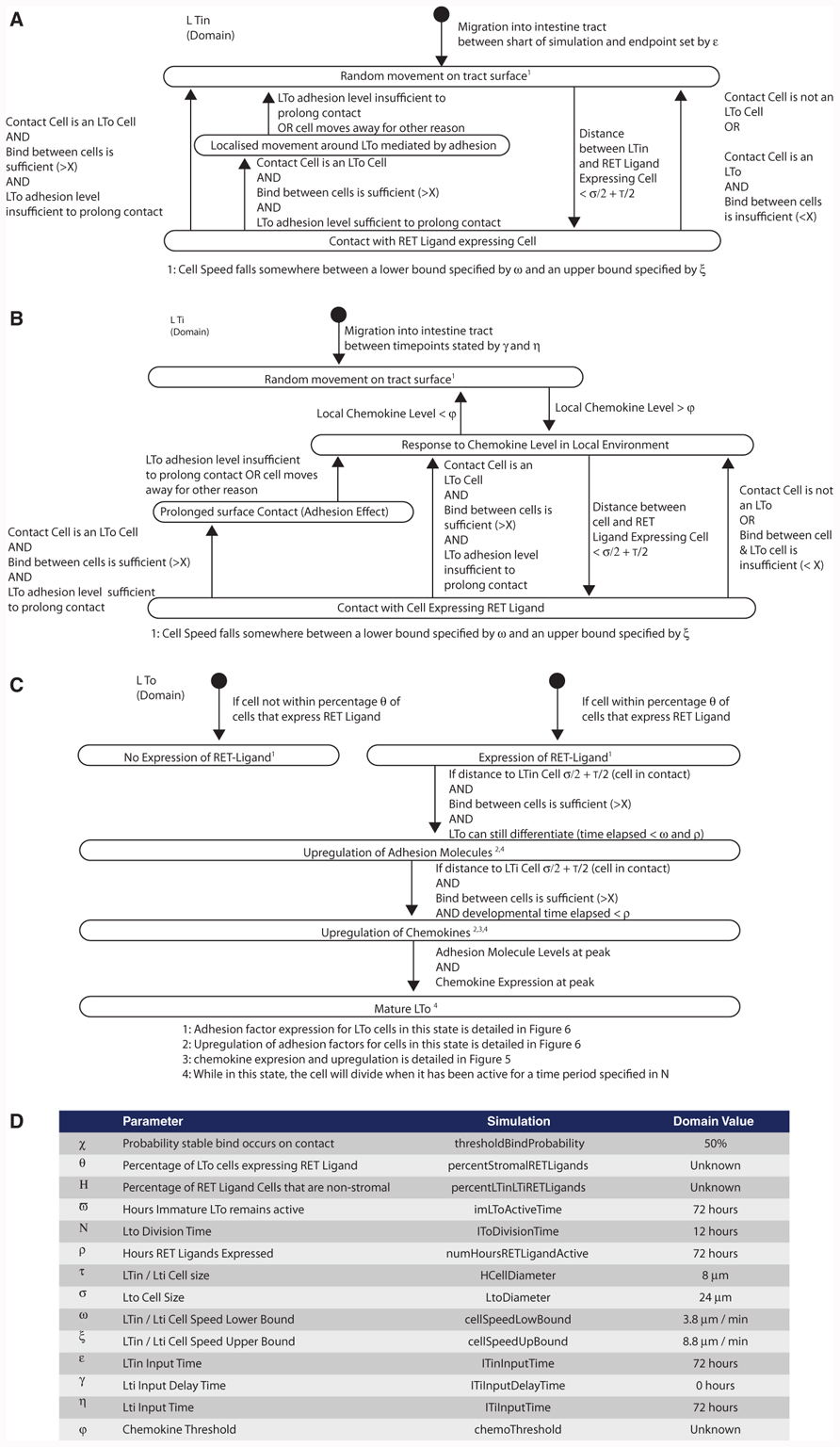
FIGURE 2. The domain model captures an abstraction of the biological domain. The state diagrams, created using a modified version of Unified Modeling language, provide a description of the states in which the identified agents (cell type) may exist within (the boxes), and the biological event that must take place for that agent to transition into the next state (the arrow). This does not contain any simulation-specific detail. (A) LTin cell, (B) LTi cell, (C) LTo cell, and (D) biological parameters identified in the creation of the domain model.
State Diagrams
Each of the key cell types identified in the literature is represented explicitly in the domain model. For each cell type, the states (observed behaviors or gene expression profile) that the cell might exist in and the interaction(s) that must take place for that cell to change state were examined. For example, an LTo (stromal) cell (Figure 2C) initiates in the model as an undifferentiated stromal cell until LTβ receptor activation, upon which the LTo cell induces expression of cytokines, chemokines, and adhesion factors critical for PP development. Such descriptions are documented through the use of state diagrams (Figure 2), a documentation method closely related to the notation included within UML and widely used in software engineering (Bersini and Carneiro, 2006; Read et al., 2009). Through creating this model, parameters are identified and recorded. Some of these parameters have known values which have been determined experimentally, whereas the values of others are currently unknown.
Activity Diagram
A further UML diagram, an activity diagram, is utilized to specify how the cells identified in the state diagrams interact (Figure 3). It is through these interactions that the observed behavior is expected to emerge. Thus, in this model, it is the interactions between cells that causes statistically significant changes to LTi/LTin cell velocity and displacement.
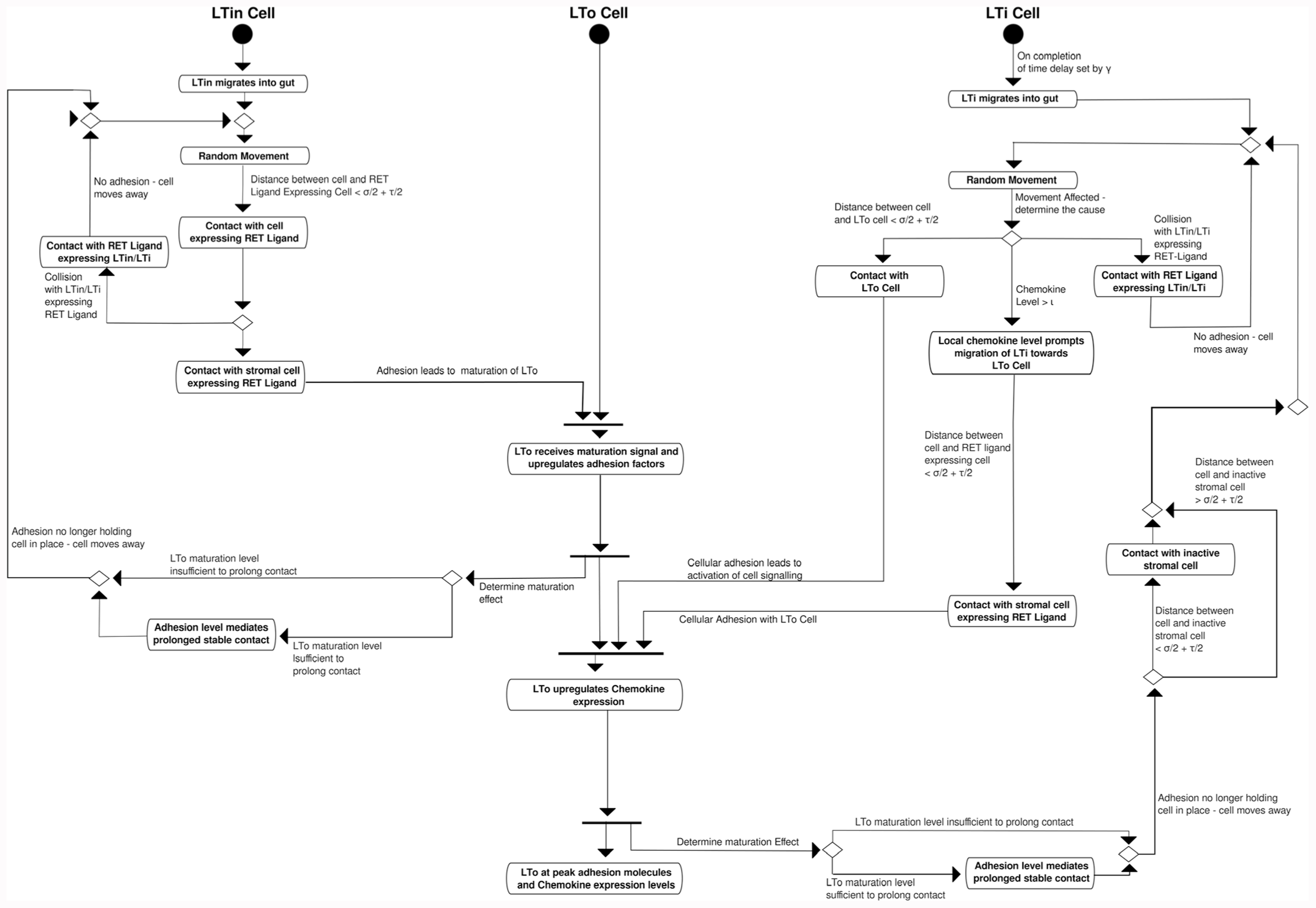
FIGURE 3. Activity diagram of domain model representing the low-level interactions between the cells (LTin, LTi, LTo cells) which lead to the formation of PP. Cellular behaviors are described in boxes, decisions points indicated by diamonds and lines. Arrows indicate potential changes to cellular behavior.
Platform Model
Utilizing the domain model the implementation of the computer simulation is documented using a platform model. This specifically details how the individual cells, the model environment and interactions described in the domain model will be implemented in the computer simulation (Figure 4). In the platform, the interactions that lead to state changes are examined and translated into a form which can be captured in computer code (the simulator). Further parameters are identified during this process and described, and as in the domain model, the numerical values of some parameters are unknown. These parameters capture the behavior of component parts such as adhesion molecules, cytokines, and chemokines. Despite the importance of these factors, the number of molecules expressed by the different cell types, the level of chemokine expression required to induce cellular chemotaxis and the diffusion distribution of chemokines and cytokines in the localized environment all are currently unknown. Thus further assumptions are made based on known biology and documented for scrutiny alongside simulation results (Tables 1–3; Figures 5 and 6). Critical to the modeling process, emergent behavior specified in the domain model is entirely removed from the platform model. Biologically observed behavior must emerge through interactions between components and not be encoded into the model, as this invalidates the simulator as a predictive experimental tool.

FIGURE 4. The Platform model details how the states and interactions captured in the domain model are coded into the simulation. The expected behavior, which emerges from interactions between components in the system, is specifically not present in the platform model. Behavior emerges from the simulation and are not coded into the simulation. In the platform model, how each cell behaves and how interactions are encoded is detailed. As this includes a variety of factors from the domain model a number of assumptions are made and documented. (A) LTin cell, (B) LTi cell, (C) LTo cell, and (D) additional simulation parameters identified in the creation of the platform model.
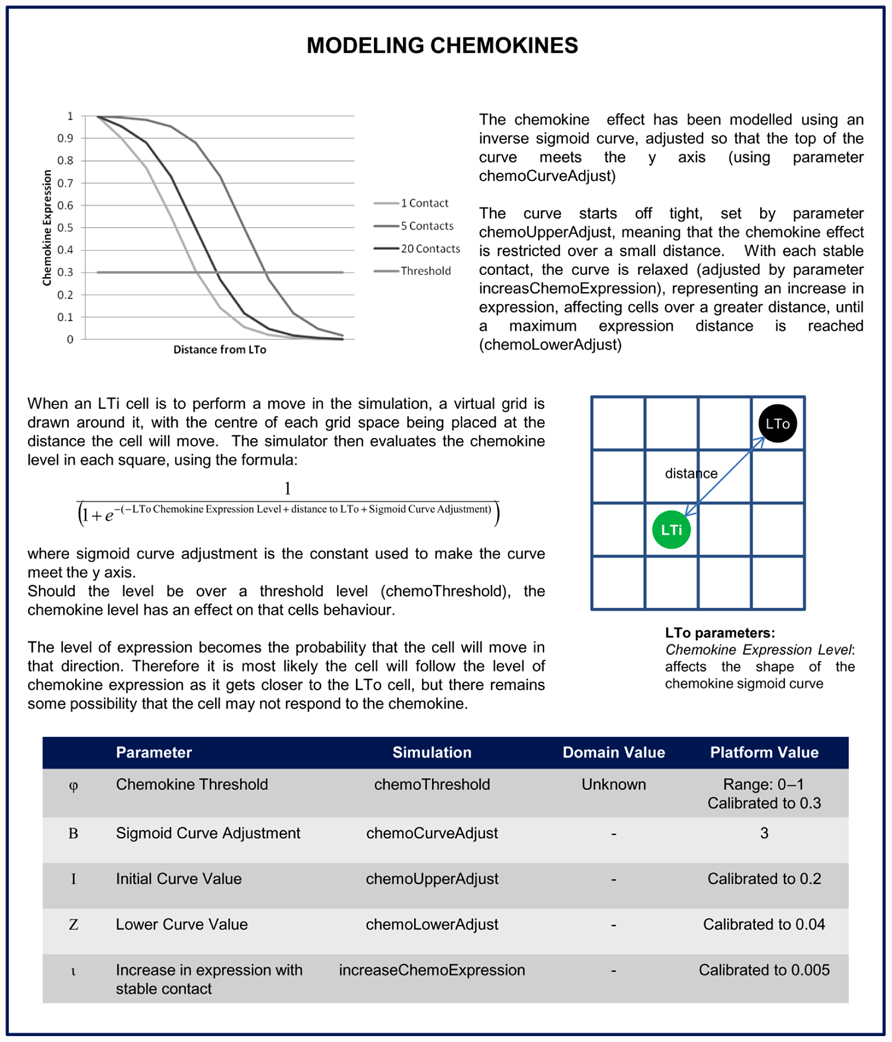
FIGURE 5. Description of how chemokines are included in the platform model. This details mechanism of chemokine diffusion in the model from the LTo cell, and how the direction of LTi cell movement is based on a calculation of local chemokine levels.
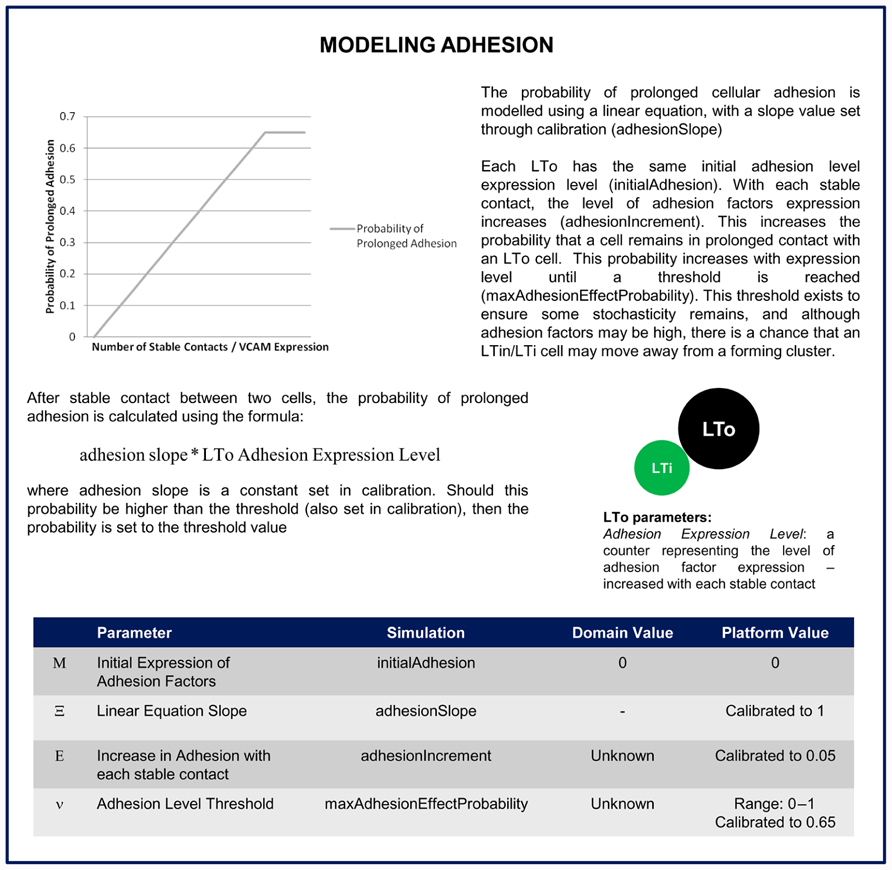
FIGURE 6. Description of how the adhesion factors are included in the platform model. This details how the LTo cell increases adhesion factor expression with each stable contact and the probability that a LTi or LTin cell remains in prolonged contact with an LTo cell is determined in the simulator.
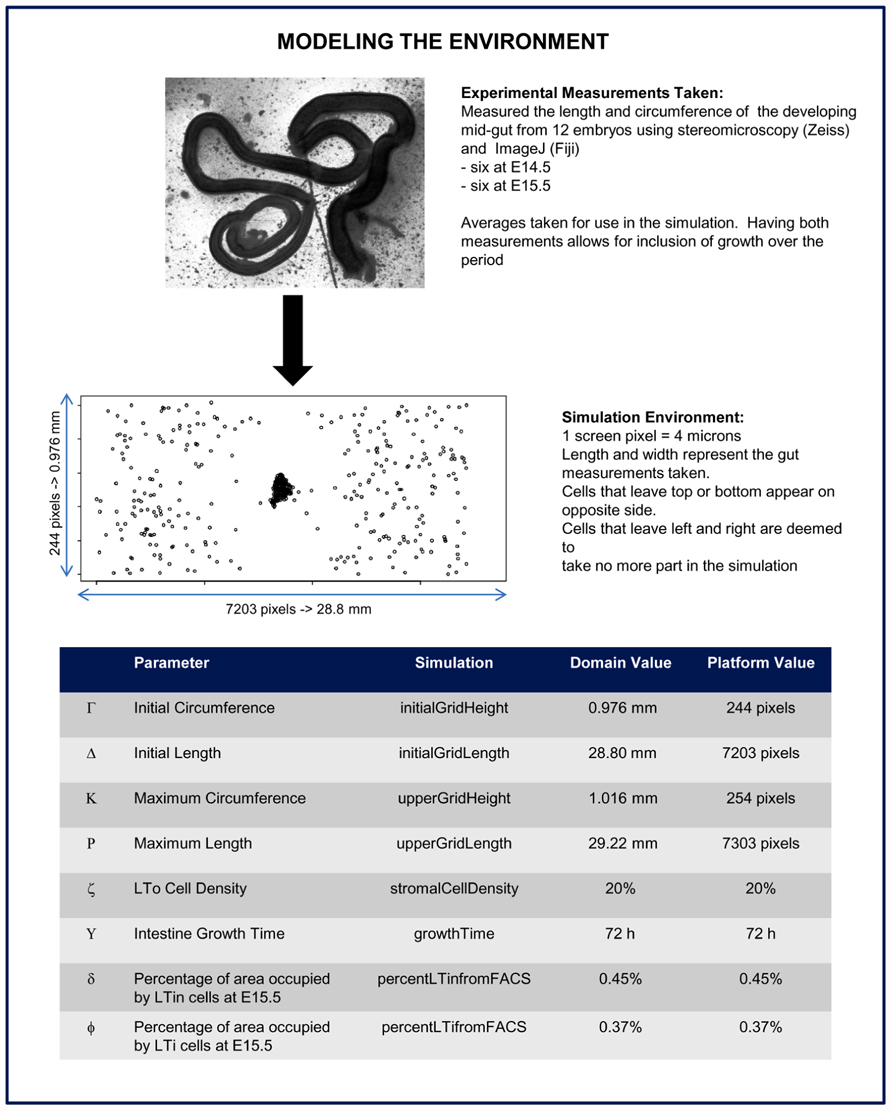
One of the strengths of agent-based simulation is the ability to consider spatial elements of the biological environment. Thus, it is critical to accurately represent the fetal intestine tract in which our agents interact, and understand how this environment changes during the time-frame of the simulation. Images were taken of the developing mid-gut from twelve embryos, six at E14.5 and six at E15.5, using stereomicroscopy (Zeiss). Measurements of the length and circumference of each were then taken using ImageJ (Fiji). Taking measurements at different time-points ensures the dynamic nature of the developing tract (model environment) was captured. Using these measurements, and known cell sizes (Veiga-Fernandes et al., 2007) a virtual environment was created which accurately represents that seen ex vivo (Figure 7), and a scale set where 1 pixel in our graphical simulation will represent four microns. The platform model also specifies how the user interacts with the simulator (e.g., graphical interface representing the environment and the control panel), and specifies how data can be extracted for further analysis (Andrews et al., 2011; Table 4).
Simulator
The computer simulation was created from the specification in the platform model. The Java-based MASON simulation environment, a cross-platform toolkit for the creation of multi-agent simulations was used (Luke, 2005). Each agent (cell) type is created as a Java class, with state transitions encoded to match those specified on the platform model. MASON simulations work in steps, where each active agent performs the behavior determined by its current state within each step. Such a feature allows for the inclusion of time in the simulation. By default, one simulation time-step represents 1 min of developmental time. A copy of the Java code for the simulation and the simulator is accessible online at http://www.cs.york.ac.uk/immunesims/frontiers.
Simulator Calibration Using Experimental Data
To identify values for parameters identified in the domain and platform models, numerical values were determined from the literature and unpublished experimental data However, obtaining a numerical value for many parameters is not currently possible due to technical experimental limitations. Calibration is the process by which values are obtained for any parameters for which a numerical value is unknown. The objective is to ensure that the simulator produces cellular behavior that is statistically similar to that observed in previously published studies (Veiga-Fernandes et al., 2007; Patel et al., 2012).
The simulation has been calibrated against the observed behavior of cells close to a PP versus those observed prior to patch formation (Patel et al., 2012). In this case, there are six parameters for which the value is uncertain: (a) probability at which an LTin/LTi cell will form a stable bind with an LTo cell upon contact, (b) the initial level of chemokine expression upon LTo differentiation, (c) the limit on chemokine expression level, (d) the level of chemokine required in the environment to induce LTi cell chemotaxis (e) the level at which adhesion factors are expressed with each stable contact, and (f) the probability that the level of adhesion factors expressed on the surface of an LTo cell will restrain LTin/LTi cell movement. Thus, values for these parameters needed to be established that lead to simulation outcomes of cellular behavior that does not differ from those observed ex vivo. To test for statistical similarity between the distributions seen experimentally and those observed in simulation, the non-parametric Mann–Whitney U test has been used, as the results will not be normally distributed. Values for all six parameters were established through a structured trial and error approach, and lead to cellular behavior that is statistically similar to that observed (Patel et al., 2012).
Reducing Uncertainty in Simulation Results
Prior to performing any analysis of simulation results, it is important to establish the number of replicate runs necessary (n) to produce a robust representative result that reflects the analysis being performed, and is not heavily influenced by uncertainty arising from inherent stochasticity within the simulation. This calculation is a pre-requisite in understanding the simulator’s sensitivity to parameter perturbation. Such a judgment cannot be made if the effect of the underlying inherent stochasticity is not appreciated. This was achieved using a technique developed by Read et al. (2012), which examines the relationship between the number of runs performed and the effect of such uncertainty for a given set of parameters, establishing an n to use in all subsequent analyses.
To establish n, a number of replicate run sizes were chosen (1, 5, 50, 100, 300, 500, and 800). Taking the sample size of five as an example, twenty simulation result sets were obtained, with each of the twenty sets containing the results from five simulation runs. From the results of each simulation run, medians are calculated for each of the cell behavior output measures captured. These are collated to form a set of medians for each of the 20 subsets. The medians from each set are compared to the first set using the Vargha–Delaney A-Test (Vargha and Delaney, 2000). The test compares the two distributions and returns a value between 0 and 1.0, with a result of 0.5 indicating no difference, and results above 0.71 and below 0.29 indicating a statistically significant difference between the two sets. To achieve a representative result, there should be no statistical difference in all 20 comparisons. In this case, this was achieved when each of the 20 subsets contained the results from 500 simulation runs (Figure 8). Therefore, n =500 was used for the remaining analyses.
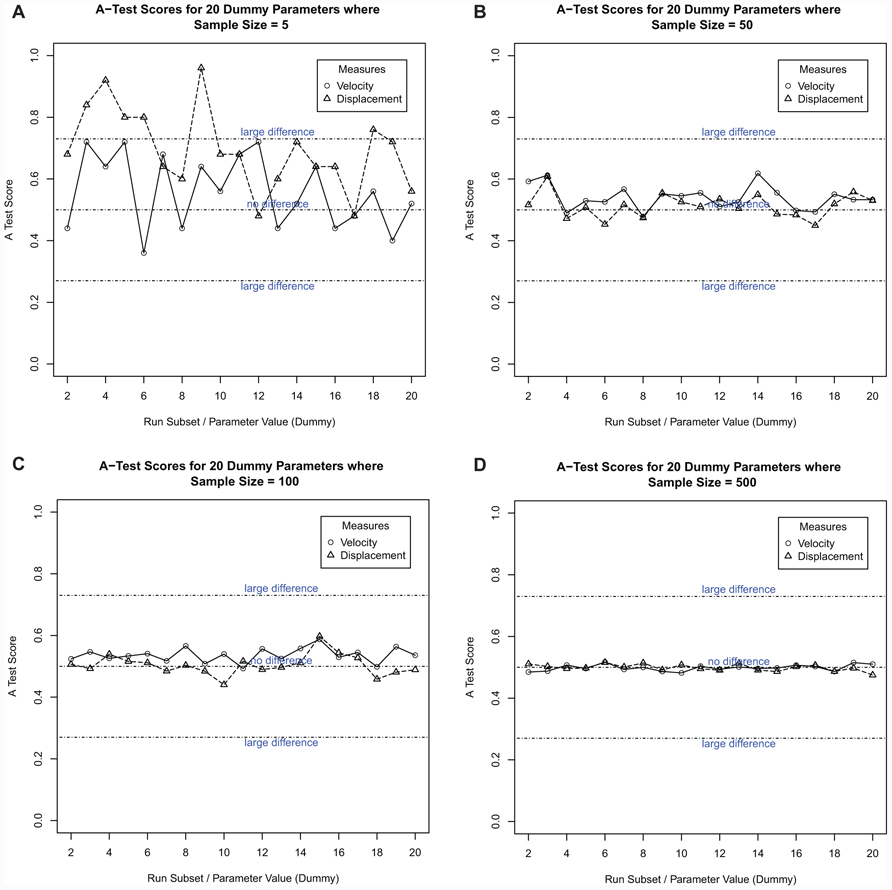
FIGURE 8. Robustness analysis to determine the number of replicate simulation runs necessary to produce a robust, representative result. The twenty result subsets are listed along the x axis, with the Vargha–Delaney A-Test score on the y axis. The subsets are labeled as “dummy parameter” sets as no parameters are being changed. The plot shows the comparison scores for both cell behavior output measures: cell velocity and cell displacement. Each of the 20 result subsets contains a number of simulation run results. From these, a set of results is generated containing the median of each cell output measure for each simulation run in the set. Each set of medians is then compared to the first set using the Vargha–Delaney A-Test. This figure shows the results for four of the sample sizes used. (A) 5, (B) 50, (C) 100, and (D) 500.
In Silico Experimentation
Simulations have been performed to test the robustness of the model to determine if PP emerge replicating gene knockout and over expression experiments published in the literature and to determine if key features of the biology are observed in the in silico model. Comparison with the observed biology was made by comparing snapshots of the simulated environment post simulation run to observed phenotypes using antibody staining of LTi and LTo cells. To simulate gene knockouts, Boolean parameters indicating the inclusion of the relevant component are set to false. To simulate changes to level of expression, values for relevant parameters were adjusted. The simulation has been run under the following conditions from the established literature (Figure 9): (Figure 9A) Normal parameter setting (control wild type mice), (Figure 9B) RET deficiency (RET– / – mice; Veiga-Fernandes et al., 2007), (Figure 9C) chemokine knockout (CXCL13– / –, CCL19/21– / – mice; Luther et al., 2003), (Figure 9D) no LTin cells (RORγ– / – mice; Eberl et al., 2004), (Figure 9E) doubling number of LTi cells (IL-7Tg mice; Meier et al., 2007). Consistent with established results no PP form in either RET, chemokine or LTi deficient mice (Figures 9B–D). In mice with increased numbers of LTi cells in the simulation (Figure 9E), more, larger PPs were observed to develop consistent with the published results.

FIGURE 9. Images of typical simulation runs at a time-point representing 72 h of PP development. Conditions have been created which replicate known phenotypes from mice: (A) Control, (B) RET– / – LTin cells (simulated knockout), (C) Chemokine deficiency (simulated CXCL13, CCL19/21 knockout), (D) LTin-deficient mice (simulated RORγ– / –mice), (E) doubling number of LTi cells (IL-7Tg mice).
Parameter Exploration in the Model
Through experimentation, literature research, and calibration, a set of parameter values has been established from which the simulator reproduces the emergent cellular behavior observed ex vivo. However, it is important to establish how sensitive the simulator output is to alteration in these values. Uncertainty and sensitivity analysis techniques can be used to quantify the effect perturbing parameter values has on simulator response, providing an insight into the sensitivity of both known biological parameter values and parameters for which a value has been established through calibration. In this case we consider the inherent epistemic uncertainty arising from parameters in the latter category, where a value is not currently known, and demonstrate statistical techniques that can be used to quantify this uncertainty. However, a full exploration of the experimentally verified parameters could also be elucidated using the same techniques.
Using the calibrated simulator, the impact on cell behavior has been investigated when the chemokine parameters are modified. These parameters are: the threshold at which chemokine expression in the environment begins to influence cell migration (chemoThreshold); the level of chemokine expressed with each LTi/LTo contact; and the distance from the LTo cell over which the chemokine can have an effect (set by parameters chemoLowerLinearAdjust and chemoUpperLinearAdjust, detailed in Figure 5). We also examine the effect of changing the parameter which specifies the probability a stable bind occurs where a hematopoietic cell (LTin/LTi) comes into contact with a stromal cell (LTo) (thresholdBindProbability). Impact on simulation response was determined using two techniques, one-a-time analysis and Latin hypercube sampling (LHS) and analysis. In one-a-time analysis, the subset of simulation parameters is examined to determine how robust the simulation is to a change in input (Read et al., 2012). Taking each in turn, the parameter is perturbed within a set range of values, with all other parameters remaining constant. For each parameter value, 500 simulation runs were performed as established through robustness analysis. The median of each cell behavior measure is calculated for the 500 runs, producing a median distribution set for each parameter value. This set of medians is compared to that gained from 500 runs of the baseline simulation, using the Vargha–Delaney A-Test (Vargha and Delaney, 2000). This determines if a change in the value of that particular component has led to behavior which is significantly different to that seen in the calibrated result.
Latin hypercube sampling and analysis, a global sensitivity analysis technique, has been performed in an attempt to identify any compound affects which become apparent when two or more of the components are varied simultaneously (Marino et al., 2008; Read et al., 2012). A range of potential values has been set for each parameter of interest, and the parameter space sampled using a LHS approach (Saltelli et al., 2000). LHS was used to produce 500 parameter value sets, with the value of each parameter falling within the set range. For each set, the simulation was run 500 times and the relevant cell behavior medians calculated. Taking each parameter of interest in turn, the sample sets were ordered by the value assigned to that parameter. A scatter plot was then generated, for each cell behavior measure, showing the parameter value in that run against the simulation result. This gives a visual representation of any correlation between the value of that cell behavior measure and the value assigned to that parameter. To gain a statistical indication of an existing correlation, the Partial Rank Correlation Coefficient was also calculated.
Determining when a Parameter Becomes Influential in the Simulation
To analyze the time-point at which a factor in the model begins to have an influence on the emergent behavior, the point at which the chemokine parameter value has a notable effect on cellular behavior (LTi cells away from a forming cluster) was determined. The simulation was run to simulate 48 h in PP development, with LTi cell behavior tracked for an hour at 12 h intervals. Five hundred simulation runs were performed, with medians recorded for each cell tracking measure for the respective run. The median results for hours 24, 36, and 48 were then compared with those from the calibrated baseline (12 h) using the Vargha–Delaney A-Test (Vargha and Delaney, 2000), to determine if there is a significant difference in cell behavior over time. All statistical analysis was performed using R.
Results
Exploring the Simulation Components Through Sensitivity Analysis
To demonstrate the use of sensitivity analysis techniques in exploration of the model, the values of the chemokine parameters, where the values are uncertain, were perturbed and the effect on the overall result analyzed.
One-a-Time Analysis
One-a-time analysis was used to determine the effect each parameter has on the cell behavior captured in the model (Figure 10). This provides an indication of how robust the simulation is to changes in parameter value, and which parameters have the greatest impact on cell behavior. To determine the effect of a parameter value perturbation, the simulation results for each value assigned to that parameter have been compared against simulation results known to be statistically similar to cell behavior seen ex vivo using the Vargha–Delaney A-Test (Vargha and Delaney, 2000). This analysis indicates that perturbing the expression and threshold level of chemokines (Figures 10A–C) at an early time-point (initiation of patch formation) has no appreciable effect on the behavior of cells in the vicinity of a forming patch. All potential values for the parameter chemoThreshold, which controls a cells response to a level of chemokine, have been explored, through never responding to presence within the environment to always responding. Although the full range has been examined, there is no significant change in cell behavior for any value in comparison to calibration results. Thus, early in PP formation the model predicts that chemokines are unlikely to be the key force driving the patch formation.
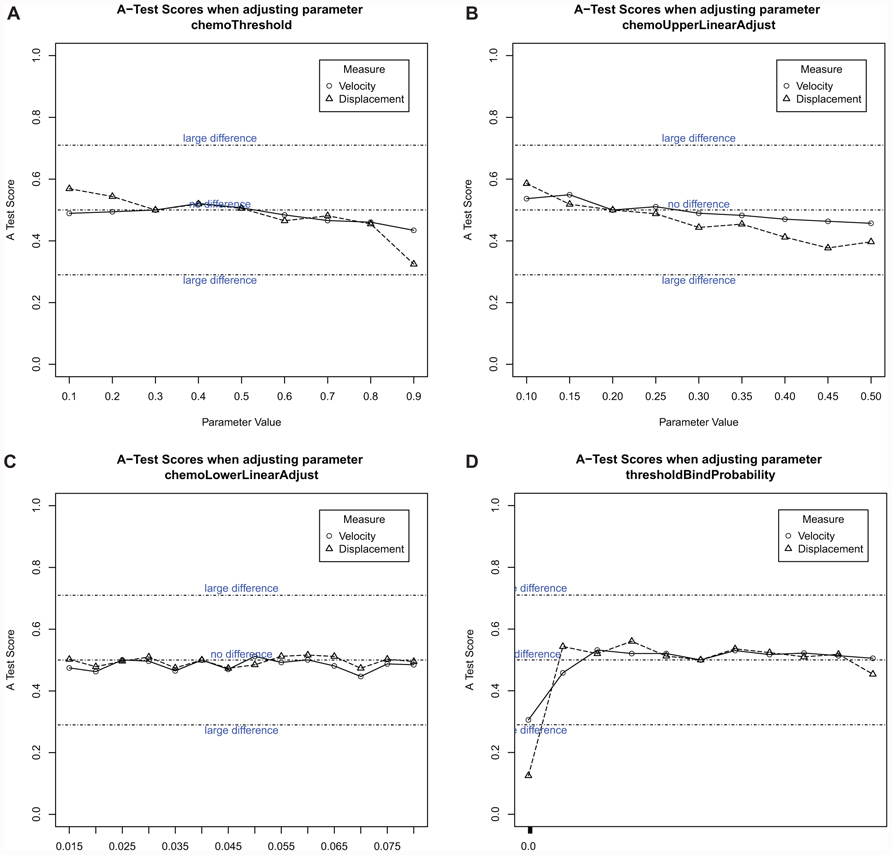
FIGURE 10. Robustness analysis of simulation use a one-parameter-at-a-time approach, which perturbs the value of just one parameter, leaving the remaining values constant in the simulation. This provides an indication of the effect perturbing each individual parameter has on simulation output. Cell behavior was compared to the calibrated baseline results using the Vargha–Delaney A-Test, which determines if two distributions statistically differ. Plots of A test score vs parameter values was plotted with the change from observed cellular behavior varies significantly from the simulation. (A) Chemokine threshold, (B) initial expression level of chemokine, (C) maximum expression level of chemokine, (D) probability of stable bind when two cells are in contact. N = 500.
Latin Hypercube Sampling and Analysis
In contrast to one-a-time analysis, LHS perturbs the values of all parameters in the subset simultaneously. Using this approach, any compound effects between parameters which do not become apparent through perturbing each individually can be identified. Analysis of these parameters (Figure 11) at the earliest phase of patch formation (12–13 h) again indicates that the chemokine parameter values are not influential at this phase in PP development. LHS analysis of the threshold value at which a chemokine begins to affect the velocity of cells close to a developing PP shows no trend in the simulation (Figure 11A). This is apparent both visually and from the calculated Partial Rank Correlation Coefficient (PRCC) values (in the header of each graph). The PRCC value gives an indication of an existing correlation between a change in output measure with a change in the input measure. However, a small trend does become apparent for the displacement output measure when the threshold value is set to its extreme value, where a cell always responds to any level of chemokine in the environment.
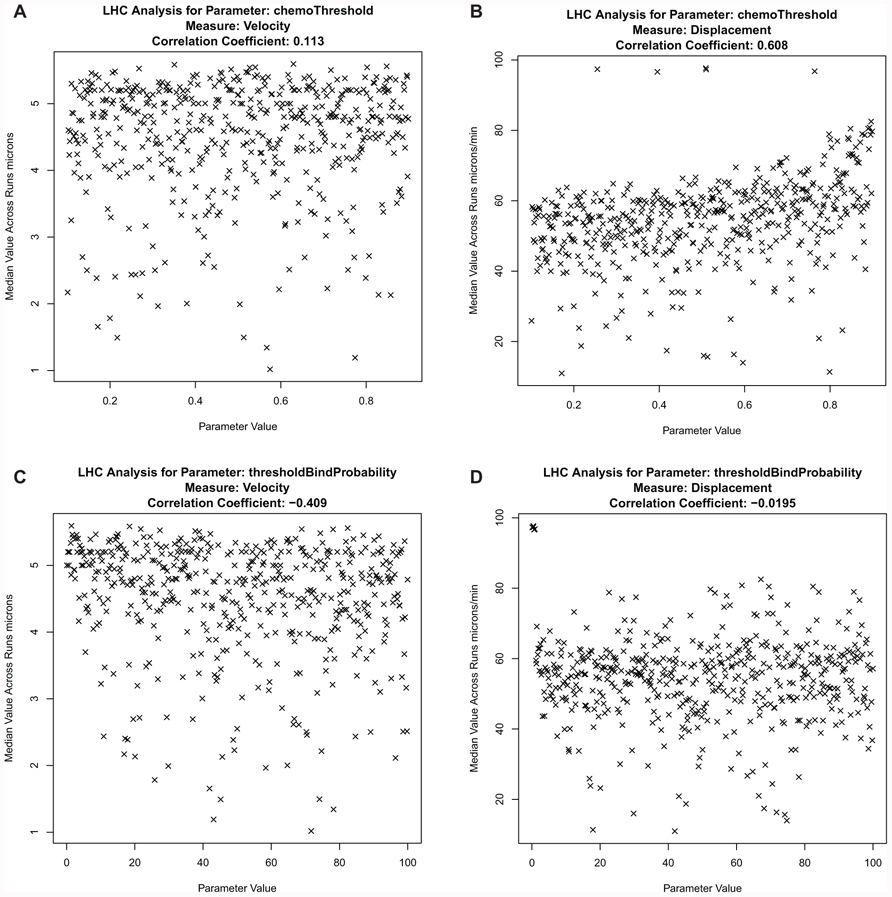
FIGURE 11. Parameter analysis, using a Latin hypercube approach, to determine the influence of parameters on simulation output measures. (A) chemokine threshold vs. velocity, (B) chemokine threshold vs displacement, (C) probability of stable bind when two cells are in contact vs velocity, and (D) probability of stable bind when two cells are in contact vs displacement. N = 500.
Investigating when a Component Becomes Influential
Chemokines have been shown to have an essential role both in vivo (Luther et al., 2003) and in silico (Figure 9C), however using both one-a-time and LHS analysis the parameter values chemoThreshold, chemoLowerLinearAdjust, and chemoUpperLinearAdjust were predicted not to have a significant affect in simulation outcome (Figures 8A and 10A). Thus to determine if and when these parameters effect cellular behavior, the simulator for was run for 48 h of simulated time (Figure 12). For each time-point, 500 sets of cell tracking data were obtained (500 runs of the simulation) with each containing a minimum of 30 tracked cells. The resultant distribution of the 500 medians for each of the 24, 36, and 48 h time-points was compared to that generated at the 12 h time-point (the calibrated baseline). Our analysis predicts that these parameters do not start to significantly change the behavior of cells until after 36 h into the simulation, a finding that can possibly be tested on a biological set-up.
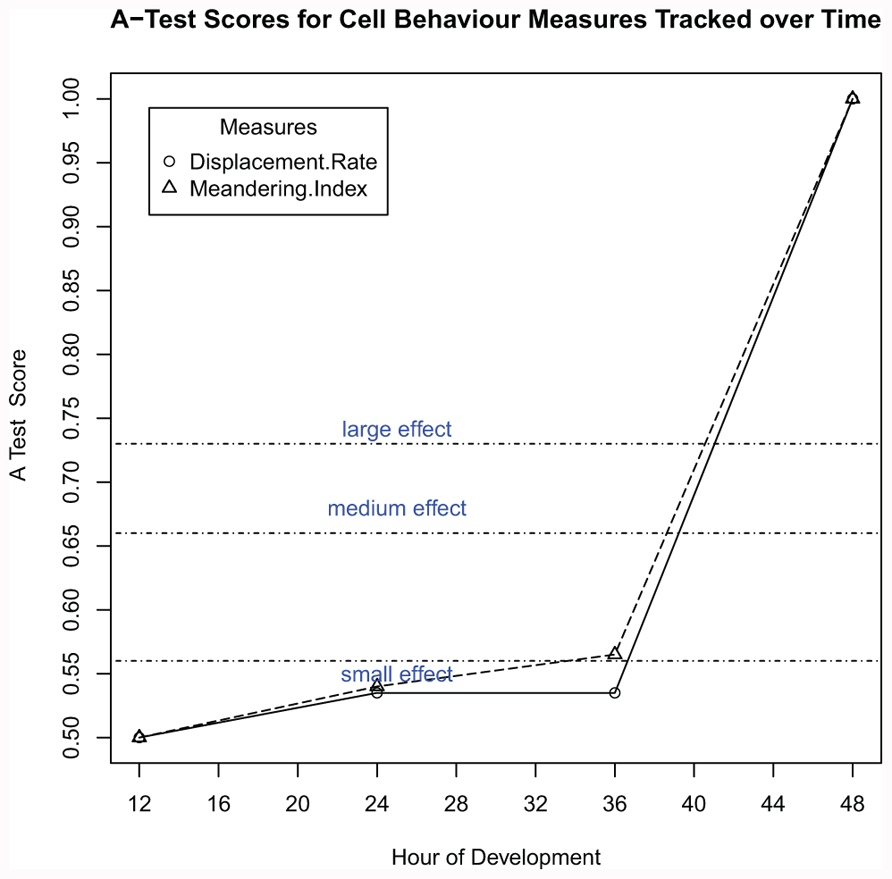
FIGURE 12. Computer simulation to predict when chemokine expression level has a significant effect on cell behavior. For 24, 36, and 48 h time-points, datasets have been generated which record the displacement of each cell in the system for a sixty minute period after that time-point. Each set of results is then compared to the simulation baseline cell behavior at 12 h using the Vargha–Delaney A-Test.
Discussion
Agent-based modeling is an important methodology for understanding complex biological systems. The ability to model time-variant stochastic systems, coupled with the environment in which the biological event occurs makes this approach highly applicable to modeling cellular function and interactions in lymphoid tissue development and function. This paper has described the process involved for the development of a robust simulation model, the application of key principles from systems engineering to translate biological understanding (the domain) into an unbiased simulator where key aspects of PP formation emerge from the model. Critically, the simulation has shown that the model faithfully recapitulates the biology leading to the stochastic formation of PPs. In fact for simulations of mice deficient in known regulatory factors of PP development (chemokines, RET tyrosine kinase, and adhesion molecules) the expected “phenotype” was observed in silico.
Creating a Framework to Utilize Simulation Modeling to Understanding Immune System Function and Development
The inherent complexity and interconnectivity of in vivo physiology has led us to develop computational simulations of an immunological process to provide novel insights into that process. Although this methodology is well established in physics, chemistry, ecology, and structural biology, the use of computational approaches has been limited due to the highly stochastic and interconnected nature of immune responses. Although mathematical ODE models are a potent methodology for understanding how populations behave, they are limited in their ability to describe complex phenomena, like lymphoid tissue formation, that emerges during immune development through interactions between individual cells. Thus, we have demonstrated a simplified non-mathematical approach that allows easy translation of the biology into a set of models that are easy to understand and interact with. Using these models in the creation of the simulator ensures the production of a tool where the scope and encapsulation of the biological understanding is clear, thus simulation results can provide meaningful insight into molecular mechanisms driving the biological process. The CoSMoS modeling process (Andrews et al., 2010) has been developed to make computational simulation accessible through breaking down the process into well documented steps that permit immunologists to develop models, understand how the agents interact and query the validity of the model. In the first step of the process the biological entity can be described using UML to create a domain model that accurately represents the biological system and the interactions between the different cell types and the environment during the process: in the PP domain model we succinctly document the key cell types (LTi, LTin, LTo), the different cellular states during PP development, and cellular interactions that are known to drive PP formation. Using the domain model, a platform model was created, again using UML, to represent the modeling environment and detail how individual cells interact and change state within the model environment. This platform model used to specify the agent-based computational model which is implemented in the Java programming language. By creating a separate model on which the simulation is generated, crucially cellular behaviors that must emerge through interactions between agents in the model are removed, and not coded into the model. By using an open source Java-based modeling environment and open source statistical tools, the technological barriers to create and utilize a computational model have been kept to a minimum. The PP simulator, the documented Java source code, all tools created for the visualization of PP formation and statistical analysis of the model are freely available for download from the web (http://www.cs.york.ac.uk/immunesims/frontiers). Making the model freely available makes it possible for immunologists to engage with the model for their own research and provide critical feedback on the future iterations of the simulator, as demonstrated in Figure 1A. Utilizing this framework it is possible to rapidly develop meaningful computational simulations of immunological processes.
Pairing Experimentation and Computational Modeling
Innate lymphoid cells have recently been shown to have essential roles in both the development of lymphoid tissue and normal lymphoid and epithelial tissue function. Bioinformatics approaches have provided novel insights into pathways that regulate cellular function; however they are limited in their capacity to understand how intracellular signals drive process during a complex stochastic process. Although knockout mice provide key insights to the functional requirement for particular pathways they often fail to capture how, when and where the pathways regulate the biological process. Although chemokines have been previously been shown to be essential in the formation of patches (verified in the model), the timing of chemokine mediated effects during PP formation are unknown. Utilizing the PP simulator and statistical analysis techniques, the parameters that control chemokine function in the model have been shown, surprisingly, to have no effect during early stages of PP development. By sampling the model over time it was possible to show that the effect of chemokines on LTi cell behavior was only found to be statistically significant 36 h into the simulation. This is consistent with biological observations that the behavior of LTi cells at E15.5, 24 h post initiation of LTi/LTin infiltration into the fetal mid-gut, the movement of all observed cells was a normal random walk (Veiga-Fernandes et al., 2007). Through using simulation we have shown that predictive models can be used to integrate mechanisms of when signaling pathways start to affect the outcome of stochastic processes, providing new insights into mechanisms driving immune development and function.
Insights that In Silico, Model Might Provide to Understanding PP Development
The utilization of a calibrated and verified computational model where behaviors emerge provides the potential to use simulation results to generate new hypothesis that can then be tested in vivo. In particular, the simulator provides a unique tool to determine potential factors and molecular mechanisms driving the initiation of PP anlagen formation and mechanisms controlling the number and location of PP development. The pairing of experimental data sets with the computational approach described in this paper has the potential to accelerate the discovery process through providing new insights into the mechanisms driving immune system development and function.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgment
The authors would like to thank Mark Read for his assistance with the statistical analysis of the model. Paul Andrews is funded by EPSRC grant EP/I005943/1 “Resilient Futures.” Jon Timmis is part funded by the Royal Society. Henrique Veiga-Fernandes is funded by Fundação para a Ciência e Tecnologia (PTDC/SAU-MII/100016/2008), Portugal, European Molecular Biology Organisation (Project 1648) and European Research Council (Project 207057). Funding for Mark Coles comes from grants from the Human Frontiers Science Program (RGP0006/2009) and the Medical Research Council (G0601156). Kieran Alden is funded by the BBSRC and EPSRC.
References
Adachi, S., Yoshida, H., Kataoka, H., and Nishikawa, S. I. (1997). Three distinctive steps in Peyer’s patch formation of murine embryo. Int. Immunol. 9, 507–514.
Andrews, P. S., Polack, F., Sampson, A. T., Timmis, J., Scott, L., and Coles, M. (2008). “Simulating biology: towards understanding what the simulation shows,” in Proceedings of the 2008 Workshop on Complex Systems Modelling and Simulation, eds S. Stepney, F. Polack, and P. Welch (UK: Luniver Press), 93–123.
Andrews, P. S., Polack, F. A. C., Sampson, A. T., Stepney, S., and Timmis, J. (2010). The CoSMoS process, Version 0.1: a process for the modelling and simulation of complex systems. Technical Report, YCS-2010-453, Department of Computer Science, University of York, 1–40.
Andrews, P. S., Stepney, S., Hoverd, T., Polack, F. A. C., Sampson, A. T., and Timmis, J. (2011). “CoSMoS process, models, and metamodels,” in CoSMoS 2011: Proceedings of the 2011 Workshop on Complex Systems Modelling and Simulation, eds S. Stepney, P. H. Welch, P. S. Andrews, and C. G. Ritson (UK: Luniver Press), 1–14.
Bersini, H., and Carneiro, J. (2006). “Immune system modeling: The OO Way,” in ICARIS 2006, Lecture Notes Computer Science, 4163, eds H. Bersini and J. Carneiro (Heidelberg: Springer), 150–163.
Chakraborty, A. K., and Das, J. (2010). Pairing computation with experimentation: a powerful coupling for understanding T cell signalling. Nat. Rev. Immunol. 10, 59–71.
Cornes, J. S. (1965). Number, size, and distribution of Peyer’s patches in the human small intestine: Part I The development of Peyer’s patches. Gut 6, 225–229.
Eberl, G., Marmon, S., Sunshine, M.-J., Rennert, P. D., Choi, Y., and Littman, D. R. (2004). An essential function for the nuclear receptor ROR gamma in the generation of fetal lymphoid tissue inducer cells. Nat. Immun. 5, 64–73.
Figge, M. T., Garin, A., Gunzer, M., Kosco-Vilbois, M., Toellner, K.-M., and Meyer-Hermann, M. (2008). Deriving a germinal center lymphocyte migration model from two-photon data. J. Exper. Med. 205, 3019–3029.
Fukuyama, S., and Kiyono, H. (2007). Neuroregulator RET initiates Peyer’s Patch tissue genesis. Immunity 26, 393–395.
Germain, R. N., Meier-schellersheim, M., Nita-lazar, A., and Fraser, I. D. C. (2011). Systems biology in immunology: a computational modeling perspective. Annu. Rev. Immunol. 29, 527–585.
Guo, Z., and Tay, J. C. (2005). “A comparative study on modeling strategies for immune system dynamics under HIV-1 infection,” in Artificial Immune Systems, 4th International Conference, ICARIS 2005, Albeta, Canada, Lecture Notes Computer Science 3627 (Heidelberg: Springer), 220–233.
Jacob, C., Litorco, J., and Lee, L. (2004). “Immunity through Swarms: agent-based simulations of the human immune system,” in Artificial Immune Systems, International Conference, ICARIS 2004 Proceedings. Lecture Notes in Computer Science 3239, eds G. Nicosia, V. Cutello, P. Bentley, and J. Timmis (Heidelberg: Springer), 400–412.
Jung, C., Hugot, J.-P., and Barreau, F. (2010). Peyer’s patches: the immune sensors of the intestine. Int. J. Inflam. 823710.
Lagreca, M. C., de Almeida, R. M. C., and dos Santos, R. M. Z. (2001). A dynamical model for the immune repertoire. Physica A 289, 191–207.
Luther, S. A., Ansel, K. M., and Cyster, J. G. (2003). Overlapping roles of CXCL13, interleukin 7 receptor alpha, and CCR7 ligands in lymph node development. J. Exp. Med. 197, 1191–1198.
Marino, S., Hogue, I. B., Ray, C. J., and Kirschner, D. E. (2008). A methodology for performing global uncertainty and sensitivity analysis in systems biology. J. Theor. Biol. 254, 178–196.
Meier, D., Bornmann, C., Chappaz, S., Schmutz, S., Otten, L. A., Ceredig, R., Acha-Orbea, H., and Finke, D. (2007). Ectopic lymphoid-organ development occurs through interleukin 7-mediated enhanced survival of lymphoid-tissue-inducer cells. Immunity 26, 643–654.
Patel, A., Harker, N., Moreira-Santos, L., Ferreira, M., Alden, K., Timmis, J., Foster, K., Garefalaki, A., Pachnis, P., Andrews, P. S., Enomoto, H., Milbrandt, J., Pachnis, V., Coles, M., Kioussis, D., and Veiga-Fernandes, H. (2012). Differential RET signaling responses orchestrate lymphoid and nervous enteric system development. Sci. Signal (in press).
van de Pavert, S. A., and Mebius, R. E. (2010). New insights into the development of lymphoid tissues. Nat. Rev. Immunol. 10, 664–674.
Randall, T. D., Carragher, D. M., and Rangel-Moreno, J. (2008). Development of secondary lymphoid organs. Annu. Rev. Immunol 26, 627–650.
Read, M., Andrews, P. S., Timmis, J., and Kumar, V. (2012). Techniques for grounding agent-based simulations in the real domain: a case study in experimental autoimmune encephalomyelitis. Math. Comput. Model. Dyn. Syst. 18, 67–86.
Read, M., Timmis, J., Andrews, P. S., and Kumar, V. (2009). “Using UML to model EAE and its regulatory network,” in ‘09 Proceedings of the 8th International Conference on Artificial Immune Systems, Lecturer Notes Computer Science 5666 (Berlin: Springer-Verlag) 4–6.
Saltelli, A., Chan, K., and Scott, E. M. (2000). “Sensitivity Analysis,” in Wiley Series in Probability and Statistics Wiley. NY: John Wiley & Sons, Inc.
Sieburg, H. B., McCutchan, J. A., Clay, O. K., Cabalerro, L., and Ostlund, J. J. (1990). Simulation of HIV infection in artificial immune systems. Physica D 45, 208–227.
Stafford, M. A., Corey, L., Cao, Y., Daar, E. S., Ho, D. D., and Perelson, A. S. (2000). Modeling plasma virus concentration during primary HIV infection. J. Theor. Biol. 203, 285–301.
Vargha, A., and Delaney, H. D. (2000). A critique and improvement of the CL common language effect size statistics of McGraw and Wong. J. Educ. Behav. Stat. 25, 101–132.
Keywords: agent-based modeling, computational modeling, development, lymphoid tissue inducing cells, lymphoid tissue organizer cells, Peyer’s patches, sensitivity analysis
Citation: Alden K, Timmis J, Andrews PS, Veiga-Fernandes H and Coles MC (2012) Pairing experimentation and computational modeling to understand the role of tissue inducer cells in the development of lymphoid organs. Front. Immun. 3:172. doi: 10.3389/fimmu.2012.00172
Received: 24 January 2012; Paper pending published: 12 March 2012;
Accepted: 07 June 2012; Published online: 18 July 2012.
Edited by:
Brigitta Stockinger, MRC National Institute for Medical Research, UKReviewed by:
Jorge Caamano, University of Birmingham, UKAndrew Yates, Albert Einstein College of Medicine, USA
Robin Callard, University College London, UK
Copyright: © 2012 Alden, Timmis, Andrews, Veiga-Fernandes and Coles. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: Mark C. Coles, The Centre for Immunology and Infection, University of York, Heslington, York, YO10 5DD, UK. e-mail:bWFyay5jb2xlc0B5b3JrLmFjLnVr

 Jon Timmis2,3
Jon Timmis2,3