- 1School of Mathematics and Statistics, University of Sydney, Sydney, NSW, Australia
- 2Department of Immuno-Oncology, Beckman Research Institute, City of Hope, Duarte, CA, United States
Therapeutic vaccines can elicit tumor-specific cytotoxic T lymphocytes (CTLs), but durable reductions in tumor burden require vaccines that stimulate high-avidity CTLs. Recent advances in immunotherapy responses have led to renewed interest in vaccine approaches, including dendritic cell vaccine strategies. However, dendritic cell requirements for vaccines that generate potent anti-tumor T-cell responses are unclear. Here we use mathematical modeling to show that, counterintuitively, increasing levels of immature dendritic cells may lead to selective expansion of high-avidity CTLs. This finding is in contrast with traditional dendritic cell vaccine approaches that have sought to harness ex vivo generated mature dendritic cells. We show that the injection of vaccine antigens in the context of increased numbers of immature dendritic cells results in a decreased overall peptide:MHC complex load that favors high-avidity CTL activation and expansion. Overall, our results provide a firm basis for further development of this approach, both alone and in combination with other immunotherapies such as checkpoint blockade.
Introduction
In principle, the immune system can eliminate cancer cells by the activation and expansion of cancer-specific cytotoxic T lymphocytes (CTLs). Immune checkpoint blockade (ICB) immunotherapies, which release T cells from various negative regulatory pathways, have demonstrated impressive clinical successes and have become standard-of-care for many malignancies (1). However, the response to ICB seems to require the pre-existence of anti-tumor T cells (2). Vaccine approaches to generate tumor-specific T cells offer a potential solution towards generating a sufficient anti-tumor T cell response. Dendritic cell (DC) vaccines in particular, offer a means to activate and expand tumor-specific T cells (3). Here we discuss the impact of DC maturation status on vaccine design strategies.
CTLs detect cancer cells by T cell receptor (TCR) recognition of peptides displayed by a major histocompatibility complex (pMHC) on the surface of target cancer cells. Each TCR-pMHC interaction occurs at a particular strength–affinity–with multiple TCR-pMHC interactions occurring for each CTL-target cell interaction. While affinity is a measure of individual TCR-pMHC bonds, avidity is an overall measure of the strength of the TCR-pMHC interaction and as such, depends on the amount of pMHC expressed by antigen presenting cells (4). Importantly, T cell avidity determines the likelihood of successful lysis (5).
Therapeutic peptide vaccines aim to capitalize on the cancer-killing ability of CTLs. Initial results of peptide-based vaccines showed the ability to elicit significant numbers of antigen-specific CTLs, but often lacked measurable clinical successes (6–8). Recent progress in vaccine construction and combinatorial strategies with other immunotherapy agents has shown renewed promise for therapeutic peptide vaccines (3). Our work suggests that the dose and modality of peptide vaccines are key considerations for the design of future clinical interventions.
Early studies of cancer-specific CTLs showed that high-avidity TCRs are necessary to effectively lyse cancer cells that express native antigens at low levels (9). Preferentially selecting for high-avidity CTLs, however, is difficult. Regarding vaccines targeting cancer-associated antigens (CAA), thymic education of CTLs may likely have removed high-avidity T cells from the T-cell repertoire via negative selection (10). As a result, primarily low-avidity CTLs are left to respond to CAA-targeting vaccines. Beyond CAA, recent therapeutic vaccine efforts have focused on targeting somatic mutation-derived neo-antigens (11, 12). As yet, neo-antigen vaccines have largely focused on peptides sought to elicit high affinity TCR responses but have not yet explored the impact of dosage on T-cell repertoire response to the vaccine (13, 14). For both CAA and neo-antigen targeting vaccines, standard dosages typically involve high antigen loads that may non-discriminately favor the expansion of both high and low avidity CTLs. However, lowering the dosage of peptides for vaccination yields sub-therapeutically relevant levels of CTL (15). Together, this highlights the need for further understanding of antigen dosage and context for efficacious vaccine design.
We previously showed that therapeutic vaccine designs were sensitive to DC-associated parameters (16). Given that DCs, which present antigen on their cell surface along with co-stimulatory molecules, facilitate CTL activation, we hypothesized that modulation of DC and peptide dosing could enhance an anti-cancer immune response. We show that by increasing the number of immature DCs (iDCs), the average DC antigen load is lowered, which in turn selects for the expansion of high-avidity CTLs. This observation suggests traditional DC vaccine approaches that intravenously inject ex vivo matured DCs (mDCs) may need to be reconsidered in favor of an injection of iDCs paired with injection of peptide and adjuvant (3, 17). Our work suggests that combinatorial therapy with vaccine antigens and increased immature DCs, either by ex vivo generation or stimulated in vivo, may have efficacy. Thus, our findings suggest an approach that could improve already existing immune-based cancer therapies for increased and more durable clinical responses.
Material and Methods
We previously developed a mathematical model to study how vaccine-induced avidity selection affects tumor clearance (16). This model was calibrated to ex vivo human data from Chung et al. (18) and then validated against data from (19, 20). Here, we extend this model to show that induction of immature DCs may improve current treatments by eliciting high-avidity CTLs. What follows is a brief description of our previously published model. We primarily use parameter estimates from the literature (see Table 1 and the references therein) and estimates generated from our prior analysis of ex vivo human data.
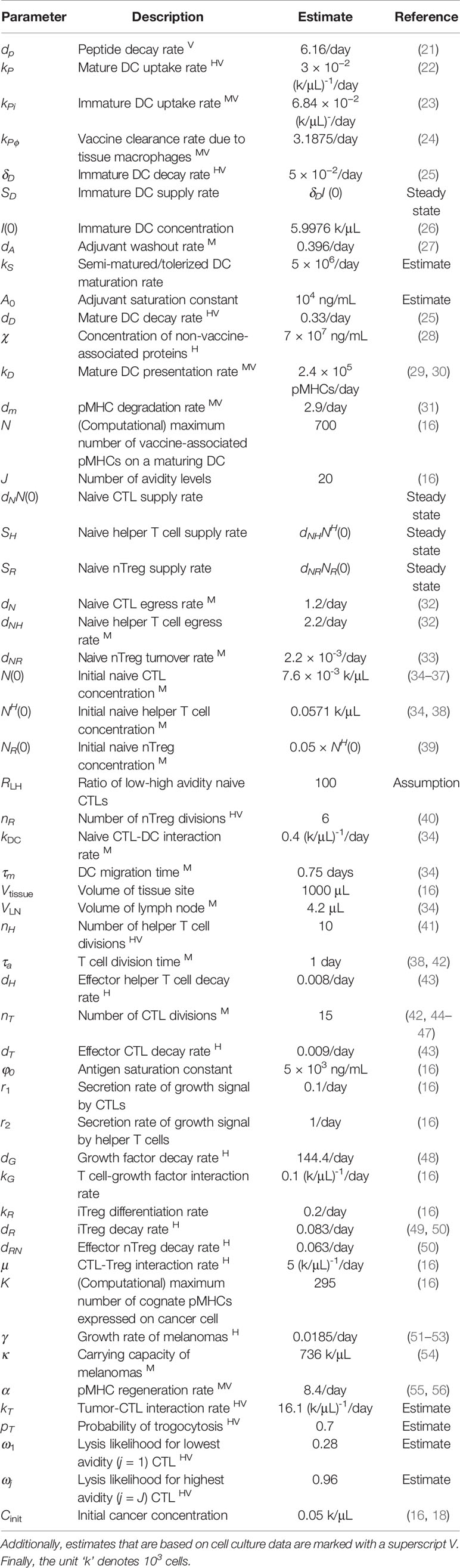
Table 1 Estimates that are characterized by human data are marked with a superscript H, while estimates based on murine data are marked with a superscript M.
Basic Model
The model consists of three major components: the activation and maturation of DCs (Eqs 1–8); the activation and proliferation of T cells (Eqs 9–16); and the lysis and trogocytosis-mediated MHC stripping of cancer cells by effector CTLs (Eqs 23–25). Figure 1 depicts a schematic of these interactions.
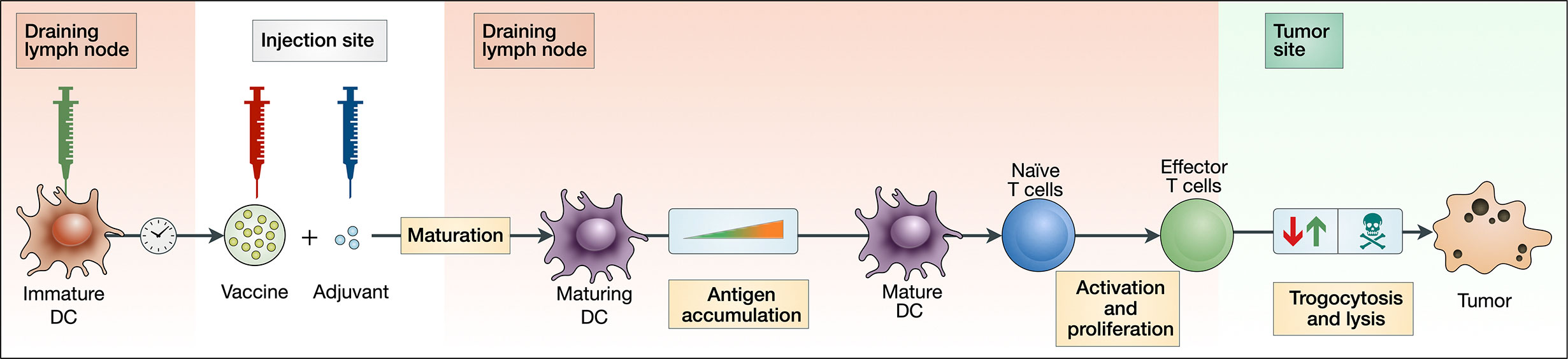
Figure 1 Block diagram depicting key aspects of our theoretical vaccination model. An injection of peptide vaccine is given intramuscularly with adjuvant. Immature DCs are injected intranodally, prompting an accumulation of antigen by maturing DCs. These maturing DCs then migrate and activate naive T cells in the lymph node, which then proliferate into effector T cells. Effector T cells can both strip peptides off the surface of cancer cells via trogocytosis and kill cancer cells.
Dendritic Cells
To model the activation and maturation of DCs at the injection site (the volume of which is Vtissue), we consider several populations: P, the concentration of vaccine peptides; A, the concentration of vaccine adjuvant; I, the concentration of immature DCs; S, the concentration of semi-mature or “tolerizing” DCs; and Mj, the concentration of maturing DCs presenting j vaccine-associated pMHCs, where j can vary between zero and N. In modelling the interactions between these populations, we assume that immature DCs become semi-mature in the presence of peptide antigen, various danger signals, and tissue-derived immunogenic signals (57, 58). Once in this semi-mature state, we assume DC maturation occurs as a result of vaccine adjuvant. DC maturation signals may in turn affect T-cell priming and activation (19). As a simplifying assumption, we assume that the strategy to optimize DC maturation is successful. That is, we do not model the pharmacodynamics of the vaccine adjuvant. Next, we model the interactions between these populations with an ODE system:
Change in vaccine peptide concentration:
Change in adjuvant concentration:
Change in immature DC concentration:
Change in semi-mature/tolerized DC concentration:
Change in mature DC concentration:
In Equation 1, vaccine peptides are injected intramuscularly at rate u(t), decay at rate dp, taken up by immature DCs at rate kPi, taken up by mature DCs at rate kp, and are competitively diminished due to consumption by tissue macrophages at rate kPϕ (note that we do not model these macrophages in our study). Here, we assume that iDCs have a greater antigen uptake rate than mDCs (59, 60). In Equation 2, vaccine adjuvants are injected intramuscularly at rate , taken up by immature DCs at rate kPi, washed out at rate dA, and are lost due to consumption by splenic macrophages at rate kPϕ. In Equation 3, immature DCs are supplied at rate sD, decay at rate and become semi-mature and acquire vaccine peptides at rate Here, kD is the rate of peptide presentation, χ is the concentration of non-vaccine peptides, and is the proportion of peptides presented that are vaccine specific.
In Equation 4, we assume that semi-mature DCs, S, turnover at a rate comparable to mature DCs dD, and mature due to adjuvant at rate Here, is the maturation rate due to adjuvant and is a adjuvant-saturation constant that ensures that for large adjuvant doses, the DC maturation tapers off. In the absence of adjuvant, however, these semi-mature DCs are unlikely to produce a functional T cell response (61). Thus, for the purposes of this study we do not track T cells that become tolerized as a result of these semi-mature/tolerized DCs.
In Eqs 5 and 6, newly matured DCs initially enter the mature DC population presenting one vaccine peptide with subsequent peptides presented at rate as described above. Additionally, surface peptides degrade at rate dm, which is proportional to the number of presented peptides, j. Finally, mature DCs decay at rate dD. Here, we assume that mature DCs decay faster than iDCs (62).
T Cells
To model the activation and proliferation of T cells both at the lymph node (the volume of which is VLN) and at the tumor site, we first model avidity as a spectrum that varies from j=1 to j=J, corresponding to the lowest and highest avidity states respectively. We then consider several populations: Nj, the concentration of naive CTLs of avidity j; , the concentration of naive helper T cells of avidity j; NR, the concentration of naive natural regulatory T cells; Tj, the concentration of effector CTLs of avidity j; Hj, the concentration of effector helper T cells of avidity j; R, the concentration of induced regulatory T cells; RN, the concentration of effector natural regulatory T cells; and G, the concentration of positive growth factors. The interactions between these populations are then modelled with an ODE system:
Change in naive helper T cell concentration:
Change in naive killer T cell concentration:
Change in naive natural regulatory T cell concentration:
Change in effector killer T cell concentration:
Change in effector helper T cell concentration:
Change in natural regulatory T cell concentration:
Change in induced regulatory T cell concentration:
Change in concentration of positive growth factors:
In Equation 9, naive CTLs in the lymph node of avidity j are supplied at rate ρjsT, where ρj is the proportion supplied that have avidity j. These naive CTLs also exit the lymph node at rate dN. The rate at which naive CTLs are activated by mature DCs that have migrated into the lymph node is
Migration is modelled with a fixed delay of τm, with being the proportion that survives migration. For intranodal injections, the value of τm is set to zero. The kinetic interaction rate between naive CTLs of avidity j and mature DCs presenting k vaccine-peptides is kDC with pj,k being the probability of an interaction leading to successful activation. This means the net kinetic rate, kDCpj,k, depends on both T cell avidity, j, and the number of pMHCs presented on a DC, k. Finally, the leading term accounts for the volume change between the injection site and the lymph node. However, for intranodal injections, this ratio is set to one as there will be no change in volume. In Equation 10, which is similar to Equation 9, naive helper T cells of avidity j are supplied at rate ρjsH, decay at rate dNH, and are activated at the net rate of
In Equation 11, which is similar to Eqs 9 and 10, naive natural regulatory T cells (nTregs) are supplied at rate sR, decay at rate dNR, and are activated at the net rate of
As we do not account nTregs of different avidities, we sum over the variable j.
Equations 12–16 describe interactions within the tumor site. In Equation 12, naive CTLs undergo nT divisions. The division program is modelled with a fixed delay of τa, with being the proportion that effectively activate and traffic to the tumor site. As a consequence, not all T cells that exit the lymph node arrive as effector T cells at the tumor site. These assumptions equate to a net supply rate of
To account for T-cell hyporesponsiveness, we multiply Equation 20 by This ensures that antigen accumulation results in diminished effector CTL expansion. We also assume effector CTLs: decay at rate dT; expand due to interactions with positive growth factors at rate kG; and are suppressed by interactions with induced regulatory T cells at rate μ. Given that induced regulatory T cells (iTregs) and effector nTregs have similar suppression rates (63, 64), we assume that nTregs suppress effector CTLs at an identical rate of μ.
In Equation 13, naive helper T cells undergo nH divisions. Following a similar argument to that in Equation 12, the net supply rate of effector helper T cells is
These effector helper T cells differentiate into induced regulatory T cells at rate kR; are suppressed by both iTregs and nTregs at rate μ; decay at rate dH; and expand due to interactions with positive growth factors at rate kG.
In Equation 14, following a similar argument to that in Equation 12, effector nTregs enter the system at rate
and decay at rate dRN. In Equation 15, iTregs enter the system as differentiated effector helper T cells and decay at rate dR. Finally, in Equation 16, effector CTLs and helper T cells secrete growth factors such as IL‑2 at rates r1 and r2. These growth factors are assumed to decay at rate dG.
Cancer Cells
To model the lysis of cancer cells and trogocytosis of cancer cell MHC by effector CTLs, we consider a population of cancer cells presenting k vaccine-associated peptides, Ck, where k varies from zero to K. The interactions between these cancer cells and effector CTLs are modelled with an ODE system:
For k = 1, ···, K – 1,
In Eqs 23–25, the total cancer population, grows logistically at rate γ and with carrying capacity κ. As a simplifying assumption, we assume that the number of surface peptides is halved after mitosis, resulting in a net compartmental growth rate of
for the population of cancer cells presenting k peptides, Ck. We also assume that surface peptides are regenerated at rate α. To model trogocytosis-mediated MHC stripping, we assume that CTLs and cancer cells presenting k peptides interact at rate kT and additionally assume the number of peptides stripped during this interaction is binomially distributed with probability pT. For brevity we let denote the probability that a CTL will trogocytose m MHC:peptides off a cancer cell presenting n surface peptides. This allows us to describe the trogocytosis rate as
Finally, to model lysis, we let λj,k denote the lysis probability between a cancer cell presenting k peptides and an effector CTL of avidity j and assume that these interactions occur at rate kT. This implies the net kinetic interaction rate depends on both T cell avidity and the amount of pMHC presented by a cancer cell. To model the lysis probability, we assume that the probability of lysis increases with cognate pMHCs but is also modulated by CTL avidity. This can be modelled by assuming a probability function of the form
where rj is an avidity-dependent rate parameter chosen so that the lysis probability at maximal levels of cognate pMHC expression, i.e., λj,k varies linearly from ω1 for the lowest avidity CTL to ωJ for the highest avidity CTL.
Functional Forms
Peptide Vaccine Injection Rate
Here, we assume that the vaccine is injected systemically at a fixed dose, u0, and at a regular interval of ζ, which corresponds to the functional form
Vaccine Adjuvant Injection Rate
We assume that the vaccine adjuvant is injected at a clinically-relevant fixed dose of 5×105 ng/mL (19), and at a regular interval of η, corresponding to the functional form
Peptide Uptake Rates
We previously used ex vivo human data from (22) to estimate a mature DC uptake rate, kP, of 3 × 10−2 (k/μL)-1/day. It is generally understood that immature DCs, relative to mature DCs, have a greater uptake rate (59, 60). To estimate the uptake rate by iDCs, we use in vitro murine data from (23), who note that antigen internalization (as quantified by staining for the antibody YAe) in iDCs is 2.28 times greater than in mDCs. Thus, we assume that the uptake by iDCs, kPi, is 2.28 × kP = 6.84 × 10−2 (k/μL)‑1/day. To account for vaccine clearance by splenic macrophage, we first note the steady-state concentration of non-activated macrophages in mice is estimated to be 1.25 × 10-1 k/μL (24). In (24), the authors also estimate the rate of phagocytosis by non-activated macrophages to be 25.2 (k/μL)‑1/day. Together, these correspond to a splenic macrophage associated vaccine clearance rate, kPϕ, of 25.2 (k/μL)‑1/day × 0.125 k/μL = 3.1875/day.
Activation Probability
The probability of a mature DC presenting k vaccine-associated pMHCs activating a naive T cell of avidity j, pj,k, is modelled with a switch:
Here, 1/(Nc – 1) and 1/(J – 1) map j and k from their respective domains to [0,1]. The dimensionless parameter v = 0.05 determines how sensitive our switching function is to pMHC expression. This characterization ensures that and high pMHC levels on DCs stimulate both high- and low-avidity CTLs (20, 65–69) and by contrast, low pMHC expression stimulates mostly high-avidity CTLs (10, 70–72). To reflect this, we assumed that beyond a critical number of pMHCs, Nc, only low-avidity CTLs were stimulated. We set Nc =N / 2 = 350, implying that DCs must have a surface antigen density below 50% to stimulate high-avidity CTLs.
Initial Conditions
We assume that the vaccine is first administered at t = 0, i.e., P(0) = u0, where u0 is the vaccine dose. Our model assumes a large number of immature DCs preexist at the injection site. In (73), the total DC population at steady-state conditions in the dermis is estimated to be approximately 23.4 k/μL. Around 92.74% of this population is expected to immature (74), equating to an initial iDC concentration at the injection site of 21.7 k/μL. Similarly, 7.26% of the total DC population is expected to be mature (74), equating to a total mDC concentration of 1.7 k/μL. For intravenous injections, we use a total DC concentration of 25 DCs/μL (75), and assume that 90% of this population is immature, equating to an iDC concentration of 22.5 DCs/μL and total mDC concentration of 2.5DCs/μL. Finally, for intranodal injections, we use a pre-existing LN iDC count of 25,190 cells, and an mDC count of 32,920 cells (26), which for a control volume of VLN, equates to an iDC concentration of 5.9976 k/μL, and a total mDC concentration of 7.8381 k/μL. Moreover, we assume that within this mature DC population, pMHCs are normally distributed with mean μ = 100 and variance σ2 = 25 (76). As a simplifying assumption, we assume the initial concentration of semi-mature/tolerizing DCs is zero.
To model the scarcity of high-avidity naive T cells, we assume that their availability decreases exponentially. Specifically, we assume Nj(0) = ρjN(0) and where Here, the model parameters a and b are chosen so that and ρ1/ρJ, i.e., the ratio low-avidity to high-avidity T cells, equates to the model parameter RLH. In our simulations, we set RLH to 100, which means that for one high-avidity T cell there are 100 low-avidity T cells. Moreover, naive natural regulatory T cells, NR, make up roughly 5% of the naive helper T cell population (39), thus, we set
Prior to vaccination, tumor-specific effector T cells exist, albeit at low concentrations (approximately 0.12% of the total CD8+ count) (77). Assuming a total CD8+ count of 600 cells/μL (78), this equates to an initial tumor-specific effector CTL concentration of 0.72 cells/μL. To estimate the initial tumor-specific effector helper T cell concentration, we assume a comparable percentage (i.e., 0.12%) also exists before vaccination. Using a circulating helper T cell concentration of 103 cells/μL (79), this corresponds to an initial tumor-specific effector helper T cell concentration of 1.2 cells/μL. Moreover, approximately 1.5% of this helper T cell pool expresses the natural regulatory T cell phenotype (39), which equates to an initial effector natural regulatory T cell concentration of RN (0) = 1.8 × 10-2 cells/μL. As a simplification, we assume that initially there are no induced regulatory T cells, i.e., R (0) = 0, and that the concentration of growth factor is zero, i.e., G (0) = 0. Finally, to account for the scarcity of high-avidity T cells, we multiply the concentrations of effector CTLs and effector helper T cells by ρj (defined in the above paragraph). Mathematically, Tj (0) = ρj × 0.72 cells/μL and Hj (0) = ρj × 1.2 cells/μL. In other words, initially, for every high-avidity tumor-specific effector T cell, there are 100 low-avidity tumor-specific effector T cells.
Finally, we assume that the total cancer cell concentration is Cinit, with cognate pMHC being normally distributed with mean μ = 148 and variance σ2 = 49. Mathematically, if then
Sensitivity Analysis
To understand how DC maturation status affects parameter sensitivity, we conduct sensitivity analysis on our modified model. We account for non-linear interactions between parameters by varying all parameters simultaneously using Latin hypercube sampling (n=250) over the ranges shown in Table 2, and measure sensitivity by calculating Spearman’s rank correlation coefficient (SRCC), ρ, for each parameter against the fold decrease. These simulations use a peptide vaccine dosage of 7 × 105 ng fortnightly, with an iDC dosage of 106 cells/μL injected at the same time as the peptide vaccine. Table 2 shows SRCC ρ for each parameter.
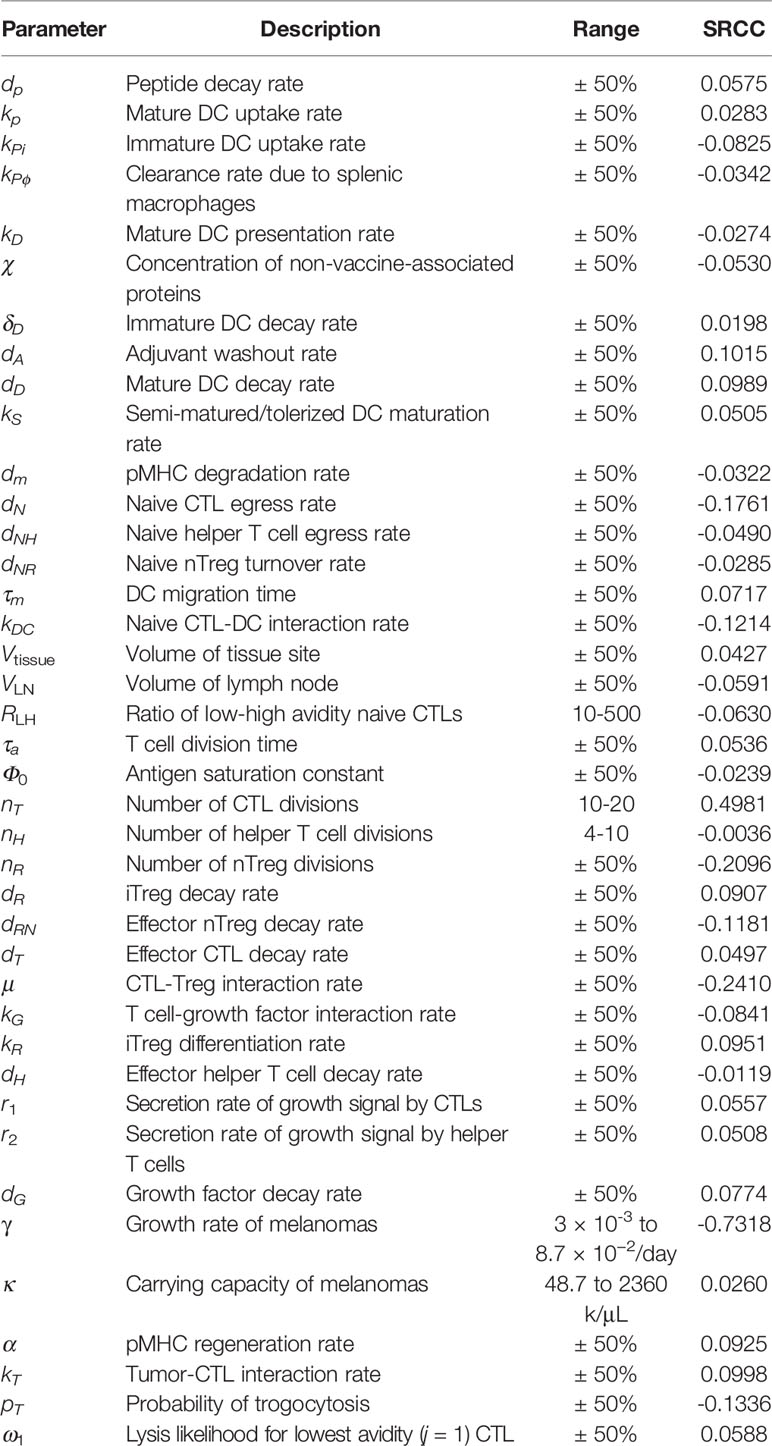
Table 2 Spearman’s rank correlation coefficient between modified model parameters and fold decreases of simulations when varied simultaneously.
In our previous model, a sensitivity analysis identified antigen presentation by DCs as a key variable for the beneficial therapeutic value of vaccines. Here, we amend our model with the induction of immature DCs, resulting in supraphysiological levels of DCs. The resulting scale difference reduces the power of DC-associated parameters. Additionally, the model is now sensitive to the tumor growth rate, γ, suggesting that characteristics such as proliferative and apoptotic cell rates may affect the clinical response to the therapeutic vaccine.
Results
Modified Mathematical Model
We previously found that the rate of antigen presentation by DCs determined the therapeutic value of an anti-tumor CTL response (16). Here, we hypothesize that inducing high levels of immature DCs would preferentially stimulate naive high-avidity CTLs by increasing the total concentration of mature DCs while lowering the average antigen density per DC. To test this proposed approach, we change Equation 2 in our original model (see Materials and Methods) to include a source term, v(t), which describes the elicitation of immature DCs, either by injection of ex vivo derived DCs or by recruitment of DC progenitors from the bone marrow via cytokine stimulation:
As a simplifying assumption, we assume that induced immature DCs (iDCs) are given at a fixed dose v0, and at dosing intervals of ξ hours after the injection of the peptide vaccine, which leads to the functional form:
Figure 1 uses a block diagram to depict the key interactions of our model.
Increased immature DC levels yields lower peptide:MHC levels and tumor cell reduction
In our example, we assume our tumor is a melanoma and assume that our vaccine either targets either neo-antigen peptides or classical antigens such as MART1. Initially, we simulate the DC context of the vaccine while leaving the peptide dosage fixed at the previously optimized value of 100 ng daily. Using this low peptide dosing, we effectively fix the pMHC levels on DCs to be low. To assess the robustness of our modified model, we next simulated iDC doses ranging from 103 cells/μL to 1012 cells/μL, with dosing intervals that range from 0 to 24 hours after a peptide injection. For these simulations, we assume that our vaccine adjuvant is delivered at a dose of 105 ng simultaneously with the peptide vaccine.
A global sweep of iDC dosages within these ranges identified multiple iDC induction magnitudes as being optimal, i.e., inducing a >90% decrease in tumor burden (Figure 2A). For example, an iDC induction magnitude of 106 iDCs/μL given at the same time as the peptide vaccine, induced a 97% decrease in tumor burden. Importantly, the substantial reduction in tumor concentration we observed is neither dose dependent nor time dependent within our parameters, with a wide range of iDC concentrations and dosing intervals achieving a high degree of tumor reduction. Indeed, for iDC doses between 102 to 107 k/μL, the percentage decrease in tumor concentration varies minimally from the local optimum regardless of the dosing interval used. We thus find that the temporal robustness of this system centered around iDC induction and high-avidity T cell induction potentially allows for the possibility of introducing other combinatorial therapeutic strategies that may synergize with vaccine strategies, including checkpoint blockade and inducers of immunogenic cell death.
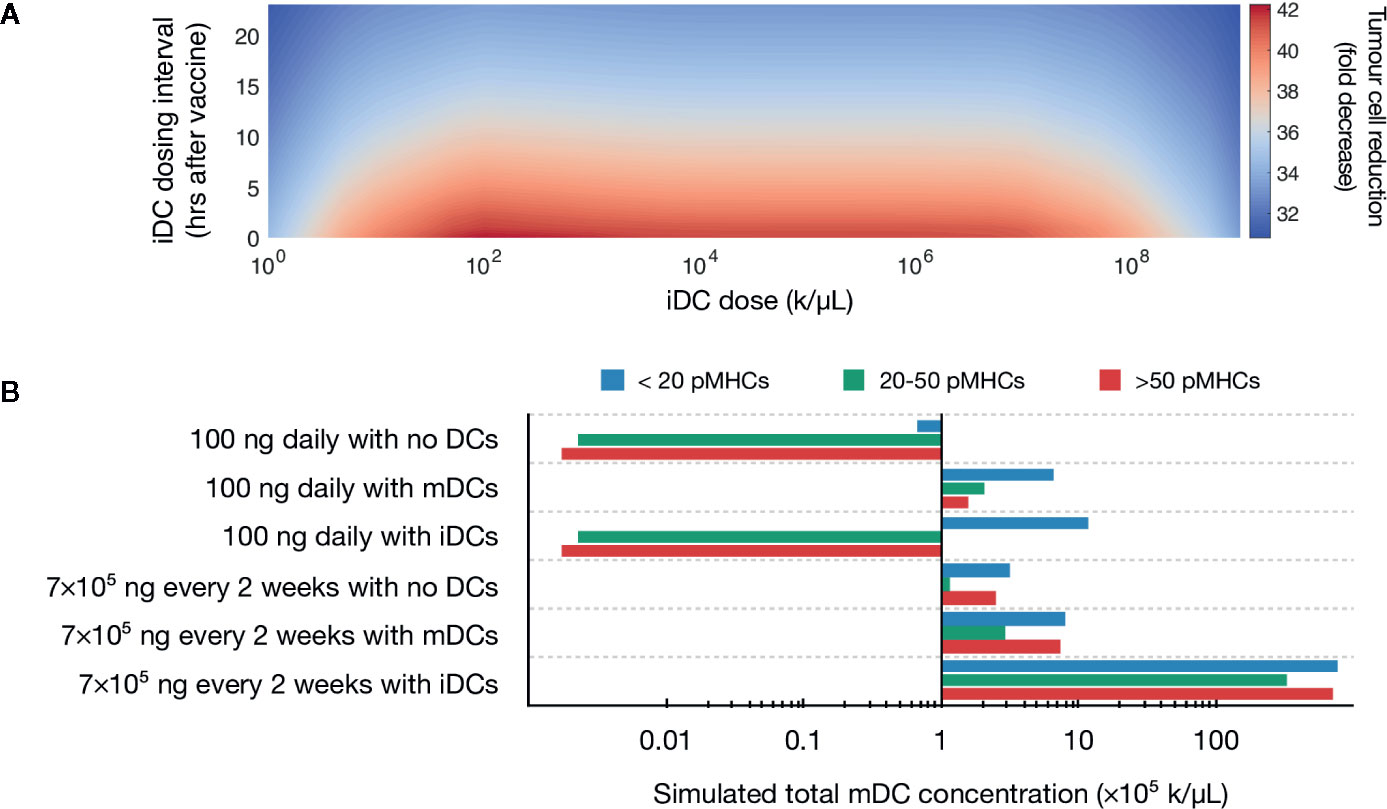
Figure 2 Simulated induction of iDCs favors tumor reduction. (A) Heatmap depicts predicted tumor cell reduction (fold change) for different iDC dosages when given with 100 ng of peptide daily. Here, the unit ‘k’ denotes 103 cells. (B) Stacked bar chart visualizing the predicted distribution of antigen on mature DCs for various vaccine protocols.
Our initial results demonstrated that increased iDC levels, rather than increased mDC levels, favor robust tumor clearing. We next set to determine if similar results could be recapitulated with clinically relevant vaccine dosages, rather than the 100 ng daily peptide dose identified by our previous model. We first compared pMHC levels in three therapeutic variations: peptide with either no DCs, induction of iDCs, or induction of mDCs with around 6 × 106 DCs (which, for a control volume of VLN =4.2 μL, equates to a concentration of 1.43 × 103 k/μL), a dosing concentration similar to previously used in a clinical setting and within optimal concentrations found in our global sweep above (80). We assume that within this population of ex vivo matured DCs (mDCs), pMHCs are normally distributed with mean μ=100 and variance σ2 = 25 (76). Additionally, we compare peptide dosing concentrations for both an ideal 100 ng daily and a clinically relevant 7 × 105 ng every 2 weeks (20). Our model shows that at both peptide doses, induction of iDCs results in increased pMHC-low mature DCs as compared to no DC or mDC conditions (Figure 2B). This reduced antigen density in the context of the same peptide injection concentrations is due to the significantly increased numbers of mDCs generated by inducing iDCs (Figure 2B). These increased numbers are due to the longer half-life of iDCs as compared to mDCs, which are thought to rapidly decay upon maturation. As a result, the same peptide concentration dispensed over a larger number of DCs results in lower pMHC levels per DC.
Immature DCs Promote High-Avidity T Cells and Tumor Clearance in Clinically Relevant Dosing Schemes
Previously, we showed lower levels of pMHC competitively favor the expansion of high-avidity T cells rather than low-avidity T cells (16). As expected, we find that at both peptide dosing schemes induction of iDCs significantly favors the generation of high-avidity T cells compared to mDCs (Figure 3A). The optimal low dose of 100 ng daily of peptide significantly favors the development of high-avidity T cells, but even with the clinically relevant dosing of 7 × 105 ng every 2 weeks, the induction of iDCs significantly shifts the balance of T cell composition to favor high-avidity T cells. This highlights that while traditional mDC or peptide-only vaccination strategies do increase T-cell induction, they do so at the expense of high-avidity T cells. In reflection of increased expansion of high-avidity T cells, our simulations further demonstrate that iDC induction results in improved cancer cell lysis (Figure 3B).
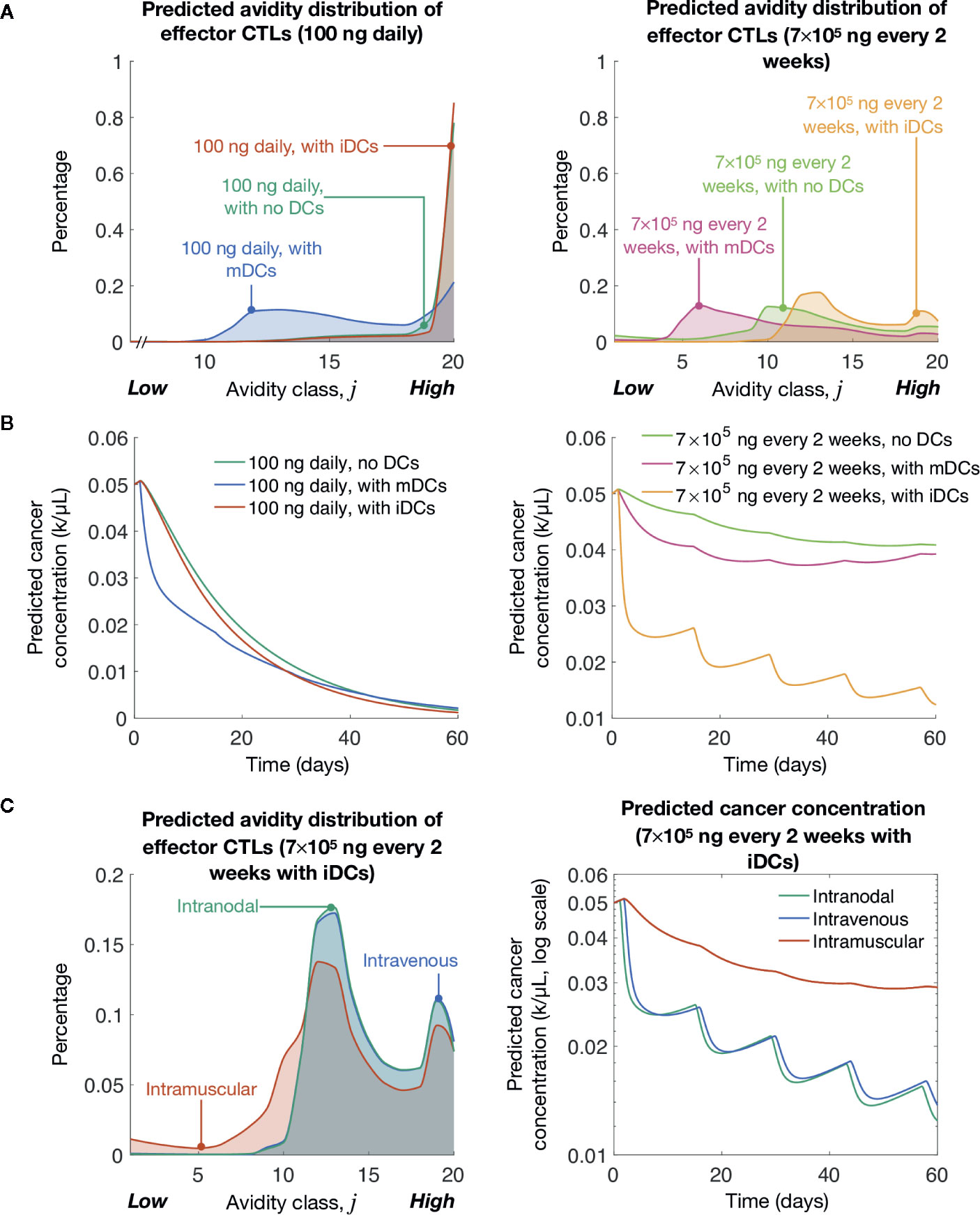
Figure 3 Simulated induction of iDCs at clinically relevant vaccination doses yields significant tumor cell clearance. (A) Simulated avidity distribution of effector T cells for various vaccine protocols. (B) Simulated cancer concentrations over time for various vaccine protocols. (C) Simulated avidity distribution of effector T cells and tumor cell reduction (fold change) for different delivery routes. The unit ‘k’ denotes 103 cells.
Finally, we compared vaccine responses in three different delivery routes: intramuscular, intravenous, and intranodal. For intramuscular case, at most, only 4% of DCs are expected to arrive at the LN (81). To model this, we multiply the source terms (described by Eqs 17–20) by 4%. To model intravenous delivery, we modify our initial conditions so that DCs in our model are characterized by blood DC data (75). Finally, to model intranodal delivery, we assume there is no migratory delay between the injection site and the LN (i.e., τm = 0), and that there is no volume change between DC compartment and the LN compartment. Our simulations suggest that in the context of avidity-selection and tumor clearance (see Figure 3C), DC vaccination route is a critical consideration for maximizing vaccine efficiency. iDCs intranodal injections followed by intravenous injection were both preferable over intradermal DC injections. This data highlights the importance of high iDC cell numbers accumulating in the LN in our vaccination model.
Discussion
Cancer immunotherapy is now a routine means of successfully treating tumors of various types in the clinic. However, improved immunotherapies to benefit greater numbers of patients with increased durability are still needed. Despite its tremendous successes, ICB therapy only benefits less than the majority of patients treated (82–84) and presents significant risks for adverse side-effects (85–87). Therapeutic peptide vaccines can robustly induce a tumor-specific CTL response with limited side effects due to induction of an antigen-specific immune response rather than broad immune activation (20). Preferential development of high avidity anti-tumor CTLs enables enhanced tumor cell killing (9, 18). Previously, we showed that vaccine dosages could be optimized to preferentially elicit high-avidity CTLs, unlike standard dosages that elicit low-avidity CTLs (16). In that study, we showed that the efficacy of a dosage-optimized approach depended on DC-related parameters, which motivated us to explore how we could harness immature DCs to boost anti-tumor activity.
High peptide antigen doses have been shown experimentally to result in low avidity and T cell responses (88, 89). However dosing timing strategy has been shown to have a significant effect on the average avidity of a T cell population (90, 91). Other work has shown that modulation of antigen presenting cells is a key component of the induction of high avidity T cells (92). We hypothesized that increasing the magnitude of iDCs given with a dosage-optimized peptide vaccine may enhance CTL responses. It is important to stress that this approach is conceptually different from traditional DC vaccines in which ex vivo matured DCs are injected (3, 17). To assess this approach, we extended our previous model to account for a hypothetical induction of iDCs. We show that induction of iDCs, and not mDCs, can significantly reduce tumor burden, improving upon the performance of a peptide vaccine. A key assumption of our model is that iDCs will have a longer half-life and inducing iDCs will result in a larger overall pool of DCs as compared to the injection of mDCs, which are known to have a shorter half-life (62). Our simulations show that these effects are tied to the increased half-life of iDCs and therefore increased DC levels in general, which results in a lower average antigen density per DC. As such, induction of iDCs favors the preferential stimulation of high-avidity CTLs and tumor cell clearance. In support of our findings, increased circulating DC levels have been associated with increased survival in certain malignancies (93–95). Further experimental or clinical evidence of the relationship between circulating DC levels and vaccination efficacy is needed.
Early cancer vaccines targeting over-expressed CAAs such as MART-1, MAGE, NYE-ESO-1, HER2, and MUC-1 demonstrated mediocre clinical results. Evidence suggests that the T cell repertoire capable of responding to these antigens are primarily composed of low-avidity T cells due to central tolerance of T cells specific for self-antigens (96). Recently, there has been renewed interest in cancer vaccines due to promising results for those targeting neoantigens (97–100). Additionally, encouraging preliminary clinical results have recently been observed in therapeutic approaches combining DC vaccines with checkpoint blockade (101). Our findings suggest that inducing increased iDC levels would benefit vaccines targeting either over-expressed CAAs or neoantigens, as the expansion of high-avidity CTLs would favor clinical responses in both scenarios.
Initial DC vaccines, such as Sipuleucel-T, were major milestones for immunotherapy-based treatments of cancer and demonstrated modest, but meaningful, clinical results (102). While DC vaccines have not achieved widespread therapeutic success, it is unclear if this is a result of targeting TAAs, the influence of previously unknown immunosuppression mechanisms in the tumor microenvironment, or difficult in manufacturing cell products (103). While traditional DC vaccines have been based on ex vivo antigen loading and maturation of autologous DCs, our model finds that injecting iDCs results in a maximal anti-tumor response. We find that intranodal injection, as compared to intradermal or intravenous injection, results in the most T cell activation as it ensures high numbers of DCs are loaded with low pMHC levels. Although repeated intranodal injection of iDCs is not an ideal clinical scenario, it highlights the importance of recent bioengineering efforts to localize tumor antigen vaccination to lymph node sites (104). However, intravenous injection of iDCs did result in substantial tumor burden reduction. We suggest that other alternatives to iDC generation and injection, such as mobilization of bone marrow DC precursors, is an attractive possibility for future consideration in tumor vaccine design. Treatments with cytokines such as Fms-like tyrosine kinase 3 ligand (Flt3L) has demonstrated efficacy in increasing levels of circulating DCs (105–107). Our model suggests that elevated levels of iDCs, rather than mDCs, favors a longer half-life of the circulating DC compartment and results in lower average pMHC levels that would then favor high-avidity T cell generation. Therefore, induction of iDCs by any of several means followed by peptide vaccination and adjuvant for in vivo DC maturation would favor tumor clearance. While our model simplistically accounts for adjuvant as a necessary requirement for DC maturation and activation of T cells, we acknowledge that different adjuvant choices may have highly variable effects on DC activation and downstream T cell differentiation (108, 109).
Our work addresses an important and less appreciated element of cancer vaccines – how vaccine design and administration can select for and enhance the proliferation of high-avidity CTLs. However, there remain many barriers to efficacy with a combination strategy that our model does not consider. For example, we do not account for potential intra-tumoral heterogeneity of antigen expression, factors influencing CTL trafficking to tumor sites, or a multitude of potential immune suppression mechanisms found within tumor microenvironments. Additionally, in modelling the T cell activation we do not explicitly model TCR signaling. Future work will involve incorporating existing validated models of TCR signaling (110), and calibrating these models to avidity data from (111, 112). Defining the minimum complexity of the immune system is challenging, and the model used in this study does not, nor does it aim to account for all known immune interactions.
The mathematical model presented here proposes that increasing the magnitude of iDCs with an optimized peptide vaccine may improve tumor clearance. The model highlights the relative importance of antigen loads on DCs, which facilitate the selective expansion of high-avidity CTLs. While pre-clinical experimental validation of our findings are necessary, our model suggests previously unappreciated aspects of vaccine design that may be necessary for the development of effective cancer treatments.
Data Availability Statement
All datasets presented in this study are included in the article.
Author Contributions
AK performed the simulations and formal analysis. AK and CE wrote the first draft of the manuscript. All authors contributed to the article and approved the submitted version.
Funding
This work was supported by an Australian Government Research Training Program Scholarship; an Australian Research Council Discovery Project [DP180101512]; and by the US Department of Defense Breast Cancer Research Program [W81XWH-11–1–0548].
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1. Zappasodi R, Merghoub T, Wolchok JD. Emerging Concepts for Immune Checkpoint Blockade-Based Combination Therapies. Cancer Cell (2018) 33(4):581–98. doi: 10.1016/j.ccell.2018.03.005
2. Trujillo JA, Sweis RF, Bao R, Luke JJ. T Cell-Inflamed versus Non-T Cell-Inflamed Tumors: A Conceptual Framework for Cancer Immunotherapy Drug Development and Combination Therapy Selection. Cancer Immunol Res (2018) 6(9):990–1000. doi: 10.1158/2326-6066.CIR-18-0277
3. Saxena M, Bhardwaj N. Re-Emergence of Dendritic Cell Vaccines for Cancer Treatment. Trends Cancer (2018) 4(2):119–37. doi: 10.1016/j.trecan.2017.12.007
4. Jandus C, Usatorre AM, Vigano S, Zhang L, Romero P. The Vast Universe of T Cell Diversity: Subsets of Memory Cells and Their Differentiation. Methods Mol Biol (2017) 1514:1–17. doi: 10.1007/978-1-4939-6548-9_1
5. Abbas AK, Lichtman AHH, Pillai S. Cellular and Molecular Immunology. Philadelphia, Pennsylvania, USA: Elsevier Health Sciences (2014).
6. Slingluff CL. The present and future of peptide vaccines for cancer: single or multiple, long or short, alone or in combination? Cancer J (2011) 17(5):343–50. doi: 10.1097/PPO.0b013e318233e5b2
7. Lollini PL, Cavallo F, Nanni P, Forni G. Vaccines for tumour prevention. Nat Rev Cancer (2006) 6(3):204–16. doi: 10.1038/nrc1815
8. Mougel A, Terme M, Tanchot C. Therapeutic Cancer Vaccine and Combinations With Antiangiogenic Therapies and Immune Checkpoint Blockade. Front Immunol (2019) 10:467. doi: 10.3389/fimmu.2019.00467
9. Stuge TB, Holmes SP, Saharan S, Tuettenberg A, Roederer M, Weber JS, et al. Diversity and recognition efficiency of T cell responses to cancer. PloS Med (2004) 1(2):e28. doi: 10.1371/journal.pmed.0010028
10. McMahan RH, Slansky JE. Mobilizing the low-avidity T cell repertoire to kill tumors. Semin Cancer Biol (2007) 17(4):317–29. doi: 10.1016/j.semcancer.2007.06.006
11. Hu Z, Ott PA, Wu CJ. Towards personalized, tumour-specific, therapeutic vaccines for cancer. Nat Rev Immunol (2018) 18(3):168–82. doi: 10.1038/nri.2017.131
12. Schumacher TN, Schreiber RD. Neoantigens in cancer immunotherapy. Science. (2015) 348(6230):69–74. doi: 10.1126/science.aaa4971
13. Pan RY, Chung WH, Chu MT, Chen SJ, Chen HC, Zheng L, et al. Recent Development and Clinical Application of Cancer Vaccine: Targeting Neoantigens. J Immunol Res (2018) 2018:4325874. doi: 10.1155/2018/4325874
14. Speiser DE, Baumgaertner P, Voelter V, Devevre E, Barbey C, Rufer N, et al. Unmodified self antigen triggers human CD8 T cells with stronger tumor reactivity than altered antigen. Proc Natl Acad Sci USA (2008) 105(10):3849–54. doi: 10.1073/pnas.0800080105
15. Kittlesen DJ, Thompson LW, Gulden PH, Skipper JC, Colella TA, Shabanowitz J, et al. Human melanoma patients recognize an HLA-A1-restricted CTL epitope from tyrosinase containing two cysteine residues: implications for tumor vaccine development. J Immunol (1998) 160(5):2099–106.
16. Kumbhari A, Kim PS, Lee PP. Optimisation of anti-cancer peptide vaccines to preferentially elicit high-avidity T cells. J Theor Biol (2019) 486:110067. doi: 10.1016/j.jtbi.2019.110067
17. Perez CR, De Palma M. Engineering dendritic cell vaccines to improve cancer immunotherapy. Nat Commun (2019) 10(1):5408. doi: 10.1038/s41467-019-13368-y
18. Chung B, Stuge TB, Murad JP, Beilhack G, Andersen E, Armstrong BD, et al. Antigen-specific inhibition of high-avidity T cell target lysis by low-avidity T cells via trogocytosis. Cell Rep (2014) 8(3):871–82. doi: 10.1016/j.celrep.2014.06.052
19. Hailemichael Y, Dai Z, Jaffarzad N, Ye Y, Medina MA, Huang X-F, et al. Persistent antigen at vaccination sites induces tumor-specific CD8+ T cell sequestration, dysfunction and deletion. Nat Med (2013) 19(4):465–72. doi: 10.1038/nm.3105
20. Rezvani K, Yong ASM, Mielke S, Jafarpour B, Savani BN, Le RQ, et al. Repeated PR1 and WT1 peptide vaccination in Montanide-adjuvant fails to induce sustained high-avidity, epitope-specific CD8+ T cells in myeloid malignancies. Haematologica (2011) 96(3):432–40. doi: 10.3324/haematol.2010.031674
21. Harndahl M, Rasmussen M, Roder G, Dalgaard Pedersen I, Sorensen M, Nielsen M, et al. Peptide-MHC class I stability is a better predictor than peptide affinity of CTL immunogenicity. Eur J Immunol (2012) 42(6):1405–16. doi: 10.1002/eji.201141774
22. Sallusto F, Cella M, Danieli C, Lanzavecchia A. Dendritic cells use macropinocytosis and the mannose receptor to concentrate macromolecules in the major histocompatibility complex class II compartment: downregulation by cytokines and bacterial products. J Exp Med (1995) 182(2):389–400. doi: 10.1084/jem.182.2.389
23. Platt CD, Ma JK, Chalouni C, Ebersold M, Bou-Reslan H, Carano RA, et al. Mature dendritic cells use endocytic receptors to capture and present antigens. Proc Natl Acad Sci USA (2010) 107(9):4287–92. doi: 10.1073/pnas.0910609107
24. Maree AF, Komba M, Dyck C, Labecki M, Finegood DT, Edelstein-Keshet L. Quantifying macrophage defects in type 1 diabetes. J Theor Biol (2005) 233(4):533–51. doi: 10.1016/j.jtbi.2004.10.030
25. Kaplan G, Nusrat A, Witmer MD, Nath I, Cohn ZA. Distribution and turnover of Langerhans cells during delayed immune responses in human skin. J Exp Med (1987) 165(3):763–76. doi: 10.1084/jem.165.3.763
26. Di Girolamo W, Coronato S, Portiansky E, Laguens G. Profile of immune cells in lymph nodes draining human malignant tumors. Med (B Aires) (2008) 68(6):423–7.
27. Dupuis M, McDonald DM, Ott G. Distribution of adjuvant MF59 and antigen gD2 after intramuscular injection in mice. Vaccine (1999) 18(5-6):434–9. doi: 10.1016/s0264-410x(99)00263-7
28. Leeman M, Choi J, Hansson S, Storm MU, Nilsson L. Proteins and antibodies in serum, plasma, and whole blood-size characterization using asymmetrical flow field-flow fractionation (AF4). Anal Bioanal Chem (2018) 410(20):4867–73. doi: 10.1007/s00216-018-1127-2
29. Delamarre L, Holcombe H, Mellman I. Presentation of exogenous antigens on major histocompatibility complex (MHC) class I and MHC class II molecules is differentially regulated during dendritic cell maturation. J Exp Med (2003) 198(1):111–22. doi: 10.1084/jem.20021542
30. Henrickson SE, Mempel TR, Mazo IB, Liu B, Artyomov MN, Zheng H, et al. T cell sensing of antigen dose governs interactive behavior with dendritic cells and sets a threshold for T cell activation. Nat Immunol (2008) 9(3):282–91. doi: 10.1038/ni1559
31. Wilson NS, El-Sukkari D, Villadangos Je A. Dendritic cells constitutively present self antigens in their immature state in vivo and regulate antigen presentation by controlling the rates of MHC class II synthesis and endocytosis. Blood. (2004) 103(6):2187–95. doi: 10.1182/blood-2003-08-2729
32. Mandl JN, Liou R, Klauschen F, Vrisekoop N, Monteiro Ja o P, Yates AJ, et al. Quantification of lymph node transit times reveals differences in antigen surveillance strategies of naive CD4+ and CD8+ T cells. Proc Natl Acad Sci (2012) 109(44):18036–41. doi: 10.1073/pnas.1211717109
33. Rubtsov YP, Niec RE, Josefowicz S, Li L, Darce J, Mathis D, et al. Stability of the regulatory T cell lineage in vivo. Science (2010) 329(5999):1667–71. doi: 10.1126/science.1191996
34. Catron DM, Itano AA, Pape KA, Mueller DL, Jenkins MK. Visualizing the first 50 hr of the primary immune response to a soluble antigen. Immunity. (2004) 21(3):341–7. doi: 10.1016/j.immuni.2004.08.007
35. Pittet MJ, Valmori D, Dunbar PR, Speiser DE, Lienard D, Lejeune F, et al. High frequencies of naive Melan-A/MART-1–specific CD8+ T cells in a large proportion of human histocompatibility leukocyte antigen (HLA)-A2 individuals. J Exp Med (1999) 190(5):705–16. doi: 10.1084/jem.190.5.705
36. Williams H, Sarapata E, Caldwell T, dePillis L. Mathematical modeling of regulatory T cell effects on renal cell carcinoma treatment. Discrete Continuous Dyn Syst Ser B (2013) 18: (4):915–43. doi: 10.3934/dcdsb.2013.18.915
37. Speiser DE, Colonna M, Ayyoub M, Cella M, Pittet MJ, Batard P, et al. The activatory receptor 2B4 is expressed in vivo by human CD8+ effector alpha beta T cells. J Immunol (2001) 167(11):6165–70. doi: 10.4049/jimmunol.167.11.6165
38. Homann D, Teyton L, Oldstone MBA. Differential regulation of antiviral T-cell immunity results in stable CD8+ but declining CD4+ T-cell memory. Nat Med (2001) 7(8):913–9. doi: 10.1038/90950
39. Valmori D, Merlo A, Souleimanian NE, Hesdorffer CS, Ayyoub M. A peripheral circulating compartment of natural naive CD4 Tregs. J Clin Invest (2005) 115(7):1953–62. doi: 10.1172/JCI23963
40. Litjens NH, Boer K, Zuijderwijk JM, Klepper M, Peeters AM, Prens EP, et al. Allogeneic Mature Human Dendritic Cells Generate Superior Alloreactive Regulatory T Cells in the Presence of IL-15. J Immunol (2015) 194(11):5282–93. doi: 10.4049/jimmunol.1402827
41. Geiger R, Duhen T, Lanzavecchia A, Sallusto F. Human naive and memory CD4+ T cell repertoires specific for naturally processed antigens analyzed using libraries of amplified T cells. J Exp Med (2009) 206(7):1525–34. doi: 10.1084/jem.20090504
42. Murali-Krishna K, Altman JD, Suresh M, Sourdive DJ, Zajac AJ, Miller JD, et al. Counting antigen-specific CD8 T cells: a reevaluation of bystander activation during viral infection. Immunity (1998) 8(2):177–87. doi: 10.1016/s1074-7613(00)80470-7
43. Hellerstein M, Hanley MB, Cesar D, Siler S, Papageorgopoulos C, Wieder E, et al. Directly measured kinetics of circulating T lymphocytes in normal and HIV-1-infected humans. Nat Med (1999) 5(1):83–9. doi: 10.1038/4772
44. Obst R. Timing T cell priming cycling. Front Immunol (2015) 6:563. doi: 10.3389/fimmu.2015.00563
45. Butz EA, Bevan MJ. Massive expansion of antigen-specific CD8+ T cells during an acute virus infection. Immunity (1998) 8(2):167–75. doi: 10.1016/s1074-7613(00)80469-0
46. Gerlach C, Rohr JC, Perie L, van Rooij N, van Heijst JW, Velds A, et al. Heterogeneous differentiation patterns of individual CD8+ T cells. Science (2013) 340(6132):635–9. doi: 10.1126/science.1235487
47. Buchholz VR, Flossdorf M, Hensel I, Kretschmer L, Weissbrich B, Graf P, et al. Disparate individual fates compose robust CD8+ T cell immunity. Science (2013) 340(6132):630–5. doi: 10.1126/science.1235454
48. Lotze MT, Matory YL, Ettinghausen SE, Rayner AA, Sharrow SO, Seipp CA, et al. In vivo administration of purified human interleukin 2. II. Half life, immunologic effects, and expansion of peripheral lymphoid cells in vivo with recombinant IL 2. J Immunol (1985) 135(4):2865–75.
49. Borghans J AM, Tesselaar K, de Boer RJ. Current best estimates for the average lifespans of mouse and human leukocytes: reviewing two decades of deuterium-labeling experiments. Immunol Rev (2018) 285(1):233–48. doi: 10.1111/imr.12693
50. Vukmanovic-Stejic M, Zhang Y, Cook JE, Fletcher JM, McQuaid A, Masters JE, et al. Human CD4+ CD25hi Foxp3+ regulatory T cells are derived by rapid turnover of memory populations in vivo. J Clin Invest (2006) 116(9):2423–33. doi: 10.1172/JCI28941
51. Carlson JA. Tumor doubling time of cutaneous melanoma and its metastasis. Am J Dermatopathol (2003) 25:291–9. doi: 10.1097/00000372-200308000-00003
52. Eskelin S, Pyrhonen S, Summanen P, Hahka-Kemppinen M, Kivela T. Tumor doubling times in metastatic malignant melanoma of the uvea: tumor progression before and after treatment. Ophthalmology. (2000) 107:1443–9. doi: 10.1016/S0161-6420(00)00182-2
53. Ollila DW, Stern SL, Morton DL. Tumor doubling time: a selection factor for pulmonary resection of metastatic melanoma. J Surg Oncol (1998) 69:206–11. doi: 10.1002/(SICI)1096-9098(199812)69:4<206::AID-JSO3>3.0.CO;2-N
54. Sarapata EA, de Pillis LG. A comparison and catalog of intrinsic tumor growth models. Bull Math Biol (2014) 76(8):2010–24. doi: 10.1007/s11538-014-9986-y
55. Carreno BM, Hansen TH. Exogenous peptide ligand influences the expression and half-life of free HLA class I heavy chains ubiquitously detected at the cell surface. Eur J Immunol (1994) 24(6):1285–92. doi: 10.1002/eji.1830240607
56. Christinck ER, Luscher MA, Barber BH, Williams DB. Peptide binding to class I MHC on living cells and quantitation of complexes required for CTL lysis. Nature. (1991) 352(6330):67–70. doi: 10.1038/352067a0
57. Coffman RL, Sher A, Seder RA. Vaccine adjuvants: putting innate immunity to work. Immunity. (2010) 33(4):492–503. doi: 10.1016/j.immuni.2010.10.002
58. Gardner A, Ruffell B. Dendritic Cells and Cancer Immunity. Trends Immunol (2016) 37(12):855–65. doi: 10.1016/j.it.2016.09.006
59. Mellman I, Steinman RM. Dendritic cells: specialized and regulated antigen processing machines. Cell. (2001) 106(3):255–8. doi: 10.1016/S0092-8674(01)00449-4
60. Trombetta ES, Mellman I. Cell biology of antigen processing in vitro and in vivo. Annu Rev Immunol (2005) 23:975–1028. doi: 10.1146/annurev.immunol.22.012703.104538
61. Steinman RM, Hawiger D, Nussenzweig MC. Tolerogenic dendritic cells. Annu Rev Immunol (2003) 21:685–711. doi: 10.1146/annurev.immunol.21.120601.141040
62. De Smedt T, Pajak B, Muraille E, Lespagnard L, Heinen E, De Baetselier P, et al. Regulation of dendritic cell numbers and maturation by lipopolysaccharide in vivo. J Exp Med (1996) 184(4):1413–24. doi: 10.1084/jem.184.4.1413
63. Benson MJ, Pino-Lagos K, Rosemblatt M, Noelle RJ. All-trans retinoic acid mediates enhanced T reg cell growth, differentiation, and gut homing in the face of high levels of co-stimulation. J Exp Med (2007) 204(8):1765–74. doi: 10.1084/jem.20070719
64. Dons EM, Raimondi G, Cooper DK, Thomson AW. Induced regulatory T cells: mechanisms of conversion and suppressive potential. Hum Immunol (2012) 73(4):328–34. doi: 10.1016/j.humimm.2011.12.011
65. Alexander-Miller MA, Leggatt GR, Berzofsky JA. Selective expansion of high- or low-avidity cytotoxic T lymphocytes and efficacy for adoptive immunotherapy. Proc Natl Acad Sci (1996) 93(9):4102–7. doi: 10.1073/pnas.93.9.4102
66. Bullock TNJ, Mullins DW, Colella TA, Engelhard VH. Manipulation of Avidity to Improve Effectiveness of Adoptively Transferred CD8+ T Cells for Melanoma Immunotherapy in Human MHC Class I-Transgenic Mice. J Immunol (2001) 167(10):5824–31. doi: 10.4049/jimmunol.167.10.5824
67. Kedl RM, Schaefer BC, Kappler JW, Marrack P. T cells down-modulate peptide-MHC complexes on APCs in vivo. Nat Immunol (2002) 3(1):27. doi: 10.1038/ni742
68. Kedl RM, Rees WA, Hildeman DA, Schaefer B, Mitchell T, Kappler J, et al. T cells compete for access to antigen-bearing antigen-presenting cells. J Exp Med (2000) 192(8):1105–14. doi: 10.1084/jem.192.8.1105
69. Kroger CJ, Amoah S, Alexander-Miller MA. Cutting edge: Dendritic cells prime a high avidity CTL response independent of the level of presented antigen. J Immunol (2008) 180(9):5784–8. doi: 10.4049/jimmunol.180.9.5784
70. Sandberg JK, Franksson L, Sundback J, Michaelsson J, Petersson M, Achour A, et al. T cell tolerance based on avidity thresholds rather than complete deletion allows maintenance of maximal repertoire diversity. J Immunol (2000) 165(1):25–33. doi: 10.4049/jimmunol.165.1.25
71. van den Boorn JG, Le Poole IC, Luiten RM. T-cell avidity and tuning: the flexible connection between tolerance and autoimmunity. Int Rev Immunol (2006) 25(3-4):235–58. doi: 10.1080/08830180600743081
72. Vigano S, Utzschneider DT, Perreau M, Pantaleo G, Zehn D, Harari A. Functional avidity: a measure to predict the efficacy of effector T cells? Clin Dev Immunol (2012) 2012:153863. doi: 10.1155/2012/153863
73. Bauer J, Bahmer FA, Worl J, Neuhuber W, Schuler G, Fartasch M. A strikingly constant ratio exists between Langerhans cells and other epidermal cells in human skin. A stereologic study using the optical disector method and the confocal laser scanning microscope. J Invest Dermatol (2001) 116(2):313–8. doi: 10.1046/j.1523-1747.2001.01247.x
74. Ferdousi M, Romanchuk K, Mah JK, Virtanen H, Millar C, Malik RA, et al. Early corneal nerve fibre damage and increased Langerhans cell density in children with type 1 diabetes mellitus. Sci Rep (2019) 9(1):8758. doi: 10.1038/s41598-019-45116-z
75. Haller Hasskamp J, Zapas JL, Elias EG. Dendritic cell counts in the peripheral blood of healthy adults. Am J Hematol (2005) 78(4):314–5. doi: 10.1002/ajh.20296
76. Walseng E, Furuta K, Bosch B, Weih KA, Matsuki Y, Bakke O, et al. Ubiquitination regulates MHC class II-peptide complex retention and degradation in dendritic cells. Proc Natl Acad Sci USA (2010) 107(47):20465–70. doi: 10.1073/pnas.1010990107
77. Gannon PO, Baumgaertner P, Huber A, Iancu EM, Cagnon L, Abed Maillard S, et al. Rapid and Continued T-Cell Differentiation into Long-term Effector and Memory Stem Cells in Vaccinated Melanoma Patients. Clin Cancer Res (2017) 23(13):3285–96. doi: 10.1158/1078-0432.CCR-16-1708
78. Murphy K. Janeway’s Immunobiology (Immunobiology: The Immune System (Janeway)). New York, New York, USA: Garland Science (2011).
79. Beers MH, Berkow R, Bogin RM, Fletcher AJ, Nace BA, Moy DE, et al. The Merck manual of diagnosis and therapy. Whitehouse Station, NJ: Merck (1999). Available at: http://www.merck.com/pubs/mmanual/.
80. Schreibelt G, Bol KF, Westdorp H, Wimmers F, Aarntzen EH, Duiveman-de Boer T, et al. Effective Clinical Responses in Metastatic Melanoma Patients after Vaccination with Primary Myeloid Dendritic Cells. Clin Cancer Res (2016) 22(9):2155–66. doi: 10.1158/1078-0432.CCR-15-2205
81. Verdijk P, Aarntzen EH, Lesterhuis WJ, Boullart AC, Kok E, van Rossum MM, et al. Limited amounts of dendritic cells migrate into the T-cell area of lymph nodes but have high immune activating potential in melanoma patients. Clin Cancer Res (2009) 15(7):2531–40. doi: 10.1158/1078-0432.CCR-08-2729
82. Camacho LH. CTLA-4 blockade with ipilimumab: biology, safety, efficacy, and future considerations. Cancer Med (2015) 4(5):661–72. doi: 10.1002/cam4.371
83. Mahoney KM, Freeman GJ, McDermott DF. The Next Immune-Checkpoint Inhibitors: PD-1/PD-L1 Blockade in Melanoma. Clin Ther (2015) 37(4):764–82. doi: 10.1016/j.clinthera.2015.02.018
84. Ott PA, Hodi FS, Robert C. CTLA-4 and PD-1/PD-L1 blockade: new immunotherapeutic modalities with durable clinical benefit in melanoma patients. Clin Cancer Res (2013) 19(19):5300–9. doi: 10.1158/1078-0432.CCR-13-0143
85. Bertrand A, Kostine M, Barnetche T, Truchetet ME, Schaeverbeke T. Immune related adverse events associated with anti-CTLA-4 antibodies: systematic review and meta-analysis. BMC Med (2015) 13:211. doi: 10.1186/s12916-015-0455-8
86. Corsello SM, Barnabei A, Marchetti P, De Vecchis L, Salvatori R, Torino F. Endocrine side effects induced by immune checkpoint inhibitors. J Clin Endocrinol Metab (2013) 98(4):1361–75. doi: 10.1210/jc.2012-4075
87. Gelao L, Criscitiello C, Esposito A, Goldhirsch A, Curigliano G. Immune checkpoint blockade in cancer treatment: a double-edged sword cross-targeting the host as an “innocent bystander”. Toxins (Basel) (2014) 6(3):914–33. doi: 10.3390/toxins6030914
88. Andersson B. Studies on the regulation of avidity at the level of the single antibody-forming cell. The effect of antigen dose and time after immunization. J Exp Med (1970) 132(1):77–88. doi: 10.1084/jem.132.1.77
89. Billeskov R, Lindenstrom T, Woodworth J, Vilaplana C, Cardona PJ, Cassidy JP, et al. High Antigen Dose Is Detrimental to Post-Exposure Vaccine Protection against Tuberculosis. Front Immunol (2017) 8:1973. doi: 10.3389/fimmu.2017.01973
90. Carretero-Iglesia L, Couturaud B, Baumgaertner P, Schmidt J, Maby-El Hajjami H, Speiser DE, et al. High Peptide Dose Vaccination Promotes the Early Selection of Tumor Antigen-Specific CD8 T-Cells of Enhanced Functional Competence. Front Immunol (2019) 10:3016. doi: 10.3389/fimmu.2019.03016
91. Narayan S, Choyce A, Fernando GJ, Leggatt GR. Secondary immunisation with high-dose heterologous peptide leads to CD8 T cell populations with reduced functional avidity. Eur J Immunol (2007) 37(2):406–15. doi: 10.1002/eji.200535688
92. Oh S, Hodge JW, Ahlers JD, Burke DS, Schlom J, Berzofsky JA. Selective induction of high avidity CTL by altering the balance of signals from APC. J Immunol (2003) 170(5):2523–30. doi: 10.4049/jimmunol.170.5.2523
93. Della Bella S, Gennaro M, Vaccari M, Ferraris C, Nicola S, Riva A, et al. Altered maturation of peripheral blood dendritic cells in patients with breast cancer. Br J Cancer (2003) 89(8):1463–72. doi: 10.1038/sj.bjc.6601243
94. Hirooka S, Yanagimoto H, Satoi S, Yamamoto T, Toyokawa H, Yamaki S, et al. The role of circulating dendritic cells in patients with unresectable pancreatic cancer. Anticancer Res (2011) 31(11):3827–34.
95. Pinzon-Charry A, Ho CS, Maxwell T, McGuckin MA, Schmidt C, Furnival C, et al. Numerical and functional defects of blood dendritic cells in early- and late-stage breast cancer. Br J Cancer (2007) 97(9):1251–9. doi: 10.1038/sj.bjc.6604018
96. Pedersen SR, Sorensen MR, Buus S, Christensen JP, Thomsen AR. Comparison of vaccine-induced effector CD8 T cell responses directed against self- and non-self-tumor antigens: implications for cancer immunotherapy. J Immunol (2013) 191(7):3955–67. doi: 10.4049/jimmunol.1300555
97. Carreno BM, Magrini V, Becker-Hapak M, Kaabinejadian S, Hundal J, Petti AA, et al. Cancer immunotherapy. A dendritic cell vaccine increases the breadth and diversity of melanoma neoantigen-specific T cells. Science (2015) 348(6236):803–8. doi: 10.1126/science.aaa3828
98. Ott PA, Hu Z, Keskin DB, Shukla SA, Sun J, Bozym DJ, et al. An immunogenic personal neoantigen vaccine for patients with melanoma. Nature (2017) 547(7662):217–21. doi: 10.1038/nature22991
99. Sahin U, Derhovanessian E, Miller M, Kloke BP, Simon P, Lower M, et al. Personalized RNA mutanome vaccines mobilize poly-specific therapeutic immunity against cancer. Nature (2017) 547(7662):222–6. doi: 10.1038/nature23003
100. Schumacher T, Bunse L, Pusch S, Sahm F, Wiestler B, Quandt J, et al. A vaccine targeting mutant IDH1 induces antitumour immunity. Nature (2014) 512(7514):324–7. doi: 10.1038/nature13387
101. Wilgenhof S, Corthals J, Heirman C, van Baren N, Lucas S, Kvistborg P, et al. Phase II Study of Autologous Monocyte-Derived mRNA Electroporated Dendritic Cells (TriMixDC-MEL) Plus Ipilimumab in Patients With Pretreated Advanced Melanoma. J Clin Oncol (2016) 34(12):1330–8. doi: 10.1200/JCO.2015.63.4121
102. Kantoff PW, Higano CS, Shore ND, Berger ER, Small EJ, Penson DF, et al. Sipuleucel-T immunotherapy for castration-resistant prostate cancer. N Engl J Med (2010) 363(5):411–22. doi: 10.1056/NEJMoa1001294
103. Mastelic-Gavillet B, Balint K, Boudousquie C, Gannon PO, Kandalaft LE. Personalized Dendritic Cell Vaccines-Recent Breakthroughs and Encouraging Clinical Results. Front Immunol (2019) 10:766. doi: 10.3389/fimmu.2019.00766
104. Liu H, Moynihan KD, Zheng Y, Szeto GL, Li AV, Huang B, et al. Structure-based programming of lymph-node targeting in molecular vaccines. Nature (2014) 507(7493):519–22. doi: 10.1038/nature12978
105. Anandasabapathy N, Breton G, Hurley A, Caskey M, Trumpfheller C, Sarma P, et al. Efficacy and safety of CDX-301, recombinant human Flt3L, at expanding dendritic cells and hematopoietic stem cells in healthy human volunteers. Bone Marrow Transplant (2015) 50(7):924–30. doi: 10.1038/bmt.2015.74
106. Maraskovsky E, Daro E, Roux E, Teepe M, Maliszewski CR, Hoek J, et al. In vivo generation of human dendritic cell subsets by Flt3 ligand. Blood (2000) 96(3):878–84. doi: 10.1182/blood.V96.3.878.015k15_878_884
107. Pulendran B, Banchereau J, Burkeholder S, Kraus E, Guinet E, Chalouni C, et al. Flt3-ligand and granulocyte colony-stimulating factor mobilize distinct human dendritic cell subsets in vivo. J Immunol (2000) 165(1):566–72. doi: 10.4049/jimmunol.165.1.566
108. Obeid J, Hu Y, Slingluff CL Jr. Vaccines, Adjuvants, and Dendritic Cell Activators–Current Status and Future Challenges. Semin Oncol (2015) 42(4):549–61. doi: 10.1053/j.seminoncol.2015.05.006
109. Palucka K, Banchereau J, Mellman I. Designing vaccines based on biology of human dendritic cell subsets. Immunity. (2010) 33(4):464–78. doi: 10.1016/j.immuni.2010.10.007
110. Lever M, Maini PK, van der Merwe PA, Dushek O. Phenotypic models of T cell activation. Nat Rev Immunol (2014) 14(9):619–29. doi: 10.1038/nri3728
111. Irving M, Zoete V, Hebeisen M, Schmid D, Baumgartner P, Guillaume P, et al. Interplay between T cell receptor binding kinetics and the level of cognate peptide presented by major histocompatibility complexes governs CD8+ T cell responsiveness. J Biol Chem (2012) 287(27):23068–78. doi: 10.1074/jbc.M112.357673
Keywords: T-cell avidity, DC vaccines, cancer vaccines, immature DCs, mathematical model
Citation: Kumbhari A, Egelston CA, Lee PP and Kim PS (2020) Mature Dendritic Cells May Promote High-Avidity Tuning of Vaccine T Cell Responses. Front. Immunol. 11:584680. doi: 10.3389/fimmu.2020.584680
Received: 17 July 2020; Accepted: 05 October 2020;
Published: 30 October 2020.
Edited by:
Graham Pawelec, University of Tübingen, GermanyReviewed by:
Markus Philipp Radsak, Johannes Gutenberg University Mainz, GermanyMichele De Palma, École Polytechnique Fédérale de Lausanne, Switzerland
Copyright © 2020 Kumbhari, Egelston, Lee and Kim. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Peter S. Kim, cGV0ZXIua2ltQHN5ZG5leS5lZHUuYXU=
†These authors share first authorship
‡These authors have contributed equally to this work
 Adarsh Kumbhari
Adarsh Kumbhari Colt A. Egelston
Colt A. Egelston Peter P. Lee
Peter P. Lee Peter S. Kim
Peter S. Kim