- 1Schweizerischer Verband der Diagnostikindustrie (SVDI), Bern, Switzerland
- 2Clinical and Diagnostic Immunology, Department of Microbiology, Immunology and Transplantation, KU, Leuven, Belgium
- 3Immunology Service, Department of Laboratory Medicine, University Hospitals, Leuven, Belgium
Introduction
Laboratory tests are an important component in the diagnostic process. From an analytical point of view, most tests have reached high technical standards resulting in quantitative results with very high precision and accuracy. The challenge for the clinician then is how to interpret those results. It is particularly difficult when different test systems use different scales and arbitrary units for a given biomarker, as is often the case in immunologic testing. For the clinician it is demanding to estimate the predictive value of a diagnostic test result. A solution to this problem that is advocated here is to provide likelihood ratios as a measure of the predictive value of test results. This approach is not only useful to harmonize interpretation between assays and assay platforms but can be employed as well in external quality control programs. However, the concept of likelihood ratios in clinical diagnostics, although not new, is not yet generally accepted and needs further promotion by demonstrating its usefulness.
Some 55 years ago, a “technic for the estimation of the predictive value of diagnostic test results in the subject tested when the sensitivity and specificity of the test and the prevalence of the disease in the population are known” was described (1). At that time, the technic was limited to dichotomous, qualitative test results. Later, the approach has been extended to intervals of test results and their likelihood ratio (LR) (2–6). The LR of a diagnostic test result is defined by its likelihood in diseased subjects (sensitivity) versus non-diseased subjects (1-specificity). In the field of autoimmunity, test result interval-specific LRs have been applied for the diagnosis of rheumatoid arthritis (7, 8), vasculitis (9, 10), systemic rheumatic diseases (11–16), inflammatory bowel disease and celiac disease (17–22).
It has been realized that expressing results in the form of LRs provides a convenient way to harmonize test results which otherwise would be expressed in various units and provider-defined scales, making it difficult to compare results. This has led to a proposal for harmonization of anti-neutrophil cytoplasmic antibody (ANCA) testing (23, 24), antinuclear antibody testing (25, 26) and autoimmunity tests in general by reporting test result-specific LRs (27, 28). The calculation of LRs of test result intervals has been further extended to arbitrary quantitative test results (29, 30) and applied, for example, for the diagnosis of Alzheimer’s disease (31), ANCA testing (24), antinuclear antibody testing (26) and celiac disease (22).
For the clinician, LRs could be a valuable diagnostic measure (32–35). Nevertheless, a wide application of LRs in diagnostic laboratory testing is not observed today. This might have different reasons, such as:
● a LR is related to a specific diagnosis and, habitually, the clinician does not inform the testing laboratory on the precise diagnostic question.
● a test might be used for screening purposes resulting in a differential diagnosis.
● there is a dearth of data on LRs (and consequently laboratories do not report LRs).
With regard to the differential diagnosis, it should be noted that LRs for each differential diagnosis are very valuable to estimate the relative weight of possible diagnoses (36, 37). Establishing LRs needs clinical studies to be performed, either by the in vitro diagnostics industry, the laboratories, or a collaboration of both. As this has a cost, reimbursement of laboratory tests should consider the additional clinical value of the diagnostic information given by the LR (38), which is not the case today.
What Needs to Be Done?
The field will benefit from applying LRs as quantifiable diagnostic values of laboratory tests and as means for harmonizing otherwise incompatible quantities of test results. The Receiver Operating Characteristics (ROC) curve of a test is a good basis for establishing LRs. Such ROC curves are routinely established to choose a cut-off for qualitative readouts and for calculating the area under the curve (AUC). On ROC curves the LR of a test result interval is given by the slope of the corresponding secant to the curve between the two endpoints of the interval (Figure 1) (39). Making the interval smaller and smaller the LR of a single test result is reached as the slope of the tangent to the ROC curve at the point corresponding to the test result (Figure 1) (39).
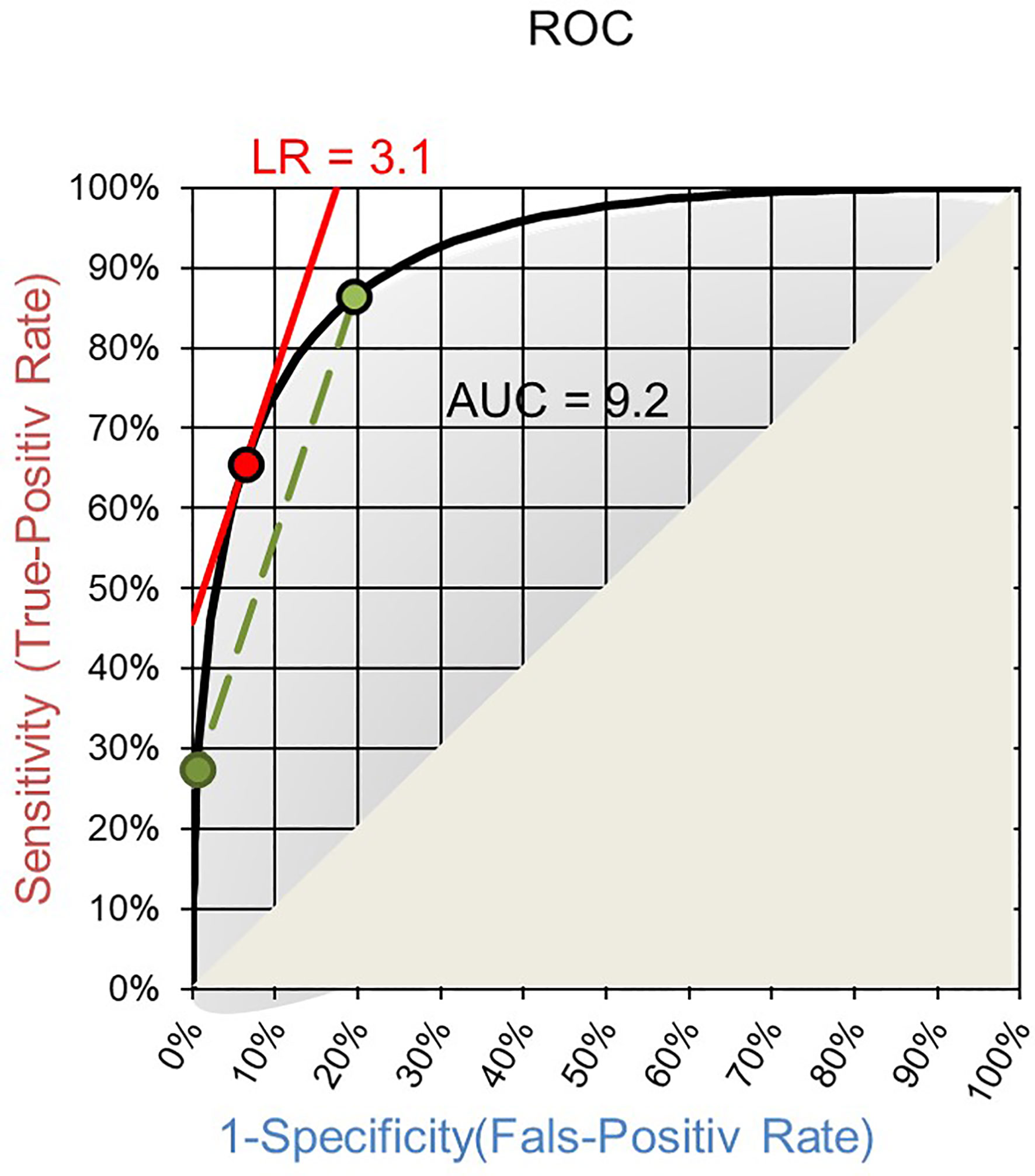
Figure 1 ROC curve with AUC. The slope of the secant (green) gives the LR of an interval of test results and the slope of the tangent (red) for a specific quantitative test result.
Since the AUC expresses the discriminant power of a test, the test producer has a high interest to publish such ROC curves. Usually only the graphical display of the curve or even only the AUC and the cut-off are published, but not the test result values corresponding to the individual points of the curve. Some publications shared the complete ROC curve dataset, which allowed to calculate the LRs using the Bézier curves method (31). Based on published ROC curves on fasting capillary glycemia testing (40), D-dimer testing (41), PSA testing (42), HbA1c testing for gestational diabetes mellitus (43), and an Alzheimer’s test (44), we determined test-result specific LRs. These data are given in Supplemental Data Figure 1.
Having access to the raw data of clinical studies and the LRs, the next step will be to guide the clinicians to understand the use of LRs. One way certainly is to apply LRs in differential diagnosis. As an example, when performing antinuclear antibody tests (ANA) for screening for connective tissue disease one would get different LRs for different diseases. This would allow the clinician to weigh the suspicions derived from other clinical data. Based on published data on antinuclear antibody testing (45), we deduced the titer-specific LR for the various systemic rheumatic diseases. The results are shown in Supplemental Data Figure 2.
Another advantage of using LRs is the harmonization of different techniques, scales, units etc. (24). It certainly would make it easier for the clinician to interpret one single scale, namely LR, than having to get acquainted with different titers, units/ml, ug/ml, mmol/l etc. Even tests using the same scale are not always comparable between different test producers but could be harmonized with LRs. Clinical guidelines giving clinical decision limits for certain test results could improve on such harmonized LRs, not only for dichotomous readouts (46, 47), but also for quantitative results.
LRs have a direct function in estimating the probability of a diagnosis. According to Bayes’ theorem the pretest odds multiplied by the LR of the test result give the posttest odds. Now, the clinician in daily practice may not be used to thinking in such numbers of probability but would rather develop an intuition for them. Nevertheless, when it comes to explain, defend, and document a diagnostic decision, LRs would be very helpful. Estimating the pretest odds might be the more difficult part. Starting from the prevalence of the disease in the population to which the patient belongs, the clinician usually adds the anamnestic and clinical findings leading to the use of a laboratory test in order to include or exclude the suspicion. A low suspicion would need a much higher LR for inclusion than a high suspicion and, conversely, a high suspicion would need a much lower LR for exclusion than a low suspicion. For example, when testing healthy pregnant women for HIV-infection the pretest odds would be around 1:100’000. Receiving now a positive screening test from the laboratory a confirmation would of course be necessary, which usually needs a second blood sample. But what should the doctor tell the patient in the meantime? Above what level of screening test results is the LR starting to get higher than 1? HIV-Screening tests have a very low cut-off to reach a maximal sensitivity, but this leads to the fact that low screening results have an LR smaller than 1. The same holds for anti-nuclear antibody screening by indirect immunofluorescence. A low titer positivity (e.g.) 1:40 or 1:80 has a low LR (<1) for systemic rheumatic disease (14).
In daily practice, the clinician probably is not thinking in terms of pretest probabilities or even pretest-odds. However, the clinical experience provides a level of premonition for a diagnosis that should be confirmed or refuted by the laboratory test. To what extend such change of suspicion is valid depends of course on the quantitative level of the test result. For standardized and frequently used tests, the clinician would intuitively have a feeling for how much the quantitative test result assures the diagnosis. But often, especially in non-harmonized test systems and when the result is at a level near the cut-off point between positivity and negativity, the information content of the result will be overestimated and therefore misleading. As an example, we recently defined for 8 different ANCA test systems assay-specific test results that corresponded to a LR of 0.1, 1, 10 and 30 (24). For the different assays, the test result that corresponded to a LR of 10 was 35 Units, 48.5 CU, 8.6 IU/mL, 2.8 AI, 10 IU/mL, 13.8 U/mL, 48 U/mL and 10.7 IU/mL (24). All these values have the same clinical meaning, namely that the chance to find such value is 10 times higher in patients with ANCA-associated vasculitis than in individuals without an ANCA-associated vasculitis. The provision of LR values would give the individual results a meaning without knowing the scales and cut-offs. When LR values will be reported by the laboratories, together with the quantitative results, the intuitive diagnostic estimation of the clinician will get with time a new dimension that is generally applicable, independent on the specific test. The diagnostic information provided by a LR of 3, 10, 30 or 100 will get a semantic content on how much secure the clinician can be in the daily routine, without calculating probabilities.
Another example that we recently worked out is on antinuclear antibodies (ANA). Lately, platforms that measure fluorescence intensities have been introduced into clinical laboratories. We defined the light intensity units that corresponded to a LR of 0.1, 0.33, 1, 3 and 10 for the NovaView, an automated ANA system from Inova Diagnostics. By doing so we found that the light intensity unit that corresponded to a LR of 0.1 was very close to the cutoff for positivity proposed by the company (26). This means that values that correspond to the cutoff are 10 times more likely to be found in individuals without an ANA-associated rheumatic disease than in patients with an ANA-associated rheumatic disease (which was in agreement with the many false positives reported by the clinicians). We report the LRs for ANA-associated rheumatic disease associated with the ANA fluorescence intensities, which helps the clinician with interpreting test results. One could even go a step further and define pattern-specific LR. Indeed, we demonstrated that the positive predictive value of ANA depends on the pattern, with the highest positive predictive values for the centromere pattern (48).
Finally, we also associated LRs to tissue transglutaminase antibody levels and this revealed that cutoffs are not aligned between manufacturers (22). Here again, test result specific LRs could help to align results between manufacturers.
A further aspect in using LRs by the laboratory is that it can be applied in external quality control. It is nowadays standard for clinical laboratories to take part in external quality controls. When starting to provide LRs of test results to the clinicians it would be important to also compare LRs with other laboratories. Upcoming differences would probably rather have their origin in the different specifications of clinical studies used to establish the ROC curves than in the technical procedures in the laboratory. This would be important to find out to improve harmonization of tests. It might lead to harmonize clinical diagnosis.
Conclusion
We here presented the concept of LR and illustrated its application in autoimmune serology. There are several advantages in applying LR to communicate the diagnostic value of a test. It allows to report test result- (or test result interval)-specific information and to harmonize interpretation between assays and assay platforms. It can not only be applied for specific diseases, but also in differential diagnosis. The concept can also be employed in external quality control programs. The advantages of using LRs in autoimmune serology is being recognized by experts and in vitro diagnostic companies and using LR has been proposed by international organizations (EASI, EFLM, …) as a convenient way to harmonize ANCA test results. Major efforts still need to be done in order to get the concept more generally accepted and applied.
Author Contributions
The authors contributed equally to the manuscript. All authors contributed to the article and approved the submitted version.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fimmu.2021.655262/full#supplementary-material
Supplementary Figure 1 | ROC curves with test result values (o) corresponding to the individual points of the curve (left) and LR as a function of test results (right) as calculated by the Bézier curves method (29). Test results with LR=1 are indicated in red. (A) Fasting capillary blood glucose as a screening test for diabetes (40). (B) D-dimer testing for suspected pulmonary embolism in outpatients (41). (C) PSA testing Gleason grade ≥7 vs Gleason grade <7 or no cancer (42). (D) HbA1c Test as a Tool in the Diagnosis of Gestational Diabetes Mellitus (43).
Supplementary Figure 2 | Based on published immunofluorescence test results (45) LRs are calculated for positive results (> 1:160) LR+, borderline results (1:40- 1:160) and negative results (<1:40) LR- in systemic lupus erythematosus (SLE), Sjogren syndrome (SS), systemic sclerosis (SSc), dermatomyositis and polymyositis (DM/PM), mixed CTD (MCTD) and rheumatoid arthritis (RA).
References
1. Vecchio TJ. Predictive value of a single diagnostic test in unselected populations. N Engl J Med (1966) 274(21):1171–3. doi: 10.1056/NEJM196605262742104
3. Brown MD, Reeves MJ. Evidence-based emergency medicine/skills for evidence-based emergency care. Interval likelihood ratios: another advantage for the evidence-based diagnostician. Ann Emerg Med (2003) 42(2):292–7. doi: 10.1067/mem.2003.274
4. Vermeersch P, Vercammen M, Holvoet A, Vande Broek I, Delforge M, Bossuyt X. Use of interval-specific likelihood ratios improves clinical interpretation of serum FLC results for the diagnosis of malignant plasma cell disorders. Clin Chim Acta (2009) 410(1–2):54–8. doi: 10.1016/j.cca.2009.09.021
5. Kohn MA, Klok FA, van Es N. D-dimer Interval Likelihood Ratios for Pulmonary Embolism. Acad Emerg Med (2017) 24(7):832–7. doi: 10.1111/acem.13191
6. Liang T, Schibeci Oraa S, Rebollo Rodríguez N, Bagade T, Chao J, Sinert R. Predicting Urinary Tract Infections With Interval Likelihood Ratios. Pediatrics (2020) 4:e2020015008. doi: 10.1542/peds.2020-015008
7. Bossuyt X, Coenen D, Fieuws S, Verschueren P, Westhovens R, Blanckaert N. Likelihood ratios as a function of antibody concentration for anti-cyclic citrullinated peptide antibodies and rheumatoid factor. Ann Rheum Dis (2009) 68(2):287–9. doi: 10.1136/ard.2007.085597
8. Bossuyt X. Anticitrullinated protein antibodies: taking into account antibody levels improves interpretation. Ann Rheum Dis (2017) 76(9):e33. doi: 10.1136/annrheumdis-2016-211039
9. Vermeersch P, Blockmans D, Bossuyt X. Use of likelihood ratios can improve the clinical usefulness of enzyme immunoassays for the diagnosis of small-vessel vasculitis. Clin Chem (2009) 55(10):1886–8. doi: 10.1373/clinchem.2009.130583
10. Bossuyt X, Rasmussen N, van Paassen P, Hellmich B, Baslund B, Vermeersch P, et al. A multicentre study to improve clinical interpretation of proteinase-3 and myeloperoxidase anti-neutrophil cytoplasmic antibodies. Rheumatol (Oxford) (2017) 56(9):1533–41. doi: 10.1093/rheumatology/kex170
11. Bossuyt X, Cooreman S, De Baere H, Verschueren P, Westhovens R, Blockmans D, et al. Detection of antinuclear antibodies by automated indirect immunofluorescence analysis. Clin Chim Acta (2013) 415:101–6. doi: 10.1016/j.cca.2012.09.021
12. Oyaert M, Bossuyt X, Ravelingien I, Van Hoovels L. Added value of indirect immunofluorescence intensity of automated antinuclear antibody testing in a secondary hospital setting. Clin Chem Lab Med (2016) 54(2):e63–6. doi: 10.1515/cclm-2015-0887
13. Op De Beéck K, Vermeersch P, Verschueren P, Westhovens R, Mariën G, Blockmans D, et al. Antinuclear antibody detection by automated multiplex immunoassay in untreated patients at the time of diagnosis. Autoimmun Rev (2012) 12(2):137–43. doi: 10.1016/j.autrev.2012.02.013
14. Op De Beeck K, Vermeersch P, Verschueren P, Westhovens R, Mariën G, Blockmans D, et al. Detection of antinuclear antibodies by indirect immunofluorescence and by solid phase assay. Autoimmun Rev (2011) 10(12):801–8. doi: 10.1016/j.autrev.2011.06.005
15. Claessens J, Belmondo T, De Langhe E, Westhovens R, Poesen K, Hüe S, et al. Solid phase assays versus automated indirect immunofluorescence for detection of antinuclear antibodies. Autoimmun Rev (2018) 17(6):533–40. doi: 10.1016/j.autrev.2018.03.002
16. Bossuyt X, Claessens J, De Langhe E, Belmondo T, Westhovens R, Hue S, et al. Antinuclear antibodies by indirect immunofluorescence and solid phase assays. Ann Rheum Dis (2020) 79(6):e65. doi: 10.1136/annrheumdis-2019-215443
17. Vermeulen N, Vermeire S, Rutgeerts P, Bossuyt X. Likelihood ratio for Crohn’s disease as a function of anti-Saccharomyces cerevisiae antibody concentration. Inflammation Bowel Dis (2010) 16(1):5–6. doi: 10.1002/ibd.20905
18. Vermeersch P, Coenen D, Geboes K, Mariën G, Hiele M, Bossuyt X. Use of likelihood ratios improves clinical interpretation of IgA anti-tTG antibody testing for celiac disease. Clin Chim Acta (2010) 411(1-2):13–7. doi: 10.1016/j.cca.2009.09.030
19. Vermeersch P, Richter T, Hauer AC, Stern M, Uhlig HH, Zimmer KP, et al. Use of likelihood ratios improves clinical interpretation of IgG and IgA anti-DGP antibody testing for celiac disease in adults and children. Clin Biochem (2011) 44(2-3):248–50. doi: 10.1016/j.clinbiochem.2010.09.026
20. Vermeersch P, Geboes K, Mariën G, Hoffman I, Hiele M, Bossuyt X. Defining thresholds of antibody levels improves diagnosis of celiac disease. Clin Gastroenterol Hepatol (2013) 11:398–403. doi: 10.1016/j.cgh.2012.10.025
21. Oyaert M, Vermeersch P, De Hertogh G, Hiele M, Vandeputte N, Hoffman I, et al. Combining antibody tests and taking into account antibody levels improves serologic diagnosis of celiac disease. Clin Chem Lab Med (2015) 53(10):1537–46. doi: 10.1515/cclm-2013-1099
22. Bogaert L, Cauchie M, Van Hoovels L, Vermeersch P, Fierz W, De Hertogh G, et al. Optimization of serologic diagnosis of celiac disease in the pediatric setting. Autoimmun Rev (2020) 19(5):102513. doi: 10.1016/j.autrev.2020.102513
23. Bossuyt X, Cohen Tervaert JW, Arimura Y, Blockmans D, Flores-Suárez LF, Guillevin L, et al. Position paper: Revised 2017 international consensus on testing of ANCAs in granulomatosis with polyangiitis and microscopic polyangiitis. Nat Rev Rheumatol (2017) 13(11):683–92. doi: 10.1038/nrrheum.2017.140
24. Bossuyt X, Damoiseaux J, Rasmussen N, van Paassen P, Hellmich B, Baslund B, et al. for (i) the European Federation of Laboratory Medicine (EFLM) Task and Finish Group “Autoimmunity Testing,” (ii) the European Autoimmune Standardization Initiative (EASI) and the (iii) European Consensus Finding Study Group on autoantibodies (ECFSG). Harmonization of antineutrophil cytoplasmic antibodies (ANCA) testing by reporting test result-specific likelihood ratios: position paper. Clin Chem Lab Med (2021) 59(2):e35–9. doi: 10.1515/cclm-2020-1178
25. Bossuyt X, De Langhe E, Borghi MO, Meroni PL. Understanding and interpreting antinuclear antibody tests in systemic rheumatic diseases. Nat Rev Rheumatol (2020) 16(12):715–26. doi: 10.1038/s41584-020-00522-w
26. Bossuyt X, Claessens J, Belmondo T, De Langhe E, Westhovens R, Poesen K, et al. Harmonization of clinical interpretation of antinuclear antibody test results by solid phase assay and by indirect immunofluorescence through likelihood ratios. Autoimmun Rev (2019) 18(11):102386. doi: 10.1016/j.autrev.2019.102386
27. Damoiseaux J. The perspective on standardisation and harmonisation: the viewpoint of the EASI president. Auto Immun Highlights (2020) 611(1):4. doi: 10.1186/s13317-020-0127-3
28. Sack U, Bossuyt X, Andreeva H, Antal-Szalmás P, Bizzaro N, Bogdanos D, et al. European Autoimmunity Standardisation Initiative. Quality and best practice in medical laboratories: specific requests for autoimmunity testing. Auto Immun Highlights (2020) 311(1):12. doi: 10.1186/s13317-020-00134-0
29. Fierz W. Likelihood ratios of quantitative laboratory results in medical diagnosis: The application of Bézier curves in ROC analysis. PloS One (2018) 13(2):e0192420. doi: 10.1371/journal.pone.0192420
30. Fierz W. A simplified method to approximate a ROC curve with a Bézier curve to calculate likelihood ratios of quantitative test results. MethodsX (2020) 7:100915. doi: 10.1016/j.mex.2020.100915
31. Fierz W. Application of Bézier Curves for Calculating Likelihood Ratios for Plasma Amyloid-β Biomarkers for Alzheimer’s Disease. Front Aging Neurosci (2018) 10:276. doi: 10.3389/fnagi.2018.00276
32. Vermeersch P, Bossuyt X. Comparative analysis of different approaches to report diagnostic accuracy. Arch Intern Med (2010) 170(8):734–5. doi: 10.1001/archinternmed.2010.84
33. Gallagher EJ. Clinical utility of likelihood ratios. Ann Emerg Med (1998) 31(3):391–7. doi: 10.1016/S0196-0644(98)70352-X
34. Grimes DA, Schulz KF. Refining clinical diagnosis with likelihood ratios. Lancet (2005) 365(9469):1500–5. doi: 10.1016/S0140-6736(05)66422-7
35. Moosapour H, Raza M, Rambod M, Soltani A. Conceptualization of category-oriented likelihood ratio: a useful tool for clinical diagnostic reasoning. BMC Med Educ (2011) 1711:94. doi: 10.1186/1472-6920-11-94
36. Lipkin M. The Likelihood Concept In Differential Diagnosis. Perspect Biol Med (1964) 7:485–97. doi: 10.1353/pbm.1964.0018
37. Brenner H. Measures of differential diagnostic value of diagnostic procedures. J Clin Epidemiol (1996) 49(12):1435–39. doi: 10.1016/S0895-4356(96)00215-6
38. Fierz W, Bossuyt X. Likelihood Ratios as Value Proposition for Diagnostic Laboratory Tests. J Appl Lab Med (2020) 15(5):1061–9. doi: 10.1093/jalm/jfaa064
39. Choi BC. Slopes of a receiver operating characteristic curve and likelihood ratios for a diagnostic test. Am J Epidemiol (1998) 1148(11):1127–32. doi: 10.1093/oxfordjournals.aje.a009592
40. Bortheiry AL, Malerbi DA, Franco LJ. The ROC curve in the evaluation of fasting capillary blood glucose as a screening test for diabetes and IGT. Diabetes Care (1994) 17(11):1269–72. doi: 10.2337/diacare.17.11.1269
41. Perrier A, Desmarais S, Goehring C, de Moerloose P, Morabia A, Unger PF, et al. D-dimer testing for suspected pulmonary embolism in outpatients. Am J Respir Crit Care Med (1997) 156(2 Pt 1):492–6. doi: 10.1164/ajrccm.156.2.9702032
42. Thompson IM, Ankerst DP, Chi C, Lucia MS, Goodman PJ, Crowley JJ, et al. Operating characteristics of prostate-specific antigen in men with an initial PSA level of 3.0 ng/ml or lower. JAMA (2005) 294(1):66–70. doi: 10.1001/jama.294.1.66
43. Renz PB, Cavagnolli G, Weinert LS, Silveiro SP, Camargo JL. HbA1c Test as a Tool in the Diagnosis of Gestational Diabetes Mellitus. PloS One (2015) 10(8):e0135989. doi: 10.1371/journal.pone.0135989
44. Nakamura A, Kaneko N, Villemagne VL, Kato T, Doecke J, Doré V, et al. High performance plasma amyloid-β biomarkers for Alzheimer’s disease. Nature (2018) 554(7691):249–54. doi: 10.1038/nature25456
45. Hayashi N, Kawamoto T, Mukai M, Morinobu A, Koshiba M, Kondo S, et al. Detection of antinuclear antibodies by use of an enzyme immunoassay with nuclear HEp-2 cell extract and recombinant antigens: comparison with immunofluorescence assay in 307 patients. Clin Chem (2001) 47(9):1649–59. doi: 10.1093/clinchem/47.9.1649
46. Solomon DH, Kavanaugh AJ, Schur PH. American College of Rheumatology Ad Hoc Committee on Immunologic Testing Guidelines. Evidence-based guidelines for the use of immunologic tests: antinuclear antibody testing. Arthritis Rheum (2002) 47(4):434–44. doi: 10.1002/art.10561
47. Kavanaugh AF, Solomon DH. American College of Rheumatology Ad Hoc Committee on Immunologic Testing Guidelines. Guidelines for immunologic laboratory testing in the rheumatic diseases: anti-DNA antibody tests. Arthritis Rheumatol (2002) 47(5):546–55. doi: 10.1002/art.10558
Keywords: clinical interpretation, laboratory tests, likelihood ratio, harmonization, quality control
Citation: Fierz W and Bossuyt X (2021) Likelihood Ratio Approach and Clinical Interpretation of Laboratory Tests. Front. Immunol. 12:655262. doi: 10.3389/fimmu.2021.655262
Received: 18 January 2021; Accepted: 23 March 2021;
Published: 16 April 2021.
Edited by:
Luis Eduardo Coelho Andrade, Federal University of São Paulo, BrazilReviewed by:
Sarah Louise Tansley, University of Bath, United KingdomCopyright © 2021 Fierz and Bossuyt. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Walter Fierz, d2FsdGVyLmZpZXJ6QHN2ZGkuY2g=
 Walter Fierz
Walter Fierz Xavier Bossuyt
Xavier Bossuyt