Antibodies and cryptographic hash functions: quantifying the specificity paradox

The specificity of the immune response is critical to its biological function, yet the generality of immune recognition implies that antibody binding is multispecific or degenerate. The current work explores and quantifies this paradox through a systems analysis approach that incorporates set theoretic ideas and an application of structural and statistical modeling to prior experimental immunological and biochemical data. Order-of-magnitude estimates are computed for the average degeneracies and specificities of antibodies and epitopes using a chemico-spatial model for epitope diversity and a binary model for antibody-antigen binding. The results illustrate and quantify how the humoral immune system achieves both high specificity and high degeneracy simultaneously by effectively decoupling the two properties, similarly to programs in cryptography called secure hash algorithms (SHAs), which display the same paradoxical features. In addition, an antibody-epitope interaction probability model is used to help show how newly formed antibodies may avoid cross-reactivity with self-antigens despite their high degree of multispecificity and how the requirement of polyclonal binding likely improves the overall specificity of the immune response. Because they describe the relationships between various statistical parameters in humoral immunity, the models developed here may also have predictive utility.

1 Introduction

Human antibodies (Abs) behave as specific to their cognate antigens (Ags) under many clinical and experimental conditions. For example, a monoclonal antibody’s specificity (1) is often critical to its therapeutic (2, 3) or diagnostic (4–6) utility. Such antibodies have commonly been referred to as “monospecific” or “monoreactive” (7–10). Early immunological thinking was, in fact, that one antibody or receptor implied one specificity (11, 12), in what has been referred to as the “one antibody, one antigen” dogma, rule or paradigm (13–15). The specificity of antibodies depends on the broad chemical and structural diversity in their variable or binding regions, which arises from a more-or-less random recombination of their coding immune gene segments (16, 17), together with several other secondary mechanisms (18–24).

Yet despite the large degree of diversity among immune cell receptors and antibodies, we know that their binding to antigens must still be highly multispecific, cross-reactive or degenerate (25–30). This is because immune recognition is thought to be inclusive of all types of antigen-sized molecules and molecular fragments (31–36)– an observation termed the postulate of antigenic totality in the present work– and while the immune repertoire of an individual is large, it is small compared to chemical space. In the language of set theory, the relation (“mapping”) of distinct antigens– or, more precisely, the parts of their structures called epitopes–to antibody species that can bind them must be many-to-one, at least on average.

The current work is an attempt to quantify and shed light on this specificity paradox. How can antibodies be both specific and multispecific? The topic has been discussed for decades with respect to both antibodies (37) and T-cells (28, 38), and estimates of T-cell receptor degeneracy have been given (25, 29). Sewell hypothesized that the capacity of T-cell receptors to retain some specificity for particular antigens despite high levels of cross-reactivity related to the sizes of their repertoires and those of their presenting peptides (28). With respect to antibodies, the current thinking is that they likely span a range of specificities, and that at least some antibodies produced late in the immune response are highly specific to their cognate antigens (39–41).

However, there has not been a formal, systematic attempt to describe the statistics of antibody-epitope interactions and to clarify–in mathematical terms–the paradoxical capacity of the adaptive immune response to display features of both multispecificity, or degeneracy, and specificity. The current study illustrates how these two properties are, in fact, distinct and statistically uncoupled. It does so by applying some set theoretic constructs and a quantitative though approximate (order-of-magnitude) systems analysis to the question. The study defines operational specificity (OpS) of antibodies precisely as how unlikely it is for an antibody to cross-react with an antigen that did not elicit it (i.e., a non-cognate antigen). It derives mathematical expressions for this quantity in regard to individual antibodies, their averages, and the antibody repertoire as a whole (systemic OpS), in terms of the other properties of the system. A binary, statistical model of antibody-antigen binding is developed (i.e., a pair either binds or it does not) and applied to prior experimental data to arrive at conservative, lower-bound estimates for antibody and epitope degeneracy, as well as cross-reactive probabilities and OpS. A related model (AEIP) is used to confirm the results and explore the frequency of antibody interaction with self-antigens, as well as the effect of polyclonality on self-interaction.

The main findings in the study are as follows:

1. A conservative, lower bound estimate for the average binding degeneracy of a human antibody is in the range of 10⁷³ to 10⁷⁶ epitopes, of which at least at least ≈10¹⁸ represent protein or peptide epitopes.

 To arrive at these estimates, a peptide-epitope chemico-spatial (PECS) model of epitope diversity is developed and combined with prior experimental data (Methods Section 2.1 and Results Sections 3.1 and 3.2).

2. An estimate for the average operational specificity (OpS) of human antibodies across a single individual’s antibody repertoire is approximately 1-10^–7 to 1-10^-12 (Results Section 3.3.1).

3. The systemic OpS–i.e. the specificity of an individual’s antibody repertoire as a whole, S_c–varies as $S_c\approx 1-\frac{{\langle D_i\rangle }^2}{N}(\text{Var}(R_j)+1)$, where ⟨D_i⟩ is the average epitope degeneracy, R_j is the distribution of normalized antibody degeneracies, and N is the size of the repertoire. (Results Section 3.3.3 and Appendix Section 6.2.3).

4. Numerical estimates of human systemic antibody OpS are in the range of ≈1-10^–7 to 1-10^–14. (Results Section 3.3.3.)

5. The specificity of individual epitopes for their cognate antigens is quite high: in the range of $1-{10}^{\mathrm{-14}}$ to $1-{10}^{\mathrm{-8}}$, but epitope space is so large that it virtually guarantees, statistically, that two randomly chosen antibodies in an immune repertoire will share many common epitopes in their binding spaces–conservatively, ≈ 10⁶ to 10¹⁶ protein or peptide epitopes, on average (Results Section 3.5), although this is a very small fraction of the total size of the relevant epitope space.

6. The average number of self-antigens to which a newly formed antibody will be complementary is in the range of ${10}^{-3}$ to 1, assuming 10,000 self-antigens and an average epitope degeneracy of 1 (see Results Section 3.7). This is consistent with experimental data.

7. The total number of antigens complementary to a polyclonal response of n antibodies increases approximately linearly with n, but the number of antigens having complementarity to multiple members (m) of that set of antibodies falls exponentially with m. (Results Section 3.8) This illustrates how the requirement of polyclonal binding in the immune response likely improves its overall specificity.

Further, it is illustrated here that the mathematical structure underlying immune specificity and degeneracy closely mirrors that of cryptographic hash functions (see ref (42) for review), also known as secure hash algorithms (SHAs). These functions take digital files as their input and generate relatively short alphanumeric codes called hash values, a.k.a. message digests, that are then attached to the files for security purposes. They are used in many types of digital security protocols, such as those generating digital signatures (43, 44). The Bitcoin mining protocol (45, 46) uses the hash algorithm SHA-256 (47, 48), which generates hash values of 256 bits in length. Mathematically, hash values and electronic files are the cryptographic counterparts of antibodies and epitopes, respectively, and they give rise to the same type of specificity paradox. Hash functions must be capable of handling any digital input, which means their outputs or digests must be highly degenerate (49), yet they must be specific enough to their originating or “cognate”¹ files to ensure digital security. In addition, although an SHA is a total, single-valued function and the relation of epitopes to antibodies in a repertoire is not, we show that the latter approximates the former in behavior (see, e.g., Results Section 3.6). To illustrate the parallels between the systems, cryptanalytic data from a single case is compared to immunologic experimental data. The example case used is an electronic file that is 4000 bits (250 16-bit words) in size, which was approximately the size of the average Bitcoin transaction over most the 2010’s (50, 51).

By integrating experimental data into a newly developed mathematical framework that describes the relationships among key immune system properties or parameters, such as size and specificity, the present work aims to improve our understanding of the statistics of antibody-antigen complementarity. It shows that antibodies, at least on average, must have very high binding degeneracies or multispecificities and illustrates how they are able to maintain high clinical and laboratory specificity despite this. It further demonstrates how this capability relies on a statistical decoupling of specificity and multispecificity, similar to the case in cryptographic hash systems. The findings here also suggest that human immune system parameters have been evolutionarily optimized to permit universal antigen recognition while limiting cross- and self-reactivity. The study focuses on the statistics of humoral immunity–i.e., B-cell receptors and antibodies–but many of the general principles are applicable to T-cell receptors as well.

2 Methods

2.1 Peptide/protein epitope chemico-spatial model

We define an epitope here as that portion of a molecular structure or set of structures (e.g., a set of amino acids) in a particular 3-D conformation, allowing for local fluctuations, that is involved in close interactions with an antibody. (See Glossary in Supplementary Material 2 for the definitions of terms used in this work.) Further, “epitopes” in this work generally refers to distinct epitopes, as opposed to copies, unless otherwise indicated.² The size of epitope space depends not only on varying amino acid sequences, but also on conformational diversity, because antibodies can discriminate conformation (52, 53). Modeling this can be complex, but the approach is simplified here by use of a peptide/protein epitope chemico-spatial (PECS) model. In this model, each amino acid in a protein or peptide epitope can occur in any of q distinct (x,y) positions, where the hypothetical (x,y) plane is defined as roughly parallel to the paratope-epitope (Ab-Ag) interface. See Figure 1. In addition, each residue can occur at different depths, or z-positions, relative to the plane. The z-coordinate is decomposed into the position of the protein surface relative to the plane and that of the residue (as defined by its alpha-carbon) relative to the surface. The decomposition is important because the set of amino acids in an epitope is not necessarily continuous on the protein polypeptide chain (54). Most epitopes, in fact, are of the discontinuous or “conformational” type (55–59). This also suggests that the z-positions of the residues be considered as mutually independent. Hence, if N_r amino acid types can occur at any one of d depths (z-positions) relative to the interfacial plane, the number of possible chemico-spatial configurations is $M_{prot}={(N_{r}d)}^q$. Because we are seeking a conservative, lower bound estimate for epitope diversity, the PECS model intentionally underestimates the total number of distinct protein/peptide epitopes (see also Appendix, Section 6.1).

Figure 1

Figure 1. Peptide/protein epitope chemico-spatial (PECS) model. Ab–antibody; red border–region of antibody interfacing with epitopes; $a_1$ through $a_6$–6 possible (x, y)-positions for epitope amino acids; red discs–α carbons of amino acids; $z_1$ through $z_5$–5 possible z-positions for the α-carbons. The (hypothetical) interfacial plane, and additional $a_k$ positions, extend from the x-axis in the y-dimension, which would run perpendicular to the page. The α carbons can occur at any of three depths within each amino acid, and the local epitope surface can, itself, occur at one of three depths relative to the interfacial plane. The model intentionally undercounts the total number of epitopes by ignoring amino acid side chain and backbone conformational diversity, as well as possible shifts in amino acid $(a_k)$ position in the (x, y) plane.

2.2 Degeneracy and operational specificity

2.2.1 Problem and solution element degeneracy

Consider finite sets Φ and Ψ containing M and N elements, respectively, and the relation

$\begin{array}{ll}H\subseteq \text{Φ}\times \text{Ψ}.& (1)\end{array}$

We refer to Φ as the problem set, its elements ϕ_i as problem elements, Ψ as the solution set, and its elements ψ_j as solution elements. For simplicity and symmetry, throughout this work, the “i” subscripts–i.e., inputs–are reserved for problem elements and the “j” subscripts for solution elements.

As illustrated in Figure 2, Φ_H is the preimage of the H relation, Ψ is considered both the image and codomain of H and is embedded in a larger set of elements, Ψ^C, the analysis of which is beyond the scope of the present study. In the immunologic context, Φ is the set of all possible epitopes, Ψ is the set of all antibodies in an individual’s repertoire, Φ_H is the set of epitopes that are complementary to (would bind to) at least 1 antibody (variable region) in Ψ, and Ψ^C is the set of all possible human antibodies (“Ψ complete”). In the cryptographic context, Φ and Ψ are the sets of all possible input files (in this work, of size 4000 bits) and all possible SHA-generated hash values (here, of 256 bits in length), respectively. Φ_H is the preimage of the SHA function, which is equal to Φ, and Ψ^C is the space of possible hash values producible by any SHA function. In both contexts, we assume that H is surjective–in other words, there is no need to consider the subset of Ψ called Ψ_H because all codomain elements (antibodies, hash values) are involved in the relation.³

Figure 2

Figure 2. Diagram of relations associating problem and solution elements in the current study. Green trapezoid ($\Phi$)–the set of all epitopes (problem elements, domain), $\left\{{\varphi }_1,{\varphi }_2, {\varphi }_3,\dots {\varphi }_{12}\right\}$; red oval ($\Psi$)–one individual’s Ab (variable region) repertoire (solution elements, codomain, image of $H$), $\left\{{\psi }_1,{\psi }_2,{\psi }_3\right\}$; $H$ (ring)–the relation associating $\text{Φ}$ and $\text{Ψ}$; grey oval (${\text{Φ}}_{\text{H}}$)–the subset of $\text{Φ}$ that is related to $\text{Ψ}$ by $H$–i.e., the preimage of $H$– which is the set of epitopes that bind to at least one Ab in $\text{Ψ}$; orange oval (${\Psi }^{\text{C}}$)–set of all possible human Ab species, of which $\text{Ψ}$ is a subset; $\text{arrows}$–complementary $(\varphi ,{\psi }^{\text{C}})$ pairs, ${\psi }^{\text{C}}\in {\text{Ψ}}^C$; blue arrows–primary or cognate $(\varphi ,\psi )$ pairs; solid, black arrows–potential collisions, i.e., ($\varphi ,\psi$) pairs involving non-cognate $\varphi$; yellow arrows– $(\varphi ,{\psi }^{\text{C}})$ pairs involving Abs outside of $\text{Ψ}$; solid, yellow arrows–pairs involving epitopes that bind only to Abs outside of $\text{Ψ}$. The subset of problem elements, here $\left\{{\varphi }_1,{\varphi }_7,{\varphi }_{12}\right\}$, involved in cognate pairs (blue arrows) is called ${\text{Φ}}_{cog}$ (see text). The dashed arrows represent pairs potentially involved in anticollisions: dashed, yellow–potential extra-repertoire anticollisions; dashed, black–a potential intra-repertoire anticollision (${\psi }_1,{\varphi }_7,{\psi }_2$). The (${\varphi }_7,{\psi }_1$) pair also gives rise to a potential collision (${\varphi }_1,{\psi }_1,{\varphi }_7$). See text for the definitions of these variables in the cryptographic context. In both contexts, ${\text{Φ}}_{\text{H}}$ is many orders of magnitude larger than $\text{Ψ}$ (not drawn to scale), and the $H$ relation is presumed to be “onto”–i.e., covers the entire codomain $\text{Ψ}$.

For convenience, we define the relations H_B and H_K as instances of the H relation (Equation 1) corresponding to immune recognition and SHAs, respectively. H_K is a total, single-valued function, whereas this study explores the extent to which H_B is or is not.

We also define the N × M relation matrix R_ij according to whether the element ϕ_i in Φ is associated with the element ψ_j in Ψ as

$${\text{R}}_{ij}=\{\begin{array}{r}\hfill 1, \text{if\hspace{0.17em}yes} \\ \hfill 0, \text{if\hspace{0.17em}no}. \end{array}$$

See also Figure 3. The degeneracy, $D_j$, of solution element $j$ is the number of correspondences or “yeses” across all problem elements⁴: $D_j$ = ${\text{R}}_{*,j}={\displaystyle {\sum }_{i=1}^M{\text{R}}_{ij}}$, and the average degeneracy⁵ across all solution elements is $\langle D_j\rangle ={\displaystyle {\sum }_{j=1}^N{D}_j/N}$. See Table 1 for a list of the variables used in this work and their definitions. Similarly, the degeneracy of problem element $i$ is $D_i={\text{R}}_{i,*}={\displaystyle {\sum }_{j=1}^N{\text{R}}_{ij}}$, and the average degeneracy across all problem elements is $\langle D_i\rangle ={\displaystyle {\sum }_{i=1}^M{D}_i/M}$. In immunity, $D_j$ is the binding degeneracy of antibody $j$ across all epitopes, and $D_i$ that of epitope $i$ across all antibodies in the repertoire. Since double sums over all ${\text{R}}_{ij}$ in the system can be carried out in either order without changing the result, we know that ${\displaystyle {\sum }_{i=1}^M{D}_i}={\displaystyle {\sum }_{j=1}^N{D}_j}$, and hence $M\langle D_i\rangle =N\langle D_j\rangle ,$which is the relation size, or the sum of all the “1”s in ${\text{R}}_{ij}$. In immunity, this is the total number of possible epitope-Ab pairs involving an individual immune repertoire. Then, $\langle D_j\rangle =\langle D_i\rangle M/N$.

Figure 3

Figure 3. Relation matrix R. ϕ_i and ψ_j–problem and solution elements as described in Figure 2; D_i and D_j– the degeneracies for problem element i and solution element j, respectively. For each possible (ϕ_i,ψ_j) pair, the corresponding matrix value indicates whether ϕ_i associates with ψ_j (in which case, R_ij =1), or not (R_ij =0). For example, problem element ϕ₁ associates with solution element ψ₁ but not with ψ₂. The primary or cognate pairs are indicated with a blue”1”. The matrix elements excluding the D_i =0 columns (ϕ₂,ϕ₁₀, and ϕ₁₁) correspond to the H relation described in Figure 2. In real-world humoral immunity, many, and perhaps most, of the D_i’s are 0 (e.g., solid yellow arrows in Figure 2; see Results Section 3.2.2). By contrast, in SHA algorithms, D_i is always 1. The rows and columns of the matrix have been transposed here for illustration purposes.

Table 1

Table 1. The main variables used in this work.

The probability, $P_{0j}$, that a randomly chosen problem element will be associated with solution element $j$ is $P_{0j}={\displaystyle {\sum }_{i=1}^M{\text{R}}_{ij}/M=D_j/M}.$ In immunity, the probability that a randomly chosen epitope will bind to (i.e., be complementary to) antibody $j$ is the degeneracy of that Ab as a fraction of the number of possible epitopes. The normalized degeneracy of each solution element can be given as the degeneracy relative to the mean, $R_j=D_j/\langle D_j\rangle$, so that $P_{0j}=R_j\langle D_j\rangle /M=R_j\langle D_i\rangle /N$. Similarly, the normalized degeneracies of the problem elements are $R_i=D_i/\langle D_i\rangle$, and the probability that a randomly chosen Ab will bind to epitope $i$ is $P_{0i}={\displaystyle {\sum }_{j=1}^N{\text{R}}_{ij}/N}=D_i/N=R_i\langle D_i\rangle /N=R_i\langle D_j\rangle /M.$

2.2.2 Operational specificity

If an antigen contains ϵ_i epitopes, E_i = {i₁,i₂,…i_ϵi}, then the number of Ab interactions it will have is $m_i={\displaystyle {\sum }_{k=1}^{{ϵ}_i}{1}_{\left\{D_{i_k}=1\right\}}}$. Assuming $D_i$ is usually 0 or 1 for most epitopes (see Section 4.2.2), then $\langle D_i\rangle <1$ and, very approximately, $m_i\approx \langle D_i\rangle {ϵ}_i$, Over all antigens, the average number of Ab interactions per antigen, $\langle m\rangle$, will more closely approximate $\langle m\rangle \approx \langle D_i\rangle \langle ϵ\rangle$. Hence, for $\langle D_i\rangle <1$, a fair approximation is $\langle D_i\rangle \approx \langle m\rangle /\langle ϵ\rangle$.

To define operational specificity, or OpS, we first establish the idea of primary or cognate pairs, which are problem element-solution element pairs that we define to be elements of a “special” or primary subset of the overall relation and that are uniquely paired. By “uniquely paired”, we mean they form a partial bijection or a bijective subset of the overall relation. Namely, they are a subset, H′, of H:

$$H^{\prime }=\left\{({\varphi }_{g(j)},{\psi }_j)\right|j\in \left\{1,2,3,\dots N\right\}\},$$

where g: Ψ → Φ_cog is a bijection (unique pairing) and Φ_cog is the subset of Φ for which each element is cognate to a corresponding element in Ψ. This assumes that M ≥ N. See Figure 2. The set of pairs of tested epitopes and their cognate antibodies is a cognate subset, as is the set of pairs of digital messages to be secured and their corresponding hash values.

As shown in Table 2, there are three possible relationships between a cognate ordered pair $({\varphi }_{i_1}, {\psi }_{j_1})$and any other ordered pair $({\varphi }_{i_2},$ ${\psi }_{j_2})$. For simplicity, the table assumes that $g(j)=j$. That is, the indices of cognate problem and solution elements are equal. 1) If $i_1\ne i_2, j_1=j_2$, the pairs share only the same solution element, and we call the relationship a collision or cross-reaction (solid, black arrows in Figure 2); 2) If $i_1=i_2, j_1\ne j_2$, the pairs share only the problem element, and the relationship is an anticollision (dashed, black arrow in Figure 2; see also Section 3.5). Finally, 3) If $i_1\ne i_2, j_1\ne j_2$, the pairs share neither element and participate in a non-collision. Throughout this work, the term “collision” will be assumed to include the idea of antibody cross-reaction with non-cognate epitopes, and “specificity” will refer to collision specificity, rather than anticollision specificity, unless otherwise stated. Notably, there are no anticollisions in SHA algorithms; the present study explores how close humoral immunity comes to this, if at all.

Table 2

Table 2. Examples of the three types of relationships between a cognate ordered pair and other ordered pairs (assuming i = j for cognate ordered pairs).

The operational specificity of an element, S, measures how unlikely it is for the element to participate in a collision or cross-reaction. For individual elements or their averages, S = 1 − P, where P is the probability of a collision⁶. If P_j = 0 and S_j = 1, then no non-cognate problem elements point to solution element j, and it has perfect specificity for its cognate problem element. In immunity, this would mean an antibody is truly monospecific. In cryptography, no alternative files would hash to primary or originating message digest j. Conversely, S_j = 0 implies that all problem elements collide: all non-cognate epitopes cross-react with antibody j and all alternative files hash to message digest j. This is illustrated in Figure 4.

Figure 4

Figure 4. Dependence of specificity (OpS) on degeneracy. The operational specificity, S_j, of a solution element (e.g., an antibody or hash value) for its cognate problem element (e.g., epitope or digital file), relative to a randomly selected problem element, is plotted on the vertical axis as a function of its degeneracy, D_j. The various lines represent different sizes, M, for the problem space, which determine the line’s slope. The point (D_j,S_j) = (1,1), labeled the “point of monospecificity,” is the only point where the solution element is absolutely specific for its cognate problem element. It is also where the specificity is independent of the size of problem space. When D_j = M, (e.g., D_j =10,000 for M =10,000), the specificity is zero.

Collision probabilities and OpS can be considered in the context of individual antibodies, P_j, S_j, or system averages, ⟨P_j⟩, ⟨S_j⟩. In addition, the systemic probability of a collision, P_c, is the probability of a cross-reaction between a solution element and one non-cognate problem element anywhere across the entire solution space, and the systemic OpS, S_c, is the corresponding specificity.

For individual solution elements and $D_j\gg 1$, $P_j\approx \frac{D_j}{M}=P_{0j}$ and $S_j\approx 1-\frac{D_j}{M}$. Hence, as depicted in Figure 4, the specificity is a function of the degeneracy and the size of the problem space. The latter expression is similar in form, though not exactly the same, as the measure called specificity used in binary medical tests (60).⁷ Similarly, For $D_j\gg 1$, averages across the system are

$\begin{array}{ll}\langle P_j\rangle \approx \frac{\langle D_j\rangle }{M}=\frac{\langle D_i\rangle }{N}& (2)\end{array}$

and $\langle S_j\rangle$ is 1 minus those quantities.

For large problem/solution spaces, systemic OpS is generally S_c ≈ e^−Pc, which reduces to S ≈ 1 − P_c for P_c ≪ 1. The forms for P_c and S_c in terms of other system variables, as well as all derivations, are provided in the Appendix (Section 6.2) and Supplementary Material 3.

2.2.3 Phenomenological simulations related to systemic OpS

In this set of calculations, N antibodies in the system were assigned degeneracies (D_j’s) conforming to a positive-valued Gaussian distribution. Then, D_j epitopes were randomly associated with each antibody, j, one Ab per epitope (D_i =1). Pairs of epitopes were then selected at random–the first representing the cognate epitope in an antibody-epitope pair. If the second happened to bind the same antibody as the first, then the epitope pairing was counted as an Ab cross-reaction. This was repeated for the entire set of epitopes, so that there were a maximum of 100,000 ×99,999/2 ≈ 5 x 10⁹ epitope pairs per trial. The probability of cross-reaction was calculated as the number of positive cross-reactions divided by the total number of epitope pairs, and this was compared to the theoretical result. A number of trials were carried out, varying the spread of the degeneracies (σ of the Gaussian distribution). The actual number of epitope pairs per trial varied between 2 and 5 billion, because of the effect of truncating the Gaussian (at D_j=0), which varied with the spread parameter.

2.3 Antibody-epitope interaction probability model

2.3.1 AEIP model form

The above models do not take into account sampling of subsets of antibodies from larger pools, as occurs in polyclonal immune responses to an antigen. To guarantee the generation of accurate statistics for multi-epitope, multi-antibody interactions involving such sampling across all size scales, the antibody-epitope interaction probability (AEIP) model was developed. This model generates the probability, P(ϵ, m, n, N), of an antigen having ϵ epitopes that will participate in m interactions with a set of n distinct antibodies or B-cell clones selected from a larger pool of N clones in the immune repertoire. The total number of expected complementary interactions, or “matches,” ⟨W⟩, given A tested antigens, is then simply ⟨W⟩ = AP. The assumptions are that 1) H_B is total (no unassigned epitopes), 2) H_B is random; 3) the antigens are each assigned random epitopes, 4) duplicate epitope-antibody matches for a given antigen are not allowed (no combinatoric replacement), and 5) the antigenic binding spaces of the Abs are of the same size (all D_j are equal). This last condition is why the Ab degeneracies do not appear explicitly in the model. Conditions 2, 3, and 5 imply that the antigenic space is apportioned more-or-less evenly among the N antibodies.

The probability is the product of four terms:

$\begin{array}{ll}P(ϵ,m,n,N),=S_{ϵ}{C}_n{T}_1{T}_2& (3)\end{array}$

where

$$S_{ϵ}=\frac{ϵ!}{(ϵ-m)!},C_n=\frac{n!}{(n-m)!m!},T_1=\frac{(N-n)!}{(N-n-ϵ+m)!},T_2=\frac{(N-ϵ)!}{N!},$$

provided that the arguments of the factorials are all greater than zero–i.e., N ≥ {ϵ,n} ≥ m, and N ≥ n + ϵ − m. This expression is exact, in the sense that statistical results will converge to it over a large number of trials.

In the special case of n =1 (a single selected or tested Ab), the number of cross-reactive matches, m, can be either 0 or 1, and the probability reduces to

$$P(ϵ,m,1,N)=\{\begin{array}{l}1-ϵ/N\text{ if }m=0,\hfill \\ ϵ/N\text{ if }m=1,\hfill \end{array}$$

and ⟨W⟩ = Aϵ/N for a single match. Since ⟨D_i⟩ = 1 in the AEIP model, from Equation 2 the average probability of collision for an individual Ab is ⟨P_j⟩ ≈ 1/N and ⟨W⟩ = Aϵ⟨P_j⟩, as in the example given in Results Section 3.7.

As discussed in the Appendix (Section 6.3), for arbitrary n ≥ ϵ ≥ m > 0 and N ≫ {n,ϵ,m}, the probability simplifies to P(ϵ,m,n,N) ≈ S_ϵC_n/N^m.

Various other approximations to the exact model are derived and other details are also provided in the Appendix (Section 6.3).

2.3.2 Phenomenological simulations related to the AEIP model

Several sets of trial calculations, or phenomenological simulations, were carried out to quantify the probabilities of interaction between sets of selected antibodies and arbitrary antigens, and the results were compared to the theoretical estimates from the AEIP model. For each calculation, a set of n antibodies was randomly selected out of a larger pool of N Abs, which also correspond to the N partitions into which epitope space was subdivided. Then, ϵ epitopes were randomly selected from those partitions and assigned to a test antigen and checked for complementarity with the n selected Abs. The number of non-redundant matches was then tabulated for each of A test antigens. The results were compared with the theoretical results, using the exact formulation (log form of Equation 3) and either of four approximations for the probabilities, which are described in the Appendix (Section 6.3). For most trials, ϵ = 5 was used, because that is a typical number of immunodominant epitopes involved in an immune response (61, 62) and it also allows for smaller repertoire sizes to be explored, given the constraint N > ϵ. In one set of trials (see Figure 5), ϵ =1000, which is a high-end estimate of the number of recognizable epitopes on an antigen (Supplementary Material 4).

Figure 5

Figure 5. Log plot of the probability of interaction between antibodies raised in a polyclonal response to a non-self antigen and the set of all self-antigens in the human body, according to the AEIP model. W–the average number of self-antigens, out of 10000, that will likely interact with any of 10 selected antibodies, assuming 1000 epitopes per Ag, for various sizes of antibody repertoires (base-10 log plot). m–the number of cross-reactions per antigen. It is unlikely for even one self-antigen to find two Ab matches, and the probabilities decrease exponentially from there with the number of matches.

3 Results

3.1 Size of the problem domains, Φ

3.1.1 The size of electronic file space

The size of digital file space grows exponentially with file size. The contents of a 4000-bit input file can be arranged in 2⁴⁰⁰⁰ or approximately 10¹²⁰⁴ ways, and hence the size of the file space, M = 10¹⁰²⁴. For comparison, the number of particles in the known universe is very approximately 10⁸⁰.

3.1.2 The size of peptide/protein epitope space

The number of possible epitopes that the humoral immune system could be tasked with recognizing also grows roughly exponentially with molecular or fragment size. As described in Methods, the PECS model gives a lower-bound estimate for the size of epitope space as M_prot = (N_rd)^q, where N_r is the number of residue types, q is the number of (x,y) positional “slots” for the amino acids across the binding interface and d is the number of possible z-positions, which are the depths of the α-carbons relative to the binding interface.

This is illustrated in Figure 1. As to an estimate of q, multiple studies have shown that the average protein or peptide epitope–i.e., the set of amino acids interacting at the antibody-antigen interface–consists of about 15–25 residues (58, 59, 63), and many epitope interfaces contain 30 amino acids or more. Because a reasonable lower bound is sought here, we choose 15 as the maximal number of amino acids and, in addition, we limit the number of positional slots to the number of amino acids, so that q =15. Since any of 20 possible amino acid types can occur at each of those (x,y) slots, N_r =20. To estimate d, we partition the depth of residues relative to the hypothetical interfacial plane into a number of regions, as shown in the figure. The great majority of epitope amino acids are centered at a Chakravarty depth (distance of an atom from the nearest surface water molecule) of 8Å or less, and most are between 3.5 Å and 6 Å (64). Hence, we can reasonably discretize the problem by allowing the α-carbon of an amino acid to occupy any one of three depths relative to the epitope surface, each separated by roughly 2.0-2.5Å. This separation is large enough to capture typical local fluctuations, as measured, for example, by RMS deviations of α-carbons in MD simulations of stable structures (65, 66), or between homologous α-carbons in conserved regions of different proteins (67).

The depth of the epitope surface, itself, can also vary relative to the interfacial plane. Since, again, we are erring on the side of undercounting possible configurations, we suppose only three different possible depths for the surface at each amino acid position and assume the separation to be roughly equal to that between the possible depths of the amino acids relative to the surface. Hence, each residue can be at any of d =5 depths relative to the plane (any of 3 possible positions relative to the surface, with two possible shifts of the surface). Further, since epitopes can be discontinuous, the model assumes the amino acid positions are all independent of each other. Hence, the overall estimate arising from the model is M_prot ≈ (20 · 5)¹⁵, or 10³⁰. For multiple reasons cited above and in the Appendix (Section 6.1), this is likely a very conservative lower-bound estimate for the number of possible protein epitopes that the adaptive immune response must be capable of recognizing/binding.

3.1.3 The size of hapten space

In addition to proteins and peptides, the immune system recognizes any number of molecular types, including sugars, lipids, carbohydrates, drugs and small molecules. These molecules can function as immunogens, provided they are coupled with carrier proteins. It is estimated that there are about 10⁶³ possible small organic compounds of molecular weight 500 Da or less that are stable in water at room temperature, if only C, H, O, N, P, S and halide atom types are included (68). Restricting our analysis to molecules of this size and assuming only one conformation per molecule, we can set 10⁶³ as the lower bound for the number of possible haptens that the immune system is tasked with recognizing. Further, assuming that carrier proteins contribute up to 10 amino acids to the combined hapten/protein epitope and using the PECS model described above for the chemical and conformational diversity of the amino acids, the total number of possible, distinct structures comprised of hapten and protein is M ≈ 10⁶³ × (20 · 5)¹⁰or about 10⁸³. This likely represents a very conservative, lower-bound estimate of the number of possible molecular structures to which the immune system could be challenged to respond, because 1) larger haptens (e.g., digoxin at a M.W. of 781 Da) (69), haptens containing different atom types (70, 71), and larger protein epitopes (72) are known to exist, and 2) the estimate does not take into account the conformational diversity of the haptens. In addition, M or |Φ| is likely to be significantly larger than the number of structures, because humoral immunity generally recognizes multiple epitopes on each hapten-carrier conjugate. Put another way, although antigenic totality suggests M is at least as large as the number of hapten/carrier protein structures, it could be larger (see also Glossary, Supplementary Material 2).

3.2 Size of the repertoires (Ψ) and the degeneracies of ψ_j

As described in Methods (Section 2.2), the average degeneracy of solution elements (e.g., Abs) is ⟨D_j⟩ = ⟨D_i⟩ M/N, where M = |Φ| and N = |Ψ| are the problem and solution set sizes, and ⟨D_i⟩ is the average degeneracy of the problem elements (e.g., epitopes).⁸ When ⟨D_i⟩< 1, it can be considered a measure of the coverage fraction of the H relation, f_H = |Φ_H|/|Φ| –that is, the “completeness” of the binding repertoire. On the other hand, when ⟨D_i⟩ > 1, it is a measure of the “multivalued-ness” or multiplicity of H–e.g., the binding space overlap of the antibodies.

3.2.1 A hash function’s repertoire

In the cryptographic case, ⟨D_i⟩ is the average degeneracy of all files or messages, and because hash functions (H_K) behave as total mathematical functions–i.e., each digital file maps to one and only one hash value– D_i = ⟨D_i⟩ = 1, and the average degeneracy of the hash values reduces to ⟨D_j⟩ = M/N. For our example case involving SHA-256, M ≈ 10¹²⁰⁴, the size of the solution domain is N = 2²⁵⁶ ≈ 10⁷⁷, and ⟨D_j⟩≈ 10¹²⁰⁴/10⁷⁷ = 10¹¹²⁷. Hence, the H_K relation (here, SHA-256) is highly many-to-one or non-injective. In this absolute sense, hash values are not at all specific to a given file.

3.2.2 The antibody repertoire

Analogously to the cryptographic case, if M is the number of (distinct) epitopes, N the number of (distinct) antibodies or cellular receptors, and ⟨D_i⟩ the average degeneracy of epitopes with respect to an individual’s immune repertoire, then the average Ab degeneracy in the system is ⟨D_j⟩ = ⟨D_i⟩ M/N. The estimate for M was given above. Now, we estimate N and ⟨D_i⟩.

There are ≈ 10¹¹ to 10¹² T and B cells in the human body (73, 74) and because there tend to be multiple copies of each cellular clone, the number of chemically distinct antibodies/immune receptors in an individual–i.e., the size an individual’s immune repertoire, N–is thought to be⁹ in the range of 10⁷ to 10¹⁰ (75–78).

As described in Methods (Section 2.2), a fair estimate of ⟨D_i⟩ is ≈⟨m⟩/⟨ϵ⟩, where m is the number of antibody interactions per antigen and ϵ is the number of epitopes per antigen. It is known that different antibodies can bind similar epitopes (79–84), but in this work, an epitope is defined such that similar, but distinct chemical compounds are counted as different epitopes. We know that D_i is often< 1, since individual immune responses tend not to produce antibodies against all epitopes on an antigen (85–89). As discussed in Section 3.7 below and in Supplementary Material 4, a generous estimate for ⟨ϵ⟩ is 1000, and individual immune responses typically generate antibodies to a few tens of epitopes (⟨m⟩), so a reasonable lower bound for ⟨D_i⟩ is ≈ 10/1000=1/100. For simplicity, throughout this work ⟨D_i⟩ = 1 is often used as a first approximation for the immunologic case.

Combining estimates for M, N, and ⟨D_i⟩, a conservative lower bound estimate for ⟨D_j⟩ is a range of ≈ (1/100) × 10⁸³/10¹⁰ = 10⁷¹ to 1 × 10⁸³/10⁷ = 10⁷⁶. This is a very low-end estimate of the number of epitopes, as defined here, that each Ab species, on average, is tasked with being able to bind. The number of protein/peptide epitopes is likely to be at least ⟨D_j,prot⟩ ≈ (1/100) × 10³⁰/10¹⁰ to 1 × 10³⁰/10⁷ = 10¹⁸ to 10²³. Hence, the H_B relation is highly many-to-one as well, at least on average.

These are fairly robust results. Using a much more restrictive approximation of the size of chemical space (90, 91) for the size of the hapten domain changes the conclusions quantitatively but not qualitatively.

3.3 Operational specificity

We define operational specificity (OpS), S, as the unlikelihood of an element pairing with a non-cognate partner (See Methods, Section 2.2.2) It can be considered in at least three contexts: 1) that of averages over all solution elements, 2) that of individual solution elements and 3) that of the system as a whole. We will consider each in turn, here. We discuss anticollision probabilities and epitope OpS, with the corresponding results, in Section 3.5 and Supplementary Material 3.2.

3.3.1 Average OpS over all solution elements

Since the human immune repertoire contains 10⁷ to 10¹⁰ distinct Ab variable region species (N), conservative, lower bound estimates of $\langle P_j\rangle =\langle D_i\rangle /N$ are $\approx {10}^{-10}$ to ${10}^{-7}$ for $\langle D_i\rangle =1$, and ${10}^{-12}$ to ${10}^{-9}$ for $\langle D_i\rangle =1/100$. The corresponding estimates for $\langle S_j\rangle$ are a range of $1-{10}^{-7}$ to $1-{10}^{-10}$ and $1-{10}^{-9}$ to $1-{10}^{-12}$, respectively. It is in this sense that antibodies are, at least on average, highly specific. As depicted in Figure 6, cross-reactivity is improbable for each randomly selected antibody-epitope, on average, though not nearly as improbable as a random collision (second preimage) in a cryptographic algorithm such as SHA-256. In the case of SHA-256, ⟨S_j⟩ is about 1-10^-77. The statistical comparison between the two systems is summarized in Table 3.

Figure 6

Figure 6. Binning of chemical (or message) space. For both panels, the inner, colored circular area represents the set of possible epitopes; each of the 64 circular sectors (out to the dashed circular boundary) is the slice of chemical space to which each distinct Ab is complementary, assuming no overlap and complete coverage; ϕ₁through ϕ₆–different epitopes; crosses (+)–epitopes cognate to their respective antibodies; dots (•)–random, non-cognate epitopes. In (A) the probability that a randomly selected (•) epitope would be in the same bin as a cognate (+) epitope is 1/64, because the chemical space is divided equally. In (B) four antibodies dominate the space, so that the odds of such a cross-reaction are much higher. In this way, the probability of a cross-reaction or collision increase with the variance in the degeneracies. In cryptology, the circle represents the set of all possible digital messages that a hash function could receive as input; each slice represents a subset of messages that result in a particular digest or hash value. For SHA-256, there would be ≈10⁷⁷ slices. In humoral immunity, there are 10 million slices, or more. An expansion of the set of possible epitopes or digital files, depicted here as an enlargement of the colored circular area to the dashed outer circle, does not change the probability of a cross-reaction or collision, provided the new ϕ are randomly distributed across the solution space.

Table 3

Table 3. Basic statistical comparison between the SHA-256 model system used in this study (SHA-256 System column) and the B cell receptor/antibody immune recognition system (Humoral Immunity column).

3.3.2 Operational specificity of individual solution elements

As derived in the Appendix, Section 6.2, for high solution element degeneracies, ⟨D_j⟩ ≫ 1, the collision probability for an individual solution element (antibody or hash value), j, is P_j ≈ R_j⟨D_i⟩/N, where R_j is the normalized degeneracy of solution element j. This holds provided there are no prior correlations between problem and solution elements. In the case of SHA functions in current use, the distribution of the M files among the N − 1 non-cognate hash values is close to random and uniform (92–94). Although the output of these functions is exactly reproducible for each unique input, it varies chaotically with small changes in the input, in what is known as the avalanche effect (95), resulting in a pseudo-random distribution. And since the solution elements (hash values) are all of the same size, this pseudo-random mapping also ensures that each member of the solution set has very nearly the same number of files mapping to it (preimage cardinality). Thus, the probability distribution of R_j is spiked, with all R_j ≈ 1. Further, since ⟨D_i⟩ = 1, it is clear that P_j = ⟨D_i⟩/N ≈ 1/N, for each hash value, j. This is analogous to randomly assigning M possible problem elements into N equally sized bins, as depicted in Figure 6. The OpS for each hash value is then S_j ≈ 1 − 1/N = ⟨S_j⟩, which for the example case is, again, ≈1-10^-77.

The situation in immunity is analogous. Absent prior exposure, the distribution of epitopes across the repertoire of N − 1 non-cognate antibodies is likely very close to random, because the recombination of the coding segments for antibodies is known to be largely random (16, 17). In addition, small changes in structure tend to have disproportionate effects in antibody-antigen affinity (96–101), in what could be called the immunological version of the avalanche effect. Hence, in the general case, two epitopes with structures that vary more than slightly are no more likely to bind the same antibody than by chance.

As to the size distribution of the binding spaces of individual antibodies, there is a paucity of data, but the distribution of CDR3 lengths, which has been considered a proxy for binding site diversity, is reported to be roughly a truncated Gaussian (76, 102, 103). In any symmetric distribution of positive-valued data, the largest data point value cannot exceed twice the mean (because x_max = 2 × mean − x_min, and x_min > 0). Hence, a size distribution that is approximately a truncated Gaussian, or otherwise symmetric, implies a maximal normalized degeneracy for solution elements of R_j,max ≈ 2, and a maximal cross-reaction probability of P_j,max ≈ 2⟨D_i⟩/N = 2⟨P_j⟩. The minimal OpS of an antibody taken from a symmetric distribution of Ab degeneracies is then S_j,min ≈ 1−2⟨D_i⟩/N. Assuming, again, that ⟨D_i⟩ = 1, this means S_j,min =1 - 2 × 10^–7 to 1 - 2 × 10^-10, which is the same order of magnitude as the average OpS across all antibodies (1-10^–7 to 1-10^-10). Thus, truncated Gaussian or other symmetric binding space distributions do not, in general, lead to order-of-magnitude drops in individual Ab operational specificities, relative to the mean.

At the other extreme, the bounds for the maximal OpS (S_j,max) and minimal cross-reactivity (P_j,min) for individual antibodies are less clear. While affinity differences between different antibodies have been quantified–e.g., affinity maturation may confer an increase in binding affinity of one or two orders of magnitude (86, 104, 105)–differences in binding space sizes or specificities have not.

3.3.3 Systemic OpS

The systemic OpS takes into account all possible pairwise combinations of members of the problem repertoire (e.g., epitopes) with all (single) elements in the solution (Ab) repertoire. As detailed in the Appendix (Section 6.2), assuming large problem spaces (M ≫ 1) and solution element degeneracies (⟨D_j⟩≫ 1), and assuming complementary (ϕ,ψ) pairings are uncorrelated, the systemic probability of collision, P_c, is approximately

$\begin{array}{ll}{P}_c\approx {\frac{\langle D_i\rangle }{N}}^2(\text{Var}(R_j)+1)=\frac{{\langle D_j\rangle }^{2}N}{M^2}(\text{Var}(R_j)+1),& (4)\end{array}$

where (Var(R_j) + 1) = $K_c^{†}$ is the high-mean distribution coefficient for solution elements. The systemic OpS is given by S_c ≈ 1−P_c, provided P_c ≪ 1. As also discussed in the Appendix (Section 6.2), the P_c term is minimized, and S_c is maximized, when the probability distribution of D_j is singular (i.e., “spiked”; see Figure 7), and all R_j =1, so that the variance Var(R_j) is essentially zero and $S_c\approx 1-P_c=1-\frac{{\langle D_i\rangle }^2}{N}$. Hence, in the case of a spiked distribution, $K_c^{†}$ = 1. Notably, cryptographic hash algorithms such as SHA-256 are thought to have a spiked preimage size distribution (93, 106). For our example cryptographic case, then, we can estimate P_c for the hash function to be the same as ⟨P_j⟩, i.e., $P_c\approx \frac{{\langle D_i\rangle }^2}{N}=\frac{1^2}{{10}^{77}}=$10^-77 $\approx$ $\langle P_j\rangle$ and, similarly, $S_c\approx \langle S_j\rangle \approx$1-10^-77.

Figure 7

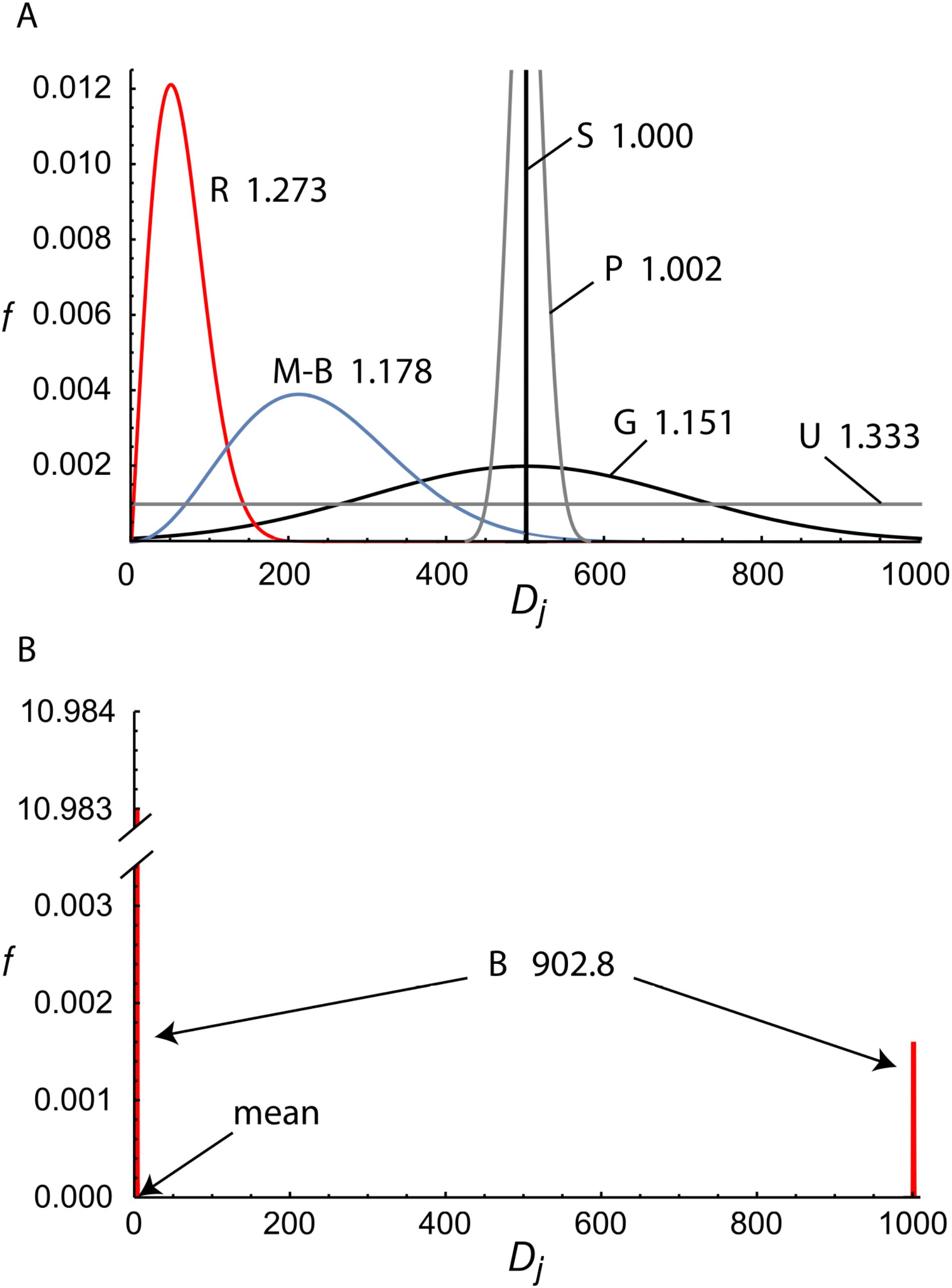
Figure 7. Unimodal and bimodal distributions for antibody or hash value degeneracies. Panel (A) shows five different unimodal distributions for solution element degeneracies, normalized to the interval D_j ∈ [0,1000], and their associated (high-mean) distribution coefficients, K_c^†. They are: R–a Rayleigh distribution (red curve) with σ =50; M-B–a Maxwell-Boltzmann distribution (blue curve) with σ =150; G–a Gaussian (black curve) with σ =200 and µ = ⟨D_j⟩ = 500; S–a singular distribution (black spike) at D_j =500, P–a Poisson distribution (grey curve) with λ = ⟨D_j⟩ = 500,; and U–a uniform distribution (grey line). The singular distribution minimizes the variance and, hence, the distribution coefficient, and it therefore maximizes the system specificity. However, the distribution coefficients of the other unimodal curves do not differ from that optimal case by more than a factor of 1.333 in these examples, despite their varying forms. By contrast, Panel (B) shows a skewed and widely split bimodal distribution (red spikes, “B”) in which a small number of elements (100) account for most (95.0%) of the system’s degeneracy and the vast majority (100,000) account for very little, resulting in a large variance and K_c^† (902.8, as well as K_c =901.9). This greatly diminishes the system OpS and increases the chances for cross reactivity or collision relative to the optimal case.

From Equation 4, note that as M is increased, so long as the solution element degeneracies, D_j, increase proportionately, P_c remains unchanged, as Var(R_j) is constant under uniform scaling of D_j. Hence, similar to the case for the average antibody OpS, as long as H_B is random, the systemic probability (P_c) and specificity (OpS) are unchanged as the number of epitopes to which the system is exposed (M) is increased. See also Figure 6 and Appendix (Section 6.2).

As mentioned above, the actual size distribution of Ab binding spaces is unclear, but there is some data to suggest that it is approximately Gaussian. Since the maximal variance of any Gaussian distribution over its positive support is the mean squared or, here, ⟨R_j⟩² (107–109), and since, by definition, ⟨R_j⟩ = 1, it must be true that max(Var(R_j)) = 1² = 1 for Ab binding degeneracies conforming to Gaussian distributions. Hence, the maximal $K_c^{†}$ for a Gaussian distribution of Ab degeneracies is 2, and for large ⟨D_j⟩ and fixed N and ⟨D_i⟩, the maximal probability of a collision across the system is $P_{c,max}=\frac{2{\langle D_i\rangle }^2}{N} ,$or twice the optimal value, and the minimal OpS, $s_{c,min}=1-\frac{2{\langle D_i\rangle }^2}{N}$. Further, what is conventionally considered a Gaussian distribution of positive data generally has a location parameter $\mu$ > 0, and in these cases, the maximal variance over the Gaussian’s positive support is ${\langle R_j\rangle }^2(\pi -2)/2$, which implies a maximal $K_c^{†}$ of $\pi /2\approx 1.5708$ and $P_{c,max}\approx \frac{1.57{\langle D_i\rangle }^2}{N}$. Table 4 shows the results of statistical trials calculating rates of epitope-Ab cross-reactivity as a function of varying spread parameter, (σ), of the (truncated) Gaussian distribution of antibody degeneracies, given fixed repertoire size N and location parameter µ. The cross-reactivity rates closely track Var(R_j), which here achieves a peak value of ≈ 0.452 at about σ =20. The rates then plateau at that of a uniform distribution (4/3N), to within discretization error.

Table 4

Table 4. Rates of cross-reactivity of 100,000 epitopes with 100 Abs for different spreads (σ) in Ab degeneracies.

As illustrated in Figure 7 and discussed in the Appendix (Section 6.4), other, related unimodal distributions, such as Rayleigh, Maxwell-Boltzmann, Poisson, and uniform distributions, have similar maximal $K_c^{† }$values and therefore give similar results. At the other extreme, systems having widely split and skewed bimodal distributions–i.e., two sub-populations with very different population sizes and degeneracies–can have a much lower OpS, as also depicted in the figure. As described in detail in the Appendix (Section 6.2.4), a split distribution will always have a higher variance and a lower OpS than a spiked distribution. The effect is much more pronounced if the lower-degeneracy peak is much taller (and thus has a significant total probability mass). Other distributions (e.g., multimodal, less widely split/less asymmetric bimodal) give intermediate results (not shown). These facts together suggest that as long as Ab degeneracies conform approximately to Gaussian or similar unimodal distributions, the systemic probability of cross-reaction is never more than twice the minimum value, and more commonly less than ≈1.57 times the minimum value, for fixed N and ⟨D_i⟩. Given our prior estimates for N, P_c,max in human immunity would fall in a range of $\approx$2 $\times$10^–10 to $\approx$2 $\times$10^–7 for $\langle D_i\rangle =1,$ and 2 $\times$10^–14 to $\approx$2 $\times$10^–11 for $\langle D_i\rangle =0.01,$ with corresponding $S_{c,min}$ ranges of 1 - $P_{c,max}$.

3.4 Statistical trial calculations of Ab-Ag cross-reaction probabilities for varying repertoire size

As mentioned earlier and described in Methods (Section 2.3), the AEIP model was developed to predict the number of interactions between arbitrary antigens and a set of antibodies selected randomly from a larger Ab pool. Several sets of corresponding trial calculations, or phenomenological simulations, were carried out, and the results were compared to those of the model. In the main set of calculations, 10 antibodies were selected at random from Ab repertoires of varying sizes and tested against 100 billion antigens, each having 5 epitopes. For the sake of simplicity and interpretability, the model assumes that at each repertoire size, the repertoires are both complete and non-overlapping–i.e., D_i =1. Hence, the model does not illustrate the effect of subtracting or adding antibodies with similar degeneracies to the immune repertoire; rather, it can be used to compare the behavior of immune systems designed with different repertoire sizes and corresponding Ab degeneracies.

The results for the number of antigens having a single cross-reactive antibody match, W, as a function of repertoire size are shown as a log-log plot in Figure 8. The plot is linear, with slope -0.988, indicating that W drops off inversely with N, approximately in proportion to N^−0.988. The theoretical and trial results are nearly superposable. The raw results, along with those of several approximations to the AEIP model, are given in Supplementary Table S1 of Supplementary Material 1.2. For a repertoire size of N = 100, over 33.9% of the antigens cross-react once, whereas for N = 1000, only ≈ 4.8% cross-react once, with similarly decreasing results for larger N.

Figure 8

Figure 8. Base-10 log-log plot of the number of single, cross-reactive Ab-Ag matches between randomly selected antigens and sets of 10 antibodies selected randomly from larger repertoires (as in a polyclonal response), as a function of repertoire size. LogW–log of the number of antigens having complementarity to exactly one antibody in the selected set. LogN–log of the size of the Ab repertoire. The red dots are the trial (simulation) results, while the blue line is a least-squares-fit of the theoretical results (from the AEIP model). The number of antigens tested is 100 billion, and the number of epitopes per Ag (ϵ) was fixed at 5.

3.5 Anticollision (epitope cross-reaction) probability and OpS

The average epitope cross-reaction probability ⟨P_i⟩ is the average probability that an epitope will be complementary to a non-cognate antibody (e.g., see dashed black arrow in Figure 2). It is given by $\langle P_i\rangle =\frac{\langle D_i^{*}\rangle }{N}$, where $\langle D_i^{*}\rangle =\langle D_i\rangle -1+L_0$ is the average non-cognate degeneracy over all epitopes–i.e., the average number of non-cognate Abs to which an epitope is complementary–and $L_0$ is the fraction of epitopes having degeneracy 0 (see Supplementary Material 3.2). Since in immunity, $\langle D_i\rangle$ is likely small, a Poisson distribution for the degeneracies is plausible–i.e., $L_k=\frac{e^{-\langle D_i\rangle }{\langle D_i\rangle }^k}{k!}$, where $L_k$is the probability of epitope $i$ having $D_i=k$. This is because, if it is fairly rare for an epitope to be complimentary to any single antibody, then the probability of complementarity to $m$ antibodies might be expected to fall off exponentially with $m$. Assuming that this is the case, $L_0=e^{-\langle D_i\rangle },$ and given our estimate of $0.01<\langle D_i\rangle <1$, $\langle D_i^{*}\rangle$ would be in a range between $\approx 5\times {10}^{-5}\text{ and }0.37$.

Further, given our previous estimates for $N$, $\langle P_i\rangle$ falls in the range of $\langle P_i\rangle \approx {10}^{-14}$ to ${10}^{-8}$, with $\langle S_i\rangle$ in the range of $\approx 1-{10}^{-8}$ to $1-{10}^{-14}$. Hence, individual epitopes would appear to be quite specific for their cognate antibodies.

However, the same is not true for systemic epitope OpS. The systemic anticollision (epitope cross-reaction) probability, $P_a$, is given by.

$\begin{array}{ll}{P}_a=\frac{{\langle D_i\rangle }^{2}M}{N(N-1)}\left(\frac{\text{Var}(D_i)}{{\langle D_i\rangle }^2}+1-\frac{1}{\langle D_i\rangle }\right),& (5)\end{array}$

where the term in parentheses is the distribution coefficient, K_a. Note that since P_a is a sum over individual probabilities over the system, it can (greatly) exceed 1, in which case it is interpreted as the expected number of epitopes complementary to two antibodies throughout the system. For N ≫ 1 and a Poisson distribution of $D_i$, $P_a \approx \frac{{\langle D_i\rangle }^{2}M}{N^2}$ (see Supplementary Material 3.2). Given our previous estimates for $N$ and $\langle D_i\rangle$, the systemic epitope cross-reaction probability, $P_a$, falls in the range of $P_a\approx {\left(\frac{0.01}{{10}^{10}}\right)}^{2}M$to ${\left(\frac{1}{{10}^7}\right)}^{2}M={10}^{-24}M$to ${10}^{-14}M.$ Even using our conservative, lower-bound estimates for $M$ and $M_{prot},$ this implies $P_a\approx {10}^{49}$ to ${10}^{59}$ across all epitopes and $P_a\approx {10}^6$to ${10}^{16}$ across only protein/peptide epitopes. Correspondingly, the systemic OpS across all epitopes, $S_a\approx e^{-P_a}=e^{-{10}^{59}}$ to $e^{-{10}^{49}}$ (see Addendum Section 8.2.3 for derivation), which is effectively zero. Hence, the large size of these epitope spaces virtually guarantees that two randomly selected antibodies will, on average, contain many of the same epitopes in their binding spaces, although this group of shared epitopes represents only a tiny fraction (e.g., ${10}^{-24}$) of the total.¹⁰

By contrast, in the cryptographic case, $L_0=0$ and $\langle D_i\rangle =1$ (each digital file maps reproducibly to a single digital signature) and hence $\langle P_i\rangle =\frac{\langle D_i\rangle -1+L_0 }{N}=0$–i.e., there are no anticollisions. Likewise, $\text{Var}(D_i)=0$ for SHAs, and hence $P_a =\frac{M}{N(N-1)}(0+1-1)=0$. Thus, with respect to systemic problem element OpS, the mathematical behavior of immune recognition and SHA functions diverges, due to the strict single-valuedness of SHAs and the size of the problem spaces. See also Discussion.

3.6 Average multiplicity and coverage fraction of the H relation

A quantity related to ⟨D_i^∗⟩ and ⟨D_i⟩ is the average multiplicity of H, which is the average number of solution elements pointed to by each problem element in Φ_H,

$$\overline{mult}(H)=\frac{{\sum }_{k=1}^{N}P(D_i=k)k}{{\sum }_{k=1}^{N}P(D_i=k)}=\frac{\langle D_i\rangle }{\left|{\Phi }_{\text{H}}\right|/\left|\Phi \right|}=\frac{\langle D_i\rangle }{f_H}.$$

In immunity, this is the average epitope degeneracy divided by the epitope coverage fraction. For a Poisson distribution of D_i, f_H = 1 − e^−⟨D_i⟩, and, hence, given our estimates for ⟨D_i⟩, approximate ranges for the coverage fraction and average multiplicity in immunity are $0.01<f_{\text{H}}<0.63$ and $1.005\le \overline{mult}(H_B)\le 1.58$, respectively. This means that, although a considerable fraction of all epitopes bind to at least one antibody in a given repertoire, most of the epitopes within that fraction bind to only one antibody–i.e., the $H_B$ relation is near-total and yet generally single-valued. For SHAs, $f_H=\overline{mult}(H_K)=1$.

3.7 Estimate of Ab cross-reactivity with self-antigens

We can estimate the expected number of antigens that will bind, or the probability of a single binding interaction, to a given (fixed) antibody. This is relevant to autoimmunity, for example. The AEIP model indicates that the probability of a single Ab-Ag interaction is linear in the number of epitopes per Ag, ϵ (see Methods section 2.3.1). For large N, the total number of interactions, can be expressed using the relation ⟨W⟩ = Aϵ⟨P_j⟩, where A is the number of antigens accessible to an antibody. In particular, we can ask, when a new Ab is randomly generated, say by somatic mutation in the periphery, what are the chances that it will cross-react with one of the body’s own antigens? As described in Supplementary Material 4, a reasonable estimate for A, in the case of self-antigens, is 10,000, and a generous estimate for ϵ is 1000.

Assuming ⟨D_i⟩ = 1, ⟨P_j⟩ has been shown in the present study to be 10^-10 to 10^-7. Taking A ≈ to be 10,000, the average local degeneracy (i.e., “local” to a restricted set of antigens), ⟨W⟩ = Aϵ⟨P_j⟩, is, therefore, in a range of about 0.001 to 1. This is the average number of self-antigens/epitopes that a single newly produced Ab species will have in its chemical binding space. Studies of polyclonal animal antibodies raised against animal proteins and tested against large arrays of human proteins have shown frequencies of strong binding events that are consistent with these statistics (110), as have studies of monoclonal Abs using panels of recombinant human antigen arrays (111). On the other hand, the lower-end estimate for ⟨D_i⟩ of 0.01 results in an estimate for ⟨W⟩ of 10⁻⁵ to 10⁻², which is somewhat lower than that expected from experiment.

3.8 The effect of polyclonal binding requirements on specificity

Although monoclonal Abs can elicit immune responses (112, 113), polyclonal Abs are generally more effective at activating the complement system (114, 115) and neutralizing soluble proteins or viral particles (116, 117), for example, because they more readily result in stable, multimeric Ab-Ag complexes. Thus, the probabilities with which non-cognate antigens will bind to multiple Abs, e.g., in a typical polyclonal immune response, is of interest with regard to autoimmunity. The dependence of these binding probabilities on the number of antibodies present in the response, the size of the repertoire, and the number of epitope-antibody complementarities, or matches, was explored in a set of theoretical calculations using the AEIP model, as well as a number of corresponding statistical calculations, or phenomenological simulations.

3.8.1 The probability of polyclonal self-reaction.

First, consider the self-reactivity example described above, but now suppose that self-antigens are exposed to ten non-cognate antibodies instead of one. As shown in Table 5, the AEIP model demonstrates that the average number of self-antigens that will cross-react once (m =1) is, as expected, higher by a factor of ≈ 10–that is, ⟨W⟩ varies in a range from 0.010 to 9.99, depending on the repertoire size and assuming ⟨D_i⟩ = 1.

Table 5

Table 5. Number of self-antigens (out of 10,000 total), each having 1000 epitopes, participating in m crossreactions with 10 test antibodies selected randomly out of the total repertoire, which varies in size here from 10⁷ to 10¹⁰, as calculated from the AEIP model.

However, as also shown in the table, as well as in Table 6 and Figure 5, and as described analytically in the Appendix (Section 6.3), the chances that an individual antigen will participate in m cross-reactive interactions –i.e., m of its epitopes interacting with m distinct, non-cognate antibodies–falls off approximately exponentially with m. Table 5 shows that the chances of any of the self-antigens in the prior example cross-reacting with any two of the selected antibodies is about 5 in a billion to 5 in 1000. Figure 5 shows a log plot of the probability of m cross-reactive matches between any of the 10,000 self-antigens in the body and 10 antibodies selected randomly from repertoires of sizes ranging from 10⁷ to 10¹⁰, assuming 1000 epitopes per Ag (ϵ =1000). The log plot is roughly linearly decreasing with m, which means the probability is exponentially decreasing. Even with this high number of epitopes per Ag, the total probability that any of the self-antigens will cross-react with two of the ten selected Abs is only ≈ 4% in the smallest repertoire (N = 10⁷ Abs), and the chances that any will cross-react with all 10 Abs is on the order of 10^-66 to 10^-36 across the various repertoire sizes.

Table 6

Table 6. Probability of cross-reactive matching for various sizes of the total Ab repertoire, N, and varying numbers of cross-reactive matches per Ag, m, assuming complete coverage of epitope space without overlap (i.e., D_i =1).

3.8.2 Phenomenological simulations of multiple cross-reactions with single antigens

This general pattern of a linearly increasing probability of single cross-reactions per Ag as a function of the number of distinct antibodies in a response, accompanied by an exponentially decreasing probability of multiple cross-reactions per Ag, is also shown in a set of phenomenological simulations (see also Methods Section 2.3.2).

An increasingly large subset of antibodies (n =1 to 10) was randomly selected from a repertoire of fixed size (N =10 million) and tested against a panel of 100 million antigens, with each having 5 epitopes per Ag. Supplementary Figure S1 in Supplementary Material 1.1 shows the number of antigens cross-reacting once with one of the n selected antibodies, according to both the numerical results of the simulations as well as the exact AEIP results. (The results of 4 different approximations to the exact model, which correspond to within ±0.0004%, are given in Supplementary Material 1.2, Supplementary Table S2). Although there is some statistical variation in the numerical trial results, the overall results indicate a linear increase in the number of epitope-antibody matches as a function of the number of antibodies present (e.g., in the polyclonal response). Hence, as expected, polyclonal antibodies are likely to result in proportionately more single cross-reactive matches than a monoclonal Ab.

However, Table 6 shows that the number of antigens, out of 100 billion, cross-reacting with m of the 10 antibodies selected randomly out of Ab repertoires of various sizes (N) decreases approximately exponentially with m. At larger N, the probability of each additional cross-reactive match drops by a factor of $\approx \frac{N(m+1)}{(5-m)(10-m)}$ for fixed N, as expected (see Appendix Section 6.3, Equation 13). In addition, the probabilities diminish in inverse proportion to N, also as expected. At a repertoire size of 10⁷, the chances of an antigen being complementary to two or more Abs are on the order of 1 in 10¹¹. Hence, in humans, the probability that multiple antibodies raised in a polyclonal response would cross-react with a given non-cognate antigen, (e.g., a self-antigen) thereby triggering a potent immune response to that antigen, is normally very small.

In cryptography, the equivalent of requiring n Ab matches for a single antigen would be to require that the digest of an input file correspond to n concatenated hash values, rather than one. This would mean effectively increasing the size of the solution space of the hash function by a factor of n, e.g., from SHA-256 to SHA-512, which exists as part of the SHA-2 standard (118, 119), or SHA-1024, which does not.

4 Discussion

This study has described the statistics that underlie the human immune system’s paradoxical ability to recognize an extremely large set of possible antigens (Ags) while retaining apparent specificity for particular cognate antigens. As has been illustrated, immunity accomplishes this by using strategies that mathematically parallel those used by cryptographic hash functions such as SHA-256. Both systems employ solution elements (antibodies, hash values) that are, at least on average, highly degenerate or multispecific toward their problem elements (epitopes, digital files), yet appear to maintain specificity for their originating or primary problem elements in real-world operation. Moreover, the study illustrates in a quantitative, albeit approximate, manner why multispecificity and specificity are viewed most usefully not as different points along the same parameter axis, but as distinct parameters or properties with different, though related, mathematical forms. In particular, specificity is a function of the degree of multispecificity, as well as other system variables.

4.1 Antibody degeneracy

The large size of epitope space, together with the need for completeness of antigen recognition, implies that antibodies must have high binding degeneracies, at least on average. This is a straightforward application of the pigeonhole principle (120) to humoral immunity. Other authors have pointed out that T-cell receptors must be multispecific (25, 38), because of the large number of possible presenting peptides. In 1998, Mason estimated that one T-cell can respond to 10⁸ different 11-mer peptides, and T-cell multispecificity has been experimentally confirmed (29). Multispecificity, or degeneracy, has also been understood to be a property of at least some antibodies (26, 33, 39, 40, 121–124). It is well-known that a single Ab variable region can have within it multiple distinct binding sites or paratopes (125), or different paratope states (27, 126, 127), that bind completely different epitopes. A single Ab paratope can bind different, unrelated epitopes (128–130), or different epitopes on the same Ag (59). Germline or “natural” antibodies–those found in human serum in the apparent absence of antigenic stimulation and which are primarily of the IgM class–are known to be “polyreactive” (26, 121), although often with low affinity. Conventionally, it has been believed that the binding regions of polyreactive antibodies tend to be more flexible (123, 131, 132), although there is evidence against this (133, 134), and a 2020 analysis indicated that polyreactive antibodies also tended to be less strongly negatively charged and less hydrophilic, while tending to have longer CDR loops in the heavy chain (135). In general, however, antibodies, and particularly affinity-matured antibodies (41, 136–139), are believed to be more specific than T-cell receptors. Overall, it has remained unclear as to how antibody multispecificity should be interpreted in the context of cases in which antibodies demonstrate exquisite specificity for particular antigenic targets.

Moreover, a global, systematic, quantitative analysis of human antibody degeneracy and its relation to specificity has not been previously undertaken. Some authors have characterized the number of possible, distinct antigens as “infinite” (39, 40). Here, through straightforward modeling and the use of prior experimental data, we arrive at conservative lower-bound estimates for the number of possible, hapten-related epitopes and protein/peptide epitopes of M =10⁸³ and M_prot =10³⁰, respectively.¹¹ These results imply a conservative, lower-bound estimate for the average degeneracy of antibodies to be ≈10⁷¹ epitopes, of which at least ≈10¹⁸ represent protein or peptide epitopes. Hence, H_B, the relation which takes epitopes to antibodies in an individual repertoire, is very highly many-to-one, at least on average.

The cryptographic case is similar: hash functions must be capable of handling any of an enormous number of possible digital files–far greater, even, than the number of possible epitopes. For a 4000-bit digital file space (roughly 100 English words), this number is M ≈ 10¹²⁰⁴, which implies an average hash value degeneracy of ≈ 10¹¹²⁷ files or messages. Thus, as is known, the hash values generated from, and assigned to, input digital files as distinguishing markers are, in fact, not at all specific in an absolute sense (140–143). In this same sense, antibodies, at least on average, are far from being absolutely specific to their cognate epitope or antigen.

4.2 The specificity paradox

The specificity paradox is that, despite this necessary degeneracy, multispecificity, or “promiscuity”, antibodies often appear to be specific to their cognate antigens in laboratory testing or clinical use (144–146), and hash functions such as SHA-256 are, in practice, highly effective digital security tools. The explanation is that the utility of these systems depends not as much on absolute specificity as it does on the degree of specificity. This idea, expressed in other terms, is well known in cryptography, but it is not widely appreciated for antibodies. In the immunological literature, the notion of polyspecificity, multispecificity or degeneracy has often been conceived of as a sort of opposite of specificity, implying a many-to-one relationship as opposed to a one-to-one relationship. This has led to some confusion.

Degeneracy is the number of complementary partners an element has in a relation–e.g., the number of epitopes to which an antibody is complementary. By contrast, specificity, strictly defined here as operational specificity, is an element’s unlikelihood of being complementary to an arbitrary, non-cognate partner–e.g., of an antibody’s being complementary to a non-cognate epitope. Hence, an element in a relation can be both highly degenerate–i.e., highly multispecific–with respect to its possible partners and, simultaneously, highly specific, without contradiction.

As described by the models and simulations in this work, the average solution element OpS is very high in both types of systems: $\approx$ 1-10^-77 for SHA-256, and $\approx$ 1-10^-7 to 1-10^-12 for the human antibody repertoire.

Hence, the solution elements in either system are sufficiently large, non-overlapping, and, as discussed below, uncorrelated to exhibit the specificity required for them to work as intended in their contexts of use. Although an Ab recognizes many molecular structures, those structures are scattered throughout chemical space and the binding repertoire. Thus, as proposed by prior authors for T-cell receptors (28), the probability that a given Ab will recognize a single, randomly selected antigen or epitope is still low. The same holds true for digital files and hash values (141, 143, 147). Since the probability of collisions or cross-reactions varies inversely with solution repertoire size, N, repertoires in these systems must be large enough to make those events sufficiently rare, yet small enough to be feasible. In addition, because the average and systemic cross-reactive probabilities $\langle P_j\rangle$ and $P_c$, depend on $\langle D_j\rangle /M$ and ${\langle D_j\rangle }^2/M^2$, respectively, it is true that as epitope spaces increase in size (M), the cross-reactive probabilities and corresponding OpS’s remain constant so long as the antibody degeneracies, ⟨D_j⟩, grow proportionately– and they do if epitopes are distributed randomly across the antibody binding spaces. Similarly, in cryptography, doubling the digital file size (squaring M) does not change the average OpS of a hash value, since ⟨D_j⟩ increases proportionately (by a factor of M). On the other hand, when the size of the solution space, N, increases, the average specificity rises, presuming the problem element degeneracy, ⟨D_i⟩, is fixed.

The meaning of systemic OpS differs substantially from that of individual OpS or its average across the system. For solution elements (e.g., antibodies), the latter two quantities are measures of whether a randomly chosen problem element (e.g., epitope) is likely to be complementary to a particular solution element. Systemic OpS, by contrast, measures how improbable it is for a collision or cross-reaction to occur anywhere across the entire system. For high average solution element degeneracies (⟨D_j⟩ ≫ 1), it has been shown here that the systemic probability of collision varies approximately as $P_c\approx \frac{{\langle D_i\rangle }^2}{N}(\text{Var}(R_j)+1)$, where R_j is the degeneracy normalized to the mean. For small individual collision probabilities (i.e., large spaces), the systemic OpS is, then, S_c ≈ e^−P_c, which reduces to 1 − P_c when P_c is ≪ 1, as it is for antibodies in a human immune repertoire or hash values generated by an SHA.

In the case of SHA functions, since all D_i =1, and the spread of hash value degeneracies (Var(D_j) or Var(R_j)) is effectively 0, these collision probabilities and the associated OpS’s are likely very close to the solution element average (1-10^-77), which is the minimum possible value for fixed, large N. Less is known about the distributions of antibody degeneracies, but there is some evidence that they are approximately Gaussian. The current work, together with the results of prior studies on statistical distributions (107–109), has illustrated that, for a fixed repertoire size and average epitope degeneracy, ⟨D_i⟩, Gaussian and many other unimodal, Gaussian-like distributions give rise to maximal cross-reaction probabilities of, at most, twice that of the minimum, and more often less than ≈ 1.57 times the minimum. Hence, systemic OpS is rather insensitive to shifts within and between these kinds of unimodal degeneracy distributions, for a large, fixed repertoire size. By contrast, a system with a widely split, bimodal degeneracy distribution and a tall left-hand peak, for example, would have a specificity that is significantly lower, by virtue of an increased variance, than that of the optimal configuration. All of this would seem to apply to hash values as well.

In humoral immunity, the current work has illustrated that, as expected, the average epitope degeneracy–i.e., the average number of distinct Abs capable of binding a particular epitope, ⟨D_i⟩–increases linearly with the number of Ab species available, assuming the average size of the individual Ab binding spaces is constant. Further, the quadratic dependence of the probability of Ab cross-reactivity, P_c, on ⟨D_i⟩, underscores why it is important for the immune system to have as low a ⟨D_i⟩ as possible while still ensuring, statistically, that the immune response will recognize multiple epitopes on any arbitrary antigen.

A related, unforeseen result of this analysis has been that while the average epitope OpS is fairly high–estimated here to be ≈ 1 − 10⁻¹⁴ to 1 − 10⁻⁸, the systemic epitope OpS, S_a, is effectively zero. This arises from the fact that for large problem/solutions spaces, systemic OpS is S_a ≈ e^−Pa and that, in contrast to the case of antibody cross-reactions or collisions, the probability (or, here, the number) of anticollisions–i.e., the expected number of epitopes complementary to any two randomly selected antibodies– $P_a \approx \frac{{\langle D_i\rangle }^{2}M}{N^2}\left(\frac{\text{Var}(D_i)}{{\langle D_i\rangle }^2}+1-\frac{1}{\langle D_i\rangle }\right)$ is very high in absolute terms. For protein or peptide epitopes, it is at least 10⁶ − 10¹⁶, and for the set of all epitopes, far higher. In this way, the immune system diverges from SHAs, for which P_a = 0 and S_a = 1. This occurs because, although the prefactor $\frac{{\langle D_i\rangle }^{2}M}{N^2}$ is extremely large in both systems due to the large problem spaces, the distribution coefficient $\left(\frac{\text{Var}(D_i)}{{\langle D_i\rangle }^2}+1-\frac{1}{\langle D_i\rangle }\right)$ for SHA digital file degeneracies is 0, while that for epitope degeneracies is > 0 (and equal to 1 for a Poisson distribution). Hence, while an individual epitope will, on average, be very specific for its cognate antibody in an immune repertoire, chemical/epitope space is so large that two antibodies selected randomly from that repertoire will still be statistically guaranteed to be complementary to many of the same epitopes, although the fraction of such epitopes relative to the total is extremely small (10⁻²⁴ to 10⁻¹⁴).¹² We have thus demonstrated that in humoral immunity, the H_B relation is almost certainly multivalued over at least part of its domain, but that this “multivalued-ness”, or multiplicity, is limited, estimated here to be ≈ 1.005 to 1.58 antibodies per epitope, on average, assuming a Poisson distribution of epitope degeneracies. Along those same lines, the average non-cognate degeneracy of an epitope is estimated to be only ≈ 0.00005 to 0.37 antibodies. Thus, while it appears that potential anticollisions (epitope cross-reactions) must exist in humoral immunity in large numbers, they are expected to actually occur fairly infrequently as long as epitopes are randomly distributed across antibody binding space.

This helps demonstrate that although the H_B relation does not mirror cryptographic hash functions exactly, in that it is not exactly a total, single-valued function, it does approximate one. The average epitope degeneracy, ⟨D_i⟩, which is a measure of the coverage fraction of H_B–i.e., the number of epitopes recognized by an individual’s repertoire (Φ_H) relative to the number of all possible epitopes (Φ)– while not exactly 1, is likely within an order of magnitude or two less than one. In fact, assuming a Poisson distribution, it implies a coverage fraction of ≈ 0.01 to 0.6, which is remarkably high, given the size of Φ (M or M_prot). Interestingly, calculated rates of Ab cross-reactivity assuming ⟨D_i⟩ = 1 were more consistent with experiment here than those assuming ⟨D_i⟩ = 0.01 (Results Section 3.7). At the same time, H_B is not highly multivalued, as just mentioned. The human immune repertoire thus seems to have been evolutionarily tuned in size and specificity to cover all of antigenic space in any single individual without much redundancy in epitope binding. If ⟨D_i⟩ were higher, for example, there would be more cross-reactivity, and if it were lower, immune recognition might be incomplete–i.e., antigenic totality might not hold.

4.3 Random association

One might argue, especially with regard to antibodies, that the specificity for local changes in epitope structure is significantly worse than the above estimates would imply, because local changes in antigen structure may not, in some cases, produce large changes in Ab binding affinity (148). It is true that immunological cross-reactions are more probable in nearby (82) than more distant (110, 111) regions of chemical/epitope space. Finding cross-reactivity is easier among related drug molecules (149), homologous antigens across species (150, 151), or surface antigens in different strains of a virus (152), for example, than it is among distantly related or unrelated antigens. This effect is mirrored by some types of cryptanalytic attacks, such as differential attacks, which exploit the fact that collisions are more apt to be found through local perturbations of digital messages than through large changes (153–155). It is also true that, over the course of an individual’s lifetime, there will be constant modification of the Ab repertoire due to affinity maturation and the filtering out of self-reactive antibodies (156, 157), so that some non-randomness is introduced (158).

However, because of 1) the randomness involved in immune gene recombination (16, 17) described earlier, 2) avalanche-type effects in Ab-Ag structure-affinity relationships (96–101), which, while often not as great as those in SHA functions, are still significant, and 3) the sheer size of chemical space, the vast majority of epitopes to which the immune system is naïve will still be more-or-less randomly distributed across Ab variable regions. This is the immunological equivalent of hash functions generating pseudo-random hash value output for each unique digital message input (92, 159).

In this way, degeneracy and specificity are decoupled in these systems. As long as hash functions generate random output, they can take on digital messages of arbitrary length (increases in M) without any significant loss of OpS in their hash values–what in cryptography is known collision resistance (160). Similarly, in adaptive immunity, as long as there are no correlations between new epitopes and, for example, antibodies/cell receptors directed against self-antigens, the immune system can afford complementarity to any arbitrarily large number of different, random epitopes without incurring higher rates of cross-reactivity. In the case of some autoimmune diseases, epitopes on pathogens can “mimic” self-epitopes such that their cognate antibodies or cell receptors are very likely to cross-react with self (161, 162) and thus the normal statistics do not hold. In a similar way, correlations between new inputs and target hash values “break” an SHA, which means they negate its security or utility (155). Hence, in both systems, randomness is a key design feature–not just to create diversity in the solution space, but to create uncorrelated diversity.

4.4 Affinity maturation and absolute specificity

Affinity-matured antibodies have a higher affinity for their cognate antigens because of the diversification and amplification of selected combining site populations that occurs during the maturation process (163, 164). One line of thinking has been that these antibodies are also more specific than primary or germline antibodies (136–139), possibly because they are more rigid (165–168). However, other studies indicate that the higher affinity may arise from a number of mechanisms unrelated to flexibility (166, 169–171).

In either case, the body’s ability to respond effectively to an antigen to which it is naïve depends critically on the diversity that exists prior to the initiation of the affinity maturation process with respect to that particular antigen. An immune repertoire that has undergone many affinity maturation events must still retain sufficient degeneracy to respond to any arbitrary antigens in the context of a limited, albeit large, total number of immune receptor species. As illustrated in this work, and as mentioned above, an immune repertoire with a bimodal distribution of antibody degeneracies has a lower systemic operational specificity than one with a singular distribution, more so if the split in the distribution is wide, with the taller peak at lower degeneracies. Not surprisingly, even antibodies that have undergone affinity maturation have been shown to cross-react with both related (80–83, 110, 149, 172, 173) and unrelated epitopes (110, 111, 128, 129, 174–177).

These findings and the statistics of immune receptors and molecular diversity as detailed in this work and as paralleled by the statistics of SHA collisions, would suggest that cross-reactive antigens to any antibody, affinity-matured or primary, probably exist somewhere in chemical/peptide space, although they may be difficult to find. Experimental data on the size of the binding spaces of individual antibodies is currently scarce, and nothing in the present work rules out the existence of particular antibodies that are absolutely specific to their cognate epitopes. However, it appears to be highly statistically, chemically and functionally improbable. Terms like “monospecific” or “monoreactive” should be understood in this context.

4.5 Factors limiting cross-reactions and collisions

As also illustrated in the current work, factors that reduce the number of cross-reactions or collisions are 1) restriction of the effective problem domains, 2) multiple-match requirements (at least in the case of immunity), and 3) low-variance degeneracy distributions, which were discussed above. In real-world operation, the absolute number of collisions or cross-reactions depends not only on the antibody specificity, which is essentially a ratio or “rate,” but on the number of problem element inputs with which the system will actually be presented, which is generally much smaller than the set of all possible inputs. As described in Supplementary Material 6, the average person will be exposed to an extremely small fraction of all possible antigenic molecular structures over his/her lifetime, and the number of self-antigens to which a novel Ab will be exposed is also relatively small. Similarly, cryptanalysts, Bitcoin miners, and thieves are limited in their searches for collisions by computational capacity and cost.

As to multiple-match requirements, this analysis illustrates the statistics by which the linkage between polyclonal antibody binding and a potent immune response likely boosts operational specificity for whole antigens relative to individual epitopes. Although there are exceptions, a potent immune response generally requires the binding of multiple antibodies to an antigen and the formation of immune complexes (see ref (178) for a review). Because they bind to different epitopes on the antigen, polyclonal antibodies facilitate the formation of these complexes. They are commonly thought of as being less specific than monoclonal antibodies (179–181), and this is true, as measured by their collective degeneracy. As illustrated in the current work, a set of multiple, distinct antibodies will have a proportionately larger antigenic binding space than an individual (monoclonal) Ab. For this reason, it has been surmised by some that polyclonal immune responses may contribute to autoimmunity (182). However, as is also illustrated here, the probability that the same antigen (e.g., a self-antigen) will cross-react with several non-cognate antibodies raised in an immune response is low, dropping off exponentially with the number of epitope-antibody matches. Because the binding spaces of the constituent antibodies in a polyclonal response are (randomly) different, the likelihood of a non-cognate antigen cross-reacting with several of them is approximately the product of the individual likelihoods. In this way, the requirement that the immune system imposes on a given antigen to participate in multiple Ab-Ag interactions before allowing it to trigger a potent immune response very likely helps to prevent autoimmunity and other non-targeted responses. The mechanism may be likened to multi-step authentication in digital security.

4.6 Other parallels and potential applications

There are other parallels between adaptive immunity and cryptology that have not been mentioned in this analysis. In some cases, these cross-disciplinary connections may provide insights or suggest avenues of investigation.

For example, although SHAs are often modeled as random oracles (92), and although their outputs are in fact close to randomly uniform distributions, cryptanalysts exploit deviations from uniformity in many types of attack by localizing target hash values to more highly populated regions of the hash value domain (e.g., references (155, 183)). In a similar way, recombination in immune cell receptor genes is not entirely random and uniform (184), and rates of somatic hypermutation, a genomic process that occurs as part of affinity maturation, also show some location- (21) and sequence-related (185, 186) biases. It is known that in B-cells that are not naïve to antigens, the heavy chain tends to determine the light chain, a phenomenon called light chain coherence (158). It is not yet clear whether any of these deviations from randomness also result in non-uniformity in the Ab binding repertoire as it affects the coverage of antigenic space; presumably, they may. Through antigenic drift (187–189) and shift (190), pathogens like viruses and bacteria mutate or genetically reassort to evade the adaptive immune response. However, the extent to which they may “attack” binding repertoire non-uniformity–i.e., occupy or mutate into regions of epitope chemical space whose cognate antibodies reside in “cold spots” in their coding sequences–has not yet been well explored and represents a potential area of research. Additional parallels between adaptive immunity and cryptography, some of which suggest other avenues of inquiry, are discussed in Supplementary Material 7.

Finally, the analytic framework developed here and its future extensions and refinements may have applications in predictive calculations–for example, in quantitative predictions of cross-reactivity among sets or pools of antibodies (191–193), particularly as more data is collected with respect to immunologic parameters such as antibody binding space sizes and epitope degeneracies. Knowledge of the mathematical relationships among system parameters should enable the determination of any single parameter, given data on the others (e.g., by rearrangement of Equation 4), or, when data on all the parameters is available, enable checks on their mutual consistency.

5 Conclusion

This study has used a probabilistic systems analysis approach to describe the statistics that underlie human antibody-antigen complementarity. It has provided conservative, lower-bound, order-of-magnitude estimates for antibody degeneracy, or multispecificity, while also defining, formulating, and quantifying the concept of operational specificity. It has illustrated why the degeneracy of human antibodies must be extremely high, at least on average, and that the properties of degeneracy and operational specificity (OpS) are distinct and, in an important sense, decoupled: as long as the assignment of epitopes to antibodies–i.e., the H_B relation–is random, OpS remains constant as the size of epitope space varies. This helps to explain and quantify the specificity paradox–namely, that antibodies can be highly degenerate, or “multispecific,” in their binding to epitopes and still display significant clinical and laboratory specificity. In particular, antibodies are specific enough for the body to be able to tolerate the production of new ones, given the number of self-antigens that they are likely to encounter, and given that the binding of cognate and non-cognate epitopes is generally uncorrelated. In addition, it has been shown here how the immune system’s imposition of multi-epitope recognition requirements, executed via the polyclonal response, increases specificity and likely helps avert autoimmunity.

The present study has also illustrated that adaptive immunity shares many similarities with cryptographic hash algorithms in its organization and function. The digital fingerprints produced by hash functions such as SHA-256 are even more highly degenerate than antibodies, but they are also more operationally specific, because of the greater size of their solution spaces, again illustrating how the two properties are uncoupled. Further, H_B approximates the behavior of SHAs, which are total, single-valued functions, by being near-total while managing to avoid high multiplicity. The parameters in humoral immunity have apparently been “tuned” to statistically ensure that multiple epitopes will be recognized on an arbitrary antigen, while minimizing the chances that any epitope will be recognized by multiple antibodies.

This work is intended as a first attempt at formalizing the analysis of degeneracy and specificity in these types of systems; it is expected that the analysis will be extended in the future to include Ψ^C, the set of all possible human antibody species, and that the numerical estimates will improve. By delineating the relationships between system parameters involved in humoral immunity, the current models extend our understanding of the statistics of cross-reactivity and could contribute to predictive calculations. The parallels between immunity and cryptography may suggest cross-disciplinary research.

Data availability statement

The original contributions presented in the study are included in the article/Appendix/Supplementary Material. Further inquiries can be directed to the corresponding author.

Ethics statement

Ethical approval was not required for the study involving humans in accordance with the local legislation and institutional requirements. Written informed consent to participate in this study was not required from the participants or the participants’ legal guardians/next of kin in accordance with the national legislation and the institutional requirements.

Author contributions

RP: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review & editing.

Funding

The author(s) declare financial support was received for the research and/or publication of this article. This work was supported in part by NIH Grant R01GM103695-05.

Acknowledgments

The author thanks Victor Ovchinnikov, Yoshitatsu Sei, the late Martin Karplus, and several Frontiers reviewers for their reading of the manuscript and suggestions. He thanks Antoine Joux, Joan Daemen, Dan Boneh and Morris J. Dworkin for helpful discussion. He also thanks the Karplus group, Harvard Medical School, Dan Kahne and the Department of Chemistry and Chemical Biology at Harvard, and Paul Conlin and the Boston VA Medical Center for support.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fimmu.2025.1585421/full#supplementary-material

Footnotes

1. ^ Here, we extend the notion of cognate, which denotes a primary (or causal) and unique pairing between an epitope and an antibody, to the general case of any system containing problem and solution elements that can be identified as having such a relationship, including cryptographic hash systems.
2. ^ The same is true for “antibodies”, which refers to a set of unique antibody species–more specifically, unique variable regions, as well as the terms “solution elements”, “problem elements”, “hash values”, and “digital files”.
3. ^ It is highly probable that all (fully formed) antibodies bind at least one epitope. Similarly, all hash values are thought to have at least one possible originating file, although this has not been proven.
4. ^ The degree of the element, in set theory. This is similar to the preimage cardinality of the element under H but degeneracy (or degree) is a property that extends to all domain or codomain elements, including those with degeneracy 0.
5. ^ The units here are problem elements, or, e.g., epitopes, but we will ignore units for conciseness in most of this work.
6. ^ Technically, a second preimage, in cryptography.
7. ^ Specificity $=1-\left(\text{false}(+)/\text{cond}(-)\right),$ where “$\text{false}(+)$” is the number of individuals in a population testing falsely positive and “$\text{cond}(-)$” the number who do not have the illness or condition.
8. ^ As mentioned, the “i” subscripts here always correspond to problem elements (e.g., epitopes) and the “j” subscripts to solution elements (e.g., Abs).
9. ^ This is significantly less than the upper limit of diversity that can, in theory, arise from immune cell gene recombination (21, 194, 195), illustrating that only a small fraction of total possible antibody and receptor variable region diversity (Ψ^C) is realized in any one individual (Ψ).
10. ^ i.e., a single epitope would cross-react with one of these randomly selected antibody pairs very infrequently, provided epitopes are randomly distributed throughout the Ab binding space.
11. ^ Since there are ≈10³² total (i.e., not unique) protein molecules in the entire human population (196) and ≈10⁸⁰ atoms in the known universe (197), this illustrates that only a small fraction of all possible species of epitopes or antigens are ever instantiated. Still, there is no evidence to suggest the immune repertoire would fail to recognize any of them.
12. ^ This is also the approximate probability that two randomly selected epitopes will cross-react with a given antibody, since ⟨D_i⟩²/N² = ⟨D_j⟩²/M².

References

1. Lipman NS, Jackson LR, Trudel LJ, and Weis-Garcia F. Monoclonal versus polyclonal antibodies: Distinguishing characteristics, applications, and information resources. ILAR J. (2005) 46:258–68. doi: 10.1093/ilar.46.3.258

PubMed Abstract | Crossref Full Text | Google Scholar

2. Bang LM and Keating GM. Adalimumab. BioDrugs. (2004) 18:121–39. doi: 10.2165/00063030-200418020-00005

PubMed Abstract | Crossref Full Text | Google Scholar

3. Quinteros DA, Bermúdez JM, Ravetti S, Cid A, Allemandi DA, and Palma SD. Therapeutic use of monoclonal antibodies: general aspects and challenges for drug delivery. In: Andronescu E. and Grumezescu A. M. (eds). Nanostructures for Drug Delivery. Micro and Nano Technologies. (Elsevier, 2017)807–833. doi: 10.1016/B978-0-323-46143-6.00025-7

Crossref Full Text | Google Scholar

4. Siddiqui MZ. Monoclonal antibodies as diagnostics; an appraisal. Indian J Pharm Sci. (2010) 72:12. doi: 10.4103/0250-474x.62229

PubMed Abstract | Crossref Full Text | Google Scholar

5. Yang M, van Bruggen R, and Xu W. Generation and diagnostic application of monoclonal antibodies against Seneca Valley virus. J Veterinary Diagn Invest. (2011) 24:42–50. doi: 10.1177/1040638711426323

PubMed Abstract | Crossref Full Text | Google Scholar

6. Lian X, Scott-Thomas A, Lewis JG, Bhatia M, MacPherson SA, Zeng Y, et al. Monoclonal antibodies and invasive aspergillosis: Diagnostic and therapeutic perspectives. Int J Mol Sci. (2022) 23:5563. doi: 10.3390/ijms23105563

PubMed Abstract | Crossref Full Text | Google Scholar

7. Wikipedia. Monospecific antibody(2022). Available online at: https://en.wikipedia.org/wiki/Monospecific_antibody (Accessed December of 2024).

Google Scholar

8. Borowska MT, Boughter CT, Bunker JJ, Guthmiller JJ, Wilson PC, Roux B, et al. Biochemical and biophysical characterization of natural polyreactivity in antibodies. Cell Rep. (2023) 42:113190. doi: 10.1016/j.celrep.2023.113190

PubMed Abstract | Crossref Full Text | Google Scholar

9. Lopes JA, Garnier NE, Pei Y, Yates JGE, Campbell ESB, Goens MM, et al. AAV-vectored expression of monospecific or bispecific monoclonal antibodies protects mice from lethal Pseudomonas aeruginosa pneumonia. Gene Ther. (2024) 31:400–12. doi: 10.1038/s41434-024-00453-1

PubMed Abstract | Crossref Full Text | Google Scholar

10. Ray CMP, Yang H, Spangler JB, and Mac Gabhann F. Mechanistic computational modeling of monospecific and bispecific antibodies targeting interleukin-6/8 receptors. PLoS Comput Biol. (2024) 20:e1012157. doi: 10.1371/journal.pcbi.1012157

PubMed Abstract | Crossref Full Text | Google Scholar

11. Ehrlich P. Croonian lecture.—on immunity with special reference to cell life. Proc R Soc Lond. (1900) 66:424–48.. doi: 10.1098/rspl.1899.0121

Crossref Full Text | Google Scholar

12. Burnet FM. A modification of Jerne’s theory of antibody production using the concept of clonal selection. Nat Immunol. (2007) 8:1024–6. (reprinted from Australian journal of science, vol 20, 1957). doi: 10.3322/canjclin.26.2.119

PubMed Abstract | Crossref Full Text | Google Scholar

13. van der Neut Kolfschoten M, Schuurman J, Losen M, Bleeker WK, Martínez-Martínez P, Vermeulen E, et al. Anti-inflammatory activity of human IgG4 antibodies by dynamic Fab arm exchange. Science. (2007) 317:1554–7. doi: 10.1126/science.1144603

PubMed Abstract | Crossref Full Text | Google Scholar

14. Tieri P, Grignolio A, Zaikin A, Mishto M, Remondini D, Castellani GC, et al. Network, degeneracy and bow tie. Integrating paradigms and architectures to grasp the complexity of the immune system. Theor Biol Med Model. (2010) 7:32. doi: 10.1186/1742-4682-7-32

PubMed Abstract | Crossref Full Text | Google Scholar

15. Jiang G, Lee CW, Wong PY, and Gazzano-Santoro H. Evaluation of semi-homogeneous assay formats for dual-specificity antibodies. J Immunol Methods. (2013) 387:51–6. doi: 10.1016/j.jim.2012.09.010

PubMed Abstract | Crossref Full Text | Google Scholar

16. Tonegawa S. Somatic generation of antibody diversity. Nature. (1983) 302:575–81. doi: 10.1038/302575a0

PubMed Abstract | Crossref Full Text | Google Scholar

17. Alt FW, Blackwell TK, and Yancopoulos GD. Development of the primary antibody repertoire. Science. (1987) 238:1079–87. doi: 10.1126/science.3317825

PubMed Abstract | Crossref Full Text | Google Scholar

18. Weigert MG, Cesari IM, Yonkovich SJ, and Cohn M. Variability in the lambda light chain sequences of mouse antibody. Nature. (1970) 228:1045–7. doi: 10.1038/2281045a0

PubMed Abstract | Crossref Full Text | Google Scholar

19. Li Z, Woo CJ, Iglesias-Ussel MD, Ronai D, and Scharff MD. The generation of antibody diversity through somatic hypermutation and class switch recombination. Genes Dev. (2004) 18:1–11. doi: 10.1101/gad.1161904

PubMed Abstract | Crossref Full Text | Google Scholar

20. Briney BS, Willis JR, and Crowe JE. Human peripheral blood antibodies with long HCDR3s are established primarily at original recombination using a limited subset of germline genes. PLoS One. (2012) 7:e36750. doi: 10.1371/journal.pone.0036750

PubMed Abstract | Crossref Full Text | Google Scholar

21. Elhanati Y, Sethna Z, Marcou Q, Callan CG, Mora T, and Walczak AM. Inferring processes underlying B-cell repertoire diversity. Philos Trans R Soc Lond B Biol Sci. (2015) 370:20140243. doi: 10.1098/rstb.2014.0243

PubMed Abstract | Crossref Full Text | Google Scholar

22. Chi X, Li Y, and Qiu X. V(D)J recombination, somatic hypermutation and class switch recombination of immunoglobulins: mechanism and regulation. Immunology. (2020) 160:233–47. doi: 10.1111/imm.13176

PubMed Abstract | Crossref Full Text | Google Scholar

23. Lebedin M, Foglierini M, Khorkova S, Vázquez García C, Ratswohl C, Davydov AN, et al. Different classes of genomic inserts contribute to human antibody diversity. Proc Natl Acad Sci. (2022) e2205470119. doi: 10.1073/pnas.2205470119

PubMed Abstract | Crossref Full Text | Google Scholar

24. Chang X, Krenger P, Krueger CC, Zha L, Han J, Yermanos A, et al. TLR7 signaling shapes and maintains antibody diversity upon virus-like particle immunization. Front Immunol. (2022) 12:827256. doi: 10.3389/fimmu.2021.827256

PubMed Abstract | Crossref Full Text | Google Scholar

25. Mason D. A very high level of crossreactivity is an essential feature of the T-cell receptor. Immunol Today. (1998) 19:395–404. doi: 10.1016/s0167-5699(98)01299-7

PubMed Abstract | Crossref Full Text | Google Scholar

26. Zhou Z, Zhang Y, Hu Y, Wahl L, Cisar J, and Notkins A. The broad antibacterial activity of the natural antibody repertoire is due to polyreactive antibodies. Cell Host Microbe. (2007) 1:51–61. doi: 10.1016/j.chom.2007.01.002

PubMed Abstract | Crossref Full Text | Google Scholar

27. Zimmermann J, Romesberg FE, Brooks CL, and Thorpe IF. Molecular description of flexibility in an antibody combining site. J Phys Chem B. (2010) 114:7359–70. doi: 10.1021/jp906421v

PubMed Abstract | Crossref Full Text | Google Scholar

28. Sewell AK. Why must T cells be cross-reactive? Nat Rev Immunol. (2012) 12:669–77. doi: 10.1038/nri3279

PubMed Abstract | Crossref Full Text | Google Scholar

29. Wooldridge L, Ekeruche-Makinde J, van den Berg H, Skowera A, Miles J, Tan M, et al. A single autoimmune T cell receptor recognizes more than a million different peptides. J Biol Chem. (2012) 287:1168–77. doi: 10.1074/jbc.m111.289488

PubMed Abstract | Crossref Full Text | Google Scholar

30. Gunti S and Notkins AL. Polyreactive antibodies: Function and quantification. J Infect Dis. (2015) 212:S42–6. doi: 10.1093/infdis/jiu512

PubMed Abstract | Crossref Full Text | Google Scholar

31. Janeway C, Travers P, Walport M, and Shlomchik M. Autoimmune responses are directed against self antigens. 5th edn. New York: Garland Science (2001).

Google Scholar

32. Collins AM, Sewell WA, and Edwards MR. Immunoglobulin gene rearrangement, repertoire diversity, and the allergic response. Pharmacol Ther. (2003) 100:157–70. doi: 10.1016/j.pharmthera.2003.07.002

PubMed Abstract | Crossref Full Text | Google Scholar

33. Peng HP, Lee KH, Jian JW, and Yang AS. Origins of specificity and affinity in antibody–protein interactions. Proc Natl Acad Sci. (2014) 111:E2656–E2665. doi: 10.1073/pnas.1401131111

PubMed Abstract | Crossref Full Text | Google Scholar

34. Goulet DR and Atkins WM. Considerations for the design of antibody-based therapeutics. J Pharm Sci. (2020) 109:74–103. doi: 10.1016/j.xphs.2019.05.031

PubMed Abstract | Crossref Full Text | Google Scholar

35. Ehlers AM, den Hartog Jager CF, Kardol-Hoefnagel T, Katsburg MMD, Knulst AC, and Otten HG. Comparison of two strategies to generate antigen-specific human monoclonal antibodies: Which method to choose for which purpose? Front Immunol. (2021) 12:660037. doi: 10.3389/fimmu.2021.660037

PubMed Abstract | Crossref Full Text | Google Scholar

36. Zhang Y. Evolution of phage display libraries for therapeutic antibody discovery. mAbs. (2023) 15. doi: 10.1080/19420862.2023.2213793

PubMed Abstract | Crossref Full Text | Google Scholar

37. Eisen HN. Specificity and degeneracy in antigen recognition: Yin and yang in the immune system. Annu Rev Immunol. (2001) 19:1–21. doi: 10.1146/annurev.immunol.19.1.1

PubMed Abstract | Crossref Full Text | Google Scholar

38. Frank S. Specificity and Cross-Reactivity. Princeton: Princeton University Press (2002). p. 35. book section 4.

Google Scholar

39. Dimitrov JD, Planchais C, Roumenina LT, Vassilev TL, Kaveri SV, and Lacroix-Desmazes S. Antibody polyreactivity in health and disease: Statu variabilis. J Immunol. (2013) 191:993–9. doi: 10.4049/jimmunol.1300880

PubMed Abstract | Crossref Full Text | Google Scholar

40. Jaiswal D, Verma S, Nair DT, and Salunke DM. Antibody multispecificity: A necessary evil? Mol Immunol. (2022) 152:153–61. doi: 10.1016/j.molimm.2022.10.012

PubMed Abstract | Crossref Full Text | Google Scholar

41. Rosenberg AM, Ayres CM, Medina-Cucurella AV, Whitehead TA, and Baker BM. Enhanced T cell receptor specificity through framework engineering. Front Immunol. (2024) 15:1345368. doi: 10.3389/fimmu.2024.1345368

PubMed Abstract | Crossref Full Text | Google Scholar

42. Sobti R and Geetha G. Cryptographic hash functions: A review. Int J Comput Sci Issues. (2012) 9:461–79.

Google Scholar

43. Diffie W and Hellman ME. New directions in cryptography. IEEE Trans Inf Theory. (1976) 22:644–54. doi: 10.1109/TIT.1976.1055638

Crossref Full Text | Google Scholar

44. Schnorr C. P.. Efficient Identification and Signatures for Smart Cards. In: Brassard G. (ed). Advances in Cryptology — CRYPTO’89 Proceedings. Lecture Notes in Computer Science. (1990) 435. Springer, New York, NY.doi: 10.1007/0-387-34805-0_22

Crossref Full Text | Google Scholar

45. Nakamoto S. Bitcoin: A peer-to-peer electronic cash system(2008). Available online at: https://bitcoin.org/bitcoin.pdf.

Google Scholar

46. Chaudhary K., Fehnker A., van de Pol J., and Stoelinga M.. Modeling and verification of the Bitcoin protocol. In: van Glabbeek R., Groote J. F., and Höfner P. (eds). Proceedings of the Workshop on Models for Formal Analysis of Real Systems (MARS 2015). Electronic Proceedings in Theoretical Computer Science. (2015)196:46–60. Open Publishing Association. doi: 10.4204/EPTCS.196.5

Crossref Full Text | Google Scholar

47. Gilbert H and Handschuh H. Security analysis of SHA-256 and sisters. In: Matsui M and Zuccherato RJ, editors. Selected Areas in Cryptography. Springer: Berlin Heidelberg (2003). p. 175–93.

Google Scholar

48. National Institute of Standards and Technology. FIPS 180-4: Secure hash standard (SHS). National Institute of Standards and Tech. (2015). doi: 10.6028/NIST.FIPS.180-4

Crossref Full Text | Google Scholar

49. Stack Exchange. SHA’s finite character set and collision(2018). Available online at: https://crypto.stackexchange.com/questions/61428/shas-finite-character-set-and-collision.

Google Scholar

50. Kasahara S and Kawahara J. Effect of Bitcoin fee on transaction-confirmation process. J Ind Manage Optimization. (2019) 15:365–86. doi: 10.3934/jimo.2018047

Crossref Full Text | Google Scholar

51. Visuals B. Transaction size: Daily median transaction size statistics per block, excluding coinbase transaction (miner reward)(2023). Available online at: https://bitcoinvisuals.com/chain-tx-size.

Google Scholar

52. Irving M, Craig L, Menendez A, Gangadhar B, Montero M, van Houten N, et al. Exploring peptide mimics for the production of antibodies against discontinuous protein epitopes. Mol Immunol. (2010) 47:1137–48. doi: 10.1016/j.molimm.2009.10.015

PubMed Abstract | Crossref Full Text | Google Scholar

53. Brown M, Joaquim T, Chambers R, Onisk D, Yin F, Moriango J, et al. Impact of immunization technology and assay application on antibody performance – a systematic comparative evaluation. PloS One. (2011) 6:e28718. doi: 10.1371/journal.pone.0028718

PubMed Abstract | Crossref Full Text | Google Scholar

54. Van Regenmortel MHV. Specificity, polyspecificity, and heterospecificity of antibody-antigen recognition. J Mol Recognition. (2014) 27:627–39. doi: 10.1002/jmr.2394

PubMed Abstract | Crossref Full Text | Google Scholar

55. Barlow DJ, Edwards MS, and Thornton JM. Continuous and discontinuous protein antigenic determinants. Nature. (1986) 322:747–8. doi: 10.1038/322747a0

PubMed Abstract | Crossref Full Text | Google Scholar

56. Pellequer JL, Westhof E, and Van Regenmortel MHV. Predicting location of continuous epitopes in proteins from their primary structures. Methods in Enzymology. Academic Press, San Diego, CA. (1991). 203:176–201. doi: 10.1016/0076-6879(91)03010-E

PubMed Abstract | Crossref Full Text | Google Scholar

57. Benjamin D and Perdue SS. Site-directed mutagenesis in epitope mapping. Methods Enzymol. (1996) 9:508–15. doi: 10.1006/meth.1996.0058

PubMed Abstract | Crossref Full Text | Google Scholar

58. Stave JW and Lindpaintner K. Antibody and antigen contact residues define epitope and paratope size and structure. J Immunol. (2013) 191:1428–35. doi: 10.4049/jimmunol.1203198

PubMed Abstract | Crossref Full Text | Google Scholar

59. Reis PBPS, Barletta GP, Gagliardi L, Fortuna S, Soler MA, and Rocchia W. Antibody-antigen binding interface analysis in the big data era. Front Mol Biosci. (2022) 9:945808. doi: 10.3389/fmolb.2022.945808

PubMed Abstract | Crossref Full Text | Google Scholar

60. Baratloo A, Hosseini M, and Negida A. El Ashal G. Part 1: Simple definition and calculation of accuracy, sensitivity and specificity. Emerg (Tehran). (2015) 3:48–9.

PubMed Abstract | Google Scholar

61. Han J, Schmitz AJ, Richey ST, Dai YN, Turner HL, Mohammed BM, et al. Polyclonal epitope mapping reveals temporal dynamics and diversity of human antibody responses to H5N1 vaccination. Cell Rep. (2021) 34:108682. doi: 10.1016/j.celrep.2020.108682

PubMed Abstract | Crossref Full Text | Google Scholar

62. Tarke A, Sidney J, Kidd CK, Dan JM, Ramirez SI, Yu ED, et al. Comprehensive analysis of T cell immunodominance and immunoprevalence of SARS-CoV-2 epitopes in COVID-19 cases. Cell Rep Med. (2021) 2:100204. doi: 10.1016/j.xcrm.2021.100204

PubMed Abstract | Crossref Full Text | Google Scholar

63. Rubinstein ND, Mayrose I, Halperin D, Yekutieli D, Gershoni JM, and Pupko T. Computational characterization of B-cell epitopes. Mol Immunol. (2008) 45:3477–89. doi: 10.1016/j.molimm.2007.10.016

PubMed Abstract | Crossref Full Text | Google Scholar

64. Zheng W, Ruan J, Hu G, Wang K, Hanlon M, and Gao J. Analysis of conformational B-cell epitopes in the antibody-antigen complex using the depth function and the convex hull. PloS One. (2015) 10:e0134835. doi: 10.1371/journal.pone.0134835

PubMed Abstract | Crossref Full Text | Google Scholar

65. Li X, Hassan SA, and Mehler EL. Long dynamics simulations of proteins using atomistic force fields and a continuum representation of solvent effects: Calculation of structural and dynamic properties. Proteins: Structure Function Bioinf. (2005) 60:464–84. doi: 10.1002/prot.20470

PubMed Abstract | Crossref Full Text | Google Scholar

66. Knaggs MH, Salsbury FR, Edgell MH, and Fetrow JS. Insights into correlated motions and long-range interactions in Chey derived from molecular dynamics simulations. Biophys J. (2007) 92:2062–79. doi: 10.1529/biophysj.106.081950

PubMed Abstract | Crossref Full Text | Google Scholar

67. Stuart AD, McKee TA, Williams PA, Harley C, Shen S, Stuart DI, et al. Determination of the structure of a decay accelerating factor-binding clinical isolate of Echovirus 11 allows mapping of mutants with altered receptor requirements for infection. J Virol. (2002) 76:7694–704. doi: 10.1128/jvi.76.15.7694-7704.2002

PubMed Abstract | Crossref Full Text | Google Scholar

68. Bohacek RS, McMartin C, and Guida WC. The art and practice of structure-based drug design: a molecular modeling perspective. Med Res Rev. (1996) 16:3–50. doi: 10.1002/(sici)1098-1128(199601)16:1⟨3::Aid-med1⟩3.0.Co;2-6

PubMed Abstract | Crossref Full Text | Google Scholar

69. Griffiths NM, Hewick DS, and Stevenson IH. The serum pharmacokinetics of digoxin as an immunogen and hapten in the rabbit. Int J Immunopharmacol. (1985) 7:697–703. doi: 10.1016/0192-0561(85)90154-7

PubMed Abstract | Crossref Full Text | Google Scholar

70. Westhoff CM, Lopez O, Goebel P, Carlson L, Carlson RR, Wagner FW, et al. Unusual amino acid usage in the variable regions of mercury-binding antibodies. Proteins. (1999) 37:429–40. doi: 10.1002/(SICI)1097-0134(19991115)37:3⟨429::AID-PROT10⟩3.0.CO;2-P

PubMed Abstract | Crossref Full Text | Google Scholar

71. Thierse H, Gamerdinger K, Junkes C, Guerreiro N, and Weltzien H. T cell receptor (TCR) interaction with haptens: metal ions as non-classical haptens. Toxicology. (2005) 209:101–7. doi: 10.1016/j.tox.2004.12.015

PubMed Abstract | Crossref Full Text | Google Scholar

72. Haste Andersen P, Nielsen M, and Lund O. Prediction of residues in discontinuous B-cell epitopes using protein 3D structures. Protein Sci. (2006) 15:2558–67. doi: 10.1110/ps.062405906

PubMed Abstract | Crossref Full Text | Google Scholar

73. Janeway C, Travers P, Walport M, and Shlomchik M. The generation of diversity in immunoglobulins. 5th edition. New York: Garland Science (2001).

Google Scholar

74. Alberts B, Johnson A, Lewis J, Raff M, Roberts K, and Walter P. Lymphocytes and the cellular basis of adaptive immunity. In: Molecular Biology of the Cell, 4th edn. Garland Science, New York (2002).

Google Scholar

75. Arstila T, Casrouge A, Baron V, Even J, Kanellopoulos J, and Kourilsky P. A direct estimate of the human α β T cell receptor diversity. Science. (1999) 286:958–61. doi: 10.1126/science.286.5441.958

PubMed Abstract | Crossref Full Text | Google Scholar

76. Glanville J, Zhai W, Berka J, Telman D, Huerta G, Mehta G, et al. Precise determination of the diversity of a combinatorial antibody library gives insight into the human immunoglobulin repertoire. Proc Natl Acad Sci. (2009) 106:20216–21. doi: 10.1073/pnas.0909775106

PubMed Abstract | Crossref Full Text | Google Scholar

77. Robins H, Campregher P, Srivastava S, Wacher A, Turtle C, Kahsai O, et al. Comprehensive assessment of T-cell receptor β-chain diversity in αβ T cells. Blood. (2009) 114:4099–107. doi: 10.1182/blood-2009-04-217604

PubMed Abstract | Crossref Full Text | Google Scholar

78. Qi Q, Liu Y, Cheng Y, Glanville J, Zhang D, Lee J, et al. Diversity and clonal selection in the human T-cell repertoire. Proc Natl Acad Sci. (2014) 111:13139–44. doi: 10.1073/pnas.1409155111

PubMed Abstract | Crossref Full Text | Google Scholar

79. Portefaix JM, Thebault S, Bourgain-Guglielmetti F, Del Rio M, Granier C, Mani JC, et al. Critical residues of epitopes recognized by several anti-p53 monoclonal antibodies correspond to key residues of p53 involved in interactions with the mdm2 protein. J Immunol Methods. (2000) 244:17–28. doi: 10.1016/S0022-1759(00)00246-5

PubMed Abstract | Crossref Full Text | Google Scholar

80. Bard F, Barbour R, Cannon C, Carretto R, Fox M, Games D, et al. Epitope and isotype specificities of antibodies to β-amyloid peptide for protection against Alzheimer’s disease-like neuropathology. Proc Natl Acad Sci. (2003) 100:2023–8. doi: 10.1073/pnas.0436286100

PubMed Abstract | Crossref Full Text | Google Scholar

81. Niederfellner G, Lammens A, Mundigl O, Georges GJ, Schaefer W, Schwaiger M, et al. Epitope characterization and crystal structure of GA101 provide insights into the molecular basis for type i/ii distinction of CD20 antibodies. Blood. (2011) 118:358–67. doi: 10.1182/blood-2010-09-305847

PubMed Abstract | Crossref Full Text | Google Scholar

82. Buus S, Rockberg J, Forsström B, Nilsson P, Uhlen M, and Schafer-Nielsen C. High-resolution mapping of linear antibody epitopes using ultrahigh-density peptide microarrays. Mol Cell Proteomics. (2012) 11:1790–800. doi: 10.1074/mcp.m112.020800

PubMed Abstract | Crossref Full Text | Google Scholar

83. Faleri A, Santini L, Brier S, Pansegrau W, Surdo PL, Scarselli M, et al. Two cross-reactive monoclonal antibodies recognize overlapping epitopes on Neisseria meningitidis factor H binding protein but have different functional properties. FASEB J. (2013) 28:1644–53. doi: 10.1096/fj.13-239012

PubMed Abstract | Crossref Full Text | Google Scholar

84. Wong WK, Robinson SA, Bujotzek A, Georges G, Lewis AP, Shi J, et al. Ab-ligity: identifying sequence-dissimilar antibodies that bind to the same epitope. mAbs. (2021) 13. doi: 10.1080/19420862.2021.1873478

PubMed Abstract | Crossref Full Text | Google Scholar

85. Edwards BM, Barash SC, Main SH, Choi GH, Minter R, Ullrich S, et al. The remarkable flexibility of the human antibody repertoire; isolation of over one thousand different antibodies to a single protein, BLyS. J Mol Biol. (2003) 334:103–18. doi: 10.1016/j.jmb.2003.09.054

PubMed Abstract | Crossref Full Text | Google Scholar

86. Poulsen TR, Meijer PJ, Jensen A, Nielsen LS, and Andersen PS. Kinetic, affinity, and diversity limits of human polyclonal antibody responses against tetanus toxoid. J Immunol. (2007) 179:3841–50. doi: 10.4049/jimmunol.179.6.3841

PubMed Abstract | Crossref Full Text | Google Scholar

87. Naqid IA, Owen JP, Maddison BC, Spiliotopoulos A, Emes RD, Warry A, et al. Mapping polyclonal antibody responses to bacterial infection using next generation phage display. Sci Rep. (2016) 6:24232. doi: 10.1038/srep24232

PubMed Abstract | Crossref Full Text | Google Scholar

88. Guo JY, Liu IJ, Lin HT, Wang MJ, Chang YL, Lin SC, et al. Identification of COVID-19 B-cell epitopes with phage-displayed peptide library. J Biomed Sci. (2021) 28:43 doi: 10.1186/s12929-021-00740-8

PubMed Abstract | Crossref Full Text | Google Scholar

89. Haynes WA, Kamath K, Bozekowski J, Baum-Jones E, Campbell M, Casanovas-Massana A, et al. High-resolution epitope mapping and characterization of SARS-CoV-2 antibodies in large cohorts of subjects with COVID-19. Commun Biol. (2021) 4:1317. doi: 10.1038/s42003-021-02835-2

PubMed Abstract | Crossref Full Text | Google Scholar

90. Ertl P. Cheminformatics analysis of organic substituents: identification of the most common substituents, calculation of substituent properties, and automatic identification of drug-like bioisosteric groups. J Chem Inf Comput Sci. (2002) 43:374–80. doi: 10.1021/ci0255782

PubMed Abstract | Crossref Full Text | Google Scholar

91. Polishchuk PG, Madzhidov TI, and Varnek A. Estimation of the size of drug-like chemical space based on GDB-17 data. J Comput Aided Mol Des. (2013) 27:675–9. doi: 10.1007/s10822-013-9672-4

PubMed Abstract | Crossref Full Text | Google Scholar

92. Koblitz N and Menezes AJ. The random oracle model: a twenty-year retrospective. Des Codes Cryptogr. (2015) 77:587–610. doi: 10.1007/s10623-015-0094-2

Crossref Full Text | Google Scholar

93. Gupta S., Yadav S. K., Singh A. P., and Maurya K. C.. A Comparative Study of Secure Hash Algorithms. In: Satapathy S. and Das S. (eds). Proceedings of First International Conference on Information and Communication Technology for Intelligent Systems: Volume 2. Smart Innovation, Systems and Technologies. (2016)51. Springer, Cham. doi: 10.1007/978-3-319-30927-9_13

Crossref Full Text | Google Scholar

94. Kaminsky A. Testing the randomness of cryptographic function mappings(2019). Available online at: https://eprint.iacr.org/2019/078.

Google Scholar

95. Feistel H. Cryptography and computer privacy. Sci Am. (1973) 228:15–23. doi: 10.1038/scientificamerican0573-15

Crossref Full Text | Google Scholar

96. Ingram VM. Gene mutations in human hæmoglobin: the chemical difference between normal and sickle cell hemoglobin. Nature. (1957) 180:326–8. doi: 10.1038/180326a0

PubMed Abstract | Crossref Full Text | Google Scholar

97. Rudikoff S, Giusti AM, Cook WD, and Scharff MD. Single amino acid substitution altering antigenbinding specificity. Proc Natl Acad Sci. (1982) 79:1979–83. doi: 10.1073/pnas.79.6.1979

PubMed Abstract | Crossref Full Text | Google Scholar

98. Feldhammer M, Durand S, and Pshezhetsky AV. Protein misfolding as an underlying molecular defect in mucopolysaccharidosis III type C. PloS One. (2009) 4:e7434. doi: 10.1371/journal.pone.0007434

PubMed Abstract | Crossref Full Text | Google Scholar

99. Montagut C, Dalmases A, Bellosillo B, Crespo M, Pairet S, Iglesias M, et al. Identification of a mutation in the extracellular domain of the epidermal growth factor receptor conferring cetuximab resistance in colorectal cancer. Nat Med. (2012) 18:221–3. doi: 10.1038/nm.2609

PubMed Abstract | Crossref Full Text | Google Scholar

100. Chiu ML, Goulet DR, Teplyakov A, and Gilliland GL. Antibody structure and function: The basis for engineering therapeutics. Antibodies. (2019) 8:55. doi: 10.3390/antib8040055

PubMed Abstract | Crossref Full Text | Google Scholar

101. Xavier JS, Nguyen TB, Karmarkar M, Portelli S, Rezende PM, Velloso JPL, et al. ThermoMutDB: a thermodynamic database for missense mutations. Nucleic Acids Res. (2020) 49:D475–9. doi: 10.1093/nar/gkaa925

PubMed Abstract | Crossref Full Text | Google Scholar

102. Gibson KL, Wu Y, Barnett Y, Duggan O, Vaughan R, Kondeatis E, et al. B-cell diversity decreases in old age and is correlated with poor health status. Aging Cell. (2009) 8:18–25. doi: 10.1111/j.1474-9726.2008.00443.x

PubMed Abstract | Crossref Full Text | Google Scholar

103. Wang F, Ekiert D, Ahmad I, Yu W, Zhang Y, Bazirgan O, et al. Reshaping antibody diversity. Cell. (2013) 153:1379–93. doi: 10.1016/j.cell.2013.04.049

PubMed Abstract | Crossref Full Text | Google Scholar

104. Simons JF, Lim YW, Carter KP, Wagner EK, Wayham N, Adler AS, et al. Affinity maturation of antibodies by combinatorial codon mutagenesis versus error-prone PCR. mAbs. (2020) 12:1803646. doi: 10.1080/19420862.2020.1803646

PubMed Abstract | Crossref Full Text | Google Scholar

105. Chan DTY and Groves MAT. Affinity maturation: highlights in the application of in vitro strategies for the directed evolution of antibodies. Emerging Topics Life Sci. (2021) 5:601–8. doi: 10.1042/etls20200331

PubMed Abstract | Crossref Full Text | Google Scholar

106. Cortez D. M. A., Sison A. M., and Medina R. P.. Cryptanalysis of the Modified SHA256. Proceedings of the 2020 4th High Performance Computing and Cluster Technologies Conference & 2020 3rd International Conference on Big Data and Artificial Intelligence (HPCCT & BDAI '20). Association for Computing Machinery, New York, NY, USA. (2020)179–183. doi: 10.1145/3409501.3409513

Crossref Full Text | Google Scholar

107. Bera A and Sharma S. Estimating production uncertainty in stochastic frontier production function models. J Productivity Anal. (1999) 12:187–210. doi: 10.1023/A:1007828521773

Crossref Full Text | Google Scholar

108. Horrace WC. Moments of the truncated normal distribution. J Productivity Anal. (2014) 43:133–8. doi: 10.1007/s11123-013-0381-8

Crossref Full Text | Google Scholar

109. Petrella R. The maximal variance of unilaterally truncated Gaussian and chi distributions. (2025). In submission.

Google Scholar

110. Lemass D, O’Kennedy R, and Kijanka G. Referencing cross-reactivity of detection antibodies for protein array experiments. F1000Research. (2017) 5:73. doi: 10.12688/f1000research.7668.2

PubMed Abstract | Crossref Full Text | Google Scholar

111. Kijanka G, IpCho S, Baars S, Chen H, Hadley K, Beveridge A, et al. Rapid characterization of binding specificity and cross-reactivity of antibodies using recombinant human protein arrays. J Immunol Methods. (2009) 340:132–7. doi: 10.1016/j.jim.2008.10.008

PubMed Abstract | Crossref Full Text | Google Scholar

112. Weiner LM, Dhodapkar MV, and Ferrone S. Monoclonal antibodies for cancer immunotherapy. Lancet. (2009) 373:1033–40. doi: 10.1016/s0140-6736(09)60251-8

PubMed Abstract | Crossref Full Text | Google Scholar

113. Schoofs T, Klein F, Braunschweig M, Kreider EF, Feldmann A, Nogueira L, et al. HIV-1 therapy with monoclonal antibody 3BNC117 elicits host immune responses against HIV-1. Science. (2016) 352:997–1001. doi: 10.1126/science.aaf0972

PubMed Abstract | Crossref Full Text | Google Scholar

114. Huber M, von Wyl V, Ammann CG, Kuster H, Stiegler G, Katinger H, et al. Potent Human Immunodeficiency Virus-neutralizing and complement lysis activities of antibodies are not obligatorily linked. J Virol. (2008) 82:3834–42. doi: 10.1128/jvi.02569-07

PubMed Abstract | Crossref Full Text | Google Scholar

115. Diebolder CA, Beurskens FJ, de Jong RN, Koning RI, Strumane K, Lindorfer MA, et al. Complement is activated by IgG hexamers assembled at the cell surface. Science. (2014) 343:1260–3. doi: 10.1126/science.1248943

PubMed Abstract | Crossref Full Text | Google Scholar

116. Zwick MB, Wang M, Poignard P, Stiegler G, Katinger H, Burton DR, et al. Neutralization synergy of Human Immunodeficiency Virus type 1 primary isolates by cocktails of broadly neutralizing antibodies. J Virol. (2001) 75:12198–208. doi: 10.1128/jvi.75.24.12198-12208.2001

PubMed Abstract | Crossref Full Text | Google Scholar

117. Nowakowski A, Wang C, Powers DB, Amersdorfer P, Smith TJ, Montgomery VA, et al. Potent neutralization of botulinum neurotoxin by recombinant oligoclonal antibody. Proc Natl Acad Sci. (2002) 99:11346–50. doi: 10.1073/pnas.172229899

PubMed Abstract | Crossref Full Text | Google Scholar

118. National Institute of Standards and Technology. Announcing the secure hash standard(2002). Available online at: https://csrc.nist.gov/csrc/media/publications/fips/180/2/archive/2002-08-01/documents/fips180-2.pdf.

Google Scholar

119. Rhodes D. SHA-512 hashing algorithm overview(2020). Available online at: https://komodoplatform.com/en/academy/sha-512/.

Google Scholar

120. Heeffer A and Rittaud B. The pigeonhole principle, two centuries before Dirichlet. Math Intell. (2014) 36:27–9. doi: 10.1007/s00283-013-9389-1

Crossref Full Text | Google Scholar

121. Casali P and Notkins AL. Probing the human B-cell repertoire with EBV: polyreactive antibodies and CD5+ B lymphocytes. Annu Rev Immunol. (1989) 7:513–35. doi: 10.1146/annurev.iy.07.040189.002501

PubMed Abstract | Crossref Full Text | Google Scholar

122. Wucherpfennig K, Allen P, Celada F, Cohen IR, De Boer R, Garcia K, et al. Polyspecificity of T cell and B cell receptor recognition. Semin Immunol. (2007) 19:216–24. doi: 10.1016/j.smim.2007.02.012

PubMed Abstract | Crossref Full Text | Google Scholar

123. Bhowmick A and Salunke DM. Limited conformational flexibility in the paratope may be responsible for degenerate specificity of HIV epitope recognition. Int Immunol. (2012) 25:77–90. doi: 10.1093/intimm/dxs093

PubMed Abstract | Crossref Full Text | Google Scholar

124. Jones DD, DeIulio GA, and Winslow GM. Antigen-driven induction of polyreactive IgM during intracellular bacterial infection. J Immunol. (2012) 189:1440–7. doi: 10.4049/jimmunol.1200878

PubMed Abstract | Crossref Full Text | Google Scholar

125. Bhattacharjee A and Glaudemans C. Dual binding specificities in Mopc 384 and 870 murine myeloma immunoglobulins. J Immunol. (1978) 120:411–3. doi: 10.4049/jimmunol.120.2.411

PubMed Abstract | Crossref Full Text | Google Scholar

126. Goel M, Krishnan L, Kaur S, Kaur KJ, and Salunke DM. Plasticity within the antigen-combining site may manifest as molecular mimicry in the humoral immune response. J Immunol. (2004) 173:7358–67. doi: 10.4049/jimmunol.173.12.7358

PubMed Abstract | Crossref Full Text | Google Scholar

127. Fernández-Quintero M, Pomarici N, Math B, Kroell K, Waibl F, Bujotzek A, et al. Antibodies exhibit multiple paratope states influencing VH–VL domain orientations. Commun Biol. (2020) 3:589. doi: 10.1038/s42003-020-01319-z

PubMed Abstract | Crossref Full Text | Google Scholar

128. Keitel T, Kramer A, Wessner H, Scholz C, Schneider-Mergener J, and Höhne W. Crystallographic analysis of anti-p24 (HIV-1) monoclonal antibody cross-reactivity and polyspecificity. Cell. (1997) 91:811–20. doi: 10.1016/s0092-8674(00)80469-9

PubMed Abstract | Crossref Full Text | Google Scholar

129. Pinilla C, Appel J, Campbell G, Buencamino J, Benkirane N, Muller S, et al. All-D peptides recognized by an anti-carbohydrate antibody identified from a positional scanning library. J Mol Biol. (1998) 283:1013–25. doi: 10.1006/jmbi.1998.2137

PubMed Abstract | Crossref Full Text | Google Scholar

130. Gras-Masse H, Georges B, Estaquier J, Tranchand-Bunel D, Tartar A, Druilhe P, et al. Convergent peptide libraries, or mixotopes, to elicit or to identify specific immune responses. Curr Opin Immunol. (1999) 11:223–8. doi: 10.1016/s0952-7915(99)80038-7

PubMed Abstract | Crossref Full Text | Google Scholar

131. Notkins AL. Polyreactivity of antibody molecules. Trends Immunol. (2004) 25:174–9. doi: 10.1016/j.it.2004.02.004

PubMed Abstract | Crossref Full Text | Google Scholar

132. Guthmiller JJ, Lan LY, Fernández-Quintero ML, Han J, Utset HA, Bitar DJ, et al. Polyreactive broadly neutralizing B cells are selected to provide defense against Pandemic Threat Influenza Viruses. Immunity. (2020) 53:1230–44.e5. doi: 10.1016/j.immuni.2020.10.005

PubMed Abstract | Crossref Full Text | Google Scholar

133. Jeliazkov JR, Sljoka A, Kuroda D, Tsuchimura N, Katoh N, Tsumoto K, et al. Repertoire analysis of antibody CDR-H3 loops suggests affinity maturation does not typically result in rigidification. Front Immunol. (2018) 9:413. doi: 10.3389/fimmu.2018.00413

PubMed Abstract | Crossref Full Text | Google Scholar

134. Burnett DL, Schofield P, Langley DB, Jackson J, Bourne K, Wilson E, et al. Conformational diversity facilitates antibody mutation trajectories and discrimination between foreign and selfantigens. Proc Natl Acad Sci. (2020) 117:22341–50. doi: 10.1073/pnas.2005102117

PubMed Abstract | Crossref Full Text | Google Scholar

135. Boughter CT, Borowska MT, Guthmiller JJ, Bendelac A, Wilson PC, Roux B, et al. Biochemical patterns of antibody polyreactivity revealed through a bioinformatics-based analysis of CDR loops. eLife. (2020) 9:e61393. doi: 10.7554/elife.61393

PubMed Abstract | Crossref Full Text | Google Scholar

136. Yin Y, Wang XX, and Mariuzza RA. Crystal structure of a complete ternary complex of T-cell receptor, peptide–MHC, and CD4. PNAS. (2012) 109:5405–10. doi: 10.1073/pnas.1118801109

PubMed Abstract | Crossref Full Text | Google Scholar

137. Adhikary R, Yu W, Oda M, Walker RC, Chen T, Stanfield RL, et al. Adaptive mutations alter antibody structure and dynamics during affinity maturation. Biochemistry. (2015) 54:2085–93. doi: 10.1021/bi501417q

PubMed Abstract | Crossref Full Text | Google Scholar

138. Adams RM, Kinney JB, Walczak AM, and Mora T. Physical epistatic landscape of antibody binding affinity. arXiv arXiv:1712.04000. (2017). doi: 10.48550/arXiv.1712.04000

Crossref Full Text | Google Scholar

139. Adams RM, Kinney JB, Walczak AM, and Mora T. Epistasis in a fitness landscape defined by antibodyantigen binding free energy. Cell Syst. (2019) 8:86–93.e3. doi: 10.1016/j.cels.2018.12.004

PubMed Abstract | Crossref Full Text | Google Scholar

140. Stack Exchange. How can hashes be unique if they are limited in number?(2018). Available online at: https://crypto.stackexchange.com/questions/58214/how-can-hashes-be-unique-if-they-are-limitedin-number.

Google Scholar

141. Kelsey J and Schneier B. Second preimages on n-bit hash functions for much less than 2ⁿ work. IACR Cryptology ePrint Arch In Proceedings of the 24th Annual International Conference on Theory and Applications of Cryptographic Techniques (EUROCRYPT'05). Springer-Verlag, Berlin, Heidelberg. (2005)474–490. doi: 10.1007/11426639_28

Crossref Full Text | Google Scholar

142. Haitner I, Horvitz O, Katz J, Koo CY, Morselli R, and Shaltiel R. Reducing complexity assumptions for statistically-hiding commitment. J Cryptology. (2007) 22:283–310. doi: 10.1007/s00145-007-9012-8

Crossref Full Text | Google Scholar

143. Andreeva E, Bouillaguet C, Dunkelman O, Fouque PA, Hoch J, Kelsey J, et al. New second-preimage attacks on hash functions. J Cryptology. (2015) 29:657–96. doi: 10.1007/s00145-015-9206-4

Crossref Full Text | Google Scholar

144. Sterner E, Peach ML, Nicklaus MC, and Gildersleeve JC. Therapeutic antibodies to ganglioside GD2 evolved from highly selective germline antibodies. Cell Rep. (2017) 20:1681–91. doi: 10.1016/j.celrep.2017.07.050

PubMed Abstract | Crossref Full Text | Google Scholar

145. Rajewsky K. The advent and rise of monoclonal antibodies. Nature. (2019) 575:47–9. doi: 10.1038/d41586-019-02840-w

PubMed Abstract | Crossref Full Text | Google Scholar

146. Singh R, Chandley P, and Rohatgi S. Recent advances in the development of monoclonal antibodies and next-generation antibodies. ImmunoHorizons. (2023) 7:886–97. doi: 10.4049/immunohorizons.2300102

PubMed Abstract | Crossref Full Text | Google Scholar

147. Isobe T and Shibutani K. Preimage attacks on reduced tiger and SHA-2. In: Dunkelman O, editor. Fast Software Encryption. Springer, Berlin Heidelberg (2009). p. 139–55.

Google Scholar

148. Frank F, Keen MM, Rao A, Bassit L, Liu X, Bowers HB, et al. Deep mutational scanning identifies SARS-CoV-2 nucleocapsid escape mutations of currently available rapid antigen tests. Cell. (2022) 185:3603–16.e13. doi: 10.1016/j.cell.2022.08.010

PubMed Abstract | Crossref Full Text | Google Scholar

149. Wang Z, Zhu Y, Ding S, He F, Beier R, Li J, et al. Development of a monoclonal antibody-based broad-specificity ELISA for fluoroquinolone antibiotics in foods and molecular modeling studies of cross-reactive compounds. Anal Chem. (2007) 79:4471–83. doi: 10.1021/ac070064t

PubMed Abstract | Crossref Full Text | Google Scholar

150. Kwong LS, Thom M, Sopp P, Rocchi M, Wattegedera S, Entrican G, et al. Production and characterization of two monoclonal antibodies to bovine tumour necrosis factor alpha (TNF-α) and their cross-reactivity with ovine TNF-α. Vet Immunol Immunopathol. (2010) 135:320–4. doi: 10.1016/j.vetimm.2010.01.001

PubMed Abstract | Crossref Full Text | Google Scholar

151. Rozemuller H, Prins HJ, Naaijkens B, Staal J, Bühring HJ, and Martens AC. Prospective isolation of mesenchymal stem cells from multiple mammalian species using cross-reacting anti-human monoclonal antibodies. Stem Cells Dev. (2010) 19:1911–21. doi: 10.1089/scd.2009.0510

PubMed Abstract | Crossref Full Text | Google Scholar

152. Wrammert J, Koutsonanos D, Li GM, Edupuganti S, Sui J, Morrissey M, et al. Broadly cross-reactive antibodies dominate the human B cell response against 2009 pandemic H1N1 influenza virus infection. J Exp Med. (2011) 208:181–93. doi: 10.1084/jem.20101352

PubMed Abstract | Crossref Full Text | Google Scholar

153. Biham E and Shamir A. Differential cryptanalysis of DES-like cryptosystems. J Cryptol. (1991) 4:3–72. doi: 10.1007/BF00630563

Crossref Full Text | Google Scholar

154. Biham E. On the applicability of differential cryptanalysis to hash functions. E.I.S.S Workshop Cryptographic Hash Functions (Oberwolfach(D)). (1992).

Google Scholar

155. Wang X, Yin Y, and Yu H. Finding collisions in the full SHA-1. In: Shoup V, editor. Advances in Cryptology – CRYPTO 2005. Lecture Notes in Computer Science, vol. 3621 . Springer, Berlin Heidelberg (2005). p. 17–36. doi: 10.1007/115352182

Crossref Full Text | Google Scholar

156. Russell DM, Dembić Z, Morahan G, Miller JFAP, and Bürki K. Nemazee D. Peripheral deletion of self-reactive B cells. Nature. (1991) 354:308–11. doi: 10.1038/354308a0

PubMed Abstract | Crossref Full Text | Google Scholar

157. Goodnow CC, Sprent J, Fazekas de St Groth B, and Vinuesa CG. Cellular and genetic mechanisms of self tolerance and autoimmunity. Nature. (2005) 435:590–7. doi: 10.1038/nature03724

PubMed Abstract | Crossref Full Text | Google Scholar

158. Jaffe DB, Shahi P, Adams BA, Chrisman AM, Finnegan PM, Raman N, et al. Functional antibodies exhibit light chain coherence. Nature. (2022) 611:352–7. doi: 10.1038/s41586-022-05371-z

PubMed Abstract | Crossref Full Text | Google Scholar

159. Bellare M. and Rogaway P.. Random oracles are practical: a paradigm for designing efficient protocols. Proceedings of the 1st ACM Conference on Computer and Communications Security (CCS '93). Association for Computing Machinery, New York, NY, USA. (1993)62–73. doi: 10.1145/168588.168596

Crossref Full Text | Google Scholar

160. Rogaway P and Shrimpton T. Cryptographic hash-function basics: Definitions, implications, and separations for preimage resistance, second-preimage resistance, and collision resistance. In: Roy B and Meier W, editors. Fast Software Encryption. Springer, Berlin Heidelberg (2004). p. 371–88.

Google Scholar

161. Karlsen AE and Dyrberg T. Molecular mimicry between non-self, modified self and self in autoimmunity. Semin Immunol. (1998) 10:25–34. doi: 10.1006/smim.1997.0102

PubMed Abstract | Crossref Full Text | Google Scholar

162. Wekerle H and Hohlfeld R. Molecular mimicry in multiple sclerosis. New Engl J Med. (2003) 349:185–6. doi: 10.1056/nejmcibr035136

PubMed Abstract | Crossref Full Text | Google Scholar

163. Jacob J, Kassir R, and Kelsoe G. In situ studies of the primary immune response to (4-hydroxy-3nitrophenyl)acetyl. I. @ the architecture and dynamics of responding cell populations. J Exp Med. (1991) 173:1165–75. doi: 10.1084/jem.173.5.1165

PubMed Abstract | Crossref Full Text | Google Scholar

164. Lee JH, Sutton HJ, Cottrell CA, Phung I, Ozorowski G, Sewall LM, et al. Long-primed germinal centres with enduring affinity maturation and clonal migration. Nature. (2022) 609:998–1004. doi: 10.1038/s41586-022-05216-9

PubMed Abstract | Crossref Full Text | Google Scholar

165. Thorpe IF and Brooks CL. Molecular evolution of affinity and flexibility in the immune system. Proc Natl Acad Sci. (2007) 104:8821–6. doi: 10.1073/pnas.0610064104

PubMed Abstract | Crossref Full Text | Google Scholar

166. Mishra AK and Mariuzza RA. Insights into the structural basis of antibody affinity maturation from next-generation sequencing. Front Immunol. (2018) 9:117. doi: 10.3389/fimmu.2018.00117

PubMed Abstract | Crossref Full Text | Google Scholar

167. Ovchinnikov V, Louveau JE, Barton JP, Karplus M, and Chakraborty AK. Role of framework mutations and antibody flexibility in the evolution of broadly neutralizing antibodies. eLife. (2018) 7:e33038 doi: 10.7554/elife.33038

PubMed Abstract | Crossref Full Text | Google Scholar

168. Fernández-Quintero ML, Loeffler JR, Bacher LM, Waibl F, Seidler CA, and Liedl KR. Local and global rigidification upon antibody affinity maturation. Front Mol Biosci. (2020) 7:182. doi: 10.3389/fmolb.2020.00182

PubMed Abstract | Crossref Full Text | Google Scholar

169. Cauerhff A, Goldbaum FA, and Braden BC. Structural mechanism for affinity maturation of an antilysozyme antibody. Proc Natl Acad Sci. (2004) 101:3539–44. doi: 10.1073/pnas.0400060101

PubMed Abstract | Crossref Full Text | Google Scholar

170. De Genst E, Handelberg F, Van Meirhaeghe A, Vynck S, Loris R, Wyns L, et al. Chemical basis for the affinity maturation of a camel single domain antibody. J Biol Chem. (2004) 279:53593–601. doi: 10.1074/jbc.M407843200

PubMed Abstract | Crossref Full Text | Google Scholar

171. Sheng Z, Bimela JS, Katsamba PS, Patel SD, Guo Y, Zhao H, et al. Structural basis of antibody conformation and stability modulation by framework somatic hypermutation. Front Immunol. (2022) 12:811632. doi: 10.3389/fimmu.2021.811632

PubMed Abstract | Crossref Full Text | Google Scholar

172. Throsby M, van den Brink E, Jongeneelen M, Poon L, Alard P, Cornelissen L, et al. Heterosubtypic neutralizing monoclonal antibodies cross-protective against H5N1 and H1N1 recovered from human IgM+ memory B cells. PloS One. (2008) 3:e3942. doi: 10.1371/journal.pone.0003942

PubMed Abstract | Crossref Full Text | Google Scholar

173. Vu DM, Pajon R, Reason DC, and Granoff DM. A broadly cross-reactive monoclonal antibody against an epitope on the N-terminus of meningococcal fHbp. Sci Rep. (2012) 2:341. doi: 10.1038/srep00341

PubMed Abstract | Crossref Full Text | Google Scholar

174. Bostrom J, Yu SF, Kan D, Appleton BA, Lee CV, Billeci K, et al. Variants of the antibody herceptin that interact with HER2 and VEGF at the antigen binding site. Science. (2009) 323:1610–4. doi: 10.1126/science.1165480

PubMed Abstract | Crossref Full Text | Google Scholar

175. Tapryal S, Gaur V, Kaur KJ, and Salunke DM. Structural evaluation of a mimicry-recognizing paratope: Plasticity in antigen–antibody interactions manifests in molecular mimicry. J Immunol. (2013) 191:456–63. doi: 10.4049/jimmunol.1203260

PubMed Abstract | Crossref Full Text | Google Scholar

176. Vojdani A. Reaction of monoclonal and polyclonal antibodies made against infectious agents with various food antigens. J Clin Cell Immunol. (2015) 6:1000359. doi: 10.4172/2155-9899.1000359

Crossref Full Text | Google Scholar

177. Vojdani A, Vojdani E, and Kharrazian D. Reaction of human monoclonal antibodies to SARS-CoV-2 proteins with tissue antigens: Implications for autoimmune diseases. Front Immunol. (2021) 11. doi: 10.3389/fimmu.2020.617089

PubMed Abstract | Crossref Full Text | Google Scholar

178. Oostindie SC, Lazar GA, Schuurman J, and Parren PWHI. Avidity in antibody effector functions and biotherapeutic drug design. Nat Rev Drug Discov. (2022) 21:715–35. doi: 10.1038/s41573-022-00501-8

PubMed Abstract | Crossref Full Text | Google Scholar

179. Voskuil JLA. Commercial antibodies and their validation. F1000Research. (2014) 3:232. doi: 10.12688/f1000research.4966.2

PubMed Abstract | Crossref Full Text | Google Scholar

180. Creative Diagnostics. Polyclonal vs. monoclonal antibodies protocol(2025). Available online at: https://www.creative-diagnostics.com/polyclonal-vs-monoclonal-antibodies.htm?gad_source=1&gclid=EAIaIQobChMItbWouZPaiwMVfG9HAR1bMQv2EAAYASAAEgLnAfD_BwE.

Google Scholar

181. Proteintech Group. Polyclonal vs. monoclonal antibodies(2024). Available online at: https://www.ptglab.com/news/blog/polyclonal-vs-monoclonal-antibodies/.

Google Scholar

182. Wikipedia. Polyclonal B cell response(2023). Available online at: https://en.wikipedia.org/wiki/Polyclonal_B_cell_response.

Google Scholar

183. Kuwakado H and Hirose S. Pseudorandom-function property of the step-reduced compression functions of SHA-256 and SHA-512. In: Chung KI, Sohn K, and Yung M, editors. Information Security Applications. Lecture Notes in Computer Science, vol. 5379 . Springer, Berlin Heidelberg (2008). p. 174–89. doi: 10.1007/978-3-642-00306-613

Crossref Full Text | Google Scholar

184. Kidd MJ, Jackson KJL, Boyd SD, and Collins AM. DJ pairing during VDJ recombination shows positional biases that vary among individuals with differing IGHD locus immunogenotypes. J Immunol. (2016) 196:1158–64. doi: 10.4049/jimmunol.1501401

PubMed Abstract | Crossref Full Text | Google Scholar

185. Dunn-Walters DK, Dogan A, Boursier L, MacDonald CM, and Spencer J. Base-specific sequences that bias somatic hypermutation deduced by analysis of out-of-frame human IgVH genes. J Immunol. (1998) 160:2360–4. doi: 10.4049/jimmunol.160.5.2360

PubMed Abstract | Crossref Full Text | Google Scholar

186. Cowell LG and Kepler TB. The nucleotide-replacement spectrum under somatic hypermutation exhibits microsequence dependence that is strand-symmetric and distinct from that under germline mutation. J Immunol. (2000) 164:1971–6. doi: 10.4049/jimmunol.164.4.1971

PubMed Abstract | Crossref Full Text | Google Scholar

187. Finlay BB and McFadden G. Anti-immunology: Evasion of the host immune system by bacterial and viral pathogens. Cell. (2006) 124:767–82. doi: 10.1016/j.cell.2006.01.034

PubMed Abstract | Crossref Full Text | Google Scholar

188. van de Sandt CE, Kreijtz JHCM, and Rimmelzwaan GF. Evasion of Influenza A Viruses from innate and adaptive immune responses. Viruses. (2012) 4:1438–76. doi: 10.3390/v4091438

PubMed Abstract | Crossref Full Text | Google Scholar

189. Keck ZY, Angus AG, Wang W, Lau P, Wang Y, Gatherer D, et al. Non-random escape pathways from a broadly neutralizing human monoclonal antibody map to a highly conserved region on the hepatitis C virus E2 glycoprotein encompassing amino acids 412-423. PLoS Pathog. (2014) 10:e1004297. doi: 10.1371/journal.ppat.1004297

PubMed Abstract | Crossref Full Text | Google Scholar

190. Weber F and Elliott RM. Antigenic drift, antigenic shift and interferon antagonists: how bunyaviruses counteract the immune system. Virus Res. (2002) 88:129–36. doi: 10.1016/s0168-1702(02)00125-9

PubMed Abstract | Crossref Full Text | Google Scholar

191. Li F, Liu YH, Li YW, Li YH, Xie PL, Ju Q, et al. Construction and development of a mammalian cell-based full-length antibody display library for targeting hepatocellular carcinoma. Appl Microbiol Biotechnol. (2012) 96:1233–41. doi: 10.1007/s00253-012-4243-5

PubMed Abstract | Crossref Full Text | Google Scholar

192. Hanson KE, Gabriel N, Mchardy I, Hoffmann W, Cohen SH, Couturier MR, et al. Impact of IVIG therapy on serologic testing for infectious diseases. Diagn Microbiol Infect Dis. (2020) 96:114952. doi: 10.1016/j.diagmicrobio.2019.114952

PubMed Abstract | Crossref Full Text | Google Scholar

193. Veggiani G and Sidhu SS. Beyond natural immune repertoires: Synthetic antibodies. Cold Spring Harbor Protoc. (2024) 2024. doi: 10.1101/pdb.top107768

PubMed Abstract | Crossref Full Text | Google Scholar

194. Davis MM. Bjorkman PJ. T-cell antigen receptor genes and T-cell recognition. Nature. (1988) 334:395–402. doi: 10.1038/334395a0

PubMed Abstract | Crossref Full Text | Google Scholar

195. Mora T. and Walczak A. M.. Quantifying lymphocyte receptor diversity. bioRxiv. (2016)046870. doi: 10.1101/046870

Crossref Full Text | Google Scholar

196. Milo R. What is the total number of protein molecules per cell volume? A call to rethink some published values. BioEssays. (2013) 35:1050–5. doi: 10.1002/bies.201300066

PubMed Abstract | Crossref Full Text | Google Scholar

197. Bennett T. How many particles are in the observable universe(2017). Available online at: https://www.popularmechanics.com/space/a27259/how-many-particles-are-in-the-entire-universe/.

Google Scholar