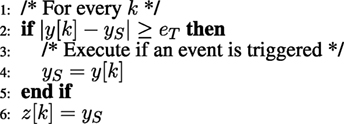- Department of Electronic and Telecommunication Engineering, University of Moratuwa, Moratuwa, Sri Lanka
Frequently, a physical plant of a control system has an optimum operating point such as the spark (or injection) time of an internal combustion engine that results in maximum torque. Extremum Seeking Control (ESC) is a method of adaptive control capable of locating and maintaining a plant at such an optimum operating point in real time. It is capable of doing so with minimal a priori knowledge of the plant and can also track slowly varying changes. Input perturbed ESC schemes that use periodic dither signals have the disadvantage of requiring a high bandwidth for sampling and correlating the plant output with the dither signal. If the feedback path was to be implemented over a packet switched communication network, the high bandwidth requirement could result in increased congestion and consequently packet delays and dropouts. As a solution encoding using sporadic (aperiodic) sampling techniques can be used in the feedback path of the ESC scheme to reduce the required bandwidth. However, in order to ensure convergence of the ESC scheme with encoding, the effect of the signal reconstruction error due to encoding on the critical correlation stage has to be investigated. The contribution of this paper is an investigation of the convergence requirements and bandwidth performance of two encoding schemes; Memory-Based Event Triggering (MBET) and Event Triggered Adaptive Differential Modulation (ETADM). The results show that MBET can fail for objective functions with plateaus. ETADM fails when the number of ETADM steps used for reconstructing the plant output per perturbation cycle is too low to allow correlation. In terms of bandwidth reduction MBET performs better than ETADM (97% and 70%, respectively). However, the use of MBET results in a longer convergence time.
1. Introduction
When a plant is time invariant, known a priori and not subject to exogenous disturbances, finding an optimum operating point offline can be computationally intensive but achievable. The amount of computation would generally grow exponentially with the number of variables. When the plant is time variant and subject to exogenous disturbances, this task becomes more challenging since the optimum operating point has to be sought and maintained online (i.e., in real time).
Extremum Seeking Control (ESC) is a potential solution to this problem. It is a type of adaptive control capable of seeking an optimal operating point and maintaining the plant near it. Since ESC is capable of achieving this without much a priori knowledge of the plant, it can handle plant perturbations and exogenous disturbances. ESC has been applied to a wide range of real world problems such as handling thermoacoustic instability in Banaszuk et al. (2004). Beaudoin et al. (2006) use ESC for bluff body drag reduction, while in Dixon and Frew (2006), it is used for optimizing sensor networks. This technique is used for vehicle control in Stankovich and Stipanovic (2009). Recent publications such as Munteanu and Bratcu (2015), Li et al. (2016), and Bizon (2016) suggest a significant interest in using ESC for maximum power point tracking in photovoltaic cells. Other state-of-the-art applications include those in thermodynamic process optimization such as Mu et al. (2015) and Hu et al. (2015). It has also been used for online optimization of anaerobic digestion as in Lara-Cisneros et al. (2015).
The prevalent form of ESC uses a dither (i.e., excitation) signal to explore the search space of the control problem by perturbing the control inputs. This can be periodic as in Tan et al. (2010) and Krstic and Wang (2000) or stochastic as in Spall (1992) and Manzie and Krstic (2009).
1.1. Motivation
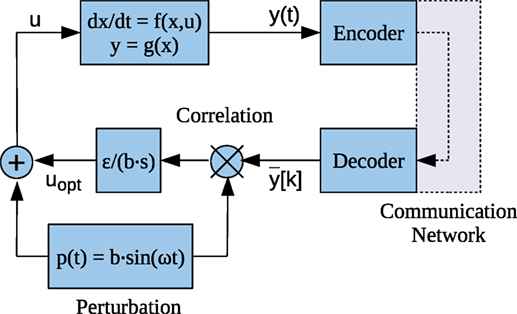
In a networked control system (NCS) that is packet switched, when a periodically sampled variable is transmitted over the communication network it can be subject to the congestion related issues such as delay, delay variation, and packet drops as reported in Zampieri (2008), Donkers et al. (2011), and Premaratne (2014). In Wu et al. (2013), it is demonstrated that congestion can lead to increased packet drops. If the bandwidth intensive feedback loop from the plant output sensor to the correlator (Figure 1) is transmitted over a communication network, it would be subjected to the issues mentioned above.
A realistic example of such a control system is an extremum seeking control scheme such as that of Scotson and Wellstead (1990) being used for optimizing the ignition timing of a ship. Since, the sensor that measures the torque of the propeller shaft is often located at a significant distance from the engine timing controller as mentioned in Hao and Ji (2012), the use of a communication network to complete the feedback path is a justifiable solution. A furnace with a gas emission sensor located at a significant distance due to the operating temperature range of the sensor is another realistic example.
The rational for using sporadic (i.e., aperiodic) sampling is to mitigate congestion due to periodic sampling by decreasing the effective sampling rate. Studies by Arzen (1999), Astrom and Bernhardsson (2002), and Henningsson et al. (2008) have demonstrated the ability of sporadic sampling to reduce the effective sampling rate provided the exogenous disturbances of the control system have a bounded rate of change. Table V of Premaratne et al. (2017) provides empirical evidence that sporadic sampling can reduce the likelihood of packet drops due to decreased transmission. This is an additional advantage.
Possible sporadic sampling techniques include Memory-Based Event Triggering (MBET) proposed by Arzen (1999) and further developed in Lehmann and Lunze (2010) and Lunze and Lehmann (2010). In Event Triggered Adaptive Delta Modulation (ETADM) proposed by Premaratne et al. (2013), event triggering is combined with Adaptive Delta Modulation (ADM). The main motivation for investigation is the effect of the reconstruction error of the above sporadic sampling techniques on the vital correlation stage of the ESC scheme.
1.2. Contribution
The contribution of this paper is the investigation of the convergence requirements and bandwidth performance of MBET and ETADM when used in the feedback path of a sinusoidally perturbed ESC scheme.
1.3. Outline of This Paper
The background of the encoding schemes used is discussed under the Preliminaries (Section 2). In Section 3, the main results are discussed. These include the requirements for convergence of MBET (Section 3.1) and ETADM (Section 3.2). In Section 3.3, the bandwidth reduction of both encoding methods is compared.
2. Preliminaries
2.1. Notations
The set of real numbers and positive integers (excluding zero) is represented by and , respectively. The absolute value of a variable is given by |z|. The letter k in square brackets is used to denote a periodic (clocked) discrete time sample. A class function is a two-argument function . The first argument is a function (known as a class function) which is continuous, strictly increasing, and zero when the argument is zero. The second argument of a function is strictly decreasing. The definitions of and functions are taken from page 144 of Khalil (2002).
2.2. Control System Model
The control system considered consists of an encoded feedback loop (Figure 1). The system description is given by,
where is the plant state, is the control input, and is the output . Both F and G are globally Lipschitz with respect to their arguments. Typically G is a concave (or convex) function with a single isolated optimum point. The high pass and low pass filters are excluded due to possible interference with the bandwidth limiting encoding scheme.
Assumption 1. There exists a globally Lipchitz x*: such that for all , F(x*(u), u) = 0.
Assumption 2. F(x*(u), u) = 0 is uniformly globally asymptotically stable in u.
Let ϕ(u): = G(x*(u)) be the steady state plant output with an isolated maximum v. Assumptions 1 and 2 ensure the stability of the ESC scheme such that for any bounded input u, the state x will remain bounded and converge to the unique equilibrium point determined by the diffeomorphism x*(u).
Definition 1. From Tan et al. (2006) and Nesic (2009): The system , where x ∈ Rn, t ∈ R ≥ 0, and ε ∈ Rl > 0 are, respectively, the state of the system, the time variable, and the parameter vector, is said to be semi-globally practically asymptotically (SPA) stable, uniformly in (εi, …, εj), j ∈ 1, …, l, if there exists β ∈ KL such that the following holds. For each pair of strictly positive real numbers (Δ,ν), there exist real numbers , k = 1, 2, …, j, and for each fixed , k = 1, 2, …, j, there exist εi = εi(ε1, ε2, …, εi−1, Δ, ν), with i = j + 1, j + 2, …, l, such that the solutions of with the so constructed parameters ε = (ε1, …, εl) satisfy:
for all t ≥ t0 ≥ 0, x(t0) = x(t0) with |x0| ≤ Δ. If we have that j = l, then we say that the system is SPA stable, uniformly in ε.
Assumption 3. The ESC scheme of (1) is SPA stable.
If a dynamical system such as equation (1) is SPA stable its output can start from an arbitrarily large initial bound Δ (||x0|| ≤ Δ) and converging to an arbitrarily small bound μ such that ||y(t) − yv|| ≤ μ where yv = ϕ(v) is the desired steady state value of y(t) (i.e., the optimum). Assumption 3 extends the results of Assumptions 1 and 2 to the practical situation where the continuous periodic dither input results in an output perturbed by the bounded harmonics of the periodic input dither.
2.3. Encoding Scheme and Communication Network Model
The purpose of an encoding scheme is to reduce the bandwidth of a signal by minimizing redundancy. A common redundancy in control systems is the high dependence of adjacent samples. This enables the low bandwidth difference between two adjacent samples to be used instead of the entire sample itself. However, according to Premaratne et al. (2013), the transmission of the difference is only beneficial in systems that use time division multiple access (TDMA). An alternative to this is to use sporadic sampling (aperiodic sampling) where the transmission takes place only when there is a significant change in the signal. This makes them more suitable for packet switched NCS. Both encoding schemes considered in this paper fall into this category.
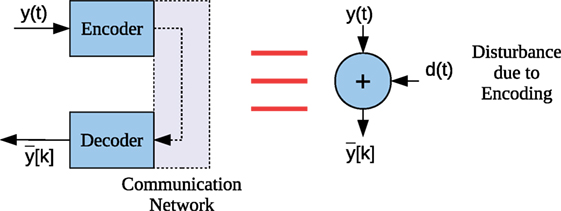
When an encoding scheme is used it is necessary to sample the encoded variable (i.e., the output of the plant) at a sufficient rate TS. The encoded variable will then have to be reconstructed and held for the sampling time TS. This results in an error which can be modeled as a disturbance d(t) = (Figure 2) where k is the discretized time of the reconstruction due to holding. Due to this error further assumptions are necessary.
Assumption 4. For the sufficient sampling time TS, there exists an error bound Δq where for t ∈ [(k − 1) TS, kTS). For convenience, Δq is taken as the upper bound of the quantization error.
Assumption 5. Ideal synchronized clocks are used for periodic sampling and reconstruction of y(t).
Assumption 6. The communication network uses packet switched multiple access with a negligible channel access time compared to TS.
From Assumption 4, the ESC scheme of equation (1) need not be considered as a discrete system as in Choi et al. (2002). Assumptions 5 and 6 are necessary to neglect any effect due to delay and delay variation (jitter), which is inevitable in a packet switched communication network according to the results of Zampieri (2008), Donkers et al. (2011), and Premaratne (2014).
In Tan et al. (2010), it is mentioned that dither signal p(t) cannot be correlated to the disturbance d(t). This can be expressed as:
where T is the perturbation period and p(t) = b sin(ωt). If the two correlate, the direction of update u may be wrongly inferred. This is one of the assumptions used in Tan et al. (2010) to prove convergence of the system. In addition, it is also mentioned that in practice a small correlation can be tolerated provided that the integral of equation (3) is sufficiently small. Therefore, it is possible to relax the requirement of equation (3) such that
will suffice for . The requirement of equation (3) can be used to prove convergence when the reconstruction error can be obtained analytically as in the case of MBET (Lemma 1). When this becomes difficult as for ETADM; equation (4) or empirical correlation of the integrator input of (Figure 1) has to be used.
2.4. Encoding Schemes
In this section, the two encoding schemes used (MBET and ETADM) are introduced in terms of their functionality and main parameters. Based on this in Section 3, the scenarios under which these encoding schemes fail for ESC are derived.
2.4.1. Memory-Based Event Triggering
In MBET of Arzen (1999), Lehmann and Lunze (2010), and Lunze and Lehmann (2010), a periodically sampled input is used. A subsequent sampling event takes place when the difference between the input and the stored input value during the previously triggered event exceed a threshold. The event-based sample is then transmitted across the communication network and at the receiver a Zero Order Hold (ZOH) is used to reconstruct the original signal. The pseudo code of a MBET encoder is given by Figure 3.
The output z[k] becomes the reconstruction once it is held at the ZOH. According to the results of Premaratne et al. (2013), this method is highly efficient in reducing network traffic. However, according to Hirche and Buss (2004), it can become unstable when a packet drop occurs. The main parameter for MBET is the event triggering threshold eT. From the result of Lemma 1 of Premaratne (2016), an MBET encoded signal can be practically approximated to a biased quantizer with a step size of eT. This makes it relatively simple to apply to a practical system.
2.4.2. Event Triggered Adaptive Differential Modulation
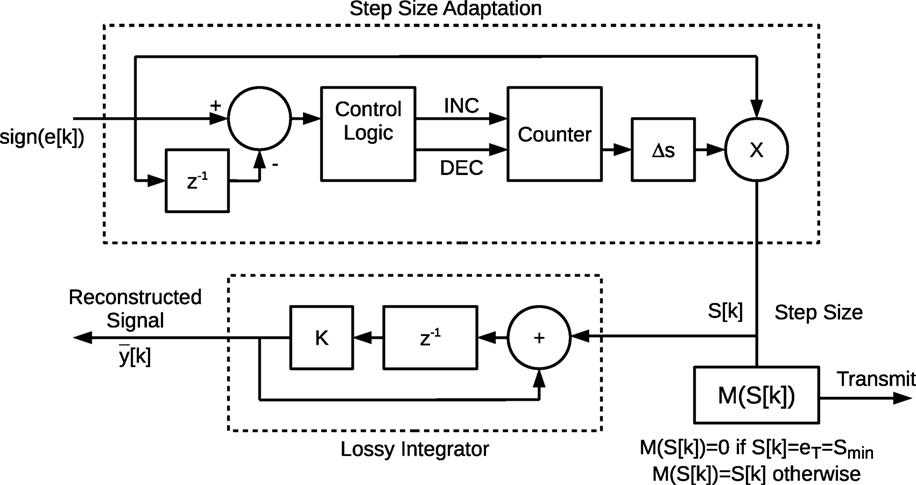
In ETADM of Premaratne et al. (2013), the error between the input and locally reconstructed signal is first encoded at the transmitter by an Adaptive Differential Modulation (ADM) encoder (Figures 6 and 7). The ADM encoder encodes the difference into a variable step size S[k] (for a given time), ranging from a minimum step size Smin to a maximum step size Smax with a step increment of ΔS. When the ADM encoder converges to the input, the step size forms a periodic cycle S[k] = − S[k − 1] = ± Smin. From Theorem 3 of Premaratne et al. (2013), this periodic cycle can be blocked by a subsequent encoder such that
The non-zero output of M(⋅) is then transmitted across the communication network (Figure 8). At the receiver, the signal is reconstructed (i.e., decoded) by a lossy integrator similar to that of the encoder instead of a ZOH. The lossy integrator makes ETADM robust to bounded packet drops compared to MBET. When compared to MBET, the computational complexity of ETADM is significantly higher. Encoding MBET requires only three lines of pseudo code (Figure 3). One the other hand, ETADM requires two lossy integrators, the block M(⋅) and a sign function calculation and the step adaptation of Figure 7. The step adaptation itself has to detect the input sequence of continuous −1 or 1 and increment the step size. If there is a transition in the input (i.e., −1 becomes 1 or vice versa), the step size has to be decremented. Furthermore, the selection of parameters for a particular application is heuristic.
3. Main Results
In this section, the effects of using encoding schemes for ESC are analyzed from a theoretical perspective and empirically verified using Simulink. Reasonable parameters are selected for the simulated ESC example with b = 0.2 and G = ϵ/b = 1. The system dynamics of the simulated example are given by . The objective function and frequency are selected according to the scenario. Each simulation has a sampling time of 0.01 s and is run for 5000 s.
3.1. Memory-Based Event Triggering
Lemma 1. The sinusoidally perturbed ESC system described by (1) that satisfies Assumptions 1 to 6 will converge under MBET encoding if there exists no ux, such that |ϕ(ux) − ϕ(uy)| < eT and |(ux − uy)| > 2b where b > 0 is the amplitude of the sinusoidal perturbation.
Proof. At steady state for an initial value u0 ∈ [ux, uy] such that u ∈ [u0 − b, u0 + b] ⊂ [ux, uy], no events will be triggered since |ϕ(ux) − ϕ(uy)| < eT. Therefore, , where yS is a constant since no events are triggered. Therefore from equation (3),
The correlation is non-zero due to the fact that since ϕ is Lipschitz for all ϕ such that , ϕ(u0 + b sin(ωt)) consists of a fundamental at ω and harmonics.
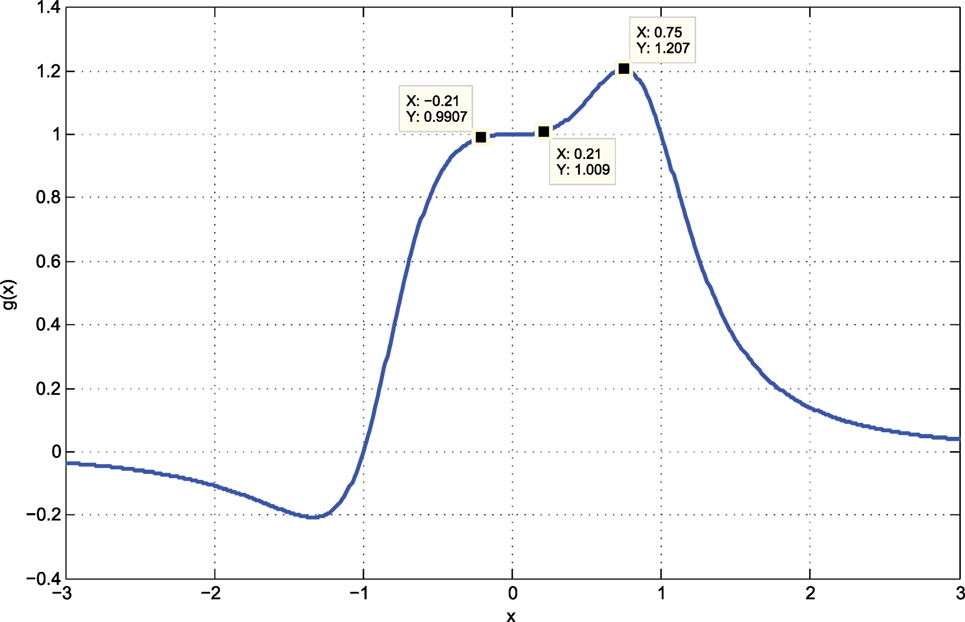
Example 1. Consider the system of (1) with u = x and the plant input-output map:
From the plot of Figure 4, the optimum input, v ≈ 0.75, and the corresponding optimum output is ϕ(v) ≈ 1.2. The output map has a plateau at u = x ∈ [−0.21, 0.21] where y ≈1. When b = 0.2 and perturbation frequency f = ω/(2π) = 10 Hz, the system fails to converge when eT = 0.1 (Figure 5A) and succeeds only when eT is reduced to 0.01 (Figure 5B).
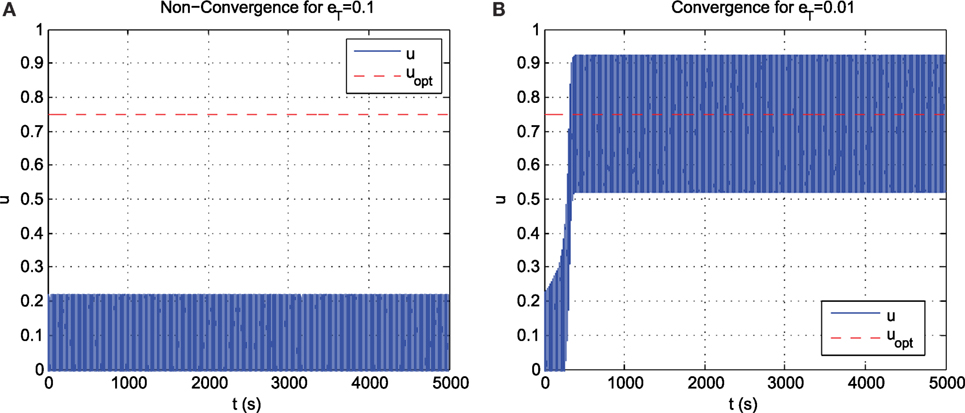
Figure 5. MBET encoded ESC performance for the plant of example 1. (A) Non-convergence for eT = 0.1. (B) Convergence for eT = 0.01.
Remark 1. In order to guarantee convergence when using MBET, prior knowledge of the non-existence of a plateau in the function ϕ(u) is required. This may not be possible in a time variant objective function.
3.2. Event Triggered Adaptive Differential Modulation
Unlike in MBET, the error d(t) of ETADM is complex to model. This is due to the complex state transitions of the ETADM encoder that are highlighted in Theorem 2 of Premaratne et al. (2013). Therefore, it is necessary to ensure that the reconstruction and p(t) are correlated unless y(t) = ϕ(v). Thus, if the perturbation frequency f can by tracked by a cycle of the encoder state S[k], this requirement can be satisfied. Taking the minimum number of samples to maintain a cycle as λ, the value of f would be given by
Finding a suitable value for λ requires insight into the cyclic behavior of S[k] of the ADM encoder based upon its implementation (Figures 6 and 7).
From the proof of Theorem 2 of Premaratne et al. (2013), the possible values of S[k] are discrete and range from Smax, −(Smax + ΔS), …, −Smin, and Smin, Smin + ΔS … Smax. Thus, these discrete values can be taken as individual states. By denoting the state (i.e., value of S[k]) at time k is denoted by the subscript Sk and the sign of e[k] as Ek = sgn(e[k]) = {−1, 0, 1} the state transitions can be represented as:
if Sk is positive and
if Sk is negative.
Since the cycle given by S[k] = − S[k − 1] = ± Smin would be blocked by equation (5), from equations (8) and (9), the cycle with the next largest step size (i.e., ±(Smin + ΔS)) is given by
This cycle becomes {0, Smin + ΔS, 0, −Smin − ΔS} after blocking by equation (5).
From equation (10), the minimum value of λ is four. However, since the lossy integrator with an equation given by x[k + 1] = Kx[k] + KM(S[k]) (K < 1 with K being as close as possible to one) attenuates the signal when M(S[k]) = 0, additional transitions of S[k] = ± (Smin + ΔS) would be required to compensate for the attenuation x[k + 1] = Kx[k]. Thus, the perturbation frequency of equation (7) will have to satisfy the condition
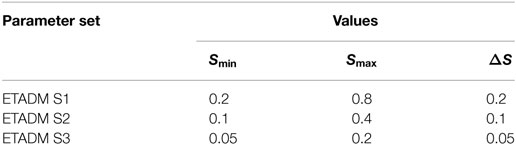
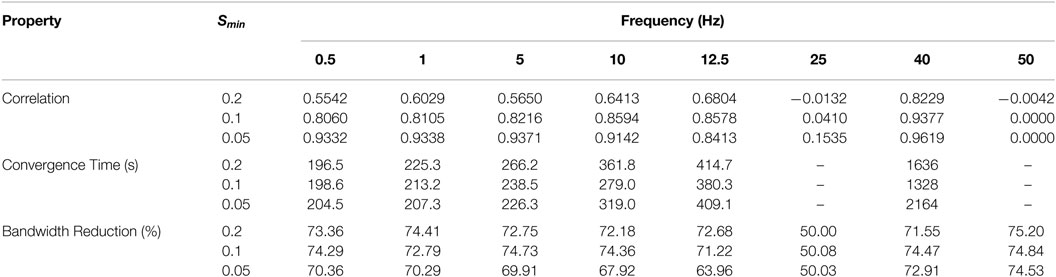
This result is verified for a bell function ϕ(u) = exp[−(u − 2)2/2] with a maximum at u = 2. Three sets of parameters for ETADM encoding (S1, S2, and S3) are selected such that Smin is comparable with the perturbation amplitude b (Table 1). For these results and the sampling time of 0.01 s, f < 25 Hz.
Table 2 shows the results in terms of correlation, convergence, and bandwidth reduction. Out of the multiple frequencies used 50 Hz and 25 Hz are selected so that the perturbation cycle can only be reconstructed by two and four ETADM step values, respectively. For both of these frequencies, there is no significant correlation and convergence as predicted by equation (11). The frequency of 40 Hz is selected in between 50 Hz and 25 Hz for observation of the intermediate behavior. In this case, though there is an unexpectedly high correlation, the convergence time is very large compared to the remaining values. Consistent results are obtained for frequencies below 25 Hz where there is a sufficiently high correlation and rapid convergence.
3.3. Performance Comparison
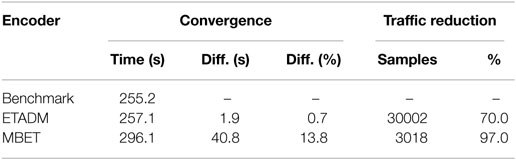
Table 3 compares the performance of MBET and ETADM with eT = Smin = 0.1 with a periodically sampled benchmark. The results show that for comparable parameters MBET outperforms ETADM in terms of bandwidth reduction. This confirms the previously published results of (Premaratne et al., 2013). However, though MBET is more bandwidth efficient than ETADM, it is increases the convergence time compared to the benchmark.
4. Discussion
Extremum Seeking Control (ESC) is an effective method capable of locating and maintaining a plant at an optimum operating point. It can do so with minimal a priori knowledge of the plant. When the ESC scheme uses sinusoidal input perturbation a high bandwidth is required for sampling and correlating the plant output with the dither signal. This can be reduced by using an encoding scheme for the feedback path. In this paper the convergence requirements and bandwidth performance of two encoding schemes, Memory-Based Event Triggering (MBET) and Event Triggered Adaptive Differential Modulation (ETADM) are investigated.
The result of Lemma 1 proves that MBET will not converge if the objective function has a plateau such that the plateau range is greater than the perturbation amplitude and height is less that the MBET threshold. ESC is expected to function without a priori knowledge of the objective function. As mentioned in Remark 1, when MBET encoding is used, knowledge of the non-existence of a plateau in the objective function is necessary.
In the case of ETADM, the convergence result depends on the correlation between the plant output and its reconstruction. The requirement of f < 1/(4TS) [equation (11)] was obtained for the perturbation frequency which were confirmed in the empirical results of Table 2.
In terms of bandwidth reduction, MBET performs better than ETADM with 97% and 70% bandwidth reduction, respectively. However, the use of MBET results in a longer convergence time. Out of the two methods, the authors prefer ETADM due to this reason because the convergence time is significantly less than that of MBET. Furthermore, ETADM can mimic the periodic output of the plant due to its cyclic behavior and is also robust to packet drops. The effects of packet drops on control systems have been subjected to numerous recent studies, such as Cloosterman et al. (2008), Quevedo et al. (2011), and Quevedo and Nesic (2011). Of particular interest is the use of Markovian chains for modeling the dropout as in Wei et al. (2014a,b, 2015b) and Wei et al. (2015a) for application in ESC.
In this paper, the benchmark of Smin = eT was used. The main future direction is to develop a more comprehensive benchmark in terms of parameters and dynamical systems for comparing diverse sporadic sampling methods. In addition, for any problem, the parameters of ETADM have to be selected heuristically. Developing a framework for selecting suitable parameters for ETADM encoding for a particular application is another required future direction. The possibility of using low bandwidth asymptotic cycles similar to that reported in Premaratne (2016) instead of a sinusoidal perturbation for ESC is another interesting research avenue.
Author Contributions
VW did the fundamental research, formulated the basic theory of the paper, and wrote the initial paper. UP supervised the first author, refined the theoretical and empirical work, and did the final editing of the paper.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors would like to acknowledge Dr. Prathapasinghe Dharmawansa for his support and constructive comments.
References
Arzen, K. E. (1999). “A simple event-based PID controller,” in IFAC Congress (Beijing: IFAC), 423–428.
Astrom, K. J., and Bernhardsson, B. M. (2002). “Comparison of Riemann and Lebesgue sampling for first order stochastic systems,” in Proceedings of the 41st IEEE Conference on Decision and Control, Vol. 2 (Las Vegas, NV: IEEE), 2011–2016.
Banaszuk, A., Ariyur, K. B., Krstic, M., and Jacobsen, C. A. (2004). An adaptive algorithm for control of thermoacoustic instability. Automatica 40, 1965–1972. doi: 10.1016/j.automatica.2004.06.008
Beaudoin, J. F., Cadot, O., Aider, J. L., and Wesfried, J. (2006). Bluff body drag reduction by extremum seeking control. J. Fluids Struct. 22, 973–978. doi:10.1016/j.jfluidstructs.2006.04.010
Bizon, N. (2016). Global maximum power point tracking (GMPPT) of photovoltaic array using the extremum seeking control (ESC): a review and a new gmppt esc scheme. Renew. Sustain. Energ. Rev. 57, 524–539. doi:10.1016/j.rser.2015.12.221
Choi, J. Y., Krstic, M., Ariyur, K. B., and Lee, J. S. (2002). Extremum seeking control for discrete-time systems. IEEE Trans. Automat. Contr. 47, 318–323. doi:10.1109/9.983370
Cloosterman, M. B. G., van de Wouw, N., Heemels, W. P. M. H., and Nijmeijer, H. (2008). “Stabilization of networked control systems with large delays and packet dropouts,” in American Control Conference (Seattle, WA: IEEE), 4991–4996.
Dixon, C., and Frew, E. W. (2006). “Controlling the mobility of network nodes using decentralized extremum seeking,” in Proceedings of the 45th IEEE Conference on Decision and Control (San Diego, CA: IEEE), 1291–1296.
Donkers, M., Heemels, W., van de Wouw, N., and Hetel, L. (2011). Stability analysis of networked control systems using a switched linear systems approach. IEEE Trans. Automat. Contr. 56, 2101–2115. doi:10.1109/TAC.2011.2107631
Hao, H., and Ji, Q. (2012). “A design of marine propulsion shaft power telemetry system,” in Advances in Mechanical and Electronic Engineering, eds D. Jin and S. Lin (Berlin and Heidelberg: Springer), 185–189.
Henningsson, T., Johannesson, E., and Cervin, A. (2008). Sporadic event-based control of first-order linear stochastic systems. Autamatica 44, 2890–2895. doi:10.1016/j.automatica.2008.03.026
Hirche, S., and Buss, M. (2004). “Packet loss effects in passive telepresence systems,” in Decision and Control, 2004. CDC. 43rd IEEE Conference On, Vol. 4 (Paradise Islands, Bahamas: IEEE), 4010–4015.
Hu, B., Li, Y., Cao, F., and Xing, Z. (2015). Extremum seeking control of COP optimization for air-source transcritical CO2 heat pump water heater system. Appl. Energy 147, 361–372. doi:10.1016/j.apenergy.2015.03.010
Krstic, M., and Wang, H. H. (2000). Stability of extremum seeking feedback for general nonlinear dynamic systems. Automatica 36, 595–601. doi:10.1016/S0005-1098(99)00183-1
Lara-Cisneros, G., Aguilar-López, R., and Femat, R. (2015). On the dynamic optimization of methane production in anaerobic digestion via extremum-seeking control approach. Comput. Chem. Eng. 75, 49–59. doi:10.1016/j.compchemeng.2015.01.018
Lehmann, D., and Lunze, J. (2010). “Event-based control using quantized state information,” in IFAC Proceedings, Vol. 43 (Sinaia Romania), p. 1–6.
Li, X., Li, Y., Seem, J. E., and Lei, P. (2016). Detection of internal resistance change for photovoltaic arrays using extremum-seeking control MPPT signals. IEEE Trans. Control Syst. Technol. 24, 325–333. doi:10.1109/TCST.2015.2424857
Lunze, J., and Lehmann, D. (2010). A state-feedback approach to event-based control. Automatica 46, 211–215. doi:10.1016/j.automatica.2009.10.035
Manzie, C., and Krstic, M. (2009). Extremum seeking with stochastic perturbations. IEEE Trans. Automat. Contr. 54, 580–585. doi:10.1109/TAC.2008.2008320
Mu, B., Li, Y., Seem, J. E., and Hu, B. (2015). A multivariable Newton-based extremum seeking control for condenser water loop optimization of chilled-water plant. J. Dyn. Syst. Meas. Control 137, 111011. doi:10.1115/1.4031051
Munteanu, I., and Bratcu, A. I. (2015). Mppt for grid-connected photovoltaic systems using ripple-based extremum seeking control: analysis and control design issues. Solar Energy 111, 30–42. doi:10.1016/j.solener.2014.10.027
Nesic, D. (2009). “Extremum seeking control: convergence analysis,” in 2009 European Control Conference (ECC) (Budapest: IEEE), 1702–1715.
Premaratne, U. (2014). “Empirical network jitter measurements for the simulation of a networked control system,” in International Conference on Advances in ICT for Emerging Regions (ICTer) (Colombo: IEEE), 235–240.
Premaratne, U. (2016). “Limit cycle like asymptotic dynamics in feedback loops with memory based event triggering,” in Moratuwa Engineering Research Conference (MERCon) (Colombo: IEEE), 427–431.
Premaratne, U., Halgamuge, S. K., and Mareels, I. M. Y. (2013). Event triggered adaptive differential modulation: a new method for traffic reduction in networked control systems. IEEE Trans. Automat. Contr. 58, 1696–1706. doi:10.1109/TAC.2013.2242571
Premaratne, U., Halgamuge, S. K., and Mareels, I. M. Y. (2017). “Traffic reduction in packet switched networked control systems using deadband error modulation,” in IEEE Transactions on Automatic Control. doi:10.1109/TAC.2016.2615685
Quevedo, D. E., and Nesic, D. (2011). Input-to-state stability of packetized predictive control over unreliable networks affected by packet-dropouts. IEEE Trans. Automat. Contr. 56, 370–375. doi:10.1109/TAC.2010.2095950
Quevedo, D. E., Ostergaard, J., and Nesic, D. (2011). Packetized predictive control of stochastic systems over bit-rate limited channels with packet loss. IEEE Trans. Automat. Contr. 56, 2854–2868. doi:10.1109/TAC.2011.2139410
Scotson, P. G., and Wellstead, P. E. (1990). Self-tuning optimization of spark ignition automotive engines. IEEE Commun. Mag. 10, 94–101.
Spall, J. C. (1992). Multivariate stochastic approximation using a simultaneous perturbation gradient approximation. IEEE Trans. Automat. Contr. 37, 332–341. doi:10.1109/9.119632
Stankovich, M. S., and Stipanovic, D. M. (2009). “Discrete time extremum seeking by autonomous vehicles in a stochastic environment,” in Joint 48th IEEE Conference on Decision and Control 28th Chinese Control Conference (Shanghai: IEEE), 4541–4546.
Tan, Y., Moase, W. H., Manzie, C., Nesic, D., and Mareels, I. (2010). “Extremum seeking from 1922 to 2010,” in Proceedings of the 29th Chinese Control Conference (Beijing: IEEE).
Tan, Y., Nesic, D., and Mareels, I. (2006). On non-local stability properties of extremum seeking control. Automatica 42, 889–903. doi:10.1016/j.automatica.2006.01.014
Wei, Y., Qiu, J., Karimi, H. R., and Wang, M. (2014a). Filtering design for two-dimensional Markovian jump systems with state-delays and deficient mode information. Inf. Sci. 269, 316–331. doi:10.1016/j.ins.2013.12.042
Wei, Y., Qiu, J., Karimi, H. R., and Wang, M. (2014b). Model reduction for continuous-time markovian jump systems with incomplete statistics of mode information. Int. J. Syst. Sci. 45, 1496–1507. doi:10.1080/00207721.2013.837545
Wei, Y., Qiu, J., Karimi, H. R., and Wang, M. (2015a). Model approximation for two-dimensional markovian jump systems with state-delays and imperfect mode information. Multidimens. Syst. Signal Process. 26, 575–597. doi:10.1007/s11045-013-0276-x
Wei, Y., Qiu, J., and Karimi, H. R. (2015b). Quantized H-infinity filtering for continuous-time Markovian jump systems with deficient mode information. Asian J. Control 17, 1914–1923. doi:10.1002/asjc.1052
Wu, H., Feng, Z., Guo, C., and Zhang, Y. (2013). ICTCP: incast congestion control for TCP in data-center networks. IEEE/ACM Trans. Netw. 21, 345–358. doi:10.1109/TNET.2012.2197411
Keywords: extremum seeking control, networked control systems, network traffic reduction, encoding schemes, memory-based event triggering, event triggered adaptive differential modulation
Citation: Wijesinghe VS and Premaratne UK (2016) Bandwidth Reduction and Convergence Analysis of Extremum Seeking Control with Feedback Encoding. Front. Mech. Eng. 2:11. doi: 10.3389/fmech.2016.00011
Received: 06 August 2016; Accepted: 04 November 2016;
Published: 28 November 2016
Edited by:
Hamid Reza Karimi, Polytechnic University of Milan, ItalyReviewed by:
Sachin Prakash Wadikhaye, Eaton Technologies Pvt. Ltd, IndiaJianbin Qiu, Harbin Institute of Technology, China
Copyright: © 2016 Wijesinghe and Premaratne. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Upeka Kanchana Premaratne, dXBla2FAdW9tLmxr
 Vikum S. Wijesinghe
Vikum S. Wijesinghe Upeka Kanchana Premaratne
Upeka Kanchana Premaratne