Effects of Viscous Dissipation on Unsteady Mixed Convection Heat Transfer from a Circular Cylinder for Parallel and Contra Flows

Introduction

Heat transfer from a circular cylinder has been the subject of research due to its occurrence in many industrial and engineering applications such as heat exchanger tubes, chimney stacks, cooling towers, measuring probes, and sensors (Sarkar et al., 2011), drying of different materials (textiles, veneer, paper, and film materials), cooling of glass, plastics, and industrial devices, from turbine blades to electronic circuits, anemometry, and chemical or radioactive contamination/purification (Juncu, 2004), nuclear reactors, hot wires, and steam pipes (Mahfouz, 2003). In some processes, it takes place only by free convection or forced convection. However, there are some processes where the forced and free convection are of comparable order, and then the process of heat transfer is known as combined convection or mixed convection. This paper investigates the heat-transfer characteristics of the combined free and forced convection from a horizontal circular cylinder, which is placed to a transverse flow whose direction is either in the free convection flow (parallel flow) or opposite to it (contra flow).

Dennis and Chang (1970) investigated the steady incompressible flow around a circular cylinder for a range of Reynolds numbers from 5 to 100. The dimensionless governing equations are solved employing finite-difference method, but in effect, it appears to be failed because of being very slow at higher Reynolds numbers. Results have been elucidated by the drag coefficient, the angle of separation, and the pressure and vorticity distributions over the cylinder surface. Almost a decade later, Fornberg (1980) considered the same problem and carried out an efficient numerical method based on Newton’s method, which can provide solutions beyond a Reynolds number of 100. Numerical solutions showed that just before a Reynolds number of 300, the wake region is reduced or elongated when the vorticity regenerates from the end of the wake region.

Mahfouz (2003) considered the transient free convection from an isothermal cylinder placed horizontally in a micropolar fluid. The local and average Nusselt numbers and the flow and thermal fields have been discussed for different values of the controlling parameters. The natural convection heat transfer from an isothermal horizontal cylinder of elliptic cross section has been examined by Cheng (2006). The viscosity of the fluid is assumed to vary proportional to an inverse linear function of temperature and a suitable coordinate transformation, and the cubic spline collocation method was used. Moreover, Juncu (2008) investigated the transient heat transfer from an elliptic cylinder placed in a free stream fluid, and the temperature of the cylinder varies in time.

A good work on the forced convection heat transfer from a circular cylinder has been done by Kurdyumov and Fernández (1998). Results are illustrated in terms of the Nusselt number for small values of Reynolds number. Nguyen et al. (1996) studied the heat transfer from a rotating circular cylinder. It was embedded in a spatially uniform and time-dependent convective environment under the effect of buoyancy force. The equations of the vorticity, stream function, and energy were solved using a hybrid spectral scheme. The Reynolds number, Grashof number, rotational speed, and the gravity direction had considerable influence on the heat-transfer rate. The effects of Prandtl number and Richardson number on the wake dynamics and heat transfer past a circular cylinder in crossflow have been examined by Sarkar et al. (2011). The effects of the Reynolds number and Prandtl number have been illustrated in terms of the local and average Nusselt.

In the nineteenth century, Badr and his coworkers published a series of papers (Badr, 1983, 1984; Badr and Dennis, 1985; Badr et al., 1990) on the flow and heat transfer around a cylinder. Badr (1983) examined the laminar mixed convection from a horizontal cylinder placed in the free stream, which is directed to horizontal and perpendicular to the cylinder axis. Results are presented in terms of vorticity, pressure, temperature, and local Nusselt number around the surface. The author also considered the same problem taking the forced flow directed either vertically upward (parallel flow) or vertically downward (contra flow). The vorticity and Nusselt number distributions are illustrated with the change of the Grashof number and the Reynolds number for both parallel and contra flows. Mahfouz and Badr (2000) numerically demonstrated the characteristics of the flow in the wake of a circular cylinder, which was kept in a cross-stream and made rotational oscillation about its own axis.

Biswas and Sarkar (2009) examined the effects of thermal buoyancy on vortex shedding behind a circular cylinder, which is placed in a crossflow at low Reynolds numbers. The dimensionless governing equations have been solved using streamline upwind Petrov–Galerkin (SUPG) based finite element method. Sarkar et al. (2010) studied the flow and heat-transfer characteristics for mixed convection flow past two tandem square cylinders which were kept in a uniform upward flow at a Reynolds number of 100. Numerical solutions of the problem are obtained using the aforementioned SUPG based finite element method, and the results have been demonstrated for various Richardson numbers taking into consideration the influences of aiding and opposing buoyancy.

A long time ago, Nakai and Okazaki (1975) examined the heat-transfer characteristics from a horizontal infinite fine wire by mixed convections for parallel, contrary, and crossflows. The problem was analyzed theoretically considering the dominant behavior of one of the forced or free convection to the other. They also conducted an experiment and found a good agreement with the analytical solutions. Gebhart (1962) performed boundary layer analysis in order to comprehend the influence of the viscous dissipation for vertical surfaces under different thermal conditions. The situations where viscous dissipation is important have been illustrated elaborately. He concluded that the magnitude of the viscous dissipation effect is dependent on a dissipation number; however, it cannot be expressed in terms of the Grashof or the Prandtl number. Abu-Hijleh et al. (1998) studied the effect of viscous dissipation on the local entropy generation due to natural convection from a heated horizontal isothermal cylinder. They mentioned that the comprehensive knowledge about the overall natural convective heat transfer around circular cylinders is important for the development of heat exchangers, hot water and steam pipes, heaters, refrigerators, and electrical conductors. Recently, Chhabra et al. (2007) investigated the effects of viscous dissipation on the heat transfer between banks of long cylinders and power law fluids.

From the above literature survey, it can be concluded that a very few studies have considered the mixed convection heat transfer from a circular cylinder for both parallel and contra flows. Moreover, the previous studies except Abu-Hijleh et al. (1998) and Chhabra et al. (2007) have neglected the influences of viscous dissipation, but it is always not realistic. For this reason, the objective of this study is to investigate the unsteady mixed convection heat transfer from a circular cylinder for both parallel and contra flows in the presence of viscous dissipation. The system of governing equations is transformed into a suitable form of integration, and the resulting equations are solved using finite-difference method. Numerical results are presented in terms of the Nusselt number and the vorticity distribution as well as the streamlines and the isotherms.

Mathematical Formulation

We consider a horizontal circular cylinder of radius a in a uniform free stream of velocity U_∞ and temperature T_∞ while the surface of the cylinder is kept at constant temperature T_s. The flow direction of the free stream has been taken in two ways: vertically upward and vertically downward. We also assume that the temperature difference (T_s − T_∞) between the cylinder surface and the ambient fluid has a negligible effect on the fluid properties; however, it can significantly affects the buoyancy forces in the momentum equation. Moreover, the cylinder is presumed to be long enough that produces negligible end effects. In this manner, we can consider the flow field to be two-dimensional. Therefore, the governing equations can be expressed in terms of vorticity, stream function, and energy equations as

$\frac{\partial {\mathrm{\omega }}^{\star }}{\partial t^{\star }}+u^{\star }\frac{\partial {\mathrm{\omega }}^{\star }}{\partial r^{\star }}+\frac{v^{\star }}{r^{\star }}\frac{\partial {\mathrm{\omega }}^{\star }}{\partial r^{\star }}=\mathrm{\nu }{\nabla }^2{\mathrm{\omega }}^{\star }\pm \frac{1}{\mathrm{\rho }}\left(\frac{\partial F_{\mathrm{\theta }}}{\partial r^{\star }}-\frac{1}{r^{\star }}\frac{\partial F_{r^{\star }}}{\partial \mathrm{\theta }}+\frac{F_{\mathrm{\theta }}}{r^{\star }}\right),$ (1)

${\mathrm{\omega }}^{\star }={\nabla }^2{\mathrm{\psi }}^{\star },$ (2)

$\frac{\mathit{\partial T}}{\partial t^{\star }}+u^{\star }\frac{\mathit{\partial T}}{\partial r^{\star }}+\frac{v^{\star }}{r^{\star }}\frac{\mathit{\partial T}}{\partial \mathrm{\theta }}=\frac{\mathrm{\kappa }}{\mathrm{\rho }c}{\nabla }^{2}T+\frac{\mathrm{\nu }}{c}{\mathrm{\Phi }}^{\star },$ (3)

where

${\nabla }^2=\frac{{\partial }^2}{\partial {r^{\star }}^2}+\frac{1}{r^{\star }}\frac{\partial }{\partial r^{\star }}+\frac{1}{{r^{\star }}^2}\frac{{\partial }^2}{\partial {\mathrm{\theta }}^2},$

and Φ* is the viscous dissipation term and given by

${\mathrm{\Phi }}^{\star }={\left(\frac{1}{r^{\star }}\frac{\partial u^{\star }}{\partial \mathrm{\theta }}+\frac{\partial v^{\star }}{\partial r^{\star }}-\frac{v^{\star }}{r^{\star }}\right)}^2+2\left\{{\left(\frac{\partial u^{\star }}{\partial r^{\star }}\right)}^2+\frac{1}{{r^{\star }}^2}{\left(u^{\star }+\frac{\partial v^{\star }}{\partial \mathrm{\theta }}\right)}^2\right\}.$

In the above equations, t* is the time, u* and v* are the velocities in the r* and θ directions, T is the temperature, ρ is the density, ν is the kinematic viscosity, κ is the thermal conductivity, and c is the specific heat. Moreover, $F_{r^{\star }}$ and F_θ are the radial and transverse components of the body force and defined as

$F_{r^{\star }}=-\mathrm{\rho }g\mathrm{\beta }\left(T-T_{\infty }\right)\text{cos}\mathrm{\theta }\text{and}{F}_{\mathrm{\theta }}=\mathrm{\rho }g\mathrm{\beta }\left(T-T_{\infty }\right)\text{sin}\mathrm{\theta }\text{,}$ (4)

where g is the gravitational acceleration, β is the coefficient of thermal expansion, and T_∞ is the fluid temperature far away from the cylinder. The vorticity ω and stream function ψ are related to the velocity field by

$\mathrm{\omega }=-\frac{1}{r^{\star }}\left(r^{\star }\frac{\partial v^{\star }}{\partial r^{\star }}+v^{\star }-\frac{\partial u^{\star }}{\partial \mathrm{\theta }}\right)$ (5)

and

$u^{\star }=\frac{1}{r^{\star }}\frac{\partial {\mathrm{\psi }}^{\star }}{\partial \mathrm{\theta }},v^{\star }=-\frac{\partial {\mathrm{\psi }}^{\star }}{\partial r^{\star }}.$ (6)

The associated boundary conditions are

$u^{\star }=v^{\star }=0,T=T_s\text{at}r=a,$ (7)

$u^{\star }=U_{\infty }\text{cos}\mathrm{\theta },v^{\star }=-U_{\infty }\text{sin}\mathrm{\theta },{\mathrm{\omega }}^{\star }=0,\text{and}T=T_{\infty }\text{as}r\to \infty .$ (8)

We now introduce the following dimensionless variables

$\begin{array}{llll}\hfill u& =\frac{u^{\star }}{U_{\infty }},v=\frac{v^{\star }}{U_{\infty }},r=\frac{r^{\star }}{a},t=\frac{U_{\infty }{t}^{\star }}{a},& \hfill & \\ \hfill \mathrm{\psi }& =\frac{{\mathrm{\psi }}^{\star }}{a{U}_{\infty }},\mathrm{\omega }=\frac{a{\mathrm{\omega }}^{\star }}{U_{\infty }},\text{and}\mathrm{\varphi }=\frac{T-T_{\infty }}{T_s-T_{\infty }},\end{array}$ (9)

where U_∞ is the velocity of the uniform stream.

Thus the system of Eqs 1–3 reduces to

$\frac{\partial \mathrm{\omega }}{\mathit{\partial t}}+u\frac{\partial \mathrm{\omega }}{\mathit{\partial r}}+\frac{v}{r}\frac{\partial \mathrm{\omega }}{\partial \mathrm{\theta }}=\frac{2}{\mathrm{Re}}{\nabla }^2\mathrm{\omega }\pm \frac{\text{Gr}}{2{\mathrm{Re}}^2}\left(\text{sin}\mathrm{\theta }\frac{\partial \mathrm{\varphi }}{\mathit{\partial r}}+\text{cos}\mathrm{\theta }\frac{\partial \mathrm{\varphi }}{\partial \mathrm{\theta }}\right),$ (10)

$\mathrm{\omega }={\nabla }^2\mathrm{\psi },$ (11)

$\frac{\partial \mathrm{\varphi }}{\mathit{\partial t}}+u\frac{\partial \mathrm{\varphi }}{\mathit{\partial r}}+\frac{v}{r}\frac{\partial \mathrm{\varphi }}{\mathit{\partial Y}}=\frac{2}{\mathrm{Pr}\mathrm{Re}}{\nabla }^2\mathrm{\varphi }+\text{Ec}\mathrm{\Phi },$ (12)

where

$\begin{array}{llll}\hfill {\nabla }^2& =\frac{{\partial }^2}{\partial r^2}+\frac{1}{r}\frac{\partial }{\mathit{\partial r}}+\frac{1}{r^2}\frac{{\partial }^2}{\partial {\mathrm{\theta }}^2},& \hfill & \\ \hfill \mathrm{\Phi }& ={\left(\frac{1}{r}\frac{\mathit{\partial u}}{\partial \mathrm{\theta }}+\frac{\mathit{\partial v}}{\mathit{\partial r}}-\frac{v}{r}\right)}^2+2\left\{{\left(\frac{\mathit{\partial u}}{\mathit{\partial r}}\right)}^2+\frac{1}{r^2}{\left(u+\frac{\mathit{\partial v}}{\partial \mathrm{\theta }}\right)}^2\right\}.& \hfill & \end{array}$

Also the velocity components u and v used in the above equations are given by

$u=\frac{1}{r}\frac{\partial \mathrm{\psi }}{\partial \mathrm{\theta }},v=-\frac{\partial \mathrm{\psi }}{\mathit{\partial r}}.$ (13)

In Eqs 10 and 12, Gr = gβ(2a)³(T_s − T_∞)/ν² is the Grashof number, Re = 2aU_∞/ν is the Reynolds number, Pr = μc/κ is the Prandtl number, and Ec = νU_∞/ca(T_s − T_∞) is the Eckert number.

The boundary conditions take the form

$u=v=0,\mathrm{\varphi }=1\text{at}r=1,$ (14)

$u=\text{cos}\mathrm{\theta },v=-\text{sin}\mathrm{\theta },\mathrm{\omega }=0,\text{and}\mathrm{\varphi }=0\text{as}r\to \infty .$ (15)

Finally, we transform the polar coordinates (r, θ) into (ξ, θ) using the relation ξ = ln r so that Eqs 10–12 become

$e^{\mathrm{2\xi }}\frac{\partial \mathrm{\omega }}{\mathit{\partial t}}+U\frac{\partial \mathrm{\omega }}{\partial \mathrm{\theta }}+V\frac{\partial \mathrm{\omega }}{\partial \mathrm{\xi }}=\frac{2}{\mathrm{Re}}\left(\frac{{\partial }^2\mathrm{\omega }}{\partial {\mathrm{\theta }}^2}+\frac{{\partial }^2\mathrm{\omega }}{\partial {\mathrm{\xi }}^2}\right)\pm \frac{\text{Gr}}{2{\mathrm{Re}}^2}{e}^{\mathrm{\xi }}\left(\text{sin}\mathrm{\theta }\frac{\partial \mathrm{\varphi }}{\partial \mathrm{\theta }}+\text{cos}\mathrm{\theta }\frac{\partial \mathrm{\varphi }}{\partial \mathrm{\xi }}\right),$ (16)

$e^{\mathrm{2\xi }}\mathrm{\omega }=\frac{{\partial }^2\mathrm{\psi }}{\partial {\mathrm{\theta }}^2}+\frac{{\partial }^2\mathrm{\psi }}{\partial {\mathrm{\xi }}^2},$ (17)

$e^{\mathrm{2\xi }}\frac{\partial \mathrm{\varphi }}{\partial \mathrm{\tau }}+U\frac{\partial \mathrm{\varphi }}{\partial \mathrm{\theta }}+V\frac{\partial \mathrm{\varphi }}{\partial \mathrm{\xi }}=\frac{2}{\mathrm{Pr}\mathrm{Re}}{\nabla }^2\mathrm{\varphi }+e^{-\mathrm{2\xi }}\text{Ec}\mathrm{\Phi }\text{,}$ (18)

where we have used the relations

$V=\frac{\partial \mathrm{\psi }}{\partial \mathrm{\theta }},U=-\frac{\partial \mathrm{\psi }}{\partial \mathrm{\xi }},$ (19)

$\mathrm{\Phi }={\left(\frac{\mathit{\partial U}}{\partial \mathrm{\theta }}+\frac{\mathit{\partial V}}{\partial \mathrm{\xi }}-2V\right)}^2+2\left\{{\left(\frac{\mathit{\partial U}}{\partial \mathrm{\xi }}\right)}^2+{\left(U+\frac{\mathit{\partial V}}{\partial \mathrm{\theta }}\right)}^2\right\}.$ (20)

The corresponding boundary conditions are

$\begin{array}{llll}\hfill \mathrm{\psi }& =\frac{\partial \mathrm{\psi }}{\partial \mathrm{\xi }}=0\text{and}\mathrm{\varphi }=1\text{at}\mathrm{\xi }=0,& \hfill & \\ \hfill \frac{\partial \mathrm{\psi }}{\partial \mathrm{\theta }}& =e^{\mathrm{\xi }}\text{cos}\mathrm{\theta },\frac{\partial \mathrm{\psi }}{\partial \mathrm{\xi }}=e^{\mathrm{\xi }}\text{sin}\mathrm{\theta },\mathrm{\omega }=0,\mathrm{\varphi }=0\text{as}\mathrm{\xi }\to \infty .\end{array}$ (21)

From physical point of view, the local Nusselt number, Nu, and the average skin friction, ${\overline{C}}_f$, and Nusselt number, $\overline{\text{Nu}}$, are of great importance. These are defined as

$\text{Nu}=\frac{\mathit{ah}}{k},{\overline{C}}_f=\frac{a{\overline{\mathrm{\tau }}}_w}{\mathrm{\mu }{U}_{\infty }},\text{and}\overline{\text{Nu}}=\frac{a\overline{h}}{k},$ (22)

where h and $\overline{h}$ are, respectively, the local and overall heat-transfer coefficients, which are given by

${\overline{\mathrm{\tau }}}_w=\frac{\mathrm{\mu }}{\mathrm{\pi }}{\int }_0^{\mathrm{\pi }}{\left(\frac{\partial u^{\star }}{\partial r^{\star }}\right)}_{r^{\star }=a}d\mathrm{\theta },h=\frac{\mathrm{\kappa }}{T_s-T_{\infty }}{\left(\frac{\mathit{\partial T}}{\partial r^{\star }}\right)}_{r^{\star }=a},\text{and}\overline{h}=\frac{1}{\mathrm{2\pi }}{\int }_0^{\mathrm{2\pi }}\mathit{hd}\mathrm{\theta }.$ (23)

Numerical Method

In this study, we have solved the dimensionless governing Eqs 16–18 in the modified coordinates (ξ, θ) using finite-difference method. In particular, we use SOR method with residual tolerance of order 10⁻⁶ for the stream function defined in Eq. 17. Taking ξ_max = 4.0, we consider the uniform meshes of sizes Δθ = 2π/(m − 1) and Δξ = ξ_max/(n − 1), where m = 257 and n = 129 are the number of intervals along the θ and ξ directions. The relaxation parameter, say “δ” is determined from the relation (Roache, 1998):

$\mathrm{\delta }=2\left(\frac{1-\sqrt{1-\mathrm{\epsilon }}}{\mathrm{\epsilon }}\right),$ (24)

where

$\mathrm{\epsilon }=\frac{1}{4}{\left[\text{cos}\left(\frac{\mathrm{\pi }}{m-1}\right)+\text{cos}\left(\frac{\mathrm{\pi }}{n-1}\right)\right]}^2.$ (25)

Having found the stream function, we calculate the velocity components using Eq. 19 at each time step. Then the alternate direct implicit (ADI) method is used for the transient vorticity transport and energy Eqs 16 and 18. In this manner, using the values of ω and ϕ at any time step, we compute their values at the next time step from Eqs 16 and 18. It is noted that the transient and diffusion terms in the ADI method are discretized using forward-time central-space technique. Moreover, we use second upwind differencing technique for the convective terms. Although ADI method is unconditionally stable, a grid independency test has been performed taking different number of mesh points, and the results are presented in Table 1. Here, we calculate the percentage error (%) for a variable Ω using two computed values with different number of grid points, which is given by

$\text{Error}\left(\%\right)=\left|\frac{\mathrm{\Omega }\left(m_{k+1}\times n_{k+1}\right)-\mathrm{\Omega }\left(m_k\times n_k\right)}{\mathrm{\Omega }\left(m_k\times n_k\right)}\right|\times 100,$ (26)

where m_k = 2^k + 1 and n_k = 2^k−1 + 1 denote the number of grids in θ and ξ directions, respectively. In order to justify the grid dependency test, the average Nusselt number is calculated considering different number of mesh points. When we determine the percentage error of Ω for 65 × 33 grids, the value of Ω for 33 × 17 grids is taken as a reference value. It is clear that the maximum error in the average Nusselt number calculated for mesh size 257 × 129 and 513 × 257 becomes less than 2%. Accordingly, we choose a grid of size 257 × 129 as a standard grid for the entire computation. Above all, the reduction in relative error validates the grid independence of the solution.

TABLE 1

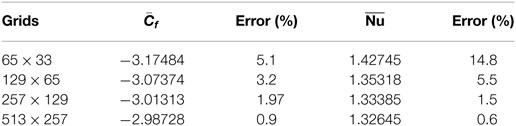
Table 1. Comparison of average skin friction and Nusselt number for parallel flow at τ = 10 when Pr = 0.7, Re = 20, Ec = 0.01, Gr = 100, and Δτ = 10⁻⁴.

Results and Discussion

In Figure 1, a comparison is made of the average Nusselt number obtained by the present method and Badr (1983). As mentioned by Badr (1983), the cylinder was heated instantaneously to the constant surface temperature T_s after a certain time. So the result indicates the decrease of average Nusselt after a certain time. However, the present study evaluates the time from 0. Thus, the initial time taken by Badr (1983) has been transformed into 0 for the validation purpose. It is evident from the result that the present method gives a good agreement with Badr (1983). Moreover, Figure 2 shows the comparison of vorticity distribution obtained by the present method and Badr (1983). In this case, there is found an excellent agreement between the present method and Badr (1983).

FIGURE 1

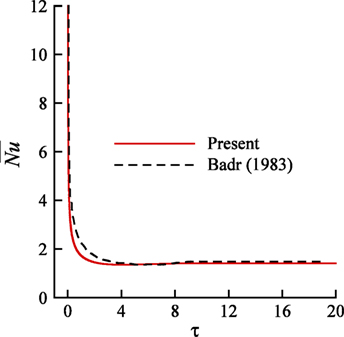
Figure 1. A comparison with the result obtained by Badr (1983) for Pr = 0.73, Re = 5, and Gr = 100.

FIGURE 2

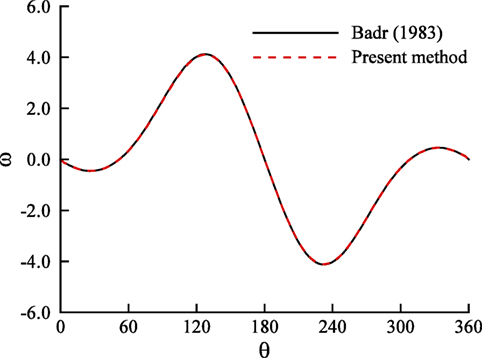
Figure 2. Vorticity distribution obtained by the present method and Badr (1983) when Pr = 0.7, Re = 20, and Gr = 100.

The transient development of streamlines and isotherms for the parallel flow is demonstrated in Figures 3A–C and 4A–C, respectively. As time goes by, the size of the vortex and the momentum boundary layer gradually increase. On the other hand, Figure 4A–C shows that the temperature distribution is elongated with time in the downstream region. Moreover, it becomes thick at the rear stagnation point (θ = 180). The reasons for increasing the vortex and the momentum boundary layer and thickening the temperature distribution are attributed to the convection of fluid and heat along the direction of the free stream.

FIGURE 3

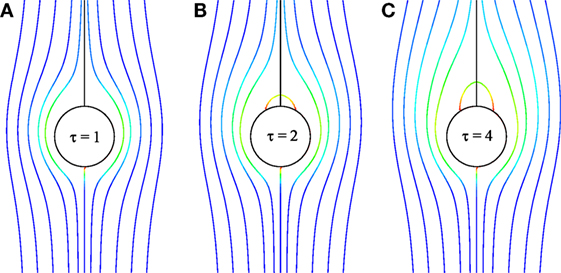
Figure 3. Transient development of streamlines for the parallel flow for Pr = 0.7, Re = 20, Ec = 0.01, and Gr = 100.

FIGURE 4

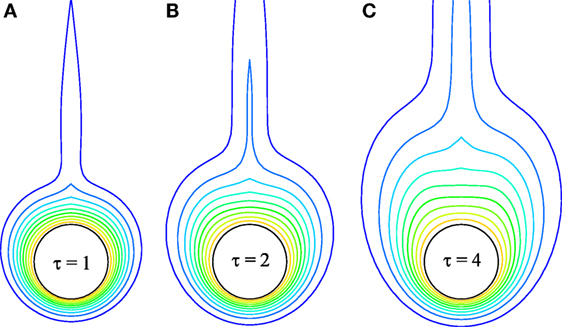
Figure 4. Transient development of isotherms for the parallel flow for Pr = 0.7, Re = 20, Ec = 0.01, and Gr = 100.

Figures 5A–C and 6A–C depict the transient development of streamlines and isotherms, respectively, for the contra flow. It is found that there occurs vortex within a short period of time. With increase of time, it significantly increases. This is due to the fact that the fluid erupts against the buoyancy force which induces negative pressure at the rear stagnation point. It is evident from Figure 6A–C that the temperature distribution is drastically elongated with time in the downstream region. Also the thickness of the temperature distribution increases at the rear stagnation point (θ = 180), which helps to increase the size of the vortex. Since the hot fluid near the circular cylinder is transferred by the free stream, hence the temperature distribution is extended in the downstream region.

FIGURE 5

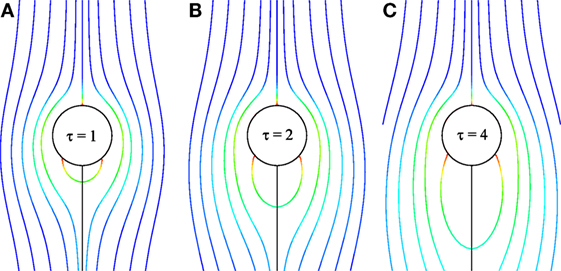
Figure 5. Transient development of streamlines for the contra flow for Pr = 0.7, Re = 20, Ec = 0.01, and Gr = 100.

FIGURE 6

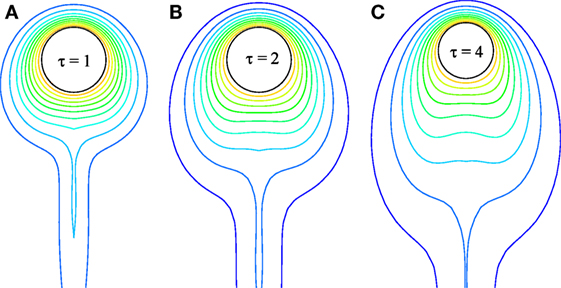
Figure 6. Transient development of isotherms for the contra flow for Pr = 0.7, Re = 20, Ec = 0.01, and Gr = 100.

The effects of the Eckert number on the local Nusselt number for parallel and contra flows are shown in Figures 7A,B, respectively. When Ec = 0.0, the Nusselt number for parallel flow gradually increases along the surface of the cylinder from the front stagnation point θ = 0 and gets a maximum at the rear stagnation point θ = π. In the presence of viscous dissipation, that is, when Ec ≠ 0, the Nusselt number for parallel flow demonstrates the non-monotonous behavior in the interval 0 ≤ θ ≤ 2π/3 and then it increases with θ up to θ = π. The similar characteristics are observed when the angular distance changes from 2π to π. But for contra flow, the Nusselt number corresponding to any of the Eckert number changes almost in the same manner of parallel flow for Ec = 0.0. In both cases, the Eckert number has strong effect on the Nusselt number and, it decreases with increasing values of the Eckert number. In particular, the Nusselt number relating to Ec ≠ 0 has distinct characteristics from that for Ec = 0.0 in the interval 0 ≤ θ ≤ 2π/3.

FIGURE 7

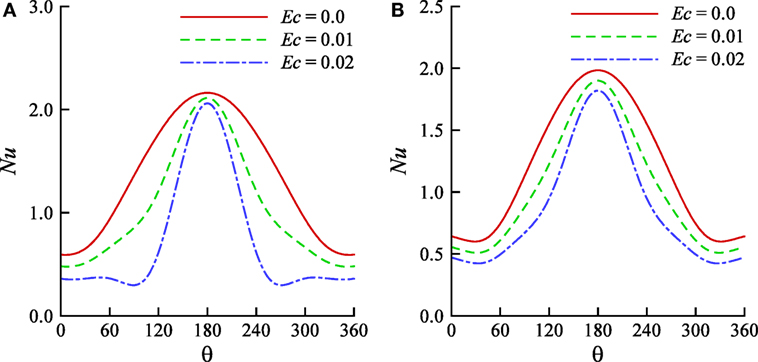
Figure 7. Effects of the Eckert number on the local Nusselt number for (A) parallel and (B) contra flows when Pr = 0.7, Gr = 100.0, and Re = 20.

The effects of the Eckert number on the vorticity distribution for parallel and contra flows are demonstrated in Figures 8A,B, respectively. It is found from Figure 8A that whatever be the value of Ec the vorticity first increases in the interval (0, 2π/3) and then decreases up to the point θ = π. However, it varies in a reverse way as θ changes from 2π to π. There is seen weak effect of the Eckert number on the vorticity distribution. In the case of parallel flow, the maximum value of the Nusselt number occurred at θ = 2π/3 increases, and its minimum value at θ = 4π/3 decreases as the value of Ec increases. The similar characteristics are observed for contra flow. But the effect of the Eckert number on the vorticity distribution for contra flow seems to be higher than that for parallel flow.

FIGURE 8

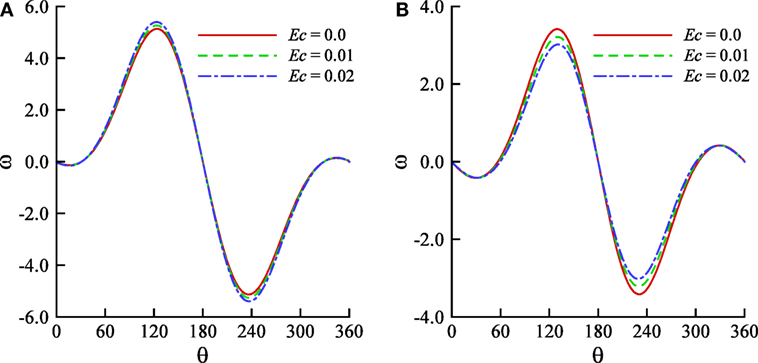
Figure 8. Effects of the Eckert number on the vorticity distribution for (A) parallel and (B) contra flows when Pr = 0.7, Gr = 100.0, and Re = 20.

Figures 9A,B illustrate the variations of the steady state streamlines and isotherms for parallel and contra flows. Results indicate that the momentum boundary layer and the thermal boundary layer become thinner for parallel flow compared to those for contra flow. The reason is that in the case of parallel flow the forced convection aids the buoyancy force owing to their same direction which accordingly accelerates the fluid flow. Moreover, the points of separation for parallel flow are delayed in comparison with contra flow. This is due to the fact that in the case of parallel flow, the forced convection assists the free convection flow resulting in increasing the fluid flow, which inhibits the flow field to be separated from the surface of the cylinder.

FIGURE 9

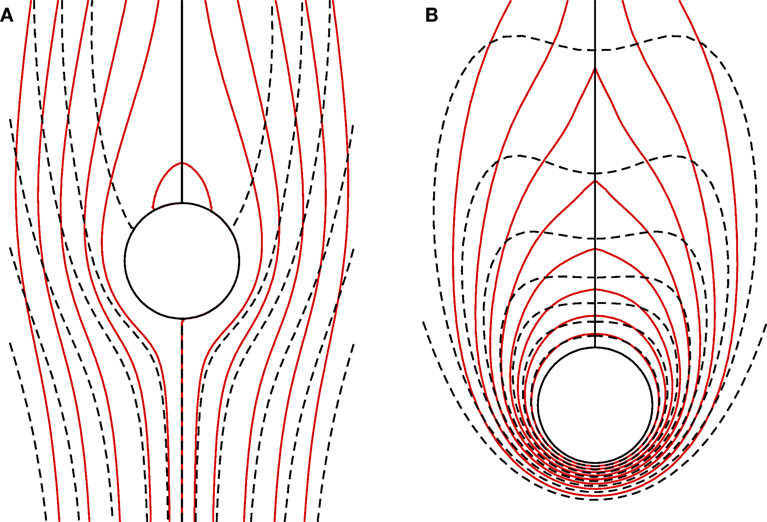
Figure 9. Steady state (A) streamlines and (B) isotherms for the parallel (solid lines) and contra (dashed lines) flows for Pr = 0.7, Re = 20, Gr = 100, and Ec = 0.01.

The influences of the Eckert number on the streamlines and isotherms for the parallel flow are shown in Figures 10A,B, respectively. It is clear from Figure 10A that there is weak effect of the Eckert number on the fluid flow, and it thickens the momentum boundary layer at a small amount. It is because heat is dissipated around the circular cylinder, which is then transferred in the direction of free convection flow. However, the Eckert number has tremendous effect on the temperature distribution. Due to dissipation of heat, the temperature distribution erupts not only in the downstream region but also in the radial direction. For this reason, the thermal boundary layer increases with Eckert number.

FIGURE 10

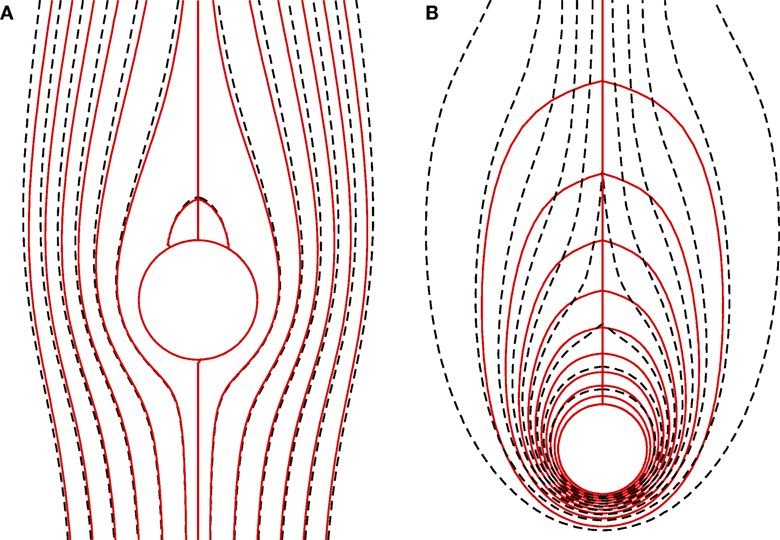
Figure 10. Steady state (A) streamlines and (B) isotherms for the parallel flow when Pr = 0.7, Re = 20, Gr = 100, Ec = 0.0 (solid lines), and Ec = 0.02 (dashed lines).

Figures 11A,B exhibit the effects of the Eckert number on the streamlines and isotherms, respectively. Figure 11B shows that heat is dissipated around the cylinder in a wide region with the presence heat dissipation. Also the temperature distribution is significantly elongated owing to the combined effect of buoyancy and forced convection. That is why the thermal boundary layer considerably increases with the dissipation of heat. Besides it is evident from Figure 11A that there is negligible effect of the Eckert number on the streamlines, especially in the upstream region. However, the size of the vortex increases with the dissipation of heat, although the point of separation remains almost same. In comparison with Ec = 0.0, the cause of increase of the momentum and thermal boundary layer for Ec = 0.02 is the dissipation of heat, which results in the eruption of the fluid against the buoyancy force owing to density differences.

FIGURE 11

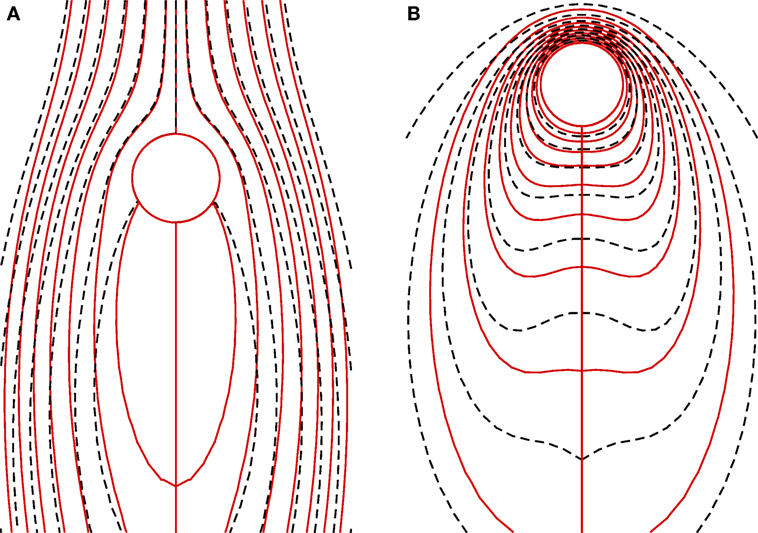
Figure 11. Steady state (A) streamlines and (B) isotherms for the contra flow when Pr = 0.7, Re = 20, Gr = 100, Ec = 0.0 (solid lines), and Ec = 0.02 (dashed lines).

Conclusion

The unsteady mixed convection heat transfer from a circular cylinder is investigated in the presence of heat dissipation. Two types of flow configurations, namely, parallel and contra flows have been considered depending on the directions of the forced convection and the free convection. The dimensionless equations are solved using finite-difference method. For both parallel and contra flows, the Nusselt number and the isotherms strongly depend on the viscous dissipation. The vorticity distribution of the contra flow is relatively more dependent on the viscous dissipation compared to the parallel flow. In contrast to the parallel flow, the point of separation occurs quickly, and the size of the vortex is large for contra flow under the same boundary conditions.

Author Contributions

The development of the model and code has been done by MH. Computations of the model equations have been accomplished by NR. AA-R kept his contribution by adding idea on the discussion from the obtained results jointly with MH.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Abu-Hijleh, B. A./K., Jadallah, I. N., and Nada, E. A. (1998). Entropy generation due to natural convection from a horizontal isothermal cylinder in oil. Int. Commun. Heat Mass Transf. 25, 1135–1143. doi: 10.1016/S0735-1933(98)00104-3

CrossRef Full Text | Google Scholar

Badr, H. M. (1983). A theoretical study of laminar mixed convection from a horizontal cylinder in cross stream. Int. J. Heat Mass Transf. 26, 639–653. doi:10.1016/0017-9310(83)90014-5

CrossRef Full Text | Google Scholar

Badr, H. M. (1984). Laminar combined convection from a horizontal cylinder—parallel and contra flow regimes. Int. J. Heat Mass Transf. 27, 15–27. doi:10.1016/0017-9310(84)90233-3

CrossRef Full Text | Google Scholar

Badr, H. M., Coutanceau, M., Dennis, S. C. R., and Ménard, C. (1990). Unsteady flow past a rotating circular cylinder at Reynolds numbers 10³ and 10⁴. J. Fluid Mech. 220, 459–484. doi:10.1017/S0022112090003342

CrossRef Full Text | Google Scholar

Badr, H. M., and Dennis, S. C. R. (1985). Time dependent viscous flow past an impulsively started rotating and translating circular cylinder. J. Fluid Mech. 158, 447–488. doi:10.1017/S0022112085002725

CrossRef Full Text | Google Scholar

Biswas, G., and Sarkar, S. (2009). Effect of thermal buoyancy on vortex shedding past a circular cylinder in cross-flow at low Reynolds numbers. Int. J. Heat Mass Transf. 52, 1897–1912. doi:10.1016/j.ijheatmasstransfer.2008.08.034

CrossRef Full Text | Google Scholar

Cheng, C.-Y. (2006). The effect of temperature-dependent viscosity on the natural convection heat transfer from a horizontal isothermal cylinder of elliptic cross section. Int. Commun. Heat Mass Transf. 33, 1021–1028. doi:10.1016/j.icheatmasstransfer.2005.10.012

CrossRef Full Text | Google Scholar

Chhabra, R. P., Soares, A. A., Ferreira, J. M., and Caramelo, L. (2007). Effects of viscous dissipation on heat transfer between an array of long circular cylinders and power law fluids. Can. J. Chem. Eng. 85, 808–816. doi:10.1002/cjce.5450850602

CrossRef Full Text | Google Scholar

Dennis, S. C. R., and Chang, G.-Z. (1970). Numerical solutions for steady flow past a circular cylinder at Reynolds numbers up to 100. J. Fluid Mech. 42, 471–489. doi:10.1017/S0022112070001428

CrossRef Full Text | Google Scholar

Fornberg, B. (1980). A numerical study of steady viscous flow past a circular cylinder. J. Fluid Mech. 98, 819–855. doi:10.1017/S0022112080000419

CrossRef Full Text | Google Scholar

Gebhart, B. (1962). Effects of viscous dissipation in natural convection. J. Fluid Mech. 14, 225–232. doi:10.1017/S0022112062001196

CrossRef Full Text | Google Scholar

Juncu, G. (2004). Unsteady conjugate heat/mass transfer from a circular cylinder in laminar crossflow at low Reynolds numbers. Int. J. Heat Mass Transf. 47, 2469–2480. doi:10.1016/j.ijheatmasstransfer.2003.10.035

CrossRef Full Text | Google Scholar

Juncu, G. (2008). Unsteady heat transfer from an elliptic cylinder. Int. J. Heat Mass Transf. 51, 920–928. doi:10.1016/j.ijheatmasstransfer.2007.11.001

CrossRef Full Text | Google Scholar

Kurdyumov, V. N., and Fernández, E. (1998). Heat transfer from a circular cylinder at low Reynolds numbers. J. Heat Transfer 120, 72–76. doi:10.1115/1.2830067

CrossRef Full Text | Google Scholar

Mahfouz, F. M. (2003). Transient free convection from a horizontal cylinder placed in a micropolar fluid. Heat Mass Transf. 39, 455–462. doi:10.1007/s00231-002-0329-4

CrossRef Full Text | Google Scholar

Mahfouz, F. M., and Badr, H. M. (2000). Flow structure in the wake of a rotationally oscillating cylinder. J. Fluids Eng. 122, 290–301. doi:10.1115/1.483257

CrossRef Full Text | Google Scholar

Nakai, S., and Okazaki, T. (1975). Heat transfer from a horizontal circular wire at small Reynolds and Grashof numbers-II. Int. J. Heat Mass Transf. 18, 397–413. doi:10.1016/0017-9310(75)90029-0

CrossRef Full Text | Google Scholar

Nguyen, H. D., Paik, S., and Douglass, W. (1996). Unsteady mixed convection about a rotating circular cylinder with small fluctuations in the free-stream velocity. Int. J. Heat Mass Transf. 39, 511–525. doi:10.1016/0017-9310(95)00149-4

CrossRef Full Text | Google Scholar

Roache, P. J. (1998). Computational Fluid Dynamics, 2nd Edn. Albuquerque: Hermosa.

Google Scholar

Sarkar, S., Dalal, A., and Biswas, G. (2010). Mixed convective heat transfer from two identical square cylinders in cross flow at Re = 100. Int. J. Heat Mass Transf. 53, 2628–2642. doi:10.1016/j.ijheatmasstransfer.2010.02.053

CrossRef Full Text | Google Scholar

Sarkar, S., Dalal, A., and Biswas, G. (2011). Unsteady wake dynamics and heat transfer in forced and mixed convection past a circular cylinder in cross flow for high Prandtl numbers. Int. J. Heat Mass Transf. 54, 3536–3551. doi:10.1016/j.ijheatmasstransfer.2011.03.032

CrossRef Full Text | Google Scholar