- Advanced Design and Analysis Group, Central Mechanical Engineering Research Institute (CSIR), Durgapur, India
A comparative assessment is done on the effectiveness of some developed and reported macroscopic and mesoscopic models deployed for addressing the three-dimensional thermo-fluidic transport during high-power laser surface alloying process. The macroscopic models include the most celebrated k–ε turbulence model and the large eddy simulation (LES) model, whereas a kinetic theory-based lattice Boltzmann (LB) approach is invoked under the mesoscopic paradigm. The time-dependent Navier–Stokes equations are transformed into the k–ε turbulence model by performing the Reynolds averaging technique, whereas a spatial filtering operation is used to produce the LES model. The models are suitably modified to address the turbulent melt-pool convection by using a modified eddy viscosity expression including a damping factor in the form of square root of the liquid fraction. The LB scheme utilizes three separate distribution functions to monitor the underlying hydrodynamic, thermal and compositional fields. Accordingly, the kinematic viscosity, thermal and mass diffusivities are adjusted independently. A single domain fixed-grid enthalpy-porosity approach is utilized to model the phase change phenomena in conjunction with an appropriate enthalpy updating closure scheme. The performance of these models is recorded by capturing the characteristic nature of the thermo-fluidic transport during the laser material processing. The maximum values of the pertinent parameters in the computational domain obtained from several modeling efforts are compared to assess their capabilities. The comparison shows that the prediction from the k–ε turbulence model is higher than the LES and LB models. In addition, the results from all three models are compared with the available experimental results in the form of dimensionless composition of the alloyed layer along the dimensionless depth of the pool. The comparison reveals that the LB and the LES approaches are better than the k–ε turbulence approach in reproducing the experimental results.
Introduction
Laser surface alloying is a surface modification process, where the intense heat from a laser source causes local melting of the engineered surface thereby producing a molten pool with simultaneous addition of some alloying materials in the form of powder into the laser generated melt pool. The alloying material also melts along with the substrate material and mixes with it and after the removal of heat by removing the laser, the molten pool gets solidified with formation of an alloyed layer on the surface of the base material. The thermo-fluidic transport in the melt pool actually dictates the mechanical and metallurgical characteristics of the final alloyed layer on the substrate. Hence, a thorough understanding of the molten pool transport is required in predicting the behavior of the alloyed layer accurately.
Such transport process is characterized by a dynamic evolution of the interface between two phases, namely, solid and liquid. Hence, this class of problems is commonly referred to as the “moving boundary problems.” The mathematical modeling for such problems becomes further complicated due to the complex boundary conditions and temperature-dependent variable thermal and physical properties. Laminar flow theories were used in earlier studies to address the thermo-fluidic transport in laser melted pools (Chan et al., 1984; Kou and Wang, 1986; Sarkar et al., 2002). However, it was not quite successful in predicting the experimental behavior. In fact, it has been emphasized that depending on the surface tension Reynolds number or Marangoni number (given by the ratio of surface tension gradient force to viscous force as , where lref,v is the characteristic length given by the viscous boundary layer thickness, the other terms are defined later), the transport in the molten pool may become turbulent in nature. As such, it has been observed that in case of surface tension-driven flows, the flow becomes turbulent if the surface tension Reynolds number is greater than 100 (Aboutalebi et al., 1995). It can be shown that typically for a high-power laser melting, the surface tension Reynolds number is much greater than 100. Accordingly, in most laser melting situations where the power input is high, the melt-pool convection can be turbulent. Accordingly, research has been directed to address the turbulent transport for the solid–liquid two-phase flow encountering in the high-energy material processing application such as a laser surface alloying process (Mohanraj et al., 2002; Chakraborty et al., 2004). Majority of the turbulence models in this regard follow the simple and most celebrated k–ε model. It should be emphasized that the k–ε turbulence model uses the Reynolds-averaged Navier–Stokes (RANS) equations for the mean flow quantities, where all the scales of the turbulence are apparently modeled. In some cases, the model performs very accurately, however, it might not be very much appropriate for all kind of time-dependent flows, since the averaging technique wipes out most of the important characteristics of the transient and large-scale coherent flows. On the contrary, the large eddy simulation (LES) model provides an alternative to the RANS approach where the large eddies are computed in a transient flow by using a set of filtered equations. Filtering operation is applied to the exact Navier–Stokes equations to remove the eddies only that are smaller than the filter size, which is commonly taken as the mesh size. The smaller eddies are having a more “universal” behavior since they contain less turbulent kinetic energy. This makes them more isotropic in nature and hence easier to be modeled (Chatterjee and Chakraborty, 2005; Chatterjee, 2011). Furthermore, it can be observed that often, the solidification-melting phenomena occur in varying scales between the subatomic micro to macro. Hence, the macroscopic modeling may not be always the best practice since they are incapable of capturing the complex microscopic phenomena. The multiscale mesoscopic approach based on the lattice Boltzmann (LB) method has recently emerged to offer great potential for solving complicated fluid dynamic problems with morphological development (Chen and Doolen, 1998). The approach is very simple in implementation, having good numerical stability and accuracy, and inherently parallelizable. Hence, the method can be used as a powerful tool to solve complicated phase change problems, characterized by the evolution of complex interfacial topologies (Chakraborty and Chatterjee, 2007).
In view of the above, there is a need for comparative assessment of various macroscopic and mesoscopic models developed for addressing the transport characteristics during laser material processing. Such comparison can provide an appropriate prediction of the numerical model to be used for simulating the transport phenomena associated with the high-energy material processing applications. This should be categorically mentioned here that the models have already been developed and reported in the contemporary literature by the same author group. Hence, the details in regard to the various categories of modeling are not given here for the purpose of brevity. Only some salient features are mentioned, and the major emphasis is given to understand the comparison of the different modeling strategies for solving a common problem and predict the best possible method for such class of problems. The intricate modeling details can be had from the respective works published in the literature as mentioned in Section “Physical Problem and Mathematical Models.”
Physical Problem and Mathematical Models
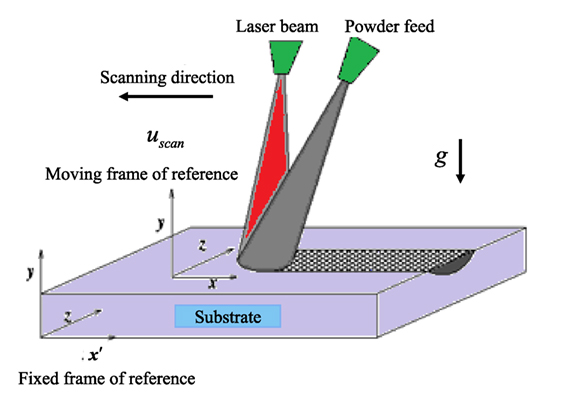
Figure 1 shows schematically the underlying processes of a typical laser surface alloying technique. A part of the energy from the laser source (specified by a laser heating efficiency) heats the surface of the substrate material and forms a molten pool. Simultaneously, an alloying material in the powder form is added to the melt pool. The powder melts by the heat from the laser and mixes with the molten base material by convective and diffusion dominated transport. When the laser source moves away (with a constant scanning speed, uscan in the negative x-direction), the molten materials get solidified and form an alloyed layer over the substrate surface.
Following the macroscopic paradigm, the pertinent governing equations for the thermo-fluidic transport inside the laser generated molten pool essentially constitutes the mass, momentum, energy, and species conservation equations. The governing equations considering the laminar fluid flow theory (Sarkar et al., 2002) for the problem presented in Figure 1 can be given in a generalized form as follows:
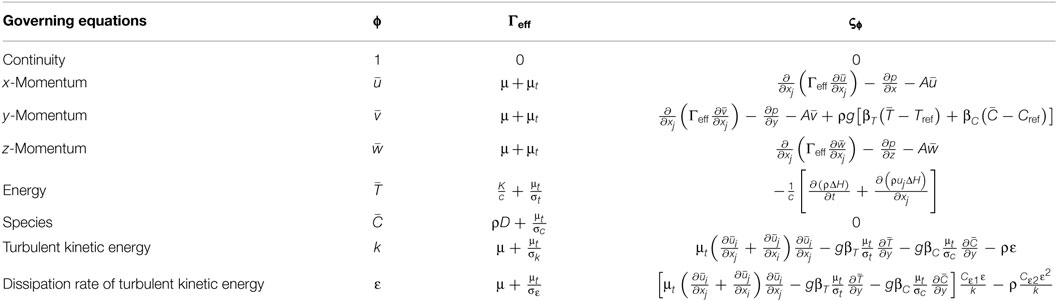
where ϕ is a vector of conserved quantities, such as mass, momentum, or energy, xi is the coordinate in the Cartesian system, ui is the component of mean velocity in the direction xi, Γeff is the effective diffusion coefficient for the variable ϕ, and ςϕ is the source term for the dependent variable ϕ. The second term on the r.h.s. of Eq. 1 comes from the coordinate transformation x = x′ − (−uscan)t, where (x′, y, z) are the stationary coordinates and (x, y, z) are coordinates in a frame moving with the torch.
Following the Reynolds averaging technique, the equivalent single-phase governing equations (Chakraborty et al., 2004) for the k–ε turbulence model can be constructed in a Cartesian coordinate system fixed with the moving laser source (since it is a moving heat source problem, a moving coordinate system is adopted to formulate the governing equations and consequently, source terms will arise as a result of the coordinate transformation) and the corresponding values of ϕ, Γeff, and ςϕ for various conservation equations are given in Table 1. In Table 1, g is the acceleration due to gravity, βT and βC are the volumetric expansion coefficient of heat and solute, respectively, Tref is taken to be equal to the melting temperature of the base material, and Cref is taken to be equal to the concentration of the alloying species at that reference temperature. Adopting an enthalpy formulation for the energy transport equation, one can express the total enthalpy in terms of sensible heat and the variable nodal latent heat of fusion (ΔH). Furthermore, μ is the dynamic viscosity, μt is the eddy viscosity, c represents the specific heat of the material, K is the thermal conductivity, represents the concentration of the alloying element, and D represents mass diffusivity of the same in the substrate material, σt is the turbulent Prandtl number, σc is turbulent Schmidt number, σk = 1 and σε = 1.3, Cμ = 0.09, Cε1 = 1.44, and Cε2 = 1.92.
A single domain fixed-grid enthalpy-porosity approach (Brent et al., 1988) in conjunction with an appropriate enthalpy updating closure scheme (Voller et al., 1989) is utilized for modeling the phase change phenomena in presence of a continuously evolving solid–liquid interface. In this method, the morphology of the phase change domain can be treated as an equivalent porous medium that offers a frictional resistance toward fluid flow in that region. This resistance can be conveniently formulated using Darcy’s model in association with the Kozeny–Carman relationship, which leads to the source term in the momentum equation, where A is given as follows:
where fl is the liquid fraction given by ΔH/L, with ΔH being the latent enthalpy content of a control volume, and L being the latent heat of fusion. The term ΔH can be expressed as follows:
where Ts and Tl are the solidus and liquidus temperatures, respectively. It is assumed that the liquid fraction within the mushy region varies linearly with temperature as . In Eq. 2, Km is a large number (~108) and b is a small number (~10−3) to avoid division by 0. The above formulation effectively ensures that the velocity undergoes a smooth transition from a 0 value in the solid region to a finite value in the liquid region.
The governing equations employed for LES are obtained by filtering the time-dependent Navier–Stokes equations in either Fourier (wave number) space or configuration (physical) space. The spatially filtered Navier–Stokes equations along with the detailed schemes for subgrid closures are available in Chatterjee and Chakraborty (2005) and Chatterjee (2011).
The transformed boundary conditions both for the k–ε and LES models along with the fixed-grid enthalpy-porosity approach for modeling phase change in conjunction with the enthalpy updating closure scheme, details of numerical procedures, grid requirements and its sensitivity, and all the special attentions needed for capturing the near wall turbulence are available in Chakraborty et al. (2004), Chatterjee and Chakraborty (2005), and Chatterjee (2011).
In the mesoscopic paradigm of computation, we deploy the kinetic theory-based LB method for obtaining the macroscopic flow, thermal and compositional variables. The LB scheme utilizes three separate distribution functions in such cases following the passive scalar approach (He et al., 1998). These three scalars are introduced to address the fluid flow velocity, the temperature, and the composition (mass fraction) for complete description of the momentum, energy, and mass transport. This feature of the passive scalar approach in the LB paradigm helps in adjusting the kinematic viscosity, thermal and mass diffusivities independently making the approach suitable for a wide variety of solid–liquid phase change problems. Appropriate source terms are added in the respective kinetic equations of the LB model to handle the phase changing aspects along with an enthalpy updating procedure (Chatterjee and Chakraborty, 2006) following the enthalpy-porosity approach. The mathematical details of the LB model, the applied boundary conditions, and the implementation procedure can be found elsewhere (Chatterjee, 2012).
Transport Characteristics
The general transport characteristics obtained from various modeling strategies are presented here in a concise manner. The simulation domain for the laser surface alloying process is fixed as, 8 mm × 4 mm × 8 mm. Numerical results are presented for the following pertinent controlling parameters: laser power = 2.4 kW, laser efficiency = 15%, laser torch radius = 0.9 mm, scanning speed = 0.012 m/s, and powder feed rate = 0.02 g/s. Iron is taken as the substrate material, and aluminum powder is chosen as the cladding material for the purpose of numerical computation. The thermophysical property values used in the computation can be found in Chakraborty et al. (2004).
The flow and the thermal fields obtained from the k–ε turbulence model studies are shown in Figure 2, the LES model predictions are depicted in Figure 3, and the LB model results are presented in Figure 4. Since the surface tension coefficient of temperature (defined as ∂σsur/∂T) is negative (taken as −0.00049 N/mK) for the present case, a fluid element located in the vicinity of the laser source will have a lower surface tension than another fluid element located further away from the source, both fluid elements being located on the top (free) surface. This differential of surface tension gives rise to a radially outward fluid flow at the top surface. It can easily be observed from the above figures that among all the influencing forces, surface tension force is predominant and the most important one in terms of governing the melt-pool dynamics, since it initiates the flow within the molten pool. This kind of pool shape is a consequence of a rather anisotropic nature of an enhanced diffusion process in case of turbulent molten pool. In the present case, the net thermal energy available to the pool is predominantly transported along the longitudinal and sidewise directions by the Marangoni advection along with molecular as well as eddy thermal diffusion process. The downward advection of heat is small compared to longitudinal and spanwise advection because of much smaller magnitude of downward velocity component, as compared to magnitudes of longitudinal and spanwise components. In case of turbulent transport, due to an enhanced mixing process, the mean advection strength goes down, which results in a decrease in longitudinal and sidewise advection strength. On the other hand, an enhanced effective diffusion process due to interactions between fluctuating velocity components of eddies in a turbulent pool tries to increase the length and width of the pool by propagating the influence of thermal disturbance across a relatively larger distance. The resultant pool geometry is, therefore, a consequence of the above two counteracting effects active in tandem.
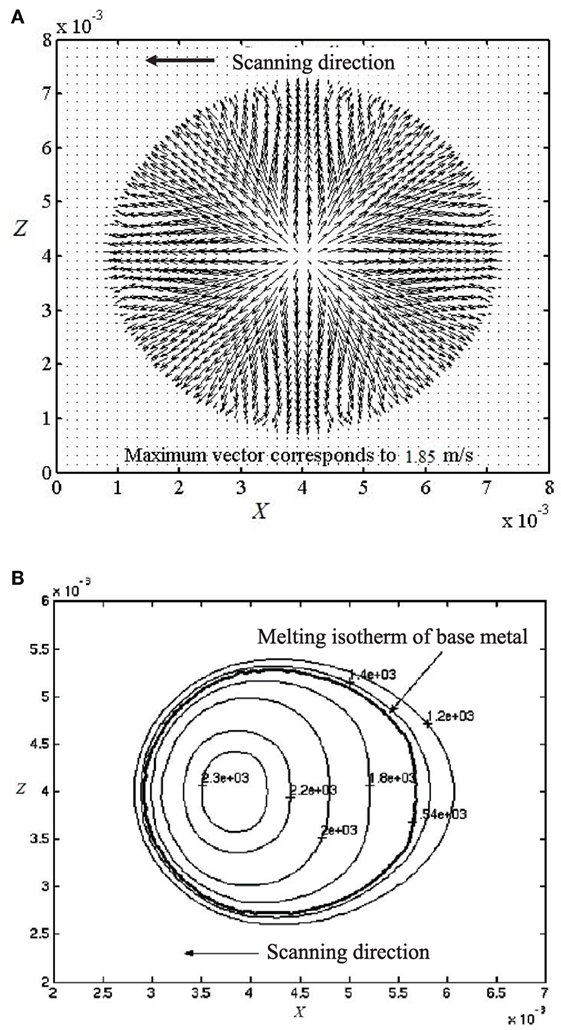
Figure 2. (A) Velocity and (B) temperature fields on the top surface of the substrate obtained from the k–ε turbulence model.
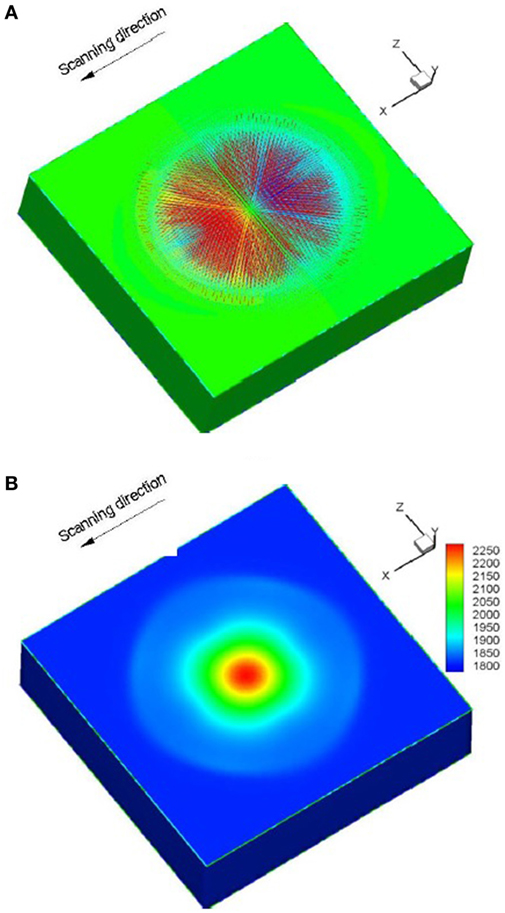
Figure 3. (A) Velocity vectors and (B) temperature contours at the top surface of the substrate obtained from the large eddy simulation.
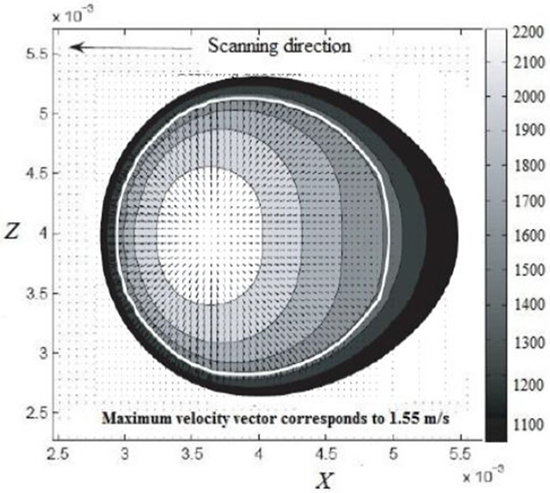
Figure 4. Velocity and temperature profiles on the top surface of the substrate obtained from the lattice Boltzmann simulation.
Comparative Assessment
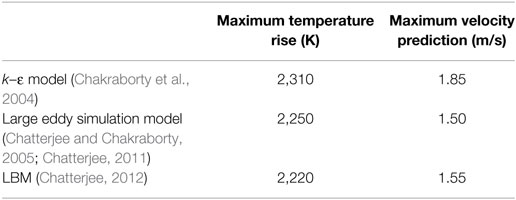
The various macroscopic and mesoscopic model predictions are first presented in Table 2 to understand the capabilities and shortcomings of the models. In a latter attempt, the modeling predictions are compared with the available experimental results. It can be observed that the LES model predictions are found less compared to the results form the k–ε turbulence model. This is attributable to the more realistic consideration of the energy cascading mechanisms and the subsequent dissipation over the diffusive length scales. The LB model predictions are, however, found close to those predicted by the LES model. This is an extremely important observation in regard to the potential applicability of the LB model for such class of problems. The LB model is intrinsically based on the kinetic theory, which accounts for the particle transport. These particles are assumed to be composed of thousands of molecules constituting the system under consideration. Hence, the model is virtually accounting for the intricate microscopic details. Although in the molecular dynamics simulation strategy each and every individual molecule are modeled, which is not the case with the LB model. Still, it is quite capable of addressing the microscopic issues in a macroscopic framework. Accordingly, the LB predictions are much better compared to the laminar flow model, and also it is observed that to some extent it predicts better than the standard k–ε model and it is at par with the LES model predictions at least for the present problem under consideration.
In the laser surface alloying process, the most important aspect is the distribution of the alloying element along the depth of the substrate since this finally characterizes the microstructural behavior of the alloyed layer. A comprehensive comparison of the various modeling strategies with the available experimental result (Mohanraj et al., 2002) is shown in Figure 5 for the dimensionless composition of the solidified layer along the dimensionless depth of the pool. The depth is non-dimensionalized by the maximum depth of the alloyed layer. It is evident from Figure 5 that the k–ε turbulence model qualitatively captures the correct trend. However, the LES model as well as the LB model provides more accurate matching with the experimental data. It can also be observed from the figure that the composition of the solute is the highest at the top surface and decreases gradually toward the substrate. The numerical results based on the k–ε turbulence model overestimate the solute concentration, whereas the predictions from the LES and the LB models are closer to the experimental results.
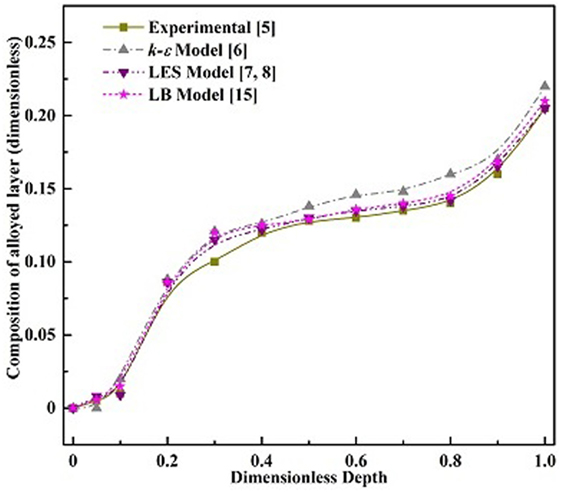
Figure 5. Composition of the solidified layer along the depth of the pool obtained from different models and experiment.
To understand the capabilities and limitations of various models adopted for simulating the transport phenomena occurring during the high-power laser surface alloying process, a final discussion is presented here. At the ouset, it is imperative to say that the laminar flow theory has purposefully been omitted here since the flow is believed to be turbulent with a surface tension Reynolds number greater than 100. Ideally, a direct numerical simulation (DNS) would turn out to be the best choice, because of its inherent capability to solve for all time and spatial scales associated with the turbulence. However, from a practical perspective, DNS is virtually ruled out for most of the complicated computational fluid dynamics (CFD) problems, such as the laser surface melting problem referred to here, since it is too computationally intensive. In practice, to resolve all spatial and temporal scales in a laser surface melting problem, the time and space resolutions would need to be extremely refined, resulting in a discretization that would take an extraordinarily long time to solve, even with the best of computational facilities available these days. Accordingly, to address the turbulent nature of the problem, first, the standard k–ε model is used with a modified eddy viscosity expression including a damping factor in the form of square root of the liquid fraction. The k–ε model simply attempts to capture the turbulence by performing time or space averaging. Under certain conditions, this method can be very accurate, but it might not be very suitable for all transient flows, since the averaging process wipes out most of the important characteristics of a time-dependent and large-scale coherent flow structure. Further, the k–ε model may not perform satisfactorily in recirculating flows, since it is based on the Boussinesq hypothesis that does not take into account the rotationality in motion and turbulence anisotropy. LES is thought to be a more realistic approach that computes the larger eddies occurring in the computational domain. This approach addresses the underlying physics in a much more mathematically consistent manner. It should, however, be emphasized here that the application of LES to phase change materials processing simulations is currently at its infancy. Typical applications to date have been only documented for simple geometries, without involving any changes in phase. This is mainly because of the extremely rich computational resources required to resolve the turbulent eddies. Till date, most successful LES simulations have been executed using high-order spatial discretization schemes, with great care being taken to resolve all scales larger than the inertial subrange. The degradation of accuracy in the mean flow quantities with poorly resolved LES is, however, not well documented. Significant research needs to be executed in this regard to standardize LES-based models for simulation of transport phenomena in phase change materials processing with a greater level of confidence. On the other hand, the kinetic theory-based LB method has proved to have extremely encouraging potential to solve complex thermo-fluidic problems characterized by complicated phase boundaries such as the problem of phase separation of two immiscible fluids. Since it is based on the kinetic theory, it can be useful for predicting the intricate microscopic issues evolving in case of solid–liquid phase transformation. However, this approach is often suffering from the numerical instability, which develops when the viscosity becomes small.
Conclusion
A comparative study is performed to assess the performances of various modeling strategies commonly employed in predicting the thermo-fluidic transport in case of a high-energy laser surface alloying process. Two different paradigms are chosen, namely, macroscopic and mesoscopic modeling. In the macroscopic paradigm, the conventional CFD technique is used that involves solution of the RANS equations and the filtered Navier–Stokes equations in capturing the turbulence following the celebrated k–ε model and the LES model, respectively. The kinetic theory-based LB technique is used in the mesoscopic paradigm that involves solution of three kinetic equations to address the fluid flow, heat transfer, and species transport. All these models have already been used to solve a generic case of a laser surface alloying process. The k–ε turbulence model overpredicts all the pertinent hydrodynamic, thermal and mass transfer quantities. In predicting the experimental trends, it is observed that the LES and the LB models are closer compared to the k–ε turbulence model. Hence, the LES model or alternatively the LB model can be successfully used for simulating the real-life moving boundary phase change problems.
Author Contributions
The author confirms being the sole contributor of this work and approved it for publication.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The reviewer, SN-M, and handling editor declared their shared affiliation, and the handling editor states that the process nevertheless met the standards of a fair and objective review.
Acknowledgments
The author thanks the other authors in his group for carrying out the numerical modeling and simulation work. Also, the author gratefully acknowledges the financial support provided by the Department of Science & Technology (DST), Govt. of India through the sanction order no. SR/S3/MERC-051/2010 (C) and SR/S3/MERC-051/2010 (G).
References
Aboutalebi, M. R., Hassan, M., and Guthrie, R. I. L. (1995). Numerical study of coupled turbulent flow and solidification for steel slab clusters. Numer. Heat Transfer 28, 279–299. doi: 10.1080/10407789508913746
Brent, A. D., Voller, V. R., and Reid, K. J. (1988). Enthalpy-porosity technique for modeling convection-diffusion phase change: application to the melting of a pure metal. Numer. Heat Transfer 13, 297–318. doi:10.1080/10407788808913615
Chakraborty, N., Chatterjee, D., and Chakraborty, S. (2004). Modeling of turbulent transport in laser surface alloying. Numer. Heat Transfer 46, 1009–1032. doi:10.1080/10407780490517629
Chakraborty, S., and Chatterjee, D. (2007). An enthalpy based hybrid lattice Boltzmann method for modeling solid-liquid phase transition in presence of convective transport. J. Fluid Mech. 592, 155–175. doi:10.1017/S0022112007008555
Chan, C. L., Mazumdar, J., and Chen, M. M. (1984). Two dimensional transient model for convection in laser melted pool. Metall. Trans. A 15, 2175–2184. doi:10.1007/BF02647100
Chatterjee, D. (2011). Computational modeling of transport phenomena in high energy materials processing application: large eddy simulation and parallelization. Int. J. Comput. Mat. Sci. Surf. Eng. 4, 1–22. doi:10.1504/IJCMSSE.2011.037349
Chatterjee, D. (2012). A lattice Boltzmann model for high energy materials processing application. Int. J. Multiscale Comput. Eng. 10, 229–247. doi:10.1615/IntJMultCompEng.2012002280
Chatterjee, D., and Chakraborty, S. (2005). Large eddy simulation of laser induced surface tension driven flow. Metall. Trans. B 36, 743–754. doi:10.1007/s11663-005-0078-0
Chatterjee, D., and Chakraborty, S. (2006). A hybrid lattice Boltzmann model for solid–liquid phase transition in presence of fluid flow. Phys. Lett. A 351, 359–367. doi:10.1016/j.physleta.2005.11.014
Chen, S., and Doolen, G. D. (1998). Lattice Boltzmann method for fluid flows. Annu. Rev. Fluid Mech. 30, 329–364. doi:10.1146/annurev.fluid.30.1.329
He, X., Chen, S., and Doolen, G. D. (1998). A novel thermal model for the lattice Boltzmann method in incompressible limit. J. Comput. Phys. 146, 282–300. doi:10.1006/jcph.1998.6057
Kou, S., and Wang, Y. H. (1986). Three-dimensional convection in laser melted pools. Metall. Trans. A 17, 2265–2270. doi:10.1007/BF02645924
Mohanraj, P., Sarkar, S., Chakraborty, S., Phanikumar, G., Dutta, P., and Chattopadhyay, K. (2002). Modeling of transport phenomena in laser surface alloying with distributed species mass source. Int. J. Heat Fluid Flow 23, 298–307. doi:10.1016/S0142-727X(02)00177-7
Sarkar, S., MohanRaj, P., Chakraborty, S., and Dutta, P. (2002). Three dimensional computational modeling of momentum, heat and mass transfer in a laser surface alloying process. Numer. Heat Transfer A 42, 307–326. doi:10.1080/10407780290059576
Keywords: laser surface alloying, transport phenomena, numerical simulation, k–ε turbulence model, large eddy simulation, lattice Boltzmann model
Citation: Chatterjee D (2017) A Comparison of Numerical Strategies for Modeling the Transport Phenomena in High-Energy Laser Surface Alloying Process. Front. Mech. Eng. 3:4. doi: 10.3389/fmech.2017.00004
Received: 23 February 2017; Accepted: 12 May 2017;
Published: 01 June 2017
Edited by:
Guillermo Rein, Imperial College London, United KingdomReviewed by:
Wolfram Jahn, Pontificia Universidad Católica de Chile, ChileRandall McDermott, National Institute of Standards and Technology, United States
Salvador Navarro-Martinez, Imperial College London, United Kingdom
Copyright: © 2017 Chatterjee. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Dipankar Chatterjee, ZF9jaGF0dGVyamVlQGNtZXJpLnJlcy5pbg==
 Dipankar Chatterjee
Dipankar Chatterjee