Advances in Thermionic Energy Conversion through Single-Crystal n-Type Diamond

Thermionic energy conversion, a process that allows direct transformation of thermal to electrical energy, presents a means of efficient electrical power generation as the hot and cold side of the corresponding heat engine are separated by a vacuum gap. Conversion efficiencies approaching those of the Carnot cycle are possible if material parameters of the active elements at the converter, i.e., electron emitter or cathode and collector or anode, are optimized for operation in the desired temperature range. These parameters can be defined through the law of Richardson–Dushman that quantifies the ability of a material to release an electron current at a certain temperature as a function of the emission barrier or work function and the emission or Richardson constant. Engineering materials to defined parameter values presents the key challenge in constructing practical thermionic converters. The elevated temperature regime of operation presents a constraint that eliminates most semiconductors and identifies diamond, a wide band-gap semiconductor, as a suitable thermionic material through its unique material properties. For its surface, a configuration can be established, the negative electron affinity, that shifts the vacuum level below the conduction band minimum eliminating the surface barrier for electron emission. In addition, its ability to accept impurities as donor states allows materials engineering to control the work function and the emission constant. Single-crystal diamond electrodes with nitrogen levels at 1.7 eV and phosphorus levels at 0.6 eV were prepared by plasma-enhanced chemical vapor deposition where the work function was controlled from 2.88 to 0.67 eV, one of the lowest thermionic work functions reported. This work function range was achieved through control of the doping concentration where a relation to the amount of band bending emerged. Upward band bending that contributed to the work function was attributed to surface states where lower doped homoepitaxial films exhibited a surface state density of ∼3 × 10¹¹ cm⁻². With these optimized doped diamond electrodes, highly efficient thermionic converters are feasible with a Schottky barrier at the diamond collector contact mitigated through operation at elevated temperatures.

Introduction

In 2014 the estimated energy consumption in the United States was about 100 Exajoules (Fichman, 2015). About 39% of the total U.S. energy supply is used to producing electricity with nuclear (8.5%), natural gas (8.5%), and coal (16.7%) the main energy sources (wind 1.7% and hydro 2.5%) while photovoltaics account for 0.17% of the total energy usage. Coal fired power plants operate on a modified Rankine cycle with maximum efficiency of 42%, and gas fired plants slightly lower at 38% similar to nuclear power plant thermal efficiency. Coal and nuclear power plants typically have a lifetime that exceeds 30 years while for various photovoltaic plants (poly- and monocrystalline cells) a mean degradation rate of 0.8%/year was reported for commercially useful lifetimes of 25 years (Jordan and Kurtz, 2013). For transportation, including cars, trucks, buses, trains, ships, and planes, oil is the main energy source and accounts for 28% of the total energy use. Cars, light trucks, and motorcycles consume about 58% of the transportation energy budget signifying the importance of electrical power demands with a shift to electrical propulsion. The efficiency for various electrical power generation technologies, as displayed in Figure 1, presents a critical comparison of thermoelectric and thermionic conversion capability (Vining, 2009). With a thermionic converter collector work functions of 1 eV an efficiency similar to thermal power plants is indicated and lowering of the collector work function to 0.5 eV would allow an efficiency exceeding 50%.

FIGURE 1

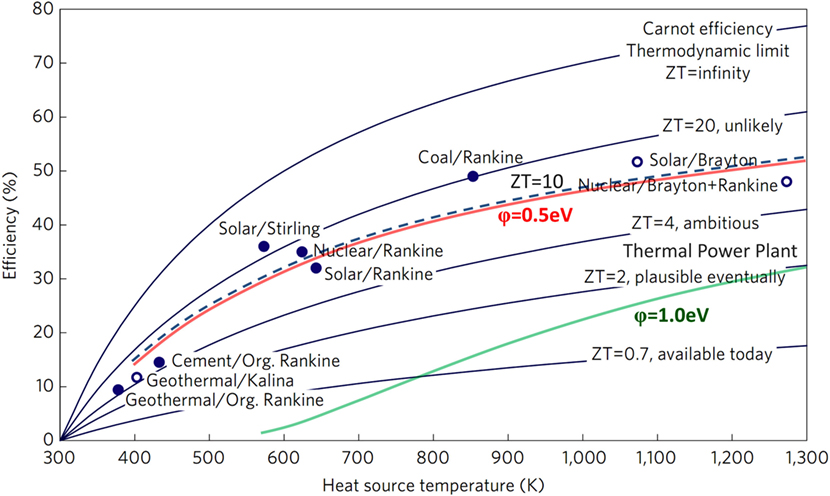
Figure 1. Efficiency for various power generators compared to thermoelectric conversion with figure of merit ZT and thermionic conversion efficiency enabled by low work function collectors (Vining, 2009). With a collector work function of φ = 1.0 eV efficiencies compare to thermal power plants and for a work function of φ = 0.5 eV a conversion efficiency of ∼50% is possible.

Vacuum Thermionic Electron Emission and Energy Conversion

Vacuum Thermionic Electron Emission

One of the first scientific observation of electron emission was conducted by Elster and Geitel and reported in 1882 (Elster and Geitel, 1882). In a glass bulb, a sealed platinum wire could be heated to incandescence by an electrical current and an opposed metal electrode connected to an electrometer indicated the charge status. It was concluded that a dependence exists between the electric charge and its type and the type and quality of the electrode surface as well as the state of incandescence of the electrode. After observation of current flow from a carbon filament to a platinum plate positioned “preferably between the limbs of the carbon conductor” Edison filed the “Electrical Indicator” patent in November 1883 (Edison, 1884). In 1884, Edison demonstrated to Preece an attempt to regulate the current flow in a circuit using his glow lamps and provided him several specimens of different design. Preece, in an elaborate investigation of phenomena concerning Edison’s lamps, coined the term “Edison effect,” which should lead to the development of the thermionic diode (Preece, 1884; Fleming, 1895). In an investigation of the nature of the discharge, the cathode rays were identified by Thomson as negatively charged particles of fundamental importance (Thomson, 1897, 1899) for which Stoney had suggested the term electron (Stoney, 1894). Further studies of electron emission sought to describe the physical phenomena in terms of kinetic gas theory where Richardson presented an approach (Richardson, 1901) that was independently arrived at by Thomson in a theoretical discussion (Richardson, 1903) and that quantified the electron emission current i by

$i=A{T}^{1∕2}{e}^{-\mathrm{\omega }∕\mathit{RT}}$ (1)

where T is the temperature, ω is the work an electron has to do to escape, R is the universal gas constant in the equation pv = RT, and A is the pre-exponent factor that is independent of temperature. In a similar approach equating electron emission from a metal with evaporation of a mono-atomic gas Dushman arrived at an expression assuming that the specific heat of free electrons in a metal is negligible and the specific heat of the evaporated electrons is the same as that of a mono-atomic gas (Dushman, 1923). Electron emission from a solid was thus quantified by

$I=A{T}^2{e}^{-b_0∕T}$ (2)

with b₀ the only material-dependent parameter and A an universal constant which based on a quantum-mechanical derivation included a dimensionless constant, k²me/h³, with k Boltzmann’s constant, m and e the electron mass and charge, respectively, and h Plank’s constant (Richardson, 1914). As electrons traverse the solid–vacuum boundary, the properties of the quantum-mechanical wave function of the electrons can modify the value of A. In addition, variations in the value of A can arise from surface properties that deviate from smooth and uniform potentials. These contributions can be addressed by including a factor (1−r) in A where r is the reflection coefficient for electrons with sufficient energy allowing escape from the solid (Nordheim, 1928). For most smooth, clean metal surfaces the reflection coefficient is <10% and the term (1−r) neglected. However, adsorbates or thin films can present abrupt changes in the surface potential curves (Knapp, 1973).

The saturated electron emission current from a metallic emitter can thus be expressed by

$J\left(T\right)=A_R{T}^2{e}^{-\frac{\mathrm{\phi }}{k_{\mathit{\text{B}}}T}}$ (3)

where

$A_R=\mathit{CF}\cdot A_0,$ (4)

with a correction factor (CF) which varies with material parameters and temperature and

$A_0=\frac{\mathrm{4\pi }m{k}_B^{2}e}{h^3},$ (5)

the theoretical value of Richardson’s constant, 120 A cm⁻² K⁻².

From experimental data, it was observed that the work functions for metals display a linear temperature dependence, φ = φ₀ + αT, with values of α of the order of 10⁻⁴ eV K⁻¹ with theoretical calculations arriving at values typically an order of magnitude smaller (Wilson, 1966a,b; Kiejna et al., 1979; Durakiewicz et al., 2001; Ibragimov and Korol’kov, 2001).

The saturated thermionic electron emission current tacitly implies the application of a sufficient extracting field that prevents an electronic charge accumulation adjacent to the emitter boundary. These space charge effects described by Child (1911) and Langmuir (1913, 1923) impede electron emission with the maximum current between planar electrodes at a distance L and potential V given by

$J_{\mathit{CL}}={\frac{V}{L^2}}^{3∕2}\frac{1}{\mathrm{9\pi }}{\left(\frac{2e}{m}\right)}^{1∕2}.$ (6)

In absence of externally applied extraction fields, as is the case for thermionic converters, the electron current transported across the inter-electrode spacing is prohibitively small for applications and consequently points to small gaps as a space charge mitigating method.

Vacuum Thermionic Energy Conversion

Prominent interest in phenomena surrounding glow effects around electrically heated solids directed Schlichter in 1915 to study a process that would “in principle present a possibility to directly convert heat energy to electrical energy as the economical method of such a procedure would be of great technical importance” (Schlichter, 1915). In the same report, the efficiency of the converter, then termed glow-element, was described similarly to a Carnot process by

$N_0=\frac{T_2-T_1}{T_2},$ (7)

independent of the material but the temperature of the electrodes with T₂, the temperature of the glow-electrode and T₁, the temperature of the counter-electrode. In this first experimental demonstration of thermionic energy conversion utilizing a platinum element at 1,000°C, an efficiency of 1.5 × 10⁻¹¹ was reported and its magnitude mainly attributed to radiation losses, however, space charge phenomena were not addressed. An energy diagram for a space charge limited converter is presented in Figure 2A and an ignited cesium converter operating in plasma mode is shown in Figure 2B (Hatsopoulos, 1963).

FIGURE 2

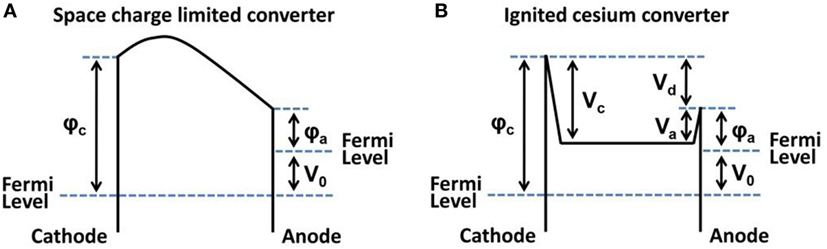
Figure 2. Energy diagram for a space charge limited converter (A) and an ignited cesium converter in plasma mode (B); the work function of cathode (emitter) is φ_c and anode (collector) φ_a.

It was about 40 years later that Hernqvist et al. postulated two key efficiency limiting factors, i.e., electrode work function differential and inter-electrode space charge effects, that need to be addressed for practical applications (Hernqvist et al., 1958). Assuming space charge free condition the efficiency of a thermionic converter was derived to

$\mathrm{\eta }\cong \frac{{\mathrm{\phi }}_c-{\mathrm{\phi }}_a}{{\mathrm{\phi }}_c+\frac{\mathrm{\sigma }{ϵ}_t}{B}\frac{A_r}{A_e}{T}^2\text{exp}\left(e{\mathrm{\phi }}_c∕k_{B}T\right)},$ (8)

with φ_c and φ_a cathode and anode work function, respectively, ϵ_t the thermal emissivity of the cathode, σ the Stefan–Boltzmann constant, A_r the radiating cathode area, A_e the electron emitting cathode area, and B the emission constant. Methods of reducing the adverse space charge effects are detailed in Table 1, an updated version from Hernqvist et al. (1958) with a focus on most recent advances. Technological improvements in micromachining and semiconductor device processing through lithography should enable micron-sized electrode spacing that could enable a new generation of energy converters previously not possible to manufacture (Lee et al., 2012a,b; Belbachir et al., 2014). To increase the electron velocity, a high voltage is paired with a magnetic field or a gate electrode is introduced between cathode and anode which has been of interest recently (Meir et al., 2013; Wanke et al., 2016). A suitable electron transparent grid electrode was suggested by utilizing graphene that exhibited an electron transparency of ∼99.9% (Srisonphan et al., 2014). Mitigation of the electronic space charge has also been reported through the introduction of positive ions which can be generated through impact ionization for lower cathode temperatures of 1,200–1,500°C in an ignited or arc-mode converter (Hernqvist, 1963). A recent modification of the arc-mode converter demonstrated a confined plasma discharge that generated positive ions for its surrounding lower work function cathode region (Rasor, 2017). Application of laser excitation of cesium atoms for continuous ion generation was also suggested (Hansen et al., 1976).

TABLE 1

Table 1. Approaches for reducing space charge effects in thermionic converters.

Novel Materials for Thermionic Converter Electrodes

Work Function Requirements for Emitter and Collector

With the law of Richardson–Dushman (Eq. 3) governing electron emission practical current densities required for thermionic converters define values for the emitter work function. Similarly, the efficiency dependency on electrode work functions dictates the use of a sufficiently low work function for the collector. It was early discovered that electron emission from a partially cesium covered tungsten filament resulted in an increase in electron emission (Ito and Cappelli, 2012). This phenomenon of work function reduction due to adsorbed alkali-metal atoms is still exploited in thermionic conversion research and applications with more recent interest in solar or photo-enhanced thermionic conversion (Langmuir and Kingdon, 1925; El-Genk and Momozaki, 2002; Zhang et al., 2003; Ogino et al., 2004; Lee et al., 2009; Makdisi et al., 2014). An extensive experimental investigation of various metal work functions under cesium coverage is presented in Table 2 (Reck et al., 2014).

TABLE 2

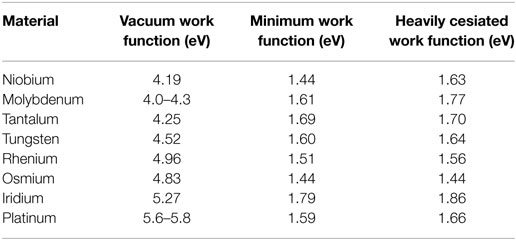
Table 2. Work functions of various metal surfaces in vacuum and in cesium vapor with the minimum work function under optimized cesium coverage and for surfaces with increased cesium coverage.

For a thermionic converter operating in ignited mode, a figure of merit was suggested by the barrier index V_B given by

$V_B={\mathrm{\phi }}_a+V_d+V_{\mathit{att}}\cong {\mathrm{\phi }}_a+0.45\text{eV},$ (9)

where φ_a is the anode (collector) work function, V_d is the arc voltage drop, and V_att is the attenuation coefficient arising from the current reduction due to the plasma or non-ideal electrode surfaces (Wilson, 1966c; Verhoef and Asscher, 1997; Luke, 2005; Shefsiek, 2010). As the ideal work function for a collector at room temperature has been calculated to ∼0.5 eV for a conversion efficiency >50% (see Figure 1), the ideal thermionic converter would then be described by V_B = φ_a identifying the efficiency limit for cesium-based converter technology (Hatsopoulos and Gyftopoulos, 1973, 2007; Rasor, 1991).

Engineered Materials for Low Work Function Electrodes

As the efficiency or figure of merit for a thermionic converter after (Eq. 9) is primarily defined by the value of the collector work function, the search for novel low work function materials is of ongoing interest. In the following sections, diamond based converter electrodes will be discussed in more detail.

Properties of Diamond As Wide Band-Gap Semiconductor

Diamond exhibits a set of unique materials properties that distinguishes it from other semiconductors and suggests its application in solid-state and vacuum electronics. Foremost, the material is characterized by a high-thermal conductivity >2,000 Wm⁻¹ K⁻¹, a high carrier mobility 4,500 cm²V⁻¹s⁻¹ for electrons and the ability of its lattice to accept impurities in acceptor and donor configuration (Yamamoto et al., 1997; Kalish, 1999; Isberg et al., 2002). With a wide band gap of E_g = 5.47 eV donor states can be formed by introduction of phosphorus at ∼0.6 eV below the conduction band minimum (CBM) and nitrogen at 1.7 eV below the CBM; boron establishes acceptor states at 0.37 eV above the valence band maximum (Farrer, 1969; Shiomi et al., 1991; Koizumi et al., 1997; Kato et al., 2005a).

The surfaces of diamond exhibit one of the most relevant properties for electron emission applications in the nature of its electron affinity that can shift to negative values under certain surface terminations, most readily prepared utilizing a hydrogen passivation process (see Figure 3) (Pickett, 1994; van der Weide et al., 1994; Takeuchi et al., 2005).

FIGURE 3

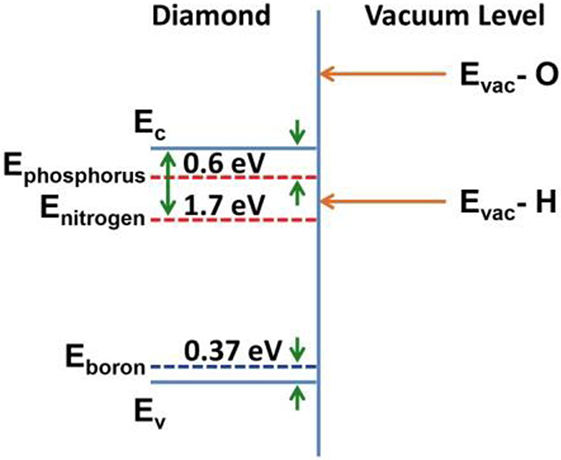
Figure 3. Schematic band structure of diamond with donor levels (nitrogen, phosphorus), boron acceptor, and negative electron affinity for hydrogen passivated surface, conduction, and valence band indicated by E_c and E_v, respectively.

The donor states in conjunction with the negative electron affinity (NEA) suggest the feasibility of low and ultra-low work function surfaces ideally suited for thermionic conversion applications and with research into diamond electron sources of ongoing interest (Lin et al., 2014).

Low Work Function Doped Diamond Surfaces

The evidence of shallow donor states established by phosphorus warrants an investigation of phosphorus-doped diamond with respect to thermionic electron emission and low work function electrode applications. To more accurately discern phenomena arising from donor states doped single-crystal diamond substrates and homoepitaxial diamond growth were utilized to prepare the doped diamond material discussed in the following sections.

Single-Crystal Nitrogen-Doped Diamond

For nitrogen-doped diamond, a commercially available high-pressure, high temperature (HPHT) plate with (100) surface orientation was re-polished to an average roughness Ra < 10 nm followed by a wet-chemical cleaning procedure including a boil in H₂SO₄/H₂O₂/H₂O, 3:1:1 at 220°C for 15 min followed by HF treatment for 5 min and a final boil in NH₄OH/H₂O₂/H₂O, 1:1:5 at 75°C for 15 min with a rinse with DI water after each treatment step. The sample was then loaded into a CVD reactor with a base pressure in the low 10⁻⁸ Torr where the sample surface was exposed to a pure hydrogen plasma. A hydrogen plasma was ignited under a hydrogen flow rate of 400 sccm, a pressure of 65 Torr and a microwave power of 1,300 W that resulted in a sample temperature of ∼850°C as recorded by an optical pyrometer. After an exposure time of 5 min, the process was terminated and the thus hydrogen passivated sample loaded into the measurement chamber with a base pressure in the low 10⁻¹⁰ Torr.

Thermionic electron emission characterization commenced after the sample was annealed at 600°C for 5 min to desorb atmospheric species. Recording the temperature of the diamond plate with an optical pyrometer the electron emission current was measured and a fit to the Richardson–Dushman relation as shown in Figure 4 allowed determination of the thermionic work function φ and the Richardson constant A_R.

FIGURE 4

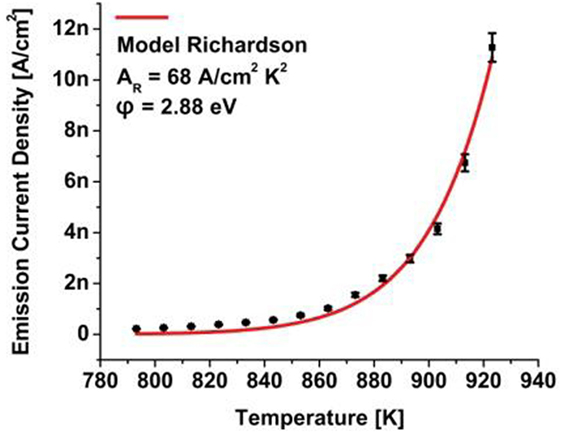
Figure 4. Thermionic electron emission from a high-pressure, high temperature (100) nitrogen-doped, single-crystal diamond sample with negative electron affinity surface properties induced by hydrogen passivation.

The same nitrogen-doped sample was characterized by secondary ion mass spectroscopy (SIMS) communicating a nitrogen concentration of 3.3 × 10¹⁹ cm⁻³ and from thermionic electron emission characterization a work function of φ = 2.88 eV and a Richardson constant of A_R = 68 A cm⁻²K⁻² was derived.

In reference to the nitrogen level at 1.7 eV, the observation of a work function of 2.88 eV indicated an emission barrier increase that was attributed to upward band bending in the amount of 1.18 eV. A photoelectron spectroscopy study elsewhere reported upward band bending of 1.7 eV for a nitrogen-doped single-crystal (100) diamond sample with a nitrogen concentration of 10²⁰ cm⁻³ (Diederich et al., 1998a). These results indicate a relation between the doping concentration and the amount of band bending.

The value of the experimentally determined Richardson constant of 68 A cm⁻²K⁻² deviated from the theoretical value of 120 A cm⁻²K⁻² which advised a discussion. With the effective work function, φ_e, defined by φ_e = k_B⋅T⋅ln(AT²/J) where A = 120 A cm⁻²K⁻² the Richardson work function can be derived from a fit to the current density data plot J = A_R⋅T²⋅exp(−φ/k_BT). As the effective work function was observed to follow φ_e = φ + αT it follows that α = dφ_e/dφ = k⋅ln(120/A_R). Thus, for materials that do not exhibit a temperature-dependent work function, the value for the Richardson constant will be 120 A cm⁻²K⁻² (Hensley, 1961). A further evaluation of expression (Eq. 5) for the Richardson constant with an effective electron mass for diamond of 0.54 m_e arrives at a Richardson constant of ∼64 A cm⁻²K⁻² which is in good agreement with the experimentally obtained value. In a more detailed description, a quantum simulation for the Richardson constant was based on the density of states, g(E), and the Fermi–Dirac distribution, f (T, E), through

$A\left(T\right)\propto \sqrt{\frac{k_B}{\mathrm{2\pi }{m}_e}}\int g\left(E\right)f\left(T,E\right)\mathit{dE},$ (10)

which allowed a more accurate calculation of the emission current for wide band-gap materials as these exhibit a different density of states than metals (Musho et al., 2013). In the same report, wide band-gap material with E_c−E_f = 1 eV and work function of 2 eV presented a Richardson constant of ∼60 A cm⁻²K⁻². These values are in agreement with thermionic emission reports where polycrystalline boron doped diamond with a boron concentration of ∼10¹⁹ cm⁻³ was characterized with a Richardson constant of 60 A cm⁻²K⁻² and nitrogen-doped nanocrystalline diamond with a nitrogen concentration of 2.4 × 10²⁰ cm⁻³ evaluated with a Richardson constant of ∼70 A cm⁻²K⁻² (Suzuki et al., 2009; Paxton et al., 2012).

The significant value for the Richardson constant confirms the nitrogen-doped diamond plate as a suitable substrate material for homoepitaxial doped diamond films and their application as thermionic cathode as the electron emission current should not be limited by the substrate.

Single-Crystal Phosphorus-Doped Diamond

Phosphorus-doped diamond was prepared utilizing plasma-enhanced chemical vapor deposition (PECVD) in a dedicated reactor for the growth of electronic grade material and a base pressure in the low 10⁻⁸ Torr regime. The system employs a complete dry pumping solution including a turbomolecular and scroll pump for a high vacuum background ambient and a positive displacement pump for processing. In addition to the water-cooled reactor chamber a custom designed, water-cooled sample stage is used.

Process gases include research grade hydrogen and methane and as phosphorus source a 200 ppm trimethylphosphine (TMB), P(CH₃)₃, in hydrogen gas mixture, a less toxic source than phosphine gas, PH₃. In a growth study elsewhere different phosphorus sources, tertiarybutylphosphine, TBM, and phosphine were used to prepare and characterize the doped and n-type diamond films grown on (111) oriented type Ib (nitrogen-doped, HPHT) substrates (Kato et al., 2005b). It was observed that there is no significant difference in doping profile and electronic properties when either phosphorus doping source is used indicating similar decomposition of the molecules in the hot plasma.

Prior to phosphorus-doped diamond growth the wet-chemical cleaning process detailed in section “Single-Crystal Nitrogen-Doped Diamond” was employed to remove contaminants from the HPHT nitrogen-doped single-crystal diamond substrate with (100) surface orientation. A pure hydrogen plasma excited under 400 sccm hydrogen flow rate, pressure of 50 Torr, and microwave power of 1,300 W was timed for 15 min after which conditions were adjusted for phosphorus-doped diamond growth. In this growth step, the hydrogen flow rate was reduced to 388 sccm, methane flow was established at 2 sccm, and the TMB/H₂ gas mixture introduced at 10 sccm. With a microwave power of 2,500 W and a pressure of 85 Torr, the substrate was heated to about 950°C as measured by a dual-wavelength optical pyrometer. The growth time under these conditions was timed at 7 min after which microwave power and process gases were shut off and the reactor evacuated. A SIMS profile for a typical sample is displayed in Figure 5A and communicates a phosphorus doping concentration of ∼10¹⁷ cm⁻³ and a film thickness of ∼10 nm. An optical microscopy image of the surface shown in Figure 5B presents a smooth surface morphology without any significant defects observed.

FIGURE 5

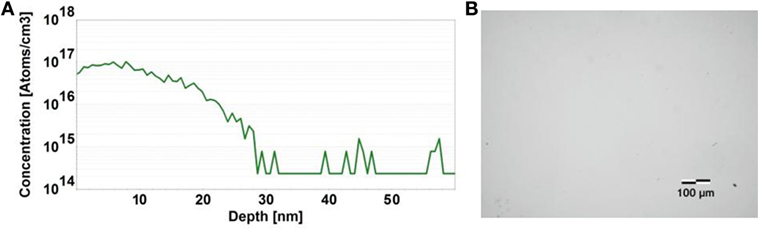
Figure 5. Secondary ion mass spectroscopy profile of a phosphorus-doped diamond film grown on a (100) oriented surface (A) and the corresponding surface morphology acquired via optical microscopy indicating no detectable growth defect formation (B).

Characterization of the thermionic electron emission commenced after an annealing step where the sample was heated to a temperature of 600°C controlled by an optical pyrometer. The electron emission current was recorded as a function of diamond sample temperature with the results shown in Figure 6 (solid square data points.).

FIGURE 6

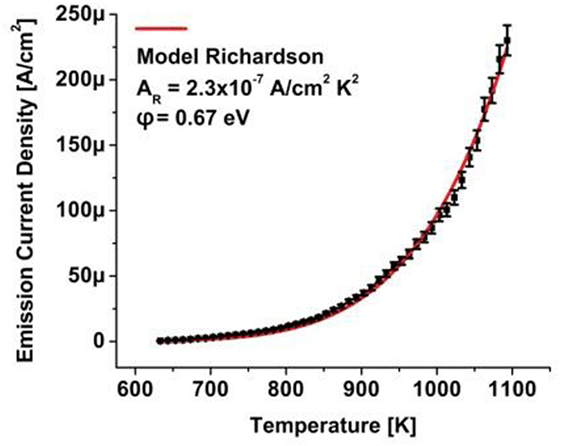
Figure 6. Thermionic electron emission (square data points) from a phosphorus-doped diamond film with negative electron affinity surface grown on a high-pressure, high temperature (100) nitrogen-doped, single-crystal diamond substrate. A fit to the Richardson relation (solid curve) communicates a work function of φ = 0.67 eV.

A fitting procedure to the Richardson relation (solid line) with a determination coefficient R² > 0.99 allows extraction of the work function and Richardson constant. An ultra-low work function of φ = 0.67 eV indicates negligible band bending in reference to the phosphorus levels at ∼0.6 eV. The reduced value of the Richardson constant of ∼10⁻⁷ A cm⁻²K⁻² may be attributed to the doping concentration of ∼10¹⁷ cm⁻³ phosphorus. Operation of the thermionic electrode under current flow at temperatures exceeding 825°C indicates the stability of the hydrogen passivation layer that induces the NEA surface which eliminates the surface emission barrier and contributes to the low work function. This is one of the lowest work function values reported; comparable to the measured work function of 0.82 eV for 12CaO–7Al₂O₃, or C12A7:electride and 0.9 eV for polycrystalline phosphorus-doped diamond (Koeck et al., 2009; Rand et al., 2011).

To evaluate the influence of the doping concentration on the work function, a phosphorus-doped diamond film was prepared similarly but with an increase in the TMP/H₂ flow rate from 10 to 30 sccm which corresponds to a phosphorus doping concentration of ∼10¹⁸ cm⁻³. Thermionic electron emission displayed in Figure 7 (solid triangles) allows fitting to the law of Richardson (dashed curve) with a work function of φ = 0.84 eV increased from φ = 0.64 eV for the lower doped film. The work function increase was attributed to more prominent upward band bending that increased the emission barrier. In an annealing step, the temperature of the diamond substrates was increased to ∼1,050°C for 30 min during which the pressure in the measurement chamber increased to ∼5 × 10⁻⁸ Torr. This process desorbed hydrogen that induced the NEA characteristics from the phosphorus-doped diamond surface.

FIGURE 7

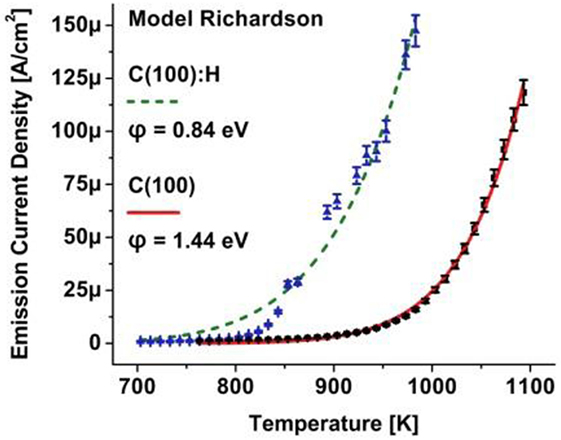
Figure 7. Thermionic electron emission from a phosphorus-doped diamond film with hydrogen passivated surface (triangular data points) with a fit to the Richardson relation (dashed curve) presenting a work function of 0.84 eV; the same surface, annealed to desorb hydrogen, exhibits electron emission (square data points) that communicates a work function of 1.44 eV.

In a successive thermionic electron emission measurement of the clean doped diamond surface, the emission current shown as square data points in Figure 5 followed the law of Richardson and a work function of φ = 1.44 eV was derived indicating a barrier increase by 0.6 eV. This is one of the lowest thermionic work functions reported for a clean doped diamond surface. An ab initio molecular dynamics investigation of the bare C(100)-2 × 1 surface presented a positive electron affinity of +0.8 eV due to its large surface dipole from electronic charge in the dangling-bond orbitals from the dimer atoms (Van Der Weide et al., 1994). The calculations were substantiated by experiment on a practically hydrogen-free boron doped type IIb (100) diamond surface that exhibited a positive electron affinity of 0.5 eV (Diederich et al., 1996). Similarly, for a clean nitrogen-doped type Ib (100) diamond surface, a positive electron affinity of 0.5 ± 0.1 eV was reported from photoelectron emission spectroscopy (Diederich et al., 1998b). For heavily phosphorus-doped diamond with a doping concentration of 7 × 10¹⁹ cm⁻³, these data are also in agreement with the reported barrier height of 0.53 eV attributed to the positive electron affinity of the (111)-2 × 1 reconstructed diamond surface (Yamada et al., 2006).

To further extend the study of work function and Richardson constant evolvement with phosphorus doping concentration HPHT type Ib nitrogen-doped substrates with (111) surface orientation were utilized for phosphorus-doped diamond homoepitaxy. On the (111) diamond surface phosphorus is more readily incorporated which was first demonstrated by Koizumi et al. (1997) who utilized PECVD to grow n-type, phosphorus-doped diamond on type Ib substrates.

Similar to the (100) oriented substrate pre-treatment detailed in the previous sections, the HPHT type Ib nitrogen-doped plates with (111) surface orientation were chemically cleaned and a hydrogen plasma step employed prior to phosphorus-doped diamond homoepitaxy. SIMS characterization shown in Figure 8A presented an increased phosphorus concentration of 4.4 × 10¹⁸ cm⁻³ and a film thickness of ∼275 nm. The same sample was evaluated by thermionic electron emission plotted in Figure 8B and a work function of 1.45 eV was derived from a fit to the Richardson relation with a value for the Richardson constant of A_R = 0.011 A cm⁻²K⁻². With the work function of 1.45 eV upward band bending in the amount of 0.86 eV is derived.

FIGURE 8

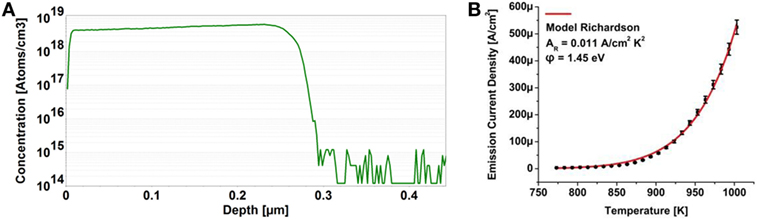
Figure 8. Secondary ion mass spectroscopy profile of a phosphorus-doped diamond film grown on a (111) oriented high-pressure, high temperature type Ib nitrogen-doped diamond surface (A) and the corresponding thermionic electron emission characterization with respect to the Richardson formalism (B).

In a schematic shown in Figure 9, the band structure for the diamond electrodes is depicted with a doping concentration of 2 × 10¹⁷ cm⁻³ for a phosphorus-doped diamond film and the higher doped nitrogen-doped diamond with a doping concentration of 3.3 × 10¹⁹ cm⁻³. Band bending values are derived from thermionic work function measurements and the depletion width L_d calculated from the relation L_d = (2ϵ₀ϵ_sW_d/qN_d)^1/2 where ϵ₀ is the permittivity in vacuum, ϵ_s is the dielectric constant of diamond, q is the elementary charge, N_d the donor concentration, and W_d the barrier height. The surface state density relates to the depletion width via qN_dL_d = qN_ss.

FIGURE 9

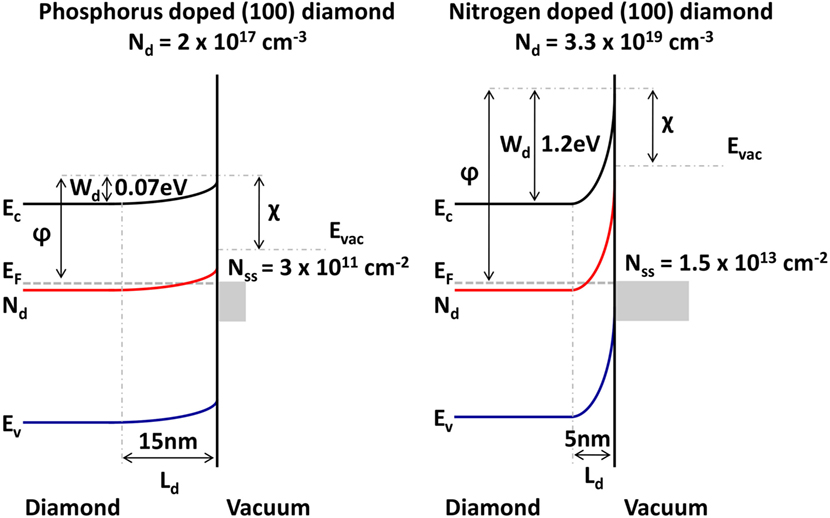
Figure 9. Band bending schematic for single-crystal (100) diamond with different doping concentration of 2 × 10¹⁷ cm⁻³ for phosphorus-doped diamond and 3.3 × 10¹⁹ cm⁻³ for nitrogen-doped diamond.

The experimental thermionic emission data for doped diamond suggests a relation between the thermionic emission parameters, work function and Richardson constant, and the doping concentration. As the amount of band bending presented in this research has been corroborated by photoemission spectroscopy studies by various groups its origin may be related more fundamentally to the doping density and corresponding defect states as well as surface properties.

Thermionic Energy Conversion Approaches and Considerations Utilizing Diamond Electrodes

The demonstration of low and ultra-low work function single-crystal diamond surfaces should be well suited as electrode material for thermionic conversion applications. To demonstrate a thermionic converter approach based on single-crystal diamond, a nitrogen-doped HPHT (100) plate with a nitrogen incorporation of ∼10¹⁹ cm⁻³, the emitter, was paired with an electrode comprised a phosphorus-doped film with a phosphorus incorporation of ∼10¹⁷ cm⁻³, grown on a nitrogen-doped HPHT (100) plate, the collector, with the schematic configuration presented in Figure 10A. This configuration would verify thermionic current flow from emitter to collector, however, the electrode spacing of 75 μm would result in space charge limited operation and its mitigation was achieved through application of a small, variable bias. For the electron emitter, a nitrogen-doped diamond was characterized as shown in Figure 10B with a work function of 2.21 eV providing sufficient current for operation. Under application of a bias to mitigate space charge effects a barrier in the current flow was observed, shown in Figure 10C, and attributed to Schottky effects at the lower temperature collector attributed to the low phosphorus doping. At 800°C, the measured current was fitted to the Child–Langmuir relation, indicated by the dashed line in Figure 10C, that indicated a space charge regime where a deviation at higher bias values was attributed to resistivity effects at the doped diamond electrodes and their contacts. With an increase in the operating temperature to 850°C the collector temperature increased sufficiently to reduce the Schottky barrier at the collector electrical contact. This issue can also be addressed by utilizing an increased phosphorus concentration for the electrical contact including selective growth, a technique demonstrated for solid-state diamond devices (Kato et al., 2009).

FIGURE 10

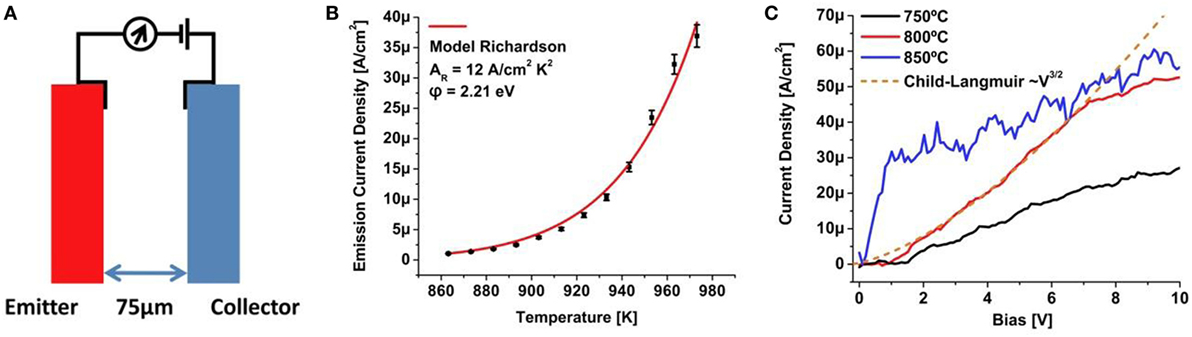
Figure 10. Schematic of a thermionic converter cell utilizing a nitrogen-doped diamond emitter and phosphorus-doped diamond collector (A) with emitter thermionic characterization (B) and thermionic current flow through the converter by application of a bias to mitigate space charge that indicates a Schottky barrier at the collector at lower temperatures, a space charge regime, indicated by the dashed line at 800°C, and a regime that may be attributed in part to resistivity effects at the doped diamond electrodes and contacts (C).

Conclusion

Thermionic energy conversion allows efficient conversion of heat into electrical energy through thermionic electron emission from an emitter with a suitable low work function. As the efficiency of a thermionic converter is related to the work function differential between emitter and collector a lower work function collector is preferred with an ideal value of ∼0.5 eV. Diamond, a wide band-gap semiconductor, displays unique materials properties that suggests its application as electrode material in thermionic conversion. The NEA that shifts the vacuum level below the CBM eliminates a surface barrier for electron emission. In conjunction with donor states established at 1.7 eV and 0.6 eB below the CBM for nitrogen and phosphorus, respectively, low work function electrodes are feasible. Utilizing diamond homoepitaxy via PECVD a phosphorus-doped diamond film with a doping concentration of ∼10¹⁷ cm⁻³ and a film thickness of ∼10 nm was grown on a (100) oriented single-crystal diamond substrate and an ultra-low work function of 0.67 eV was demonstrated. For higher phosphorus-doped films with a doping concentration of 4.4 × 10¹⁸cm⁻³ and a film thickness of ∼275 nm, a (111) oriented substrates was utilized and the work function was increased to 1.45 eV. For nitrogen-doped single-crystal (100) oriented diamond with a nitrogen concentration of 3.3 × 10¹⁹ cm⁻³, a work function of 2.88 eV was measured. The increase in the work function due to increased upward band bending was attributed to an increase in the surface states from 3 × 10¹¹ to 1.5 × 10¹³cm⁻² for the low phosphorus and higher nitrogen-doped diamond, respectively. Employing doped diamond electrodes in a thermionic converter cell demonstrated thermionic current flow in the device. Schottky effects at the collector, due to the reduced phosphorus doping concentration, were mitigated through operation at elevated temperatures and were suggested to be addressed through selective growth of high phosphorus-doped diamond for electrical contacts.

Author Contributions

FK was responsible for preparing the material and performing and evaluating the experimental measurements; he composed the manuscript and reviewed the literature. RN provided support and guidance for this research study.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Funding

This research was supported by the Office of Naval Research through grant # N00014-10-1-0540.

References

Belbachir, R. Y., An, Z., and Ono, T. (2014). Thermal investigation of a micro-gap thermionic power generator. J. Micromech. Microeng. 24, 085009. doi: 10.1088/0960-1317/24/8/085009

CrossRef Full Text | Google Scholar

Child, C. D. (1911). Discharge from hot CaO. Phys. Rev. 32, 492. doi:10.1103/PhysRevSeriesI.32.492

CrossRef Full Text | Google Scholar

Diederich, L., Küttel, O. M., Aebi, P., and Schlapbach, L. (1998a). Electron affinity and work function of differently oriented and doped diamond surfaces determined by photoelectron spectroscopy. Surf. Sci. 418, 219–239. doi:10.1016/S0039-6028(98)00718-3

CrossRef Full Text | Google Scholar

Diederich, L., Küttel, O. M., Ruffieux, P., Pillo, T., Aebi, P., and Schlapbach, L. (1998b). Photoelectron emission from nitrogen-and boron-doped diamond (100) surfaces. Surf. Sci. 417, 41–52. doi:10.1016/S0039-6028(98)00638-4

CrossRef Full Text | Google Scholar

Diederich, L., Küttel, O. M., Schaller, E., and Schlapbach, L. (1996). Photoemission from the negative electron affinity (100) natural hydrogen terminated diamond surface. Surf. Sci. 349, 176–184. doi:10.1016/0039-6028(95)01117-X

CrossRef Full Text | Google Scholar

Durakiewicz, T., Arko, A. J., Joyce, J. J., Moore, D. P., and Halas, S. (2001). Thermal work function shifts for polycrystalline metal surfaces. Surf. Sci. 478, 72–82. doi:10.1016/S0039-6028(01)00898-6

CrossRef Full Text | Google Scholar

Dushman, S. (1923). Electron emission from metals as a function of temperature. Phys. Rev. 21, 623. doi:10.1103/PhysRev.21.623

CrossRef Full Text | Google Scholar

Edison, T. A. (1884). Electrical Indicator, US Patent No. 307031.

Google Scholar

El-Genk, M. S., and Momozaki, Y. (2002). An experimental investigation of the performance of a thermionic converter with planar molybdenum electrodes for low temperature applications. Energy Convers. Manag. 43, 911–936. doi:10.1016/S0196-8904(01)00084-X

CrossRef Full Text | Google Scholar

Elster, J., and Geitel, H. (1882). Ueber die Electricität der Flamme. Ann. Physik und Chemie Neue Folge 16, 193–222. doi:10.1002/andp.18822520602

CrossRef Full Text | Google Scholar

Farrer, R. G. (1969). On the substitutional nitrogen donor in diamond. Solid State Commun. 7, 685–688. doi:10.1016/0038-1098(69)90593-6

CrossRef Full Text | Google Scholar

Fichman, B. T. (2015). Monthly Energy Review March 2015, Washington, DC: U.S. Energy Information Administration, Office of Energy Statistics, Office of Survey Development and Statistical Integration, Integrated Energy Statistics Team. DOE/EIA-0035(2015/03).

Google Scholar

Fleming, J. A. (1895). A further examination of the Edison effect in glow lamps. Proc. Phys. Soc. London 14, 187. doi:10.1088/1478-7814/14/1/318

CrossRef Full Text | Google Scholar

Hansen, L. K., Hatch, G. L., Fitzpatrick, G. O., and Rasor, N. S. (1976). “The plasmatron as an advanced performance thermionic converter,” in 11th Intersociety Energy Conversion Engineering Conference, Stateline, NV, 1630–1634.

Google Scholar

Hatsopoulos, G. N. (1963). Transport effects in cesium thermionic converters. Proc. IEEE 51, 725–733. doi:10.1109/PROC.1963.2265

CrossRef Full Text | Google Scholar

Hatsopoulos, G. N., and Gyftopoulos, E. P. (1973). Thermionic Energy Conversion, Vol. 1. Cambridge, MA: Mit Press.

Google Scholar

Hatsopoulos, G. N., and Gyftopoulos, E. P. (2007). “Thermionic power generator,” in McGraw Hill’s Encyclopedia of Science and Technology, ed. E. Geller (New York: McGraw-Hill), 343.

Google Scholar

Hensley, E. B. (1961). Thermionic emission constants and their interpretation. J. Appl. Phys. 32, 301–308. doi:10.1063/1.1735994

CrossRef Full Text | Google Scholar

Hernqvist, K. G. (1963). Analysis of the arc mode operation of the cesium vapor thermionic energy converter. Proc. IEEE 51, 748–754. doi:10.1109/PROC.1963.2267

CrossRef Full Text | Google Scholar

Hernqvist, K. G., Kanefsky, F., and Norman, F. H. (1958). Thermionic energy converter. RCA Rev. 19, 244–258.

Google Scholar

Ibragimov, K. I., and Korol’kov, V. A. (2001). Temperature dependence of the work function of metals and binary alloys. Inorg. Mater. 37, 567–572. doi:10.1023/A:1017556031226

CrossRef Full Text | Google Scholar

Isberg, J., Hammersberg, J., Johansson, E., Wikström, T., Twitchen, D. J., Whitehead, A. J., et al. (2002). High carrier mobility in single-crystal plasma-deposited diamond. Science 297, 1670–1672. doi:10.1126/science.1074374

PubMed Abstract | CrossRef Full Text | Google Scholar

Ito, T., and Cappelli, M. A. (2012). Optically pumped cesium plasma neutralization of space charge in photon-enhanced thermionic energy converters. Appl. Phys. Lett. 101, 213901. doi:10.1063/1.4767349

CrossRef Full Text | Google Scholar

Jordan, D. C., and Kurtz, S. R. (2013). Photovoltaic degradation rates—an analytical review. Prog. Photovolt Res. Appl. 21, 12–29. doi:10.1002/pip.1182

CrossRef Full Text | Google Scholar

Kalish, R. (1999). Doping of diamond. Carbon N. Y. 37, 781–785. doi:10.1016/S0008-6223(98)00270-X

CrossRef Full Text | Google Scholar

Kato, H., Makino, T., Ogura, M., Tokuda, N., Okushi, H., and Yamasaki, S. (2009). Selective growth of buried n+ diamond on (001) phosphorus- doped n-type diamond film. Appl. Phys. Express 2, 055502. doi:10.1143/APEX.2.055502

CrossRef Full Text | Google Scholar

Kato, H., Yamasaki, S., and Okushi, H. (2005a). n-type doping of (001)-oriented single-crystalline diamond by phosphorus. Appl. Phys. Lett. 86, 222111. doi:10.1063/1.1944228

CrossRef Full Text | Google Scholar

Kato, H., Futako, W., Yamasaki, S., and Okushi, H. (2005b). Growth of phosphorus-doped diamond using tertiarybutylphosphine and trimethylphosphine as dopant gases. Diamond Relat. Mater. 14, 340–343. doi:10.1016/j.diamond.2004.11.032

CrossRef Full Text | Google Scholar

Kiejna, A., Wojciechowski, K. F., and Zebrowksi, J. (1979). The temperature dependence of metal work functions. J. Phys. F Metal Phys. 9, 1361. doi:10.1088/0305-4608/9/7/016

CrossRef Full Text | Google Scholar

Knapp, A. G. (1973). Surface potentials and their measurement by the diode method. Surf. Sci. 34, 289–316. doi:10.1016/0039-6028(73)90120-9

CrossRef Full Text | Google Scholar

Koeck, F. A. M., Nemanich, R. J., Lazea, A., and Haenen, K. (2009). Thermionic electron emission from low work-function phosphorus doped diamond films. Diamond Relat. Mater. 18, 789–791. doi:10.1016/j.diamond.2009.01.024

CrossRef Full Text | Google Scholar

Koizumi, S., Kamo, M., Sato, Y., Ozaki, H., and Inuzuka, T. (1997). Growth and characterization of phosphorous doped {111} homoepitaxial diamond thin films. Appl. Phys. Lett. 71, 1065–1067. doi:10.1063/1.119729

CrossRef Full Text | Google Scholar

Langmuir, I. (1913). The effect of space charge and residual gases on thermionic currents in high vacuum. Phys. Rev. 2, 450. doi:10.1103/PhysRev.2.450

CrossRef Full Text | Google Scholar

Langmuir, I. (1923). The effect of space charge and initial velocities on the potential distribution and thermionic current between parallel plane electrodes. Phys. Rev. 21, 419. doi:10.1103/PhysRev.21.419

CrossRef Full Text | Google Scholar

Langmuir, I., and Kingdon, K. H. (1925). Thermionic effects caused by vapours of alkali metals. Proc. R. Soc. London A Contain. Papers Math. Phys. Character 107, 61–79. doi:10.1098/rspa.1925.0005

CrossRef Full Text | Google Scholar

Lee, J. H., Bargatin, I., Provine, J., Clay, W. A., Schwede, J. W., Liu, F., et al. (2009). “Thermionic emission from microfabricated silicon-carbide filaments,” in Power MEMS 2009; 2009 Dec 1–4; Washington, DC, USA, 149–152.

Google Scholar

Lee, J.-H., Igor, B., Melosh, N. A., and Howe, R. T. (2012a). Optimal emitter-collector gap for thermionic energy converters. Appl. Phys. Lett. 100, 173904. doi:10.1063/1.4707379

CrossRef Full Text | Google Scholar

Lee, J. H., Bargatin, I., Gwinn, T. O., Vincent, M., Littau, K. A., Maboudian, R., et al. (2012b). “Microfabricated silicon carbide thermionic energy converter for solar electricity generation,” in 2012 IEEE 25th International Conference on Micro Electro Mechanical Systems (MEMS) (Paris: IEEE), 1261–1264.

Google Scholar

Lin, I.-N., Koizumi, S., Yater, J., and Koeck, F. (2014). Diamond electron emission. MRS Bull. 39, 533–541. doi:10.1557/mrs.2014.101

CrossRef Full Text | Google Scholar

Luke, J. R. (2005). “Advanced thermionic converter technology development,” in AIP Conference Proceedings, Vol. 746 (Albuquerque: AIP), 918–925.

Google Scholar

Makdisi, Y., Kokaj, J., Afrousheh, K., Mathew, J., Thomas, N., and Pichler, G. (2014). Collision induced phenomena in the autoionizing spectrum of Ba and Sr. J. Phys. Conf. Series 548, 012054. doi:10.1088/1742-6596/548/1/012054

CrossRef Full Text | Google Scholar

Meir, S., Stephanos, C., Geballe, T. H., and Mannhart, J. (2013). Highly-efficient thermoelectronic conversion of solar energy and heat into electric power. J. Renew. Sustain. Energy 5, 043127. doi:10.1063/1.4817730

CrossRef Full Text | Google Scholar

Musho, T. D., Paxton, W. F., Davidson, J. L., and Greg Walker, D. (2013). Quantum simulation of thermionic emission from diamond films. J. Vacuum Sci. Technol. B Nanotechnol. Microelectron. 31, 021401. doi:10.1116/1.4792522

CrossRef Full Text | Google Scholar

Nordheim, L. W. (1928). The effect of the image force on the emission and reflexion of electrons by metals. Proc. R. Soc. London A Contain. Papers Math. Phys. Character 121, 626–639. doi:10.1098/rspa.1928.0222

CrossRef Full Text | Google Scholar

Ogino, A., Muramatsu, T., and Kando, M. (2004). Output characteristics of solar-power-driven thermionic energy converter. Jpn. J. Appl. Phys. 43, 309. doi:10.1143/JJAP.43.309

CrossRef Full Text | Google Scholar

Paxton, W. F., Wade, T., Howell, M., Tolk, N., Kang, W. P., and Davidson, J. L. (2012). Thermionic emission characterization of boron-doped microcrystalline diamond films at elevated temperatures. Physica Status Solidi 209, 1993–1995. doi:10.1002/pssa.201228114

CrossRef Full Text | Google Scholar

Pickett, W. E. (1994). Negative electron affinity and low work function surface: cesium on oxygenated diamond (100). Phys. Rev. Lett. 73, 1664. doi:10.1103/PhysRevLett.73.1664

CrossRef Full Text | Google Scholar

Preece, W. H. (1884). On a peculiar behaviour of glow-lamps when raised to high incandescence. Proc. R. Soc. London 38, 219–230. doi:10.1098/rspl.1884.0093

CrossRef Full Text | Google Scholar

Rand, L. P., Waggoner, R. M., and Williams, J. D. (2011). “Hollow cathode with low work function electride insert,” in ASME 2011 International Mechanical Engineering Congress and Exposition (Denver: American Society of Mechanical Engineers), 317–323.

Google Scholar

Rasor, N. S. (1991). Thermionic energy conversion plasmas. IEEE Trans. Plasma Sci. 19, 1191–1208. doi:10.1109/27.125041

CrossRef Full Text | Google Scholar

Rasor, N. S. (2017). Hybrid mode cesium diode thermionic converter. J. Appl. Phys. 121, 203304. doi:10.1063/1.4983816

CrossRef Full Text | Google Scholar

Reck, K., Dionigi, F., and Hansen, O. (2014). “Photon-enhanced thermionic emission in cesiated p-type and n-type silicon,” in 29th European Photovoltaic Solar Energy Conference and Exhibition, Amsterdam, 328–330.

Google Scholar

Richardson, O. W. (1901). On the negative radiation from hot platinum. Camb. Philos. Proc. I, 286.

Google Scholar

Richardson, O. W. (1903). The electrical conductivity imparted to a vacuum by hot conductors. Philos. Trans. R. Soc. Lond. Ser. A 201, 497–549.

Google Scholar

Richardson, O. W. (1914). Electron theory and gas molecule distribution in field of force. Philos. Mag. 28, 633–647. doi:10.1080/14786441108635246

CrossRef Full Text | Google Scholar

Schlichter, W. (1915). Die spontane Elektronenemission glühender Metalle und das glühelektrische Element. Ann. Phys. 352, 573–640. doi:10.1002/andp.19153521302

CrossRef Full Text | Google Scholar

Shefsiek, P. (2010). Describing and correlating the performance of the thermionic converter: a historical perspective. IEEE Trans. Plasma Sci. 38, 2041–2047. doi:10.1109/TPS.2010.2050910

CrossRef Full Text | Google Scholar

Shiomi, H., Nishibayashi, Y., and Fujimori, N. (1991). Characterization of boron-doped diamond epitaxial films. Jpn. J. Appl. Phys. 30, 1363. doi:10.1143/JJAP.30.1363

CrossRef Full Text | Google Scholar

Srisonphan, S., Kim, M., and Kim, H. K. (2014). Space charge neutralization by electron-transparent suspended graphene. Sci. Rep. 4, 1–4. doi:10.1038/srep03764

CrossRef Full Text | Google Scholar

Stoney, G. J. (1894). Of the “Electron” or Atom of Electricity, Philosophical Magazine. Series 5, Vol. 38, 418–420.

Google Scholar

Suzuki, M., Ono, T., Sakuma, N., and Sakai, T. (2009). Low-temperature thermionic emission from nitrogen-doped nanocrystalline diamond films on n-type Si grown by MPCVD. Diamond Relat. Mater. 18, 1274–1277. doi:10.1016/j.diamond.2009.05.004

CrossRef Full Text | Google Scholar

Takeuchi, D., Kato, H., Ri, G. S., Yamada, T., Vinod, P. R., Hwang, D., et al. (2005). Direct observation of negative electron affinity in hydrogen-terminated diamond surfaces. Appl. Phys. Lett. 86, 152103. doi:10.1063/1.1900925

CrossRef Full Text | Google Scholar

Thomson, J. J. (1897). XL. Cathode rays. London Edinburgh Dublin Philos. Mag. J. Sci. 44, 293–316. doi:10.1080/14786449708621070

CrossRef Full Text | Google Scholar

Thomson, J. J. (1899). LVIII. On the masses of the ions in gases at low pressures. London Edinburgh Dublin Philos. Mag. J. Sci. 48, 547–567. doi:10.1080/14786449908621447

CrossRef Full Text | Google Scholar

Van Der Weide, J., Zhang, Z., Baumann, P., Wensell, M., Bernholc, R., and Nemanich, R. J. (1994). Negative-electron-affinity effects on the diamond (100) surface. Phys. Rev. B 50, 5803–5806. doi:10.1103/PhysRevB.50.5803

CrossRef Full Text | Google Scholar

van der Weide, J. Z., Baumann, P. K., Wensell, M. G., Bernholc, J., and Nemanich, R. J. (1994). Negative-electron-affinity effects on the diamond (100) surface. Phys. Rev. B 50, 5803. doi:10.1103/PhysRevB.50.5803

CrossRef Full Text | Google Scholar

Verhoef, R. W., and Asscher, M. (1997). The work function of adsorbed alkalis on metals revisited: a coverage-dependent polarizability approach. Surf. Sci. 391, 11–18. doi:10.1016/S0039-6028(97)00399-3

CrossRef Full Text | Google Scholar

Vining, C. B. (2009). An inconvenient truth about thermoelectrics. Nat. Mater. 8, 83. doi:10.1038/nmat2361

PubMed Abstract | CrossRef Full Text | Google Scholar

Wanke, R., Hassink, G. W. J., Stephanos, C., Rastegar, I., Braun, W., and Mannhart, J. (2016). Magnetic-field-free thermoelectronic power conversion based on graphene and related two-dimensional materials. J. Appl. Phys. 119, 244507. doi:10.1063/1.4955073

CrossRef Full Text | Google Scholar

Wilson, R. G. (1966a). Vacuum thermionic work functions of polycrystalline Be, Ti, Cr, Fe, Ni, Cu, Pt, and type 304 stainless steel. J. Appl. Phys. 37, 2261–2267. doi:10.1063/1.1708797

CrossRef Full Text | Google Scholar

Wilson, R. G. (1966b). Vacuum thermionic work functions of polycrystalline Nb, Mo, Ta, W, Re, Os, and Ir. J. Appl. Phys. 37, 3170–3172. doi:10.1063/1.1703180

CrossRef Full Text | Google Scholar

Wilson, R. G. (1966c). Electron and ion emission from polycrystalline surfaces of Nb, Mo, Ta, W, Re, Os, and Ir in cesium vapor. J. Appl. Phys. 37, 4125–4131. doi:10.1063/1.1708061

CrossRef Full Text | Google Scholar

Yamada, T., Okano, K., Yamaguchi, H., Kato, H., Shikata, S.-I., and Nebel, C. E. (2006). Field emission from reconstructed heavily phosphorus-doped homoepitaxial diamond (111). Appl. Phys. Lett. 88, 212114. doi:10.1063/1.2206552

CrossRef Full Text | Google Scholar

Yamamoto, Y., Imai, T., Tanabe, K., Tsuno, T., Kumazawa, Y., and Fujimori, N. (1997). The measurement of thermal properties of diamond. Diamond Relat. Mater. 6, 1057–1061. doi:10.1016/S0925-9635(96)00772-8

CrossRef Full Text | Google Scholar

Zhang, C., Najafi, K., Bernal, L. P., and Washabaugh, P. D. (2003). “Micro combustion-thermionic power generation: feasibility, design and initial results,” in 12th International Conference on TRANSDUCERS, Solid-State Sensors, Actuators and Microsystems, Vol. 1 (Boston: IEEE), 40–44.

Google Scholar