- Department of Mechanical Engineering, The University of Hong Kong, Pokfulam, Hong Kong
It is a great challenge to efficiently convert low-grade heat (<100°C) to electricity. Currently available heat-to-current converters, such as thermoelectric generators, operating in a low-grade heat regime reach efficiencies no higher than a few percent (<3%). Herein, we illustrated a thermal capacitive electrochemical cycle (TCEC) using electrochemical cell, where the connection to the hot or cold reservoirs alternates in a cyclic charging–heating–discharging–cooling mode to convert heat into electricity, which performs as an electrochemical heat engine. TCEC technology is a cost-effective method for exploiting the temperature-dependent electrostatic potential in an electric double layer (EDL) at carbon electrode/electrolyte interfaces; it produces net electricity by altering the EDL thickness via heating and cooling. In this paper, TCEC on supercapacitor was confirmed on commercial supercapacitor, which showed a poor conversion efficiency. To improve the performance, we redesigned the cell by employing the pouch cell setup with activated carbon as electrode materials and homemade temperature controlling system, which boosted the efficiency from 0.5% of commercial supercapacitor to 3.05% when cycling between 10 and 65°C. A higher efficiency of 3.95% could be reached by using microwaved exfoliated graphene nanosheets (MEG) and nitric acid-treated MEG, which could help in decreasing the energy loss caused by charge leakage.
Introduction
A vast amount of low-grade heat (<100°C) exists in the environment and in the form of waste heat in industrial processes. Efficient conversion of this low-grade heat to electricity is challenging due to the low temperature differential and the distributed nature of these heat sources (Bell, 2008; Rattner and Garimella, 2011; Chu and Majumdar, 2012). Solid-state thermoelectric materials, which work on the temperature difference between two heat reservoirs, have been studied as major candidates for heat to electricity conversion (Rosi, 1968; DiSalvo, 1999; Poudel et al., 2008; Snyder and Toberer, 2008). The figure of merit (ZT) of thermoelectric materials can reach 2 at high temperatures but is limited to 1.5 below 100°C, resulting in a low conversion efficiency of <3% in harvesting low-grade heat (Vining, 2009; Kraemer et al., 2011; Zebarjadi et al., 2012; Feng et al., 2013). The Seebeck effect in electrochemical thermogalvanic cells has also been investigated, but the poor ionic mass transport between two heat reservoirs gives a poor efficiency of <0.5% (Quickenden and Mua, 1995; Hu et al., 2010). Other technologies, such as thermoionic and ultracold-atom thermoelectric engines, have also attracted interest but are typically expensive and inefficient (Brantut et al., 2013; Meir et al., 2013). Currently available heat-to-current converters operating in the low-grade heat regime reach efficiencies no higher than a few percent.
Recent studies of the thermodynamic cycle using electrochemical cells show great potential. In these systems, the connection to either the hot or cold reservoir alternates in a cycle (Lee et al., 2014; Yang et al., 2014a,b; Härtel et al., 2015b). This electrochemical heat engine converts heat into electricity by operating in the charging–heating–discharging–cooling mode, which resembles the Stirling and Carnot heat engine that generates mechanical work via a heating–expansion–cooling–compression cycle. There are two categories of thermo-electrochemical cycles: thermally regenerative electrochemical cycle (TREC) and thermal capacitive electrochemical cycle (TCEC). The TREC is based on the temperature-dependent redox reaction (faradic) in a battery system. The battery voltage is dependent on temperature and is determined by the Nernst equation (Hammond and Risen, 1979; Chum, 1981; Wessells et al., 2011), thus tuning along with changing temperature. Net energy is produced by the voltage difference, originating from the heat absorption and the entropy change in the system. Lee et al. (2014) developed a TREC using a copper hexacyanoferate (CuHCF) cathode and a Cu/Cu+ anode. They used NaNO3 and Cu(NO3)2 electrolytes for CuHCF and Cu electrodes, respectively, which were separated by an anion exchange membrane. The system showed a heat-to-current conversion efficiency of 3.7% when cycling between 10 and 60°C. An efficiency of 5.7% can be achieved under 50% heat recuperation, which is comparable to thermoelectric materials with ZT ≈ 3.5 at this small temperature gradient. However, some limitations must be considered in the further development of TREC technology, such as limited potential materials for electrodes due to the harsh requirements in this system, long waiting time for each cycle and poor efficiency along with high cost.
The TCEC exploits the temperature-dependent electrostatic potential (non-faradic) in an electric double layer (EDL) to construct a thermodynamic cycle (Härtel et al., 2015b). The energy storage in an EDL, which has been widely used in supercapacitors, is based on the electrostatic separation of charges upon polarization at the carbon electrode/electrolyte interface (Frackowiak and Beguin, 2001; Goodenough et al., 2007; Zhang and Zhao, 2009; Zhu et al., 2011; Conway, 2013). The Gouy–Chapman–Stern (GCS) theory models the ion distribution close to the planar electrodes, and the potential distribution (φ) can be described by Poisson–Boltzmann equation (Von Helmholtz, 1879; Gouy, 1910; Chapman, 1913; Stern, 1924; López-García et al., 2011):
where kb is the Boltzmann constant, T is the absolute temperature, e is the electron charge, σ is the surface charge density, C is the ion concentration in bulk solution, NA is Avogadro’s constant, ε0 is the vacuum permittivity, εr is the relative permittivity of the electrolyte, and L is the EDL effective thickness.
As described in Eq. 1, the energy extraction of the capacitive mixing (CAPMIX) technique has been studied by mixing sea saltwater with river freshwater (Brogioli, 2009; Brogioli et al., 2012, 2013; Hatzell et al., 2014; Härtel et al., 2015a). The tendency of the charged ions to move away from the electrode when decreasing the salt concentration leads to the expansion of the EDL; this is referred to as “capacitive double-layer expansion” (CDLE). The increased EDL thickness decreases the capacitance and thus increases the electrode potential at a fixed electrode charge. Therefore, the positive electrode becomes more positive and the negative electrode becomes more negative, resulting in the full cell voltage rise. The potential also shows a near-linear increase with temperature because the first term of kbT provides the predominant T dependence (Rica et al., 2012; Janssen et al., 2014). Based on this temperature dependence, TCEC could be designed. A schematic diagram of the charge–voltage cycle is shown in Figure 1A. The supercapacitor is externally charged at Tc (step 1) and is then heated up to Th at an open circuit (step 2). A temperature rise increases the ion thermal motion and thus the ions move farther into solution, leading to CDLE. Moreover, εr usually decreases with increasing temperature, and so the capacitance further decreases and thus the electrode potential increases. The cell is then discharged at a higher potential at Th, and the energy can be harvested through an external circuit (step 3). The cycle is completed by cooling from Th to Tc at an open circuit, which compresses the EDL (step 4). The efficiency (η) can be calculated as:
where is the maximum work between discharge and charge in a cycle. Eloss is the energy loss in the system. Qh is the total heat input from the hot reservoir to the device and consists of heat flows during heating that occurs in step 2 and the isothermal discharging in step 3. During the isothermal operation at Tc and Th, the system efficiency can be improved by heat recuperation (Qrec), as part of the heat rejected in cooling step 4 can be used for heating in step 2 (Bejan and Kraus, 2003; Serth and Lestina, 2014). A recuperation efficiency of 50–70% can be readily achieved (Lee et al., 2014; Yang et al., 2014a). Recently, Härtel et al. (2015b) presented a thermocapacitive cycle that harvested low-grade heat using a commercial 10 F supercapacitor between Tc = 0°C and Th = 65°C. However, the efficiency calculated by equation (2) is only 0.5% without heat recuperation, which is one order of magnitude lower than the theoretical model shown in Figure 1B (Janssen et al., 2014; Härtel et al., 2015b).
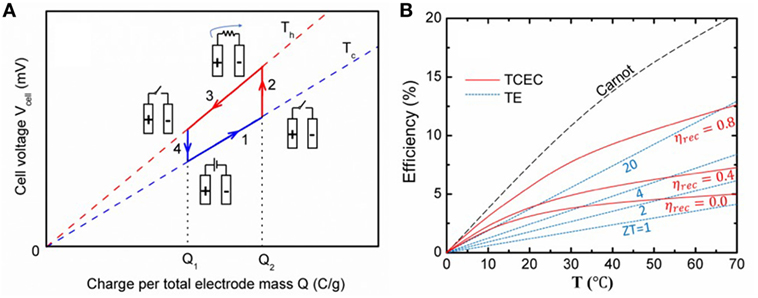
Figure 1. (A) Schematic diagram of charge–voltage cycle for thermal capacitive electrochemical cycle (TCEC). (B) Theoretical efficiency of TE and TCEC (ηrec: heat recuperation efficiency).
Herein, we improved the performance of TCEC cells by optimizing the cell design and applying carbon materials to weak the non-uniform heating and self-discharge. Homemade pouch cell assembled with activated carbon achieved a thermal-to-electricity conversion efficiency of 3.05% when cycling between 10°C and 65°C without heat recuperation. And this efficiency could be further improved to 3.95% by employing microwaved exfoliated graphene nanosheets (MEG) and nitric acid-treated MEG. The TCEC on grapheme-based supercapacitor also showed a higher stability and durability.
Materials and Methods
Electrode Materials Preparation
Our low-cost solution method allows preparation of few-layer MEG by mild oxidation (Zheng et al., 2011; Zhai et al., 2014). About 1 g of natural graphite flakes (Sigma Aldrich) were added into 50 ml mild oxidizer, which consisted of concentrated H2SO4 (96%; Sigma Aldrich) and hydrogen peroxide (30%; Prolabo) at a volume ratio of 9:1. The resulting mixture was stirred under room temperature for 2 h and then washed with deionized water for several time to remove residual reactants. The MEG nano sheets were obtained after irradiating the dried powder from previous oxidation in microwave oven (700 W) for 1 min.
Pouch Cell Fabrication
Uniform heating is difficult to achieve in a matter of minutes in a commercial cylinder-type supercapacitor, and as a result only a small amount of CDLE occurs before the self-discharge. This indicates that the whole cell must be rapidly and uniformly heated in order to maximize the thermal voltage rise and the subsequent discharge. Therefore, a two-electrode pouch cell configuration was used. For electrochemical cell based on activated carbon, activated carbon powder (Kuraray Chemical Co., 1,300 m2/g) and 5 wt% polytetrafluoroethylene (PTFE, 60% dispersion in water) was mixed into a paste and then coated on the Al current collector (Frackowiak and Beguin, 2001; Zhang and Zhao, 2009; Zhu et al., 2011). After drying overnight at 100°C in vacuum, two carbon electrodes (40 µm, ~5 mg) and a porous polypropylene separator (Celgard3501) were sandwiched with 250 µl electrolyte [1.5 M tetraethylammonium tetrafluoroborate (TEA-BF4) solvated in acetonitrile (AN)] (Stoller and Ruoff, 2010). The typical thickness of a cell was 1–1.5 mm.
The MEG electrodes will be prepared by coating slurry (MEG powders with 5wt% PTFE) on graphite rods for the electrode potential measurement, and on Al foil for TCEC pouch cell assembly. The electrodes will be dried overnight at 100°C under vacuum, washed with ethanol, and then soaked in electrolytes (1.5 M TEA-BF4 solvated in AN).
Microstructure Characterization
The cross-sectional structure of the MEG electrode was determined through Scanning Electron Microscope (Hitachi S-4800). The MEG films were approximately 32 µm thick with a mass of 2–3 mg (Figure 2).
Electrochemical Measurement
The open circuit voltage (OCV) changes of supercapacitor during heating or cooling were measured by potentiostats with a two-electrode configuration (Gamry reference 3000). The charging or discharging process was also conducted in the same potentiostats under constant current of 100 mA/g.
Results and Discussion
We measured the cell voltage by placing a fully charged Panasonic 4.7 F supercapacitor in a hot water reservoir at 65°C (Figure 3A). After heating, the voltage increased in the first 100 s and then decreased over time. Thus, the response time of CDLE is faster than the self-discharge. A temperature coefficient of 0.593 mV/K was measured by thermal voltage rise at different temperatures for the fully charged supercapacitor (black squares, Figure 3B), which is consistent with previously reported results (Härtel et al., 2015b). However, uniform heating is difficult to achieve in a matter of minutes in a commercial cylinder-type supercapacitor, and as a result only a small amount of CDLE occurs before self-discharge. This indicates that the whole cell must be rapidly and uniformly heated in order to maximize the thermal voltage rise and the subsequent discharge. Therefore, a two-electrode pouch cell configuration was used in a follow-up experiment (Figure 3C). A homemade thermoelectric-based temperature cycler was used to control heating and cooling using LabVIEW programs. Thermopaste (Omega) was applied to all of the interfaces to ensure good thermal contact (Kraemer et al., 2011; Feng et al., 2013; Yang et al., 2014a). Figure 3D shows the experimental charge–voltage curve of pouch cell using activated carbon electrodes; the work obtained was 1.6 J/g when cycling between Tc = 10°C and Th = 65°C. The measured α was 1.09 mV/K (red spot, Figure 3B), which is higher than that of a commercial supercapacitor.
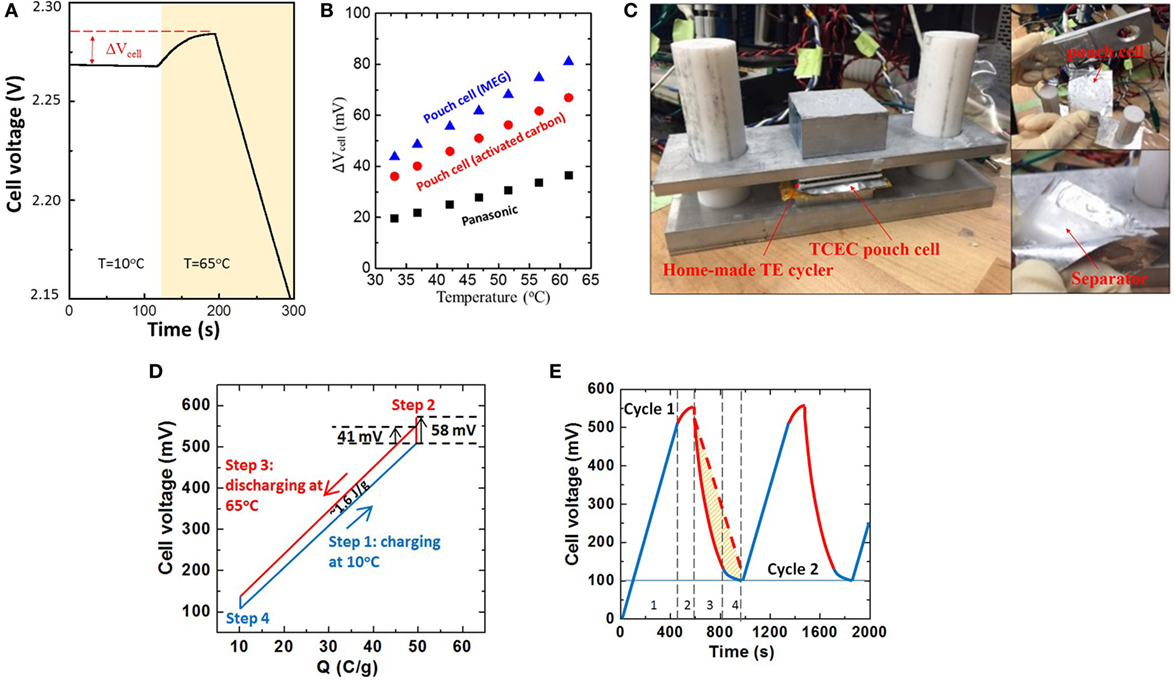
Figure 3. (A) OCV for fully charged supercapacitor (Panasonic 4.7 F) at 65°C. (B) Cell voltage rise vs. temperature. (C) Home-made TE temperature cycler and pouch cell. (D) Charge–voltage cycle for the pouch cell using activated carbon electrodes. (E) Cell voltage vs. time plot for first and second thermal cycles (Imeasure = 100 mA/g, t3/t1 ~ 0.65).
The efficiency of TECE could be obtained after knowing the output work and input heat. The amount of total thermal energy used in the primary heat source (here, the thermoelectric module was used) is dependent on the setup of temperature controlling system, which is difficult to be determined. Referring to other research works in the related field (Lee et al., 2014; Yang et al., 2014a,b; Härtel et al., 2015a,b), it confirms that the calculated efficiency only includes thermal energy absorbed by the device and does not include the total energy used in the primary heat resource. Unlike the thermoelectric device, TCEC works in the isothermal operation, indicating that no extra energy is required to maintain the temperature difference. Basically, the total thermal energy Qh needed comes from two parts: one is for the increase of temperature in device (step 2) and the other is the heat absorbed in high temperature for energy conversion (step 3). Given the mass ratio of each material, the specific heat (Cp) of the pouch cell was 0.685 J/gK. Therefore, Qh equals 52.4 J/g, and an efficiency of 3.05% can be achieved. The efficiency can be raised to ~4.76% under 50% heat recuperation.
To further improve the conversion efficiency, one of the most promising ways is to decrease the significant energy loss caused by charge leakage. As shown in Figure 3D, the cell voltage rise of AC pouch cell was 58 mV in step 2, which is close to the calculated value of 59.95 mV (ΔV = αΔT). However, the significant voltage drop caused by charge leakage decreased the effective voltage rise to 41 mV. As seen in Figure 3E, the charge leakage also occurred during the isothermal discharging (step 3) because the amount of discharge in step 3 is less than the amount of charge transferred to the cell in step 1, causing a coulombic efficiency of ~65%. The ideal discharge curve should follow the red dash line; the yellow area represents energy loss. When the TCEC cell with both identical carbon electrodes is completely discharged at Tc, the base potentials of the positive (φTc+) and negative (φTc−) electrodes should be at the same value as their given self potential (φTc0), and thus the cell voltage Vcell = φTc+ − φTc− = 0. With external charging at the voltage of Vext at Tc (step 1), the base potential of the positive electrode increases to φTc+ = Vext/2, and that of the negative electrode decreases to φTc− = −Vext/2, resulting in a cell voltage Vcell ≈ Vext. When heating from Tc to Th (step 2) and discharging at Th (step 3), the Vcell increases as a result of CDLE but the temperature rise also enhances the charge leakage due to the self-discharge in the EDL, which is driven by two mechanisms. In the electrolyte, the ions tend to move away from the electrode to increase their solvation (Reszko-Zygmunt et al., 2005; Fletcher et al., 2010; Andreas, 2015). In the carbon electrode, the base potential of each charged electrode (φTc+, φTc−) tends to come back to their self potential (Brogioli, 2009; Brogioli et al., 2012). Our previous study shows that self potential is tunable by adjusting the concentration of strong acid groups on the carbon electrode. Therefore, to address the slow ion diffusion (Brogioli, 2009; Fletcher et al., 2010), ion desolvation (Levy et al., 2012; Bankura et al., 2013), and partial overlap of EDLs (Schaldach et al., 2004; Huang et al., 2008; Biesheuvel et al., 2014) in the complex geometry of the narrow pores in activated carbon during heating, we used few-layer MEG (Zheng et al., 2011; Zhai et al., 2014) and HNO3-treated MEG (N-MEG) as electrodes materials.
Figure 4A is the electrode base potential vs. the thermal potential change for the individual as-prepared MEG electrode. The measured data under different Vext can be fitted by GCS theory as a solid black curve (Brogioli, 2009; Brogioli et al., 2012; Hatzell et al., 2014) (Note: we only show the data points of Vext = 500 mV in Figure 4A.). For the identical electrode system using the MEG for both positive and negative electrodes, the green spot represents the self potential φTc0 of MEG electrode at Tc = 10°C, and the green squares (φTc+, φTc−) are the base potentials for the positive and negative charged MEG electrodes under the external voltage of 500 mV and their corresponding thermal potential change (φTc+, φTc−) after heating to Th = 65°C. As noted, the external charging dominates the electrode base potentials to φTc+ and φTc−, and thus the corresponding Δφ+ and Δφ− are determined along the GCS curve. The blue spot is the self potential of the MEG electrode treated with nitric acid for 12 h, which decreases to a less positive value (φTc0−) and roughly falls on the same GCS curve. By using HNO3-treated MEG as the negative electrode, the charge leakage in TCEC could be improved by operating in a smaller driving force between φTc− and φTc0− (blue arrow) than that between φTc− and φTc0 (green arrow). Figure 4B shows the charge–voltage cycle performed by a pouch cell using MEG and HNO3-treated MEG as positive and negative electrodes, respectively. The measured α is 1.32 mV/K (blue triangle, Figure 3B), which could generate a higher thermal-stimulated voltage increase than that of activate carbon pouch cell and obtain more net electricity of ~2.6 J/g. Therefore, the system achieves a high conversion efficiency of 3.95% without heat recuperation as the estimated Cp is 0.87 J/g. From the voltage vs. time plot shown in Figure 4C, we observe that the charge leakage can be improved with a more linear discharging curve, thus the coulombic efficiency was improved to ~80%.
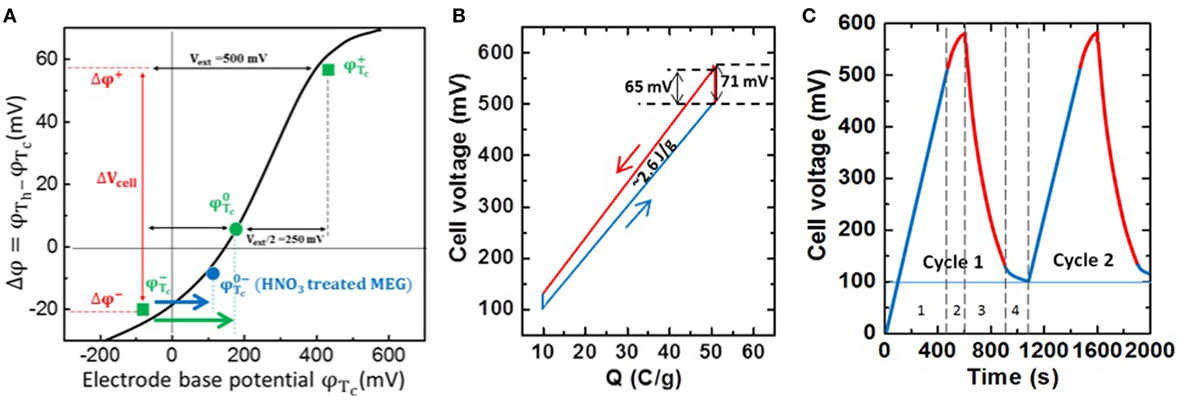
Figure 4. (A) Base potential of MEG electrode vs. thermal potential change (Tc = 10°C, Th = 65°C). (B) Charge–voltage cycle for the pouch cell using MEG (positive) and HNO3-treated MEG (negative) electrodes. (C) Cell voltage vs. time plot for first and second thermal cycles (t3/t1 ~ 0.8).
Conclusion
In summary, we tested TCEC on commercial supercapacitor, activated carbon-based supercapacitor and MEG-based supercapacitor. TCEC on commercial supercapacitor gave a low conversion efficiency (<1%), which resulted from the nonuniform heating on cylinder-type structure. In order to maximize the thermal voltage rise, and then subsequent discharge, we built up a homemade temperature control system and employed a two-electrode configuration cell based on activated carbon, which successfully enhanced the thermoelectric efficiency to a higher level of 3.05%. It was illustrated that the performance could be further improved as if we could decrease the energy loss resulted from the charge leakage. Self potential of MEG was tuned by nitric acid treatment. Pouch cell of MEG as anode and HNO3-treated MEG as cathode showed a larger temperature coefficient and a climbing energy conversion efficiency of 3.95% while TCEC on it had a better durability and stability with over 80% coulombic efficiency. This work proves that TCEC is a cost-effective electrochemical heat engine as it could use readily available carbon materials and operate without expensive ion-selective membranes. A TCEC is expected to have a faster cycle time than a TREC because the equilibration time to achieve a fully charged EDL and the CDLE response time are on a scale of minutes. Meanwhile, adjusting the concentration of strong acid group on the carbon electrode is proved to be an effectual way to increase the potential difference between the charged electrode and its self-potential, which provides opportunities for TCEC optimization.
A thermal cycle can be achieved with adequate mechanical design; for example, a heat wheel equipped with an electrochemical cell rotating between a hot and cold side, which could broaden the application of this technology in industry. Unlike temperature gradient technologies operating at low temperature differentials, the isothermal operation of a thermal cycle enables effective heat recuperation (50–70%) from the cooling process back to the heating process, which can considerably boost overall system efficiency.
Author Contributions
S-PF developed the expert ideas and supervised the project. XW and S-PF provided experimental data for the manuscript and wrote the manuscript.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Funding
This work was primarily supported by the General Research Fund under Award Number HKU 712213E and 17202314 (S-PF) from the Research Grants Council of Hong Kong Special Administrative Region, China. This work was also partially supported by the Strategic Research Theme on Clean Energy from the University of Hong Kong, and HKU-Zhejiang Institute of Research and Innovation (HKU-ZIRI).
References
Andreas, H. A. (2015). Self-discharge in electrochemical capacitors: a perspective article. J. Electrochem. Soc. 162, A5047–A5053. doi: 10.1149/2.0081505jes
Bankura, A., Carnevale, V., and Klein, M. L. (2013). Hydration structure of salt solutions from ab initio molecular dynamics. J. Chem. Phys. 138, 014501. doi:10.1063/1.4772761
Bell, L. E. (2008). Cooling, heating, generating power, and recovering waste heat with thermoelectric systems. Science 321, 1457–1461. doi:10.1126/science.1158899
Biesheuvel, P., Porada, S., Levi, M., and Bazant, M. (2014). Attractive forces in microporous carbon electrodes for capacitive deionization. J. Sol. St. Electrochem. 18, 1365–1376. doi:10.1007/s10008-014-2383-5
Brantut, J.-P., Grenier, C., Meineke, J., Stadler, D., Krinner, S., Kollath, C., et al. (2013). A thermoelectric heat engine with ultracold atoms. Science 342, 713–715. doi:10.1126/science.1242308
Brogioli, D. (2009). Extracting renewable energy from a salinity difference using a capacitor. Phys. Rev. Lett. 103, 058501. doi:10.1103/PhysRevLett.103.058501
Brogioli, D., Ziano, R., Rica, R., Salerno, D., Kozynchenko, O., Hamelers, H., et al. (2012). Exploiting the spontaneous potential of the electrodes used in the capacitive mixing technique for the extraction of energy from salinity difference. Energy Environ. Sci. 5, 9870–9880. doi:10.1039/c2ee23036d
Brogioli, D., Ziano, R., Rica, R., Salerno, D., and Mantegazza, F. (2013). Capacitive mixing for the extraction of energy from salinity differences: survey of experimental results and electrochemical models. J. Colloid Interface Sci. 407, 457–466. doi:10.1016/j.jcis.2013.06.050
Chapman, D. L. (1913). LI. A contribution to the theory of electrocapillarity. Lond. Edinburgh Dublin Philos. Mag. J. Sci. 25, 475–481. doi:10.1080/14786440408634187
Chu, S., and Majumdar, A. (2012). Opportunities and challenges for a sustainable energy future. Nature 488, 294. doi:10.1038/nature11475
Chum, H. L. (1981). Review of Thermally Regenerative Electrochemical Systems. Golden, CO: Solar Energy Research Institute.
Conway, B. E. (2013). Electrochemical Supercapacitors: Scientific Fundamentals and Technological Applications. Ottawa: Springer Science & Business Media.
DiSalvo, F. J. (1999). Thermoelectric cooling and power generation. Science 285, 703–706. doi:10.1126/science.285.5428.703
Feng, S.-P., Chang, Y.-H., Yang, J., Poudel, B., Yu, B., Ren, Z., et al. (2013). Reliable contact fabrication on nanostructured Bi 2 Te 3-based thermoelectric materials. Phys. Chem. Chem. Phys. 15, 6757–6762. doi:10.1039/c3cp50993a
Fletcher, S., Sillars, F., Carter, R., Cruden, A., Mirzaeian, M., Hudson, N., et al. (2010). The effects of temperature on the performance of electrochemical double layer capacitors. J. Power Sources 195, 7484–7488. doi:10.1016/j.jpowsour.2010.05.043
Frackowiak, E., and Beguin, F. (2001). Carbon materials for the electrochemical storage of energy in capacitors. Carbon N. Y. 39, 937–950. doi:10.1016/S0008-6223(00)00183-4
Goodenough, J. B., Abruna, H., and Buchanan, M. (2007). “Basic research needs for electrical energy storage,” in Report of the Basic Energy Sciences Workshop for Electrical Energy Storage. doi:10.2172/935429
Gouy, M. (1910). Sur la constitution de la charge électrique à la surface d’un électrolyte. J. Phys. Theor. Appl. 9, 457–468. doi:10.1051/jphystap:019100090045700
Hammond, R. H., and Risen, W. M. (1979). An electrochemical heat engine for direct solar energy conversion. Solar Energy 23, 443–449. doi:10.1016/0038-092X(79)90153-1
Härtel, A., Janssen, M., Samin, S., and van Roij, R. (2015a). Fundamental measure theory for the electric double layer: implications for blue-energy harvesting and water desalination. J. Phys. 27, 194129. doi:10.1088/0953-8984/27/19/194129
Härtel, A., Janssen, M., Weingarth, D., Presser, V., and van Roij, R. (2015b). Heat-to-current conversion of low-grade heat from a thermocapacitive cycle by supercapacitors. Energy Environ. Sci. 8, 2396–2401. doi:10.1039/C5EE01192B
Hatzell, M. C., Raju, M., Watson, V. J., Stack, A. G., van Duin, A. C., and Logan, B. E. (2014). Effect of strong acid functional groups on electrode rise potential in capacitive mixing by double layer expansion. Environ. Sci. Technol. 48, 14041–14048. doi:10.1021/es5043782
Hu, R., Cola, B. A., Haram, N., Barisci, J. N., Lee, S., Stoughton, S., et al. (2010). Harvesting waste thermal energy using a carbon-nanotube-based thermo-electrochemical cell. Nano Lett. 10, 838–846. doi:10.1021/nl903267n
Huang, J., Sumpter, B. G., and Meunier, V. (2008). Theoretical model for nanoporous carbon supercapacitors. Angew. Chem. Int. Ed. 47, 520–524. doi:10.1002/anie.200703864
Janssen, M., Härtel, A., and Van Roij, R. (2014). Boosting capacitive blue-energy and desalination devices with waste heat. Phys. Rev. Lett. 113, 268501. doi:10.1103/PhysRevLett.113.268501
Kraemer, D., Poudel, B., Feng, H.-P., Caylor, J. C., Yu, B., Yan, X., et al. (2011). High-performance flat-panel solar thermoelectric generators with high thermal concentration. Nat. Mater. 10, 532. doi:10.1038/nmat3013
Lee, S. W., Yang, Y., Lee, H.-W., Ghasemi, H., Kraemer, D., Chen, G., et al. (2014). An electrochemical system for efficiently harvesting low-grade heat energy. Nat. Commun. 5, 3942. doi:10.1038/ncomms4942
Levy, A., Andelman, D., and Orland, H. (2012). Dielectric constant of ionic solutions: a field-theory approach. Phys. Rev. Lett. 108, 227801. doi:10.1103/PhysRevLett.108.227801
López-García, J. J., Horno, J., and Grosse, C. (2011). Poisson–Boltzmann description of the electrical double layer including ion size effects. Langmuir 27, 13970–13974. doi:10.1021/la2025445
Meir, S., Stephanos, C., Geballe, T., and Mannhart, J. (2013). Highly-efficient thermoelectronic conversion of solar energy and heat into electric power. J. Renew. Sustain. Energy 5, 043127. doi:10.1063/1.4817730
Poudel, B., Hao, Q., Ma, Y., Lan, Y., Minnich, A., Yu, B., et al. (2008). High-thermoelectric performance of nanostructured bismuth antimony telluride bulk alloys. Science 320, 634–638. doi:10.1126/science.1156446
Quickenden, T., and Mua, Y. (1995). A review of power generation in aqueous thermogalvanic cells. J. Electrochem. Soc. 142, 3985–3994. doi:10.1149/1.2048446
Rattner, A. S., and Garimella, S. (2011). Energy harvesting, reuse and upgrade to reduce primary energy usage in the USA. Energy 36, 6172–6183. doi:10.1016/j.energy.2011.07.047
Reszko-Zygmunt, J., Sokołowski, S., Henderson, D., and Boda, D. (2005). Temperature dependence of the double layer capacitance for the restricted primitive model of an electrolyte solution from a density functional approach. J. Chem. Phys. 122, 084504. doi:10.1063/1.1850453
Rica, R., Ziano, R., Salerno, D., Mantegazza, F., and Brogioli, D. (2012). Thermodynamic relation between voltage-concentration dependence and salt adsorption in electrochemical cells. Phys. Rev. Lett. 109, 156103. doi:10.1103/PhysRevLett.109.156103
Rosi, F. (1968). Thermoelectricity and thermoelectric power generation. Solid State Electron. 11, 833–68. doi:10.1016/0038-1101(68)90104-4
Schaldach, C., Bourcier, W. L., Paul, P. H., and Wilson, W. (2004). Electrostatic potentials and fields in the vicinity of engineered nanostructures. J. Colloid Interface Sci. 275, 601–611. doi:10.1016/j.jcis.2004.02.092
Serth, R. W., and Lestina, T. (2014). Process Heat Transfer: Principles, Applications and Rules of Thumb. Oxford, UK: Academic Press.
Snyder, G. J., and Toberer, E. S. (2008). Complex thermoelectric materials. Nat. Mater. 7, 105–114. doi:10.1038/nmat2090
Stern, O. (1924). Zur theorie der elektrolytischen doppelschicht. Berichte der Bunsengesellschaft f elektrolytischen doppe 30, 508–516.
Stoller, M. D., and Ruoff, R. S. (2010). Best practice methods for determining an electrode material’s performance for ultracapacitors. Energy Environ. Sci. 3, 1294–1301. doi:10.1039/c0ee00074d
Vining, C. B. (2009). An inconvenient truth about thermoelectrics. Nat. Mater. 8, 83. doi:10.1038/nmat2361
Wessells, C. D., Huggins, R. A., and Cui, Y. (2011). Copper hexacyanoferrate battery electrodes with long cycle life and high power. Nat. Commun. 2, 550. doi:10.1038/ncomms1563
Yang, Y., Lee, S. W., Ghasemi, H., Loomis, J., Li, X., Kraemer, D., et al. (2014a). Charging-free electrochemical system for harvesting low-grade thermal energy. Proc. Natl. Acad. Sci. U.S.A. 111, 17011–17016. doi:10.1073/pnas.1415097111
Yang, Y., Loomis, J., Ghasemi, H., Lee, S. W., Wang, Y. J., Cui, Y., et al. (2014b). Membrane-free battery for harvesting low-grade thermal energy. Nano Lett. 14, 6578–6583. doi:10.1021/nl5032106
Zebarjadi, M., Esfarjani, K., Dresselhaus, M., Ren, Z., and Chen, G. (2012). Perspectives on thermoelectrics: from fundamentals to device applications. Energy Environ. Sci. 5, 5147–5162. doi:10.1039/C1EE02497C
Zhai, P., Chang, Y.-H., Huang, Y.-T., Wei, T.-C., Su, H., and Feng, S.-P. (2014). Water-soluble microwave-exfoliated graphene nanosheet/platinum nanoparticle composite and its application in dye-sensitized solar cells. Electrochim. Acta 132, 186–192. doi:10.1016/j.electacta.2014.03.145
Zhang, L. L., and Zhao, X. (2009). Carbon-based materials as supercapacitor electrodes. Chem. Soc. Rev. 38, 2520–2531. doi:10.1039/b813846j
Zheng, R., Gao, J., Wang, J., Feng, S.-P., Ohtani, H., Wang, J., et al. (2011). Thermal percolation in stable graphite suspensions. Nano Lett. 12, 188–192. doi:10.1021/nl203276y
Keywords: low-grade heat, electrochemical heat engine, thermoelectric, thermal cycle, supercapacitor
Citation: Wang X and Feng S-P (2017) Thermal Capacitive Electrochemical Cycle on Carbon-Based Supercapacitor for Converting Low-grade Heat to Electricity. Front. Mech. Eng. 3:20. doi: 10.3389/fmech.2017.00020
Received: 28 August 2017; Accepted: 09 November 2017;
Published: 30 November 2017
Edited by:
Tengfei Luo, University of Notre Dame, United StatesReviewed by:
Xinyan Huang, University of California, Berkeley, United StatesLiang Chen, Xi’an Jiaotong University, China
Copyright: © 2017 Wang and Feng. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Shien-Ping Feng, aHBmZW5nQGhrdS5oaw==
 Xun Wang
Xun Wang Shien-Ping Feng
Shien-Ping Feng