Adhesive Strength of Contacts of Rough Spheres

The adhesive contact between a parabolic indenter with superimposed roughness and an elastic half space is studied in the JKR-limit (infinitely small range of action of adhesive forces) using the boundary element method with mesh-dependent detachment criterion suggested in 2015. Three types of superimposed roughness are considered: one- and two-dimensional waviness and randomly rough roughness. It is shown that in the case of regular waviness, the character of adhesion is governed by the Johnson adhesion parameter. For our randomly rough surfaces a new adhesion parameter has been identified numerically, which uniquely determines the adhesive strength of the contact.

Introduction

It is well-known that neutral bodies attract each other by van der Waals forces. However, adhesive forces in macroscopic systems often are negligible. Kendall expressed this with his famous statement “solids are expected to adhere; the question is to explain why they do not, rather than why they do!” (Kendall, 2001). The reason for the weakness of adhesion in macroscopic contacts is the roughness of surfaces. It is the roughness which prevents intimate contact on the atomic scale (Fuller and Tabor, 1975; Luan and Robbins, 2005; Ciavarella, 2017). However, it was shown both theoretically and experimentally that roughness sometimes can even enhance adhesion. Briggs and Briscoe have observed that a small roughness increases the adhesion energy compared to the smooth surface in the pull-off experiment of smooth rubber against a Perspex cylinder, but large roughness can reduce the adhesion significantly (Briggs and Briscoe, 1977). The analysis of a sphere with axially-symmetrical waviness studied by Guduru and numerically by Wu also shows an increase in the adhesive force (Guduru, 2007; Wu, 2012).

The influence of simplified roughness in form of regular waviness on adhesion in the whole range of roughness amplitudes from “very rough” to “practically smooth” was studied by Johnson in 1995. He introduced a dimensionless parameter governing the adhesion behavior. He found that above a critical value of this “Johnson parameter,” surfaces jump into complete contact even at zero load (Johnson, 1995). This study was based on the solution of non-adhesive contact given by Westergaard (1939) and the Griffith idea of energy balance as used in the original Johnson-Kendall-Robert (JKR) theory for parabolic contacts (Johnson et al., 1971). In recent years a few attempts have been undertaken to generalize this work of Johnson. Afferrante et al. proposed an analytical solution for rough surfaces containing a series of superposed sinewaves defined by the Weierstrass function (Afferrante et al., 2015). Persson and Scaraggi used a DMT-type model (Derjaguin-Muller-Toporov) to study the effect of roughness on adhesion in DMT-limit (Persson and Scaraggi, 2014). Ciavarella proposed a simple approach for rough adhesive contact, the so-called bearing-area model (BAM) (Ciavarella, 2018a) and also an approximation in the JKR regime (Ciavarella, 2018b). Numerically, the adhesion of rough surfaces has been studied using molecular dynamics (Pastewka and Robbins, 2014, 2016), finite element method based on molecular dynamics (Eid et al., 2011), Boundary Element Method (BEM) (Carbone et al., 2009; Joe et al., 2017; Rey et al., 2017) and the method of non-linear boundary integral equations (Galanov, 2011).

In the present paper we numerically study contacts of parabolic bodies with superimposed roughness either in form of a regular waviness or multi-scale roughness. We restrict ourselves to the limiting case of very short ranged adhesive forces which we will call the JKR-limit, because the JKR theory uses exactly the same assumption. Application of the Boundary Element Method for simulation of adhesive contacts in the JKR limit was made possible in 2015 by means of a mesh-size dependent detachment criterion proposed by Pohrt and Popov (Pohrt and Popov, 2015). This numerical approach has been validated by comparison with existing analytical solutions including axisymmetric contacts (Popov et al., 2017), elliptic contacts (Li et al., 2018) and toroidal contacts (Argatov et al., 2016). The method was applied to solve a number of contact problems, such as brush-like structures (Li and Popov, 2018a,b) and flat-ended indenters with complicated face shapes (Popov et al., 2017). Recently this method was developed further to include functionally graded material and layered material (Li and Popov, 2017; Li et al., 2018). The present paper closes the gap in the classes of systems considered so far by considering adhesion of curved contacts with superimposed roughness—the problem which in some sense can be considered as the generic case of any real adhesive contact.

The structure of this paper is the following. In section Adhesive Contact of One- and Two-Dimensional Wavy Surface With Periodic Boundary Conditions we recapitulate the known analytical results for adhesive contact between a wavy surface (one- and two-dimensional waviness) and an elastic half space and reproduce them by numerical simulation. In section Adhesive Contact of a Sphere With a Two-Dimensional Wavy Roughness the adhesive contact of a curved surface with superimposed waviness is considered. We show that the character of adhesion in this case is essentially governed by the Johnson parameter. In section Adhesive Contact of a Parabolic Indenter With a Random Roughness contacts of curved surfaces with superimposed random roughness are investigated. It is noted that the numerical simulation in sections Adhesive Contact of a Sphere With a Two-Dimensional Wavy Roughness and Adhesive Contact of a Parabolic Indenter With a Random Roughness are carried out only for the pull-off (unloading). Section Conclusion gives conclusions on the above cases.

Adhesive Contact of One- and Two-Dimensional Wavy Surface With Periodic Boundary Conditions

One-Dimensional Waviness

Basic understanding of the role of roughness on adhesion has been achieved by Johnson (Johnson, 1995). He considered adhesion between a regular slightly wavy surface with amplitude h and wavelength λ:

$\begin{array}{ll}f\left(x\right)=h\left[1-\cos \left(2\pi x/\lambda \right)\right]& (1)\end{array}$

and an elastic half space with effective elastic modulus E* = E/(1 − ν²), where E is elastic modulus and ν is Poisson's ratio. The relation between the mean pressure p and the contact half-width a (within one wavelength λ) in a dimensionless form is given by

$\begin{array}{ll}p/p_{1D}^{*}={\sin }^2{\psi }_a-\alpha {\left(\tan {\psi }_a\right)}^{1/2},& (2)\end{array}$

where $p_{1D}^{*}=\pi E^{*}h/\lambda$ is the pressure needed for complete contact in the corresponding non-adhesive problem and ψ_a = πa/λ. The dimensionless parameter α is defined as

$\begin{array}{ll}\alpha ={\left(\frac{2\lambda \gamma }{{\pi }^2{h}^2{E}^{*}}\right)}^{1/2},& (3)\end{array}$

where γ is the work of adhesion per unit area. In the following, we will refer to α as the “Johnson parameter.”

The relation is shown in Figure 1 for different values of Johnson parameter α (solid lines). Numerically we simulated the same contact using the Boundary Element Method with periodic boundary conditions. Dependences of the normalized average pressure on the normalized half-width of the contact are represented with symbols. The subplot shows a 3D representation of a sample contact configuration. Numerical simulations were carried out under controlled approach of surfaces. This allows us to reach steady states which are not obtained in force-control. The reason is that when the force is controlled and increased from zero for α < 0.57, small values of πa/λ are not reached. Instead, the first touch of the surfaces leads to a sudden jump into the contact configuration corresponding to the intersection of the corresponding curve and the axis p = 0. Further increase of pressure leads to increase of the contact area until the maximum of the force is achieved. At further approach, the system jumps into complete contact. At the values of Johnson parameter α > 0.57 the maximum of the force is negative; this means that the system jumps into complete contact immediately at first touch.

FIGURE 1

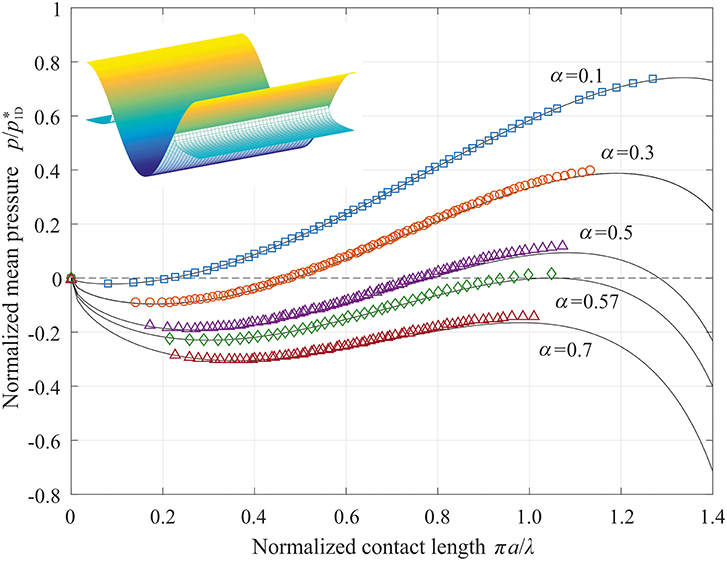
Figure 1. Dependence of the mean pressure on the contact half-width in “one-dimensional” adhesive contact. Solid lines show analytical solution and symbols present results of numerical simulation with BEM.

Two-Dimensional Waviness

In the paper by Johnson (1995) contacts with two-dimensional waviness of the form

$\begin{array}{ll}f\left(x,y\right)=h\left[1-\cos \left(2\pi x/\lambda \right)\text{ cos }\left(2\pi y/\lambda \right)\right]& (4)\end{array}$

were also briefly discussed. An analytical solution was given only for the extreme case of large load (approaching the complete contact) based on the asymptotic solution of non-adhesive contact (Johnson et al., 1985) while the non-contact area was assumed to be circular. This solution is also governed by the same Johnson parameter α as given in equation (3):

$\begin{array}{ll}p/p_{2D}^{*}=1-4/3·{\psi }_b^2-\pi /\left(2\sqrt{2}\right)\alpha ·{\left(1/{\psi }_b\right)}^{1/2}.& (5)\end{array}$

Here $p_{2D}^{*}=\sqrt{2}\pi E^{*}h/\lambda$ is the pressure needed for achieving complete contact in the non-adhesive problem and ψ_b = πb/λ. Note that here b is the radius of the non-contact area.

Dependencies of the average pressure on the normalized contact radius obtained by BEM are shown in Figure 2. The “contact radius” is formally defined as $a^{*}=\sqrt{A_{\text{con}}/\pi }$. At the full contact we have $a^{*}=\sqrt{{\lambda }^2/\pi }$ or $\pi a^{*}/\lambda =\sqrt{\pi }\approx 1.77$, so the value of 1.77 in x-axis of Figure 2 indicates the complete contact. The relation between load and contact radius for different parameter α is presented in Figure 2A. More details can be seen in Figure 2B, where the force-radius dependence and the contact configurations are shown for the case of a moderate value α = 0.4. As already pointed out by Johnson, adhesive contact with a two dimensional waviness is similar to that of one-dimensional waviness but has also some differences. One can see that there are two contact stages during detachment: From point A to C, adjacent contact areas are connected and the shape of the non-contact region resembles a square with rounded corners. The transition from point C to point D is not continuous. Instead, the contact drops from the connected state to the multi-area contact. The amplitude of the discontinuity depends on the value of α. For very small values of α, the curve is more connected (see Figure 2A at α = 0.1). In the opposite case of α larger than a critical value of ~0.57, a stable multi-contact configuration cannot be reached during detachment. Instead the contact is lost entirely. Please note that this value of 0.57 has different interpretation from that in one-dimensional contact.

FIGURE 2

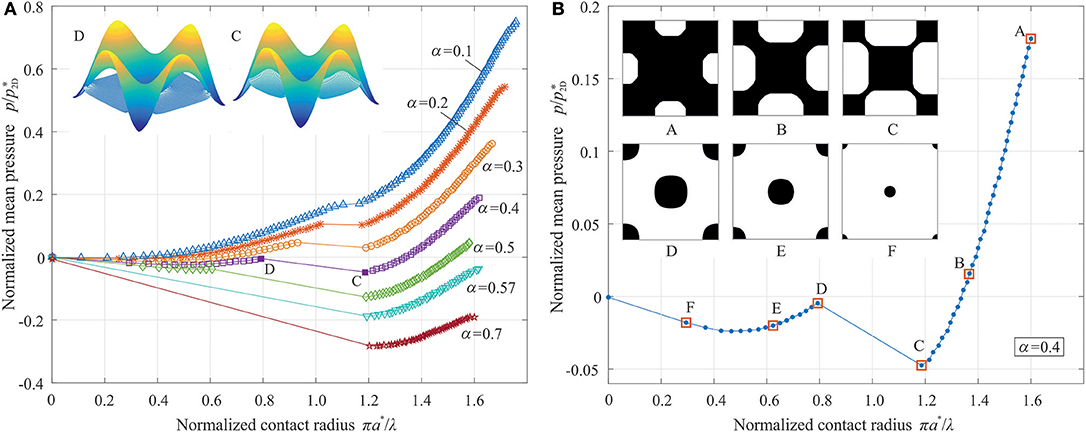
Figure 2. Dependence of the normalized average pressure on the normalized contact radius with two-dimensional waviness (A) for different parameters α; (B) Details of the non-continuous evolution of the contact configuration for α = 0.4.

Adhesive Contact of a Sphere With a Two-Dimensional Wavy Roughness

Consider a parabolic shape with a superimposed waviness:

$\begin{array}{ll}f\left(x,y\right)=\frac{x^2+y^2}{2R}+h\left[1-\cos \frac{2\pi x}{\lambda }\cos \frac{2\pi y}{\lambda }\right]& (6)\end{array}$

where R is the radius of curvature of the parabolic profile and other parameters are the same as defined in section Adhesive Contact of One- and Two-Dimensional Wavy Surface With Periodic Boundary Conditions. An example of such a surface is illustrated in Figure 3A. For a smooth sphere, the well-known analytical solution (JKR theory) for the load-displacement dependence is plotted in Figure 4A with solid line. Normal force and displacement are normalized by the critical values

$\begin{array}{ll}{F}_{\text{JKR}}=-\frac{3}{2}\pi \gamma R,& (7)\end{array}$

$\begin{array}{ll}{d}_{\text{JKR}}=-{\left(\frac{3{\pi }^2{\gamma }^{2}R}{64E^{*2}}\right)}^{1/3}.& (8)\end{array}$

FIGURE 3

Figure 3. Illustration of a regularly (A) and randomly (B) rough sphere in contact with an elastic half-space.

FIGURE 4

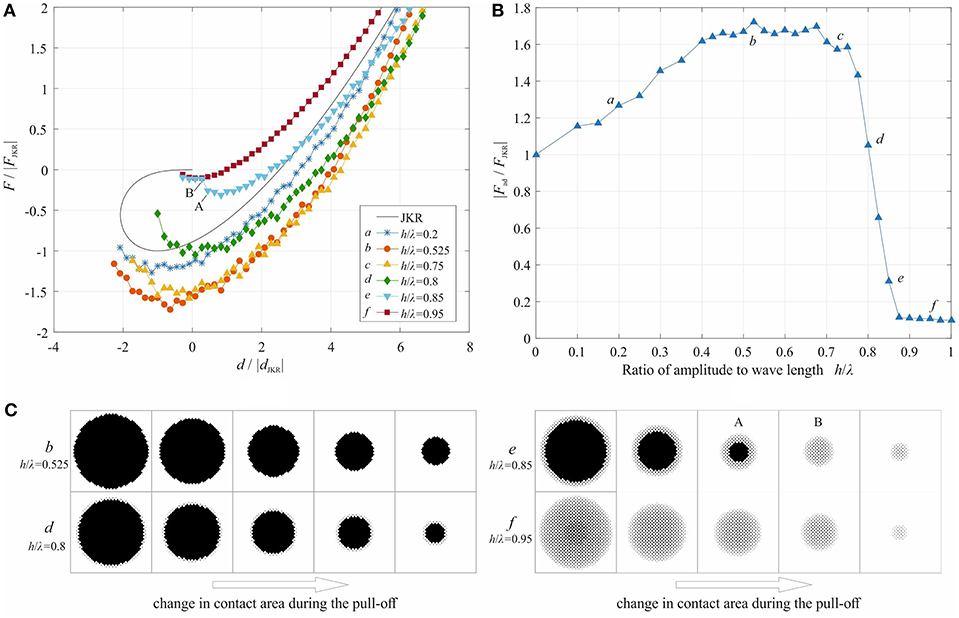
Figure 4. Adhesive contact of a rough sphere. (A) Load-displacement dependence for different amplitudes of waviness; (B) dependence of adhesive force on the amplitude of the waviness; (C) four exemplary evolutions of the contact area during pull-off.

Numerical simulation of the pull-off was again carried out using the BEM under the displacement-controlled condition. In this series of simulations we did not use periodic boundary conditions but free boundaries like in Hertz-theory. Due to the macroscopic curvature, a new dimensionless parameter λ/R appears in the present problem. We begin our consideration with an illustration of the influence of waviness on adhesion in the special case λ/R = 0.05, with the amplitudes of waviness h/λ varying from 0.2 to 1. The mesh size was chosen in such a way that one period of waviness has at least 42×42 grid points. The dependencies of the normal force on the displacement are shown in Figure 4A. To compare the results with the JKR solution, we focus on the adhesive force F_ad defined as the greatest tensile force corresponding to the minimum of the force-displacement relation. The absolute values of this force for different amplitudes of waviness are shown in Figure 4B. One can see that the adhesive force first increases with the amplitude of waviness and then drops to a very low value for amplitudes exceeding some threshold value.

Figure 4C shows a series of typical contact configurations during the pull-off for four increasing wave amplitudes, corresponding to the curves b, d, e, f in Figure 4A. The last picture always corresponds to the last stable configuration before complete detachment. For small enough roughness amplitude, as represented by the case b, the contact area represents basically a complete circle with a rough border. The maximum adhesive force is in this case larger than for the smooth sphere (JKR). From Figure 4B it can be seen that maximum enhancement is by the factor 1.7 for such situation. The case d is similar to b, but here the contact area is not continuous: there are some isolated points at the border around the rough circle. With increasing the amplitude of waviness, this effect becomes more pronounced, as exemplified with the case e: a circular area at the center is surrounded by a ring of separated points around the border. The pictures A and B in case e illustrate a transition between a state having a compact center contact to a cloud of point contacts. The two configurations are marked in Figure 4A: one can see the jump in the force from A to B. In case f, the contact always consists of unconnected points. The adhesive force in such a configuration is very small and further decreases when the amplitude of the waviness is increased (Figure 4B). There is an intuitive explanation of the described behavior. When the Johnson parameter for the chosen waviness is much larger than the critical one, the macroscopic profile can be considered as smooth. Only at the border there will be some perturbation as in the case b. In the opposite case of very small Johnson parameter, the contact occurs only at the summits of the waviness. Our hypothesis is thus that the Johnson parameter determines which one of the two scenarios will be realized.

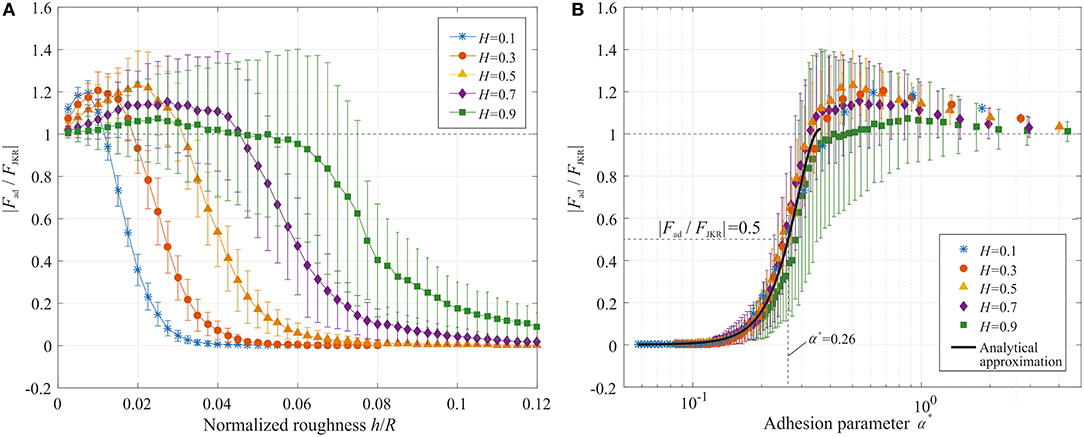
To prove this hypothesis, we replotted Figure 4B to show the dependence of the adhesive force on the Johnson parameter. For different values of the elastic modulus, surface energy, radius of the sphere and the wave length, the adhesive detachment shows a universal behavior: the maximum pull-off force expressed in terms of the JKR value indeed depends strongly on the Johnson parameter and only very weak on the normalized wavelength λ/R. At the critical value of the Johnson parameter α ≈ 0.24, the transition from the “compact area” to the “point cloud” solution occurs and the adhesive force drops drastically. For smaller Johnson parameter (α < 0.24), the adhesive force is very small and approximately proportional to the Johnson parameter, as shown in Figure 5B the encircled part corresponding to the area in Figure 5A.

FIGURE 5

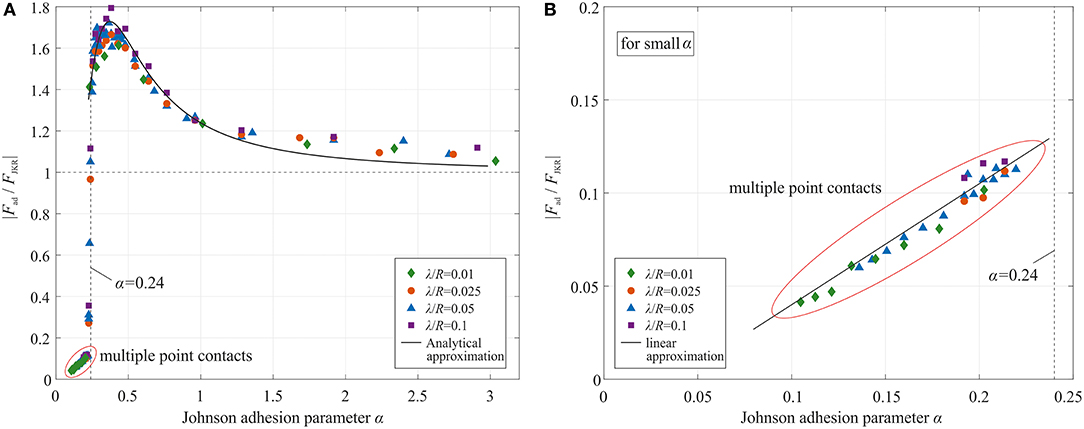
Figure 5. Dependence of adhesive force on the Johnson parameter (A) in a large range (B) for small Johnson parameter. Solid line shows the approximation following equation (9).

The dependence of adhesive force on the Johnson parameter can be approximated as

$\begin{array}{ll}\frac{F_{\text{ad}}}{F_{\text{JKR}}}\approx \Lambda \left(\alpha \right)=\{\begin{array}{cc}\frac{0.27}{{\alpha }^2}·\exp \left(-\frac{0.14}{{\alpha }^2}\right)+1,& \text{for }\alpha >0.24\\ 0.65·\alpha -0.025,& \text{for }\alpha <0.24\end{array}& (9)\end{array}$

The maximum tensile force during adhesive detachment of a sphere with superposed regular waviness can thus be expressed as

$\begin{array}{ll}{F}_{ad}\approx -\frac{3}{2}R\pi \gamma \Lambda \left(\alpha \right).& (10)\end{array}$

Adhesive Contact of a Parabolic Indenter With a Random Roughness

In this section we consider the adhesion of a rough sphere. On the one hand, it is widely accepted that roughness can significantly reduce adhesion. In Fuller and Tabor (1975), this was shown for a contact between a smooth sphere and a rough flat surface having asperities with Gaussian height distribution. In some cases, however, roughness can enhance adhesion. Early in 1977 the experimental investigation of a smooth rubber against a Perspex cylinder has shown that some small roughness can enhance the adhesion but the opposite is true for larger roughness (Briggs and Briscoe, 1977). The theoretical and numerical study of a sphere covered with only one regular waviness also showed an increase of adhesive force (Guduru, 2007; Wu, 2012). In Fuller (2011) it was found experimentally that adhesion in the rolling contact of a cylinder on an elastomer could substantially increase if the surfaces were rough. This enhancement was only observed when the elastomer was soft enough. The enhancement of adhesion was associated with the bulk viscoelastic effects of materials. Kesari et al. found that the surface roughness increases the energy hysteresis in the adhesion experiment of depth-dependent hysteresis using both AFM and nanoindentation apparatus and it was stated that the hysteresis is contributed by several factors and surface roughness could be an important one (Kesari et al., 2010). Medina and Dini found a similar increase of the adhesive pull-off force at low roughness for large values of Tabor parameter (= 5) in a numerical study. They used the Lennard-Jones potential for calculating van der Waals forces between elements (Medina and Dini, 2014). Recently an indentation test of spheres with micro-force tester showed that the highest pull-off force was found not on the smooth sample but that with micro roughness (Pepelyshev et al., 2018). It was argued that the increase of the contact area is the main cause for the increase pull-off force. In our numerical simulation, we also find the same behavior in the adhesive contact of rough spheres.

Consider a parabolic profile with curvature radius R superposed with a random roughness (Figure 3B). In the present paper, we use a roughness generator described in Pohrt and Li (2014). It produces a randomly rough surface by using the back Fourier transformation from a Fourier-density with a power-law dependency of it absolute value on the absolute value of the wave-vector, q, as well as vectors q₀, q₁ and the rms roughness h. The minimum and maximum random phases, while integration is performed between two “cut-off” wave vectors q₀, q₁. The exponent of the power-law dependency, H, (ranging from 0 to 1), is sometimes called the “Hurst exponent.” The roughness generated by the above mentioned procedure is unambiguously determined by the exponent H, the cut-off wave wave vectors which can be realized in a finite discrete system are given by q_min = 2π/L and q_max = π/Δx, where L is the length of simulation area and Δx is the mesh size. In the simulation, we assume L = R and put q₀ = q_min and q₁ = q_max. Note that the roughness produced in the described way does not necessarily represent real surfaces, which normally show strong phase correlation (Borodich et al., 2016). However, we consider the described generator as a way for producing well-defined comparable rough topography. We avoid calling these surfaces “fractal” but will further use for H the notation “Hurst exponent”

The pull-off was simulated for a number of increasing amplitudes of roughness and for different Hurst exponents. A few examples of force-distance curve are shown in Figure 6. One can see that, similarly to the case in section Adhesive Contact of a Sphere With a Two-Dimensional Wavy Roughness, small roughness leads to an increase of the adhesive force. Further increase of roughness reduces the force of adhesion. This behavior can be observed more clearly in Figure 7A, where the average values of pull-off force for 15 realizations of rough surfaces are shown as well as the corresponding standard deviations. The phenomenon of enhanced adhesion is observed for small Hurst exponents from 0.1 to 0.5, but not always for large Hurst exponent 0.7 and 0.9: the pull-off force for some rough surfaces with H = 0.7 or 0.9 decreases with roughness. In direct comparison it can be seen that surfaces with higher Hurst exponent have generally a wider range of roughness for which the adhesive force is enhanced. Results presented in Figure 7A suggest that there is no critical value of the Hurst exponent.

FIGURE 6

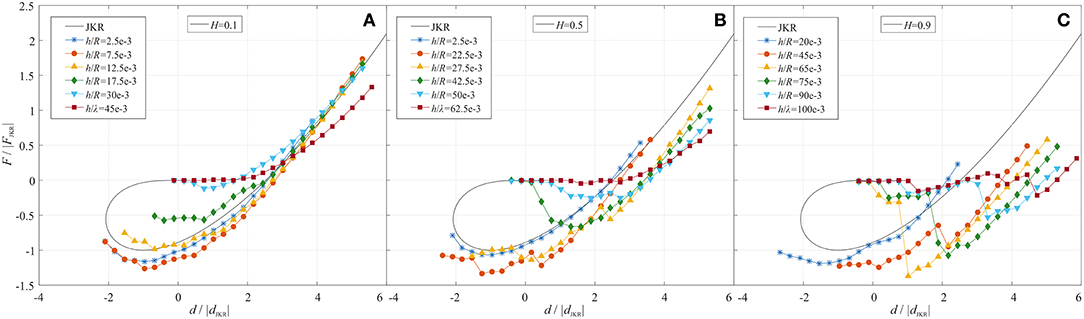
Figure 6. Force-distance curves for different roughnesses and Hurst exponents (A) H = 0.1; (B) H = 0.5; (C) H = 0.9.

FIGURE 7

Figure 7. Dependence of adhesive force on (A) roughness and (B) adhesion parameter α*.

As we have seen in sections Adhesive Contact of One- and Two-Dimensional Wavy Surface With Periodic Boundary Conditions and Adhesive Contact of a Sphere With a Two-Dimensional Wavy Roughness, the main governing parameter for adhesion of wavy surfaces is the Johnson parameter. In the case of randomly rough surfaces, this parameter cannot be determined from the waviness because the roughness is a superposition of a large number of waves with various amplitudes. If any, a series of Johnson parameters for different scales would have to be defined. If a single governing parameter similar to the Johnson parameter does exist in this case, it may depend on all material and geometric parameters of the contact problem: elastic modulus E*, surface energy γ, surface roughness h, Hurst exponent H and cutoff wave vectors q₀ and q₁. Based on the results presented in Figure 7A we suggest the following definition for an “adhesion parameter” of this kind of rough surfaces:

$\begin{array}{ll}{\alpha }^{*}={\left(\frac{4\gamma q_1^{0.8H-1}}{\pi E^{*}{h}^2{q}_0^{0.8H}}\right)}^{1/2}.& (11)\end{array}$

Note that if there is only one wave vector q₀ = q₁, equation (11) reduces to the original Johnson parameter equation (3). When the force of adhesion is plotted as function of α*, all results collapse to a single dependency shown in Figure 7B.

Different from the case of regular waviness in section Adhesive Contact of a Sphere With a Two-Dimensional Wavy Roughness, the pull-off force here doesn't drop dramatically at some critical value apparently, so we give an analysis of the relation of pull-off force and the adhesion parameter in this transition region. It is found that the following Gaussian-type expression gives a good approximation:

$\begin{array}{ll}\left|\frac{F_{\text{ad}}}{F_{\text{JKR}}}\right|\approx {\Lambda }^{*}\left({\alpha }^{*}\right)=1.023·\exp \left(-\frac{{\left({\alpha }^{*}-0.3619\right)}^2}{{0.1188}^2}\right).& (12)\end{array}$

It covers the range from very low force |F_ad/F_JKR| ≈ 0 transiting to the value |F_ad/F_JKR| ≈ 1 for α* = 0.344. In the range for larger α*, enhanced adhesion is not always observed for large Hurst exponents, so an analytical approximation is not given in this study. Furthermore, there is not a clear critical value of α* as in the case of regular waviness, therefore we give here only a value of adhesion parameter α* = 0.26 for |F_ad/F_JKR| ≈ 0.5.

Figure 8 presents details of contact configurations corresponding to numerical results presented in Figure 6 and Figure 7. For each Hurst exponent, three values of h are shown, related to their effect on the obtained adhesive force: In the left column of Figure 8, the amplitude of roughness is small and corresponds to the maximum of the adhesive force (see Figure 7), the second column represents intermediate roughness with |F_ad/F_JKR| ≈ 0.8. In the third column, a large roughness value is chosen with |F_ad/F_JKR| < 0.1. If the roughness is small enough, the contact area is almost compact. This is particularly pronounced for large H and small h.

FIGURE 8

Figure 8. Series of contact configurations during the pull-off process.

Conclusion

The adhesive detachment of curved surfaces with two-dimensional waviness from an elastic half space was numerically simulated using the boundary element method. We found that waviness can both increase and decrease the adhesive force compared to the smooth JKR solution. The deviation from JKR behavior depends mainly on the unmodified Johnson adhesion parameter α. At some critical value a ≈ 0.24, a transition occurs from a compact contact with rough boundary to a contact consisting of multiple separated contact spots and the obtained tensile force is reduced significantly.

In the case of added random roughness, the simulation was carried out for different Hurst exponents and amplitudes of roughness. In all cases we observed that the adhesive force at small roughness amplitudes is increased. For roughness amplitudes above some critical value, the adhesion is decreased significantly. This observation is in agreement with experiments, such as those conducted by Briggs and Briscoe (1977). For the investigated class of randomly rough surfaces, we identified an adhesive parameter determining the force of adhesion.

Author Contributions

VP and RP conceived the study. VP carried out analytical analysis. QL carried out numerical simulations. All authors drafted and reviewed the manuscript.

Funding

Authors acknowledge financial support of the Deutsche Forschungsgemeinschaft (DFG PO 810-55-1) and the German ministry for research and education BMBF, grant No. 13NKE011A. This research was also partially supported by the Tomsk State University competitiveness improvement program.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Afferrante, L., Clavarella, M., and Demelio, G. (2015). Adhesive contact of the weierstrassprofile. Proc. R. Soc. A Math. Phys. Eng. Sci. 471, 387–405. doi: 10.1098/rspa.2015.0248

CrossRef Full Text

Argatov, I., Li, Q., Pohrt, R., and Popov, V. L. (2016). Johnson-kendall-roberts adhesive contact for a toroidal indenter. Proc. R. Soc. London A Math. Phys. Eng. Sci. 472:20160218. doi: 10.1098/rspa.2016.0218

PubMed Abstract | CrossRef Full Text | Google Scholar

Borodich, F. M., Pepelyshev, A., and Savencu, O. (2016). Statistical approaches to description of rough engineering surfaces at nano and microscales. Tribol. Int. 103, 197–207. doi: 10.1016/j.triboint.2016.06.043

CrossRef Full Text | Google Scholar

Briggs, G. A. D., and Briscoe, B. J. (1977). The effect of surface topography on the adhesion of elastic solids. J. Phys. D Appl. Phys. 10, 2453–2466. doi: 10.1088/0022-3727/10/18/010

CrossRef Full Text | Google Scholar

Carbone, G., Scaraggi, M., and Tartaglino, U. (2009). Adhesive contact of rough surfaces: Comparison between numerical calculations and analytical theories. Eur. Phys. J. E 30, 65–74. doi: 10.1140/epje/i2009-10508-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Ciavarella, M. (2017). On pastewka and robbins' criterion for macroscopic adhesion of rough surfaces. J. Tribol. 139:031404. doi: 10.1115/1.4034530

CrossRef Full Text | Google Scholar

Ciavarella, M. (2018a). A very simple estimate of adhesion of hard solids with rough surfaces based on a bearing area model. Meccanica 53, 241–250. doi: 10.1007/s11012-017-0701-6

CrossRef Full Text | Google Scholar

Ciavarella, M. (2018b). An approximate JKR solution for a general contact, including rough contacts. J. Mech. Phys. Solids 114, 209–218. doi: 10.1016/j.jmps.2018.03.005

CrossRef Full Text | Google Scholar

Eid, H., Adams, G. G., Mcgruer, N. E., Fortini, A., Buldyrev, S., and Srolovitz, D. (2011). A combined molecular dynamics and finite element analysis of contact and adhesion of a rough sphere and a flat surface. Tribol. Trans. 54, 920–928. doi: 10.1080/10402004.2011.615638

CrossRef Full Text | Google Scholar

Fuller, K. (2011). Effect of surface roughness on the adhesion of elastomers to hard surfaces. Mater. Sci. Forum 662, 39–51. doi: 10.4028/www.scientific.net/MSF.662.39

CrossRef Full Text | Google Scholar

Fuller, K. N. G., and Tabor, D. (1975). The effect of surface roughness on the adhesion of elastic solids. Proc. R. Soc. A Math. Phys. Eng. Sci. 345, 327–342. doi: 10.1098/rspa.1975.0138

CrossRef Full Text | Google Scholar

Galanov, B. A. (2011). Models of adhesive contact between rough elastic bodies. Int. J. Mech. Sci. 53, 968–977. doi: 10.1016/j.ijmecsci.2011.07.010

CrossRef Full Text | Google Scholar

Guduru, P. R. (2007). Detachment of a rigid solid from an elastic wavy surface: theory. J. Mech. Phys. Solids 55, 445–472. doi: 10.1016/j.jmps.2006.09.004

CrossRef Full Text | Google Scholar

Joe, J., Scaraggi, M., and Barber, J. R. (2017). Effect of fine-scale roughness on the tractions between contacting bodies. Tribol. Int. 111, 52–56. doi: 10.1016/j.triboint.2017.03.001

CrossRef Full Text | Google Scholar

Johnson, K. L. (1995). The adhesion of two elastic bodies with slightly wavy surfaces. Int. J. Solids Struct. 32, 423–430. doi: 10.1016/0020-7683(94)00111-9

CrossRef Full Text | Google Scholar

Johnson, K. L., Greenwood, J. A., and Higginson, J. G. (1985). The contact of elastic regular wavy surfaces. Int. J. Mech. Sci. 27, 383–396. doi: 10.1016/0020-7403(85)90029-3

CrossRef Full Text | Google Scholar

Johnson, K. L., Kendall, K., and Roberts, A. D. (1971). Surface energy and the contact of elastic solids. Proc. R. Soc. London A. 324, 301–313. doi: 10.1098/rspa.1971.0141

CrossRef Full Text | Google Scholar

Kendall, K. (2001). Molecular Adhesion and Its Applications. New York, NY: Springer US.

Google Scholar

Kesari, H., Doll, J. C., Pruitt, B. L., Cai, W., and Lew, A. J. (2010). Role of surface roughness in hysteresis during adhesive elastic contact. Philos. Mag. Lett. 90, 891–902. doi: 10.1080/09500839.2010.521204

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, Q., Argatov, I., and Popov, V. L. (2018). Onset of detachment in adhesive contact of an elastic half-space and flat-ended punches with non-circular shape: analytic estimates and comparison with numeric analysis. J. Phys. D. Appl. Phys. 51:145601. doi: 10.1088/1361-6463/aab28b

CrossRef Full Text | Google Scholar

Li, Q., Pohrt, R., Lyashenko, I. A., and Popov, V. L. (2018). Boundary element method for non-adhesive and adhesive contacts of a coated elastic half-space. arXiv:1807.01885.

Google Scholar

Li, Q., and Popov, V. L. (2017). Boundary element method for normal non-adhesive and adhesive contacts of power-law graded elastic materials. Comput. Mech. 61, 319–329. doi: 10.1007/s00466-017-1461-9

CrossRef Full Text | Google Scholar

Li, Q., and Popov, V. L. (2018a). Adhesive force of flat indenters with brush-structure. Facta Univ. Ser. Mech. Eng. 16, 1–8. doi: 10.22190/FUME171220005L

CrossRef Full Text | Google Scholar

Li, Q., and Popov, V. L. (2018b). Adhesive contact of rough brushes. Beilstein J. Nanotechnol. 9, 2405–2412. doi: 10.3762/bjnano.9.225

PubMed Abstract | CrossRef Full Text | Google Scholar

Luan, B., and Robbins, M. O. (2005). The breakdown of continuum models for mechanical contacts. Nature 435, 929–932. doi: 10.1038/nature03700

PubMed Abstract | CrossRef Full Text | Google Scholar

Medina, S., and Dini, D. (2014). A numerical model for the deterministic analysis of adhesive rough contacts down to the nano-scale. Int. J. Solids Struct. 51, 2620–2632. doi: 10.1016/j.ijsolstr.2014.03.033

CrossRef Full Text | Google Scholar

Pastewka, L., and Robbins, M. O. (2014). Contact between rough surfaces and a criterion for macroscopic adhesion. Proc. Natl. Acad. Sci. U.S.A. 111, 3298–3303. doi: 10.1073/pnas.1320846111

PubMed Abstract | CrossRef Full Text | Google Scholar

Pastewka, L., and Robbins, M. O. (2016). Contact area of rough spheres: large scale simulations and simple scaling laws. Appl. Phys. Lett. 108:221601. doi: 10.1063/1.4950802.

CrossRef Full Text | Google Scholar

Pepelyshev, A., Borodich, F. M., Galanov, B. A., Gorb, E. V., and Gorb, S. N. (2018). Adhesion of soft materials to rough surfaces: experimental studies, statistical analysis and modelling. Coatings 8:350. doi: 10.3390/coatings8100350

CrossRef Full Text | Google Scholar

Persson, B. N., and Scaraggi, M. (2014). Theory of adhesion: role of surface roughness. J. Chem. Phys. 141:124701. doi: 10.1063/1.4895789

PubMed Abstract | CrossRef Full Text | Google Scholar

Pohrt, R., and Li, Q. (2014). Complete boundary element formulation for normal and tangential contact problems. Phys. Mesomechan. 17, 334–340. doi: 10.1134/s1029959914040109

CrossRef Full Text | Google Scholar

Pohrt, R., and Popov, V. L. (2015). Adhesive contact simulation of elastic solids using local mesh-dependent detachment criterion in boundary elements method. Facta Univ. Ser. Mech. Eng. 13, 3–10.

Google Scholar

Popov, V. L., Pohrt, R., and Li, Q. (2017). Strength of adhesive contacts: influence of contact geometry and material gradients. Friction 5, 308–325. doi: 10.1007/s40544-017-0177-3

CrossRef Full Text | Google Scholar

Rey, V., Anciaux, G., and Molinari, J. F. (2017). Normal adhesive contact on rough surfaces: efficient algorithm for FFT-based BEM resolution. Comput. Mech. 60, 69–81. doi: 10.1007/s00466-017-1392-5

CrossRef Full Text | Google Scholar

Westergaard, H. M. W. (1939). Bearing pressures and cracks. J. Appl. Mech. 6, 49–53.

Google Scholar

Wu, J. J. (2012). Numerical simulation of the adhesive contact between a slightly wavy surface and a half-space. J. Adhes. Sci. Technol. 26, 331–351. doi: 10.1163/016942411X576527

CrossRef Full Text | Google Scholar