Are There Limits to Superlubricity of Graphene in Hard, Rough Contacts?

Yes, there are. They result from the splitting of a large correlated contact into many small patches. When the lubricant consists of thin solid sheets, like graphene, the patches are expected to act independently from each other. Crude estimates for the friction forces between hard, stiff solids with randomly rough surfaces are given, which apply to surfaces with Hurst roughness exponents H > 0.5. The estimates are obtained by combining realistic contact-patch-size distributions with friction-load relations deduced for isolated contact patches. The analysis reveals that load is carried predominantly by large patches, while most frictional forces stem from small contact patches. Low friction is favored when the root-mean-square height gradients are small, while a large roll-off wavelength and thus large root-mean-square roughness is predicted to lead to small friction. Moreover, friction is found to increase sublinearly with load in a nominally flat, structurally lubric contact.

1. Introduction

When two solids are pressed against each other, surface atoms experience large normal and lateral forces from the counterbody in the true contact points. While normal forces on atoms in the top layer are, for the most part, unidirectional with minor relative fluctuations, lateral forces are expected to quickly change sign on small scales (Hirano and Shinjo, 1990; Shinjo and Hirano, 1993), because atoms are (statistically) pushed as many times to the left as to the right. If this expectation were generally true, solid friction would be generally super small. However, plastic deformation, e.g., in the form of dislocations that are nucleated by corner-stress concentrations (Sørensen et al., 1996; Sharp et al., 2016) or by strong interfacial interactions (Dietzel et al., 2017) but also the presence of loosely bonded atoms (lubricant, airborne contamination, etc.) (He et al., 1999; Dietzel et al., 2008) can lead to a systematic interlocking of solids and thereby to significant interfacial shear stresses and thus noticeable friction during sliding. Significant friction can also arise when two solids with identical lattice spacings are perfectly aligned with each other or when the solids happen to be one-dimensional (Aubry, 1983), or, in some other exotic situation that may interest some physicists (Müser et al., 2003) but does not relate to applications.

Real solids happen to be three-dimensional and their surfaces tend to be chemically passivated. Under these circumstances, simulations of flat, clean, crystalline, and amorphous model systems (Hirano and Shinjo, 1990; Müser et al., 2001; Verhoeven et al., 2004; Dietzel et al., 2018), scaling arguments (Müser et al., 2001) and even experiments on small antimony particles adsorbed on graphite (Dietzel et al., 2008, 2013, 2017) show that friction can be a sublinear function of the contact area. In this case, the ratio of the (static) shear force and the normal force would disappear in the thermodynamic or macroscopic limit. The effect has been called structural lubricity (Müser, 2004). It is revealed most prominently by graphite flakes rotated against a graphite substrate (Dienwiebel et al., 2004) but also by misoriented MoS₂ transfer films (Martin et al., 1993).

Structural lubricity is a special form of superlubricity (Baykara et al., 2018). The latter term only implies friction coefficients below 0.01, irrespective of its molecular origin (Martin and Erdemir, 2018). Soft-matter systems, in which a liquid lubricant remains in the contact, such as in hydrogels or solvated polymer brushes, may have tiny friction coefficients (Lee and Spencer, 2008; Martin and Erdemir, 2018) but are not addressed in this work.

The critical question to be addressed for flat, clean interfaces is whether—or more precisely to what contact length (Sharp et al., 2016)—do elastic restoring forces dominate the interfacial deformation forces so that multistability is avoided? Multistability means that different microscopic equilibrium configurations are possible for identical macroscopic set-ups. It is a necessary condition for hysteresis at small velocities and thus for Coulomb friction (no or weak dependence of friction on the sliding velocity) to occur, as explained so beautifully in Prandtl's work on the origin of friction (Prandtl, 1928; Popov and Gray, 2012). Simple scaling arguments (on static friction) suggest that elastic restoring forces should keep the upper hand in contacts between three-dimensional crystals and that there is a tie when one or both solids are amorphous (Müser, 2004). Even if corrections to these simple scaling laws might always turn the interfacial interactions into the winner (Sharp et al., 2016), friction forces should remain extremely small, because the domains moving as a correlated, effectively rigid unit would supposedly be extremely large. In fact, Sharp et al. (2016) found that the (kinetic) friction between a circular disk with a flat surface and an essentially infinite substrate dropped exponentially with the ratio of the shear modulus G and the local maximum traction τ_max. Whenever G is given by relatively strong covalent or metallic bonds but τ_max results from weak van-der-Waals interactions, friction forces can remain extremely small.

The situation is sensitive to the dimension of the objects (Shinjo and Hirano, 1993; Müser, 2004), because one-dimensional solids become effectively softer at large scales, while three-dimensional objects become stiffer. This is ultimately at the root for elasticity to “outperform” interfacial interactions up to large scales and thereby to allow for superlubricity of three-dimensional solids. In contrast, one-dimensional chains are rather prone to elastic instabilities (Aubry, 1983), while the onset of (local) elastic instabilities in more highly-dimensional objects should almost unavoidably induce non-elastic deformations (Hammerberg et al., 1998; Müser, 2001). This conclusion is inline with the observation that wearless (Coulomb) friction with atomic-force microscope tips can generally only be observed with soft cantilevers (Socoliuc et al., 2004).

The symmetry of solids (amorphous vs. crystalline) in direct contact matters for static friction, because it determines how systematic lateral forces add up or cancel each other (Müser et al., 2001; Müser, 2004). Even the shape of contact patches and their orientation to a substrate can affect the static friction in this regard (de Wijn, 2012, 2014).

When assessing the effect of interfacial symmetry on structural lubricity, kinetic friction is more difficult to address than static friction, as a better geometric interlocking (and thus higher static friction) does not automatically lead to more or more intense instabilities (Müser et al., 2003). In fact, when a thin layer of weakly adsorbed molecules mediates the locking between solids, kinetic friction is expected to turn out substantially smaller for commensurate than for incommensurate surfaces, while the opposite is true for their static friction (Müser, 2002). Interestingly, the symmetry of the surfaces appears to be surprisingly irrelevant for kinetic friction when interlocking is due to the contact-induced generation of dislocations (Sharp et al., 2016).

Thus, if chemically passivated solids are hard enough to not deform plastically during contact, the only possible mechanism mediating a significant friction stress between solids across the interface is related to the presence of mobile atoms or molecules in the interface. Contaminants may induce a linear scaling of shear forces with contact area (He et al., 1999; Müser and Robbins, 2000; He and Robbins, 2001; Dietzel et al., 2008) and in fact, super low friction forces have first been reported to necessitate ultra-high vacuum (Martin et al., 1993; Dietzel et al., 2008). However, it recently turned out that contaminants (e.g., airborne molecules) do not have to act that way and that the concept of structural lubricity may persist even under ambient conditions (Cihan et al., 2016; Özoğul et al., 2017), for example, when the contaminants can easily glide past a smooth surface, as is the case for graphite.

Given the analysis of friction between flat solids, friction coefficients appear possible that might be even smaller than so-far reported experimental values near 10⁻³ for molybdenum disulfide (MoS₂) (Martin et al., 1993) or hydrogen-enriched diamond-like carbon coatings (Erdemir and Eryilmaz, 2014). However, the multi-scale roughness on almost any natural or technical surface induces interfacial stress distributions that are much more heterogeneous than those encountered in model systems (Persson, 2001, 2008; Campañá et al., 2008), such as graphene and flat antimony islands moving past graphite, or the plane-parallel walls that are routinely studied with molecular dynamics. Superlubricity is then suppressed even more strongly than in the case of circular disks (Sharp et al., 2016). Individual contact patches could act independently, so that the static friction force rather than the kinetic friction force of individual patches would need to be considered.

In this paper, an attempt is made to estimate the friction coefficient for situations, in which individual contact patches are too small for dislocations to be nucleated, while the separation between them is large enough so that they can act essentially independently. Solids separated by thin, solid lubricants should match this category. Within a contact patch, the lubricant's large in-plane stiffness makes it act like a rigid sheet. However, a lubricant sheet can bend rather easily outside contact patches (Lee et al., 2010). This allows it to minimize its energy in a given contact patch without being much constrained by the energy minimization in an adjacent contact patch, if the given sheet happens to extend over more than one contact patch. While in-plane, intra-bulk deformation might also add to the ability of graphite flakes to locally minimize their free energy, the pertinant transverse deflections of asperities are assumed to be negligibly small in comparison.

2. Theory

The following set-up, which is sketched in Figure 1, is considered in the theory: the substrate is treated as an infinitely stiff solid composed of discrete atoms. It is supposed to adhere weakly to a solid, two-dimensional lubricant, which is going to be called graphene, because graphene is the most appropriate material for the theoretical considerations pursued here. We will be predominantly concerned with estimating the maximum possible lateral forces between the stiff substrate and graphene. The layer separates the substrate from a rough, but elastically deformable counterface. Due to its compliance, the top layer is assumed to be able to accommodate the corrugation of graphene much better than the more rigid substrate, such that slip occurs between the substrate and graphene. None of the results identified hereafter would be affected if compliance or elasticity were divided up more evenly between the two solids in contact. However, the treatment would become rather cumbersome and thereby its simplicity be hidden.

FIGURE 1

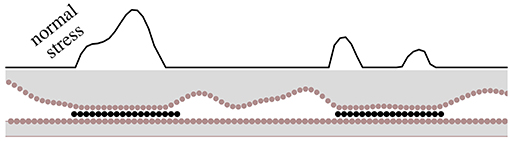
Figure 1. Schematic of the considered system: flat, rigid substrate separated from a rough, elastic indenter through two-dimensional solid lubricant particles. Normal forces on atoms can be estimated from continuum theory. Lateral forces fluctuate wildly from one atom to the next whenever the (projected) lattice constants of the solid bodies do not match closely.

Three main assumptions are made, which the author of this paper believes to be reasonable even if they are uncontrolled approximations. (i) The graphene sheets are so large that in general not more than one sheet resides within a connected contact patch. (ii) A given sheet can accommodate each microscale contact patch to essentially the best of its abilities without being affected by the geometry of adjacent patches, i.e., it can move back and forth small distances within a patch without having to pay significant elastic or surface energy for the associated deformation (in particular bending) between the patches. (iii) Within a contact patch, the in-plane bonds of graphene are too stiff to allow for elastic multistability. Free bending of the sheet is suppressed by the relatively large normal stresses within a patch, but possible, for example in-between the two stress bumps in the double asperity contact of Figure 1.

Last but not least, a model for the relation between local normal and lateral forces needs to be identified. Two extreme points of view can be taken toward this end. One extreme would be to claim that in contact, the lateral force of a substrate on a graphene atom can only depend on an atom's lateral position relative to the substrate irrespective of the normal force squeezing it against the substrate. This would automatically lead to a shear force independent of the normal force and perhaps be a model assumption favored by those who believe that microscopic shear stresses are independent of the microscopic normal stresses. This viewpoint indeed makes sense if adhesive forces exceed the external forces, e.g., in soft-matter systems or potentially also for flat solids moving under their own adhesive force over a surface. The other extreme view would be to treat the interactions between chemically passivated solids in zones of high pressures within a hard-disk picture. In this case the determination of the relation between normal and shear forces reduces to a geometrical exercise, whose result is that the tangential force is the tangent of an effective slope times the normal force. The same relation is obtained in the case of short-range repulsion and large contact pressures (Müser, 2008).

To incorporate the two just-discussed limits, the following (interfacial) lateral force component f_nx of atom n is assumed

$\begin{array}{ll}{f}_{nx}=u_n·{\mu }_{\text{m}}·\left(f_{nz}+f_z^{\text{off}}\right),& (1)\end{array}$

when the atom is squeezed at a random lateral position with a normal force f_nz against a rigid substrate, while $f_z^{\text{off}}$ invokes an additional offset to the lateral force, which can be due to adhesion. Here μ_m can be interpreted as a microscopic friction coefficient (which would be the static friction coefficient for commensurate surfaces), while u_n can be treated as a random number of zero mean distributed on (−1,1) for non-commensurate surfaces. In a first approximation, u_n can be treated as uniformly distributed. In section 2.2, we show that a more realistic distribution does not lead to relevant changes of the presented treatment.

Determining a reasonable value for μ_m is certainly more important than reflecting the correct distribution function of u_n. The classical hard-sphere value for μ_m is close to 0.3, which is also obtained for Lennard-Jones atoms moving past Lennard-Jones systems. The graphene bond, however, is relative strong while the bond length is relatively short. This leads to a reduction of μ_m, which is estimated to be 0.1 from a set of small simulation runs of various atoms sliding over graphite.

Estimating a net friction force from Equation (1) can be broken up into three steps. First, the distribution of contact patch size needs to be identified. Second, an expression for the rms-lateral force in a contact patch of size A carrying a load L needs to be found. Third, the results from the first two steps need to be merged and ballpark estimates for materials coefficient be made.

Since the main target of this paper is the analysis of rough, stiff contacts, adhesion is assumed to be small enough to barely affect the contact-patch statistics, i.e., adhesion should be small enough so that in the relevant load range the proportionality coefficient between true contact area and load is not increased by more than order 10% compared to the adhesion-free case. However, adhesion will be included in as far as that adhesive effects can increase the rms lateral force of a patch of a given size A. Moreover, it will be assumed that the normal pressure is small enough for the relative contact area to be much less than unity but sufficiently large for more than two or three meso-scale asperities to be in contact so that a linear dependence of the real contact area on load is a good approximation (Pastewka et al., 2013).

2.1. Contact-Patch Statistics

Many surfaces in nature and technology can be described as being randomly rough. The most common characterization is in terms of their height spectrum C(q) (Persson, 2014), which is essentially defined with four numbers, that is, the Hurst roughness exponent H, the short wavelength cutoff λ_s, the roll-off wavelength λ_r, and the spectrum at either one of the two wavelengths, or, alternatively, the root-mean-square height gradient ḡ. The part of the spectrum, which is the most relevant to this work, is the so-called self-affine branch, on which C(q) is proportional to q^−2·(1+H), i.e., for λ_s < 2π/q ≤ λ_r, where q denotes the magnitude of a given wavevector.

In addition to the four numbers needed to define C(q), it also matters to some degree if the transition from self-affine scaling to the roll-off regime is smooth or abrupt. The findings for the contact-patch size distribution n(A) summarized in this section are predominantly based on computer simulations (Müser and Wang, 2018) using the more realistic smooth transition (Palasantzas, 1993; Jacobs et al., 2017).

Computer simulations of continuum models for surfaces reveal three scaling regimes for the n(A) dependence. At small A, n(A) is approximately constant (Campañá, 2008), up to a small-scale cross-over area of Müser and Wang (2018)

$\begin{array}{ll}{A}_{\text{s}}\approx \frac{3\pi (2-H)}{16{\kappa }^2(1-H)}{\lambda }_{\text{s}}^2,& (2)\end{array}$

where κ is the proportionality coefficient relating the true relative contact area a_r and the mean macroscopic pressure p₀ via

$\begin{array}{ll}{a}_{\text{r}}=\frac{\kappa p_0}{E^{*}\overline{g}}.& (3)\end{array}$

The value of κ turns out close to two for typical values of Hurst exponents. Thus, if the generic value of H = 0.8 is used, A_s turns out close to λ_s.

Individual contact patches of size A < A_s show a relation between contact area and load similar to that of Hertzian contacts. Note, however, that the identification of this scaling regime necessitates the contact mechanics treatment to use discretizations that are much finer than λ_s. Real surfaces appear to show self-affine scaling of the height topography almost down to the smallest measurable scales, i.e., even down to the nanometer scale (Jacobs et al., 2017). It could be argued that λ_s was only introduced as a means to have a well-defined continuum model for contact mechanics, in which contact patches are true areas rather than isolated points. Because of the self-affine branch extending almost to atomic scales, it is doubtful that the small-A scaling regime exists in reality. In fact, when the self-affine scaling was taken down to (twice) the discretization length, a Hertzian scaling regime was not identified (Hyun et al., 2004). For this reason, but also because the net load carried by the (hypothetical) quasi-Hertzian patches is minuscule and even more importantly because thermal activation most certainly assists the sliding motion in sub-nanometer scale contacts, the effect of these ultra-small patches on both friction and normal force will be ignored. Instead, it will be assumed that a contact area of A > A_min is needed to convey a (quasi-) static shear force in a given contact patch, where A_min should be larger but not much larger than atomic dimensions. In the following, A_min will be set equal to the (hypothetical) A_s and estimated to be of order 1 nm².

The distribution of medium- and large patches was observed to obey (Müser and Wang, 2018)

$\begin{array}{ll}n(A)=n(A_{\text{ref}}){\left(\frac{A_{\text{ref}}}{A}\right)}^{2-H/2}{e}^{-(A-A_{\text{ref}})/A_{\text{max}}},& (4)\end{array}$

where A_ref is a reference patch size on the self-affine scaling branch and A_max is a characteristic (maximum) patch size. Thus, the probability for patch areas exceeding A_max is suppressed exponentially. To keep the closed-form mathematical description simple, the exponential factor in Equation (4) will therefore be replaced with a Heaviside step function Θ(A_max − A). A numerical analysis of the relative errors of this approximation on the final friction coefficient shows that this approximation only leads to effects of the order of 10%.

A central question to address is, how large is A_max? For H = 0.8, A_max was found to depend on the ratio ϵ_f ≡ λ_s/λ_r with a rather steep power law of $A_{\text{max}}\propto {ϵ}_{\text{f}}^{\beta }$, where β(H = 0.8) = 1.5 ± 0.1, and a more moderate power law on the normal stress through $A_{\text{max}}\propto p_0^{\gamma }$ with γ(H = 0.8) = 0.55 ± 0.05 for normal pressures well below the pressure, at which contact percolates. Combining these two laws results in

$\begin{array}{ll}{A}_{\text{max}}=g(H)·{ϵ}_{\text{f}}^{\beta (H)}·{\left(\frac{\kappa p_0}{E^{*}\overline{g}}\right)}^{\gamma (H)}·{\lambda }_{\text{s}}^2& (5)\end{array}$

The simulation data presented in reference Müser and Wang (2018) is consistent with a numerical value of g(H = 0.8) ≈ 0.023. When p₀ is so small and/or ϵ_f so large that A_max does not turn out at least ten times A_s, the conditions for the derivation of Equation (5) are obviously violated. Likewise, A_max should not be anywhere near ${\lambda }_{\text{r}}^2$. Sensitivity by the reader regarding the used parameters and range of applicability is required.

Similar relations as that in Equation (5) are expected to hold for other Hurst exponents >0.5, however, with changed numerical values for g(H), β(H), and γ(H). The reason why interfaces with a Hurst exponent less than one half should behave differently than those above it is that the elastic energy in full contact stems predominantly from the long- (short-) wavelength roughness above (below) H = 0.5, Indeed, A_max reveals a power law dependence neither on ϵ_f nor on p₀ for H = 0.3 (Müser and Wang, 2018).

2.2. Relation Between Load and Friction Force in a Meso-Scale Patch

This section is concerned with the question of how the mean-square force within a contact patch increases with its area under the assumption that the area is small enough to prevent the nucleation of a dislocation. To facilitate the treatment, the adhesion-free case is considered first.

2.2.1. Adhesion-Free Case

In the hard-disk, adhesion-free limit, the effective normal offset force $f_z^{\text{off}}$ is neglected. Given Equation (1), the square of the lateral force that the substrate exerts onto a randomly placed graphene sheet in contact patch p then reads

$\begin{array}{ll}{F}_{\text{l}p}^2={\mu }_{\text{m}}^2{\left({\displaystyle \sum _{n\in \text{patch }p}}{u}_{nz}{f}_{nz}\right)}^2.& (6)\end{array}$

To calculate the expectation value of that expression, we neglect correlation of the lateral forces acting on adjacent graphene atoms. This assumption is ultimately justified when the substrate has significant elements of randomness, as it occurs in disordered systems. [Commensurate contacts are not considered here, also because the lubricant patches and the two (single-crystal, but randomly rough) confining walls would have to have identical in-plane elementary cells and all three would have to be perfectly oriented—a situation that appears to be rather irrelevant]. Equation (6) then simplifies to

$\begin{array}{llll}\langle F_{\text{l}p}^2\rangle & =& {\mu }_{\text{m}}^2\langle {\displaystyle \sum _{n\in \text{patch }p}}{u}_{nz}^2{f}_{nz}^2\rangle .& (7)\end{array}$

$\begin{array}{lll}\approx & {\mu }_{\text{m}}^2{N}_p\langle u_n^2\rangle {\langle f_{nz}^2\rangle }_{\text{patch }p},& (8)\end{array}$

$\begin{array}{lll}=& {\mu }_{\text{m}}^2{N}_p\Delta A^2\langle u_n^2\rangle {\langle {\sigma }^2\rangle }_{\text{patch }p}.& (9)\end{array}$

By going from Equations (7, 8), it was assumed that the relative lateral position of graphene atoms to substrate atoms is independent of pressure, which can be motivated by the strong in-plane bonds of graphene. In Equation (9), the average over the normal stress is taken over the contact patch area in the continuum approximation and a constant area ΔA is assigned to each graphene atom. Moreover σ refers by default (that is, when no indices are added) to the normal stress, while 〈… 〉_{patch p} indicates an average over patch p.

Thus, to evaluate typical lateral forces, we need to evaluate the second moment of the random numbers u_n and the second moment of the stress in individual patches. The second moment of a uniform random number on (−1, 1) is 1/3. If we had distributed u_n according to u_n = cos(φ_n), where φ_n is a uniform random number on (0, 2π) the result would have been 1/2. If instead, it had been chosen as $u_n=cos({\phi }_n^{(x)})cos({\phi }_n^{(y)})$, it would have been 1/4. Both numbers results in a negligible difference for the final friction coefficient in the semi-quantitative analysis presented here.

The second moment of the stress in a patch as a function of its patch size A_p needs to be determined next. The overwhelming part of contact points resides in patches belonging to the Pr(A) ∝ A^−(2−H/2) scaling regime. Campana observed a linear relation between load and contact area on that branch with rather small scatter in the proportionality constant from one patch to the next (Campañá, 2008). Our own simulations supported his finding (Müser and Wang, 2018). It is therefore meaningful to approximate the distribution of normal stresses with the function that describes the full stress distribution.

Stress distributions in elastic contacts are well-described by Persson (2001) and Campañá and Müser (2007)

$\begin{array}{llll}Pr(\sigma )& \propto & e^{-2{(\sigma -p_0)}^2/{(E^{*}\overline{g})}^2}-e^{-2{(\sigma +p_0)}^2/{(E^{*}\overline{g})}^2}.& (10)\end{array}$

Evaluating the second moment of σ over the ideal distribution and normalizing it to the true contact area, which satisfies $a_{\text{r}}\approx 2p_0/E^{*}\overline{g}$ (assuming that $p_0\ll E^{*}\overline{g}$),

$\begin{array}{ll}\langle {\sigma }^2\rangle \approx \frac{1}{\sqrt{2\pi }}{(E^{*}\overline{g})}^2& (11)\end{array}$

is obtained while the first moment of the normal stress reads 〈σ〉 ≈ E*ḡ/2.

Putting all things together and forming the ratio $\mu \equiv \sqrt{\langle F_{\text{r}p}^2\rangle }/L_p$, where L_p is the load carried by the meso-scale patch, yields

$\begin{array}{lll}\frac{\mu }{{\mu }_{\text{m}}}& =& \sqrt{\frac{2}{3·\sqrt{2\pi }}}\sqrt{N_p}\\ & \approx & 0.5·\sqrt{N_p}.& (12)\end{array}$

Except for a slightly reduced pre-factor of ≈ 0.5, this relation is identical to that obtained for a delta-distributed normal force. A similar result is obtained for any other stress distribution that does not change with contact area and that is not too broad. Thus, corrections to the normal stress distribution used here can scarcely matter.

2.2.2. General Case

The calculation starting from Equation (6) can be repeated for the general case by replacing f_nz with $f_{nz}+f_z^{\text{off}}$. The mean-square lateral force in patch p is readily obtained as

$\begin{array}{ll}\langle F_{lp}^2\rangle ={\mu }_m^2·\langle u_n^2\rangle ·\left(\langle f_{nz}^2\rangle +2\langle f_{\text{nz}}\rangle ·f_z^{\text{off}}+{\left(f_z^{\text{off}}\right)}^2\right)·N_p& (13)\end{array}$

Results for $\langle u_n^2\rangle$ or $\langle f_{nz}^2\rangle$ can then be taken from the above treatment of the adhesionless case.

2.2.3. Sanity Check

It is certainly not possible to compute high-precision lateral forces from models that are as simple as the one pursued here. It might yet be useful to check if the correct order of magnitude of experimental results is reproduced. Toward this end, the model is now applied to estimate the friction between a disordered cluster sitting under its own adhesive load on a graphite substrate.

In order to conduct a comparison, an adhesive stress needs to be ascertained first. Assuming 12-6 Lennard Jones interactions between atoms residing in opposite solids, the surface energy between two planes (after integrating over the volume of the counterbody and the line below a material point at the surface) is obtained to

$\begin{array}{ll}\gamma (z)=\frac{4·2^{2/3}}{3}·{\gamma }_0·\left\{{\left(\frac{\zeta }{z}\right)}^8-{\left(\frac{\zeta }{z}\right)}^2\right\},& (14)\end{array}$

where γ₀ is the true cleavage energy and σ can be gauged to be $\zeta =\sqrt[3]{2}{z}_{\text{eq}}$ so that a realistic interlayer spacing (z_eq = 3.4 Å for graphite) is obtained. γ₀ = 0.37 J/m² is taken for the cleavage energy of graphite (Wang et al., 2015).

After differentiation of the second summand on the r.h.s. of Equation (14) with respect to z, the magnitude of the adhesive pressure per unit area at the equilibrium distance thus turns out to be

$\begin{array}{ll}{p}_{\text{a}}=\frac{16·2^{1/3}}{3}·\frac{{\gamma }_0}{z_{\text{eq}}}.& (15)\end{array}$

The numerical value for the case study conducted here is about 1 GPa. It is obtained for graphite interacting with graphite, but a similar order of magnitude should be obtained, for example, for antimony on graphite. Both fall in-between a clear classification of being insulators or metals and thus have a similar electronic polarizability, which determines the magnitude of dispersive interactions.

Using the result from Equation (13), the (maximum) shear stress in the absence of an external normal force is then simply estimated to be

$\begin{array}{ll}\tau ={\mu }_{\text{m}}·p_{\text{a}}·\sqrt{\frac{\Delta A}{2·A}},& (16)\end{array}$

where ΔA is the surface area per graphite atom.

Using an atomic friction coefficient of μ_m = 0.1, the correct value of $\Delta A=2·a_{\text{ip}}^2/\sqrt{3}$, where a_ip = 1.4 Å is taken as the in-plane distance between two graphite atoms, the relation $\tau =(0.1/\sqrt{A})$ J/m² is obtained. This ballpark estimate fits experimental results extremely well, see, e.g., the structural-lubricity branches shown in Figure 2 of reference Dietzel et al. (2017). While difficult to prove, the author wishes to state that none of the (many) ad-hoc numbers used in this ballpark estimate had been adjusted to achieve this level of agreement with the experimental data. The level of agreement certainly benefits from some fortuitous error cancelation, also because the repulsion in the 12-6 Lennard Jones interaction law (the starting point for the p_a = 1 GPa-estimate) is significantly less accurate than the exponential repulsion in a Buckingham potential, provided the 1/R⁶ singularity is screened in the Buckingham potential at small R.

2.3. Merging Single-Patch Friction Laws With Patch-Area Statistics

The results from sections 2.1, 2.2 remain to be combined. In the limit of weak coupling between adjacent patches, each isolated patch is supposed to contribute to the maximum of its ability so that the total friction force and total load need to be summed up over the various patch-size scaling regimes. In other words, each graphite sheet is assumed to resist the sliding motion with the maximum of its abilities, or more precisely, with the rms of the lateral force. When replacing a sum over discrete patches with a continuous integral, net force components of

$\begin{array}{ll}\langle F_{\alpha }\rangle =\int dAn(A)F_{\alpha }(A),& (17)\end{array}$

are obtained.

As argued in section 2.1, the dominant contribution for both normal and lateral force stems from the self-affine scaling branch of n(A). The central difference between normal and lateral force is that the normal load grows linearly with A while the lateral force only scales with $\sqrt{A}$. As a consequence, the load is carried predominantly by the large patches for the n(A) = c · A^−2+H/2 relation:

$\begin{array}{ll}{F}_z=\frac{2·c·F_z^{\text{char}}}{H}·\left\{{\left(\frac{A_{\text{max}}}{\Delta A}\right)}^{H/2}-{\left(\frac{A_{\text{s}}}{\Delta A}\right)}^{H/2}\right\}·& (18)\end{array}$

where c is a normalization constant and $F_z^{\text{char}}$ a characteristic normal force per (surface) atom, i.e.,

$\begin{array}{ll}{F}_z^{\text{char}}=E^{*}\overline{g}\Delta A/\kappa & (19)\end{array}$

for a randomly rough surface.

In contrast, the lateral force turns out to be dominated by the small patches for H < 1:

$\begin{array}{ll}{F}_x=\frac{2·c·F_x^{\text{char}}}{1-H}·\left\{{\left(\frac{\Delta A}{A_{\text{s}}}\right)}^{\frac{1-H}{2}}-{\left(\frac{\Delta A}{A_{\text{max}}}\right)}^{\frac{1-H}{2}}\right\},& (20)\end{array}$

where the characteristic atomic lateral force can be deduced to be

$\begin{array}{ll}{F}_x^{\text{char}}=\frac{{\mu }_{\text{m}}}{\sqrt{2}}\sqrt{{\left(F_z^{\text{char}}\right)}^2+2F_z^{\text{char}}{p}_{\text{a}}+p_{\text{a}}^2}.& (21)\end{array}$

When H is very close to unity, Equation (20) is well approximated by

$\begin{array}{ll}{F}_x(H\to 1)=c·F_x^{\text{char}}·ln(A_{\text{max}}/A_{\text{s}}).& (22)\end{array}$

Defining the friction coefficient as the ratio of lateral and normal force gives

$\begin{array}{ll}\mu \approx \frac{F_x^{\text{char}}}{F_z^{\text{char}}}·\frac{H}{1-H}\sqrt{\frac{\Delta A}{A_{\text{s}}}}·{\left(\frac{A_{\text{s}}}{A_{\text{max}}}\right)}^{H/2}& (23)\end{array}$

for Hurst exponents that do not approach H = 1 too closely from below,

At this point, elaborate guesses could be inserted for the various quotients that arise in Equation (23). However, a quick estimate might be more instructive. The ratio $F_x^{\text{char}}/F_z^{\text{char}}$ will be in the order of 0.1. For H = 0.8, the ratio H/(1 − H) is equal to 5. The minimum size of a contact patch that does not move in a thermally activated matter is of order A_s = π · 1 nm², while the surface area associated with a single (graphite) atom is roughly ΔA = π · 3 Ų (bond length of 1.4Å and a packing fraction of the honeycomb lattice of 0.68). The crucial number is the value for A_max. According to a review on solid friction and contact aging (Baumberger and Caroli, 2006), it usually lies in the micrometric range, so let us call a typical radius 1 μm. This turns the last factor of the r.h.s. of Equation (23) into 1/1, 000^H. Combining all these factors yields μ = 3.5 · 10⁻⁴. This value should be clearly below the detection limit for macroscopic friction experiments. At the same time, it only applies to the friction between two nominally flat surfaces and not to a pin-on-disk geometry. For the latter, friction coefficients should turn out distinctly larger, because many small contact patches should exist near the macroscopic contact line.

It is interesting to note that the precise estimate for the size A_s is not particularly relevant. It almost enters only in a logarithmic fashion into Equation (23). For H = 0.8, μ_s is predicted to decrease only by 25% if A_s is increased by a factor of ten. The only truly critical variable in Equation (23) is A_max.

Rather than taking a potentially arbitrary number from experiment, results for A_max obtained from contact-mechanics simulations can be used, i.e., those summarized in section 2.1. However, the author fears that the resulting formula might be over-interpreted even if it is labeled with clear caution signs. Mathematically literate readers, however, are invited to insert the pertinent expression for A_max into Equation (23). They will find that the friction coefficient in the model is predicted to decrease with a weak power law of the nominal contact pressure squeezing the surfaces together. At the same time, μ_s is found to decrease quite quickly with the ϵ_f, i.e., for H = 0.8 roughly according to ${ϵ}_{\text{f}}^{0.78}$. This leads to the counterintuitive result that more roughness (on large wavelength) leads to less friction. Yet, roughness at small wavelengths increases friction—unless adhesive effects start to contribute significantly. The important restriction for these results to be borne out experimentally is that the dominant source of friction is a structural interlocking in the absence of dislocations and contaminants on the surfaces.

3. Discussion and Conclusions

In this work, a theory for structural lubricity of hard randomly rough surfaces that are lubricated with thin lamellar solids (graphene) was developed. The main assumptions entering the theory was that each individual contact patch is structurally lubric and that non-connected contact patches could act independently from each other. This is because different patches are lubricated by different sheets and/or thin sheets can buckle in-between two patches so that they are able to accommodate the local interface to the best of their abilities and as if there were no constraints on the sheet locally from other patches.

This study also included a back-of-the-envelope type calculation for the friction of flat, amorphous antimony particles moving in ultra-high vacuum on graphite (Dietzel et al., 2017). Results turned out rather promising thereby giving credibility to the possibility of structural lubricity.

The theory finds the friction coefficient to quickly decrease with the characteristic contact patch size, which itself increases with load. Thus, if none of the usual friction mechanisms matters significantly, the ratio of lateral and normal force should decrease with increasing load, up to the point where the externally imposed stress induces dislocations. Assuming that maximum or characteristic contact patches are micrometer sized, a minimum friction coefficient of order 5 · 10⁻⁴ is identified for nominally flat surfaces. For larger maximum contact patches, plastic deformation might be difficult to avoid.

A potentially counter-intuitive result of the theory is that increasing the roll-off wavelength λ_r and thus the rms-roughness is predicted to reduce friction, at least until plasticity sets in. The reason is that larger values of λ_r (while keeping the surface height spectrum at smaller wavelengths unchanged—whereby the rms-gradient would remain essentially unaltered) increases the typical distance between meso-scale contact patches. As a consequence, individual contact patches tend to carry more load, whereby the characteristic size of individual small-scale patches within the meso-scale patch increases. Finally, large individual contact patches have a small ratio of (maximum) shear forces and load.

For pin-on-disk type experiments, the microscopic scaling theory would have to be folded with the macroscopic Hertzian stress profile of the tip, as done, for example, in reference Müser (2016). It seems clear that this procedure leads to many more small patches near the (macroscopic) contact line and thereby to a substantial increase of the estimated friction coefficient. In addition, the predicted power law dependence of μ on the load would become (even) weaker.

Obviously, the results presented in this paper should be taken as crude order-of-magnitude guesses, even if much effort was made to provide reasonable pre-factors. In fact, most of the effort was made to provide reasonable pre-factors, which hopefully did not hide the simplicity of the scaling arguments. It would yet be interesting to apply the theory to a well-characterized contact, in which height spectra—or even better height topographies—of both surfaces are provided. In the case of a surface whose profile violates the random-phase approximation and/or for the regular pin-on-disk measurement, a full contact-mechanics analysis might have to be conducted first so that contact-patch statistics are accurate.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

MM acknowledges helpful discussions with Sergej Sukhomlinov.

References

Aubry, S. (1983). The twist map, the extended Frenkel-Kontorova model and the devil's staircase. Phys. D Nonlinear Phenomena 7, 240–258. doi: 10.1016/0167-2789(83)90129-X

CrossRef Full Text | Google Scholar

Baumberger, T., and Caroli, C. (2006). Solid friction from stick–slip down to pinning and aging. Adv. Phys. 55, 279–348. doi: 10.1080/00018730600732186

CrossRef Full Text | Google Scholar

Baykara, M. Z., Vazirisereshk, M. R., and Martini, A. (2018). Emerging superlubricity: a review of the state of the art and perspectives on future research. Appl. Phys. Rev. 5:041102. doi: 10.1063/1.5051445

CrossRef Full Text | Google Scholar

Campañá, C. (2008). Using green's function molecular dynamics to rationalize the success of asperity models when describing the contact between self-affine surfaces. Phys. Rev. E 78:026110. doi: 10.1103/PhysRevE.78.026110

PubMed Abstract | CrossRef Full Text | Google Scholar

Campañá, C., and Müser, M. H. (2007). Contact mechanics of real vs. randomly rough surfaces: A Green's function molecular dynamics study. Europhys. Lett. 77:38005. doi: 10.1209/0295-5075/77/38005

CrossRef Full Text | Google Scholar

Campañá, C., Müser, M. H., and Robbins, M. O. (2008). Elastic contact between self-affine surfaces: comparison of numerical stress and contact correlation functions with analytic predictions. J. Phys. Condensed Matter 20:354013. doi: 10.1088/0953-8984/20/35/354013

CrossRef Full Text | Google Scholar

Cihan, E., İpek, S., Durgun, E., and Baykara, M. Z. (2016). Structural lubricity under ambient conditions. Nat. Commun. 7:12055. doi: 10.1038/ncomms12055

PubMed Abstract | CrossRef Full Text | Google Scholar

de Wijn, A. S. (2012). (In)commensurability, scaling, and multiplicity of friction in nanocrystals and application to gold nanocrystals on graphite. Phys. Rev. B 86:085429. doi: 10.1103/PhysRevB.86.085429

CrossRef Full Text | Google Scholar

de Wijn, A. S. (2014). Erratum: (in)commensurability, scaling, and multiplicity of friction in nanocrystals and application to gold nanocrystals on graphite. Phys. Rev. B 90:039906. doi: 10.1103/PhysRevB.90.039906

CrossRef Full Text | Google Scholar

Dienwiebel, M., Verhoeven, G. S., Pradeep, N., Frenken, J. W. M., Heimberg, J. A., and Zandbergen, H. W. (2004). Superlubricity of graphite. Phys. Rev. Lett. 92:126101. doi: 10.1103/PhysRevLett.92.126101

PubMed Abstract | CrossRef Full Text | Google Scholar

Dietzel, D., Brndiar, J., Štich, I., and Schirmeisen, A. (2017). Limitations of structural superlubricity: Chemical bonds versus contact size. ACS Nano 11, 7642–7647. doi: 10.1021/acsnano.7b02240

PubMed Abstract | CrossRef Full Text | Google Scholar

Dietzel, D., de Wijn, A. S., Vorholzer, M., and Schirmeisen, A. (2018). Friction fluctuations of gold nanoparticles in the superlubric regime. Nanotechnology 29:155702. doi: 10.1088/1361-6528/aaac21

PubMed Abstract | CrossRef Full Text | Google Scholar

Dietzel, D., Feldmann, M., Schwarz, U. D., Fuchs, H., and Schirmeisen, A. (2013). Scaling laws of structural lubricity. Phys. Rev. Lett. 111:235502. doi: 10.1103/PhysRevLett.111.235502

PubMed Abstract | CrossRef Full Text | Google Scholar

Dietzel, D., Ritter, C., Mönninghoff, T., Fuchs, H., Schirmeisen, A., and Schwarz, U. D. (2008). Frictional duality observed during nanoparticle sliding. Phys. Rev. Lett. 101:125505. doi: 10.1103/PhysRevLett.101.125505

PubMed Abstract | CrossRef Full Text | Google Scholar

Erdemir, A., and Eryilmaz, O. (2014). Achieving superlubricity in DLC films by controlling bulk, surface, and tribochemistry. Friction 2, 140–155. doi: 10.1007/s40544-014-0055-1

CrossRef Full Text | Google Scholar

Hammerberg, J., Holian, B., Röder, J., Bishop, A., and Zhou, S. (1998). Nonlinear dynamics and the problem of slip at material interfaces. Phys. D Nonlinear Phenomena 123, 330–340. doi: 10.1016/S0167-2789(98)00132-8

CrossRef Full Text | Google Scholar

He, G., Müser, M. H., and Robbins, M. O. (1999). Adsorbed layers and the origin of static friction. Science 284, 1650–1652.

PubMed Abstract | Google Scholar

He, G., and Robbins, M. O. (2001). Simulations of the kinetic friction due to adsorbed surface layers. Tribol. Lett. 10, 7–14. doi: 10.1023/A:1009030413641

CrossRef Full Text | Google Scholar

Hirano, M., and Shinjo, K. (1990). Atomistic locking and friction. Phys. Rev. B 41, 11837–11851.

PubMed Abstract | Google Scholar

Hyun, S., Pei, L., Molinari, J.-F., and Robbins, M. O. (2004). Finite-element analysis of contact between elastic self-affine surfaces. Phys. Rev. E 70:026117. doi: 10.1103/PhysRevE.70.026117

PubMed Abstract | CrossRef Full Text | Google Scholar

Jacobs, T. D. B., Junge, T., and Pastewka, L. (2017). Quantitative characterization of surface topography using spectral analysis. Surf. Topogr. Metrol. Prop. 5:013001. doi: 10.1088/2051-672X/aa51f8

CrossRef Full Text | Google Scholar

Lee, C., Li, Q., Kalb, W., Liu, X. Z., Berger, H., Carpick, R. W., et al. (2010). Frictional characteristics of atomically thin sheets. Science 328, 76–80. doi: 10.1126/science.1184167

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, S., and Spencer, N. D. (2008). Sweet, hairy, soft, and slippery. Science 319, 575–576. doi: 10.1126/science.1153273

PubMed Abstract | CrossRef Full Text | Google Scholar

Martin, J. M., Donnet, C., Mogne, T. L., and Epicier, T. (1993). Superlubricity of molybdenum disulphide. Phys. Rev. B 48, 10583–10586. doi: 10.1103/PhysRevB.48.10583

PubMed Abstract | CrossRef Full Text | Google Scholar

Martin, J. M., and Erdemir, A. (2018). Superlubricity: friction's vanishing act. Phys. Today 71, 40–46. doi: 10.1063/PT.3.3897

CrossRef Full Text | Google Scholar

Müser, M. (2001). Dry friction between flat surfaces: multistable elasticity vs. material transfer and plastic deformation. Tribol. Lett. 10, 15–22. doi: 10.1023/A:1009086631388

CrossRef Full Text | Google Scholar

Müser, M. H. (2002). Nature of mechanical instabilities and their effect on kinetic friction. Phys. Rev. Lett. 89:224301. doi: 10.1103/PhysRevLett.89.224301

PubMed Abstract | CrossRef Full Text | Google Scholar

Müser, M. H. (2004). Structural lubricity: role of dimension and symmetry. Europhys. Lett. 66, 97–103. doi: 10.1209/epl/i2003-10139-6

CrossRef Full Text | Google Scholar

Müser, M. H. (2008). Rigorous field-theoretical approach to the contact mechanics of rough elastic solids. Phys. Rev. Lett. 100:055504. doi: 10.1103/PhysRevLett.100.055504

PubMed Abstract | CrossRef Full Text | Google Scholar

Müser, M. H. (2016). On the contact area of nominally flat hertzian contacts. Tribol. Lett. 64:14. doi: 10.1007/s11249-016-0750-3

CrossRef Full Text | Google Scholar

Müser, M. H., and Robbins, M. O. (2000). Conditions for static friction between flat crystalline surfaces. Phys. Rev. B 61, 2335–2342. doi: 10.1103/PhysRevB.61.2335

CrossRef Full Text | Google Scholar

Müser, M. H., Urbakh, M., and Robbins, M. O. (2003). “Statistical mechanics of static and low-velocity kinetic friction,” in Advances in Chemical Physics, eds I. Prigogine and S. A. Rice (New York, NY: John Wiley & Sons), 187–272.

Google Scholar

Müser, M. H., and Wang, A. (2018). Contact-patch-size distribution and limits of self-affinity in contacts between randomly rough surfaces. Lubricants 6:85. doi: 10.3390/lubricants6040085

CrossRef Full Text | Google Scholar

Müser, M. H., Wenning, L., and Robbins, M. O. (2001). Simple microscopic theory of amontons's laws for static friction. Phys. Rev. Lett. 86, 1295–1298. doi: 10.1103/PhysRevLett.86.1295

PubMed Abstract | CrossRef Full Text | Google Scholar

Özoğul, A., İpek, S., Durgun, E., and Baykara, M. Z. (2017). Structural superlubricity of platinum on graphite under ambient conditions: the effects of chemistry and geometry. Appl. Phys. Lett. 111:211602. doi: 10.1063/1.5008529

CrossRef Full Text | Google Scholar

Palasantzas, G. (1993). Roughness spectrum and surface width of self-affine fractal surfaces via the k-correlation model. Phys. Rev. B 48, 14472–14478.

PubMed Abstract | Google Scholar

Pastewka, L., Prodanov, N., Lorenz, B., Müser, M. H., Robbins, M. O., and Persson, B. N. J. (2013). Finite-size scaling in the interfacial stiffness of rough elastic contacts. Phys. Rev. E 87:062809. doi: 10.1103/PhysRevE.87.062809

PubMed Abstract | CrossRef Full Text | Google Scholar

Persson, B. N. J. (2001). Theory of rubber friction and contact mechanics. J. Chem. Phys. 115:3840. doi: 10.1063/1.1388626

CrossRef Full Text | Google Scholar

Persson, B. N. J. (2008). On the elastic energy and stress correlation in the contact between elastic solids with randomly rough surfaces. J. Phys. Condensed Matter 20:312001. doi: 10.1088/0953-8984/20/31/312001

CrossRef Full Text | Google Scholar

Persson, B. N. J. (2014). On the fractal dimension of rough surfaces. Tribol. Lett. 54, 99–106. doi: 10.1007/s11249-014-0313-4

CrossRef Full Text | Google Scholar

Popov, V., and Gray, J. (2012). Prandtl-Tomlinson model: history and applications in friction, plasticity, and nanotechnologies. ZAMM J. Appl. Math. Mech. 92, 683–708. doi: 10.1002/zamm.201200097

CrossRef Full Text | Google Scholar

Prandtl, L. (1928). Ein Gedankenmodell zur kinetischen Theorie der festen Körper. Z. Angew. Math. Mech. 8:85.

Google Scholar

Sharp, T. A., Pastewka, L., and Robbins, M. O. (2016). Elasticity limits structural superlubricity in large contacts. Phys. Rev. B 93:121402. doi: 10.1103/PhysRevB.93.121402

CrossRef Full Text | Google Scholar

Shinjo, K., and Hirano, M. (1993). Dynamics of friction: superlubric state. Surf. Sci. 283, 473–478.

Google Scholar

Socoliuc, A., Bennewitz, R., Gnecco, E., and Meyer, E. (2004). Transition from stick-slip to continuous sliding in atomic friction: entering a new regime of ultralow friction. Phys. Rev. Lett. 92:134301. doi: 10.1103/PhysRevLett.92.134301

PubMed Abstract | CrossRef Full Text | Google Scholar

Sørensen, M. R., Jacobsen, K. W., and Stoltze, P. (1996). Simulations of atomic-scale sliding friction. Phys. Rev. B 53, 2101–2113.

PubMed Abstract | Google Scholar

Verhoeven, G. S., Dienwiebel, M., and Frenken, J. W. M. (2004). Model calculations of superlubricity of graphite. Phys. Rev. B 70:165418. doi: 10.1103/PhysRevB.70.165418

CrossRef Full Text | Google Scholar

Wang, W., Dai, S., Li, X., Yang, J., Srolovitz, D. J., and Zheng, Q. (2015). Measurement of the cleavage energy of graphite. Nat. Commun. 6:8853. doi: 10.1038/ncomms8853

PubMed Abstract | CrossRef Full Text | Google Scholar