Physics-Based Simulation of Heat Load on Structures for Improving Construction Standards for Bushfire Prone Areas

Australian building standard AS 3959 provides mandatory requirements for the construction of buildings in bushfire prone areas in order to improve the resilience of the building to radiant heat, flame contact, burning embers, and a combination of these three bushfire attack forms. The construction requirements are standardized based on the bushfire attack level (BAL). BAL is based on empirical models which account for radiation heat load on structure. The prediction of the heat load on structure is a challenging task due to many influencing factors: weather conditions, moisture content, vegetation types, and fuel loads. Moreover, the fire characteristics change dramatically with wind velocity leading to buoyancy or wind dominated fires that have different dominant heat transfer processes driving the propagation of the fire. The AS 3959 standard is developed with respect to a quasi-steady state model for bushfire propagation assuming a long straight line fire. The fundamental assumptions of the standard are not always valid in a bushfire propagation. In this study, physics based large-eddy simulations were conducted to estimate the heat load on a model structure. The simulation results are compared to the AS 3959 model; there is agreement between the model and the simulation, however, due to computational restrictions the simulations were conducted in a much narrower domain. Further simulations were conducted where wind velocity, fuel load, and relative humidity are varied independently and the simulated radiant heat flux upon the structure was found to be significantly greater than predicted by the AS 3959 model. The effect of the mode of fire propagation, either buoyancy-driven or wind dominated fires, is also investigated. For buoyancy dominated fires the radiation heat load on the structure is enhanced compared to the wind dominated fires. Finally, the potential of using physics based simulation to evaluate individual designs is discussed.

1. Introduction

Bushfire or wildfire is an integral part of the Australia environment and costs millions of dollars every year in terms of losses to the economy. The infamous Black Saturday bushfire of 2009 alone had an estimated economic cost of AUD 4.4 billion and destroyed ~3,500 structures (McLeod et al., 2010; Ronchi et al., 2017). Previously, the 2003 Canberra fire (Blanchi and Leonard, 2005) destroyed roughly 390 houses and cost an estimated AUD 0.35 billion in losses. Over the past decade, the frequency of bushfire around the world has increased (Jolly et al., 2015). Ronchi et al. reported some of the economic costs of wildfire in North America to be between 0.4 and 7 billion USD in the last decade. The size of fires is also increasing. Recently, large and devastating bushfires, termed mega bushfire or mega wildfire, have emerged. Wildfires are classified as mega wildfires if the fire occurs at large spatial scale coupled with strong wind reaching up to 100 km/h, firestorm events and massive ember generation can cause massive evacuation, devastation, and loss of life. These fires are dynamic and difficult to manage (Mell et al., 2010). Dynamic bushfire behavior is also present in smaller bushfires. Empirically-based operational fire models struggle to account for extreme and dynamic bushfire behavior and existing operational fire model show significant difference in predicting the bushfire propagation (Cruz and Alexander, 2013). Some of the recent “mega wildfires” are the 2016 Fort McMurray fire, Canada; the 2017 Californian wildfires, USA; the 2017 Portugal wildfires, Portugal (Ronchi et al., 2017). The effect of these bushfires is not limited to economical damages, the fires also cause massive evacuation of communities and present challenges to emergency personnel. The Black Saturday fire, Australia, caused 7500 people to evacuate (McLeod et al., 2010). Many people, who did not evacuate early, died during their attempted late evacuation. The high number (173) of fatalities in 2009 Black Saturday fire is one such identified bushfire case where late evacuation resulted in the loss of life (McLeod et al., 2010; Whittaker et al., 2013). Expansion of suburban areas into previously undeveloped forest and grassland also increases the impact of fires on the population. As the populations of major cities grows, so does the area of residential areas bordering fire prone bushland. City planners and building authorities must therefore plan new developments to be resilient to the risks of bushfires.

1.1. Building in Bushfire Prone Areas

A recent study in the US (Radeloff et al., 2018) showed that there is a significant increase in the wildland-urban-interface (WUI), WUI houses, and people living in WUI from 1990-2010. One definition of the WUI (Radeloff et al., 2005) is as an area in which:

• There are at least 6.17 housing units/km² with vegetation area of more than 50% of terrestrial area, or

• There are more than 6.17 housing unit/km² with vegetation area less than 50% of terrestrial area and is less than 2.4 km away from vegetation which has an area of greater than 5 km² and have vegetation area of greater than 75%.

These definitions depend somewhat on the jurisdiction. In Australia, bushfire prone areas (BPA) are classified by Australian Standard 3959 (AS 3959, 2009). The BPA is classified into three classes:

• Bushfire hazard level 2 (BHL2): Areas of forest, woodlands, scrub, shrublands, mallee, and rainforest where there is potential for bushfire behavior such as a crown fire, extreme levels of radiant heat, and extreme ember attack. BHL2 does not include grasslands. An area of BHL2 that is larger than 4 hectares will be mapped as BPA including a buffer of 300 m.

• Bushfire hazard level 1 (BHL1): Areas of forest, woodlands, scrub, shrublands, mallee, rainforest, and unmanaged grasslands where there is potential for bushfire behavior such as crown fire, grassfire, and ember attack. An area of BHL1 that is between 2 and 4 hectares that is not unmanaged grassland will be mapped as BPA including a buffer of 150 m. An area of unmanaged grassland larger than 2 hectares will be mapped as BPA including a buffer of 60 m.

• Bushfire hazard level low (BHL low): Areas where extent of bushfire attack is very low e.g., managed grassland park, airports, or botanical gardens.

Australian standard 3959 (AS 3959, 2009) was developed to specify the necessary design for the structures located at BPA. The intention of AS 3959 was improving the resilience of buildings against the bushfire attack (radiant heat, direct flame contact, burning ember, or a combination of these three factors) to mitigate the risk of bushfire through better adaptability of structures situated in the WUI. While the topic of this paper is limited to AS 3959, the US standard developed by National Fire Protection Association (NFPA). NFPA 1144 (NFPA 1144, 2013) uses a similar model to prescribe design requirements for structures in the WUI areas of the US. There are several drawbacks of AS 3959 that have previously been reported (Roberts et al., 2017; Sharples, 2017). A particular limitation of AS 3959 is the lack of quantified ember loading during a fire event. Embers are the leading cause of house loss; in the Canberra 2003 fires, 229 houses were destroyed in the suburb of Duffy and 106 of the houses were ignited by embers alone (Blanchi and Leonard, 2005). AS 3959 only provides a small amount of guidance about ember attack increasing with fire danger. AS 3959 is based upon an empirical model for radiation heat load upon the structure. The model and its limitations will now be discussed.

1.2. Empirical Models and FDI

Fire danger index (FDI) is a measure of the degree of fire danger quantified based on wind speed, relative humidity, some measure of fuel load, and fuel moisture content. Fuel moisture content is typically modeled based upon the dryness of fuel, rainfall, vegetation type, and past fire history. For this discussion, we will assume only flat terrain, however, there are multiplicative corrections for slopes that can be applied. FDI is a scaled version of the quasi-steady rate of fire spread on flat ground expected under the weather and fuel conditions. The McArthur Forest fire danger index FDI has a reference value set to 100 for the 1939 Black Friday bushfire (McArthur, 1967). There are many instances where this reference value was breached, for example, the Black Saturday bushfire of 2009, where FDI value for forest was more than 172 and 241 for grass lands (Tollhurst, 2009). In the state of New South Wales, Australia, FDI of above 100 suggests that structures will not survive and hence evacuation of occupants is required. There are several versions of the fire danger index for different fuel types and for different fire spread models and all FDI are based on the same principles. Given that this work focus on grassland fuels, the relevant fire danger index is the grassland fire danger index (GFDI):

$\begin{array}{ll}GFDI=\{\begin{array}{l}3.35w\exp \left(-0.097m_c+0.0403u\right)m_c\le 18.8\%,\hfill \\ 0.299w\exp \left(-1.686m_c+0.0403u\right)\left(30-m_c\right)\hfill \\ 18.8\%<m_c<30\%.\hfill \end{array}& (1)\end{array}$

where w is the fuel weight (T/Ha), m_c is fuel moisture content as a percentage, and u is the wind speed at 10 m high in km/h. The moisture content is modeled by the following correlation

$\begin{array}{ll}{m}_c=\frac{97.7+4.06RH}{T+6}-0.00854RH+\frac{3000}{C}-30,& (2)\end{array}$

where RH is relative humidity (%), T is ambient temperature (°C) is the curing index (0 − 100%), a measure of the amount of dead material in the grassland. The GFDI is used to determine the rate of spread of the fire RoS, which is used to model the intensity of the fire. The RoS is

$\begin{array}{ll}RoS=0.13GFDI.& (3)\end{array}$

The fire intensity model for grassland [AS 3959 fuel class G, and also class C (shrubland), D (scrub), and E (Mallee/Mulga)] is given by Byram's model:

$\begin{array}{ll}I=\frac{HwRoS}{36},& (4)\end{array}$

where H is heat of combustion (in the Byram model H = 18.6 MJ/kg) and flame length L_f is subsequently calculated using

$\begin{array}{ll}{L}_f=0.0775I^{0.46},& (5)\end{array}$

and flame height may be determined using:

$\begin{array}{ll}{F}_h=L_{f}cos\alpha ,& (6)\end{array}$

where α is the angle between the ground surface and the flame height which is not subsequently modeled. An algorithm in AS 3959 is provided to compute the flame angle which gives the maximum view factor between the flame and the structure to provide an estimate of heat load in the worst-case scenario. On a flat ground the view factor will be maximized at α = π/2. The lack of a model of α is a limitation of the standard, especially since some limited flame angle correlations, for example Weise and Biging (1996), do exist in the literature. To calculate emitted radiant heat flux, an estimated flame temperature (1090 K) is used instead of fire intensity; note that intensity does determine the flame length.

The emitted radiant heat flux is computed from the flame temperature, flame height, and flame width. Here flame width refers to the length of the fire front taken as arbitrarily as 100 m in the AS 3959 standard. These fire behavior parameters are used to compute the emitted radiant heat flux load available from the fire present in the particular vegetation. The radiant heat emitted by the flame is

$\begin{array}{ll}{q}_{r,emitted}=L_{f}cos\alpha F_w\sigma ϵT_f^4,& (7)\end{array}$

where T_f is the flame temperature (K), σ is the Stefan-Boltzmann constant (5.67⁻⁸W/m²K⁴), ϵ is called emissivity and represents the non-ideal blackbody characteristics of the material. ϵ is taken as the value for soot (0.9). F_w is the flame width.

AS 3959 assumes a constant value of flame temperature of 1090 K however the instantaneous value of flame temperature can be higher than 1200 K (Worden et al., 1997). It can be seen from Equation (7) that the thermal radiation is proportional to the fourth power of the flame temperature and directly proportional to effective area of the flame. Because the flame temperature is raised to the fourth power and so any errors in flame temperature lead to much larger errors in emitted radiant heat flux. The radiant heat flux received at the structure depends on two more parameters: the view factor F_1,2, which represents the effective solid angle between the flame in the classified vegetation and structure, and ϕ, the atmospheric transmissivity to account for how much radiative heat is absorbed before reaching the structure. These two parameters are combined with the calculation of heat flux load at the site to estimate effective radiant heat flux at the structure. That is,

$\begin{array}{ll}{q}_{r,effective}=L_{f}cos\alpha F_w{F}_{1,2}\varphi \sigma ϵT_f^4.& (8)\end{array}$

AS 3959 (table 3.1) classifies the bushfire attack level (BAL) into six categories based on the radiant heat flux q_r,effective at the structure

• BAL- LOW: considered safe situation for heat flux less 12.5 kW/m² and no ember attack. Hence, no special construction requirements.

• BAL- 12.5, 19, 29, 40: special construction is required, the numbers correspond to heat fluxes of 12.5, 19, 29, and 40 kWm⁻², respectively. These cases involve ember attack however there is no quantification of ember attack, only that ember attach is suggested to increase with the heat flux.

• BAL- FZ: are considered situations in which direct flame contact in addition to heat flux more than 40 kWm⁻² and ember showers are expected to the structure.

There are several drawbacks in the AS 3959 approach. Firstly, there is no model for ember attack, and only limited guidance (see above) about when embers can be expected. Other limitations include a fixed value of flame temperature, limitations to the flame length calculation, an ambiguous flame angle, the view factor model, and assumption of a planar flame. Hence, the AS 3959 radiation model in certain situations and generally in mega-bushfire might severely under predict radiation heat flux load. In the 2017 Iberian wildfires, Portugal, social media posts showed that many of the structure were exposed to multiple fire fronts showing a higher heat flux exposure on the structure (Viegas, 2017). The other aspect that radiant heat flux depends upon is view factor. The dynamic nature of a fire front changes the structure of flame hence affecting the view factor. The view factor can also change significantly due to different topography that is, if the fire is progressing down a slope toward the structure would have higher view factor than a fire progressing up the slope toward the structure. AS 3959 does include the topography in the computation of the view factor. Because we are only considering flat ground for this study, we omit discussion of the slope corrections to view factor. Another potential limitation of the AS 3959 approach is the lack of consideration of any flame geometry. The lack of a flame angle model may also be a critical flaw; it has been established for some time that there are two modes of fire propagation in wild, industrial, and building fires (Apte et al., 1991; Morvan and Frangieh, 2018). Grassfires have been characterized as wind dominated and buoyancy dominated fires (Dold and Zinoviev, 2009; Moinuddin et al., 2018; Morvan and Frangieh, 2018). In the wind dominated mode the shearing fluid flow (that is, the wind) dominates over the buoyant flow (the updraft from the fire plume). The flame is elongated and confined to a boundary layer structure, Figure 1A. In the buoyancy dominated mode, the updraft from the fire is sufficient to overcome the shearing forces of the driving wind and the flame becomes more vertical, see Figure 1B. In the wind dominated mode, the flame height is low and so the view factor will be small compared to the buoyancy dominated mode, however, because the fire plume is confined to a boundary layer there will be a high convective heat flux downstream of the fire. In the buoyancy dominated mode the plume is vertical and therefore the convective heat flux ahead of the fire will be small compared to the wind dominated mode. However, because the flame is vertical, the radiant heat flux ahead of the fire will be high compared to the wind dominated mode. For a realistic parameter range, wind dominated fires will have high GFDI (Equation 1) because of the exponential growth with wind speed. As a fire transitions from a buoyancy dominated fire to a wind dominated fire due to an increase in wind speed the GFDI will increase. The fire intensity is expected to increase due to the increase in GFDI and RoS (Equation 3). The AS 3959 model (Equation 5) predicts monotonic increase in flame height with increasing RoS and therefore, assuming flat ground, increased radiation load upon a structure. However, we hypothesize that if the fire becomes wind dominated the flame height will decrease and the corresponding increase in intensity may not be sufficient to ensure that the heat load on the structure increases with increasing wind speed.

FIGURE 1

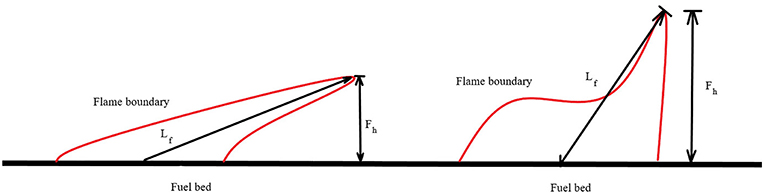
Figure 1. Cartoon showing a sketch of the two different flame geometries expected from the two fire propagation modes. (left) A wind dominated flame, (right) a buoyancy dominated flame.

The Byram convective number, N_c is used to quantify if a fire is buoyancy dominated or wind dominated (Morvan and Frangieh, 2018). The Bryam number is defined by

$\begin{array}{ll}{N}_c=\frac{2gI}{C_p\rho T_a{(u_{10}-RoS)}^3},& (9)\end{array}$

where g = 9.8 ms⁻² is the gravitation acceleration constant, T_ais the ambient temperature, T_a = 305 K in the simulations presented here, the density ρ = 1.2 kg/m³ and specific heat of air C_p = 1.0 kJ/kg K. u₁₀ is the driving wind speed at 10 m high. u₁₀ is a chosen because wind speed measured at 10 m is a meteorological standard. The factor of two in the definition of N_c is merely conventional. Fires are conclusively buoyancy dominated if N_c ≥ 10, wind dominated if N_c ≤ 2, and ambiguous if 2 < N_c < 10.

1.3. Present Study

In this work we conduct simulations to compare the radiation heat load upon a structure, as close as computationally possible, from the fire scenario in AS 3959 predicted by the BAL set out in the standard, to the radiation heat load simulated by a physics based model. The idea is to assess the validity of the standard as it stands, rather than looking to extend the standard to include new features such as ember attack. Specifically, we will

1. identify if the BAL classification values are supported by physics-based simulation,

2. assess the sensitivity of the radiation heat load to the wind speed, fuel load, and relative humidity,

3. and examine the differences in heat load on a structure between buoyancy dominated fires and wind dominated fires.

The simulations are as close to the AS 3959 standard as computationally practical. However, due to computational restrictions the fire width is considerably reduced from 100 to 20 m. However, if the radiative heat load predicted by a 20 m wide fire is larger than predicted by AS 3959, it is reasonable to assume that the 100 m wide fire will exceed the standard by a larger amount. For simplicity we consider a grassland fuel at GFDI = 50 to match the fuel class G in AS 3959. Further simulations are conducted to assess the effect of varying the driving wind speed and fuel load on the heat flux received by a structure and to determine if the different modes (wind dominated or buoyancy dominated) fire propagation effects the radiative heat load upon a structure. This work is intended to provide an introductory framework for the use of physics-based models in construction standards for properties in bushfire prone areas.

2. Physics Based Simulation

2.1. Fire Dynamics Simulator (FDS)

The code used to conduct the simulations is FDS (McGrattan et al., 2013a). FDS uses a large eddy simulation (LES) methodology to solve the equations governing fluid momentum. LES resolves large scale fluid motions but smaller, subgrid scale, turbulent motions are modeled with an eddy viscosity approach. The grass is modeled as fuel particles located in a layer on the ground using the boundary fuel model. The boundary fuel model assumes that the fuel bed is thin and that the combustion largely occurs above the fuel bed. The gas phase to be resolved on a user-specified coarse grid and the fuel pyrolysis and the heat transfer to the fuel bed is resolved on a finer grid (in this case determined by the program). As the solid fuel decays due to heating, the fuel acts as a source of combustible gas. The height and structure of the grass, which exerts an aerodynamic drag force, is also represented as a momentum sink in the Navier-Stokes equations. Conduction within the solid fuel is modeled, but the contribution of conduction to the overall heat transfer is negligible. The convective heat transfer from the flame to the fuel bed is modeled using an empirical correlation for convective heat transfer to vertical circular cylinders. Radiation heat transfer is approximated by solving the radiation transport equation using a discrete ordinates method. A problem arises with this approach; because the combustion zone is difficult to resolve with LES the gas temperature can be under predicted in the flame. Because radiation depends on the fourth power of flame temperature, care is required so that unacceptable errors in radiative heat flux do not occur. The source of radiation is modeled by a piecewise function for the flaming and non-flaming regions. Outside the flaming zone, where T is well resolved and there is no difficulty. Inside the flaming zone the radiation source is a function of the local heat release per unit volume.

FDS uses a fast chemistry model of combustion and where the mixture fraction of fuel and air is higher than the stoichiometric value, the fuel is considered burnt. See Mell et al. (2007), Mell et al. (2009), and McGrattan et al. (2013b) for a full and careful discussion of the physics-based model and the numerical methods used. FDS has been carefully validated for the simulation of grassfires. Both Mell et al. (2007) and Moinuddin et al. (2018) have compared simulation results to experimental results from Cheney et al. (1998). The simulations were shown to reproduce the measured rate-of-spread.

2.2. Model Setup

AS 3959 assumes a straight line fire of width 100 m, that is, the fire is assumed to behave like a two-dimensional line fire. However, due to computational restrictions a fire width of 20 m is used here. Linn et al. (2012) has demonstrated that this width is adequate for quasi-two-dimensional simulations. Linn et al. (2012) notes that the RoS of a straight-line fire is significantly greater than the RoS of a naturally curved fire. It is important to note that the fire is still three dimensional, although the fire is similar at every location in the span-wise direction. This approach was adopted for these simulations because the standard assumes a straight line fire. In reality, a perfectly straight line fire is unlikely, fire fronts often propagate in an elliptical shape. As such, the distance from the fire front to the structure, and therefore the radiative heat load, would vary as a function of position along the curved fire line.

The lateral boundaries are free slip to ensure that the fireline remains approximately straight as the fire progresses through the domain. The total domain height is chosen to be at four times the structure height, to avoid spurious fluid acceleration above the canopy (Bou-Zeid et al., 2009). The ground is a no-slip boundary and the top boundary is a free-slip surface as is standard for atmospheric surface layer simulations.

The driving wind is prescribed using a logarithmic mean velocity profile that is

$\begin{array}{ll}{u}_{inlet}=Alog(\frac{z}{z_0}),& (10)\end{array}$

The roughness length is taken as z₀ = 0.03 m, representative of open grassland (Rüedi, 2006). The amplitude A is chosen so u(0, 10)= 5.83, 8.33, and 12.50 ms⁻¹. To introduce turbulent fluctuations, the synthetic eddy method of Jarrin et al. (2006) is used. This method introduces artificial perturbations in with randomized length and velocity scale. N_eddy synthetic eddies with length scale L_eddy and velocity scale σ_eddy are prescribed on the inlet plane x = 0.

A structure of size 5x5x2.5 is located at 240x10x2.5. The structure is a solid object with no-slip boundary conditions and thermally inactive material properties. Therefore, no re-radiation from the structure to the fire is included in the simulations and combustion of the structure is not simulated; these assumptions are also implicitly made by AS 3959. The wind-only flow is firstly allowed to spin-up for a time of 300 s, to ensure a statistically stationary wind field throughout the domain. The fire was ignited by a temperature anomaly of 1200 K imposed for 10 s over a line which runs across the domain at x = 40 m and this causes the fuel to ignite. A schematic of the domain is sketched in Figure 2.

FIGURE 2

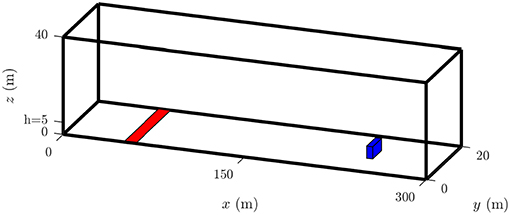
Figure 2. The simulation domain showing the line ignition source (red strip), and the house structure (blue object).

The resolution follows Moinuddin et al. (2018) with a uniform grid spacing in all variables δx = δy = δz = 0.25 m. δx is approximately half of the extinction length scale (Morvan et al., 2013). Moinuddin et al. (2018) found that a stretched grid, as used by Morvan et al. (2013) converged more slowly than a uniform grid. The other parameters for the fuel properties are shown in Table 1.

TABLE 1

Table 1. Simulation parameter values and characteristics.

The quantities measured in the simulations are the radiative and convective heat fluxes located on the walls of the structure and the boundary temperature. The heat fluxes are measured at a single point on each face of the structure, although only the face of the structure nearest to the approaching fire front is relevant. The boundary temperature allows measurement of the fire front location and correspondingly the RoS of the fire. The pyrolysis model used in these simulations is the linear model of Morvan and Dupuy (2004). Thus, fuel with a temperature above T = 400 K is pyrolyzing. The T = 400 K contour is then a clear measure of the pyrolysis front and the fire front location is taken as midpoint of the pyrolysis region. Because the fire is a straight line fire in the spanwise direction, the pyrolysis region may be averaged in the y−direction to give a single mean fire location x_*. Because the flame may be quite long and elongated, the fire front location based on the center of the pyrolysis region may be significantly further away from the structure than the location of the leading edge of the flame. The effect of different flame measurements on the radiative heat load was tested.

Seven simulations are conducted, notice that some cases in the parametric study are duplicates. The first simulation is control case aimed at replicating the AS 3959 scenario as faithfully as possible. Three further sets of simulations are conducted systematically varying driving wind velocity, vegetation load, and relative humidity to assess how the radiative heat flux upon the structure depends on these quantities. Assuming that the lowest wind velocity fire is buoyancy dominated. As the driving wind speed increases (with all other parameters constant), the fires should be more dominated by wind than buoyancy. If the fire is wind dominated, the radiative heat flux should be low but the convective heat flux should be high relative to a fire where the fire is buoyancy dominated. However, if the fire is buoyancy dominated, the increase in wind speed should tilt the flame, allowing more fuel to be involved in the fire and thus increase the intensity of the fire. Correspondingly the radiative heat flux on the structure will increase. As the vegetation load increases (with all other parameters constant), the intensity of the fire should increase and correspondingly the radiative heat flux should increase. Decreasing the relative humidity with other parameters fixed should lead to a increase in fire intensity and radiative heat flux on the structure. The parameters for all cases are shown in Table 2.

TABLE 2

Table 2. Parameters for base case and parametric study.

3. Results And Analysis

3.1. Basecase

To check that the simulation is reasonable we examine the frontal position as a function of time and the RoS (ie the time derivative of the position) of the fire. The frontal location and RoS are shown in Figure 3. Because of the noise in the RoS results, a five-point moving average smoothing was applied to the data to reveal informative trends. The frontal location in time shows a brief ignition phase over the first 5 s of the simulation before becoming approximately linear, indicative of a quasi-steady fire. The RoS shows a slight decreasing trend after the ignition phase. The average rate of spread (~2.2 ms⁻¹) is commiserate with the observations of Cheney et al. (1998), simulations of Linn et al. (2012) and Moinuddin et al. (2018), and empirical model predictions (Moinuddin et al., 2018) for similar wind speeds and fuel conditions.

FIGURE 3

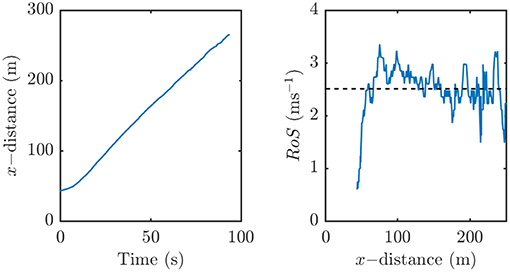
Figure 3. The frontal location (left) and RoS (right) as a function of time. The RoS has been smoothed using a five-point moving average. The dashed line shows the mean RoS over the simulation.

The simulated heat load of the basecase, following AS 3959 as closely as possible, is compared to the AS 3959 BAL predictions. The radiative and convective heat fluxes received on all surfaces of the structure as a function of fire front distance from the structure are shown in Figure 4. Because the fire location moves over time the distances between the fire and the structure changes in time. Because AS 3959 quantifies BAL in terms of distance and because different fire parameters lead to different RoS, these plots are made with respect to fire distance, rather than time. The radiative heat flux on the structure is irregular, although some trends are observable. The heat flux on the front surface increases most quickly as the flame makes contact with the structure. The heat flux on the rear surface increases after the fire has passed the structure. The heat fluxes on the left and right sides both increase at the same distance (~–10 m) but the peak radiative heat load on the left hand side is much greater than on the right hand side and on the front of the structure. The asymmetry is likely due to a complicated wake behind the structure which leads to intensification of the fire on one side of the structure. While this phenomenon is interesting, a full investigation is beyond the scope of the present study. Furthermore, the peak of radiant heat flux, when the fire is in direct contact with the structure is not important because the structure will likely ignite. The radiant heat flux on the top of the structure is minimal because the top surface is flat and not exposed to the flame. The radiation heat load can be used to estimate the duration of the heat load on the structure. The heat load on all faces is summed and the peak total heat load is measured. The duration of heat exposure is taken as the time period where the heat load exceeds 1% of the peak total heat load. For the basecase the exposure duration is 22 s. Note that all other cases give similarly short exposure periods. The duration of exposure is important when considering ignition by radiation alone, however, in reality most house losses ignitions are piloted by embers (Blanchi and Leonard, 2005).

FIGURE 4

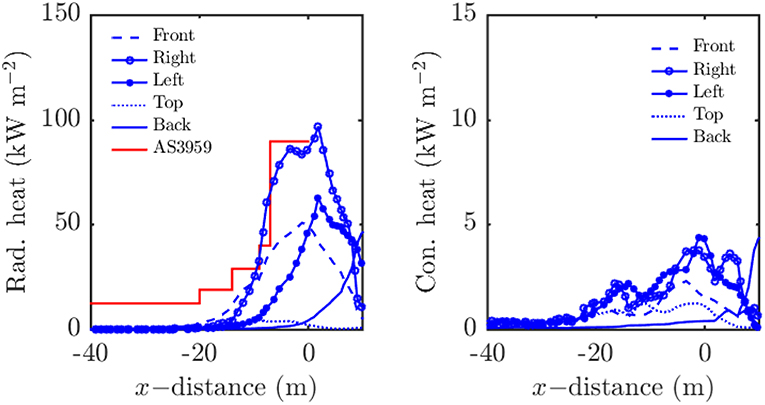
Figure 4. Radiation (left) and convective heat load (right) on the structure for the base case. The distance is measured to the center of the pyrolysis region.

The convective heat flux on the structure is approximately an order of magnitude less than the corresponding radiative heat flux on the structure and therefore negligible in terms of BAL in this case. However, this does not imply that the convective heat load on the structure is always negligible nor does this imply that the increased windload due to the convective plume can be neglected.

The Byram number is computed from Equation (9) using the quasi-steady rate of spread before the fire impacts on the structure and the mean total heat release rate over the time before the fire impacts on the structure. The Bryam numbers and the RoS from the simulations are also listed in Table 2. The simulated RoS are realistic compared to the grassfire experiments of Cheney et al. (1998). The simulated RoS exceeds that of previous simulations by Moinuddin et al. (2018) although we use a straight line fire as opposed to a naturally curved fire which makes significant differences to the RoS (Linn et al., 2012). The values of, and the variation in, RoS computed here are of similar magnitude to the observations of Linn et al. (2012). The Byram numbers indicate that most of the cases are wind dominated, except the vel. case 2, which is ambiguous and vel. case 3 which is buoyancy dominated. The Bryram numbers are unsurprising; high fuel load and low wind speed should give a buoyancy dominated fire.

The total heat flux, that is the sum of radiant and convective heat flux, and radiation heat flux are also shown in Figure 5 to see the relative contribution of convective heat load. In this figure, the front face of the structure is located at the origin and the distance to the fire front is measured along the x−axis. The fire location is measured by the fire front and leading edge approaches. The simulated heat flux follows the same trends as the BAL model, however, the BAL-12.5 and BAL-19 are apparently excessive. That is, the standard predicts heat flux far greater (between two and more than 10 times) the simulated heat flux. The BAL-29 and BAL-40 regions agree with the simulation results. Recall that the simulated fire is one fifth of the width of the fire modeled by AS 3959. The radiant heat load can be expected to increase with increasing fire width. Therefore, while the simulation results may apparently support the model in the standard, the simulated heat flux from a 100 m wide fire will likely exceed the standard. While this discrepancy could be severe, the standard could be revised fairly easily. The BAL regions are fairly narrow so the regions could be made wider to accommodate larger anticipated heat fluxes. Measuring the distance from the leading edge of the flame shifts the heat flux curve to the right. Consequently the peak heat flux is received well after the fire front has passed the house structure. The flame center measurement, which leads to greatest heat flux when the fire impacts upon the structure is more intuitive. The total heat flux and radiation heat flux are also shown in Figure 5 to see the relative contribution of convective heat load and, as expected, the contribution of convection to total heat load is negligible in this case.

FIGURE 5

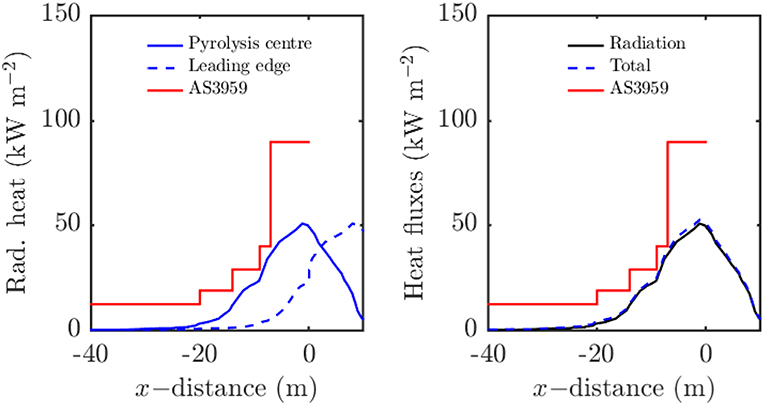
Figure 5. Comparison of heat load with AS 3959 data; the origin is the position of structure. (Left) Radiation heat load, (right) radiation and total heat load. For (left) the fire location is estimated from the center of the pyrolysis region (fire front) and from the leading edge of the fire. For (right), only the center of the pyrolysis region is used.

3.2. Variation of Driving Velocity

The driving wind velocity is varied with fixed vegetation load (0.75 kgm⁻² and fixed relative humidity (25%). The wind velocities are decreased from the value of 12.5 to 5.55 ms⁻¹, or 45 to 20 kmh⁻¹.

In this set of simulations the fuel load is high and as such a buoyancy dominated fire may be expected at low wind speeds, whereas the fire will tend to be more wind dominated at high wind speeds. Buoyancy dominated fires tend to have taller and more vertical flames than wind dominated fires, so more radiative heat load on the structure may occur at low wind speeds due to the size of the flame. Increased wind speed wind provides increased fresh oxygen to the fire, this enhances the fuel burning rate, in turn creating a larger fire. If the shear force from the wind is significant relative to the buoyant force from the fire plume, the increased wind speed also inclines the fire plume at a more acute angle, increasing heat transfer to the virgin fuel, subsequently increasing the pyrolysis region and fire intensity. Because the fire intensity increases the flame height and flame temperature both increase leading to greater radiative heat load on the structure. However, if the fire becomes wind dominated (i.e., wind shear dominates buoyancy forces) the flame will effectively attach to the ground (Sharples et al., 2010) leading to a very small flame height and a decrease in radiative heat load on the structure.

Figure 6 shows the heat load with varying wind velocities; 5.55, 8.33, and 12.5 ms⁻¹, respectively. The figure supports the hypothesized effect of buoyancy dominated fire yielding higher radiative heat loads at lower wind velocities. The radiative heat load for the 12.5 ms⁻¹ case is systematically lower than the other two cases. The radiative heat load at distance 0 m (i.e., where the flame makes contact with the structure) for the 5.55 and the 8.33 ms⁻¹ case wind speed case is ~90 kWm⁻². However, for the 12.5 ms⁻¹ wind speed case the radiative heat load at distance zero is much lower than the other two cases: ~45 kWm⁻². Unexpectedly, the intermediate wind speed 8.33 ms⁻¹ case yields the highest heat load, suggesting that the radiative heat load dependence on the fire dynamics is complicated. For example buoyancy dominated fires with very upright flames may not burn as intensely as a buoyancy dominated fire with a slightly inclined flame. The inclination of the flame will lead to increased preheating and pyrolysis of unburnt fuel and a more intense fire overall, while still yielding a large flame area that enhances radiative heat fluxes on the structure. A more comprehensive investigation of the flame dynamics is required to fully understand this behavior.

FIGURE 6

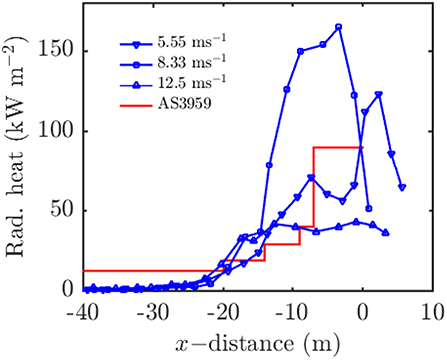
Figure 6. Radiation heat load on the front of the structure as the wind velocity varies. Distance is measured to the pyrolysis center.

The maximum convective heat flux on the structure was measured to be ~ 7% of the maximum radiative heat flux on the structure, consistent with the findings in Figure 4.

The flame profiles are examined when the fire is located at x ≈ −20 m and x ≈ 0 m. Here we use the term flame profile to refer to a cross section of the flame determined from the stoichometric mixture fraction contour and are shown in Figure 7. Because FDS uses a mixed-is-burnt combustion model these contours in the xz−plane represent the simulated flame boundary, with combustion occurring in the region enclosed by the contours. The three fires at x = −20 m have different characteristics. For the u₁₀ = 5.55 and u₁₀ = 8.33 ms⁻¹ cases the average flame height is ~0.75 m, whereas for the u₁₀ = 12.5 ms⁻¹ case the flame height is less than 0.5 m. This is consistent with the notion that the u₁₀ = 12.5 ms⁻¹ case is wind dominated and the other two cases are buoyancy dominated. When the fire is at x = 0, the flame height behavior is no longer systematic, which is likely due to the complexities of the fire engulfing the structure.

FIGURE 7

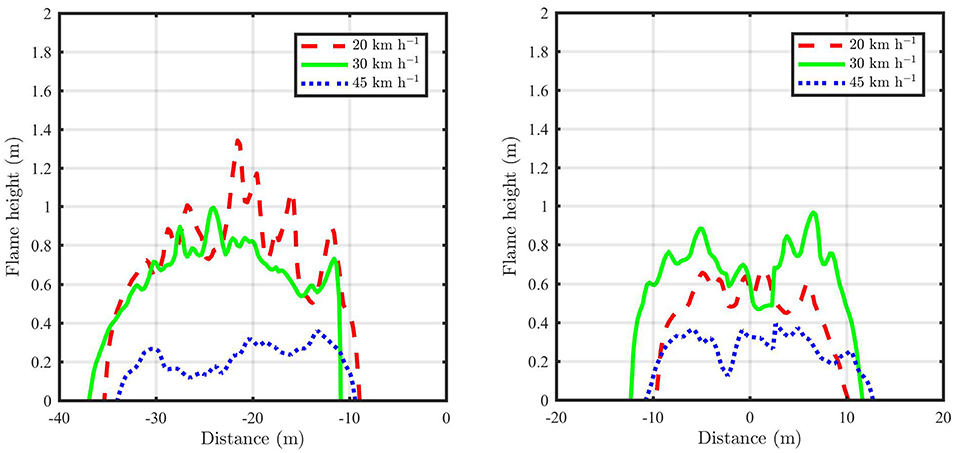
Figure 7. Flame profiles showing characteristics of the flame at different velocities. (Left) Flame profiles at 20 m distance, (right) flame profiles at the structure location.

The AS 3959 model predicts that the flame height increases monotonically with wind speed. In these cases the GFDI = 34, 50, and 92 for u₁₀ = 5.55, 8.33, and 12. ms⁻¹ respectively. AS 3959 considers tussock moorland fires at GFDI = 50 and the computed GFDI values are in the very high to severe fire danger rating categories. Basic manipulation of Equations (1)–(5), i.e., substituting all quantities into Equation (5) and assuming only u varies gives the following equation for L_f

$\begin{array}{ll}{L}_f=0.0775B{e}^{0.0185u_{10}},& (11)\end{array}$

where B is a constant:

$\begin{array}{ll}B=\{{ }_{{\left(\frac{0.299w^{2}H}{36}\exp \left(-1.686m_c\right)\left(30-m_c\right)\right)}^{0.46}18.8\%<m_c<30\%.}^{{\left(\frac{3.35w^{2}H}{36}\exp \left(-0.097m_c\right))\right)}^{0.46}{m}_c\le 18.8\%,}& (12)\end{array}$

Recall L_f is the flame length, H is relative humidity, m_c is fuel moisture content, and u₁₀ is the driving wind speed.

Because the ground is flat the view factor will be maximized at α = π/2. Therefore, L_f is the only variable in Equation (8). Hence the AS 3959 model predicts that the (maximum possible) radiation flux at the structure will increase with increasing wind speed; this prediction is not supported by these simulations. The predictions of the standard are also breached, for all wind speed cases, with the exception of the BAL-40 region in the 12.5 ms⁻¹ case. The maximum heat flux (from the 8.33 ms⁻¹ cases) received in the BAL-19 region is ~30 kWm⁻², 100 kWm⁻² in the BAL-29 region, and 150 kWm⁻² in the BAL-40 region not breached in this case. Not correctly predicting the worse-case scenario is a problem for the standard. Structures may be built to withstand the predicted worse-case scenario and receive far greater heat flux from a fire with lower GFDI.

3.3. Variation of Vegetation Load

Because the base case (wind speed 12.5 ms⁻¹, 25% relative humidity, and a fuel load of 0.375 kgm⁻²) is wind dominated, increasing the fuel load should increase the intensity of the fire, and subsequently the radiative heat flux at the structure should increase. The results shown in Figure 8 support the aforementioned hypothesis. The general trend is that the radiative heat flux at the structure increases with increasing heat load; especially before the fire impacts upon the structure. There is a peak in radiative heat flux in the highest fuel load case, at around x = −20 m. The exact cause of the peak is not investigated, but the peak in radiation heat flux corresponds to a peak in total heat release rate suggesting that fire has instantaneously flared up around that point.

FIGURE 8

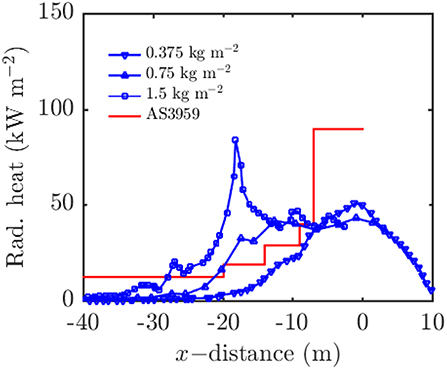
Figure 8. Radiation heat load on the front of the structure with varying vegetation load. Distance is measured to the pyrolysis center.

3.4. Variation of Relative Humidity

Following the equation for GFDI (1), increasing the relative humidity decreases the GFDI and thus the radiative heat flux at the structure. However, increasing the relative humidity also will modify the fuel moisture content, which will decrease the burning rate of the fuel and the intensity of the fire. Here, in order to systematically investigate the effect of different parameters, we modify the relative humidity without changing the fuel moisture content. Three relative humidities are selected: 6.25, 12, and 25% (basecase) with wind speed and fuel load held constant at 12.5 ms⁻¹ and 0.375 kgm⁻², respectively. The results in these cases are complicated: the relative humidity (with constant fuel moisture content) does modify the radiative heat flux at the structure however the results are not completely systematic. The general trend is that lower relative humidity yields the peak higher radiative heat load as shown in Figure 9. However, the 25% relative humidity case yields the highest radiative heat flux when −20 < x < −10 m. At x = −15 m the 25% case gives radiative heat flux of ~30 kWm⁻², the 12% case gives radiative heat flux of ~22 kWm⁻², and the 6.25% case gives radiative heat flux of ~18 kWm⁻². At greater distances from the structure, x < −20 m, the order of the curves changes again. However, the difference in between the heat fluxes are relatively small for x < −20 m and this observation may simply be due to turbulent fluctuations in the fires or some other source of noise in the data. While relative humidity on its own does yield some changes in radiative heat flux at the structure, the changes are not entirely systematic. We therefore conclude that relative humidity largely acts as a proxy for fuel moisture content in the GFDI equation and further work is required to assess the effect of fuel moisture content upon the radiative heat flux at the structure.

FIGURE 9

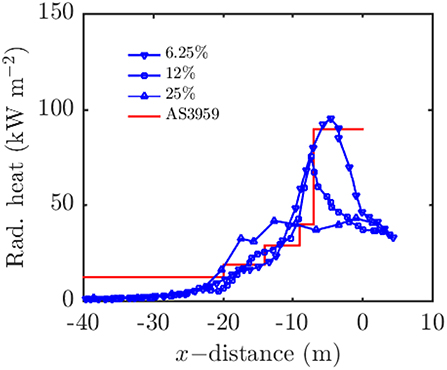
Figure 9. Radiation heat load on the front face of the structure as a function of distance to the flame center with varying relative humidity. Distance is measured to the pyrolysis center.

3.5. The Case to Improve Building Standards With Physics-Based Modeling

Designing building standards is arguably a very difficult task. In the case of building in bushfire prone areas, the basic requirements of the standard are to ensure that a building is resilient to a realistic fire event and the standard is simple and straightforward to apply. Idealized simulations, such as those conducted here, can be considered as a first attempt at providing a framework that can be used to revise existing standards. Controlled physical experiments can also serve as a validation for proposed structural integrity discussed in AS 3959 in a bushfire attack. The controlled experiments have significant cost, risk, and safety, which limits it utilization. Numerical modeling reduces the cost, risk, and safety in exploring the bushfire attack on structure. Previously, numerical simulations have been successfully applied to simulate experimental grassfires (Mell et al., 2007; Moinuddin et al., 2018). Here, we have demonstrated that the same physics-based models can simulate the radiant heat load upon a structure. The computational effort required to simulate fire impact on a structure is currently too great to allow the possibility of simulating a general proposed structure in a given location in detail. However in the future, simulation of fire impact on a proposed design may become part of the design and approval process.

For the data presented here, the idealized models included in AS 3959 were found to under predict the simulations results near the structure. Furthermore, the models in AS 3959 do not account for the differences between buoyancy dominated and wind dominated fires. Given these limitations and the omission of any kind of ember attack model, in the AS 3959 the standard should be re-examined.

Because computational technology and physics-based simulation have advanced considerably since the standard was originally implemented, physics-based simulations of bushfire attack on a structure could be used to strengthen the standard. It is important to examine the limitations of the approach presented here. Firstly, it is unlikely that a house structure would be built in unmaintained grasslands; most houses have a garden with watered or mowed grass forming a buffer region from the fire. Nonetheless the simulations conducted here reflect the situations outlined in AS 3959. The present research only considers surface fuels whereas the standard is mostly concerned with elevated forest or shrub like fuels. In planning this study, it was thought that surface fuels were likely to be better predicted by the idealized model used by the standard. The geometry of the vegetation, the possibility of crown fuel involvement, and wind reduction due to the vegetation are expected to complicate the fire impact upon a structure. Similarly this study did not address the effect of sloping terrain on the fire spread and radiative heat load. Therefore, a further study should be conducted in future to address these limitations.

4. Conclusions

Physics based simulations are performed following the model outlined in the building standard AS 3959. The basecase simulation was designed to replicate the AS 3959 grassland (tussock moorland) fire as close as computationally feasible. That is, a straight line fire approaching a small cubiod structure was simulated and the radiative heat flux at the front face of the structure was analyzed as a function of the distance from fire front to the structure. The AS 3959 standard is based upon the radiative heat flux received at the structure. The standard sets several BAL levels; the BAL level is the radiative heat flux permitted if the fire is a particular difference away from the structure. Due to computational constraints, the width of the simulated fire is 20 m instead of the 100 m outlined in the standard. As the fire width increases, the radiative heat flux on the structure should also increase. The simulated radiative heat flux was similar in magnitude to the modeled radiative heat flux. However, the simulation was conducted at a much smaller width than the standard considers. Because radiative heat flux will increase with increasing fire width, therefore, the standard is likely insufficient for these fires. A parametric study shows that the relative humidity alone does vary the radiative heat flux on a structure, but not entirely in a systematic manner. Relative humidity will also vary the fuel moisture content, held constant in these simulations, and effect of varying the fuel moisture content needs to be investigated. The fuel load increases the radiative heat flux on a structure. As wind speed increases the fire changes from a buoyancy dominated fire leading to high radiative heat flux upon a structure, to a wind dominated fire with lower heat flux on the structure and this occurs despite the GFDI monotonically increasing.

Overall, building standards based on radiative heat flux alone will require revision to account for other forms of bushfire impact such as ember attack. Physics based modeling has the potential to simulate realistic fires and physics based simulations could be used to revise the radiative heat flux levels used in AS 3959. As computational capacity increases, physics based simulations may be used in performance based design of structures in bushfire prone areas.

Author Contributions

NK conducted and analyzed the bulk of the simulations presented in this work and contributed to writing the manuscript. DS conducted preliminary simulations, proposed the study presented, and contributed writing the manuscript. RW conducted a literature review, performed an assessment of AS 3959, and contributed to writing the manuscript. KM contributed to writing the manuscript and provided guidance and expertise throughout the project.

Funding

This project was funded by the Commonwealth of Australia through the Bushfire and Natural Hazards Cooperative Research Centre. Project: Fire spread prediction across fuel types, 2014–2020.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors are grateful to the administrators of Spartan, a high performance computing cluster at the University of Melbourne.

Abbreviations

FDI, Fire Danger Index; GFDI, Grass Fire Danger Index; RoS, Rate-of-spread (of a fire); BAL, Bushfire attack level.

References

Apte, V., Bilger, R., Green, A., and Quintiere, J. (1991). Wind-aided turbulent flame spread and burning over large-scale horizontal pmma surfaces. Combust. Flame 85, 169–184. doi: 10.1016/0010-2180(91)90185-E

CrossRef Full Text | Google Scholar

AS 3959 (2009). Construction of Buildings in Bush Fire Prone Areas (as 3959). Technical report, Standards Australia, Sydney, NSW.

Blanchi, R., and Leonard, J. (2005). Investigation of Bushfire Attack Mechanisms Resulting in House Loss in the Act Bushfire 2003. Technical report, Bushfire Cooperative Research Centre (CRC) Report.

Bou-Zeid, E., Overney, J., Rogers, B. D., and Parlange, M. B. (2009). The effects of building representation and clustering in large-eddy simulations of flows in urban canopies. Bound. Layer Meteorol. 132, 415–436. doi: 10.1007/s10546-009-9410-6

CrossRef Full Text | Google Scholar

Cheney, N., Gould, J., and Catchpole, W. R. (1998). Prediction of fire spread in grasslands. Int. J. Wildland Fire 8, 1–13. doi: 10.1071/WF9980001

CrossRef Full Text | Google Scholar

Cruz, M. G., and Alexander, M. E. (2013). Uncertainty associated with model predictions of surface and crown fire rates of spread. Environ. Model. Softw. 47, 16–28. doi: 10.1016/j.envsoft.2013.04.004

CrossRef Full Text | Google Scholar

Dold, J., and Zinoviev, A. (2009). Fire eruption through intensity and spread rate interaction mediated by flow attachment. Combust. Theor. Model. 13, 763–793. doi: 10.1080/13647830902977570

CrossRef Full Text | Google Scholar

Jarrin, N., Benhamadouche, S., Laurence, D., and Prosser, R. (2006). A synthetic-eddy-method for generating inflow conditions for large-eddy simulations. Int. J. Heat Fluid Flow 27, 585–593. doi: 10.1016/j.ijheatfluidflow.2006.02.006

CrossRef Full Text | Google Scholar

Jolly, W. M., Cochrane, M. A., Freeborn, P. H., Holden, Z. A., Brown, T. J., Williamson, G. J., et al. (2015). Climate-induced variations in global wildfire danger from 1979 to 2013. Nat. Commun. 6:7537. doi: 10.1038/ncomms8537

PubMed Abstract | CrossRef Full Text | Google Scholar

Linn, R., Canfield, J., Cunningham, P., Edminster, C., Dupuy, J.-L., and Pimont, F. (2012). Using periodic line fires to gain a new perspective on multi-dimensional aspects of forward fire spread. Agric. For. Meteorol. 157, 60–76. doi: 10.1016/j.agrformet.2012.01.014

CrossRef Full Text | Google Scholar

McArthur, A. G. (1967). Fire Behaviour in Eucalypt Forests. Leaflet number 107.

Google Scholar

McGrattan, K., Hostikka, S., and Floyd, J. (2013a). Fire Dynamics Simulator, User's Guide. Gaithersburg, MD: NIST special publication, 1019.

Google Scholar

McGrattan, K., Hostikka, S., Floyd, J., Baum, H. R., Rehm, R. G., Mell, W., et al. (2013b). Fire Dynamics Simulator (Version 6), Technical Reference Guide. Gaithersburg, MD: NIST special publication, 1018.

Google Scholar

McLeod, R. N., Pascoe, S. M., and Teaguea, B. G. (2010). Final Report, Royal Commission into Victoria's Bushfires. Technical report, State of Victoria.

Mell, W., Jenkins, M. A., Gould, J., and Cheney, P. (2007). A physics-based approach to modelling grassland fires. Int. J. Wildland Fire 16, 1–22. doi: 10.1071/WF06002

CrossRef Full Text | Google Scholar

Mell, W., Maranghides, A., McDermott, R., and Manzello, S. L. (2009). Numerical simulation and experiments of burning douglas fir trees. Combust. Flame 156, 2023–2041. doi: 10.1016/j.combustflame.2009.06.015

CrossRef Full Text | Google Scholar

Mell, W. E., McDermott, R. J., and Forney, G. P. (2010). “Wildland fire behavior modeling: perspectives, new approaches and applications,” in Proceedings of 3rd Fire Behavior and Fuels Conference (Birmingham, AL), 25–29.

Google Scholar

Moinuddin, K., Sutherland, D., and Mell, W. (2018). Simulation study of grass fire using a physics-based model: striving towards numerical rigour and the effect of grass height on the rate of spread. Int. J. Wildland Fire 27, 800–814. doi: 10.1071/WF17126

CrossRef Full Text | Google Scholar

Morvan, D., and Dupuy, J. (2004). Modeling the propagation of a wildfire through a mediterranean shrub using a multiphase formulation. Combust. Flame 138, 199–210. doi: 10.1016/j.combustflame.2004.05.001

CrossRef Full Text | Google Scholar

Morvan, D., and Frangieh, N. (2018). Wildland fires behaviour: wind effect versus byram's convective number and consequences upon the regime of propagation. Int. J. Wildland Fire 27, 636–641. doi: 10.1071/WF18014

CrossRef Full Text | Google Scholar

Morvan, D., Meradji, S., and Mell, W. (2013). Interaction between head fire and backfire in grasslands. Fire Saf. J. 58, 195–203. doi: 10.1016/j.firesaf.2013.01.027

CrossRef Full Text | Google Scholar

NFPA 1144 (2013). Nfpa 1144 Standard for Reducing Structure Ignition Hazards from Wildland Fire. Technical report, National Fire Protection Association and others.

Radeloff, V. C., Hammer, R. B., Stewart, S. I., Fried, J. S., Holcomb, S. S., and McKeefry, J. F. (2005). The wildland–urban interface in the united states. Ecol. Appl. 15, 799–805. doi: 10.1890/04-1413

CrossRef Full Text | Google Scholar

Radeloff, V. C., Helmers, D. P., Kramer, H. A., Mockrin, M. H., Alexandre, P. M., Bar-Massada, A., et al. (2018). Rapid growth of the us wildland-urban interface raises wildfire risk. Proc. Natl. Acad. Sci. U.S.A. 115, 3314–3319. doi: 10.1073/pnas.1718850115

PubMed Abstract | CrossRef Full Text | Google Scholar

Roberts, M., Sharples, J., and Rawlinson, A. (2017). “Incorporating ember attack in bushfire risk assessment: a case study of the Ginninderry region,” in MODSIM2017 Proceedings - MSSANZ, Modelling and Simulation Society of Australia and New Zealand, The 22nd International Congress on Modelling and Simulation (Hobart, TAS), 1152–1158.

Google Scholar

Ronchi, E., Gwynne, S. M., Rein, G., Wadhwani, R., Intini, P., and Bergstedt, A. (2017). e-Sanctuary: Open Multi-Physics Framework for Modelling Wildfire Urban Evacuation. Technical report, National Fire Protection Association.

Google Scholar

Rüedi, I. (2006). WMO Guide to Meteorological Instruments and Methods of Observation: WMO-8 Part i: Measurement of Meteorological Variables. Geneva: World Meteorological Organization.

Sharples, J. J. (2017). Risk Implications of Dynamic Fire Propagation. Report for Ginninderra Falls Association (Non-peer reviewed report).

Google Scholar

Sharples, J. J., Gill, A. M., and Dold, J. W. (2010). “The trench effect and eruptive wildfires: lessons from the kings cross underground disaster,” in Proceedings of Australian Fire and Emergency Service Authorities Council 2010 Conference (Darwin, NT), 8–10.

Google Scholar

Tollhurst, K. (2009). Report on the Physical Nature of the Victorian Fires Occurring on the 7th of February 2009. Technical report, University of Melbourne.

Google Scholar

Viegas, D. X. (2017). O Complexo de Incéndios de Pedr og ao Grande e Concelhos limtrofes, Iniciado a 17 de Junho de 2017. Technical report, Universidade de Coimbra.

Weise, D., and Biging, G. (1996). Effects of wind velocity and slope on flame properties. Can. J. For. Res. 26, 1849–1858. doi: 10.1139/x26-210

CrossRef Full Text | Google Scholar

Whittaker, J., Haynes, K., Handmer, J., and McLennan, J. (2013). Community safety during the 2009 Australian ‘Black Saturday’ bushfires: an analysis of household preparedness and response. Int. J. Wildland Fire 22, 841–849. doi: 10.1071/WF12010

CrossRef Full Text | Google Scholar

Worden, H., Beer, R., and Rinsland, C. P. (1997). Airborne infrared spectroscopy of 1994 western wildfires. J. Geophys. Res. Atmos. 102, 1287–1299. doi: 10.1029/96JD02982

CrossRef Full Text | Google Scholar

Nomenclature