Passive and Active Control on 3D Convective Flow of Viscoelastic Nanofluid With Heat Generation and Convective Heating

1. Introduction

Fluids are much used to transfer heat in heat transfer equipment in industrial and engineering processes. Such processes are die casting, catalysis, distillation, synthesis in petrochemical industry, gas processing, hot-mix paving in concrete industry and steam generators in industrial laundry. In the above applications, thermal conductivity plays a vital role in heat transfer equipment. Conventional heat transfer of ordinary fluids, like water and oil, have low thermal conductivity, and poor heat transfer characters. The nanofluid is an advanced type of fluid incorporating nanometer-sized particles. This fluid is more stable, has high thermal conductivity, high mobility, a larger heat transfer surface between particles and fluids, low pumping power compared with ordinary fluids, low particle clogging, and low volume concentrations. Ahmed et al. (2014) addressed the uncertainties of dynamic viscosity and thermal conductivity of nanofluid flow in a permeable stretching tube under the influence of a heat sink/source. They proved that the skin friction coefficient of Ag–water nanofluid is smaller compared to the TiO₂ nanofluid. The dual solutions of nanofluid flow past a moving semi-infinite flat plate are derived by Bachok et al. (2010), who found that a smaller heat transfer rate occurs in higher values of the Prandtl number. Khan and Pop (2010) explored the impact of Brownian motion and thermophoresis on a nanofluid flow in a flat surface. It is seen that Brownian motion suppresses the reduced Nusselt number and strengthens the reduced Sherwood number. The impact of Brownian motion and thermophoresis of nanofluid fluid flow between two parallel plates was recently investigated by Derakhshan et al. (2019). They proved that the Nusselt number is suppressed with enhanced thermophoretic and Brownian motion parameters. A few important works on this direction are (Hassani et al., 2011; Makinde and Aziz, 2011; Kasmani et al., 2015, 2016, 2017).

In recent years, many researchers have concerned themselves with the study of non-Newtonian materials because they have more usages in food processing, petroleum production, drawing of plastic films, metal spinning, etc. Viscoelastic fluid is one of the non-Newtonian fluids and contains viscous and elastic behaviors. Cortell (2006) discussed the MHD flow of a viscoelastic fluid past a stretching sheet with suction. He found that the viscoelastic parameter leads to an improvement of the heat transfer gradient. MHD viscoelastic boundary layer flow over a flat sheet with non-uniform heat source and radiation was analytically and numerically solved by (Abel and Mahesha, 2008). Eswaramoorthi et al. (2016) explored the effect of thermal radiation of a viscoelastic fluid over a stretching surface. They found that the velocity boundary layer thickness decays with a more enhanced viscoelastic parameter. All the above studies reported only viscoelastic fluid without nanofluid. However, in recent years, many researchers dealt with viscoelastic nanofluids because they have more industrial applications. Shit et al. (2016) examined the viscoelastic nanofluid over a stretching surface. Their result showed that the fluid temperature decays in the presence of the viscoelasticity of the nanofluid. Very recently, Hayat et al. (2018) studied the three-dimensional flow of viscoelastic nanofluid over a stretching surface with heat generation/absorption. They implemented the Cattaneo-Christov double-diffusion theory for their study. They observed that the skin friction coefficient enhances upon increasing the ratio parameter. Some useful investigations of this direction are (Ramzan and Yousaf, 2015; Ramzan et al., 2016; Seth et al., 2016). In some practical applications, such as cooling of nuclear reactors, underground disposal of radioactive waste material, and storage of foodstuffs, the heat absorption/generation effects are essential. MHD boundary layer flow of a viscoelastic nanofluid with source/sink was investigated by Goyal and Bhargava (2014) and they found that the thermal boundary layer thickens with large values for the heat source/sink parameter. Some recent discussions on heat absorption/generation can be seen in Azim et al. (2010), Eswaramoorthi et al. (2017), and Halim et al. (2017).

In nanofluids, the base fluid does not obey Newtonian fluid properties, so it becomes more justified to imagine them as viscoelastic fluids, as for example with Ethylene glycol-ZnO, Ethylene glycol-CuO and Ethylene glycol-Al₂O₃. This type of work can be explored on two- and three-dimensional viscoelastic fluids, but less research has been done for viscoelastic nanofluids, especially three-dimensional viscoelastic nanofluids. To overcome this, we investigated the impact of passive and active controls on 3D viscoelastic nanofluid flow upon a stretching plate with heat generation and convective heating.

2. Mathematical Formulation

Let us consider the time-independent 3D convective flow of a heat generating viscoelastic nanofluid upon a stretched plate. Assume that the nanofluid has a single phase as well as uniform shape and size. The thermophoresis and Brownian motion effects are considered in this model. The bottom side of the plate is heated with hot fluid of temperature T_c and makes a heat transfer coefficient h_c (see Eswaramoorthi et al., 2015, 2016). Under the above assumptions, the governing equations of the present model are given as (see Ramzan and Yousaf, 2015):

$\begin{array}{llll}{u}_x+v_y+w_z& =& 0& (1)\end{array}$

$\begin{array}{l}u{u}_x+v{u}_y+w{u}_z=\nu u_{zz}\\ -k_1[u{u}_{xzz}+w{u}_{zzz}-u_x{u}_{zz}-u_z{w}_{zz}\\ -2u_z{u}_{xz}-2w_z{u}_{zz}]& (2)\end{array}$

$\begin{array}{l}u{v}_x+v{v}_y+w{v}_z=\nu v_{zz}\\ -k_1[v{v}_{xzz}+w{v}_{zzz}-v_x{v}_{zz}-v_z{w}_{zz}\\ -2v_z{v}_{xz}-2w_z{v}_{zz}]& (3)\end{array}$

$\begin{array}{ll}u{C}_x+v{C}_y+w{C}_z=D_B{C}_{zz}+\frac{D_T}{T_{\infty }}{T}_{zz}& (4)\end{array}$

$\begin{array}{l}u{T}_x+v{T}_y+w{T}_z={\alpha }_m{T}_{zz}+\tau \left[D_B{C}_z{T}_z+\frac{D_T}{T_{\infty }}{T}_z^2\right]\\ +\frac{Q}{\rho c_p}(T-T_{\infty })& (5)\end{array}$

where, u, v, w, ν, k₁, D_B, C, D_T, T, T_∞, α_m, τ, Q, ρ, and c_p are the x− direction velocity, y− direction velocity, z− direction velocity, kinematic viscosity, material parameter of fluid, Brownian motion coefficient, fluid concentration, thermophoretic diffusion coefficient, temperature of the fluid, free stream temperature, thermal diffusivity, ratio of effective heat capacity of the nanoparticle material to heat capacity of the fluid, heat generation/absorption coefficient, density of the fluid and specific heat, respectively.

The corresponding boundary conditions are,

$\begin{array}{l}u(x,y,0)=ax,v(x,y,0)=by,w(x,y,0)=0,C(x,y,0)=C_w(x),\\ -k\frac{\partial T}{\partial z}(x,y,0)=h_c(T_c(x,y,0)\\ -T(x,y,0)),u(x,y,\infty )=0,v(x,y,\infty )=0,u_z(x,y,\infty )=0,\\ v_z(x,y,\infty )=0,C(x,y,\infty )=C_{\infty },T(x,y,\infty )=T_{\infty }& (6)\end{array}$

Now, we introduce the following dimensionless similarity variables,

$\begin{array}{l}u=ax{f}^{\prime }(\eta ),\eta =\sqrt{\frac{a}{\nu }}z,v=ay{g}^{\prime }(\eta ),\\ w=-\sqrt{a\nu }\left[f(\eta )+g(\eta )\right]\\ \varphi (\eta )=\frac{C-C_{\infty }}{C_w},\left(\text{for PC}\right)\varphi (\eta )=\frac{C-C_{\infty }}{C_w-C_{\infty }}\left(\text{for AC}\right),\\ \theta (\eta )=\frac{T-T_{\infty }}{T_c-T_{\infty }}& (7)\end{array}$

Substituting Equation (7) in Equations (2-5), we have

$\begin{array}{l}\frac{d^{3}f}{d{\eta }^3}-{\left(\frac{df}{d\eta }\right)}^2+\left(f+g\right)\frac{d^{2}f}{d{\eta }^2}\\ +K[\left(f+g\right)\frac{d^{4}f}{d{\eta }^4}+\left(\frac{d^{2}f}{d{\eta }^2}-\frac{d^{2}g}{d{\eta }^2}\right)\frac{d^{2}f}{d{\eta }^2}\\ -2\left(\frac{df}{d\eta }+\frac{dg}{d\eta }\right)\frac{d^{3}f}{d{\eta }^3}]=0& (8)\end{array}$

$\begin{array}{l}\frac{d^{3}g}{d{\eta }^3}-{\left(\frac{dg}{d\eta }\right)}^2+\left(f+g\right)\frac{d^{2}g}{d{\eta }^2}\\ +K[\left(f+g\right)\frac{d^{4}g}{d{\eta }^4}+\left(\frac{d^{2}f}{d{\eta }^2}-\frac{d^{2}g}{d{\eta }^2}\right)\frac{d^{2}g}{d{\eta }^2}\\ -2\left(\frac{df}{d\eta }+\frac{dg}{d\eta }\right)\frac{d^{3}g}{d{\eta }^3}]=0& (9)\end{array}$

$\begin{array}{ll}\frac{d^2\varphi }{d{\eta }^2}+PrLe\left(f+g\right)\frac{d\varphi }{d\eta }+\frac{Nt}{Nb}\frac{d^2\theta }{d{\eta }^2}=0& (10)\end{array}$

$\begin{array}{ll}\frac{d^2\theta }{d{\eta }^2}+Pr\left(f+g\right)\frac{d\theta }{d\eta }+Nb\frac{d\varphi }{d\eta }\frac{d\theta }{d\eta }+Nt{\left(\frac{d\theta }{d\eta }\right)}^2+PrHg\theta =0& (11)\end{array}$

Boundary conditions (6) in terms of f, g, ϕ and θ become:

$\begin{array}{l}f(0)=0,g(0)=0,\frac{df(0)}{d\eta }=1,\frac{dg(0)}{d\eta }=c,\frac{df(\infty )}{d\eta }=0,\\ \frac{dg(\infty )}{d\eta }=0,\frac{d^{2}f(\infty )}{d{\eta }^2}=0,\frac{d^{2}g(\infty )}{d{\eta }^2}=0,\\ Nb\frac{d\varphi (0)}{d\eta }+Nt\frac{d\theta (0)}{d\eta }=0,\varphi (\infty )=0(\text{for PC}),\\ \varphi (0)=1,\varphi (\infty )=0(\text{for AC})\\ \frac{d\theta (0)}{d\eta }=-Bi\left[1-\theta (0)\right],\theta (\infty )=0& (12)\end{array}$

where $K=\frac{k_{1}a}{\nu }$ is the viscoelastic parameter, $Pr=\frac{\nu }{{\alpha }_m}$ is the Prandtl number, $Nb=\frac{\tau D_B(C_w-C_{\infty })}{\nu }$ is the Brownian motion parameter, $Nt=\frac{\tau D_T(T_c-T_{\infty })}{\nu T_{\infty }}$ is the thermophoresis parameter $Hg=\frac{Q}{a\rho c_p}$ is the heat generation/absorption parameter, $Le=\frac{{\alpha }_m}{De}$ is the Lewis number, $c=\frac{b}{a}$ is the stretching ratio and $Bi=\frac{h_c\sqrt{\frac{v}{a}}}{k}$ is the Biot number.

The skin friction coefficients and Nusselt number are defined as follows:

$\begin{array}{l}{\tau }_{wx}=\nu u_z+k_1[u{u}_{xz}+v{u}_{yz}+w{u}_{zz}+u_z{u}_x+v_z{v}_x+2w_z{w}_x\\ -w_z{u}_z{]}_{z=0}\\ {\tau }_{wy}=\nu v_z+k_1[u{v}_{xz}+v{v}_{yz}+w{v}_{zz}+u_z{u}_y+v_z{v}_y+2w_z{w}_y\\ -w_z{v}_z{]}_{z=0}\\ Nu=-\frac{x{k}_T{\left[\frac{\partial T}{\partial z}\right]}_{z=0}}{k_T(T_w-T_{\infty })}\end{array}$

Then, the dimensionless form of the skin friction coefficients (C_fx & C_fy) and Nusselt number (Nu) are defined as:

$\begin{array}{lll}{C}_{f_x}\sqrt{Re}& =& {\left[\frac{d^{2}f}{d{\eta }^2}+K\left\{2\frac{df}{d\eta }\frac{d^{2}f}{d{\eta }^2}-(f+g)\frac{d^{3}f}{d{\eta }^3}+\left(\frac{df}{d\eta }+\frac{dg}{d\eta }\right)\frac{d^{2}f}{d{\eta }^2}\right\}\right]}_{\eta =0}\\ C_{f_y}\sqrt{Re}& =& {\left[\frac{d^{2}g}{d{\eta }^2}+K\left\{2\frac{dg}{d\eta }\frac{d^{2}g}{d{\eta }^2}-(f+g)\frac{d^{3}g}{d{\eta }^3}+\left(\frac{df}{d\eta }+\frac{dg}{d\eta }\right)\frac{d^{2}g}{d{\eta }^2}\right\}\right]}_{\eta =0}\\ Nu/\sqrt{Re}& =& -{\left[\frac{d\theta }{d\eta }\right]}_{\eta =0}.\end{array}$

3. HAM Solutions

We define the initial assumptions of HAM as f⁰(η) = 1 − Exp(−η), g⁰(η) = c(1 − Exp(−η)), ${\varphi }^0(\eta )=-\frac{NtBiExp(-\eta )}{Nb(1+Bi)}$ (for PC), ϕ⁰(η) = Exp(−η) (for AC) and ${\theta }_0(\eta )=\frac{BiExp(-\eta )}{1+Bi}$ and the linear operators are $L_f=\frac{d^{3}f}{d{\eta }^3}-\frac{df}{d\eta }$, $L_g=\frac{d^{3}g}{d{\eta }^3}-\frac{dg}{d\eta }$, $L_{\varphi }=\frac{d^2\varphi }{d{\eta }^2}-\varphi$ and $L_{\theta }=\frac{d^2\theta }{d{\eta }^2}-\theta$ with $L^f\left[E_1+E_{2}Exp(\eta )+E_{3}Exp(-\eta )\right]$, $L^g\left[E_4+E_{5}Exp(\eta )+E_{6}Exp(-\eta )\right]$, $L^{\varphi }\left[E_{7}Exp(\eta )+E_{8}Exp(-\eta )\right]$ and $L^{\theta }\left[E_{9}Exp(\eta )+E_{10}Exp(-\eta )\right]$, where E_j(j = 1 − 10) are constants. After simplifying the m^th order HAM equations, we get the following:

$\begin{array}{l}{f}^m(\eta )=f^{m^{+}}(\eta )+E_1+E_{2}Exp(\eta )+E_{3}Exp(-\eta )\\ g^m(\eta )=g^{m^{+}}(\eta )+E_4+E_{5}Exp(\eta )+E_{6}Exp(-\eta )\\ {\varphi }^m(\eta )={\varphi }^{m^{+}}(\eta )+E_{7}Exp(\eta )+E_{8}Exp(-\eta )\\ {\theta }^m(\eta )={\theta }^{m^{+}}(\eta )+E_{9}Exp(\eta )+E_{10}Exp(-\eta )\end{array}$

where f^m+(η), g^m+(η), ϕ^m+(η) and θ^m+(η) are the particular solutions and these solutions have the axillary parameters h_f, h_g, h_ϕ and h_θ. These parameters are important in the convergence of the HAM solutions. The range values are −2.0 ≤ h_f, h_g ≤ −0.2, −1.7 ≤ h_ϕ ≤ 0.1, (for PC), −1.4 ≤ h_ϕ ≤ −0.2 (for AC) and −1.5 ≤ h_θ ≤ 0.1, see Figure 1. We found that the h value for the whole region of η is -1.

FIGURE 1

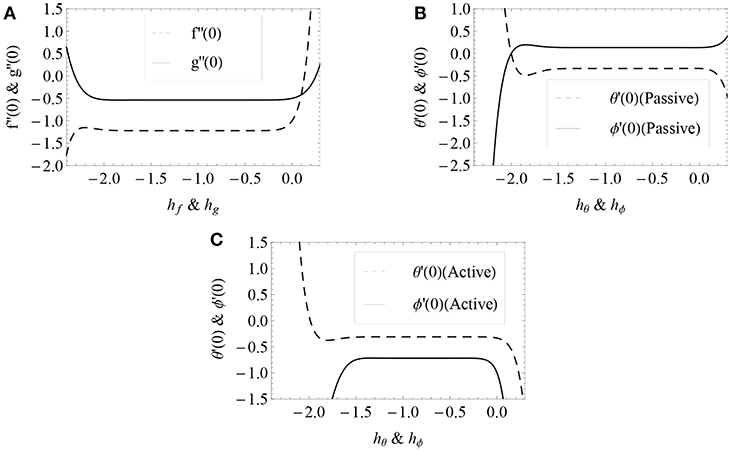
Figure 1. h curves of f″(0) & g″(0) (A) and θ′(0) & ϕ′(0) for PC (B) and AC (C) with K = 0.1, c = 0.5, Nb = 0.5, Nt = 0.2, Hg = −0.3 and Bi = 0.5.

Table 1 represents the different order of −f″(0), −g″(0), ϕ′(0) and −θ′(0). It is clear the that 10^th order is adequate for both velocity profiles and the 25^th order is needed for both nanoparticle volume fraction and temperature profiles. Table 2 presents the comparison of −f″(0) and −g″(0) for various values of c (Qayyum et al., 2014) and found that our results are in excellent agreement.

TABLE 1

Table 1. Order of approximation.

TABLE 2

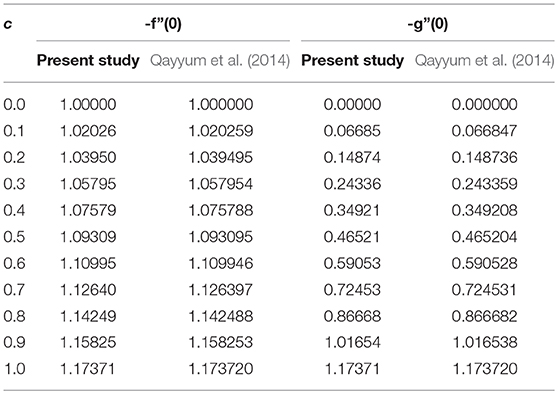
Table 2. Comparison of −f″(0) and −g″(0) for different values of c with (Qayyum et al., 2014).

4. Correlation Analysis

For the design of the thermal system and to analyze their performance, the correlation equations are essential. Linear regression analysis is used to derive the correlation equations from the obtained numerical values. The correlation equations of the skin friction coefficients and Nusselt number for both controls are given by:

$\begin{array}{l}{C}_{f_x}\sqrt{Re}=-0.713767-6.6843K-0.616636c\\ C_{f_y}\sqrt{Re}=0.439078-2.827825K-1.932749c\\ Nu/\sqrt{Re}=0.289679-0.137205K+0.034461c-0.142392Hg\\ -0.003866Nt-0.000646Nb(\text{for PC})\\ Nu/\sqrt{Re}=0.279397-0.119256K+0.024824c-0.198675Hg\\ -0.01164Nt-0.053518Nb(\text{for AC})\end{array}$

This equation is valid for 0 ≤ K ≤ 0.3, 0 ≤ c ≤ 1, −0.3 ≤ Hg ≤ 0.3, 0.2 ≤ Nt ≤ 1.2 and 0.4 ≤ Nb ≤ 1.2 with a maximum error of 0.05.

5. Results and Discussion

The impacts of pertinent parameters on x− direction velocity profile (f′(η)), y− direction velocity profile (g′(η)), nanoparticle volume fraction (ϕ(η)), temperature profile (θ(η)) and local Nusselt number ($Nu/\sqrt{Re}$) with fixed value of Prandtl number (Pr = 1.2) and Lewis number (Le = 1) are delineated in this section. Figures 2A,B portray the impact of viscoelastic parameter (K) on (f′(η)) and (g′(η)). In general, viscoelasticity generates tensile stress that opposes the fluid motion, and hence both velocities reduce when the values of K are enhanced. The consequences of thermophoresis parameter (Nt) and Biot number (Bi) on ϕ(η) for both controls are plotted in Figures 3A–D, and it was found that ϕ(η) is an enhancing function of both Nt and Bi for both controls. Physically, Nt creates a thermal conductivity of the nanoparticles. Larger thermal conductivity reveals more concentration between the nanoparticles. So, increasing the values of Nt would enrich the nanoparticle volume fraction boundary thickness. In addition, nanoparticle volume fraction is an increasing function of the Biot number. The nanoparticle volume fraction depends on the fluid temperature. A higher Biot number causes higher fluid temperature and this causes the nanoparticle volume fraction to be enhanced. It can be seen in Figures 4A,B that the nanoparticle volume fraction increased along with the rising heat absorption/generation parameter (Hg) and it dropped when the values of the Brownian motion parameter (Nb) increased. This is an important result for thermal engineering applications. Physically, larger values of Nb give more kinetic energy, and this energy increases the collision between the nanoparticles. This causes the reduction of nanoparticle volume fraction layer. The impacts of Hg and Bi on θ(η) profile for both controls are illustrated in Figures 5A–D. The positive values of Hg generate heat energy inside the boundary and this causes fluid temperature to increase. On the contrary, the negative values of Hg absorb heat energy inside the boundary and this causes a reduction of the fluid temperature. Physically, the large Biot number increases the heat transfer coefficient, and this creates a higher surface temperature. So, a larger Biot number escalates the thickness of the thermal boundary layer. This result is used to enhance heat transfer characteristics in the petroleum industry, thermal energy storage and heat exchangers. The changes of the local Nusselt number for various combinations of Hg, K and Nt are illustrated in Figures 6A–D for both controls. These figures shows that the heat transfer gradient is reduced when the values of Hg, K and Nt are high.

FIGURE 2

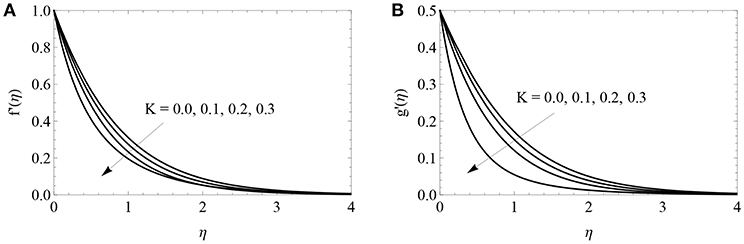
Figure 2. x− direction velocity (A) and y− direction velocity (A) profiles for different values of viscoelastic parameter with c = 0.5.

FIGURE 3

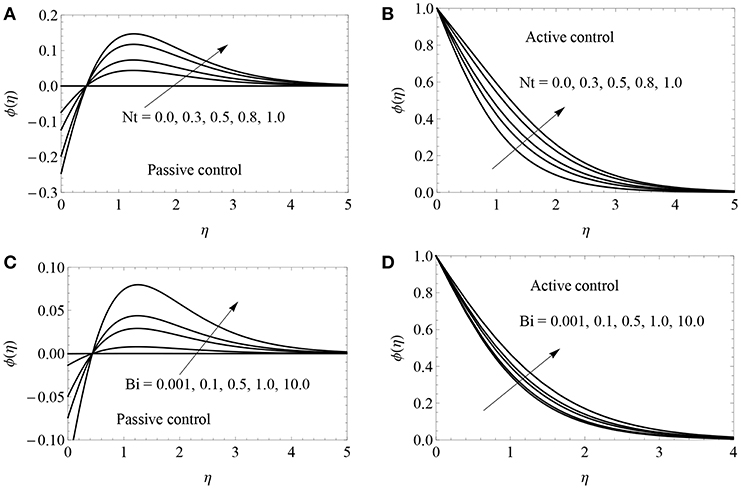
Figure 3. Nanoparticle volume fraction profile of different values of Nt (A,B) and Bi (C,D) for both passive and active cases with K = 0.1, c = 0.5, Nb = 0.5 and Hg = −0.3.

FIGURE 4

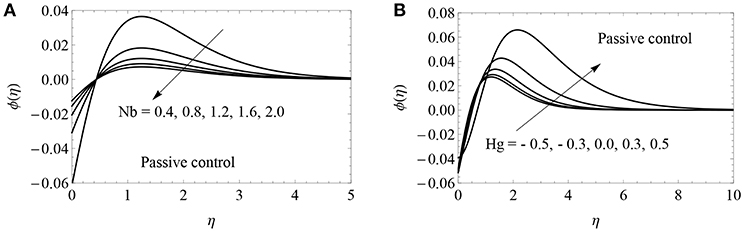
Figure 4. Nanoparticle volume fraction profile of different values of Nb (A) and Hg (B) for passive case with K = 0.1, c = 0.5, Nt = 0.2 and Bi = 0.5.

FIGURE 5

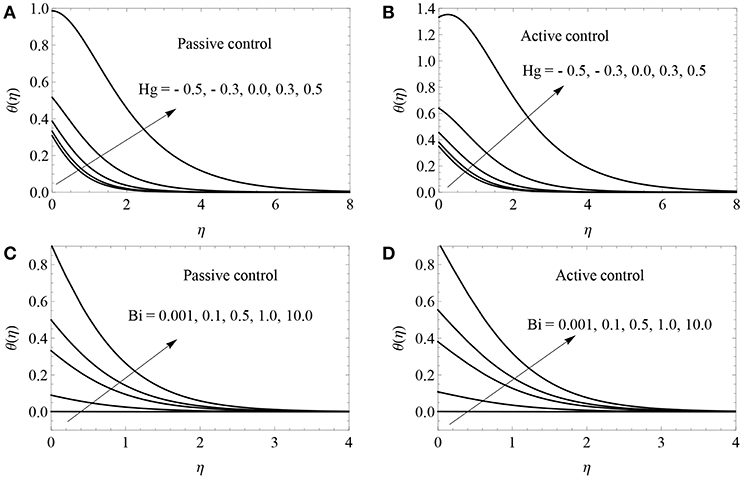
Figure 5. Temperature profile for different values of Hg (A,B) and Bi (C,D) for both passive and active cases with K = 0.1, c = 0.5, Nb = 0.5 and Nt = 0.2.

FIGURE 6

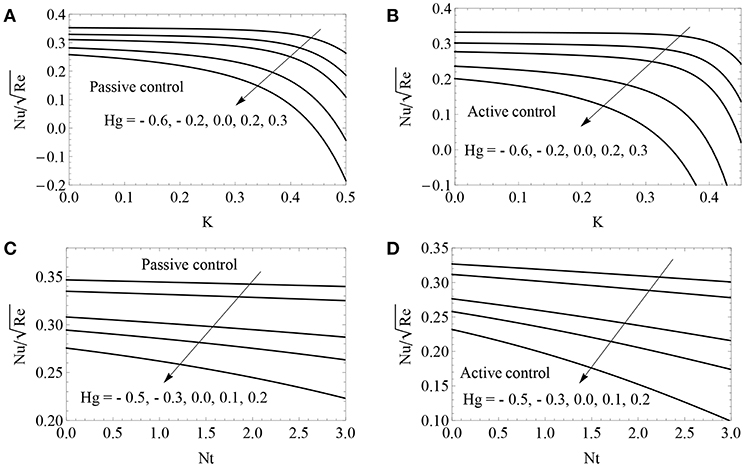
Figure 6. Local Nusselt number for different combination of Hg, K (A,B) and Nt (C,D) with K = 0.1, c = 0.5 and Bi = 0.5.

6. Conclusions

In this work, we address the impact of passive control and active control on 3D viscoelastic nanofluid flow upon a stretching membrane with heat absorption/generation and convective heating. The system of appearing non-linear PDEs is converted into a couple of ODE's by using suitable similarity transformations. Convergent series solutions are obtained using the homotopy analysis method (HAM). The following findings are observed in our study.

• Both x− direction and y− direction velocities are weakened with increasing K values.

• The nanoparticle volume fraction is strengthened when the values of Nt and Bi are high for both controls.

• The fluid temperature improves when the values of Hg and Bi increase for both controls.

• The heat transfer gradient drops when the values of Hg, K and Nt rise for both controls.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Abel, M. S., and Mahesha, N. (2008). Heat transfer in MHD viscoelastic fluid flow over a stretching sheet with variable thermal conductivity, non-uniform heat source and radiation. Appl. Math. Model. 32, 1965–1983. doi: 10.1016/j.apm.2007.06.038

CrossRef Full Text | Google Scholar

Ahmed, S. E., Hussein, A. K., Mohammed, H. A., and Sivasankaran, S. (2014). Boundary layer flow and heat transfer due to permeable stretching tube in the presence of heat source/sink utilizing nanofluids. Appl. Math. Comp. 238, 149–162. doi: 10.1016/j.amc.2014.03.106

CrossRef Full Text | Google Scholar

Azim, M. A., Mamun, A. A., and Rahman, M. M. (2010). Viscous Joule heating MHD-conjugate heat transfer for a vertical flat plate in the presence of heat generation. Int. Commu. Heat Mass Transf. 37, 666–674. doi: 10.1016/j.icheatmasstransfer.2010.02.002

CrossRef Full Text | Google Scholar

Bachok, N., Ishak, A., and Pop, I. (2010). Boundary-layer flow of nanofluids over a moving surface in a flowing fluid. Int. J. Ther. Sci. 49, 1663–1668. doi: 10.1016/j.ijthermalsci.2010.01.026

CrossRef Full Text | Google Scholar

Cortell, R. (2006). Effects of viscous dissipation and work done by deformation on the MHD flow and heat transfer of a viscoelastic fluid over a stretching sheet. Physics Letters A. 357, 298–305. doi: 10.1016/j.physleta.2006.04.051

CrossRef Full Text | Google Scholar

Derakhshan, R., Ahmadreza Shojaei, Hosseinzadeh, K. H., Nimafar, M., and Ganji, D. D. (2019). Hydrothermal analysis of magneto hydrodynamic nanofluid flow between two parallel by AGM. Case Studies Ther. Engin. 14, 100439. doi: 10.1016/j.csite.2019.100439

CrossRef Full Text | Google Scholar

Eswaramoorthi, S., Bhuvaneswari, M., Sivasankaran, S., and Rajan, S. (2015). Effect of radiation on MHD convective flow and heat transfer of a viscoelastic fluid over a stretching surface. Procedia Eng. 127, 916–923. doi: 10.1016/j.proeng.2015.11.364

CrossRef Full Text | Google Scholar

Eswaramoorthi, S., Bhuvaneswari, M., Sivasankaran, S., and Rajan, S. (2016). Soret and Dufour effects on viscoelastic boundary layer flow, heat and mass transfer in a stretching surface with convective boundary condition in the presence of radiation and chemical reaction. Scientia Iranica Transactions B: Mech. Engin. 23, 2575–2586. doi: 10.24200/sci.2016.3967

CrossRef Full Text | Google Scholar

Eswaramoorthi, S., Bhuvaneswari, M., Sivasankaran, S., and Rajan, S. (2017). Effect of partial slip and chemical reaction on convection of a viscoelastic fluid over a stretching surface with Cattaneo-Christov heat flux model. IOP Conf. Ser. Mater. Sci. Eng. 263, 1–8. doi: 10.1088/1757-899X/263/6/062009

CrossRef Full Text | Google Scholar

Goyal, M., and Bhargava, R. (2014). Boundary layer flow and heat transfer of viscoelastic nanofluids past a stretching sheet with partial slip conditions. Appl. Nanosci. 4, 761–767. doi: 10.1007/s13204-013-0254-5

CrossRef Full Text | Google Scholar

Halim, N. A., Sivasankaran, S., and Noor, N. F. M. (2017). Active and passive controls of the Williamson stagnation nanofluid flow over a stretching/shrinking surface. Neural Comput. Appli. 28, 1023–1033. doi: 10.1007/s00521-016-2380-y

CrossRef Full Text | Google Scholar

Hassani, M., Mohammad Tabar, M., Nemati, H., Domairry, G., and Noori, F. (2011). An analytical solution for boundary layer flow of a nanofluid past a stretching sheet. Int. J. Ther. Sci. 50, 2256–2263. doi: 10.1016/j.ijthermalsci.2011.05.015

CrossRef Full Text | Google Scholar

Hayat, T., Qayyum, S., Shehzad, S. A., and Alsaedi, A. (2018). Cattaneo-Christov double-diffusion theory for three-dimensional flow of viscoelastic nanofluid with the effect of heat generation/absorption. Res. Phys. 8, 489–495. doi: 10.1016/j.rinp.2017.12.060

CrossRef Full Text | Google Scholar

Kasmani, R. M., Sivasankaran, S., Bhuvaneswari, M., and Hussein, A. K. (2017). Analytical and numerical study on convection of nanofluid past a moving wedge with Soret and Dufour effects. Int. J. Numer. Methods Heat Fluid Flow. 27, 2333–2354. doi: 10.1108/HFF-07-2016-0277

CrossRef Full Text | Google Scholar

Kasmani, R. M., Sivasankaran, S., Bhuvaneswari, M., and Siri, Z. (2015). Effect of thermal radiation and suction on convective heat transfer of nanofluid along a wedge in the presence of heat generation/absorption. AIP Conf. Proc. 1682, 020008-1–020008-7. doi: 10.1063/1.4932417

CrossRef Full Text | Google Scholar

Kasmani, R. M., Sivasankaran, S., Bhuvaneswari, M., and Siri, Z. (2016). Effect of chemical reaction on convective heat transfer of boundary layer flow in nanofluid over a wedge with heat generation/absorption and suction. J. Appl. Fluid Mech. 3, 379–388. doi: 10.18869/acadpub.jafm.68.224.24151

CrossRef Full Text | Google Scholar

Khan, W. A., and Pop, I. (2010). Boundary-layer flow of a nanofluid past a stretching sheet. Int. J. Heat Mass Transf. 53, 2477–2483. doi: 10.1016/j.ijheatmasstransfer.2010.01.032

CrossRef Full Text | Google Scholar

Makinde, O. D., and Aziz, A. (2011). Boundary layer flow of a nanofluid past a stretching sheet with a convective boundary condition. Int. J. Ther. Sci. 50, 1326–1332. doi: 10.1016/j.ijthermalsci.2011.02.019

CrossRef Full Text | Google Scholar

Qayyum, A., Hayat, T., Alhuthali, M. S., and Malaikah, H. M. (2014). Newtonian heating effects in three-dimensional flow of viscoelastic fluid. IChin. Phys. B. 23, 054703. doi: 10.1088/1674-1056/23/5/054703

CrossRef Full Text | Google Scholar

Ramzan, M., and Yousaf, F. (2015). Boundary layer flow of three-dimensional viscoelastic nanofluid past a bi-directional stretching sheet with Newtonian heating. AIP Advances 5, 057132-1-057132-15. doi: 10.1063/1.4921312

CrossRef Full Text | Google Scholar

Ramzan, M., Yousaf, F., Farooq, M., and Chung, J. D. (2016). Mixed convective viscoelastic nanofluid flow past a porous media with Soret-Dufour effects. Commu. Theoret. Phys. 66, 133–142. doi: 10.1088/0253-6102/66/1/133.

CrossRef Full Text | Google Scholar

Seth, G. S., Mishra, M. K., and Chamkha, A. J. (2016). Hydromagnetic convective flow of viscoelastic nanofluid with convective boundary condition over an inclined stretching sheet. J. Nanofluids. 5, 511–521. doi: 10.1166/jon.2016.1249

CrossRef Full Text | Google Scholar

Shit, G. C., Haldar, R., and Ghosh, S. K. (2016). Convective heat transfer and MHD viscoelastic nanofluid flow induced by a stretching sheet. Int. J. Appl. Comput. Math. 2, 593–608. doi: 10.1007/s40819-015-0080-4

CrossRef Full Text | Google Scholar