The Combined Thermal and Mechanical Effect of an Interstitial Gas on Thermal Rectification Between Periodically Grooved Surfaces

This paper presents a study on the combined thermal and mechanical effect of interstitial gas on thermal rectification between a periodically grooved surface and a flat one. To evaluate the interstitial medium influence, the analytico-numerical solution to the corresponding thermoelastic contact problem is constructed taking into account the effect of thermal strains on gap deformation. The results are provided for the Stainless Steel AISI 304—Aluminum Alloy A380 pair in the presence of air or krypton in the interface gaps. The effects of the gas thermal conductivity and pressure, the imposed pressure and heat flux, and the maximum groove height on the effective thermal contact resistance and the level of thermal rectification are analyzed. It is revealed that taking into account the mechanical effect of the gap filler leads to lower values of thermal rectification level. Also, the change of the gap filler thermal conductivity has more pronounced effect that the change of its pressure.

Introduction

Today the tribological mechanical components of many modern devices are often regularly textured with grooves, dimples, protrusions, etc. of small height in order to improve their surface properties significantly (Etsion, 2004, 2005; Stepien, 2011). When textured surfaces are in contact, periodic arrays of gaps are present at the contact interface. The contacting textured surfaces are often subject to the action of not only normal and shear mechanical loads, but also thermal load. The thermal strains caused by the imposed heat flow can have a significant effect on the contact parameters of the bodies, especially dimensions of contact regions/interface gaps and thermal contact resistance.

The results of theoretical studies of thermoelastic contact between bodies of dissimilar materials in a vacuum environment (Barber, 1971; Dundurs and Panek, 1976; Stevenson et al., 1991; Kharitonov and Yakutin, 1997; Chumak and Martynyak, 2012) showed that the contact parameters and thermal contact resistance of the bodies depend not only on the heat flow density but also on the reversal of its direction. This phenomenon was repeatedly observed experimentally [a review of these experimental observations is available in Roberts and Walker (2011)] and is known as thermal rectification or the directional effect. The essence of thermal rectification is that the thermal contact resistance between two bodies is greater in one heat flow direction across the interface than in the reverse direction. Thermal rectification between textured surfaces is poorly investigated [the only study available was conducted by Chumak and Martynyak (2019)].

The interface gaps between textured surfaces are commonly filled with natural (gas, liquid) or operational (grease, coolant) substance. The interstitial medium exerts pressure on the contacting surfaces and offers additional thermal resistance, and thus can significantly affect the distribution of stress-strain state and temperature in the contacting bodies, and the level of thermal rectification.

The vast majority of investigations of the effect of the interface gap filler on the contact of bodies have been conducted taking into account either only filler pressure or only filler thermal conductivity.

The influence of the interstitial medium filling the interface gaps on the mechanical behavior of bodies has been studied by Machyshyn and Nagórko (2003), Slobodyan et al. (2014), Kozachok et al. (2017), Malanchuk et al. (2017), Serednytska et al. (2019) (gas-filled gaps), Evtushenko and Sulim (1981), Kuznetsov (1985), Kit et al. (2003), and Martynyak and Slobodyan (2009) (liquid-filled gaps). A number of works studied the influence of liquid bridges in interface gaps on contact interaction when the remainder of the gap is filled with a vacuum (Peng and Bhushan, 2002; Boer, 2007; Xue and Polycarpou, 2007; Persson, 2008; Wang et al., 2009) or with a gas (Martynyak and Slobodyan, 2008; Martynyak et al., 2009; Slobodyan, 2012; Kozachok et al., 2016; Kozachok and Martynyak, 2018). The normal contact approach and contact compliance of the bodies with periodically grooved or wavy surfaces and medium-filled interface gaps was investigated by Kozachok et al. (2018a,b).

The comprehensive review of the investigations of the thermal effect of the interface gap filler is provided in Chumak (2018) and Chumak and Martynyak (2019), where this effect and thermal rectification phenomena was studied for periodically grooved and wavy surfaces, respectively.

The works that take into account both gap filler pressure and thermal conductivity are limited to Yovanovich et al. (1982), Song et al. (1993), and Bahrami et al. (2004a,b). However, they did not take into account the influence of thermal strains that did not allow them to study thermal rectification.

To summarize, thermal rectification between textured surfaces has been poorly investigated. The previous studies of the contact between textured surfaces do not take into account the combined mechanical and thermal effect of the interstitial medium in the interface gaps and effect of thermal strains on the deformation of interface gaps at the same time. Considering only thermal or mechanical effect of the interface gap filler may greatly influence the outcome on the one hand, and neglecting the influence of thermal strains does not enable investigating thermal rectification phenomenon on the other hand.

The aims of the present study are:

(1) To construct the solution of the thermoelastic contact problem for a body with a periodically grooved surface and a body with a smooth surface in the presence of an interstitial gas in the interface gaps, which exerts pressure as well as offers thermal resistance.

(2) To investigate the combined pressure and thermal conductivity effect of the interstitial gas on thermal rectification between the contacting bodies.

Statement of Problem

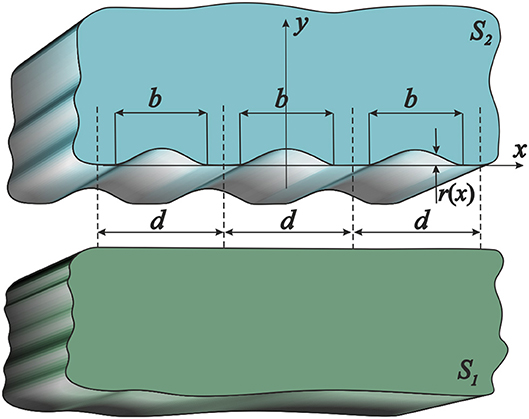
Consider two bodies that are made from isotropic and dissimilar materials with Poisson's ratios ν₁, ν₂, shear moduli μ₁, μ₂, coefficients of linear thermal expansion α₁, α₂, and thermal conductivities λ₁, λ₂ (Figure 1). The surface of the lower body S₁ is perfectly flat, and the surface of the upper body has regular surface texture in the form of periodically arranged grooves. The shape of the textured surface is described by the smooth periodic function r(x) of the coordinate x:

$\begin{array}{ll}\mathit{r}\left(\mathit{x}\right)=\{\begin{array}{c}{r}_0\left(1-\frac{{\left(\tan \left(\frac{\pi x}{d}\right)\right)}^2}{{\left(\tan \left(\frac{0.5\pi b}{d}\right)\right)}^2}\right),\left|x-md\right|<0.5b\\ 0,\left|x-md\right|\ge 0.5b\end{array},m\in R.& (1)\end{array}$

Here, b denotes the width of each groove, r₀ is the maximum height of the grooves, d denotes the period of the surface pattern (d > b ).

FIGURE 1

Figure 1. The bodies prior to loading.

The groove height is assumed to be small in comparison to the groove width, i.e., r₀ ≪ b. This assumption will allow us to impose the boundary conditions not on the actual surfaces but write them on the plane y = 0 (Dundurs et al., 1973).

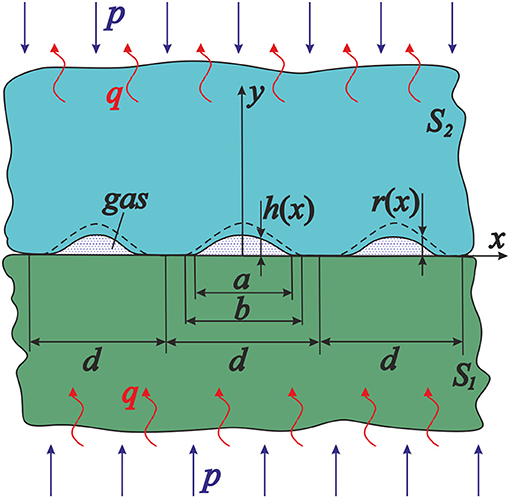
Since the problem is posed in the framework of linear thermoelasticity, assuming plane strain conditions, we consider the contact of two half-planes (Figure 2). They are compressed against each other by a remotely applied uniform pressure p, and a far-field uniform heat flux q is imposed in the direction normal to the interface.

FIGURE 2

Figure 2. The model of the contact.

Two opposite directions of heat flow are considered: heat flows from body S₁ into body S₂ when q > 0 (as in Figure 2), and heat flows from body S₂ into body S₁ when q < 0.

Due to the initial regular surface texture of the upper body, the interface between the solids consists of a periodic array of gaps and a periodic array of contacts.

Every gap is supposed to be filled with an equal amount of an ideal gas. The mechanical influence of the gap filler is simulated by pressure p_g, which, according to the Pascal's law, is the same in each point of the gas. To simulate the thermal influence of the interstitial gas, we will use the following gap thermal resistance model (Chumak, 2018):

$\begin{array}{ll}{R}_g(x)=h(x)/{\lambda }_g,& (2)\end{array}$

where h(x) denotes the gap height, and λ_g denotes the thermal conductivity of the gas. This model provides for gap deformation due to both mechanical and thermal loads. Also, it assumes that heat is transferred through the interstitial medium only by conduction in the y-direction.

The interface offers no thermal resistance outside the gaps.

The values of contact parameters lie within two limiting cases—frictionless contact (zero coefficient of friction) and complete stick (infinite coefficient of friction). As shown in Popov et al. (2019), the difference between the limiting values of the contact parameters is not large for normal contact of bodies. Based on this fact and since the allowance for friction forces will greatly increase complexity of the problem, we assume frictionless contact in the work.

If the magnitude of the imposed heat flow is to be the same for the contact with interface gaps and the contact without interface gaps, the additional far-field difference in temperatures ΔT must be supplied in the case of the periodic array of gaps. ΔT is clearly the cumulative effect of temperature disturbances arising out of each gap in the array, and equals to the average temperature jump across the interface (Das and Sadhal, 1997; Manners, 2000; Chumak, 2018):

$\begin{array}{ll}\Delta T=\frac{1}{d}{\displaystyle {\int }_{-a/2}^{a/2}\gamma \left(x\right)dx,}& (3)\end{array}$

where a denotes the interface gap width, γ(x) = T ⁻ (x, 0) − T⁺(x, 0) is the temperature jump across the interface, T(x, y) is the temperature, the superscripts + and − denote boundary values of a function on the x-axis in the upper and lower half-planes, respectively.

The effective thermal contact resistance, which is defined as R_eff = ΔT/q (Madhusudana and Fletcher, 1986), is then

$\begin{array}{ll}{R}_{eff}=\frac{1}{qd}{\displaystyle {\int }_{-a/2}^{a/2}\gamma \left(x\right)dx.}& (4)\end{array}$

The boundary conditions at the interface are:

on the gap surfaces (|x − md| < 0.5a ):

$\begin{array}{llll}{T}^{-}(x,0)& =& T^{+}(x,0)+R(x)q_y^{+}(x,0),q_y^{+}(x,0)=q_y^{-}(x,0),& (5)\end{array}$

$\begin{array}{llll}{\sigma }_{yy}^{+}& =& {\sigma }_{yy}^{-},{\sigma }_{yy}^{+}=-p_g,{\sigma }_{xy}^{+}=0,{\sigma }_{xy}^{-}=0;& (6)\end{array}$

in the contact regions (|x − md| ≥ 0.5a ):

$\begin{array}{llll}{T}^{-}(x,0)& =& T^{+}(x,0),q_y^{+}(x,0)=q_y^{-}(x,0),& (7)\end{array}$

$\begin{array}{llll}{\sigma }_{yy}^{+}& =& {\sigma }_{yy}^{-},{\sigma }_{xy}^{+}=0,{\sigma }_{xy}^{-}=0,u_y^{+}=u_y^{-}-r(x).& (8)\end{array}$

The boundary conditions at the far-field are:

$\begin{array}{ll}\underset{y\to \pm \infty }{\lim }{q}_x\left(x,y\right)=0,\underset{y\to \pm \infty }{\lim }{q}_y\left(x,y\right)=q,& (9)\end{array}$

$\begin{array}{ll}\underset{y\to \pm \infty }{\lim }{\sigma }_{yy}\left(x,y\right)=-p,\underset{y\to \pm \infty }{\lim }{\sigma }_{xy}\left(x,y\right)=0,& (10)\end{array}$

$\begin{array}{ll}\underset{y\to \pm \infty }{\lim }{\sigma }_{xx}\left(x,y\right)=q{\theta }_{j}y,{\theta }_j=\frac{2{\mu }_j{\delta }_j}{\left(1-{\nu }_j\right)},j=1,2.& (11)\end{array}$

Here and further on, q_x(x, y), q_y(x, 0) are components of heat flow, σ_xx, σ_xy, σ_yy are stress components, u_y is a displacement component, and the quantity ${\delta }_j=\frac{{\alpha }_j(1+{\nu }_j)}{{\lambda }_j}$ is called the thermal distortivity of a material (Dundurs and Panek, 1976). The condition (11) describes application of linearly distributed stress to prevent the global warping of the contacting bodies and provide periodic contact along the whole interface (Panek and Dundurs, 1979).

Solution to Problem

Using the approach described in Chumak (2018), the considered thermoelastic contact problem has been reduced to the following system of singular integro-differential equations for the gap height h(ξ) and the temperature jump γ(ξ):

$\begin{array}{l}\frac{2}{d}{\displaystyle {\int }_{-\alpha }^{\alpha }\frac{h^{\prime }\left(\eta \right)}{\eta -\xi }}d\eta +\frac{{\lambda }_{12}\delta \left(\gamma \left(\xi \right)-\Delta T\right)}{{\xi }^2+1}\\ =-\frac{6\pi r_0}{d\beta }\left(\frac{{\xi }^2}{{\beta }^2}-\frac{1}{2}\right)+\frac{K\left(p-p_g\right)}{{\xi }^2+1},\left|\xi \right|<\alpha ;& (12)\end{array}$

$\begin{array}{ll}{\lambda }_g\frac{\gamma \left(\xi \right)}{h\left(\xi \right)}-\frac{{\lambda }_{12}}{2d}{\displaystyle {\int }_{-\alpha }^{\alpha }\frac{{\gamma }^{\prime }\left(\eta \right)}{\eta -\xi }}d\eta =q,\left|\xi \right|<\alpha ,& (13)\end{array}$

where $\delta ={\delta }_2-{\delta }_1,{\lambda }_{12}=\frac{2{\lambda }_1{\lambda }_2}{\left({\lambda }_1+{\lambda }_2\right)},$ $K=2\left(\frac{\left(1-{\nu }_1\right)}{{\mu }_1}+\frac{\left(1-{\nu }_2\right)}{{\mu }_2}\right),$ $\xi =\tan \left(\frac{\pi x}{d}\right)$, $\eta =\tan \left(\frac{\pi t}{d}\right)$, $\alpha =\tan \left(0.5\frac{\pi a}{d}\right)$, $\beta =\tan \left(0.5\frac{\pi b}{d}\right)$, $\Delta T=\frac{1}{\pi }{\displaystyle {\int }_{-\alpha }^{\alpha }\frac{\gamma \left(\xi \right)}{{\xi }^2+1}d\xi ,}$ $f^{\prime }\left(\eta \right)=\frac{df}{d}\eta .$

The system (12, 13) is supplemented with the conditions (Chumak, 2018)

$\begin{array}{ll}h(\pm \alpha )=0,h^{\prime }(\pm \alpha )=0,\gamma (\pm \alpha )=0,{\gamma }^{\prime }(\pm \alpha )=0,& (14)\end{array}$

which ensure that the contact stresses and heat flows are bounded at the gap ends.

The system of singular integro-differential equations of a similar form was obtained by Chumak (2018) when solving the thermoelastic contact problem for wavy surfaces. To solve the system, the iterative procedure, developed by Martynyak and Chumak (2012), was adapted. For the sake of brevity, we omit the details, which can be found in Martynyak and Chumak (2012) and Chumak (2018), and provide only the final result:

$\begin{array}{ll}h\left(\xi \right)=-\frac{\sqrt{{\alpha }^2-{\xi }^2}}{\alpha }{\displaystyle \sum _{n-0}^N\left(A_n-B_n\frac{{\displaystyle {\sum }_{k-0}^N{A}_k}}{{\displaystyle {\sum }_{k-0}^N{B}_k}}\right)\frac{U_{2n}\left(\frac{\xi }{\alpha }\right)}{2n+1}},\left|\xi \right|\le \alpha ;& (15)\end{array}$

$\begin{array}{ll}\gamma \left(\xi \right)=-\frac{dq\sqrt{{\alpha }^2-{\xi }^2}}{\pi {\lambda }_{12}}\left(\frac{2}{\chi }+\ln \frac{\chi -\sqrt{{\alpha }^2-{\xi }^2}}{\chi +\sqrt{{\alpha }^2-{\xi }^2}}+\frac{{\lambda }_g}{q}{\displaystyle \sum _{m=1}^M{C}_m}\left(\frac{U_{2m}\left(\frac{\xi }{\alpha }\right)}{2m+1}-\frac{U_{2m-2}\left(\frac{\xi }{\alpha }\right)}{2m-1}\right)\right),\left|\xi \right|\le \alpha .& (16)\end{array}$

$\begin{array}{ll}p=\frac{p_g-{\displaystyle {\sum }_{n-0}^N{A}_n}}{{\displaystyle {\sum }_{n-0}^N{B}_n}},& (17)\end{array}$

$\begin{array}{ll}T=\frac{2d}{\pi {\lambda }_{12}}\left(\frac{q}{\chi }\left(\chi \ln \chi -\chi +1\right)-\frac{{\lambda }_g}{2}{\displaystyle \sum _{m=1}^M{\left(-1\right)}^m{C}_m{\alpha }^{-2m}{\left(\chi -1\right)}^{2m-1}\left(\frac{{\left(\chi -1\right)}^2}{2m+1}+\frac{{\alpha }^2}{2m-1}\right)}\right).& (18)\end{array}$

Here, $\chi =\sqrt{{\alpha }^2+1}$, α is supposed to be known value, U_n(ξ) is the Chebyshev polynomial of the second kind, A_n, B_n, C_m are known constants. On each iteration step, these constants are determined from the corresponding systems of linear algebraic equations (for more details, see section 3.2 of Chumak, 2018).

The solution of the problem includes an unknown gas pressure p_g. To calculate it, we can use the ideal gas law:

$\begin{array}{ll}{p}_g{V}_g=\frac{m_g}{{\mu }_g}R{T}_g,& (19)\end{array}$

where m_g denotes the mass of the gas, μ_g is the molar mass of the gas, V_g denotes the volume of the gas, T_g is the absolute temperature of the gas, and R denotes the universal gas constant (R = 8.3145 JK⁻¹mol⁻¹).

Expressing the gas volume in terms of the gap height h(ξ),

$\begin{array}{ll}{V}_g=l{\displaystyle {\int }_{-a/2}^{a/2}h\left(x\right)dx}=\frac{ld}{\pi }{\displaystyle {\int }_{-\alpha }^{\alpha }\frac{h\left(\xi \right)}{{\xi }^2+1}d\xi },& (20)\end{array}$

substituting (15) into (20) and performing the integration, we obtain

$\begin{array}{ll}{V}_g=ld{\displaystyle \sum _{n=0}^N{\left(-1\right)}^{n+1}{\alpha }^{-2n-1}}{\left(\chi -1\right)}^{2n+1}\left(A_n-B_n\frac{{\displaystyle {\sum }_{k-0}^N{A}_k}}{{\displaystyle {\sum }_{k-0}^N{B}_k}}\right),& (21)\end{array}$

where l = 1 m.

We relate the absolute gas temperature to the temperatures of the gap surfaces as

$\begin{array}{ll}{T}_g=\frac{1}{a}{\displaystyle {\int }_{-a/2}^{a/2}\frac{T^{-}\left(x,0\right)+T^{+}\left(x,0\right)}{2}dx}+T_0,& (22)\end{array}$

where T₀ = 273.15 K.

Since $T^{-}(x,0)=\frac{{\lambda }_{12}\gamma (x)}{(2{\lambda }_1)}$ and $T^{+}(x,0)=\frac{-{\lambda }_{12}\gamma (x)}{(2{\lambda }_2)}$ (Chumak, 2018),

$\begin{array}{ll}{T}_g=\frac{{\lambda }_{12}^{*}\pi }{4arctan(\alpha )}\Delta T+T_0,& (23)\end{array}$

where ${\lambda }_{12}^{*}=\frac{({\lambda }_2-{\lambda }_1)}{({\lambda }_1+{\lambda }_2)}.$

Substitution of (21) and (23) into (19) yields

$\begin{array}{l}{p}_g=\frac{R{m}_g}{4ld{\mu }_g\arctan (\alpha )}\\ \frac{{\lambda }_{12}^{s\ast }\text{π}\Delta T+4T_0\arctan (\alpha )}{{\displaystyle {\sum }_{n=0}^N{\left(-1\right)}^{n+1}}{\alpha }^{-2n-1}{\left(\chi -1\right)}^{2n+1}\left(A_n-B_n\frac{{\displaystyle {\sum }_{k-0}^N{A}_k}}{{\displaystyle {\sum }_{k-0}^N{B}_k}}\right)}.& (24)\end{array}$

Then, the applied pressure p can be calculated using (17).

Results and Discussion

Calculations are performed for the Stainless Steel AISI 304 (the material of the body S₁)—Aluminum Alloy A380 (the material of the body S₂) pair in the presence of air or krypton in the interface gaps. The properties of the materials and the interstitial gases are listed in Tables 1, 2, respectively. The other parameters are chosen to be: b = 1 mm, d = 4 mm. The notations that are used in the figures below are provided in Table 3.

TABLE 1

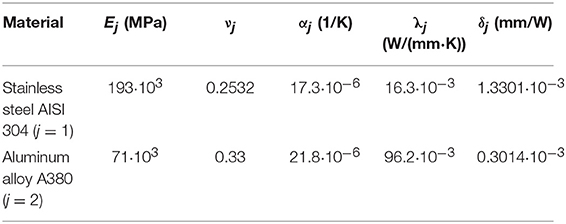
Table 1. The properties of the materials (Harvey, 1982; NADCA, 2015).

TABLE 2

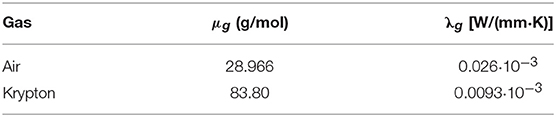
Table 2. The properties of the interstitial gases (Dorf, 2003).

TABLE 3

Table 3. The notations used in the figures.

Since the thermal distortivity δ₁ of Stainless Steel AISI 304 is greater than the thermal distortivity δ₂ of Aluminum Alloy A380, q > 0 corresponds to the case of heat flowing into the material with the smaller thermal distortivity (blue lines in the figures) and q < 0 corresponds to the case of heat flowing into the material with the larger thermal distortivity (red lines in the figures).

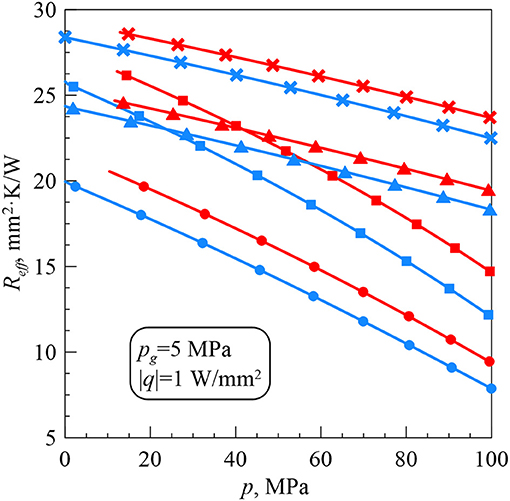
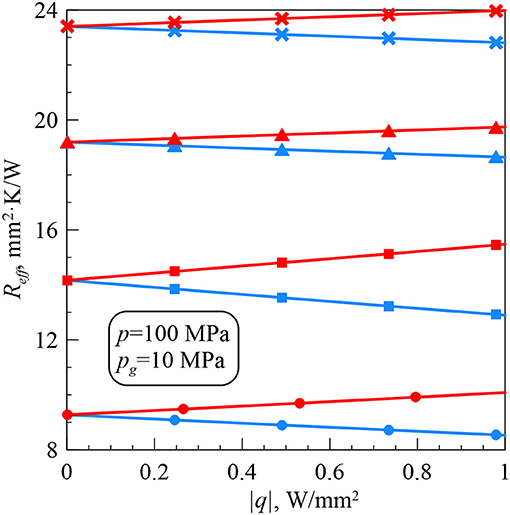
Figure 3 shows the dependences of the effective thermal contact resistance R_eff on the applied pressure p. The results are presented for the gas pressure p_g = 5 MPa and two values of heat flux: q = 1 W/mm² and q = −1 W/mm². The effective thermal contact resistance changes upon reversal of the direction in which heat is flowing, i.e., thermal rectification between the contacting bodies takes place. At fixed values of input parameters, R_eff is always greater when heat flows into the material with the larger thermal distortivity (red lines). For the two opposite directions of heat flow, R_eff decreases as p increases and is always larger in the case of krypton. The greater is the maximum height r₀ of the grooves, the greater is R_eff.

FIGURE 3

Figure 3. The effective thermal contact resistance R_eff vs. the applied pressure p.

It should be noted that red curves in Figure 3 do not intersect the axis p = 0. This is connected with the fact that the solution of the thermoelastic contact problem has been constructed under the assumption that the gap width cannot exceed the groove width (a ≤ b). However, the heat flow directed to the material with higher thermal distortivity has prevailing influence on the gap deformation at low applied pressures and causes spread of the gap outside the initial groove boundaries. In this case, the thermoelastic contact problem must be solved for a > b. This adds certain complexity to construction of the problem solution and goes beyond the scope of the investigations performed in the work.

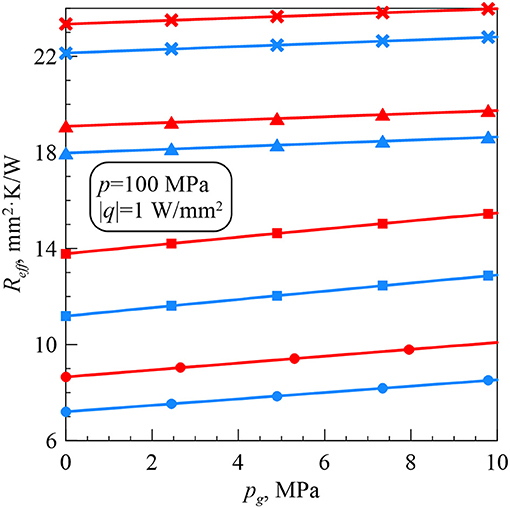
The effective thermal contact resistance R_eff vs. the gas pressure p_g is shown in Figure 4 for p = 100 MPa and |q| = 1 W/mm². An increase in p_g leads to an increase in R_eff.

FIGURE 4

Figure 4. The effective thermal contact resistance R_eff vs. the gas pressure p_g.

R_eff for p_g = 10 MPa is greater R_eff for p_g = 0 MPa by

• 15.58% when r₀ = 0.005 mm, the interstitial gas is air and q = 1 W/mm²;

• 14.24% when r₀ = 0.005 mm, the interstitial gas is air and q = −1 W/mm²;

• 13.26% when r₀ = 0.005 mm, the interstitial gas is krypton and q = 1 W/mm²;

• 10.96% when r₀ = 0.005 mm, the interstitial gas is krypton and q = −1 W/mm².

R_eff for krypton is greater R_eff for air by

• 35.62% when r₀ = 0.005 mm, p_g = 0 MPa, and q = 1 W/mm²;

• 37.24% when r₀ = 0.005 mm, p_g = 0 MPa, and q = −1 W/mm²;

• 33.85% when r₀ = 0.005 mm, p_g = 10 MPa, and q = 1 W/mm²;

• 34.85% when r₀ = 0.005 mm, p_g = 10 MPa, and q = −1 W/mm².

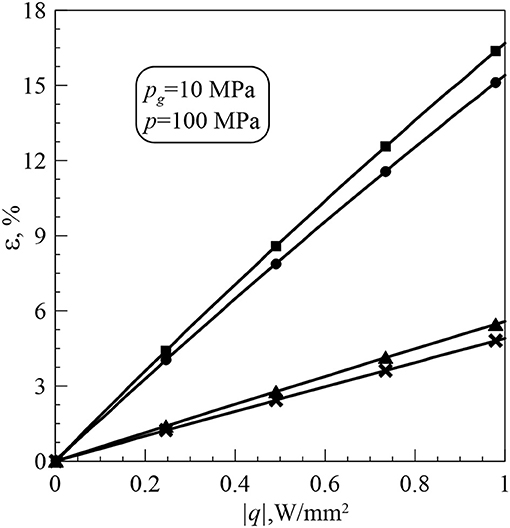
As an absolute value of increases, R_eff decreases when heat flows into the aluminum alloy and increases when heat flows into the stainless steel (Figure 5).

FIGURE 5

Figure 5. The effective thermal contact resistance R_eff vs. the heat flux |q|.

To assess a level of thermal rectification for a given |q|, we use the rectification index ε defined by the formula $\epsilon =(R_{eff}^{Al\to SS}-R_{eff}^{SS\to Al})/R_{eff}^{Al\to SS}*100\%$ (Snaith et al., 1986; Madhusudana, 1993). Here, $R_{eff}^{Al\to SS}$ denotes the effective resistance in the case of heat flowing from the aluminum alloy to the stainless steel and $R_{eff}^{SS\to Al}$ denotes the effective resistance in the case of heat flowing from the stainless steel to the aluminum alloy.

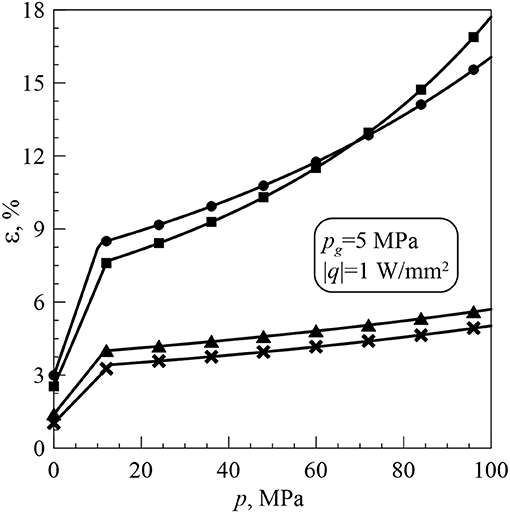
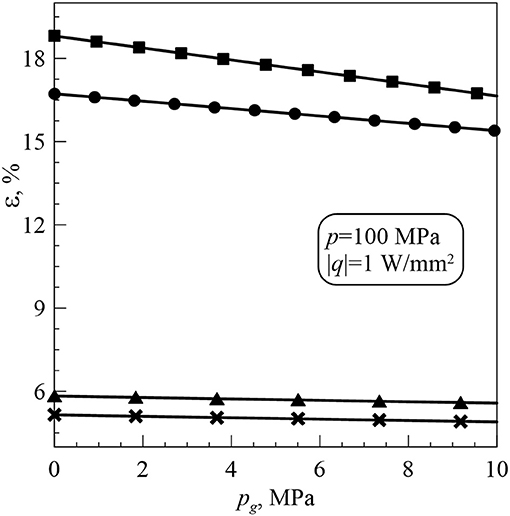
Figures 6–8 provide the dependences of the rectification index ε on the applied pressure p, gas pressure p_g and heat flux |q|, respectively.

FIGURE 6

Figure 6. The thermal rectification index ε vs. the applied pressure p.

FIGURE 7

Figure 7. The thermal rectification index ε vs. the gas pressure p_g.

FIGURE 8

Figure 8. The thermal rectification index ε vs. the heat flux |q|.

ε increases with increasing p, besides more rapidly for lower pressures (Figure 6). When r₀ = 0.005 mm, ε for air is greater than ε for krypton up to approx. p = 67 MPa, but ε for air is smaller than ε for krypton for larger values of p. When r₀ = 0.01 mm, ε for air is greater than ε for krypton within the whole considered range of p.

A decrease in p_g or an increase in |q| causes an increase in ε (Figures 7, 8). The thermal rectification level can reach up to 18% for the considered range of input parameters.

ε for p_g = 10 MPa is greater ε for p_g = 0 MPa by

• 7.93% when r₀ = 0.005 mm, the interstitial gas is air and |q| = 1 W/mm²;

• 11.44% when r₀ = 0.005 mm, the interstitial gas is krypton and |q| = 1 W/mm².

ε for krypton is greater ε for air by

• 11.16% when r₀ = 0.005 mm, p_g = 0 MPa and |q| = 1 W/mm²;

• 7.64% when r₀ = 0.005 mm, p_g = 10 MPa and |q| = 1 W/mm².

Conclusions

The thermoelastic contact between a periodically grooved surface and a flat surface in the presence of an ideal gas in the interface gaps has been investigated. The combined thermal and mechanical effect of the interstitial medium was taken into account. The thermal influence of the gas was simulated by the gap thermal resistance that is directly proportional to the gap height and inversely proportional to the gas thermal conductivity. The mechanical influence of the gas was taken into account by its pressure.

The contact problem was reduced to a system of singular integro-differential equations for a temperature jump across the gap and a gap height. To solve the system, the iterative procedure, developed recently by the authors, was adapted. The relationship between the gas pressure and the applied pressure was obtained using the condition of boundedness of contact stresses at the gap ends. Expressing the gas volume in terms of the gap height and relating the absolute gas temperature to the temperatures of the gap surfaces, the ideal gas law was used to calculate the gas pressure.

To evaluate the effective thermal contact resistance and the level of thermal rectification, the Stainless Steel AISI 304—Aluminum Alloy A380 interface in the presence of air or krypton in the interface gaps was examined. It was revealed that the effective thermal contact resistance is greater when heat flows from the aluminum alloy to the stainless steel (into the material with the higher thermal distortivity) than for the reverse heat flow direction. The effective resistance for krypton-filled gaps is always larger than the effective resistance for air-filled gaps. The effective resistance increases as the applied pressure decreases or the gas pressure increases. An increase in the absolute value of heat flow leads to a decrease/an increase in the effective resistance when heat flows into the aluminum alloy/stainless steel. It is observed that the level of thermal rectification increases with increasing heat flow magnitude, decreasing gas pressure and increasing applied pressure. The rectification level changes variously with the thermal conductivity of the interstitial gas depending on the applied pressure.

Taking into account the mechanical effect of the gap filler leads to lower values of thermal rectification level. Also, the change of the gap filler thermal conductivity has more pronounced effect that the change of its pressure.

Author Contributions

RM designed the model and the study, and supervised the findings of this work. KC wrote the manuscript with support from RM, performed the analytic calculations and the numerical simulations, and designed the figures. All authors discussed the results and contributed to the final manuscript.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Bahrami, M., Yovanovich, M. M., and Culham, J. R. (2004a). Thermal joint resistances of conforming rough surfaces with gas-filled gaps. J. Thermophys. Heat Transf. 18, 318–325. doi: 10.2514/1.5480

CrossRef Full Text | Google Scholar

Bahrami, M., Yovanovich, M. M., and Culham, J. R. (2004b). Thermal joint resistances of nonconforming rough surfaces with gas-filled gaps. J. Thermophys. Heat Transf. 18, 326–332. doi: 10.2514/1.5482

CrossRef Full Text | Google Scholar

Barber, J. R. (1971). The effect of thermal distortion on constriction resistance. Int. J. Heat Mass. Transf. 14, 751–766. doi: 10.1016/0017-9310(71)90105-0

CrossRef Full Text | Google Scholar

Boer, M. P. (2007). Capillary adhesion between elastically hard rough surfaces. Exp. Mech. 47:171. doi: 10.1007/s11340-006-0631-z

CrossRef Full Text | Google Scholar

Chumak, K. (2018). The thermoelastic contact problem for wavy surfaces with a heat-conducting medium in interface gaps. Math. Mech. Solids 23, 1389–1406. doi: 10.1177/1081286517726369

CrossRef Full Text | Google Scholar

Chumak, K., and Martynyak, R. (2012). Thermal rectification between two thermoelastic solids with a periodic array of rough zones at the interface. Int. J. Heat Mass. Transf. 55, 5603–5608. doi: 10.1016/j.ijheatmasstransfer.2012.05.049

CrossRef Full Text | Google Scholar

Chumak, K. A., and Martynyak, R. M. (2019). Effective thermal contact resistance of regularly textured bodies in the presence of intercontact heat-conducting media and the phenomenon of thermal rectification. J. Math. Sci. 236, 160–171. doi: 10.1007/s10958-018-4103-7

CrossRef Full Text | Google Scholar

Das, A. K., and Sadhal, S. S. (1997). A note on the evaluation of thermal constriction resistance for finite thickness gaps. ASME J. Heat Transf. 119, 177–180. doi: 10.1115/1.2824084

CrossRef Full Text | Google Scholar

Dorf, R. C. (2003). CRC Handbook of Engineering Tables. Boca Raton, FL: CRC Press.

Google Scholar

Dundurs, J., and Panek, C. (1976). Heat conduction between bodies with wavy surfaces. Int. J. Heat Mass. Transf. 19, 731–736. doi: 10.1016/0017-9310(76)90125-3

CrossRef Full Text | Google Scholar

Dundurs, J., Tsai, K. C., and Keer, L. M. (1973). Contact between elastic bodies with wavy surfaces. J. Elast. 3, 109–115. doi: 10.1007/BF00045817

CrossRef Full Text | Google Scholar

Etsion, I. (2004). Improving tribological performance of mechanical components by laser surface texturing. Tribol. Lett. 17, 733–737. doi: 10.1007/s11249-004-8081-1

CrossRef Full Text | Google Scholar

Etsion, I. (2005). State of the art in laser surface texturing. ASME J. Tribol. 127, 248–253. doi: 10.1115/1.1828070

CrossRef Full Text | Google Scholar

Evtushenko, A. A., and Sulim, G. T. (1981). Stress concentration near a cavity filled with a liquid. Mater. Sci. 16, 546–549. doi: 10.1007/BF00723078

CrossRef Full Text | Google Scholar

Harvey, P. D. (1982). Engineering Properties of Steel. Metals Park, OH: American Society for Metals.

Kharitonov, V. V., and Yakutin, N. V. (1997). Contact heat transfer between dissimilar materials. Tech. Phys. 42, 125–129. doi: 10.1134/1.1258613

CrossRef Full Text | Google Scholar

Kit, G. S., Martynyak, R. M., and Machishin, I. M. (2003). The effect of a fluid in the contact gap on the stress state of conjugate bodies. Int. Appl. Mech. 39, 292–299. doi: 10.1023/A:1024414302961

CrossRef Full Text | Google Scholar

Kozachok, O., and Martynyak, R. (2018). Contact problem for wavy surfaces in the presence of an incompressible liquid and a gas in interface gaps. Math. Mech. Solids 1–13. doi: 10.1177/1081286518781679

CrossRef Full Text | Google Scholar

Kozachok, O. P., Martynyak, R. M., and Slobodian, B. S. (2018a). Interaction Between Bodies With Regular Relief in the Presence of an Interstitial Medium. Lviv: Rastr-7.

Kozachok, O. P., Slobodian, B. S., and Martynyak, R. M. (2017). Interaction of two elastic bodies in the presence of periodically located gaps filled with a real gas. J. Math. Sci. 222, 131–142. doi: 10.1007/s10958-017-3287-6

CrossRef Full Text | Google Scholar

Kozachok, O. P., Slobodian, B. S., and Martynyak, R. M. (2018b). Contact of two elastic bodies with wavy topography in the presence of gases in gaps. Mater. Sci. 54, 194–201. doi: 10.1007/s11003-018-0173-4

CrossRef Full Text | Google Scholar

Kozachok, O. P., Slobodyan, B. S., and Martynyak, R. M. (2016). Contact of elastic bodies in the presence of gas and incompressible liquid in periodic interface gaps. Mater. Sci. 51, 804–813. doi: 10.1007/s11003-016-9905-5

CrossRef Full Text | Google Scholar

Kuznetsov, Y. A. (1985). Effect of fluid lubricant on the contact characteristics of rough elastic bodies in compression. Wear 102, 177–194. doi: 10.1016/0043-1648(85)90217-0

CrossRef Full Text | Google Scholar

Machyshyn, I., and Nagórko, W. (2003). Interaction between a stratified elastic half-space and an irregular base allowing for the intercontact gas. J. Theor. Appl. Mech. 41, 271–288. Available online at: http://www.ptmts.org.pl/jtam/index.php/jtam/article/view/v41n2p271

Google Scholar

Madhusudana, C. V. (1993). Thermal contact conductance and rectification at low joint pressures. Int. Comm. Heat Mass Transf. 20, 123–132. doi: 10.1016/0735-1933(93)90013-L

CrossRef Full Text | Google Scholar

Madhusudana, C. V., and Fletcher, L. S. (1986). Contact heat transfer - The last decade. AIAA J. 24, 510–523. doi: 10.2514/3.9298

CrossRef Full Text | Google Scholar

Malanchuk, N., Slobodyan, B., and Martynyak, R. (2017). Frictional contact of two solids with a periodically grooved surface in the presence of an ideal gas in interface gaps. J. Theor. Appl. Mech. 55, 1181–1192. doi: 10.15632/jtam-pl.55.4.1181

CrossRef Full Text | Google Scholar

Manners, W. (2000). Heat conduction through irregularly spaced plane strip contacts. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 214, 1049–1057. doi: 10.1243/0954406001523515

CrossRef Full Text | Google Scholar

Martynyak, R., and Chumak, K. (2012). Effect of heat-conductive filler on interface gap on thermoelastic contact of solids. Int. J. Heat Mass Transf. 55, 1170–1178. doi: 10.1016/j.ijheatmasstransfer.2011.09.053

CrossRef Full Text | Google Scholar

Martynyak, R. M., and Slobodyan, B. S. (2008). Influence of liquid bridges in the interface gap on the contact of bodies made of compliant materials. Mater. Sci. 44, 147–155. doi: 10.1007/s11003-008-9068-0

CrossRef Full Text | Google Scholar

Martynyak, R. M., and Slobodyan, B. S. (2009). Contact of elastic half spaces in the presence of an elliptic gap filled with liquid. Mater. Sci. 45, 66–71. doi: 10.1007/s11003-009-9156-9

CrossRef Full Text | Google Scholar

Martynyak, R. M., Slobodyan, B. S., and Zelenyak, V. M. (2009). Pressure of an elastic half space on a rigid base with rectangular hole in the case of a liquid bridge between them. J. Math. Sci. 160, 470–477. doi: 10.1007/s10958-009-9511-2

CrossRef Full Text | Google Scholar

NADCA. (2015). NADCA Product Specification Standards for Die Casting, 9th Edn. Arlington Heights, IL: North American Die Casting Association.

Panek, C., and Dundurs, J. (1979). Thermoelastic contact between bodies with wavy surfaces. ASME J. Appl. Mech. 46, 854–860. doi: 10.1115/1.3424667

CrossRef Full Text | Google Scholar

Peng, W., and Bhushan, B. (2002). Sliding contact analysis of layered elastic/plastic solids with rough surfaces. ASME J. Tribol. 124, 46–61. doi: 10.1115/1.1401018

CrossRef Full Text | Google Scholar

Persson, B. N. J. (2008). Capillary adhesion between elastic solids with randomly rough surfaces. J. Phys. Condens. Matter. 20, 315007. doi: 10.1088/0953-8984/20/31/315007

CrossRef Full Text | Google Scholar

Popov, V. L., Heß, M., and Willert, E. (2019). Handbook of Contact Mechanics - Exact Solutions of Axisymmetric Contact Problems. Berlin; Heidelberg: Springer-Verlag.

Roberts, N. A., and Walker, D. G. (2011). A review of thermal rectification observations and models in solid materials. Int. J. Therm. Sci. 50, 648–662. doi: 10.1016/j.ijthermalsci.2010.12.004

CrossRef Full Text | Google Scholar

Serednytska, K. R., Martynyak, R., and Chumak, K. (2019). The thermoelastic state of a bi-material with an open gas-filled interface crack. J. Theor. Appl. Mech. 57, 331–341. doi: 10.15632/jtam-pl/104587

CrossRef Full Text | Google Scholar

Slobodyan, B. S. (2012). Pressure of an elastic body on a rigid base with a recess partially filled with a liquid that does not wet their surfaces. Mater. Sci. 47, 561–568. doi: 10.1007/s11003-012-9428-7

CrossRef Full Text | Google Scholar

Slobodyan, B. S., Malanchuk, N. I., Martynyak, R. M., Lyashenko, B. A., and Marchuk, V. E. (2014). Local sliding of elastic bodies in the presence of gas in the intercontact gap. Mater. Sci. 50, 261–268. doi: 10.1007/s11003-014-9716-5

CrossRef Full Text | Google Scholar

Snaith, B., Probert, S. D., and O'Callaghan, P. W. (1986). Thermal resistances of pressed contacts. Appl. Energy 22, 31–84. doi: 10.1016/0306-2619(86)90073-5

CrossRef Full Text | Google Scholar

Song, S., Yovanovich, M. M., and Goodman, F. O. (1993). Thermal gap conductance of conforming surfaces in contact. ASME J. Heat Transf. 115, 533–540. doi: 10.1115/1.2910719

CrossRef Full Text | Google Scholar

Stepien, P. (2011). Deterministic and stochastic components of regular surface texture generated by a special grinding process. Wear 271, 514–518. doi: 10.1016/j.wear.2010.03.027

CrossRef Full Text | Google Scholar

Stevenson, P. F., Peterson, G. P., and Fletcher, L. S. (1991). Thermal rectification in similar and dissimilar metal contacts. ASME J. Heat Transf. 113, 30–36. doi: 10.1115/1.2910547

CrossRef Full Text | Google Scholar

Wang, J., Qian, J., and Gao, H. (2009). Effects of capillary condensation in adhesion between rough surfaces. Langmuir 25, 11727–11731. doi: 10.1021/la900455k

PubMed Abstract | CrossRef Full Text | Google Scholar

Xue, X., and Polycarpou, A. A. (2007). An improved meniscus surface model for contacting rough surfaces. J.Colloid Interface Sci. 311, 203–211. doi: 10.1016/j.jcis.2007.02.038

PubMed Abstract | CrossRef Full Text | Google Scholar

Yovanovich, M. M., DeVaal, J. W., and Hegazy, A. H. (1982). A Statistical Model to Predict Thermal Gap Conductance Between Conforming Rough Surfaces. AIAA paper No. 82-0888, 1–7.