- DIMEAS - Department of Mechanical and Aerospace Engineering, Politecnico di Torino, Turin, Italy
Legged animals are capable of rapid movements, are efficient from the energy point of view, and are able to adapt their gaits to environmental conditions. Motions like walking, trotting, galloping, and jumping, are difficult to evaluate and replicate due to their being consequences of complex interactions of different systems (such as the musculoskeletal system and the central and peripheral nervous systems, including also the influence of the environment). In this paper, we analyzed the behavior of a four-legged robot constituted by one active DOF in each leg (using commercial servomotors) and one passive DOF in each knee and in the spine (using springs). Our objective was to increase the motion performances of the robot by varying the stiffness of the springs. The results obtained from the simulation underline how the stiffness of the spine influences the performance of the robot by increasing the speed and reducing the energy required by the servomotors.
1. Introduction
Nowadays, in a society where everything is influenced by innovation and every area of human knowledge can be supported and improved by the use of technology, robotics has a central role in our lives.
Mobile robots have many applications from military to space exploration, from industrial use to implementation in daily life. There are two main branches of mobile robots depending on their structure: wheeled and legged. The combination of these two branches provides an opportunity to conceive novel architectures, such as those in Boston Dynamics (2017), Muscolo and Recchiuto (2017), and Muscolo et al. (2017).
Wheeled mobile robots are famous for their use in land exploration and for many other robotic applications (Muscolo and Recchiuto, 2016). The advantage of their structure is underlined by their simplicity to construct and to control, but they are also less flexible for motion in rough terrains. Legged robots have important characteristics of mobility and versatility, which allow more complex functions respect to the wheeled one (Raibert et al., 2008; Nelson et al., 2019). However, legged locomotion presents some disadvantages: these systems are more complex and unstable and are harder to control.
The mechanism of mammalian movement has been studied from the biological point of view (Alexander, 1984), and it has been shown that big mammals preserve a lot of energy during their stride through an elastic structure in their legs; the spring-mass model has been proposed on this basis (Blickhan, 1989; Alexander, 1990). On the same topic, Chatzakos and Papadopoulos (2007) studied the passive dynamics of four-legged robots, underlining the importance of forward speed vs. touchdown angle in the self-stabilized Spring-Loaded Inverted Pendulum (SLIP). Additionally, in Poulakakis et al. (2006), simple control laws for asymmetric gaits implemented on a robot were presented. The authors of Farley et al. (1993) studied the effect of a musculoskeletal spring in legged animals and they modeled trotting and hopping as a spring-mass system in different animals. Furthermore, analysis of a wide size range of animals at equivalent speed indicated that larger animals have stiffer leg springs, proportional to the body mass, but that the angle swept by the leg spring is nearly independent of the body mass. The authors of Gehring et al. (2013) proposed a control framework for a quadrupedal robot able to drive locomotion with different gaits. Also, in a study based on SLIP (Wang et al., 2015), the authors presented a stability criterion that establishes the necessary and sufficient condition of galloping stability for the quadruped robot to attain a controlled thrust. The results demonstrated that an imbalanced posture of the trunk could be stabilized by adjusting the stiffness of the four legs. In Iida and Pfeifer (2004), the authors presented a new “cheap” method for achieving a bounding gait in four-legged robots with a minimalistic approach. Another simple control method is presented in Buchli et al. (2006); in this method, the controller works through adaptive frequency oscillators that autonomously tune the intrinsic frequency of the oscillators to the resonant frequency of a compliant four-legged robot. A computational model that unifies the well-known scale effects in running quadrupeds is presented in Herr et al. (2002). The model is constructed through a physics-based simulation of six running mammals of different sizes.
An important aspect of quadruped motion to study is the contribution provided by the presence of the spine in the system. Its effect on the leg behavior is presented in Deng et al. (2012) and Wei et al. (2015), where the researchers proposed a simplified model, on the sagittal plane, of quadruped mammals with an articulated spine joint. In Silva et al. (2013), the authors presented a four-legged robot modeled with SimMechanics.
In this paper, a novel virtual model of a four-legged robot with a flexible spine and compliant legs using springs is conceived. The robot has one active DOF for each leg, using commercial servomotors. The aim of our research is to study the behavior of the four-legged system when the stiffness of each spring joint is modified; furthermore, the impact that the flexible spine has on the system is also shown. The simulations are performed in an environment simulated in Matlab using both a general Matlab model and a CAD model with commercial products. In each model, the simulations converge to the same result.
Many studies have been performed on the same research subject, but we noted that our contribution introduces a research not underlined in the cited works. Although our research approach has been proposed for biped robots in Maiorino and Muscolo (2020), including the stiffness variation in compliant legs during locomotion, in this work, we introduce a four-legged robot with compliance in spine and legs. The novelty of our contribution can be underlined by the following four points:
• We made a comparison among compliant/rigid legs and compliant/rigid spine;
• We always used the same input without modifying the control but only the stiffness of legs and spine;
• Our system has a completely passive spine;
• Our system is low cost and simple to reproduce by the research community with simple, low-cost, readily available servomotors.
In contrast, in the work of Galloway et al. (2013), they studied the influence of the stiffness of legs without considering the spine. Culha and Saranli (2011) studied an active spine joint and compared it with a blocked one. In their study, they highlight comparative analysis of the passive motion of the spine and of passive legs as necessary future work. Such future work (that they had not yet performed or shown in the paper), is in line with the work presented in this paper. Khoramshahi et al. (2013) compared the control motion of a quadruped robot using active and fixed spines. No comparisons with the passive spine and passive legs were underlined; future work with passive-active spines was only proposed. In Eckert et al. (2015), it seems that no stiffness in the leg was analyzed in combination with spine stiffness, though passive and active spines were analyzed.
The paper is structured as follows: section 2 shows the four-legged robot model; section 3 presents the control architecture; section 4 shows the simulation tests. Sections 5 and 6 show, respectively, the discussion and conclusion.
2. Four-Legged Robot Model
2.1. Physical and Analytical Modeling
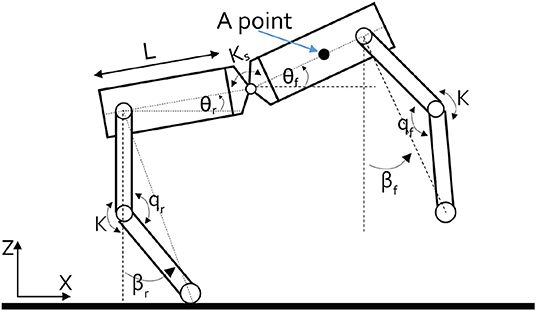
In order to understand the dynamic properties of a quadruped robot, a simple planar model is presented in Figure 1. The planar four-legged robot is divided into two symmetrical parts; each one is constituted by two symmetrical links, connected by a torsional spring and constituting the leg, which is connected to another link (the trunk) using a servomotor. The two trunks are connected with a torsional spring, functioning as the spine. Equation (1) describes the dynamic behavior of the system:
This equation is widely described in Deng et al. (2012) and Wei et al. (2015). is the mass matrix, is a matrix that includes the velocity-dependent forces, spring force, and gravitational forces. The vector contains the generalized coordinates of the model. The orientation angles of legs are is used to indicate the state of the legs. If λ = 1 (or 0) represents the leg landing (or not landing) on the ground. is the matrix containing the friction forces, driving forces, and driving torques. Q represents the actuation and dissipation elements. If these terms are ignored in (1), the dynamics is described by (2).
= [x z θf θr]T, is the mass matrix:
where m is the mass of the robot, J represents the inertia of the body, and the other terms are shown in Figure 1; k indicates the stiffness of the springs for each leg. l0 indicates the resting length of the springs. The leg angle is characterized by β. The orientation angle of the front part of the body is characterized by θf. The orientation angle of the rear part of the body is characterized by θr. L indicates the length of each half of the body. F represents the force of the leg, and its orientation coincides with the orientation of the leg.
C= [C1 C2 C3 C4]T is obtained from Deng et al. (2012) and Wei et al. (2015).
The structure of the model presented in Deng et al. (2012) and Wei et al. (2015) is slightly different from that shown in Figure 1. Indeed, our model presents a torsional spring in the knee (K) that creates momentum on the leg structure, so in this case, unlike in the case of Deng et al. (2012) and Wei et al. (2015), the forces acting parallel with the line between the contact point and the motor must be computed.
2.2. 3D Virtual Model
In order to design the 3D virtual model of the four-legged robot, in the first phase, we used Simscape Multibody™, developed by MathWorks®, which provides a simulation environment for 3D mechanical robots. The model of a four-legged robot was made using simple blocks, such as spheres, cylinders, and bricks. Broadly, it is possible to split the model into two sections: torso and legs. In the second phase, we designed a realistic 3D model with CAD, which was imported in Simscape Multibody and simulated. The results of this simulation are reported in this paper. The dimensions of the model are small, and the total weight of our four-legged robot is about 63.5g. All details are shown in Table 1, while images of the quadruped in the simulation environment are shown in Figures 2, 3.
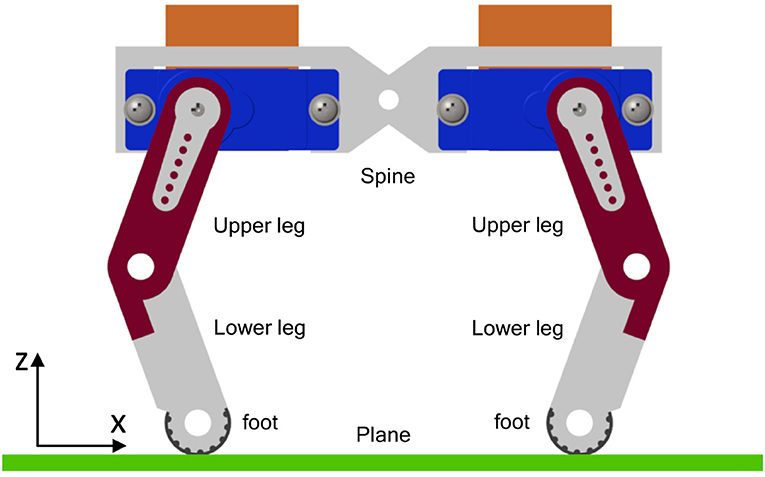
Figure 2. Side view of the robot. The blue part is the SG90 servomotor shown in Figure 4.
The trunk is divided into two identical parts separated by the spine. The four legs are identical and are composed of the upper leg, lower leg, and foot. The actuation is provided by four servomotors located at the connection point between hip and trunk. These servomotors drive the four hip joints for walking. We take the servomotor SG90 as the real model of the motors for potential future prototyping. In a first step, we planned to use the MoPei SG90 micro servomotor, which has a weight of 9g and a maximum torque of 1.6kgcm (0.1569Nm), as shown in Figure 4. In a second step, we provided to use another servomotor with a weight of 14g and capable of providing a maximum torque of 2.5kgcm (0.2452Nm). The material selected for the model is ABS (a techno-polymer), which can be developed by 3D printing and has a density of 1.12g/cc. Rubber was chosen as the material for the foot to reduce sliding and with density of 1.7g/cc. In order to enable a complete understanding of the research work performed, we included two videos of the 3D robot model walking.
3. Control Architecture
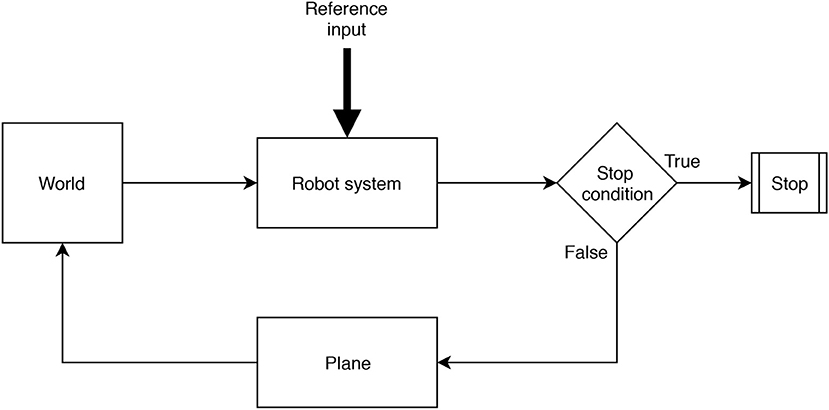
The Simscape model is composed by subsystems: the world environment, the plane and the Robot subsystem. Figure 5 shows the general architecture of the system. In the World block, the basic settings like the direction of the gravitational force and the origin of the reference system are defined. The robot system block contains the 3D model, composed of the torso and four legs, with all the blocks that define them.
The stop condition is the logic block that compares the input received from the sensor with the stop condition defined by us (for example, the maximum time of the simulation or the maximum × displacement performed by the robot). In our case, the stop conditions compare the displacement along the x, y, and z axes, measured at point A defined in Figure 1, with the world reference. If the stopping conditions are not met at the moment t, the simulation continues; in this case, the contact force library of Simscape (Miller, 2019) returns the reaction of the plane, which allows the system moving to respect the initial reference frame defined by the world.
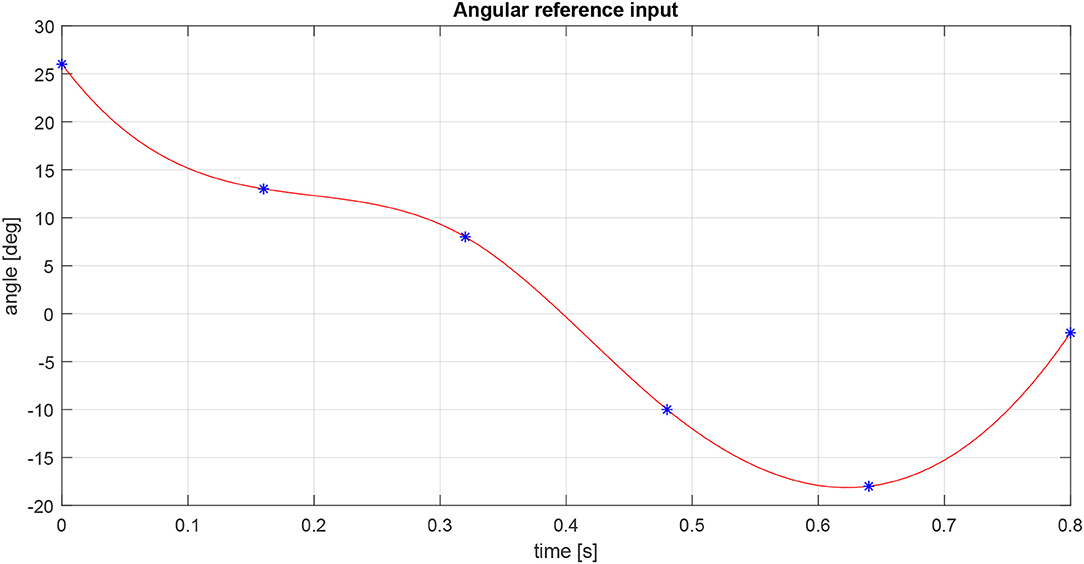
In order to allow robot movements, four hip joint actuators are used to connect the legs and torso, while the spine and knees are passive joints with torsional springs. The gait is achieved by sending the angular joint positions directly to the actuator with a gait period of 0.8s. During the walk, the right anterior and left posterior legs are activated simultaneously, while the other two legs are shifted by a half period. To find good values for the angular position to drive the hip joints, we used the Genetic Algorithm in the Matlab Global Optimization Toolbox. Figure 6 shows the trend of the reference angular joint used as input.
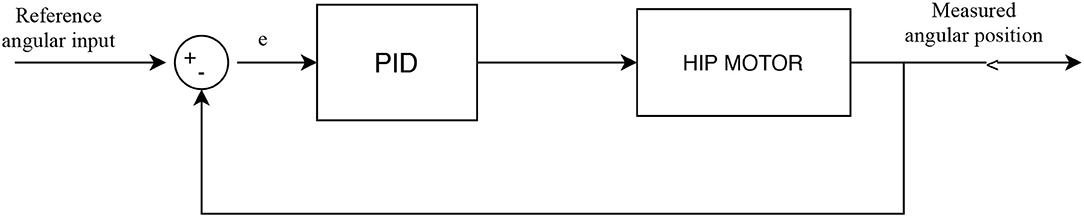
Within the scope of this paper, the robot should be capable to walk in a straight line. So, in order to fulfill this requirement, a system with a dedicated controller is not necessary. The only check of the robot stride is to stop the simulation when point A has traveled 50cm. A PID controller is used for each leg to act if there is some discrepancy between the reference angular input and that output. The parameters of the PID controller are computed through PID tune in Simulink. A general scheme of this controller is presented in Figure 7.
4. Simulation Tests
4.1. Overview
Different trials were carried out to test the performances of the robot. The performance measurements are the time spent to travel from 0 to 50 cm of displacement of point A, the torque supplied by motors, and the power spent. The directions of the x and z axes are shown in Figure 2.
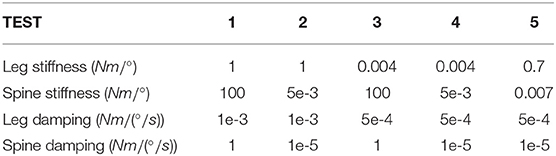
Five tests were performed using the same angular input on the servomotors in order to analyze the response of the system at different stresses.
• TEST 1: rigid (legs)—rigid (spine). In the first test, we chose to simulate a walking robot with higher values of spring stiffness in the legs and the spine.
• TEST 2: rigid (legs)—compliant (spine). In the second test, the behavior of the system is shown for the legs' spring with higher stiffness and the spine's spring compliant.
• TEST 3: compliant (legs)—rigid (spine). The third test shows the response of the robot when the springs of legs are compliant and the spring of the spine has high stiffness.
• TEST 4: compliant (legs)—compliant (spine). The fourth test shows the behavior of the robot when all springs are compliant.
• TEST 5: optimized compliant (legs)—optimized compliant (spine). TEST 5 is an optimization of the TEST 4.
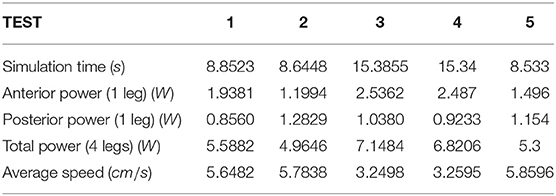
Table 2 shows the values used for all performed tests.
4.2. TEST 1: Rigid (Legs)—Rigid (Spine)
For this test, the value of the spring stiffness on legs and spine are set to allow a very small joint oscillation.
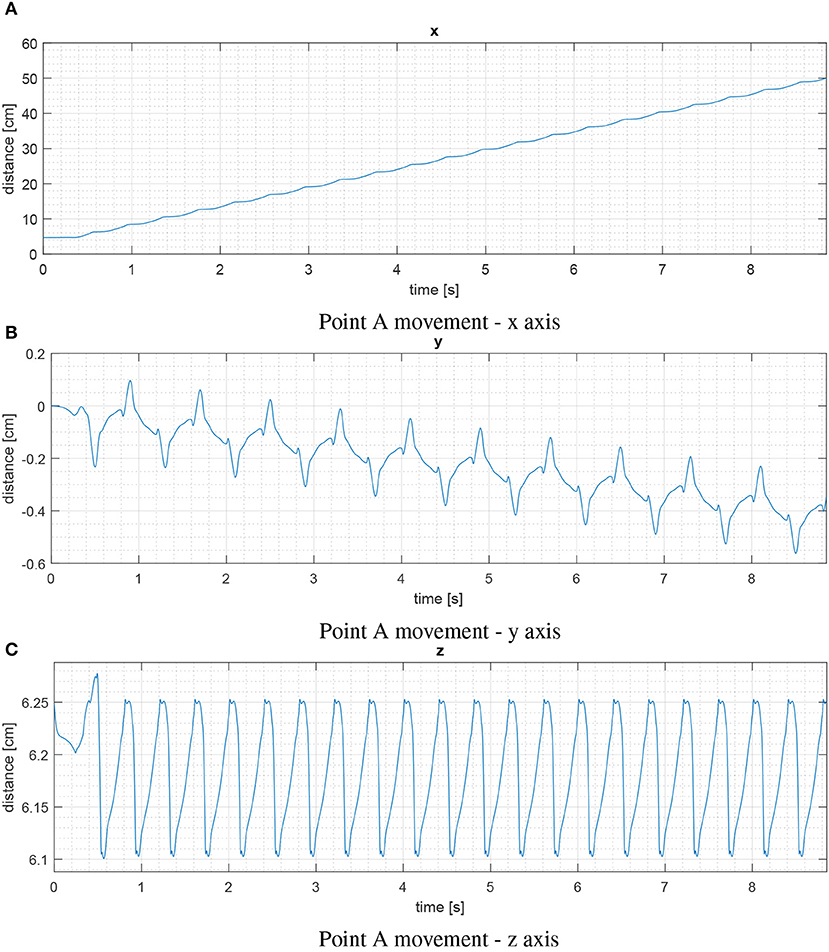
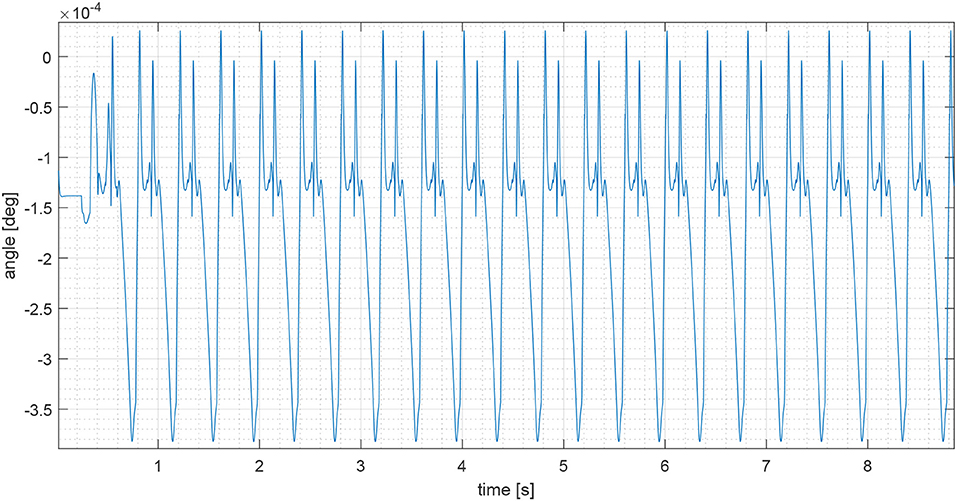
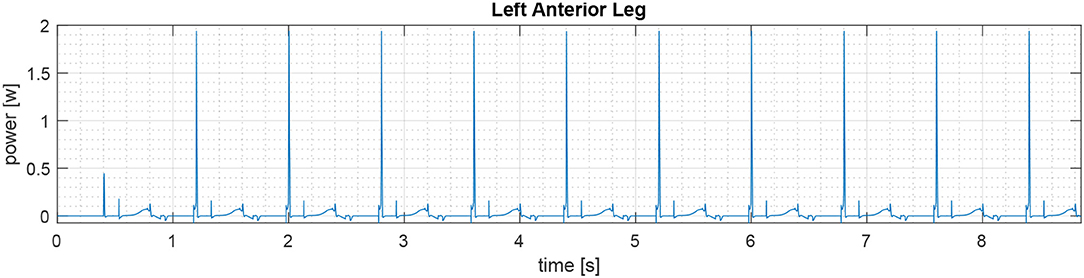
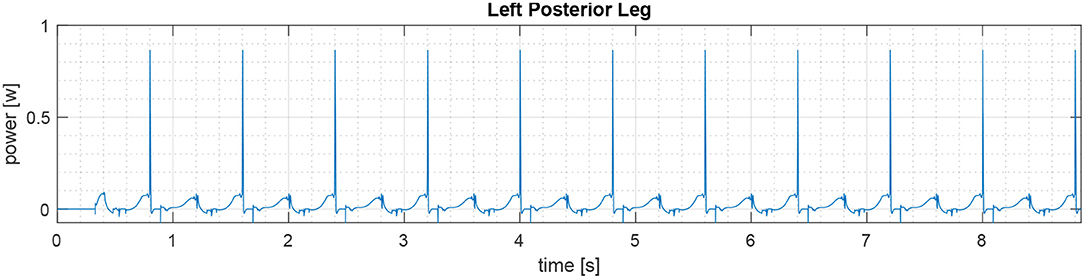
Figure 8 shows the trend of point A during the gait. In particular, we can see that the time spent to travel from 0 to 50 cm is 8.8523s, the maximum deviation on the y axis is 0.5621cm, and the trend on the z axis is between 6.1005 cm and 6.2776 cm. Figure 9 shows the angular displacement of the spine. These oscillations are very small with a range from −3.8237·10−4 degrees to 2.5945·10−5 degrees. The maximum torque, in absolute terms, is produced by the anterior legs. Its value is 0.2212Nm. The maximum torque generated by the hip joint of the posterior legs is 0.0771Nm. Regarding the power spent in walking, the maximum power is provided by the left anterior leg. Its value is 1.9381W (see Figure 10), while the maximum value of posterior leg power is 0.8560W (Figure 11).
4.3. TEST 2: Rigid (Legs)—Compliant (Spine)
The time to travel from 0 to 50 cm is 8.6448s; the maximum deviation in the module on y axis is 1.1627cm, and the trend on z axis is between 6.0846 cm and 6.2485 cm. The displacements of the spine are larger than in TEST 1 with a range from −8.2228 degrees to 0 degrees. The maximum torque is produced by the left anterior leg and is 0.2110Nm. In this test, the maximum value of power spent in walking is provided by the right posterior leg. Its value is 1.2829W.
4.4. TEST 3: Compliant (Legs)—Rigid (Spine)
The third simulation is the opposite of the TEST 2. The time to travel from 0 to 50 cm is 15.3855s, the maximum deviation on the y axis is 3.3962cm, and the trend on the z axis is between 6.0480cm and 6.3150cm. The oscillations of the spine are very small and range from −2.1677·10−4 degrees to 1.5007 · 10−4 degrees. The torque produced by the right anterior leg is 0.2347Nm. The max power in absolute terms is provided by the right anterior leg and has a value of 2.5362W.
4.5. TEST 4: Compliant (Legs)—Compliant (Spine)
In TEST 4, the time spent to travel from 0 to 50 cm is 15.34s. The maximum power spent for walking is provided by the right anterior leg. Its value is 2.487W.
4.6. TEST 5: Optimized Compliant (Legs)—Optimized Compliant (Spine)
In this test, we optimized the combination of the spring stiffness in the legs and spine of the TEST 4 obtaining, as a result, a time spent to travel from 0 to 50 cm of 8.533s. The average speed of the robot is 5.8596cm/s.
5. Discussion
Table 3 shows a summary of the results of the five tests performed.
From Table 3, it is clear that TEST 1 and TEST 2 have similar behavior with about the same forward speed. The robot performances in TEST 3 and TEST 4 differ somewhat from those in the aforementioned tests. For example, it is possible to see that, in these two tests, the robot is approximately twice slower than in the first two. The simulation time to go from 0 to 50 cm is about 8.8s in TEST 1 and TEST 2 and is about 15.3s in TEST 3 and TEST 4. It is important to underline that, in all of the tests performed, a marked difference in the torque generated by the anterior motors with respect to the posterior ones is discovered. For example, comparing the torque of one anterior and posterior leg in TEST 1, it can be seen that the peak torque generated by the former is twice the peak torque of the latter.
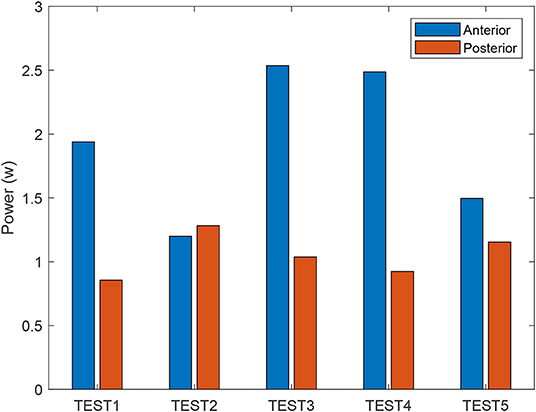
Figure 12 shows the power requested for each test performed. It can be noted that TEST 2 is the best combination of springs.
TEST 2, with rigid legs and a compliant spline, presents slightly higher performance with respect to TEST 1. This is because the introduction of a compliant spine assists with walking during the lifting and landing of the foot, with the effect of incrementing the forward speed and providing a better distribution of torque and power. If a compliant spine is included in the robot, more redistribution of the energy in the different actuators is noted. In TEST 5, where the spring stiffness is set to 0.7Nm/° and the spine stiffness to 0.007Nm/°, we may obtain a very small increment of average forward speed with respect to TEST 2, from 5.7838cm/s for TEST 2 to 5.8596cm/s for TEST 5. However, the difference in the power consumption of the two anterior and posterior legs is higher in TEST 5 with respect to TEST 2.
6. Conclusion
In this paper, we presented the design and simulation, in a 3D environment, of a simple four-legged robot modeled with CAD and Matlab. The quadruped has passive knees and a spine made by passive joints, provided by rotational springs. Each leg has one active DOF actuated by a commercial servomotor, SG90. The modification of the spring stiffness in the legs and spine allows the modification of the behavior of the system. With proper calibration, a reduction of the energy required for the movement of the robot could be obtained, increasing the performance of the system. In conclusion, we found that, with the right combination of the stiffness spring in knees and spine, it is possible to obtain better performances. However, the influence of the spine stiffness with respect to the leg stiffness is higher if the final aim is to increase robot performance in terms of reducing power consumption and allowing an optimized redistribution of the energy in the whole robotic system.
Data Availability Statement
The datasets generated for this study are available on request to the corresponding author.
Author Contributions
FS designed the robot model and performed the simulation. GM conceived, proposed, and started the research topic idea, managing, supervising, and optimizing the research work.
Funding
This work was partially funded by the Politecnico di Torino thanks to the Starting Grant for Assistant Professorship and partially funded by the author GM.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
Many thanks to Politecnico di Torino for a Starting Grant for Assistant Professorship.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmech.2020.00016/full#supplementary-material
In order to enable a complete understanding of the research work performed, we included two videos of the 3D robot model walking.
References
Alexander, R. (1990). Three uses for springs in legged locomotion. Int. J. Robot. Res. 9, 53–61. doi: 10.1177/027836499000900205
Alexander, R. M. (1984). Elastic energy stores in running vertebrates. Am. Zool. 24, 85–94. doi: 10.1093/icb/24.1.85
Blickhan, R. (1989). The spring-mass model for running and hopping. J. Biomech. 22, 1217–1227. doi: 10.1016/0021-9290(89)90224-8
Boston Dynamics (2017). Introducing Handle. Available online at: https://www.youtube.com/watch?v=-7xvqQeoA8cs (accessed January 21, 2020).
Buchli, J., Iida, F., and Ijspeert, A. J. (2006). “Finding resonance: adaptive frequency oscillators for dynamic legged locomotion,” in 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems (Beijing: IEEE), 3903–3909. doi: 10.1109/IROS.2006.281802
Chatzakos, P., and Papadopoulos, E. (2007). “Parametric analysis and design guidelines for a quadruped bounding robot,” in 2007 Mediterranean Conference on Control & Automation (Athens: IEEE), 1–6. doi: 10.1109/MED.2007.4433668
Culha, U., and Saranli, U. (2011). “Quadrupedal bounding with an actuated spinal joint,” in 2011 IEEE International Conference on Robotics and Automation (Shanghai: IEEE), 1392–1397. doi: 10.1109/ICRA.2011.5980176
Deng, Q., Wang, S., Xu, W., Mo, J., and Liang, Q. (2012). Quasi passive bounding of a quadruped model with articulated spine. Mech. Mach. Theory 52, 232–242. doi: 10.1016/j.mechmachtheory.2012.02.003
Eckert, P., Spröwitz, A., Witte, H., and Ijspeert, A. J. (2015). “Comparing the effect of different spine and leg designs for a small bounding quadruped robot,” in 2015 IEEE International Conference on Robotics and Automation (ICRA) (Seattle, WA: IEEE), 3128–3133. doi: 10.1109/ICRA.2015.7139629
Farley, C. T., Glasheen, J., and McMahon, T. A. (1993). Running springs: speed and animal size. J. Exp. Biol. 185, 71–86.
Galloway, K. C., Clark, J. E., and Koditschek, D. E. (2013). Variable stiffness legs for robust, efficient, and stable dynamic running. ASME. J. Mech. Robot. 5:011009. doi: 10.1115/1.4007843
Gehring, C., Coros, S., Hutter, M., Bloesch, M., Hoepflinger, M. A., and Siegwart, R. (2013). “Control of dynamic gaits for a quadrupedal robot,” in 2013 IEEE International Conference on Robotics and Automation (Karlsruhe: IEEE), 3287–3292. doi: 10.1109/ICRA.2013.6631035
Herr, H. M., Huang, G. T., and McMahon, T. A. (2002). A model of scale effects in mammalian quadrupedal running. J. Exp. Biol. 205, 959–967.
Iida, F., and Pfeifer, R. (2004). “Cheap rapid locomotion of a quadruped robot: self-stabilization of bounding gait,” in Intelligent Autonomous Systems, Vol. 8 (Amsterdam: IOS Press), 642–649.
Khoramshahi, M., Spröwitz, A., Tuleu, A., Ahmadabadi, M. N., and Ijspeert, A. J. (2013). “Benefits of an active spine supported bounding locomotion with a small compliant quadruped robot,” in 2013 IEEE International Conference on Robotics and Automation (Karlsruhe: IEEE), 3329–3334. doi: 10.1109/ICRA.2013.6631041
Maiorino, A., and Muscolo, G. G. (2020). Biped robots with compliant joints for walking and running performance growing. Front. Mech. Eng. 6:11. doi: 10.3389/fmech.2020.00011
Miller, S. (2019). Simscape Multibody Contact Forces Library. Available online at: https://www.github.com/mathworks/Simscape-Multibody-Contact-Forces-Library (accessed March 3, 2020).
Muscolo, G. G., Caldwell, D., and Cannella, F. (2017). “Biomechanics of human locomotion with constraints to design flexible-wheeled biped robots,” in 2017 IEEE International Conference on Advanced Intelligent Mechatronics (AIM) (Munich: IEEE), 1273–1278. doi: 10.1109/AIM.2017.8014193
Muscolo, G. G., and Recchiuto, C. T. (2016). TPT a novel taekwondo personal trainer robot. Robot. Auton. Syst. 83, 150–157. doi: 10.1016/j.robot.2016.05.009
Muscolo, G. G., and Recchiuto, C. T. (2017). Flexible structure and wheeled feet to simplify biped locomotion of humanoid robots. Int. J. Hum. Robot. 14:1650030. doi: 10.1142/S0219843616500304
Nelson, G., Saunders, A., and Playter, R. (2019). “The PETMAN and Atlas robots at boston dynamics,” in Humanoid Robotics: A Reference, eds A. Goswami and P. Vadakkepat (Dordrecht: Springer), 169–186. doi: 10.1007/978-94-007-6046-2_15
Poulakakis, I., Smith, J. A., and Buehler, M. (2006). “On the dynamics of bounding and extensions: towards the half-bound and gallop gaits,” in Adaptive Motion of Animals and Machines (Tokyo: Springer), 79–88.
Raibert, M., Blankespoor, K., Nelson, G., and Playter, R. (2008). Bigdog, the rough-terrain quadruped robot. IFAC Proc. 41, 10822–10825. doi: 10.3182/20080706-5-KR-1001.01833
Silva, M., Barbosa, R. S., and Castro, T. S. (2013). “Development of a quadruped robot model in simmechanics™,” in Nature-Inspired Mobile Robotics 709–716. doi: 10.1142/9789814525534_0089
Wang, C., Zhang, T., Wei, X., Long, Y., and Wang, S. (2015). Dynamic imbalance analysis and stability control of galloping gait for a passive quadruped robot. Appl. Bionics Biomech. 2015:479615. doi: 10.1155/2015/479615
Keywords: four-legged robots, compliant joints, multibody model, legged robots, small legged robot, torsional spring
Citation: Spadaro FT and Muscolo GG (2020) Influence of Compliant Joints in Four-Legged Robots. Front. Mech. Eng. 6:16. doi: 10.3389/fmech.2020.00016
Received: 22 January 2020; Accepted: 10 March 2020;
Published: 07 May 2020.
Edited by:
Nicola Ivan Giannoccaro, University of Salento, ItalyReviewed by:
Yoshitaka Nakanishi, Kumamoto University, JapanFrancesco Dal Corso, University of Trento, Italy
Copyright © 2020 Spadaro and Muscolo. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Giovanni Gerardo Muscolo, Z2lvdmFubmkubXVzY29sb0Bwb2xpdG8uaXQ=
 Francesco Tracuzzi Spadaro
Francesco Tracuzzi Spadaro Giovanni Gerardo Muscolo
Giovanni Gerardo Muscolo