Stress Distributions in the Cattaneo–Mindlin Problem on a Contact With Slip and Adhesion of Two Cylindrical Bodies

Two-dimensional Cattaneo–Mindlin problem on a contact with slip and adhesion between two elastic bodies of the same material is considered in classical statement for circular cylinders as well as in more general statements: for non-circular cylinders with higher order of touch and cylindrical bodies with a wavy periodic surface. Stress distributions are found both in the contact area and inside the bodies. The question of how the friction affects a formation of adhesion zone in the contact area and distribution of maximum tangential stress within the bodies is investigated.

Introduction

If elastic bodies are made of the same material and their sizes as well as the radii of curvature of their surfaces are much larger than the size of contact area, then a mutual slip of contacting surfaces will not occur in the case of normal contact. It means that friction forces do not appear in the contact area (Johnson, 1985). If a shear loading is applied to such contacted bodies, then depending on its magnitude, compared with a normal loading, two cases are possible. The first one is full mutual slip of surfaces of the bodies in whole contact area, which occurs under ultimate shear loading. In the second case, surfaces of the bodies clutch in the middle of contact area under the friction influence and slide against each other at its edges. In the last case, we have a contact with slip and adhesion. The size of adhesion zone is unknown in advance and depends, in particular, on a friction coefficient.

Contact with slip and adhesion between elastic bodies of the same material, first considered independently by Cattaneo (1938) and Mindlin (1949), is commonly called the Cattaneo–Mindlin problem (Johnson, 1985). In a two-dimensional case, this problem involves the contact of elastic cylindrical bodies under conditions of plane strain. In a three-dimensional case, it is about the contact of elastic spheres or bodies, which have smooth convex surfaces and touch each other previously at a point. The Cattaneo (1938) and Mindlin (1949) have found distribution of tangential stress in the contact area. The stress within the bodies, in particular, a parameter corresponding to the von Mises yield criterion was investigated in Dini and Hills (2004).

The generalization of the Cattaneo–Mindlin problem on the cases of higher-order touch, multiple contact areas and periodic contact are presented in Ciavarella (1998a,b), Jager (1998), Block and Keer (2008), Papangelo and Ciavarella (2015), and Papangelo et al. (2015). The stress distributions inside the contacting bodies were not studied in these papers. Periodic contact with slip and adhesion problems of plane strain between two elastic bodies with the same material (one is a half-space and another has a complex shape surface) were considered in Goryacheva et al. (2012), Chumak et al. (2014), Goryacheva and Martynyak (2014), and Malanchuk et al. (2017).

This article deals with two-dimensional Cattaneo–Mindlin problem as in classical statement for circular cylinders and also in two more general statements: for non-circular cylinders with higher order of touch and cylindrical bodies with a wavy periodic surface. In addition to the distribution of contact stresses, the distribution of stresses is found inside the bodies, in particular, the distribution of maximum tangential stress. Previously, a study of distribution of maximum tangential stress in elastic bodies, which are under conditions of smooth and sliding contact, was performed by Belyaev (1924), Sneddon (1946, 1948), Kuznetsov (1978), Kuznetsov and Gorokhovsky (1978), Johnson (1985), Ostryk (2015a,b), Klimchuk and Ostrik (2017), and Klimchuk and Ostryk (2018). Results of such studies enable to reveal zones with high values of tangential stresses, where a plastic flow of material appears according to the Tresca yield criterion.

Contact of Circular Cylinders

Let us consider two elastic cylinders, which have radii R₁ and R₂ as well as the same elastic constants (G is a shear modulus and ν a Poisson's ratio). Cylinders touch previously along the common generatrix (Figure 1A). They are being compressed by normal forces of intensity P uniformly distributed through the axial coordinate and form a contact area −a ≤ x ≤ a (Figure 1B). After that, cylinders are applied by uniformly distributed tangential forces of intensity Q, perpendicular to generatrix (Figure 1C). Under the friction influence, the contact area divides into the adhesion zone c ≤ x ≤ c in the middle as well as slip zones −a ≤ x < c, c < x ≤ a at its edges. Boundary points of cylinders have the same tangential displacements in the adhesion zone. Tangential and normal stresses are subjected to the Amonton friction law in slip zones. Thus, they are proportional with a friction coefficient μ₀. The plane strain independent of the axial coordinate takes place within the cylinders. Owing to the assumption that a contact area is small (a < < R₁, R₂), the problem is formulated for two elastic half-planes. Surfaces of the bodies near the contact area are approximated by parabolic cylinders $y=x^2/(2R_1)$, $y=-x^{2/}/(2R_2)$.

FIGURE 1

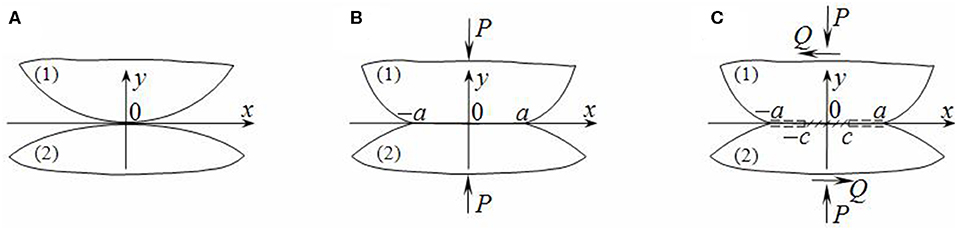
Figure 1. Scheme of contact: (A) bodies prior to loading and (B) the first stage and (C) the second stage of loading.

On the first stage of normal loading, boundary conditions of the problem have the form

$\begin{array}{l}(u_y^{(2)}-u_y^{(1)}){|}_{y=0}=\frac{x^2}{2R^{*}},{\sigma }_y^{(1)}{|}_{y=0}={\sigma }_y^{(2)}{|}_{y=0},\\ -a\le x\le a,{\sigma }_y^{(1)}{|}_{y=0}={\sigma }_y^{(2)}{|}_{y=0}=0,|x|>a,\\ {\tau }_{xy}^{(1)}{|}_{y=0}={\tau }_{xy}^{(2)}{|}_{y=0}=0,-\infty <x<\infty ,\frac{1}{R^{*}}=\frac{1}{R_1}+\frac{1}{R_2}& (1)\end{array}$

where R^* is a combined radius of curvature. According to the last condition, shear stresses are absent in the contact area due to the problem symmetry with respect to axis Oy. With the use of a solution of this problem (Johnson, 1985), the contact pressure function

$\begin{array}{ll}p(x)=-\frac{1}{2G}{\sigma }_y^{(1)}{|}_{y=0}=-\frac{1}{2G}{\sigma }_y^{(2)}{|}_{y=0},-a\le x\le a& (2)\end{array}$

has a following form:

$\begin{array}{ll}p(x)=\frac{P}{\pi a^{2}G}\sqrt{a^2-x^2}.& (3)\end{array}$

A half-width of contact area is determined by an equality

$\begin{array}{ll}a=2\sqrt{\frac{(1-\nu )P{R}^{*}}{\pi G}},& (4)\end{array}$

which follows from an equilibrium condition

$\begin{array}{ll}{\displaystyle \underset{-a}{\overset{a}{\int }}}p(x)dx=\frac{P}{2G}.& (5)\end{array}$

On the second stage of loading by tangential forces Q, considered in Cattaneo (1938) and Mindlin (1949), boundary conditions are the following:

$\begin{array}{l}\left(u_x^{(2)}-u_x^{(1)}\right){|}_{y=0}=0,-c\le x\le c,{\tau }_{xy}^{(1)}{|}_{y=0}\\ ={\mu }_0{\sigma }_y^{(1)}{|}_{y=0},c<|x|\le a,\\ \left(u_y^{(2)}-u_y^{(1)}\right){|}_{y=0}=\frac{x^2}{2R^{*}},{\sigma }_y^{(1)}{|}_{y=0}={\sigma }_y^{(2)}{|}_{y=0},{\tau }_{xy}^{(1)}{|}_{y=0}\\ ={\tau }_{xy}^{(2)}{|}_{y=0},-a\le x\le a,\\ {\sigma }_y^{(1)}{|}_{y=0}={\sigma }_y^{(2)}{|}_{y=0}={\tau }_{xy}^{(1)}{|}_{y=0}={\tau }_{xy}^{(2)}{|}_{y=0}=0,|x|>a.& (6)\end{array}$

Normal stress ${\sigma }_y^{(1)}{|}_{y=0}$ in the contact area remains the same as on the first stage. It is determined by equalities (2) and (3). According to the Cattaneo–Mindlin solution, a dimensionless function of tangential contact tractions

$\begin{array}{ll}q(x)=-\frac{1}{2G}{\tau }_{xy}^{(1)}{|}_{y=0}=-\frac{1}{2G}{\tau }_{xy}^{(2)}{|}_{y=0},-a\le x\le a& (7)\end{array}$

in slip and adhesion zones has the forms

$\begin{array}{l}q(x)=\frac{{\mu }_{0}P}{\pi a^{2}G}\left(\sqrt{a^2-x^2}-\sqrt{c^2-x^2}\right),-c\le x\le c,\\ q(x)={\mu }_{0}p(x),c<|x|\le a.& (8)\end{array}$

The relative size of adhesion zone

$\begin{array}{ll}\frac{c}{a}=\sqrt{1-\frac{Q}{{\mu }_{0}P}}& (9)\end{array}$

is determined by an equilibrium condition

$\begin{array}{ll}{\displaystyle \underset{-a}{\overset{a}{\int }}}q(x)dx=\frac{Q}{2G}.& (10)\end{array}$

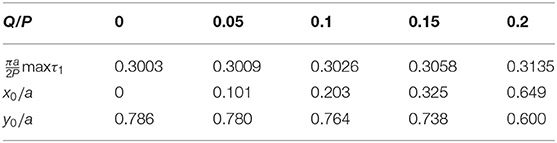
Figure 2 shows the distribution of normalized normal $\bar{p}(x)=(2Ga/P)$ and tangential $\bar{q}(x)=(2Ga/P)q(x)$ contact tractions in the case μ₀ = 0.25 for different values of ratio Q/P. The distribution of contact pressure $\bar{p}(x)$ is permanent, and the distribution of tangential tractions $\bar{q}(x)$ has characteristic breaks at points x = ±c of transition from the adhesion zone to slip zones. For values Q/P = 0.05, 0.1, 0.15, and 0.2, the relative size c/a of the adhesion zone is 0.894, 0.775, 0.633, and 0.447, respectively. In the case of Q/P = 0, tangential tractions do not appear (q(x) ≡ 0) in the contact area (corresponding to a smooth contact). In the case of Q/P = μ₀, we have a sliding contact. Herewith, the adhesion zone disappears (c/a = 0).

FIGURE 2

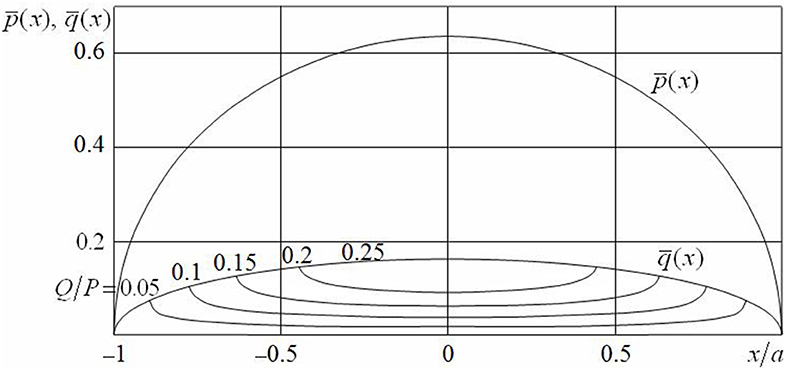
Figure 2. Distribution of normal $\bar{p}(x)$ and tangential $\bar{q}(x)$ contact tractions (μ₀ = 0.25, ν = 0.3, Q/P = 0.05, 0.1, 0.15, 0.2, 0.25).

Stresses at each point (x, y) of elastic half-plane (cylinder 1) are found with use of the Kolosov formulas (Muskhelishvili, 1966):

$\begin{array}{l}\frac{1}{2G}({\sigma }_x+{\sigma }_y)=-4\Re \Phi (z),\frac{1}{2G}({\sigma }_y-{\sigma }_x+2i{\tau }_{xy})\\ =2[\overline{\Phi }(z)+\Phi (z)+(z-\overline{z}){\Phi }^{\prime }(z)],& (11)\end{array}$

where Φ(z) is the Kolosov–Muskhelishvili potential, an analytic function of complex variable z = x + iy, presented by the Cauchy type integral

$\begin{array}{ll}\Phi (z)=\frac{1}{2\pi i}{\displaystyle \underset{-a}{\overset{a}{\int }}}\frac{p(s)-iq(s)}{s-z}ds.& (12)\end{array}$

According to formulas (3) and (8), density of integral (12) has the form

$\begin{array}{ll}p(s)-iq(s)=\frac{P}{\pi a^{2}G}\{\begin{array}{l}(1-i{\mu }_o)\sqrt{a^2-s^2}+i{\mu }_0\sqrt{c^2-s^2},-c\le s\le c,\hfill \\ (1-i{\mu }_o)\sqrt{a^2-s^2},-a\le s<-c,c<s\le a.\hfill \end{array}& (13)\end{array}$

Taking into account (Equation 13), we write the function Φ(z) from Equation (12) as follows:

$\begin{array}{l}\Phi (z)=\frac{P}{\pi a^{2}G}\frac{1}{2\pi i}[(1-i{\mu }_0){\displaystyle \underset{-a}{\overset{a}{\int }}\frac{\sqrt{a^2-s^2}}{s-z}}ds\\ +i{\mu }_0{\displaystyle \underset{-c}{\overset{c}{\int }}\frac{\sqrt{c^2-s^2}}{s-z}ds}].& (14)\end{array}$

With the use of a value of integral

$\begin{array}{ll}{\displaystyle \underset{-a}{\overset{a}{\int }}}\frac{\sqrt{a^2-s^2}}{s-z}ds=\pi \left(\sqrt{z^2-a^2}-z\right),& (15)\end{array}$

obtained by the contour integration method (Muskhelishvili, 1966), finally, we find that

$\begin{array}{ll}\Phi (z)=-\frac{iP}{2\pi a^{2}G}\left[(1-{\mu }_0)\sqrt{z^2-a^2}+i{\mu }_0\sqrt{z^2-c^2}-z\right].& (16)\end{array}$

With the use of formula (11), the combinations of stresses are determined:

$\begin{array}{l}{\sigma }_x+{\sigma }_y=-\frac{4P}{\pi a^2}\Im \left[(1-i{\mu }_0)\sqrt{z^2-a^2}+i{\mu }_0\sqrt{z^2-c^2}-z\right],\\ {\sigma }_x-{\sigma }_y+2i{\tau }_{xy}=\frac{4P}{\pi a^2}[{\mu }_0\left(\sqrt{z^2-a^2}-\sqrt{z^2-c^2}\right)\\ +y\left(\frac{(1-i{\mu }_0)z}{\sqrt{z^2-a^2}}+\frac{i{\mu }_{0}z}{\sqrt{z^2-c^2}}-1\right)].& (17)\end{array}$

To find separate components of stress tensor from Equation (17), we set distances $r_1^{\pm }$, $r_2^{\pm }$, ρ and angles ${\vartheta }_1^{\pm }$, ${\vartheta }_2^{\pm }$, ϑ by the following dependences:

$\begin{array}{ll}z\mp a={r_1}^{\pm }{e^i}^{{\vartheta }_1^{\pm }},z\pm c={r_2}^{\pm }{e^i}^{{\vartheta }_2^{\pm }},z=\rho e^{i\vartheta }.& (18)\end{array}$

Then we get

$\begin{array}{l}{\sigma }_x+{\sigma }_y=-\frac{4P}{\pi a^2}[\sqrt{{r_1}^{+}{r_1}^{-}}(\text{sin}\frac{{\vartheta }_1^{+}+{\vartheta }_1^{-}}{2}-{\mu }_0\text{cos}\frac{{\vartheta }_1^{+}+{\vartheta }_1^{-}}{2})\\ +\sqrt{{r_2}^{+}{r_2}^{-}}{\mu }_0\text{cos}\frac{{\vartheta }_2^{+}+{\vartheta }_2^{-}}{2}-y],\\ {\sigma }_x-{\sigma }_y+2i{\tau }_{xy}=\frac{4P}{\pi a^2}[-{\mu }_0\sqrt{{r_1}^{+}{r_1}^{-}}{e}^{i\frac{{\vartheta }_1^{+}+{\vartheta }_1^{-}}{2}}\\ +{\mu }_0\sqrt{{r_2}^{+}{r_2}^{-}}{e}^{i\frac{{\vartheta }_2^{+}+{\vartheta }_2^{-}}{2}}\\ +(1-i{\mu }_0)\frac{\rho y}{\sqrt{{r_1}^{+}{r_1}^{-}}}{e}^{i(\vartheta -\frac{{\vartheta }_1^{+}+{\vartheta }_1^{-}}{2})}+i{\mu }_0\frac{\rho y}{\sqrt{{r_2}^{+}{r_2}^{-}}}{e}^{i(\vartheta -\frac{{\vartheta }_2^{+}+{\vartheta }_2^{-}}{2})}-y].& (19)\end{array}$

Equality (19) yields the following stresses:

$\begin{array}{l}{\sigma }_x=-\frac{2P}{\pi a^2}\{\sqrt{r_1^{+}{r}_1^{-}}\left(\sin \frac{{\vartheta }_1^{+}+{\vartheta }_1^{-}}{2}-2{\mu }_0\cos \frac{{\vartheta }_1^{+}+{\vartheta }_1^{-}}{2}\right)\\ +2{\mu }_0\sqrt{r_2^{+}{r}_2^{-}}\cos \frac{{\vartheta }_2^{+}+{\vartheta }_2^{-}}{2}\\ +\frac{\rho }{2a}\sqrt{r_1^{+}{r}_1^{-}}[\cos \left(\vartheta -\frac{{\vartheta }_1^{+}+{\vartheta }_1^{-}}{2}\right)\\ +{\mu }_0\sin \left(\vartheta -\frac{{\vartheta }_1^{+}+{\vartheta }_1^{-}}{2}\right)]\sin \left({\vartheta }_1^{+}-{\vartheta }_1^{-}\right)\\ -{\mu }_0\frac{\rho }{2c}\sqrt{r_2^{+}{r}_2^{-}}\sin \left(\vartheta -\frac{{\vartheta }_1^{+}+{\vartheta }_1^{-}}{2}\right)\sin \left({\vartheta }_2^{+}-{\vartheta }_2^{-}\right)\\ -\frac{1}{a}{r}_1^{+}{r}_1^{-}\sin \left({\vartheta }_1^{+}-{\vartheta }_1^{-}\right)\},\\ {\sigma }_y=-\frac{2P}{\pi a^2}\{\sqrt{r_1^{+}{r}_1^{-}}\sin \frac{{\vartheta }_1^{+}+{\vartheta }_1^{-}}{2}\\ +{\mu }_0\frac{\rho }{2c}\sqrt{r_2^{+}{r}_2^{-}}\sin \left(\vartheta -\frac{{\vartheta }_2^{+}+{\vartheta }_2^{-}}{2}\right)\sin \left({\vartheta }_2^{+}-{\vartheta }_2^{-}\right)\\ -\frac{\rho }{2a}\sqrt{r_1^{+}{r}_1^{-}}[\cos \left(\vartheta -\frac{{\vartheta }_1^{+}+{\vartheta }_1^{-}}{2}\right)\\ +{\mu }_0\sin \left(\vartheta -\frac{{\vartheta }_1^{+}+{\vartheta }_1^{-}}{2}\right)]\sin \left({\vartheta }_1^{+}-{\vartheta }_1^{-}\right)\},\\ {\tau }_{xy}=\frac{2P}{\pi a^2}\{-{\mu }_0\sqrt{r_1^{+}{r}_1^{-}}\sin \frac{{\vartheta }_1^{+}+{\vartheta }_1^{-}}{2}\\ +{\mu }_0\sqrt{r_2^{+}{r}_2^{-}}\sin \frac{{\vartheta }_2^{+}+{\vartheta }_2^{-}}{2}+\frac{\rho }{2a}\sqrt{r_1^{+}{r}_1^{-}}[\sin \left(\vartheta -\frac{{\vartheta }_1^{+}+{\vartheta }_1^{-}}{2}\right)\\ -{\mu }_0\cos \left(\vartheta -\frac{{\vartheta }_1^{+}+{\vartheta }_1^{-}}{2}\right)]\sin \left({\vartheta }_1^{+}-{\vartheta }_1^{-}\right)\\ +{\mu }_0\frac{\rho }{2c}\sqrt{r_2^{+}{r}_2^{-}}\cos \left(\vartheta -\frac{{\vartheta }_2^{+}+{\vartheta }_2^{-}}{2}\right)\sin \left({\vartheta }_2^{+}-{\vartheta }_2^{-}\right)\}.& (20)\end{array}$

In addition, we find the principal normal σ₁, σ₂, σ₃ and tangential τ₁, τ₂, τ₃ stresses (Timoshenko and Goodyear, 1979)

$\begin{array}{l}{\sigma }_{1,2}=\frac{1}{2}({\sigma }_x+{\sigma }_y)\pm {\tau }_1,{\sigma }_3=\nu ({\sigma }_x+{\sigma }_y),{\tau }_1\\ =\frac{1}{2}|{\sigma }_y-{\sigma }_x+2i{\tau }_{xy}|,{\tau }_{2,3}=\frac{1}{2}|{\sigma }_{2,1}-{\sigma }_3|& (21)\end{array}$

as well as maximum tangential stress

$\begin{array}{ll}{\tau }_{max}=max({\tau }_1,{\tau }_2,{\tau }_3).& (23)\end{array}$

Figures 3, 4 present the level lines of maximum tangential stress τ_max, calculated for Poisson's ratio ν = 0.3. The solid lines correspond to τ_max, and the dashed ones point to τ₁, if τ₁ < τ_max = τ₂. Figure 3A refers to a smooth contact (Q/P = 0), Figure 3B (μ₀ = 0.25, Q/P = 0.15), and Figure 4A (μ₀ = 0.5, Q/P = 0.3) refer to a contact with slip and adhesion, and Figure 3C (μ₀ = Q/P = 0.25) and Figure 4B (μ₀ = Q/P = 0.5) refer to a sliding contact. Distribution of stress τ_max for a contact with slip and adhesion is transitional between the same distribution for the smooth and sliding contacts. In this case, the largest values of stress τ_max increase, while the force ratio Q/P moves from 0 to μ₀. If a friction coefficient μ = 0.25, then the value max τ_max = max τ₁ is reached at point x = ± x₀, y = ± y₀ inside each of contacting bodies. This point is shifting in a direction of shear loading and closer to the surface of the body in comparison with a smooth contact (Table 1). If a friction coefficient μ₀ = 0.5, then with increase in Q/P, this point comes first to the surface of the body; and second, while moving to a sliding contact, the value τ_max becomes the largest at all points of contact area ($max{\tau }_{max}=max{\tau }_1=0.5\frac{2P}{\pi a}$, −1 < x/a < 1, Figure 4B). In addition, under sliding contact conditions for μ₀ = 0.25 (as shown in Figure 3C), the largest value ${\tau }_{max}=0.331\frac{2P}{\pi a}$, slightly bigger than the value $max{\tau }_1=0.330\frac{2P}{\pi a}$ inside a half-plane, is reached within the slip zone at points x/a = ± 0.243 by stresses τ₂ and τ₃, respectively. For μ₀ = 0.5 and Q/P = 0.3 (Figure 4A), the largest value ${\tau }_{max}={\tau }_1=0.387\frac{2P}{\pi a}$ is the same at all points of slip zones (0.633a < |x| < a).

FIGURE 3

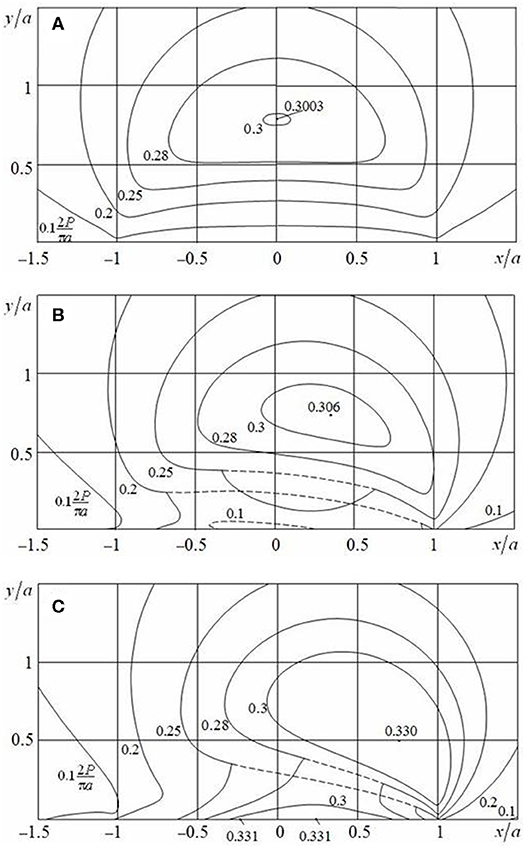
Figure 3. Distribution of maximum tangential stress τ_max in the cases of (A) smooth contact (μ₀ = 0, Q/P = 0), (B) contact with slip and adhesion (μ₀ = 0.25, Q/P = 0.15), and (C) sliding contact (μ₀ = Q/P = 0.25).

FIGURE 4

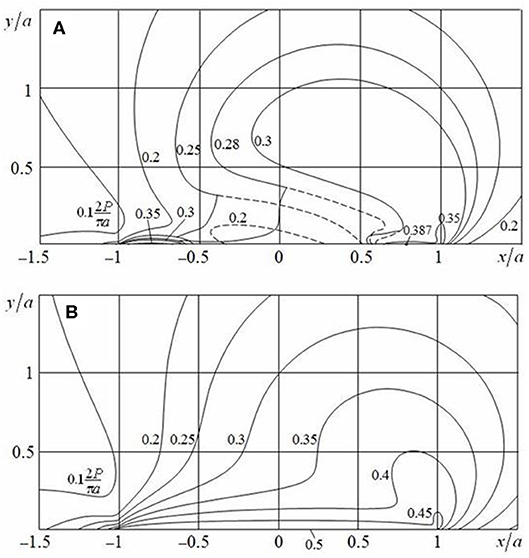
Figure 4. Distribution of maximum tangential stress τ_max in the cases of (A) contact with slip and adhesion (μ₀ = 0.5, Q/P = 0.3) and (B) sliding contact (μ₀ = Q/P = 0.5).

TABLE 1

Table 1. Points with the largest value of maximum tangential stress.

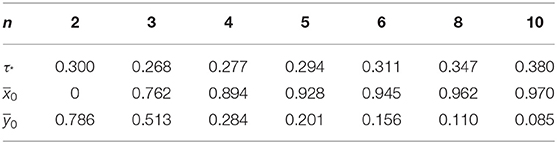
A more detailed numerical analysis shows that for friction coefficients from μ₀ < 0.25 and for any ratio of forces in range 0 ≤ Q/P ≤ μ₀, the value max τ_max is reached at point inside a body. For each μ₀ ≥ 0.25, there is such a transient value (Q/P)_* that the value max τ_max is realized inside a half-plane while 0 ≤ Q/P < (Q/P)_* and at the boundary of a half-plane in slip zones while (Q/P)_* ≤ Q/P ≤ μ₀. Values (Q/P)_* are given in Table 2 for various friction coefficients. The largest value τ_max = τ_{2, 3} is reached at certain symmetrical points x = ±x₁ inside the right and left slip zones, while 0.25 ≤ μ₀ < 0.5. The largest value τ_max = τ₁ is constant along both slip zones while μ₀ ≥ 0.5.

TABLE 2

Table 2. Transient values (Q/P)_* for various friction coefficients μ₀.

To summarize these results, we have obtained in analytical form the largest values τ_max in slip zones. With the use of relations (17), (21), and (22), the following expressions are found for the principal tangential stresses:

$\begin{array}{l}{\tau }_1={\mu }_0\frac{2P}{\pi a}\sqrt{1-{\left(\frac{c}{a}\right)}^2},{\tau }_{2,3}\\ =\frac{P}{\pi a^2}|(1-2\nu )\left(\sqrt{a^2-x^2}+\text{sgn}x·{\mu }_0\sqrt{x^2-c^2}\right)\\ \pm {\mu }_0\sqrt{a^2-c^2}|,\\ y=0,c<|x|<a.& (23)\end{array}$

Here, we find that

$\begin{array}{l}\underset{c<|x|<a}{\max }{\tau }_{\max }{|}_{y=o}=\{\begin{array}{l}{\tau }_{2,3}{|}_{y=0,x=\pm x_1}=\frac{P}{\pi a^2}\sqrt{a^2-c^2}\\ \left[(1-2\nu )\sqrt{1+{\mu }_0^2}+{\mu }_0\right],{\mu }_0\le {\mu }_0^{*},\\ {\tau }_1{|}_{y=0,c<\left|x\right|<a}={\mu }_0\frac{2P}{\pi a}\sqrt{1-{(c/a)}^2},{\mu }_0\ge {\mu }_0^{*},\end{array}\\ x_1=\sqrt{\frac{{\mu }_0^2{a}^2+c^2}{1+{\mu }_0^2}}\text{, }{\mu }_0^{*}=\frac{1-2\nu }{2\sqrt{\nu (1-\nu )}}.& (24)\end{array}$

In particular, ${\mu }_0^{*}=0.436$ for ν = 0.3. Values $\underset{c<|x|<a}{max}{\tau }_{max}{|}_{y=0}$ in Equation (24) become the largest values τ_max, if they are bigger than the values max τ₁ inside a half-plane. This is illustrated in Figures 3C, 4A,B.

We note that in the case μ₀ = 0.5, Q/P = 0.15, the distribution of maximum tangential stress is almost the same as for μ₀ = 0.25, Q/P = 0.15 (shown in Figure 3B). This fact indicates that the distribution of maximum tangential stresses is not almost affected by the distribution of tangential tractions in the contact area, but only the main vector of tractions is significant.

Touch of Higher Order

Consider the Cattaneo–Mindlin problem for non-circular cylinders, if their prior contact along the common generatrix has higher order. In this case, we set surfaces of bodies near the contact area by equations $y=B_1|x{|}^n$, $y=-B_2|x{|}^n$ (B₁ > 0, B₂ > 0; n = 2, 3, …). If n = 2, then we have the classic Cattaneo–Mindlin problem for circular cylinders.

Further, we use singular integral relations (Johnson, 1985):

$\begin{array}{l}\frac{\partial u_x^{(1,2)}}{\partial x}{|}_{y=0}=-(1-2\nu )p(x)\pm 2(1-\nu )\frac{1}{\pi }\underset{-a}{\stackrel{a}{\int }}\frac{q(s)}{s-x}ds,\\ \frac{\partial u_y^{(1,2)}}{\partial x}{|}_{y=0}=(1-2\nu )q(x)\pm 2(1-\nu )\frac{1}{\pi }\underset{-a}{\stackrel{a}{\int }}\frac{p(s)}{s-x}ds,& (25)\end{array}$

where functions p(x) and q(x) are determined by Equations (2) and (7), respectively, while −a ≤ x ≤ a and equal to zero at |x| > a.

The boundary conditions for the first stage of normal loading are set in Equation (1), except the first condition, which should be written as follows:

$\begin{array}{ll}\left(u_y^{(2)}-u_y^{(1)}\right){|}_{y=0}=B{|x|}^n,-a\le x\le a,B=B_1+B_2.& (26)\end{array}$

Satisfying differentiated condition (26) by the second relation (25) with q(x) ≡ 0, we obtain a singular integral equation

$\begin{array}{ll}\frac{1}{\pi }\underset{-a}{\stackrel{a}{\int }}\frac{p(s)}{s-x}ds=-\frac{nB\text{sgn}x}{4(1-\nu )}{|x|}^{n-1},-a<x<a.& (27)\end{array}$

With the solution of Equation (27), bounded at the edges of interval −a < x < a, we find in the form (Gakhov, 1963)

$\begin{array}{ll}p(x)=\frac{nB}{4(1-\nu )\pi }\sqrt{a^2-x^2}{I}_n(x),I_n(x)=\underset{-a}{\stackrel{a}{\int }}\frac{{|s|}^{n-1}\text{sgn}s}{\sqrt{a^2-s^2}}\frac{ds}{s-x}.& (28)\end{array}$

The recurrent relation holds for an integral in Equation (28),

$\begin{array}{r}{I}_n(x)=x^2{I}_{n-2}(x)+2J_{n-2},n=3,4,\dots ,\\ J_n={\displaystyle \underset{0}{\overset{a}{\int }}}\frac{s^n}{\sqrt{a^2-s^2}}ds=\frac{n-1}{n}{a}^2{J}_{n-2}=a^n{J}_n^{\prime },\\ J_{2m}^{\prime }=\frac{(2m-1)!!}{(2m)!!}\frac{\pi }{2},J_{2m-1}^{\prime }=\frac{(2m-2)!!}{(2m-1)!!},m=1,2,\dots ,& (29)\end{array}$

with initial values

$\begin{array}{l}{I}_1(x)=\frac{2}{\sqrt{a^2-x^2}}1\text{n}\frac{a+\sqrt{a^2-x^2}}{|x|},I_2(x)=\pi .\end{array}$

Applying a recurrent formula (29) several times, we find

$\begin{array}{l}{I}_{2m}(x)=2\left(J_{2m-2}+J_{2m-4}{x}^2+\dots +J_2{x}^{n-4}\right)+I_2(x)x^{2(m-1)},\\ I_{2m-1}(x)=2\left(J_{2m-3}+J_{2m-5}{x}^2+\dots +J_1{x}^{2m-4}\right)+I_1(x)x^{2(m-1)}.\end{array}$

Therefore, on the basis of Equation (28), we obtain the distribution of contact pressure

$\begin{array}{l}p(x)=\frac{P}{2\pi a^{2}G}\tilde{p}(x,a),\\ \tilde{p}(x,a)=\frac{1-{(-1)}^n}{2}\frac{n!!}{(n-1)!!}\frac{x^{n-1}}{a^{n-2}}1\text{n}\frac{a+\sqrt{a^2-x^2}}{|x|}\\ +\sqrt{a^2-x^2}{\displaystyle \sum _{k=1}^{\left[n/2\right]}}{\frac{{\left[n/2\right]}_k}{\left[(n-1)/2\right]}}_k{\left(\frac{x}{a}\right)}^{2k-2},-a\le x\le a,& (30)\end{array}$

where [n/2] is an entire part of n/2, [n]_k = n(n − 1)…(n − k + 1). Dependence of half-width a of the contact area on the force P

$\begin{array}{ll}a=\sqrt[n]{\frac{(1-\nu )P}{n{J}_n^{\prime }BG}}& (31)\end{array}$

is found from an equilibrium condition (5).

In the case of even n, formulas (30) and (31) have been obtained by Shtayerman (1949).

Figure 5 shows the dimensionless contact pressure $\bar{p}(x)=(2Ga/P)p(x)$ distribution on half-width of contact area (0 ≤ x ≤ a) for different values of indicator n. It can be noticed that with increase in n, the contact pressure decreases inside the contact area but increases at its edge.

FIGURE 5

Figure 5. Distribution of contact pressure $\bar{p}(x)$ for different n.

On the second stage, elastic bodies are loaded by tangential forces Q. Contact area −a ≤ x ≤ a divides into the adhesion zone −c ≤ x ≤ c and the slip zones −a ≤ x < −c, c < x ≤ a. In boundary condition (6), the third condition should be replaced by Equation (26) and the normal stress ${\sigma }_y^{(1)}{|}_{y=0}$ in the contact area should take the form of Equations (2) and (30). Satisfying differentiated first condition (6) by the first relation (25), we obtain an integral equation with respect to the function of tangential contact tractions q(x) in the adhesion zone

$\begin{array}{ll}\underset{-a}{\overset{a}{\int }}\frac{q(s)}{s-x}ds=0,-c<x<c.& (32)\end{array}$

Because the normal and tangential tractions in slip zones are connected by equality

$\begin{array}{ll}q(x)={\mu }_{0}p(x),c<|x|\le a,& (33)\end{array}$

Equation (32) is written as follows:

$\begin{array}{ll}\underset{-c}{\overset{c}{\int }}\frac{q(s)}{s-x}ds=-{\mu }_0\left(\underset{c}{\overset{a}{\int }}+\underset{-a}{\overset{-c}{\int }}\right)\frac{p(s)}{s-x}ds,-c<x<c.& (34)\end{array}$

The substitution of unknown function

$\begin{array}{ll}{q}_0(x)=q(x)-{\mu }_{0}p(x),-c<x<c& (35)\end{array}$

yields the following equation:

$\begin{array}{ll}\underset{-c}{\overset{c}{\int }}\frac{q_0(s)}{s-x}ds=-{\mu }_0\underset{-a}{\overset{a}{\int }}\frac{p(s)}{s-x}ds,-c<x<c.& (36)\end{array}$

Taking into account (Equation 27), integral Equation (36) takes the form

$\begin{array}{ll}\frac{1}{\pi }\underset{-c}{\overset{c}{\int }}\frac{q_0(s)}{s-x}ds={\mu }_0\frac{nB\text{sgn}x}{4(1-\nu )}{|x|}^{n-1},-c<x<c& (37)\end{array}$

and differs from the integral Equation (27) in both an integration interval (a is replaced by c) and the multiplier −μ₀ at the right part. Therefore, with respect to Equation (30), we obtain its bounded solution in the form

$\begin{array}{ll}{q}_0(x)=-\frac{{\mu }_{0}P}{2\pi a^{2}G}{\left(\frac{c}{a}\right)}^{n-2}\tilde{p}(x,c).& (38)\end{array}$

With the use of Equations (35) and (38), the function of tangential contact tractions is found in the adhesion zone

$\begin{array}{ll}q(x)=q_0(x)+{\mu }_{0}p(x)=\frac{{\mu }_{0}P}{2\pi a^{2}G}\left[\tilde{p}(x,a)-{\left(\frac{c}{a}\right)}^{n-2}\tilde{p}(x,c)\right].& (39)\end{array}$

With the use of an equilibrium condition (10), the relative size of adhesion zone is determined

$\begin{array}{ll}\frac{c}{a}=\sqrt[n]{1-\frac{Q}{{\mu }_{0}P}}.& (40)\end{array}$

Stresses in half-plane y ≥ 0 are found with use of formula (11), in which the potential density Φ(z) from Equation (12) is given as follows:

$\begin{array}{ll}p(s)\text{}-\text{}iq(s)\text{ }=\text{ }\frac{P}{2\pi a^{2}G}\{\begin{array}{l}(1-i{\mu }_0)\tilde{p}(s,a)\\ +i{\mu }_0{\left(\frac{c}{a}\right)}^{n-2}\tilde{p}(s,c),-c\le s\le c,\\ (1-i{\mu }_0)\tilde{p}(s,a),-a\le s<-c,c<s\le a.\end{array}& (41)\end{array}$

Taking into account (Equation 41), the function Φ(z) from Equation (12) is presented as

$\begin{array}{l}\Phi (z)=\frac{P}{2\pi a^{2}G}\left[(1-i{\mu }_0)\tilde{\Phi }(z,a)+i{\mu }_0{\left(\frac{c}{a}\right)}^{n-2}\tilde{\Phi }(z,c)\right],\\ \tilde{\Phi }(z,a)=\frac{1}{2\pi i}\underset{-a}{\overset{a}{\int }}\frac{\tilde{p}(s,a)}{s-z}ds.& (42)\end{array}$

Further, to find the function $\tilde{\Phi }(z,a)$ in Equation (42), we consider two cases.

1. The case of even n. Using the second formula of Equation (30), we have that

$\begin{array}{l}\tilde{\Phi }(z,a)=\frac{1}{2\pi i}(\frac{n}{n-1}{U}_0(z)+\frac{n(n-2)}{(n-1)(n-3)}\frac{U_1(z)}{a^2}\\ +\mathrm{...}+\frac{n!!}{(n-1)!!}\frac{U_{n/2-1}(z)}{a^{n-2}}),\\ U_k(z)=\underset{-a}{\overset{a}{\int }}\frac{s^{2k}\sqrt{a^2-s^2}}{s-z}ds,k=0,1,\mathrm{...}.& (43)\end{array}$

The following recurrent formula is true for integral U_k(z) in Equation (43):

$\begin{array}{l}{U}_k(z)=z^2{U}_{k-1}(z)+2z{V}_{k-1},k=1,2,\dots ,\\ V_k=\underset{0}{\overset{a}{\int }}{s}^{2k}\sqrt{a^2-s^2}ds=\frac{J_{2k+2}}{2k+1},k=0,1,\dots .& (44)\end{array}$

According to Equation (15), the integral U₀(z) in Equation (43), which is an initial value for formula (44), can be presented as

$\begin{array}{ll}{U}_0(z)=\pi \left(\sqrt{z^2-a^2}-z\right).& (45)\end{array}$

Consistently applying recurrent formula (44) and taking into account Equation (45), we find

$\begin{array}{l}{U}_k(z)=\pi z[\frac{(2k-3)!!}{(2k)!!}{a}^{2k}+\frac{(2k-5)!!}{(2k-2)!!}{a}^{2k-2}{z}^2\\ +\mathrm{...}+\frac{(-1)!!}{2!!}{a}^2{z}^{2k-2}+z^{2k-1}\left(\sqrt{z^2-a^2}-z\right)],k=0,1,\mathrm{...}.& (46)\end{array}$

Substituting U_k(z)(k = 0, 1, .. . , n/2-1) from Equation (46) into the first formula of Equation (43), after transformations, we get

$\begin{array}{l}\tilde{\Phi }(z,a)=-\frac{i}{2}{\displaystyle \sum _{k=1}^{n\backslash 2}}\left(a_{nk}\sqrt{z^2-a^2}+c_{nk}z\right){\left(\frac{z}{a}\right)}^{2k-2},\\ a_{nk}=\frac{{\left[n/2\right]}_k}{{\left[(n-1)/2\right]}_k},c_{nk}={\displaystyle \sum _{m=k}^{n/2}}\frac{(2m-2k-3)!!}{(2m-2k)!!}{a}_{nm},& (47)\end{array}$

assuming that (−)!! = 1, (−3)!! = −1, and

$\begin{array}{l}{{\tilde{\Phi }}^{\prime }}_z(z,a)=\frac{i}{2}{\displaystyle \sum _{k=1}^{n/2}\left(b_{nk}\frac{z}{\sqrt{z^2-a^2}}-(2k-1)c_{nk}\right){\left(\frac{z}{a}\right)}^{2k-2},}\\ b_{nk}=\frac{{[n/2]}_k}{[(n-3)/2_k},n=2,4,\mathrm{...};k=1,2,\mathrm{...},n/2.& (48)\end{array}$

In particular, for the case of n = 4 we have

$\begin{array}{l}{a}_{41}=\frac{4}{3},a_{42}=\frac{8}{3},b_{42}=4,b_{41}=-8,c_{41}=0,c_{42}=-\frac{8}{3},\\ \tilde{\Phi }(z,a)=-\frac{2i}{3}\left[\left(1+2\frac{z^2}{a^2}\right)\sqrt{z^2-a^2}-2\frac{z^3}{a^2}\right].& (49)\end{array}$

On the basis of Equations (42), (47), and (48), we find the stresses with use of formula (11).

1. The case of odd n. Similar to the case of even n, we obtain

$\begin{array}{l}\tilde{\Phi }(z,a)=-\frac{ia}{2}[\frac{n!!}{(n-1)!!}(\frac{1}{\pi }{\displaystyle \sum _{k=1}^{n-1}\frac{J_{n-k-1}^{\prime \prime }}{n-k}{\left(\frac{z}{a}\right)}^{k-1}}\\ +i{\left(\frac{z}{a}\right)}^{n-1}\ln \frac{ia+\sqrt{z^2-a^2}}{z})\\ +\frac{1}{a}\sqrt{z^2-a^2}{\displaystyle \sum _{k=1}^{\left(n-1\right)/2}\left(a_{nk}+c_{nk}^{\prime }\frac{z}{a}\right){\left(\frac{z}{a}\right)}^{2k-2}}],c_{nk}^{\prime }\\ ={\displaystyle \sum _{m=k}^{(n-1)/2}\frac{(2m-2k-3)!!}{(2m-2k)!!}{a}_{nm}},\\ {\tilde{\Phi }}_z^{\prime }(z,a)=-\frac{i}{2}[\frac{n!!}{(n-1)!!}\frac{1}{\pi }{\displaystyle \sum _{k=2}^{n-1}\frac{k-1}{n-k}{J}_{n-k-1}^{\prime \prime }{\left(\frac{z}{a}\right)}^{k-2}}\\ -\frac{a}{\sqrt{z^2-a^2}}{\displaystyle \sum _{k=1}^{(n-3)/2}{b}_{nk}{\left(\frac{z}{a}\right)}^{2k-1}}\\ +\frac{n!!}{(n-3)!!}\left(i\ln \frac{ia+\sqrt{z^2-a^2}}{z}+\frac{a}{\sqrt{z^2-a^2}}\right){\left(\frac{z}{a}\right)}^{n-2}\\ +{\displaystyle \sum _{k=1}^{(n-1)/2}(2k-1)}{c}_{nk}^{\prime }{\left(\frac{z}{a}\right)}^{2k-2}],\\ J_{2k}^{\prime \prime }=2J_{2k}^{\prime },J_{2k-1}^{\prime \prime }=0.& (50)\end{array}$

values ${\tau }_{*}=\frac{\pi a}{2P}max{\tau }_{max}=\frac{\pi a}{2P}max{\tau }_1$ calculated for ν = 0.3 in the case of smooth contact (Q/P = 0) are given in Table 3 as well as relative coordinates $\pm {\overline{x}}_0=\pm x_0/a,{\overline{y}}_0=y_0/a$ of points, in which these values are reached. With increase in n, these points approach the edges of contact area.

TABLE 3

Table 3. Points with values of τ_* for different n.

The distribution of maximum tangential stress τ_max in the case n = 4, ν = 0.3 is given in Figure 6. Figure 6A refers to a smooth contact (Q/P = 0), Figure 6B to a contact with slip and adhesion (μ₀ = 0.25, Q/P = 0.15), and Figure 6C to a sliding contact (μ₀ = Q/P = 0.25). As in Contact of Circular Cylinders, solid lines correspond to τ_max and dashed ones to τ₁, if τ₁ < τ_max = τ₂. By comparing with a second order touch (n = 2, Figure 3), the stress concentration is observed closer to the edges of contact area.

FIGURE 6

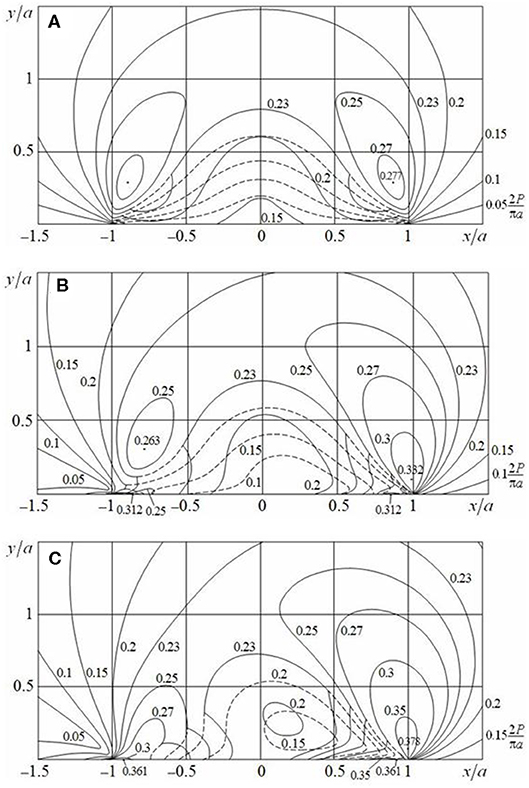
Figure 6. Distribution of maximum tangential stress τ_max in the cases of (A) smooth contact (μ₀ = 0, Q/P = 0), (B) contact with slip and adhesion (μ₀ = 0.25, Q/P = 0.15), and (C) sliding contact (μ₀ = Q/P = 0.25) for n = 4.

Periodic Case

Assume that surfaces of elastic cylindrical bodies are l-periodic along the axis Ox and touch previously through the lines x = kl(k = 0, ±1, ±2, …). Surfaces are set mathematically by equations y = $-B_1(cos\frac{2\pi x}{l}-1),$ y = $B_2(cos\frac{2\pi x}{l}-1)$ (B₁ > 0, B₂ > 0). In this variant of the Cattaneo–Mindlin problem, the bodies are compressed at infinity by the normal forces of intensity p_∞, creating the contact areas −a + kl ≤ x ≤ a + kl. After this, the tangential forces of intensity q_∞ are applied at infinity and contact areas divide into adhesion −c + kl ≤ x ≤ c + kl and slip c + kl < |x| ≤ a + kl(k = 0, ±1, ±2, …) zones.

Singular integral relation (25) in the periodic case takes the form

$\begin{array}{l}{\displaystyle {\frac{\partial u_x^{(1,2)}}{\partial x}|}_{y=0}=-(1-2v)p(x)\pm 2(1-v)\frac{1}{l}\underset{-a}{\overset{a}{\int }}q(s)cot\frac{\pi }{l}(s-x)ds,}\\ {\displaystyle {\frac{\partial u_y^{(1,2)}}{\partial x}|}_{y=0}=-(1-2v)q(x)\pm 2(1-v)\frac{1}{l}\underset{-a}{\overset{a}{\int }}p(s)cot\frac{\pi }{l}(s-x)ds,}& (51)\end{array}$

where functions p(x), q(x) are l-periodic and defined by equalities (2) and (7).

On the first stage of normal loading, boundary conditions are as follows:

$\begin{array}{l}{\left(u_y^{(2)}-u_y^{(1)}\right)|}_{y=0}=B\left(cos\frac{2\pi x}{l}+1\right),{{\sigma }_y^{(1)}|}_{y=0}={{\sigma }_y^{(2)}|}_{y=0},\\ -a+kl\le x\le a+kl,\\ {{\sigma }_y^{(1)}|}_{y=0}={{\sigma }_y^{(2)}|}_{y=0}=0,a+kl<x<l-a+kl,\\ {{\tau }_{xy}^{(1)}|}_{y=0}={{\tau }_{xy}^{(2)}|}_{y=0}=0,-\infty <x<\infty ,B\\ =B_1+B_2,k=0,\pm 1,\pm 2,\dots .& (52)\end{array}$

Satisfying differentiated first condition (52) by the second relation (51) with q(x) ≡ 0, we obtain a singular integral equation.

$\begin{array}{ll}\underset{-a}{\overset{a}{\int }}p(s)cot\frac{\pi }{l}(s-x)ds=-\frac{\pi B}{1-v}sin\frac{2\pi x}{l},-a<x<a.& (53)\end{array}$

The solution of Equation (53), bounded at the ends of interval −a < x < a, has the form (Shtayerman, 1949)

$\begin{array}{l}p(x)=\frac{2\pi B}{(1-v)l}cos\frac{\pi x}{l}.\sqrt{sin\frac{\pi }{l}(a-x)sin\frac{\pi }{l}(a+x)},\\ -a\le x\le a.& (54)\end{array}$

With the use of an equilibrium condition,

$\begin{array}{ll}\underset{-a}{\overset{a}{\int }}p(x)dx=\frac{p_{\infty }l}{2G},& (55)\end{array}$

a half-width of each contact area is determined

$\begin{array}{ll}a=\frac{l}{\pi }arcsin\sqrt{\frac{(1-v)p_{\infty }l}{\pi BG}}.& (56)\end{array}$

The boundary conditions on the second stage of tangential loading are as follows:

$\begin{array}{l}{\left(u_x^{(2)}-u_x^{(1)}\right)|}_{y=0}=0,-c+kl\le x\le c+kl,{{\tau }_{xy}^{(1)}|}_{y=0}\\ ={\mu }_0{{\sigma }_y^{(1)}|}_{y=0},c+kl<|x|\le a+kl,\\ {\left(u_y^{(2)}-u_y^{(1)}\right)|}_{y=0}=B\left(cos\frac{2\pi x}{l}+1\right),{{\sigma }_y^{(1)}|}_{y=0}\\ ={{\sigma }_y^{(2)}|}_{y=0},{{\tau }_{xy}^{(1)}|}_{y=0}={{\tau }_{xy}^{(2)}|}_{y=0},\\ -a+kl\le x\le a+kl,\\ {{\sigma }_y^{(1)}|}_{y=0}={{\sigma }_y^{(2)}|}_{y=0}={{\tau }_{xy}^{(1)}|}_{y=0}{={\tau }_{xy}^{(2)}|}_{y=0}=0,a\\ +kl<x<l-a+kl,k=0,\pm 1,\pm 2,\dots .& (57)\end{array}$

Here, the normal stress ${\sigma }_y^{(1)}{|}_{y=0}$ is known and presented by formulas (2) and (54).

Using the first boundary condition (57) and the first relation (51), in similar way to Touch of Higher Order, we obtain the integral equation with respect to l-periodic function q₀(x) from Equation (35)

$\begin{array}{ll}\underset{-c}{\overset{c}{\int }}{q}_0(s)cot\frac{\pi }{l}(s-x)ds={\mu }_0\frac{\pi B}{1-v}sin\frac{2\pi x}{l},-c<x<c.& (58)\end{array}$

The last one is similar to Equation (53). Its bounded solution has the form

$\begin{array}{l}{q}_0(x)=-{\mu }_0\frac{2\pi B}{(1-v)l}cos\frac{\pi x}{l}.\sqrt{sin\frac{\pi }{l}(c-x)sin\frac{\pi }{l}(c+x)},\\ -c\le x\le c.& (59)\end{array}$

From Equations (35) and (59), we find l-periodic function of tangential contact tractions

$\begin{array}{l}q(x)={\mu }_{0}p(x),c<\left|x\right|\le a,\\ q(x)=-{\mu }_0\frac{2\pi B}{(1-v)l}\cos \frac{\pi x}{l}.(\sqrt{\sin \frac{\pi }{l}(c-x)\sin \frac{\pi }{l}(c+x)}\\ -\sqrt{\sin \frac{\pi }{l}(a-x)\sin \frac{\pi }{l}(a+x)}),\\ -c\le x\le c.& (60)\end{array}$

From an equilibrium condition,

$\begin{array}{ll}\underset{-a}{\overset{a}{\int }}q(x)=\frac{q_{\infty }l}{2G}& (61)\end{array}$

the relative width of adhesion zones is determined as

$\begin{array}{ll}\frac{c}{a}=\frac{1}{\pi }arcsin\left(\sqrt{1-\frac{Q}{{\mu }_{0}P}}sin\frac{\pi a}{l}\right).& (62)\end{array}$

The stresses in half-plane y ≥ 0 are found with use of formula (11), where the potential Φ(z) has the form

$\begin{array}{l}\Phi (z)=\frac{1}{2il}\underset{-a}{\overset{a}{\int }}\left[p(s)-iq(s)\right]\cot \frac{\pi }{l}(s-z)ds,\\ p(s)-iq(s)=\{\begin{array}{l}(1-i{\mu }_0)p(s)-i{q}_0(s),-c\le s\le c,\\ (1-i{\mu }_0)p(s),-a\le s<-c,c<s\le a,\end{array}& (63)\end{array}$

or

$\begin{array}{ll}\Phi (z)=\frac{1-i{\mu }_0}{2il}\underset{-a}{\overset{a}{\int }}p(s)cot\frac{\pi }{l}(s-z)ds-\frac{1}{2l}\underset{-c}{\overset{c}{\int }}{q}_0(s)cot\frac{\pi }{l}(s-z)ds.& (64)\end{array}$

Calculating the integral

$\begin{array}{l}\underset{-a}{\overset{a}{\int }}cos\frac{\pi s}{l}.\sqrt{sin\frac{\pi }{l}(a-s)sin\frac{\pi }{l}(a+s)}cot\frac{\pi }{l}(s-z)ds\\ =lcos\frac{\pi z}{l}.\left(\sqrt{sin\frac{\pi }{l}(z-a)sin\frac{\pi }{l}(z+a)}-sin\frac{\pi z}{l}\right)& (65)\end{array}$

and taking into account (Equation 56), we obtain

$\begin{array}{l}\Phi (z)=-\frac{i{p}_{\infty }\cos (\pi z/l)}{G{\sin }^2(\pi a/l)}[(1-i{\mu }_0)\sqrt{\sin \frac{\pi }{l}(z-a)\sin \frac{\pi }{l}(z+a)}\\ +i{\mu }_0\sqrt{\sin \frac{\pi }{l}(z-c)\sin \frac{\pi }{l}(z+c)}-\sin \frac{\pi z}{l}],\\ \overline{\Phi }(z)+\Phi (z)=-\frac{2{\mu }_0{p}_{\infty }\cos (\pi z/l)}{G{\sin }^2(\pi a/l)}(\sqrt{\sin \frac{\pi }{l}(z-a)\sin \frac{\pi }{l}(z+a)}\\ -\sqrt{\sin \frac{\pi }{l}(z-c)\sin \frac{\pi }{l}(z+c)}),\\ {\Phi }^{\prime }(z)=-\frac{i\pi p_{\infty }\cos (\pi z/l)}{Gl{\sin }^2(\pi a/l)}[(1-i{\mu }_0)\frac{[\cos (2\pi z/l)+{\sin }^2(\pi a/l)]\sin (\pi z/l)}{\sqrt{\sin [(\pi /l)(z-a)]\sin [(\pi /l)(z+a)]}}\\ +i{\mu }_0\frac{[\cos (2\pi z/l)+{\sin }^2(\pi c/l)]\sin (\pi z/l)}{\sqrt{\sin [(\pi /l)(z-c)]\sin [(\pi /l)(z+c)]}}].& (66)\end{array}$

Substituting expressions from Equation (66) into Equation (11), the stresses are determined.

In Figure 7, the distribution of maximum tangential stress τ_max (ν = 0.3, l/a = 8) is shown in cases (A) μ₀ = 0.25, Q/P = 0.15; (B) μ₀ = 0.5, Q/P = 0.3. The solid lines correspond to τ_max, and the dashed and dash-dotted lines correspond to τ₁, if τ₁ < τ_max = τ₂ and τ₁ < τ_max = τ₃, respectively. The maximum tangential stress τ_max = τ₁ reaches the largest value within a half-plane [case (A)] or at half-plane boundary in points x ± c[c/a = 0.623 case (B)]. In the last case, the maximum tangential stress slightly decreases (within 0.6%) along the slip zones. The presented distribution differs a little from the stress distribution in the corresponding cases for a single contact area (l/a = ∞, Contact of Circular Cylinders, Figures 3B, 4A) and coincides with them at l/a ≥ 20.

FIGURE 7

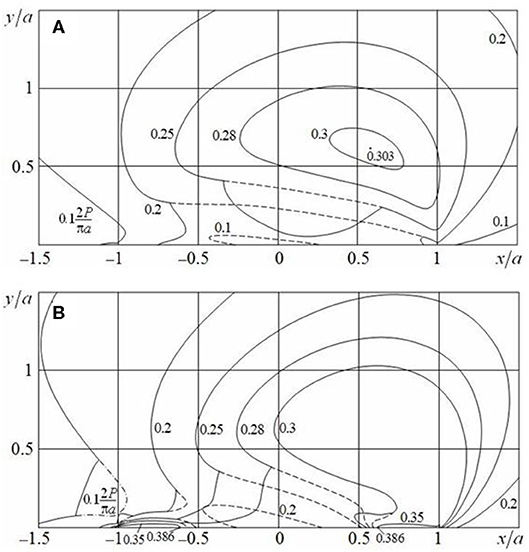
Figure 7. Distribution of maximum tangential stress τ_max in the periodic case (l/a = 8) for (A) μ₀ = 0.25, Q/P = 0.15 and (B) μ₀ = 0.5, Q/P = 0.3.

Conclusions

With the use of numerical analysis of obtained stress distributions in the Cattaneo–Mindlin problem, it is established that the point, in which maximum tangential stress reaches its largest value, is located inside each of contacting elastic bodies for a friction coefficient μ < 0.25. With increase in a friction coefficient and a shear loading, this point moves gradually to the boundary of the body (in the contact area). In the case of a touch of higher order, this point moves closer to the far edge (x = a) of contact area. At the same time, the local increase of stress occurs near the edge x = −a. Comparing with the case of a single contact area, in the periodic problem, the distribution of maximum tangential stress is almost unchanged, if a contact area does not exceed a quarter of period (l/a ≥ 8).

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

VO set a problem and performed the analytical calculations. TK created the code and performed the numerical calculations. VO and TK analyzed the results.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Belyaev, M. M. (1924). “Local stresses during compression of elastic bodies,” in Engineering Structures and Structural Mechanics (Saint Petersburg: The Way), 30–43.

Google Scholar

Block, J. M., and Keer, L. M. (2008). Periodic contact problems in plane elasticity. J. Mech. Mater. Struct. 3, 1207–1237. doi: 10.2140/jomms.2008.3.1207

CrossRef Full Text | Google Scholar

Cattaneo, C. (1938). Sul contatto di due corpi elastici: distribuzione locale degli sforzi. Rendiconti dell' Accademia nazionale dei Lincei. 27, 474–478.

Google Scholar

Chumak, K., Malanchuk, N., and Martynyak, R. (2014). Partial slip contact problem for solids with regular surface texture assuming thermal insulation or thermal permeability of interface gaps. Int. J. Mech. Sci. 84, 138–146. doi: 10.1016/j.ijmecsci.2014.04.015

CrossRef Full Text | Google Scholar

Ciavarella, M. (1998a). The generalized Cattaneo partial slip plane contact problem. I – theory. Int. J. Solids Struct. 35, 2349–2362. doi: 10.1016/S0020-7683(97)00154-6

CrossRef Full Text | Google Scholar

Ciavarella, M. (1998b). The generalized Cattaneo partial slip plane contact problem. II – examples. Int. J. Solids Struct. 35, 2363–2378. doi: 10.1016/S0020-7683(97)00155-8

CrossRef Full Text | Google Scholar

Dini, D., and Hills, D. A. (2004). Bounded asymptotic solutions for incomplete contacts in partial slip. Int. J. Solids Struct. 41, 7049–7062. doi: 10.1016/j.ijsolstr.2004.05.058

CrossRef Full Text | Google Scholar

Gakhov, F. D. (1963). Boundary Value Problems. Moscow: Fizmatgiz.

Google Scholar

Goryacheva, I. G., Malanchuk, N. I., and Martynyak, R. M. (2012). Contact interaction of bodies with a periodic relief during partial slip. J. Appl. Math. Mech. 76, 695–709. doi: 10.1016/j.jappmathmech.2013.03.002

CrossRef Full Text | Google Scholar

Goryacheva, I. G., and Martynyak, R. M. (2014). Contact problems for textured surfaces involving frictional effects. Proc. Inst. Mech. Eng. Part J. 228, 707–716. doi: 10.1177/1350650114528318

CrossRef Full Text | Google Scholar

Jager, J. (1998). A new principle in contact mechanics. ASME J. Tribol. 120, 677–684. doi: 10.1115/1.2833765

CrossRef Full Text | Google Scholar

Johnson, K. L. (1985). Contact Mechanics. Cambridge: Cambridge University Press. doi: 10.1017/CBO9781139171731

CrossRef Full Text | Google Scholar

Klimchuk, T. V., and Ostrik, V. I. (2017). Frictional contact between an elastic strip and a semi-infinite punch with rounded edge. Acta Mechanica 228, 3619–3631. doi: 10.1007/s00707-017-1866-8

CrossRef Full Text | Google Scholar

Klimchuk, T. V., and Ostryk, V. I. (2018). Smooth contact of a semi-infinite punch with rounded edge and an elastic strip. J. Math. Sci. 231, 650–664. doi: 10.1007/s10958-018-3842-9

CrossRef Full Text | Google Scholar

Kuznetsov, Y.A., and Gorokhovsky, G. A. (1978). The effect of roughness on the stress state of frictionally contacting bodies. Appl. Mech. 14, 62–68. doi: 10.1007/BF00885748

CrossRef Full Text | Google Scholar

Kuznetsov, Y. A. (1978). The superposition principle in the solution of contact – friction stress problems. Wear 50, 183–189. doi: 10.1016/0043-1648(78)90255-7

CrossRef Full Text | Google Scholar

Malanchuk, N., Slobodyan, B., and Martynyak, R. (2017). Frictional contact of two solids with a periodically grooved surface in the presence of an ideal gas in interface gaps. J. Theor. Appl. Mech. 55, 1181–1192. doi: 10.15632/jtam-pl.55.4.1181

CrossRef Full Text | Google Scholar

Mindlin, R. D. (1949). Compliance of elastic bodies in contact. J. Appl. Mech. 16, 259–268.

Google Scholar

Muskhelishvili, N. I. (1966). Some Basic Problems of the Mathematical Theory of Elasticity. Moscow: Nauka.

Google Scholar

Ostryk, V. I. (2015a). Contact Mechanics. Kyiv: Kyiv University Press.

Google Scholar

Ostryk, V. I. (2015b). Smooth contact of a polynomial profile stamp with an elastic half-plane. Bull. Kyiv Univ. 1, 41–44.

Google Scholar

Papangelo, A., and Ciavarella, M. (2015). Cattaneo – Mindlin plane problem with Griffith friction. Wear 342, 398–407. doi: 10.1016/j.wear.2015.10.005

CrossRef Full Text | Google Scholar

Papangelo, A., Ciavarella, M., and Barber, J. R. (2015). Fracture mechanics implications for apparent static friction coefficient in contact problems involving slip-weakening laws. Proc. R Soc. A 471:271. doi: 10.1098/rspa.2015.0271

CrossRef Full Text | Google Scholar

Shtayerman, I. Y. (1949). Contact Problem of the Theory of Elasticity. Moscow: Gostekhizdat.

Google Scholar

Sneddon, I. N. (1946). Boussinesq's problem for a flat-ended cylinder. Proc. Camb. Philos. Soc. 42, 29–39. doi: 10.1017/S0305004100022702

CrossRef Full Text | Google Scholar

Sneddon, I. N. (1948). Boussinesq's problem for a rigid cone. Proc. Camb. Philos. Soc. 44, 492–507. doi: 10.1017/S0305004100024518

CrossRef Full Text | Google Scholar

Timoshenko, S. P., and Goodyear, J. N. (1979). Theory of Elasticity. Moscow: Nauka.

Google Scholar