A Simplified Theory of Electroadhesion for Rough Interfaces

1. Introduction

An electric voltage applied between two contacting rough elastic bodies leads to accumulation of charges of opposite signs on the surfaces, which obviously produces electrostatic attraction. The electrostatic load adds to the external repulsive loads and possibly to van der Waals adhesive interactions. Also, it influences the intimate contact area and therefore the frictional force when the solids are sliding, which is of great interest for new touch screen applications (Vardar et al., 2017). It is therefore of utmost importance to understand the fundamentals of friction and adhesion, particularly their relation with tactile perception. This is a very active field of research nowadays, and electroadhesion is a promising technology in this area. The discovery of electroadhesion dates back to 1923, when Johnsen and Rahbek (1923) described the physical phenomenon.

Persson (2018) has extended his theory of contact mechanics (Persson, 2001, 2007) and developed a general mean-field theory that includes electroadhesion in a way similar to the Persson and Scaraggi theory for van der Waals adhesion (Persson and Scaraggi, 2014). These theories use the “Derjaguin-Muller-Toporov (DMT) assumption” (Derjaguin et al., 1975; Ciavarella et al., 2019), namely that the contact can be considered similar to that in the absence of adhesion (repulsive problem), and the effect of the adhesive forces is estimated based on the gap distribution by simply convoluting the force-separation law. The theory of Persson (2018) is developed for two limiting cases: (i) the case where an electric insulating film (actually two films in general) is interposed between the two conducting bodies, and (ii) the case of two electric conducting solids, which results in contact resistance and a voltage drop over a narrow region at the interface; in the latter case a theorem of Barber (2003) on repulsive contact is used, which states that the contact conductance is proportional to the mechanical contact stiffness. A simplified theory was also proposed by Popov and Hess (2018).

It is, however, unclear from the full Persson theories which are the main parameters governing the problem, since Persson's theories were developed in very general settings, particularly in terms of the full spectrum of roughness and the complex details of the gap between the surfaces. This results in quite elaborate theories which may not be easy to apply or interpret. A simpler theory was proposed for van der Waals adhesion by Ciavarella (2018) and Ciavarella and Papangelo (2019), called the bearing area model (BAM) as it provides a simple estimate of the adhesion forces between rough hard surfaces using an extremely simple and therefore closed-form geometric estimate of the adhesive area. The BAM is also loosely a DMT model similar to that of Persson and Scaraggi (2014), but thanks to the geometrical estimate for the bearing area, it is completely expressible in simple closed-form equations in the case of a power-law power spectrum density (PSD) of the roughness. The main goal of the present paper is to generalize this theory to electroadhesion.

As suggested in a recent paper by Dalvi et al. (2019), surface topography can easily have more than seven orders of magnitude of almost-power-law spectrum, including down to the Ångström scale (see Figure S2 in Dalvi et al., 2019, which gives the 2D isotropic PSD). But in the end, as originally suggested by Persson and Tosatti (2001), the effective adhesive force depends only on the large-wavelength components of the PSD; see also the stickiness criteria derived by Ciavarella (2019). We shall also extend the stickiness criteria to electroadhesion, and we find surprisingly universal results, despite the very different origins of the various proposals we compare. However, the real contact area, and therefore the friction force, depends crucially on the truncation of the PSD spectrum, implying a rather difficult choice which will ultimately require a best-fit exercise.

2. Electroadhesion

Let us consider the contact configuration shown in Figure 1. We have an elastic rough solid which is brought into contact with a rigid flat surface. Both solids are made of conducting materials, but they are coated with electric insulating (and rigid) films of thicknesses d₁ and d₂, respectively, and relative dielectric constants ε₁ and ε₂ (see Figure 1). A (remote) electric voltage difference V is applied at the two conducting solids. As the elastic solid is rough, the local interfacial separation u = u(x) depends on the in-plane coordinate x = (x, y).

FIGURE 1

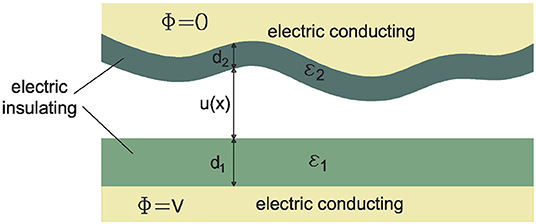
Figure 1. Sketch of the geometry considered: A rough elastic solid is squeezed against a flat rigid solid. Both solids are made of conducting materials, with insulating coatings of thicknesses d₁ and d₂ and dielectric constants ε₁ and ε₂. An electric voltage difference V is applied at the two solids. The interfacial separation u = u(x) depends on the in-plane coordinate x = (x, y).

By writing the variation of the electric potential through the contact pair, Persson (2018) obtained the z component of the electric field at the interface:

$\begin{array}{ll}{E}_z(x)=-\frac{V}{u(x)+h_0},& (1)\end{array}$

where

$\begin{array}{ll}{h}_0=\frac{d_1}{{\epsilon }_1}+\frac{d_2}{{\epsilon }_2}.& (2)\end{array}$

The normal pressure acting at the solid-vacuum interface is given by the zz component of the Maxwell stress tensor, ${\sigma }_{zz}(x)=\frac{{\epsilon }_0}{2}{E}_z^2,$ i.e.,

$\begin{array}{ll}{\sigma }_{zz}(x)=\frac{{\epsilon }_0}{2}{\left(\frac{V}{u(x)+h_0}\right)}^2,& (3)\end{array}$

where ${\epsilon }_0\simeq 8.8542\times 10^{-12}$ N/V² is the vacuum permittivity. Hence, we have an adhesive mean pressure

$\begin{array}{ll}{p}_{\text{ad}}=\frac{{\epsilon }_0}{2}{V}^2{\displaystyle {\int }_0^{\infty }}{\left(\frac{1}{u(x)+h_0}\right)}^{2}P(p|u)du,& (4)\end{array}$

where P(p|u) is the probability distribution of interfacial gaps at pressure p for given u, including the contact area. For insulating solids, the theory of Persson (2018) indeed accounts for the adhesive interactions within the contact area [u(x) = 0 in Equation 3] and for those exerted outside the contact patches. The probability distribution of gaps is in fact

$\begin{array}{ll}P(p|u)=\frac{A}{A_0}\delta (u)+P_1(p|u),& (5)\end{array}$

where δ(u) is the delta function, A is the contact area, A₀ is the nominal contact area, and P₁(p|u) is normalized so that

$\begin{array}{ll}{\displaystyle {\int }_0^{\infty }}{P}_1(p|u)du=1-\frac{A}{A_0}.& (6)\end{array}$

From the above analysis, the applied external pressure p_ext at a given mean separation $\overline{u}$ can be obtained by summing the repulsive p and the adhesive pressure p_ad (pressure is negative when compressive), which results in

$\begin{array}{l}{p}_{\text{ext}}=p+p_{\text{ad}}=p+\frac{{\epsilon }_0}{2}{\left(\frac{V}{h_0}\right)}^2\frac{A}{A_0}\\ +\frac{{\epsilon }_0}{2}{V}^2{\displaystyle {\int }_0^{\infty }}{\left(\frac{1}{u(x)+h_0}\right)}^2{P}_1(p|u)du,& (7)\end{array}$

where the adhesive terms are estimated by following the DMT method (Derjaguin et al., 1975; Ciavarella et al., 2019), i.e., neglecting the elastic deformations induced by the adhesive interactions.

In what follows, we shall assume for simplicity self-affine fractal rough surfaces that have a typical power-law PSD

$\begin{array}{ll}C(q)=Z{q}^{-2(1+H)},q_0<q<q_1,& (8)\end{array}$

where C(q) = 0 elsewhere, H = 3 − D is the Hurst exponent with D being the fractal dimension of the surface, $q=\frac{2\pi }{\lambda }$ is the wavenumber associated with the wavelength λ, q₁, and q₀ are respectively the largest and smallest wavenumbers in the surface representation, and $Z=\frac{H}{\pi }{\left(\frac{h_{\text{rms}}}{q_0}\right)}^2{\left(\frac{1}{q_0}\right)}^{-2(H+1)}$ is a constant multiplier, with h_rms being the root mean square (rms) amplitude of roughness (see Figure 2).

FIGURE 2

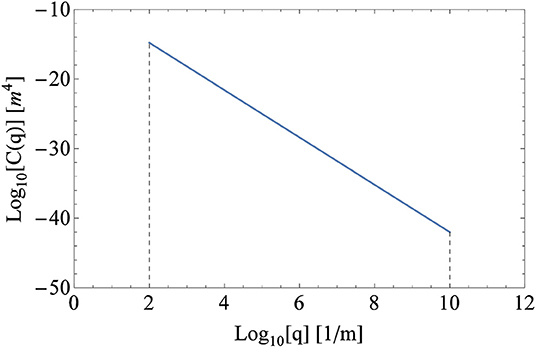
Figure 2. Typical power-law PSD of a self-affine randomly rough surface. In this figure, Z = 10⁻⁸ m^0.6, with $q_0=10^2$ 1/m, $q_1=10^{10}$ 1/m, and H = 0.7.

3. Bearing Area Method for Electroadhesion

3.1. General Equations

Determining the external load p_ext by Equation (7) requires in general that the probability distribution P₁(p|u) of interfacial separations be known, which can be achieved by using Persson's theories (see Almqvist et al., 2011). Instead, we propose here a simpler theory, which builds on the previous BAM (Ciavarella, 2018; Ciavarella and Papangelo, 2019) and gives a very simple estimate of the adhesion of hard rough solids based on a bearing area estimation of the adhesive contact area (Ciavarella, 2018). The theory is not an approximation of the DMT theory of Persson, since it is based on a different approximation. We first replace the electrostatic potential (3) with a Maugis–Dugdale equivalent, for which the adhesive traction is defined as a function of the gap u (see Figure 3):

$\begin{array}{ll}{p}_{\text{ad}}(u)=\{\begin{array}{ll}{\sigma }_0,& u\le h_0,\\ 0,& u>h_0.\end{array}& (9)\end{array}$

Upon integration for nominally flat surfaces, the work of the adhesion Δγ is given by

$\begin{array}{ll}\Delta \gamma =\frac{{\epsilon }_0}{2}{V}^2{\displaystyle {\int }_0^{\infty }}{\left(\frac{1}{u(x)+h_0}\right)}^{2}du=\frac{{\epsilon }_0}{2h_0}{V}^2.& (10)\end{array}$

For this to be equal to the surface energy in the Maugis-Dugdale approximation, i.e., $\Delta \gamma ={\int }_0^{h_0}{\sigma }_{0}du={\sigma }_0{h}_0$, we need to have

$\begin{array}{ll}{\sigma }_0=\frac{{\epsilon }_0}{2h_0^2}{V}^2,& (11)\end{array}$

and hence the results in Ciavarella (2018) apply (BAM).

FIGURE 3

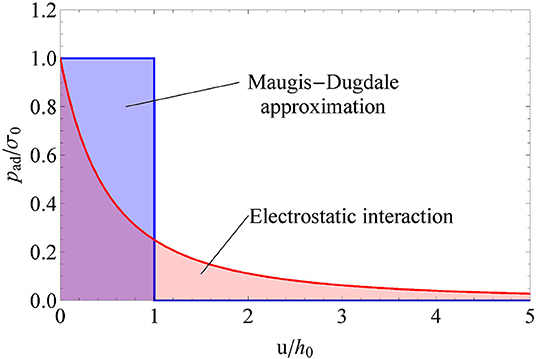
Figure 3. Typical electrostatic attraction force law replaced by a Maugis step function law, plotted in dimensionless form with ${\tilde{p}}_{\text{ad}}/{\tilde{\sigma }}_0$ vs. $\tilde{u}=u/h_0$.

For a nominally flat surface with Gaussian distribution of heights, the main idea is to estimate the adhesive area¹ analogously to a bearing area estimate which works very well for the sphere problem (see Ciavarella, 2018); for the nominally flat Gaussian roughness this results in

$\begin{array}{ll}\frac{A_{\text{ad}}}{A_0}=\frac{1}{2}\left[erfc\left(\frac{\overline{u}-h_0}{\sqrt{2}{h}_{\text{rms}}}\right)-erfc\left(\frac{\overline{u}}{\sqrt{2}{h}_{\text{rms}}}\right)\right],& (12)\end{array}$

where $\overline{u}$ is the mean separation of the surfaces and h_rms is the rms amplitude of roughness.

For intermediate mean separations, the repulsive pressure can be obtained by using Persson's theory (Persson, 2007; Papangelo et al., 2017), which for self-affine fractal surfaces with power-law PSD and fractal dimension D ≃ 2.2 gives (negative when compressive)

$\begin{array}{ll}p(\overline{u})\simeq -E^{*}{q}_0{h}_{\text{rms}}exp\left(\frac{-\overline{u}}{\gamma h_{\text{rms}}}\right),& (13)\end{array}$

where γ ≃ 0.5 is a constant parameter and E^* is the composite elastic modulus of the material.

3.2. Insulating Solids

While for the spherical problem the bearing area estimate above excludes the contact area itself, for Gaussian roughness the expression (12) tends to 1 in the limit, so it would be inconsistent to add separately the true contact area A/A₀: hence, in our theory there will be no effect of rms slopes, which in Persson's (2018) theory certainly enter the picture. Further, we sum the repulsive (13) and attractive contributions to obtain an external applied pressure (positive when tensile)

$\begin{array}{l}\frac{p_{\text{ext}}(\overline{u})}{E^{*}}\simeq -q_0{h}_{\text{rms}}exp\left(\frac{-\overline{u}}{\gamma h_{\text{rms}}}\right)\\ +\frac{{\upsilon }^2}{2}\left[erfc\left(\frac{\overline{u}-h_0}{\sqrt{2}{h}_{\text{rms}}}\right)-erfc\left(\frac{\overline{u}}{\sqrt{2}{h}_{\text{rms}}}\right)\right],& (14)\end{array}$

where we have defined an “electroadhesive” dimensionless voltage

$\begin{array}{ll}\upsilon =\sqrt{\frac{{\sigma }_0}{E^{*}}}=\sqrt{\frac{{\epsilon }_0}{2E^{*}}}\frac{V}{h_0}.& (15)\end{array}$

For very low voltage the external load $p_{\text{ext}}(\overline{u})$ coincides with the repulsive load p, while for very high voltage the two surfaces will stick together. By introducing the dimensionless parameters

$\begin{array}{l}{\tilde{p}}_{\text{ext}}=\frac{p_{\text{ext}}}{E^{*}},{\tilde{\sigma }}_0=\frac{{\sigma }_0}{E^{*}},\tilde{\overline{u}}=\frac{\overline{u}}{h_0},\\ {\tilde{h}}_{\text{rms}}=\frac{h_{\text{rms}}}{h_0},{\tilde{\lambda }}_L=\frac{{\lambda }_L}{h_0},& (16)\end{array}$

Equation (14) can be written as

$\begin{array}{l}{\tilde{p}}_{\text{ext}}(\tilde{\overline{u}})\simeq -\frac{2\pi }{{\tilde{\lambda }}_L}{\tilde{h}}_{\text{rms}}exp\left(\frac{-\tilde{\overline{u}}}{\gamma {\tilde{h}}_{\text{rms}}}\right)\\ +\frac{{\upsilon }^2}{2}\left[erfc\left(\frac{\tilde{\overline{u}}-1}{\sqrt{2}{\tilde{h}}_{\text{rms}}}\right)-erfc\left(\frac{\tilde{\overline{u}}}{\sqrt{2}{\tilde{h}}_{\text{rms}}}\right)\right],& (17)\end{array}$

where λ_L is the longest wavelength in the surface representation, i.e., q₀ = 2π/λ_L. Notice that in the standard case of van der Waals forces, $\frac{{\sigma }_0}{E^{*}}\simeq \frac{\Delta \gamma /ϵ}{E^{*}}=\frac{l_a}{ϵ}$ with $l_a=\Delta \gamma /E^{*}$ defines a characteristic adhesion length, where ϵ is the characteristic length of interaction of the order of the interatomic distance. In the electroadhesion case, ${\upsilon }^2=\frac{{\epsilon }_0{V}^2}{2E^{*}{h}_0^2}$ replaces l_a/ϵ, and by changing the voltage it can be varied by many orders of magnitude. Hence, adhesion is favored at high applied voltage V, low elastic modulus E^*, and thin insulating layer thickness. Clearly, if both the van der Waals adhesion forces and the electroadhesive tractions are present, they should be summed.

3.3. Conducting Solids

If an electric voltage is applied between two contacting solids with certain electric conductivity, then one has to account for the electric current flow through the contact patches; hence, there would be attraction only outside of the contact areas. However, the voltage drop V across the (non-)contacting interface will depend on the electric conductivities κ₁ and κ₂ of the solids. Barber's (2003), using Persson (2018) theorem for the analogy between electrical conduction and mechanical stiffness, finds approximately that the actual voltage drop $\Delta V(\overline{u})$ decreases with the applied voltage V in a manner² depending on the mean separation $\overline{u}$:

$\begin{array}{ll}\Delta V(\overline{u})=\frac{V}{1+4\frac{d_0}{h_{\text{rms}}}\frac{p(\overline{u})}{E^{*}}},& (18)\end{array}$

where

$\begin{array}{ll}{d}_0=\left(\frac{{\kappa }_1{d}_2+{\kappa }_2{d}_1}{{\kappa }_1+{\kappa }_2}\right).& (19)\end{array}$

By Equation (11), for conducting materials the adhesive strength will be dependent on the mean separation $\overline{u}$. From Equation (11), we define

$\begin{array}{ll}{\sigma }_{0,\text{cond}}(\overline{u})=\frac{{\epsilon }_0{V}^2}{2h_0^2}\frac{1}{{\left(1+4\frac{d_0}{h_{\text{rms}}}\frac{p(\overline{u})}{E^{*}}\right)}^2}=\frac{{\sigma }_0}{{\left(1+4\frac{d_0}{h_{\text{rms}}}\frac{p(\overline{u})}{E^{*}}\right)}^2},& (20)\end{array}$

where ${\sigma }_{0,\text{cond}}(\overline{u})\le {\sigma }_0$ and we recall that σ₀ is the adhesive strength for insulating bodies. Hence, for a fixed separation one obtains

$\begin{array}{l}\frac{p_{\text{ext}}(\overline{u})}{E^{*}}\simeq -q_0{h}_{\text{rms}}exp\left(\frac{-\overline{u}}{\gamma h_{\text{rms}}}\right)\\ +\frac{{\sigma }_0}{2E^{*}}\frac{\left[erfc\left(\frac{\overline{u}-h_0}{\sqrt{2}{h}_{\text{rms}}}\right)-erfc\left(\frac{\overline{u}}{\sqrt{2}{h}_{\text{rms}}}\right)\right]}{{\left(1+4d_0{q}_{0}exp\left(\frac{-\overline{u}}{\gamma h_{\text{rms}}}\right)\right)}^2}& (21)\end{array}$

or, in dimensionless form,

$\begin{array}{l}{\tilde{p}}_{\text{ext}}\left(\tilde{\overline{u}}\right)\simeq -\frac{2\pi }{{\tilde{\lambda }}_L}{\tilde{h}}_{\text{rms}}exp\left(\frac{-\tilde{\overline{u}}}{\gamma {\tilde{h}}_{\text{rms}}}\right)\\ +\frac{{\upsilon }^2}{2}\frac{\left[erfc\left(\frac{\tilde{\overline{u}}-1}{\sqrt{2}{\tilde{h}}_{\text{rms}}}\right)-erfc\left(\frac{\tilde{\overline{u}}}{\sqrt{2}{\tilde{h}}_{\text{rms}}}\right)\right]}{{\left(1+\frac{8\pi }{{\tilde{\lambda }}_L}{\tilde{d}}_{0}exp\left(\frac{-\tilde{\overline{u}}}{\gamma {\tilde{h}}_{\text{rms}}}\right)\right)}^2},& (22)\end{array}$

where we have defined ${\tilde{d}}_0=d_0/h_0.$

4. Voltage Near Full Contact

As noted by Persson, adhesion increases very slowly as the voltage increases, but above a certain threshold the increase becomes very rapid as the surfaces approach each other. It may be useful in certain applications to have an estimate of the voltage at which the rough surfaces would be near full contact. Assuming in our simplified theory that this occurs already at $\frac{\overline{u}}{h_{\text{rms}}}=1$, for insulating bodies imposing a given p_ext results in the following condition for υ:

$\begin{array}{ll}{\upsilon }_{\text{full}}=\sqrt{\frac{{\epsilon }_0{V}_{\text{full}}^2}{2E^{*}{h}_0^2}}=\sqrt{2\left(\frac{{\tilde{p}}_{\text{ext}}+\frac{2\pi }{{\tilde{\lambda }}_L}{\tilde{h}}_{\text{rms}}exp\left(-\frac{1}{\gamma }\right)}{erfc\left(\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{2}{\tilde{h}}_{\text{rms}}}\right)-erfc\left(\frac{1}{\sqrt{2}}\right)}\right)},& (23)\end{array}$

where we take γ = 0.5. For conducting solids, using Equation (22) we obtain

$\begin{array}{l}{\upsilon }_{\text{full}}=\sqrt{\frac{{\epsilon }_0{V}_{\text{full}}^2}{2E^{*}{h}_0^2}}\\ =\sqrt{2\left(\frac{\left({\tilde{p}}_{\text{ext}}+\frac{2\pi }{{\tilde{\lambda }}_L}{\tilde{h}}_{\text{rms}}exp\left(-\frac{1}{\gamma }\right)\right){\left(1+\frac{8\pi }{{\tilde{\lambda }}_L}{\tilde{d}}_{0}exp\left(-\frac{1}{\gamma }\right)\right)}^2}{erfc\left(\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{2}{\tilde{h}}_{\text{rms}}}\right)-erfc\left(\frac{1}{\sqrt{2}}\right)}\right)}.& (24)\end{array}$

We see that the main parameters on which υ_full depends are q₀ and h_rms.

5. Numerical Results

Figure 4 shows the external pressure ${\tilde{p}}_{\text{ext}}/{\tilde{\sigma }}_0$ as a function of the mean separation $\tilde{\overline{u}}$ for ${\tilde{\lambda }}_L=2,048,$ ${\tilde{h}}_{\text{rms}}=1$, and varying υ = [0.01, 0.02, 0.04, 0.08, 0.2]. In Figure 4 solid lines refer to insulating solids, while dashed lines are used for conducting solids with ${\tilde{d}}_0=1,000.$ Upon increasing the applied voltage, the mean load vs. mean separation curve becomes more and more attractive so that macroscopic adhesion becomes important. Clearly differences between the two cases of insulating and conducting bodies are more evident at higher voltages υ (see Equation 18).

FIGURE 4

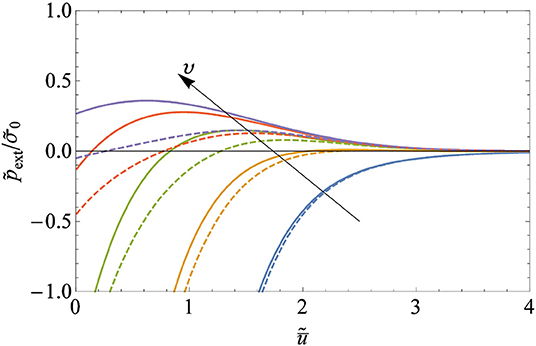
Figure 4. External pressure ${\tilde{p}}_{\text{ext}}/{\tilde{\sigma }}_0$ (> 0 when tensile) as a function of the mean separation $\tilde{\overline{u}}$ for ${\tilde{\lambda }}_L=2,048,$ ${\tilde{h}}_{\text{rms}}=1$, and varying υ = [0.01, 0.02, 0.04, 0.08, 0.2]. Solid lines correspond to insulating solids and dashed lines to conducting solids with ${\tilde{d}}_0=1,000$.

If max[${\tilde{p}}_{\text{ext}}(\tilde{\overline{u}}\in [0,+\infty ))]={\tilde{p}}_{\text{ext}}^{max}>0$, then the surfaces are sticky and a positive external pressure is needed to separate them. Figure 5 shows the abrupt decay in the pull-off pressure ${\tilde{p}}_{\text{ext}}^{max}/{\tilde{\sigma }}_0$ with ${\tilde{h}}_{\text{rms}}$, for a constant voltage υ = 0.08 and increasing ${\tilde{\lambda }}_L=2,048\times \left[0.1,1,5,10\right]$ for both insulating (solid lines) and conducting (with ${\tilde{d}}_0=1,000$, dashed lines) solids. It can be seen that for a given ${\tilde{h}}_{\text{rms}}$, the pull-off pressure ${\tilde{p}}_{\text{ext}}^{max}$ increases for surfaces with longer wavelengths ${\tilde{\lambda }}_L$. In Figure 6, the decay of the pull-off pressure with ${\tilde{h}}_{\text{rms}}$ is plotted for constant ${\tilde{\lambda }}_L=2,048$ and varying υ = [0.01, 0.02, 0.04, 0.08, 0.2]. Increasing the dimensionless voltage υ increases the tensile traction needed to separate the rough surfaces and makes the surfaces more prone to adhesion. We infer from Figures 4–6 that conducting solids are less inclined to exhibit macroscopic adhesion due to the smaller voltage drop experienced at the interface.

FIGURE 5

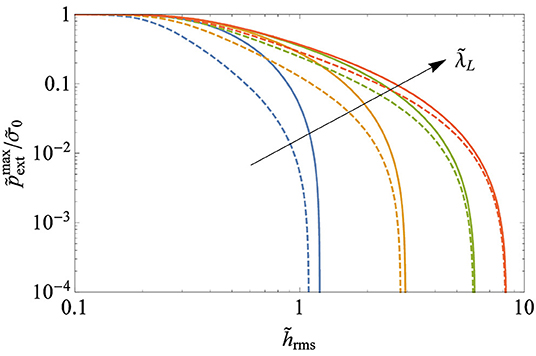
Figure 5. Pull-off mean pressure ${\tilde{p}}_{\text{ext}}^{max}/{\tilde{\sigma }}_0$ vs. ${\tilde{h}}_{\text{rms}}$ (log-log scale), with a constant voltage υ = 0.08 and increasing ${\tilde{\lambda }}_L=2,048\times \left[0.1,1,5,10\right]$ for both insulating (solid lines) and conducting (with ${\tilde{d}}_0=1,000$, dashed lines) solids.

FIGURE 6

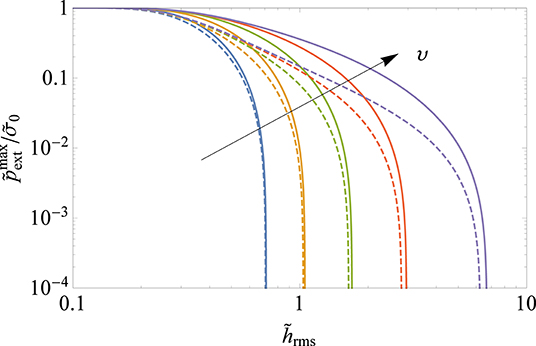
Figure 6. Pull-off mean pressure ${\tilde{p}}_{\text{ext}}^{max}/{\tilde{\sigma }}_0$ vs. ${\tilde{h}}_{\text{rms}}$ (log-log scale) for ${\tilde{\lambda }}_L=2,048$ and varying υ = [0.01, 0.02, 0.04, 0.08, 0.2]. Solid lines correspond to insulating solids and dashed lines to conducting solids with ${\tilde{d}}_0=1,000$.

6. Stickiness Criteria

The above results show that the pull-off traction is principally determined by h_rms, q₀, and υ. Indeed, for a low contact area, neither the repulsive nor the attractive tractions depend on the surface “magnification” ζ = q₁/q₀ as in the adhesionless load-separation relation (13). By adopting the BAM approach to estimate the adhesive contact area and using the results in Ciavarella (2019) for the case of van der Waals interactions, we easily obtain in our electroadhesion case that for stickiness,

$\begin{array}{ll}{h}_{\text{rms}}<{\left(0.6\frac{{\sigma }_0{h}_0}{E^{*}}{\lambda }_L\right)}^{0.5}=0.775\upsilon \sqrt{h_0{\lambda }_L},& (25)\end{array}$

where we recognize that in the electroadhesive case the adhesive energy depends on the applied dimensionless voltage υ.

Alternatively, a stickiness criterion could be defined using the energy balance proposed by Persson and Tosatti's theory for classical van der Waals adhesion. Persson and Tosatti (2001) proposed that for a rough interface the effective adhesive energy Δγ_eff available at pull-off is

$\begin{array}{ll}\Delta {\gamma }_{\text{eff}}=\frac{A}{A_0}\Delta \gamma -\frac{U_{\text{el}}}{A_0},& (26)\end{array}$

where the term $\frac{A}{A_0}(>1)$ is the ratio between the contact area A in full contact and the nominal contact area A₀ and is greater than 1 because of a roughness-induced effect, and U_el is the elastic strain energy stored to squeeze the roughness, with isotropic power spectrum C(q) in full contact³ given by

$\begin{array}{ll}\frac{U_{\text{el}}(\zeta )}{A_0}=\frac{\pi E^{*}}{2}{\displaystyle {\int }_{q_0}^{q_1}}{q}^{2}C(q)dq,& (27)\end{array}$

which depends on the magnification. With electroadhesion, we replace Δγ with the term $\frac{{\epsilon }_0}{2h_0}{V}^2$, resulting in (omitting the van der Waals contribution and for A/A₀ ≃ 1)

$\begin{array}{ll}\Delta {\gamma }_{\text{eff}}=\frac{{\epsilon }_0}{2h_0}{V}^2-\frac{U_{\text{el}}}{A_0}.& (28)\end{array}$

Using the results in Ciavarella (2019), a new stickiness criterion, akin to that of “Persson and Tosatti”, is derived by imposing Δγ_eff = 0 in (28), which can be cast in terms of the roughness rms amplitude as

$\begin{array}{ll}{h}_{\text{rms}}<\upsilon \sqrt{h_0{\lambda }_L\frac{2H-1}{\pi H}}.& (29)\end{array}$

For the typical Hurst exponent H = 0.8 (Persson, 2014), this becomes

$\begin{array}{ll}{h}_{\text{rms}}<0.5\upsilon \sqrt{h_0{\lambda }_L},& (30)\end{array}$

which, except for the threshold (0.5 instead of 0.775), compares well with the other criteria obtained with BAM.

We can rewrite the stickiness criteria in dimensionless form:

$\begin{array}{lll}{\tilde{h}}_{\text{rms}}<0.5\upsilon \sqrt{{\tilde{\lambda }}_L}& \left(\text{Persson-Tosatti}\right),& (31)\end{array}$

$\begin{array}{lll}{\tilde{h}}_{\text{rms}}<0.775\upsilon \sqrt{{\tilde{\lambda }}_L}& \left(\text{BAM}\right).& (32)\end{array}$

Figure 7 shows two contour plots of the pull-off mean pressure ${\tilde{p}}_{\text{ext}}^{max}/{\tilde{\sigma }}_0$ as a function of υ and ${\tilde{h}}_{\text{rms}}$ (log-log scale) with ${\tilde{\lambda }}_L=2,048$, for insulating solids (Equation 17) in Figure 7A and for conducting solids (Equation 22, with ${\tilde{d}}_0=200$) in Figure 7B. The stickiness boundaries obtained with (32) and (31) for H = 0.8 are represented by thick black solid and dashed lines, respectively. Even though the two criteria have been obtained from different arguments, it is noteworthy that they yield very similar outcomes, which agree satisfactorily with the numerical results obtained from Equations (17) and (22). In general the pull-off force increases with increasing voltage υ and decreasing amplitude roughness ${\tilde{h}}_{\text{rms}}$. We have also distinguished a “no sticky” region for ${\tilde{p}}_{\text{ext}}^{max}/{\tilde{\sigma }}_0<10^{-4}$, which corresponds to very rough hard solids and low voltage.

FIGURE 7

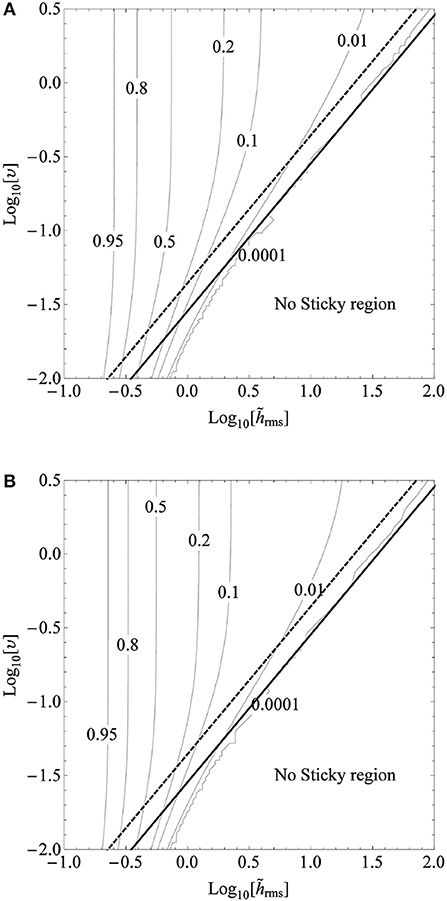
Figure 7. Pull-off mean pressure ${\tilde{p}}_{\text{ext}}^{max}/{\tilde{\sigma }}_0$ as a function of υ and ${\tilde{h}}_{\text{rms}}$ (log-log scale) for ${\tilde{\lambda }}_L=2,048$: (A) insulating solids; (B) conducting solids with ${\tilde{d}}_0=200$. The thick black solid and dashed lines indicate the stickiness limits obtained, respectively, with BAM (Equation 32) and by following the Persson and Tosatti energy balance for H = 0.8 (Equation 31).

Finally, in Figure 8 we provide a qualitative estimate of the friction coefficient $\mu /\tilde{\tau }$ as a function of the external pressure $-{\tilde{p}}_{\text{ext}}$:

$\begin{array}{ll}\mu /\tilde{\tau }=\frac{A/A_0}{\left(-{\tilde{p}}_{\text{ext}}\right)},& (33)\end{array}$

where we have defined a dimensionless shear strength of the interface, $\tilde{\tau }=\tau /E^{*}$. The normalized contact area is computed according to Persson's (2001) theory as

$\begin{array}{ll}\frac{A}{A_0}=erf\left(\frac{\sqrt{\pi }}{h_{\text{rms}}^{\prime }}\frac{2\pi }{{\tilde{\lambda }}_L}{\tilde{h}}_{\text{rms}}exp\left(\frac{-\tilde{\overline{u}}}{\gamma {\tilde{h}}_{\text{rms}}}\right)\right),& (34)\end{array}$

where $h_{\text{rms}}^{\prime }$ is the surface rms slope and $\frac{A}{A_0}$ is corrected by a factor of $\sqrt{\pi }$ in the brackets to give it the correct slope at the origin (see Putignano et al., 2012; Violano et al., 2019). In Figure 8, we used ${\tilde{\lambda }}_L=2,048$, ${\tilde{h}}_{\text{rms}}=1$ and $h_{\text{rms}}^{\prime }=2.5$ and varied the dimensionless electrical voltage as υ = [0.01, 0.02, 0.03, 0.04] for both insulating (solid lines) and conducting (with ${\tilde{d}}_0=250$, dashed lines) solids. Figure 8 shows that the friction coefficient increases with increasing voltage and gets very high for low normal forces, as a finite contact area is possible under a vanishing normal load. The curves are consistent with what has been observed in experiments (Shultz et al., 2015; Ayyildiz et al., 2018; Sirin et al., 2019).

FIGURE 8

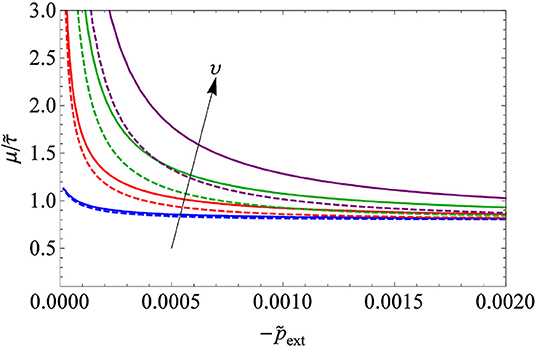
Figure 8. Friction coefficient $\mu /\tilde{\tau }=\frac{A/A_0}{(-{\tilde{p}}_{\text{ext}})}$ as a function of the external pressure −p_ext for ${\tilde{h}}_{\text{rms}}=1,$ $h_{\text{rms}}^{\prime }=2.5$ and dimensionless electrical voltage υ = [0.01, 0.02, 0.03, 0.04].

7. Further Results

In this section we provide a possible example with dimensional results based on a typical rough surface with the PSD shown in Figure 2, for which Z = 10⁻⁸ m^0.6 with $q_0=10^2$ 1/m, $q_1=10^{10}$ 1/m and H = 0.7, so that the surface rms height is h_rms = 8.43 μm and the surface rms slope is $h_{\text{rms}}^{\prime }=0.324$. Figure 9A shows the adhesive pressure p_ad = p_ext − p, in Figure 9B the mean separation $\overline{u}$, and in Figure 9C the normalized contact area A/A₀ as a function of the applied voltage for E^* = [1, 10, 100] MPa and for both insulating (solid lines) and conducting (with d₀ = 10 mm, dashed lines) solids. All the plots are for a constant external pressure p_ext = 100 Pa, and the normalized contact area is computed according to Equation (34). For harder solids we get lower adhesive contact pressure, higher mean separation, and smaller contact area. Figure 9C effectively shows that A/A₀ remains very small over the entire range of applied voltage, indicating that the approximation we used is correct. In general, for a given voltage, conducting bodies show less adhesion, higher average separation, and smaller contact area. As in Persson (2018), a critical voltage can be identified above which a sharp increase in p_ad is observed and which can be estimated using Equations (23) and (24); see the black circles and squares in Figure 9.

FIGURE 9

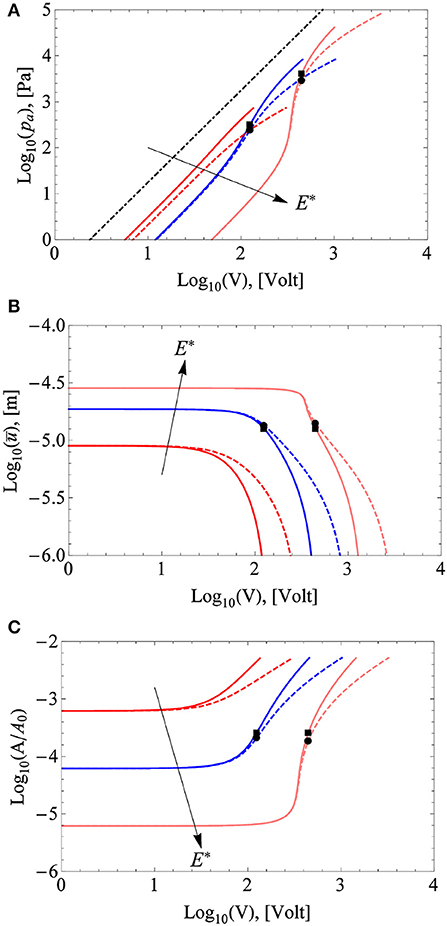
Figure 9. (A) Adhesive pressure p_ad = p_ext − p, (B) mean separation $\overline{u},$ and (C) normalized contact area A/A₀ as functions of the applied voltage V for E^* = [1, 10, 100] MPa and for both insulating (solid lines) and conducting (with d₀ = 10 mm, dashed lines) solids. All plots are for a constant external pressure p_ext = 100 Pa. In (A), the dot-dashed line represents the theoretical electroadhesive strength σ₀. In all panels the black circles and squares represent estimates of the critical voltage υ_full using Equations (23) and (24).

8. Discussion: Alternating Current

Electroadhesion with direct current is not as easy to detect as it is when alternating current (AC) is applied. However, in terms of the mathematical model, very few changes are needed to translate the above results to the case of AC voltage. Indeed, when the applied voltage oscillates in time, V(t), one should take into account the variation of the dielectric properties of the media with the applied frequency and replace h₀ in Equation (2) with a function

$\begin{array}{ll}{h}_0(\omega )=\frac{d_1}{{\epsilon }_1(\omega )}+\frac{d_2}{{\epsilon }_2(\omega )},& (35)\end{array}$

where ε_i(ω) are the dielectric functions of the two media. In the classical case of sinusoidal voltage, V(t) = V₀cos(ω₀t), we have to change (3) to

$\begin{array}{ll}{\sigma }_{zz}(x,t)=\frac{{\epsilon }_0}{4}{\left(\frac{V_0}{|u(x)+h_0({\omega }_0)|}\right)}^2\left(1+cos(2{\omega }_{0}t+2\varphi )\right),& (36)\end{array}$

where ϕ is defined by

$\begin{array}{ll}u(x)+h_0({\omega }_0)=\left|u(x)+h_0({\omega }_0)\right|exp(i\varphi ).& (37)\end{array}$

Notice that in this case we have that the adhesive traction σ_zz(x, t) oscillates in time about its mean value

$\begin{array}{ll}{\sigma }_{zz}(x)={\displaystyle \underset{0}{\overset{\frac{2\pi }{{\omega }_0}}{\int }}}{\sigma }_{zz}(x,t)dt=\frac{{\epsilon }_0}{4}{\left(\frac{V_0}{|u(x)+h_0({\omega }_0)|}\right)}^2,& (38)\end{array}$

which coincides with Equation (3) for constant voltage.

9. Conclusions

Using the bearing area model of Ciavarella, we have developed a simple theory for electroadhesion between two hard rough surfaces. The model is derived for the cases of insulating and conducting bodies, where in the latter case the voltage drop near the interface needs to be evaluated by taking into account the current flowing through the asperity contact regions. We have shown that the friction coefficient increases with increasing voltage and can reach very high values for low normal forces, in agreement with experimental results. We have introduced a new dimensionless parameter for electroadhesion, which governs the behavior of the proposed model. Pull-off forces depend mostly on well-defined quantities, such as the applied voltage, the surface rms height, and the longest wavelength in the surface representation. In the limit of small contact area, two stickiness criteria have been derived based on the present theory and on the energy balance proposed by Persson and Tosatti, which turns out to give very similar results (except for a prefactor) for pure-power-law power spectral densities.

Data Availability Statement

All datasets generated for this study are included in the article/supplementary material.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

MC and AP acknowledge support from the Italian Ministry of Education, University and Research under the Programme Department of Excellence Legge 232/2016 (grant no. CUP-D94I18000260001). AP is thankful to the DFG (German Research Foundation) for funding the project PA 3303/1-1, and acknowledges support from PON Ricerca e Innovazione 2014-2020-Azione I.2 - D.D. n. 407, 27/02/2018, bando AIM (grant no. AIM1895471).

Footnotes

1. ^The adhesive area is defined as the portion of surface on which tensile stress is applied.

2. ^Notice that we are following a DMT-like approach, so from Equation (13) we have written the contact stiffness K_⊥ = p/(γh_rms); see Persson (2018).

3. ^Notice that we use the original convention and notation for C(q) of Persson and not the definition of Dalvi et al. (2019), which is C^iso(q) = 4π²C(q).

References

Almqvist, A., Campana, C., Prodanov, N., and Persson, B. N. J. (2011). Interfacial separation between elastic solids with randomly rough surfaces: comparison between theory and numerical techniques. J. Mech. Phys. Solids 59:2355. doi: 10.1016/j.jmps.2011.08.004

CrossRef Full Text | Google Scholar

Ayyildiz, M., Scaraggi, M., Sirin, O., Basdogan, C., and Persson, B. N. (2018). Contact mechanics between the human finger and a touchscreen under electroadhesion. Proc. Natl. Acad. Sci. U.S.A. 115, 12668–12673. doi: 10.1073/pnas.1811750115

PubMed Abstract | CrossRef Full Text | Google Scholar

Barber, J. R. (2003). Bounds on the electrical resistance between contacting elastic rough bodies. Proc. R. Soc. A 459:53. doi: 10.1098/rspa.2002.1038

CrossRef Full Text | Google Scholar

Ciavarella, M. (2018). A very simple estimate of adhesion of hard solids with rough surfaces based on a bearing area model. Meccanica 53, 241–250. doi: 10.1007/s11012-017-0701-6

CrossRef Full Text | Google Scholar

Ciavarella, M. (2019). Universal features in “stickiness” criteria for soft adhesion with rough surfaces. arXiv [Preprint]. arXiv:1908.06380. doi: 10.1016/j.triboint.2019.106031

CrossRef Full Text | Google Scholar

Ciavarella, M., Joe, J., Papangelo, A., and Barber, J. R. (2019). The role of adhesion in contact mechanics. J. R. Soc. Interface 16:20180738. doi: 10.1098/rsif.2018.0738

PubMed Abstract | CrossRef Full Text | Google Scholar

Ciavarella, M., and Papangelo, A. (2019). Extensions and comparisons of BAM (Bearing Area Model) for stickiness of hard multiscale randomly rough surfaces. Tribol. Int. 133, 263–270. doi: 10.1016/j.triboint.2018.10.001

CrossRef Full Text | Google Scholar

Dalvi, S., Gujrati, A., Khanal, S. R., Pastewka, L., Dhinojwala, A., and Jacobs, T. D. (2019). Linking energy loss in soft adhesion to surface roughness. arXiv [Preprint]. arXiv:1907.12491. doi: 10.1073/pnas.1913126116

PubMed Abstract | CrossRef Full Text | Google Scholar

Derjaguin, B. V., Muller, V. M., and Toporov, Y. P. (1975). Effect of contact deformations on the adhesion of particles. J. Colloid Interface Sci. 53, 314–326. doi: 10.1016/0021-9797(75)90018-1

CrossRef Full Text | Google Scholar

Johnsen, A., and Rahbek, K. (1923). A physical phenomenon and its applications to telegraphy, telephony, etc. J. Inst. Electr. Eng. 61, 713–725. doi: 10.1049/jiee-1.1923.0092

CrossRef Full Text | Google Scholar

Papangelo, A., Hoffmann, N., and Ciavarella, M. (2017). Load-separation curves for the contact of self-affine rough surfaces. Sci. Rep. 7:6900. doi: 10.1038/s41598-017-07234-4

PubMed Abstract | CrossRef Full Text

Persson, B. N., and Scaraggi, M. (2014). Theory of adhesion: role of surface roughness. J. Chem. Phys. 141:124701. doi: 10.1063/1.4895789

PubMed Abstract | CrossRef Full Text | Google Scholar

Persson, B. N. J. (2001). Theory of rubber friction and contact mechanics. J. Chem. Phys. 115:3840. doi: 10.1063/1.1388626

CrossRef Full Text | Google Scholar

Persson, B. N. J. (2007). Relation between interfacial separation and load: a general theory of contact mechanics. Phys. Rev. Lett. 99:125502. doi: 10.1103/PhysRevLett.99.125502

PubMed Abstract | CrossRef Full Text | Google Scholar

Persson, B. N. J. (2014). On the fractal dimension of rough surfaces. Tribol. Lett. 54, 99–106. doi: 10.1007/s11249-014-0313-4

CrossRef Full Text | Google Scholar

Persson, B. N. J. (2018). The dependency of adhesion and friction on electrostatic attraction. J. Chem. Phys. 148:144701. doi: 10.1063/1.5024038

PubMed Abstract | CrossRef Full Text | Google Scholar

Persson, B. N. J., and Tosatti, E. (2001). The effect of surface roughness on the adhesion of elastic solids. J. Chem. Phys. 115, 5597–5610. doi: 10.1063/1.1398300

PubMed Abstract | CrossRef Full Text | Google Scholar

Popov, V. L., and Hess, M. (2018). Voltage induced friction in a contact of a finger and a touchscreen with a thin dielectric coating. arXiv [Preprint]. arXiv:1805.08714. Available online at: https://arxiv.org/abs/1805.08714

Google Scholar

Putignano, C., Afferrante, L., Carbone, G., and Demelio, G. (2012). A new efficient numerical method for contact mechanics of rough surfaces. Int. J. Solids Struct. 49, 338–343. doi: 10.1016/j.ijsolstr.2011.10.009

CrossRef Full Text | Google Scholar

Shultz, C. D., Peshkin, M. A., and Colgate, J. E. (2015). “Surface haptics via electroadhesion: Expanding electrovibration with Johnsen and Rahbek,” in 2015 IEEE World Haptics Conference (WHC) (Evanston, IL), 57–62. doi: 10.1109/WHC.2015.7177691

CrossRef Full Text | Google Scholar

Sirin, O., Ayyildiz, M., Persson, B. N. J., and Basdogan, C. (2019). Electroadhesion with application to touchscreens. Soft Matter 15, 1758–1775. doi: 10.1039/C8SM02420K

PubMed Abstract | CrossRef Full Text | Google Scholar

Vardar, Y., Guclu, B., and Basdogan, C. (2017). Effect of waveform on tactile perception by electrovibration displayed on touch screens. IEEE Trans. Haptics 10:488. doi: 10.1109/TOH.2017.2704603

PubMed Abstract | CrossRef Full Text | Google Scholar

Violano, G., Afferrante, L., Papangelo, A., and Ciavarella, M. (2019). On stickiness of multiscale randomly rough surfaces. J. Adhes. 1–19. doi: 10.1080/00218464.2019.1685384

CrossRef Full Text | Google Scholar