- Department of System Dynamics and Friction Physics, Institute of Mechanics, Technische Universität Berlin, Berlin, Germany
The stress state in the volume of contacting bodies may essentially influence the material behavior. For evaluating various modes of inelastic behavior and/or failure, such as plastic deformation, crack initiation, and propagation or fatigue, the complete stress tensor beneath the contact interface may be of importance. For many geotechnical and biomechanical applications, the hydrostatic pressure gradient beneath the contact is of interest as well. However, most theories for normal and tangential contact provide only few stress components in the contact surface. In the present paper, we show that the full stress state in the half-space can be easily found for axisymmetric bodies. We provide expressions in form of one-dimensional integrals for all components of the stress tensor and the hydrostatic pressure gradient inside the half-space. In terms of numerical complexity, the proposed method can be advantageous to other elaborate methods.
Introduction
Since Huber's (1904) solution of the Hertzian contact, it is known that the von Mises equivalent stress and, thus, the endangered region for plastic failure, lies beneath the surface of the indented half-space. It was later shown that the same holds for the tangentially loaded Hertzian contact under sliding conditions for coefficients of frictions below 0.3 (Hamilton and Goodman, 1966) and for other indenter shapes (Ciavarella et al., 1998). However, many solutions for contact problems are limited to few components of surface stresses and, thus, do not allow for predictions with respect to plastic failure or more complicated failure mechanisms.
Another example, where the stress state inside the half-space or, more precisely, the hydrostatic pressure gradient is of interest, are natural joints such as knee or hip joints. When layers of cartilage are in contact, it was found experimentally that dynamic compression that may result from activities like walking and running promotes regenerative processes. In this loading scenario, a high rate of in- and outflow of interstitial fluid in the surface zone of the porous, fluid saturated medium is measured (Wong and Carter, 2003). It is believed that the fluid flow is responsible for transport of nutrients and waste and is, thus, crucial for cartilage health (Zhang et al., 2009). Hence, Popov (2019) proposed a growth law for cartilage based on the changing rate of the hydrostatic pressure gradient. Here, following Darcy's law for fluid flow in porous media, the hydrostatic pressure gradient is considered a measure for fluid flow.
The brute force method to obtain the stresses in the half space is to use superpositions of the point force solutions by Boussinesq (1885) and Cerruti (1882). However, the resulting numerical integrations are very expensive in terms of computational complexity. On a three-dimensional n×n×n grid, the complexity of this method is . This is inconvenient, whenever the stresses must be computed repeatedly due to changing indenter shapes (in case of wear or growth) or due to variations in loading. Of course, more elaborate methods with lower complexity exist. An example with the complexity is the FFT-based boundary element method (BEM) for the half-space (Pohrt and Li, 2014).
In the present paper, we employ the superposition idea first described by Mossakovski (1963) to derive expressions in form of one-dimensional integrals for the whole stress tensor in the half-space. Starting point for the frictionless normal contact problem is the complete analytical solution for the Hertzian contact by Huber (1904). For the tangential contact problem, we operate in the Cattaneo-Mindlin approximation and base our derivation on the Hertzian solution by Hamilton (1983). The resulting expressions may be used to numerically or analytically determine stresses and hydrostatic pressure gradients for arbitrary axisymmetric indenters and arbitrary loading histories. Employing the same method, Willert et al. (2020) derived simple analytic expressions for the stresses and the hydrostatic pressure gradient, but only for contact plane. In terms of complexity, we show that the proposed method can be advantageous, even compared to elaborate methods such as the FFT-based BEM.
The paper is organized as follows: sections Frictionless Normal Contact and Tangential Contact in the Cattaneo-Mindlin Approximation are concerned with the normal and tangential contact problem, respectively. In both sections, we first obtain the respective solution for the cylindrical flat punch from the Hertzian solution and then derive expression for arbitrary indenter shapes by superposition of flat punch solutions. In case of the tangential contact, we also discuss the states of partial and full slip and arbitrary loading histories. In the end of both sections, the von Mises stresses and hydrostatic pressure gradients are shown for some examples. The paper closes with a discussion and some conclusive remarks.
Frictionless Normal Contact
In this section, we derive expressions for the stress state and the pressure gradient in the half-space for the axisymmetric Boussinesq problem. As suggested by Mossakovski (1963), the solution for arbitrary axisymmetric profiles can be obtained by superimposing incremental flat punch solutions.
Conversely, this superposition idea can also be employed to obtain the flat punch solution from any known axisymmetric solution. Thus, we first derive the flat punch solution inside the half-space using the well-known Hertzian solution provided by Huber (1904) and later use this solution to derive expressions for arbitrary axisymmetric profiles.
Hence, the stress components for the indentation by a rigid cylindrical flat punch (superscript FP) with the radius a can be derived from the Hertzian solution (superscript H) using
with the indentation depth δ and δH = a2 / R in the Hertzian case. The obtained flat punch solution is presented in Appendix A.
Now, we consider the case of general axisymmetric profiles. Under the assumption of a convex smooth profile f = f (r), the relation between penetration depth and contact radius is a unique function
In the framework of the MDR (Popov and Heß, 2015), it is shown that this function can be derived from the profile f(r) by the simple Abel integral transform,
By again employing the superposition idea described above, we obtain expressions for the general axisymmetric profile (superscript AS) via
Thus, we interpret the indentation process as a series of incremental indentations of flat punches with increasing contact radii. The obtained expressions read
where u as well as its derivative ua are shortcuts for
In Equation (5), FN is the total normal force,
E* = E/(1 − ν2) is the effective Young's modulus and ν is the Poisson's ratio. In the contact plane (z = 0) and in the axis of contact (r = 0), Equation (5) simplify significantly. The resulting expressions are presented in Appendices B and C, respectively. Using the same procedure as described above, the expressions of the stress components at the surface were already presented by Willert et al. (2020).
It is elemental that the superposition idea also works with any linear operation on the stress components. As an example, the hydrostatic pressure phs = (σrr + σφφ + σzz)/3 and the components of the gradient of the hydrostatic pressure are obtained as well. Again, we first calculate the flat punch solutions from the Hertzian solution (presented in Appendix A) and then obtain expressions for the axisymmetric case:
with the derivatives
The corresponding expressions at the contact plane and at the axis of contact (r = 0) are, again, presented in Appendices B and C, respectively.
Examples for the Frictionless Normal Contact
The two already discussed indenter shapes, the paraboloid (Hertzian contact) and the cylindrical flat punch, as well as two more imperfect shapes, the paraboloid with a parabolic cap and the cylindrical flat punch with rounded edges, serve as examples for the frictionless normal contact in the following. The profiles and the relation between penetration depth δ and contact radius a are listed in Popov et al. (2019):
a) Paraboloid with radius of curvature R (see Figure 1A):
b) Cylindrical flat punch (see Figure 1B):
c) Paraboloid with a parabolic cap with radius of the cap b and radii of curvature R1 and R2 (see Figure 1C):
where and .
d) Cylindrical flat punch with rounded edges with radius of the blunt end b and radius of curvature R (see Figure 1D):
With these relations, the integrals in Equations (5) and (8) and are evaluated numerically, with exception of the flat punch where stress components and pressure gradients are explicitly given in Equations (26) and (28) of Appendix A.
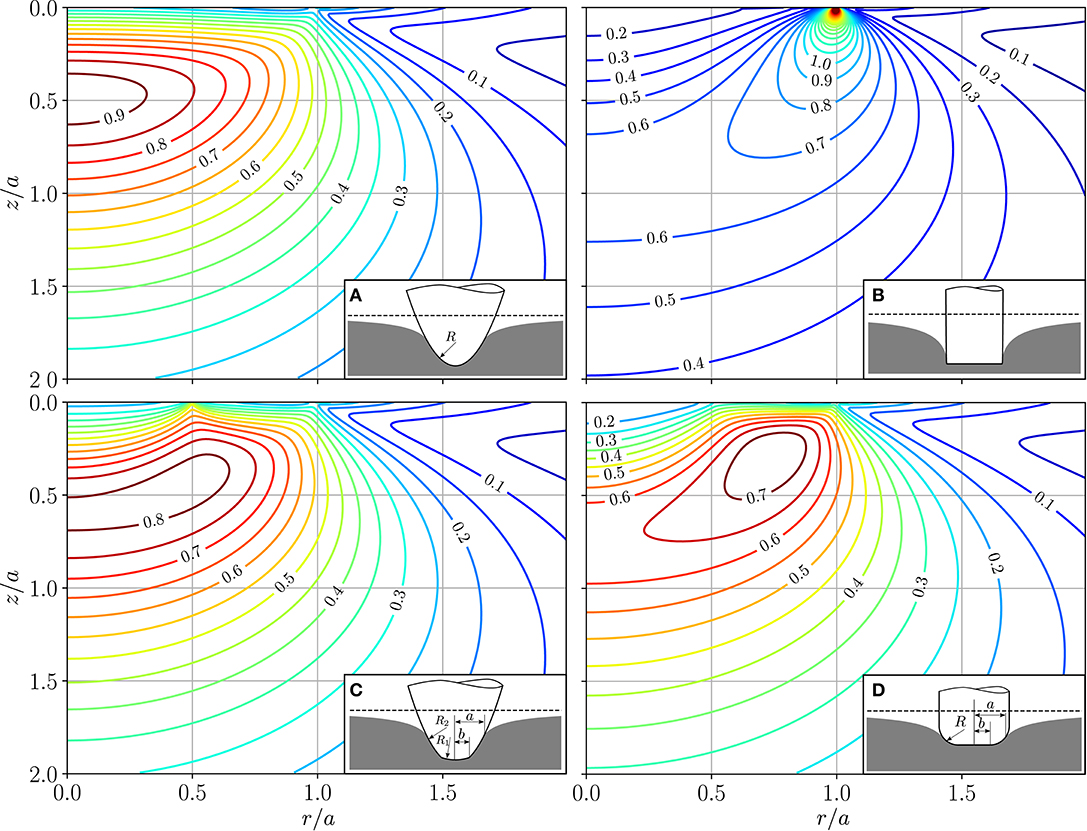
Figure 1. Von Mises equivalent stress in the half-space normalized with the average pressure p0 assuming ν = 0.3 for different indenter shapes with indentation depth δ: (A) Parabolical indenter, (B) Cylindrical flat punch, (C) paraboloid with a parabolical cup with b/a = 0.5 and R1 = 3R2, (D) Cylindrical flat punch with rounded edge with b/a = 0.5.
As a common measure for plastic failure, we calculate the von Mises equivalent stress
The von Mises stress normalized with the average pressure in contact is plotted in Figure 1. Of course, the well-known distribution for the paraboloid with the maximum at z/a = 0.5 is simply the reproduction of the solution by Huber (1904). For the paraboloid with a parabolic cap with b/a = 0.5 and R1 = 3R2, the maximum is widened and is located below the surface as well. Due to the small kink at b/a = 0.5 where the curvature changes, the distribution beneath is distorted toward the surface. The flat punch produces a stress singularity at the surface owing to the sharp edge. The lowest maximum with a normalized von Mises stress of 0.74 is obtained for the Cylindrical flat punch with rounded edges. It occurs under the rounded outer area of the indenter at a depth of z/a ≈ 0.3.
In Figure 2, the absolute value of the hydrostatic pressure gradient,
is plotted. It is normalized by the pressure gradient in the center of the contact plane produced by the equivalent parabolical indenter with the same contact radius and indentation depth,
Unlike the von Mises stress, the pressure gradient reaches its maximum at the surface in all cases. Maxima in form of singularities are found at the contact edge and at places of sudden geometrical change. Thus, the paraboloid with a parabolic cup and the flat punch with rounded edges exhibit additional singularities at r = b. Furthermore, the comparison of the pressure gradient under flat and curved section shows that, apart from the above-mentioned singularities, it is much larger for small radii of curvature.
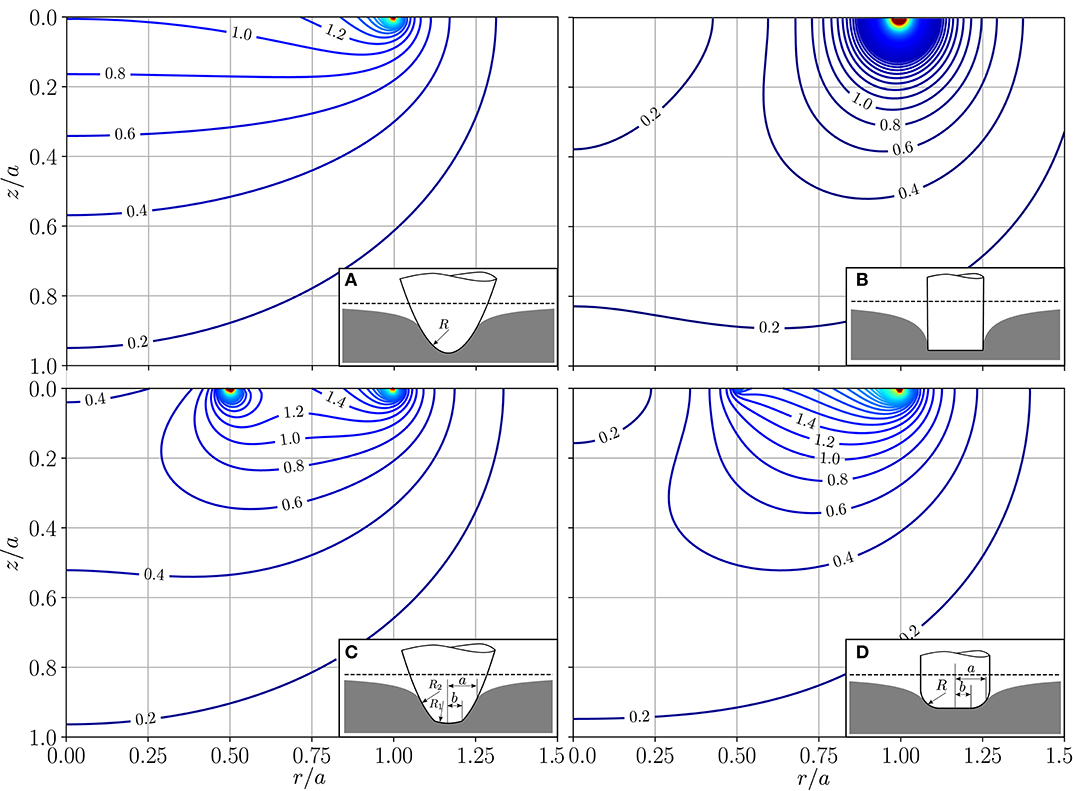
Figure 2. Normalized absolute value of the hydrostatic pressure gradient assuming ν = 0.3 for different indenter shapes with indentation depth δ: (A) Parabolical indenter, (B) Cylindrical flat punch, (C) paraboloid with a parabolical cup with b/a = 0.5 and R1 = 3R2, (D) Cylindrical flat punch with rounded edge with b/a = 0.5.
Tangential Contact in the Cattaneo-Mindlin Approximation
In this section, we consider the stress state and pressure gradient in the half-space due to tangential surface loads in the form
In the Cattaneo-Mindlin approximation, the tangential contact can be reduced to superpositions of contact pressure distributions resulting from the frictionless normal indentation problem (Jäger, 1995). Thus, we can use the same procedure as for the frictionless normal contact. Further, we will discuss the cases of partial slip and complete slip, that is, if the stick condition |σxz(r)| < μ p(r) is violated.
For the Hertzian contact, the tangential surface loading of a globally sliding indenter is
with the coefficient of friction μ. The resulting stresses were given by Hamilton and Goodman (1966) as imaginary parts of a complex function and, later, more conveniently, in explicit form by Hamilton (1983) (note, that in the equation for σxx it should be x2z2/S instead of x2z2/3).
With these expression, we, again, obtain the flat punch solutions via Equation (1). The surface loading for a sliding flat punch, for example, is
A flat punch can either completely slip or completely stick (Popov et al., 2019). The solutions for the case of complete stick, are given by the substitution
in the solutions for the sliding flat punch with the effective shear modulus G* = 4G/(2 − ν) and the tangential rigid body displacement ux,0. For the sake of brevity, the complete set of equations for the tangentially loaded flat punch is not explicitly presented here. It is more convenient to compute and store the derivatives in Equation (1) using a symbolic engine such as Wolfram Mathematica.
For the axisymmetric sliding contact with a convex smooth profile, we, again, determine the stresses from a superposition of incremental sliding flat punch indentations with increasing radii. Hence, the stresses in the half-space, resulting only from the tangential surface loading, are given by Equation (4) and the computed flat punch solutions. It should be noted that for the full stress state, the stresses (5) caused by normal loading must be added.
For monotonic tangential loading, under constant normal force, partial slip will occur for convex profiles. Starting with the tangential loading, slip will propagate from the edge of contact. Following Jäger (1995, 1998) and Ciavarella (1998), the surface stresses σxz in the partial slip case can be written as a superposition
with the surface stress due to normal loading given in Equation of Appendix B and the radius c of the stick area, giving
The radius of the stick area is determined by
Popov et al. (2019), with FN given in Equation (7). Hence, the stresses in the half-space for arbitrary profiles resulting from the tangential loading are given by a superposition of incremental sliding flat punch contacts with radii increasing from the stick radius to the contact radius,
with ij in {xx, yy, zz, xy, yz, zx} and the solutions for a sliding flat punch .
In the case of arbitrary loading histories, the solution is simply a finite number of superpositions in the form of Equation (21). Most conveniently, this can be modeled as one-dimensional tangential spring deflections ux,1D in the framework of MDR (see (Popov et al., 2019) for details), yielding
Obviously, as for the normal contact, the integral Equations (24) and (25) also hold for the hydrostatic pressure and the components of the hydrostatic pressure gradient, if the stress components of the sliding flat punch are substituted with hydrostatic pressure phs and the components of the pressure gradient, respectively.
Examples for Monotonic Tangential Loading
As examples for the tangential contact, we discuss the parabolical indenter and the cylindrical flat punch with rounded edges (see section Examples for the Frictionless Normal Contact for details) under monotonic tangential loading. For a coefficient of friction of μ = 0.3 and tangential rigid body displacement of δ/4 and δ/2, respectively, we obtain the cases of partial slip and complete slip for both indenter shapes.
Figure 3 shows the von Mises equivalent stress for both indenters and loading scenarios in the x-z-plane. In all cases, the tangential surface loading leads to an additional local maximum at the trailing edge in the contact plane and the maximum beneath the surface is shifted toward the leading edge. For the parabolical indenter in the state of partial slip, the global maximum is beneath the surface as for the frictionless normal contact. In case of a complete slip, however, both maxima are of similar magnitude. This corresponds with the statement of Johnson (1985), that the maximum travels to the contact plane for μ > 0.3 in the case of a sliding Hertzian contact. For the flat punch with rounded edges in the partial slip scenario, both maxima are of similar magnitude, while a distinct global maximum at the trailing edge in the contact plane is found in the case of complete slip.
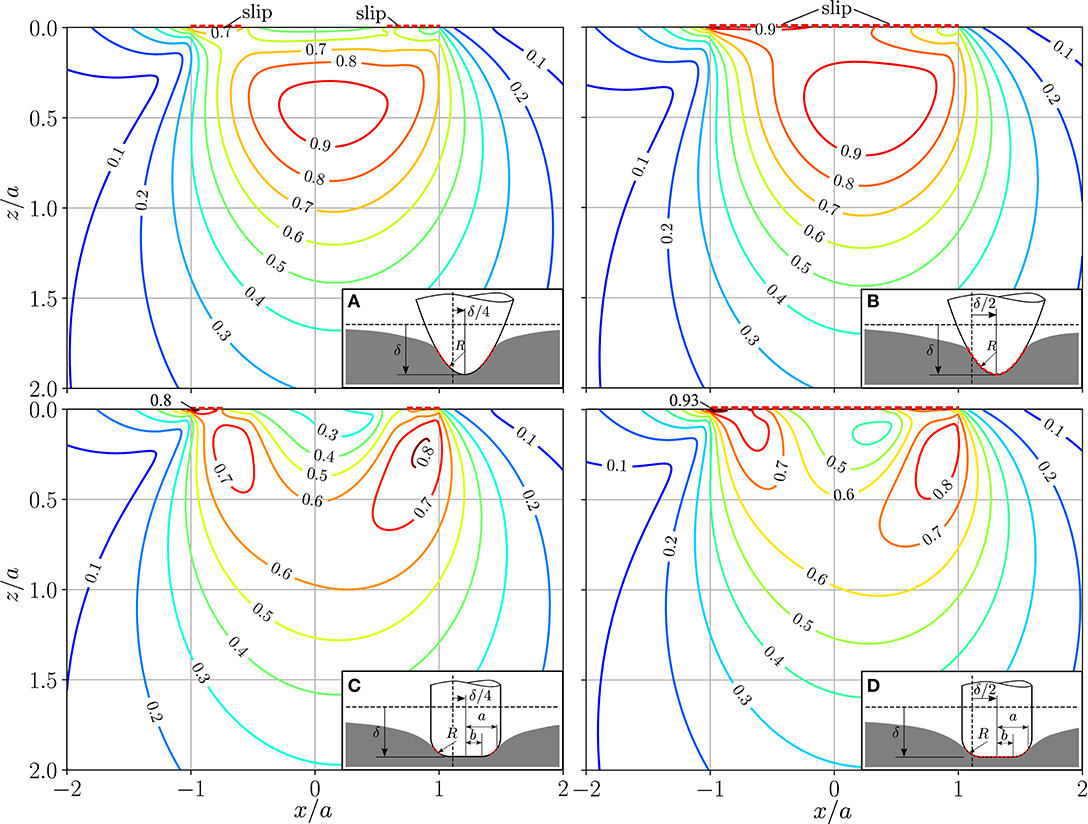
Figure 3. Von Mises equivalent stress in the half-space at y = 0 normalized with the average pressure p0 assuming ν = 0.3 and coefficient of friction μ = 0.3 for different indenter shapes with indentation depth δ and tangential displacement ux,0 = δ/4 for (A,C) and ux,0 = δ/2 for (B,D). Indenter shapes: (A,B) Parabolical indenter, (C,D) Cylindrical flat punch with rounded edge with b/a = 0.5. Dashed red lines mark contact areas with slip.
Figure 4 shows the absolute value of the hydrostatic pressure gradient for the same indenter shapes and loading scenarios. In the case of complete slip, the gradient is increased at the leading edge and decreased at the trailing edge compared to the frictionless normal contact. However, the contribution of the tangential contact is, at least for μ = 0.3, small in comparison to the normal contact. In the case of partial slip, the discontinuity due to the beginning slip area yields an additional minimum at the leading edge and an additional maximum at the trailing edge.
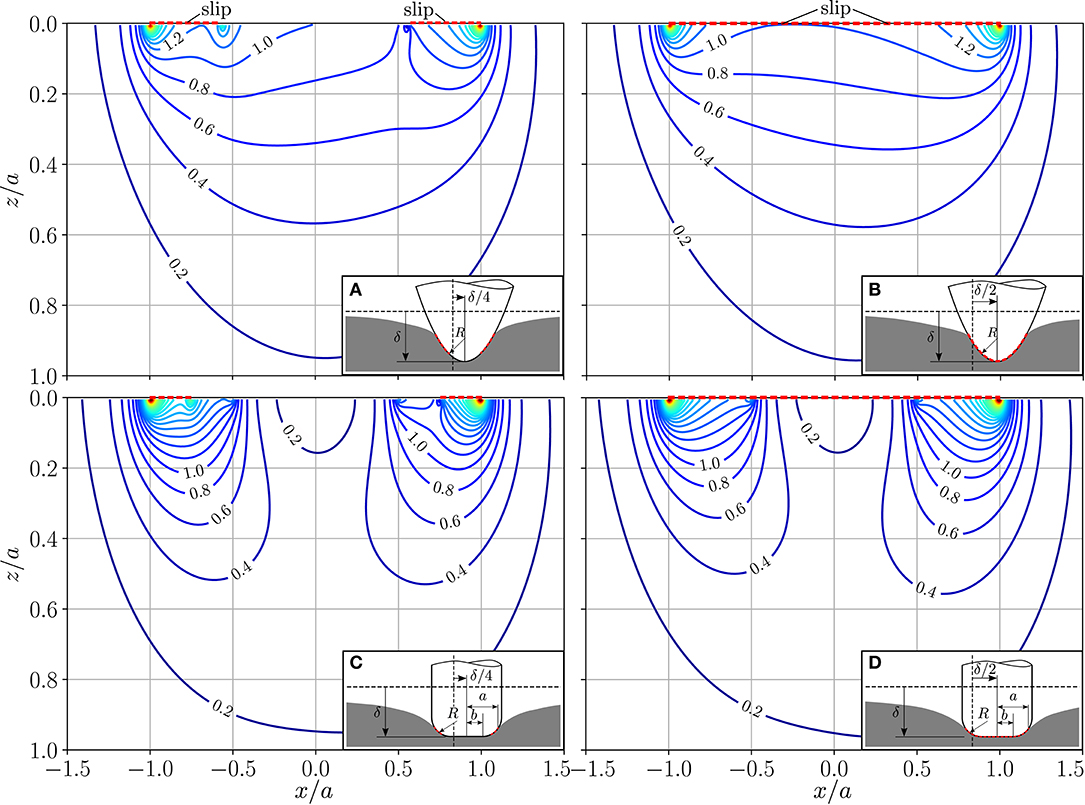
Figure 4. Normalized absolute value of the hydrostatic pressure gradient at y = 0 assuming ν = 0.3 and coefficient of friction μ = 0.3 for different indenter shapes with indentation depth δ and tangential displacement ux,0 = δ/4 for (A,C) and ux,0 = δ/2 for (B,D). Indenter shapes: (A,B) Parabolical indenter, (C,D) Cylindrical flat punch with rounded edge with b/a = 0.5. Dashed red lines mark contact areas with slip.
Discussion
The evaluation of the integral kernels of the one-dimensional integrals (5) or (6) comes, of course, with some computational cost. It is thus advantageous to evaluate the analytic expressions numerically on a grid over the half-space domain of interest and save the resulting matrices. These matrices can then be used to calculate the stress state for arbitrary axisymmetric indenters and loading histories.
For a grid of n × n points in the x − z plane, the one-dimensional integrals can be reduced to n matrix-vector multiplications of complexity , where m is the number of flat punch superpositions. Thus, the overall complexity simply scales with the number of points (in this case n2) and flat punch superpositions, . As it is not necessary to compute the stresses in more points than needed, the proposed formulation can be advantageous compared to other effective methods such as the FFT-based boundary element method (BEM) for the half-space (Pohrt and Li, 2014). For this example, the FFT-based BEM is of complexity because it requires evaluation of stresses on a three-dimensional n × n × n grid. However, if stresses in n × n points in a x − y plane beneath the surface are sought for, the proposed method still has , whereas the FFT-based BEM is only of complexity .
We used stresses derived with the superposition idea to calculate the von Mises equivalent stresses for different indenter shapes and loadings. The examples showed that the endangered regions with respect to plastic failure often lie beneath the surface. Further, we provided expressions for direct calculation of the components of the hydrostatic pressure gradient. In fluid saturated media like cartilage, pressure gradients promote fluid flow which can be linked to tissue growth (Popov, 2019). The examples show that the absolute values of the pressure gradient are higher under small radii of curvature of the indenting body and singular at the surface, where discontinuities such as contact radius, stick radius, or sudden topography changes of the indenting body are located. It should be noted that the superposition idea is not bound to homogenous half-spaces, but can, for example, also be used for layered, graded media like cartilage (Argatov et al., 2018).
The provided expressions for the stress state and pressure gradient in the half-space beneath an axisymmetric indenter in terms of the relation of indentation depth to contact radius δ = g(a) can, thus, be seen as a useful addition to the framework of the Method of Dimensionality Reduction (MDR) (Popov and Heß, 2015). Here, the same function g(x) is interpreted as a one-dimensional profile pressed into a spring bedding. The MDR allows for rapid numerical simulations of profile changes due to wear or growth (in biological joints). However, the presented method of obtaining the full stress tensor can also be generalized with regard to other contact solutions for arbitrary loading histories such as the Method of Memory Diagrams (MMD) (Aleshin et al., 2015).
Conclusions
By exploiting the superposition idea by Mossakovski (1963) and Jäger (1998), we derived expressions in form of one-dimensional integrals for the full stress tensor and the components of the hydrostatic pressure gradient in the half-space beneath normally and tangentially loaded axisymmetric contacts. These expressions allow for efficient pointwise numerical evaluation for arbitrary indenter shapes and are suitable for contact simulations involving shape change due to wear or growth. With respect to plastic failure, we showed the importance of considering the whole half-space for selected indenter shapes and loadings. Further, we calculated hydrostatic pressure gradient distributions and discussed the relevance with respect to growth in biological contacts.
Data Availability Statement
All datasets generated for this study are included in the article/supplementary material.
Author Contributions
The author confirms being the sole contributor of this work and has approved it for publication.
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
I am very grateful to Valentin Popov and Emanuel Willert for valuable discussions on the topic.
References
Aleshin, V., Bou Matar, O., and Van Den Abeele, K. (2015). Method of memory diagrams for mechanical frictional contacts subject to arbitrary 2D loading. Int. J. Sol. Struct. 60, 84–95. doi: 10.1016/j.ijsolstr.2015.02.016
Argatov, I., Heß, M., and Popov, V. L. (2018). The extension of the method of dimensionality reduction to layered elastic media. J. Appl. Math. Mech. ZAMM 98, 622–634. doi: 10.1002/zamm.201700213
Boussinesq, J. (1885). Applications des potentiels à l'étude de l'équilibre et du mouvement des solides élastiques. Paris: Gauthiers-Villars (in French).
Cerruti, V. (1882). Ricerche intorno all' equilibrio de'corpi elastici isotropi. Memorie Dell'accademia Nazionale Dei Lincei 13, 81–122 (in Italian).
Ciavarella, M. (1998). Tangential loading of general three-dimensional contacts. J. Appl. Mech. 65, 998–1003. doi: 10.1115/1.2791944
Ciavarella, M., Hills, D. A., and Monno, G. (1998). The influence of rounded edges on indentation by a flat punch. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci. 212, 319–327. doi: 10.1243/0954406981521259
Hamilton, G. M. (1983). Explicit equations for the stresses beneath a sliding spherical contact. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci. 197, 53–59. doi: 10.1243/PIME_PROC_1983_197_076_02
Hamilton, G. M., and Goodman, L. E. (1966). The stress field created by a circular sliding contact. J. Appl. Mech. 33, 371–376. doi: 10.1115/1.3625051
Huber, M. T. (1904). Zur theorie der berührung fester elastischer körper. Ann. Phys. 14, 153–163. doi: 10.1002/andp.19043190611
Jäger, J. (1995). Axi-symmetric bodies of equal material in contact under torsion or shift. Arch. Appl. Mech. 65, 478–487. doi: 10.1007/BF00835661
Jäger, J. (1998). A new principle in contact mechanics. J. Tribol. 120, 677–684. doi: 10.1115/1.2833765
Johnson, K. L. (1985). Contact Mechanics. Cambridge: Cambridge University Press. doi: 10.1017/CBO9781139171731
Mossakovski, V. I. (1963). Compression of elastic bodies under conditions of (axisymmetric case). J. Appl. Math. Mech. PMM 27, 630–643. doi: 10.1016/0021-8928(63)90150-3
Pohrt, R., and Li, Q. (2014). Complete boundary element formulation for normal and tangential contact problems. Phys. Mesomech. 17, 334–340. doi: 10.1134/S1029959914040109
Popov, V. L. (2019). Active bio contact mechanics: concepts of active control of wear and growth of the cartilage in natural joints. AIP Conf. Proc. 2167:020285. doi: 10.1063/1.5132152
Popov, V. L., and Heß, M. (2015). Method of Dimensionality Reduction in Contact Mechanics and Friction. Berlin: Springer Verlag. doi: 10.1007/978-3-642-53876-6
Popov, V. L., Heß, M., and Willert, E. (2019). Handbook of Contact Mechanics: Exact Solutions of Axisymmetric Contact Problems. Berlin: Springer Verlag. doi: 10.1007/978-3-662-58709-6
Willert, E., Forsbach, F., and Popov, V. L. (2020). Stress tensor and gradient of hydrostatic pressure in the contact plane of axisymmetric bodies under normal and tangential loading. ZAMM. doi: 10.20944/preprints202003.0157.v1
Wong, M., and Carter, D. R. (2003). Articular cartilage functional histomorphology and mechanobiology: a research perspective. Bone 33, 1–13. doi: 10.1016/S8756-3282(03)00083-8
Zhang, L., Hu, J., and Athanasiou, K. A. (2009). The role of tissue engineering in articular cartilage repair and regeneration. Crit. Rev. Biomed. Eng. 37, 1–57. doi: 10.1615/critrevbiomedeng.v37.i1-2.10
Appendix
Appendix A: Flat Punch Solution for the Frictionless Normal Contact Problem
The stress components of the cylindrical flat punch are obtained by Equation (1) with the Hertzian solution by Huber (1904):
with the shortcuts
where A = r2 + z2 − a2 and . With the components in Equation (26), the hydrostatic pressure phs = (σrr + σϕϕ + σzz)/3 and the components of the hydrostatic pressure gradient can be obtained as well:
with the derivatives
Appendix B: Axisymmetric Solution at the Surface for the Frictionless Normal Contact
At the surface (z = 0), the non-vanishing stress components in Equation (5) simplify to
The hydrostatic pressure and the pressure gradient components in Equation (8) simplify to
at the surface. All of the above equations except were already derived by Willert et al. (2020).
Appendix C: Axisymmetric Solution in the Axis of Contact for the Frictionless Normal Contact
In the axis of contact (r = 0), the non-vanishing stress components in Equation (5) simplify to
The hydrostatic pressure and the non-vanishing pressure gradient component in Equation (5) simplify to
in the axis of contact.
Keywords: stress state, pressure gradient, normal contact, tangential contact, friction, axial symmetry, method of dimensionality reduction
Citation: Forsbach F (2020) Stress Tensor and Gradient of Hydrostatic Pressure in the Half-Space Beneath Axisymmetric Bodies in Normal and Tangential Contact. Front. Mech. Eng. 6:39. doi: 10.3389/fmech.2020.00039
Received: 10 March 2020; Accepted: 13 May 2020;
Published: 26 June 2020.
Edited by:
Marco Paggi, IMT School for Advanced Studies Lucca, ItalyReviewed by:
Liran Ma, Tsinghua University, ChinaVladislav Aleshin, UMR8520 Institut d'Électronique, de Microélectronique et de Nanotechnologie (IEMN), France
Copyright © 2020 Forsbach. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Fabian Forsbach, ZmFiaWFuLmZvcnNiYWNoQHR1LWJlcmxpbi5kZQ==
 Fabian Forsbach
Fabian Forsbach