Analysis of Elastic Normal Contact of Surfaces With Regular Microgeometry Based on the Localization Principle

Introduction

In general case, a surface topography is represented by a combination of deterministic and random functions (Whitehouse, 1994) determined by natural factors or technological treatment of the surface. Deterministic components are formed either as a result of imperfections in the operation of technological equipment or in stationary operating conditions (for example, the steady shape of a worn surface Goryacheva, 1997). In addition, a regular microgeometry on the surface can be created to control the operational properties of friction pairs, in particular their tribological characteristics. The geometric structure of surfaces has a great significance on the friction processes in an elastic contact under the condition of minimal wear. Prediction of the contact characteristics of surfaces with a given regular microgeometry, as well as the control of its optimal microgeometry are the urgent problems for micro- and nanotribology (Myshkin and Goryacheva, 2016).

The term “regular microgeometry” suggests that on the surface there is a periodic or a non-periodic system of asperities (or grooves) of a certain shape, mathematically described by a continuous or a piecewise function. The most common types of microgeometry used in tribological applications include isotropic (created in the transverse and longitudinal directions) and anisotropic (created in one direction only) ones.

Many operational characteristics of joints, such as stiffness, thermal and electrical conductivity, tightness, adhesion strength, etc. are determined by characteristics of normal contact such as the contact pressure distribution, the real contact area and the additional compliance caused by the existence of microgeometry. For their correct calculation, it is necessary to formulate and to solve a periodic contact problem that takes into account the density of contact spots and the interaction of asperities. Such problems and methods for solving them have been extensively investigated. Most of the results obtained relate to the solution of the plane periodic problem of the linear elasticity theory, corresponding to the anisotropic (two-dimensional) geometric texture. The approaches for solving this class of problems are well developed. The main analytical ones are based on the methods using complex potentials (Westergaard, 1939; Kuznetsov, 1976; Krishtafovich et al., 1994; Manners, 1998; Soldatenkov, 2013; Xu and Jackson, 2018), the method of superposition of Flamant solutions (Schmueser and Comninou, 1979; Block and Keer, 2008; Tsukanov, 2018a,b), the dual series equations method (Dundurs et al., 1973; Carbone and Mangialardi, 2004), and also their modifications. Based on these methods, problems were also solved with more complex boundary conditions, for example, taking friction into consideration, or the influence of adhesion forces (e.g., see the review of Goryacheva and Martynyak, 2014). The two-dimensional (2D) periodic problems including ones, having several segments of integration within one period can be also effectively solved numerically, e.g., with the use of iterative methods (Chekina and Keer, 1999; Manners, 2003). Boundary element method (BEM) (Ciavarella et al., 2005) and finite element method (FEM) (Paggi and Reinoso, 2018) are also successfully applied for solving problems of that type. Unlike the problems for a single contact zone, the close-form solution of a 2D periodic contact problem commonly contains trigonometric functions and it can be cumbersome for engineering analysis, particular if the shape of asperities is not simple.

In contrast to the case of 2D problem, the three-dimensional (3D) problem corresponding to an isotropic microgeometry was solved only by using semi-analytical and numerical methods (e.g., BEM, FEM) due to the lack of a direct inverse of the corresponding integral equations. The non-periodic contact problems for a system of asperities, having various shape, location and height distribution were solved by semi-analytical iteration methods (Goryacheva, 1997; Shen et al., 2018). The significant influence of contact spots density, depending on the number of asperities and relative distance between them, is emphasized. The numerical methods for 3D periodic contact problems in linear elasticity are well developed now (Müser et al., 2017). They usually include the Fast Fourier transform (FFT) technique to meet the periodic boundary conditions and to reduce the calculation costs (Stanley and Kato, 1997; Yastrebov et al., 2015). A rather effective approximate approach for estimating the distribution of contact pressures on the real contact spots for the surfaces with regular microgeometry, taking into account the asperities interaction, is the use of the localization principle (Goryacheva, 2006). It allows calculating the real contact areas and pressure distribution on them for periodic systems of asperities, having equal or different heights. This method was further developed to analyze the contact pressure distribution during the indentation of a multilevel periodic system of spherical asperities into a two-layer half-space and to analyze the influence of asperities density on the surface layer stress state and the additional compliance due to the existence of surface microgeometry (Goryacheva and Torskaya, 2019).

The main purpose of this study is the development of the approximate analytical method of solution for periodic contact problems, involving regular surface microgeometry on the basis of localization principle. This class of contact problems is widely used in modeling of artificial texture; however, the close-form solutions are rarely available, especially for 3D problems. In this paper, the unified approximate method to solve 3D and 2D contact problems for a periodic system of asperities of equal height is analytically developed. The accuracy of the method is estimated based on the known exact solutions of the corresponding contact problems. New approximate solutions of 2D contact problems for a periodic system of parabolic asperities with single and double contact segments within a period are obtained. Also, new features of the dependences of contact characteristics (pressure distribution, contact zone size) on load are revealed.

Localization Principle in Solving the Discrete Contact Problems

In general case, the problem of discrete contact of a nominally flat surface, having regular microgeometry, with an elastic half-space can be formulated as follows. There is a finite or an infinite system of punches with a given shape, loaded with a constant nominal pressure, which is penetrated into the elastic half-space. For solving the problem it is necessary to determine the contact pressure distribution on the real contact spots, taking into account the curvature of the deformed half-space surface due to the interaction of punches (asperities). The main point of the localization principle (Goryacheva, 2006) is that the real contact pressure on a single contact spot with a sufficient accuracy is determined by setting the exact contact conditions only on the fixed spot under consideration and adjacent to it. The influence of the remaining spots is replaced by the action of the nominal (averaged over the remaining part of the surface) pressure. With this approach, the normal displacements of the half-space surface under an arbitrary fixed asperity from the action of the remaining asperities are taken into account. They are approximately calculated from the distributed nominal pressure acting outside the certain region which depends on the contact density.

The general formulation of the linear elastic 3D periodic contact problem for a system of asperities (with equal or different heights) and its solution using the localization principle are given in Goryacheva (1998). In particular, the results of a numerical analysis of the integral relations obtained (Goryacheva, 1998) show that for a system of periodically arranged axisymmetric asperities with equal height, the pressure distribution p(r) on the real contact spot (for not very intimate contact) with sufficient accuracy is determined by the expression:

$\begin{array}{ll}p(r)=\frac{E^{*}}{4{\pi }^2}{\displaystyle \underset{0}{\overset{a}{\int }}}\Delta f(\rho )H_1(r,\rho )d\rho +\frac{2}{\pi }\overline{N}{P}_s\text{arctan}\left(\frac{\sqrt{a^2-r^2}}{\sqrt{A^2-a^2}}\right)& (1)\end{array}$

where f (r) is the function describing the shape of the punch contact surface, Δf (r) is the Laplacian of the function f (r); $\stackrel{-}{N}$ is the average number of contact spots per unit area, P_sis the load acting on a single contact spot, a is the contact spot radius, $A={(\pi \stackrel{-}{N})}^{-1}$ is the radius of circle outside which the value of nominal pressure acting on the elastic half-space is taken into account (Figure 1), E^* is the reduced modulus of elasticity of the contacting bodies, determined by the following expression

$\begin{array}{ll}\frac{1}{E^{*}}=\frac{1-{\nu }_1^2}{E_1}+\frac{1-{\nu }_2^2}{E_2},& (2)\end{array}$

where E₁, ν₁ and E₂, ν₂ are the Young's moduli and Poisson's ratios of the materials of contacting bodies, respectively.

FIGURE 1

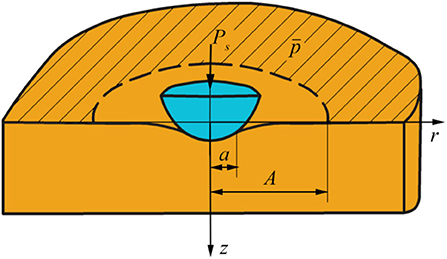
Figure 1. Representation of contact interaction of a system of axisymmetric asperities with an elastic half-space according to the localization principle.

The kernel of the integral operator in Equation (1) is determined for the circular contact region in the case of bounded contact pressure as Goryacheva (1998):

$\begin{array}{l}{H}_1(r,\rho )={\displaystyle \underset{0}{\overset{2\pi }{\int }}}\frac{2\rho }{\pi \sqrt{r^2-2r\rho \text{ cos }\theta +{\rho }^2}}\text{arctan}\\ \left(\frac{\sqrt{a^2-r^2}\sqrt{a^2-{\rho }^2}}{a\sqrt{r^2-2r\rho \text{ cos }\theta +{\rho }^2}}\right)d\theta .& (3)\end{array}$

The total load acting on a single contact spot is determined by the equilibrium equation

$\begin{array}{ll}{P}_s=2\pi {\displaystyle \underset{0}{\overset{a}{\int }}}p(r)rdr.& (4)\end{array}$

To increase the accuracy of contact characteristics calculation, especially at high contact density, it is necessary to solve the inhomogeneous integral equation of the second kind when determining the contact pressure (Goryacheva, 1998).

This approach was used (Goryacheva and Torskaya, 1995; Goryacheva, 1998) for calculation of contact pressures and internal stresses at indentation of a periodic system of equally high asperities into an elastic homogeneous and an inhomogeneous (coated) half-space. The calculation results show a significant effect of the asperities density on the distribution of contact pressures under a single asperity (Figure 2A) and on the dependence of radius of a single contact spot on the nominal pressure $\stackrel{-}{p}=P\stackrel{-}{N}$ (Figure 2B).

FIGURE 2

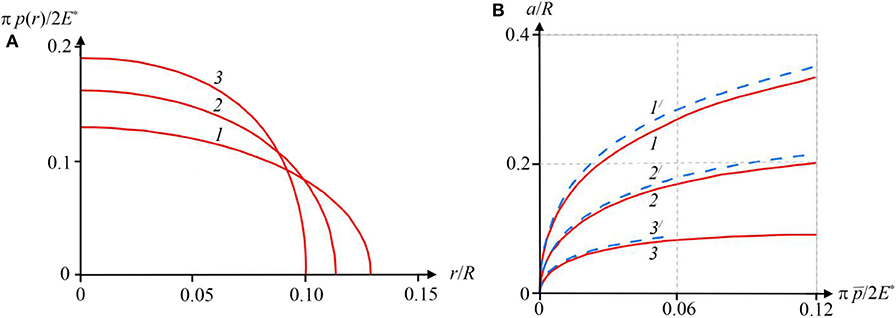
Figure 2. Pressure distribution under a single asperity (A) at $\stackrel{-}{p}=\pi P/2E^{*}{R}^2$ = 0.0044; l/R = 1 (1), l/R = 0.25 (2), l/R = 0.2 (3) and dependence of the radius of a contact spot on dimensionless nominal pressure (B) for l/R = 1 (1,1^/), l/R = 0.5 (2, 2^/), l/R = 0.2 (3, 3^/); curves 1, 2, 3 are calculated from Equations (1–4) and 1^/, 2^/, 3^/—from the Hertz theory.

In the case of indentation of periodic system of asperities with different heights into an elastic homogeneous or layered half-space the penetration of the highest asperities is calculated firstly. Then the curvature of the half-space boundary between asperities is calculated, and the nominal pressure at which the asperities of the next height level come into contact is determined. The described method for 3D problems with several height levels of asperities is suggested by Goryacheva (1997, 1998).

Determination of the Contact Characteristics of Surfaces With a Microrelief in the Conditions of a Plane Elasticity Problem

In the general case, a plane-strain periodic contact problem without friction involves solving the following integral equation having a Hilbert kernel (Schtaierman, 1949; Barber, 2018):

$\begin{array}{ll}\frac{E^{*}}{2}{h}^{\prime }(x)=\frac{1}{2\pi }{\displaystyle \underset{-a}{\overset{a}{\int }}}p(\xi )cot\frac{x-\xi }{2}d\xi ,& (5)\end{array}$

here h′(x) is the derivative of the initial gap function between surfaces, p(x) is the contact pressure distribution; a is the half-width of the contact zone.

In the absence of a direct inversion of Equation (5) on an arbitrary segment [–a, a] a closed form expression for determining the distribution of contact pressure is possible only for certain initial gap functions.

The method to solve the contact problems based on the localization principle, in the simplest formulation, involves the contact problem solution for a single asperity (determination of contact pressure distribution) taking into account the normal displacements of a half-plane boundary inside the considered single contact zone from action of the averaged pressure, applied outside the certain region (see section Localization Principle in Solving the Discrete Contact Problems).

The contact problem for a single contact segment is described by the integral equation with the Cauchy kernel (Muskhelishvili, 1953):

$\begin{array}{ll}\frac{E^{*}}{2}{h}^{\prime }(x)=\frac{1}{2\pi }{\displaystyle \underset{-a}{\overset{a}{\int }}}\frac{p(\xi )}{x-\xi }d\xi ,& (6)\end{array}$

having for a symmetric initial gap function and bounded pressure on both ends of contact segment the following inversion (Muskhelishvili, 1953):

$\begin{array}{ll}p(x)=\frac{E^{*}}{2\pi }\sqrt{a^2-x^2}{\displaystyle \underset{-a}{\overset{a}{\int }}}{h}^{\prime }(\xi )\frac{1}{\sqrt{a^2-{\xi }^2}}\frac{1}{\xi -x}d\xi .& (7)\end{array}$

The initial gap function within the contact zone is determined by the following condition:

$\begin{array}{ll}h(x)=\delta -(f(x)+f_2(x)),& (8)\end{array}$

where f (x) is the asperity shape function, δ is the contact approach, f ₂(x) is the function, describing curvature of the half-plane boundary caused by the action of the remaining asperities except for the one under consideration.

According to the localization principle, the action of the remaining asperities is replaced by a uniform pressure acting outside a strip of width 2b. The value of 2b is determined from the condition of equality of the mean pressure inside and outside of this strip. The mean pressure in a plane periodic contact problem is determined as $\stackrel{-}{p}=P_s/L$, where P_s is the total load on a single contact segment, L is the distance between the peaks of asperities (period); therefore 2b = L. To determine the total load on a single contact zone P_s, the equilibrium equation is used

$\begin{array}{ll}{P}_s={\displaystyle \underset{-a}{\overset{a}{\int }}}p(x)dx.& (9)\end{array}$

The function f ₂(x) can be represented as a difference between displacements from a uniform load distributed over the entire half-plane and displacements from the same load inside a strip of width L (Johnson, 1985):

$\begin{array}{ll}{f}_2(x)=-\frac{2}{\pi E^{*}}\frac{P_s}{L}\left(C-{\displaystyle \underset{-a}{\overset{x}{\int }}}ln\left[\frac{L/2+\xi }{L/2-\xi }\right]d\xi \right).& (10)\end{array}$

Displacements from a uniform load distributed over the all half-plane are constant. This statement can be justified as follows. If one represents the uniform pressure distributed over a strip of arbitrary width 2b in the form of Fourier series with a period L as

$\begin{array}{ll}p(x)=\stackrel{-}{p}\frac{2b}{L}+\frac{2}{\pi }\stackrel{-}{p}{\displaystyle \sum _{n=1}^{\infty }}\frac{1}{n}\text{sin}\left(\frac{2\pi nb}{L}\right)\text{cos}\left(\frac{2\pi nx}{L}\right),& (11)\end{array}$

then the derivative of vertical displacements of the half-plane boundary from the pressure distribution (11) is determined by the Hilbert transform (Srivastava and Lowengrub, 1970):

$\begin{array}{ll}{{ū}_z}^{\prime }(x)=H\left\{p(x)\right\}=\frac{4}{\pi }\stackrel{-}{p}{\displaystyle \sum _{n=1}^{\infty }}\frac{1}{n}\text{sin}\left(\frac{2\pi nb}{L}\right)\text{sin}\left(\frac{2\pi nx}{L}\right).& (12)\end{array}$

Taking into account that 2b = L, the right-hand side of Equation (12) becomes zero, and the half-plane displacements are constant. After differentiating Equation (10) and substitution the result in Equation (8), we obtain the expression for the derivative of the gap function inside the single contact zone:

$\begin{array}{l}{h}^{\prime }(x)=f^{\prime }(x)+\frac{2}{\pi E^{*}}\frac{P_s}{L}\left(ln\left[\frac{L/2+x}{L/2-x}\right]\right)\\ =f^{\prime }(x)+\frac{4}{\pi E^{*}}\frac{P_s}{L}\text{artanh}\left(\frac{2x}{L}\right),& (13)\end{array}$

Using Equation (7), one can determine the contact pressure taking into account the elastic interaction of asperities.

$\begin{array}{l}p(x)=\frac{E^{*}}{2\pi }\sqrt{a^2-x^2}{\displaystyle \underset{-a}{\overset{a}{\int }}}\left[f^{\prime }(\xi )+\frac{4}{\pi E^{*}}\frac{P_s}{L}\text{artanh}\left(\frac{2\xi }{L}\right)\right]\\ \frac{1}{\sqrt{a^2-{\xi }^2}}\frac{1}{\xi -x}d\xi .& (14)\end{array}$

The total load on the asperity, taking into account the symmetry of the function f (x), is determined directly using Equation (13) (Schtaierman, 1949; Barber, 2018):

$\begin{array}{ll}P=\frac{E^{*}}{2}{\displaystyle \underset{-a}{\overset{a}{\int }}}\frac{f^{\prime }(\xi )\xi d\xi }{\sqrt{a^2-{\xi }^2}}+\frac{2}{\pi }\frac{P_s}{L}{\displaystyle \underset{-a}{\overset{a}{\int }}}\frac{\xi }{\sqrt{a^2-{\xi }^2}}\text{artanh}\left(\frac{2\xi }{L}\right)d\xi .& (15)\end{array}$

Calculation of the integral in the second term of Equation (15) with condition of 2a < L gives the following expression for the load:

$\begin{array}{ll}P=\frac{E^{*}}{2}{\displaystyle \underset{-a}{\overset{a}{\int }}}\frac{f^{\prime }(\xi )\xi d\xi }{\sqrt{a^2-{\xi }^2}}+\frac{P_s}{L}\left(L-\sqrt{L^2-4a^2}\right).& (16)\end{array}$

Using Equation (16), it is possible to simplify the integration of the second term in square brackets in Equation (14). For this purpose the method based on the Abel transform of the function ∂P/∂a (Barber, 2018) was used. Then Equation (14) is reduced to the following form

$\begin{array}{l}p(x)=\frac{1}{\pi }{\displaystyle \underset{x}{\overset{a}{\int }}}\frac{{P^{\prime }}_a(\xi )d\xi }{\sqrt{{\xi }^2-x^2}}=\frac{E^{*}}{2\pi }\sqrt{a^2-x^2}{\displaystyle \underset{-a}{\overset{a}{\int }}}\frac{f^{\prime }(\xi )d\xi }{\sqrt{a^2-{\xi }^2}(\xi -x)}\\ +\frac{2P_s}{\pi L}\text{arctan}\left(\frac{2\sqrt{a^2-x^2}}{\sqrt{L^2-4a^2}}\right),& (17)\end{array}$

where ${P^{\prime }}_a=\partial P/\partial a$.

It should be noted that in the 2D periodic problem the effect of elastic interaction on the contact pressure under the central asperity is characterized by a function similar to the 3D case for axisymmetric asperities arranged at the nodes of hexagonal lattice (see Equation 1).

Let us consider some examples of using the localization principle in 2D periodic contact problems for specific types of microgeometry, common in engineering applications.

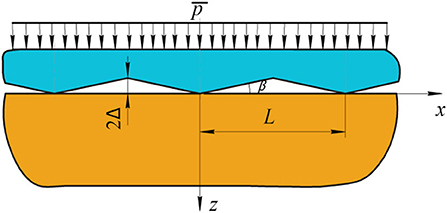
Sinusoidal Profile

A two-dimensional profile described by the function f(x) = Δ(1 − cos(2πx/L)), where Δ, L are the amplitude and the period, is the simplest way to describe waviness or roughness of a surface formed along one direction (longitudinal or transverse). Expressions for determining the contact pressure distribution and the dependence of mean pressure $\stackrel{-}{p}$ on a contact zone half-width were first obtained by Westergaard (1939):

$\begin{array}{ll}p(x)=\frac{\sqrt{2}\pi E^{*}\Delta }{L}\text{cos}(\pi x/L)\sqrt{\text{cos}(2\pi x/L)-\text{cos}(2\pi a/L)};& (18)\end{array}$

$\begin{array}{ll}\stackrel{-}{p}=p^{*}{\text{sin}}^2(\pi a/L).& (19)\end{array}$

Here p^* = πE^*Δ/L is the pressure required to achieve complete contact between surfaces.

Consider the solution of this problem using the localization principle. The initial and the equivalent schemes of the problem are shown in Figure 3.

FIGURE 3

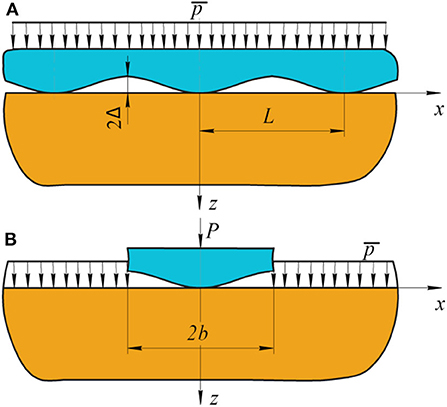
Figure 3. Contact of a wavy surface with an elastic half-plane (A) and the equivalent scheme in accordance with the localization principle (B).

An analytical expression for contact pressure distribution under a single sinusoidal asperity, which is a solution of Equation (6), was obtained by Tsukanov (2018a) in the form of an infinite series of Chebyshev polynomials:

$\begin{array}{l}{p}_s(x)=\frac{2\pi \Delta E^{*}}{L}\sqrt{1-{(x/a)}^2}\\ {\displaystyle \sum _{k=0}^{\infty }}{(-1)}^k{\text{J}}_{2k+1}(2\pi a/L)U_{2k}(x/a),& (20)\end{array}$

where U_i(x) is the Chebyshev polynomial of the second kind of degree i; J_k(x) is the Bessel function of the first kind of integer order k.

Equations for determining the total force, applied to a single asperity and the maximum pressure are obtained in closed form Tsukanov (2018a):

$\begin{array}{ll}{P}_s=\frac{{\pi }^2\Delta E^{*}}{L}a{\text{J}}_1(2\pi a/L);& (21)\end{array}$

$\begin{array}{ll}{p}_{smax}=p_s(x){|}_{x=0}=\frac{\pi \Delta E^{*}}{L}{\displaystyle \underset{0}{\overset{2\pi a/L}{\int }}}{\text{J}}_0(t)dt.& (22)\end{array}$

Using Equations (16–17) and (20–22), the approximate expressions can be obtained to determine the contact characteristics of a wavy surface indenting into an elastic half-plane. The expressions for the mean and the maximum pressure have the following form

$\begin{array}{ll}\stackrel{-}{p}=\frac{{\pi }^2\Delta E^{*}}{L^2}a{\text{J}}_1(2\pi a/L)\left(2-\frac{\sqrt{L^2-4a^2}}{L}\right);& (23)\end{array}$

$\begin{array}{l}{p}_{max}=\frac{\pi \Delta E^{*}}{L}{\displaystyle \underset{0}{\overset{2\pi a/L}{\int }}}{\text{J}}_0(t)dt+\frac{2\pi \Delta E^{*}}{L^2}a{\text{J}}_1(2\pi a/L)\\ \left(\text{arctan}\left(\frac{2a}{\sqrt{L^2-4a^2}}\right)\right).& (24)\end{array}$

Wedged Profile

This type of microrelief can be found on surfaces after very rough edge machining. The radius of curvature of asperities is much smaller than their height, and it can be considered as negligible. The scheme of the problem is shown in Figure 4. The equivalent scheme according to localization principle is similar to Figure 3.

FIGURE 4

Figure 4. Contact of a wedged profile with an elastic half-plane.

For the possibility of applying the methods of the linear theory of elasticity, the angleβ = arctan(4Δ/L) should be small.

The exact solution of this problem was obtained by Block and Keer (2008):

$\begin{array}{ll}p(x)=\frac{E^{*}\text{ tan }\beta }{\pi }\text{arcosh}\left(\frac{\text{tan}(\pi a/L)}{\text{tan}(\pi \left|x\right|/L)}\right).& (25)\end{array}$

In accordance with the localization principle (see Equations 16, 17) and using well-known expressions for determining contact pressure and total load on a single blunt wedge (Johnson, 1985), the following approximate equations for determining the contact characteristics have been reduced:

$\begin{array}{l}p(x)=\frac{E^{*}\text{ tan }\beta }{\pi }\text{arcosh}\left(\frac{a}{x}\right)\\ +\frac{2E^{*}a\text{ tan }\beta }{\pi L}\text{arctan}\left(\frac{2\sqrt{a^2-x^2}}{\sqrt{L^2-4a^2}}\right);& (26)\end{array}$

$\begin{array}{ll}\stackrel{-}{p}=\frac{E^{*}a\text{ tan }\beta }{L}\left(2-\frac{\sqrt{L^2-4a^2}}{L}\right).& (27)\end{array}$

Periodic System of Parabolic Asperities With a Single Contact Segment Within a Period

A common in practical applications type of texture (e.g., after laser surfacing) is a periodic system of cylindrical (parabolic) asperities in which the radius of curvature significantly exceeds their height. The scheme of the problem is shown in Figure 5.

FIGURE 5

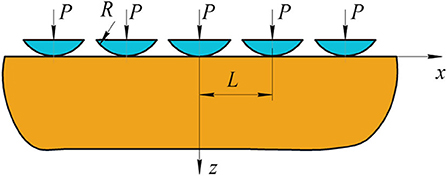
Figure 5. Contact of a system of parabolic asperities and an elastic half-plane with a single contact segment within a period.

This problem was previously considered by Kuznetsov (1978). An exact expression to calculate the contact pressure distribution in a closed form has not been derived, however the relation between the half-width a of a contact zone and the total load per one asperity P_s was found (Kuznetsov, 1978):

$\begin{array}{ll}a=\frac{L}{\pi }arccos\left(exp\left(-\frac{2\pi P_{s}R}{L^2{E}^{*}}\right)\right).& (28)\end{array}$

Using the well-known equations for determining the contact characteristics of a single smooth indenter (Johnson, 1985) and Equations (16, 17), the following expressions for the pressure distribution and the total load on a single asperity, taking into account elastic interaction are derived:

$\begin{array}{ll}p(x)=\frac{E^{*}}{2R}\sqrt{a^2-x^2}+\frac{E^{*}{a}^2}{2RL}\text{arctan}\left(\frac{2\sqrt{a^2-x^2}}{\sqrt{L^2-4a^2}}\right);& (29)\end{array}$

$\begin{array}{ll}{P}_s=\frac{\pi E^{*}{a}^2}{4R}\left(2-\frac{\sqrt{L^2-4a^2}}{L}\right).& (30)\end{array}$

Periodic System of Asperities With Two Contact Segments Within a Period

The more complicated problem arises, if there are multiple contact segments within one period. Without significant loss of generality let us consider the contact problem for a periodic non-uniform system of parabolic asperities and an elastic half-plane, with two interacting asperities within a single period. This type of contact problem has no exact solution, but can be approximately solved in a close-form using the localization principle.

The problem scheme is shown in Figure 6. Pairs of parabolic asperities form a periodic system with a period L. The shape of two interconnected asperities (see Figure 6) can be expressed by a biquadratic function:

$\begin{array}{ll}f(x)=\frac{x^4}{8R{c}^2}-\frac{x^2}{4R}.& (31)\end{array}$

Here R is a curvature radius of each asperity and 2c is a distance between asperity centers. The system of asperities is under the action of the nominal pressure $\stackrel{-}{p}$.

FIGURE 6

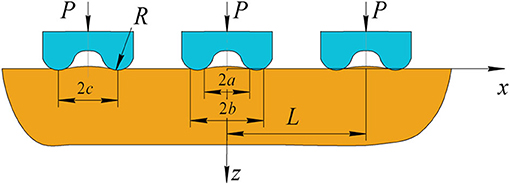
Figure 6. Contact of a system of parabolic asperities and an elastic half-plane with two contact segments within a period.

For the two contact segments and asperities shape, defined by Equation (31), the contact pressure and the total load on one contact segment are determined by the following expressions (Gladwell, 1980):

$\begin{array}{ll}{p}_0(x)=\frac{E^{*}\sqrt{x^2\left(x^2-{b_0}^2\right)\left({a_0}^2-x^2\right)}}{4R{c}^2},a_0\le |x|\le b_0;& (32)\end{array}$

$\begin{array}{ll}{P}_s=\frac{\pi E^{*}{\left({b_0}^2-{a_0}^2\right)}^2}{64R{c}^2},& (33)\end{array}$

where $2c=\sqrt{2({b_0}^2+{a_0}^2)}$.

The contact pressure in a general case of multizone 2D contact problem is determined by the following expression (Schtaierman, 1949; Muskhelishvili, 1953):

$\begin{array}{ll}p(x)=\frac{E^{*}}{2\pi X(x)}{\displaystyle \sum _{k=1}^n}{\displaystyle \underset{a_k}{\overset{b_k}{\int }}}\frac{h^{\prime }(\xi )X(\xi )d\xi }{\xi -x}+\frac{2i{Q}_{n-1}(x)}{X(x)}.& (34)\end{array}$

Here h(x) is an initial gap function; n is a number of contact segments, k = 1…n; a_k, b_k are the coordinates of the k-th contact segment; $X(x)=\sqrt{(x-a_1)(x-b_1)\dots (x-a_n)(x-b_n)}$; $Q_{n-1}(x)=D_0{x}^{n-1}+D_1{x}^{n-2}+\dots +D_{n-1}$; coefficients D₀…D_n−1 are determined from the system of equations taking into account continuity and boundary conditions at the contact segment ends (Ghanati and Adibnazari, 2019).

According to the localization principle, to obtain a solution of a periodic problem we must consider the contact of the asperities at one period taking into account an additional curvature f₂(x) of the half-plane boundary within the contact zones due to the influence of the other asperities. It follows from Equation (13), that the derivative of the initial gap function within each contact zone, can be expressed as:

$\begin{array}{ll}{h}^{\prime }(x)=f^{\prime }(x)+{f^{\prime }}_2(x)=\frac{x^3}{2R{c}^2}-\frac{x}{2R}+\frac{4\stackrel{-}{p}}{\pi E^{*}}\text{artanh}\left(\frac{2x}{L}\right).& (35)\end{array}$

Taking into account the boundary conditions within one period and approximating the hyperbolic arctangent function in Equation (35) by the cubic polynomial under the assumption that 2c < L, from Equation (34) we obtain the following expression for the contact pressure in periodic problem:

$\begin{array}{ll}p(x)=\frac{E^{*}\sqrt{Z(x)}}{2\pi }{\displaystyle \underset{a}{\overset{b}{\int }}}\frac{h^{\prime }(\xi )d\xi }{(\xi -x)\sqrt{Z(\xi )}},& (36)\end{array}$

Here Z(x) = (x² − b²)(a² − x²) (a and b are the ends of the contact zones in periodic contact problem) and h′(x) is approximated by the following expression:

$\begin{array}{ll}{h}^{\prime }(x)=\left(\frac{1}{2R{c}^2}+\frac{32\stackrel{-}{p}}{3\pi E^{*}{L}^3}\right)x^3+\left(\frac{8\stackrel{-}{p}}{\pi E^{*}L}-\frac{1}{2R}\right)x.& (37)\end{array}$

Substituting Equations (35) and (37) in Equation (36) and following Gladwell (1980), we derive the following expression for the contact pressure in the periodic contact problem with two parabolic asperities within the period:

$\begin{array}{l}p(x)=E^{*}\left(\frac{1}{4R{c}^2}+\frac{16\stackrel{-}{p}}{3\pi E^{*}{L}^3}\right)\\ \sqrt{x^2\left(x^2-b^2\right)\left(a^2-x^2\right)}.a\le |x|\le b,& (38)\end{array}$

where the ends of the contact zones follow the relation b² + a² = 2c².

A more general problem, involving multiple contact zones, can be treated similarly using numerical methods for solution of Equation (34).

For comparison of the results obtained in the periodic contact problem with the contact pressure distribution (32) for two asperities we assume that the distance between asperities 2c and the nominal (mean) pressure $\stackrel{-}{p}$ are the same; the value of the nominal pressure is calculated from the relation

$\begin{array}{ll}\stackrel{-}{p}=\frac{2P_s}{L},& (39)\end{array}$

where P_s is given by Equation (33).

Results and Discussion

The analytical solutions derived from the method of localization were used for the analysis of the contact characteristics in the periodic contact problems and for comparison with the available exact solutions. The dimensionless pressure distributions for the contact of a sinusoidal wavy surface and an elastic half-plane at two values of a dimensionless contact zone width are shown in Figure 7. The results indicate that the solution based on the localization principle allows predicting the distribution of contact pressures with sufficient accuracy up to high loads (high contact density, characterizing by the ratio 2a/L). The comparison of the dependencies of the dimensionless mean and maximum contact pressures vs. contact zone width 2a for the exact and the approximate solutions is presented in Figure 8. The results indicate that a significant discrepancy between the exact and the approximate values of contact characteristics begins only at high contact density (2a/L ≈ 0.7). Note, that for such high values of contact density the solution for almost complete contact can be applied (Johnson, 1985).

FIGURE 7

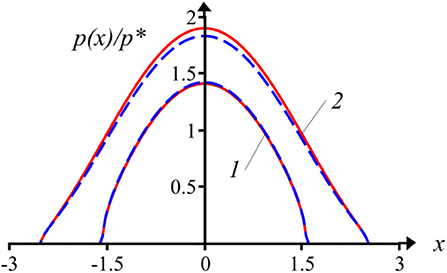
Figure 7. Pressure distribution for sinusoidal waviness contacting with an elastic half-plane at 2a/L = 0.5 (1) and 2a/L = 0.8 (2): exact solution (solid line), localization principle solution (dashed line).

FIGURE 8

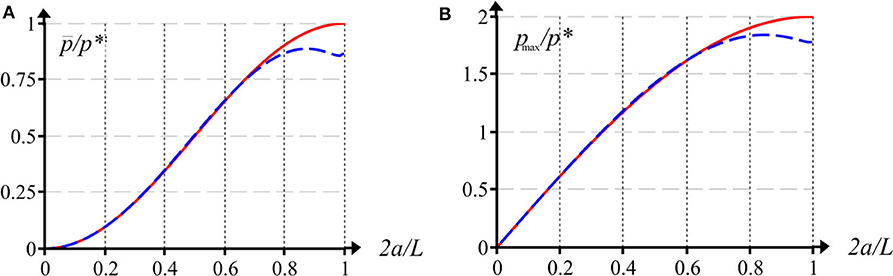
Figure 8. The dependence of the mean (A) and the maximum (B) pressures on a contact zone width: exact solution (solid line), approximate solution (dashed line).

The distributions of contact pressure for a wedged profile indented into an elastic half-plane at two values of dimensionless contact zone width are shown in Figure 9. Comparison of the results calculated based on the exact solution and the localization principle makes it possible to conclude that the approximate pressure distribution is close to the exact one even for the case with infinite peaks due to angle point in the wedged profile. The dependences of the dimensionless contact zone width on the dimensionless mean pressure for the wedged profile, indenting into an elastic half-plane are shown in Figure 10. For the wedged profile, as well as for the wavy one, the discrepancy of the dependencies of the contact width on the mean contact pressure begins at 2a/L ≈ 0.7. At further increase of the applied pressure the approximate solution gives overestimated values of contact zone width.

FIGURE 9

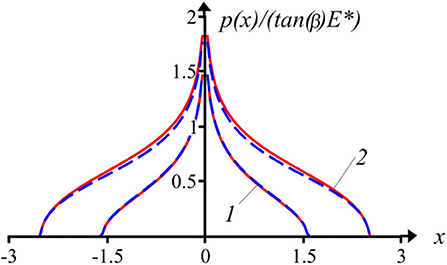
Figure 9. Contact pressure distribution for the wedged profile at 2a/L = 0.5 (1) and 2a/L = 0.8 (2): exact solution (solid line), localization principle solution (dashed line).

FIGURE 10

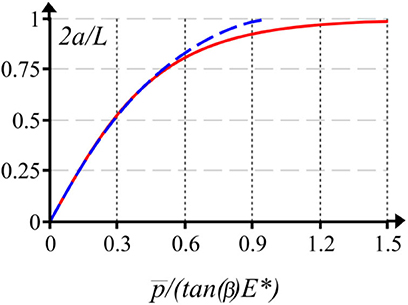
Figure 10. Dependencies of the contact width on the mean pressure for a wedged profile: numerical integration of Equation (25) (solid line), approximate solution (dashed line).

The pressure distributions calculated for a periodic system of cylindrical (parabolic) asperities with use of Equation (29) in comparison with the Hertz theory (in a two-dimensional formulation) are shown in Figure 11. The asperity interaction effect is revealed in a decrease in the contact zone size and an increase in the peak pressure. With a further increase in load or asperities density, the pressure profile is significantly different from the Hertzian one. This result is in good agreement with the 3D case for spherical asperities (see Figure 2). The comparative graphs of a/L ratio on the dimensionless load for a periodic system of parabolic asperities with a single contact segment within a period are shown in Figure 12. The curve corresponding to the localization principle solution is close to the exact solution up to the value a/L ≈ 0.35 (2a/L ≈ 0.7), as well as for other considered profiles. The discrepancy with the Hertzian curve corresponding to non-interacting asperities begins at a/L ≈ 0.125. For the values of a/L < 0.125 the error of calculation using the Hertz theory is <3%. The last result is similar to the case of a 3D system of spherical asperities (see Figure 2). At the large values of load the approximate solution overestimates the contact zone size in comparison with the exact Equation (28), however the discrepancy is smaller than for a wedged profile.

FIGURE 11

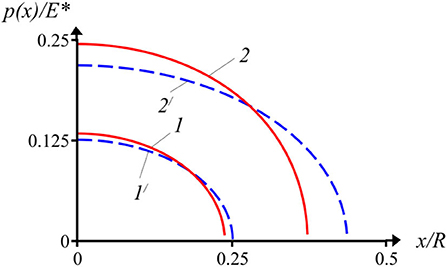
Figure 11. The contact pressure distribution under the cylindrical asperity for the periodic system (1, 2) and from the Hertz solution (1^/, 2^/) at $\stackrel{-}{p}/E^{*}$ = 0.05 (1, 1^/) and [[Inline Image]] = 0.15 (2, 2^/).

FIGURE 12

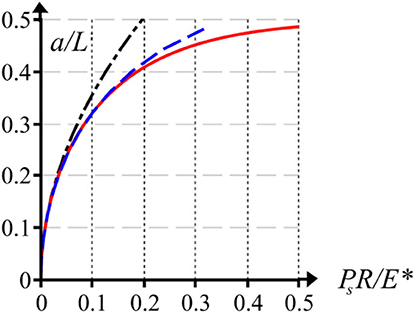
Figure 12. The dependence of a/L ratio on the dimensionless load for a periodic system of cylindrical asperities: exact solution (solid line), localization principle solution (dashed line), the Hertz theory (dash-dot line).

Contact pressure distributions for a periodic system of parabolic asperities with two contact segments within a period (L = 2.4c) are shown in Figure 13 in comparison with the non-periodic double asperity contact. The graphs show, that as well as for a single contact segment within a period (see Figure 11) the increase in the density of asperities leads to an increase in the peak pressure, and also to the reduction of contact width (b–a) at fixed nominal pressure. The considered case can be used in the analysis of a short-range and a long-range elastic interaction between asperities. The short-range elastic interaction, depending mainly on the distance between two asperities, leads to asymmetry of the contact pressure distribution between the adjacent sides of the asperities. The long-range interaction is determined by the number and the shape of asperities within one period and the value of L. Effect of the long-range interaction is smaller than of the short-range; approximately it can be considered on the basis of localization principle. The maximum effect of the long-range elastic interaction is reached at merging of contact zones between the asperities (a = 0).

FIGURE 13

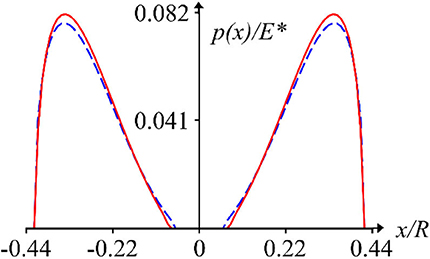
Figure 13. Distribution of contact pressures for a periodic system of asperities with two contact segments within a period (solid lines) in comparison with a non-periodic double asperity contact (dashed lines): $\stackrel{-}{p}/E^{*}$ = 0.05; 2c = 0.6.

Conclusions

The unified approximate analytical method to solve 3D and 2D contact problems for a regular surface microgeometry penetrating the elastic half-space (half-plane) is developed. The equations derived for 3D and 2D cases, using the localization principle, show the identical structure for different dimensionality of the problem. The accuracy of the obtained method for two-dimensional problems was estimated for wavy and wedged profiles, by comparison with the exact solutions. New approximate solutions of 2D contact problems for a periodic system of parabolic asperities with single and double contact segments within a period are obtained.

The results obtained show that the application of the presented method in a plane contact problem for bodies with a periodic regular microrelief allows to calculate the contact characteristics with high accuracy up to large contact densities (2a/L ≈ 0.7). Further increasing of the applied load or contact density leads to moderate overestimation of contact characteristics in comparison with the exact solutions. For all considered cases the increase in asperities density leads to an increase in the peak pressure, and also to the reduction of the contact half-width at a fixed load. Qualitatively, the form of contact pressure distribution is generally defined by the shape of asperities.

The advantage of the developed approach is the ability to separately consider the effects associated with the shape of asperities and the relative distance between them. The method allows to simplify the calculation of contact characteristics for a complex-shaped regular texture, for which a straightforward analytical solution does not exist, including more general multizone contact problems. The approach developed can be also used for the solution of the 2D and 3D periodic contact problems with complicated boundary conditions (e.g., with adhesion of different nature at the interface Makhovskaya, 2003).

Data Availability Statement

All datasets generated for this study are included in the article and the supplementary material.

Author Contributions

IG, localization principle formulation with applications to 3D contact problems. IT, development of the localization method to 2D contact problems.

Funding

This research was funded by the Russian Foundation for Basic Research, grant 20-01-00400. The solution and analysis of contact characteristics for wavy surface falls under the framework of the grant from the Russian Foundation for Basic Research 19-08-00615.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Barber, J. R. (2018). Contact Mechanics. Cham: Springer International Publishing.

Google Scholar

Block, J. M., and Keer, L. M. (2008). Periodic contact problems in plane elasticity. J. Mech. Mater. Struct. 3, 1207–1237. doi: 10.2140/jomms.2008.3.1207

CrossRef Full Text | Google Scholar

Carbone, G., and Mangialardi, L. (2004). Adhesion and friction of an elastic half-space in contact with a slightly wavy rigid surface. J. Mech. Phys. Solids. 52, 1267–1287. doi: 10.1016/j.jmps.2003.12.001

CrossRef Full Text | Google Scholar

Chekina, O. G., and Keer, L. M. (1999). A new approach to calculation of contact characteristics, J. Tribol. 121, 20–27. doi: 10.1115/1.2833804

CrossRef Full Text | Google Scholar

Ciavarella, M., Demelio, G., and Murolo, G. (2005). A numerical algorithm for the solution of two-dimensional rough contact problems. J. Strain Anal. Eng. 40, 463–476. doi: 10.1243/030932405X15936

CrossRef Full Text | Google Scholar

Dundurs, J., Tsai, K. C., and Keer, L. M. (1973). Contact between elastic bodies with wavy surfaces. J. Elast. 3, 109–115. doi: 10.1007/BF00045817

CrossRef Full Text | Google Scholar

Ghanati, P., and Adibnazari, S. (2019). A study on the extent of the contact and stick zones in multiple contacts. Arch. Appl. Mech. 89, 1825–1836. doi: 10.1007/s00419-019-01545-w

CrossRef Full Text | Google Scholar

Gladwell, G. M. L. (1980). Contact Problems in the Classical Theory of Elasticity. Sijthoff, Noordhoff.

Google Scholar

Goryacheva, I. (1997). Contact Mechanics in Tribology. Dordrecht: Springer.

Google Scholar

Goryacheva, I. G. (1998). Periodic contact problem for the elastic half-space. J. Appl. Math. Mech. 62, 1036–1044. doi: 10.1016/S0021-8928(98)00122-1

CrossRef Full Text | Google Scholar

Goryacheva, I. G. (2006). Mechanics of discrete contact. Trib. Int. 39, 381–386. doi: 10.1016/j.triboint.2005.04.020

CrossRef Full Text | Google Scholar

Goryacheva, I. G., and Martynyak, R. M. (2014). Contact problems for textured surfaces involving frictional effects. P. I. Mech. Eng. J. J. Eng. 228, 707–716. doi: 10.1177/1350650114528318

CrossRef Full Text | Google Scholar

Goryacheva, I. G., and Torskaya, E. V. (1995). Periodic contact problem for a system of punches and the elastic layer bonded to the elastic half-space. J. Frict. Wear. 17, 642–652.

Goryacheva, I. G., and Torskaya, E. V. (2019). Contact of multi-level periodic system of indenters with coated elastic half-space. FU Mech. Eng. 17, 149–159. doi: 10.22190/FUME190511022G

CrossRef Full Text | Google Scholar

Johnson, K. L. (1985). Contact Mechanics. Cambridge: University Press.

Google Scholar

Krishtafovich, A. A., Martynyak, R. M., and Shvets, R. N. (1994). Contact between anisotropic half-plane and rigid body with regular microrelief. J. Frict. Wear. 15, 15–21.

Kuznetsov, E. A. (1976). Periodic contact problem for half-plane allowing for forces of friction. Sov. Appl. Mech. 12, 1014–1019. doi: 10.1007/BF00885047

CrossRef Full Text | Google Scholar

Kuznetsov, Ye. A. (1978). The use of automorphic functions in the plane theory of elasticity. Mech. Solids. 6, 35–44.

Makhovskaya, Y. Y. (2003). Discrete contact of elastic bodies in the presence of adhesion. Mech. Solids. 38, 39–51.

Google Scholar

Manners, W. (1998). Partial contact between elastic surfaces with periodic profiles. Proc. R. Soc. Lond. 454, 3203–3221. doi: 10.1098/rspa.1998.0298

CrossRef Full Text | Google Scholar

Manners, W. (2003). Methods for analysing partial contact between surfaces. Int. J. Mech. Sci. 45, 1181–1199. doi: 10.1016/S0020-7403(03)00143-7

CrossRef Full Text | Google Scholar

Müser, M. H., Dapp, W. B., and Bugnicourt, R. (2017). Meeting the contact-mechanics challenge. Tribol. Lett. 65:118. doi: 10.1007/s11249-017-0900-2

CrossRef Full Text | Google Scholar

Muskhelishvili, N. I. (1953). Some Basic Problems of the Mathematical Theory of Elasticity. Holland: Noordhoff.

Google Scholar

Myshkin, N. K., and Goryacheva, I. G. (2016). Tribology: trends in the half-century development. J. Frict. Wear. 37, 513–516. doi: 10.3103/S106836661606009X

CrossRef Full Text | Google Scholar

Paggi, M., and Reinoso, J. (2018). A variational approach with embedded roughness for adhesive contact problems. Mech. Adv. Mater. Struct. 1–17. doi: 10.1080/15376494.2018.1525454

CrossRef Full Text | Google Scholar

Schmueser, D., and Comninou, M. (1979). The periodic array of interface cracks and their interaction. Int. J. Solids Struct. 15, 927–934. doi: 10.1016/0020-7683(79)90022-2

CrossRef Full Text | Google Scholar

Schtaierman, I. Y. (1949). Contact Problem of Theory of Elasticity. Moscow: Gostekhizdat.

Google Scholar

Shen, L., Quanzhou, Y., Qunyang, L., Xi-Qiao, F., and Huajian, G. (2018). Contact stiffness of regularly patterned multi-asperity interfaces. J. Mech. Phys. Solids 111, 277–289. doi: 10.1016/j.jmps.2017.10.019

CrossRef Full Text | Google Scholar

Soldatenkov, I. A. (2013). The periodic contact problem of the plane theory of elasticity. Taking friction, wear and adhesion into account. J. Appl. Math. Mech. 77, 245–255. doi: 10.1016/j.jappmathmech.2013.07.017

CrossRef Full Text | Google Scholar

Srivastava, K. N., and Lowengrub, M. (1970). Finite Hilbert transform technique for triple integral equations with trigonometric kernels. Proc. Roy. Soc. Edn. LXVIII, 309–321. doi: 10.1017/S0080454100008463

CrossRef Full Text | Google Scholar

Stanley, H. M., and Kato, T. (1997). An FFT-based method for rough surface contact. J. Tribol. 119, 481–485. doi: 10.1115/1.2833523

CrossRef Full Text | Google Scholar

Tsukanov, I. Y. (2018a). Partial contact of a rigid multisinusoidal wavy surface with an elastic half-plane. Adv. Tribol. 1–8. doi: 10.1155/2018/8431467

CrossRef Full Text | Google Scholar

Tsukanov, I. Y. (2018b). Periodical contact problem for a surface with two-level waviness. Mech. Solids. 53, 129–136. doi: 10.3103/S0025654418030160

CrossRef Full Text | Google Scholar

Westergaard, H. M. (1939). Bearing pressures and cracks. J. Appl. Mech. T. ASME. 6, 49–52.

Google Scholar

Whitehouse, D. J. (1994). Handbook of Surface Metrology. Bristol: Inst. of Physics.

Google Scholar

Xu, Y., and Jackson, R. L. (2018). Periodic contact problems in plane elasticity – the fracture mechanics approach. J. Tribol. 140, 404–415. doi: 10.1115/1.4036920

CrossRef Full Text | Google Scholar

Yastrebov, V. A., Anciaux, G., and Molinari, J. F. (2015). From infinitesimal to full contact between rough surfaces: evolution of the contact area. Int. J. Solids Struct. 52, 83–102. doi: 10.1016/j.ijsolstr.2014.09.019

CrossRef Full Text | Google Scholar