- 1Meta Acoustic Lab, George W. Woodruff School of Mechanical Engineering, Georgia Institute of Technology, Atlanta, GA, United States
- 2Parker H. Petit Institute for Bioengineering and Bioscience, Georgia Institute of Technology, Atlanta, GA, United States
High resolution diagnostic ultrasound imaging requires the use of high frequency acoustic transmission deep into the body. However, the presence of high impedance, lossy barriers such as the skull scatters and damps the energy delivered to the targeted region, limiting the usefulness of ultrasound for brain imaging and brain therapies. Non-Hermitian complementary metamaterials (NHCMM) are precisely designed to enable total and bidirectional acoustic transmission through lossy barriers, poising these metamaterials as a useful tool for non-invasive diagnostic brain imaging and brain therapies. Here, we apply NHCMMs to skull surfaces with unique geometries and irregularities to evaluate the performance of NHCMMs under near realistic imaging circumstances. We employ a multi-step imaging process by collecting the initial reflected pressure field caused by an irregular skull region and an initial metamaterial layer that is not perfectly matched, tailor the metamaterial parameters to complement the skull region, and collect a second pressure field with the tumor present. The tumor location is ascertained by calculating the contrast to noise ratio of the higher amplitude backscattered pressure field compared to the rest of the pressure field. Even with the skull irregularities, the imaging information of an acoustic scatterer, in this paper represented as a brain tumor, is preserved through the bilayer and reconstructible despite the scattering effect caused by the skull imperfections. Evaluating the performance of NHCMMs with various defects is critical to understanding its effectiveness for non-invasive neurological procedures and diagnostic imaging; the success of tumor detection through the NHCMM/skull bilayer illustrated in this paper will ideally lead to implementation in ultrasound diagnostics for neurological disorders.
Introduction
Ultrasound is considered one of the most biocompatible imaging modalities as it requires no ionizing radiation, penetrates deep into biological tissues, and offers superior resolution compared to other imaging techniques (Bushberg et al., 2012, Ch. 1). As a result, ultrasound is a proficient tool for a variety of non-invasive medical applications, with researchers actively investigating its potential uses. For example, high intensity focused ultrasound (HIFU) concentrates acoustic energy to a focal point within the body to ablate tumors (Kennedy et al., 2003, 2004; Wu et al., 2003, 2004; Kennedy, 2005; Ninet et al., 2005), pulverize kidney stones (Sapozhnikov et al., 2007; Neisius et al., 2014), and open the blood brain barrier for direct drug delivery to the brain (Kinoshita et al., 2006). Further ultrasound based, non-invasive therapies clear aortic plaque (Nishida et al., 2004; Takakuwa et al., 2018), accelerate bone fracture healing (Heckman et al., 1994; Hadjiargyrou et al., 1998; Busse et al., 2002), and assist in gene therapies (Kim et al., 1996; Bednarski et al., 1997). In addition to direct therapeutic applications, high frequency ultrasound is commonly used to image organs and tissue for diagnostic purposes (Hynynen et al., 1996; Tran et al., 2003; Tanter and Fink, 2014; Errico et al., 2015; Wang et al., 2016). With the help of microbubble and nanodroplet contrast agents, ultrasound serves as a high resolution, deep tissue imaging modality used to track blood flow and detect locations of arterial plaque build-up throughout the body (Yan et al., 2018). Ultrasonic therapies have even been proposed to treat neurological disorders, and some researchers have implemented these therapies. Monti et al. targeted short, low-intensity energy pulses of ultrasound at the thalamus of a patient suffering from a disorder of consciousness due to a severe traumatic brain injury, after which the patient almost immediately exhibited vast improvement and continued to dramatically improve over a several-day time span (Monti et al., 2016).
Although high frequency ultrasound increases the precision and spatial resolution of the aforementioned biomedical applications, major challenges exist to adapt these techniques for brain imaging and brain therapies. The primary problem is the presence of the skull acting as a highly mismatched impedance barrier with strong attenuative effects. This lossy acoustic barrier drastically limits the transmission of ultrasound energy into the brain, inhibits the effectiveness of HIFU and prevents diagnostic imaging capabilities (Fry and Barger, 1978; Pichardo et al., 2010).
To mitigate the scattering and loss caused by the skull, acoustic metamaterials use transformation acoustics to enable bidirectional acoustic transmission into the brain, paving the way to non-invasive diagnostic brain imaging and non-invasive brain therapies. Complementary metamaterials (CMM) are designed with the negative real acoustic properties of the aforementioned acoustic barrier to effectively counteract any impedance mismatch effects to transmit through lossless impedance barriers (Shen et al., 2014). However, CMMs are ineffective for acoustic transmission through the skull, as the porosity of cranial bone creates a lossy interior structure; as a result, the purely real-valued sound speed and density will not fully characterize the acoustic impedance, resulting in an impedance mismatch when using a CMM on a lossy barrier. In addition, the CMM doesn't contain effective acoustic gain that compensates the intrinsic loss of the skull. To overcome the loss of the skull and achieve total acoustic transmission, non-Hermitian complementary metamaterials (NHCMM) are designed with an active energy input to directly counteract the loss of the skull (Craig et al., 2019). Since the NHCMM considers both the real and imaginary material parameters of the lossy barrier, the bilayer acts as an invisible media to ultrasound, allowing bidirectional acoustic transmission.
Previous investigations on NHCMMs illustrate the effectiveness of the material for biomedical applications, with full-wave simulations exhibiting perfect bidirectional transmission and the ability to preserve imaging information through the bilayer (Craig et al., 2019). However, these simplified models do not accurately consider the internal geometry of a human skull.
Here, we study the effectiveness of NHCMMs for ultrasonic imaging by considering several bone irregularities typical to the skull, including changes in curvature, thickness, and the presence of cavities in the skull; the NHCMM must be adaptable to ensure lossless transmission through any skull geometry for practical use of NHCMMs in the future. We construct a multilayer system consisting of the NHCMM, skull, brain tissue, and a tumor structure, with physiologically accurate geometries and material parameters. After studying the initial pressure field and finely tuning the NHCMM parameters to optimize it for the complex geometry of the skull, we can detect the acoustic shadows caused by the tumor in the reflected pressure fields, demonstrating significantly improved acoustic transmission capable of detecting the tumor presence.
Methods
General Model Conditions
We use COMSOL Multiphysics to simulate acoustic wave propagation through the NHCMM-skull bilayer with determined material properties. The effect of shear waves can be modeled with Biot theory (Craig et al., 2019) and is neglected in this study. In each case, two material layers representing the skull and metamaterial are modeled with acoustic plane wave incidence from the exterior of the metamaterial surface. The metamaterial is directly adjacent to the external surface of the skull and the brain tissue is along the interior surface of the skull. The exterior environment is modeled as water with density ρ = 1,000 kg/m3 and sound speed c = 1,500m/s, and due to the similarities between brain tissue and water, the healthy brain tissue is modeled with the same density and sound speed as water. Each material layer is 10 mm thick unless specified otherwise and modeled with density, ρ = 1,900 + 50i kg/m3 and sound speed, c = 2,835 + 80i m/s (Fry and Barger, 1978). The material properties of the NHCMM are set to match the skull. A diagram of this set-up and the corresponding pressure fields, as well as a control case with no NHCMM present, is illustrated in Figure 1. To avoid singularities in the calculations, the density of the metamaterial is set as ρ = −0.9999*(1,900 + 50i) kg/m3 and the sound speed is c = −0.9999*(2,835 + 80i) m/s. Since this study focuses on the imaging capabilities of NHCMMs, we simulate a brain tumor with a 10 mm radius with sound speed c = 2,000 m/s and density ρ = 1,500 kg/m3. A 1.5 MHz imaging frequency was selected to conform with typical biomedical ultrasound frequencies, which range from 1 to 15 MHz. Additionally, control simulations of only the tumor in an aqueous environment and tumor surrounded by an idealized NHCMM-skull bilayer are included for comparison.
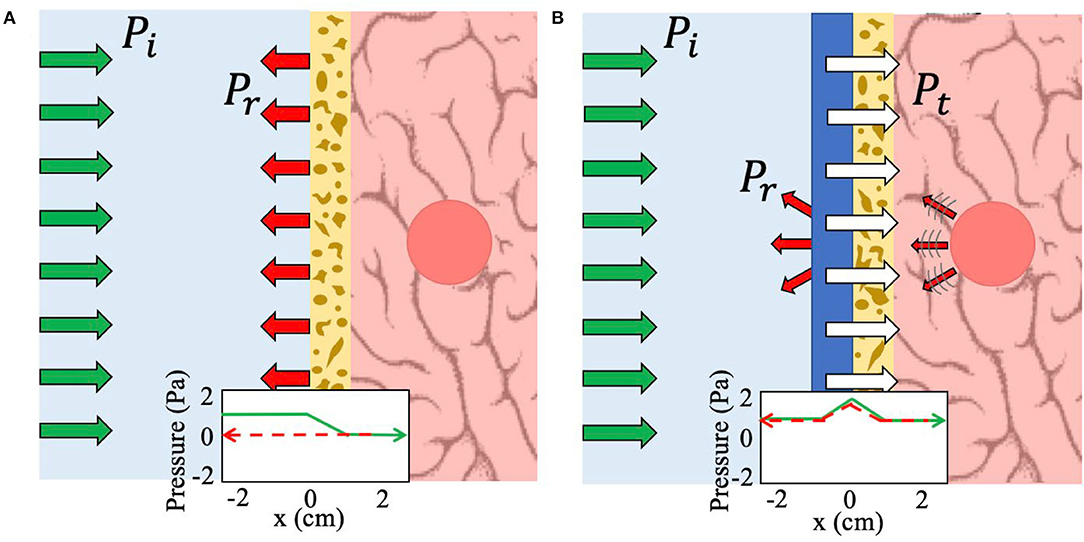
Figure 1. Schematic of the working principle of NHCMM. Green arrows indicate incident pressure (Pi), red arrows reflected pressure (Pr), and white arrows transmitted pressure (Pt). (A) Imaging without any metamaterial compensation results in complete reflection and scattering due to the lossy skull. A graphical representation of the bidirectional acoustic pressure field demonstrates this loss as the pressure amplitude falls to zero as the acoustic wave passes through the skull at x = 0 (green arrow) and thus no reflected pressure can be detected (red dashed arrow). (B) Imaging with the NHCMM results in complete bidirectional transmission of the acoustic wave, including ultrasound imaging information of the tumor presence and location. The corresponding graph of the acoustic pressure field shows clear acoustic gain to counteract the subsequent loss caused by the skull as the signal passes into the brain (green arrow). The reflected pressure amplitude is also preserved through the NHCMM/skull bilayer (red dashed arrow).
We evaluate the backscattered pressure field for each case to determine the efficacy of the NHCMM with near realistic skull conditions. Specifically, we measure the two-dimensional backscattered pressure field that is 60 mm wide for the sloped and blood vessel cases or 50 mm wide for the curved skull cases, and extends up 20 mm. For the curved cases, this measurement area is directly above the NHCMM boundary, and for the sloped and blood vessel cases the measurement area is 10 mm above the NHCMM. This region is illustrated in the model set-up diagrams as a rectangular region marked by a black dashed line. Additionally, we compute the pressure amplitude at the midpoint of the backscattered pressure field, indicated by a red dashed line through the center of the backscattered pressure field region. To quantify the backscattered signal coming from the tumor region, the contrast to noise ratio (CNR) is calculated by taking the average pressure amplitude of the pressure profile between x = ±15 mm (directly above the tumor) and comparing it to the standard deviation of the noise floor taken between x = ±25 mm and x = ±20 mm. The formula for this calculation is
, where Si and So are the signal amplitudes inside and outside the region of interest, respectively, and δi and δo are the standard deviations of the noise inside and outside the region of interest, respectively. The exact coordinates of where the signal and background measurements are taken vary slightly from case to case, but the CNR measurements for one experimental design with tuned NHCMM and its corresponding control case with a flat non-adjusted NHCMM are calculated using the same coordinates. The CNR for ultrasound tends to be lower than optical imaging modalities due to the inherent noisiness of the background, or speckle, so a CNR of 1.3 or greater was considered sufficient for distinguishing the tumor presence, which is greater than or on par with ultrasound and MRI papers using CNR as a quantifying metric for the quality of their images (Geissler et al., 2007; Dahl et al., 2011; Deng et al., 2017).
Skull Sloping Models
We construct skull geometries with an internally varying thickness to understand its effect on the imaging capabilities of NHCMM. Several sloped cases are modeled, ranging from a 0.5 mm rise over a 60 mm distance (0.8% slope) to a 2 mm rise (3.3% slope), and an additional case is modeled of the skull thickness changing to be 2 mm thicker in the center of the field as compared to the edges of the imaging window (±6.67% slope). In all circumstances, the minimum skull thickness is 10 mm. The first metamaterial for each case has a constant 10 mm thickness, matching the thickness of a uniform skull. The second metamaterial condition of each case mirrors the varying thickness of the skull; this can be accomplished by controlling the active circuit components of the NHCMM to compensate for the varying thickness, rather than altering the physical thickness of the metamaterial each time. In all the simulations, the material parameters are kept consistent to that of the general model.
Skull Curvature Models
We test the effect of skull curvature on ultrasonic imaging by simulating the NHCMM-skull bilayer with two distinct geometric configurations and two curvatures. We designed the skull curvature using two different configurations to ensure that the method of creating curvature in the computer model did not significantly impact the simulation nor the NHCMM performance. The first geometric configuration considers the metamaterial and skull as a concentric bilayer of circular shells with thickness along the radial direction being 10 mm, and the skull layer having an external radius of 100 and 50 mm for the smaller and larger degrees of curvatures, respectively. The second geometric configuration models the skull and metamaterial as the overlapping regions of shifted circular shells with equal radii. We construct this configuration by modeling three circular arcs with center points spaced 10 mm from one another, resulting in two shell regions that represent the metamaterial and skull. Once again, this setup is studied with the two different curvatures with the radii of the skull being either 100 or 50 mm. Consequently, the metamaterial and skull have a slightly different thickness along the radial direction for this geometric configuration. With these geometric configurations, we evaluate the imaging capability of NHCMM compensating a skull with curvature. Each of these simulations have the same material parameters as the general model. The reflected pressure fields with and without a tumor present in the brain tissue are observed.
Skull With Blood Vessel Models
Blood vessels in the brain may form local skull abnormalities and cause the appearance of unwanted artifacts in ultrasound images (Al-Refai, 2016). Using microbubbles as an ultrasound contrast agent, the location and geometry of major blood vessels along the interior of the skull can be determined (Errico et al., 2015, 2016). In this case, the scattered pressure field from a blood vessel-induced indent in the skull through the NHCMM can be approximated. Simulations were modeled with hemispherical portions removed from the skull to mimic this defect. The half-ellipse portions were created using Bezier lines in COMSOL. The smaller blood vessel ellipse had a minor axis radius of 0.8 mm and a major axis radius of 4 mm, while the larger blood vessel had minor and major axis radii of 1.6 and 8 mm, respectively. Since the actual blood vessel has similar material properties to the tissue and water, it was modeled with the same material parameters of water. Each simulation applies the same material parameters as the general model and observes the reflected pressure field with and without tumor presence.
Tumor Detection
For the sloped skull cases, the tumor detection is calculated by collecting measurements of the scattered pressure field with the uniform 10 mm thick NHCMM and comparing the CNR of that measurement to the CNR of the scattered pressure field when the NHCMM is adjusted to match the sloping condition. For the curved, blood vessel, and combination cases, the detection of tumors through the NHCMM/skull bilayer is done by comparing the backscattered pressure field of each geometric configuration with and without the tumor present, analyzed using Matlab 2019a. An example of this process is exhibited in Figure 2, which observes the total pressure field scattered by a tumor with 10 mm radius surrounded by a curved skull with a 100 mm outer radius formed by concentric circles (Figure 2A). The total pressure field from the curved skull layer with no tumor is also calculated as a control case illustrated in Figure 2B. Adding a tumor in the same geometry results in a different backscattering pressure field, but is not easily distinguishable (see Figure 2C). We subtract these pressure fields to determine the backscattering from only the tumor (see Figure 2D) and filter the result with a 2D Fourier transform with the known frequency and propagation direction of the wave. An inverse Fourier transform on the filtered k-space yields the backscattered pressure field in Figure 2E that corresponds to the absolute value of the reflected pressure field from the tumor. Afterwards, the CNR is taken for the filtered reflected pressure field from the tumor (Figure 2E) as well as the unfiltered case (Figure 2C) which serves as a control CNR value.
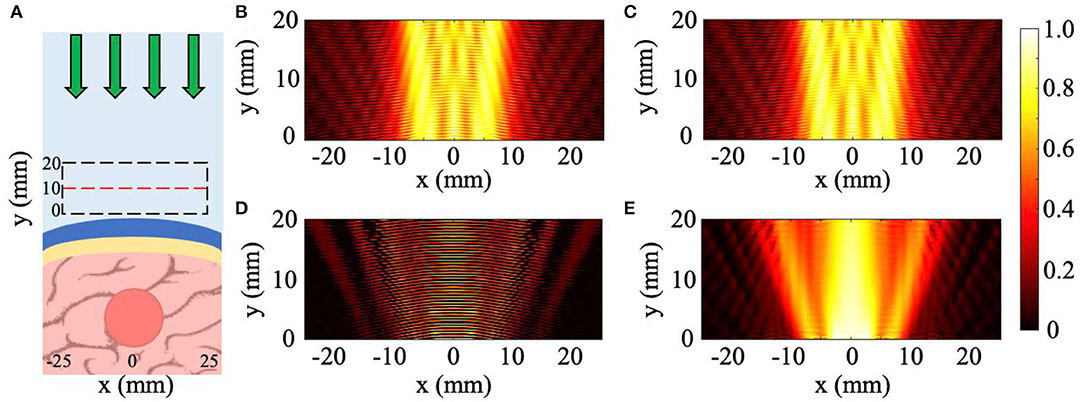
Figure 2. Method to retrieve tumor scattering from the total pressure field. (A) Diagram of tumor-skull-NHCMM with incident pressure (green arrows). (B) Incident and reflected acoustic pressure field of an imaging plane wave incident on a concentric NHCMM-skull bilayer with a skull radius of 100 mm. (C) Incident and reflected acoustic pressure field of the same geometry in (B) but with a brain tumor. (D) The subtraction of the measured pressure fields in (B,C). (E) Filtering the results in (D) using a 2D Fourier transform to isolate the backscattering from just the tumor. The colorbar represents the normalized pressure amplitude.
Results
Skull Sloping
The general setup for imaging through a skull with varying thickness is illustrated in Figure 3A with a plane wave incident on the NHCMM-skull bilayer with an increase in thickness of 1 and 2 mm (1.67 and 3.33% slope), and results shown in Figures 3B–E. The backscattered pressure field is observed in a rectangular region denoted by the dashed black rectangle in Figure 3A to evaluate the performance of the metamaterial. In this case, the area is shifted 10 mm away from the metamaterial with a 60 mm width and 20 mm height. The pressure amplitude on the red dashed line in the middle of the area is also plotted. The backscattered pressure fields through the sloped skulls compensated by a metamaterial with constant thickness (10 mm) are plotted in Figures 3B,C for the 1.67 and 3.33% sloping geometries, respectively. In Figure 3B, the backscattered pressure field of the tumor is not distinguishable from the noise, indicated by the pressure field. Interestingly, the skull with greater internal slope of 3.33% (2 mm rise) has a region of minimal reflection (see Figure 3C). This is due to the accidental satisfaction of Fabry-Perot condition at this bilayer thickness (Lu et al., 2007), resulting in a reduced pressure reflection and masking the backscattering of the tumor. Since the flat metamaterial is ineffective for imaging through the sloped skull, we alter its design to directly mirror the skull geometry. In order to non-invasively determine the internal geometry of the skull, we sweep the effective thickness of the metamaterial to satisfy the Fabry-Perot condition with its effects on the reflected pressure field illustrated in Figure 3C. Since the NHCMM is designed with active circuit elements, we can change the resistance and capacitance values that control the active response of each unit cell in the metamaterial to alter its local effective thickness (Craig et al., 2019). Given that the skull has sloped internal geometry, sweeping the metamaterial thickness results in a reduced pressure reflection wherever the Fabry-Perot condition is satisfied. It is important to note that when the thickness of the metamaterial exceeds the thickness of the skull, the reduced reflection that indicates the satisfaction of the Fabry-Perot condition is no longer observed. Therefore, we begin sweeping the effective metamaterial thickness at values near zero and denote the locations of reduced pressure reflections to determine the slope of the interior of the skull. Once the thickness variation is determined, the NHCMM is designed to mirror this skull geometry. With this metamaterial compensating the exterior of the skull, the resulted backscattered pressure fields imaging the tumor are illustrated in Figures 3D,E for the smaller and larger slopes, respectively. These pressure fields indicate the presence of the tumor with acoustic shadows located at x = ±15 mm. CNR values of 1.78 for the 1.67% slope (1 mm rise) case and 1.87 for the 3.33% slope (2 mm rise) case confirm significant contrast between the backscattered tumor signal and the surrounding brain tissue. In comparison, the CNR of the 1.67 and 3.33% slope cases with a uniform metamaterial are 0.20 and −1.64, respectively. The 3.33% slope control CNR is negative due to the Fabry-Perot resonance, causing a sharp decrease in the pressure amplitude. From these plots, it is clear that a uniform metamaterial cannot possibly resolve fluctuations in backscattered pressure caused by tumorous tissue, but adjusting the metamaterial parameters such that the metamaterial matches the sloping profile enables tumor region detection with good precision.
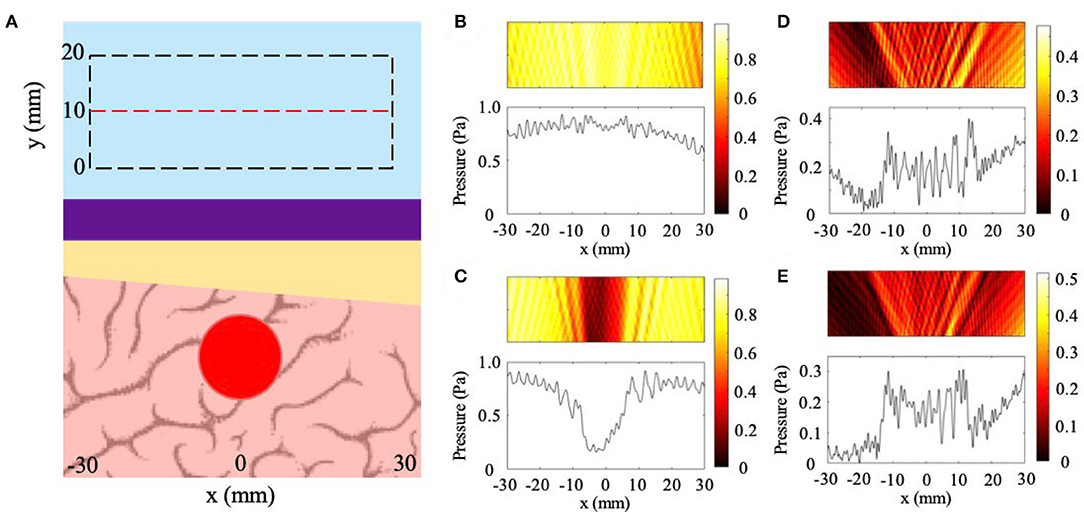
Figure 3. Effects of skull sloping on ultrasound imaging with NHCMM. (A) Illustration of the skull sloping model used in full wave simulations. Plane wave incidence from the top of the subfigure. Reflected pressure fields are taken in the black dashed rectangles with the pressure amplitude recorded on the red dashed line. (B) Scattered pressure field from imaging through a skull with an internal slope of 1.67% compensated by a flat metamaterial. (C) Scattered pressure field from imaging through a skull with a larger internal slope of 3.33% compensated by a flat metamaterial. (D) Scattered pressure field from imaging through a skull with a 1.67% slope compensated by a metamaterial with the mirrored skull geometry. (E) Scattered pressure field from imaging through a skull with a 3.33% slope compensated by a metamaterial with the mirrored skull geometry. The colorbars represent pressure amplitudes in Pa.
In addition to cases with a 1 and 2 mm rise, we considered 10 mm thick skull with sloped regions increasing by 0.5 mm (.83% slope), 0.75 mm (1.25% slope), and 1.5 mm (2.5% slope). These cases are presented in Figure 4 with both the uniform metamaterial compensation and the perfectly matched metamaterial conditions plotted. The uniform metamaterial is the same one designed in Craig et al. (2019), which models the impact of a 10 mm thick NHCMM on the lossless transmission of ultrasound through a flat, equally thick skull region. As can be seen from the pressure amplitude profile of the backscattered pressure in the control cases (Figures 4A–C), it is impossible to detect the presence of abnormal brain tissue if an improperly matched NHCMM is used. Once the metamaterial is tuned to match the slope gradient (Figures 4D–F), an elevated pressure signal is seen in the center of the amplitude profile. The CNR values for the tuned 0.5 mm rise, 0.75 mm rise, and 1.5 mm rise NHCMM cases are 2.40, 1.49, and 2.52, respectively, and the CNR for the uniform metamaterial cases are 0.85, 0.83, and 0.09, respectively. Even if the skull increases in thickness by only 0.5 mm over a 60 mm imaging region corresponding to a slope of 0.83%, the uniform metamaterial is completely ineffective at non-healthy tissue detection. This further demonstrates the importance of an appropriately designed NHCMM for biological conditions, and that ultrasound can diagnose tumor presence once the NHCMM matches the skull geometry.
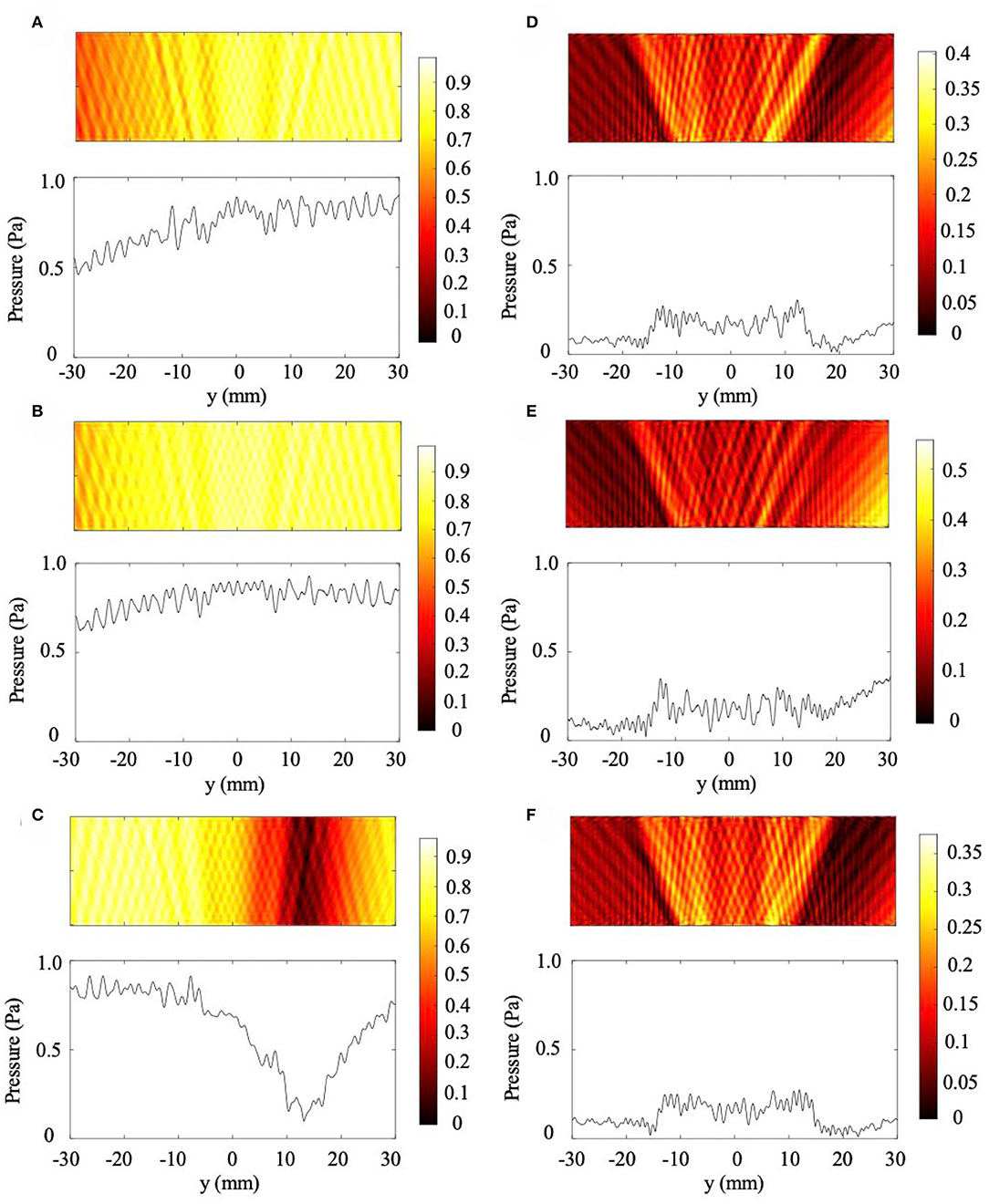
Figure 4. Additional skull sloping cases. (A–C) are scattered pressure fields from skull thicknesses increasing by 0.5, 0.75, and 1.5 mm, respectively, with a 10 mm uniform NHCMM. (D–F) are corresponding 0.83% (0.5 mm rise), 1.25% (0.75 mm rise), and 2.5% (1.5 mm rise) sloped cases with tuned NHCMM layers to match the skull thickness. The colorbars represent pressure amplitudes in Pa.
Lastly, to determine if a tunable NHCMM can work with more complex skull geometries, the NHCMM is tested against a skull region that increases in thickness by 2 mm in the center of the imaged region (6.67% slope) and decreases back to a 10 mm thickness at the edge of the imaging region (−6.67% slope). The multi-slope model set-up and the filtered scattered pressure field with properly designed NHCMM are presented in Figure 5. The tumor is directly underneath the skull when it peaks in thickness (Figure 5A). When the flat, uniform NHCMM is applied to this skull, multiple regions of Fabry-Perot resonance appear and no tumorous tissue can be detected (Figure 5B). Once the NHCMM is tuned to match the skull sloping pattern, the tumorous tissue reveals itself through the increased backscattered pressure amplitude compared to the healthy brain tissue, which has a weak reflected amplitude close to zero (Figure 5C). The CNR of the tumor region compared to the background is 1.36, indicating a strong and detectable difference in pressure reflection. If a uniform, 10 mm thick NHCMM metamaterial is used instead, the CNR is −0.51, meaning the tumor tissue is completely undetectable. The variety of cases considered in this section demonstrate that the NHCMM can significantly improve glioblastoma and other brain tumor detection, so long as the NHCMM is tuned to match the skull sloping condition.
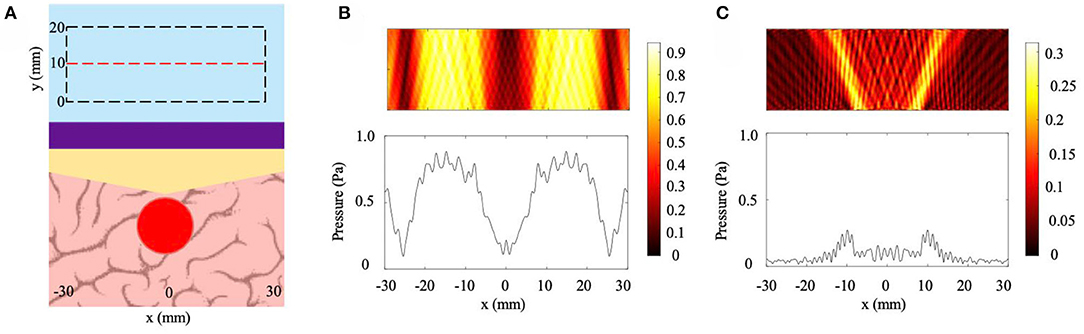
Figure 5. Multi-slope condition. (A) Diagram of the skull/NHCMM condition with the skull slope changing by ±6.67%, peaking in thickness at the center of the imaging region, coupled with a uniform 10 mm thick NHCMM. (B) Scattered pressure field from the multi-slope skull coupled with a 10 mm thick NHCMM. (C) Scattered pressure field from the multi-slope skull with a NHCMM layer that matches the changes in thickness of the skull. The colorbars represent pressure amplitudes in Pa.
Skull Curvature
The results from the skull curvature studies are presented in Figure 6. The general setup described in the Methods section is shown in Figure 6A with a plane wave incident on the NHCMM-skull bilayer having two different curvatures. The backscattered pressure field in the rectangular area enclosed by the dashed black lines is analyzed to characterize the imaging performance of the metamaterial in Figure 6A. The area is adjacent to the exterior of the metamaterial with a 50 mm width and 20 mm height. Within the area, the amplitude of the pressure field is measured along the red dashed line 10 mm away from the metamaterial to detect the presence of the tumor (see Figure 6A). We use two control cases as a basis for comparison. In the first case, a full wave simulation models plane wave incidence onto a tumor without NHCMM or skull. Without the bilayer, the observed rectangular area is shifted 20 mm closer to the tumor. The plot of the pressure amplitude indicates the presence of a tumor with acoustic shadows located at x = ±13 mm (see Figure 6B). For a second control case, we observe the scattered pressure field from a flat skull compensated by NHCMM. The backscattered pressure field is similar to the previous case with the acoustic shadows at x = ±15 mm to indicate the presence of the tumor in Figure 6C, demonstrating the effectiveness of the metamaterial. The CNR value for this condition is 1.99. For the concentric skull geometries, Figures 6D,E illustrate the reflected pressure fields with skull radii of 100 and 50 mm for the smaller and larger curvatures, respectively. Here, we note that the similarity between the two cases; both indicate the presence of a tumor with acoustic shadows at x = ±16 mm. The CNR values for the 100 and 50 mm radii are 3.14 and 2.74, respectively. For the bilayer constructed with shifted circular arcs, Figures 6F,G illustrate the reflected pressure fields with the skull outer radii equal to 100 and 50 mm for the smaller and larger curvatures, respectively. The backscattered pressure field obtained through the bilayer with the smaller curvature in Figure 6F shows similar results to the pressure fields in Figures 6D,E with an acoustic shadow at x = ±16 mm. However, the pressure field resulted from imaging through the larger curvature has an acoustic shadow at x = ±11 mm (see Figure 6G). The CNR values for the 100 and 50 mm shifted arc cases are 2.80 and 2.70, respectively. While both of the curvature cases modeled by the shifted arcs indicate the presence of a tumor, the difference in their acoustic shadows illustrate how the curvature affects the backscattered pressure field. On the other hand, the consistency of the pressure fields in Figures 6D,E demonstrates the effectiveness of the concentric bilayer geometry, illustrating that the skull curvature has a minimal effect on the resulted backscattered pressure field. Proper filtering of the backscattered pressure helps to strengthen the tumor signal and increase the CNR values, but even in the unfiltered case the CNR value is above the 1.3 threshold. Based on these models, properly designed NHCMMs that match the local skull curvature are shown to be effective for ultrasonic imaging with different degrees of curvature.
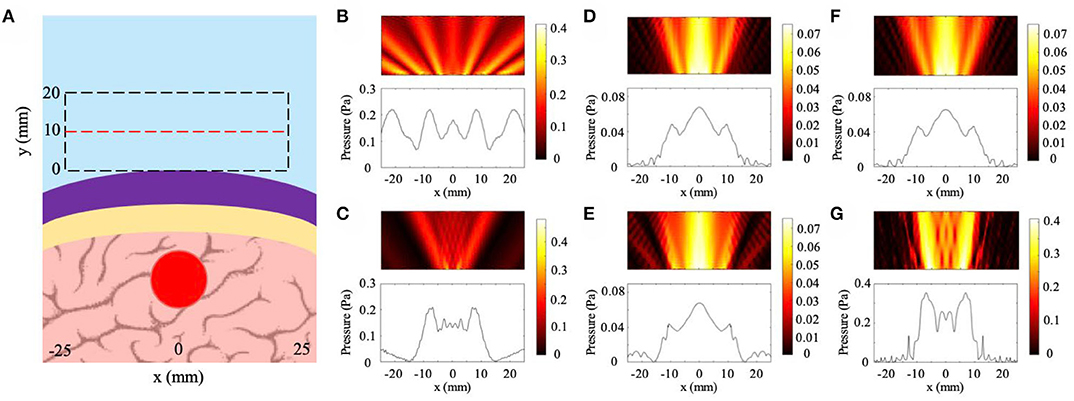
Figure 6. Effects of skull curvature on ultrasound imaging with NHCMM. (A) Illustration of the curved NHCMM-skull setup with a plane wave incident from the top of the subfigure. Reflected pressure fields are taken in the black dashed rectangles with the pressure amplitude recorded on the red dashed line. (B) Backscattered pressure field and pressure amplitude from a tumor without either NHCMM or skull layers. (C) Backscattered pressure field amplitude resulted from imaging through a flat NHCMM-skull bilayer. (D) Filtered pressure field amplitude resulted from imaging through a curved, concentric NHCMM-skull bilayer with an outer skull radius of 100 mm. (E) Filtered pressure field amplitude resulted from imaging through a curved, concentric NHCMM-skull bilayer with an outer skull radius of 50 mm. (F) Filtered pressure field amplitude resulted from imaging through a curved NHCMM-skull bilayer modeled by shifted circular arcs having radii of 100 mm. (G) Filtered pressure field amplitude resulted from imaging through a curved NHCMM-skull bilayer modeled by shifted circular arcs having radii of 50 mm. The colorbars represent pressure amplitudes in Pa.
Blood Vessel
The results for blood vessel irregularity cases are shown in Figure 7 with the general geometric configuration illustrated in Figure 7A. The location and dimensions of the pressure field observation window match that of the variable thickness study. In particular, we study the cases of blood vessel indentations with three different locations and two different sizes. The dimensions are discussed in detail in the Methods section. In Figures 7B,C, we observe the backscattered pressure fields of the NHCMM-skull bilayer with the smaller and larger blood vessel geometries, respectively. For these cases, the locations of the blood vessel indentations lie on the same axis as the tumor, resulting in the symmetric reflected fields. Here, we observe the presence of a tumor with the acoustic shadow illustrated in the plotted pressure amplitudes located at x = ±18 mm for both smaller and larger blood vessels. The CNR values for the small and large blood vessel geometries are 1.78 and 1.52, respectively. In comparison, the CNR of the scattered pressure field from the small and large blood vessel conditions without proper signal filtering is 0.37 and 0.44, respectively. The resultant pressure fields for the cases where the locations of the blood vessels shift 10 mm to the right are illustrated in Figures 7D,E. This shift was included in the simulation to observe the effect of blood vessel and tumor overlap on the imaging performance. The backscattered pressure fields indicate the presence of an acoustic scatterer with shadows at x = −17 mm and x = 20 mm for the small blood vessel and x = −18 mm and x = 14 mm for the larger blood vessel. The CNR values for filtered signals of the small and large blood vessel geometries shifted 10 mm to the right are 1.92 and 1.60, respectively, compared to the unfiltered signal CNR values of 0.29 and 0.47, respectively. Reconstructing the tumor geometry from this backscattered pressure field results in a shift in the tumor location. However, shifting the blood vessel another 10 mm to the right improves the symmetry of the backscattered field with acoustic shadows located at x = ±17 mm for the small blood vessel and x = −17 mm and x = 18 mm for the large blood vessel (see Figures 7F,G). This improvement is due to the blood vessel and tumor shift being far enough to avoid overlap. The CNR values of the filtered signals from the small and large blood vessel shifted 20 mm to the right are 1.71 and 1.78, respectively, above the CNR threshold. The control CNR values for the small and large blood vessel 20 mm shifted case are 0.29 and 0.27, respectively. The results from these models indicate the effectiveness of NHCMMs for imaging through the skull with blood vessels. In order to detect the tumor presence with acceptable signal contrast it is critical to properly filter the pressure signal, as indicated by the filtered signals consistently having above-threshold CNR values compared to the unfiltered signals having CNR values of 0.27–0.47. This filtering can be accomplished by tuning the NHCMM parameters to compensate for the skull indents caused by the blood vessel after using microbubble contrast agents to determine the location of the blood vessel.
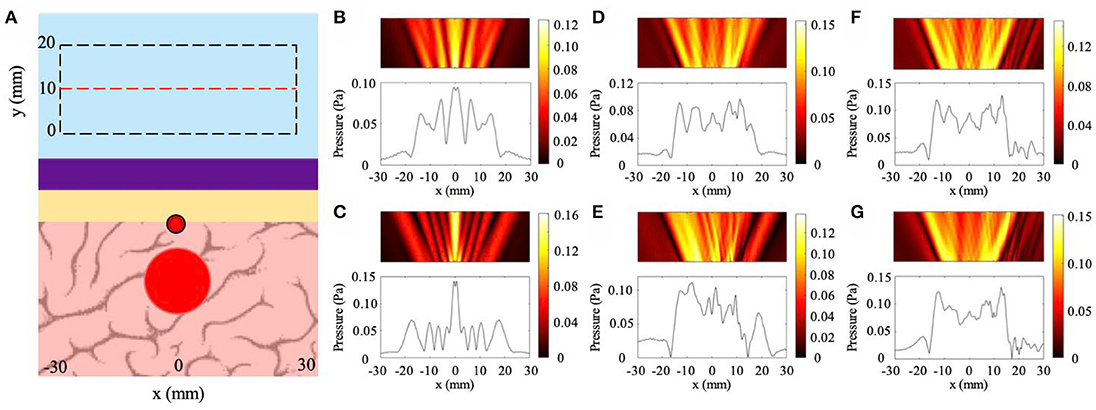
Figure 7. Effects of blood vessel induced indentation on ultrasound imaging with NHCMM. (A) Illustration of the NHCMM-skull bilayer with a blood vessel imprinting on the interior side of the skull. Reflected pressure fields are taken in the black dashed rectangles with the pressure amplitude recorded on the red dashed line. (B) Scattered pressure field from imaging through a skull having a small blood vessel vertically aligned with the tumor and compensated by NHCMM. (C) Scattered pressure field from imaging through a skull having a larger blood vessel vertically aligned with the tumor and compensated by NHCMM. (D) Scattered pressure field from imaging through a skull having a small blood shifted 10 mm to the right from its location in (B) compensated by NHCMM. (E) Scattered pressure field from imaging through a skull having a medium blood vessel shifted 10 mm to the right from its location in (C) compensated by NHCMM. (F) Scattered pressure field from imaging through a skull having a small blood vessel shifted 20 mm to the right from its location in (B) compensated by NHCMM. (G) Scattered pressure field from imaging through a skull having a medium blood vessel shifted 20 mm to the right from its location in (C) compensated by NHCMM. The colorbars represent pressure amplitudes in Pa.
Combination of Non-uniformities
To ensure that the NHCMM is tunable for any skull geometry, we created a model of a skull region with a combination of skull sloping, skull curvature, and skull aberrations caused by blood vessel presence. The skull curvature was modeled by creating layers of shifted concentric circles, each with a 100 mm radius, as described in section Skull Curvature Models. We tested this geometry both with a uniform circular tumor with a 10 mm radius as well as a pear-shaped, irregular tumor 24 mm in length. The results for this case are shown in Figure 8, with the model conditions for the non-uniform tumor reproduced in Figure 8A. The skull is curved slightly and increases in thickness at the right edge of the imaging window, with a large blood vessel and corresponding hemispherical skull indent directly above the tumor. As shown in Figure 8B, which has the scattered pressure field from this skull shape condition and circular tumor with a precisely tuned NHCMM to match the skull properties, an increase in the pressure amplitude appears in the center of the pressure field, an indicator of abnormal tissue which causes this backscatter. In Figure 8C, the pressure amplitude caused by the pear-shaped tumor also increases in the center of the pressure field and has a distinctly different profile from that in Figure 8B. The CNR of these pressure fields are 1.39 for the circular tumor and 1.96 for the irregular tumor, compared to CNR values of 0.96 and 1.39 for the circular and irregular tumor cases, respectively. Based on the CNR values for the irregular tumor, the unfiltered pressure field can still detect the tumor presence, but the filtered case provides greater contrast to help distinguish the tumor. This model provides further evidence that a properly matched NHCMM can resolve tissue abnormalities through a lossy barrier such as the skull.
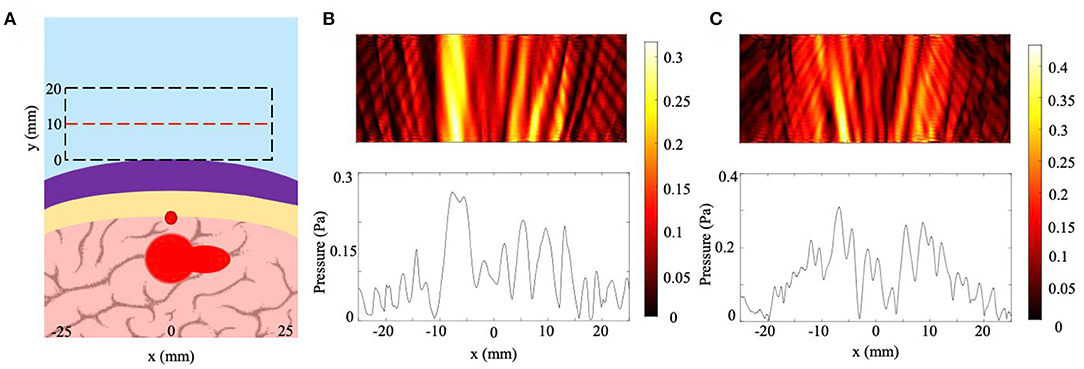
Figure 8. Effects of multiple skull inhomogeneities on ultrasound imaging with NHCMM. (A) Diagram of the skull, NHCMM, blood vessel, and tumor arrangement. The skull was modeled to be curved and increased in thickness toward the right end of the imaging window. The tumor in the diagram is the shape of the pear-shaped irregular tumor. A large blood vessel is located above the tumor which creates a hemispherical indent in the skull. (B) The scattered pressure field of the inhomogeneous skull with a uniform tumor and precisely tuned NHCMM. (C) The scattered pressure field of the inhomogeneous skull and irregular tumor with a precisely tuned NHCMM to match the skull geometry. The colorbars represent pressure amplitudes in Pa.
Discussions
The tunable NHCMM in this paper is capable of achieving lossless acoustic transmission through lossy barriers such as the skull, regardless of the skull shape or internal geometry. Previous research has investigated NHCMMs for brain imaging (Craig et al., 2019) but confined its research to a flat and homogenous skull layer, lacking consideration of the complexity of different skull regions. We prove that using a uniform NHCMM, such as the one in Craig et al. (2019), fails to locate a brain tumor through a non-uniform skull layer in Figures 3B,C, 4A–C, 5B; even slight variations in the skull thickness throughout the imaging window caused the uniform NHCMM to be completely ineffective at detecting the abnormal tissue region. By incorporating active circuit components in the NHCMM, taking an initial measurement of the acoustic reflection caused by the unique skull geometry, and tuning each circuit such that the effective metamaterial parameters precisely match that skull region's geometry, perfect acoustic transmission can be achieved through lossy barriers. More specifically, the NHCMM calibration procedure for each patient would begin by applying the NHCMM to a relatively flat skull region and adjusting the circuit components until the known reflection pulse signal from the skull disappear. When imaging through skull regions with more complex geometry, the pre-calibrated parameters will be used for fine tuning of the unit cells based on the skull non-uniformity as described in this work. Thus, this NHCMM imaging technique can be implemented in patients of all ages, head sizes, or tumor locations in the brain, as the acoustic properties of the skull are determined on a case-by-case basis and the tunable NHCMM can be altered to match those acoustic properties.
Ultrasound is already widely used for tumor detection in a variety of biological systems. In patients with early stage cervical cancer, ultrasound was capable of detecting both large (>4 cm) and small (<2 cm) tumors with high fidelity and performed better than MRI (Epstein et al., 2013). Furthermore, computer-aided ultrasound systems are capable of detecting tumors on the millimeter-scale (Moon et al., 2012). Additionally, ultrasound is implemented in several types of neurological therapies, such as thalamic stimulation for comatose patients, and has been implemented in resolving brain vasculature in combination with microbubble ultrasound contrast agents. However, the frequency used in thalamic stimulation is much lower than typical diagnostic ultrasound such that it cannot be used for imaging. By implementing a tunable NHCMM system, collecting a preliminary backscattered pressure field and altering the NHCMM parameters to compensate for variations in that pressure field caused by the skull geometry, tumors can be detected through the skull with high fidelity. Based on the findings in this paper as well as those in the literature cited above, we anticipate that this NHCMM/skull imaging system coupled with high frequency diagnostic ultrasound can easily image millimeter-scale tumors, suggesting that tunable NHCMMs could lead to significant advances in medical imaging technology for the early diagnosis and treatment of brain tumors.
It is important to note that the NHCMM designed in this paper only uses plane-wave ultrasound. The resolution limits of plane-wave ultrasound imaging is determined by the full-width half max of the ultrasound beamwidth, given by the formula FWHM = 1.206λz/L, where λ is the wavelength of the ultrasound in a given medium, calculated by dividing the incident frequency by the medium sound speed, z is the imaging depth, and L is the length of the transducer face (Szabo, 2014). Using a 1.5 MHz linear array transducer, the smallest resolvable object is approximately 600 μm, and this resolution limit improves as the frequency increases. When this NHCMM is physically realized, the resolution will be dependent on the unit cell size of the metamaterial as governed by manufacturing limitations. However, advances in microfabrication techniques can help ensure that the physically realized metamaterial unit cell size remains on the 100 μm to mm scale, not significantly hindering the fundamental resolution limit of this technology. As for the upper limit of the tumor detection, this is dependent on the imaging window length; in order to reveal a clear difference in pressure amplitude contrast from the tumor vs. the background signal, the tumor cannot fill the entire ultrasound imaging window. In the CNR analysis used in this paper, a 10 mm region on both ends of the imaging window was used to establish the background signal and noise values. Since most medical imaging transducers range from 50 to 150 mm in length, this means that an absolute maximal tumor size detectable by this ultrasound/NHCMM design is about 130 mm. In a study by Dempsey et al., the researchers noted an average malignant glioma tumor size to be 78 mm with minimum and maximum tumor sizes of 2.8 and 206.6 mm (Dempsey et al., 2005). It is important to note that the maximum size in that paper is inflated as it is a combination of measurements taken from multiple regions, so most tumor sizes will not reach that large. Based on this information, the NHCMM should be capable of detecting the vast majority of brain tumors, especially if used for early diagnosis.
This manuscript modeled the NHCMM working with a variety of skull inhomogeneities, including skull curvature, aberrations caused by blood vessels, and changing skull thickness. One environmental condition not explicitly considered in these simulations is the presence of the scalp at the surface. The scalp was not included in the simulations due to having acoustic properties similar to tissue; based on the findings in Chopra et al. (2015), the thickness of skin on the scalp and forehead ranges from 1.2 to 1.8 mm depending on the studied region, and the change in thickness between different areas ranges from 30 to 100 μm, much smaller (thickness < λ/10) than the wavelength from the ultrasound transducer. Because of the scalp uniformity, we predict that the scalp presence would cause a slight phase variation in the signal, and thus was deemed not critically important in the NHCMM/skull models. In addition, the irregularities considered in this study may be more extreme than the irregularities in a thinner region of the skull. The thickness and curvature of a real human skull differs depending on the cranial bone being imaged, so imaging through a thin layer of temporal bone will be easier than through thick parietal bone at the back of the skull. Furthermore, the 10 mm skull thickness used in the simulations is representative of a worst-case scenario; in reality, most skulls range from 5.3 to 7.5 mm in thickness and is dependent on sex but not age (Moreira-Gonzalez et al., 2006). We used such a thick skull layer to prove that bone thickness was not a limitation to the usefulness of NHCMM for brain tumor detection, and in reality, the resulting pressure signal from tumor/ultrasound interaction will be even stronger and more obvious.
Conclusion
In this paper, we evaluated the performance of NHCMMs for imaging through the skull with near realistic conditions by modeling cases where the skull exhibited curving, sloping, and interior surface aberrations. In all of these cases, the acoustic pressure field revealed the presence of a tumor when NHCMMs with material parameters calibrated to each unique skull condition were applied to the skull surfaces, as determined by both qualitative observations as well as calculating the contrast to noise ratio of the pressure signal. In contrast, ultrasound imaging through the skull with no NHCMM present or with an improperly designed NHCMM, one that was not tailored to match the skull profile, failed to resolve the tumor regardless of the skull shape. Thus, tunable NHCMMs are a functional and novel tool for diagnostic ultrasound imaging and can be applied to detect tumor presence for any skull geometry. Future directions include research into the physical realization of a NHCMM for ultrasound imaging and subsequent application to diagnose brain tumor severity.
Data Availability Statement
All datasets generated for this study are included in the article. Further inquiries can be directed to the corresponding author.
Author Contributions
CS conceived the idea and advised the research. SC and PW conducted the research. All authors contribute to the manuscript writing. All authors contributed to the article and approved the submitted version.
Funding
This research is supported by Georgia Tech Faculty Startup Funding.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Bednarski, M. D., Lee, J. W., Callstrom, M. R., and Li, K. C. (1997). In vivo target-specific delivery of macromolecular agents with MR-guided focused ultrasound. Radiology 204, 263–268. doi: 10.1148/radiology.204.1.9205257
Bushberg, J., Seibert, J. A., Leidholdt, E. M. Jr., and Boone, J. M. (2012). The Essentials Physics of Medical Imaging, 3rd Edn. Philadelphia, PA: Lippincott Williams & Wilkins.
Busse, J. W., Bhandari, M., Kulkarni, A. V., and Tunks, E. (2002). The effect of low-intensity pulsed ultrasound therapy on time to fracture healing: a meta-analysis. Can. Med. Assoc. J. 166, 437–441.
Chopra, K., Calva, D., Sosin, M., Tadisina, K. K., Banda, A., De La Cruz, C., et al. (2015). A comprehensive examination of topographic thickness of skin in the human face. Aesthetic Plast. Surg. 35, 1007–1013. doi: 10.1093/asj/sjv079
Craig, S. R., Welch, P. J., and Shi, C. (2019). Non-hermitian complementary acoustic metamaterials for lossy barriers. Appl. Phys. Lett. 115:051903. doi: 10.1063/1.5110501
Dahl, J. J., Hyun, D., Lediju, M., and Trahey, G. E. (2011). Lesion detectability in diagnostic ultrasound with short-lag spatial coherence imaging. Ultrason. Imaging 33, 119–133. doi: 10.1177/016173461103300203
Dempsey, M. F., Condon, B. R., and Hadley, D. M. (2005). Measurement of tumor “size” in recurrent malignant glioma: 1D, 2D, or 3D? Am. J. Neuroradiol. 26, 770–776.
Deng, Y., Palmeri, M. L., Rouze, N. C., Trahey, G. E., Haystead, C. M., and Nightingale, K. R. (2017). Quantifying image quality improvement using elevated acoustic output in B-mode harmonic imaging. Ultrasound Med. Biol. 43, 2416–2425. doi: 10.1016/j.ultrasmedbio.2017.06.024
Epstein, E., Testa, A., Gaurilcikas, A., Di Legge, A., Ameye, L., Atstupenaite, V., et al. (2013). Early-stage cervical cancer: tumor delineation by magnetic resonance imaging and ultrasound—a European multicenter trial. Gynecol. Oncol. 128, 449–453. doi: 10.1016/j.ygyno.2012.09.025
Errico, C., Osmanski, B. F., Pezet, S., Couture, O., Lenkei, Z., and Tanter, M. (2016). Transcranial functional ultrasound imaging of the brain using microbubble-enhanced ultrasensitive Doppler. Neuroimage 124, 752–761. doi: 10.1016/j.neuroimage.2015.09.037
Errico, C., Pierre, J., Pezet, S., Desailly, Y., Lenkei, Z., Couture, O., et al. (2015). Ultrafast ultrasound localization microscopy for deep super-resolution vascular imaging. Nature 527, 499–502. doi: 10.1038/nature16066
Fry, F. J., and Barger, J. E. (1978). Acoustical properties of the human skull. J. Acoust. Soc. Am. 63, 1576–1590. doi: 10.1121/1.381852
Geissler, A., Gartus, A., Foki, T., Tahamtan, A. R., Beisteiner, R., and Barth, M. (2007). Contrast-to-noise ratio (CNR) as a quality parameter in fMRI. J. Magn. Reson. Imaging 25, 1263–1270. doi: 10.1002/jmri.20935
Hadjiargyrou, M., McLeod, K., Ryaby, J. P., and Rubin, C. (1998). Enhancement of fracture healing by low intensity ultrasound. Clin. Orthop. Relat. Res. 355, S216–S229. doi: 10.1097/00003086-199810001-00022
Heckman, J. D., Ryaby, J. P., McCabe, J., Frey, J. J., and Kilcoyne, R. F. (1994). Acceleration of tibial fracture-healing by non-invasive, low-intensity pulsed ultrasound. J. Bone Joint Surg. Am. 76, 26–34. doi: 10.2106/00004623-199401000-00004
Hynynen, K., Freund, W. R., Cline, H. E., Chung, A. H., Watkins, R. D., Vetro, J. P., et al. (1996). A clinical, noninvasive, MR imaging-monitored ultrasound surgery method. Radiographics 16, 185–195. doi: 10.1148/radiographics.16.1.185
Kennedy, J. E. (2005). High-intensity focused ultrasound in the treatment of solid tumours. Nat. Rev. Cancer 5:321. doi: 10.1038/nrc1591
Kennedy, J. E., Ter Haar, G. R., and Cranston, D. (2003). High intensity focused ultrasound: surgery of the future? Br. J. Radiol. 76, 590–599. doi: 10.1259/bjr/17150274
Kennedy, J. E., Wu, F., Ter Haar, G. R., Gleeson, F. V., Phillips, R. R., Middleton, M. R., and Cranston, D. (2004). High-intensity focused ultrasound for the treatment of liver tumours. Ultrasonics 42, 931–935. doi: 10.1016/j.ultras.2004.01.089
Kim, H. J., Greenleaf, J. F., Kinnick, R. R., Bronk, J. T., and Bolander, M. E. (1996). Ultrasound-mediated transfection of mammalian cells. Hum. Gene Ther. 7, 1339–1346. doi: 10.1089/hum.1996.7.11-1339
Kinoshita, M., McDannold, N., Jolesz, F. A., and Hynynen, K. (2006). Noninvasive localized delivery of Herceptin to the mouse brain by MRI-guided focused ultrasound-induced blood-brain barrier disruption. Proc. Natl. Acad. Sci. U.S.A. 103, 11719–11723. doi: 10.1073/pnas.0604318103
Lu, M. H., Liu, X. K., Feng, L., Li, J., Huang, C. P., Chen, Y. F., et al. (2007). Extraordinary acoustic transmission through a 1D grating with very narrow apertures. Phys. Rev. Lett. 99:174301. doi: 10.1103/PhysRevLett.99.174301
Monti, M. M., Schnakers, C., Korb, A. S., Bystritsky, A., and Vespa, P. M. (2016). Non invasive ultrasonic thalamic stimulation in disorders of consciousness after severe brain injury: a first-in-man report. Brain Stimul. 9, 940–941. doi: 10.1016/j.brs.2016.07.008
Moon, W. K., Shen, Y.-W., Bae, M. S., Huang, C.-S., Chen, J.-H., and Chang, R.-F. (2012). Computer-aided tumor detection based on multi-scale blob detection algorithm in automated breast ultrasound images. IEEE Trans. Med. Imaging 32, 1191–1200. doi: 10.1109/TMI.2012.2230403
Moreira-Gonzalez, A., Papay, F. E., and Zins, J. E. (2006). Calvarial thickness and its relation to cranial bone harvest. Plast. Reconstr. Surg. 117, 1964–1971. doi: 10.1097/01.prs.0000209933.78532.a7
Neisius, A., Smith, N. B., Sankin, G., Kuntz, N. J., Madden, J. F., Fovargue, D. E., et al. (2014). Improving the lens design and performance of a contemporary electromagnetic shock wave lithotripter. Proc. Natl. Acad. Sci. U.S.A. 111, E1167–E1175. doi: 10.1073/pnas.1319203111
Ninet, J., Roques, X., Seitelberger, R., Deville, C., Pomar, J. L., Robin, J., et al. (2005). Surgical ablation of atrial fibrillation with off-pump, epicardial, high-intensity focused ultrasound: results of a multicenter trial. J. Thorac. Cardiov. Sur. 130, 803–809. doi: 10.1016/j.jtcvs.2005.05.014
Nishida, T., Shimokawa, H., Oi, K., Tatewaki, H., Uwatoku, T., Abe, K., et al. (2004). Extracorporeal cardiac shock wave therapy markedly ameliorates ischemia-induced myocardial dysfunction in pigs in vivo. Circulation 110, 3055–3061. doi: 10.1161/01.CIR.0000148849.51177.97
Pichardo, S., Sin, V. W., and Hynynen, K. (2010). Multi-frequency characterization of the speed of sound and attenuation coefficient for longitudinal transmission of freshly excised human skulls. Phys. Med. Biol. 56, 219–250. doi: 10.1088/0031-9155/56/1/014
Sapozhnikov, O. A., Maxwell, A. D., MacConaghy, B., and Bailey, M. R. (2007). A mechanistic analysis of stone fracture in lithotripsy. J. Acoust. Soc. Am. 121, 1190–1202. doi: 10.1121/1.2404894
Shen, C., Xu, J., Fang, N. X., and Jing, Y. (2014). Anisotropic complementary acoustic metamaterial for canceling out aberrating layers. Phys. Rev. X 4:041033. doi: 10.1103/PhysRevX.4.041033
Szabo, T. L. (2014). Diagnostic Ultrasound Imaging: Inside Out, 2nd Edn. Boston, MA: Academic Press.
Takakuwa, Y., Sarai, M., Kawai, H., Yamada, A., Shiino, K., Takada, K., et al. (2018). Extracorporeal shock wave therapy for coronary artery disease: relationship of symptom amelioration and ischemia improvement. Asia Ocean. J. Nucl. Med. Biol. 6, 1–9. doi: 10.22038/aojnmb.2017.9899
Tanter, M., and Fink, M. (2014). Ultrafast imaging in biomedical ultrasound. Trans. Ultrason. Ferroelectr. Freq. Control 61, 102–119. doi: 10.1109/TUFFC.2014.2882
Tran, B. C., Seo, J., Hall, T. L., Fowlkes, J. B., and Cain, C. A. (2003). Microbubble-enhanced cavitation for noninvasive ultrasound surgery. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 50, 1296–1304. doi: 10.1109/TUFFC.2003.1244746
Wang, S., Lin, J., Wang, T., Chen, X., and Huang, P. (2016). Recent advances in photoacoustic imaging for deep-tissue biomedical applications. Theranostics 6, 2394–2413. doi: 10.7150/thno.16715
Wu, F., Wang, Z. B., Chen, W. Z., Bai, J., Zhu, H., and Qiao, T. Y. (2003). Preliminary experience using high intensity focused ultrasound for the treatment of patients with advanced stage renal malignancy. J. Urol. 170, 2237–2240. doi: 10.1097/01.ju.0000097123.34790.70
Wu, F., Wang, Z. B., Chen, W. Z., Zou, J. Z., Bai, J., Zhu, H., et al. (2004). Extracorporeal focused ultrasound surgery for treatment of human solid carcinomas: early Chinese clinical experience. Ultrasound Med. Biol. 30, 245–260. doi: 10.1016/j.ultrasmedbio.2003.10.010
Keywords: ultrasound, acoustics metamaterials, diagnostics, imaging, ultrasonic therapies
Citation: Craig SR, Welch PJ and Shi C (2020) Non-Hermitian Complementary Acoustic Metamaterials for Imaging Through Skull With Imperfections. Front. Mech. Eng. 6:55. doi: 10.3389/fmech.2020.00055
Received: 31 January 2020; Accepted: 12 June 2020;
Published: 21 July 2020.
Edited by:
Oscar Vazquez Mena, University of California, San Diego, United StatesReviewed by:
Mariana Amorim Fraga, Federal University of São Paulo, BrazilLuis Guillermo Villanueva, École Polytechnique Fédérale de Lausanne, Switzerland
Copyright © 2020 Craig, Welch and Shi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Chengzhi Shi, Y2hlbmd6aGkuc2hpQGdhdGVjaC5lZHU=
†These authors share first authorship
 Steven R. Craig
Steven R. Craig Phoebe J. Welch
Phoebe J. Welch Chengzhi Shi
Chengzhi Shi