Hallmarks of Life in Single Cell Contact Mechanics: Outstanding Challenges and Perspectives

Introduction

Cells are the smallest living units/machines engineered by Nature. In a volume that may vary from 30 to 4 10⁶ μm³ they comprise the most refined machineries for self-division, molecular synthesis, assembly and metabolism, that on the whole regulate their development and secure their survival (Alberts et al., 2008). But all those activities would not be possible if the cells were not capable of interacting with their surroundings. Many of these interactions, like cellular adhesion, are mediated by mechanical cues (Schwarz and Safran, 2013), the mechanisms of which are so important and complex, and yet mostly unknown. It is for that reason that Cell Mechanobiology has become a major focus of continuous research and review, with (Kamm et al., 2017; Dufrene and Persat, 2020; Hallou and Brunet, 2020; Miller and Hu, 2020) being just a few of the most recent and multiple examples.

Indeed, cells can sense and generate forces and other mechanical stimuli as a result of the interaction with their surroundings, which usually trigger a functional response or are triggered by a cellular activity (Huang et al., 2004; Vogel and Sheetz, 2006). The response or activity can be physiological, transformative or motional (Figure 1) and involve the interplay of intracellular and exocellular components at different spatio-temporal scales. The mechanisms that convert mechanical cues into biochemical responses or viceversa, define the capacity of the cell to transduce mechanical signals and, in doing so, regulate its physiological activity and maintain the chemical balance. Cell mechanotransduction is hence key in sustaining life.

FIGURE 1

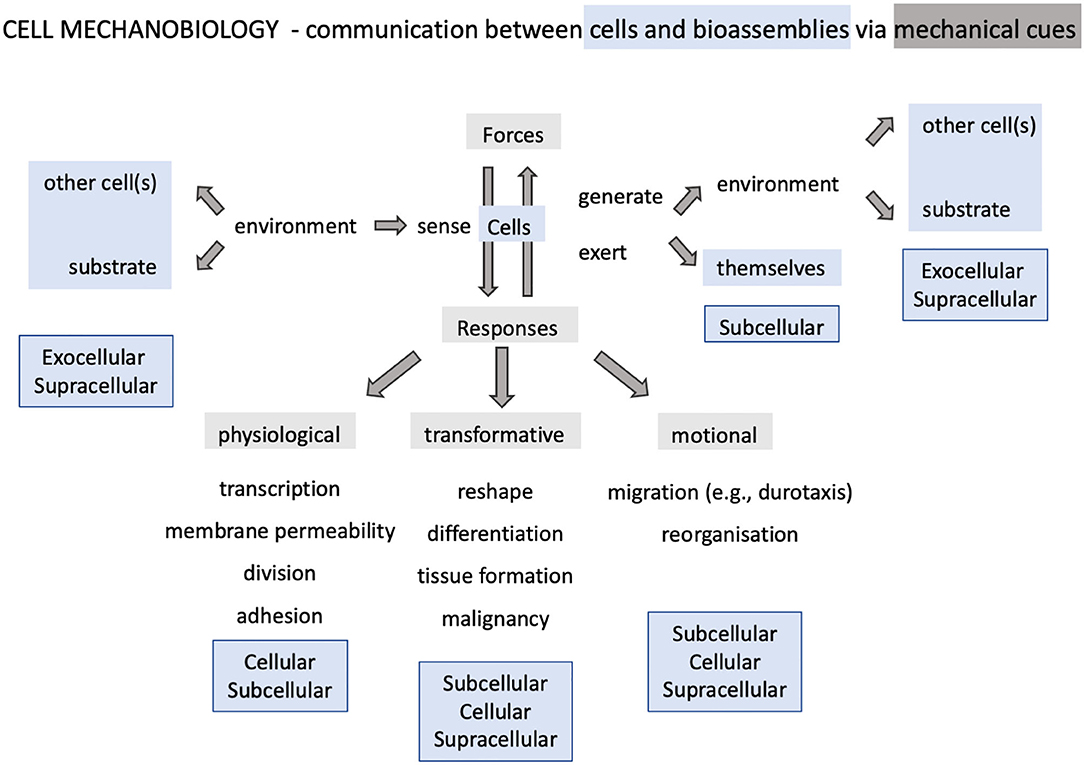
Figure 1. Landscape of cellular mechanobiology. The discipline revolves about single cell behavior and encompasses phenomena involving supracellular, intracellular and exocellular bioassemblies.

Mechanics is intertwined and evolves in parallel with cellular activity in these highly dynamic systems. This fact, together with the relatively high variability in cell behavior, adds a level of complexity that is not present in inanimate materials. Notwithstanding, the mechanical tests traditionally employed in the study of material properties have also been the experimental approach of choice for cells. Those methods became routine in their mechanical characterization, even though the results produced by different groups and with different techniques may differ from one another (Nawaz et al., 2012). The reason for this lack of consensus has been subject of thorough discussion (Hoffman and Crocker, 2009), but mainly attributed to the specifics of the technique used and the experimental conditions, which on the whole prompt the manifestation of a particular behavioral aspect above others. Therefore, it has been difficult to identify a universal behavior, even for cells of the same type. A particularly illustrative example of the latter is the work of Wu et al. (2018). The result of a large-scale, multi-institutional cooperation, a total of seven different techniques were put in place to measure the mechanical properties of MCF-7 cells, only to demonstrate the discrepancy between the experimental data. In stating the variability in cell behavior, even for those of the same type, the work actually evinces the fundamental issue of characterizing cells by a unique set of mechanical parameters, on the one hand. On the other hand, it demonstrates the limited capability of single techniques and routine experimental protocols for the detection and qualitative assessment of cell mechanical behavior as a complex whole. Does this/the above mean that we might require an arsenal of techniques for a complete assessment of the cell mechanics? In a way, it does. If the purpose is to find a thorough description of general validity.

Despite the continuous effort of the last few decades to understand the mechanical behavior of cells, there are still many open questions and the scientific challenge remains high. In the context of theory, we might be facing a similar situation, if not more severe: “… cell mechanics is but the tip of the iceberg, while a more profound approach would have to consider inelastic or plastic rather than elastic deformations and kinematic hardening rather than differential stiffening as the most salient mechanical characteristics of live cells.” (Kroy, 2008). Similarly, from the experimental perspective, a study concluded that: “…the mechanical properties of a cell are not static but dynamic and responsive to environmental conditions. Therefore, mechanical models of a cell must include a dependence on time and physiological conditions” (Pelling et al., 2007). These statements are now more than 10 years ago, and yet has as much validity as if they were made yesterday.

This review does not aim to describe as to build up on the state of the art in single cell mechanics, scrutinizing common scientific approaches and pinpointing current issues, outstanding challenges and directions worth further exploring.

State of the Art

Experimental Techniques and the Importance of Combined and Synchronous Detection

In comparison with inanimate matter, cells are a very special kind of materials; they possess a unique architecture of interconnected membrane compartments and molecular networks that are in constant evolution and physiological activity, ready to respond to intra and exocellular cues of the most diverse kind, via multiple processes that may occur sequentially or simultaneously, and at different locations in a three-dimensional space.

Methods exist that allow to exert the smallest mechanical perturbations with great precision and sensitivity, as well as quantitatively detect and/or visualize the mechanical response at different times and precise locations. Most of them make use of microsized or nanosized probes, either mechanical, optical, electric or magnetic, to apply and/or quantitatively detect, even map, forces or deformations, and some kind of optical microscopy to precisely locate the application of stimuli and visualize the mechanical response. But none of the experimental, state-of-the-art techniques can, separately, apply and detect any mechanical perturbation, anytime and anywhere, in ways and magnitudes that can be relevant for cells (Figure 2). In this context, relevant to define cellular behavior as completely and thoroughly as possible.

FIGURE 2

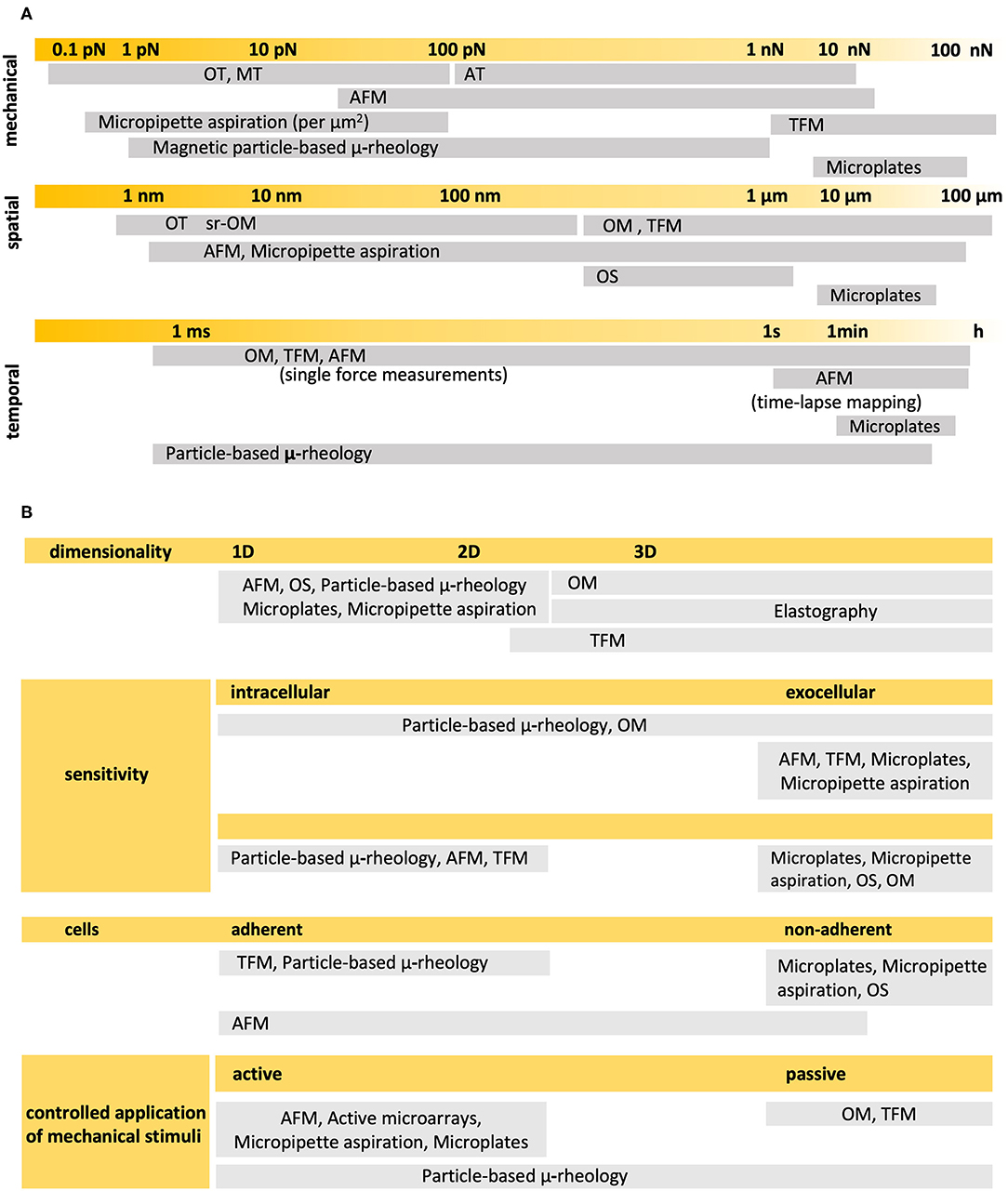
Figure 2. Experimental techniques most commonly used in single cell mechanics (A) Detection ranges in the mechanical, spatial and temporal scales of relevance. (B) Main characteristics. OM, Optical Microscopy; AFM, Atomic Force Microscopy; TFM, Traction Force Microscopy; OT, Optical Tweezers; MT, Magnetic Tweezers; AT, Acoustic Tweezers; OS, Optical Stretcher. Particle-based techniques may comprise optical or magnetic drag, tweezers or traps, and twist cytometry. Sources: (Thoumine and Ott, 1997; Hochmuth, 2000; Lau et al., 2003; Wottawah et al., 2005; Basoli et al., 2018; Septiadi et al., 2018; Wu et al., 2018).

It is for that reason that the behavioral complexity of cells demands a proportionate and suitable combination of measuring setups for the in-situ detection of relevant mechanical phenomena, in two and three dimensions, and at the relevant mechanical, spatial, and temporal scales.

In the context of single cells, probe-based microscopies deserve special mention (Figure 3A). Collectively, this family of techniques can precisely apply and register mechanical forces in the pico- and nanonewton range, deformations of the order of nano and micrometers, as well as optically track phenomena at the nano and micrometer scales, ranging from the millisecond to the hour. The atomic force microscope (AFM) can nominally apply compressive and tensile loads and detect the normal and horizontal components of forces and vertical deformations at the upper surface of the cells. These should be preferably attached to a substrate, meaning that the technique is sensitive to phenomena occurring at or at the vicinity of the apical membrane and, in any case, close enough to the cantilever-probe. The in-plane spatial resolution is hence determined, and limited, by the size of the probe as it applies tensions or compressions across the cell surface. But the major limitation is that the technique alone cannot provide a direct measure of the contact area, let al.one the geometry of the contact region between cell and probe. To that end, the integration of an optical-interference technique may be required, such as total reflection interference contrast microscopy (RICM). The combined set-up has been earlier applied to study ligand-receptor interactions at the molecular level (Stuart and Hlady, 1999), leveraging the capacity of AFM and RICM to detect forces and separation distances, respectively, with sub-nanoscale precision. Previously, RICM had been proven effective in measuring gap distances between cell basal membranes and the underlying substrate, in the calculation of contact areas (Curtis, 1964; Verschueren, 1985), and of their changes in cells under stress, either in a stand-alone configuration (Hategan et al., 2003), or in combination with the method of micropipette aspiration (Heinrich et al., 2001). But despite its high measuring potential, the tandem AFM-RICM has not been so much applied in the study of cell mechanics as in the investigation of inert materials (Dubreuil et al., 2003). Instead, contact areas are calculated based on geometrical assumptions, which restrict the probes to a limited range of sizes and geometries of high symmetry, and in turn limits the measuring potential of the technique. The cantilever itself, poses a limitation in the rates at which forces and deformations can be applied: loading rates should be fast enough to minimize the instrumental drift, and slow enough to avoid the dominance of the hydrodynamic drag, and to quantise its effect in the measurement of forces (Alcaraz et al., 2003; Mahaffy et al., 2004). Also, the amplitudes of oscillatory stimuli are kept relatively low so that it is possible to reasonably assume that cells behave as linearly viscoelastic materials, which in turn allows for the determination of meaningful dynamic elastic moduli. As a result, the maximal forces and deformations applied are of the order of hundreds of pN or a few nanometres (2–50 nm), respectively, with frequency windows between 0.1 and 10² Hz, which limits the overall detection range of the technique (Alcaraz et al., 2003; Mahaffy et al., 2004; Hiratsuka et al., 2009). On the other hand, Traction Force Microscopy (TFM) (Figure 3B) heavily relies on optical microscopy to detect cell deformations, primarily, through the lateral displacement of fluorescent probes embedded in the substrate onto which the cells are adhered (Polacheck and Chen, 2016). The optical device is usually an inverted microscope that provides bottom-side views of cells at a particular (focal) plane or set of planes (should a confocal or a structured illumination microscope be used). Hence, the technique is particularly appropriate to detect and track lateral deformations and obtain in-plane components of cell-generated forces at the vicinity of the basal membrane of adherent cells. In comparison with AFM, TFM is faster in optically detecting concurrent mechanical events at different cell locations, and the hydrodynamic drag nor the obtention of contact areas poses critical issues. However, the spatial resolution lies at its best in the (sub)micrometer range, and the data processing, including the computation of traction forces from observed in-plane displacements, is highly laborious, challenging and time-consuming. Henceforth, the technique is particularly responsive in detecting displacements at the (sub)cellular level, but not in tracking events that occur at the molecular scale and cannot generate mechanical maps on the fly. Also, the technique is not most appropriate to track out-of-plane events, i.e., normal components of forces or concurrent out-of-plane deformations. The limitations of TFM are common to other similar techniques that trace external deformations (i.e., by means of micropillars), or particle-based techniques that trace internal displacements of cell structures and organelles.

FIGURE 3

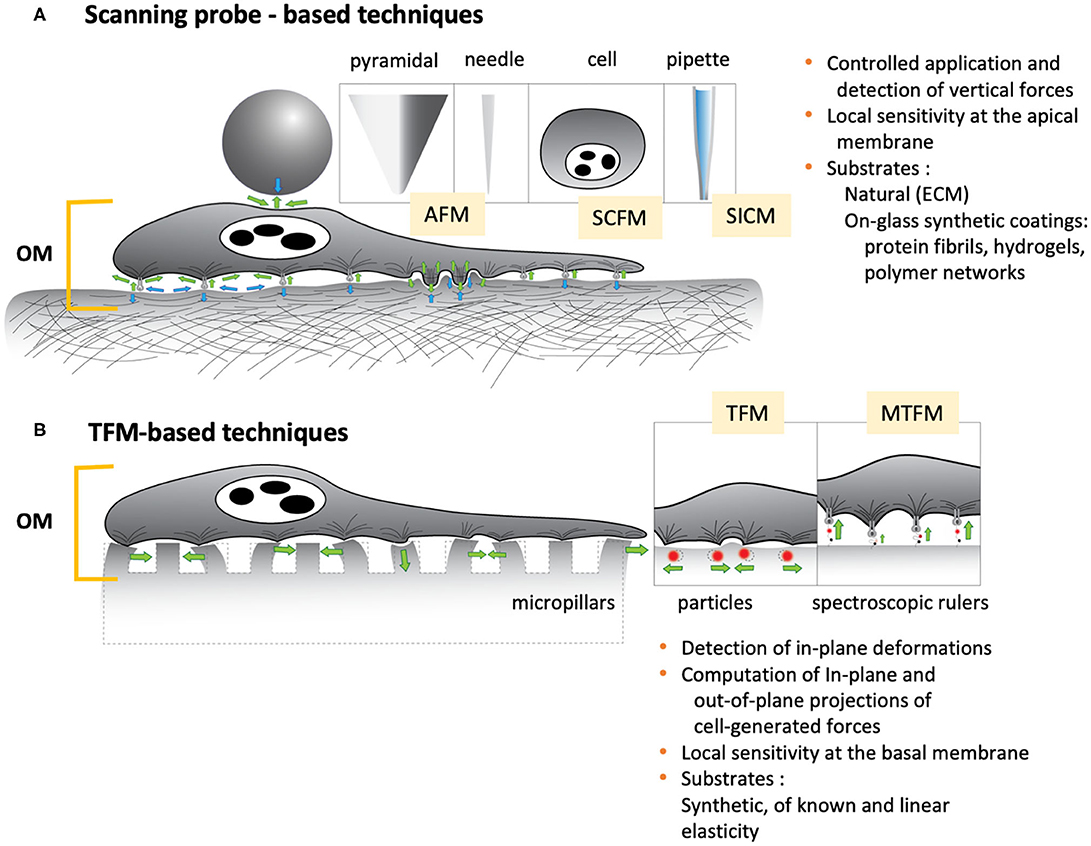
Figure 3. Two of the most common contact-based technique to study cell mechanics. (A) Scanning probe-based techniques. Microbeads, pyramidal tips, needles, cells or pipettes are usually employed as stand-alone probes or attached to microcantilevers. (B) TFM-based techniques. Rigid materials or non-degradable silicone or polyacrylate are used as substrates, featuring micropillars, embedded fluorescent particles or spectroscopic rulers, i.e., fluorophore-quencher pairs attached to unfolding molecule (a repetitive protein construct, DNA hairpin, or PEG) that acts as a force sensor (Liu et al., 2017). Both sets of techniques heavily profit from or rely on the combination with optical microscopies. Green arrows: forces exerted by the cell; Blue arrows: exocellular forces.

Other techniques, such as optical tweezers or the recently developed molecular tension fluorescence microscopy (MTFM) (Liu et al., 2017), are sensitive to mechanical events at the molecular scale, and in that sense have the highest spatial and temporal resolution. But also in these cases, the information they provide is restricted to one or, at the most, two spatial dimensions, and lack comparable significance at the (sub)cellular level.

As shown above, there is indeed a panoply of high-end technologies from which to define suitable combinations that allow a thorough investigation of the mechanical behavior of cells in the widest detection range. These combinations should assist in finding missing links between mechanics, structure and physiology, going beyond purely observational correlations into the causal relations and underpinning mechanisms.

To date, some promising efforts to combine techniques have been recently reported and to some extent, provided significant evidence in that sense. For example, Schierbaum et al. (2019) recently employed a combined AFM-TFM setup to find statistical correlations between viscoelastic parameters and contractile stresses in endothelial cells (Figure 4). Although the observations clearly indicate that, on average, stiffer cells exert higher traction forces, at a subcellular scale this does not seem to be the case. Indeed, for a given cell, the highest traction forces were located mainly around the more compliant and fluid regions. This apparent discrepancy of results across length scales questions the significance of such correlations, especially if the specifications of each measuring technique, their synchronized use, and the underlying mechanism(s) of force transmission inside cells are not sufficient considered. In this particular case, stiffness and fluidity were obtained from creep maps at the apical region of the cells, whereas traction moments were computed from local displacements of fluorescent beads in proximity with the basal membrane. The set-up combination was not so much used synchronously as sequentially, at different unspecified times, and given the disparate spatial resolution of the techniques employed, most presumably on different subcellular regions of dissimilar size.

FIGURE 4

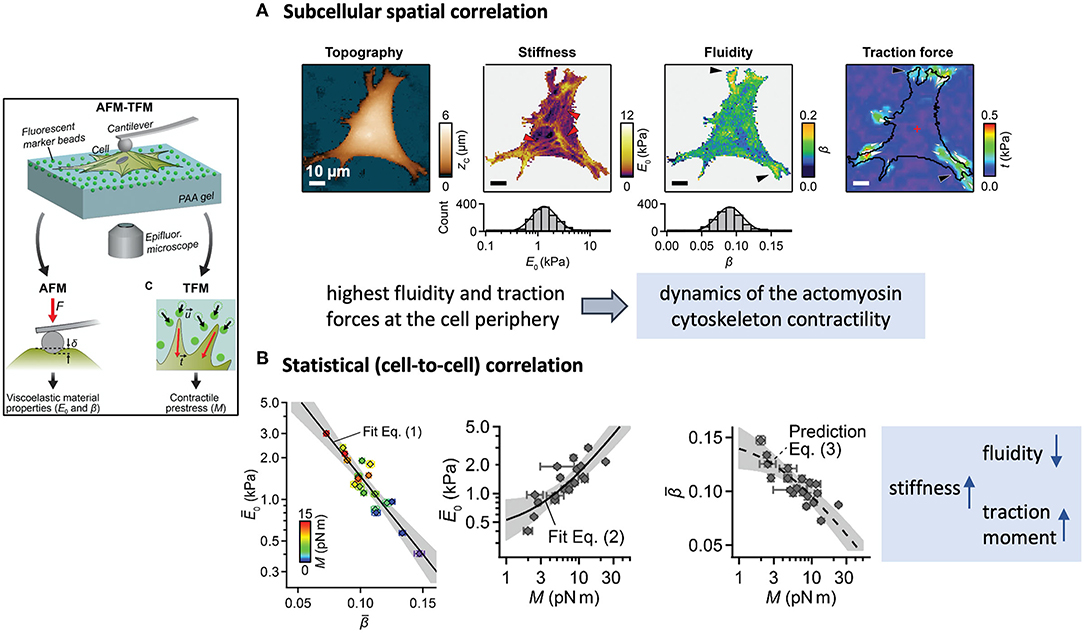
Figure 4. Example of a scientific study based on the combination of an AFM and an TFM to find spatial and statistical correlations between cell mechanical parameters. The framed inset on the left outlines the experimental approach. (A) Multiparametric maps of a fibroblast showing examples of colocalization of areas of high traction activity with regions of high fluidity. (B) The average results show however that stiffer cells exert higher traction moments than more fluid cells. (Figures reproduced from Schierbaum et al., 2019 with permission of the Royal Society of Chemistry).

A significant step in achieving synchronicity of mechanical and optical data, has been made by Beicker et al. (2018). In their combined set-up, they were able to laterally visualize the morphology of a single cell as it was mechanically tested with an AFM (Figure 5). The integration of vertical light sheet illumination and sideways microscopy in an AFM literally introduces a new perspective and makes it possible to directly observe the influence of the mechanical stimuli and the nature of the response in relation to the cell morphology, structure and behavior alongside the lateral region and as a function of time. Through this combination, the authors show evidence of structural and mechanical coupling between the cell membrane and the nucleus, an unprecedent finding of significant relevance that potentially shows the interplay of cell organelles in the transmission of forces within the cell.

FIGURE 5

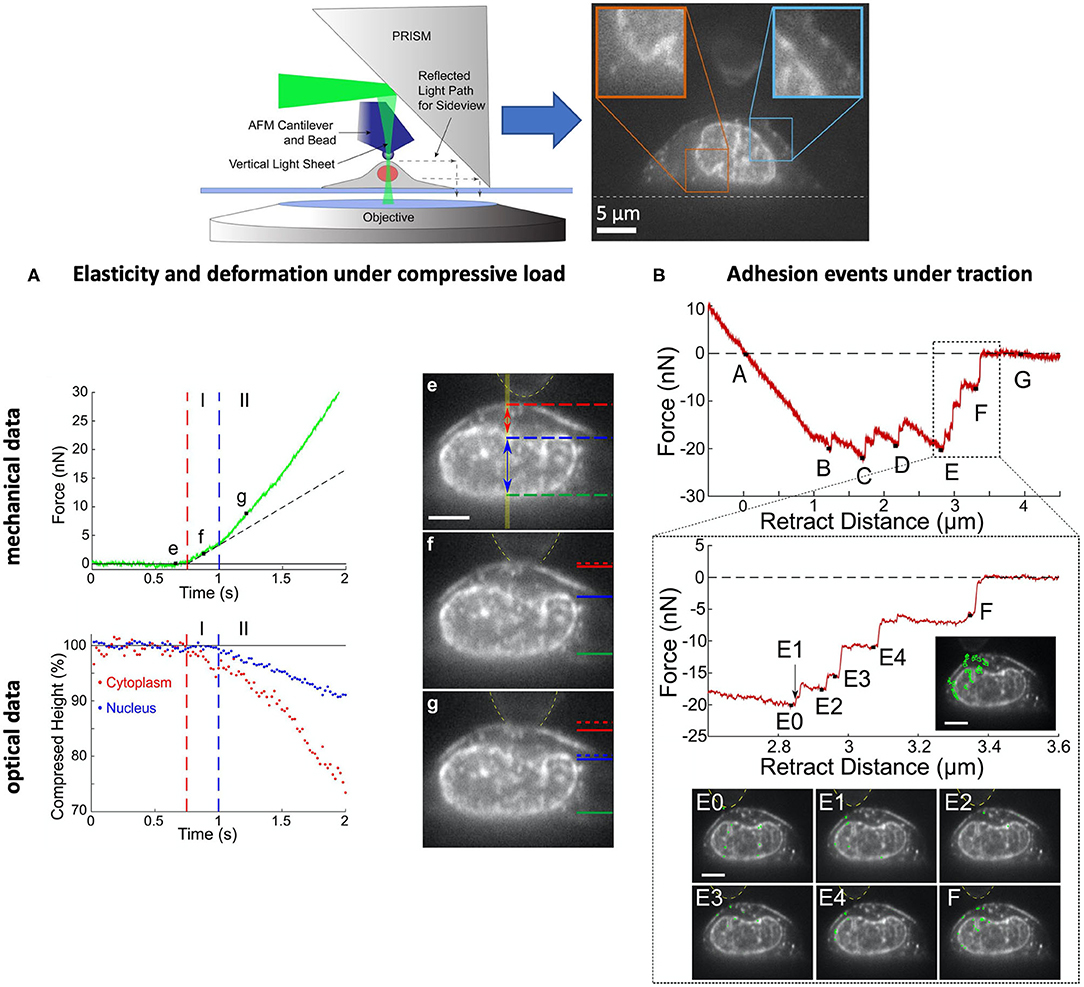
Figure 5. Example of a scientific study based on a combination of AFM, pathway rotated imaging for sideways microscopy (PRISM) vertical light sheet illumination (VLS) for the synchronous detection of optical and mechanical events of single ovarian cancer cells (SKOV3). Inset on the top: experimental set-up. (A) The compression tests reveal two regimes, I and II, where the cell displays a stiffness of 2.9 and 3.9 kPa, respectively, and associated with the deformation of the cytoplasm (I) and the nucleus (II). (B) The decompression tests reveal a series of adhesion signatures (B–F) that can be associated to snap-off events between the membrane and the fibronectin-coated bead (B–E) and the membrane, nucleus and bead (E,F). The results evince a mechanical coupling between cell membrane and nucleus, a type of interconnection that mediates cell adhesion. [Figures reproduced from (Beicker et al., 2018) with permission¹].

More recently, the work of Skamrahl et al. (2019) has provided further evidence of dynamical mechano-adaptation of cells by a suitable combination of AFM and optical fluorescence microscopy (Figure 6). Indeed, the report shows alterations in the turnover rate and length of basal F-actin stress fibers as cells are subjected to apical loads between 0.1 and 1 nN. The findings constitute a clear evidence of apical-basal force transmission or “action at a distance,” whereby the application of local mechanical stress at the top of a cell results in the modulation of cytoskeletal activity and remodeling, i.e., an active response, at the bottom. In this respect, the work adds to the pioneering findings (Mathur et al., 2000), and follows the experimental approach of Charras and Horton (2002a). Marthur et al. had reported on a similar manifestation of apical-basal force transmission, whereby apical loads applied on single HUVEC cells induce the reorganization of focal adhesions at the immediacy of their basal membranes within minutes. Charras and Horton on the other hand, combined AFM and confocal microscopy to unveil for the first time the effect that mechanical strains have in modulating Ca-mediated mechanotransduction pathways in osteoblasts. Through this approach, they were able to identify threshold cellular strains triggering the chemical response, to precisely define the experimental timeframe for the whole process within seconds, to assess the contribution of the cytoskeletal structures, and to propose a sensible model for the mechanism by which bone cells sense mechanical strains. Although Skamrahl et al. provide characteristic time scales of stress fiber dynamics, they do not propose a molecular model or mechanism in line with their results and those reported by Mathur et al. (2000), nor do they provide a measure of the timeframe for the force transmission and transduction events. The question remains open, as to when and how, in the interval of 2 min between the application of the mechanical stress and the time when the observation begins, force propagates and triggers the physiological response.

FIGURE 6

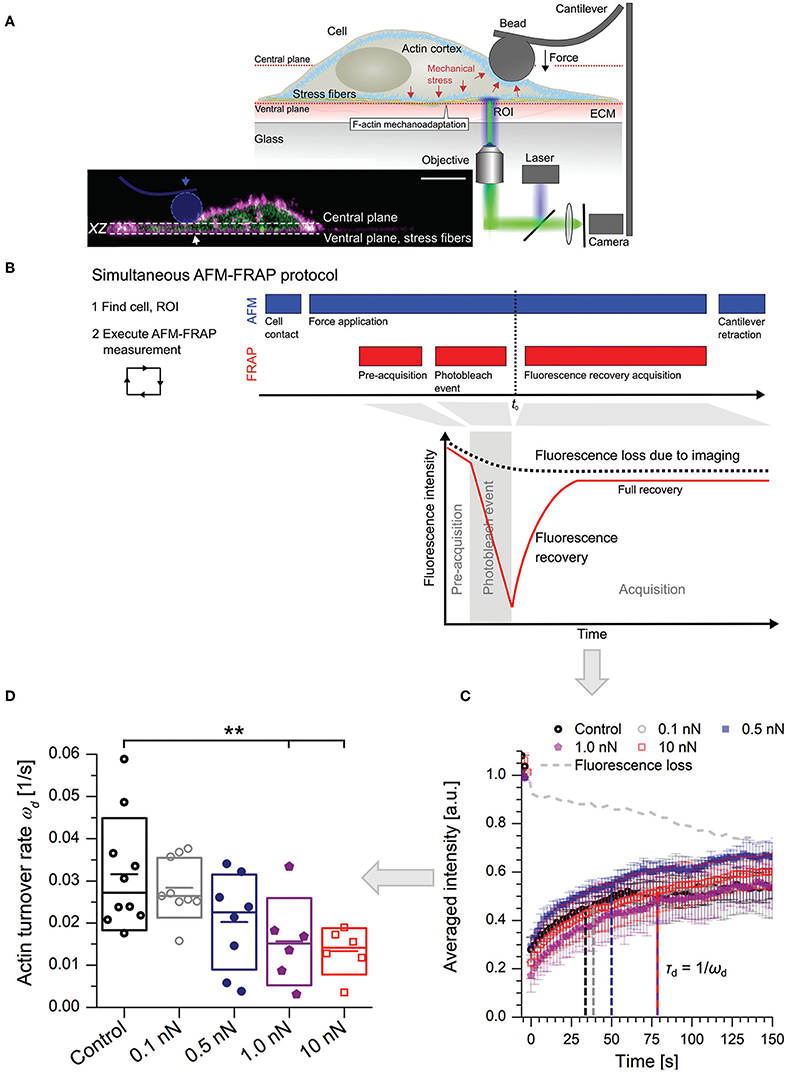
Figure 6. Combined AFM-FRAP for the detection of a physiological response in the immediacy of the basal membrane of cells subjected to apical stress. (A) The experimental set-up. The inset features a real-life cross-section of an adherent cell. (horizontal scale bar = 10 μm, distance between planes = 4μm). (B) Experimental protocol. Force is kept constant and applied at least two minutes before acquisition of fluorescence recovery data. (C) Typical fluorescence recovery curves as a function of applied force. The turnover rate is indicated in relation with the characteristic recovery time. (D) Statistical results of turnover rates (**, level of significance p < 0.01). (Figures reproduced from Skamrahl et al., 2019 with permission²).

Although a complete mechanistic picture remains elusive at the cellular scale, it may not be the case at the subcellular level. A remarkable example of the latter is the work of Bouissou et al. (2017), which provides a detailed mechanism of the way podosomes work in motile cells. Built upon the podosome architecture, and consistent with the experimental results, the authors manage to relate mechanical function to key molecules and structures. The work is exemplary in that it manages to obtain a mechanism of how a subcellular structure mechanically works, via an original experimental approach that comprises the combination of AFM, super-resolution optical microscopy with numerical simulations and protein expression knock-down techniques (Figure 7, see also section Experimental Approaches and Protocols). Though the work eludes discussing the podosome as a dynamic structure that emerges and disappears with time, as the time-lapse AFM experiments show, studies of such nature and caliber very well deserve to be considered as gold standards in the study of cell mechanics.

FIGURE 7

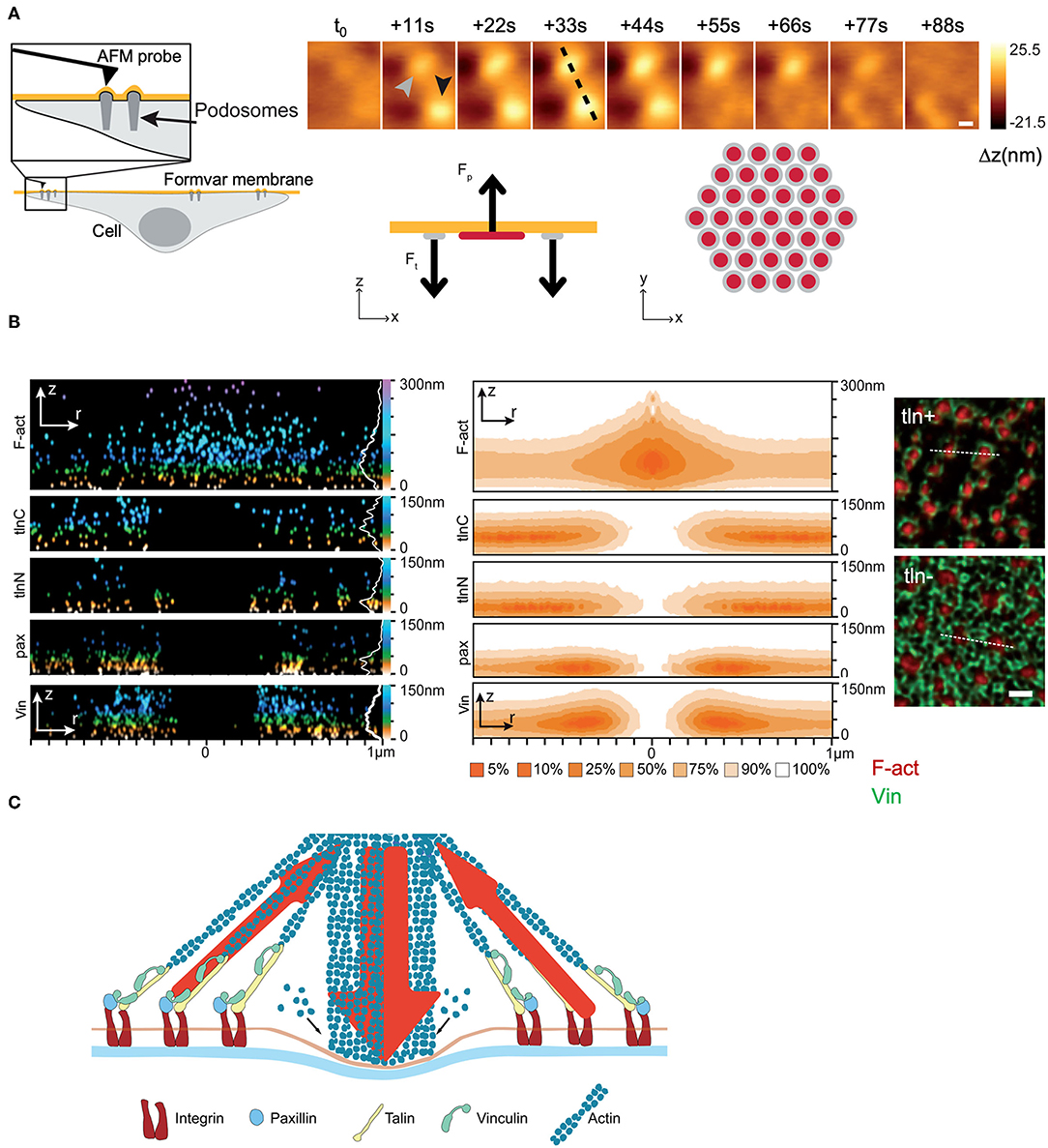
Figure 7. Experimental study of the podosome structure and working mechanism. (A) AFM measurements: Topology of a pair of podosomes from fingerprint tracks left on a Formvar membrane. Simulation results: Protrusion-traction model of a single podosome in agreement with the experimental results. The stability of the podosome at a certain time is the result of a mechanical balance between protrusion forces (F_p) at the center of the podosome (red) and peripheral traction forces (F_t) (gray). (B) DONALD measurements. Spatial distribution of key structures and molecules (F-actin, talin, paxillin and vinculin) in a single podosome (left), and their corresponding probability density distributions (center). The immunofluorescence images (right) show the distribution of F-actin and vinculin in single podosomes and evince the contribution of talin in co-maintaining the annular structure. (C) Proposed general model of a podosome, featuring the molecular structure and the mechanical configuration of exerted forces. (Figures reprinted and adapted with permission from Bouissou et al., 2017). Copyright 2017 American Chemical Society.

Outside the AFM context, a recent study combining TFM and arrays of micropillar actuators particularly stands out (Shi et al., 2019). Unlike the classical micro-rheological techniques, the experimental set-up allows to obtain rheological maps of cell basal regions, along with spatial distributions of cellular fluctuations (Figure 8). Such a configuration was applied to thoroughly describe the cytoskeletal dynamics of single fibroblasts as a function of time and space. Via a sound and comprehensive statistical analysis of the experimental data, the authors were able to detect and locate distinctive behavioral traits of the cell cortex and stress fibers, and establish meaningful spatial correlations in the observed displacements, which showed on the one hand, the highly cooperative dynamics of the actomyosin network, and on the other hand, the avalanche-like dynamics of the actin cortex. The results were not discussed in comparable depth, and although they seemed to be in agreement with the theoretical predictions of Ferrero et al. (2014) and Hwang et al. (2016), they are based on different dynamic mechanisms, neither of which could be ruled out.

FIGURE 8

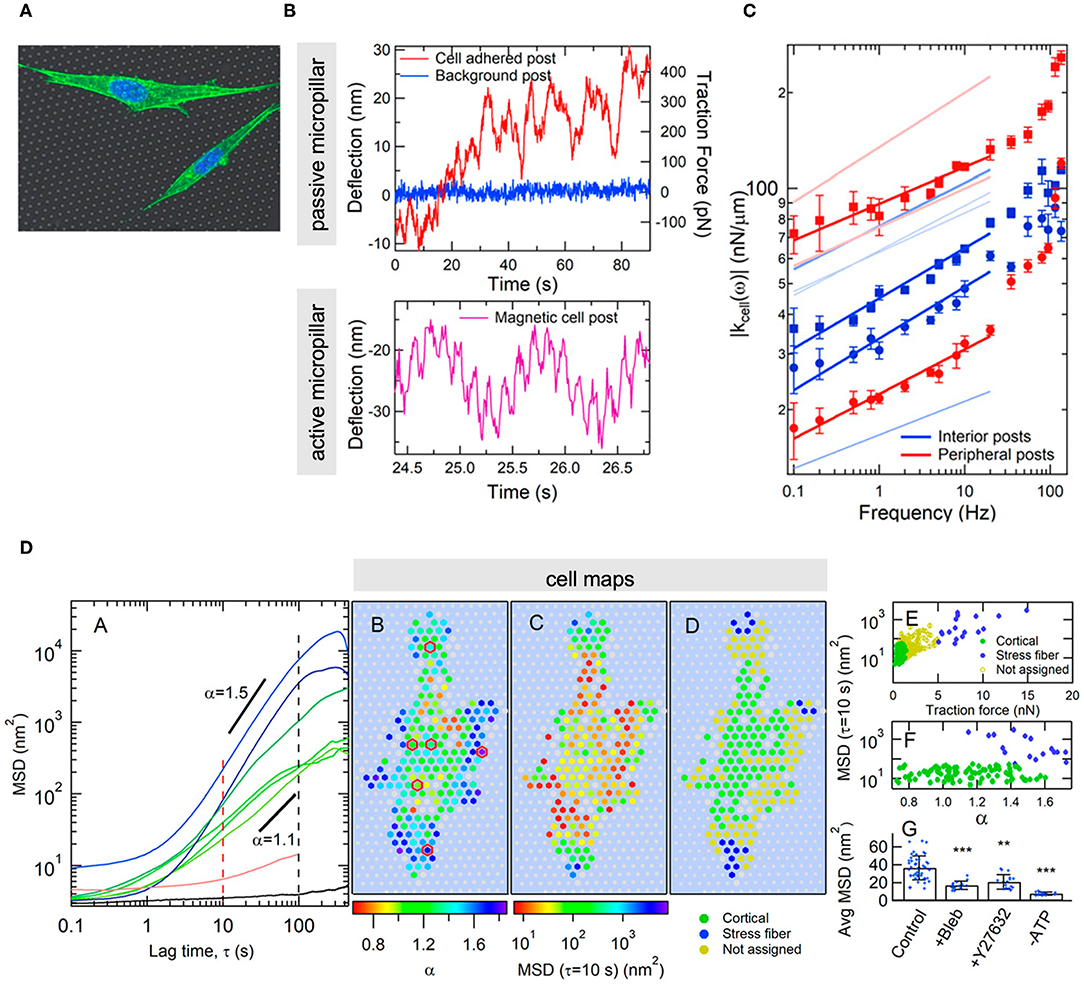
Figure 8. Example of combining TFM and actuator arrays to obtain microrheological data and map cell-generated fluctuations at the basal membrane of adherent cells. (A) Image of cells on the microstructured substrate. (B) Typical experimental output of a non-actuated (upper graph) and an actuated micropillar driven by a double-sinusoidal magnetic field at 1 and 7 Hz (lower graph). (C) Dynamic stiffness as a function of frequency for micropillars situated in the central (blue) and the peripheral (red) regions of the cell, exhibiting different power-law dependences. (D) From left to right: mean square displacements of passive micropillar deflections and MSD exponents that differ in the central (cortical) and the peripheral (dense in stress fibers) regions and show superdifusive behavior. Spatial distributions of MSD exponents, mean square displacements and traction forces across the cell and according to the regions rich in actin cortex and stress fibers. MSD values and traction forces according to type of micropillar (level of significance: **p < 0.01; ***p < 0.001). The effect of cytoskeletal disrupting agents on the cellular fluctuations reveal that the structure involved is the actomyosin network. (Figures reproduced from Shi et al., 2019).

The existing reports reveal the great measuring and detection potential of combining state-of-the-art techniques, and the incipient effort in that direction. But also, that their application in cell mechanical studies is far from being fully exploited. Other relevant aspects to consider are the simultaneous determination of contact areas and the influence of lateral forces in cell behavior. AFM, being one of the most versatile techniques in its diverse operational modes (Figure 9), can also detect the lateral component of forces, but these are usually ignored in non-rheological studies, most of the time under the assumption, not fully justified, that the forces are applied normally and hence the horizontal component is negligible or irrelevant. This assumption may appear valid when the experiment is performed at the apex of the cells, but not necessarily, and much less elsewhere. The reason is simple: the cell surface is not horizontally flat, its curvature profile is complex, adaptive and site-dependent. Experimentally, this magnitude is not directly measurable, and can only be assumed a-priori, or, at its best, indirectly inferred from optical cross sections of limited spatial resolution and asynchronously obtained. As a consequence, the experimental study of friction at the cellular scale remains as challenging as unexplored, with a potential biological relevance still in process of being discovered.

FIGURE 9

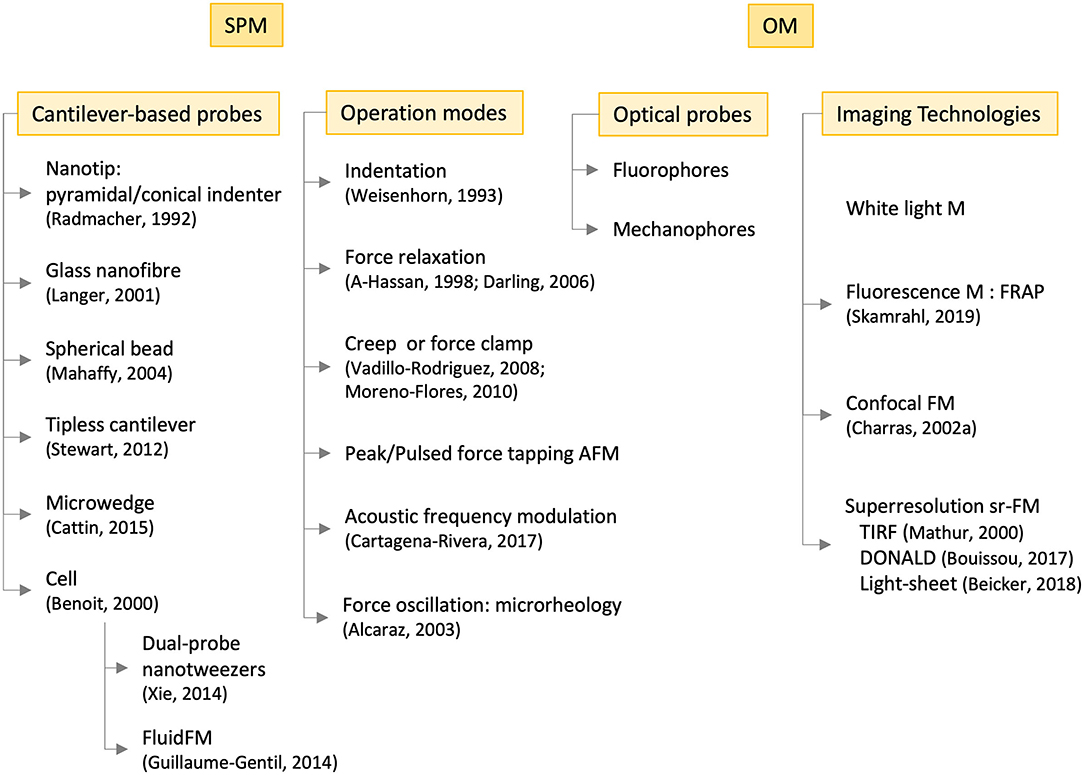
Figure 9. Operational modes and technologies employed in the experimental study of cell mechanics with scanning probe microscopies (SPM, left-hand side) and optical microscopies (OM, right-hand side), the latter in combination with the former. Some references are included of pioneering or outstanding works. M, microscopy; F, fluorescence; FRAP, fluorescence recovery after photobleaching; TIRF, total internal reflection fluorescence; DONALD, direct optical nanoscopy with axially localized detection; sr, super-resolution.

Methodologies and Protocols

As in the case of inert materials, mechanical assays alone do not suffice to understand the relation between behavior and structure in cells. To ascertain the relative influence of individual variables, the usual approach has consisted in manipulating the material, either chemically or physically, in a controlled manner and in such a way that either the nature of its constituents, relative composition, or a particular environmental condition during its synthesis or treatment is selectively altered. The effect of such manipulation can be visualized optically, via the use of molecular dyes (i.e., fluorophores) that selectively label specific cellular structures or organelles. In the case of cells, mechanical assays are often accompanied by chemical or genetic interventions, whereby the cells are subjected to the action of certain drugs of known effect or to manipulation treatments of their genetic material or gene expression machinery. In both cases, the interventions are mostly focused on causing alterations of diverse nature in their cytoskeletal structure, and most recently, dynamics. The interventions are mainly used to test molecular hypotheses, usually with a substantial biological background, whereby the molecule or structure believed to play a decisive role in the process is selectively altered. The mechanical essay is then used to either confirm or refute the working hypothesis and draw conclusions in this regard. How generally valid this conclusion might be, depends on the level of statistical significance of the observation (reproducibility or repeatability of a particular behavior) across cells of the same type and across cell types. Unlike inanimate materials, making generalizations on cellular behavior or on their mechanical properties from experimental results is audacious: cell-to-cell variability is an intrinsic feature that is far more superior and depends on far more numerous factors as batch-to-batch variability in inanimate matter. Hence, reproducible behavior must be interpreted in statistical terms, and based on a proportionate number of experiments on comparably numerous cell strains and cell types.

The vast majority of studies have been mainly focussed on unveiling the connection between mechanics and certain components of the cellular architecture and/or the cellular membrane; in other words, the main structural elements. In this regard, and in the context of chemical interventions, the use of disruptive or stabilizing agents of actin filaments and microtubules in the experimental protocols has become commonplace ever since the early works of Rotsch and Radmacher (2000) and Charras and Horton (2002a). Drugs such as cytochalasin B, D or latrunculin A are often employed to inhibit the formation of actin fibers, whereas nocodazole, colchicine and colcemide exert a similar effect on microtubules. Paclitaxel, on the other hand, has been the drug of choice to stabilize microtubules. Less common, but important if the purpose is to disrupt cytoskeletal activity or mechanotransduction pathways, is the employment of enzyme or pathway inhibitors. Blebbistatin and ML-7 disrupt the activity of enzymes associated to the actomyosin network, whereas gadolinium ions, verapamil or thapsigargin supress the calcium entry pathway, each in a different way (Charras and Horton, 2002a). Interestingly, these chemical agents do not disrupt cellular structures so much as physiological processes in a selective manner. In the first case, it is the mechanism of cytoskeletal contractility as example of active cellular response or hallmark of dynamic cellular behavior. In the second, the trafficking of Ca ions as part of a mechano-transducing pathway. In this sense, those substances and similar others with tuneable and controllable effects and well-known mechanisms of action at the single cell level, hold great scientific potential and hence are much in need. They enable to ascertain the relevance and influence of physiologically active processes, and hence to understand the mechanical behavior of cells as living entities.

Chemical intervention can be easily incorporated in the mechanical assays; drugs can be added or removed in-situ without major practical complications, allowing the study of their effect on the same cells and in one single experiment. A major objection to the use of drugs is that these may cause perturbations on cells that may not be controllable, measurable, reproducible or selective enough at the cellular scale. Besides, a substantial knowledge of their effects and mechanism of action, also in the appropriate dose(s), is required prior to their utilization. Factors such as the extent of drug intake or resistance at the single cell level are critical but likely to vary among cells, resulting in an added variability of behavior that cannot be experimentally controlled. In this regard, the physical investigation heavily relies on (and lags behind) the biological and pharmaceutical investigations pertaining drug development and associated effects in-vitro. As positive as this interaction may be in enhancing cross-disciplinarity, it also limits the gain in physical knowledge in that it restricts the nature and number of hypotheses to test.

Genetic manipulation may be more precise and a method of choice when it comes to modulate the presence of key molecules inside cells. These molecules are proteins, and usually constituents of the cellular skeleton or of molecular complexes putatively relevant in determining the mechanical characteristics of cells, such as cell-substrate (e.g., focal adhesions) and cell-cell anchors (e.g., cell-cell junctions. The manipulations, which usually occur at the DNA level, aim at the up-regulation, down-regulation or suppression (knock-out) of the expression of the corresponding target protein. Correspondingly, the process usually results in the increase, decrease or absence of intracellular protein, with the corresponding alterations in the processes or structures the protein is part of. In this sense, the genetic approach introduces a higher level of control and versatility in the type and number of processes it can modify. However, the manipulations are complicated and laborious, which rules out a simple, in-situ implementation, require numerous materials and dedicated equipment, not to mention the expertise and know-how of geneticists and biologists. Also in this case, the biological and genetic knowledge is key in defining the appropriate course of action (i.e., choice of relevant proteins and genes to manipulate and how) for the intended outcome (alteration of cellular activity or structure).

Data Analysis and Interpretation

Despite the advancement in the measuring technologies and the level of sophistication of the experimental methodologies, the analysis and interpretation of (opto-)mechanical data have not witnessed a comparable development. Indeed, the current techniques can generate big sets of data with relative ease, but only a relatively small portion can be easily explained or is susceptible of routine analysis and interpretation.

Also in the context of living matter, a typical mechanical experiment allows to obtain the relations between forces and deformations, also as a function of time or of frequency. Reports abound in which the behavior of many types of cells have been investigated via “indentation” tests³, which have become a routine procedures, or through stress relaxation, creep or rheological experiments at the microscale. In all these cases, the results have been analyzed in analogous ways as for inanimate materials, borrowing the traditional models of contact mechanics, in particular of the theory of linear viscoelasticity (Figure 10). It is hence not uncommon to find elastic or complex moduli (usually tensile or shear), as characterizing parameters for various cell types or subcellular regions. The models range from those of purely elastic and homogeneous bodies, tension-based models whereby cells are considered as pre-stressed entities characterized by a homogenous membrane tension, to those of linear viscoelastic bodies, either homogeneous or not. When the cells are treated as viscoelastic bodies, the models employed vary according to the type of mechanical assay performed; in the case of transient-type experiments (stress relaxation, creep), the spring-dashpot-based representation and its variants is usually the model of choice, with Kelvin-type or Voight-type elements representing the contribution of cell components to the observed behavior. Whichever cell components these may be, remain a matter of data interpretation, usually in the form of hypotheses that may or not be confirmed by chemically intervention experiments of the type described above. In dynamic microrheological tests, the power-law model is predominantly applied, whereby the elastic component of the shear modulus (G') is expected to depend linearly on the logarithm of the frequency. The slope, denoted as β, is taken as a measure of the fluidity of the material, a value between 0 (linear elastic solid) and 1 (linear fluid). Typical β values for cells are 0.1–0.3 at low frequencies, increasing with frequency toward the value of 0.75 (Hoffman and Crocker, 2009).

FIGURE 10

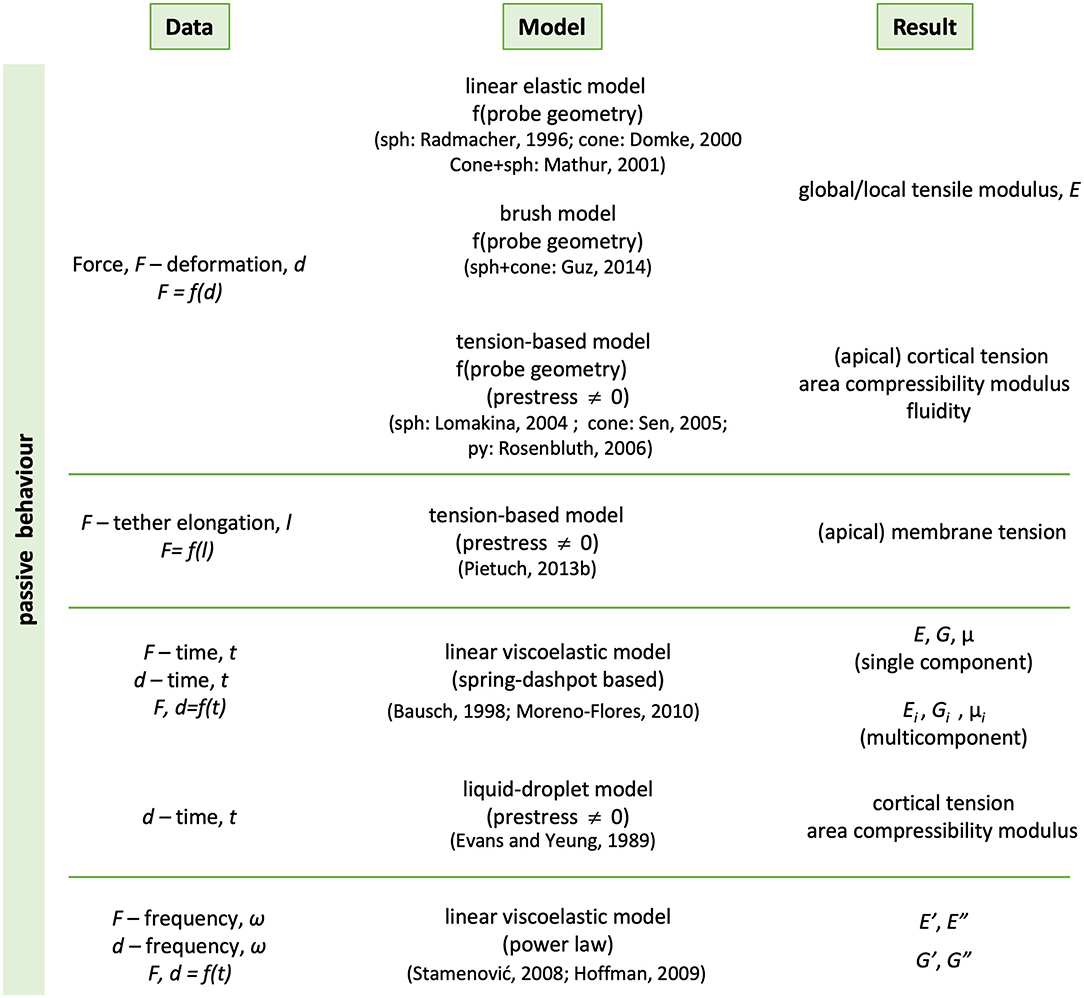
Figure 10. Summary of the phenomenological descriptions most commonly used to analyse experimental data of living cells. The methods are traditional of Contact Mechanics and used to characterize at least the passive behavior of materials. Representative references are included in brackets. sph, cone, py stand for spherical, conical and pyramidal indenter, respectively.

The significance of giving mechanical constants as intensive magnitudes is relative in the sense that they allow to easily compare and classify cell types based on their mechanical characteristics, as for any other kind of material. But, to which extent these values are a faithful and complete representation of the cellular mechanical behavior is a matter that, surprisingly, has not been settled or discussed extensively enough. And it should, for various reasons:

Calculation of moduli and compliance. The problem of the contact area. The fundamental relations are based on intrinsic magnitudes, stress and strains that, in order to be properly and accurately calculated, require the knowledge of the contact area between the cell and the surface, or surfaces, where forces and deformations are applied. A parameter that cannot be obtained experimentally via the techniques usually employed and previously described. Indeed, the geometry of the contact region is either unknown or poorly defined, and prone to vary among locations on the cell surface, if local probes are used in the mechanical tests. For the sake of simplification, the type of mechanical probes for the experiments are intently chosen to be highly symmetrical or geometrically simple, mainly flat planes or spheres. But still assumptions need to be made that concern the contact mechanical behavior of cells, including values for parameters such as the Poisson's ratio, with typical values ranging between 0.35 and 0.5 (Trickey et al., 2006; Liu et al., 2019). This is nothing other than paradoxical, as that is precisely what one wants to find out through the experiment. The procedure appears at times inconsistent, especially when contact areas or Young's moduli are calculated from indentation-type experiments under the assumption that cells behave elastically, while, at the same time, transient data, from force relaxation or creep compliance tests, are being analyzed with viscoelastic models (Gullekson et al., 2017; Liu et al., 2019). Another challenge related to the contact area is, particularly in the case of cells and in long experiments, its dependence with time. This aspect is most frequently overlooked, but its relevance can compromise the validity of the assumptions and the analysis approach as a whole.

The intentional search for simplicity. The use and abuse of Hertzian models. Many experimental studies have been done under conditions, usually small deformations (i.e., few nm) and/or forces (i.e., <1 nN) and during short periods of time (i.e., <1–2 s), whereby the instantaneous response of cells is registered and found to be similar to that of linearly elastic, even rigid and semi continuous bodies. As much as this approach simplifies the data treatment and interpretation, a question remains regarding the actual relevance and significance of the results and the calculated parameters. The treatment has become routine to an extent that it is now possible to obtain stiffness maps of whole cells automatically (Figure 11), without so much as a simple calculation of slopes, or of Young's moduli, mostly according to the Hertz model (Hertz, 1882). The Hertzian approach for a spherical indenter, and to a less extent the later modifications introduced by Sneddon and Bilodeau for axisymmetric (Sneddon, 1965) and pyramidal indenters (Bilodeau, 1992), have gained widespread acceptance and use in cellular studies, although their validity is far from evident in this experimental context. Indeed, the issue of applying Hertz-based models in cell mechanics has been discussed as early as 2002 (McElfresh et al., 2002): these models work on the assumption that the material is relatively hard, linearly elastic, and represented as a continuous, isotropic and homogeneous half-space. Besides, the material should have a flat and non-adhesive surface for test and analysis. But the vast experimental evidence on cells amassed in the last 30 years clearly indicates that, in rigor, none of these assumptions can faithfully approximate the nature and behavior of cells. More realistic contact mechanical models have been reported that consider the effect of surface (Ding et al., 2018), i.e., membrane tension (references in Figure 10) and glycocalyx (Sokolov et al., 2013; Guz et al., 2014) and that have been applied to cells. Despite their good performance, they have not gained the widespread popularity of the hertzian models. In the same line of thought and to the author's knowledge, classical models that consider the effect of adhesion, such as the Johnson-Kendall-Roberts (JKR) model (Johnson et al., 1971), the Derjaguin-Muller-Toporow (DMT) model (Derjaguin et al., 1975) or the generalization of Maugis and Pollock (1984), their solutions for different contact geometries and approaches for viscoelastic materials (Popov et al., 2019), as well as derived models (e.g., Hui et al., 2015; Long et al., 2016) have so far not been applied to cells.

FIGURE 11

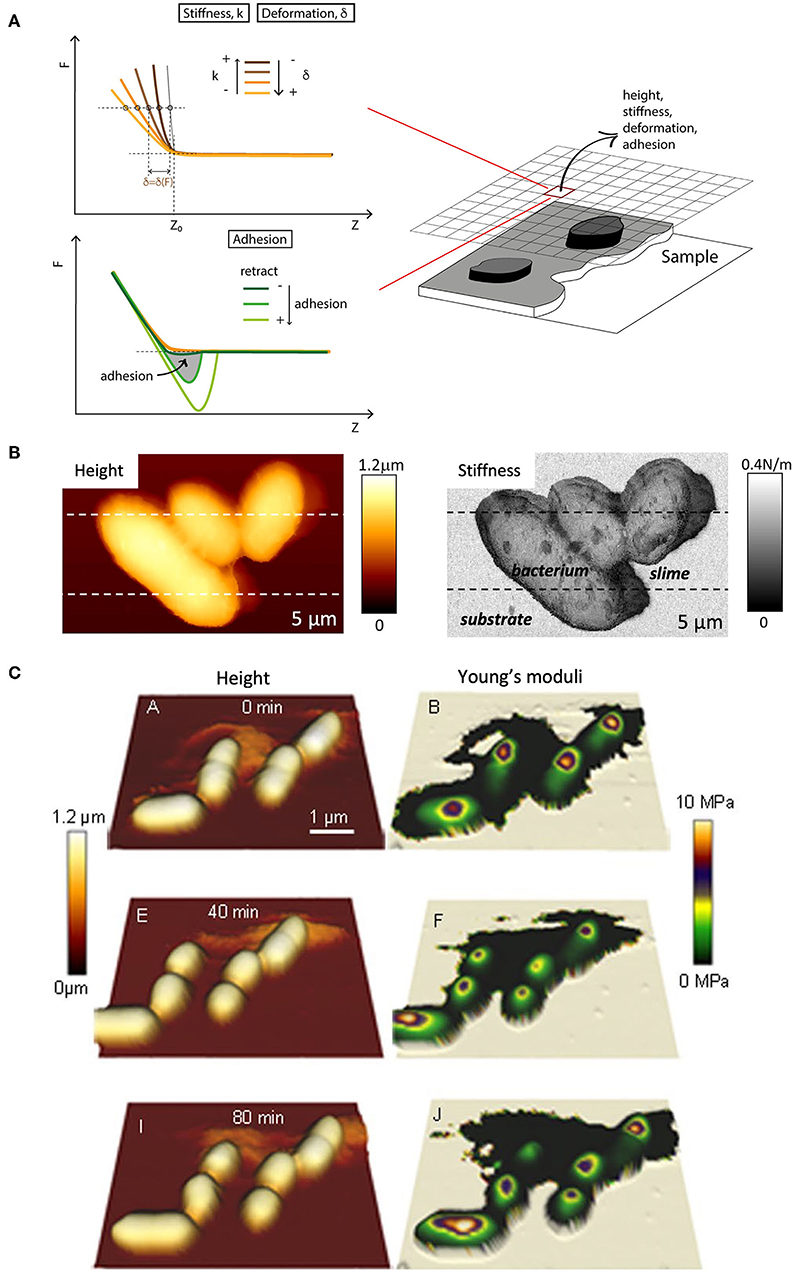
Figure 11. Multiparametric imaging on the fly. (A) Generation of multiplexed data from AFM force-displacement curves. Stiffness are computed as slopes from linear fits of parts of the loading curve contact region (traces in shides of orange). The fitting limits are either preset or readjusted a posteriori (graphics adapted from Moreno-Flores and Toca-Herrera, 2013, fig. 7.9). (B) Height and stiffness maps of motile bacterial leaving a trace of, presumably, slime of distinctive softness (figure reproduced from Dhahri et al., 2013 with permission²). (C) Time-lapse topological and mechanical maps of single bacteria (E. Coli) undergoing cell division. The Young moduli were calculated according to the Hertz model via a data analysis software of the AFM manufacturer (figure reproduced from Bhat et al., 2018 with permission²).

Passive vs. active responses. Influence of structure and physiology. Cells are active and living materials, and in this sense, they constitute a special kind of smart matter. Irrespective of the categorization in elastic or viscoelastic materials, the mechanism of the response may be active or passive, a mixture of both and non-linear. In this sense, the experiments have not been conclusive enough, and the methods for data analysis routinely employed do not allow making distinctions of such kind. Although chemical and genetic interventions can throw some light on the influence of certain structural elements and molecular roles, the issue lacks sufficient experimental evidence. Instead, it remains a subject of interpretation and hence, debatable.

Cell heterogeneity. Influence of the immediate environment and time. As mentioned before, a contact-based technique such as AFM can map the viscoelastic properties of whole cells by systematically and sequentially probing their local response to an applied force or deformation at specific locations across the cell body. Cells are not homogeneous materials nor do they have a defined shape, and in this respect, the maps reveal certain spatial variability of the mechanical behavior. This variability may be attributed to multiple factors, such as local variations in the morphology and structure, variations in cell thickness (i.e., cell height) and cell adherence. But neither are cells inert, and their dynamics and interactions with their immediate surroundings can play a significant role in the observed behavioral diversity. In this sense, the underlying substrate, its nature and mechanics, as well as the presence of neighboring cells (cell confluency) are relevant aspects that should be considered. In particular, whether these factors are intrinsic or extrinsic to the cellular behavior are issues worth debating, as only in the latter case, and depending on the technique employed, may constitute an environmental factor that should be at least considered in the analysis (Managuli and Roy, 2017; Ding et al., 2018), rather than corrected. In the case of tissue-forming adherent cells, such as epithelial cells, for which the contact with substrates and other cells is essential in order to properly develop function, both cells and substrate are constitutive of the system and their role an integral part of the cellular response. Contrarily, suspension cells, such as blood cells, reproductive cells or certain types of bacteria, the existence of which does not depend on contact with substrates or with other cells, those factors may not be part of the system but can influence the response in one way or another. It remains to consider if this response has any biological significance, and in this sense, the cellular response should be correctly identified and interpreted.

Cells as in vitro samples. Reproducibility of cell behavior. Cells are no ordinary materials, and this also extends to the ways in which the cells samples are produced, which should also be considered. Animal cells for in vitro studies can be purchased as batches of cell lines, or obtained from primary cultures. The former are “modified versions” of naturally-occurring cells, which can be maintained at the laboratory, in principle indefinitely (Freshney, 2005). This is possible due to the capability of these cells to continuously grow and proliferate, if cultured with the appropriate growing medium and in suitable amounts. The cell lines, called immortal for that reason, share characteristics with and originate from tumors. Cell lines are maintained in-vitro via a procedure named cell passaging, in which the cells, when reaching a certain limiting confluence, are detached from the old substrate, dispersed, diluted and transferred to a new substrate, in a fresh medium. Cell passaging is a routine practice, but relative aggressive to cells, which in practice limits the number of times it can be performed without irreversibly and uncontrollably altering the integrity of cultured cells. The frequency at which cells should be passaged, as well as maximum number of cell passages vary with each cell line, and when applicable, are recommendations determined by biological practice and integrated in the experimental protocols of cell culture. Though expected to bring changes, the variability in biological behavior and cell function, also phenotype and genotype, between cells of the same type but from different passages is not well determined. This includes the physical behavior. Contrarily, primary cells are directly extracted from living tissue, tumor or not, and have limited capacity to survive. They are much more sensitive to passaging, and hence do not stand in-vitro maintenance. Also in this case, primary cells may display different behavior depending on the tissue, the subject they have been extracted from, as well as the procedure of preparation and maintenance of the integrity of the samples prior to experiment. Taking the above into account, it is reasonable to ask the extent to which the parameters experimentally obtained are actually influenced by the preparation method and in-culture pre-treatment.

Different experimental methodologies and models of analysis. As suggested before, different technologies have distinctive experimental sensitivities and hence likely to provide divergent perspectives of the cellular mechanical behavior. Therefore, it is reasonable to expect that the respective results may not be necessarily coincident or comparable in quantitative terms. Besides, the mechanical parameters are likely to differ if disparate methods of data analysis and interpretation are chosen for the same kind of experimental data.

Theory and Simulation

Theoretical models. Just as with notions of the theory of linear (visco)elasticity to obtain mechanical properties of cells, single cell biophysics has also borrowed pre-existent theories and models of material science to explain and understand the mechanical behavior (see the summary of Figure 12). Among the latter, rigid scaffolds and various types of soft matter such as polymer-based gels, soft glassy (foams and emulsions) or biphasic (sol-gel) materials have been considered as references with which to compare the behavioral features of certain cell components, especially the cytoskeleton. Indeed, the theories/models employed so far have been able to explain particular aspects of the cellular behavior, but none of them has stood out as a “theory for everything” in cell mechanics; a model that can account for the behavior of cells in all its experimental manifestations and complexity.

FIGURE 12

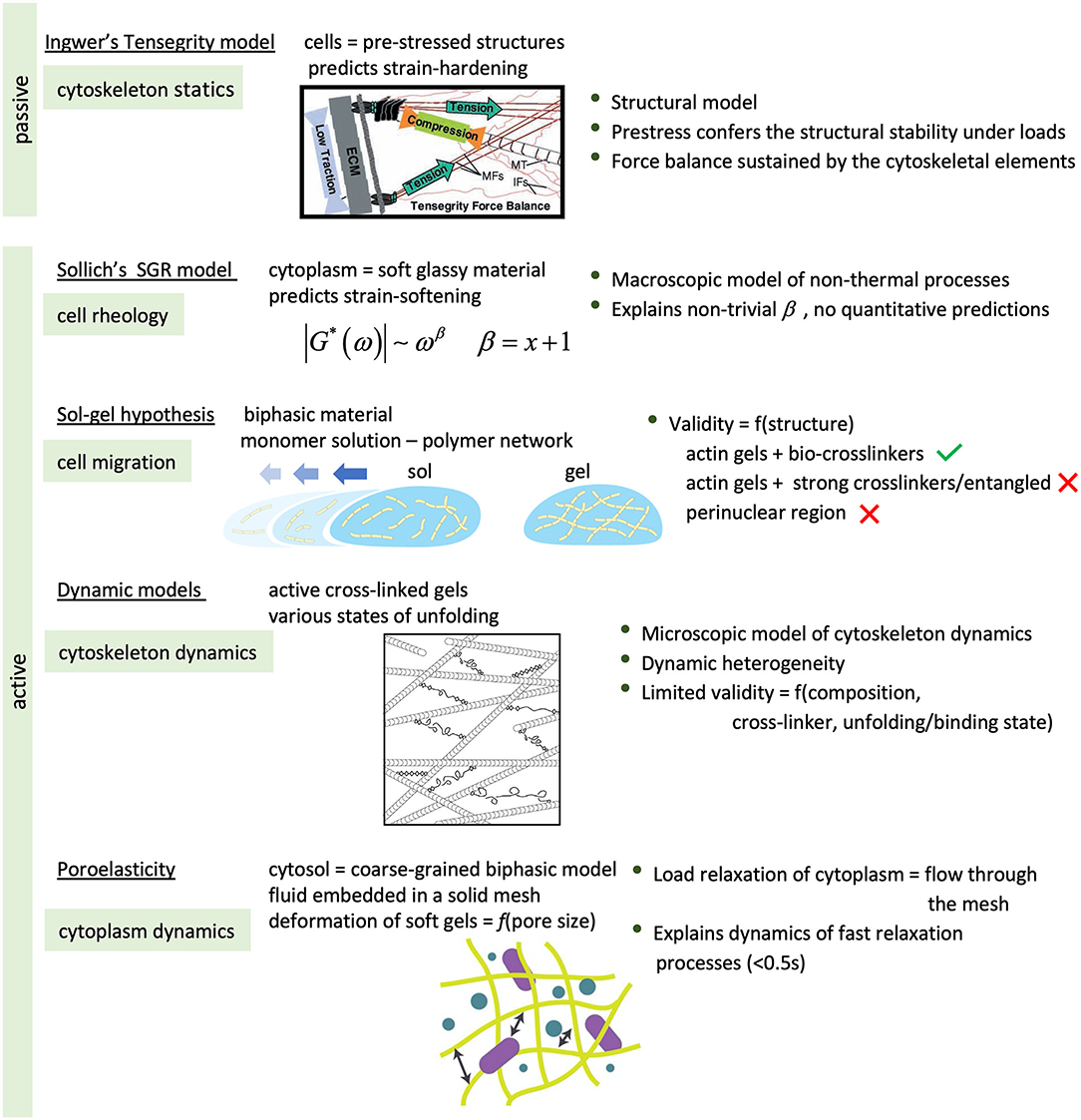
Figure 12. Summary of some of the theories to understand the behavior of living cells, in particular cell components, under mechanical stress or deformation. [Artworks of tensegrity, dynamic models and poroelasticity reproduced from (Ingber, 2003), (Hoffman et al., 2007), and (Hasse and Pelling, 2015), respectively, with permission].

Ingber's theory of Tensegrity (Ingber, 1993) explains the static mechanics of structural scaffolds. In this sense the model accounts for the passive behavior of cells, as long as these are viewed as pre-stressed structures with capacity to maintain their mechanical and structural stability under loads. In the model, the cytoskeletal network is the resilient structure that sustains the mechanical forces and preserves the mechanical equilibrium, with the actin microfilaments and microtubules the elements supporting tensions and compressions, respectively. The disruption of either of these elements disturbs the force balance between the cells and their surroundings, increasing tractions on the substrate (MT) or in the cell (MF). The theory provides a macroscopic view of the passive behavior of biopolymer fibers and cytoskeletal networks and in this sense, it can explain strain-induced stiffening exhibited by some type of cells. But it fails to explain their dynamics and hence the active behavior to compensate the mechanical unbalance, the strain-softening behavior of other cells, also from a microscopic point of view (Hoffman and Crocker, 2009; Hasse and Pelling, 2015).

The mechano-dynamic aspects of cellular behavior have been usually identified with those of the cytoplasm. From a macroscopic point of view, the interior of cells can be considered as made of a (homogeneous) material capable of dynamically responding to transient stimuli. In this case, cells have been found to behave as soft glassy materials when subjected to periodic shear^4, but also relax under steady loads as though they were poroelastic (Moeendarbary et al., 2013). In each case, the mechanical response could be described by a power-law behavior in frequency and time, in qualitative agreement with the predictions of Sollich, or of the poroelasticity theory (Biot, 1941), respectively. Indeed, the SGR theory of Solich (1998) predicts a power-law-like behavior, whereby the availability of non-thermal⁵ free energy, rather than temperature, is the determining factor that elicits the dynamic response. This is defined by the parameter x, with values lower than 1 characteristic of a glassy state, of frozen dynamics, and values between 1 and 2 defining the dynamic range. x is related to the power-law exponent, β, by a simple relation (β = x+1). In this sense, the SGR theory can be useful in explaining the mechanical behavior of cells driven by ATP-dependent processes. Although able to explain some relevant experimental observations such as strain-induced softening or non-trivial rheological behavior, the quantitative predictions do not seem to square with the observations (Hoffman and Crocker, 2009). More successful in its quantitative predictions has been the poroelastic model (Moeendarbary et al., 2013). In it, the cytoplasm is coarsely-grained modeled as a bicomponent material; an elastic, porous mesh embedded in an aqueous fluid. The dynamics is determined by the movement of liquid through the mesh pores in response to an applied load, resulting in characteristic times defined by the pore size, the elasticity of the mesh, and the properties of the fluid.

Neither of these models take into consideration the microscopic dimension, and cannot provide a mechanistic view that integrates, at least, the most relevant molecular components. Consequently, they cannot fully explain the dynamic heterogeneity observed in single cells, as well as among cells and cell types. The microscopic models such as the sol-gel hypothesis, the glassy worm like chain model (GWLC) or active gels, consider the interior of cells as dynamic networks of protein fibers, interconnected or not, in a fluid medium. In each respective model, the dynamic response is viewed as a consequence of reversible molecular processes of fibrillar assembly and disassembly, of hindered fibrillar motion and, in the case of active gels, either of cross-link formation/disruption, or of the activity of motor proteins/binding proteins (Lau et al., 2003; Mizuno et al., 2007). However, these models can only explain a relatively narrow range of non-universal cellular behavior, strain-softening (Kroy, 2008) or strain-stiffening (Mizuno et al., 2007), provide a partial view of the structural dynamics and heterogeneity of the cytoskeletal network, and they are structure-specific⁶, which limits their validity. Besides, the sol-gel hypothesis cannot provide a rational explanation of non-thermally driven dynamics and fails to describe cell crawling (Hoffman and Crocker, 2009; Hasse and Pelling, 2015). Also, the GWLC model and the model of an active biopolymer gel differ notably in their fundamental assumptions despite their structural similarity, with one attributing the dynamic molecular response to equilibrium fluctuations and the other to non-equilibrium fluctuations. And in all cases, the influence of non-cytoskeletal and non-cytoplasmic constituents in the mechanical response is either overlooked or not considered. This might result in an oversimplification, taking into account that organelles such as the nucleus accounts for 10–20% of the total cell volume (e.g., 16% in NIH/3T3 fibroblasts), exhibit distinctive mechanical characteristics of singular physiological relevance and responsiveness (Guilak et al., 2000; Lherbette et al., 2017; Stephens et al., 2017), are actively involved in mechanotransduction processes (Burridge et al., 2019) and mechanically coupled with other structural elements, as suggested by the work of Beicker et al. (2018).

Simulations. Computational approaches such as the Finite Element Method (FEM) have been regularly employed to reproduce the response (i.e., force and deformations) of materials to mechanical stimuli. Basically, these materials are modeled as/discretized as bi- or tridimensional meshed objects with a specific geometry and material properties, and a well-defined set of boundary conditions or assumptions. In the context of cell mechanics, this type of simulations has provided a “proof of model,” confirming or refuting the working hypotheses of the wet-bench (experimental) studies. Cells have been represented as axisymmetric constructs (Unnikrishnan et al., 2007), spheres or ellipsoids (Liu et al., 2019), with or without structural components (Bursa and Fuis, 2009). The former are the structural models, whereby some of the cell constituents, namely the membrane cortex, cytoplasm and nucleus, are modeled as homogeneous continua or discrete elements. The non-structural models were relatively simple and the first to be developed; these represented the cell as a homogeneous, isotropic continuum (Charras and Horton, 2002b). Both the structural and non-structural models have been combined in the so-called bendo-tensegrity model (Bansod et al., 2018). The model combines continuous and discrete elements to simulate the nucleus and cytoplasm on the one hand, and the cytoskeletal fibrillar network (actin filaments, microtubules and intermediate filaments) on the other hand. In all the previous cases, calculations have been made under the assumption that the mechanical characteristics of the object or of its critical components are known, and they focus on simulating the structural response based on an assumed architecture. Something that, in the case of cells and in view of the above and the observed behavioral variability, is still a matter of discussion and speculation, as is the identification and contribution of those critical components. Other assumptions include the nature of the contact region, the interaction between simulated components, and the Poisson's ratio. In this sense, simulations rely heavily on experimental background data, and mechanical parameters obtained through experiment. Consequently, the simulation results may be as reliable or questionable as the experimental data, and hence subjected to a similar kind of discussion.

Discussion

Single cell mechanics has undergone a considerable and significant development, that continues today. The non-stopping effort and intensive research have led to numerous and significant findings as regards the importance of mechanics in shaping cell type and behavior. Although with certain lack of consensus in the quantitative details and important questions still open, it is generally agreed that, from the materials point of view, cells are heterogeneously complex, viscoelastic materials, that exhibit linear and non-linear behavior depending on the environmental conditions. Indeed, the mechanical behavior of cells highly depends, among other factors:

• on the time during which the mechanical stimulus is applied, and on the speed with which this is applied

• on the integrity and dynamics of interconnected structural elements

• on cell type, topology and density (confluency).

Likewise, the cellular elasticity and adherence have proved mechanical signatures of cell type, tumor cell malignancy, and cell-cell communication, that are mainly determined by the cytoskeletal network, in particular the microfilaments, or F-actin. Also, the substrate stiffness and the mechanical state of the cell can affect its shape, pre-stress, adhesion on substrates, differentiation, and motility.

The body of work supporting the statements above is considerable. If anything, it evinces the high complexity and variability of cellular behavior, including the interaction with its surroundings, and the interconnection between external and internal, structural and non-structural factors. It has enabled to stablish statistical correlations between cellular structure, behavior and function, but without hardly providing a mechanistic view or proof of mechanisms that can account for all the observations as yet. How could one tackle the outstanding challenges?

Time matters in cell mechanics. In principle, many of the experimental methodologies available today are capable of capturing events occurring in different locations inside and outside the cell, as well as in the course of time (Figure 2). Given that cells are highly dynamic systems, this kind of experiments can be paramount in finding causal correlations out of the time sequence of physical, chemical and physiological events that take place inside the cell, and in identifying the agents (molecules, organelles and structures) actually involved. This type of information may prove valuable in discovering the mechanisms by which cells sense, generate, transduce and transmit mechanical cues. So far, the efforts have been mainly focussed in finding statistical correlations between cell mechanical parameters and the functionality of the cell cytoskeleton, particularly the actin-actomyosin network. In most of these works, time is not considered as experimental variable, and hence the degree of interconnection between the different behaviors is missing in those studies.

Time may also be behind the question of how important the cytoskeletal microtubules are in shaping the mechanical response of cells. The pivotal work of Rotsch and Radmacher (2000) set an influential precedent in experimentally showing that microtubules are not particularly relevant in defining cell elasticity of fibroblasts, as much as the microfilament network is, and quite a number of later reports have supported this idea. The conclusions are mainly based on loading tests under conditions—low compressive loads (of the order of 10² pN), short times (barely tens of seconds to seconds)—where cells may mostly reveal an elastic response of structural nature, mainly determined by the actin cortex. A discussion in terms of dynamics and the interconnectivity of the microfilament and microtubular networks are in most cases, if not in all, missing. And yet, there is sufficient evidence of the importance that the architecture and dynamics of the microtubular network has in cell division⁷, polarization and locomotion (Alberts et al., 2008), in sensing sound-induced vibrations (Schwander et al., 2010), as well as in sustaining high compressive loads (Brangwynne et al., 2006), in determining the response to mechanical strains (Charras and Horton, 2002a), or in maintaining local stiffness (Pelling et al., 2007). Likewise, there is an established importance that intermediate filaments have in shaping mechanics of cells and tissues (Broussard et al., 2020). It is thus reasonable to suppose that, as the works described in the previous section, the mechanical role and dynamics of microtubules as well as intermediate filaments manifest at larger mechanical and spatio-temporal scales that have been either scarcely or not thoroughly explored on the experimental ground, nor have they been studied in mutual interconnection, or in relation to other molecular complexes and cell organelles.

Is Cell Plasticity Actually Plasticity? The Passive, Active or a Physiological Contributions

Cells are living entities, and unlike inanimate matter, have an added level of behavioral complexity. The structural, dynamical and physiological nature of the cell mechanical response is ever-present and intertwined in yet unknown ways. Although experiments can be devised in such a way that cell responsiveness is predominantly inert and hence determined by structure, any conclusions that may be drawn from these studies may have very limited, if not questionable, validity.

It is therefore essential to include the dynamical and physiological aspects of cell behavior in the study of cell mechanics, if the purpose is to gain a solid and comprehensive knowledge. In this respect, some fundamental questions arise: to what extent is the mechanical behavior of cells a consequence of dynamics or physiology? How all these contributions interconnect to one another and deployed? Is it possible to identify them experimentally? All this boils down to prove the following hypothesis: that the physiological processes have their own mechanical fingerprint, and this is dependent on the timing and duration of each process. As far as cytoskeleton remodeling is concerned, it has been evinced that stem cells are particularly sensitive to shear oscillations of low frequency (i.e., 0.1–0.5 Hz) at the basal membrane, modulating their adherence and triggering their differentiation accordingly (Kang et al., 2017); oscillations of slightly higher frequency, i.e., 2 Hz, have not such effect, which suggests a possible frequency window for the manifestation of such physiological response. For the particular case of cell mitotic division, the proof of concept of the hypothesis mentioned above, was early reported by Matzke et al. (2001), and only much later was it further explored by Stewart et al. (2011) and Cattin et al. (2015). At the level of molecules, the outstanding work of Guo et al. (2014) and particularly their original experimental approach, deserves special mention. The authors smartly leveraged the measuring potential of optical traps and tweezers and combined active and passive microrheology, in order to obtain force spectra out of spatial fluctuations of intracellular particle tracers. In this way, they were capable of identifying the active forces caused by motor proteins in the cytoskeleton and detect differences in the cytoplasm activity between normal and cancer cells of the same type. From this perspective, the work sets a remarkable precedent and evinces once more the great benefit of combining experimental capabilities and analytical resources in gaining fundamental knowledge of the active mechanics of cells. In consequence, it is to be expected that the integration of multiple techniques for synchronous detection, measurement and data analysis holds great potential in providing qualitative and quantitative evidence of interrelated processes, as well as in identifying mechanical signatures and characteristic time scales.

Cell confluency: the role of cell-cell interactions in the mechanical response. Cells that form tissues need to establish connections with other cells in order to develop properly. Therefore, it is rational to expect that the mechanical behavior of these cells be different if studied in isolation or in the presence of other neighboring cells. In this respect, the cell density can be an important parameter to consider in the study of cell mechanics (Brückner and Janshoff, 2018; Broussard et al., 2020). In the context of two-dimensional in-vitro cell culture models, cell confluency, or the percentage of substrate area covered by a monolayer of cells, has proven to be an influential factor in determining the mechanics of healthy epithelial cells, as compared to invasive tumor cells of the same type (Schierbaum et al., 2017), in enhancing membrane tension (Pietuch et al., 2013a,b) or in modifying the cell elasticity, although with quite different results in the latter case (Efremov et al., 2013; Schierbaum et al., 2017). In the context of 3D in vitro cell culture models, recent attempts have been reported to characterize the elasticity and cell-cell interfacial tensions of multicellular spheroids by cavitation rheology (Blumlein et al., 2017), as well as the overall viscoelasticity of epithelial cysts (Shen et al., 2017) and elasticity of multicellular spheres of mesenchymal stromal cells by AFM (Tietze et al., 2019). Both latter works provide evidence of characteristic relaxation dynamics and indentation mechanics that differ substantially to those of single cells. It is thus reasonable to expect “transitions” in the mechanical behavior as cell proliferate and develop into mature spheroids (Moreno-Flores and Küpcü, 2015).

These findings are in line with the underlying idea that the mechanical signatures of cells evolve as they network and eventually develop into tissues and organelles, or in case of cancer cells, as they develop tumors with a certain invasiveness. Stablishing the connection between mechanics and cell development at the fundamental level (Hallou and Brunet, 2020), can thus be critical in gaining a deeper understanding of morphogenesis (Keller, 2012), as well as tumor development and metastasis (Kumar and Weaver, 2009; Wirtz et al., 2011). In this regard, the clinical application of the cell mechanotype and of micromechanical techniques in cancer detection does no longer seem to be a far-fetched possibility (Nautiyal et al., 2018; Stylianou et al., 2018).

The 3D view. Cell anisotropy is a property that varies according to cell type and may evolve in the course of time, i.e., cell life cycle and physiological activity. The basal-apical polarity of epithelial cells, and the dendrite-to-axon transmission of electrical signals in neurons are two classical examples. Likewise, cells in vivo are subjected to, and exert, a characteristic set of mechanical cues that determine their development, function and shape in a three-dimensional space. The in-vivo scenario heavily contrasts with most of the experimental studies in cell mechanics, whereby the application of stimuli and the observation of the response are limited to a single direction or plane. Hence, technologies enabling 3D visualization and mapping of micromechanical interactions between cells and their environment in a dynamic manner would be much needed. These in combination with 3D scaffolds of controlled structure—pore size, fiber length and diameter—dynamic behavior and degradability, capable of active sensing and responsiveness, fluidization and remodeling (Kennedy et al., 2017; Lemma et al., 2019), may prove promising in defining the new state of the art in the methodology for cell mechanobiology.

Single cell tribology. Friction can cause or aggravate tissue damage and inflammation, induce bone, tooth wear and blister formation, and lead to commonplace pathologies such as osteoarthritis. Therefore, a considerable effort has been put in place to understand tissue resilience and degradation, as well as to investigate restorative treatments or, alternatively and whenever applicable, replacement materials for implants (Gebeshuber et al., 2008; Correa and Lietman, 2017; Pina et al., 2018). A recurrent model material in the characterization and engineering studies has been the articular cartilage, for which a wealth of reported research exists (Correa and Lietman, 2017; Pina et al., 2018). However, much is still unknown at the level of single cells, in particular about the relation between cell rheology and cell tribology and the impact that friction may have on the mechanical and physiological behavior. A significant contribution in that direction suggests a relation between cell deformability and surface friction, and that both characteristics may determine the metastatic potential of cancer cells (Byun et al., 2013). Just recently, friction-induced mechanisms for cellular inflammation and cellular death have been proposed for corneal epithelial cells and chondrocytes from multicellular experiments (Bonnevie et al., 2018; Pitenis et al., 2018), and, in view of the relevance of the findings, this type of investigations are expected to gain momentum. In this respect, active microrheological techniques able to apply and detect shear stress and strains inside and outside single cells, in combination with microfluidic approaches can make a significant difference.

Conclusions and Outlook

Despite the impressive record of research work, single cell mechanics has still a long way to go in reaching consensus and thorough understanding. There is great need in putting the reported findings in relation to one another, and from this perspective, revise the vast knowledge amassed so far. On the other hand, tackling the questions still open in the field requires integrative approaches and methodologies on a par with the still unfathomed cell complexity. The search for a complete and universal mechanistic view of cell mechanics remains to be a formidable task and an outstanding challenge that absolutely depends on extensive crossdisciplinarity to be fruitful. A roadmap toward such aim should consider the variable time as key experimental and theoretical parameter, the development of rigorous gold standards for the routine mechanical characterization of cells, and the conception of dynamic models that integrate the biological, physical and chemical knowledge, as well as resources in computation and engineering. Synchronous or combined multi-instrumental and multidimensional methods of cell manipulation and detection emerge as key experimental approaches to ascertain and identify the plausible active and physiological contributions to the overall cell behavior, the anisotropic nature, the relevant structural and functional interconnections, the role of friction, as well as the implications to cell communication and development.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Footnotes

1. ^Granted by the terms and conditions of the Creative Commons CC BY License (https://creativecommons.org/licenses/).

2. ^According to the terms of Creative Commons Attribution 4.0 International License: http://creativecommons.org/licenses/by/4.0/.

3. ^Although the term indentation could be in this case misleading, as this may not be what it actually occur when cells are subjected to normal loads, and especially if these forces are non-local.

4. ^An enlightening summary of experimental and theoretical works supporting the statement can be found in Hwang et al. (2016) and Shi et al. (2019).

5. ^Meaning chemical and ATP-dependent.

6. ^The sol-gel hypothesis relies on the dynamics of the fibre assembly/disassembly to explain a particular type of active response of cells (cell migration, cell deformation), whereas the behaviour of cross-linked gels is determined by the polymer composition, the nature of the cross-linker or the active molecule.

7. ^Though not explicitly shown (Matzke et al., 2001) hints at the relevance that microtubules may well have in shaping cell shape and stiffness prior cell division by the following brief remark: “Adding of 10 μM nocodazole blocked the increases in both height and stiffness that occur before furrowing and cell division (data not shown)”. The comment appears even though the discussion uniquely revolves about actin microfilaments being key in the process. Nocodazole does not disrupt microfilaments so much as microtubules (see section “Experimental Approaches and Protocols”), and yet has such a distinctive effect that nonetheless is left out from the discussion.

References

A-Hassan, E., Heinz, W. F., Antonik, M. D., D'Costa, N. P., Nageswaran, S., Schoenenberger, C.-A., et al. (1998). Relative microelasticity mapping of living cells by atomic force microscopy. Biophys. J. 74, 1564–1578. doi: 10.1016/S0006-3495(98)77868-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Alberts, B., Johnson, A., Lewis, J., Raff, M., Roberts, K., and Walter, P. (2008). Molecular Biology of the Cell, 5th Edn. New York, NY: Garland Science.

Google Scholar

Alcaraz, J., Buscemi, L., Grabulosa, M., Trepat, X, Fabry, B., Farré, R., et al. (2003). Microrheology of human lung epihelial cells measured by atomic force microscopy. Biophys. J. 84, 2071–2079. doi: 10.1016/S0006-3495(03)75014-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Bansod, Y. D., Matsumoto, T., Nagayama, K., and Bursa, J. (2018). A finite element bendo-tensegrity model of eukaryotic cell. J. Biomech. Eng. 140:101001. doi: 10.1115/1.4040246

PubMed Abstract | CrossRef Full Text | Google Scholar

Basoli, F., Giannitelli, S. M., Gori, M., Mozetic, P., Bonfanti, A., Trombetta, M., et al. (2018). Biomechanical characterization at the cell scale: present and prospects. Front. Physiol. 9:1449. doi: 10.3389/fphys.2018.01449

PubMed Abstract | CrossRef Full Text | Google Scholar

Bausch, A. R., Ziemann, F., Boulbitch, A. A., Jacobson, K., and Sackmann, E. (1998). Local measurements of viscoelastic parameters of adherent cell surfaces by magnetic bead microrheometry. Biophys. J. 75, 2038–2049. doi: 10.1016/S0006-3495(98)77646-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Beicker, K., O'Brien, E. T. III., Falvo, M. R., and Superfine, R. (2018). Vertical light sheet enhanced side-view imaging for AFM cell mechanics studies. Sci. Rep. 8:1504. doi: 10.1038/s41598-018-19791-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Benoit, M., Gabriel, D., Gerisch, G., and Gaub, H. E. (2000). Discrete interactions in cell adhesion measured by single-molecule force spectroscopy. Nat. Cell. Biol. 2, 313–317. doi: 10.1038/35014000

PubMed Abstract | CrossRef Full Text | Google Scholar

Bhat, S. V., Sultana, T., Körnig, A., McGrath, S., Shahina, Z., and Dahms, T. E. S. (2018). Correlative atomic force microscopy quantitative imaging-laser scanning confocal microscopy quantifies the impact of stressors on live cells in real-time. Sci. Reports 8:8305. doi: 10.1038/s41598-018-26433-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Bilodeau, G. G. (1992). Regular pyramid punch problem. J. Appl. Mech. 59, 519–523. doi: 10.1115/1.2893754

CrossRef Full Text | Google Scholar

Biot, M. A. (1941). General theory of three-dimensional consolidation. J. Appl. Phys. 12, 155–164. doi: 10.1063/1.1712886

CrossRef Full Text | Google Scholar

Blumlein, A., Williams, N., and McManus, J. J. (2017). The mechanical properties of individual cell spheroids. Sci. Rep. 7:7346. doi: 10.1038/s41598-017-07813-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Bonnevie, E. D., Delco, M. L., Bartell, L. R., Jasty, N., Cohen, I., Fortier, L. A., et al. (2018). Microscale frictional strains determine chondrocyte fate in loaded cartilage. J. Biomech. 74, 72–78. doi: 10.1016/j.jbiomech.2018.04.020

PubMed Abstract | CrossRef Full Text | Google Scholar

Bouissou, A., Proag, A., Bourg, N., Pingris, K., Cabriel, C., Balor, S., et al. (2017). Podosome force generation machinery: a local balance between protrusion at the core and traction at the ring. ACS Nano 11, 4028–4040. doi: 10.1021/acsnano.7b00622

PubMed Abstract | CrossRef Full Text | Google Scholar

Brangwynne, C. P., MacKintosh, F. C., Kumar, S., Geisse, N. A., Talbot, J., Mahadevan, L., et al. (2006). Microtubules can bear enhanced compressive loads in living cells because of lateral reinforcement. J. Cell Biol. 173, 733–741. doi: 10.1083/jcb.200601060

PubMed Abstract | CrossRef Full Text | Google Scholar

Broussard, J. A., Jaiganesh, A., Zarhoob, H., Conway, D. E., Dunn, A. R., Espinosa, H. D., et al. (2020). Scaling up single-cell mechanics to multicellular tissues – the role of the intermediate filament-desmosome network. J. Cell Sci. 133:jcs228031. doi: 10.1242/jcs.228031

PubMed Abstract | CrossRef Full Text | Google Scholar

Brückner, B. R., and Janshoff, A. (2018). Importance of integrity of cell-cell junctions for the mechanics of confluent MDCK II cells. Sci. Rep. 8:14117. doi: 10.1038/s41598-018-32421-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Burridge, K., Monaghan-Benson, E., and Graham, D. M. (2019). Mechanotransduction: from the cell surface to the nucleus via RhoA. Phil. Trans. R. Soc. B 374:0229. doi: 10.1098/rstb.2018.0229

PubMed Abstract | CrossRef Full Text | Google Scholar

Bursa, J., and Fuis, V. (2009). “Finite element simulation of mechanical tests of individual cells,” in IFMBE Proceedings WC, Vol 25, eds O. Dössel and W. C. Schlegel (Springer Verlag), 16–19.

PubMed Abstract | Google Scholar

Byun, S., Son, S., Amodei, D., Cermak, N., Shaw, J., Kang, J. H., et al. (2013). Characterizing deformability and surface friction of cancer cells. Proc. Natl. Acad. Sci. U.S.A. 110, 7580–7585. doi: 10.1073/pnas.1218806110

PubMed Abstract | CrossRef Full Text | Google Scholar

Cartagena-Rivera, A. X., Van Itallie, C. M., Anderson, J. M., and Chadwick, R. S. (2017). Apical surface supracellular mechanical properties in polarized epithelium using noninvasive acoustic force spectroscopy. Nature Comm. 8:1030. doi: 10.1038/s41467-017-01145-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Cattin, C. J., Düggelin, M., Martinez-Martin, D., Gerber, C., Müller, D. J., and Stewart, M. P. (2015). Mechanical control of mitotic progression in single animal cells. Proc. Natl. Acad. Sci. U.S.A. 112, 11258–11263. doi: 10.1073/pnas.1502029112

PubMed Abstract | CrossRef Full Text | Google Scholar

Charras, G. T., and Horton, M. A. (2002a). Single cell mechanotransduction and its modulation analyzed by atomic force microscope indentation. Biophys. J. 82, 2970–2981. doi: 10.1016/S0006-3495(02)75638-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Charras, G. T., and Horton, M. A. (2002b). Determination of cellular strains by combined atomic force microscopy and finite element modeling. Biophys. J. 83, 858–879. doi: 10.1016/s0006-3495(02)75214-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Correa, D., and Lietman, S. A. (2017). Articular cartilage repair: current needs, methods and research directions. Sem. Cell Develop. Biol. 62, 67–77. doi: 10.1016/j.semcdb.2016.07.013

PubMed Abstract | CrossRef Full Text | Google Scholar

Curtis, A. S. G. (1964). The mechanism of adhesion of cells to glass: a study by interference reflection microscopy. J. Cell Biol. 20, 199–215. doi: 10.1083/jcb.20.2.199

PubMed Abstract | CrossRef Full Text | Google Scholar

Darling, E. M., Zauscher, S., and Guilak, F. (2006). Viscoelastic properties of zonal articular chondrocytes measured by atomic force microscopy. Osteoarthritis Cartilage 14, 571–579. doi: 10.1016/j.joca.2005.12.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Derjaguin, B. V., Muller, V. M., and Toporov, Y. P. (1975). Effect of contact deformations on the adhesion of particles. J. Colloid Interface Sci. 53, 314–325. doi: 10.1016/0021-9797(75)90018-1

CrossRef Full Text | Google Scholar

Dhahri, S., Ramonda, M., and Marlière, C. (2013). In-situ determination of the mechanical properties of gliding or non-motile bacteria by atomic force microscopy under physiological conditions without immobilization. PLoS ONE 8:e61663. doi: 10.1371/journal.pone.0061663

PubMed Abstract | CrossRef Full Text | Google Scholar

Ding, Y., Wang, J., Xu, G.-K., and Wang, G.-F. (2018). Are elastic moduli of biological cells depth dependent or not? Another explanation using a contact mechanics model with surface tension. Soft Matter. 14, 7534–7541. doi: 10.1039/C8SM01216D

CrossRef Full Text | Google Scholar

Domke, J., Dannöhl, S., Parak, W. J., Müller, O., Aicher, W. K., and Radmacher, M. (2000). Substrate dependent differences in morphology and elasticity of living osteoblasts investigated by atomic force microscopy. Coll. Int. B Bioint. 19, 367–379. doi: 10.1016/S0927-7765(00)00145-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Dubreuil, F., Elsner, N., and Fery, A. (2003). Elastic properties of polyelectrolyte capsules studied by atomic-force microscopy and RICM. Eur. Phys. J. E 12, 215–221. doi: 10.1140/epje/i2003-10056-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Dufrene, Y. D., and Persat, A. (2020). Mechanomicrobiology: how bacteria sense and respond to forces. Nat. Rev. Microbiol. 18, 227–240. doi: 10.1038/s41579-019-0314-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Efremov, Y. M., Dokrunova, A. A., Bagrov, D. V., Kudryashova, K. S., Sokolova, O. S., and Shaitan, K. V. (2013). The effects of confluency on cell mechanical properties. J. Biomech. 46, 1081–1087. doi: 10.1016/j.jbiomech.2013.01.022

PubMed Abstract | CrossRef Full Text | Google Scholar

Evans, E., and Yeung, A. (1989). Apparent viscosity and cortical tension of blood granulocytes determined by micropipet aspiration. Biophys. J. 56, 151–160. doi: 10.1016/S0006-3495(89)82660-8

CrossRef Full Text | Google Scholar

Ferrero, E. E., Martens, K., and Barrat, J. L. (2014). Relaxation in yield stress systems through elastically interacting activated events. Phys. Rev. Lett. 113:248301. doi: 10.1103/PhysRevLett.113.248301

PubMed Abstract | CrossRef Full Text | Google Scholar

Freshney, R. I. (2005). Culture of Animal Cells : A Manual of Basic Techniques. Hoboken, NJ: John Wiley & Sons. doi: 10.1002/9780471747598

CrossRef Full Text | Google Scholar

Gebeshuber, I. C., Drack, M., and Scherge, M. (2008). Tribology in biology. Tribology 2, 200–212. doi: 10.1179/175158308X383206

CrossRef Full Text | Google Scholar

Guilak, F., Tedrow, J. R., and Burgkart, R. (2000). Viscoelastic properties of the cell nucleus. Biochem. Biophys. Res. Comm. 269, 781–786. doi: 10.1006/bbrc.2000.2360

PubMed Abstract | CrossRef Full Text | Google Scholar

Guillaume-Gentil, O., Potthoff, E., Ossola, D., Franz, C. M., Zambelli, T., and Vorholt, J. A. (2014). Force-controlled manipulation of single cells: from AFM to FluidFM. Trends Biotech. 32, 381–388. doi: 10.1016/j.tibtech.2014.04.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Gullekson, C., Cojoc, G., Schürmann, M., Guck, J., and Pelling, A. (2017). Mechanical mismatch between Ras transformed and untransformed epithelial cells. Soft Matter 13, 8483–8491. doi: 10.1039/C7SM01396E

PubMed Abstract | CrossRef Full Text | Google Scholar

Guo, M., Ehrlicher, A. J., Jensen, M. H., Renz, M., Moore, G. R. D., et al. (2014). Probing the stochastic, motor-driven properties of the cytoplasm using force spectrum microscopy. Cell 158, 822–832. doi: 10.1016/j.cell.2014.06.051

PubMed Abstract | CrossRef Full Text | Google Scholar

Guz, N., Dokukin, M., Kalaparthi, V., and Sokolov, I. (2014). If cell mechanics can be described by elastic modulus: study of different models and probes used in indentation experiments. Biophys. J. 107, 564–575. doi: 10.1016/j.bpj.2014.06.033

PubMed Abstract | CrossRef Full Text | Google Scholar

Hallou, A., and Brunet, T. (2020). On growth and force: mechanical forces in development. Development 147:dev187302. doi: 10.1242/dev.187302

PubMed Abstract | CrossRef Full Text | Google Scholar

Hasse, K., and Pelling, A. E. (2015). Investigating cell mechanics with atomic force microscopy. J. R. Soc. Interface 12:20140970. doi: 10.1098/rsif.2014.0970

PubMed Abstract | CrossRef Full Text | Google Scholar

Hategan, A., Law, R., Kahn, S., and Discher, D. E. (2003). Adhesively-tensed cell membranes: lysis kinetics and atomic force microscopy probing. Biophys. J. 85, 2746–2759. doi: 10.1016/S0006-3495(03)74697-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Heinrich, V., Ritchie, K., Mohandas, N., and Evans, E. (2001). Elastic thickness compressibility of the red cell membrane. Biophys. J. 81, 1452–1463. doi: 10.1016/S0006-3495(01)75800-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Hertz, H. (1882). Über die Berührung fester elastischer Körper. J. Reine Angew. Math. 92, 156–171. doi: 10.1515/crll.1882.92.156

CrossRef Full Text | Google Scholar

Hiratsuka, S., Mizutani, Y., Tsuchiya, M., Kawahara, K., Tokumoto, H., and Okajima, T. (2009). The number distribution of complex shear modulus of single cells measured by atomic force microscopy. Ultramicroscopy 109, 937–941. doi: 10.1016/j.ultramic.2009.03.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Hochmuth, R. M. (2000). Micropipette aspiration of living cells. J. Biomechs. 33, 15–22. doi: 10.1016/S0021-9290(99)00175-X

PubMed Abstract | CrossRef Full Text | Google Scholar

Hoffman, B. D., and Crocker, J. C. (2009). Cell mechanics: dissecting the physical responses of cells to force. Annu. Rev. Biomed. Eng. 11, 259–288. doi: 10.1146/annurev.bioeng.10.061807.160511

PubMed Abstract | CrossRef Full Text | Google Scholar

Hoffman, B. D., Massiera, G., and Crocker, J. C. (2007). Fragility and mechanosensing in a thermalized cytoskeleton model with forced protein unfolding. Phys. Rev. E 76:051906. doi: 10.1103/PhysRevE.76.051906

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, H., Kamm, R. D., and Lee, R. T. (2004). Cell mechanics and mechanotransduction: pathways, probes, and physiology. Am. J. Physiol. Cell Physiol. 287, 1–11. doi: 10.1152/ajpcell.00559.2003

PubMed Abstract | CrossRef Full Text | Google Scholar

Hui, C.-Y., Liu, T., Salez, T., Raphael, E., and Jagota, A. (2015). Indentation of a rigid sphere into an elastic substrate with surface tension and adhesion. Proc. R. Soc. A Math. Phys. Eng. Sci. 471:727. doi: 10.1098/rspa.2014.0727

PubMed Abstract | CrossRef Full Text | Google Scholar

Hwang, H. J., Riggleman, R. A., and Crocker, J. C. (2016). Understanding soft glassy materials using an energy landscape approach. Nat. Mater. 15, 1031–1036. doi: 10.1038/nmat4663

PubMed Abstract | CrossRef Full Text | Google Scholar

Ingber, D. E. (1993). Cellular tensegrity: defining new rules of biological design that govern the cytoskeleton. J. Cell Sci. 104, 613–627.

PubMed Abstract | Google Scholar

Ingber, D. E. (2003). Tensegrity I. Cell structure and hierarchical systems. J. Cell Sci. 116, 1157–1173. doi: 10.1242/jcs.00359

PubMed Abstract | CrossRef Full Text | Google Scholar

Johnson, K. L., Kendall, K., and Roberts, A. D. (1971). Surface energy and the contact of elastic solids. Proc. R. Soc. Lond. A 324, 301–313. doi: 10.1098/rspa.1971.0141

CrossRef Full Text | Google Scholar

Kamm, R. D., Lammerding, J., and Mofrad, M. R. K. (2017). “Cellular Nanomechanics,” in Springer Handbook of Nanotechnology, ed B. Bhushan (Berlin: Springer Handbooks; Heidelberg: Springer), 1069–1100.

Google Scholar

Kang, H., Wong, D. S. H., Yan, X., Jung, H. J., Kim, S., Lin, S., et al. (2017). Remote control of multimodal nanoscale ligand oscillations regulates stem cell adhesion and differentiation. ACS Nano 11, 9636–9649. doi: 10.1021/acsnano.7b02857

PubMed Abstract | CrossRef Full Text | Google Scholar

Keller, R. (2012). Physical biology returns to morphogenesis. Science 338, 201–203. doi: 10.1126/science.1230718

PubMed Abstract | CrossRef Full Text | Google Scholar

Kennedy, K. M., Bhaw-Lusimon, A., and Jhurry, D. (2017). Cell-matrix mechanical interaction in electrospun polymeric scaffolds for tissue engineering: Implications for scaffold design and performance. Acta Biomaterialia 50, 41–55. doi: 10.1016/j.actbio.2016.12.034

PubMed Abstract | CrossRef Full Text | Google Scholar

Kroy, K. (2008). Dynamics of wormlike and glassy wormlike chains. Soft Matter 4, 2323–2330. doi: 10.1039/b807018k

CrossRef Full Text | Google Scholar

Kumar, S., and Weaver, V. M. (2009). Mechanics, malignancy and metastasis: the force journey of a tumor cell. Cancer Metastasis Rev. 28, 113–127. doi: 10.1007/s10555-008-9173-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Langer, M. G., Fink, S., Koitschev, A., Rexhausen, U., Heinrich Hörber, J. K., and Ruppersberg, J. P. (2001). Lateral mechanical coupling of stereocilia in cochlear hair bundles. Biophys. J. 80, 2608–2621. doi: 10.1016/S0006-3495(01)76231-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Lau, A. W. C., Hoffman, B. D., Davies, A., Crocker, J. C., and Lubensky, T. C. (2003). Microrheology, stress fluctuations and active behavior of living cells. Phys. Rev. Lett. 91:198101. doi: 10.1103/PhysRevLett.91.198101

PubMed Abstract | CrossRef Full Text | Google Scholar

Lemma, E. D., Spagnolo, B., De Vittorio, M., and Pisanello, F. (2019). Studying cell mechanobiology in 3D: the two-photon lithography approach. Trends in Biotech. 37, 358–372. doi: 10.1016/j.tibtech.2018.09.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Lherbette, M., dos Santos, A., Hari-Gupta, Y., Fili, N., Toseland, C. P., and Schaap, I. A. T. (2017). Atomic Force Microscopy microrheology reveals large structural inhomogeneities in single cell-nuclei. Sci. Rep. 7:8116. doi: 10.1038/s41598-017-08517-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, Y., Galior, K., Ma, V. P.-Y., and Salaita, K. (2017). Molecular tension probes for imaging forces at the cell surface. Acc. Chem. Res. 50, 2915–2924. doi: 10.1021/acs.accounts.7b00305

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, Y., Mollaeian, K., and Ren, J. (2019). Finite element modeling of living cells for AFM indentation-based biomechanical characterization. Micron 116, 108–115. doi: 10.1016/j.micron.2018.10.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Lomakina, E. B., Spillmann, C. M., King, M. R., and Waugh, R. E. (2004). Rheological analysis and measurement of neutrophil indentation. Biophys. J. 87:4246–4258. doi: 10.1529/biophysj.103.031765

PubMed Abstract | CrossRef Full Text | Google Scholar

Long, J., Wang, G., Feng, X.-Q., and Yu, S. (2016). Effects of surface tension on the adhesive contact between a hard sphere and a soft substrate. Int. J. Solids Struct. 84, 133–138. doi: 10.1016/j.ijsolstr.2016.01.021

CrossRef Full Text | Google Scholar

Mahaffy, R. E., Park, S., Gerde, E., Käs, J., and Shih, C. K. (2004). Quantitative analysis of the viscoelastic properties of thin regions of fibroblasts using atomic force microscopy. Biophys. J. 86, 1777–1793. doi: 10.1016/S0006-3495(04)74245-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Managuli, V., and Roy, S. (2017). Simultaneous analysis of elstic and nonspecific adhesive properties of thin sample and biological cell considering bottom substrate effect. J. Biomech. Eng. 139:9. doi: 10.1115/1.4037289

PubMed Abstract | CrossRef Full Text | Google Scholar

Mathur, A. B., Collinsworth, A. M., Reichert, W. M., Kraus, W. E., and Truskey, G. A. (2001). Endothelial, cardiac muscle and skeletal muscle exhibit different viscous and elastic properties as determined by atomic force microscopy. J. Biomech. 34, 1545–1553. doi: 10.1016/S0021-9290(01)00149-X

PubMed Abstract | CrossRef Full Text | Google Scholar

Mathur, A. B., Truskey, G. A., and Reichert, W. M. (2000). Atomic force and total internal reflection fluorescence microscopy for the study of force transmission in endothelial cells. Biophys. J. 78, 1725–1735. doi: 10.1016/S0006-3495(00)76724-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Matzke, R., Jacobson, K., and Radmacher, M. (2001). Direct, high-resolution measurement of furrow stiffening during division of adherent cells. Nature Cell Biol. 3, 607–610. doi: 10.1038/35078583

PubMed Abstract | CrossRef Full Text | Google Scholar

Maugis, D., and Pollock, H. M. (1984). Surface forces, deformation and adherence at metal microcontacts. Acta Metal. 32, 1323–1334. doi: 10.1016/0001-6160(84)90078-6

CrossRef Full Text | Google Scholar

McElfresh, M., Baesu, E., Balhorn, R., Belak, J., Allen, M. J., and Rudd, R. E. (2002). Combining constitutive materials modeling with atomic force microscopy to understand the mechanical properties of living cells. Proc. Natl. Acad. Sci. U.S.A. 99, 6493–6497. doi: 10.1073/pnas.082520599

PubMed Abstract | CrossRef Full Text | Google Scholar

Miller, A. E., Hu, Pi, and Barker, T. H. (2020). Feeling things out: bidirectional signaling of the cell-ECM interface, implications in the mechanobiology of cell spreading, migration, proliferation, and differentiation. Adv. Healthcare Mat. 9:1901445. doi: 10.1002/adhm.201901445

PubMed Abstract | CrossRef Full Text | Google Scholar

Mizuno, D., Tardin, C., Schmidt, C. F., and MackKintosh, F. C. (2007). Nonequilibrium mechanics o active cytoskeletal networks. Science 315, 370–373. doi: 10.1126/science.1134404

PubMed Abstract | CrossRef Full Text | Google Scholar

Moeendarbary, E., Valon, L., Frizsche, M., Harris, A. R., Moulding, D. A., Thrasher, A. J., et al. (2013). The cytoplasm of living cells behaves as a poroelastic material. Nat. Mater. 12, 253–261. doi: 10.1038/nmat3517

PubMed Abstract | CrossRef Full Text | Google Scholar

Moreno-Flores, S., Benitez, R., Vivanco, M., and Toca-Herrera, J. L. (2010). Stress relaxation and creep on living cells with the atomic force microscope: a means to calculate elastic moduli and viscosities of cell components. Nanotechnology 21:445101. doi: 10.1088/0957-4484/21/44/445101

PubMed Abstract | CrossRef Full Text | Google Scholar

Moreno-Flores, S., and Küpcü, S. (2015). 2D protein arrays induce 3D in vivo-like assemblies of cells. Soft Matter 11, 1259–1264. doi: 10.1039/C4SM02278E

PubMed Abstract | CrossRef Full Text | Google Scholar

Moreno-Flores, S., and Toca-Herrera, J. L. (2013). Hybridizing Surface Probe Microscopies. Toward a Full Description of the Meso- and Nanoworlds. Boca Raton, FL: CRC Press.

Google Scholar

Nautiyal, P., Alam, F., Balani, K., and Agarwal, A. (2018). The role of nanomechanics in healthcare. Adv. Healthcare Mat. 7:1700793. doi: 10.1002/adhm.201700793

PubMed Abstract | CrossRef Full Text | Google Scholar

Nawaz, S., Sánchez, P. L, Bodensiek, K., Li, S., Simons, M., and Shaap, I. A. (2012). Cell viscoelasticity measured with AFM and optical trapping at sub-micrometer deformations. PLoS ONE 7:e45297. doi: 10.1371/journal.pone.0045297

PubMed Abstract | CrossRef Full Text | Google Scholar

Pelling, A. E., Dawson, D. W., Carreon, D. M., Chirstiansen, J. J., Shen, R. R., Teitell, M. A., et al. (2007). Distinct contributions of microtubule subtypes to cell membrane shape and stability. Nanomed. Nanotech. Biol. Med. 3, 43–52. doi: 10.1016/j.nano.2006.11.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Pietuch, A., Brückner, B. R., and Janshoff, A. (2013b). Membrane tension homeostasis of epithelial cells through surface area regulation in response to osmotic stress. Biochim. Biophys. Acta: Mol. Cell Res. 1833, 712–722. doi: 10.1016/j.bbamcr.2012.11.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Pietuch, A., Rouven Brückner, B., Fine, T., Mey, I., and Janshoff, A. (2013a). Elastic properties of cells in the context of confluent cell monolayers: impact of tension and surface area regulation. Soft Matter. 9:11490. doi: 10.1039/c3sm51610e

CrossRef Full Text | Google Scholar

Pina, S., Rebelo, R., Correlo, V. M., Oliveira, J. M., and Reis, R. L. (2018). Bioceramics for Osteochondral Tissue Engineering and Regeneration. Adv. Exp. Med. Biol. 1058:53–75. doi: 10.1007/978-3-319-76711-6_3

CrossRef Full Text | Google Scholar

Pitenis, A. A., Urueña, J. M., Hart, S. M., O'Bryan, C. S., Marshall, S. L., Levings, P. P., et al. (2018). Friction-Induced Inflammation. Tribol. Lett. 66:81. doi: 10.1007/s11249-018-1029-7

CrossRef Full Text | Google Scholar

Polacheck, W., and Chen, C. S. (2016). Measuring cell-generated forces: a guide to the available tools. Nat. Methods 13, 415–423. doi: 10.1038/nmeth.3834

PubMed Abstract | CrossRef Full Text | Google Scholar

Popov, V. L., He, ß, M., and Willert, E. (2019). Handbook of Contact Mechanics – Exact Solutions of Axisymmetric Contact Problems. Berlin: Springer. doi: 10.1007/978-3-662-58709-6

CrossRef Full Text | Google Scholar

Radmacher, M., Fritz, M., Kacher, C. M., Cleveland, J. P., and Hansa, P. K. (1996). Measuring the viscoelastic properties of human platelets with the atomic force microscopy. Biophys. J. 70, 556–567. doi: 10.1016/S0006-3495(96)79602-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Radmacher, M., Tillmann, R. W., Fritz, M., and Gaub, H. E. (1992). From molecules to cells: imaging soft samples with the atomic force microscope. Science 257, 1900–1905. doi: 10.1126/science.1411505

PubMed Abstract | CrossRef Full Text | Google Scholar

Rosenbluth, M. J., Lam, W. A., and Fletcher, D. A. (2006). Force microscopy of nonadherent cells:a comparison of leukemia cell deformability. Biophys. J. 90, 2994–3003. doi: 10.1529/biophysj.105.067496

PubMed Abstract | CrossRef Full Text | Google Scholar

Rotsch, C., and Radmacher, M. (2000). Drug-induced changes of cytoskeletal structure and mechanics in fibroblasts: an atomic microscopy study. Biophys. J. 78, 520–535. doi: 10.1016/S0006-3495(00)76614-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Schierbaum, N., Rheinlaender, J., and Schäffer, T. E. (2017). Viscoelastic properties of normal and cancerous human breast cells are affected differently by contact to adjacent cells. Acta Biomaterialia 55, 239–248. doi: 10.1016/j.actbio.2017.04.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Schierbaum, N., Rheinlaender, J., and Schäffer, T. E. (2019). Combined atomic force microscopy (AFM) and traction force microscopy (TFM) reveals a correlation between viscoelastic material properties and contractile prestress of living cells. Soft Matter. 15, 1721–1729. doi: 10.1039/C8SM01585F

PubMed Abstract | CrossRef Full Text | Google Scholar

Schwander, M., Kachar, B., and Müller, U. (2010). The cell biology of hearing. J. Cell Biol. 190, 9–20. doi: 10.1083/jcb.201001138

PubMed Abstract | CrossRef Full Text | Google Scholar

Schwarz, U. S., and Safran, S. A. (2013). Physics of adherent cells. Rev. Mod. Phys. 85, 1327–1381. doi: 10.1103/RevModPhys.85.1327

PubMed Abstract | CrossRef Full Text | Google Scholar

Sen, S., Subramanian, S., and Discher, D. E. (2005). Indentation and adhesive probing of a cell membrane with afm: theoretical model and experiments. Biophys. J. 89, 3203–3213. doi: 10.1529/biophysj.105.063826

PubMed Abstract | CrossRef Full Text | Google Scholar

Septiadi, D., Crippa, F., Moore, T. L., Rothen-Rutishauser, B., and Petri-Fink, A. (2018). Nanoparticle-cell interaction: a cell mechanics perspective. Adv. Mat. 30:1704463. doi: 10.1002/adma.201704463

PubMed Abstract | CrossRef Full Text | Google Scholar

Shen, Y., Guan, D., Serien, D., Takeuchi, S., Tong, P., Yobas, L., et al. (2017). Mechanical characterization of microengineered epithelial cysts by using atomic force microscopy. Biophys. J. 112, 398–409. doi: 10.1016/j.bpj.2016.12.026

PubMed Abstract | CrossRef Full Text | Google Scholar

Shi, Y., Porter, C. L., Crocker, J. C., and Reich, D. H. (2019). Dissecting fat-tailed fluctuations in the cytoskeleton with active micropost arrays. Proc. Natl. Acad. Sci. U.S.A. 116, 13839–13846. doi: 10.1073/pnas.1900963116

PubMed Abstract | CrossRef Full Text | Google Scholar

Skamrahl, M., Colin-York, H., Barbieri, L., and Fritzsche, M. (2019). Simultaneous quantification of the interplay between molecular turnover and cell mechanics by AFM-FRAP. Small 15:1902202. doi: 10.1002/smll.201902202

PubMed Abstract | CrossRef Full Text | Google Scholar

Sneddon, I. N. (1965). The relation between load and penetration in the axisymmetric Boussinesq problem for a punch of arbitrary profile. Int. J. Eng. Sci. 3, 47–57. doi: 10.1016/0020-7225(65)90019-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Sokolov, I., Dokukin, M. E., and Guz, N. V. (2013). Method for quantitative measurements of the elastic modulus of biological cells in AFM indentation experiments. Methods 60, 202–213. doi: 10.1016/j.ymeth.2013.03.037

PubMed Abstract | CrossRef Full Text | Google Scholar

Solich, P. (1998). Rheological constitutive equation for a model of soft glassy materials. Physical Rev E. 58, 738–759. doi: 10.1103/PhysRevE.58.738

CrossRef Full Text | Google Scholar

Stamenović, D. (2008). Rheological behavior of mammalian cells. Cell. Mol. Life Sci. 65, 3592–3605. doi: 10.1007/s00018-008-8292-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Stephens, A. D., Banigan, E. J., Adam, S. A., Goldman, R. D., and Marko, J. F. (2017). Chromatin and lamin A determine two different mechanical response regimes of the cell nucleus. Mol. Biol. Cell 28, 1984–1996. doi: 10.1091/mbc.e16-09-0653

PubMed Abstract | CrossRef Full Text | Google Scholar

Stewart, M. P., Helenius, J., Toyoda, Y., Ramanathna, S. P., Müller, D. J., and Hyman, A. A. (2011). Hydrostatic pressure and the actomyosin cortex drive mitotic cell rounding. Nature 469, 226–230. doi: 10.1038/nature09642

PubMed Abstract | CrossRef Full Text | Google Scholar

Stewart, M. P., Toyoda, Y., Hyman, A. A., and Müller, D. J. (2012). Tracking mechanics and volume of globular cells with atomic force microscopy using a constant-height clamp. Nature Protocols 7, 143–154. doi: 10.1038/nprot.2011.434

PubMed Abstract | CrossRef Full Text | Google Scholar

Stuart, J. K., and Hlady, V. (1999). Reflection interference contrast microscopy combined with scanning force microscopy verifies the nature of protein-ligand interaction force measurements. Biophys. J. 76, 500–508. doi: 10.1016/S0006-3495(99)77218-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Stylianou, A., Lekka, M., and Stylianopoulos, T. (2018). AFM assessing of nanomechanical fingerprints for cancer early diagnosis and classification: from single cell to tissue level. Nanoscale 10:20930. doi: 10.1039/C8NR06146G

PubMed Abstract | CrossRef Full Text | Google Scholar

Thoumine, O., and Ott, A. (1997). Time scale dependent viscoelastic and contractile regimes in fibroblasts probed by microplate manipulation. J. Cell Sci. 110, 2109–2116.

PubMed Abstract | Google Scholar

Tietze, S., Kräter, M., Jacobi, A., Taubenberger, A., Herbig, M., Wehner, R., et al. (2019). Spheroid culture of mesenchymal stromal cells results in morphorheological properties appropriate for improved microcirculation. Adv. Sci. 6:1802104. doi: 10.1002/advs.201802104

CrossRef Full Text | Google Scholar

Trickey, W. R., Baaijens, F. P., Laursen, T. A., Alexopooulos, L. G., and Guilak, F. (2006). Determination of the Poisson's ratio of the cell: recovery properties of chondrocytes after release from complete micropipette aspiration. J. Biomech. 39, 78–87. doi: 10.1016/j.jbiomech.2004.11.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Unnikrishnan, G. U., Unnikrishnan, V. U., and Reddy, J. N. (2007). Constitutive material modeling of cell: a micromechanics approach. J. Biomech. Eng. 129, 315–323. doi: 10.1115/1.2720908

PubMed Abstract | CrossRef Full Text | Google Scholar

Vadillo-Rodriguez, V., Beveridge, T. J., and Dutcher, J. R. (2008). Surface viscoelasticity of individual gram-negative bacterial cells measured using atomic force microscopy. J. Bacteriol. 190, 4225–4232. doi: 10.1128/JB.00132-08

PubMed Abstract | CrossRef Full Text | Google Scholar

Verschueren, H. (1985). Interference reflection microscopy in cell biology: methodology and applicatons. J. Cell Sci. 75, 279–301.

PubMed Abstract | Google Scholar

Vogel, V., and Sheetz, M. (2006). Local force and geometry sensing regulate cell functions. Nat. Rev. Mol. Ce. Biol. 7, 265–275. doi: 10.1038/nrm1890

PubMed Abstract | CrossRef Full Text | Google Scholar

Weisenhorn, A. L., Khorsandi, M., Kasas, S., Gotzos, V., and Butt, H.-J. (1993). Deformation and height anomaly of soft surfaces studied with an AFM. Nanotechnology 4, 106–113. doi: 10.1088/0957-4484/4/2/006

CrossRef Full Text | Google Scholar

Wirtz, D., Konstantopoulos, K., and Searson, P. C. (2011). The physics of cancer: the role of physical interactions and mechanical forces in metastasis. Nat. Rev. Cancer. 11, 512–522. doi: 10.1038/nrc3080

PubMed Abstract | CrossRef Full Text | Google Scholar

Wottawah, F., Schinkinger, S., Lincoln, B., Ananthakrishnan, R., Romeyke, M., Guck, J., et al. (2005). Optical rheology of biological cells. Phys. Rev. Lett. 94:098103. doi: 10.1103/PhysRevLett.94.098103

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, P.-H., Aroush, D. R.-B., Asnacios, A., Chen, W.-C., Dokukin, M. E., Doss, B. L., et al. (2018). A comparison of methods to assess cell mechanical properties. Nat. Methods 15, 491–498. doi: 10.1038/s41592-018-0015-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Xie, H., Yin, M., Rong, W., and Sun, L. (2014). In situ quantification of living cell adhesion forces: single cell force spectroscopy with a nanotweezer. Langmuir 30, 2952–2959. doi: 10.1021/la500045q

PubMed Abstract | CrossRef Full Text | Google Scholar