Metal Transfer and Wear

Introduction

These thoughts are offered as a reminder that Tribology is not all about the normal contact of fractal surfaces, and indeed, not all about elastic contact of rubber and polymers, or even about dry contact. Machines do still contain metal surfaces sliding past each other, hopefully separated by an oil film; and sometimes, when tolerances have been pushed too far, or running with starved lubrication when the oil or grease supply is inadequate, with some metal to metal contact. Fortunately this is not always disastrous: surfaces do often run-in, so that after running with contact and a contribution of dry-contact friction, there is steady wear and contacts no longer occur. The traditional design criterion for gears and ball races was, and still is, the Λ − ratio: the ratio of the predicted film thickness for smooth surfaces to the rms roughness. Certainly a Λ − ratio of 3 or more¹ usually leads to full-film lubrication: but to anyone with the slightest background in surface roughness this is an absurd rule. Assuming, as is usually done, that the predicted smooth-surface film thickness refers to the distance between the mean planes of the roughness, the rms roughness says nothing about the how much contact there will be. And if running-in is successful, and the high points of the surface wear away, the rms (and the Λ − ratio) may hardly change, but there will be successful operation.

But when will running-in be successful? What determines when instead of running-in there will be scuffing, and disaster?

The traditional picture of the “mixed friction” regime is that when the local film thickness falls to zero, additives (or perhaps happy accidents) provide a boundary lubricant in the oil: some form of long chain polymer, which has a reactive end which attaches itself to the metal, and carries the load on its free ends: with low friction but, more importantly, preventing metal to metal contact. The Blok scuffing criterion was that the maximum surface temperature must be below a specific value: and there was the problem, what should it be? In Bowden and Tabor's laboratory experiments, using a known, pure, organic compound, clear links with the known properties could be found; but in engineering practice perhaps all that can be done is to ensure that the calculated maximum temperature in a new application is no more than in an existing application: the ISO guide concentrates on the temperature calculation, not on the temperature found.

But what happens when boundary lubrication fails? Fortunately it seems that we do not move completely into the dry wear scenario. The failure will usually be local, and the dry wear process interrupted. An earlier work (Sakmann et al., 1944) reported that in a pin on disc experiment, flooding the surface with a plain mineral oil halved the transfer at a light load, but produced only a small reduction at a heavier load. But flooding with oleic acid largely eliminated transfer.

Here it seems desirable to review what has been learnt about dry wear, and perhaps, forgotten.

Transfer and Wear

The obvious starting point is the “Archard” wear equation. This was predicted by Holm in 1938 [Holm (1938)], by postulating that for every encounter of a pair of atoms (within the contact area found as W/p_m) there was a fixed probability of one being pulled out of its parent surface. Detailed experimental confirmation was provided by Burwell and Strang (1952), but from electron micrographs of transfer particles they argue that the unit event is the encounter of two asperities. Both models predict that the volume of wear V is proportional to the distance slid L and the load W, and inversely proportional to the hardness p_m: V = k · L · (W/p_m). Archard's contribution was to show that it is not necessary to assume that the average size of the contact areas or wear particles is constant, and to calculate the probabilities k implied by the results of all the available experimental wear combinations … and to go on to contribute to the great wear research program of Hirst's group at AEI (Associated Electrical Industries) Aldermaston (see Archard, 1953; Kerridge, 1955, etc.).

Wear of Soft Steel Against Hard Steel

The natural meaning of the term “wear” is the weight, or volume, lost from the device concerned: and early researchers merely noted that this could become either transfer particles attached to the “wrong” partner, or loose wear debris. The important distinction between transfer and wear was first made when Kerridge (1955) found that when a (radioactive) steel pin was loaded against a rotating hard steel ring (“hollow drum” perhaps conveys the picture), a radioactive transfer layer built up on the ring, but the radioactivity (and therefore the amount of transfer) then became constant. When the active pin was replaced by an inactive one, the activity reduced, mirroring the path of the increase: it was not that the transfer layer had a maximum size, and could build up no further, but that a steady state had been reached where the transfer to the ring equaled the rate of loss from the ring. At this point the pin wear rate fell to the steady rate required by the wear law. The wear fragments were carefully collected and monitored, little radioactivity being found at first, but ultimately matching the wear rate of the pin: and consisting of relatively large, oxidized, particles. The detachment of the transfer layer, and so presumably its oxidation rate, was the rate-determining process. Experiments in air at 10⁻³ mm mercury found the wear rate reduced to a tenth (or lower at low loads) of the atmospheric value, confirming this.

Thus, for this combination, wear is a multi-stage process. First, metallic transfer from pin to ring as submicroscopic particles. These are then smeared out to form a (harder) transfer layer. The transfer layer then oxidizes, helped by the temperature produced by frictional heating, weakening its attachment to the ring, and finally the oxidized layer is rubbed off as large oxide particles to form the wear debris.

Wear of Brass Against Hard Steel (Severe Wear)

Kerridge and Lancaster (1956) followed this by replacing the soft steel pin by an irradiated (60/40) brass pin. Initially both wear of the pin and transfer increased exponentially at almost the same rate, with nothing left over to form wear fragments. When the experiment was repeated with a load 5× higher but lubricated with cetane, the same was true, but the amounts reduced to one quarter. The significant feature was that as the transfer film reached its limiting value, the wear rate fell to its uniform rate. As in Kerridge's experiments, when the active pin was replaced by an inactive one, the decrease from the limiting activity rate to zero mirrored the growth from zero to limiting activity. And when an inactive pin was replaced by an active one, there was at first no activity in the wear debris: wear particles are not produced directly from the pin. Convincing evidence was given that individual wear particles at a given time after a pin replacement all had the same activity, i.e., each had the same mix of “new” and “old” transfer fragments.

The authors emphasize that the term “transfer film” is misleading; the transfer layer is composed of identifiable fragments. These grow by accretion of further fragments to become incipient wear particles, perhaps 50× larger than the transfer fragments, before becoming detached as wear particles. But the fragments are themselves much larger than the likely size of asperity contacts, more approximating to “the total real area of contact as estimated from the ratio of the load to the flow pressure of 60/40 brass,” so it seems (although the authors do not quite say this) that incipient transfer fragments form on the pin by accretion from individual intermetallic junctions.

Thus, for this combination, wear is again a multi-stage process: first, transfer fragments are assembled on the pin, which then transfer from pin to ring, and then become larger by accretion: these are smeared out to become harder, thicker, flakes, which finally become detached as wear particles.

The authors, rather as an aside, report that both the transfer rate and the wear rate are proportional to the load, and that the same applies to the sizes of transfer fragments and wear particles: concluding that “the number of individual events occurring … is the same at all loads.” This is a flat contradiction of the Archard (and Greenwood!) belief, that the typical event is the same at all loads, and that only the number of events is proportional to load.

The authors also make the very perceptive remark (in view of the work of Cocks and Antler to be described below), “Once a fragment has been transferred to the ring, the load will be concentrated on that fragment during subsequent passages beneath the pin.”

Wear of Hard Steels Against Hard Steel (Mild Wear)

One might expect mild wear to be the more straightforward process, but this was not what Archard and Hirst (1957) found. When rubbing hardened tool steel pins against a disk of the same material, the initial behavior was as described above (but on a scale two orders of magnitude less): the pin wore by transfer to the disk, the transfer fragments then aggregated into larger (metallic) fragments which became detached as wear particles. But as the conformity between pin and disk improved, many of the transferred fragments were worn away by a much smaller scale process. And then in a final stage the wear rate increased by a factor of five, and seems to have occurred as abrasion by large (oxidized) wear particles. At this stage the transfer “layer” consisted of areas with no transfer and patches very much thicker than the average (50–100 Å) thickness.

Wedges (Prows)

Tribologists have long regretted the impossibility of directly examining the area of contact between sliding metals: but in 1962 two researchers reported the results of looking sideways at the contact²… which “of course” could reveal nothing. But it did!

When Cocks (1962) loaded a hemispherically ended copper rider against the surface of a rotating large cylindrical copper drum (load 700 g, speed 0.038 cm/s) he found: “This immediately revealed some unexpected phenomena. Most of the time during sliding, the drum and rider were separated by a wedge of displaced metal which emerged from the drum surface and became trapped between them.”

The same was found for other metal pairs. Rider and drum were polished up to grade 0000 paper, and then cleaned to be wettable by water and yielding a high coefficient of friction (1.1–1.4). The rider was given a slight transverse movement to avoid repeating the same path on the drum.

A wedge of metal displaced from the drum becomes trapped between the two sliding members and holds them apart. Thus, the drum surface slides against the wedge instead of the rider itself. As the sliding proceeds, the wedge continuously receives more metal from the drum. At the same time fragments of metal from the wedge are intermittently redeposited back on the drum, and can be seen emerging from the contact on the drum surface. From time to time the wedge itself breaks away from the rider, and is carried away on the drum surface. However, when this happens a new wedge immediately begins to form and the surfaces are soon visibly separated again.

Neither the hardness, nor the relative hardnesses of rider and drum appeared to matter.

The whole assembly of rider, wedge and part of the drum could be mounted in a cold-setting plastic without ever separating them, and then sectioned, polished and etched. Figure 1 shows a result. The wedge is initiated by transfer from the drum, and remains bonded to the rider. It is “a relatively compact mass of metal, not an aggregate of individual fragments ….” The wedge grows by accretion, at the front, where “the material of the wedge is continuous with that of the drum”: so the relative motion must cause shearing of the metal, presumably rather similar to what happens in the formation of a chip in the machining of a ductile metal.

FIGURE 1

Figure 1. Section through the wedge linking drum and rider, both of oxygen-free high-conductivity copper, after sliding at a speed of 0.038 cm/s with a load of 710 g. (A) Complete wedge. Magnification 100×. (B) Right-hand portion of the section in (A). Magnification 340× [Reproduced from Cocks (1962), with the permission of AIP Publishing].

The life of a wedge is very variable: as short as 20 s (sliding distance 0.8 cm): often 10–20 min (sliding distance 25–45 cm) and sometimes longer. After perhaps 1 min it seems an equilibrium size is reached where continued accretion at the front is balanced by fragments breaking of from the rear (and sometimes the entire wedge breaks away).

Cocks (1964) showed that the wedge formation and consequent separation of the sliding bodies occurs in the same way between two flat surfaces, usually with several wedges in action at once. The wedge may be formed by accretion from either disk, and occasionally (see one beautiful micrograph of a wedge formed by a pair of SAE1020 steel disks at 5 kg load) by accretion at both ends. These later experiments showed that the wedge mechanism seemed able to continue indefinitely (copper on copper), to reduce to a much smaller scale (steel on steel), or apparently to cease completely (nickel on nickel).

Antler (1962), working with metals suited to electrical contacts, mostly using lighter loads (100 g) and longer runs (40 m sliding distance) found similar behavior. He emphasizes the irrelevance of the relative hardnesses of rider and flat, and how the prow (his term, but also “wedge-shaped prow”) becomes very much harder than either, making its resemblance to a machining tool clearer. But he gives many examples of the complexity of the process: one example being for a gold rider sliding on a palladium flat:

(a) First pass: gold rider deposits adherent particles on palladium flat with little palladium transfer to gold;

(b) Second and third passes: rider removes gold from flat;

(c) Subsequent passes: a severely work hardened gold prow gouges [the] flat, producing palladium particles that adhere to the rider;

(d) From this point, sliding is identical to the all-palladium system, regardless of length of run. Practically all debris is palladium.

Note the hardnesses: Gold, 79 kg/mm²; Palladium, 142 kg/rnm²: but it is the soft gold which wears away the hard palladium!

Antler (1964) notes that wear by the prow-formation mechanism tends to change to the rider-wear severe regime on prolonged sliding in the same track. This was observed with a variety of metals, including aluminum, copper, gold, palladium, and silver sliding on themselves. This differs from what Cocks reports for his pin on disc experiments, but he never ran on the same track.

Rabinowicz's Contribution

The first use of radioactivity to study transfer was when Sakmann et al. (1944) slid an inactive slider over an activated block, and measured the transfer with a Geiger counter. Gregory (1946) slid a radioactive lead slider³ over an inactivated flat surface: this permitted the use of autoradiography to study the transfer. He noted average film thicknesses between 10 and 100 lead atoms thick. Rabinowicz and Tabor (1951) modestly state:

This paper describes an extension of Gregory's autoradiographic method to a study of the friction and pick-up occurring between stationary and sliding metal surfaces in the absence and in the presence of lubricant films.

carrying understatement too far! They established the proportionality between pick-up and load: that for like metals there was no correlation between pick-up and hardness: that for dissimilar metals the pick-up was typically less by a factor 50, mainly due to the smaller size of the transfer fragments, typically 10⁻⁸ g compared to 10⁻⁶ g. They conclude that metallic transfer does not occur as a uniform smear but as a relatively small number of discrete fragments.

which seems to be the first clear statement of this fact⁴. But sadly for the present purpose, the main thrust of the paper is to study the effect of lubrication, certainly on both friction and transfer, but really hoping to get some clue to the origin of friction.

However, Rabinowicz and Tabor make the important discovery that transfer takes place under purely normal loading, although on a much reduced scale, with transfer fragments typically 10⁻¹¹ g: still enormous by atomic standards (10¹⁰ atoms). Rabinowicz (1952) followed this up more carefully, finding the total transfer (copper to copper: load 4 kg) of 3 × 10⁻⁸ to 3 × 10⁻⁹ g, but falling to 10⁻¹⁰ g when great care was taken to avoid lateral motion.

Are such transfer fragments consistent with an atom by atom transfer process?

We note with interest Rabinowicz (1953) “A quantitative study of the wear process” –which is entirely about transfer fragments, with no mention of wear fragments! However, following Kerridge (1955) and Kerridge and Lancaster (1956), Rabinowicz (1958) recognized the distinction between transfer and wear, and propounded a criterion for the size of wear fragments (The AEI publications contain estimates of the sizes of transfer and wear fragments, but make no attempt to predict them). Rabinowicz starts from the basic Bowden and Tabor idea of a lump of metal torn out of the base and crushed against the slider so that it adheres and becomes a transfer fragment. When the crushing load is removed, the fragment relaxes, but remains stretched because it adheres to the slider, and residual stresses remain. A fragment of volume V with mean residual stresses ${\bar{\sigma }}_r$ will have a strain energy $({\bar{\sigma }}_r^2/2E)·V$. Rabinowicz explain that to separate the transfer particle from the slider involves the creation of new free surface, so for an area A and a work of adhesion w_ab for the pair of materials will require an energy A(w_ab): the first introduction of surface energy into Tribology⁵. Thus, the minimum size of loose wear fragments will be when $({\bar{\sigma }}_r^2/2E)·V=A(w_{ab})$. Accordingly, for a hemispherical fragment of radius r, we must have $r\ge (3E/{\bar{\sigma }}_r^2)·(w_{ab})$.

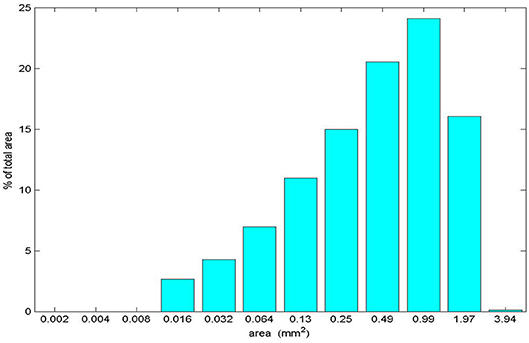
The maximum possible strain energy density is Y²/2E where Y is the yield stress in tension, and clearly the mean residual stress after unloading will be less. Rabinowicz (1958) suggests that the strain energy might be perhaps 10% of the maximum possible [In his 1961 paper, Rabinowicz (1961) suggests residual stresses are often found to be σ_r = νY, which when Poisson's ratio ν = 0.3 gives 9%]⁶. He goes on to argue that for most metals the elastic strain at yield may be taken as 3 · 10⁻³, so sets Y/E = 3 · 10⁻³, and takes Y = p_m/3 where p_m is the hardness, so a simplified, practical criterion is r ≥ 30, 000‘(w_ab)/p_m. But in wear tests to confirm this, he switches from the predicted minimum fragment size to the “average” size (total weight of larger particles equals total weight of smaller ones): despite some scatter, the agreement is reasonable. But what then do we deduce about the origin of the multitude of smaller fragments contributing half the total weight? The size distribution of the wear fragments is not given, but the Kerridge and Lancaster paper described above, and Figure 2 shows their results.

FIGURE 2

Figure 2. Size distribution of wear particles for brass pin sliding on hard steel (load 22.5 kg).

There is no evidence in these experiments of a minimum size for wear particles. And it should be noted that in experiments in which active and inactive pins were interchanged, individual wear fragments had different specific activities: i.e., each particle contained a mixture of active and inactive atoms. No particle has a life history like that postulated in the Rabinowicz model.

Discussion

We all know that the underlying problem in studying wear is the multiplicity of wear mechanisms. Even when considering a given materials pair, as the mild wear of hard steel against itself as studied by Archard and Hirst (above) or gold against platinum as described by Antler, there was a sequence of different mechanisms. Challen and Oxley (1979) used a slip-line field solution to model the steady motion when a hard slider traversed a rigid/perfectly plastic half-space, and found three modes of deformation; (1) plastic flow of the surface by a wave pushed ahead of the slider, referred to by Challen and Oxley as “rubbing mode”; (2) a deformed “prow” which becomes detached from the surface; (3) a cutting mode in which a “chip” is continuously cut from the surface. Kayaba et al. (1986) refer to all three as abrasive wear: the rubbing mode, rather inappropriately, as plowing (though they do sometimes find a gentle trace). They experimented with a hard steel pin against brass, mild steel and stainless steel. All three combinations, when unlubricated, show each of the three modes, as the parameter $\sqrt{W/R^2{H}_V}$ (where R is the pin radius, H_V the hardness, and W the load) increases. They show scanning electron micrographs of prow formation (with no reference to Cocks or Antler), and similar pictures for steel against brass, where the prow material passes under the slider and becomes a chip. When lubricated with a smear of silicone grease, with the two steels all three modes are found: however lubricated brass gave just two modes: the rubbing mode at higher loads but changing at light loads to flaking: the flakes then forming wear debris. This appears to be the delamination wear mode studied by Suh (1973), and caused by incremental plastic flow as the Challen and Oxley plastic wave moves over the surface and produces below the surface an almost reversible plastic strain cycle. I cannot resist including his conclusion (Suh, 1977) “(2) The wear rate of metals may be predicted in the near future, based on first principles and fundamental material properties.”

And of course these are just a few wear mechanisms: one should certainly add metallographic phase transformations [Welsh (1965) and his demonstration that increasing the load or speed not only changes wear from mild to severe, but, because of the frictional temperature rise, there are “three transitions: (1) a change from mild to severe wear at relatively light loads (T₁): (2) a change from severe wear back to mild wear at higher loads, (T₂): (3) a perturbation in the mild-wear rate at even higher loads, (T₃) with the wear rates of the pin and ring diverging”].

Others emphasize the development of subsurface cracks, or tribochemistry, or simple corrosion.

I have confined my attention to the largely forgotten classic contributions.

For they are largely forgotten. Exceptionally, deRooij and Schipper (2001) and deRooij et al. (2013) know of Cocks and Antler's work, so are able to build on it in their investigation of how hard transfer fragments build up on a deep-drawing tool and ruin the finish. In contrast, a recent admirable paper (Tarasov et al., 2017) studies the sliding of a hard steel pin on an aluminum disk. Their interest is in Friction Stir Welding, so they contribute new information about the effect of temperature on the iron/aluminum combination: but they rediscover prow formation, the formation of a transfer layer, and back transfer to the disk—all without noticing that it has been discovered already 60 years ago. But no radiography, so they do not learn that transfer particles are formed by accretion over time, not torn out bodily as lumps.

Is it all right to forget all this, because prows and riders are just examples of Godet's “Third Body,” so need not be treated separately? There seems no doubt that Antler's “riders” are indeed third bodies. It is less clear that Cocks' prows are: certainly sometimes they are the very opposite: they are the link which makes the first and second bodies into one! There are not two bodies sliding past each other: there is a single body shearing along a neck. It seems clear that the formation of transfer layers is not a three body process: and the transfer layer is not itself a third body any more than the oxide film can usefully be treated as such: perhaps there has been insufficient study of the five-body problem, where debris particles on their way out of the conjunction roll about between two oxide films?

Yes, study the behavior of trapped particles: but if all transfer and wear is attributed to third bodies, the term has become too wide to be useful. But at least stop studying the purely normal contact of rough surfaces.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Funding

This research has received no funding. I hope, and trust, that the University of Cambridge will provide the open access publication fee.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Footnotes

1. ^The “traditional” requirement is Λ > 3. But see Cann et al. (1994), or Greenwood (2020) for alternatives.

2. ^Cocks (1958) reported preliminary results in 1958 (cited by Antler, 1962), so undoubtedly has priority.

3. ^A lead slider containing a radioactive isotope (of radon?); by implication all that was available in Australia at the time.

4. ^But sliding was not completely steady, with some stick-slip. Did this matter?

5. ^Or should one count Derjaguin's (1934) estimate of the force of adhesion?

6. ^I find these estimates hard to accept: stresses of order Y may well be found near the interface, but will these not be very local?

References

Antler, M. (1962). Wear, friction, and electrical noise phenomena in severe sliding systems. ASLE Trans. 5, 297–307. doi: 10.1080/05698196208972473

CrossRef Full Text | Google Scholar

Antler, M. (1964). Processes of metal transfer and wear. Wear 7, 181–203. doi: 10.1016/0043-1648(64)90053-5

CrossRef Full Text | Google Scholar

Archard, J. F. (1953). Contact and rubbing of flat surfaces. J. Appl. Phys. 24, 981–988. doi: 10.1063/1.1721448

CrossRef Full Text | Google Scholar

Archard, J. F., and Hirst, W. (1957). An examination of a mild wear process. Proc. R. Soc. A 238, 515–528. doi: 10.1098/rspa.1957.0015

CrossRef Full Text | Google Scholar

Burwell, J. T., and Strang, D. C. (1952). On the empirical law of adhesive wear. J. Appl. Phys. 23, 18–28. doi: 10.1063/1.1701970

CrossRef Full Text | Google Scholar

Cann, P., Ioannides, E., Jacobson, B., and Lubrecht, A. A. (1994). The lambda ratio–a critical re-examination. Wear 175, 177–188. doi: 10.1016/0043-1648(94)90181-3

CrossRef Full Text | Google Scholar

Challen, J. M., and Oxley, P. L. B. (1979). An explanation of different regimes of friction and wear using asperity deformation models. Wear 53, 229–243. doi: 10.1016/0043-1648(79)90080-2

CrossRef Full Text | Google Scholar

Cocks, M. (1958). Wear debris in contact between sliding metals. J. Appl. Phys. 29, 1609–1610. doi: 10.1063/1.1723007

CrossRef Full Text | Google Scholar

Cocks, M. (1962). Interaction of sliding metal surfaces. J. Appl. Phys. 33, 2152–2161. doi: 10.1063/1.1728920

CrossRef Full Text | Google Scholar

Cocks, M. (1964). Role of displaced metal in the sliding of flat metal surfaces. J. Appl. Phys. 35, 1807–1814. doi: 10.1063/1.1713746

CrossRef Full Text | Google Scholar

Derjaguin, B. V. (1934). Theorie des Anhaftens kleiner teilchen. Kolloid Zeitschrift. 69, 155–164. doi: 10.1007/BF01433225

CrossRef Full Text

deRooij, M. B., and Schipper, D. J. (2001). Analysis of material transfer from a soft workpiece to a hard tool: part I—lump growth model: part II: experimental verification: ASME. J. Tribol. 123, 474–478. doi: 10.1115/1.1308023

CrossRef Full Text | Google Scholar

deRooij, M. B., van der Linde, G., and Schipper, D. J. (2013). Modelling material transfer on a single asperityscale. Wear 307, 198–208. doi: 10.1016/j.wear.2013.09.006

CrossRef Full Text | Google Scholar

Greenwood, J. A. (2020). “Elastohydrodynamic Lubrication,” in Encyclopedia of Tribology, eds Q. J. Wang and Y. W.Chung (Boston, MA: Springer), 51–80.

Google Scholar

Gregory, J. N. (1946). Radioactive tracers in the study of friction and lubrication. Nature 157, 443–444. doi: 10.1038/157443b0

CrossRef Full Text | Google Scholar

Holm, R. (1938). Wiss. Veroffent. Siemens-Werken 17:43.

Kayaba, T., Hokkirigawa, K., and Kato, K. (1986). Analysis of the abrasive wear mechanism by successive observations of wear processes in a scanning electron microscope. Wear 110, 419–430. doi: 10.1016/0043-1648(86)90115-8

CrossRef Full Text | Google Scholar

Kerridge, M. (1955). Metal transfer and the wear process. Proc. Phys. Soc. B 68, 400–407. doi: 10.1088/0370-1301/68/7/302

CrossRef Full Text | Google Scholar

Kerridge, M., and Lancaster, J. K. (1956). The stages in a process of severe metallic wear. Proc. R. Soc. A 236, 250–264. doi: 10.1098/rspa.1956.0133

CrossRef Full Text | Google Scholar

Rabinowicz, E. (1952). Metal transfer during static loading and impacting. Proc. Phys. Soc. B. 65:630.

Google Scholar

Rabinowicz, E. (1953). On the looseness of wear fragments. J. Appl. Phys. 24:367. doi: 10.1063/1.1721285

CrossRef Full Text | Google Scholar

Rabinowicz, E. (1958). The effect of size on the looseness of wear fragments. Wear 2, 4–8. doi: 10.1016/0043-1648(58)90335-1

CrossRef Full Text | Google Scholar

Rabinowicz, E. (1961). Influence of surface energy on friction and wear phenomena. J. Appl. Phys. 32, 1440–1444. doi: 10.1063/1.1728375

CrossRef Full Text | Google Scholar

Rabinowicz, E., and Tabor, D. (1951). Metallic transfer between sliding metals: an autoradiographic study. Proc. R. Soc. Lond. A 208, 455–475. doi: 10.1098/rspa.1951.0174

CrossRef Full Text | Google Scholar

Sakmann, B. W., Burwell, J. T., and Irvine, W. J. (1944). Measurements of the adhesion component in friction by means of radioactive indicators. J. Appl. Phys. 15, 459–473. doi: 10.1063/1.1707457

CrossRef Full Text | Google Scholar

Suh, N. P. (1973). The delamination theory of wear. Wear 25, 111–124.

Google Scholar

Suh, N. P. (1977). An overview of the delamination theory of wear. Wear 44, l−16. doi: 10.1016/0043-1648(77)90081-3

CrossRef Full Text | Google Scholar

Tarasov, S. Y., Filippov, A. V., Kolubaev, E. A., and Kalashnikova, T. A. (2017). Adhesion transfer in sliding a steel ball against an aluminum alloy. Tribol. Int. 115, 191–198. doi: 10.1016/j.triboint.2017.05.039

CrossRef Full Text | Google Scholar

Welsh, N. C. (1965). The dry wear of steels part I. The general pattern of behaviour. Phil. Trans. R. Soc. A 257, 31–70. doi: 10.1098/rsta.1965.0001

CrossRef Full Text | Google Scholar