Probabilistic, Fractal, and Related Techniques for Analysis of Engineering Surfaces

In many engineering fields surface topography is of crucial importance solving problems of friction and other problems of tribology. A review of mathematical approaches for description of topography of engineering surfaces is presented. Firstly, we give a brief introduction to some of statistical parameters used for description of surface roughness. It is argued that although some of these parameters may be quite useful for specific engineering problems, a set of finite numbers of parameters cannot describe contact properties of rough surfaces. Then we discuss various models of surface roughness based on Gaussian models of the asperity heights. The results of application of various modern tests of normality for checking whether the distribution of the asperity heights is Gaussian, are presented. Further fractal models of roughness are discussed. Using fractal parametric-homogeneous (PH) surfaces, it is demonstrated that tribological properties of a rough surface cannot be characterized just by the fractal dimension of the surface. It is also shown that models based solely on the power-spectral density function (PSDF) are quite similar to fractal models and these models do not reflect tribological properties of surfaces. In particular, it is demonstrated that different profiles may have the same PSDF.

1. Introduction

The paper deals mainly with surfaces used in engineering practice that will be referred to as engineering surfaces. It is known that all engineering surfaces are rough (see e.g., Archard et al., 1975; Whitehouse, 2011) and therefore, contact between engineering surfaces is realized by a number of contact spots (see e.g., Zhuravlev, 1940, 2007; Holm, 1941; Goryacheva, 1998; Borodich, 2007). If the surface profile z(x) is studied using Fourier decomposition, and the term 'roughness' is attributed to the short wavelength shapes, while the long wavelength shapes are referred to as “waviness” of the surface (see e.g., Morales-Espejel et al., 2000; Borodich and Bianchi, 2013). If the waviness is extracted from the surface profile then the rough surface may be considered as nominally flat (see e.g., Greenwood and Williamson, 1966). Roughness of engineering surfaces is a crucial factor for performance of tribological components. The energy dissipation during sliding of dry engineering surfaces and correspondingly, the friction are enormously influenced by the surface profile (see e.g., Borodich and Savencu, 2017). Here we present a critical review of some popular statistical, fractal and related techniques for modeling and analysis of the surface roughness.

One of the first attempts to employ statistical methods for description of surface roughness was presented by Abbott and Firestone (1933) who calculated the cumulative distribution function of the surface heights. In tribology this parameter is called the Abbott-Firestone curve or the bearing area curve. Independently, Zhuravlev (1940) employed this parameter in his statistical model of contact between rough surfaces that were represented as collection of spherical protuberances having identical radii. He explained that the number of contacting spheres a specific height increases as the surfaces approach each other. In the English language literature this model is usually attributed to Greenwood and Williamson (1966).

After the bearing area curve parameter was introduced, there was a period that can be referred to as “the parameter rash” because a huge number of statistical parameters of roughness were introduced (Whitehouse, 1982). These characteristics were related to both the vertical distribution of heights and the horizontal distribution of the rough profiles (Nowicki, 1985).

The next step in surface roughness characterization was the idea that it may be modeled using theory of random processes. In 1953 Linnik and Khusu presented a seminar talk where they suggested to use graphs of a stationary Gaussian random process in order to describe surface roughness, see Linnik and Khusu (1954a) for detail, as well as Linnik and Khusu (1954b) and Khusu et al. (1975). Linnik and Khusu (1954a) suggested to study the following correlation function for the Gaussian random process

$\begin{array}{ll}K(x)=K(0)·{\text{e}}^{-\alpha |x|},& (1)\end{array}$

where K(0) and α are some parameters of the roughness. Independently, the same idea was introduced later by Whitehouse and Archard (1970). They presented an absolutely correct statement that if a profile z(x) of a random rough surface is Gaussian then it can be fully described by a distribution of asperity heights and the correlation (auto-correlation) function of the process R. The auto-correlation is defined as

$\begin{array}{l}R(\delta )={\displaystyle \underset{T\to \infty }{lim}}\frac{1}{2T}{\displaystyle {\int }_{-T}^T}\left[z(x+\delta )-\bar{z}\right]\left[z(x)-\bar{z}\right]dx\\ =\langle \left[z(x+\delta )-\bar{z}\right]\left[z(x)-\bar{z}\right]\rangle & (2)\end{array}$

If one takes the Fourier transform of R(δ) then the power spectrum G(ω) or the power-spectral density function (PSDF) is obtained. If the signal frequency is denoted as ω then the PSDF is defined as

$\begin{array}{l}G(\omega )=\frac{2}{\pi }{\displaystyle {\int }_0^{\infty }}R(\delta )cos\omega \delta d\delta \text{ and}\\ \bar{z}={\displaystyle \underset{T\to \infty }{lim}}\frac{1}{2T}{\displaystyle {\int }_{-T}^T}z(x)dx.\end{array}$

Developing the random signal approach, Sayles and Thomas (1978) presented experimental relations between wavelength and the scaled power spectral density for many different surfaces. They argued that the scaled spectral density functions of many surface profiles can be approximately presented as G(ω) = 2πΛ/ω². Sayles and Thomas (1978) referred to Λ as the surface topothesy. As Dr. Sayles said to one of the authors (FB), they never claimed that the real surfaces are fractal; in fact the fractal terminology to surface roughness description was triggered by Berry and Hannay (1978) who presented a comment to Sayles and Thomas (1978) paper where they claimed that geometric properties of rough surfaces can be characterized by a new concept 'fractal' that was described in detail by Mandelbrot (1977).

Another important step in the promotion of the fractal approach to surface roughness description was the studies of the Weierstrass-Mandelbrot fractal function by Berry and Lewis (1980). Later the Weierstrass type functions were used by many researchers as a model of rough surfaces (see e.g., Roques-Carmes et al., 1988; Majumdar and Bhushan, 1990). For some period of time, the fractal models became very popular, there were even statements that “fractals are everywhere.” Fractal approach to surface topography were so popular that one could say that it became an “emperor” of many research areas. Speaking about fractal approaches in fracture mechanics Borodich (1999) argued that instead of careful presentations of the state-of-the-art, the papers dedicated to fractal analysis are often based on repetition of common myths about fractals (we call this as vulgar fractal approaches). Hence, in most of the papers dedicated to fractal approaches to fracture and surface topography, the state-of-the-street is ruling. Borodich (2002) listed examples introduced earlier by Borodich and Onishchenko (1993) and Borodich (1993) and reminded that “the fractal dimensions alone cannot characterize the features of contact.” The same situation is related to the papers dedicated to fractal approaches to surface topography, nevertheless there is still a stream of papers based on vulgar interpretation of the fractal approaches. One could mention here a statement by Mandelbrot (1998) that “fractals are not a panacea; they are not everywhere.” Using examples introduced by Borodich and his co-authors, we will show that quite often there is no meaning in fractal analysis of surface roughness.

Nowadays another tendency is quite popular, namely to describe rough surfaces using solely the PSDFs of surface topography. We argue that these papers are in essence an attempt to resurrect the fractal approach. Indeed, these papers contain usually a mixture of correct statements related to Gaussian processes and wrong statements based on attempts to extend the power-spectral analysis to non-Gaussian surfaces. In addition, these papers suffer often by employment of the ill-defined terms, such as the Hurst exponent, non-accurate statements about self-affinity of surface roughness and vulgar interpretation of fractal models. We will show that the power-spectral analysis applied to non-Gaussian surfaces is a kind of reformulation of the vulgar fractal approach. Using an analogy to Andersen's tail about new clothes produced by cunning weavers, we can say that attempts to model surfaces solely by the use of the PSDF of its roughness are “the emperor's new clothes.”

The paper is organized as follows. In section 2 probabilistic characteristics of rough surfaces are discussed. In section 3 we consider some approaches to modeling of surface roughness using graphs of random processes that in turn, assume that the asperity heights are normally distributed or they employ similar assumptions that involve normal distributions. We give a brief description of statistical methods employed for checking normality of distributions and some results of application of these tests to roughness of engineering surfaces. In section 4 we discuss briefly the fractal approaches to surface roughness, in particular using a kind of parametric-homogeneous functions having fractal graphs, e.g., the Weierstrass-Mandelbrot functions, we clarify some common misinterpretations of statements by Berry and Lewis (1980). Finally in section 5 we discuss the models of surface roughness based solely on properties of the auto-correlation function or its Fourier transform (the PDSF). We argue that these models do not reflect tribological properties of surfaces. In particular, it is demonstrated that rather different profiles may have the same inclination of the PSDF in logarithmic coordinates, or they may have even the same PSDF. Thus, there is very small scientific value (if any) of a number of papers that model surface roughness only by its PSDF.

2. Probabilistic Characteristics of Surface Roughness

If one considers a nominally flat surface and a plane perpendicular to the surface, then the surface profile is the cross-section between the plane and the rough surface. The rough profile may be presented as graph of a function z(x). Let $\bar{z}$ denote the mean profile line. If the origin level of the height measurements is taken at $\bar{z}$ then

$\frac{1}{2L}{\displaystyle {\int }_{-L}^L}\left[z(x)-\bar{z}\right]dx=0.$

Let us mention here several popular height parameters: R_max is the maximum height of the profile z(x) defined on an interval [−L, L], R_a is the arithmetical mean deviation of the surface, and the root mean square (rms) height R_q or σ² that is the square root of the mean square deviation with respect to the mean profile line $\bar{z}=0$. The mathematical expressions for these parameters are given by

$R_{max}={\displaystyle \underset{x\in \left[-L,L\right]}{max}}z(x),$

$\begin{array}{l}\hfill R_a=\frac{1}{2L}{\displaystyle {\int }_{-L}^L}|z(x)|dx\approx \frac{{\displaystyle {\sum }_{i=1}^n}|z(x_i)|}{n},\hfill \\ \hfill R_q=\sigma ={\left[\frac{1}{2L}{\displaystyle {\int }_{-L}^L}{\left[z(x)\right]}^{2}dx\right]}^{1/2},\hfill & (3)\end{array}$

where n is the number of points of measurements on the interval and z(x_i) is the measured height at the interval point x_i. In addition, the arithmetic mean height R_z is often used for practical applications. This parameter may be calculated as the average distance between the five highest picks and the five lowest points of the profile, i.e.,

$\begin{array}{ll}{R}_z=\frac{1}{5}\left[{\displaystyle \sum _{i=1}^5}{(z_i)}_{max}-{\displaystyle \sum _{i=1}^5}{(z_i)}_{min}\right].& (4)\end{array}$

One can introduce the density probability function ϕ(z). This function shows the probability that the height z(x) at a surface point x is between z and z + dz. Then, the expressions for R_a and σ² in (3) is written as

$\begin{array}{ll}{R}_a={\displaystyle {\int }_{-\infty }^{\infty }}|z|\varphi (z)dz,{\sigma }^2={\displaystyle {\int }_{-\infty }^{\infty }}{z}^2\varphi (z)dz.& (5)\end{array}$

It is natural that the roughness parameters depend on the scale of considerations. For example, if z_i = z(x_i) are measured with a stylus steps h then one can calculate the curvature of the profile peaks κ(x_i)

$\kappa (x_i)=-(z_{i-1}-2z_i+z_{i+1})/h^2.$

However, it was found that the mean curvature varies depending on the sampling intervals (Greenwood, 1992). There was a hope that the fractal dimension could provide a scale independent parameter of surface roughness. It will be discussed later that actually this assumption was not justified.

Kragelsky (1948) published one of the first papers where he claimed that the roughness heights distribution is Gaussian (normal). Although Zhuravlev (1940) presented the general expressions of his model for arbitrary bearing area curve, his example that employed linear dependence as an approximation of the bearing area curve was criticized by Kragelsky (1948) who wrote that the normal distribution of heights should be used.

We will not list here a number of parameters used in literature on tribology to describe the surface roughness. Various attempts to describe surface topography using several statistical parameters of surface roughness are described in detail in many books and papers, see e.g., Khusu et al. (1975), Nowicki (1985), and Whitehouse (2011). Some of these parameters are useful but most are not (Whitehouse, 1982).

An example of a very useful parameter is the Abbott-Firestone curve of the surface heights (bearing area curve) or the cumulative distribution function Φ(z)

$\begin{array}{ll}\Phi (z)={\displaystyle {\int }_z^{\infty }}\varphi (t)dt.& (6)\end{array}$

For example, the Φ(z) was used by Zhuravlev (1940).

Let us demonstrate that for rough surfaces their contact properties are correlated with Φ(z) that is equal to the length of a horizontal slice of the surface profile at the level h. Sometimes this curve can be used to estimate the force acting of a rough solid penetrating into an elastic foundation. Indeed, it if the characteristic size of contact region between a blunt punch and a thin elastic layer is larger than the layer thickness then the leading term of the asymptotic solution may be modeled as the Fuss-Winkler foundation (see e.g., Aleksandrov, 1963; Borodich et al., 2019b; Erbaş et al., 2019; and references therein). The Fuss foundation can be represented by a collection of independent springs attached to a rigid flat or as an elastic “mattress” (Winkler, 1867; Johnson, 1985) or as a punch acting on a liquid layer (Fus, 1801). Of course, there are restrictions on the use of the Fuss-Winkler foundation (Johnson, 1985; Popov, 2010). As Fus (more often his surname is written as Fuss) noted himself: “when a crumbly surface has a rigid substrate and does not have such depth as it should be for penetration of wheels into it by laws of hydrostatic, therefore the angle GOR” (the angle between the wheel and the surface flat) “should not be determined just by actual penetration depth but rather by the depth of the rigid support” (Fus, 1801). The Fuss-Winkler foundation was employed to model contact between an elastic foundation and (i) a nominally flat C_B profile (Borodich and Mosolov, 1991, 1992); (ii) the rough hierarchical multi-level profile (Borodich and Onishchenko, 1993, 1999), and (iii) both nominally concave and convex fractal parametric-homogeneous punches (Borodich, 1998b).

The roughness parameters used may be formally divided in the following groups (Nowicki, 1985): (i) various parameters related to the shape of asperities, e.g., the rms curvature of the asperities; (ii) various parameters related to the asperity heights; (iii) horizontal parameters; (iv) parameters connected with amplitude of the asperities and their spatial extend, like the high spot count.

3. Gaussian Random Processes as Models of Rough Surfaces

As it has been mentioned above, the surface roughness may be considered as graphs of random processes. The question if the process is Gaussian (normal) or not is crucial for estimation of validity of the models. Indeed, the overwhelming majority of papers on surface topography use statistical models of surface roughness based on explicit or implicit assumption of normality of roughness heights, see e.g., Fuller and Tabor (1975), Galanov (2011), and a discussion by Borodich et al. (2016).

3.1. Tests for Normality of Surface Roughness

There are many tests of normality (Thode, 2002). Each of these tests provides a quantitative estimation of proximity between the theoretical Gaussian distribution and an observed sample of measurements by producing the so-called p-value. The estimations are based on a particular test statistic. Borodich et al. (2016, 2019a) and Pepelyshev et al. (2018) used the most popular tests of normality to check normality of roughness of various surfaces. The afollowing tests were employed: Kolmogorov-Smirnov (KS), Anderson-Darling (AD), Cramer-von Mises (CVM), Shapiro-Wilk (SW), Shapiro-Francia (SF), Lilliefors (LF), and the Pearson. The p-value is a number that characterizes for the observed measurements, the significance at the scale [0, 1] that the normality hypothesis is true. It is possible to nominate the acceptable significance level. In our tests it was 5%. If the p-value is more than this level then the hypothesis should be accepted. This subject is a current challenging task in contact mechanics description and comprehension of nano-related phenomena as highlighted by Carpick (2018).

Let us mention here a model of dry friction developed by Borodich and Savencu (2017). In this model molecular and chemical interactions are mainly connected to the nano-scale asperities, while mechanical interlocking between surfaces are connected to the micro-scale asperities. According to this model, for proper modeling of friction, one needs to get data about the surface roughness at both atomic/nano and at micro-scales. Using the above mentioned tests of normality some data obtained for grinding surfaces was tested and results of the normality tests were negative at both nano and microscales (Borodich et al., 2016).

Then the test of normality were applied to surfaces of the epoxy resin replicas of polishing papers of various nominal asperity sizes. A white light interferometer (Zygo NewView 6000; Zygo Corporation, Middlefield, CT, USA) at a magnification of 50 was used for characterization of the surface roughness. The normality tests showed that the height distribution of the surfaces of nominal 0.3 and 1 μm are Gaussian (Pepelyshev et al., 2018). Finally, normality of roughness of carbon-based coatings deposited by direct current pulsed magnetron sputtering at two different substrate bias voltages was checked. The same as in the case of grinding surfaces, the roughness was measured at atomic/nano scales by AFM (Atomic Force Microscopy), while a profilometer was used for measuring of micro-asperity heights (Borodich et al., 2019b). It was found that surfaces at micrometer scale are normal. It is interesting to note that the AFM measurements with the 117 nm steps showed that the roughness of surfaces was Gaussian, while the AFM measurements with the 10 nm steps showed that the assumption of normality of roughness is not satisfied. This means that the use of the above mentioned statistical models of contact between nominally flat surfaces are justified only up to nanoscale, while their applicability at atomic and few nanometers scales may be questionable.

3.2. Stochastic Models of Surface Roughness

The normality of roughness is related to vertical distribution of profile heights. However, it is also very important to consider the horizontal distribution of the asperities. As it has been noted by Maugis (2000), two profiles may have the same peak height (local extrema) distributions, but the roughness may be rather different in the horizontal extension. If process is Gaussian then the horizontal properties may be fully described by the auto-correlation (correlation) function R of the process (2). Instead of R, one can use the PSDF (3), its Fourier transform G(ω).

Khusu et al. (1975) presented results of very detailed studies of Gaussian processes in applications to surface roughness. In addition to (1), they considered three other correlation functions. An extended list of various correlation functions was presented by Dette et al. (2015). However, we would like to emphasize again that the above results are effective if the roughness is Gaussian. If the roughness is not normal then the properties of the sample paths are not fully determined by the mean and covariance functions (see e.g., Ghosal and Van der Vaart, 2017).

It is known (see e.g., Aldous, 1989 and Bibby et al., 2005) that a non-Gaussian processes can be generated by the mean-reversing stochastic differential equation

$\begin{array}{ll}dX(x)=-\theta (X(x)-\mu )dx+\sigma (X(x))d{W}_B(x),& (7)\end{array}$

where x ≥ 0 and W_B(x) is the standard Brownian motion (Wiener process). Choosing the appropriate value of the parameter μ and the function σ(·), we obtain a certain height distribution of the process X(x), while the auto-correlation function is ρ(x) = e^−θ|x| and the power spectra is $G(\omega )=\frac{2}{\pi }\theta /({\theta }^2+{\omega }^2)$ for any choice of μ and σ(·). For example, the height distribution of X(x) has the gamma density with parameters λ and β if μ = β/λ and $\sigma (X)=\sqrt{2\theta X/\lambda }$ and the beta density with parameters α and β if μ = α/(α + β) and $\sigma (X)=\sqrt{2\theta X(1-X)/(\alpha +\beta )}$. Figure 1 shows simulated profiles with various height distributions and the same auto-correlation function R(x) = e^−θ|x|.

FIGURE 1

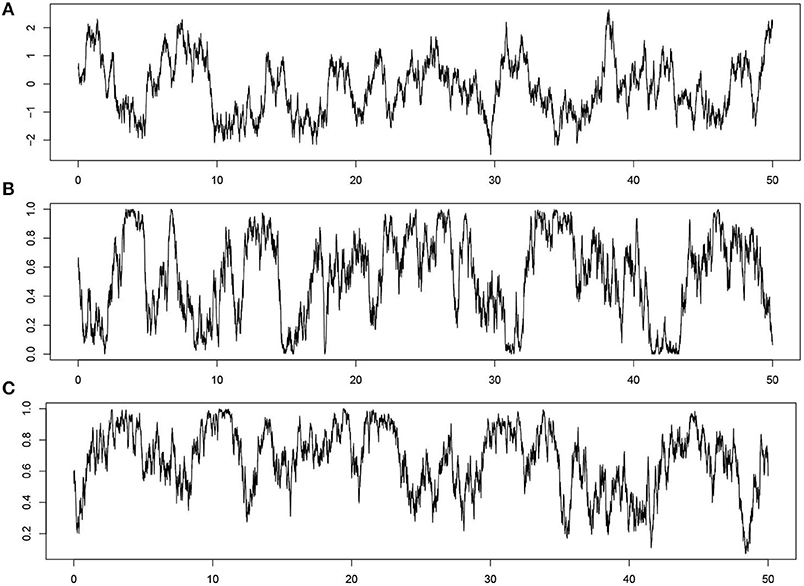
Figure 1. The simulated profiles X(x): (A) θ = 1, μ = 0, σ(X) = 2, and the height distribution of X(x) is the Gaussian distribution; (B) θ = 1, μ = 0.5, σ(X) = 2X(1 − X), the height distribution of X(x) is the uniform distribution; (C) θ = 1, a = 2.2, b = 1.2, μ = a/(a + b), σ(X) = 2X(1 − X)/(a + b), the height distribution of X(x) is the beta distribution with parameters a and b.

In general, using (7), one can construct non-Gaussian processes with flexible auto-correlation function as the sum

$h(x)={\displaystyle \sum _{i=1}^m}{X}_i(x),$

where X₁(x), …, X_m(x) are independent and each X_i(x) is the solution of the stochastic differential equation

$d{X}_i(x)=-{\theta }_i(X(x)-{\varphi }_i{\mu }_i)dx+{\sigma }_i(X(x))d{W}_i(x),$

ϕ_i > 0 and $\sum _{i=1}^m{\varphi }_i=1$, see Bibby et al. (2005). Such the process h(x) has the auto-correlation function and the power spectra

$R(x)={\displaystyle \sum _{i=1}^m}{\varphi }_i{e}^{-{\theta }_i|x|},G(\omega )=\frac{2}{\pi }{\displaystyle \sum _{i=1}^m}\frac{{\varphi }_i{\theta }_i}{{\theta }_i^2+{\omega }^2}.$

The above examples support the statement that the mean and covariance functions of a random non-Gaussian process do not determine the finite-dimensional distributions of a random process (Gusak et al., 2012).

4. Fractals Approaches to Surface Topography

Concepts of fractal, fractal geometry and fractal dimension (FD) were introduced by Mandelbrot (1975). However, he did not give any definition of fractals. Later he defined fractal sets in a metric space saying “a fractal will be defined as a set for which the Hausdorff-Besicovitch dimension strictly exceeds the topological dimension” (Mandelbrot, 1977). Finally he withdrew the definition and suggested to use the term “without a pedantic definition” (Mandelbrot, 1983). This was the reason for a comment by Greenwood (1992): “Mandelbrot is somewhat reluctant to define ‘fractals' or ‘fractal dimension' preferring to offer examples.” A popular description of many self-similar sets studied by fractal geometry, such as the Cantor staircase, von Koch snowflake, Sierpinski carpet, Menger sponge, along with Peano curve and other sets may be found in the book for school children published by Vilenkin (1968). Definitely Mandelbrot (1975) wrote his book under influence of Vilenkin's book. Indeed, at least 20% of Figures presented by Mandelbrot (1975) had analogs in the book by Vilenkin (1968). The above mentioned sets are out the scope of mathematical programmes for schools and for non-mathematical specializations of universities because the sets are more irregular than sets considered in common courses on Euclidean geometry. To encourage children for studies of set theory, Vilenkin used many funny stories and terms, e.g., he used the term the Devil staircase to describe the Cantor staircase. The Devil staircase term was later used and popularized by Mandelbrot (1983).

Because there is no generally accepted definition, we will define fractals as objects with a non-integer FD. Evidently, the term FD must be defined separately. One of the authors (FB) and his co-authors have already published several reviews related to fractals, in particular a review related to the use of fractal concepts in fracture mechanics (Borodich, 1999). There are reviews of application of fractal ideas in contact problems (Borodich and Onishchenko, 1999; Borodich, 2013c) and several articles about the use of fractal concepts in tribology (Borodich, 2013a,b; Borodich and Evans, 2013). Borodich introduced the C_B profile that is also known as the Cantor set model (Warren and Krajcinovic, 1996), and as the Cantor-Borodich profile, structure or fractal, see e.g., Abuzeid and Eberhard (2007); Soldatenkov (2015), and Thielen et al. (2016). At least two kind of contact problems can be solved for a punch described by the C_B profile (Borodich and Mosolov, 1991, 1992). The model was developed further by Borodich and Onishchenko (1993), Warren and Krajcinovic (1996), Plesha and Ni (2001), and others. Although Archard (1957) introduced the idea of hierarchical structure of roughness, there were no papers developing the idea of “bump on bump” structure of roughness until Borodich and Onishchenko (1993, 1999) introduced the multilevel hierarchical model of roughness. Now this idea of hierarchy of surface structures is quite popular due to discoveries of Gorb and his co-workers along with other experts in biological objects. In particular, the hierarchical structures were discovered in adhesive setae of geckos (Gao et al., 2005) and spiders (Schaber et al., 2019); water-repellent coatings of whip-spiders (Wolff et al., 2016); attachment discs of spiders (Wolff et al., 2015), and super-black snake skin (Spinner et al., 2013). Applications of fractal concepts to surface roughness were also discussed by Borodich and Galanov (2002) and by Borodich et al. (2016). Thus, here we will just remind some basic features of the fractal approach to surface roughness.

4.1. Mathematical and Physical Fractals

Unfortunately, many papers dedicated to applications of fractals do not provide definitions of used terminology. Often such papers are just a mess of vague discussions and non-justified statements. To clarify the subject, we split fractals into mathematical and physical (natural) fractals (see e.g., Borodich, 1997). Both mathematical and physical fractals use the concepts of a cover. This means that the object (set) is covered by cubes of size at most or equal to δ. Fractal geometry deals with mathematical fractals. The mathematical methods of fractal geometry are described in many books and papers (see e.g., Falconer, 1990; Tricot, 1995) where various FD are studied in application to mathematical objects. Various FDs are used in the studies, mainly the Hausdorff dimension and box-counting dimensions usually attributed to Minkowski, Bouligand, Pontrjagin, Schnirelman, and Kolmogorov. These FDs can be calculated by taking the limits when δ → 0. In addition, fractal geometry term is also quite often applied loosely to a collection of semi-empirical or empirical methods for estimations of the FDs of objects.

If real world or numerically simulated objects demonstrate the power-law of the number-radius relation then these objects are physical fractals. The power-law of the number-radius relation is

$\begin{array}{ll}N(\delta )~{\delta }^{-D},{\delta }_{*}\le \delta \le {\Delta }_{*},N(R)~{(R/\delta )}^D,r_{*}\le R\le R_{*}& (8)\end{array}$

where N(δ) is the number of cubes of size δ used to cover the object, D is a FD of the object, Δ_* and δ_* are the upper and lower cut-offs of the physical fractal law, respectively. The former relation of (8) is used when the cover size δ is varied and the object size R is fixed, while in the latter relation is used when the cover size δ is fixed and the object size R is varied. In this latter case R_* and r_* are the upper and lower cut-offs. The the slope of linear approximation of ln(N(δ_*)) against ln(${R}$) is used to estimate the value of D. The main distinction between these kinds of fractals is the following: the physical fractal behavior (8) is observed on a bounded region of scales only, while to study mathematical fractals one has to scale of consideration to zero limit.

4.1.1. Self-Similar Sets

Introduction to fractals starts often by presenting self-similar sets mentioned above (see examples given by Vilenkin (1968) and Mandelbrot, 1975). Due to such examples, there is a myth that all fractals are self-similar. However, self-similar sets are a very specific kind fractals. In general, self-similarity is not related to mathematical fractals. Their scaling properties are based on scaling of fractal measure or quasi-measure (see a discussion by Borodich and Feng, 2010, and Borodich, 2019), while for physical fractals their scaling properties are reflected by the relation (8).

4.1.2. Some Specific Features of Mathematical Fractals

Speaking about mathematical fractals, one has to specify the FD used. It is wrong to say that all FDs are equal to each other. For example, the Hausdorff dimension dim_HS of a set S may be not equal to its box-counting dimension dim_BS. However it is known that dim_HS ≤ dim_BS.

The statement that all nowhere differentiable curves are fractals is wrong. For example, Borodich (1998a) introduced the Moscow University function U_M that is nowhere differentiable, while it is a non-fractal curve and each finite subinterval of [1, 2] contains an infinite number of reduced copies of the whole function, i.e., it is a self-similar curve.

A mathematical fractal curve has an infinite length. Borodich (1997) formulated the following paradox in application to fractal fracture: if the crack surface is modeled as a mathematical fractal and the concept of the Griffith surface energy is used, then the propagation of the fractal crack is impossible.

If a surface is smooth then it is not a mathematical fractal (see e.g., Falconer, 1990). Even if a mathematical fractal curve is continuous everywhere, it is nowherehas differentiable. Therefore, it is often very difficult to formulate a boundary-value problem for solids having fractal boundary (see a discussion by Borodich and Volovikov, 2000). Indeed, such nowhere differentiable profile do not have even normal vector.

4.1.3. Some Specific Features of Physical Fractals

If the FD is specified then it is convenient to use the fractional part of the FD D^*. Then the FDs of fractal profiles and surfaces are 1 + D^* and 2 + D^*, respectively.

Sayles and Thomas (1978) presented the experimental relations between normalized PSDF and wavelength in logarithmic coordinates as a very impressive united line for many different surfaces. One could think that the relation spans from micrometers to many meters. However, Berry and Hannay (1978) noted that for each individual type of topography the span was over much smaller ranges. They argued that these experimental results could be represented as a united line lg(G) ~ lg(ω) due to a specific normalization of the results. Further, researchers from Jerusalem presented results of an analysis of data published by Physical reviews journals and showed that in average the physical fractals span about 1.5 orders of magnitude (Avnir et al., 1998). Mandelbrot (1998) argued that the published limited-range examples of power law correlations may be explained as unfortunate side effects of enthusiasm, imperfectly controlled by refereeing. However, the Jerusalem group disagreed with his arguments and believed that the limited-range relations for natural fractal are the dominant fractals observed in Nature (Biham et al., 1998). However, if the value of the FD is stable for less than two or three decades then fractal concept is not useful, as it was stated by Whitehouse (2001).

In general, the FD values obtained by various practical methods are not reliable (see a discussion by Borodich and Evans, 2013). For example, the power spectrum method is often employed for estimation of FD values of self-similar or self-affine fractals, in particular rough profiles (see e.g., Dubuc et al., 1989; Schmittbuhl et al., 1995). The method is based on a not very accurate statement when the power spectrum obeys a power law G(ω) ~ c/ω^α. it is reasonable to expect a signal with a ω^−α power spectrum to have a graph of dimension (5 − α)/2 (see Falconer, 1990). Normally the exponent α is in the range 1 < α ≤ 3.

As Whitehouse (2001) noted there is a very small spread of the FD values obtained for surfaces produced by different manufacturing processes. In addition, there is no well-established algorithm for estimations of the fractal law cut-offs. Thus, the physical significance of the fractal approach is very limited. We can add that if one can attribute the fractal scaling for a small range that spans for just 1.5 or 2 decades then fractals do not provide a scale-independent description of surface roughness.

4.2. Parametric-Homogeneity

One of the authors (FB) and his co-authors introduced different types of fractal profiles that allowed to handle rough fractal surfaces rigorously. There were introduced : (i) the C_B profile (Borodich and Mosolov, 1991, 1992), (ii) multilevel Hierarchical profile (Borodich and Onishchenko, 1993, 1999), and (iii) graphs of parametric-homogeneous functions (Borodich, 1993, 1998a,b). The first two profiles were based on an iterative procedure and they has been already mentioned above, while PH-functions will be described below. Note that the general statements obtained by Borodich and his co-authors about the contact problems for all these three types of surfaces do not depend on the statements about their FDs, i.e., they are valid for both fractal and non-fractal cases.

The same author (FB) introduced also the concept of parametric-homogeneity. The concept includes parametric quasi-homogeneous (PQH) transformations (in particular parametric-homogeneous (PH) transformations), corresponding functions, and PH- and PQH-sets. The PH and PQH-functions can be considered as a natural generalization of concepts of homogeneous and quasi-homogeneous functions. If the latter kind of functions is based on the use of the classical scaling with arbitrary positive scaling factor λ, PH-functions and PQH-functions are based on the use of discrete self-similarity with a fixed rescaling parameter p. Let ℤ be the set of integer numbers. Then one can employ the discrete group of coordinate dilations (${\Gamma }_{p^{\alpha k}}$) apply the following PH-transformation

${\Gamma }_{p^{\alpha k}}\text{x}=(p^{k{\alpha }_1}{x}_1,...,p^{k{\alpha }_n}{x}_n),p>0,k\in \mathbb{Z}.$

4.2.1. Parametric Quasi-Homogeneous Functions

The parametric-quasi-homogeneous function of degree d and parameter p with weights α = (α₁, …, α_l) is denoted by $B_d:{ℝ}^l\to ℝ$ and it obeys the following scaling law for a positive parameter p, p ≠ 1 and any k ∈ ℤ

$B_d({\Gamma }_{p^{\alpha k}}\text{x};p)=B_d(p^{k{\alpha }_1}{x}_1,...,p^{k{\alpha }_l}{x}_l;p)=p^{kd}{B}_d(\text{x};p),$

The parameter should be unique in some domain (Borodich, 1998a,b). I α₁ =... = α_l then PQH-functions is called a PH-functions. It is clear that if p is a parameter of the PH-transformation then p^k can be also used as a parameter. Hence, as the parameter, the least p:p > 1 is taken. The graphs of these functions can have various properties, in particular they can be smooth or fractal. The following fractal Weierstrass type functions and smooth sinusoidal log-periodic functions are examples of PH-functions

$\begin{array}{l}\hfill b_{\beta }(x,p)={\displaystyle \sum _{n=-\infty }^{\infty }}{p}^{-\beta n}f(p^{n}x)\hfill \\ \hfill \text{ or }{b}_0(x;p)=Acos(2\pi lnx/lnp+\Phi ),\hfill \end{array}$

where A and Φ are arbitrary constants and f is an arbitrary function. For any point x₀, the PH-functions are repeated $b_d(p^k{x}_0;p)=p^{kd}{b}_d(x_0;p)$ in scaling form near all points $p^k{x}_0,k\in \mathbb{Z}$.

4.2.2. Weierstrass-Mandelbrot Functions

Mandelbrot (1977) generalized the Weierstrass function, whose graph is continuous everywhere and differentiable nowhere, and introduced the complex value Weierstrass-Mandelbrot (W-M) function W(x) and its particular real case C(x; p)

$\begin{array}{l}W(x;p)={\displaystyle \sum _{n=-\infty }^{\infty }}{p}^{-\beta n}(1-e^{i{p}^{n}x})e^{i{\varphi }_n},\\ C(x;p)={\displaystyle \sum _{n=-\infty }^{\infty }}{p}^{-\beta n}(1-cos(p^{n}x)),p>1,0<\beta <1& (9)\end{array}$

where ϕ_n are arbitrary phases. Properties of these functions were studied in detail by Berry and Lewis (1980). The box dimension of C(x; p) graphs is D = 2 − β. There is no rigorous mathematical proof that its Hausdorff dimension is the same.

It is evident that C(x; p) is a particular PH-function (9) of degree β. As it has been mentioned above, the graph of C(x; p) function was used often for modeling rough profiles.

In addition, Berry and Lewis (1980) were first who studied the discrete power spectrum G(ω) of the W graphs (9) and approximated it by a continuous spectrum $\overline{G(\omega )}~{\omega }^{-(5-2D)}$. This is in agreement with the above mentioned statement by Falconer (1990).

4.2.3. Self-Affine Scaling and the Hurst Exponent Terms

Many papers dedicated to studies of surface roughness mention the concept of self-affine fractals without any definition of the concept. However, one should be very careful using such terms as self-affine scaling. Actually, it is known from mathematical courses that mapping on a plane is self-affine if it is a one-to-one mapping whose images of any three collinear points in turn belong to a line. Under this mapping the angle between two straight lines is normally not preserved. A particular case of such mapping is the quasi-homogeneous (QH) or anisotropic coordinate dilation

$\begin{array}{ll}{x}^{\prime }=e^{{\alpha }_1}x,y^{\prime }=e^{{\alpha }_2}y& (10)\end{array}$

where α₁ and α₂ are weights, ${\lambda }_x=e^{{\alpha }_1}$ and ${\lambda }_y=e^{{\alpha }_2}$ are scaling factors. This means that if a coordinate system x, y was Cartesian one then the x′, y′ system is also rectangular. However, papers on fractals reduce usually the term self-affine mapping to the above particular QH case.

In 1980 the concept of fractal was very novel. Perhaps for popularization of the concept, they used some explanations and statements that were not mathematically rigorous. For example, studying W-M functions, they wrote The fractal nature of W implies that repeated magnification of its graph reveals ever-finer levels of detail. The levels of detail are self-similar under an affine scaling in which the x axis is stretched by a factor p and W axis by p^2−D [note we have changed γ and t used by Berry and Lewis (1980) to p and x, respectively]. Unfortunately, these statements of Berry and Lewis (1980) were misinterpreted and used in many papers as generally accepted and mathematically rigorous statements applicable to all so-called self-affine fractals.

There was an attempt by Mandelbrot (1986) to develop further the concept of self-affinity. He formulated several statements about self-affine fractals that were not supported by any strict definition of these fractals. In essence, his statements are: there are both local and global scaling for self-affine fractals and each version of FD for self-affine fractals has a local and a global value, separated by a crossover. However, these statements have no mathematical meaning.

Schmittbuhl et al. (1995) wrote that the scaling (10) means that the heights h are homogeneous functions of the scaling factors (putting λ_x = λ_y)

$h({\lambda }_{x}x,{\lambda }_{x}y)={\lambda }_x^{H}h(x,y)$

where the homogeneity exponent H is the self-affine exponent, or the Hurst exponent. Unfortunately, the statement by Schmittbuhl et al. (1995) about the homogeneity of the fractal graphs is not very accurate, while the meaning of the Hurst exponent is ill-defined. It would be better if they would say that the fractal roughness to obey a discrete dilation homogeneity, i.e., it obeys the PH-law. Indeed, the scaling properties of C(x; p) function are connected with the discrete group of coordinate dilation

$\begin{array}{ll}C(p^{k}x;p)=p^{(2-D)k}C(x;p).& (11)\end{array}$

Although this scaling is quite often attributed to FD of the C(x; p) graph, saying that H = 1 − D^*, these statements are wrong because the scaling properties are governed by the degrees d of PH-functions. (Borodich, 1998a,b) showed that he can construct PH-functions with prescribed global trend h ~ x^d and given value of FD, while the Hausdorff and box-counting FDs of the Weierstrass type functions preserve their values under action of quasi-homogeneous transformation. For example, taking constants A and 0 < ϵ < < 1 one can construct PH-functions b_β(x, p) = C(x; p), b₀(x; p), b₁(x; p) and b₂(x; p)

$\begin{array}{l}\hfill b_0(x;p)=x^{-\beta }C(x;p),b_1(x;p)=Ax\left[1+ϵb_0(x;p)\right],\\ \hfill b_2(x;p)=A{x}^2\left[1+ϵb_0(x;p)\right]& (12)\end{array}$

have the same values of the Hausdorff and box dimensions and absolutely different trends. On the other hand, if one uses the above self-affine terminology then b_β(x, p) and b₂(x; p) are self-affine fractals, while b₁(x; p) is self-similar fractal because

$\begin{array}{l}{b}_1(p^{k}x;p)=p^k{b}_1(x;p).\end{array}$

It follows from the above discussion that Hurst exponent is an ill-defined term and it is not connected to FDs of the PH-graphs.

A statement by Mandelbrot (1983) is often cited. Mandelbrot (1983) wrote that coastlines are not circles, clouds are not spheres, and mountains are not cones, assuming that they have to be modeled as fractals. Borodich and Onishchenko (1999) extended Mandelbrot's statement saying that roughness of real bodies is not a mathematical fractal and all these geometrical objects: spheres, cones, circles as well as fractals are only mathematical idealizations of complex shapes of natural objects. Mathematical and physical fractals should not be confused. Certainly one can employ mathematical fractal as a possible model that reflect the power-law number-radius relation or PSDF of a natural object within a bounded interval of scales. However, the obtained problem may be a very complicated.

5. Power Spectral Density Function Approaches to Rough Surfaces

The last 20 years or so the PSDF approach became very popular in tribology community (see e.g., Persson, 2006). In fact, the authors of the papers reduce the properties of rough surfaces just to their PSDF G(ω). This approach was criticized by Borodich (2002). He wrote: two punches having the same fractal surface but situated either above or below the surface show usually different asymptotics in both load-displacement and load-area relations. As an example he considered C_B profile and solutions presented by Borodich and Onishchenko (1993). Then Borodich et al. (2016) showed that any surface and its replica have the same power spectral density, therefore one cannot characterize contact properties of rough surfaces just by surface “spectrum.” Indeed, one can consider an absolutely flat smooth surface having many sharp dents and its complementary replica (an inverted replica): a surface having many sharp asperities of the surface roughness. Evidently, they gave absolutely different contact properties (see e.g., examples by Borodich and Onishchenko, 1993).

Moreover quite often the PSDF approach is reduced to the so-called self-affine surfaces by employment of the Hurst exponent term. As we have discussed above the term is ill-defined and such papers just create “new clothes” for the vulgar fractal approach.

Using examples, we will show below that the many common statements about rough non-Gaussian surfaces are wrong or just meaningless.

5.1. Smooth Functions May Have a Power-Law PSDF

Let us show that connections of FDs and the slopes of PSDFs in logarithmic coordinates are meaningless. As an example, consider a very simple and smooth PH-function, namely a sin log-periodic function. Figure 2 shows the power spectra for h(x) = sin(2π ln(x)/ln(p)) with x ∈ [0.0001, 1].

FIGURE 2

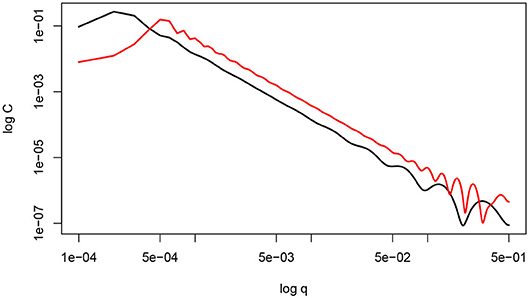
Figure 2. The power spectra of the profile h(x) = sin(2π ln(x)/ln(p)) for x ∈ [0.0001, 1] with p = 2 (black) and p = 1.3 (red).

It is clear that the function is non-fractal, nevertheless its power spectra in logarithmic coordinates located along a straight line within a bounded range of scales.

5.2. PSDFs Are Almost the Same for Different Truncated Weierstrass-Mandelbrot Functions

Let us consider two truncated Weierstrass-Mandelbrot functions

$\begin{array}{l}{C}_t(x;p)={\displaystyle \sum _{n=-N}^N}{p}^{-(2-D)n}(1-cos(p^{n}x)),\\ \end{array}$

$\begin{array}{l}A(x;p)={\displaystyle \sum _{n=-N}^N}{(-1)}^n{p}^{-(2-D)n}sin(p^{n}x),\end{array}$

where N is large natural number, p > 1 and D ∈ (1, 2). In addition, let us consider a function $x^{D-2}{C}_t(x;p)$. If N → ∞ then C_t(x; p) → C(x; p) and D is their box-dimension, however they have different trends.

Let us fix the values p = 1.5 and D = 1.5 and vary N. Let us calculate numerically the PSDFs for obtained graphs. The results are presented in logarithmic coordinates in Figure 3.

FIGURE 3

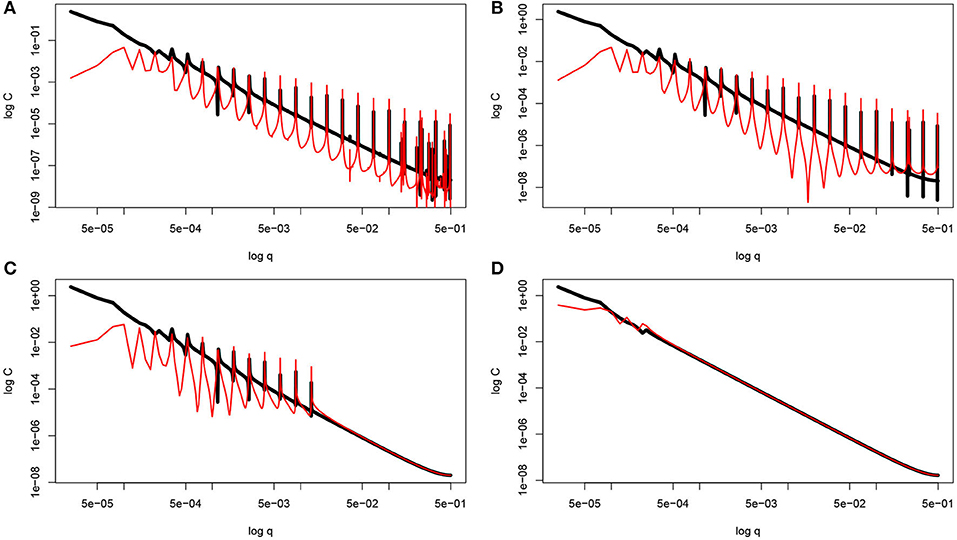
Figure 3. The power spectra of the profile C_t(x; p) (black) and the profile $x^{D-2}{C}_t(x;p)$ (red) for x ∈ [0, 1] with p = 1.5, D = 1.5 and varying N (A) N = 100; (B) N = 30; (C) N = 20; and (D) N = 10.

One can see that the average PSDFs are approximately the same while the functions are rather different.

Now let us fix the values p = 1.5, and N = 100 and vary D and calculate numerically the PSDFs for obtained functions. The results are presented in logarithmic coordinates in Figure 4. Note that for N = 100, the graphs of C_t(x; p) and $x^{D-2}{C}_t(x;p)$ are very close to graphs of PH-functions of degrees d = 2 − D and d = 0, respectively. We know that these functions have the same FD D and different trends (see a discussion above), while their PSDFs are very similar to each other.

FIGURE 4

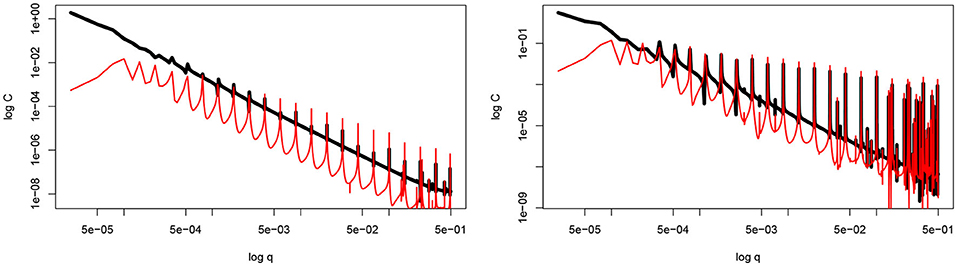
Figure 4. The power spectra of the profile C_t(x; p) (black) and the profile $x^{D-2}{C}_t(x;p)$ (red) for x ∈ [0, 1] with p = 1.5, and N = 100 for D = 1.3 (left), D = 1.7 (right).

The same procedure can be applied to the profiles A(x; p) and x^{D − 2}A(x; p). The results are shown in Figure 5. The results lead to the same conclusion as above.

FIGURE 5

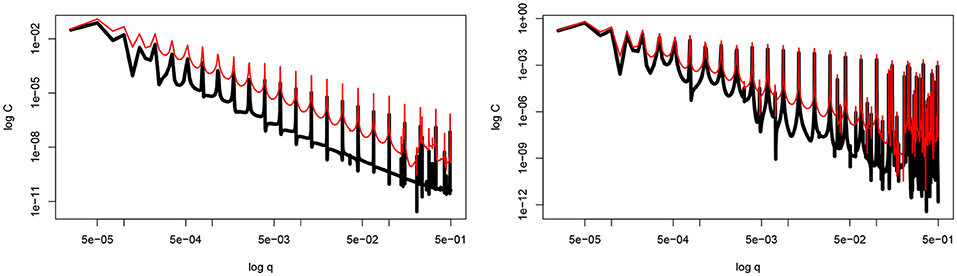
Figure 5. The power spectra of the profile A(x; p) (black) and the profile x^{D − 2}A(x; p) (red) for x ∈ [0, 1] for x ∈ [0, 1] with p = 1.5, and N = 100 for D = 1.3 (left), D = 1.7 (right).

5.3. PSDF Does Not Characterize Tribological Properties of Polished Surfaces

It is known that the tribological properties of gears can be greatly extended by improved surface finish (Krantz et al., 2001). This fact was employed by Harris et al. in a series of papers dedicated to the use of modern hard carbon-based coatings. Indeed, these hard carbon-based films can remove protuberances on the steel counterparts, reducing the values of high intensity stresses and the total number the stress concentration points. On the other hand, due to polishing of the coating asperities, the rate at which the coatings abrade steel declines as a power-law of the cycle numbers, i.e., very rapidly. The coated surface become super smooth even after just 500 cycles (see SEM images by Borodich et al., 2003). Let us consider the following thought experiment. An intact surface is modeled by a Gaussian function f₁(x) shown in Figure 1A (this assumption is in accordance with roughness measurements of intact surfaces by Pepelyshev et al., 2018 and Borodich et al., 2019a). Then the asperities of the surface have been polished away and the roughness of the polished parts are described by 0.1f₂(t) where the profile f₂(x) is shown in Figure 1B. Hence, the full polished surface is described by f₃(t) = min[f₁(x), 0.1f₂(x)] shown in Figure 6.

FIGURE 6

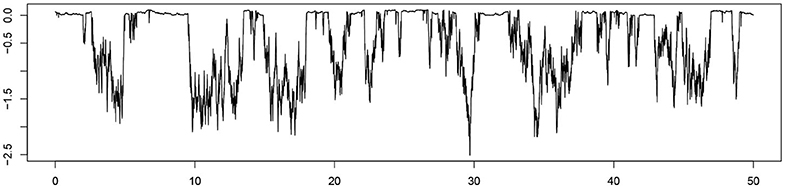
Figure 6. The “polished” profile f₃(t) = min[f₁(x), 0.1f₂(x)], where the profile f₁(x) is shown in Figure 1A and the profile f₂(x) is shown in Figure 1B.

Figure 7 shows the power spectra for the profile f₁(x) (black), the profile f₂(x) (red), and the “polished” profile f₃(x) = min[f₁(x), 0.1f₂(x)] (blue).

FIGURE 7

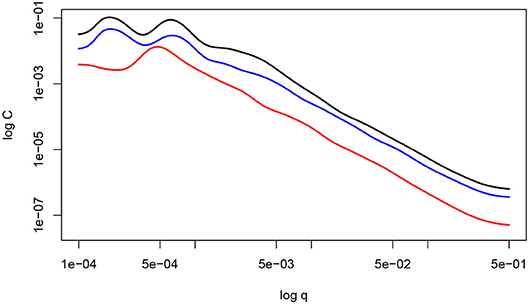
Figure 7. The power spectra for the profile f₁(x) (black) shown in Figure 1A, the profile f₂(x) (red) shown in Figure 1B, and the “polished” profile f₃(x) = min[f₁(x), 0.1f₂(x)] (blue).

These three profiles have the different outlook and tribological properties, however have the same exponent 1.9 in the power spectra, i.e., G(ω) ~ 1/ω^1.9.

6. Conclusions

A review of mathematical approaches for description of topography of engineering surfaces has been presented. It has been shown that in spite of huge amount of parameters used to characterize the surface topography, only some of the parameters are quite useful. However, their use is rather bounded, e.g., these parameters may be helpful at meso or even microscales, however they could be useless at the nanoscale.

There are many models of random processes, however just the case of Gaussian processes is well-elaborated. Some statistical methods employed for checking normality of distributions of asperity heights are reviewed. The preliminary results showed that the intact surfaces are quite often Gaussian at both micro and nanoscales, while the grinding surfaces are not normal.

Then the fractal approaches to surface roughness are discussed. Some common misinterpretations of statements by Berry and Lewis (1980) are also discussed. Some disadvantages of the fractal approaches and commonly reported wrong statements about fractals are listed. It is argued that the practical usefulness of the fractal approaches is rather doubtful. One should not expect that the employment of a mathematical fractal model of a rough surface will provide considerable advantages. In fact, such models may cause many mathematical difficulties. Thus, a strict approach to fractal modeling may substitute a difficult problem to another more difficult than the original one. Further, dimensions of physical fractals cannot be used as scale independent parameters. One should provide proper explanations of the fractal concepts used, otherwise this could lead to misinterpretation of the results. Unfortunately, quite often the answer to the question by Jelinek et al. (1998): Is there meaning in fractal analyses?, is “No.”

Finally the models of surface roughness based solely on properties of the auto-correlation function or its Fourier transform (the PDSF) are discussed. It has been noted that the PDSF approach to non-Gaussian surfaces are in essence the new clothes for the vulgar fractal approaches. We argue that these PDSF models do not reflect tribological properties of surfaces. In particular, it is demonstrated that rough profiles may have the same slopes of the PSDF in logarithmic coordinates, while they have rather different tribological properties. Thus, there is a bounded scientific value (if any) of a number of papers based on the PSDF approach.

Author Contributions

FB: substantial contributions to the conception of the work, analysis, and interpretation of published data for the work. XJ: analysis and interpretation of published data for the work. AP: statistical analysis of the results and numerical simulations for the work. All authors contributed to the article and approved the submitted version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors were grateful to support of Chongqing University enabled one of the authors (FB) to visit the University in 2019. One of the authors (XJ) would like to acknowledge the support from the National Science Foundation of China (Grant Nos. 11932004 and 51875059).

References

Abbott, E. J., and Firestone, F. A. (1933). Specifying surface quality: a method based on accurate measurement and comparison. Mech. Eng. 55, 569–572.

Google Scholar

Abuzeid, O. M., and Eberhard, P. (2007). Linear viscoelastic creep model for the contact of nominal flat surfaces based on fractal geometry: standard linear solid (SLS) material. J. Tribol. 129, 461–466. doi: 10.1115/1.2736427

CrossRef Full Text | Google Scholar

Aldous, D. (1989). Probability Approximations via the Poisson Clumping Heuristic. New York, NY: Springer-Verlag.

Google Scholar

Aleksandrov, V. M. (1963). On the solution of certain contact problems of the theory of elasticity. PMM J. Appl. Math. Mech. 27, 1490–1494.

Google Scholar

Archard, J. F. (1957). Elastic deformation and the laws of friction. Proc. R. Soc. A 243, 190–205.

Google Scholar

Archard, J. F., Hunt, R. T, and Onions, R. A. (1975). “Stylus profilometry and the analysis of the contact of rough surfaces,” in Proceedings of the IUTAM Symposium, eds A. D. de Pater and J. J. Kalker (Delft: Delft University Press), 282–303.

Google Scholar

Avnir, D., Biham, O., Lidar, D., and Malcai, O. (1998). Is the geometry of nature fractal? Science. 279, 39–40.

Google Scholar

Berry, M. V., and Hannay, J. H. (1978). Topography of random surfaces. Nature 273:573.

Google Scholar

Berry, M. V., and Lewis, Z. V. (1980). On the Weierstrass-Mandelbrot fractal function. Proc. R. Soc. A 370, 459–484.

Google Scholar

Bibby, B. M., Skovgaard, I. M., and Sorensen, M. (2005). Diffusion-type models with given marginal distribution and autocorrelation function. Bernoulli 11, 281–299. doi: 10.3150/bj/1116340291

CrossRef Full Text | Google Scholar

Biham, O., Malcai, O., Lidar, D. A., and Avnir, D. (1998). Fractality in nature: response. Science. 279, 785–786.

Google Scholar

Borodich, F. M. (1993). Similarity properties of discrete contact between a fractal punch and an elastic medium. C. R. Ac. Sc. (Paris) Ser. 2 316, 281–286.

Google Scholar

Borodich, F. M. (1997). Some fractal models of fracture. J. Mech. Phys. Solids 45, 239–259.

Google Scholar

Borodich, F. M. (1998a). Parametric homogeneity and non-classical self-similarity. I. Mathematical background. Acta Mech. 131, 27–45.

Google Scholar

Borodich, F. M. (1998b). Parametric homogeneity and non-classical self-similarity. II. Some applications. Acta Mech. 131, 47–67.

Google Scholar

Borodich, F. M. (1999). Fractals and fractal scaling in fracture mechanics. Int. J. Fracture 95, 239–259.

Google Scholar

Borodich, F. M. (2002). Comment on “Elastoplastic contact between randomly rough surfaces.” Phys. Rev. Lett. 88:069601. doi: 10.1103/PhysRevLett.88.069601

PubMed Abstract | CrossRef Full Text | Google Scholar

Borodich, F. M. (2007). Translation of historical paper. Introduction to V. A. Zhuravlev's historical paper: ‘on the question of theoretical justification of the Amontons-Coulomb law for friction of unlubricated surfaces’. Proc. Inst. Mech. Eng. J J. Eng. Tribol. 221, 893–894.

Google Scholar

Borodich, F. M. (2013a). “Fractal geometry,” in Encyclopedia of Tribology, eds Q. J. Wang and Y. W. Chung (New York, NY: Springer), 1258–1264.

Google Scholar

Borodich, F. M. (2013b). “Fractal nature of surfaces,” in Encyclopedia of Tribology, eds Q. J. Wang and Y. W. Chung (New York, NY: Springer), 1264–1269.

Google Scholar

Borodich, F. M. (2013c). “Fractal contact mechanics,” in Encyclopedia of Tribology, eds Q. J. Wang and Y. W. Chung (New York, NY: Springer), 1249–1258.

Google Scholar

Borodich, F. M. (2019). Development of Barenblatt's scaling approaches in solid mechanics and nanomechanics. Phys. Mesomech. 22, 73–82. doi: 10.1134/S1029959919010119

CrossRef Full Text | Google Scholar

Borodich, F. M., and Bianchi, D. (2013). “Surface synthesis based on surface statistics,” in Encyclopedia of Tribology, eds Q. J. Wang and Y. W. Chung (New York, NY: Springer), 3472–3478.

Google Scholar

Borodich, F. M., Brousseau, E., Clarke, A., Pepelyshev, A., and Sanchez-Lopez, J. C. (2019a). Roughness of deposited carbon-based coatings and its statistical characteristics at nano and microscales. Front. Mech. Eng. 5, 73–82. doi: 10.3389/fmech.2019.00024

CrossRef Full Text | Google Scholar

Borodich, F. M., and Evans, H. P. (2013). “Fractal characterization of surfaces,” in Encyclopedia of Tribology, eds Q. J. Wang and Y. W. Chung (New York, NY: Springer), 1246–1249.

Google Scholar

Borodich, F. M., and Feng, Z. (2010). Scaling of mathematical fractals and box-counting quasi-measure. ZAMP 61, 21–31. doi: 10.1007/s00033-009-0010-6

CrossRef Full Text | Google Scholar

Borodich, F. M., and Galanov, B. A. (2002). Self-similar problems of elastic contact for non-convex punches. JMPS 50, 2441–2461. doi: 10.1016/S0022-5096(02)00031-5

CrossRef Full Text | Google Scholar

Borodich, F. M., Galanov, B. A., Perepelkin, N. V., and Prikazchikov, D. A. (2019b). Adhesive contact problems for a thin elastic layer: Asymptotic analysis and the JKR theory. Math. Mech. Solids 24, 1405–1424. doi: 10.1177/1081286518797378

CrossRef Full Text | Google Scholar

Borodich, F. M., Keer, L. M., and Harris, S. J. (2003). Self-similarity in abrasiveness of hard carbon-containing coatings. J. Tribol. Trans. ASME 125, 1–7. doi: 10.1115/1.1509773

CrossRef Full Text | Google Scholar

Borodich, F. M., and Mosolov, A. B. (1991). Fractal contact of solids. Sov. Phys. Tech. Phys. 36, 995–997.

Google Scholar

Borodich, F. M., and Mosolov, A. B. (1992). Fractal roughness in contact problems. PMM J. Appl. Math. Mech. 56, 681–690.

Google Scholar

Borodich, F. M., and Onishchenko, D. A. (1993). Fractal roughness for problem of contact and friction (the simplest models). J. Friction Wear 14, 452–459.

Google Scholar

Borodich, F. M., and Onishchenko, D. A. (1999). Similarity and fractality in the modelling of roughness by a multilevel profile with hierarchical structure. Int. J. Solids Struct. 36, 2585–2612.

Google Scholar

Borodich, F. M., Pepelyshev, A., and Savencu, O. (2016). Statistical approaches to description of rough engineering surfaces at nano and microscales. Tribol. Int. 103, 197–207. doi: 10.1016/j.triboint.2016.06.043

CrossRef Full Text | Google Scholar

Borodich, F. M., and Savencu, O. (2017). “Hierarchical models of engineering rough surfaces and bioinspired adhesives,” in Bio-Inspired Structured Adhesives, eds L. Heepe, S. Gorb, and L. Xue (Springer), 179–219. doi: 10.1007/978-3-319-59114-8_10. Available online at: https://www.springer.com/gp/book/9783319591131

CrossRef Full Text | Google Scholar

Borodich, F. M., and Volovikov, A. Y. (2000). Surface integrals for domains with fractal boundaries and some applications to elasticity. Proc. R. Soc. Lond. A 456, 1–23. doi: 10.1098/rspa.2000.0506

CrossRef Full Text | Google Scholar

Carpick, R. W. (2018). The contact sport of rough surfaces. Science 359:38. doi: 10.1126/science.aaq1814

PubMed Abstract | CrossRef Full Text | Google Scholar

Dette, H., Pepelyshev, A., and Zhigljavsky, A. (2015). “Design for linear regression models with correlated errors,” in Handbook of Design and Analysis of Experiments, eds A. Dean, M. Morris, J. Stufken, and D. Bingham (Boca Raton, FL: CRC Press; Taylor and Francis Group), 237–276.

PubMed Abstract | Google Scholar

Dubuc, B., Quiniou, J. F., Roques-Carmes, C., Tricot, C., and Zucker, S. W. (1989). Evaluating the fractal dimension of profiles. Phys. Rev. A 39, 1500–1512.

PubMed Abstract | Google Scholar

Erbaş, B., Aydın, Y. E., and Borodich, F. M. (2019). Indentation of thin elastic films glued to rigid substrate: Asymptotic solutions and effects of adhesion. Thin Solid Films 683, 135–143. doi: 10.1016/j.tsf.2019.05.038

CrossRef Full Text | Google Scholar

Falconer, K. J. (1990). Fractal Geometry: Mathematical Foundations and Applications. Chichester: John Wiley.

Google Scholar

Fuller, K. N. G., and Tabor, D. (1975). The effect of surface roughness on the adhesion of elastic solids. Proc. R. Soc. Lond. A 345, 327–342.

Google Scholar

Fus, N. (1801). “An experience of theory on resistance by roads of various types to four-wheeled and two-wheeled carriages with definition of circumstances for which ones of these carriages are more useful than others,” in Academic Papers Selected From the First Volume of “Activities of Academy of Sciences” under title “Nova Acta Academiae Scientiarum Imperialis Petropolitanae”, Part 1 (in Russian) (Saint Petersburg), 373–422.

Google Scholar

Galanov, B. A. (2011). Models of adhesive contact between rough elastic bodies. Int. J. Mech. Sci. 53, 968–977. doi: 10.1016/j.ijmecsci.2011.07.010

CrossRef Full Text | Google Scholar

Gao, H., Wang, X., Yao, H., Gorb, S. N., and Arzt, E. (2005). Mechanics of hierarchical adhesion structures of geckos. Mech. Mater. 37, 275–285. doi: 10.1016/j.mechmat.2004.03.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Ghosal, S., and Van der Vaart, A. (2017). Fundamentals of Nonparametric Bayesian Inference. Vol. 44. Cambridge: Cambridge University Press.

Google Scholar

Goryacheva, I. G. (1998). Contact Mechanics in Tribology. Dordrecht: Kluwer Academic Publishers.

Google Scholar

Greenwood, J. A. (1992). “Problems with surface roughness,” in Fundamentals of Friction: Macroscopic and Microscopic Processes, eds I. L. Singer and H. M. Pollock (Boston, MA: Kluwer), 57–73.

Google Scholar

Greenwood, J. A., and Williamson, J. B. P. (1966). Contact of nominally flat surfaces. Proc. R. Soc. Lond. A 370, 300–319.

Google Scholar

Gusak, D., Kukush, A., Kulik, A., Mishura, Y., and Pilipenko, A. (2012). Theory of Stochastic Processes. New York, NY: Springer-Verlag.

Google Scholar

Holm, R. (1941). Die technisffie Physik der elektrischen Kontakte. Berlin: Springer-Verlag.

Google Scholar

Jelinek, H., Jones, C. L., and Warfel, M. D. (1998). Is there meaning in fractal analyses? Complex. Int. 98, 144–149.

Google Scholar

Johnson, K.L. (1985). Contact Mechanics. Cambridge, UK: Cambridge University Press.

Google Scholar

Khusu, A. P., Vitenberg, Y. R., and Palmov, V. A. (1975). Roughness of Surfaces: Theoretical Probabilistic Approach. Moscow: Nauka

Google Scholar

Kragelsky, I. V. (1948). Static friction between two rough surfaces. Bul. USSR Acad. Sci. Div. Tech. Sci. 10, 1621–1625.

Google Scholar

Krantz, T. L., Alanou, M. P., Evans, H. P., and Snidle, R. W. (2001). Surface fatigue lives of case-carburized gears with an improved surface finish. ASME J. Tribol. 123, 709–716.

Google Scholar

Linnik, Yu. V., and Khusu, A. P. (1954a). Mathematical and statistical description of unevenness of surface profile at grinding. Uspekhi Matematich. Nauk 9:255.

Google Scholar

Linnik, Yu. V., and Khusu, A. P. (1954b). Mathematical and statistical description of unevenness of surface profile at grinding. Bul. USSR Acad. Sci. Div. Techn. Sci. 20, 154–159.

Google Scholar

Majumdar, A., and Bhushan, B. (1990). Role of fractal geometry in roughness characterization and contact mechanics of surfaces. J. Tribol. 112, 205–216.

Google Scholar

Mandelbrot, B. B. (1975). Les Objects Fractals: Forme, Hasard et Dimension. Paris: Flammarion.

Google Scholar

Mandelbrot, B. B. (1977). Fractals: Form, Chance, and Dimension. San Francisco, CA: W. H. Freeman.

Google Scholar

Mandelbrot, B. B. (1983). The Fractal Geometry of Nature. New York, NY: Freeman.

PubMed Abstract | Google Scholar

Mandelbrot, B. B. (1986). “Self-affine fractal sets, I: the basic fractal dimensions,” in Fractals in Physics, eds L. Pietronero and E. Tosatti (Amsterdam), 3–15. Available online at: https://www.elsevier.com/books/fractals-in-physics/pietronero/978-0-444-86995-1

Google Scholar

Mandelbrot, B. B. (1998). Is nature fractal? Science 229:783.

Google Scholar

Maugis, D. (2000). Contact, Adhesion and Rupture of Elastic Solids. Berlin: Springer-Verlag.

Google Scholar

Morales-Espejel, G. E., Venner, C. H., and Greenwood, J. A. (2000). Kinematics of transverse real roughness in elastohydrodynamically lubricated 0line contacts using Fourier analysis. Proc. Inst. Mech. Eng. J. J. Eng. Trib. 214, 523–534. doi: 10.1243/1350650001543395

CrossRef Full Text | Google Scholar

Nowicki, B. (1985). Multiparameter representation of surface roughness. Wear 102, 161–176.

Google Scholar

Pepelyshev, A., Borodich, F. M., Galanov, B. A., Gorb, E. V., and Gorb, S. N. (2018). Adhesion of soft materials to rough surfaces: experimental studies, statistical analysis and modelling. Coatings 8:350. doi: 10.3390/coatings8100350

CrossRef Full Text | Google Scholar

Persson, B. N. L. (2006). Contact mechanics for randomly rough surfaces. Surf. Sci. Rep. 61, 201–227. doi: 10.1016/j.surfrep.2006.04.001

CrossRef Full Text | Google Scholar

Plesha, M. E., and Ni, D. (2001). Scaling of geological discontinuity normal load-deformation response using fractal geometry. Int. J. Num. Anal. Meth. Geomech. 25, 741–756. doi: 10.1002/nag.149

CrossRef Full Text | Google Scholar

Popov, V. L. (2010). Contact Mechanics and Friction. Berlin: Springer.

Google Scholar

Roques-Carmes, C., Wehbi, D., Quiniou, J. F., and Tricot, C. (1988). Modelling engineering surfaces and evaluating their non-integer dimension for application in material science. Surf. Topogr. 1, 435–443.

Google Scholar

Sayles, R. S., and Thomas, T. R. (1978). Surface topography as a nonstationary random process. Nature 271, 431–434.

Google Scholar

Schaber, C. F., Flenner, S., Glisovic, A., Krasnov, I., Rosenthal, M., Stieglitz, H., et al. (2019). Hierarchical architecture of spider attachment setae reconstructed from scanning nanofocus X-ray diffraction data. J. R. Soc. Interface 16:20180692. doi: 10.1098/rsif.2018.0692

PubMed Abstract | CrossRef Full Text | Google Scholar

Schmittbuhl, J., Vilotte, J.-P., and Roux, S. (1995). Reliability of self-affine measurements. Phys. Rev. E 51, 131–147.

PubMed Abstract | Google Scholar

Soldatenkov, I.A. (2015). Calculation of friction for indenter with fractal roughness that slides against a viscoelastic foundation. J. Frict. Wear 36, 193–196. doi: 10.3103/S1068366616060131

CrossRef Full Text | Google Scholar

Spinner, M., Kovalev, A., Gorb, S. N., and Westhoff, G. (2013). Snake velvet black: hierarchical micro- and nanostructure enhances dark colouration in Bitis rhinoceros. Sci. Rep. 3, 1–8. doi: 10.1038/srep01846

PubMed Abstract | CrossRef Full Text | Google Scholar

Thielen, S., Magyar, B., and Piros, A. (2016). Reconstruction of three-dimensional turned shaft surfaces with fractal functions. Tribol. Int. 95, 349–357. doi: 10.1016/j.triboint.2015.11.028

CrossRef Full Text | Google Scholar

Thode, H. C. (2002). Testing for Normality. New York, NY: Marcel Dekker.

Google Scholar

Tricot, C. (1995). Curves and Fractal Dimension. Berlin: Springer-Verlag.

PubMed Abstract | Google Scholar

Vilenkin, N. Ya. (1968). Stories About Sets. New York, NY; London: Academic Press.

Google Scholar

Warren, T. L., and Krajcinovic, D. (1996). Random Cantor set models for the elastic perfectly plastic contact of rough surfaces. Wear 196, 1–15.

Google Scholar

Whitehouse, D. J. (1982). The parameter rash–is there a cure? Wear 83, 75–78.

Google Scholar

Whitehouse, D. J. (2001). Fractal or fiction. Wear 249, 345–353. doi: 10.1016/S0043-1648(01)00535-X

CrossRef Full Text | Google Scholar

Whitehouse, D. J. (2011). Handbook of Surface and Nanometrology. Boca Raton, FL: CRC Press.

Google Scholar

Whitehouse, D. J., and Archard, J. F. (1970). The properties of random surfaces of significance in their contact. Proc. R. Soc. Lond. A 316, 97–121.

Google Scholar

Winkler, E. (1867). Die Lehre von der Elastizität und Festigkeit, mit Besonderer Rücksicht auf ihre Anwendung in der Technik, für Polytechnische Schulen, Bauakademien, Ingenieure, Maschinenbauer, Architekten, etc. Prague: Verlag H. Dominicus.

Google Scholar

Wolff, J. O., Grawe, I., Wirth, M., Karstedt, A., and Gorb, S. N. (2015). Spider's super-glue: thread anchors are composite adhesives with synergistic hierarchical organization. Soft Matter 11, 2394–2403. doi: 10.1039/c4sm02130d

PubMed Abstract | CrossRef Full Text | Google Scholar

Wolff, J. O., Schwaha, T., Seiter, M., and Gorb, S. N. (2016). Whip spiders (Amblypygi) become waterrepellent by a colloidal secretion that selfassembles into hierarchical microstructures. Zool. Lett. 2:23. doi: 10.1186/s40851-016-0059-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhuravlev, V. A. (1940). On question of theoretical justification of the Amontons-Coulomb law for friction of unlubricated surfaces. Zh. Tekh. Fiz. 10, 1447–1452.

Google Scholar

Zhuravlev, V. A. (2007). On question of theoretical justification of the Amontons-Coulomb law for friction of unlubricated surfaces. Proc. Instn. Mech. Engrs. Part J: J. Eng. Trib. 221, 894–898. doi: 10.1243/13506501JET176

CrossRef Full Text | Google Scholar