Auto-Ignition and Reaction Front Dynamics in Mixtures With Temperature and Concentration Stratification

Introduction

Due to diesel-like thermal efficiency and low emissions, advanced compression ignition (ACI) engines operating in the low temperature combustion regime have recently attracted extensive research interest (Dec, 2009; Dempsey et al., 2016; Cung et al., 2017; Pachiannan et al., 2019). Such engine combustion concepts include the homogeneous charge compression ignition (HCCI), HCCI with partial fuel stratification (PFS), partially premixed compression ignition (PPCI), reactivity-controlled compression ignition (RCCI), etc. Typically, combustion in these engines is globally fuel lean and highly diluted. In addition, another essential characteristic of ACI combustion is the omnipresent temperature and concentration stratification induced by fuel injection as well as in-cylinder flow and conjugate heat transfer. Controlled stratifications can offer high flexibility to modulate heat release rate and adjust engine combustion phasing (Dempsey et al., 2016), yet result in substantial challenges in the understanding of ignition and subsequent combustion evolution in ACI conditions.

Recently, a framework by overlapping the engine thermodynamic pressure-temperature trajectory and the fuel ignition delay iso-contour has been developed, aiming to provide general insights on the knock in spark-ignition (SI) engines and bulk combustion phasing in ACI engines (Szybist and Splitter, 2017; Szybist et al., 2017; Tao et al., 2019). Manifested by the changes in fuel ignition delay iso-contour and engine thermodynamic trajectory, this framework can qualitatively show the effects of conventional fuel reactivity metrics such as research and motor octane numbers (RON and MON) and octane sensitivity (OS), as well as the effects of engine operating condition, e.g., intake conditions, global equivalence ratio and level of exhaust gas recirculation (EGR). This approach is fundamentally an extension of the Livengood-Wu integration (Livengood and Wu, 1955) facilitated by the recent developments of fuel surrogate and kinetic models, and is able to explain features of engine auto-ignition as observed from experiments, for example, the reduced effectiveness of EGR to mitigate knock in boosted SI engines (Szybist et al., 2017). Useful as it is, a key dimension that this P-T framework is missing is the mixture thermal and concentration stratification in ACI engines, in that the ignition of a gas pocket occurs in the existence of temperature and equivalence ratio gradient (Dec, 2009; Dempsey et al., 2016).

With challenges to conduct well-controlled experiment and fast progress in computational combustion and chemical kinetics, extensive computational investigations have recently been conducted on the flame propagation and ignition process in mixtures with temperature and fuel stratifications. Among these studies, a representative approach is to adopt the counterflow and diffusion mixing layer configuration (Sankaran and Im, 2005; Mukhopadhyay and Abraham, 2011). For example, Sankaran and Im (2005) studies the auto-ignition characteristics of lean premixed iso-octane/air stream impinging onto a hot stream of exhaust gas. The ignition delay and front propagation speed across the mixing layer were determined as a function of a local mixture fraction variable as well as the scalar dissipation rate. Another widely-adopted approach is to perform transient computations in the 1-D planar domain with initially non-uniform temperature or fuel concentration profiles and the emphasis is placed on the subsequent reaction front development and propagation (Sun et al., 2015; Dai et al., 2017; Qi et al., 2017; Shi et al., 2017). These studies include laminar flame propagation in a stratified mixture, detonation development with temperature or concentration gradient, ignition to flame transition in stratified charge. Beyond the theoretical framework of a premixed flame, a widely adopted theory to describe reaction wave propagation in a mixture with non-uniform temperature or concentration is the reactivity gradient theory of Zeldovich (Zeldovich, 1980), which introduces the spontaneous propagation (SP) combustion waves driven by the sequential auto-ignition of adjacent particles. Such a reaction front is completely kinetics-driven and fundamentally different from the classical flame through the coupling between convective-diffusive transport and reaction.

More recently, rapid compression machine (RCM) experiment has shown that three distinct stages of oxidation exhibit in lean n-heptane/air ignition (Sarathy et al., 2019), controlled by cool flame chemistry under low temperature (Zhao et al., 2016), H₂O₂ chain branching under intermediate temperature, and CO oxidation during high temperature. It is therefore intriguing to investigate the relevance of such kinetic behaviors in the ignition of stratified mixtures under ACI conditions, and to see if these distinct stages of oxidation can form novel reaction front and provide further insights into combustion evolution and heat release profile in lean ACI combustion. Next, we shall introduce the computational platform, configuration, case setup and the concept of three-stage ignition.

Methodology

The numerical simulation of ignition in mixture with thermal and concentration stratification is conducted using a novel in-house reacting flow CFD code reactingFOAM-SCT based on OpenFOAM 6.0 (Yang et al., 2019). The new features of this open-source platform include an advanced accurate mid-point Splitting scheme (Lu et al., 2017), a fast and accurate stiff Chemistry solver (Imren and Haworth, 2016) and a detailed transport property evaluation package (Dasgupta et al., 2019). The performance of these advanced features has been extensively validated against either DNS results or analytical solutions in different configurations, including those from a diffusion-convection problem, homogeneous ignition delay, laminar premixed flame, shock wave, 1D spherical flame initiation and propagation, 2D premixed flame instabilities, 1D non-premixed counterflow flame and 2D non-premixed co-flow flame. More details of the governing equation, numerical scheme, spatial and temporal accuracy, and validation results are available in Yang et al. (2019). More recently, this code has been utilized to demonstrate the minimum ignition energy, regimes, and propagation dynamics of direct cool flame initiation (Yang and Zhao, 2020).

In the current work, first-order implicit Euler scheme is utilized to discretize the unsteady term, a second-order Gauss linear scheme is used for spatial terms, including both convection and diffusion terms. CFL number is set as 0.4. The upgraded algorithm named PIMPLE which combines PISO and SIMPLE is used for iteration. The current computational configuration is a 1D planar domain of 8 cm in length including a stratified segment from the left boundary x = 0 to x = x₁ and a uniform segment from x = x₁ to x = 8 cm, as shown in Figure 1. This domain is under adiabatic conditions with initial pressure 40 atm. At x = 0, zero gradient boundary condition is applied for temperature, pressure, and species mass fraction; at the other boundary of x = 8 cm, zero gradient is applied for temperature and species mass fraction, while wave-transmissive boundary condition is applied for pressure. As such, unlike (Dai and Chen, 2015) where substantial effects of pressure wave and shock are observed with a reflective boundary condition, there is no reflection of pressure waves from the right boundary in the current study, and the pressure in the domain eventually will drop to 40 atm. The fuel involved in the computation is n-heptane, one of the primary reference fuels representing long-chain n-alkane with low-temperature chemistry. The mechanism we adopt is from Andrae (2013), which includes 137 species and 635 reactions, and has been extensively validated and applied in engine combustion.

FIGURE 1

Figure 1. 1-D Computational domain to investigate stratified combustion.

The computation cases we select in the current work are summarized in Table 1. The range of equivalence ratio covers 0.3 to 2.0 and the temperature covers 800–1,000 K, adopted from the operating conditions of typical low temperature combustion conditions (Kokjohn et al., 2012, 2015; Wang et al., 2014; Luong et al., 2017; Naser et al., 2017; Liu et al., 2019). For example, as in Liu et al. (2019), thermal stratifications up to 30 K/cm is observed near wall region. In our simulation, the temperature gradient is set at 16, 33, and 66 K/cm. A large gradient of 66 K/cm is adopted to showcase the effect of large temperature gradient on the combustion modes. According to Kokjohn et al. (2012), in an RCCI engine, non-uniform equivalence ratio distribution is observed at a distance from 30 to 65 mm away from the center of bore, and the gradient of equivalence ratio varies approximately from 0.1 to 1.1 per centimeter. In our simulation, the equivalence ratio gradient is set from 0.1 to 0.6 cm⁻¹. Among these cases, Cases 1, 2, and 3 share the same domain length of temperature stratification at 3 cm, while their temperature gradients are different as induced by different temperature ranges. Cases 6, 7, and 8 share the same domain length of equivalence ratio stratification at 3 cm, while their ϕ gradients are different as induced by different ϕ ranges. Cases 1, 4 and 5 share the same temperature range in the segment of stratification, but with different temperature gradients due to different length of stratification segment. Similarly, Cases 6, 9, and 10 share the same ϕ range in the segment of stratification, but with different ϕ gradients due to different length of stratification segment. Beyond the stratification segment, temperature and equivalence ratio are set as uniform at 800 K and 0.3, respectively. It is shown later that due to the different initial stratifications, reaction fronts propagating into the same final uniform segment can experience different thermal-chemical states and exhibit very different structure and propagation behaviors.

TABLE 1

Table 1. Case setup including initial temperature and concentration stratification.

Concepts of Three-Stage Oxidation

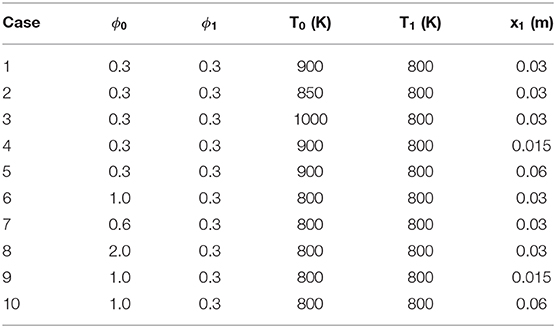
Recent RCM experiment has suggested three distinct oxidation stages for lean n-heptane/air at engine relevant conditions (Sarathy et al., 2019). As shown in Figure 2, a comparison has been made between the RCM ignition data and the simulation results for n-heptane/air at equivalence ratio 0.3, under 780 K and 21.6 atm. Quantitative difference has been observed in the pressure and CO evolution from the comparison, yet both simulation and experiment evidently exhibit three-stage oxidation phenomena. It is observed that while pressure keeps increasing throughout this process, the mole fraction of CO increases at the first and second stage ignition, while decreases at the third stage oxidation.

FIGURE 2

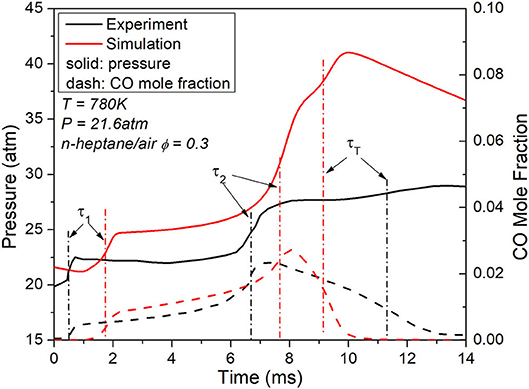
Figure 2. Measured and simulated temperature and CO evolution for the RCM ignition of n-heptane/air at ϕ = 0.3, P = 21.6 atm and T = 780 K.

To further show the detailed kinetic behavior of this three-stage oxidation phenomena, simulated temperature, heat release rate (HRR) and major species profiles are shown in Figure 3, for constant pressure adiabatic ignition for n-heptane/air at ϕ = 0.3, P = 40 atm and T = 800 K. Here the delay time for the first, second and total ignition stages are defined at the instant with local maximum temperature rise rate, as τ₁, τ₂ and τ_T respectively, as shall be adopted in the rest of this study. Three distinct peaks appear at each stage with similar orders of magnitude. Under this specific condition, the first-stage ignition occurs at lowest temperature (~850 K), which is the well-known “cool flame” stage. The dominant kinetics is the low temperature chemistry, leading to mild temperature rise and formation of H₂O₂, CO, and CH₂O, etc. The second-stage ignition occurs at intermediate temperature (~1,100 K), featured by depletion of H₂O₂, CH₂O and formation of CO. This stage is driven by the H₂O₂ chain branching via reaction H₂O₂+M=OH+OH+M. Due to the relatively low temperature at the second-stage, CO is not immediately oxidized to CO₂, instead, its oxidation occurs at a much higher temperature around 1,400 K, via a major exothermic reaction CO+OH=CO₂+H. For a near stoichiometric mixture, the difference between τ₂ and τ_T is usually not discernible due to the higher temperature rise rate at the second-stage, which immediately triggers the third-stage. As such, two-stage ignition is more commonly observed and discussed in the literature. Due to the absence of non-reactive pressure trace from experiment and additional kinetic targets, it is difficult to evaluate the heat loss and hence the effective volume evolution during the actual RCM experiment, for a more quantitative comparison. The qualitative agreement between the simulation and experiment nevertheless substantiates the three-stage oxidation during lean auto-ignition and provides necessary justification of the current work. Also, beyond the goal of the current work, more detailed combustion target measurement should be conducted under these engine relevant conditions, along with other novel combustion regimes and configurations (Zhao et al., 2016; Reuter et al., 2017) for the sake of kinetic model development.

FIGURE 3

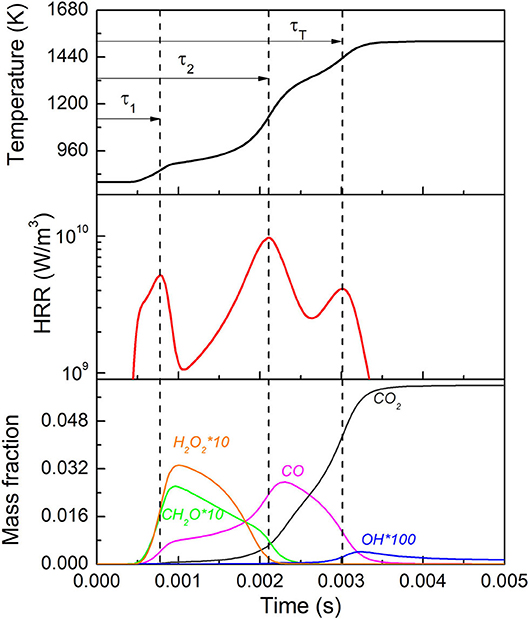
Figure 3. Ignition delay, HRR and key species profile during a typical three-stage oxidation of n-heptane/air with ϕ = 0.3, P = 40 atm and T = 800 K.

The temperature dependence of the delay time τ₁, τ₂ and τ_T for lean n-heptane/air with ϕ = 0.3 and P = 40 atm is shown in Figure 4A. All three stages exhibit the phenomena of negative temperature coefficient (NTC). As temperature becomes either lower or higher outside of the NTC regime, the difference between τ₂ and τ_T becomes less discernible and eventually the three-stage oxidation transitions into two-stage ignition. Figure 4B shows the equivalence ratio dependence of τ₁, τ₂ and τ_T for n-heptane/air with P = 40 atm and T = 800 K. As ϕ increases from lean to rich, all three stages advance. For mixtures with ϕ between 0.45 and 0.85, second and third stages merge and exhibit two-stage ignition only. The three-stage ignition is most obvious under lean conditions, yet can still be identified for richer mixtures. In addition, the first-stage ignition delay τ₁ shows much lower ϕ-sensitivity compared with τ₂ and τ_T. In the following, we shall demonstrate how these ignition delay information and sensitivity can be used to explain the ignition evolution and reaction wave propagation.

FIGURE 4

Figure 4. (A) Three-stage ignition delay as a function of temperature for lean n-heptane/air with ϕ = 0.3 and P = 40 atm; (B) Three and two-stage ignition delay as a function of equivalence ratio for n-heptane/air with P = 40 atm and T = 800 K.

Results and Discussion

Thermal Stratification

We first show the detailed combustion development in Case 1, as a demonstration for ignition and combustion evolution in scenarios with thermal stratification. As shown in Figure 5A, at t = 0.32 ms, the first-stage ignition occurs at some intermediate temperature in the stratification segment, corresponding to the minimum point of τ₁ in Figure 4A, before it occurs in the whole domain. At t = 1.245 ms, the second-stage ignition first occurs in the high temperature part in the stratified segment, followed by the third-stage ignition in the same region. Meanwhile, at t = 1.49 ms, second-stage ignition occurs in the low temperature part of the stratified segment, consequently forming a reaction front with double peak HRR, which continues to propagate throughout the domain. As shown in Figure 5B, the reaction front at t = 1.73 ms includes double heat release peaks that separate apart. The one around x = 0.04 m, corresponds to H₂O₂ chain branching and CO generation; while the other one is located at x = 0.02 m, corresponding to CO oxidation and CO₂ formation. It is noted that at this instant, the reaction progress of the upstream mixture is in between the first- and the second-stage ignition, with considerable amount of H₂O₂ and CH₂O accumulation. Such observation on the ignition and reaction front evolution qualitatively holds for all Cases 1–5 with temperature stratifications. The final reaction front including two separate heat release peaks contributed by H₂O₂ chain branching and CO oxidation is a key feature for ignition evolution with temperature gradient. As suggested by budget term analysis, the role of diffusion is negligible in all of the reaction fronts involved and the double-peak reaction wave is hence completely kinetics-driven.

FIGURE 5

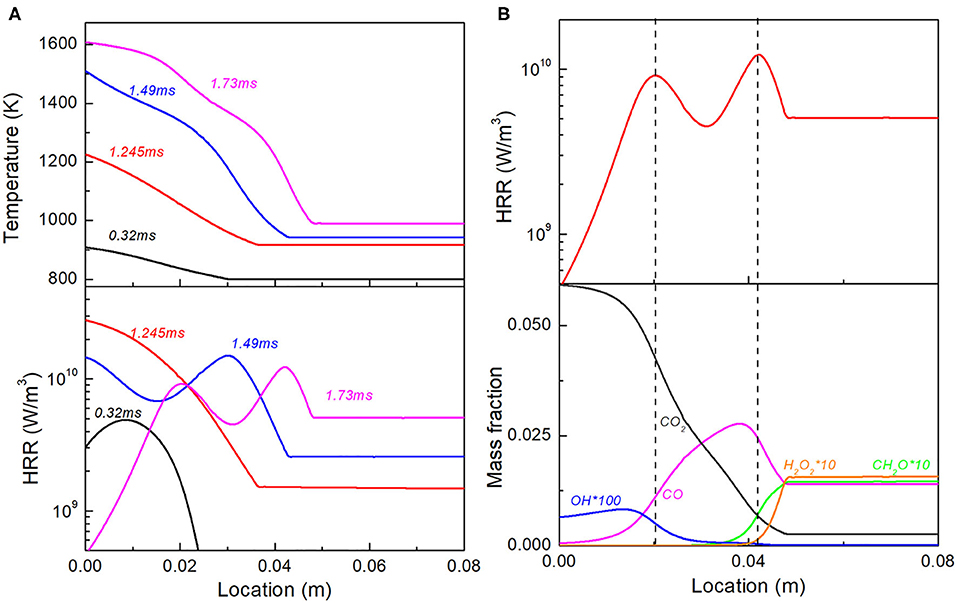
Figure 5. (A) Temperature and heat release rate profile at selected time instants for Case 1; (B) Double peak heat release and profiles of representative species for reaction front at t = 1.73 ms.

Among all cases from 1 to 5, Cases 1, 4, and 5 are associated with the same range of temperature stratification, consequently their different temperature gradients are induced by the different lengths of the stratification segment. It would be interesting to trace each stage of ignition and compare the propagation speed of the corresponding reaction front. As shown in Figure 6, for all the cases, the reaction front tends to quickly accelerate, then gradually decelerate afterwards, until eventually reaches the final, uniform segment. More importantly, regardless the local reaction front is induced by the first-, second-, or the third- stage ignition chemistry, Case 5 with the longest stratification segment and hence lowest level of thermal stratification always propagates the fastest. If we try to use the Zeldovich reactivity gradient theory to explain such a trend, we have $S=\frac{1}{|\nabla \tau |}$. Considering that τ = f(T, ϕ) where T = T(x) and ϕ = ϕ(x) at any instant, we can easily derive $\nabla \tau =\frac{\partial \tau }{\partial \varphi }\frac{d\varphi }{dx}+\frac{\partial \tau }{\partial T}\frac{dT}{dx}$. For Cases 1, 4, and 5 with thermal stratification only, it is clear that $\frac{d\varphi }{dx}$ is zero and $\frac{dT}{dx}$ increases as x₁ decreases from 0.06 to 0.015 m, as such ∇τ increases with $\frac{dT}{dx}$, and consequently, the propagation of the reaction front S decreases with $\frac{dT}{dx}$ following the order of Case 5, 1, and 4.

FIGURE 6

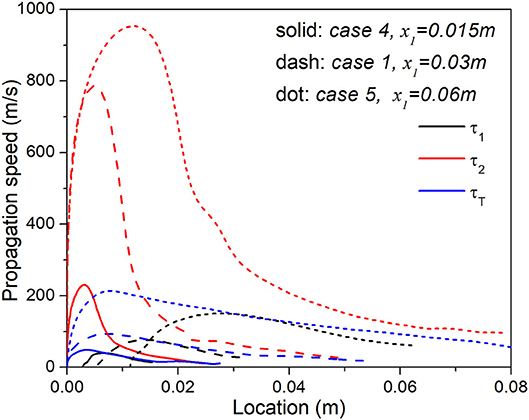
Figure 6. Comparison of the propagation velocity of each heat release peak in Case 1, 4, and 5 with the same temperature range but different lengths of stratification segment.

In addition to the zone length of the stratification segment, the temperature gradient of the thermal stratification can also be affected by the temperature range of the stratification segment, as shall be demonstrated by the comparison of Cases 1, 2, and 3 with different T₀ but the same x₁. These three cases share the length of stratification region of 3 cm. Due to the strong non-linear dependence of ignition on temperature, the reaction wave evolution exhibits strong non-linearity and it is challenging to summarize any qualitative behavior among them. However, if we focus on the reaction wave dynamics in the uniform segment, it will be intriguing to see how the distinct ignition processes among these cases affect the eventual reaction wave kinetics and dynamics. After all, these cases share the same temperature and equivalence ratio in the uniform segment, and the reaction front should exhibit similar behavior as approaching this region.

Surprisingly, the simulation shows that the final reaction fronts in the uniform segment do exhibit big difference, with Case 2 propagating the fastest, followed by Case 1 and Case 3 the slowest. To explain such trend, Figure 7 shows the temperature, pressure, HRR and key species concentration profiles as well as budget analysis of CO mass fraction in Case 1, 2, and 3, as the reaction wave arrives at the same location 0.05 m. For all these cases, the unburnt region has also finished the second-stage oxidation, as indicated by the trace amount of H₂O₂ and large amount of CO. Case 2 has the lowest amount of CO and highest temperature in unburnt region, implying relatively later development of the third-stage heat release process; while the highest amount of CO and lowest upstream temperature in Case 3 implies a lower extent of reaction progress toward the third-stage oxidation. This reaction front is hence an auto-ignitive wave induced by sequential third-stage ignition. As a result, the longer it takes for reaction front to arrive, the higher the reaction progress toward the third-stage ignition and the faster the wave propagation will be. The three-stage auto-ignition controlled by distinct chemistry has therefore granted richer theoretical meaning to the spontaneous propagation theory of Zeldovich and creates novel understanding to the auto-ignition reaction wave dynamics. As further confirmed by the budget term analysis, diffusion plays a negligible role among all the cases, and hence the final reaction front in Cases 1–3 is indeed an unsteadiness-reaction dominant auto-ignition front.

FIGURE 7

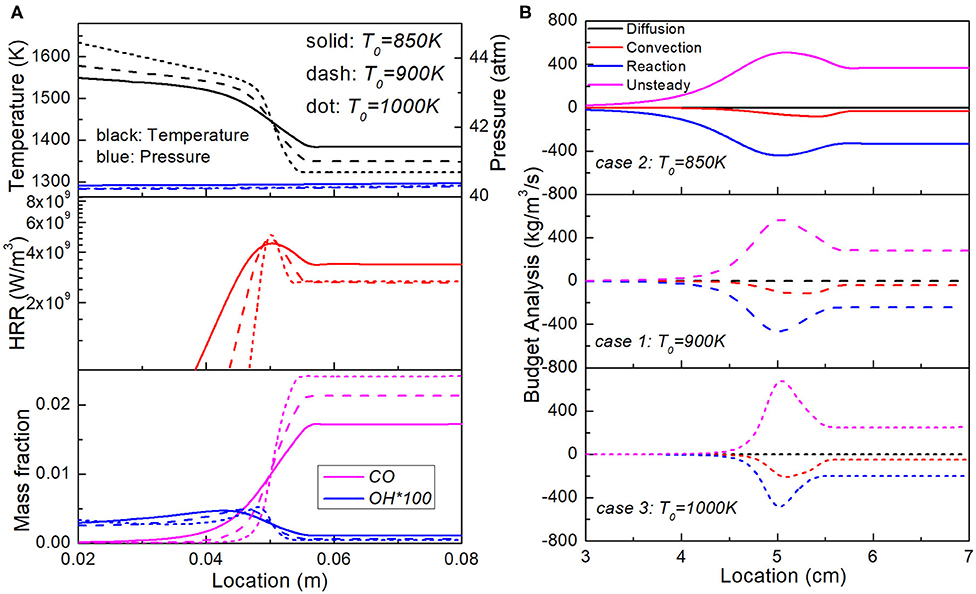
Figure 7. Comparison of the (A) Temperature, pressure, heat release rate and key species fraction profiles and (B) budget analysis of CO mass fraction in Case 1, 2, and 3 with the same lengths of temperature stratification segment but different temperature range.

Equivalence Ratio Stratification

Cases from 6 to 10 compare the ignition and reaction waves under different equivalence ratio stratifications. Figure 8 shows the detailed combustion evolution for Case 6. As shown in Figure 8A, at t = 0.535 ms, due to the lowest τ₁ in Figure 4B, the first-stage ignition occurs at the richest region in the stratification segment, and a spontaneous auto-ignition wave induced by the first-stage starts to propagate down to the ϕ gradient. At t = 0.575 ms, the second-stage ignition also occurs at the richest region in the stratification segment, consistent with the lowest τ₂ in Figure 4B, thus initiating another heat release peak in the spontaneous propagation reaction front. At t = 0.77 ms, as this reaction front with separated double heat release rate peaks propagates toward the unburnt gas, the first-stage ignition in the uniform unburnt region starts to occur. At t = 1.15 ms, the heat release peak triggered by first-stage ignition disappears. This is because the residence time is long enough such that the first-stage ignition is completed in the uniform lean region, as can be seen from the large amount of H₂O₂ and CH₂O. The heat release rate profile is further divided into two separate peaks. As shown in Figure 8B, the one around x = 0.075 m corresponds to H₂O₂ branching and CO generation, which is obviously controlled by the second-stage ignition; while the one near x = 0.072 m corresponds to CO oxidation and CO₂ formation, as induced by the third-stage ignition. By performing budget analysis, it is found that the role of diffusion is negligible in all of the reaction fronts involved.

FIGURE 8

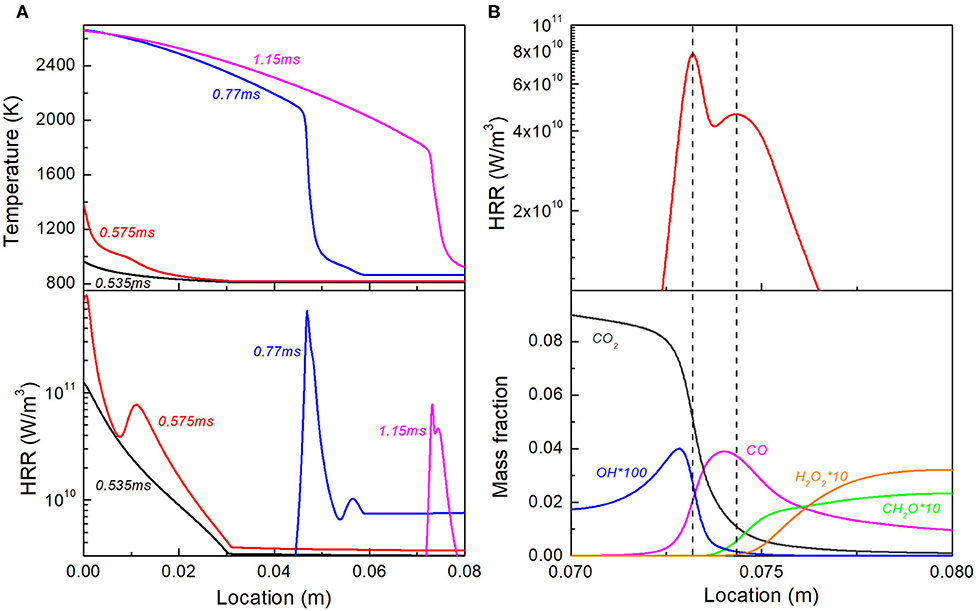
Figure 8. (A) Temperature and heat release rate profile at selected time instants for Case 6; (B) Double peak heat release and profiles of representative species for reaction front at t = 1.15 ms.

Compared with Case 6, Case 10 shares the same range of equivalence ratio, but has a longer stratification segment, resulting in a smaller equivalence ratio gradient. Figure 9 shows the detailed combustion evolution of Case 10. Similar to Case 6, first-, second-, and third-stage ignition all occurs first in the rich region of stratification segment, forming the propagating reaction front with two heat release peaks. However, a milder ϕ gradient in Case 10 leads to a milder ignition delay gradient, and consequently leads to a faster spontaneous propagation speed. The residence time for the uniform lean mixture upstream is hence not long enough for the first-stage ignition τ₁ to complete. As shown in Figure 9A, no obvious cool flame temperature rise is observed in upstream mixture at 0.68 ms. Therefore, the reaction front induced by the first-stage ignition continues propagation and will not merge into the upstream region. As shown in Figure 9B, the heat release peak around x = 0.07 m corresponds to the formation of H₂O₂, CO and CH₂O, which represents the low-temperature combustion chemistry; while the other one near x = 0.06 m corresponds to H₂O₂ branching, OH generation, CO oxidation and CO₂ formation, which represents the combination of second- and third- stage ignition.

FIGURE 9

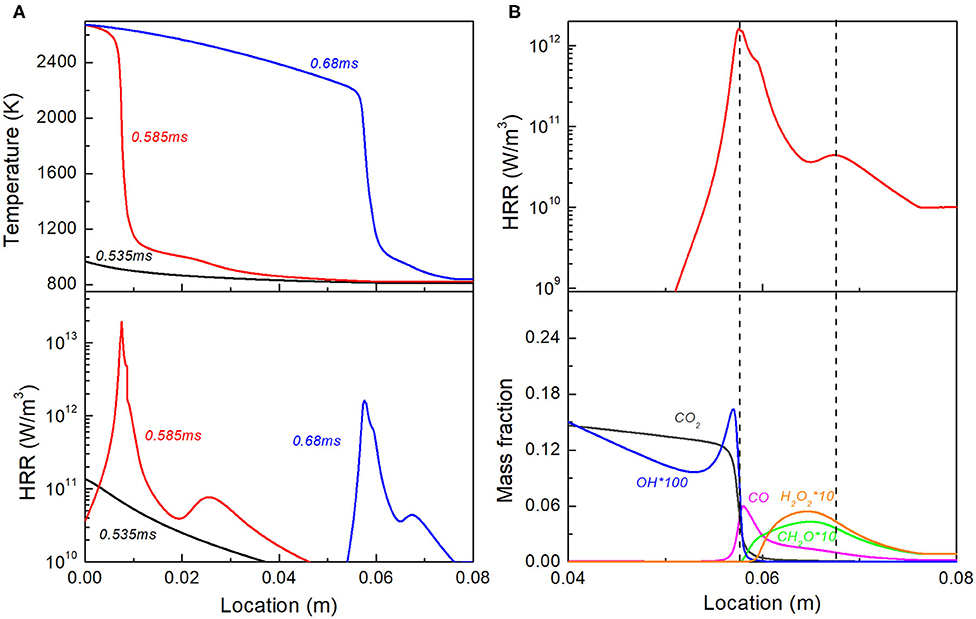
Figure 9. (A) Temperature and heat release rate profile at selected time instants for Case 10; (B) Double peak heat release and profiles of representative species for reaction front at t = 0.68 ms.

The three cases 6, 9, and 10 are associated with the same ϕ₀ but different x₁, and their reaction front propagation speed is compared in Figure 10. As expected, reaction fronts in Case 10 with the lowest level of ϕ stratification always propagate the fastest, while the propagation speed of the reaction front in Case 9 with the largest ϕ gradient is always the lowest. The classical reactivity gradient theory can explain the spontaneous wave propagation in the stratification segment, it nevertheless cannot explain the substantial difference in reaction wave dynamics in the same uniform segment. Different propagation speed in the stratification segment will influence the residence time and hence chemical reaction progress of upstream mixture in the uniform segment, which eventually leads to the different heat release rate profiles and thermal structure. In case 10, although the reaction progress of the unburnt mixture in the uniform segment is much lower, and further away from main ignition, propagation velocity of its final reaction wave is much higher due to its unique reaction wave chemistry and structure.

FIGURE 10

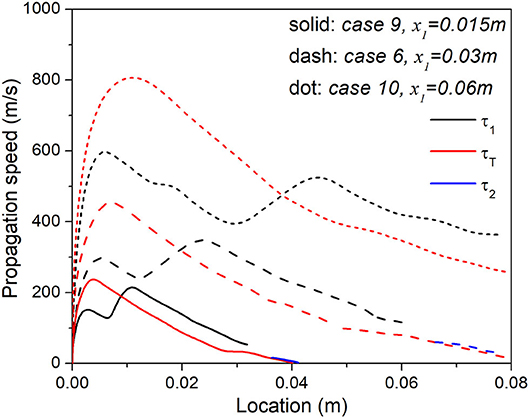
Figure 10. Comparison of the propagation velocity of each heat release peak in Case 6, 9, and 10 with the same equivalence ratio range but different lengths of stratification segment.

Concentration stratification can also be generated due to different ϕ range over the same spatial distance. Figure 11 shows the comparison of propagation speed among Cases 6, 7, and 8, with the same length of stratification segment x₁ but different equivalence ratio range ϕ₀. Case 7 has the smallest ϕ gradient while Case 8 has the largest ϕ gradient. Different from the trend shown in Figure 10, here the case with larger ϕ gradient exhibits the faster propagation speed. Within the length of stratification segment, $\frac{dT}{dx}$ is negligible as no thermal stratification is applied, and $\frac{d\varphi }{dx}$ increases as ϕ₀ increases from 0.6 to 2.0, i.e., $\frac{d\varphi }{dx}{|}_{{\varphi }_0=2.0}~2.4\frac{d\varphi }{dx}{|}_{{\varphi }_0=1.0}~5.6\frac{d\varphi }{dx}{|}_{{\varphi }_0=0.6}$. However, as shown in Figure 4B, $\frac{\partial \tau }{\partial \varphi }$ decreases as ϕ increases, $\frac{\partial \tau }{\partial \varphi }{|}_{{\varphi }_0=2.0}~\frac{1}{5}\frac{\partial \tau }{\partial \varphi }{|}_{{\varphi }_0=1.0}~\frac{1}{20}\frac{\partial \tau }{\partial \varphi }{|}_{{\varphi }_0=0.6}$. Consequently, Case 8 with ϕ₀ = 2.0 has the lowest $\frac{\partial \tau }{\partial \varphi }\frac{d\varphi }{dx}$, i.e., the lowest gradient of ignition delay following $\nabla \tau =\frac{\partial \tau }{\partial \varphi }\frac{d\varphi }{dx}+\frac{\partial \tau }{\partial T}\frac{dT}{dx}$. Therefore, Case 8 exhibits the highest spontaneous propagation speed in the stratification segment and Case 7 the slowest.

FIGURE 11

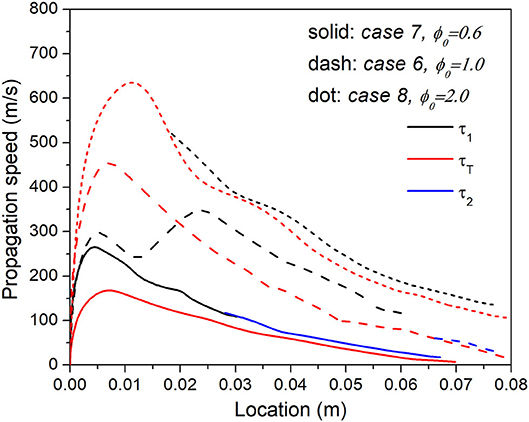
Figure 11. Comparison of the propagation velocity of each heat release peak in Case 6, 7, and 8 with the same length of the stratification segment but different equivalence ratio range.

As the reaction front propagates into the upstream uniform region, the residence time and hence reaction progress of upstream mixture in Case 8 are both the lowest, due to its fastest propagation speed. However, from Figure 11 it is observed that Case 8 maintains the highest propagation speed throughout the whole domain. To explain this trend, Figure 12 shows the temperature, pressure, HRR, and key species profiles as well as budget analysis of CO mass fraction in Case 6, 7, and 8, as the reaction wave arrives at the same location 0.06 m. It is seen that upstream mixture of Case 7 with ϕ₀ = 0.6 has the highest temperature, decreasing H₂O₂ and increasing CO approaching the reaction front, indicating the dominant process of second-stage ignition; while the upstream mixture of Case 8 with ϕ₀ = 2.0 has the lowest temperature, increasing H₂O₂ and CO approaching the reaction front, indicating an early stage of first-stage ignition. As ϕ₀ increases from 0.6 to 2.0, due to more intense combustion in the stratification segment, larger magnitude of pressure fluctuation is observed, resulting in elevated pressure distribution in the whole domain. Such pressure increase has fundamentally changed the wave structure and heat release rate. As shown in Figure 12B, influenced by the pressure elevation, the convection term becomes more and more significant as ϕ₀ increases from 0.6 to 2.0, and the unsteadiness-reaction balanced reaction front transforms into unsteadiness-convection balanced reaction front, consequently leading to the thinnest reaction front and highest propagation speed of Case 8.

FIGURE 12

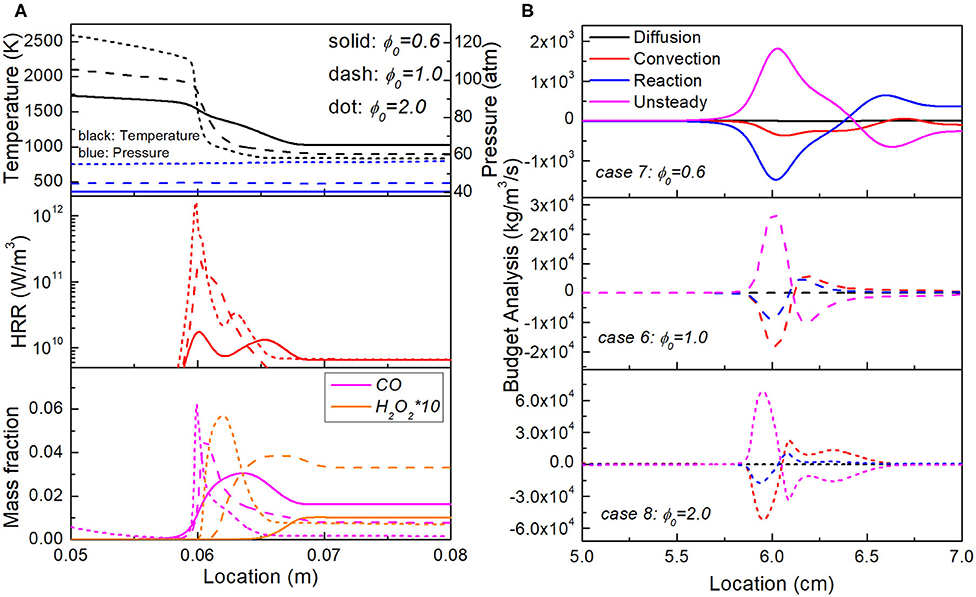
Figure 12. Comparison of the (A) Temperature, pressure, heat release rate and key species fraction profiles and (B) budget analysis of CO mass fraction in Case 6, 7, and 8 with the same lengths of equivalence ratio stratification segment but different ϕ range.

Conclusions

In this study, auto-ignition and subsequent reaction front evolution and wave dynamics in mixture with thermal and concentration stratification is computationally investigated using a recently developed computational platform with detailed chemistry and transport. The computational configuration is one-dimensional with an initially stratified segment followed by a uniform segment. Insights into stratified combustion are obtained through a combined analysis using the three-stage oxidation and the classical Zeldovich reactivity gradient theory:

1. For all the auto-ignition induced reaction fronts, it is found that diffusion plays a minor role as justified using budget term analysis.

2. It is found that for the cases with the same range of temperature in the stratification segment, the spontaneous propagation velocity of the reaction waves decreases with increasing temperature gradients induced by the length of the stratification segment. Similarly, for the cases with the same range of equivalence ratio in the stratification segment, the spontaneous propagation velocity of the reaction waves decreases with increasing ϕ gradients induced by the length of the stratification segment. For all the cases, diffusion plays a negligible role in the reaction front dynamics as suggested by budget term analysis.

3. While for the cases with the same length of the stratification segment but different range of equivalence ratio, an opposite trend has been observed between propagation velocity and the ϕ gradient, where the ϕ sensitivity of ignition delay must be carefully considered for correct prediction of reaction front dynamics.

4. For ignition in mixtures with thermal and equivalence ratio stratification, depending on the residence time and reactivity, the final reaction waves entering the uniform segment can include double or triple peaks in the heat release rate profile, which correspond to the homogeneous three-stage auto-ignition kinetics induced by low temperature chemistry, H₂O₂ chain branching and CO oxidation.

5. It is shown that the final reaction front can exhibits very different velocity when propagating into the uniform segment with the same initial thermodynamic and chemical conditions. Different propagation speed in the stratification segment will influence the residence time and hence chemical reaction progress of upstream mixture in the uniform segment, which eventually leads to the different heat release rate profiles and thermal structure of the reaction front.

6. Even though the simulation adopts a wave transmissive condition at the right boundary, due to the fast heat release rate in the domain, it is possible that the pressure profiles can be significantly elevated by the compression waves and shocks. This can lead to very unique unsteadiness-convection balanced auto-ignition reaction front with very thin structure and fast propagation speed.

7. Although the Zeldovich theory (Zeldovich, 1980) can successfully explain the qualitative effects on wave propagation speed from temperature and concentration gradient, by further comparing with the simulated reaction front propagation speed, it is found that the prediction from Zeldovich reactivity gradient theory can yield large quantitative differences, especially for the ignition reaction front corresponding to the second and third stages of auto-ignition. A probable explanation is that thermal-chemical conditions do not deviate much from the initial values before the first stage ignition occurs, therefore the corresponding propagation speed of the first-stage ignition wave is closest to the Zeldovich theory; once the first stage ignition occurs, local thermal-chemical states undergo substantial change, the initial condition of the subsequent ignition waves are substantially different from that at t = 0. Such constraints for the application of classical Zeldovich theory in the context of multistage ignition driven by distinct detailed kinetics certain merit future research.

In the future, more complexities will be included to study the combined effects of thermal and equivalence ratio gradient on charge auto-ignition and subsequent wave dynamics, for example, with either parallel or opposite temperature and concentration gradients.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

MT: validation, investigation, data processing, visualization, and writing. QY: software and tool development. PL: conceptualization, review, and editing. PZ: conceptualization, methodology, analysis, writing, and supervision. All authors contributed to the article and approved the submitted version.

Funding

This research was conducted as part of the Co-Optimization of Fuels and Engines (Co-Optima) initiative sponsored by the US Department of Energy Office of Energy Efficiency and Renewable Energy and Bioenergy Technologies and Vehicle Technologies Offices, including Co-optimization of Fuels & Engines Program with Award Number DE-EE0007985. Co-Optima is a collaborative project of multiple national laboratories initiated to simultaneously accelerate the introduction of affordable, scalable, and sustainable biofuels and high-efficiency, low-emission vehicle engines.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

Special thanks to program managers Trevor Smith and Alicia Lindauer.

References

Andrae, J. C. G. (2013). Comprehensive chemical kinetic modeling of toluene reference fuels oxidation. Fuel 107, 740–748. doi: 10.1016/j.fuel.2013.01.070

CrossRef Full Text | Google Scholar

Cung, K. D., Ciatti, S. A., Tanov, S., and Andersson, O. (2017). Low-temperature combustion of high octane fuels in a gasoline compression ignition engine. Front. Mech. Eng. 3:22. doi: 10.3389/fmech.2017.00022

CrossRef Full Text | Google Scholar

Dai, P., and Chen, Z. (2015). Supersonic reaction front propagation initiated by a hot spot in n-heptane/air mixture with multistage ignition. Combust. Flame 162, 4183–4193. doi: 10.1016/j.combustflame.2015.08.002

CrossRef Full Text | Google Scholar

Dai, P., Qi, C., and Chen, Z. (2017). Effects of initial temperature on autoignition and detonation development in dimethyl ether/air mixtures with temperature gradient. Proc. Combust. Inst. 36, 3643–3650. doi: 10.1016/j.proci.2016.08.014

CrossRef Full Text | Google Scholar

Dasgupta, A., Gonzalez-Juez, E., and Haworth, D. C. (2019). Flame simulations with an open-source code. Comput. Phys. Commun. 237, 219–229. doi: 10.1016/j.cpc.2018.11.011

CrossRef Full Text | Google Scholar

Dec, J. E. (2009). Advanced compression-ignition engines—understanding the in-cylinder processes. Proc. Combust. Inst. 32, 2727–2742. doi: 10.1016/j.proci.2008.08.008

CrossRef Full Text | Google Scholar

Dempsey, A. B., Curran, S. J., and Wagner, R. M. (2016). A perspective on the range of gasoline compression ignition combustion strategies for high engine efficiency and low NOx and soot emissions: effects of in-cylinder fuel stratification. Int. J. Eng. Res. 17, 897–917. doi: 10.1177/1468087415621805

CrossRef Full Text | Google Scholar

Imren, A., and Haworth, D. C. (2016). On the merits of extrapolation-based stiff ODE solvers for combustion CFD. Combust. Flame 174, 1–15. doi: 10.1016/j.combustflame.2016.09.018

CrossRef Full Text | Google Scholar

Kokjohn, S., Musculus, M., and Reitz, R. D. (2015). Evaluating temperature and fuel stratification for heat-release rate control in a reactivity-controlled compression-ignition engine using optical diagnostics and chemical kinetics modeling. Combust. Flame 162, 2729–2742. doi: 10.1016/j.combustflame.2015.04.009

CrossRef Full Text | Google Scholar

Kokjohn, S., Reitz, R., Splitter, D., and Musculus, M. (2012). Investigation of fuel reactivity stratification for controlling PCI heat-release rates using high-speed chemiluminescence imaging and fuel tracer fluorescence. SAE Int. J. Eng. 5, 248–269. doi: 10.4271/2012-01-0375

CrossRef Full Text | Google Scholar

Liu, H., Tang, Q., Yang, Z., Ran, X., Geng, C., Chen, B., et al. (2019). A comparative study on partially premixed combustion (PPC) and reactivity-controlled compression ignition (RCCI) in an optical engine. Proc. Combust. Inst. 37, 4759–4766. doi: 10.1016/j.proci.2018.06.004

CrossRef Full Text | Google Scholar

Livengood, J. C., and Wu, P. C. (1955). Correlation of autoignition phenomena in internal combustion engines and rapid compression machines. Proc. Combust. Inst. 5, 347–356. doi: 10.1016/S0082-0784(55)80047-1

CrossRef Full Text | Google Scholar

Lu, Z., Zhou, H., Li, S., Ren, Z., Lu, T., and Law, C. K. (2017). Analysis of operator splitting errors for near limit flame simulations. J. Comput. Phys. 335, 578–591. doi: 10.1016/j.jcp.2017.01.044

CrossRef Full Text | Google Scholar

Luong, M. B., Sankaran, R., Yu, G. H., Chung, S. H., and Yoo, C. S. (2017). On the effect of injection timing on the ignition of lean PRF/air/EGR mixtures under direct dual fuel stratification conditions. Combust. Flame 183, 309–321. doi: 10.1016/j.combustflame.2017.05.023

CrossRef Full Text | Google Scholar

Mukhopadhyay, S., and Abraham, J. (2011). Influence of compositional stratification on autoignition in n-heptane/air mixtures. Combust. Flame 158, 1064–1075. doi: 10.1016/j.combustflame.2010.10.007

CrossRef Full Text | Google Scholar

Naser, N., Jaasim, M., Atef, N., Chung, S. H., Im, H. G., and Sarathy, S. M. (2017). On the effects of fuel properties and injection timing in partially premixed compression ignition of low octane fuels. Fuel 207, 373–388. doi: 10.1016/j.fuel.2017.06.048

CrossRef Full Text | Google Scholar

Pachiannan, T., Zhong, W., Rajkumar, S., He, Z., Leng, X., and Wang, Q. (2019). A literature review of fuel effects on performance and emission characteristics of low-temperature combustion strategies. Appl. Energy 251:113380. doi: 10.1016/j.apenergy.2019.113380

CrossRef Full Text | Google Scholar

Qi, C., Dai, P., Yu, H., and Chen, Z. (2017). Different modes of reaction front propagation in n-heptane/air mixture with concentration non-uniformity. Proc. Combust. Inst. 36, 3633–3641. doi: 10.1016/j.proci.2016.06.086

CrossRef Full Text | Google Scholar

Reuter, C. B., Lee, M., Won, S. H., and Ju, Y. (2017). Study of the low-temperature reactivity of large n-alkanes through cool diffusion flame extinction. Combust. Flame 179, 23–32. doi: 10.1016/j.combustflame.2017.01.028

CrossRef Full Text | Google Scholar

Sankaran, R., and Im, H. G. (2005). Characteristics of auto-ignition in a stratified iso-octane mixture with exhaust gases under homogeneous charge compression ignition conditions. Combust. Theory. Model. 9, 417–432. doi: 10.1080/13647830500184108

CrossRef Full Text | Google Scholar

Sarathy, S. M., Tingas, E., Nasir, E. F., Detogni, A., Wang, Z., Farooq, A., et al. (2019). Three-stage heat release in n-heptane auto-ignition. Proc. Combust. Inst. 37, 485–492. doi: 10.1016/j.proci.2018.07.075

CrossRef Full Text | Google Scholar

Shi, X., Chen, J. Y., and Chen, Y. (2017). Laminar fame speeds of stratified methane, propane, and n-heptane flames. Combust. Flame 176, 38–47. doi: 10.1016/j.combustflame.2016.10.018

CrossRef Full Text | Google Scholar

Sun, W., Won, S. H., Gou, X., and Ju, Y. (2015). Multi-scale modeling of dynamics and ignition to flame transitions of high pressure stratified n-heptane/toluene mixtures. Proc. Combust. Inst. 35, 1049–1056. doi: 10.1016/j.proci.2014.05.141

CrossRef Full Text | Google Scholar

Szybist, J. P., and Splitter, D. A. (2017). Pressure and temperature effects on fuels with varying octane sensitivity at high load in SI engines. Combust. Flame 177, 49–66. doi: 10.1016/j.combustflame.2016.12.002

CrossRef Full Text | Google Scholar

Szybist, J. P., Wagnon, S. W., Splitter, D., Pitz, W. J., and Mehl, M. (2017). The reduced effectiveness of EGR to mitigate knock at high loads in boosted SI engines. SAE Int. J. Eng. 10, 2305–2318. doi: 10.4271/2017-24-0061

CrossRef Full Text | Google Scholar

Tao, M., Zhao, P., Szybist, J. P., Lynch, P., and Ge, H. W. (2019). Insights into engine autoignition: Combining engine thermodynamic trajectory and fuel ignition delay iso-contour. Combust. Flame 200, 207–218. doi: 10.1016/j.combustflame.2018.11.025

CrossRef Full Text | Google Scholar

Wang, X., Zhao, H., Xie, H., and He, B. (2014). Numerical study of the effect of piston shapes and fuel injection strategies on in-cylinder conditions in a PFI/GDI gasoline engine. SAE Int. J. Engines 7, 1888–1899. doi: 10.4271/2014-01-2670

CrossRef Full Text | Google Scholar

Yang, Q., and Zhao, P. (2020). Minimum ignition energy and propagation dynamics of laminar premixed cool flames. Proc. Combust. Inst. 38.

Yang, Q., Zhao, P., and Ge, H. (2019). reactingFoam-SCI: an open source CFD platform for reacting flow simulation. Comput. Fluids 190, 114–127. doi: 10.1016/j.compfluid.2019.06.008

CrossRef Full Text | Google Scholar

Zeldovich, Y. B. (1980). Regime classification of an exothermic reaction with nonuniform initial conditions. Combust. Flame 39, 211–214. doi: 10.1016/0010-2180(80)90017-6

CrossRef Full Text | Google Scholar

Zhao, P., Liang, W., Deng, S., and Law, C. K. (2016). Initiation and propagation of laminar premixed cool flames. Fuel 166, 477–487. doi: 10.1016/j.fuel.2015.11.025

CrossRef Full Text | Google Scholar