Continuum Model Analysis of QCM Nanotribological Data to Obtain Friction Coefficients for 304SS Contacts Lubricated by Water and TiO2 Nanoparticle Suspensions

Introduction

Quartz Crystal Microbalance (QCM) studies of tribological contacts (Rodahl and Kasemo, 1996; Laschitsch and Johannsmann, 1999; Brizmer et al., 2007; Johannsmann, 2007; Dawson et al., 2009; Krim, 2012; M'boungui et al., 2014; Borovsky et al., 2017) at both the macro and nanoscale are of increasing importance in a wide range of nano-technological and energy-related applications (Braiman et al., 2003; Kim and Kim, 2009; Zhang and Li, 2010; Krim, 2012; Hsu et al., 2014). Literature reports in this area have, to date, focused primarily on either macroscale or nanoscale contacts, and a remaining challenge in the field of tribology is to establish linkage between studies performed at wide-ranging length and time scales. One approach to establishing this linkage is to perform studies that examine the limits of macroscopic continuum mechanics, by probing where continuum methods break down as the atomic scale is approached. Nanoparticle (NP) additives are attractive candidates for such studies, as they significantly alter friction and wear at macroscopic length scales when present in a lubricated contact (Yu et al., 2016).

We report here a study of the response of QCMs with 304 Stainless Steel (304SS) sensing electrodes to rubbing contact with 304SS ball bearings, employing a continuum model to analyze the response in air, water and an aqueous TiO₂ suspensions. The QCM technique yields real-time nanotribological information at macroscale contact velocity amplitudes, typically 0.1–1 m/s. It is comprised of a thin piezoelectric quartz crystal driven at its resonance frequency by applying an AC voltage to thin metal film electrodes deposited onto each of its major faces. Contact forces and/or changes in the environment surrounding the QCM's surface electrode produce shifts in both its resonance frequency f, and quality factor Q, and the response of these quantities to probes, biological agents, and/or granular materials has been extensively studied (Borovsky et al., 2001, 2007; Krim, 2012; Dultsev and Nekrasov, 2018; Dirri et al., 2019; Han et al., 2019; Wang et al., 2019). Analysis approaches for inferring macroscopic friction coefficients from such measurements (Berg and Johannsmann, 2003; Berg et al., 2003; Leopoldes and Jia, 2010; Hanke et al., 2013; Vlachová et al., 2015; Borovsky et al., 2017, 2019) have been largely developed within the context of continuum contact models. The models must eventually break down as nanoscale length scales are approached, where systems become less uniform in nature and/or as contact regions become more poorly defined (Figure 1).

FIGURE 1

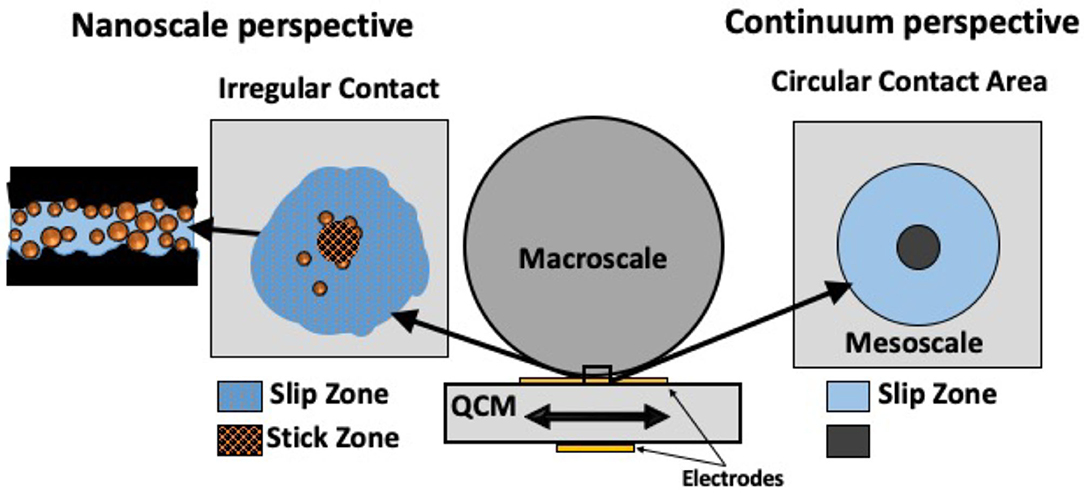
Figure 1. Nanoscale and Continuum perspectives of one ball bearing on an oscillating QCM displaying Cattaneo-Mindlin slip, with the contact area having an inner stick zone and an outer slip zone.

Vlachová et al. (2015) recently utilized a Cattaneo-Mindlin (CM) slip scenario to relate contact stiffness obtained from QCM measurements to macroscale friction coefficients, employing an analysis approach developed by Johannsmann and coworkers for QCM's loaded with spherical contacts (Berg and Johannsmann, 2003; Berg et al., 2003; Hanke et al., 2013). The CM scenario is an approximation that allows for a simplified analysis framework for two curved surfaces that are pressed with a normal load F_N into contact and then sheared tangentially (Etsion, 2010; Paggi et al., 2014; Ciavarella, 2015). Such bodies commonly remain stuck to each other in one part of the contact while slipping in other regions. The CM approximation treats the contact as rigid indenter pressed into a flat elastic surface, and assumes that sliding friction in the slip region is governed by a “Coulomb” friction law, F_f = μ_kF_N.

Berg and Johannsmann (2003), Berg et al. (2003), Hanke et al. (2013), and Vlachová et al. (2015) analysis method is based on both the linear and non-linear contact mechanics regimes associated with partially slipping contacts undergoing small amplitude reciprocal motion. It assumes that the contact area diameter is both independent of the tangential loading force and much smaller than the loading sphere diameter. Vlachová et al. obtained realistic values for friction coefficients μ_k by analyzing QCM frequency and bandwidth shifts, Δf and ΔΓ = (f/2)Δ(Q⁻¹), as a function of the amplitude of vibration for glass spheres in contact with silica or polymer-coated QCM electrodes. The values were not, however, compared to conventional macroscopic measurements of μ_k on the same materials combinations. Seed et al. (2020) very recently employed the Vlachová et al. (2015), Berg and Johannsmann (2003), Berg et al. (2003), and Hanke et al. (2013) analysis approach to infer macroscale friction coefficients μ for QCMs loaded with stainless steel spherical contacts, and also measured μ in conventional macroscale setups for the same materials combinations. They found that the values agreed well when the dependence of ΔΓ on vibrational amplitude was utilized. Overall, Seed et al. validated the combined assumptions of the continuum analysis methods, and demonstrated that the Vlachová et al. (2015), Berg and Johannsmann (2003), Berg et al. (2003), and Hanke et al. (2013) approach was viable for linkage macro and nanoscale tribological measurements (Seed et al., 2020).

The study reported by Seed et al. was performed in air on unlubricated stainless steel contacts, and the analysis was performed from a continuum perspective (Seed et al., 2020). We employ it here to examine both dry and lubricated contacts, with a particular focus on the degree to which such a continuum model can be applied to a complex liquid-nanoparticle-solid interface. TiO₂ suspensions were selected for study, as they have been reported on extensively in the tribological literature and are known to reduce friction in stainless steel contacts at both the nanoscale and macroscale (Glavatskih and Höglund, 2008; Ali et al., 2016; Acharya et al., 2019a; Wu et al., 2020). TiO₂ suspensions are also of interest in tribotronics [“active” or “smart” control of friction by combining mechanical elements with electronics (Glavatskih and Höglund, 2008; Zhang and Wang, 2016; Krim, 2019)], since they are readily repositioned by external fields for purposed of tuning of friction levels (Acharya et al., 2019b; Krim, 2019). In addition, the suspensions are of interest in energy storage applications utilizing flow batteries, where interfacial tribological properties are of importance (Wang et al., 2007; Sen et al., 2017).

Materials and Methods

Measurements were performed in air, deionized (DI) water, and DI water with suspensions of 0.67 wt% TiO₂ nanoparticles in an apparatus depicted schematically in Figure 2. The apparatus was comprised of a Ball Bearing (BB) configuration with three 304SS bearings arranged in a close packed triangular array centered on the QCM upper (liquid facing) electrode. The BB's made contact with the upper electrode at a distance of 2.29 mm from the center, which fell within the perimeter of the lower electrode and therefore within an area of active oscillation. The system weighed F_N = 0.282 N, distributed across the three contacts so as to load 0.094 N onto each of them. This loading configuration has a Hertzian contact pressure of 245 MPa in air and a contact radius of 11.05μm under the assumption of a circular contact (Popov, 2010). Measurements were performed in reciprocal motion with maximum sliding speed amplitudes ranging between 0.03 and 0.22 m/s (liquid) or 0.53 m/s (air) at the point of contact. Under these conditions, the system falls within the boundary lubrication regime where direct contact between asperities supports the load (Lu et al., 2006; Yamaguchi and Hokkirigawa, 2016). The liquid nonetheless penetrates the gaps in contact associated with roughness, allowing introduction of NP. For the liquid measurements, 0.6 mL of either DI water or the TiO₂ suspension was added to evenly cover the QCM, resulting in the tripod BBs being slightly more than half submerged. The associated buoyant force of 0.00086 N was significantly smaller than the normal force, but was nonetheless included in the model calculations. The system components were rigidly attached to each other, and, in contrast to the system employed by Vlachová' et al. were close packed. Differences in the results associated with the different experiment geometries are however expected to be minimal, as the tangential forces and local contact geometries were very similar.

FIGURE 2

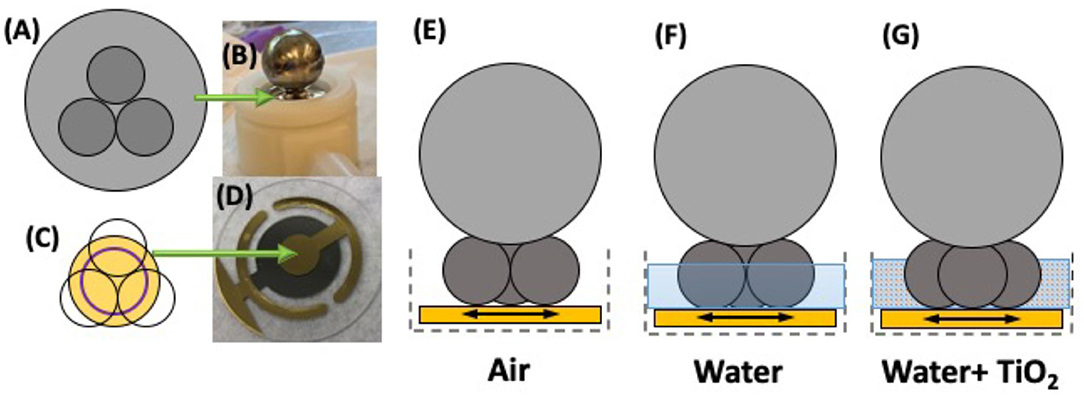
Figure 2. Images and schematics of the experimental apparatus employed here to compare friction coefficients inferred from continuum models to data recorded on QCM 304SS electrodes in contact with 304SS spheres in air, DI water, and DI water + 0.67wt% TiO₂ suspensions. Three close-packed 304SS spheres are rigidly attached to a load (A) and then placed atop an oscillating QCM electrode (B). The lower side electrode (C,D), which is smaller than the liquid-facing electrode where contacts are established (E–G), defines the active area of oscillation.

Materials

Anatase TiO₂ (titania) nanoparticles with density, Zeta potential, and radius, respectively, =4.23 g/cm³, −32.7 mV and 20 nm were obtained from US Research Nanomaterials (stock number: US7071 Houston, TX 77084, USA) at concentration ~ 20 wt% and were diluted to a concentration of 0.67 wt. The NP suspension, as prepared, had a pH of 7.7 and density of 1.00367 g/cm³. NP aggregation was not observed, but some sedimentation was observed for samples left unstirred for periods of 12–24 h. The sedimentation was readily reversible by stirring and sonication and the suspensions were stirred and sonicated for 10–15 min immediately before each experimental run, with measurements being completed within 60 min thereafter. All data were recorded within 48 h of initial preparation of the suspension.

Bulk 0.2 g 5/32” diameter Grade 100 (G100) 304SS bearings with maximum rms surface roughness 5.0 μ in (127 nm) were attached to the underside of a slider, as depicted in Figure 2. They were glued onto the holder using Gorilla Super Glue (Gorilla Glue Company, Sharonville, OH, USA).

The QCM crystals employed for the studies were AT-cut, 5 MHz, one-inch diameter QCM crystals with 304SS electrodes (FILTECH, Inc. part no. QM1022, Boston, MA). The crystals had half-inch diameter surface electrodes made of 304SS and quarter inch backside electrodes made of Au. The 304SS electrodes consisted of 200 nm 304SS films deposited atop 100 nm thick Au films deposited on 50 nm thick Ni adhesion layers, with rms surface roughness 2 ± 1 nm (Acharya et al., 2018).

Methods

Contact Angle

Contact angle measurements were performed as an independent indication of NP suspension potential for lubricity. The measurements were performed on the actual samples used for the measurements, as contact angles, and also lubricating properties, are highly dependent on surface roughness, NP concentrations, NP size and interfacial chemical compositions (Wu et al., 2020). Contact angles were measured for both DI water and TiO₂ suspensions by using a pipette to place a 10 μL drop onto the 304SS QCM electrode. An image was used to determine the contact angle on both sides of the droplets by drawing a right triangle where the base was the surface from the edge of the droplet to the center, and a line was drawn tangent to the droplet edge, forming the hypotenuse. The value for contact angle displayed in Figure 3 is the average of the right and left angles.

FIGURE 3

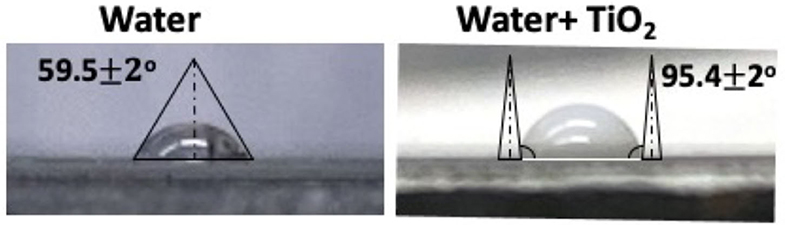
Figure 3. Images of sessile droplets of (left) pure DI water, and (right) a 0.67 wt% suspension of TiO₂ NP atop the QCM 304SS electrode, along with droplet tangents drawn to compute the contact angle.

The TiO₂ suspension exhibited a higher contact angle than that for pure water, indicating that a significantly larger slip length along with a lower friction coefficient is to be expected for contacts completely immersed in the liquid (Ellis et al., 2003; Acharya et al., 2019b). We note that this is distinct from the wetting and spreading of lubricant droplets, which also play major roles in the lubrication of dynamic mechanical systems (Wu et al., 2020).

QCM Continuum Model Analysis

Data recorded here were analyzed according to the methods described in Berg and Johannsmann (2003), Berg et al. (2003), Hanke et al. (2013), Vlachová et al. (2015), and Seed et al. (2020), which are applicable to the CM partial slip approximation in a small amplitude reciprocal motion (Figure 1). For reciprocal motion, and as the amplitude of motion increases, the partial slip regime in this model commences at the contact's edge in the form of thin annulus. The annulus progressively grows and the system transitions to full gross slippage for a sufficiently large applied tangential force (Figure 4).

FIGURE 4

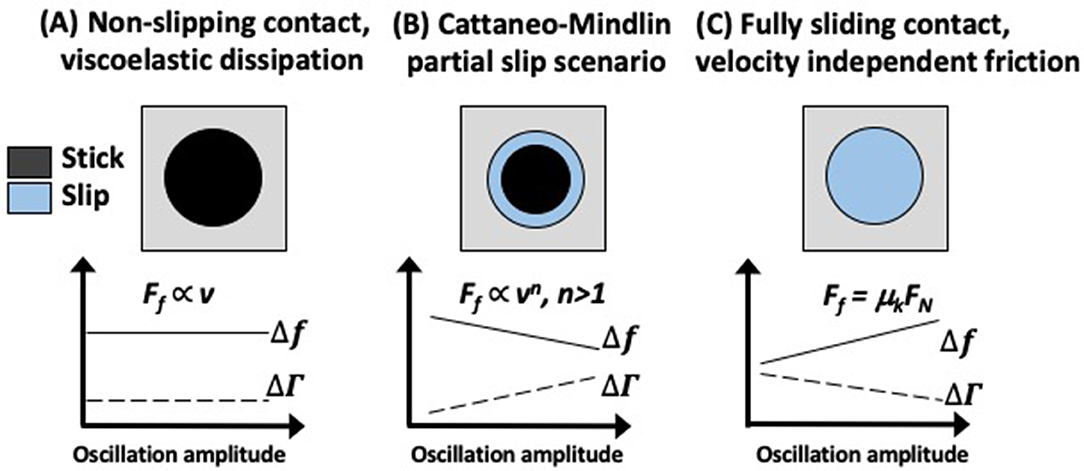
Figure 4. Schematic of the Δf and ΔΓ response of a QCM in three distinct idealized continuum contact conditions (A) A non-slipping viscoelastic contact, (B) A partially slipping contact with slipping regions governed by Coulomb friction, and (C) a fully slipping contact governed by Coulomb friction.

Values for μ in the slipping region of the contact are inferred from the shifts in resonance frequency, Δf, and half bandwidth at half height (“bandwidth,” for short), ΔΓ, of the QCM oscillating at MHz resonance frequency upon contact of a sphere with the surface (We note here that the quality factor Q, damping parameter D_f, and dissipation D, (all unitless) are all in common use to represent system dissipation. They are related to ΔΓ, which has units of Hz, as The model developed by Johannsmann and coworkers treats the system as a composite mechanical resonator consisting of a QCM in contact with a fixed load, with contact comprised of a dashpot in parallel with a spring. On a basic level, Δf and ΔΓ are proportional to the in-phase and out-of-phase component of the area-averaged periodic tangential stress at the resonator surface (Berg et al., 2003), and can be inferred from expressions for the tangential force and contact area. The time dependent tangential force at the contact is written as Hanke et al. (2013):

$\begin{array}{ll}{F}_x(t)=\kappa u(t)+\xi v(t),& (1)\end{array}$

where u is the tangential displacement, κ is the contact stiffness, v is the tangential sliding speed and ξ is a linear drag coefficient. For a viscoelastic contact small amplitude cyclic motion with amplitude u_o and tangential velocity amplitude v_o = iωu_o, the contact area A_eff is constant, all forces depend linearly on displacement, and the complex frequency shift associated with the presence of the contact can be expressed as Laschitsch and Johannsmann (1999) and Hanke et al. (2013):

$\begin{array}{ll}\Delta f+i\Delta \Gamma =\frac{n_p\kappa }{2n{\pi }^2{A}_{eff}{Z}_q}(\kappa +i\omega \xi ),& (2)\end{array}$

where A_eff is the effective area of the resonator, κ is the contact stiffness, n is the overtone order, F_N is the load, and $Z_q=8.8*{10}^6$ kg/(m²s) is the shear wave impedance. The quantities in Equation (2) are amplitude independent, and therefore both Δf and ΔΓ are constant in amplitude (Figure 4A). For the case of full slip governed by a velocity independent Coulomb friction law, Δf trending linearity upward and ΔΓ trends linearly downward as the amplitude increases (Figure 4C) (Vittorias et al., 2010).

For the case of a composite contact that is partially slipping, F_x(t) is not time harmonic, and the analysis must encompass both linear and non-linear contact mechanics regimes with proper matching of boundary conditions. The analysis developed in Berg and Johannsmann (2003), Berg et al. (2003), Hanke et al. (2013), Vlachová et al. (2015) reveals that in this regime Δf trends downward with amplitude while ΔΓ trends upward (Figure 4B). To emphasize the linear trends, the expressions in Vlachová et al. (2015), Equation 11 can be rewritten as Seed et al. (2020):

$\begin{array}{ll}\Delta f(u_o)=h-b{u}_o& (3)\end{array}$

$\begin{array}{ll}\Delta \Gamma (u_o)=\frac{4}{3\pi }b{u}_o& (4)\end{array}$

$\begin{array}{ll}h=\frac{n_p\kappa }{2n{\pi }^2{A}_{eff}{Z}_q}& (5)\end{array}$

$\begin{array}{ll}b=\frac{n_p{\kappa }^2}{6n{\pi }^2{A}_{eff}{Z}_q{F}_N}\frac{1}{\mu },& (6)\end{array}$

Where n_p is the number of BB contacts, μ is the coefficient of friction, and u_o is the amplitude of oscillation at the center of the QCM (Vlachová et al., 2015). The latter quantity is inferred from Hanke et al. (2013):

$\begin{array}{ll}{u}_0=\frac{\alpha d_q}{2\omega e_{26}{A}_{eff}}i,& (7)\end{array}$

where the parameter α is a numerical factor set equal to 1 since the QCM is modeled as a piezoelectric parallel plate, d_qis the thickness of the QCM, $e_{26}=9.65\times {10}^{-2}$ C/m² is the piezoelectric stress coefficient, i. is the current, and ω is the angular resonant frequency of the QCM (Hanke et al., 2013). In addition to the above formulation, a heuristic term representing losses linear in stress ΔΓ_off can be added to the term in Equation (4), which offsets the curve by a constant (Vlachová et al., 2015).

The value for the friction coefficient μ is inferred via two distinct methods, which were referred to by Seed et al. as “Method 1” and “Method 2,” referred to herein as “slope Model 1” and “contact Model 2.” The slope Method 1 substitutes the slope of ΔΓ vs. u_o, as determined from an amplitude sweep measurement, into Equation (4) to solve for b. The y intercept of a linear fit to the Δf vs. u_o data meanwhile yields a value for h. The values for b and h are then substituted into Equations (5, 6) to obtain μ. The contact Method 2 utilizes the Δf and ΔΓ shifts that occur at a fixed u_o to solve for μ.

Both methods must be evaluated in the CM slip regime, which is a basic assumption of the model, and predicts a negative (positive) linear slope in frequency (bandwidth) with amplitude. Friction coefficients were therefore evaluated only in amplitude regions exhibiting these linear trends, and those regions were denoted as CM slip regimes. The value of h was determined from the intercept of the Δf vs. u_o linear fit in the CM slip regime, while the value for b was obtained from the ΔΓ vs. u_o slope in the same regime. Since Equation 4 has a zero intercept, a requirement was in general enforced when finding the ΔΓ data fit, with the slope of this line used as the value of b. This condition was relaxed however for fits to the contacts lubricated by the NP suspension, as the nature of the contact geometry might be expected to change for low vibrational amplitudes.

The friction coefficient, which is a kinetic friction coefficient as determined by Seed et al. is obtained by solving Equations (5, 6) for μ in terms of h and b (Seed et al., 2020):

$\begin{array}{ll}\mu =\frac{2{\pi }^{2}n{A}_{eff}{Z}_q}{3n_p{F}_{N}b}{h}^2& (8)\end{array}$

For the present studies, a value of $A_{eff}=3.165\mathrm{\text{x}}{10}^{-5}{m}^2$ was employed for the effective area of oscillation, corresponding to the area of the smaller electrode, along with f₀ = 5 MHz for the fundamental (n = 1) resonant frequency, n_p = 3 for the number of BBs in contact with the QCM, and the acoustic impedance value $Z_q=8.8\mathrm{\text{x}}{10}^6$ kg/(m²s).

For the contact Method 2, the measured values of Δf and ΔΓ at a fixed oscillation amplitude in the CM Slip allow evaluation of μ by direct substitution of Equation (3) into Equation (4), followed by some rearrangement of terms:

$\begin{array}{ll}\mu =\frac{4\beta {\kappa }^2}{9\pi F_N\Delta \Gamma }{u}_o& (9)\end{array}$

where β and κ are given by:

$\begin{array}{ll}\beta =\frac{n_p}{2n{\pi }^2{A}_{eff}{Z}_q},\kappa =\frac{\Delta f+\frac{3\pi }{4}\Delta \Gamma }{\beta }& (10)\end{array}$

It is noted here that the contact Method 2 is straightforward in that it requires only a single measurement of Δf and ΔΓ to obtain a value for μ. The analysis is only valid however if measurement is performed at an amplitude of vibration where CM slip is occurring. This can be confirmed by imaging the contact zone or alternatively performing a local amplitude sweep that confirms a negative (positive) and linear slope for Δf (ΔΓ) vs. u_o in the region being studied.

Quartz Crystal Microbalance Apparatus and Data Recording

Measurements were performed with no contacting sphere by first installing the QCM into a Teflon holder and allowing the frequency to stabilize in air or, for the case of liquid measurements, in liquid. The tripod BB contacts were then loaded onto the QCM electrode while the system response was recorded, beginning with the minimum amplitude of vibration, and continuing on as the amplitude of vibration was increased. Variations in amplitude were achieved by introducing electrical resistance, ranging from 1,190 Ω to 0 Ω, between the QCM electrode and the oscillator circuit. This procedure was starting with 1,190 Ω and subsequently reduced every 60 s until a value of 0 Ω was attained. A baseline resonance frequency was established by using the same process for changing the QCM amplitude on the same QCM without the BB load, and for immersed contacts in the case of the lubricated measurements. Plots of Δf and ΔΓ vs. u_o were then generated. The values from these curves at equal values for u_o were used to solve for μ via the contact Method 2. To take into account the fact that the amplitude of vibration at the contact points was lower in magnitude than at the center of the electrode, the amplitude at the contacts was a modeled as a Gaussian decay, and the central maximum was calculated from Equation 11, according to Martin and Hager (1989), Josse and Lee (1998), and Lu et al. (2004):

$\begin{array}{ll}u=u_o{e}^{-\frac{a{r}^2}{R_e^2}}& (11)\end{array}$

where a = 2 is an estimated constant, r = 2.29 mm is the distance from the center, and R_e = 3.175 mm is the radius of the active oscillation region of QCM electrode. Slopes of the plots were then utilized to evaluate μ.

A QCM100 (Stanford Research Systems, Sunnyvale, CA, USA) system with the included oscillator driving circuitry, controller, and Teflon sample holder was employed to record the QCM measurements. A frequency counter (HP 53181A, Keysight Technologies, Santa Rosa, CA) and a multimeter (Keithley 2000 Series, Tektronix, Inc., Beaverton, OR) were used to measure the QCM frequency and conductance voltage via a LabView (National instruments, Austin, TX) data acquisition system. Conductance voltage V_c was converted to motional resistance R according to $\mathrm{\text{R}}={10}^{(4-V_c/5)}-75$¹, and shifts in R were converted to shifts in Γ according to Johannsmann et al. (2009):

$\begin{array}{ll}\Delta \Gamma =\frac{16A_{eff}{f}_0^{3}Zq{d}_{26}^2}{\pi }\Delta R& (12)\end{array}$

where f₀ is the fundamental resonant frequency (n=1 for these studies), $Z_q=8.8\times {10}^6$ kg/(m²s) is the acoustic impedance, and $d_{26}=3.1\times {10}^{-12}$ m/V is the piezoelectric strain coefficient.

Results

Figure 5 presents amplitude sweep data sets recorded for the response of the QCM in continuous contact with the tripod in the three environments studied. Values for μ displayed in lower panel of Figure 5 were evaluated in the respective CM regimes using the contact Method 2. All data are plotted vs. the amplitude at the actual contact (i.e., not the amplitude at the center of electrode) and range from 1 to 17 nm for air and 1 to 7 nm for the liquids, which, respectively, correspond to velocity amplitudes of 0.03–0.53 m/s and 0.03–0.22 m/s. Notably, the maximum amplitude in all cases was <40 nm diameter of the TiO₂ NP, >2 nm rms roughness of the 304SS electrodes but <127 nm maximum rms roughness of the 304SS BB's. Regions of the amplitude sweep that are consistent CM slip are shaded orange and designated as “CM slip.” The amplitude region falling between zero and the first CM slip regime is shaded purple and arbitrarily labeled the “stick regime” since the contacts are likely to transition to being stuck at the lowest amplitudes For the lubricated contacts, there are multiple regions that are consistent with CM slip (e.g., Figure 4B) that are separated by regions consistent with full slip (e.g., Figure 4C). For the water lubricated contacts the ΔΓ vs. amplitude data in the CM slip regimes trend toward zero at zero amplitude. It is difficult to identify a region of clear CM slip for the NP suspensions, as there is no extended region where the ΔΓ data exhibits a positive linear slope that extrapolates to zero.

FIGURE 5

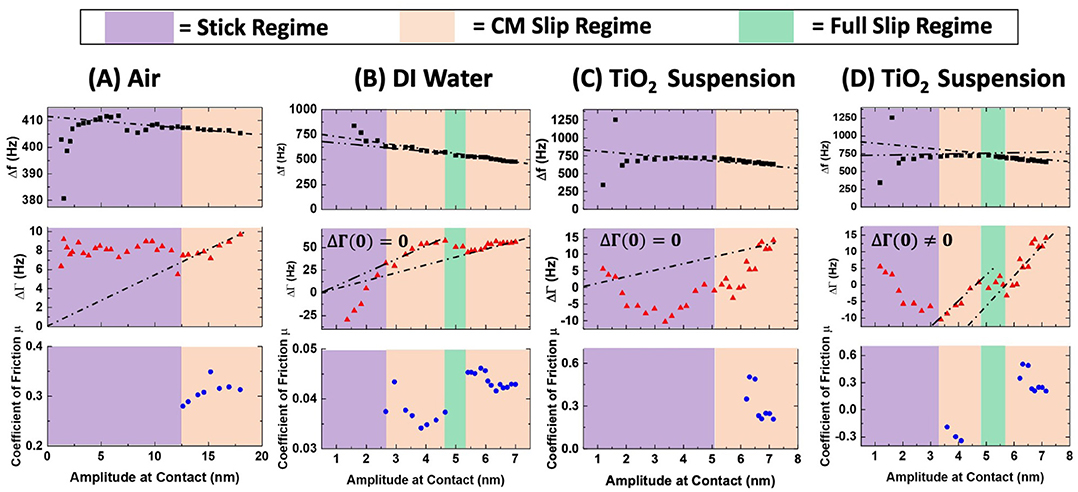
Figure 5. Plots of Δf, ΔΓ, and μ vs. QCM amplitude of vibration derived in the CM regime via Method 2, for contacts in (A) air, (B) water and (C,D) the TiO₂ suspension. Regions where Δf (ΔΓ) decrease (increase) linearly are identified as CM Slip (orange), with displayed with dashed lines. The adjacent regions are designated in purple for regions where the contact is likely to be stuck, and green in regions where the data are consistent with full slippage.

Values for friction coefficients obtained inferred from the data displayed in Figure 5 in the CM slip regimes are presented in Table 1, as well as the amplitude of vibration at which the transition from stick to a CM partial slip condition is designated. The slope Method 1 values employed the slope and intercept values from the fits displayed as black dotted lines to the ΔΓ data in Figure 5. The contact Method 2 value are inferred from the values of Δf and ΔΓ at fixed amplitudes, as denoted in the table. Since the NP suspension ΔΓ data do not trend toward zero at zero amplitude, the slope Method 1 was also applied by employing fits that were either required or not required to have a zero intercept. Relaxing the zero-intercept condition resulted in a significantly lower value for μ that was also more realistic, as discussed next.

TABLE 1

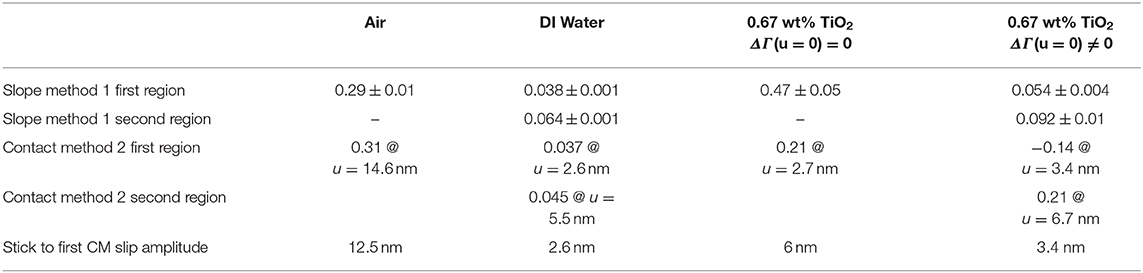
Table 1. Friction coefficients inferred from the Figure 5 data by two analysis methods, along with the transition amplitude of vibration from stick to partial slip.

Discussion

Prior measurements employing the same experimental configuration have indicated the amplitudes inferred from Equation 11 may be underestimated, causing the values for friction coefficients reported in Table 1 to be slightly underestimated by ~25% (Seed et al., 2020). Inspection of the results in Figure 5 and Table 1 for contacts in air, nonetheless reveals values of μ~0.3, which are in close agreement in close agreement with conventional ball on disk macroscale measurements (Seed et al., 2020). The continuum model therefore successfully treats this system, irrespective of the fact that the amplitude of vibration is clearly nanoscale in extent.

For the case of contacts immersed in water, the Method 1 and 2 values of μ ~ 0.04 in region 1 agree closely, and are close for the second region, at μ ~ 0.045 & 0.064. The values are also of the same order as conventional ball on disk macroscale measurements for water-immersed 304SS contacts (Curtis et al., 2017), where μ~0.1 but falling slightly lower. Overall, the continuum model can be considered to successfully treat this system, with the QCM data revealing both a lower friction coefficient and amplitude of transition from stick to partial slip that has been reduced to less than half of the value in air.

The analysis methods yield results that are far more problematic for contact immersed in the TiO₂ suspension. TiO₂ suspensions are known to lower the macroscopic friction coefficient for pure water by as much as 20–50% (Ali et al., 2016; Pardue et al., 2018; Acharya et al., 2019a; Wu et al., 2020), and this is not reflected in the Table 1 values. The Method 1 and 2 values of μ are moreover in clear disagreement with each other, and clear regions of CM slip are difficult to define. Realistic values for the friction are obtained by relaxing the zero-intercept condition. Without relaxed conditions, the model clearly fails upon introduction of NPs. The zero-intercept condition ignores viscous dissipation while calculating μ, which by the fits shown in Figure 5, is an appropriate assumption to make for air and DI water. However, the fit is poor in the case of TiO₂, suggesting that this assumption may no longer be applicable. It is possible that the presence of NP lowers the dissipation at low oscillation amplitudes, replacing the contact with a more complex granular interface. Once this condition is relaxed, however, the values still do not show the expected reductions to friction, indicating that there are still difficulties with applying the model.

One possible explanation for the continued analysis failure is that the NPs possibly change the mechanics at the contacts, which may violate some of the underlying assumptions. One possibility of NPs affecting assumptions is that the CM slip regime as defined may no longer be present if rolling and/or slipping NP are present at the interface. Additionally, the amplitude of vibration can no longer be assumed to be much smaller than the size of the contact, since the contact may be comprised of 40 nm sized objects. Other model assumptions that could become problematic by the addition of NPs include the sphere being in contact with a ridged, flat surface, ignoring surface roughness, and assuming the contact area and slip annulus are uniform circles (Hanke et al., 2013). These assumptions could also be exacerbated by the potential formation of NP film formation at the contact points and/or the embedding of NPs into the surfaces. A visible residue was observed on the QCM after the TiO₂ trial which remained even after rinsing the QCM with acetone and DI water, but we were unable to confirm the presence of embedded NP in the film by imaging. Complications to the contact introduced by the NPs could have a notable effect on the model because ΔΓ is equal to the area under the force-displacements loop divided by u_o, where the force displacement loop will have different shapesdepending on what slip regime the contact is in Hanke et al. (2013).

The sensitivity of ΔΓ tothe contact shape and conditions could also explain the behavior observed in ΔΓ in the stick regime. The small variations in ΔΓ at small amplitudes in air are likely due to small shifts and departures from the ideal model of perfect stick. This does not readily explain the largedepartures from expectation seen in the liquid trials at small amplitudes. The addition of liquids into the system resulted in low amplitude ΔΓ being largely negative with the shape either mostly concave down (DI) or concave up (TiO₂). Since this same behavior was not seen in the air experiments, it is likely the behavior is caused by the liquids. It is possible that at low amplitude, the observed ΔΓ behavior may be dominated by any energy dissipation in the liquid or behavior such as capillary action which might change the liquid barrier between contacts.

From another point of view, one might argue that the continuum model is highly successful even for the case of the TiO₂ suspension. Given that it is only applicable in CM partial slip regimes, and the lack of a clear CM slip trend in the Δf and ΔΓ vs. u data may indicate that there simply is no CM slip regime present in this complex interface, the model still manages to produce a value for TiO₂ close to water. Since the CM slip regime will potentially result in the formation of wear particles (Fouvry et al., 1998), and these wear particles do not appear to have a negative impact on the model as seen in the air and water cases, then it is possible that the wear particles formed in the CM regime are less numerous than the NPs or that the wear particles were small enough to fall in the roughness gaps while the 40 nm NPs were not. Therefore, a follow-up study with varying sized NP would be of interest to determine the size of the particulate at which, if any, the model might become more applicable. In particular, if a collection of poorly coupled collection of sliding or rolling particles were pushed into the gaps, then the continuum behavior might be recovered. In contrast, If the smaller particles formed the contract itself, then the model assumption of an amplitude of vibration being far smaller than the NP contact size would be even less applicable.

Summary and Conclusions

Using a continuum analysis model, the response of a QCM to tripod 3[4SS/304SS rubbing contacts in air, water and a TiO₂ suspension has been employed to evaluate friction coefficients. The results for dry and water lubricated contacts compare favorably with friction coefficient measurements reported in the literature for the same materials' combinations. The model appears less applicable to the case of contacts lubricates with the NP suspension. The continuum nature of the model does not however appear to be the dominant factor underlying its failure to apply to NP lubricated suspensions. The failure is likely attributed to a lack of a CM slip regime when NP are present at the interface, e.g., in the form of a poorly coupled collection of sliding or rolling particles, and/or the fact that the amplitude of vibration is no longer far smaller than the NP contact size regions.

Data Availability Statement

All datasets generated for this study are included in the article/supplementary material.

Author Contributions

CS, BA, and JK conceived the design of the experiment and constructed the apparatus. CS performed the experimental measurements and data analysis. CS and JK composed and edited the manuscript. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by the US National Science Foundation, Materials Genome Initiative Project #DMR1535082.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Abbreviations

QCN, Quartz Crystal Microbalance; CM, Cattaneo-Mindlin; SS, Stainless Steel; BB, Ball Bearing.

Footnotes

1. ^QCM200 Quartz Crystal Microbalance Digital Controller - QCM25 5 MHz Crystal Oscillator, Revision 2.

References

Acharya, B., Pardue, T. N., Avva, K. S., and Krim, J. (2018). In situ, real time studies of thermal reaction film formation temperatures for iron and 304ss surfaces immersed in 5% tricresyl phosphate in base oil. Tribol. Int. 126, 106–115. doi: 10.1016/j.triboint.2018.04.034

CrossRef Full Text | Google Scholar

Acharya, B., Pardue, T. N., Su, L., Smirnov, A. I., Brenner, D. W., and Krim, J. (2019a). Nanotribological performance factors for aqueous suspensions of oxide nanoparticles and their relation to macroscale lubricity. Lubricants 7:49. doi: 10.3390/lubricants7060049

CrossRef Full Text | Google Scholar

Acharya, B., Seed, C. M., Brenner, D. W., Smirnov, A. I., and Krim, J. (2019b). Tuning friction and slip at solid-nanoparticle suspension interfaces by electric fields. Scient. Rep. 9:18584. doi: 10.1038/s41598-019-54515-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Ali, M. K., Xianjun, H., Mai, L., Qingping, C., Turkson, R. F., and Bicheng, C. (2016). Improving the tribological characteristics of piston ring assembly in automotive engines using Al₂O₃ and TiO₂ nanomaterials as nano-lubricant additives. Tribol. Int. 103, 540–554. doi: 10.1016/j.triboint.2016.08.011

CrossRef Full Text | Google Scholar

Berg, S., and Johannsmann, D. (2003). High speed microtribology with quartz crystal resonators. Phys. Rev. Lett. 91:145505. doi: 10.1103/PhysRevLett.91.145505

PubMed Abstract | CrossRef Full Text | Google Scholar

Berg, S., Prellberg, T., and Johannsmann, D. (2003). Nonlinear contact mechanics based on ring-down experiments with quartz crystal resonators. Rev. Sci. Instrum. 74, 118–126. doi: 10.1063/1.1523647

PubMed Abstract | CrossRef Full Text | Google Scholar

Borovsky, B., Booth, A., and Manlove, E. (2007). Observation of microslip dynamics at high-speed microcontacts. Appl. Phys. Lett. 91:114101. doi: 10.1063/1.2784172

CrossRef Full Text | Google Scholar

Borovsky, B., Krim, J., Syed Asif, A., and Wahl, K. J. (2001). Measuring nanomechanical properties of a dynamic contact using an indenter probe and quartz crystal microbalance. J. App. Phys. 90:639. doi: 10.1063/1.1413493

CrossRef Full Text | Google Scholar

Borovsky, B. P., Bouxsein, C., O'Neill, C., and Sletten, L. R. (2017). An integrated force probe and quartz crystal microbalance for high-speed microtribology. Tribol. Lett. 65:148. doi: 10.1007/s11249-017-0933-6

CrossRef Full Text | Google Scholar

Borovsky, B. P., Garabedian, N. T., McAndrews, G. R., Wieser, R. J., and Burris, D. L. (2019). Integrates QCM-microtribometry: friction of single-crystal MoS₂ and gold from μm/s to m/s. ACS Appl. Mater. Interfaces. 11, 40961–40969. doi: 10.1021/acsami.9b15764

PubMed Abstract | CrossRef Full Text | Google Scholar

Braiman, Y., Barhen, J., and Protopopescu, V. (2003). Control of friction at the nanoscale. Phys. Rev. Lett. 90:094301. doi: 10.1103/PhysRevLett.90.094301

PubMed Abstract | CrossRef Full Text | Google Scholar

Brizmer, V., Kligerman, Y., and Etsion, I. (2007). A model for junction growth of a spherical contact under full stick condition. J. Tribol. 129, 783–790. doi: 10.1115/1.2772322

CrossRef Full Text | Google Scholar

Ciavarella, M. (2015). Transition from stick to slip in Hertzian contact with “Griffith” friction: The Cattaneo-Mindlin problem revisited. J. Mech. Phys. Solids. 84, 313–324. doi: 10.1016/j.jmps.2015.08.002

CrossRef Full Text | Google Scholar

Curtis, C. K., Marek, A., Smirnov, A. I., and Krim, J. (2017). A comparative study of the nanoscale and macroscale tribological attributes of alumina and stainless steel surfaces immersed in aqueous suspensions of positively or negatively charged nanodiamonds. Beil. J. Nanotechnolgy. 8, 2045–2059. doi: 10.3762/bjnano.8.205

CrossRef Full Text | Google Scholar

Dawson, B. D., Lee, S. M., and Krim, J. (2009). Tribo-induced melting transition at a sliding asperity contact. Phys. Rev. Lett. 103:205502. doi: 10.1103/PhysRevLett.103.205502

PubMed Abstract | CrossRef Full Text | Google Scholar

Dirri, F., Palomba, E., Longobardo, A., Zampetti, E., Saggin, B., and Scaccabarozzi, D. (2019). A review of quartz crystal microbalances for space applications. Sens. Actu. A Phys. 287, 48–75. doi: 10.1016/j.sna.2018.12.035

CrossRef Full Text | Google Scholar

Dultsev, F. N., and Nekrasov, D. V. (2018). Treatment of the resonance curve recorded during measurement of the signal of particle rupture from the QCM surface. Sens. Actu. B Chem. 15, 70–75. doi: 10.1016/j.snb.2018.04.029

CrossRef Full Text | Google Scholar

Ellis, J. S., McHale, G., Hayward, G. L., and Thompson, M. (2003). Contact angle-based predictive model for slip at the solid–liquid interface of a transverse-shear mode acoustic wave device. J. App. Phys. 94, 6201–6207. doi: 10.1063/1.1619195

CrossRef Full Text | Google Scholar

Etsion, I. (2010). Revisiting the cattaneo-mindlin concept of the interfacial slip in tangentially loaded compliant bodies. J. Tribol. 132:20801. doi: 10.1115/1.4001238

CrossRef Full Text | Google Scholar

Fouvry, S., Kapsa, P., and Vincent, L. (1998). Developments of fretting sliding criteria to quantify the local friction coefficient evolution under partial slip condition. Tribol. Series. 34, 161–172. doi: 10.1016/S0167-8922(98)80071-0

CrossRef Full Text | Google Scholar

Glavatskih, S., and Höglund, E. (2008). Tribotronics—towards active tribology. Tribol. Int. 41, 934–939. doi: 10.1016/j.triboint.2007.03.001

CrossRef Full Text | Google Scholar

Han, T., Nag, A., Mukhopadhyay, S. C., and Xu, Y. (2019). Carbon nanotubes and its gas-sensing applications: a review. Sens. Actu. A Phys. 291, 107–143. doi: 10.1016/j.sna.2019.03.053

CrossRef Full Text | Google Scholar

Hanke, S., Petri, J., and Johannsmann, D. (2013). Partial slip in mesoscale contacts: dependence on contact size. Phys. Rev. E. 88:032408. doi: 10.1103/PhysRevE.88.032408

PubMed Abstract | CrossRef Full Text | Google Scholar

Hsu, S., Ying, C., and Zhao, F. (2014). The nature of friction: a critical assessment. Friction 2, 1–26. doi: 10.1007/s40544-013-0033-z

CrossRef Full Text | Google Scholar

Johannsmann, D. (2007). Studies of contact mechanics with the QCM. Springer Ser Chem Sens Biosens. 5, 151–170. doi: 10.1007/5346-026

CrossRef Full Text | Google Scholar

Johannsmann, D., Reviakine, I., and Richter, R. (2009). Dissipations in films of adsorbed nanospheres studied by quartz crystal microbalance (QCM). Anal. Chem. 81, 8167–8176. doi: 10.1021/ac901381z

PubMed Abstract | CrossRef Full Text | Google Scholar

Josse, F., and Lee, Y. (1998). Analysis of the radial dependence of the mass sensitivity for modified-electrode quartz crystal resonators. Anal. Chem. 70, 237–247. doi: 10.1021/ac9706032

CrossRef Full Text | Google Scholar

Kim, H. J., and Kim, D. E. L. (2009). Nano-scale friction: a review. Precis. Eng. Manuf. 10, 141–151. doi: 10.1007/s12541-009-0039-7

CrossRef Full Text | Google Scholar

Krim, J. (2012). Friction and energy dissipation mechanisms in adsorbed molecules and molecularly thin films. Adv. Phys. 61:3, 155–323. doi: 10.1080/00018732.2012.706401

CrossRef Full Text | Google Scholar

Krim, J. (2019). Controlling friction with external electric or magnetic fields: 25 examples. Front. Mech. Eng. 5:22. doi: 10.3389/fmech.2019.00022

CrossRef Full Text | Google Scholar

Laschitsch, A., and Johannsmann, D. (1999). High frequency tribological investigations on quartz resonator surfaces. J. Appl. Phys. 85:3759. doi: 10.1063/1.369745

CrossRef Full Text | Google Scholar

Leopoldes, J., and Jia, X. (2010). Transverse shear oscillator investigation of boundary lubrication in weakly adhered films. Phys. Rev. Lett. 105:266101. doi: 10.1103/PhysRevLett.105.266101

PubMed Abstract | CrossRef Full Text | Google Scholar

Lu, F., Lee, H. P., and Lim, S. P. (2004). Quartz crystal microbalance with rigid mass partially attached on electrode surfaces. Sens. Actu. A Phys. 112, 203–210. doi: 10.1016/j.sna.2004.01.018

CrossRef Full Text | Google Scholar

Lu, X., Khonsari, M. M., and Gelinck, E. R. (2006). The Stribeck curve: experimental results and theoretical prediction. J. Tribol. 128, 789–794. doi: 10.1115/1.2345406

CrossRef Full Text | Google Scholar

Martin, B. A., and Hager, H. E. (1989). Velocity profile on quartz crystals oscillating in liquids. J. Appl. Phys. 65:2630. doi: 10.1063/1.342772

CrossRef Full Text | Google Scholar

M'boungui, G., Semail, B., Giraud, F., and Jimoh, A. A. (2014). Development of a novel plane piezoelectric actuator using Hamilton's principle based model and Hertz contact theory. Sens. Actu. A Phys. 217, 116–123. doi: 10.1016/j.sna.2014.06.026

CrossRef Full Text | Google Scholar

Paggi, M., Pohrt, R., and Popov, V. L. (2014). Partial-slip frictional response of rough surfaces. Sci Rep. 4:5178. doi: 10.1038/srep05178

PubMed Abstract | CrossRef Full Text | Google Scholar

Pardue, T. N., Acharya, B., Curtis, C. K., and Krim, J. (2018). A tribological study of Γ-Fe₂ O₃ nanoparticles in aqueous suspension. Tribol. Lett. 66:130. doi: 10.1007/s11249-018-1083-1

CrossRef Full Text | Google Scholar

Popov, V. L. (2010). “Chapter 2: qualitative treatment of contact problems- normal contact without adhesion,” in Contact Mechanics and Friction: Physical Principles and Applications (Berlin; Heidelberg: Springer Verlag), 9–25. doi: 10.1007/978-3-642-10803-7_3

CrossRef Full Text | Google Scholar

Rodahl, M., and Kasemo, B. (1996). On the measurement of thin liquid overlayers with the quartz-crystal microbalance. Sens. Actu. A Phys. 54, 448–456. doi: 10.1016/S0924-4247(97)80002-7

CrossRef Full Text | Google Scholar

Seed, C. M., Acharya, B., Andrus, R., and Krim, J. (2020). Correlation of high frequency QCM sphere-plate stiffness measurements with macroscopic frictional contacts in thin film and bulk stainless steel materials. Sens. Actu. A Phys. 36:111913. doi: 10.1016/j.sna.2020.111913

CrossRef Full Text | Google Scholar

Sen, S., Chow, C. M., Moazzen, E., Segre, C. U., and Timofeeva, E. V. (2017). Electroactive nanofluids with high solid loading and low viscosity for rechargeable redox flow batteries. J. Appl. Electrochem. 47, 593–605. doi: 10.1007/s10800-017-1063-4

CrossRef Full Text | Google Scholar

Vittorias, E., Kappl, M., Butt, H. J., and Johannsmann, D. (2010). Studying mechanical microcontacts of fine particles with the quartz crystal microbalance. Powder Technol. 203, 489–502. doi: 10.1016/j.powtec.2010.06.011

CrossRef Full Text | Google Scholar

Vlachová, J., König, R., and Johannsmann, D. (2015). Stiffness of sphere-plate contacts at MHz frequencies: dependence on normal load, oscillation amplitude, and ambient medium. Beils. J. Nanotechnol. 6, 845–856. doi: 10.3762/bjnano.6.87

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, J., Polleux, J., Lim, J., and Dunn, B. (2007). Pseudocapacitive contributions to electrochemical energy storage in TiO₂ (Anatase) nanoparticles. J. Phys. Chem. C. 111, 14925–14931. doi: 10.1021/jp074464w

CrossRef Full Text | Google Scholar

Wang, L., Junkuo, G., and Xu, J. (2019). QCM formaldehyde sensing materials: design and sensing mechanism. Sens. Actu. B Chem. 293, 71–82. doi: 10.1016/j.snb.2019.04.050

CrossRef Full Text | Google Scholar

Wu, H., Jia, F., Li, Z., Lin, F., Huo, M., Huang,. S., et al. (2020). Novel water-based nanolubricant with superior tribological performance in hot steel rolling. Int. J. Extr. Manuf. 2:025002. doi: 10.1088/2631-7990/ab82fe

CrossRef Full Text | Google Scholar

Yamaguchi, T., and Hokkirigawa, K. (2016). Friction and wear properties of PEEK resin filled with RB ceramics particles under water lubricated condition. Tribol. Online. 11, 653–660. doi: 10.2474/troll.11.653

CrossRef Full Text | Google Scholar

Yu, X., Zhou, J., and Jiang, Z. (2016). Developments and possibilities for nanoparticles in water-based lubrication during metal processing. Rev. Nanosci. Nanotechnol. 5,136–163. doi: 10.1166/rnn.2016.1072

CrossRef Full Text | Google Scholar

Zhang, C., and Wang, Z. L. (2016). Tribotronics—A new field by coupling triboelectricity and semiconductor. Nano Today. 11, 521–536. doi: 10.1016/j.nantod.2016.07.004

CrossRef Full Text | Google Scholar

Zhang, X., and Li, Q. (2010). Enhancement of friction between carbon nanotubes: an efficient strategy to strengthen fibers. ACS Nano. 4, 292–316. doi: 10.1021/nn901515j

PubMed Abstract | CrossRef Full Text | Google Scholar