- State Key Laboratory of Tribology, Department of Mechanical Engineering, Tsinghua University, Beijing, China
In this study, we propose a numerical model to investigate the contact and friction behaviors of hydration-lubricated contact in an aqueous solution confined in a gap of several molecular diameters. A force–distance curve was obtained under different surface forces, and friction behavior was determined using the modified Eyring thermal activation model. The results showed that the normal boundary contact pressure and contact gaps were obtained using the proposed numerical model. In addition, friction force increased with the logarithm of sliding velocity. Hence, the Eyring model could predict the friction behavior of hydration lubrication. Moreover, it could capture the underlying physical principles of the contact and friction behaviors of hydration lubrication.
Introduction
In nanofilm lubrication, where film thickness is in the range of a few nanometers, the physical, and chemical properties of surfaces strongly affect the friction behavior of liquid thin films, particularly of aqueous liquids. The hydration water layer is a particular form of water molecules tightly bound to ionic or hydrophilic surfaces (Kim et al., 2013, 2015). It plays an important role in specific fields, such as biolubrication (Hansen et al., 2013), hydration polymer brushes (Raviv et al., 2003; Chen et al., 2009), and nanofriction.
In the past few decades, numerous studies have investigated the physical processes of nanoscale thin film lubrication (TFL). The improvement of modern measurement techniques has considerably facilitated the study of TFL with aqueous liquids. The surface force apparatus (SFA) and atomic force microscopy (AFM) have significantly improved understanding of the tribological behavior of thin films by providing techniques for measurement of nanoscale liquid film thickness and normal and tangential forces. Jadhao and Robbins (2017), Israelachvili and Pashley (1983), Israelachvili and Wennerstroem (1990), and Israelachvili and Wennerström (1996) measured the short-range hydration repulsive force in water containing ionic or polar species. They found that a water film separates contacting surfaces, and it is not completely squeezed out even under high pressures. Additionally, they resolved several contradictions and findings that were inconsistent with hydration models. Horn et al. (2006) and Manica et al. (2008) investigated the dynamic forces maintaining relative separation between two deformable droplets. They reported that hydrodynamic and disjoining pressures strongly influence the deformation of droplets. Raviv and Klein (2002) measured the shear forces between solid surfaces sliding in aqueous salt solutions. They found strong repulsive hydration forces in these systems. Ma et al. (2015) used surface force balance to study the hydration lubrication between atomically smooth charged surfaces and found viscous losses. Diao and Espinosa-Marzal (2018) used AFM to investigate the role of water in fault lubrication. They found that a lubricating film remains confined under high pressure and friction is significantly reduced at low sliding velocities. Experimental techniques have shown that the thickness of a water film is in the nanometer range. Additionally, the film is stabilized by the hydration repulsion between hydrophilic surfaces rather than by hydrodynamic lift forces. In nanoconfined water, surface interactions consist of long-range van der Waals attraction, short-range repulsion due to hydration force, and electrostatic repulsion with an intermediate action range (longer than that of hydration repulsion but shorter than that of van der Waals attraction). These repulsive forces are effective for achieving negative adhesion (Popov, 2020).
The above literature review shows that numerous studies have experimentally examined hydration-lubricated contact. However, there is no effective numerical model that describes the hydration contact characteristics and energy dissipation during sliding. The main experimental difficulty remains the determination of separation of surfaces under hydration repulsion because AFM experiments cannot provide accurate information about surface separation and the shear rate. In this study, we propose a numerical model for the boundary friction due to hydration lubrication. This numerical model may provide a promising method for further improvement of investigation of hydration lubrication.
Governing Equations
Contact Theory Considering Hydration Effect
There are four interacting surface forces based on the interaction range: electrical double layer (EDL) force, hydration force, van der Waals force, and the repulsive force between two solid hydrophilic surfaces under nanoscale separation. Derjaguin and Landau (1941) firstly proposed the theory that surface force is the sum of EDL force and van der Waals force under long-distance interaction. Later, this theory was independently proposed by Verwey and Overbeek, and it is known as the Derjaguin–Landau–Vervey–Overbeek (DLVO) theory [also refer to Israelachvili (2011)]. The DLVO theory can be applied to accurately describe long-distance interaction forces in correlated systems. In contrast with the DLVO force, hydration repulsive force decays exponentially in the subnanometer range. Hydration repulsive force has a significant effect at subnanometer distances, and it decreases rapidly with surface separation. Therefore, different surface forces can prevail depending on the thickness of the thin film of an aqueous solution.
Based on the Lifshitz–Hamaker approach (Lifshitz, 1956; Israelachvili, 2011), van der Waals interaction and repulsive contact interaction can be obtained as the Derjaguin approximation by the integration of the Lennard-Jones interatomic potential. The contribution of van der Waals attractive interaction to overall disjoining pressure can be expressed as
The integration of the repulsive part of the Lennard-Jones potential yields
where AH is the Hamaker constant of a material, l0 is the equilibrium separation when the interatomic force between two molecules is zero (Yu and Polycarpou, 2004), and h(x, y) is the separation of contact surfaces.
Typically, two similarly charged surfaces electrostatically repel each other in a solution. However, they may interact at small separations of several molecular diameters under certain conditions. The EDL interactions of ionic aqueous liquids can be expressed as follows:
where pEDL0 is the initial EDL pressure defined by pEDL0 = 64kTρ∞[M], k is the Boltzmann constant, T is the absolute temperature, ρ∞ is the concentration of alkali metal ions, φ0 is the electrostatic potential at the midplane, and κ−1 is the Debye length.
When two hydrophilic surfaces or particles approach each other up to a distance of a few nanometers, water is arranged in an ordered manner in the vicinity of the surfaces. This structure can generate an effective repulsive force to support the external load between the surfaces. Hydration repulsive force (also referred to as non-DLVO force) becomes extremely strong in the short range. Hydration repulsive pressure can be described as a simple exponential expression (Faraudo and Bresme, 2005).
where phyd0 is the initial constant hydration pressure and λ0 is the characteristic decay length of hydration.
As analyzed above, the local distribution of the total contact pressure between two contact surfaces has four terms, namely, hydration pressure, EDL pressure, van der Waals attractive pressure, and repulsive contact pressure.
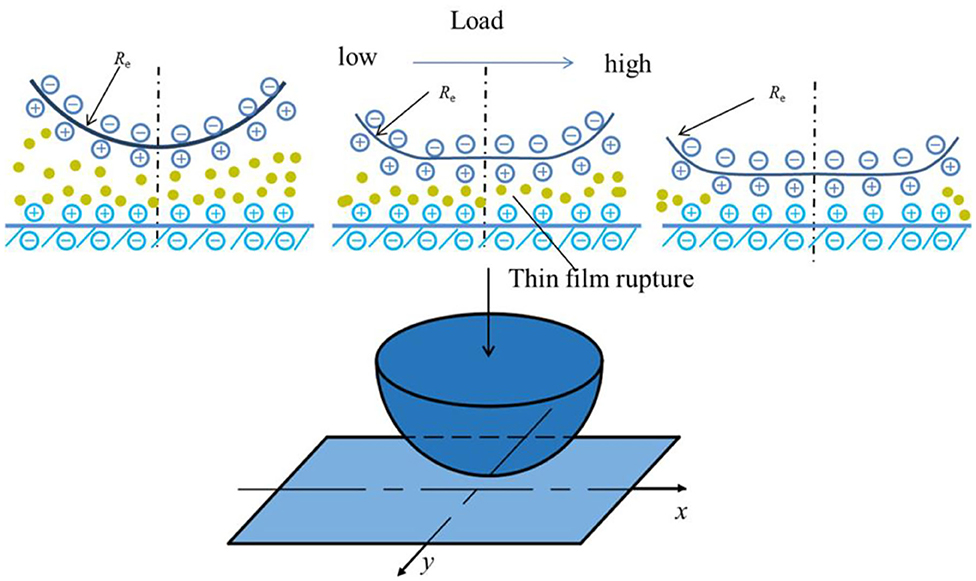
This study investigates the contact between an elastic sphere with radius R and a smooth flat surface, as shown in Figure 1. The contact profile under load can be expressed as
where h0 is the initial gap of contact surfaces and u(x, y) is the elastic deformation of the contact region. The elastic deformation can be calculated using the Boussinesq integral (Johnson, 1987) as
where E′ is the effective elastic modulus of contacting bodies, with E1, E2being the Young modulus, and ν1, ν2 the Poisson's ratio of two contacting bodies, respectively.
The total external force balanced with the surface pressure on the contact region is given by,
Friction Evaluation Based on the Eyring Model
If contact surfaces are subjected to relative tangential displacement, the molecules of a hydration lubrication layer must be rearranged. This rearrangement is supported by thermal fluctuations. The Eyring model (Eyring, 1935, 1936) describes the transition state theory of the reaction rate. It is used to evaluate and analyze the friction force of hydration-lubricated contact.
The Eyring model assumes that, in the absence of tangential loading, the heights of the energy barrier for the hopping of molecules to adjacent positions have the same value (E0) in opposite directions; thus, the net flow is zero. The application of shear force reduces the height of the energy barrier by ΔE in the direction of flow and increases it by the same amount in the opposite direction, as shown in Figure 2. When the fluid is under shear stress τ, the change in the energy barrier can be approximated as V*τ, where V* is an effective stress-activated volume. The flow rates in the forward and backward directions under shear stress are expressed as follows (Spikes, 2018):
where v0 is the frequency of the attempted rearrangements of a hydration shell. In laminar flow, the rate of relative molecular motion to a neighboring layer is given by
It is assumed that the shear strain rate is proportional to the rate of activated molecular motion. Further, based on the definitions of the Eyring stress, , and the Newtonian viscosity, , the following expression can be obtained (Jadhao and Robbins, 2017, 2019):
At a large value of τ/τE, sinh(τ/τE) ≈ 0.5 exp(τ/τE). Taking logarithms on both sides of Equation 11 and rearranging the terms, the following equation can be obtained:
Experimental investigations suggest that this equation should be extended by an additional term τ0
where τ0 is initial shear stress.
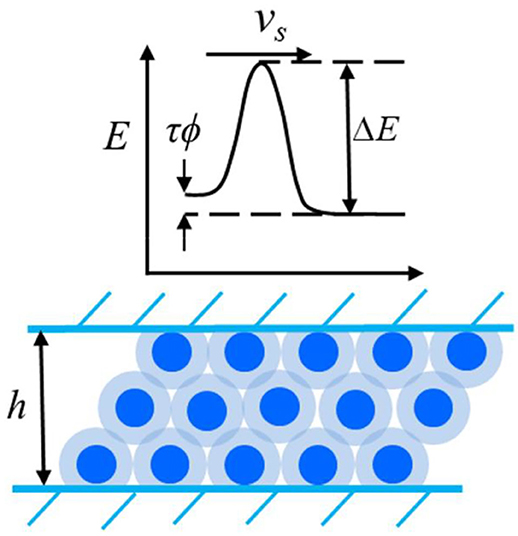
Figure 2. Schematics of the shear stress modify the energy barrier in the hydration confined liquid.
Therefore, when the shear rate is determined, shear stress can be calculated using Equation 13. The shear force under hydration-lubricated contact can be expressed as,
Numerical Scheme
In the numerical scheme, control equations were discretized and expressed in the dimensionless form using dimensionless variables as follows: , , , and . Here, a is the Hertz contact radius, and PH is the Hertz contact pressure.
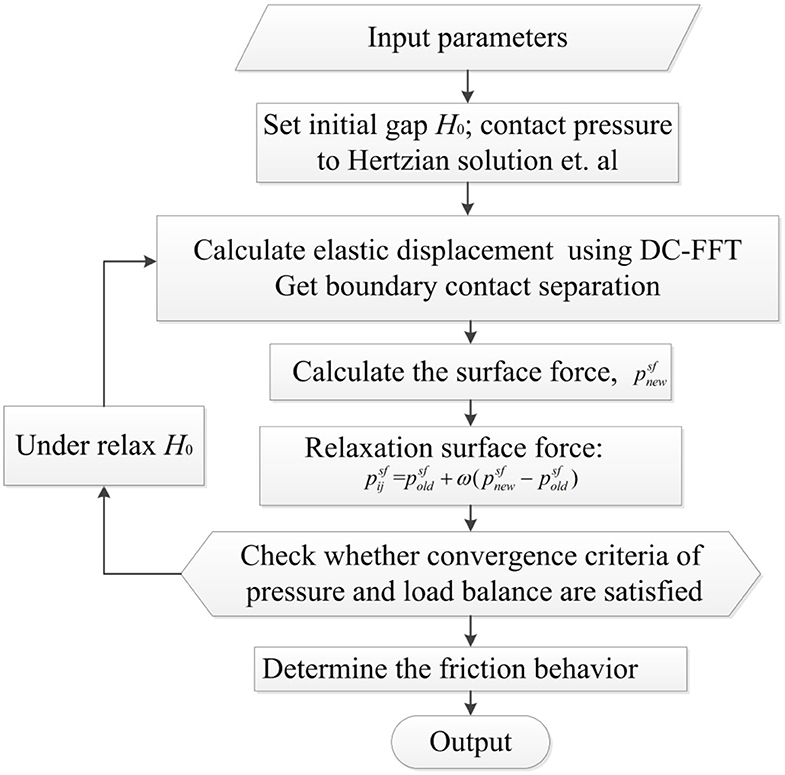
Surface repulsion force, the contact profile, and load balance were numerically calculated to determine the contact pressure of surface force and the contact separation between the two surfaces. Elastic deformation was determined by utilizing surface force; this was the most time-consuming step. The discrete convolution and fast Fourier transform (DC-FFT) technique (Liu et al., 2000) was used to improve the efficiency of calculating elastic deformation. The relaxation method was applied to ensure the robustness of the numerical scheme. The simulated area was five times larger than the Hertz diameter in the x and y directions. It was discretized into 257 × 257 nodes. The convergence criteria for pressure and load were <10−4. The converged solutions of thickness and pressure distributions were obtained after the convergence criteria were satisfied. A flow chart of the numerical scheme is shown in Figure 3.
Results and Discussion
We obtained important data on hydration capacity from a previous study (Ma et al., 2015). Then, we analyzed the surface force of a thin film of a 0.1 mol NaCl water solution using following parameters: , κ−1 = 1.36 nm, φ = 70 mV, λ0 = 0.2 nm, , , and l0 = 0.3 nm. The plots of interface pressure as a function of surface separation h were obtained using Equation 5, and they are shown in Figure 4. It can be observed that hydration repulsive pressure and EDL pressure have remarkable characteristics in the short and long ranges. Hydration repulsive pressure has a significant effect in the range of 0.5–1.5 nm, while EDL pressure may have a significant effect in the range of 2–5 nm in this case. Further, for the ultrathin gap, interface pressure increases rapidly and exceeds 1 GPa when the gap is < 0.3 nm. The sharp increase in repulsive interaction can be interpreted as a sign of the “direct contact” of the surfaces that are no longer separated by a lubricant layer. The pressure–distance curve shows that hydration pressure and EDL pressure could work synergistically to separate the contact surface, so the liquid film would be not squeezed out in contact region to produce beneficial results for TFL. These repulsive pressures could support external load so that contact surface would not contact directly.
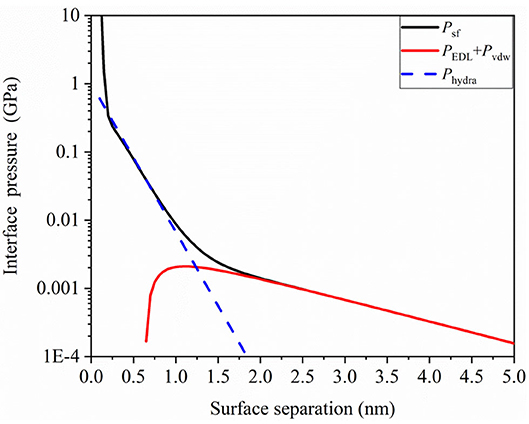
Figure 4. Interface pressure due to surface force as a function of surface separation in confined aqueous solution.
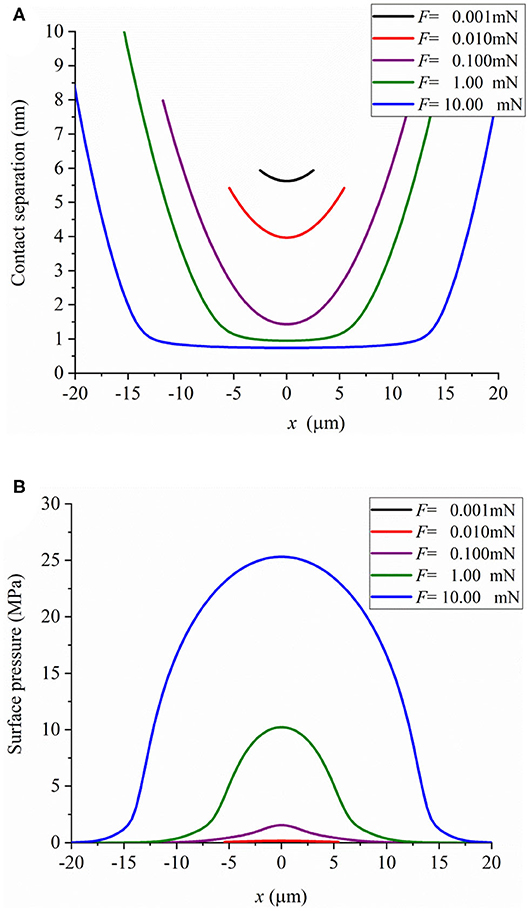
We simulated hydration-lubricated contact under the conditions of an experiment performed using the SFA. Atomically smooth mica surfaces were bent in the form of two crossed cylinders with a radius of curvature (R) of ~1 cm in salt solutions. The elastic modulus of mica is ~60 GPa (Israelachvili et al., 2004). The contact profile and surface pressure were obtained using the numerical model, and they are shown in Figure 5. The surface contact profile is negligibly affected by elastic deformation under low contact pressure mainly caused by the EDL effect. The values of pressure are < ~2.5 MPa. As contact load increases, contact separation decreases and becomes <1 nm when contact load is 10 mN. The maximum contact pressure is 25 MPa. It can be inferred that the hydration effect plays a dominant role in contact deformation. This implies that the hydration effect generates a force to support external load.
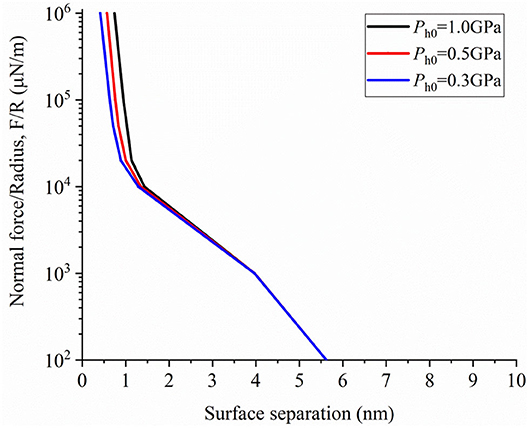
Figure 6 shows normal force as a function of surface separation under different initial constant hydration pressure changing from 1GP to 0.3GP. As surface separation decreases, normal force sharply increases at several molecular diameters. This implies that hydration load decreases exponentially when surface separation is < ~1 nm. In addition, the surface separations for the same normal force approach each other as the hydration effect decreases. The repulsive pressure generated from the interaction of solid atoms also supports a part of external load. When the separation distance of surfaces is > 2 nm, the surface force is mainly caused by EDL force and van der Waals attractive force to support the external force.
After the separation, h, between contact surfaces is calculated, the friction force due to the relative tangential motion of surfaces can be determined. In the following example, the friction behavior is shown for a load of 1 mN. The initial hydration pressure is 0.3 GPa. Other parameters remain unchanged. The minimum separation is 0.63 nm. Based on Figure 6, it can be inferred that there is hydration-lubricated contact. The effective stress-activated volume is V* = 2∗10−23 m3, and the Newtonian viscosity of the liquid is 1 mPa s−1. The constant of friction force is set to 6.5 μN in Equation 14. It should be noted that the parameters of the Eyring shear force can change in different contact stages. In this case study, we only applied the parameters given in Ma et al. (2015). Figure 7 shows the dependence of friction force on sliding velocity under hydration-lubricated contact. Friction force increases with the logarithm of sliding velocity. Energy dissipation predominantly occurs under hydration-lubricated contact. The maximum friction coefficient is ~0.003 at a sliding velocity of 3 μm/s. This reveals that, to achieve ultralow friction movement, it is extremely important to utilize surface forces such as hydration force and EDL force. Friction force mainly depends on the Eyring shear forces when rubbing surfaces are separated by a liquid hydrated structure. The hydration ions are not squeezed out and remain localized on charged surface, once the shear force applied on the hydration shells reduces the energy barrier, and thereby, promotes the thermally activated slip (Ma et al., 2015; Diao and Espinosa-Marzal, 2018). Conversely, AFM shows a new regime of ultralow friction in the transition from stick-slip to continuous sliding (Socoliuc et al., 2004). Based on this phenomenon, in future, we will consider the coupling of the proposed model with the Tomlinson model to investigate surface forces and their potential influence on friction behavior via AFM.
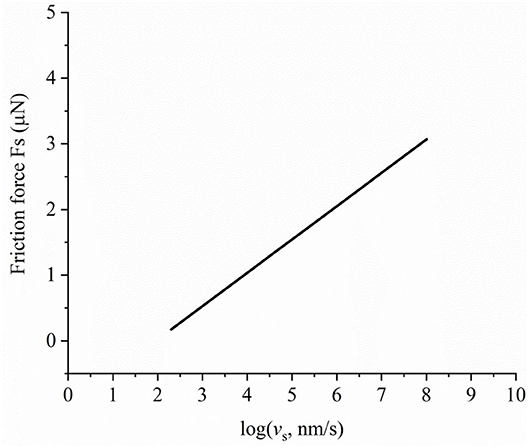
Figure 7. Dependence of friction force on sliding velocity in hydration-lubricated contact under a load of 1 mN.
Conclusions
A numerical model of hydration lubrication was proposed to evaluate contact and friction behavior at the nanoscale. The effects of hydration lubrication on contact pressure, surface profiles, and friction force were discussed. Preliminary numerical studies showed that surface forces significantly influenced boundary lubrication. Friction behavior was determined using the modified Eyring thermal activation model. It was observed that friction force increased with the logarithm of sliding velocity. This model is a preliminary investigation of the behavior of hydration-lubricated contact. The model may be further expanded to consider other factors that affect hydration lubrication, such as surface roughness, interface viscosity, and the hydrodynamic effect. The proposed numerical model may provide a new method of investigating hydration-lubricated contact at the nanoscale considering surface forces. This may be a key for understanding superlubricity in ultrathin film-lubricated contact at the nanoscale. One of the limitations of this study is that the influence of the atomic corrugation and the roughness of surfaces were not considered explicitly. In the future work, we plan to take these factors into account and expand the prediction of friction under different surface force effect.
Data Availability Statement
All datasets presented in this study are included in the article/supplementary material.
Author Contributions
YF formulated the numerical problem, carried out calculations, and drafted the manuscript. YF, LM, and XW discussed the calculation and revised the manuscript. LM and JL provided guidance on the structure and content of this paper. All authors contributed to the article and approved the submitted version.
Funding
This work was financially supported by the National Natural Science Foundation of China (51527901 and 51675297).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors would like to thank Prof. Valentin L. Popov for his constructive suggestions and the fruitful discussion for this study.
References
Chen, M., Briscoe, W. H., Armes, S. P., and Klein, J. (2009). Lubrication at physiological pressures by Polyzwitterionic brushes. Science 323, 1698–1701. doi: 10.1126/science.1169399
Derjaguin, B. V., and Landau, L. D. (1941). Theory of the stability of strongly charged lyophobic sols and of the adhesion of strongly charged particles in solutions of electrolytes. Prog. Surf. Sci. 43, 30–59. doi: 10.1016/0079-6816(93)90013-L
Diao, Y., and Espinosa-Marzal, R. M. (2018). The role of water in fault lubrication. Nat. Commun. 9:2309. doi: 10.1038/s41467-018-04782-9
Eyring, H. (1935). The activated complex in chemical reactions. J. Chem. Phys. 3, 107–115. doi: 10.1063/1.1749604
Eyring, H. (1936). Viscosity, plasticity, and diffusion as examples of absolute reaction rates. J. Chem. Phys. 4, 283–291. doi: 10.1063/1.1749836
Faraudo, J., and Bresme, F. (2005). Origin of the short-range, strong repulsive force between ionic surfactant layers. Phys. Rev. Lett. 94:077802. doi: 10.1103/PhysRevLett.94.077802
Hansen, Y. V., Gekle, S., and Netz, R. R. (2013). Anomalous anisotropic diffusion dynamics of hydration water at lipid membranes. Phys Rev Lett. 111:118103. doi: 10.1103/PhysRevLett.111.118103
Horn, R. G., Asadullah, M., and Connor, J. N. (2006). Thin film drainage: hydrodynamic and disjoining pressures determined from experimental measurements of the shape of a fluid drop approaching a solid wall. Langmuir 22, 2610–2619. doi: 10.1021/la052314b
Israelachvili, J., and Wennerström, H. (1996). Role of hydration and water structure in biological and colloidal interactions. Nature 379, 219–225. doi: 10.1038/379219a0
Israelachvili, J. N. (2011). Intermolecular and Surface Forces. 3rd Edn. Burlington, MA: Academic Press.
Israelachvili, J. N., Alcantar, N. A., Maeda, N., Mates, T. E., and Ruths, M. (2004). Preparing contamination-free mica substrates for surface characterization, force measurements, and imaging. Langmuir 20, 3616–3622. doi: 10.1021/la0352974
Israelachvili, J. N., and Pashley, R. M. (1983). Molecular layering of water at surfaces and origin of repulsive hydration forces. Nature 306, 249–250. doi: 10.1038/306249a0
Israelachvili, J. N., and Wennerstroem, H. (1990). Hydration or steric forces between amphiphilic surfaces. Langmuir 6, 873–876. doi: 10.1021/la00094a028
Jadhao, V., and Robbins, M. O. (2017). Probing large viscosities in glass-formers with nonequilibrium simulations. Proc. Natl. Acad. Sci. U.S.A. 114, 7952–7957. doi: 10.1073/pnas.1705978114
Jadhao, V., and Robbins, M. O. (2019). Rheological properties of liquids under conditions of elastohydrodynamic lubrication. Tribol. Lett. 67:66. doi: 10.1007/s11249-019-1178-3
Kim, B., Kim, Q., Kwon, S., An, S., Lee, K., Lee, M., et al. (2013). Unified stress tensor of the hydration water layer. Phys. Rev. Lett. 111:246102. doi: 10.1103/PhysRevLett.111.246102
Kim, B. H., Kwon, S., Lee, M., Kim, Q., An, S., and Jhe, W. (2015). Probing nonlinear rheology layer-by-layer in interfacial hydration water. Proc. Natl. Acad. Sci. U.S.A. 112, 15619–15623. doi: 10.1073/pnas.1515033112
Lifshitz, E. M. (1956). The theory of molecular attractive forces between solids. Sov. Phys. 2, 73–83
Liu, S., Wang, Q., and Liu, G. (2000). A versatile method of discrete convolution and FFT (DC-FFT) for contact analyses. Wear 243, 101–111. doi: 10.1016/S0043-1648(00)00427-0
Ma, L., Gaisinskaya-Kipnis, A., Kampf, N., and Klein, J. (2015). Origins of hydration lubrication. Nat. Commun. 6:6060. doi: 10.1038/ncomms7060
Manica, R., Connor, J. N., Dagastine, R. R., Carnie, S. L., Horn, R. G., and Chan, D. Y. (2008). Hydrodynamic forces involving deformable interfaces at nanometer separations. Phys. Fluids 20:32101. doi: 10.1063/1.2839577
Popov, V. L. (2020). Contacts with negative work of “adhesion” and superlubricity. Front. Mech. Eng. 5:73. doi: 10.3389/fmech.2019.00073
Raviv, U., Giasson, S., Kampf, N., Gohy, J., Jerome, R., and Klein, J. (2003). Lubrication by charged polymers. Nature 425, 163–165. doi: 10.1038/nature01970
Raviv, U., and Klein, J. (2002). Fluidity of bound hydration layers. Science 297, 1540–1543. doi: 10.1126/science.1074481
Socoliuc, A., Bennewitz, R., Gnecco, E., and Meyer, E. (2004). Transition from stick-slip to continuous sliding in atomic friction: entering a new regime of ultralow friction. Phys. Rev. Lett. 92:134301. doi: 10.1103/PhysRevLett.92.134301
Spikes, H. A. (2018). Stress-augmented thermal activation: Tribology feels the force. Friction 6, 1–31. doi: 10.1007/s40544-018-0201-2
Keywords: hydration lubricated contact, surface force, friction behaviors, Eyring model, liquid thin film, numerical model
Citation: Fang Y, Ma L, Wang X and Luo J (2020) Numerical Model for Hydration-Lubricated Contact and Its Friction Behavior at Nanoscale. Front. Mech. Eng. 6:564756. doi: 10.3389/fmech.2020.564756
Received: 22 May 2020; Accepted: 17 August 2020;
Published: 25 September 2020.
Edited by:
Alessandro Ruggiero, University of Salerno, ItalyReviewed by:
Valentin L. Popov, Technical University of Berlin, GermanyAlexander Filippov, Dnetsk Institute for Physics and Engineering, Ukraine
Copyright © 2020 Fang, Ma, Wang and Luo. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Liran Ma, bWFsaXJhbkB0c2luZ2h1YS5lZHUuY24=
 Yanfei Fang
Yanfei Fang Liran Ma
Liran Ma Xianzhang Wang
Xianzhang Wang Jianbin Luo
Jianbin Luo