- Laboratory of Computer-Aided Design of Materials, Institute of Strength Physics and Materials Science of Siberian Branch of Russian Academy of Sciences, Tomsk, Russia
We simulated wear in elastic tangential contact in partial-slip mode using the method of dimensionality reduction. The obtained numerical dependencies of wear rate on the number of loading cycles were approximated with existing analytical dependencies; at that, the estimated values of parameters of approximating equations are close to analytical estimates given before. The present results demonstrate the possibility of application of the method of dimensionality reduction to the theoretical study of fretting wear rate evolution.
Introduction
Fretting represents a specific kind of wear in contact zones appearing under multi-cycle tangential loading with relatively small amplitude providing no gross sliding to take place. The mentioned loading conditions are typical for a wide range of machine parts and joints subject to vibrations. Wear mode is determined by many parameters and conditions, including physical–mechanical properties of a material, sliding velocity, contact pressure, local, and ambient temperatures, etc. (Odfalk and Vingsbo, 1990; Goryacheva et al., 2001; Matikas and Nicolaou, 2009; Leonard et al., 2012). Variation of these parameters may lead to wear rate change by orders of magnitude (Lim and Ashby, 1987). This underlines the complexity of the problem as well as the actuality of the application of theoretical methods allowing its efficient parametric study that is difficult to carry out in full-scale experiments (Kasarekar et al., 2007).
The theoretical solution of a wear problem requires a calculation of normal and tangential stresses in contact area as well as the evolution of the shape of contacting bodies during the wear process (Dimaki et al., 2014). An equation, describing the local rate of irreversible contact shape change., represents a local wear law. This equation postulates a dependence of local wear rate on material parameters, stress–strain state, and loading conditions in a local area of contact (Popov, 2017).
The well-known assumption of wear rate proportionality to the ratio of dissipated energy to material hardness σ0 was first proposed by Reye (1860). In the present paper, we use the wear law, given in Archard and Hirst (1956) and Rabinowicz (1995) and based on the hypothesis of direct proportionality between the wear rate and work of frictional forces. The local form of this wear law for an axially symmetrical contact area reads
where Δf (r)—local change of the contact profile f (r); r—polar radius in the contact plane; —relative tangential displacement of the contacting bodies; σ0—hardness of a material; —a portion of relative displacement due to elastic deformation of the medium; τ (r)—shear stress in the contact plane; and Δ–indicates an increment of a corresponding value during a time step. Note that Equation (1) contains a non-dimensional wear coefficient kwear that includes a combination of material parameters determining the local wear rate.
As a rule, the wear process described by Equation (1) is steady because contact pressure distribution tends to uniform in the course of wearing. This is because the wear rate is higher in contact patches subject to higher normal pressure. At that, it is necessary to explicitly take into account the evolution of contact area and size (Dimaki et al., 2016).
In the paper, we use a theoretical model of wear based on the method of dimensionality reduction (Popov and Hess, 2015) and wear law (1). The model allows obtaining an exact solution to the wear problem that agrees with the analytical solutions of Galin (1961) and (Sneddon, 1965).
As it is seen from Equation (1), wear intensity varies over contact radius and time. The latter is due to time variation (as the number of cycles increases) of distributions of shear stress and strain in the contact area. Theoretical and experimental studies show that wear rate changes non-monotonically—in the beginning of the wear process, the wear rate increases, then reaches a maximum and gradually decreases to zero (as a contact profile approaches so-called “limiting” profile (Popov, 2014). In the present paper, we obtained theoretical dependencies of wear rate on the loading cycle number for different profiles of contacting bodies of revolution. The results of the theoretical study are compared with known analytical estimations.
Model and Setup
Let us briefly describe the keystones of the method of dimensionality reduction (Popov and Hess, 2014, 2015). Consider the contact of a three-dimensional body of revolution having the profile z = f (r) and an infinite elastic foundation. The given three-dimensional profile is transformed into a one-dimensional profile g (x) based on the multifactor dimensionality reduction (MDR) rules (Popov and Hess, 2014, 2015):
A transformation of the one-dimensional profile back into a three-dimensional one reads
The one-dimensional profile (2) is pressed to a certain depth d into an elastic foundation that represents a set of non-interacting springs having a spatial size Δx. The normal and tangential stiffness of the springs are given by Popov and Hess (2014):
where E* is the effective elastic modulus
and G* is the effective shear modulus
To satisfy the rules of MDR, we assume the contacting materials satisfy the “elastic similarity” condition:
that provides an ability to solve the normal and tangential contact problems independently (Johnson, 1987). The vertical displacement of an individual spring in the contact area reads
and the resulting normal force in a spring is given by
The linear force density is therefore
The contact radius a can be estimated from the following equation:
Having the value of a, it is possible to calculate the total normal force over the contact area:
According to the MDR rules, the distribution of normal pressure p in the initial three-dimensional problem can be calculated using the following integral transformation (Popov and Hess, 2014):
Assume the indenter moves to displacement in a tangential direction. A one-dimensional spring of the half-space remains in a contact state with the indenter until a tangential force in the spring reaches a critical value μfz where μ denotes the friction coefficient. After that, the spring becomes in sliding state, and the tangential force equals to μfz. This behavior is independent of an initial stress state of a spring and results in the following equations describing the relation between tangential deformation and reaction force of a spring:
The sign in Equation (14) depends on the direction of the motion of the indenter. The sign “minus” corresponds to motion along the contact plane in a positive direction of axis oX; the sign “plus” corresponds to motion in the opposite direction. Having a given time dependence of the indenter position, it is possible to calculate its increment and thus to determine a tangential deformation of a one-dimensional spring in each point of a contact area. Obviously, the tangential reaction force can also be determined as follows:
Three-dimensional radial distributions of tangential stresses τ (r) and displacements can be calculated by means of the integral transformations similar to (3):
where qx (x) is a tangential force density:
The distributions of stresses and displacements obtained above represent exact solutions of the corresponding three-dimensional problem, which is one of the main advantages of the MDR (Dimaki et al., 2014; Li et al., 2014). The transformation (2) represents a relationship between the full three-dimensional contact problem and a one-dimensional contact with an elastic foundation (Galin, 1961). Stresses and displacements in the three-dimensional contact problem with a linearly elastic foundation can be obtained using the corresponding integral transformations given earlier. The obtained solution is “exact” and can be applied to contact problems that reduce to a normal contact problem.
In this paper, we consider a contact of parabolic and comical rigid indenter with a flat elastic foundation (see Figure 1). The choice of these two shapes is conditioned by the fact that many theoretical approaches use these shapes for describing an asperity shape in single-asperity and multi-asperity models of rough surfaces [see, e.g., Popov (2017)]. For a parabolic indenter with f (r) = r2/2R, the corresponding one-dimensional profile is g (x) = x2/R. For a three-dimensional conical indenter with an initial profile given by f (r) = r tan θ, the corresponding MDR-image is .
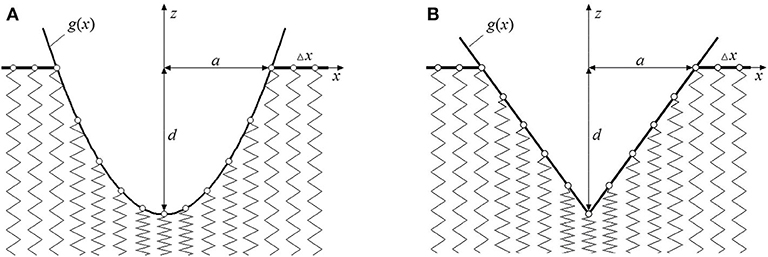
Figure 1. Profiles of contacting rigid bodies and a flat elastic foundation: (A) parabolic indenter; (B) conical indenter.
If the indenter is subject to tangential oscillations with an amplitude U(0), the characteristic wear volume per one cycle of oscillation can be roughly estimated as follows: , where a0 is the initial contact radius. At that, an estimation of several cycles needed to reach the wear depth of the indenter of an order of magnitude of d0, which reads:
In the results presented later, an actual number of cycles will be normalized to the characteristic value (19) as follows:
Further, we operate with the normalized number of cycles (20) to provide universality of the obtained results.
Simulation Results and Discussion
We carried out a theoretical study of the dependence of normalized volume wear rate on normalized cycle number Ñ for parabolic and conical indenters in partial slip mode. We assume that both bodies in contact are elastic, but only the indenter is subject to wear. It is known that for oscillations with a magnitude < μd0, the contact area separates into “stick” and “slip” regions (Jäger, 1995; Hills et al., 2009; Lengiewicz and Stupkiewicz, 2013). Wear takes place only outside the “stick” area. At that, in the absence of “gross slip” motion, the wear process finishes at the so-called “shakedown” state. After achieving the “shakedown” state (in other words, after achieving some “final” contact profile), the wear rate becomes equal to zero (Ciavarella and Hills, 1999) and after oscillations proceed in the “absence” of wear. This allows, in particular, to estimate a total wear volume for a given initial contact shape, material parameters, and loading conditions. It is necessary to note that in the mentioned conditions, wear occurs at lower spatial scales (Gnecco and Meyer, 2015).
The results of the performed numerical simulations (see Figures 2, 3) show that the wear rate initially grows, approaches a maximum value at a certain value of , and then decreases to zero that corresponds to the “shakedown.” The similar character of the dependence of wear rate on cycle number is obtained in experimental and theoretical studies (Kasarekar et al., 2007). In this connection, it is interesting to compare the quantitative estimations of parameters of the dependence w (N), obtained in the developed MDR-based model, with analytic estimations.
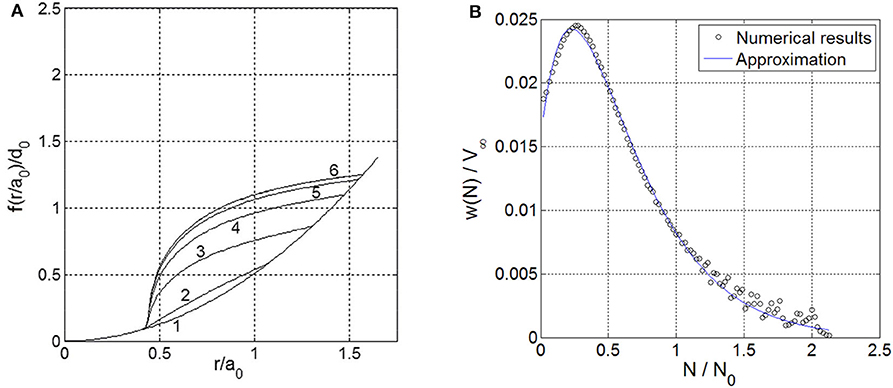
Figure 2. (A) Development of the shape of an initially parabolic profile due to fretting wear. Curve “1” shows the initial profile; further curves correspond to the following normalized number of oscillation cycles: (2) = 0.04; (3) = 0.16; (4) = 0.36; (5) = 0.64; (6) = 1. (B) Dependency of normalized wear rate on a dimensionless number of cycles for a parabolic indenter under constant normal load. Points indicate the results of numerical simulation, and solid line indicates the approximation with Equation (21).
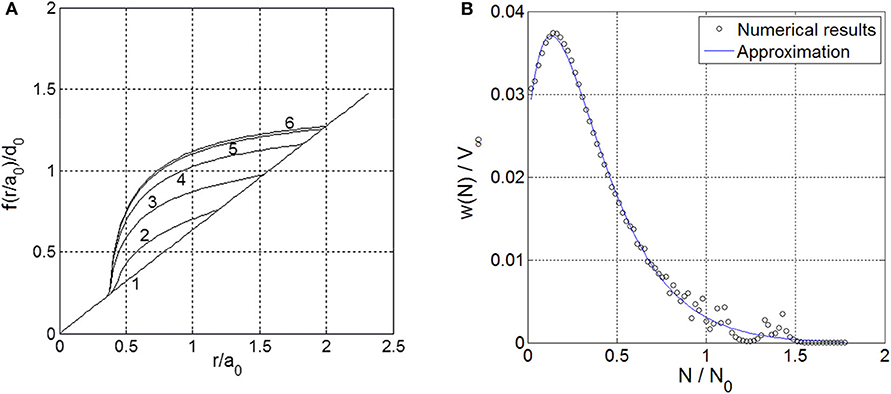
Figure 3. (A) Development of the shape of an initially conical profile due to fretting wear. Curve “1” shows the initial profile; further curves correspond to the following normalized number of oscillation cycles: (2) = 0.1; (3) = 0.4; (4) = 0.9; (5) = 1.6; (6) = 2.5. (B) Dependency of normalized wear rate on a dimensionless number of cycles for a conical indenter under a constant normal load. Points indicate the results of numerical simulation, and solid line indicates the approximation with Equation (21).
Chai and Argatov (2019) give an analytic equation for wear rate against cycle number based on the results of numerical simulation by Kasarekar et al. (2007), which reads:
where the initial wear rate w0 is defined as follows (Chai and Argatov, 2019):
where αV = kwear/μ and Δξ0—energy dissipation per first wear cycle. The parameter N1 can be estimated as follows (Chai and Argatov, 2019):
where V∞ is a total worn volume (assuming that wear rate tends to zero with an increasing number of cycles).
Simulation results for a parabolic indenter are shown in Figure 2. The obtained numerical dependence of wear rate on the number of cycles was approximated with Equation (21). The values of parameters w0 β1, and N1 were estimated by means of the non-linear least-squares method (Marquardt, 1963). It is seen that Equation (21) represents a good approximation of the numerically obtained results. The estimated values of the parameters β1 and N1 are given in Table 1. In the paper by Chai and Argatov (2019), estimation of the parameter β1 is given: β1 = 3.11. In the present study, estimation of β1 is about β1 ≈ 3 for a parabolic indenter, which is in good agreement with the given analytically obtained quantity earlier.
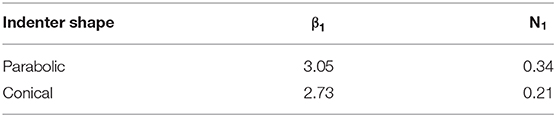
Table 1. Estimated values of the parameters of Equation (21), obtained based on the approximation of the numerical simulation results.
Simulation results for a conical indenter are presented in Figure 2. In this case, Equation (21) also allows performing a good approximation of the numerically obtained dependence of wear rate on cycle number. However, for a conical indenter, the estimated value of β1 is β1 = 2.73.
The shape and estimated values of the parameters of the dependence of wear rate on cycle numbers are in agreement with previously obtained analytic estimations (Chai and Argatov, 2019). In general, the results of performed simulations show that the method of dimensionality reduction allows us to adequately describe the dynamics of wear of arbitrary bodies of revolution.
Conclusions
We have performed numerical simulations of the evolution of wear rate of elastic bodies of revolution within a theoretical model based on the method of dimensionality reduction. It was shown that numerical dependencies of wear rate on a normalized number of cycles coincide with analytical equations for such dependencies. For a parabolic indenter, estimations of the parameter β1 ≈ 3.05 obtained in the present study and the paper (Chai and Argatov, 2019) agree. For a conical indenter, the estimation of β1 is β1 ≈ 2.73. A detailed description of the indenter shape that influences on wear rate evolution requires further studies. Summarizing, we can confirm that the present results demonstrate the applicability of the method of dimensionality reduction for analysis of wear dynamics, including quantitative prediction of wear rate and a total volume of worn material.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
AD developed the model, conducted the simulations, and wrote the manuscript.
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The author cordially acknowledges Profs. Valentin Popov and Ivan Argatov for fruitful discussions. The work was performed according to the Government research assignments for ISPMS SB RAS, Project No. III.23.1.4.
References
Archard, J. F., and Hirst, W. (1956). The wear of metals under unlubricated conditions. Proc. R. Soc. London A 236, 397–410. doi: 10.1098/rspa.1956.0144
Chai, Y. S., and Argatov, I. I. (2019). Fretting wear accumulation in partial-slip circular Hertzian contact. Mech. Res. Comm. 96, 45–48. doi: 10.1016/j.mechrescom.2019.02.005
Ciavarella, M., and Hills, A. (1999). Brief Note: some observations on the oscillating tangential forces and wear in general plane contacts. Eur. J. Mech. 18, 491–497. doi: 10.1016/S0997-7538(99)00117-5
Dimaki, A. V., Dmitriev, A. I., Chai, Y. S., and Popov, V. L. (2014). Rapid simulation procedure for fretting wear on the basis of the method of dimensionality reduction. Int. J. Solids Struct. 51, 4215–4220. doi: 10.1016/j.ijsolstr.2014.08.003
Dimaki, A. V., Dmitriev, A. I., Menga, N., Papangelo, A., Ciavarella, M., and Popov, V. L. (2016). Fast high-resolution simulation of the gross slip wear of axially symmetric contacts. Tribol. Trans. 59, 189–194. doi: 10.1080/10402004.2015.1065529
Galin, L. A. (1961). Contact Problems in the Theory of Elasticity. Raleigh, NC: North Carolina State College.
Gnecco, E., and Meyer, E. (2015). Fundamentals of Friction and Wear on Nanoscale. Cham: Springer. doi: 10.1007/978-3-319-10560-4
Goryacheva, I., Rajeev, R., and Farris, T. (2001). Wear in partial slip contact. Int. J. Precis. Engng. Manuf. 123, 848–856. doi: 10.1115/1.1338476
Hills, D. A., Sackfield, A., and Paynter, R. J. H. (2009). Simulation of fretting wear in half-plane geometries: part I – the solution for long term wear. J. Tribol. 131:031401. doi: 10.1115/1.3118785
Jäger, J. (1995). Axi-symmetric bodies of equal material in contact under torsion or shift. Arch. Appl. Mech. 65, 478–487. doi: 10.1007/BF00835661
Kasarekar, A., Bolander, N., Sadeghi, F., and Tseregounis, S. (2007). Modeling of fretting wear evolution in rough circular contacts in partial slip. Int. J. Mech. Sci. 49, 690–703. doi: 10.1016/j.ijmecsci.2006.08.021
Lengiewicz, J., and Stupkiewicz, S. (2013). Efficient model of evolution of wear in quasi-steady-state sliding contacts. Wear 303, 611–621. doi: 10.1016/j.wear.2013.03.051
Leonard, B. D., Sadeghi, F., Shinde, S., and Mittelbach, M. (2012). A numerical and experimental investigation of fretting wear and a new procedure for fretting wear maps. Tribol. Trans. 55, 313–324. doi: 10.1080/10402004.2012.654598
Li, Q., Filippov, A. E., Dimaki, A. V., Chai, Y. S., and Popov, V. L. (2014). Simplified simulation of fretting wear using the method of dimensionality reduction. Phys. Mesomech. 17, 236–241. doi: 10.1134/S1029959914030102
Lim, S. C., and Ashby, M. F. (1987). Overview no. 55. Wear-Mechanism maps. Acta Metallurg. 35, 1–24. doi: 10.1016/0001-6160(87)90209-4
Marquardt, D. (1963). An algorithm for least-squares estimation of nonlinear parameters. SIAM J. Appl. Math. 11, 431–441. doi: 10.1137/0111030
Matikas, T. E., and Nicolaou, P. D. (2009). Prediction of contact temperature distribution during fretting fatigue in titanium alloys. Tribol. Trans. 52, 346–353. doi: 10.1080/10402000802563117
Odfalk, M., and Vingsbo, O. (1990). Influence of normal force and frequency in fretting. Tribol. Trans. 33, 604–610. doi: 10.1080/10402009008981995
Popov, V. L. (2014). Analytic solution for the limiting shape of profiles due to fretting wear. Sci. Rep. 4:3749. doi: 10.1038/srep03749
Popov, V. L. (2017). Contact Mechanics and Friction. Physical principles and applications: 2nd Edn. Berlin: Springer. doi: 10.1007/978-3-662-53081-8
Popov, V. L., and Hess, M. (2014). Method of dimensionality reduction in contact mechanics and friction: a user's handbook. I. Axially-symmetric contacts. Facta Univ. Mech. Engng. 12, 1–14. Available online at: http://casopisi.junis.ni.ac.rs/index.php/FUMechEng/article/view/155
Popov, V. L., and Hess, M. (2015). Method of Dimensionality Reduction in Contact Mechanics and Friction. Berlin; Heidelberg: Springer. doi: 10.1007/978-3-642-53876-6
Keywords: fretting, wear rate, elastic contact, method of dimensionality reduction, numerical simulation
Citation: Dimaki AV (2020) Theoretical Study of Fretting Wear Rate Evolution in Axi-Symmetrical Elastic Contact Using the Method of Dimensionality Reduction. Front. Mech. Eng. 6:566703. doi: 10.3389/fmech.2020.566703
Received: 28 May 2020; Accepted: 26 August 2020;
Published: 09 October 2020.
Edited by:
Alessandro Ruggiero, University of Salerno, ItalyReviewed by:
Jiliang Mo, Southwest Jiaotong University, ChinaAlexander Filippov, Donetsk Institute for Physics and Engineering, Ukraine
Copyright © 2020 Dimaki. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Andrey V. Dimaki, ZGF2QGlzcG1zLnRzYy5ydQ==
 Andrey V. Dimaki
Andrey V. Dimaki