- Key Laboratory of Green Design and Manufacturing of Mechanical Industry, School of Mechanical Engineering, Hefei University of Technology, Hefei, China
Since the electric vehicle battery (EVB) is wildly recycled in industry, the disassembly procedures of variable EVBs is so important that can influence the efficiency and environmental impacts in remanufacturing. To improve disassembly efficiency in EVB remanufacturing, a disassembly sequence planning method based on frame-subgroup structure is proposed in this paper. Firstly, the improved disassembly relation hybrid graph and disassembly relation matrix are proposed to identify the disassembly precedence relationship and connection relationship between the components in EVB. Secondly, the frame - subgroup structure is given, and the method for solving disassembly sequence planning with frame-subgroup structure and genetic algorithm is introduced. In this method, to simplify the series of processes such as encoding, decoding, crossover and mutation, the solution space composed of all disassembly sequences is transformed into the positive integer sequence for the disassembly efficiency in battery remanufacturing. Finally, the case study of EVB disassembly sequence planning is presented to validate the feasibility of this proposed method. Comparing with other traditional methods, the advantage and application of this proposed method are introduced.
Introduction
In the past few years, governments have paid more and more attention to energy crisis, environmental protection and other related issues. At the same time, many countries attach great importance to the investment and research of electric vehicles, due to their attention to the future automotive market. Major enterprises have also produced a large number of new energy vehicles powered by batteries. The worldwide sales of electric vehicles are expected to increase from the current 1.1 million to 11 million in 2025, and 30 million in 2030 (Alfaroalgaba and Ramirez, 2020). Considering that the life cycle of EVB is between 5 and 20 years, consequently, a huge number of EVBs are expected to reach the end-of-life stage and will need to be disposed of or recycled in the coming decades (Alfaroalgaba and Ramirez, 2020). Compared with traditional engines, EVBs contain many toxic and harmful chemicals. If they cannot be disposed of properly, even if they are discarded, will cause irreversible damage to the environment. Thus in many countries, similar to normal batteries, landfilling or incineration of used EVB is prohibited (Gu et al., 2018).
The EVB is a relatively independent working system inside the electric vehicle, whose main function is to output stable and reliable power to the vehicle. Since some components inside the scrapped EVBs still have high recycling and remanufacturing value, therefore, disassembling the EVBs into components is an inevitable part to disposal of scrapped EVBs. The proper approach is to recycle its valuable components, and for the components that cannot be recycled, reused and remanufactured should be properly handled to avoid or reduce their impact on the environment (Shao et al., 2018).
The quality of scrapped EVBs is various, which is related to its life cycle and daily usage. However, the disassembly process can be controlled by human. Disassembly is a process in which the operator removes components from the assembly by a certain sequence (Kim et al., 2018). Even if the same assembly is disassembled and the same components are obtained, different disassembly sequences will lead to different results in disassembly benefit, disassembly time and so on. Therefore, how to quickly find the optimal disassembly sequence to obtain the highest recycling value or disassembly efficiency of end-of-life products is one of the most concerned issues for enterprises. This problem is also known as disassembly sequence planning (DSP) (Chang et al., 2020).
In order to optimize disassembly sequence to improve disassembly benefits, in this study, the hybrid disassembly matrix and the frame-subgroup structure is presented. And the hybrid disassembly matrix is set to identify disassembly priority and connection relationship of disassembling components, as well as the frame-subgroup structure is established to divide the solution space, and promotes computational efficiency. In the end, the disassembly experiments of the EVB is presented and discussed as the instance to validated this proposed method, and the disassembly efficiency and benefits are increased by applying the frame-subgroup structure and hybrid disassembly matrix with improved genetic algorithm.
Literature Review
Since DSP is a NP-hard combinatorial optimization problem (Lambert, 2003), when the scale or the complexity of the problem increased, the time to solve the problem will increase exponentially. The solution of the DSP problem is generally divided into two parts. The first part is to model the DSP problem, that is, to describe various relationship among components of the assembly by establishing a proper mathematical model. At present, the common modeling methods include constraints relation graph (Hu et al., 2018), disassembly tree (Liu et al., 2016), and-or graph (Tian et al., 2019), Petri net (Guo et al., 2016) and so on. Then use the constructed mathematical model to find all disassembly sequences that meet the disassembly precedence relationship. The set of all disassembly sequences is called the solution space in this paper. And the second part is to use various algorithms to try to find the optimal disassembly sequence that meets the established optimization goals in the solution space.
Different from the earlier research, which is to build mathematical model to solve the precise solution of DSP problem, a large number of DSP research currently tend to solve the problem by heuristic/meta-heuristic algorithm. Heuristic/meta-heuristic algorithms no longer blindly pursue the optimal solution of the DSP problem, and sub-optimal solutions which close to the optimal solution can also be accepted. Such algorithms sacrifice the quality of solutions, but save a lot of computing time.
Human-robot collaboration for disassembly is proposed by Xu et al. (2020) to flexibly and efficiently finish the disassembly process in remanufacturing. In this work DSP for human-robot collaboration is solved by the modified discrete Bees algorithm based on Pareto. And the proposed method is verified based on a simplified computer case. Feng et al. (2019) proposed an improved multi-objective ant colony algorithm to derive optimal target disassembly sequences. The work establishes some indices on disassembly scheme evaluation and a fuzzy integral method to evaluate the obtained disassembly scheme. And a CNC machine tool example is given to illustrate the proposed models and the effectiveness of the proposed algorithm. Laili et al. (2019) proposed a ternary bees algorithm to identify new disassembly sequences and directions. The algorithm combines the merits of a greedy search and meta-heuristic techniques. Experimental results show that the proposed approach is able to perform a rapid subassembly detection and sequence optimization for a robotic disassembly task. Due to the unorganized disassembly of electronic waste demands huge disassembly time and efforts with necessary tooling, Bahubalendruni and Varupala, (2020) developed an automated optimal disassembly sequence planning methodology to solve any product configuration. Chang et al. (2020) presents a proof-of-concept novel near real-time interactive AR-assisted product disassembly sequence planning system (ARDIS) based on product information, such as interference matrix and 3D models, and several case studies have been carried out to demonstrate and evaluate the performance of the system within the laboratory environment.
Compared with other meta heuristics algorithm, genetic algorithm has the advantages of wide application range, strong expansibility, and not easy to fall into local optimal solution, etc. it is also widely used in DSP problem solving. Lee et al. (2019) proposed interactive genetic algorithms to solve the problem of disassembly sequence planning. In their research the disassembly factor is measured by the fuzzy scoring procedure method, and then the genetic algorithm is used to select the optimal sequence. With the penalty value provided from the process, a reference is provided for the revised design. Finally, the feasibility of the proposed method is verified by examples. Tian et al. (2019) proposed a novel cooperative disassembly sequence and task planning method was proposed based on the genetic algorithm. In their work the chromosome evolution rules, such as the selection, crossover, and mutation operators, have been redesigned to obtain the (approximate) optimal multiplayer cooperative disassembly sequences and task planning. Parsa and Saadat (2019) define new optimization parameters based on the disassembly-ability and components demand. Genetic algorithm optimization method was employed to optimize the process sequence. The most demanded components with the easiest disassembly operations are disassembled first without requiring to disassemble the unwanted components and avoid complicated operations. Two case studies were analyzed to determine the effectiveness and compatibility of the method.
The above methods show that the genetic algorithm has a strong applicability in solving DSP problems. Genetic algorithm to solve DSP problem is usually divided into two steps. Firstly, formulate a set of coding and decoding methods to map the disassembly sequence to chromosome one by one. Secondly according to the relationship between the disassembly sequences, define a method for chromosome crossover and mutation to realize the iteration of the population to achieve the goal of optimization.
However, the disassembly sequences may not be continuous in the solution space. Traditional methods usually elaborate some complex coding, decoding, crossover, and mutation strategies to ensure that the child chromosome still belongs to the solution space that composed of all disassembly sequences. In this paper frame-subgroup structure combined with genetic algorithm is introduced to solve the DSP problem. In this method, the optimization problem in the solution space composed of all disassembly sequences is transformed into the optimization problem in the positive integer sequence, at the same time, a series of processes such as encoding, decoding, crossover and mutation are simplified, which improves the efficiency of solving the problem.
Methodology
Before the disassembly operation, it is necessary to have a clear understanding of the specific structure of the assembly and the interrelationship between the internal components, including the number of components to be disassembled, the connection relationship between components, and the space constraint relationship between components. In general, this information can be easily and quickly obtained by the CAD model of the assembly. Therefore, the methods and theories mentioned in this paper are based on the CAD model of the assembly.
Disassembly Relationship Hybrid Graph
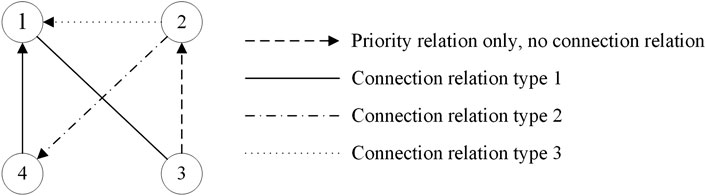
In order to clearly express the relationship between the components, in this paper, based on the constraints relation graph (Lee et al., 2019), an improved disassembly relationship hybrid graph is proposed, which can express the connection relationship and the disassembly precedence relationship between components at the same time. The disassembly precedence relationship means that there are constraints on the order of disassembly of the two parts, that is, one must be disassembled before the other, and the connection relationship refers to the mechanical connection between two parts. In the practice of disassembly, different connection relationships mean that the difficulty of disconnecting is different. For example, a DSP problem with the goal of maximizing the revenue means that the cost of disconnecting different connections is different. Therefore, the connection relationship between various components is a parameter that cannot be ignored in this type of optimization process.
The proposed disassembly relationship hybrid graph in this paper is composed of nodes and edges, for an assembly with n components, the nodes represent the n components, and the edges between nodes represent the disassembly precedence relationships and connection relationships between the components. As shown in Figure 1, The disassembly relationship hybrid graph is defined as follows:
(1) Use n nodes (circles in Figure 1) to represent the n components of the assembly, and number them with 1, 2, … , n respectively;
(2) The edges of different line types are used to represent the types of all connection relationships between components;
(3) The arrows on the edges indicate that there is a disassembly precedence relationship between the two nodes connected by the edge, and stipulate that the one pointed by the arrow needs to be disassembled before the other.
Disassembly Relationship Matrix
In order to solve the DSP problem on computer, based on adjacency matrix (Tian et al., 2018), this paper proposes a method to transform the above disassembly relation hybrid graph into disassembly relation matrix. Both of them can equally describe the relationship between the components. The disassembly relationship matrix is defined as follows:
For an assembly with n components, the matrix P of n × n is constructed in formula 1:
where the elements in matrix P are defined as follows:
In the disassembly relationship matrix P, if all elements in column j are zero, according to the definition, it means that no component can be disassembled before component j (At this time, the elements in line j should not be all zero, because if the elements in row j and column j are all zero, it indicates that there is no connection and precedence relationship between the component j and the assembly, or the component has been disassembled from the assembly). Then component j is currently in the first precedence of disassembly sequence. The disassembly operation is to release all the connection with the component j, and the all of the connection relationships of the component j is contained in the row j of the precedence relationship matrix. Thus, we only need to replace all the elements in the line j with 0, and record all the changed numbers, from which we can know which component is disconnected with component j and which kind of connection is.
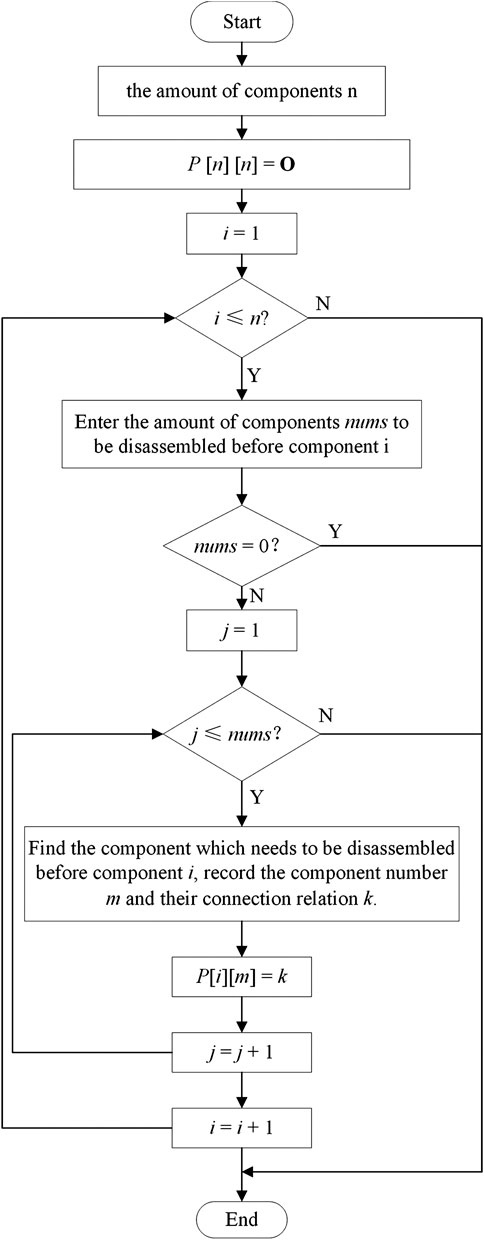
According to the definition of the disassembly relationship matrix, this paper gives a approach to generate the disassembly relationship matrix on the computer. The procedure is shown in Figure 2.
Step 1. Determine the number of components n and number these component with 1, 2, … , n.
Step 2. Create a zero matrix of size n × n.
Step 3. For each component i, find all the components that need to be disassembled before the component i, record the number m of these components and the connection relationship k between them, and assign k to the line i and column m of the matrix.
Solution Space
The disassembly precedence relationship between the components limits their order to be disassembled. The set of all disassembly sequences that meet the disassembly precedence relationship is called the solution space. In order to ensure the reliability of optimization results of the DSP problem, any proposed method of describing the relationship between components should have the feasibility of generating all disassembly sequences (solution spaces) (Ji-Bin, 2016).
Here we give a method to generate a disassembly sequence by using disassembly relationship matrix.
Step 1. For an initial disassembly relation matrix P, denoted as P0, find all its zero columns, select one of the columns (let’s assume its column i), replace all elements in row i to zero, and record all the changed numbers (the number corresponding to a certain connection relation), it means that component i is the first to be disassembled, and at the same time we get a new matrix P2.
Step 2. Find all zero columns of matrix P1, select one of the columns (let’s assume its column j) and replace the element in row j with zero, record all the changed numbers. Then component j is the second to be disassembled and we get a new matrix P2.
Step 3. Repeat the above operation until all the elements of matrix P become 0, then a disassemble path is generated.
Optimization Process
Frame-Subgroup Structure
First, we define a component relationship.
Independent: there is no disassembly precedence relationship and connection relationship between the two components. This relationship is shown on the disassembly relationship hybrid graph as: there is no edge between node i and node j, and this relationship is shown on the disassembly relationship matrix as aij = aji = 0.
Then define a set of components.
The frame-subgroup structure: the structure is a group components in the assembly, which meets the following conditions:
(1) In this group, there is one and only one component has connection relationships and precedence relationships with all other components, and the component is called the frame.
(2) All components except the frame are independent of each other, these components are called subgroups.
In engineering practice, in order to ensure that the assembly is compact, various independent components are usually constrained to a frame structure with qualified strength. Thus, the frame-subgroup structure is very common. A typical example is the printed circuit board, various electronic components on the board are subgroups, and the board carrying the electronic components is the frame.
Application of Frame-Subgroup Structure in Disassembly Sequence Planning Problem
The frame-subgroup structure has some excellent properties in the practice of DSP. The frame-subgroup structure can be simply described by Figure 3. Obviously, the components 1, 2, 3, ... , n in the figure are subgroups, and the component n+1 is frame. When disassembling the structure shown in Figure 3, the component n+1 is the last one to be disassembled, and the disassembly sequence of the previous n components is not limited. Then the feasible disassembly sequence is the full permutation of these n components, that is
After frame-subgroup structure is introduced, the structure is regarded as a whole, which will bring a lot of convenience for solving the DSP problems. Suppose the components numbered x1, x2, … , xn+1 in an assembly form a frame-subgroup structure. We can introduce notation (x1, x2, … , xn+1) to represent n! disassembly sequences of the structure, for example, put this notation in disassembly sequence like this: b1, b2, … bm (x1, x2, … , xn+1), c1, c2, … , ck, it not only can be used to replace n! disassembly sequences, but also represents a subset of the solution space, which can be called a sub-solution space. Thus this work not only realizes the division of the disassembly space, but also simplifies the expression of disassembly sequence.
The Continuity of Disassembly Sequence of Frame-Subgroup Structure
For the n! disassembly sequences indicated by the notation (x1, x2, … , xn+1), we can sort these n! sequences from small to large according to the number of components. For a simple example, when n = 3, there are six disassembly paths, the order of all disassembly paths is: 1) x1, x2, x3, x4; 2) x1, x3, x2, x4; 3) x2, x1, x3, x4; 4) x2, x3, x1, x4; 5) x3, x1, x2, x4, 6) x3, x2, x1, x4.
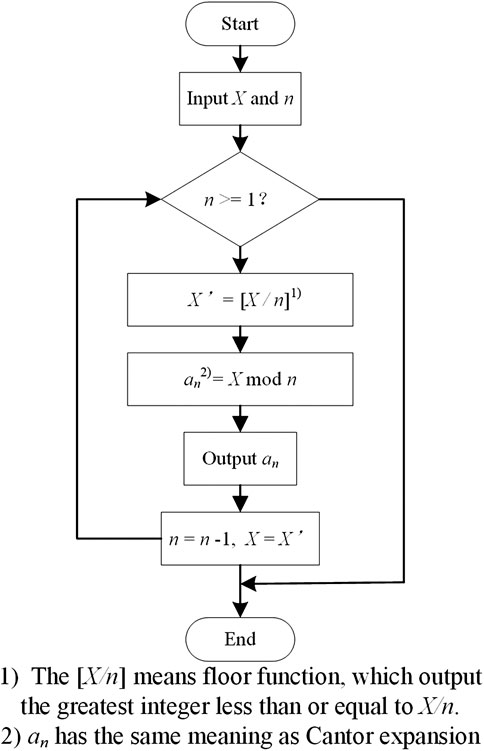
As a matter of fact, the one-to-one correspondence between these n! sequences and positive integers sequence 1, 2, …, n! can be constructed by Cantor expansion and its inverse operation.
According to Cantor expansion, the order X of a disassembly sequence xu1, xu2, …, xui, …, xun (ui ∈ {1, 2, …, n}) is calculate by formula 2.
where, an+1−i means among the components that do not currently appear, the amount of components whose subscript ui is smaller than the subscript of the component i of the disassembly sequence.
Since the Cantor expansion is a one-to-one mapping, its inverse operation can be obtained, that is, we can find the sequence ranked X in the permutations. Inverse Cantor expansion is shown in Figure 4.
By using Cantor expansion, the one-to-one correspondence between these n! sequences and positive integers 1, 2, …, n! have been constructed. It means that the disassembly sequences on the sub-solution space b1, b2, … , bm (x1, x2, … , xn+1), c1, c2, …, ck is continuous, and the optimization problem on this sub-solution space can be transformed into the optimization problem on continuous positive integer 1, 2, …, n!.
Frame-Subgroup Structure Combined With Genetic Algorithm to Solve Disassembly Sequence Planning Problem
Using the frame-subgroup structure and the genetic algorithm, this paper gives a new idea to solve DSP problem. First we find the frame-subgroup structure inside the assembly, and treat them as a whole, and obtain several disassembly sequences like this b1, b2, … , bm (x1, x2, … , xn+1), c1, c2, … , ck. This is equivalent to dividing the solution space into several unrelated sub-solution spaces. In each sub-solution space, the DSP problem can be transformed into optimization problem on continuous positive integer sequence 1, 2, … , n!. By doing so, the genetic algorithm can be easily introduced to solve the problem. Finally, by comparing the optimal solutions in each sub-solution space, the final optimal solution can be obtained.
Since it is already a mature theory to use genetic algorithm to find the optimal solution for a problem on a positive integer sequence, this paper only introduces the encoding and decoding methods of DSP problems in view of the particularity of DSP problems.
The Encoding and Decoding Strategy
First expand the positive integers, 1, 2, … , n!, to the real number interval [0, n!]. Then take a positive integer m such that 2 ^ m < n!. Use m-bit binary code as chromosome, it is equivalent to divide the real interval [0, n!] into 2 ^ m equal parts. Any m-bit binary code also can refer to a real number in interval [0, n!] by using the following approach.
For each m-bit binary chromosome substring, it refers to a real number x is calculated by formula 3.
In the formula, function decimal (substring) represents the decimal number for the binary code substring.
For example, when n = 5, n! = 120, at this time 2 ^ 8 > 120, so take m = 8, if an eight-bit binary code is 10001100, then the real number it refers to is: x = decimal (10001100) × (120)/(2 ^ 8–1) = 65.88.
Then we can round x up, i.e. [x]+1 (the [x] is floor function which output the greatest integer less than or equal to x), and find the disassembly sequence numbered [x]+1 by the inverse Cantor operation. In summary, the process of encoding and decoding are shown in Figure 5.
Fitness Function
The goal of this paper is to find the best disassembly sequence of EVB under the condition of maximum disassembly benefit.
For a m-bit binary code, its corresponding disassembly sequence can be found by using the above method. The disassembly sequence is a sequence of n elements, indicating the disassembly order of n components in the EVB. The disassembly benefit of each path is different, and we take the value of the revenue of each path as the fitness value of each chromosome.
We have the following nomenclature.
x1, x2, … , xn: Disassembly sequence; Pi, i ∈ {1, 2, … , n}: The ith disassembly relation matrix (according to the disassembly sequence x1, x2, … , xn, their is n disassembly operations of each disassembly sequence correspond to n different disassembly relationship matrices).
Ri, i∈{1, 2, … , n}: Recycling revenue of each component.
L: The fixed cost of releasing each connection.
C: Time cost per minute.
Si: Number of connection relationships needs to be released by operation i, Find the row xi of the disassembly relationship matrix Pi, and Si equal to the amount of digits one and three in that row.
Ti: Time required to complete operation i.
Tti: Transition time from operation i to operation i + 1. The value of Tti depends on the distance between component xi and component xi + 1, Find the distance between component xi and component xi + 1 from the CAD model, and record as di. Tti = coefficient × di.
Then the fitness value of each disassembly sequence x1, x2, …, xn can be obtained by formula 4.
The Model of Proposed Method
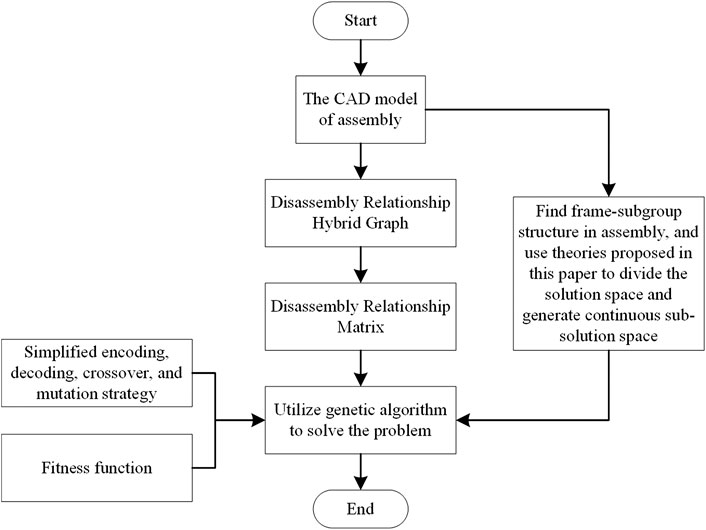
In summary, now we have established a complete theoretical model to solve the DSP problem. Compared with the existing model, the advantage of this model is that the solution space is divided into continuous subspaces by using the proposed frame subgroup structure, which simplifies the encoding, decoding, crossover, and mutation process of genetic algorithm, and improves the efficiency of the solution. The process of solving the DSP problem is shown in the Figure 6. In the following text, we will apply the theoretical model to analyze a case to prove the effectiveness of the model.
Case Study
Basic Information of a Electric Vehicle Battery
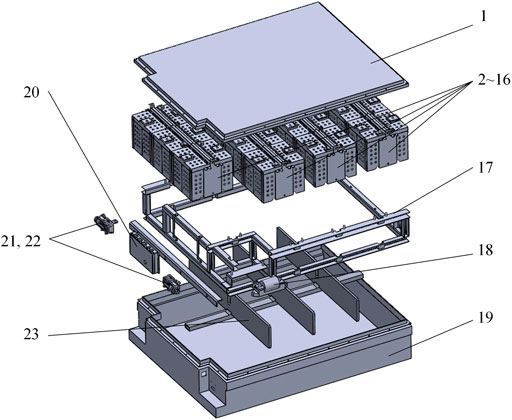
The EVB provided by partner enterprise was selected as the case study in our research in order to verify the reliability and effectiveness of the proposed method. It essentially comprises a pack of 15 modules, a battery management controller (BMC), 2 high voltage cable connector, safety device, the cooling system (heat skins) and a frame. More details of the EVB is shown in the explode view (Figure 7), and its components is listed in Table 1.
Disassembly Relationship Hybrid Graph
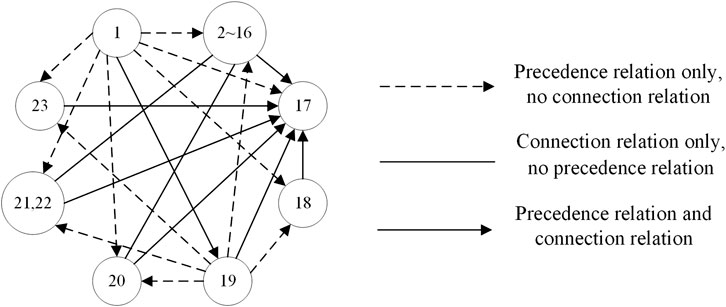
According to the exploded view of the EVB shown in Figure 7, and the previous introduction about the disassembly relationship hybrid graph, we can draw the disassembly relationship mixed graph of the EVB as shown in Figure 8.
Disassembly Relation Matrix
According to the disassembly relationship hybrid graph in Figure 8, we can get the disassembly relationship matrix of the EVB as shown in the Figure 9.
Solution Space
By analyzing the CAD model, the disassembly relationship hybrid graph and the disassembly relationship matrix of the EVB, we found that 21 components numbered from 2 to 17 and from 19 to 23 meet the definition of the frame-subgroup structure, among them, component 17 is a frame, and the remaining components are subgroups. At the same time, we found that to disassemble the EVB, firstly, we need to disassemble component 1, then disassemble component 18, and finally disassemble the above frame-subgroup structure. So the solution space in this case is relatively simple, it can be recorded as 1, 18 (2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 19, 20, 21, 22, 23, 17). According to the theory described above, there are 20! (about 2.4 × 1018) disassembly sequences in the solution space.
Using Genetic Algorithm to Solve This Problem
Encoding and Decoding
In this case, there are 20! (about 2.4 × 1018) feasible disassembly sequences in the solution space. We can construct one-to-one correspondence between these 20! disassembly sequences and positive integers, 1, 2, …, 20!, by Cantor expansion and its inverse operation.
Because 20! < 262, we use 62-bit binary code as chromosome to represent disassembly sequences. For a 62-bit binary code substring, use formula 2 to find the corresponding disassembly sequence number x, in this case that is x=1 + [decimal (substring) × (20!)/(262 − 1)], then the corresponding disassembly sequence can be found by using the inverse Cantor expansion.
Initial Population
In this case, the initial population is set to 20 chromosomes. We randomly generate 20 62-bit binary codes as the initial chromosomes, and use the above decoding operation to obtain the disassembly sequence corresponding to the chromosome.
Fitness Function
The fitness function value of a disassembly sequence x1, x2, …, x23 can be obtained by substituting the values of the following parameters into formula 4.
Ri, i∈{1,2, … ,23}: Recycling revenue of each component is listed in the Table 2.
L: Since the connections in this case are all screw connections, L is a constant of 50 CNY.
C: C = 10 CNY/min.
Ti: in this case the time to release each connection is 0.5 min. Ti = 0.5×Si (CNY).
Tti: Tti = 0.1×di (CNY).
Selection Operator
The selection operator is to select a better quality chromosome from the current population to inherit to the next generation. In this case, the strategy is roulette (Ren et al., 2019), it is based on the fitness value of chromosome. The higher the fitness value, the higher the probability of the chromosome being retained. The probability of the chromosome is retained is formulate in formula 5.
where the Ui means a disassembly sequence, and function Eual(Ui) means the fitness value of the disassembly sequence Ui.
Crossover
Select two 62-bit binary chromosomes as parents, randomly assign a position of the chromosome, and then exchange the right end parts of the two parent chromosomes to generate children. Take the crossover rate as Pc = 0.9.
Mutation
The mutation operation is applied to the gene of 62 binary chromosomes, that is, if the gene is 1, the mutation is 0, and if the gene is 0, the mutation is 1. The probability of each gene mutation is equal, take the mutation rate as Pm =0.01. That is to say, it is hoped that 1% of genes will mutate on average. In this case, there are 62 × 20 = 1240 genes in each generation, i.e., 12.4 genes are mutated on average in each generation.
Result
After the mutation operation, the next generation population is generated, then evaluate the fitness of new population, and so far, the operation of the first generation is completed, then iterate 100 more times. After performing 10 separate optimizations for this case, the one with the best fitness performance is selected, and the final optimal disassembly sequence is “1, 18, 22, 21, 2, 3, 4, 5, 9, 8, 7, 6, 10, 11, 12, 13, 16, 15, 14, 19, 20, 23, 17,” the fitness value is: 3511.2. This means following this disassembly sequence, the dismantling income should be 3511.2 in theory.
Comparison
An inevitable problem in the traditional genetic algorithm to solve the DSP problem is that complex crossover and mutation methods need to be carefully designed to ensure that the generated sub-chromosomes are still in the solution space. However, because of the introduction of the frame-subgroup structure in this paper, the problem of optimizing in the solution space, which formed by all the disassembly sequences, is transformed into the problem of optimizing on continuous positive integers. Compared with the traditional genetic algorithm for solving DSP problems, this method not only simplifies the optimization space, but also can directly uses mature coding, decoding, crossover, and mutation theories to solve the problem. Therefore, the method proposed in this paper simplified the calculation process of genetic algorithm, and should have certain advantages in solving such problems.
Aiming at the problem of EVB DSP with the goal of maximizing disassembly benefit, we compared the method proposed in this paper with the method of traditional genetic algorithm proposed by Tseng et al. (2018). However, the optimization goal of Tseng et al. is the minimum disassembly time, in order to ensure the comparability of the results, in both methods, we use the same fitness function in Selection Operator to obtain the disassembly sequence with the largest disassembly benefit.
At the same time, in both methods, we select the same crossover rate as Pc = 0.9, and the mutation rate as Pm = 0.01, and the number of iterations is 100. Due to the randomness of the genetic algorithm, we have run the two methods separately ten times, and selected the best one among them.
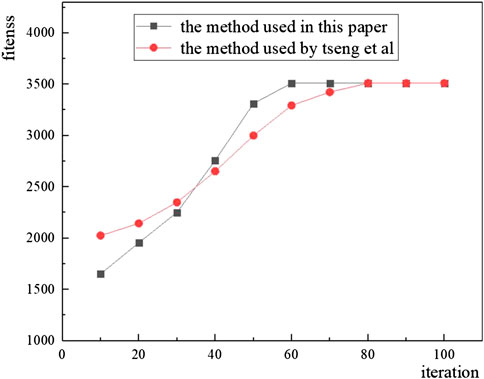
Part of the results of the two methods are shown in Table 3. The disassembly sequence generated by the comparison method is “1, 18, 22, 21, 16, 15, 14, 10, 11, 12, 13, 9, 8, 7, 6, 2, 3, 4, 5, 19, 20, 23, 17,” with the fitness value of 3506.7, which is very close to the method proposed in this paper. And the main difference between the two methods lies in disassembly sequence of the modules (components numbered 2–16), as shown in Figure 7, they gather in the middle part of EVB, and their disassembly sequence has little effect on the dismantling revenue. We record the best fitness value every 10 iterations, the relationship between fitness value with iterations of two methods are shown in Figure 10.
As shown in Figure 10, the abscissa is the number of iterations, and the ordinate is the optimal fitness value. It can be seen from Figure 10 that the method proposed in this paper converges to the maximum fitness value earlier, and both of the two methods was run on a computer with Intel Core i5 6,500 CPU at 3.2 GHz and 8 G RAM. It takes 15.3 s to generate the optimal disassembly sequence with the method proposed in this paper, and takes 25.9 s with the method of Tseng et al. Based on the above results it proved that the method proposed in this paper has certain advantage in solving the problem.
Experiment Works
Based on the above case study and the comparison with existing methods. We carried out three groups of disassembly experiments by the same skilled workers. In the first group, workers decide the disassembly sequence of the components themselves, thus there were no fixed disassembly sequence, which is also a common method utilized by resource recovery enterprises in EVB disassembly. In the second group, EVB was disassembled by workers following the disassembly sequence generated by traditional genetic algorithm, and the third group following the disassembly path generated in this paper. Three separated experiments were carried out in each group, the average value of three experiments was selected as the experimental results.
Since the components obtained from each disassembly sequence are the same, the total value of these component is fixed (show in Table 2), thus, the main factor affecting the disassembly benefit lies in the disassembly time of each sequence. In this experiment, the benefit of each disassembly sequence is equivalent to the total value of these components minus the disassembly time multiplied by the worker’s wages per unit time. Brief results of the experiment works are shown in Table 4.
The experimental results show that the disassembly sequence generated by the two theoretical models are significantly better than the conventional method utilized by resource recovery enterprises in terms of disassembly benefit and disassembly time, and there is only a small difference between the two methods. However, according to the previous statement, the advantage of the method proposed in this paper is it can get the result faster.
Conclusions and Discussions
This paper proposes a new method of frame subgroup structure combined with genetic algorithm to solve disassembly sequence planning problems with the aim of maximizing disassembly income. Firstly, this paper proposes an improved disassembly relationship hybrid graph and disassembly relationship matrix to clearly describe the disassembly priority relationship and connection relationship between components in the assembly. Secondly, this paper defines the frame-subgroup structure for the first time, and found that the disassembly sequences of this structure can be mapped one by one with positive integer sequence through Cantor expansion. The optimization problem in the solution space composed of all disassembly sequences can be transformed into the optimization problem in the positive integer sequence, which simplifies the optimization process. Thirdly, based on the properties of the frame subgroup structure, combined with genetic algorithm, this paper gives a new method to solve the DSP problem. Unlike traditional genetic algorithms for solving DSP problems, based on the proposed frame subgroup structure, this method simplifies the process of encoding, decoding, crossover, and mutation, which improves the efficiency of solving the problem. Finally, the feasibility of the method is verified by the case of the EVB, and the comparison with exist algorithm and related experiments proves that the method is superior in solving the problem.
The theory proposed in this paper has wide applicability, it can solve many disassembly sequence planning problems. For example, in the condition that most of the components inside the assembly from a frame-subgroup structure which proposed in this paper, such as when the EVB, car engine, and printed circuit board, etc. are going to be disassembled, the method proposed can get better results with higher efficiency. However, the above method still has certain limitations, when there is no frame-subgroup structure or only a few components form the frame-subgroup structure, this method does not have a particularly significant effect, which needs further study to solve this problem.
The most innovative idea of this paper is start the DSP research from the structure of EVB, but not to find a generalization algorithm. And, the result of this research proves that the proposed framework subgroup structure has certain advantages in solving the maximum benefit of EVB disassembly. There will still be other related structures with other excellent disassembly properties worth further study to make up for the limitations of existing methods and to help solving similar problems. Moreover, this paper only introduced the combination of proposed frame structure with genetic algorithm, and the application with other meta heuristic algorithms still needs comprehensive research.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author/s.
Author Contributions
QK contributed the study concepts and study design, revised the final manuscript. PZ contributed the experimental work, data analyses, edited the manuscript. LZ helped data acquisition and method comparison. SS helped literature research with constructive discussions.
Funding
This study is supported by the National Natural Science Foundation of China (Grant No. 51875162) and it is appreciated for the assistance in the Institute of Green Design and Manufacturing Engineering at Hefei University of Technology.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Alfaroalgaba, M., and Ramirez, F. J. (2020). Techno-economic and environmental disassembly planning of lithium-ion electric vehicle battery packs for remanufacturing. Resour. Conserv. Recycl. 154, 104461. doi:10.1016/j.resconrec.2019.104461
Bahubalendruni, M. V. A. R., and Varupala, P. (2020). Disassembly sequence planning for safe disposal of end-of-life waste electric and electronic equipment. Natl. Acad. Sci. Lett. doi:10.1007/s40009-020-00994-0
Chang, M. M., Nee, A. Y., and Ong, S. K. (2020). Interactive AR-assisted product disassembly sequence planning (ARDIS). Int. J. Prod. Res. 58 (16), 4916–4931. doi:10.1080/00207543.2020.1730462
Feng, Y., Zhou, M., Tian, G., Li, Z., Zhang, Z., Zhang, Q., et al. (2019). Target disassembly sequencing and scheme evaluation for CNC machine tools using improved multiobjective ant colony algorithm and fuzzy integral. Systems man and cybernetics. IEEE Trans. Syst. Man Cybern. Syst. 49 (12), 2438–2451. doi:10.1109/tsmc.2018.2847448
Gu, X., Ieromonachou, P., Zhou, L., and Tseng, M. (2018). Developing pricing strategy to optimise total profits in an electric vehicle battery closed loop supply chain. J. Clean. Prod. 203, 376–385. doi:10.1016/j.jclepro.2018.08.209
Guo, X., Liu, S., Zhou, M., and Tian, G. (2016). Disassembly sequence optimization for large-scale products with multiresource constraints using scatter search and Petri nets. IEEE Trans. Cybern. 46 (11), 2435–2446. doi:10.1109/TCYB.2015.2478486
Hu, B., Feng, Y., Zheng, H., and Tan, J. (2018). Sequence planning for selective disassembly aiming at reducing energy consumption using a constraints relation graph and improved ant colony optimization algorithm. Energies 11 (8), 2106. doi:10.3390/en11082106
Ji-Bin, J., Zhi-Feng, L., and Guang-Fu, L. (2006). Research on disassembly sequence planning algorithm based on engineering semantic information. Comput. Integrated Manufact. Syst. 12, 625–629. doi:10.1088/1742-6596/29/1/015
Kim, H., Park, C., and Lee, D. (2018). Selective disassembly sequencing with random operation times in parallel disassembly environment. Int. J. Prod. Res. 56 (24), 7243–7257. doi:10.1080/00207543.2018.1432911
Laili, Y., Tao, F., Pham, D. T., Wang, Y., and Zhang, L. (2019). Robotic disassembly re-planning using a two-pointer detection strategy and a super-fast bees algorithm. Robot. Comput. Integrated Manuf. 59, 130–142. doi:10.1016/j.rcim.2019.04.003
Lambert, A. J. D. (2003). Disassembly sequencing: a survey. Int. J. Prod. Res. 41 (16), 3721–3759. doi:10.1080/0020754031000120078
Lee, S., Tseng, H., Chang, C., and Huang, Y. (2019). Applying interactive genetic algorithms to disassembly sequence planning. Int. J. Precis. Eng. Manuf. 21 (4), 663–679. doi:10.1007/s12541-019-00276-w
Liu, X., Ni, Z., Liu, J., and Cheng, Y. (2016). Assembly process modeling mechanism based on the product hierarchy. Int. J. Adv. Manuf. Technol. 82 (1), 391–405. doi:10.1007/s00170-015-7372-z
Parsa, S., and Saadat, M. (2019). Intelligent selective disassembly planning based on disassemblability characteristics of product components. Int. J. Adv. Manuf. Technol. 104 (5), 1769–1783. doi:10.1007/s00170-019-03857-1
Ren, Y., Meng, L., Zhang, C., Zhao, F., and Sutherland, J. W. (2019). An efficient metaheuristics for a sequence-dependent disassembly planning. J. Clean. Prod. 245, 118644. doi:10.1016/j.jclepro.2019.118644
Shao, Y., Deng, X., Qing, Q., and Wang, Y. (2018). Optimal battery recycling strategy for electric vehicle under government subsidy in China. Sustainability 10 (12), 4855. doi:10.3390/su10124855
Tian, G., Ren, Y., Feng, Y., Zhou, M., Zhang, H., and Tan, J. (2019). Modeling and planning for dual-objective selective disassembly using and/or graph and discrete artificial bee colony. IEEE Trans. Industrial Inform. 15 (4), 2456–2468. doi:10.1109/tii.2018.2884845
Tian, Y., Zhang, X., Liu, Z., Jiang, X., and Xue, J. (2019). Product cooperative disassembly sequence and task planning based on genetic algorithm. Int. J. Adv. Manuf. Technol. 105 (5), 2103–2120. doi:10.1007/s00170-019-04241-9
Tian, Y., Zhang, X., Xu, J., and Li, Z. (2018). Selective parallel disassembly sequence planning method for remanufacturing. J. Comput.-Aided Design Comput. Graphics 30 (3), 531. doi:10.3724/sp.j.1089.2018.16317
Tseng, H., Chang, C., Lee, S., and Huang, Y. (2018). A Block-based genetic algorithm for disassembly sequence planning. Expert Syst. Appl. 96, 492–505. doi:10.1016/j.eswa.2017.11.004
Keywords: disassembly sequence planning, genetic algorithm, frame-subgroup structure, electric vehicle battery, disassembly relation hybrid graph, disassembly relation matrix
Citation: Ke Q, Zhang P, Zhang L and Song S (2020) Electric Vehicle Battery Disassembly Sequence Planning Based on Frame-Subgroup Structure Combined with Genetic Algorithm. Front. Mech. Eng. 6:576642. doi: 10.3389/fmech.2020.576642
Received: 26 June 2020; Accepted: 16 November 2020;
Published: 07 December 2020.
Edited by:
Zhigang Jiang, Wuhan University of Science and Technology, ChinaCopyright © 2020 Ke, Zhang, Zhang and Song. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Qingdi Ke, UWluZ2RpLmtlQGhmdXQuZWR1LmNu
 Qingdi Ke
Qingdi Ke Peng Zhang
Peng Zhang Lei Zhang
Lei Zhang