- 1Center for Mechanics of Solids, Structures and Materials, Department of Aerospace Engineering and Engineering Mechanics, The University of Texas, Austin, TX, United States
- 2Departement of Mechanical Engineering, The University of Texas, Austin, TX, United States
- 3Department of Biomedical Engineering, Texas Materials Institute, The University of Texas, Austin, TX, United States
Dry adhesion is governed by physical rather than chemical interactions. Those may include van der Waals and electrostatic forces, friction, and suction. Soft dry adhesives, which can be repeatedly attached to and detached from surfaces, can be useful for many exciting applications including reversible tapes, robotic footpads and grippers, and bio-integrated electronics. So far, the most studied Soft dry adhesives are gecko-inspired micro-pillar arrays, but they suffer from limited reusability and weak adhesion underwater. Recently cratered surfaces emerged as an alternative to micro-pillar arrays, as they exhibit many advantageous properties, such as tunable pressure-sensitive adhesion, high underwater adhesive strength, and good reusability. This review summarizes recent work of the authors on mechanical characterization of cratered surfaces, which combines experimental, modeling, and computational components. Using fundamental relationships describing air or liquid inside the crater, we examine the effects of material properties, crater shapes, air vs. liquid ambient environments, and surface patterns. We also identify some unresolved issues and limitations of the current approach, and provide an outlook for future research directions.
Introduction
Soft adhesives are conformable and deformable binding agents between two surfaces. Engineered soft adhesives have become part of our daily life, e.g., medical bandages for wound healing, stretchable brace tapes for joint protection, and double-sided tapes for paper sticking. Soft adhesives are usually categorized as either soft wet adhesives (SWAs) or soft dry adhesives (SDAs). SWAs bond surfaces together through either chemical reactions or mechanical loading (Czech et al., 2013; Cho et al., 2019; Yuk et al., 2019; Chen et al., 2020a). For example, a well-known class of SWAs is pressure-sensitive adhesives (PSAs) which consist of a viscoelastic bonding agent that can instantaneously form a bond to the adherend under applied pressure (Creton, 2003; Czech and Kowalczyk, 2011). Acrylics, polyether, silicones, polyesters, and polyurethanes are commonly used bonding agent for PSAs (Singh et al., 2011; Cilurzo et al., 2012). Due to their viscous nature, PSAs can flow to conform to rough surfaces upon compression, and the inherent tackiness and low surface energy of the adhesive materials facilitate strong bonding onto a variety of substrates (Singh et al., 2014). However, with the rapid development of bioelectronics and the increasing demand for seamless integration between humans and machines, conventional SWAs are facing some challenges. First, despite their relatively strong bonding capability, the tacky binding agent can be easily contaminated with impurities (e.g., dust, sebum, etc.), limiting both the ability to reposition and reuse. Second, the binding agent may contain chemicals harmful to humans, resulting in irritation (Kawahara and Tojo, 2007), contact dermatitis (Christoffers et al., 2014), and even injury or damage (Matsumura et al., 2013; Hwang et al., 2018). In contrast, SDAs bond by employing physical interactions such as electrostatic attraction, van der Waals (vdW) forces, suction, or friction (Eisenhaure and Kim, 2017). In general, SDAs require relatively smooth surfaces to enable such physical interactions, e.g., no air leakage or intimate contact for vdW interaction, thus they were not used as widely as SWAs. But in the last two decades, SDAs have garnered tremendous attention with great promise in the fields of healthcare, soft robotics, and human-machine interface (Brodoceanu et al., 2016; Li et al., 2016; Xiaosong et al., 2019; Chen et al., 2020b). Of particular interest are SDAs that are capable of repeated attachment and detachment, whose usefulness has been demonstrated in many exciting applications such as breathable skin patches (Kwak et al., 2011), robotic footpads or grippers (Gorb et al., 2007), and reusable bio-integrated electronics (Hwang et al., 2018).
Pillar- and Crater-Enabled Soft dry adhesives
So far, the most widely studied SDAs are surfaces with arrays of micro-pillars. The inspiration came from terrestrial species including lizards and geckos whose toe pads are covered by intricate fibrils that enable strong attachment as well as easy release (Autumn et al., 2000; Autumn et al., 2002; Arzt et al., 2003; Gao and Yao, 2004; Hansen and Autumn, 2005; Yao and Gao, 2006). Autumn et al. (2000) first discovered the hierarchical lamellae and setae structures of gecko toe pads by scanning electron microscopy (SEM). There, each seta branches into hundreds of 200 nm thin spatula, capable of conforming to curvilinear and rough surfaces. The normal adhesive strength of those toe pads was measured at of 100 kPa (Autumn et al., 2000), which is comparable to that of a 3M Scotch™ tape (200 kPa). The strong adhesion of the gecko toe pads was solely attributed to vdW forces between the nanoscale spatula and the target surface, rather than chemical bonding (Autumn et al., 2002). Aside from the remarkable attachment performance, the fibrillary system also exhibits superior reversibility and self-cleaning capability (Hansen and Autumn, 2005).
Figures 1A–E showcase several representative synthetic micro-scale surface features resembling gecko fibrils. The simplest design is micro-pillars with flat tips (Del Campo and Arzt, 2007; Del Campo et al., 2007a; Del Campo et al., 2007b) (Figure 1A). More advanced designs involve micro-pillars with hierarchy (Greiner et al., 2009; Wang et al., 2014) (Figure 1B). Spatula tips (Del Campo and Arzt, 2007; Del Campo et al., 2007a) (Figure 1C) have been designed to more closely mimic the gecko’s toe pads. Emulating the design principle of the tilting setae on gecko’s toe pads, slanted structures have been widely exploited to generate directional adhesion (Figure 1D) (Autumn et al., 2006a; Murphy et al., 2009; Moon et al., 2010; Afferrante and Carbone, 2012; Jin et al., 2014; Wang et al., 2014; Wang et al., 2015; Seo et al., 2016; Wang, 2018). This represents a breakthrough in developing reversible adhesives that truly resemble their natural prototypes. Among all the tip geometries, the mushroom-like shape (Figure 1E) stands out as it exhibits large adhesive strength by reducing the stress concentration at the pillar-substrate interfaces (Del Campo et al., 2007a; Carbone et al., 2011; Carbone and Pierro, 2012; Bae et al., 2013; Wang et al., 2014; Marvi et al., 2015; Kim et al., 2016). The vibrant research on micro-pillar-based SDAs has been summaried by many excellent review articles, with various focuses on the adhesion mechanisms, design principles, fabrication methods, and performance characterizations (Pattantyus-Abraham et al., 2013; Zhou et al., 2013; Sahay et al., 2015; Eisenhaure and Kim, 2017; Xiaosong et al., 2019). Figures 1F–L display examples of another type of SDAs, suction- or crater-based adhesives, which is the focus of this paper and will be discussed in detail later.
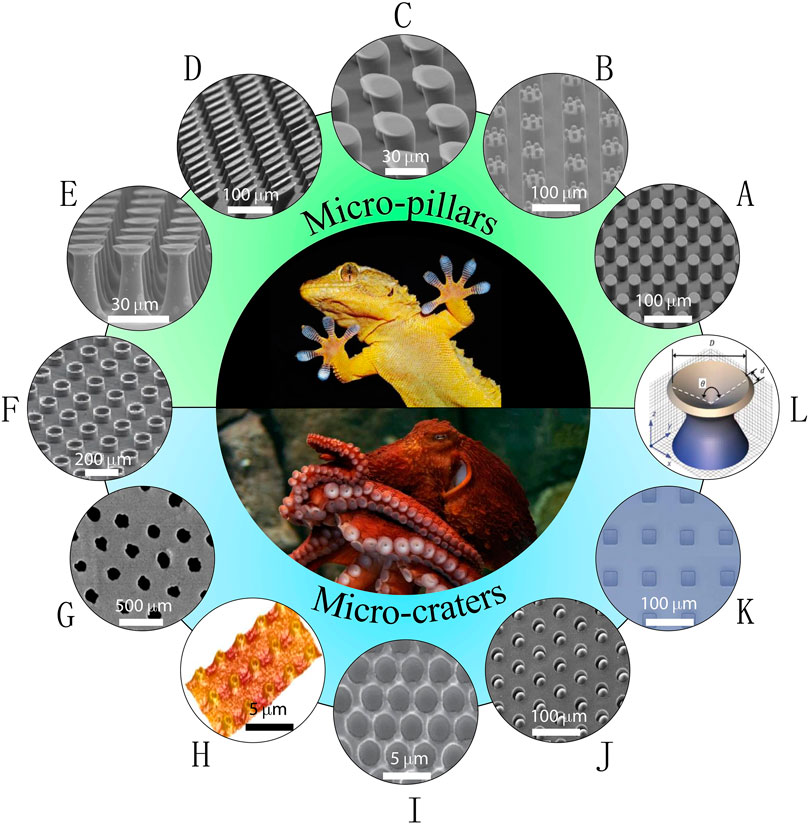
FIGURE 1. Examples of nature-inspired soft dry adhesives (SDAs). (A–E) Gecko-inspired synthetic micro-pillars with various tip geometries: (A) flat tip (reprinted with permission from ref (Del Campo et al., 2007b)); (B) hierarchical tip (reprinted with permission from ref (Greiner et al., 2009)); (C) spatular tip (reprinted with permission from ref (Del Campo and Arzt, 2007)); (D) slanted tip (reprinted with permission from ref (Murphy et al., 2009)); (E) mushroom-like tip (reprinted with permission from ref (Wang et al., 2014)). (F) A combinational structure – micro-pillars with concave tip (reprinted with permission from ref (Baik et al., 2018)). (G–K) Octopus-inspired synthetic micro-suckers or craters: (G) nano-craters on UV resin surfaces (reprinted with permission from ref (Chang et al., 2014)); (H) reversible adhesive skin patch with micro-craters on multilayer PDMS (reprinted with permission from ref (Choi et al., 2016)); (I) micro-craters on PDMS surface (reprinted with permission from ref (Akerboom et al., 2015)); (J) micro-craters with interior protuberances (reprinted with permission from ref (Baik et al., 2017)); (K) square-patterned micro-craters on PDMS surface (reprinted with permission from ref (Nanni et al., 2015)). (L) Another combinational structure – pillar with funnel-shaped tip (reprinted with permission from ref (Fischer et al., 2017)).
Despite extensive research in the last two decades, as far as applications are concerned, micro-pillar-enabled SDAs are facing some major barriers. First, according to “contact splitting” theory (Arzt et al., 2003; Chan et al., 2007; Kamperman et al., 2010), the adhesion can be enhanced by splitting up the contact with the adherend into finer subcontacts, enabled by extremely tiny fibrils. However, scaling-down the pillar size faces fundamental physical limitations and dramatically increases manufacturing difficulties and costs. Those challenges have been recognized in both electron beam lithography (Pease, 1981; Vieu et al., 2000) and nano-embossing (Becker and Heim, 2000; Kim et al., 2007). Furthermore, slender pillars are prone to buckling and collapsing, resulting in undesirable entanglements and/or mats (see Figure 2A). In fact, buckling may even lead to rupture and detachment (Chan et al., 2007; Del Campo and Arzt, 2007; Greiner et al., 2007; Kim et al., 2007; Kim et al., 2016; Eisenhaure and Kim, 2017). All of these degradation mechanisms may significantly impair the adhesive strength, leading to limited robustness and reusability. On a different note, it has been widely reported that micro-pillars may lose their van der Waals adhesion on wet surfaces or in aquatic environments (Buhl et al., 2009; Pesika et al., 2009; Baik et al., 2017; Cadirov et al., 2017; Ma et al., 2018). A typical adhesion test shown in Figure 2B unveils that humidity dramatically decreases the adhesion of micro-pillar arrays (Cadirov et al., 2017). This is consistent with another experimental observation that micro-pillar arrays almost completely lose adhesion with moisture or underwater (see the green bars in Figure 2C) (Baik et al., 2017). Figure 2D, taken from the same paper (Baik et al., 2017), highlights the adhesion of cratered surfaces, which will be discussed later.
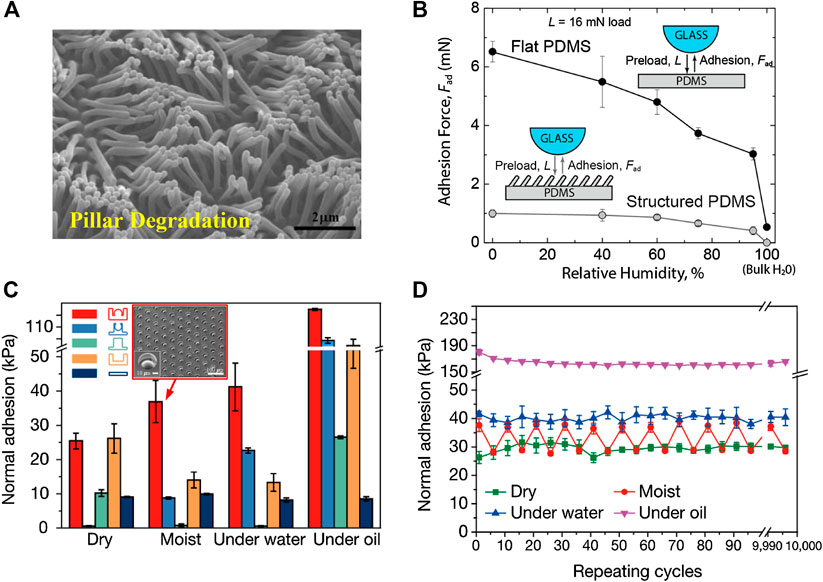
FIGURE 2. Limitations of pillared surfaces and advantages of cratered surfaces as SDAs. (A) A scanning electron microscopy (SEM) image of pillar condensation. (reprinted with permission from ref (Kim et al., 2007)). (B) Adhesion force of micro-pillars as a function of relative humidity (reprinted with permission from ref (Cadirov et al., 2017)). (C) Adhesive strengths of various pillared and cratered structures where red: protuberance-shaped crater; blue: perforated cylinders; green: cylindrical pillar; brown: cylindrical hole; black: flat surface (reprinted with permission from ref (Baik et al., 2017)). (D) Repeatable adhesion of the crater-enabled SDAs after more than 10000 cycles of attachment and detachment (reprinted with permission from ref (Baik et al., 2017)).
According to Bartlett et al. (Bartlett et al., 2012; Bartlett and Crosby, 2014), the adhesive force of micro-pillars can be scaled as
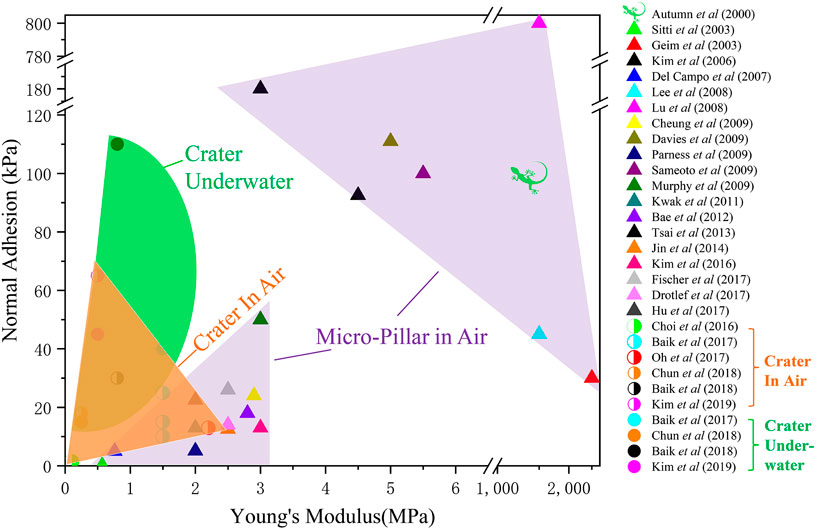
FIGURE 3. An Ashby plot of normal adhesive strength vs. material Young’s modulus for both pillar-enabled and crater-enabled SDAs. Purple regimes enclose data of pillared surfaces in air. The orange regime denotes craters in air and the green regime represents craters underwater.
Another class of reusable SDAs emerged as arrays of micro-craters (i.e., dimples or depressions engineered on polymer surfaces). In fact, utilizing suction for attachment has been widely observed in nature. The arms of aquatic cephalopods such as squid and octopus are equipped with hundreds of suckers for anchoring and object manipulation (Smith, 1991; Kier and Smith, 2002; Von Byern and Klepal, 2006; Tramacere et al., 2013;Tramacere et al., 2014b). The pressure drop inside the sucker, termed negative pressure, can reach 300 kPa for octopus and 800 kPa for decapod (Smith, 1991; Smith, 1996). Cephalopod suckers have been emulated on aquatic robots using active pumps (Wang et al., 2017c; Shintake et al., 2018) as well as passive adhesive tapes (Choi et al., 2016; Baik et al., 2017). Passive cratered surfaces have demonstrated remarkable adhesion capabilities in recent years. Just to name a few, in 2014, Chang et al. (Chang et al., 2014) created an array of submicron-sized craters on UV resin (Figure 1G) and measured adhesive shear strengths as high as 750 kPa on silicon wafers (Chang et al., 2014). In 2015, Choi et al. fabricated an array of 1 μm-diameter craters on the surface of a multilayer polydimethylsiloxane (PDMS) (Figure 1H) and the measured adhesive strength exceeded that of the same PDMS with either flat or pillared surface (Choi et al., 2016). Also in 2015, Akerboom et al. fabricated close-packed nano-dimples on 10:1 (base-to-curing agent ratio) PDMS (Figure 1I) and found a larger pull-off force in comparison to flat PDMS surfaces (Akerboom et al., 2015). In 2017, Baik et al. fabricated dome-shaped protuberances within micro-craters (Figure 1J), whose adhesive strength was found to be 2-3 times higher than micro-pillars in dry condition (Baik et al., 2017). Similarly, enhanced adhesion has been reported by Nanni et al. who engineered PDMS with square-shaped craters (Figure 1K) (Nanni et al., 2015).
Beyond simple pillars or craters, researchers have combined the pillar effects with the suction mechanism. It has been experimentally confirmed that suction contributed 20% towards the total adhesive force in mushroom-like micro-pillars (Varenberg and Gorb, 2008; Tinnemann et al., 2019). The authors argued that vacuum may be generated between the thin mushroom-like tip and the surface during the detachment. In fact, micro-pillar stalks terminated with concave dome tip (Baik et al., 2018) (Figure 1F) or funnel-shaped tip (Fischer et al., 2017) (Figure 1L) have been realized and adhesive strength has been elevated to an ultrahigh value of 5.6 MPa (Fischer et al., 2017), which is gigantic compared with kPa-range adhesive strengths for simple pillars (e.g., Figures 1A–E) or simple craters (Figures 1G–K).
Although both are SDAs, crater-enabled adhesives have the following advantages relative to pillar-enabled adhesives: ease of fabrication, pressure-sensitive adhesion, excellent wet adhesion, superior scratch resistance and reusability, and high material compliance. Generally, cratered surfaces are engineered by molding a soft elastomer on a negative template with domes. Such a fabrication method is generally easier than the process to produce hierarchical (Del Campo and Arzt, 2007; Greiner et al., 2009) or composite micro-pillars (Bae et al., 2013; Drotlef et al., 2019). Distinct from the micro-pillars whose adhesive strength is usually fixed once fabricated (Murphy et al., 2009; Mengüç et al., 2012; Chary et al., 2013), the adhesion of cratered surfaces depends on the preload (Akerboom et al., 2015; Baik et al., 2019b). It is also worth noting that crater arrays, similar to octopus suckers, show a conspicuously enhanced adhesive strength underwater or on wet surfaces (see the red bar in Figure 2C and the green domain in Figure 3). Also, without delicate protruding structures, cratered surfaces are more scratch resistant and reusable. For example, Baik et al. (Baik et al., 2017) demonstrated that the adhesive force of craters remained almost unchanged after 10,000 cycles of attachment and detachment (Figure 2D). Last but not least, as presented in Figure 3, crater-enabled SDAs are capable of producing higher adhesion while maintaining the desirable levels of material softness. Such high softness endows them with exceptional deformability as well as conformability on deformable, rough surfaces including bio-tissues (Choi et al., 2016). These advantages of crater-based adhesives have enabled many exciting applications including wall-climbing robots (Aksak et al., 2008; Sahay et al., 2015), object manipulation (Chang et al., 2014) such as wafer handling (Lee et al., 2016), and bio-integrated medical devices (Chun et al., 2018; Hwang et al., 2018; Oh et al., 2018; Baik et al., 2019a; Baik et al., 2019b; Kim et al., 2019; Iwasaki et al., 2020).
Let us point out that harnessing suction for attachment is ubiquitous. Thin-walled suction cups are widely used in everyday suction hooks and climbing robot pads (Figure 4A) (Yoshida and Ma, 2010; Manabe et al., 2012) due to their strong attachment and quick release. By assembling suction cups onto a tapered elastomeric arm, Xie et al. recently demonstrated a soft actuator that was capable of grasping objects of various shapes (Figure 4B) (Xie et al., 2020). The same group also provided a feasible solution for preventing air leakage when gripping rough surfaces by programming the compliance of the sucker. The sucker was made of electrically responsive organohydrogel, which softened under high voltage, giving rise to conformable contact with rough surfaces (Figure 4C) (Zhuo et al., 2020). Theoretical analysis and experimental measurements have been carried out to understand both the attachment and detachment behaviors of suction cups. For instance, by actively pumping out the air through a connected tube, Liu et al., (2006) has reported the relationship between the negative pressure inside the cup and the active area, i.e. the area not in contact between the cup and the substrate. The suction force can be readily obtained through negative pressure multiplied by the active area. Different from air-pumping, Ge et al. proposed a pushing-detaching framework for characterizing the suction force of a commonly used passive suction cup (Figure 4D) (Ge et al., 2015). The process is illustrated in Figure 4D. In the beginning, the cup is resting on the substrate surface. Then a preload is applied to deform the suction cup such that air inside the cup is squeezed out and the suction cup successfully attaches to the substrate. To detach it, a pulling force is applied until it reaches the pull-off force. Based on this process, the suction force of the cup has been modeled and experimentally validated. However, such analysis is only applicable to thin-walled suction cups rather than craters which are dimples on the surface surrounded by the polymer matrix.
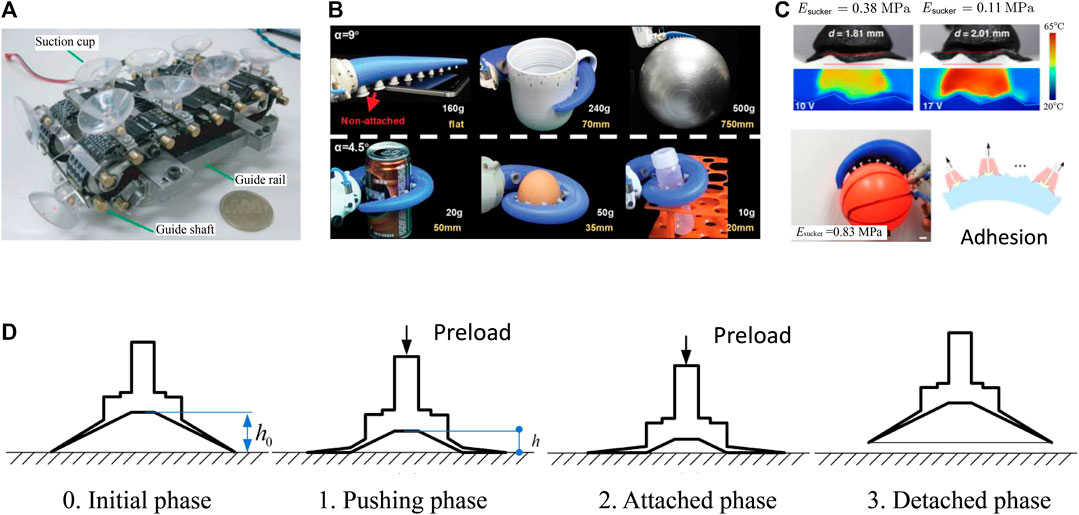
FIGURE 4. Suction cup example applications and models. (A) Wall-climbing robots with suction cups as attaching components (reprinted with permission from ref (Yoshida and Ma, 2010)). (B) A suction-cup-based tapered soft actuator capabile of gripping objects of various shapes (reprinted with permission from ref (Xie et al., 2020)). (C) An organohydrogel-based soft gripper with electrically programmable stiffness for achieving conformable contact with rough surfaces. [reprinted with permission from ref (Zhuo et al., 2020)]. (D) Schematics of a pressing-detaching process of a suction cup [reprinted with permission from ref (Ge et al., 2015)].
Despite a significant body of experimental evidence that suction is a significant adhesion mechanism for cratered surfaces, until recently, theoretical understanding and consequently model-guided design procedures were lacking. Our recent series of papers were a attempt intended to remedy this situation. We have developed an integrated computational-experimental-modeling approach for the quantitative characterization and understanding of the suction behaviors for various cratered surfaces under both dry and wet conditions. In the next section, we summarize our results by focusing on four factors controlling suction of isolated craters (Figure. 5): Young’s modulus of the polymer matrix (Figure 5A) (Qiao et al., 2017), crater shape (Figure 5B) (Qiao et al., 2017; Wang et al., 2019), air/underwater ambient environment (Figure 5C) (Wang et al., 2017b; Qiao et al., 2018), and elasto-capillary effect on micro/nano-craters (Figure 5D) (Wang et al., 2017b). In Section IV, we will discuss cratered surfaces and address the importance of the crater areal fraction as defined by the ratio between the projected area of crater and the base plane area of specimen (Figure 5E) (Wang et al., 2019) and patterns (Figure 5F) (Wang et al., 2019) of cratered arrays.
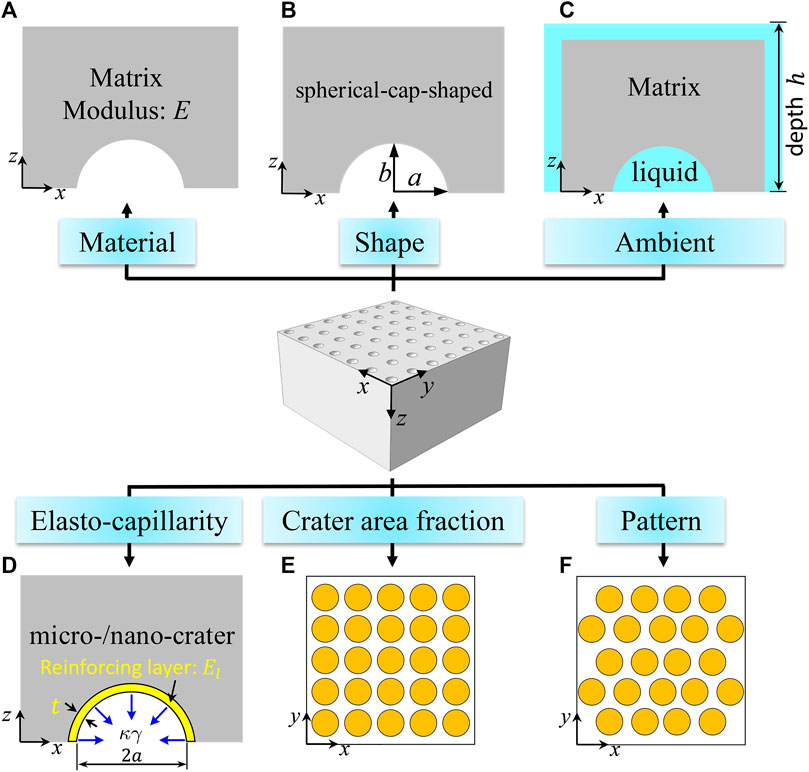
FIGURE 5. Six factors that affect the suction effects of crater arrays discussed in this review article: (A) matrix modulus; (B) crater shape, (C) ambient environment; (D) elasto-capillarity at small length scale; (E) crater area fraction; (F) the pattern of a crater array.
Isolated Craters
This section summarizes our results for isolated craters. The term isolated means that the crater dimensions are much smaller than all other specimen dimensions, and therefore the specimen can be regarded as a semi-infinite solid, where the only relevant dimensions are those of the crater.
Isolated Craters in Air
We begin this section by considering isolated craters in air as a precursor to considering the presence of liquids on the performance of isolated craters.
Modeling Framework
Following the earlier work on thin-walled suction cups (Ge et al., 2015), a loading-unloading process is established for calculating the suction force of an isolated crater, as illustrated by Figures 6A–C. Initially, the air inside the crater is characterized by the ambient pressure,
(1) The specimen is subjected to a remote compressive stress
(2) The specimen is unloaded in such a manner that air does not return to the crater and the crater springs back. This action results in a pressure drop inside the crater which produces the suction force. At the end of this step, the air in the crater is characterized by the triplet
and the suction force
where
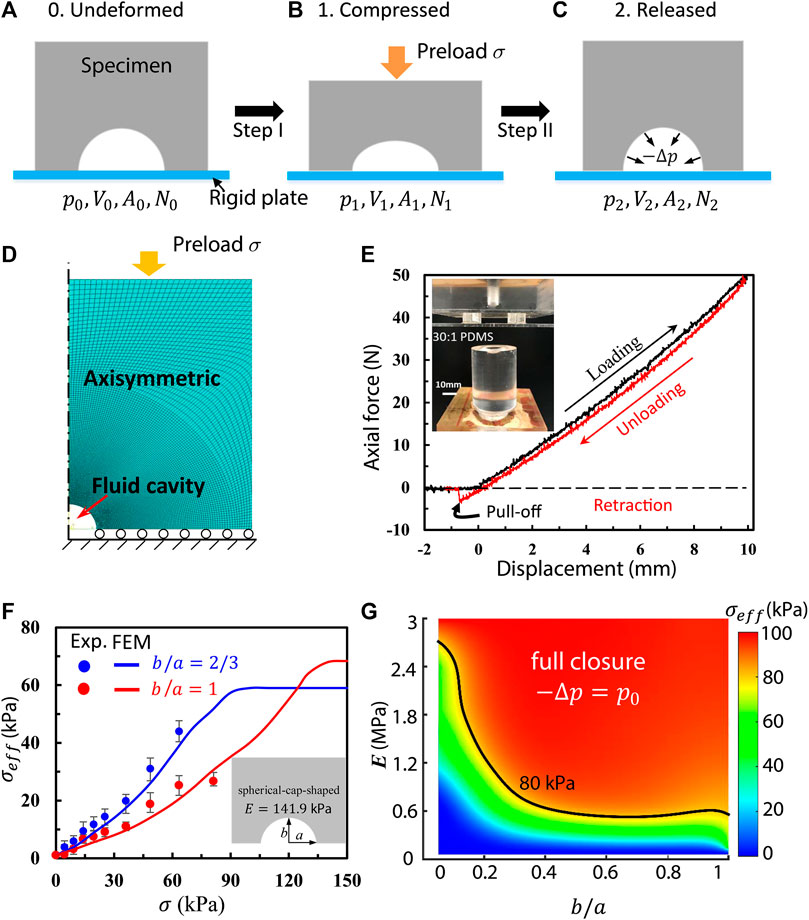
FIGURE 6. The model of a macroscopic, isolated crater in air. (A–C) Schematics of the loading-unloading process that generates suction. (D) An axisymmetric finite element model (FEM) for simulating isolated craters. (E) A representative loading-unloading-retraction curve for a cratered specimen. The inset shows the experimental setup. (F) Effective adhesive strength as a function of the preload for spherical-cap-shaped (SCS) craters with aspect ratios
Key assumptions adopted in this framework are:
a. The air flows freely out of the crater upon loading (Step 1), so that
b. No air exchange takes place upon unloading (Step 2), so that
c. The entire process is isothermal and air is an ideal gas, so that
Assumptions (a) and (b) are consistent with the abovementioned models of thin-walled suction cups (Liu et al., 2006; Ge et al., 2015). However, in our experiment, to be discussed later, Assumption (a) is hard to achieve without a vent hole drilled in the substrate. Therefore, future research is required to realize Assumption (a) without any vent hole. Furthermore, secure sealing after loading should be validated to justify Assumption (b). With these three assumptions, the pressure drop can be related to the crater volumes as
Therefore, the suction force becomes
If the ambient pressure is equal to the atmospheric pressure
According to this equation, obtaining a large value of
Simulation and Experimental Setups
Axisymmetric finite element models (FEM) for isolated craters were built to simulate the suction force using commercial software, ABAQUS 6.13 (Figure 6). The built-in function *FLUID CAVITY was implemented to model the ideal gas behavior inside the craters. The specimen/substrate interface was assumed to be frictionless, and the substrate was assumed to be rigid. The material behavior of 30:1 PDMS was characterized as an incompressible neo-Hookean model with Young’s modulus E = 141.9 kPa according to our measurements (Qiao et al., 2017). Experimentally, PDMS with base-to-curing-agent mass ratio equal to 30:1 was cured at 70°C for 12 h to mold specimens with and without craters (see inset in Figure 6E). A small vent hole with diameter of 0.8 mm was drilled in the rigid plate and roughly aligned with the center of the crater. Oil lubricant was applied at the specimen/plate interface. Loading and unloading tests were carried out with the vent hole open during loading and closed during unloading and the pull-off force was measured. A representative experimental loading-unloading curve is given in Figure 6E. The suction force can be readily calculated by subtracting the adhesive force over the contact zone (which is very small and independent of preload) from the measured pull-off force at the pull-off point (Qiao et al., 2017).
Results
Spherical-cap-shaped (SCS) craters with various aspect ratios were studied both numerically and experimentally. The schematic of a SCS crater is shown in Figure 5B where the base radius and height of the craters are labeled as
It is also worth noting that experimental and FEM results agree well. Therefore, such a simulation approach can be confidently used for characterizing other cratered specimens, e.g., of different Young’s moduli and crater shapes. A contour plot for the effective adhesive strength as a function of material Young’s modulus
Macroscopic, Isolated Craters Underwater
Similar to suction cups on aquatic cephalopods (Tramacere et al., 2014a; Tramacere et al., 2014b), craters underwater also exhibit much larger adhesive strength than those in air (see Figure 3). This is addressed by considering a cratered specimen resting on a fixed rigid platform, both submerged in liquid at depth
where
Zero Liquid Depth
We begin the discussion by first forming an understanding when
Figure 7B plots the normalized pressure drop obtained by FEM as a function of preload for both air-filled and liquid-filled hemispherical craters. The blue curve clearly shows that the pressure drop of the air-filled crater gradually increases with growing preload and eventually reaches a plateau of –Δp=pα when fully closed, i.e., vacuum, at σf =140 kPa as highlighted by the vertical dashed magenta line. However, the crater underwater undergoes a faster pressure drop than those in air such that it reaches vacuum (i.e. –Δp=pα) prior to the full closure. The intersection of the horizontal dashed black line of –Δp=pα and the curve of –Δp/pα(σ) determines a critical preload of σ0v=80 kPa. The critical preload suggests a threshold above which the liquid in the crater will vaporize. In the simplest pictureIn other words, when σ<σ0v, the liquid inside the crater remains as an incompressible fluid, while when σ≥σ0v, it should rapidly vaporize even in at room temperature. This liquid-to-gas phase transition violates the assumption of an incompressible fluid. Hence the FEM results beyond this point are no longer meaningful. It is also worth pointing out that when the craters are fully closed at σf =140 kPa, the craters in air or water behave essentially the same as –Δp=pα is realized for both craters if h=0. This explains the fully overlapped experimental results at σ=σf as highlighted by the vertical magenta dashed line in Figure 7A.
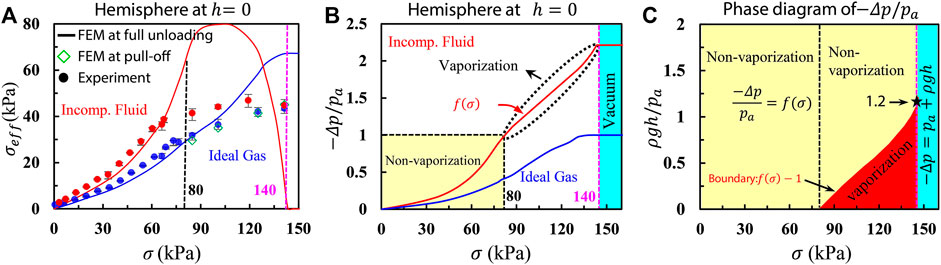
FIGURE 7. Experimental and modeling results for craters underwater. (A) Effective adhesive strength
Finite Liquid Depth
It is interesting to realize that the red curve in Figure 7B should be applicable to any
In summary, craters underwater, on the one hand, are capable of producing higher suction force than those in air due to the volume constraints; on the other hand, vaporization may take place, which undermines the suction.
Isolated Craters in Air With Surface Tension
Up to this point, we neglected polymer surface tension, which may become important for small craters on a soft matrix. The significance of surface tension can be realized by examining molded polymer surfaces. A commonly adopted fabrication method for cratered surfaces is molding polymers out of a negative template, which are usually created using either micromachining (Choi et al., 2016) or colloidal lithography (Chang et al., 2014; Akerboom et al., 2015). Such methods work well for relatively stiff polymers such as UV resin (E ∼ GPa) (Chang et al., 2014) or even 10:1 PDMS (E ∼ MPa) (Akerboom et al., 2015). However, molding microscale craters on soft polymer sheet, e.g. 40:1 PDMS (E ∼ 100 kPa) (Choi et al., 2016), resulted in much smaller crater size compared with the domes on the template after demolding. This can be attributed to the so-called elasto-capillarity effects in which the polymer surface tension is a driving force for diminishing the sizes of craters when the crater length scale is comparable to the elasto-capillary length defined as
We investigated the surface tension effect by considering isolated hemi-spherical craters with reinforcements parameterized by their thickness and Young’s modulus. A contour plot for the effective adhesive strength
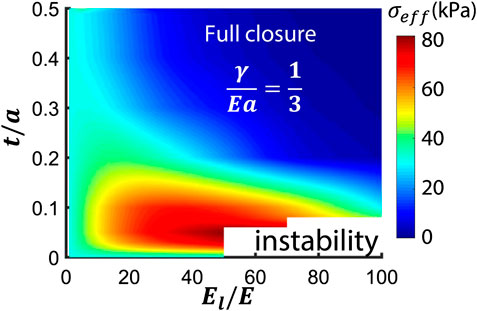
FIGURE 8. A contour plot of effective adhesive strength
In fact, adding a reinforcing layer may even enhance the suction force for craters with negligible surface tension effects. This is because a thin reinforcing layer can assist the crater to spring back upon unloading, while leaving the overall structural stiffness almost unchanged (Qiao et al., 2017). Surprisingly, a reinforced SCS crater with aspect ratio
Crater Arrays in Air
Isolated craters discussed in the previous section represent cratered surfaces with very small crater areal fraction, i.e.,
Consider two polymer sheets with the same total base plane area of
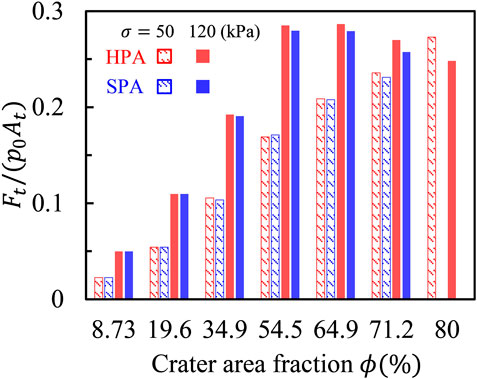
FIGURE 9. Normalized total suction force
Summary and Outlooks
Progress in the development of reversible SDAs has been rapid. So far, micro-pillared surfaces have been regarded as the primary option. In this review, we focus on cratered surfaces as an alternative, with the emphasis on our recent mechanistic understandings of suction effects of craters arrays. Through theoretical analysis, numerical simulation, and experimental measurements, the effect of polymer matrix stiffness, crater shape, air/water ambient environments, elasto-capillarity, crater area fraction, and pattern of crater arrays are systematically studied.
However, there is a major limitation in the present modeling framework, related to the simplified loading-unloading process for realizing suction effects as illustrated by Figures 6A–C. First, the substrate is assumed to be rigid and the crater/substrate interface is assumed to be frictionless. Deformable substrates (e.g., skin) and interfacial friction may prevent the venting of air/liquid during loading, and thus diminish the suction effects. Second, effective venting during loading and tight sealing during unloading and beyond, play crucial roles in strong and sustained adhesion, which should be a future direction for the design of cratered surfaces. Moreover, existing models cannot explain the experimental findings that even with exactly the same crater shape, areal fraction, and pattern, crater arrays may still exhibit different adhesive strength when the size of the crater varies (Baik et al., 2017). This size effect (not pertaining to elasto-capilarity) remains unresolved. In addition to passive cratered surfaces, reversible suction-based adhesion can also be enabled by active materials in response to external stimuli, such as temperature (Lee et al., 2016) or magnetic field (Yu et al., 2018; Linghu et al., 2019), which have not been systematically modeled.
Another potential direction for future work is to employ cohesive zone modeling in the analysis of the performance of cratered surfaces. This would allow for the intrinsic interactions (normal and shear) between contacting surfaces to be accounted for. In addition, such an approach would allow the strength and adhesion energy of different configurations to be compared, rather than relying solely on strength comparisons, which is the current practice. There may be performance regimes that are strength controlled and others that are dominated by energy considerations. This could result in the development of a richer parameter space for exploring the performance of cratered surfaces.
In summary, cratered surfaces represent a new class of SDAs with strong adhesion, remarkable reusability, and superior biocompatibility. After about 6 years of studies, research into the performance of cratered SDAs are still in its infancy. Preliminiary understandings summarized in this review were achieved under many simplifications and assumptions. The mechanics and realization of practically useful cratered SDAs are still elusive with wide open oppurtunities. Our understanding of the underlying mechanisms, exploration of optimal design, and employment of active materials require the collective wisdom of both mechanical engineers and material scientists.
Author Contributions
LW, K-HH, GR, KL, and NL participated fully to the data acquisition, analysis, and paper writing. All authors contributed to the article and approved the submitted version.
Funding
All authors acknowledge the support from the National Science Foundation (NSF) Division of Civil, Mechanical and Manufacturing Innovation (CMMI) award (Grant No. 1663551). LW acknowledges the Warren A. and Alice L. Meyer endowed graduate fellowship awarded by the Cockrell School of Engineering at the University of Texas at Austin. K-HH acknowledges the Philip C. and Linda L. Lewis Foundation Graduate Fellowship in Mechanical Engineering at the University of Texas at Austin.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Afferrante, L., and Carbone, G. (2012). Biomimetic surfaces with controlled direction-dependent adhesion. J. R. Soc. Interface. 9, 3359–3365. doi:10.1098/rsif.2012.0452
Akerboom, S., Appel, J., Labonte, D., Federle, W., Sprakel, J., and Kamperman, M. (2015). Enhanced adhesion of bioinspired nanopatterned elastomers via colloidal surface assembly. J. R. Soc. Interface. 12, 20141061. doi:10.1098/rsif.2014.1061
Aksak, B., Murphy, M. P., and Sitti, M. (2008). “Gecko inspired micro-fibrillar adhesives for wall climbing robots on micro/nanoscale rough surfaces”, in 2008 IEEE International Conference on Robotics and automation, Pasadena, CA, May 19–23 (IEEE), 3058–3063.
Arzt, E., Gorb, S., and Spolenak, R. (2003). From micro to nano contacts in biological attachment devices. Proc. Natl. Acad. Sci. Unit. States Am. 100, 10603–10606. doi:10.1073/pnas.1534701100
Autumn, K., Liang, Y. A., Hsieh, S. T., Zesch, W., Chan, W. P., Kenny, T. W., et al. (2000). Adhesive force of a single gecko foot-hair. Nature 405, 681–685. doi:10.1038/35015073
Autumn, K., Dittmore, A., Santos, D., Spenko, M., and Cutkosky, M. (2006a). Frictional adhesion: a new angle on gecko attachment. J. Exp. Biol. 209, 3569–3579. doi:10.1242/jeb.02486
Autumn, K., Majidi, C., Groff, R., Dittmore, A., and Fearing, R. (2006b). Effective elastic modulus of isolated gecko setal arrays. J. Exp. Biol. 209, 3558–3568. doi:10.1242/jeb.02469
Autumn, K., Sitti, M., Liang, Y. A., Peattie, A. M., Hansen, W. R., Sponberg, S., et al. (2002). Evidence for van der Waals adhesion in gecko setae. Proc. Natl. Acad. Sci. Unit. States Am. 99, 12252–12256. doi:10.1073/pnas.192252799
Bae, W. G., Kim, D., Kwak, M. K., Ha, L., Kang, S. M., and Suh, K. Y. (2013). Enhanced skin adhesive patch with modulus-tunable composite micropillars. Advanced healthcare materials 2, 109–113. doi:10.1002/adhm.201200098
Baik, S., Kim, D. W., Park, Y., Lee, T.-J., Ho Bhang, S., and Pang, C. (2017). A wet-tolerant adhesive patch inspired by protuberances in suction cups of octopi. Nature 546, 396–400. doi:10.1038/nature22382
Baik, S., Kim, J., Lee, H. J., Lee, T. H., and Pang, C. (2018). Highly adaptable and biocompatible Octopus‐like adhesive patches with meniscus‐controlled unfoldable 3D microtips for underwater surface and hairy skin. Adv. Sci. 5, 1800100. doi:10.1002/advs.201800100
Baik, S., Lee, H. J., Kim, D. W., Kim, J. W., Lee, Y., and Pang, C. (2019a). Bioinspired adhesive architectures: from skin patch to integrated bioelectronics. Adv. Mater. 31, 1803309. doi:10.1002/adma.201803309
Baik, S., Lee, H. J., Kim, D. W., Min, H., and Pang, C. (2019b). Capillarity-enhanced organ-attachable adhesive with highly drainable wrinkled octopus-inspired architectures. ACS Appl. Mater. Interfaces. 11, 25674–25681. doi:10.1021/acsami.9b05511
Bartlett, M. D., Croll, A. B., King, D. R., Paret, B. M., Irschick, D. J., and Crosby, A. J. (2012). Looking beyond fibrillar features to scale gecko-like adhesion. Adv. Mater. 24, 1078–1083. doi:10.1002/adma.201104191
Bartlett, M. D., and Crosby, A. J. (2014). High capacity, easy release adhesives from renewable materials. Adv. Mater. 26, 3405–3409. doi:10.1002/adma.201305593
Becker, H., and Heim, U. (2000). Hot embossing as a method for the fabrication of polymer high aspect ratio structures. Sensor Actuator Phys. 83, 130–135. doi:10.1016/s0924-4247(00)00296-x
Bico, J., Reyssat, É., and Roman, B. (2018). Elastocapillarity: when surface tension deforms elastic solids. Ann. review. 50, 629–659. doi:10.1146/annurev-fluid-122316-050130
Brodoceanu, D., Bauer, C. T., Kroner, E., Arzt, E., and Kraus, T. (2016). Hierarchical bioinspired adhesive surfaces—a review. Bioinspiration Biomimetics 11, 051001. doi:10.1088/1748-3190/11/5/051001
Buhl, S., Greiner, C., Campo, A. d., and Arzt, E. (2009). Humidity influence on the adhesion of biomimetic fibrillar surfaces. Ijmr 100, 1119–1126. doi:10.3139/146.110146
Cadirov, N., Booth, J. A., Turner, K. L., and Israelachvili, J. N. (2017). Influence of humidity on grip and release adhesion mechanisms for gecko-inspired microfibrillar surfaces. ACS Appl. Mater. Interfaces. 9, 14497–14505. doi:10.1021/acsami.7b01624
Carbone, G., Pierro, E., and Gorb, S. N. (2011). Origin of the superior adhesive performance of mushroom-shaped microstructured surfaces. Soft Matter 7, 5545–5552. doi:10.1039/c0sm01482f
Carbone, G., and Pierro, E. (2012). Sticky bio-inspired micropillars: finding the best shape. Small 8, 1449–1454. doi:10.1002/smll.201102021
Chan, E. P., Greiner, C., Arzt, E., and Crosby, A. J. (2007). Designing model systems for enhanced adhesion. MRS Bull. 32, 496–503. doi:10.1557/mrs2007.84
Chang, W.-Y., Wu, Y., and Chung, Y.-C. (2014). Facile fabrication of ordered nanostructures from protruding nanoballs to recessional nanosuckers via solvent treatment on covered nanosphere assembled monolayers. Nano Lett. 14, 1546–1550. doi:10.1021/nl4048042
Chary, S., Tamelier, J., and Turner, K. (2013). A microfabricated gecko-inspired controllable and reusable dry adhesive. Smart Mater. Struct. 22, 025013. doi:10.1088/0964-1726/22/2/025013
Chen, X., Yuk, H., Wu, J., Nabzdyk, C. S., and Zhao, X. (2020a). Instant tough bioadhesive with triggerable benign detachment. Proc. Natl. Acad. Sci. U.S.A. 117, 15497–15503. doi:10.1073/pnas.2006389117
Chen, Y., Meng, J., Gu, Z., Wan, X., Jiang, L., and Wang, S. (2020b). Bioinspired multiscale wet adhesive surfaces: structures and controlled adhesion. Adv. Funct. Mater. 30, 1905287. doi:10.1002/adfm.201905287
Cheung, E., and Sitti, M. (2009). Adhesion of biologically inspired polymer microfibers on soft surfaces. Langmuir 25, 6613–6616. doi:10.1021/la900997p
Cho, H., Wu, G., Christopher Jolly, J., Fortoul, N., He, Z., Gao, Y., et al. (2019). Intrinsically reversible superglues via shape adaptation inspired by snail epiphragm. Proc. Natl. Acad. Sci. U.S.A. 116, 13774–13779. doi:10.1073/pnas.1818534116
Choi, M. K., Park, O. K., Choi, C., Qiao, S., Ghaffari, R., Kim, J., et al. (2016). Cephalopod-inspired miniaturized suction cups for smart medical skin. Adv. Healthcare Mater. 5, 80–87. doi:10.1002/adhm.201500285
Christoffers, W. A., Coenraads, P.-J., and Schuttelaar, M.-L. (2014). Bullous allergic reaction caused by colophonium in medical adhesives. Contact Dermatitis 70, 256–257. doi:10.1111/cod.12170
Chun, S., Kim, D. W., Baik, S., Lee, H. J., Lee, J. H., Bhang, S. H., et al. (2018). Conductive and stretchable adhesive electronics with miniaturized octopus-like suckers against dry/wet skin for biosignal monitoring. Adv. Funct. Mater. 28, 1805224. doi:10.1002/adfm.201805224
Cilurzo, F., Gennari, C. G. M., and Minghetti, P. (2012). Adhesive properties: a critical issue in transdermal patch development. Expet Opin. Drug Deliv. 9, 33–45. doi:10.1517/17425247.2012.637107
Creton, C. (2003). Pressure-sensitive adhesives: an introductory course. MRS Bull. 28, 434–439. doi:10.1557/mrs2003.124
Czech, Z., and Kowalczyk, A. (2011). “Pressure-sensitive adhesives for medical applications,” in Wide spectra of quality control. Shanghai, China: InTech.
Czech, Z., Wilpiszewska, K., Tyliszczak, B., Jiang, X., Bai, Y., and Shao, L. (2013). Biodegradable self-adhesive tapes with starch carrier. Int. J. Adhesion Adhes. 44, 195–199. doi:10.1016/j.ijadhadh.2013.03.002
Davies, J., Haq, S., Hawke, T., and Sargent, J. P. (2009). A practical approach to the development of a synthetic Gecko tape. Int. J. Adhesion Adhes. 29, 380–390. doi:10.1016/j.ijadhadh.2008.07.009
Del Campo, A., and Arzt, E. (2007). Design parameters and current fabrication approaches for developing bioinspired dry adhesives. Macromol. Biosci. 7, 118–127. doi:10.1002/mabi.200600214
Del Campo, A., Greiner, C., Álvarez, I., and Arzt, E. (2007a). Patterned surfaces with pillars with controlled 3 D tip geometry mimicking bioattachment devices. Adv. Mater. 19, 1973–1977. doi:10.1002/adma.200602476
Del Campo, A., Greiner, C., and Arzt, E. (2007b). Contact shape controls adhesion of bioinspired fibrillar surfaces. Langmuir 23, 10235–10243. doi:10.1021/la7010502
Drotlef, D.-M., Amjadi, M., Yunusa, M., and Sitti, M. (2017). Bioinspired composite microfibers for skin adhesion and signal amplification of wearable sensors. Adv. Mater. 29, 1701353. doi:10.1002/adma.201701353
Drotlef, D. M., Dayan, C. B., and Sitti, M. (2019). Bio-inspired composite microfibers for strong and reversible adhesion on smooth surfaces. Integr. Comp. Biol. 59, 227–235. doi:10.1093/icb/icz009
Eisenhaure, J., and Kim, S. (2017). A review of the state of dry adhesives: biomimetic structures and the alternative designs they inspire. Micromachines 8, 125. doi:10.3390/mi8040125
Fischer, S. C. L., Arzt, E., and Hensel, R. (2016). Composite pillars with a tunable interface for adhesion to rough substrates. ACS Appl. Mater. Interfaces. 9, 1036–1044. doi:10.1021/acsami.6b11642
Fischer, S. C. L., Groß, K., Torrents Abad, O., Becker, M. M., Park, E., Hensel, R., et al. (2017). Funnel-shaped microstructures for strong reversible adhesion. Adv. Mater. Interfaces. 4, 1700292. doi:10.1002/admi.201700292
Gao, H., and Yao, H. (2004). Shape insensitive optimal adhesion of nanoscale fibrillar structures. Proc. Natl. Acad. Sci. Unit. States Am. 101, 7851–7856. doi:10.1073/pnas.0400757101
Ge, D., Matsuno, T., Sun, Y., Ren, C., Tang, Y., and Ma, S. (2015). Quantitative study on the attachment and detachment of a passive suction cup. Vacuum 116, 13–20. doi:10.1016/j.vacuum.2015.02.013
Geim, A. K., Dubonos, S. V., Grigorieva, I. V., Novoselov, K. S., Zhukov, A. A., and Shapoval, S. Y. (2003). Microfabricated adhesive mimicking gecko foot-hair. Nature Mater 2, 461–463. doi:10.1038/nmat917
Gorb, S. N., Sinha, M., Peressadko, A., Daltorio, K. A., and Quinn, R. D. (2007). Insects did it first: a micropatterned adhesive tape for robotic applications. Bioinspir. Biomim. 2, S117–S125. doi:10.1088/1748-3182/2/4/s01
Greiner, C., Arzt, E., and Del Campo, A. (2009). Hierarchical gecko-like adhesives. Adv. Mater. 21, 479–482. doi:10.1002/adma.200801548
Greiner, C., del Campo, A., and Arzt, E. (2007). Adhesion of bioinspired micropatterned surfaces: effects of pillar radius, aspect ratio, and preload. Langmuir 23, 3495–3502. doi:10.1021/la0633987
Hansen, W. R., and Autumn, K. (2005). Evidence for self-cleaning in gecko setae. Proc. Natl. Acad. Sci. Unit. States Am. 102, 385–389. doi:10.1073/pnas.0408304102
Hu, H., Tian, H., Shao, J., Li, X., Wang, Y., Wang, Y., et al. (2017). Discretely supported dry adhesive film inspired by biological bending behavior for enhanced performance on a rough surface. ACS Appl. Mater. Interfaces. 9, 7752–7760. doi:10.1021/acsami.6b14951
Huber, G., Orso, S., Spolenak, R., Wegst, U. G. K., Enders, S., Gorb, S. N., et al. (2008). Mechanical properties of a single gecko seta. Ijmr 99, 1113–1118. doi:10.3139/146.101750
Hwang, I., Kim, H. N., Seong, M., Lee, S. H., Kang, M., Yi, H., et al. (2018). Multifunctional smart skin adhesive patches for advanced health care. Adv. healthc. mater. 7, e1800275. doi:10.1002/adhm.201800275
Iwasaki, H., Lefevre, F., Damian, D. D., Iwase, E., and Miyashita, S. (2020). Autonomous and reversible adhesion using elastomeric suction cups for in-vivo medical treatments. IEEE Robotics and Automation Letters 5, 2015–2022. doi:10.1109/LRA.2020.2970633
Jin, K., Cremaldi, J. C., Erickson, J. S., Tian, Y., Israelachvili, J. N., and Pesika, N. S. (2014). Biomimetic bidirectional switchable adhesive inspired by the gecko. Adv. Funct. Mater. 24, 574–579. doi:10.1002/adfm.201301960
Kamperman, M., Kroner, E., Del Campo, A., Mcmeeking, R. M., and Arzt, E. (2010). Functional adhesive surfaces with “gecko” effect: the concept of contact splitting. Adv. Eng. Mater. 12, 335–348. doi:10.1002/adem.201000104
Kawahara, K., and Tojo, K. (2007). Skin irritation in transdermal drug delivery systems: a strategy for its reduction. Pharm. Res. (N. Y.) 24, 399. doi:10.1007/s11095-006-9165-4
Kier, W. M., and Smith, A. M. (2002). The structure and adhesive mechanism of octopus suckers. Integr. Comp. Biol. 42, 1146–1153. doi:10.1093/icb/42.6.1146
Kim, D. S., Lee, H. S., Lee, J., Kim, S., Lee, K.-H., Moon, W., et al. (2007). Replication of high-aspect-ratio nanopillar array for biomimetic gecko foot-hair prototype by UV nano embossing with anodic aluminum oxide mold, Microsyst. Technol. 13, 601–606. doi:10.1007/s00542-006-0220-1
Kim, D. W., Baik, S., Min, H., Chun, S., Lee, H. J., Kim, K. H., et al. (2019). Highly permeable skin patch with conductive hierarchical architectures inspired by Amphibians and octopi for omnidirectionally enhanced wet adhesion. Adv. Funct. Mater. 29, 1807614. doi:10.1002/adfm.201807614
Kim, S., and Sitti, M. (2006). Biologically inspired polymer microfibers with spatulate tips as repeatable fibrillar adhesives. Appl. Phys. Lett. 89, 261911. doi:10.1063/1.2424442
Kim, T., Park, J., Sohn, J., Cho, D., and Jeon, S. (2016). Bioinspired, highly stretchable, and conductive dry adhesives based on 1D-2D hybrid carbon nanocomposites for all-in-one ECG electrodes. ACS Nano. 10, 4770–4778. doi:10.1021/acsnano.6b01355
Kwak, M. K., Jeong, H.-E., and Suh, K. Y. (2011). Rational design and enhanced biocompatibility of a dry adhesive medical skin patch. Adv. Mater. 23, 3949–3953. doi:10.1002/adma.201101694
Lee, H., Um, D.-S., Lee, Y., Lim, S., Kim, H.-j., and Ko, H. (2016). Octopus-inspired smart adhesive pads for transfer printing of semiconducting nanomembranes. Adv. Mater. 28, 7457–7465. doi:10.1002/adma.201601407
Lee, J., Fearing, R. S., and Komvopoulos, K. (2008). Directional adhesion of gecko-inspired angled microfiber arrays. Appl. Phys. Lett. 93, 191910. doi:10.1063/1.3006334
Li, Y., Krahn, J., and Menon, C. (2016). Bioinspired dry adhesive materials and their application in robotics: a review. J Bionic Eng. 13, 181–199. doi:10.1016/s1672-6529(16)60293-7
Linghu, C., Wang, C., Cen, N., Wu, J., Lai, Z., and Song, J. (2019). Rapidly tunable and highly reversible bio-inspired dry adhesion for transfer printing in air and a vacuum. Soft Matter 15, 30–37. doi:10.1039/c8sm01996g
Liu, J.-L., and Feng, X.-Q. (2012). On elastocapillarity: a review. Acta Mech. Sin. 28, 928–940. doi:10.1007/s10409-012-0131-6
Liu, J., Tanaka, K., Bao, L. M., and Yamaura, I. (2006). Analytical modelling of suction cups used for window-cleaning robots. Vacuum 80, 593–598. doi:10.1016/j.vacuum.2005.10.002
Lu, G., Hong, W., Tong, L., Bai, H., Wei, Y., and Shi, G. (2008). Drying enhanced adhesion of polythiophene nanotubule arrays on smooth surfaces. ACS Nano. 2,2342–2348. doi:10.1021/nn800443m
Ma, Y., Ma, S., Wu, Y., Pei, X., Gorb, S. N., Wang, Z., et al. (2018). Remote control over underwater dynamic attachment/detachment and locomotion, Adv. Mater. 30, 1801595. doi:10.1002/adma.201801595
Manabe, R., Suzumori, K., and Wakimoto, S. (2012). “A functional adhesive robot skin with integrated micro rubber suction cups”, in 2012 IEEE international conference on Robotics and automation (ICRA), Saint Paul, MN, May 14–18 (IEEE), 904–909. doi:10.1109/ICRA.2012.6224687
Marvi, H., Song, S., and Sitti, M. (2015). Experimental investigation of optimal adhesion of mushroomlike elastomer microfibrillar adhesives. Langmuir 31, 10119–10124. doi:10.1021/acs.langmuir.5b02415
Matsumura, H., Ahmatjan, N., Ida, Y., Imai, R., and Wanatabe, K. (2013). A model for quantitative evaluation of skin damage at adhesive wound dressing removal. Int. Wound J. 10, 291–294. doi:10.1111/j.1742-481x.2012.00975.x
Mengüç, Y., Yang, S. Y., Kim, S., Rogers, J. A., and Sitti, M. (2012). Gecko-inspired controllable adhesive structures applied to micromanipulation. Adv. Funct. Mater. 22, 1246–1254. doi:10.1002/adfm.201101783
Moon, M.-W., Cha, T.-G., Lee, K.-R., Vaziri, A., and Kim, H.-Y. (2010). Tilted Janus polymer pillars. Soft Matter 6, 3924–3929. doi:10.1039/c0sm00126k
Murphy, M. P., Aksak, B., and Sitti, M. (2009). Gecko-inspired directional and controllable adhesion. Small 5, 170–175. doi:10.1002/smll.200801161
Nanni, G., Fragouli, D., Ceseracciu, L., and Athanassiou, A. (2015). Adhesion of elastomeric surfaces structured with micro-dimples. Appl. Surf. Sci. 326, 145–150. doi:10.1016/j.apsusc.2014.11.108
Oh, J. H., Hong, S. Y., Park, H., Jin, S. W., Jeong, Y. R., Oh, S. Y., et al. (2018). Fabrication of high-sensitivity skin-attachable temperature sensors with bioinspired microstructured adhesive. ACS Appl. Mater. Interfaces. 10, 7263–7270. doi:10.1021/acsami.7b17727
Parness, A., Soto, D., Esparza, N., Gravish, N., Wilkinson, M., Autumn, K., et al. (2009). A microfabricated wedge-shaped adhesive array displaying gecko-like dynamic adhesion, directionality and long lifetime. J. R. Soc. Interface. 6, 1223–1232. doi:10.1098/rsif.2009.0048
Pattantyus-Abraham, A., Krahn, J., and Menon, C. (2013). Recent advances in nanostructured biomimetic dry adhesives. Frontiers in Bioengineering and Biotechnology 1, 22. doi:10.3389/fbioe.2013.00022
Pease, R. F. W. (1981). Electron beam lithography. Contemp. Phys. 22, 265–290. doi:10.1080/00107518108231531
Pesika, N. S., Zeng, H., Kristiansen, K., Zhao, B., Tian, Y., Autumn, K., et al. (2009). Gecko adhesion pad: a smart surface? J. Phys. Condens. Matter. 21, 464132. doi:10.1088/0953-8984/21/46/464132
Qiao, S., Gratadour, J.-B., Wang, L., and Lu, N. (2015). Conformability of a thin elastic membrane laminated on a rigid substrate with corrugated surface. IEEE Trans. Compon., Packag. Manufact. Technol. 5, 1237–1243. doi:10.1109/tcpmt.2015.2453319
Qiao, S., Wang, L., Ha, K.-H., and Lu, N. (2018). Suction effects of craters under water. Soft Matter 14, 8509–8520. doi:10.1039/c8sm01601a
Qiao, S., Wang, L., Jeong, H., Rodin, G. J., and Lu, N. (2017). Suction effects in cratered surfaces. J. R. Soc. Interface. 14, 20170377. doi:10.1098/rsif.2017.0377
Roman, B., and Bico, J. (2010). Elasto-capillarity: deforming an elastic structure with a liquid droplet. J. Phys. Condens. Matter. 22, 493110. doi:10.1088/0953-8984/22/49/493101
Sahay, R., Low, H. Y., Baji, A., Shaohui, F., and Wood, K. L. (2015). A state-of-the-art review and analysis on the design of dry adhesion materials for applications such as climbing micro-robots. RSC Adv. 5, 50821–50832. doi:10.1039/C5RA06770G
Sameoto, D., and Menon, C. (2009). A low-cost, high-yield fabrication method for producing optimized biomimetic dry adhesives. J. Micromech. Microeng. 19, 115002. doi:10.1088/0960-1317/19/11/115002
Seo, J., Eisenhaure, J., and Kim, S. (2016). Micro-wedge array surface of a shape memory polymer as a reversible dry adhesive. Extreme Mechanics Letters 9, 207–214. doi:10.1016/j.eml.2016.07.007
Shintake, J., Cacucciolo, V., Floreano, D., and Shea, H. J. a. M. (2018). Soft robotic grippers. Adv Mater. 30, 1707035. doi:10.1002/adma.201707035
Singh, A. K., Mehra, D. S., Niyogi, U. K., Sabharwal, S., and Khandal, R. K. (2011). Polyurethane based pressure sensitive adhesives (PSAs) using electron beam irradiation for medical application. J. Polym. Mater. 28, 525–542.
Singh, A. K., Mehra, D. S., Niyogi, U. K., Sabharwal, S., and Singh, G. (2014). Breathability studies of electron beam curable polyurethane pressure sensitive adhesive for bio-medical application. Radiat. Phys. Chem. 103, 75–83. doi:10.1016/j.radphyschem.2014.05.015
Sitti, M., and Fearing, R. S. (2003). Synthetic gecko foot-hair micro/nano-structures as dry adhesives. J. Adhes. Sci. Technol. 17, 1055–1073. doi:10.1163/156856103322113788
Smith, A. (1996). Cephalopod sucker design and the physical limits to negative pressure. J. Exp. Biol. 199, 949–958.
Smith, A. M. (1991). Negative pressure generated by octopus suckers: a study of the tensile strength of water in nature. J. Exp. Biol. 157, 257–271.
Tao, D., Gao, X., Lu, H., Liu, Z., Li, Y., Tong, H., et al. (2017). Controllable anisotropic dry adhesion in vacuum: gecko inspired wedged surface fabricated with ultraprecision diamond cutting. Adv. Funct. Mater. 27, 1606576. doi:10.1002/adfm.201606576
Tinnemann, V., Hernández, L., Fischer, S. C., Arzt, E., Bennewitz, R., and Hensel, R. (2019). In Situ observation reveals local detachment mechanisms and suction effects in micropatterned adhesives. Adv. Funct. Mater. 29, 1807713. doi:10.1002/adfm.201807713
Tramacere, F., Beccai, L., Kuba, M., Gozzi, A., Bifone, A., and Mazzolai, B. (2013). The morphology and adhesion mechanism of Octopus vulgaris suckers. PLoS One. 8, e65074. doi:10.1371/journal.pone.0065074
Tramacere, F., Appel, E., Mazzolai, B., and Gorb, S. N. (2014a). Hairy suckers: the surface microstructure and its possible functional significance in the Octopus vulgaris sucker. Beilstein J. Nanotechnol. 5, 561–565. doi:10.3762/bjnano.5.66
Tramacere, F., Kovalev, A., Kleinteich, T., Gorb, S. N., and Mazzolai, B. (2014b). Structure and mechanical properties of Octopus vulgaris suckers. J. R. Soc. Interface. 11, 20130816. doi:10.1098/rsif.2013.0816
Tsai, C.-Y., and Chang, C.-C. (2013). Auto-adhesive transdermal drug delivery patches using beetle inspired micropillar structures. J. Mater. Chem. B 1, 5963–5970. doi:10.1039/c3tb20735h
Varenberg, M., and Gorb, S. (2008). A beetle-inspired solution for underwater adhesion. J. R. Soc. Interface. 5, 383–385. doi:10.1098/rsif.2007.1171
Vieu, C., Carcenac, F., Pépin, A., Chen, Y., Mejias, M., Lebib, A., et al. (2000). Electron beam lithography: resolution limits and applications. Appl. Surf. Sci. 164, 111–117. doi:10.1016/s0169-4332(00)00352-4
Von Byern, J., and Klepal, W. (2006). Adhesive mechanisms in cephalopods: a review. Biofouling 22, 329–338. doi:10.1080/08927010600967840
Wang, L., Ha, K.-H., Qiao, S., and Lu, N. (2019). Suction effects of crater arrays. Extreme Mechanics Letters 30, 100496. doi:10.1016/j.eml.2019.100496
Wang, L., and Lu, N. (2016). Conformability of a thin elastic membrane laminated on a soft substrate with slightly wavy surface. J. Appl. Mech. 83, 041007. doi:10.1115/1.4032466
Wang, L., Qiao, S., Ameri, S. K., Jeong, H., and Lu, N. (2017a). A thin elastic membrane conformed to a soft and rough substrate subjected to stretching/compression. J. Appl. Mech. 84,111003. doi:10.1115/1.4037740
Wang, L., Qiao, S., and Lu, N. (2017b). Effects of surface tension on the suction forces generated by miniature craters. Extreme Mechanics Letters 15, 130–138. doi:10.1016/j.eml.2017.07.004
Wang, Y., Yang, X., Chen, Y., Wainwright, D. K., Kenaley, C. P., Gong, Z., et al. (2017c). A biorobotic adhesive disc for underwater hitchhiking inspired by the remora suckerfish. Science Robotics 2, eaan8072. doi:10.1126/scirobotics.aan8072
Wang, Y., Hu, H., Shao, J., and Ding, Y. (2014). Fabrication of well-defined mushroom-shaped structures for biomimetic dry adhesive by conventional photolithography and molding. ACS Appl. Mater. Interfaces. 6, 2213–2218. doi:10.1021/am4052393
Wang, Y., Li, X., Tian, H., Hu, H., Tian, Y., Shao, J., et al. (2015). Rectangle-capped and tilted micropillar array for enhanced anisotropic anti-shearing in biomimetic adhesion. J. R. Soc. Interface. 12, 20150090. doi:10.1098/rsif.2015.0090
Wang, Z. (2018). Slanted functional gradient micropillars for optimal bioinspired dry adhesion. ACS Nano. 12, 1273–1284. doi:10.1021/acsnano.7b07493
Xiaosong, L., Dashuai, T., Hongyu, L., Pengpeng, B., Zheyu, L., Liran, M., et al. (2019). Recent developments in gecko-inspired dry adhesive surfaces from fabrication to application. Surf. Topogr. Metrol. Prop. 7 (2), 23001.
Xie, Z., Domel, A. G., An, N., Green, C., Gong, Z., Wang, T., et al. (2020). Octopus arm-inspired tapered soft actuators with suckers for improved grasping. Soft Robot. 7, 639–648. doi:10.1089/soro.2019.0082
Yao, H., and Gao, H. (2006). Mechanics of robust and releasable adhesion in biology: bottom-up designed hierarchical structures of gecko. J. Mech. Phys. Solid. 54, 1120–1146. doi:10.1016/j.jmps.2006.01.002
Yoshida, Y., and Ma, S. (2010). “Design of a wall-climbing robot with passive suction cups,” in 2010 IEEE international Conference on Robotics and biomimetics, Tianjin, China, December 14–18 (IEEE), 1513–1518. doi:10.1109/ROBIO.2010.5723554
Yu, Q., Chen, F., Zhou, H., Yu, X., Cheng, H., and Wu, H. (2018). Design and analysis of magnetic-assisted transfer printing. J. Appl. Mech. 85, 101009. doi:10.1115/1.4040599
Yuk, H., Varela, C. E., Nabzdyk, C. S., Mao, X., Padera, R. F., Roche, E. T., et al. (2019). Dry double-sided tape for adhesion of wet tissues and devices. Nature 575, 169–174. doi:10.1038/s41586-019-1710-5
Zhao, Y., Tong, T., Delzeit, L., Kashani, A., Meyyappan, M., and Majumdar, A. (2006). Interfacial energy and strength of multiwalled-carbon-nanotube-based dry adhesive. J. Vac. Sci. Technol. B 24, 331–335. doi:10.1116/1.2163891
Zhou, M., Pesika, N., Zeng, H., Tian, Y., and Israelachvili, J. (2013). Recent advances in gecko adhesion and friction mechanisms and development of gecko-inspired dry adhesive surfaces. Friction 1, 114–129. doi:10.1007/s40544-013-0011-5
Keywords: dry adhesive, suction, crater, micro-pillar, adhesive strength, underwater adhesion
Citation: Wang L, Ha K-H, Rodin GJ, Liechti KM and Lu N (2020) Mechanics of Crater-Enabled Soft Dry Adhesives: A Review. Front. Mech. Eng. 6:601510. doi: 10.3389/fmech.2020.601510
Received: 01 September 2020; Accepted: 27 October 2020;
Published: 21 December 2020.
Edited by:
Stanislav N. Gorb, University of Kiel, GermanyReviewed by:
Hyun-Joon Kim, Kyungpook National University, South KoreaÁrpád Czifra, Óbuda University, Hungary
Copyright © 2020 Wang, Ha, Rodin, Liechti and Lu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Nanshu Lu, bmFuc2h1bHVAdXRleGFzLmVkdQ==
 Liu Wang
Liu Wang Kyoung-Ho Ha
Kyoung-Ho Ha Gregory J. Rodin1
Gregory J. Rodin1 Kenneth M. Liechti
Kenneth M. Liechti Nanshu Lu
Nanshu Lu