Modeling the Electrostatic Actuation of Nanomechanical Pillar Dimers

With their unparalleled mass sensitivity, enabling single-molecule mass spectrometry, nanomechanical resonators have the potential to considerably improve existing sensor technology. Vertical pillar resonators are a promising alternative to the existing lateral resonator designs. However, one major obstacle still stands in the way of their practical use: The efficient transduction (actuation & detection) of the vibrational motion of such tiny structures, even more so when large arrays of such nanopillars need to be driven. While electrostatic forces are typically weak and, on the nanoscale even weaker when compared to a cantilever-like stiffness, it is worth revisiting the possibility of electrostatic actuation of nanomechanical pillars and other nanomechanical structures. In this paper, these forces produced by an external field are studied both analytically and numerically, and their dependencies on the geometric dimensions are discussed. Furthermore, the expected deflections for different configurations of pillar geometries are calculated and compared.

1 Introduction

Microelectromechanical systems (MEMS) have become an integral part of modern consumer products and professional medical devices, and as such have become omnipresent helpers in our lives. As an example, there are more than one dozen MEMS parts contained in a modern smartphone alone, including gyroscopes, microphones, filters, switches, oscillators, accelerometers, auto focus actuators, electronic compass, pressure sensors, proximity sensors, fingerprint sensor, etc. The sensitivity and energy efficiency of micromechanical sensors typically improve with downscaling, which has led to the development of nanoelectromechanical systems (NEMS) with feature sizes below 1 μm in two dimensions. The first NEMS were developed at the end of the last century and consisted of nano-scale mechanical silicon-based resonators (Cleland and Roukes, 1996). The mechanical oscillations of such resonators are highly sensitive to perturbations coming from the environment. This makes them excellent sensors in particular for mass sensing, since the mass responsivity inversely scales with the effective mass of the resonator (Schmid et al., 2016). Carbon nanotube resonators with an ultimately low effective mass have reached yoctogram sensitivity (Chaste et al., 2012). Besides such fundamental research, nanomechanical resonators are promising for the application in protein (Naik et al., 2009; Hanay et al., 2012; Sage et al., 2015) or aerosol mass spectrometry (Schmid et al., 2013), offering, for the first time, single-molecule sensitivity. Despite the unparalleled mass sensitivity of nanomechanical resonators, their application as practical sensors has remained challenging. The typically used horizontal nanomechanical sensors are sensitive to the landing position of the mass along their length. This requires a sophisticated dual-mode operation of the first and second normal mode (Naik et al., 2009; Dohn et al., 2010; Schmid et al., 2010), which significantly complicates the sensor design. Vertical nanomechanical pillar resonators constitute a promising design alternative with all the advantages of having a low mass. And in contrast to horizontal resonator designs, the mass loading happens at the tip of the pillars which renders dual-mode operation unnecessary.

The efficient transduction (actuation & detection of mechanical motion) of NEMS has generally remained a challenge, for pillars in particular. Typical techniques used to transduce nanomechanical resonators, such as magnetomotive (Cleland and Roukes, 1996), piezoelectric (Villanueva et al., 2011), resistive (Li et al., 2007), and dielectric polarization-based (Schmid et al., 2006; Unterreithmeier et al., 2009; Faust et al., 2012) techniques are not well suited to transduce the vertical vibration of pillars. Optical detection of mechanical motion is the most sensitive technique available. Recently it was shown that the vibration of vertical nanowires can be readily detected optically (Molina et al., 2020). When the vertical nanowires are situated at the slope maximum of the Gaussian light beam, the displacement of the light-scattering nanowires cause a modulation of the reflected light. A similar method has been used to detect the lateral motion of nanoparticles situated inside a Gaussian beam (Chien et al., 2020). A different approach relevant for this paper is to produce pillar dimers (Sadeghi et al., 2017), which allow for a plasmonic optical readout as presented with nanomechancial string resonators (Thijssen et al., 2015).

The remaining challenge is how to efficiently drive such nanomechanical pillar dimers. With typical resonance frequencies >10 MHz the actuation with an external piezoelectric shaker becomes ineffective. In this paper, we propose to drive pillar dimers electrostatically by means of an external electrostatic field. We study the case of pillar dimers featuring a conductive tip, e.g., a plasmonic gold tip (Sadeghi et al., 2017), or pillars that are made of a conductive material, such as gold (Kabashin et al., 2009) (Figure 1). The generation of local forces between two electrically isolated floating electrodes via the application of an external electrostatic field constitutes an interesting transduction scheme for NEMS. Besides the here presented specific transduction scheme of conductive nanopillars, floating electrodes are often a given design constraint, e.g., in ultrahigh-Q string or drum resonators where a metalization of the entire resonator would significantly deteriorate the quality factor (Unterreithmeier et al., 2009; Yu et al., 2012; Bagci et al., 2014; Schmid et al., 2014). Hence, the presented analytical model is applicable beyond the transduction of nanomechancial pillar dimers, specific schemes for the transduction of string or nanowire resonators, as well as drum resonators, are promising extensions.

FIGURE 1

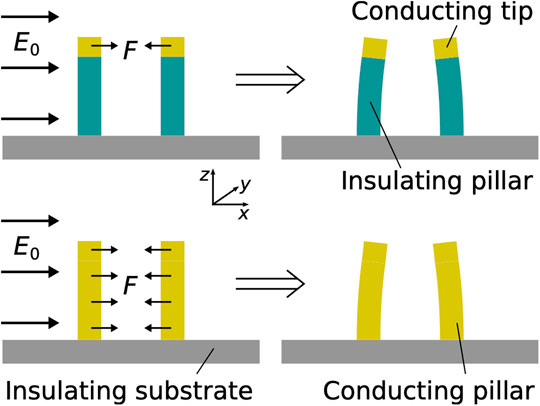
FIGURE 1. Working principle of the electrostatic pillar actuation. The applied electric field $E_0$ leads to a force between the conducting parts of the pillars. Either only the tip is conducting (top) or the whole pillar is conducting (bottom). Note that the bending here has been exaggerated for a better illustration.

2 Estimation of the Electrostatic Force

In contrast to conventional electrostatic drives where a voltage is applied between a static and a moving electrode, we intend to exploit the polarisation of conductors inside an electric field. The polarisation then leads to surface charges on the conductor, which experience a force inside the electric field. A measurable deflection can be achieved by an elastic element between the oppositely charged surface regions, which can be used as electric field sensor (Kainz et al., 2018, Kainz et al., 2019).

While for a single uncharged conductor the total force after integration over the surface of the whole conductor is zero, a net force emerges when two or more such conductors are brought close to one another (Figure 1). For the estimation of this electrostatic force between two nanomechanical pillars, a pair of conducting bodies (spheres, discs, or cylinders) is placed inside a uniform electric field E.

In many applications, rigorous analytical representations cannot be achieved without significant simplifications that generally question the reliability of the utilized modelling approach. Numerical methods have become powerful tools capable of filling this gap. Furthermore, numerical results tend to obfuscate fundamental dependencies. Reasonable analytical modelling should always be preferred. Therefore, a benchmark case in order to compare the analytical and numerical results is necessary to find solver settings and mesh quality which allow accurate results with minimum computational power. In the case of dimers, it seems best suited to use two conducting spheres embedded inside a uniform electric field for this purpose, which we’ll be presented subsequently. Forces between two cylinders will be introduced afterwards.

2.1 Two Conducting Spheres

The analytical treatment of the problem of two conducting spheres dates back at least to (Jenss, 1932) and (Morse and Feshbach, 1953). An extensive treatment of this case was done by (Davis, 1964). This quite general work is based on bispherical coordinates and treats conductive spheres of different sizes and charges, and varying distance in an electric field of arbitrary direction. Here, the resulting force for two uncharged spheres of the same radius r from this publication is used, considering only an electric field E₀ parallel to the axis between these spheres (here the z-axis). The corresponding force for a distance d between the spheres acts in the same direction and is given in electrostatic units as

$F_{\text{z}}=\frac{1}{2}{E}_0^2{r}^2{F}_1,(1)$

where

$F_1=\left(x+\frac{x^2}{4}\right){\displaystyle \sum }_{n=0}^{\infty }\frac{Y_n}{2n+1}\left(Y_n-2\text{cosh}\left({\mu }_0\right)\frac{n+1}{2n+3}{Y}_{n+1}\right),(2)$

is an infinite sum with

$x=\frac{d}{r},\text{and}{\mu }_0=\text{ln}\left(1+\frac{x}{2}+\sqrt{x+\frac{x^2}{4}}\right).(3)$

The terms Y_n can be written as

$Y_n=-\sqrt{2}\left(2n+1\right)\frac{2n+1-w_0}{2\text{sinh}\left(\left(n+\frac{1}{2}\right){\mu }_0\right)},(4)$

with

$w_0=\frac{S_1\left({\mu }_0\right)+S_1\left(0\right)}{S_0\left({\mu }_0\right)+S_0\left(0\right)}.(5)$

The terms $S_m\left(\xi \right)$ are again infinite sums given as

$S_m\left(\xi \right)={\displaystyle \sum }_{n=0}^{\infty }\frac{{\left(2n+1\right)}^m{\text{e}}^{\left(2n+1\right)\xi }}{{\text{e}}^{2\left(2n+1\right){\mu }_0}-1}.(6)$

Note that this force corresponds to the force acting on one of the spheres.

The associated numerical model was built in COMSOL using the electrostatics module. The two spheres were embedded inside a uniform field generated by two parallel plates. To model them as perfect conductors a floating potential boundary condition was applied to each. The corresponding forces were obtained by integration of the radial component of the electrostatic stress tensor over the surface of one sphere.

For comparison, a sphere radius of $r=50$ nm and an electric field strength of $E_0=100$ kV/m was chosen, while the distance was varied between 0.5 nm and 500 nm. The resulting forces are shown in Figure 2. It can be seen that the analytical and numerical forces are in good agreement. Apart from that, it can be observed that the force decreases with two different rates for increasing distance. For small distances the decrease is roughly linear, while for large distances the force decreases as $d^{-3}$. The transition between these slopes happens at r = d.

FIGURE 2

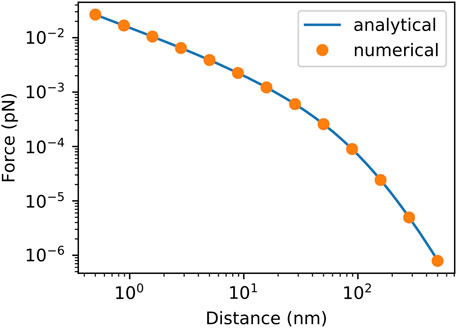
FIGURE 2. Comparison between analytically and numerically obtained forces between two uncharged conducting spheres of radius r = 50 nm in a uniform electric field with a field strength $E_0=100$ kV/m.

2.2 Two Conducting Cylinders

Unfortunately, the problem of two nanopillars cannot be described analytically in the same quality as the two spheres, since certain assumptions and simplifications have to be made. By assuming infinitely long parallel cylinders oriented in z-direction, the three-dimensional problem can be reduced to a two-dimensional one. The top and bottom faces of the actually finite-sized cylinders (height L) are neglected.

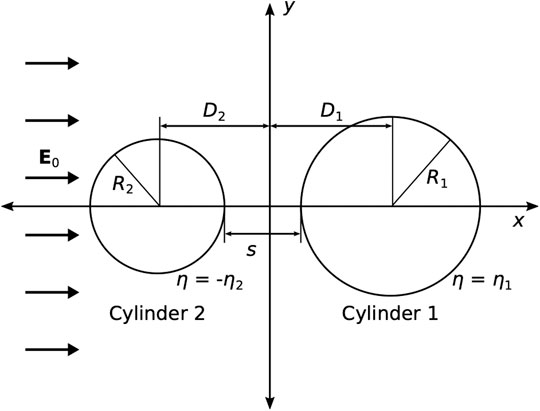
The distance between the cylinders be denoted s, the radii by R₁, R₂. The distances between the center of a cylinder to the origin are given by D₁ and D₂, respectively (Figure 3). Therefore, the centre-to-centre distance between the cylinders is d = s + R₁ + R₂ = D₁ + D₂. The electric field is assumed to be oriented in x-direction, E₀ = $E_0\widehat{x}$. The corresponding potential is therefore ${\phi }_0\left(x,y\right)=-E_{0}x$.

FIGURE 3

FIGURE 3. Cross-section of the two cylinders and important dimensions.

As for the bispherical problem, the bicylindrical problem can be treated analytically using a suitable coordinate system. Here, bipolar (BP) coordinates are a good choice for the 2D problem (Moon and Spencer, 1961). A solution for the electrostatic potential of two conducting cylinders in a uniform electric field has also been outlined in (Jenss, 1932; Morse and Feshbach, 1953). The most general treatment of the electrostatic two-cylinder problem has been presented in (Emets and Onofrichuk, 1996), however without using BP coordinates and without calculating the potential.

It pays off to perform the calculation of the potential by solving Laplace’s equation with the actual application in mind, which is outlined in the following. Cartesian (x, y) and BP ($\eta ,u$) coordinates are related by

$x=\frac{a\text{sinh}\eta }{\text{cosh}\eta -\cos u}\text{and}y=\frac{a\sin u}{\cosh \eta -\cos u}.(7)$

For now, a can be regarded as an arbitrary positive number. It corresponds to the half distance between the focal points inside the cylinders. The lines of constant η are circles in x, $y$-space encompassing one of the focal points (one for $\eta <0\iff x<0$ and one for $\eta >0\iff x>0$). The boundaries of the cylinders can therefore be expressed by $\eta ={\eta }_2<0$ for the cylinder on the left (x < 0) and $\eta ={\eta }_1>0$ for the right one (x > 0).

The η-coordinate ranges from $\left|\eta \right|=0$ (which corresponds to a circle with infinite radius touching the y-axis and therefore to Cartesian infinity) to $\left|\eta \right|=\infty$ (which corresponds to the focal points). The u-coordinate ranges from u = 0 to $u=2\pi$ (which correspond to the parts of the x-axis with x > a or $x<-a$, and $u=\pi$ to the part between the focal points $\left|x\right|<a$).

The dimensions and distances of the cylinders are related to a and ${\eta }_{\mathrm{1,2}}$ by $a^2=D_1^2-R_1^2=D_2^2-R_2^2$ and

${\eta }_{\mathrm{1,2}}=\text{ln}\left(\frac{D_{\mathrm{1,2}}+a}{R_{\mathrm{1,2}}}\right).(8)$

An expression for a in terms of $s,R_1,R_2$ can be obtained as

$a=\frac{s+R_1+R_2}{2}\sqrt{\left(1-\frac{{\left(R_1+R_2\right)}^2}{{\left(s+R_1+R_2\right)}^2}\right)\left(1-\frac{{\left(R_1-R_2\right)}^2}{{\left(s+R_1+R_2\right)}^2}\right)}.(9)$

2.2.1 Electrostatic Potential

The Laplace operator $\text{Δ}={\partial }_x^2+{\partial }_y^2$ transforms to $\text{Δ}=\left(1/h^2\right)\left({\partial }_{\eta }^2+{\partial }_u^2\right)$, with $h=h_{\eta }=h_u=a/\left(\text{cosh}\eta -\text{cos}u\right)$ being the scale factor of the BP coordinates (Moon and Spencer, 1961). Therefore, the Laplace equation looks the same in BP form, i.e., $\left({\partial }_{\eta }^2+{\partial }_u^2\right)\phi \left(\eta ,u\right)=0$. The total potential in this problem follows by superposition of the cylinder potential ${\phi }_{\text{c}}$ and the known potential of the uniform field, i.e., $\phi ={\phi }_{\text{c}}+{\phi }_0$.

The general solution for the potential due to the cylinders ${\phi }_{\text{c}}$ can therefore be written as

${\phi }_{\text{c}}\left(\eta ,u\right)=A_0+B_0\eta +{\displaystyle \sum }_{n=1}^{\infty }\left[\left(A_n{\text{e}}^{n\eta }+B_n{\text{e}}^{-n\eta }\right)\text{cos}\left(nu\right)+\left(C_n{\text{e}}^{n\eta }+D_n{\text{e}}^{-n\eta }\right)\text{sin}\left(nu\right)\right],(10)$

with $A_i,B_i,C_i,D_i$ as coefficients to be determined by the following boundary conditions.

The potential at the cylinder boundaries (and inside) is constant $\phi \left({\eta }_1,u\right)=\text{const}.=:V_1$ and $\varphi \left({\eta }_2,u\right)=\text{const}.=:V_2$. Here, ${\eta }_1<0$ and ${\eta }_2>0$. In addition, the potential of the cylinders has to vanish far away from the cylinders $\phi \left(\mathrm{0,0}\right)={\phi }_0$.

In order to obtain the coefficients, an expression for ${\phi }_0$ in terms of the eigenfunctions of the problem is needed. This can be achieved as indicated in (Morse and Feshbach, 1953) by combining the coordinates to complex variables ($z=x+\text{i}y$, $w=\eta +\text{i}u$) and exploiting the properties of analytic functions. Expanding in powers of $e^{-w\ast }$ for $\eta >0$ (lower case) and in powers of ${\text{e}}^{w\ast }$ for $\eta <0$ (upper case) leads to

${\phi }_0=-E_0\text{Re}\left(z\right)=\pm E_{0}a\left(1+2{\displaystyle \sum }_{n=1}^{\infty }{\text{e}}^{\pm n\eta }\text{cos}\left(nu\right)\right).(11)$

Ignoring the natural BC for now, the coefficients follow from exploiting the orthogonality of the sine and cosine functions. This leads to

$A_0=\frac{V_2{\eta }_1-V_1{\eta }_2}{\text{Δ}\eta }-\frac{E_{0}a\left({\eta }_1+{\eta }_2\right)}{\text{Δ}\eta },(12)$

$B_0=\frac{\text{Δ}V}{\text{Δ}\eta }+2\frac{E_{0}a}{\text{Δ}\eta },(13)$

$A_n=2E_{0}a\frac{\text{cosh}\left(n{\eta }_2\right)}{\text{sinh}\left(n\left({\eta }_1-{\eta }_2\right)\right)}{\text{e}}^{-n{\eta }_1},(14)$

$B_n=-2E_{0}a\frac{\text{cosh}\left(n{\eta }_1\right)}{\text{sinh}\left(n\left({\eta }_1-{\eta }_2\right)\right)}{\text{e}}^{n{\eta }_2},\text{and}(15)$

$C_n=D_n=0.(16)$

What remains is to determine the potentials V_1,2 the cylinders take on in the external field. This can be achieved by using the natural BC from above, ${\phi }_{\text{c}}\left(\mathrm{0,0}\right)=0$ and the fact that the cylinders are uncharged, Q₁ = Q₂ = 0. Combining these two conditions one finds

$V_1=-E_{0}a+2E_{0}a{\displaystyle \sum }_n\frac{\text{sinh}\left[n\left({\eta }_1+{\eta }_2\right)\right]}{\text{sinh}\left[n\left({\eta }_1-{\eta }_2\right)\right]},(17)$

$V_2=E_{0}a+2E_{0}a{\displaystyle \sum }_n\frac{\text{sinh}\left(n\left({\eta }_1+{\eta }_2\right)\right)}{\text{sinh}\left(n\left({\eta }_1-{\eta }_2\right)\right)}.(18)$

For ${\eta }_1=-{\eta }_2>0$, i.e., equally sized cylinders, the sum vanishes and $V_1=-V_2=-E_{0}a$.

Inserting these potentials into the above solution leads to the final result for the potential

$\phi \left(\eta ,u\right)=\pm E_{0}a+2E_{0}a\stackrel{\infty }{{\displaystyle \sum }_{n=1}}\left[\begin{array}{c}\left(\frac{\text{cosh}\left(n{\eta }_2\right){\text{e}}^{-n{\eta }_1}}{\text{sinh}\left(n\left({\eta }_1-{\eta }_2\right)\right)}{\text{e}}^{n\eta }-\frac{\text{cosh}\left(n{\eta }_1\right){\text{e}}^{n{\eta }_2}}{\text{sinh}\left(n\left({\eta }_1-{\eta }_2\right)\right)}{\text{e}}^{-n\eta }\pm {\text{e}}^{\pm n\eta }\right)\text{cos}\left(nu\right)\\ +\frac{\text{sinh}\left(n\left({\eta }_1+{\eta }_2\right)\right)}{\text{sinh}\left(n\left({\eta }_1-{\eta }_2\right)\right)}\end{array}\right],(19)$

where the + corresponds to $\eta <0$ and the $-$ to $\eta >0$.

For equally sized cylinders, ${\eta }_1\equiv -{\eta }_2>0$, φ simplifies to

$\phi \left(\eta ,u\right)=\pm E_{0}a+2E_{0}a{\displaystyle \sum }_{n=1}^{\infty }\left(2\frac{\text{cosh}\left(n{\eta }_1\right)}{\text{sinh}\left(n{\eta }_1\right)}{\text{e}}^{-n{\eta }_1}\text{sinh}\left(n\eta \right)\pm {\text{e}}^{\pm n\eta }\right)\text{cos}\left(nu\right).(20)$

A colormap of the cylinder potential and the total potential (cylinder potential plus external potential) is shown in Figure 4 for a field of E₀ = 100$E_0=100$ kV/m and cylinder radii of $R_1=75$ nm and $R_2=50$ nm.

FIGURE 4

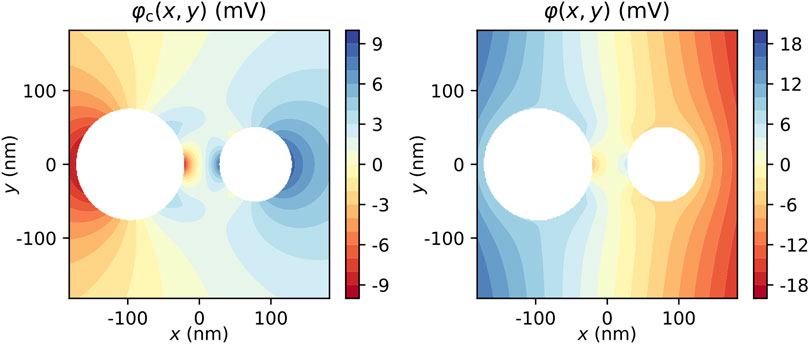
FIGURE 4. Cylinder potential (left) and total potential (right) for an external electric field of $E_0=100$ kV/m and cylinder radii $R_1=75$ nm and $R_2=50$ nm.

2.2.2 Electrostatic Force

The force follows from the integration of the surface charge density and electric field E = −grad φ over the surface S of the cylinder. The force component in a specific direction (arbitrary unit vector $\widehat{p}$) is given as

$F\cdot \widehat{p}=\frac{{\epsilon }_0}{2}{\displaystyle {\int }_S{\left(\frac{1}{h}{\partial }_{\eta }\phi \right)}^2\widehat{p}\cdot \widehat{n}dS}.(21)$

For the force in x-direction, $\widehat{p}=\widehat{x}$. The normal vector of the surface of cylinder two is $\widehat{\eta }$, which can be written in terms of Cartesian unit vectors as

$\widehat{\eta }=\frac{1}{\text{cosh}\eta -\text{cos}u}\left[\left(\text{cosh}\eta \text{cos}u-1\right)\widehat{x}-\text{sinh}\eta \text{sin}u\widehat{y}\right].(22)$

For $\eta ={\eta }_2$, the coefficients in the series of ${\partial }_{\eta }\phi$ simplify to

$g_n:=\frac{2n\text{cosh}\left(n{\eta }_1\right)}{\text{sinh}\left(n\left({\eta }_1-{\eta }_2\right)\right)},(23)$

$\Rightarrow {\partial }_{\eta }\phi =2E_{0}a\stackrel{\infty }{{\displaystyle \sum }_{n=1}}{g}_n\text{cos}\left(nu\right),(24)$

Exploiting the orthogonality of the cosines, the force in x-direction then results in

$\begin{array}{c}{F}_x=2\pi {\epsilon }_0{E}_0^2{a}^{2}L\stackrel{\infty }{{\displaystyle \sum }_{n=1}}{g}_n\left(\text{cosh}{\eta }_2{g}_{n+1}-g_n\right)\\ =2\pi {\epsilon }_0{E}_0^2{a}^{2}L{F}_{\text{c}},\end{array}(25)$

with L being the length of the cylinder and F_c an abbreviation for the sum. The orthogonality of the trigonometric functions also yields F_y = 0.

In order to study the dependence of the force on distance and radii, we assume equal radii $R_1=R_2=R=\mathrm{50,75,100}\text{nm}$ and distances varying from 0.5 to 500 nm. The field be $E_0=100$ kV/m and the length $L=1$ µm. The analytical force is again compared with the numerical one obtained with Comsol. Results are shown in Figure 5.

FIGURE 5

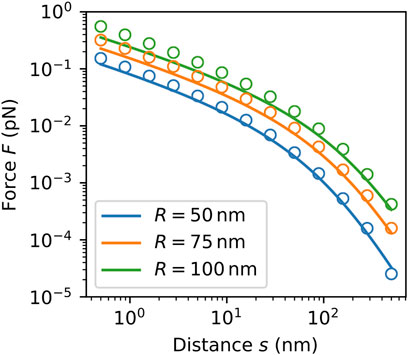
FIGURE 5. Analytical (solid lines) and numerical forces (circles) on a cylinder of length $L=1$ µm for different radii $R_1=R_2=R$ and distances for a field strength of E₀ = 100 kV/m.

The main reason for the discrepancies is that the analytical model does not consider the finite size effects and the top and bottom faces of the cylinders. The force decreases with the distance in the same way as for the two spheres. The transition between the corresponding two rates is again at roughly $s=R$. For small s, i.e., in the linear decrease regime $s<R$, the force scales with $R^2$, which stems mainly from the factor $a^2$.

Furthermore, it is interesting to investigate the force for the different cylinder radii $R_1\ne R_2$. In order to exclude other dependencies, the force is calculated for varying R_1,2 under the condition that $R_1+R_2=\text{const}\text{.}=100\text{nm}$. The corresponding results for $L=1$ µm, $E_0=100$ kV/m and $s=10$ nm are shown in Figure 6. It can be seen that having equal radii is the best case for maximising the force.

FIGURE 6

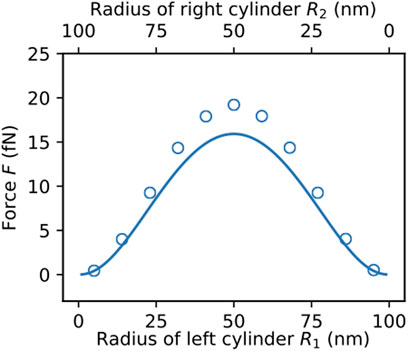
FIGURE 6. Analytical (solid lines) and numerical forces (circles) on a cylinder of length $L=1$ µm for varied radii under the condition $R_1+R_2=100\text{nm}$ for a field strength of $E_0=$ 100 kV/m and a distance $s=10$ nm.

3 Deflection as Figure of Merit

The actual deflection $\delta x$ at the tip of the nanopillar (circular cross-section, width $w=2R$, length l) depends not only on the force load but also on the effective stiffness $k=F/\delta x$ of the pillar. There are two different cases to be considered for the stiffness, since the pillar can be actuated either at the tip, (e.g., by a metal disc on top of an insulating pillar) or at the whole pillar (if the whole pillar is a conductor). Note that for now only the (quasi) static deflection is considered. Dynamical actuation at the pillar resonance yields deflections amplified by the quality factor.

For the force as a point load on the tip, the stiffness can be written as

$k_{\text{p}}=\frac{3YI}{l^3}=\frac{12\pi Y{w}^4}{l^3},(26)$

with the geometrical moment of intertia $I=\pi R^4/4=4\pi w^4$ and the Young’s modulus Y.

For nanopillars with w = 100 nm and l = 1 µm, the stiffness therefore is k_p(Si) N/m if it is made of Si ($Y\approx 150\text{GPa}$) and k_p(SiO₂) N/m if it is made of SiO2 ($Y\approx 70\text{GPa}$), which is quite large.

For the force as a uniformly distributed load, the stiffness

$k_{\text{d}}=\frac{8YI}{l^3}=\frac{32\pi Y{w}^4}{l^3},(27)$

is larger than for the point load. E.g., for a Si pillar with the same parameters as above, K_d = 1.5 kN/m. A combined expression for both cases can be written as $k_m={\alpha }_m\pi Y{w}^4/l^3$, with α_m = 12 or 32, for m = p or d, respectively.

An expression for the deflection can be obtained by inserting the force Eq. 25. It reads

$\delta x=\frac{F_{\text{x}}}{k_m}=\frac{2{\epsilon }_0{E}_0^2{F}_{\text{c}}}{{\alpha }_{m}Y}\frac{a^{2}L{l}^3}{w^4}.(28)$

Since in both cases, a force at the tip or a length-distributed force, the stiffness depends on R⁴ and the force is proportional to a², which for s < R roughly corresponds to R², the deflection is approximately proportional to $R^{-2}$. When considering the length, the deflection scales with l³ and with the length L of the conducting (part of the) cylinder. For using the whole pillar actuation L = l and the dependency is l⁴ in total. Furthermore, the force depends on the applied field strength as $E_0^2$. In summary, long, slim pillars and strong fields are beneficial for actuation. When comparing point and distributed load, it follows from the ratio $L/{\alpha }_m$ that the distributed load yields larger deflections.

For a width of w = 100 nm, a distance of d = 50 nm and an applied electric field of E₀ = 1$E_0=1$ MV/m and different lengths l of 1, 2 and 5 μm, the forces are in the order of Piconewtons. In the case of tip actuation with $L=50$ nm even smaller. This means quasistatic deflections in the order of smaller than one fm for the shortest pillars and in the order of 0.1 pm for the 5 µm ones. Considering a quality factor of the order of 10,000 (Molina et al., 2020), this results in vibrational amplitudes of the order of 1 nm.

3.1 Limitations of the Model

It is important to notice that the presented modeling approach by means of two infinitely extended cylinders is only valid as long as the neutral axes of the two considered pillars remain nearly straight and parallel to each other. This involves two subconditions: First, the maximum deflection of the individual pillars imposed by electrostatic forces must be small so that the deviations of the real electrostatic induction and the associated charge distribution remain negligible in comparison to the our simplified model. Secondly, there must be no pull-in effect between the two adjacent pillars, i.e., the restoring elastomechanical force of the individual cantilever-like pillars must always be larger than the attractive electrostatic force between the pillars (Wen-Hui and Ya-Pu, 2003; Wang et al., 2004; Zhang and pu Zhao, 2006).

If both conditions are met, then the analytical model offers the great advantage that its evaluation with common mathematical toolboxes such as Wolfram Mathematica or direct implementations in, e.g., Python provides a good estimate of the occurring electrostatic excess field strengths, the electrostatic forces, and the fundamental system behavior within fractions of a second. In contrast, a solely computational analysis with COMSOL takes several minutes yielding comparable results. In the case of a parametric sweep as, e.g., depicted in Figure 5, this may even take several hours our days.

However, as soon as the modeling prerequisites are substantially violated, our strongly, simplified two-dimensional model loses its validity and must be replaced by a three-dimensional model of dielectric cantilevers exposed to a homogenous external electric field. The rigorous mathematical description of the electromechanical interaction between the two elastic pillars and the external electric field would be usefully implemented via the energy-momentum tensor of the dielectric material composed of two components (Penfield and Haus, 1967). The first component describes the elastomechanical properties of the cantilever-like pillar while the second component incorporates the electric field interaction. Mechanical and electrical components governing the electro-elastomechanical interaction are related to each other via a suitably selected material law. From this model, the electric field distribution in the field space would have to be calculated. As soon as this is known, the resulting force of electric origin on the pillar can be derived by simple integration over a closed surface, which encloses the pillar and runs completely in free space (Penfield and Haus, 1967).

As one can see, the exact theoretical description of this problem is quite complex and very likely does not have a closed-form analytical solution. Fortunately, the two conditions mentioned above were generally fulfilled in our considerations, so that our simplified two-dimensional model can be applied for the pillars discussed above. This can be seen in the example above, which estimated dynamical deflections up to 1 nm for a pillar diameter of 100 nm and a distance of 50 nm. Nevertheless, care must be taken for larger relative deflections.

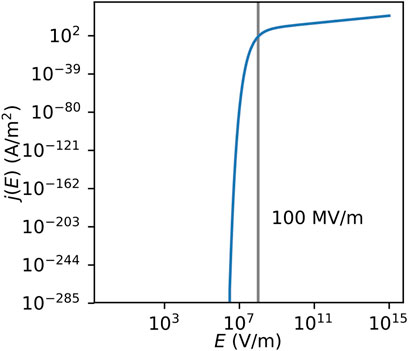
3.2 Maximum Possible Field Strength

One remaining question is how far the electric field strength can be increased, if the two aforementioned conditions of small deflections and large restoring force stay fulfilled. The limit faced here seems to be the maximum total field ($E=E_0+E_{\text{cylinders}}$) strength at which field emission of conduction electrons takes place. The following crude estimation of this limit is based on the Fowler-Nordheim description for the current density through the tunnel barrier of the material (Fowler and Nordheim, 1928). The current density can be written as

$j\left(E\right)=\frac{e^3}{8\pi h{W}_{\text{e}}}\frac{m^{\text{*}}}{m}{E}^2\text{exp}\left(-\frac{4\sqrt{2m{W}_{\text{e}}^3}}{6\pi heE}\right),(29)$

with e the electron charge, h the Planck constant, W_e the work function, m* the effective mass in the metal and m the electron mass in vacuum.

The mass ratio depends on many circumstances and is not isotropic. For Au, a value can be extracted from tables such as given in (Ashcroft and Mermin, 1976), where $m^{\text{*}}/m=1.1$. The work function also varies, for Au it is approximately W_e ≈ 5 eV = 8 · 10⁻¹⁹ J. The current density rises extremely rapidly with increasing E (Figure 7). The rate slows down at roughly 100 MV/m still being very steep. This marks the emergence of field emission.

FIGURE 7

FIGURE 7. Field emission current density vs. applied electric field strength.

The total electric field between the nanopillars is larger than E₀. The enhancement factor $E/E_0$ depends on the radii of and the distance between the pillars. Therefore, for a given applied field $E_0$, $j\left(E\right)$ depends indirectly on the radii and distance. For the dimensions considered above, a mean factor $E/E_0\approx 10$ should be considered. This means that, in theory, the applied field $E_0$ can be as high as 10 MV/m increasing the above calculated forces and deflections by a factor of 100. This is, however, a crude estimation. The actual limit has to be determined experimentally.

A possibility to provide the electric field would be to implement coplanar electrodes on the substrate. The nanopillars would then be located between these electrodes. Depending on the size of the area reserved for the nanopillars, a distance d_el between these electrodes has to be chosen. This distance, in turn, determines the voltage $V_{\text{el}}$ necessary to provide a suitable electric field. As a rough estimate, the applied field would be $E_0\approx V_{\text{el}}/d_{\text{el}}$. Thus, for a nanopillar region 10 µm wide, a voltage of around 10 V would be necessary to provide a field of 1 MV/m.

4 Conclusion

In this paper, analytical and numerical calculations for the electrostatics of two cylinders in an electric field have been used to study the possible electrostatic actuation of nanopillar dimers. While the associated electrostatic forces are very tiny, the pillars can be driven quasistatically to a deflection of up to $\sim 100\text{fm}$ for 1 µm long and 100 nm wide pillars separated by 50 nm in an applied field of 10 MV/m. If the pillars are 5 µm long, the deflection lies in the order of 10 pm. Considering the displacement amplification by the quality factor, with typical values up 10,000 (Molina et al., 2020), vibrational amplitudes in the nanometer regime can be expected.

Detection or exploiting the effects of these small deflections remains a challenging task. The limit of detection of optical methods, which are the most accurate at the moment, are already capable of detecting, e.g., nanowire motion. Moreover, they are becoming ever more effective with new promising techniques emerging such as optical plasmonic transduction.

It should also be noted that the treatment in this paper was strictly electrostatic. With rising frequencies, there can be expected an increasing magnetic contribution, which was neglected in this manuscript. A comparison of the forces with the ones obtained in an electrodynamical approach and with optical forces should be performed in a future work.

Since there are several quantities having an influence on the electrostatic force and the stiffness of the pillars, it is possible to tweak the system in order to obtain even larger deflections, both statically and dynamically. In addition to geometrical dimensions these are, e.g., the materials involved, the arrangement of (arrays of) dimers and even using other systems than pillars. The approach may also be applied to pairs of nanostrings or nanowires. Especially due to their length, they can be driven presumably more effectively than the pillar dimers.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

AK conceived the presented idea. AK and RB developed the theory and performed the computations. All authors discussed the results and contributed to the final manuscript.

Funding

This work is supported by the European Research Council under the European Union Horizon 2020 research and innovation program (Grant Agreement-716087-PLASMECS) and the Austrian Research Promotion Agency (FFG) under grant “H-iSlice” (number 869181). The Department of Integrated Sensor Systems gratefully acknowledges partial financial support by the European Regional Development Fund (ERDF) and the province of Lower Austria.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Ashcroft, N., and Mermin, D. (1976). Solid state physics. New York, NY: Holt Rinehart & Winston.

Google Scholar

Bagci, T., Simonsen, A., Schmid, S., Villanueva, L. G., Zeuthen, E., Appel, J., et al. (2014). Optical detection of radio waves through a nanomechanical transducer. Nature 507, 81–85. doi:10.1038/nature13029

PubMed Abstract | CrossRef Full Text | Google Scholar

Chaste, J., Eichler, A., Moser, J., Ceballos, G., Rurali, R., and Bachtold, A. (2012). A nanomechanical mass sensor with yoctogram resolution. Nat. Nanotechnol. 7, 301–304. doi:10.1038/nnano.2012.42

PubMed Abstract | CrossRef Full Text | Google Scholar

Chien, M. H., Steurer, J., Sadeghi, P., Cazier, N., and Schmid, S. (2020). Nanoelectromechanical position-sensitive detector with picometer resolution. ACS Photonics. 7, 2197–2203. doi:10.1021/acsphotonics.0c00701

PubMed Abstract | CrossRef Full Text | Google Scholar

Cleland, A. N., and Roukes, M. L. (1996). Fabrication of high frequency nanometer scale mechanical resonators from bulk Si crystals. Appl. Phys. Lett. 69, 2653. doi:10.1063/1.117548

CrossRef Full Text | Google Scholar

Davis, M. H. (1964). Two charged spherical conductors in a uniform electric field: forces and field strength. Q. J. Mech. Appl. Math. 17, 499–511. doi:10.1093/qjmam/17.4.499

CrossRef Full Text | Google Scholar

Dohn, S., Schmid, S., Amiot, F., and Boisen, A. (2010). Position and mass determination of multiple particles using cantilever based mass sensors. Appl. Phys. Lett. 97, 044103. doi:10.1063/1.3473761

CrossRef Full Text | Google Scholar

Emets, Y. P., and Onofrichuk, Y. P. (1996). Interaction forces of dielectric cylinders in electric fields. IEEE Trans. Dielectr. Electr. Insul. 3, 87–98. doi:10.1109/94.485519

CrossRef Full Text | Google Scholar

Faust, T., Krenn, P., Manus, S., Kotthaus, J. P., and Weig, E. M. (2012). Microwave cavity-enhanced transduction for plug and play nanomechanics at room temperature. Nat. Commun. 3, 728–736. doi:10.1038/ncomms1723

PubMed Abstract | CrossRef Full Text | Google Scholar

Fowler, R. H., and Nordheim, L. (1928). Electron emission in intense electric fields. Proc. R. Soc. Lond. - Ser. A Contain. Pap. a Math. Phys. Character 119, 173–181. doi:10.1142/9789814503464˙0087

CrossRef Full Text | Google Scholar

Hanay, M. S., Kelber, S., Naik, A. K., Chi, D., Hentz, S., Bullard, E. C., et al. (2012). Single-protein nanomechanical mass spectrometry in real time. Nat. Nanotechnol. 7, 602–608. doi:10.1038/nnano.2012.119

PubMed Abstract | CrossRef Full Text | Google Scholar

Jenss, H. (1932). Das potential isolierter sonden im homogenen felde. Archiv f. Elektrotechnik 26, 557–561. doi:10.1007/bf01660775

CrossRef Full Text | Google Scholar

Kabashin, A., Evans, P., Pastkovsky, S., Hendren, W., Wurtz, G., Atkinson, R., et al. (2009). Plasmonic nanorod metamaterials for biosensing. Nat. Mater. 8, 867–871. doi:10.1038/nmat2546

PubMed Abstract | CrossRef Full Text | Google Scholar

Kainz, A., Keplinger, F., Hortschitz, W., Kahr, M., Steiner, H., Stifter, M., et al. (2019). Noninvasive 3d field mapping of complex static electric fields. Phys. Rev. Lett. 122, 244801. doi:10.1103/PhysRevLett.122.244801

PubMed Abstract | CrossRef Full Text | Google Scholar

Kainz, A., Steiner, H., Schalko, J., Jachimowicz, A., Kohl, F., Stifter, M., et al. (2018). Distortion-free measurement of electric field strength with a mems sensor. Nat Electron 1, 68–73. doi:10.1038/s41928-017-0009-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, M., Tang, H. X., and Roukes, M. L. (2007). Ultra-sensitive nems-based cantilevers for sensing, scanned probe and very high-frequency applications. Nat. Nanotechnol. 2, 114–120. doi:10.1038/nnano.2006.208

PubMed Abstract | CrossRef Full Text | Google Scholar

Molina, J., Ramos, D., Gil-Santos, E., Escobar, J. E., Ruz, J. J., Tamayo, J., et al. (2020). Optical transduction for vertical nanowire resonators. Nano Lett. 20, 2359–2369. doi:10.1021/acs.nanolett.9b04909

PubMed Abstract | CrossRef Full Text | Google Scholar

Moon, P., and Spencer, J. (1961). Field-theory handbook. New York, NY: Springer-Verlag.

Google Scholar

Morse, P., and Feshbach, H. (1953). Methods of theoretical physics. New York, NY: McGraw-Hill.

Google Scholar

Naik, A. K., Hanay, M. S., Hiebert, W. K., Feng, X. L., and Roukes, M. L. (2009). Towards single-molecule nanomechanical mass spectrometry. Nat. Nanotechnol. 4, 445–450. doi:10.1038/nnano.2009.152

PubMed Abstract | CrossRef Full Text | Google Scholar

Penfield, P., and Haus, H. A. (1967). Electrodynamics of moving media. Cambridge, England: MIT Press. doi:10.1063/1.3034557

CrossRef Full Text

Sadeghi, P., Wu, K., Rindzevicius, T., Boisen, A., and Schmid, S. (2017). Fabrication and characterization of au dimer antennas on glass pillars with enhanced plasmonic response. Nanophotonics 7, 497–505. doi:10.1515/nanoph-2017-0011

CrossRef Full Text | Google Scholar

Sage, E., Brenac, A., Alava, T., Morel, R., Dupré, C., Hanay, M. S., et al. (2015). Neutral particle mass spectrometry with nanomechanical systems. Nat. Commun. 6, 6482–6485. doi:10.1038/ncomms7482

PubMed Abstract | CrossRef Full Text | Google Scholar

Schmid, S., Dohn, S., and Boisen, A. (2010). Real-time particle mass spectrometry based on resonant micro strings. Sensors 10, 8092–8100. doi:10.3390/s100908092

PubMed Abstract | CrossRef Full Text | Google Scholar

Schmid, S., Kurek, M., Adolphsen, J. Q., and Boisen, A. (2013). Real-time single airborne nanoparticle detection with nanomechanical resonant filter-fiber. Sci. Rep. 3, 1288. doi:10.1038/srep01288

PubMed Abstract | CrossRef Full Text | Google Scholar

Schmid, S., Bagci, T., Zeuthen, E., Taylor, J. M., Herring, P. K., Cassidy, M. C., et al. (2014). Single-layer graphene on silicon nitride micromembrane resonators. J. Appl. Phys. 115, 054513. doi:10.1063/1.4862296

CrossRef Full Text | Google Scholar

Schmid, S., Villanueva, L. G., and Roukes, M. L. (2016). Fundamentals of nanomechanical resonators. 1st Edn. New York, NY: Springer International Publishing.

CrossRef Full Text

Schmid, S., Wendlandt, M., Junker, D., and Hierold, C. (2006). Nonconductive polymer microresonators actuated by the kelvin polarization force. Appl. Phys. Lett. 89, 163506. doi:10.1063/1.2362590

CrossRef Full Text | Google Scholar

Thijssen, R., Kippenberg, T. J., Polman, A., and Verhagen, E. (2015). Plasmomechanical resonators based on dimer nanoantennas. Nano Lett. 15, 3971–3976. doi:10.1021/acs.nanolett.5b00858

PubMed Abstract | CrossRef Full Text | Google Scholar

Unterreithmeier, Q. P., Weig, E. M., and Kotthaus, J. P. (2009). Universal transduction scheme for nanomechanical systems based on dielectric forces. Nature 458, 1001–1004. doi:10.1038/nature07932

PubMed Abstract | CrossRef Full Text | Google Scholar

Villanueva, L. G., Karabalin, R. B., Matheny, M. H., Kenig, E., Cross, M. C., and Roukes, M. L. (2011). A nanoscale parametric feedback oscillator. Nano Lett. 11, 5054–5059. doi:10.1021/nl2031162

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, G.-W., Zhang, Y., Zhao, Y.-P., and Yang, G.-T. (2004). Pull-in instability study of carbon nanotube tweezers under the influence of van der waals forces. J. Micromech. Microeng. 14, 1119–1125. doi:10.1088/0960-1317/14/8/001

CrossRef Full Text | Google Scholar

Wen-Hui, L., and Ya-Pu, Z. (2003). Dynamic behaviour of nanoscale electrostatic actuators. Chin. Phys. Lett. 20, 2070–2073. doi:10.1088/0256-307x/20/11/049

CrossRef Full Text | Google Scholar

Yu, P. L., Purdy, T., and Regal, C. A. (2012). Control of material damping in high-Q membrane microresonators. Phys. Rev. Lett. 108, 083603, doi:10.1103/PhysRevLett.108.083603

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Y., and pu Zhao, Y.-p. (2006). Numerical and analytical study on the pull-in instability of micro-structure under electrostatic loading. Sensor Actuator Phys. 127, 366–380. doi:10.1016/j.sna.2005.12.045

CrossRef Full Text | Google Scholar