Theoretical and Experimental Study of the Vibration Dynamics of a 3D-Printed Sandwich Beam With an Hourglass Lattice Truss Core

3D printing (also known as additive manufacturing) has been developed for more than 30 years. The applications of 3D printing have been increasingly extended to a variety of engineering fields in recent years. The sandwich material with a high strength and overall low density is a kind of artificial material that has been extensively used in various industrial and daily life applications. This paper presents a comprehensive vibration analysis and passive control technique for a cantilevered sandwich beam with an hourglass lattice truss core fabricated with 3D printing technology. The governing equation of the beam is established by using a homogenized model and the Hamilton's principle, from which the natural frequencies are determined. The theoretical model is verified by the results from the existing literature and the finite element analysis. The frequency response of the sandwich beam measured experimentally further validates the proposed model. Subsequently, a non-linear energy sink (NES) is proposed for being employed to passively suppress the vibration of the sandwich beam. A parametric study based on the theoretical model confirms the viability of using NES to effectively control the vibration of the sandwich beam. This work presents a good demonstration of using 3D printing technology for fabricating sandwich beams with a complicated lattice core. More importantly, some guidelines regarding the dynamic analysis of sandwich beams are provided. In addition, the analytical method presented in this work provides a potential means to theoretically explore the advantages of using sandwich beams for energy harvesting in the future.

Introduction

Sandwich composite structures normally consisting of thin face sheets and a soft core have been extensively employed in industrial and daily applications, including civil, automotive engineering, and aerospace, etc., because of their light weight, high bending stiffness, outstanding sound, and thermal insulation properties (Evans et al., 2001; Kim et al., 2004; Ruzzene, 2004; Cote et al., 2007; Fan et al., 2008, 2010; Queheillalt et al., 2008; Roper, 2011). Various types of sandwich core have been proposed, such as corrugated (Buannic et al., 2003), honeycomb (Sypeck and Wadley, 2002), tetrahedral (Wadley et al., 2003), pyramidal (Queheillalt et al., 2008), and kagome cores (Wang et al., 2003). The sandwich structure is generally constructed by an axially symmetrical distribution of rods. Two thin but stiff face sheets are attached to the lightweight but thick core. It is often assumed that the thin face sheets and the core provide the most contribution to the bending stiffness and transverse shear stiffness, respectively (Lou et al., 2012).

Research on mechanical behaviors of composite structures have been vastly reported in the existing literature. Deshpande (Deshpande and Fleck, 2001) measured the collapse response of several sandwich beams with different lattice truss cores in 3-point bending experiments and derived the equivalent shear modulus of pyramidal and tetrahedral truss cores. Wang et al. (2003) studied the performance characteristics of a Kagome sandwich panel. They found that the Kagome sandwich panel exhibited a greater resistance to plastic buckling than the tetrahedron sandwich panel with the same equivalent core density. Based on the asymptotic expansion method, Buannic et al. (2003) used the periodic homogenization theory to determine the effective properties of the sandwich plate with a corrugated core, making it possible to model the alveolar plates as equivalent homogeneous plates for improving the computation efficiency. Feng et al. (2016, 2017) presented the sandwich structure with an hourglass lattice truss core whose static properties have been experimentally studied and proved to outperform those with traditional lattice cores, such as the hourglass truss structure with a relative density ranging from about 1.1–2.7% has 40–60% higher shear strength and 26–47% higher out-of-plane compressive strength than those of the pyramidal truss structure with a similar relative density, as well as a better bending strength. Therefore, it is meaningful to study the dynamics of hourglass lattice core sandwich structures.

The dynamic analysis of the sandwich structures has attracted numerous research interests in recent years. By using the Hamilton's principle, Lou et al. (2013) studied the dynamic behavior of the lattice core sandwich beam and the influences of the geometric and material parameters. Zhao et al. (2018) studied the dynamics of a two-span composite structure with a lattice core on the basis of the assumed mode method in conjunction with interpolation functions. An effective methodology was employed by Guo et al. (2017) and Yang et al. (2019) to investigate the vibration of composite structures. Because structural vibration is prone to incur noise pollution, structural damage, and even catastrophic accident, it makes great sense to explore the vibration control methods and strategies. Vibration control methods can be classified into two categories, namely, active and passive control. Li and Lyu (2014) and Li et al. (2018) realized the active vibration suppression of the lattice core sandwich structure by using the MFC actuators and PVDF sensors. In order to passively control the vibration of continuous systems, some researchers conducted the application of non-linear energy sink (NES) for achieving the vibration attenuation of sandwich structures (Zhang et al., 2016; Chen et al., 2017, 2018; Guo et al., 2020).

Although numerous research have been conducted on the dynamic analysis of sandwich structures, very few of them have been reported on the dynamics of the hourglass lattice core sandwich structures (Li et al., 2019), much less on the related experimental study. One of the potential reasons is the difficulty in fabricating the sandwich composite material with a complicated lattice truss core. The technology of 3D printing has been developed for more than 30 years with a wide application in various engineering fields (Nannan Guo, 2013; Wohlers and Gornet, 2014; Decuir et al., 2016; Deng and Suresh, 2016; Butt et al., 2018; Jiang et al., 2019). Differing from conventional manufacturing technologies, which cut materials out from solid materials, the 3D printing technique constructs objects by sequentially depositing materials to make them into pre-designed shapes. The underlying mechanism of the 3D printing technology dooms its advantages over the conventional manufacturing technologies in fabricating prototypes with complex shapes. Therefore, the 3D printing technology is very suitable for fabricating sandwich structures with complicated cores. In order to evaluate the rationality of employing the additive manufacturing of sandwich plates in the structure application, Azzouz et al. (2019) investigated the mechanical characteristics of the 3D printed lattice core. Elmadih et al. (2019) firstly used the additively manufactured (AM) lattice structures for mechanical band structures analysis, which provides a great inspiration to introduce the 3D printing technology into the field of dynamics. To the authors' best knowledge, research on the dynamics and vibrations of 3D-printed sandwich structures is still rare. Therefore, it makes great sense in this paper to study the fabrication and vibration test of the sandwich beam with an hourglass lattice truss core. Sandwich beams have the advantage of being lightweight. Given the same bending stiffness, a sandwich beam is thicker than an ordinary beam made of uniform materials. By attaching a piezoelectric transducer (IEEE Standard on piezoelectricity, 1996) on the surface of the sandwich beam, the distance between the piezoelectric transducer and the neutral plane is expected to be larger than that in the conventional case using an ordinary beam (Erturk and Inman, 2008). According to the above deduction, employing a sandwich beam in the design of a vibration energy harvester could potentially lead to the improvement of the power output. The study presented in this work also aims to lay the foundation for the research of a sandwich beam based vibration energy harvester (Liang and Liao, 2012; Hu et al., 2019) in the future.

This paper presents a comprehensive study of the dynamics of the hourglass lattice core sandwich beam. The governing equation is derived and solved by using the Hamilton's principle and assumed mode method. Theoretical results are verified by the existing literature and the finite element simulation. The 3D printing technology is employed for fabricating the physical prototype of the sandwich beam. An experiment is conducted to test the vibration response of the fabricated prototype. The experimental result agrees well with that of the theoretical model. Finally, the non-linear energy sink (NES) technology is proposed for suppressing the vibration of the sandwich structure. The feasibility of this concept is theoretically proved. The work of this paper provides a good example for the application of the 3D printing technology in the experimental study of sandwich composite structures.

Theoretical Model

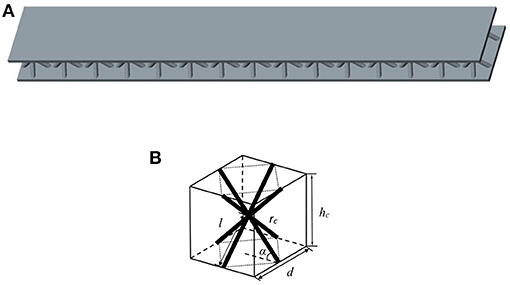
Figures 1A,B show the diagrams of the sandwich beam and the hourglass truss structure. The beam is symmetrical with respect to the neutral plane of the core layer. The thicknesses of the core layer and the sheets are h_c and h_f, respectively. The unit cell length is d, length and width of the entire sandwich beam are L and B, respectively. The inclination angle of the truss structure is denoted by α. All the struts have the same radius of circular cross-section r_c and length l. The face sheets and struts have the same material, and their mass density is ρ_f. A homogenized model for the core layer is utilized (Guo et al., 2020), the equivalent density and relative density of the core layer is calculated by ${\rho }_c=\pi r_c^2{\rho }_f/(l^{2}sin\alpha {cos}^2\alpha )$ and $\bar{\rho }={{\rho }_c/\rho }_f$, and the equivalent shear modulus can be calculated as $G_{xz}=E_s\bar{\rho }{sin}^{2}2\alpha /8$ (Deshpande and Fleck, 2001), where E_s denotes the Young's modulus.

FIGURE 1

Figure 1. Diagram of the (A) sandwich beam; and (B) hourglass truss structure.

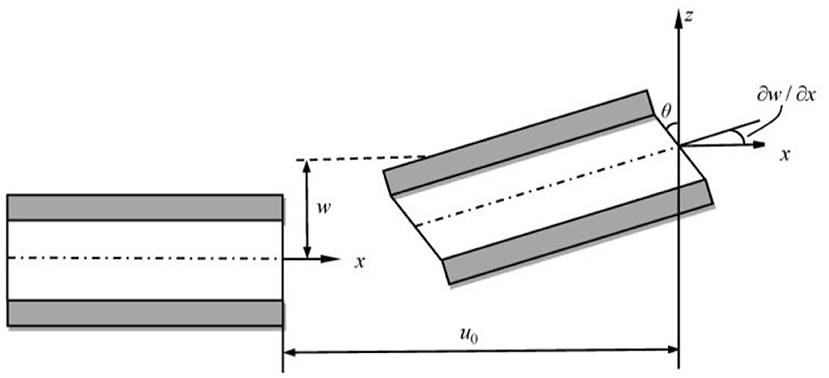
The deformation of an infinitesimal element with length dx and width dy is sketched in Figure 2. The sheets rotate by an angle ∂w/∂x, and the core layer rotates by an angle θ around the y axis.

FIGURE 2

Figure 2. Deformation diagram of the micro-unit.

Displacement fields for the sandwich beam in the x-direction and z-direction are given as

$\begin{array}{l}{u}_t=-\frac{h_c}{2}\theta -(z-\frac{h_c}{2})\frac{\partial w}{\partial x},\\ u_c=-z\theta ,\\ u_b=\frac{h_c}{2}\theta -(z+\frac{h_c}{2})\frac{\partial w}{\partial x}& (1)\end{array}$

where w is the displacement of the differential element of the sandwich beam and subscripts or superscripts b, t, and c in this work represent the bottom, top sheets, and the core of the sandwich beam, respectively. Strains of the sheets are expressed as

$\begin{array}{ll}{\epsilon }_x^i=\frac{\partial u_i}{\partial x}(i=t,b),& (2)\end{array}$

and the shear strain of the core layer as

$\begin{array}{ll}{\gamma }_{xz}^c=\frac{\partial u_c}{\partial z}+\frac{\partial w}{\partial x}& (3)\end{array}$

in which ε and γ denote the normal and shear strains, respectively. By using Hooke's law, stresses for the sandwich beam are then written as

$\begin{array}{lll}{\sigma }_x^i& =E_s{\epsilon }_x^i(i=t,b),& (4)\end{array}$

$\begin{array}{lll}{\tau }_{xz}^c& =G_{xz}{\gamma }_{xz}^c& (5)\end{array}$

in which σ and τ represent the normal and shear stresses, respectively. Hamilton's principle is used to obtain the governing equation.

$\begin{array}{ll}{\displaystyle \underset{t_0}{\overset{t_1}{\int }}}\delta (T-U)dt+{\displaystyle \underset{t_0}{\overset{t_1}{\int }}}\delta Wdt=0,& (6)\end{array}$

where U and T represent the strain energy and kinetic energy of the sandwich beam, respectively. δ is variation operator. U and T can be expressed as

$\begin{array}{lll}U& =\frac{1}{2}{\displaystyle \underset{V_t}{\int }}{\sigma }_x^t{\epsilon }_x^{t}d{V}_t+\frac{1}{2}{\displaystyle \underset{V_c}{\int }}{\tau }_{xz}^c{\gamma }_{xz}^{c}d{V}_c+\frac{1}{2}{\displaystyle \underset{V_b}{\int }}{\sigma }_x^b{\epsilon }_x^{b}d{V}_b& (7)\end{array}$

$\begin{array}{l}T=\frac{1}{2}{\displaystyle \underset{v_t}{\int }{\rho }_f}({\dot{u}}_t^2+{\dot{w}}^2)d{V}_t+\frac{1}{2}{\displaystyle \underset{v_c}{\int }{\rho }_c}({\dot{u}}_c^2\\ +{\dot{w}}^2)d{V}_c+\frac{1}{2}{\displaystyle \underset{v_b}{\int }{\rho }_f}({\dot{u}}_b^2+{\dot{w}}^2)d{V}_b& (8)\end{array}$

where V_t, V_b, and V_c are the volumes of the top face sheet, bottom face sheet, and the core layer. The virtual work of applied forces F can be given as

$\begin{array}{ll}\delta W=F\delta w{|}_{x=x_0}=F_{0}sin(\omega t)\delta w{|}_{x=x_0}& (9)\end{array}$

which is applied at x₀ of the beam, ω and F₀ denote its frequency and amplitude, respectively. w and θ are approximated by N modes and modal coordinates as

$\begin{array}{ll}w={\displaystyle \sum _{m=1}^N}{\varsigma }_m{(x)}^T{p}_m(t)={\varsigma }^T(x)\text{p}(t),& (10)\end{array}$

$\begin{array}{ll}\theta ={\displaystyle \sum _{m=1}^N}{\xi }_m{(x)}^T{q}_m(t)={\xi }^T(x)\text{q}(t),& (11)\end{array}$

where $\varsigma (x)={\left[{\varsigma }_1,...,{\varsigma }_N\right]}^T$ and $\xi (x)={\left[{\xi }_1,...,{\xi }_N\right]}^T$ represent the assumed modes satisfying the boundary condition, and $\text{p}(t)={\left[p_1,...,p_N\right]}^T$ and $\text{q}(t)={\left[q_1,...,q_N\right]}^T$ are modal coordinates. For example, the nth order mode for the cantilevered sandwich beams is

$\begin{array}{l}{\varsigma }_n(x)=\cosh ({\kappa }_n\frac{x}{L})-\cos ({\kappa }_n\frac{x}{L})-\frac{\sinh {\kappa }_n-\sin {\kappa }_n}{\cosh {\kappa }_n+\cos {\kappa }_n}\sinh ({\kappa }_n\frac{x}{L})\\ +\sin ({\kappa }_n\frac{x}{L})\\ {\xi }_n(x)=\sinh ({\kappa }_n\frac{x}{L})+\sin ({\kappa }_n\frac{x}{L})-\frac{\sinh {\kappa }_n-\sin {\kappa }_n}{\cosh {\kappa }_n+\cos {\kappa }_n}\cosh ({\kappa }_n\frac{x}{L})\\ +\cos ({\kappa }_n\frac{x}{L}),& (12)\end{array}$

where κ_n are respectively 1.875, 4.694, and 7.855 for the first three modes and (2n − 1)π/2 for the higher modes. Substituting Equations (1)–(5), (7), and (8) into (6) and performing the variation, the governing equations can be derived as

$\begin{array}{ll}\text{M}\ddot{\text{X}}(t)+\text{K}\text{X}(t)=F{\text{Q}}_0,& (13)\end{array}$

where the over dot denotes the time derivative. X(t) = [p(t)^T, q(t)^T]^T denotes the modal coordinates of the beam. M, K, and FQ₀ represent structural mass, stiffness, and modal force matrices, respectively. They are expressed as follows:

$\begin{array}{ll}\begin{array}{ll}M\hfill & =\left[\begin{array}{ll}{M}_{11}\hfill & M_{12}\hfill \\ M_{12}\hfill & M_{22}\hfill \end{array}\right],\text{K}=\left[\begin{array}{ll}{K}_{11}\hfill & K_{12}\hfill \\ K_{12}\hfill & K_{22}\hfill \end{array}\right],Q_0={[{\varsigma }^T(x_0),0]}^T\hfill \\ M_{11}\hfill & =\frac{2}{3}B{\rho }_f{h}_f^3{\int }_0^L\frac{\partial \varsigma }{\partial x}\frac{\partial {\varsigma }^T}{\partial x}dx+(2B{\rho }_f{h}_f+B{\rho }_c{h}_2]{\int }_0^L\varsigma {\varsigma }^{T}dx,\hfill \\ M_{12}\hfill & =\frac{1}{2}B{\rho }_f{h}_f^2{h}_c{\int }_0^L\frac{\partial \varsigma }{\partial x}{\xi }^{T}dx,\hfill \\ M_{22}\hfill & =(\frac{1}{2}B{\rho }_f{h}_f{h}_c^2+\frac{1}{12}B{\rho }_c{h}_c^3){\int }_0^L\xi {\xi }^{T}dx,\hfill \\ K_{11}\hfill & =\frac{2}{3}{E}_{s}B{h}_f^3{\int }_0^L\frac{{\partial }^2\varsigma }{\partial x^2}\frac{{\partial }^2{\varsigma }^T}{\partial x^2}dx+G_{xz}B{h}_c{\int }_0^L\frac{\partial \varsigma }{\partial x}\frac{\partial {\varsigma }^T}{\partial x}dx,\hfill \\ K_{12}\hfill & =\frac{1}{2}{E}_{s}B{h}_f^2{h}_c{\int }_0^L\frac{{\partial }^2\varsigma }{\partial x^2}\frac{\partial {\xi }^T}{\partial x}dx-G_{xz}B{h}_c{\int }_0^L\frac{\partial \varsigma }{\partial x}{\xi }^{T}dx,\hfill \\ K_{22}\hfill & =\frac{1}{2}{E}_{s}B{h}_f{h}_c^2{\int }_0^L\frac{\partial \xi }{\partial x}\frac{\partial {\xi }^T}{\partial x}dx+G_{xz}B{h}_c{\int }_0^L\xi {\xi }^{T}dx,\hfill \end{array}& (14)\end{array}$

Natural frequencies ω_n and modes of the sandwich beam are obtained through solving the corresponding eigenvalue of Equation (13), in which F = 0. Based on the results from the existing literature (Mead, 1966; Ahmed, 1972; Hwu et al., 2004), an example calculation is performed to verify the present method. The parameters used in the calculation are as follows (Mead, 1966; Ahmed, 1972; Hwu et al., 2004): h_f = 0.4572 mm, h_c = 12.7 mm, L = 0.7112 m, E_s = 68.9 Gpa, ρ_f = 2,680 kg/m³, G_xz = 0.08274 Gpa, ρ_c = 32.8 kg/m³. Results from the present method and the existing literature are listed in Table 1 for comparison, showing good agreement.

TABLE 1

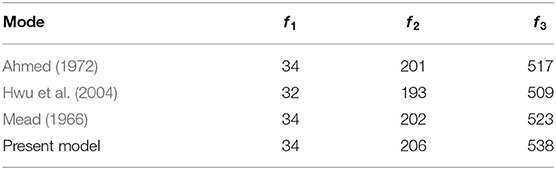
Table 1. Comparison of natural frequencies (Hz) of the cantilevered sandwich beam obtained from various theoretical models.

Finite Element Analysis

To validate the theoretical model of the sandwich beam, a finite element analysis is conducted. The material properties and parameters of the 3D-printed sandwich beam with an hourglass lattice truss core shown in the following experimental test have been listed in Table 2. The finite element model (Figure 3) is built using the commercial package ANSYS. The lattice truss core is modeled with the 1-dimensional 3-Node BEAM189 element. The face sheets are modeled with the 2-dimensional 4-Node SHELL181 element. It is noted that the coincident nodes of the shell and beam elements should be merged after creating the corresponding mesh model.

TABLE 2

Table 2. Material properties and parameters of the cantilevered sandwich beam.

FIGURE 3

Figure 3. Finite element model and mesh of the cantilevered sandwich beam.

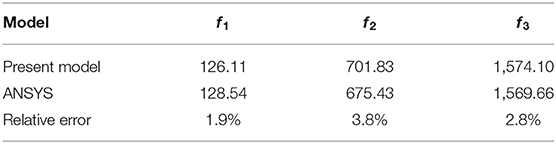
Table 3 lists the first three natural frequencies calculated from ANSYS, compared with those using the theoretical model. It is found that the relative errors between the two methods are acceptable. Moreover, the first three mode shapes obtained from the theoretical method and ANSYS are compared in Figure 4. As expected, a good consistency between the mode shapes from the theoretical and ANSYS models is observed. We can conclude that the theoretical model is verified.

TABLE 3

Table 3. Natural frequencies (Hz) of the cantilevered sandwich beam.

FIGURE 4

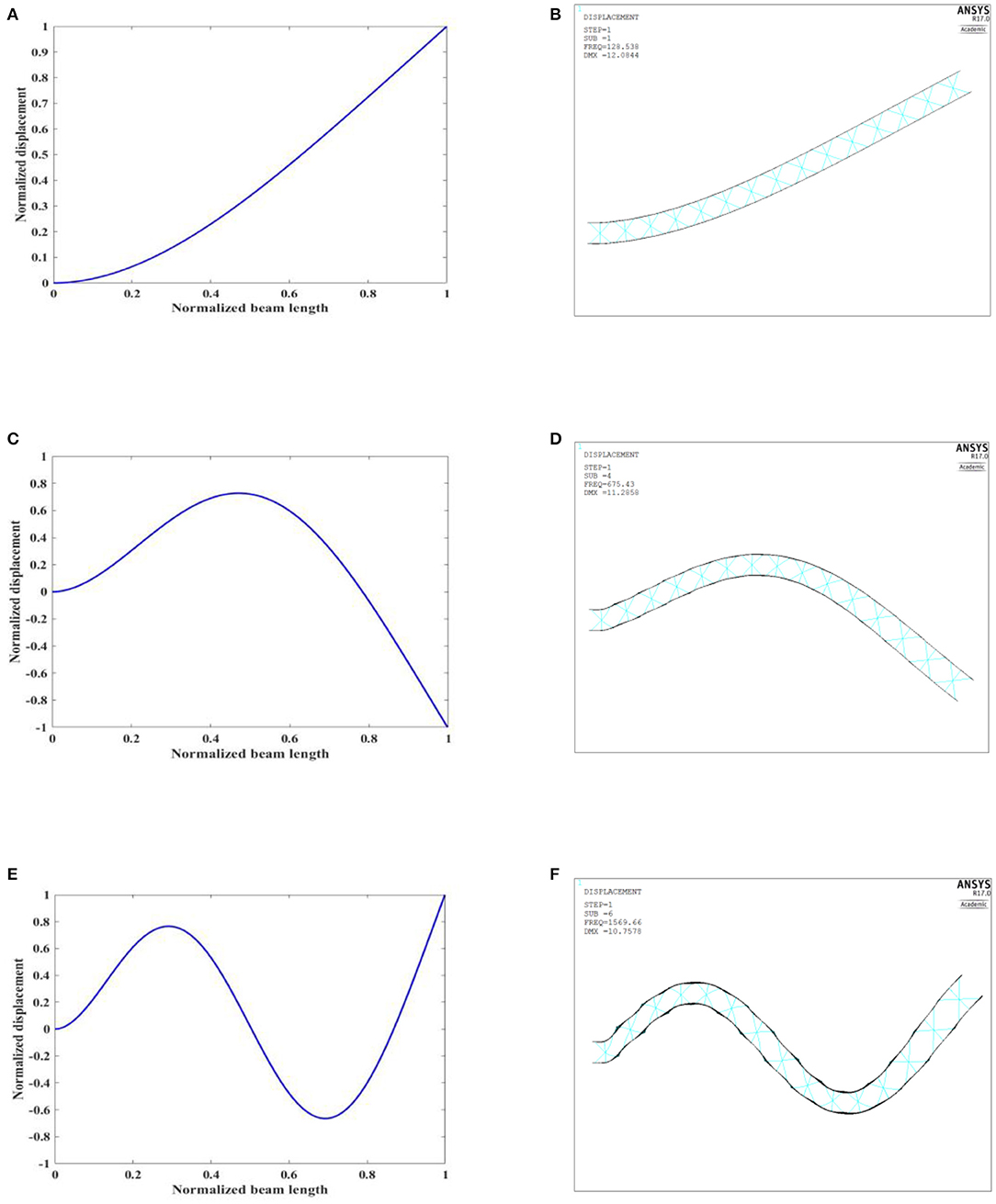
Figure 4. First three vibration modes of the cantilevered sandwich beam: (A,C,E) theoretical model; (B,D,F) ANSYS.

Prototyping and Experimental Test

Prototype Fabrication

Since the hourglass truss structure of the sandwich beam seems relatively complicated, it makes it difficult and time-consuming to fabricate such structures by using traditional manufacturing technologies. 3D printing technology is thus employed to fabricate the prototype. The equipment used for fabrication is an Original Prusa i3 MK3S printer (Figure 5) with the maximum build volume of 25 × 21 × 21 cm. Polylactic Acid (PLA) is used as a fabrication material. The printer is set with the following parameters during the printing process: printing temperature−190°C; interior fill percentage−100%; printing speed−3,600 mm/min; fan speed−100 RPM.

FIGURE 5

Figure 5. Original Prusa i3 MK3S printer used for fabricating the prototype of sandwich beam.

As pointed out in Jiang et al. (2019), due to the existence of overhanging features lying in the complicated structures, the support materials are unavoidably required for printing assistance. A good choice of printing strategy, for example, the building orientation, can significantly reduce the required support material and improve the printing quality. Figures 6A,B show two different printing strategies. As can be speculated that the strategy demonstrated in Figure 6B would be more sensible since the overhanging feature has been completely removed from both face sheets. Figures 6C,D compares the two printed samples using different printing strategies. The former sample shown in Figure 6C has obvious support materials between the two surfaces of the sandwich beam. Support materials normally need to be manually removed after fabrication. However, due to the complexity of the lattice core, manually removing the support materials becomes almost impossible. The speculation is confirmed, and a good-quality sample prototype is obtained to be used in the following experimental test.

FIGURE 6

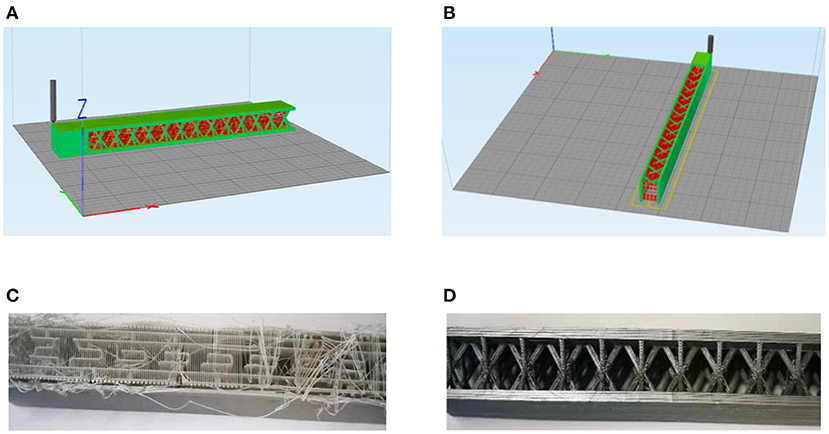
Figure 6. Two different printing strategies and printed samples: (A,C) the sandwich beam printed in the thickness direction; (B,D) the sandwich beam printed in the width direction.

Experimental Test

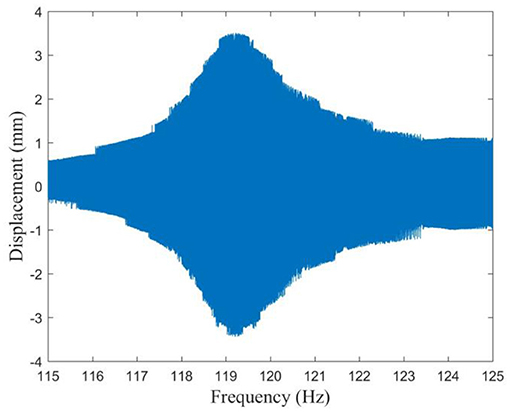
Figure 7 shows the experimental testing setup. One side of the sandwich beam is clamped to the shaker, and the other side is free. The excitation is generated by the controller, amplified by the power amplifier, and fed to the shaker. A laser sensor is used to measure the displacement at the free end of the sandwich beam during the vibration. The sinusoidal excitation at a fixed acceleration level (a_cc = 1g) is used in the experiment. The frequency is swept from 115 to 125 Hz at a rate of 0.2 Hz/s.

FIGURE 7

Figure 7. Experimental testing setup.

Figure 8 shows the frequency response of the tip displacement of the beam. It is easily found that the first natural frequency is about 119.3 Hz, which is very close to the theoretical prediction (126.11 Hz) and ANSYS (128.54 Hz) results. Considering the existence of various uncertainties during the fabrication and testing, such as the manufacturing error of the 3D printer, the material property deviation during the 3D printing process, etc., we believe that the experimental result can already be deemed a good validation for the theoretical model. It is worth mentioning that three sandwich beam samples have been 3D printed and tested to avoid experimental bias. The resonant frequencies of the three samples are 126.11, 126.05, and 126.16, respectively. A good consistency between the three samples ensures the rigor of the experiment.

FIGURE 8

Figure 8. Frequency response of the tip displacement of the sandwich around the first resonance.

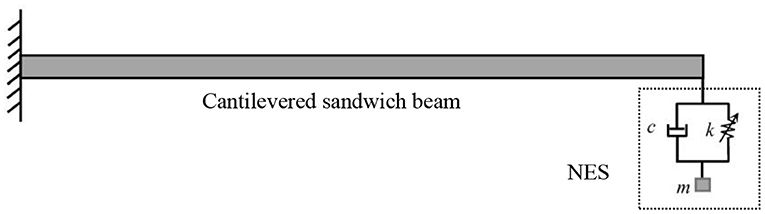
Vibration Suppression of the Sandwich Beam Using NES

Vibration suppression is of great importance in many engineering applications. Though the vibration suppression of conventional homogenous beam structures has been vastly explored, related research in terms of sandwich beams is still rare. In this section, the non-linear energy sink (NES) technique is proposed to be employed by utilizing its targeted energy transfer phenomenon to control the vibration of the sandwich beam.

As shown in Figure 9, an NES consists of a small mass block (m), a spring (k) with essential non-linearity (i.e., no linear stiffness and a strong non-linear stiffness), and a viscous damper (c). The NES is attached to the sandwich beam at the free end for energy absorption. The interaction force between the NES and the sandwich beam is dependent on the relative motion between them and can be expressed as:

$\begin{array}{ll}P=k{\left[w_N(t)-w(L,t)\right]}^3+c\left[{ẇ}_N(t)-ẇ(L,t)\right]& (15)\end{array}$

where w_N(t) and ẇ_N(t) represent the displacement and velocity of m in the NES, respectively. w(L, t) and ẇ(L, t) represent the displacement and velocity at the tip of the sandwich beam, respectively. Thus, the equation of motion of the NES can be obtained as:

$\begin{array}{ll}m{ẅ}_N(t)+k{\left[w_N(t)-w(L,t)\right]}^3+c\left[{ẇ}_N(t)-ẇ(L,t)\right]=0& (16)\end{array}$

FIGURE 9

Figure 9. The diagram of the cantilevered sandwich beam with NES.

After the introduction of the NES, the governing equation of the beam becomes:

$\begin{array}{ll}\text{M}\ddot{\text{X}}(t)+\text{C}\stackrel{\bullet }{\text{X}}(t)+\text{K}\text{X}(t)=P{\text{Q}}_0& (17)\end{array}$

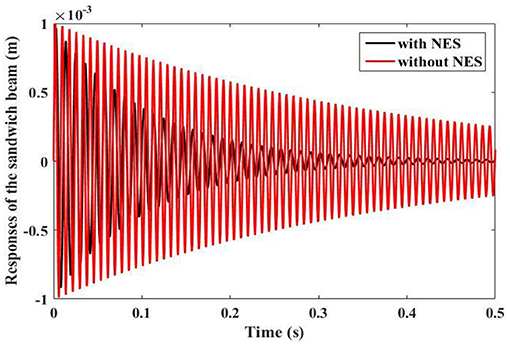
Here, Rayleigh damping is assumed, C = αM + βK with α and β being the mass-proportional and the stiffness-proportional constants, respectively. The Rayleigh damping is only applied to the sandwich beam to make the damping ratios for both the first and second modes to be 0.007. The parameters and material properties of the sandwich beam with an hourglass truss core are the same to those in the finite element analysis and experiment. By solving Equation (17) numerically with the Runge-Kutta method, one can calculate the transient response of the sandwich beam. For the given m = 0.001 kg, k = 1 × 10⁴ N/m³, and c = 100 Ns/m, Figure 10 compares the tip displacement responses of the sandwich beams with and without NES. It can be noted that as compared to the case without NES, the vibration of the sandwich beam with NES decays much faster. In addition, the quality factors (Rao and Yap, 2011) for both models are calculated to be 157 and 45, respectively.

FIGURE 10

Figure 10. Responses of the sandwich beam with and without NES.

With fixed k = 1 × 104 N/m and c = 100 Ns/m of the NES and varying m, Figure 11 reveals the effect of the mass on the vibration suppression performance of the NES. It can be observed that with the increase of m, a better vibration suppression performance for the sandwich beam increases is achieved. However, in consideration of the total weight of the entire system, certain compromise is required for good vibration suppression and the lightweight design purpose.

FIGURE 11

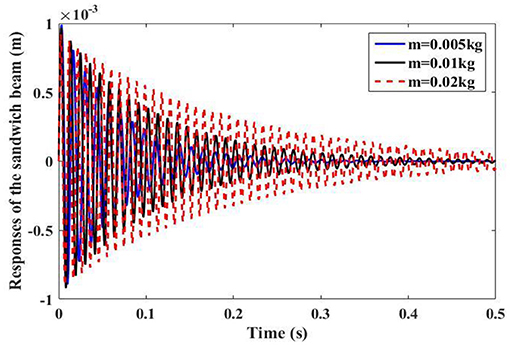
Figure 11. Transient responses of the sandwich beam with different masses of NES (m = 0.005 kg, m = 0.01 kg, m = 0.02 kg).

With fixed k = 1 × 10⁴ N/m and m = 0.01 kg of the NES and varying c, the effect of the damping coefficient on the vibration suppression performance of the NES is investigated. From Figure 12, it is noted that the increase of the damping in the NES weakens the vibration suppression for the main structure (sandwich beam). This is because the underlying mechanism of using NES for vibration suppression is based on the generation of anti-resonance for canceling the inertial force in the sandwich beam and thus suppressing its dynamic response. With the increase of the damping in the NES, the relative motion between the NES and sandwich beam is reduced, resulting in a less reacting force for suppressing the vibration of the main structure.

FIGURE 12

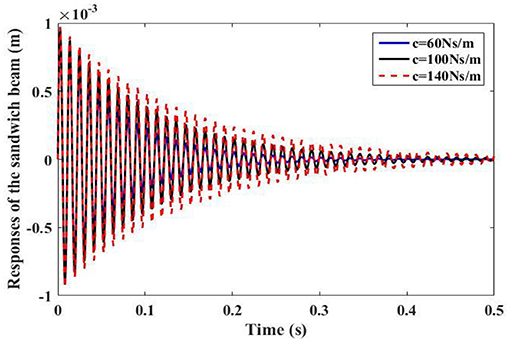
Figure 12. Transient responses of the sandwich beam with different damping coefficients of NES (c = 60 Ns/m, c = 100 Ns/m, c = 140 Ns/m).

Conclusions

In this paper, a theoretical method is proposed to study the dynamic properties of the sandwich beam with an hourglass lattice truss core. The theoretical model of the sandwich beam with an hourglass truss core is verified through the comparison with the existing literature and the finite element analysis. A good-quality 3D printed physical prototype of the sandwich beam is fabricated by using a sensible building orientation strategy. An experimental study is then performed to test the dynamic response of the 3D printed sandwich beam. The natural frequency obtained from the experiment shows a good agreement with the theoretical and finite element results. In addition, the concept of using NES to control the vibration of the sandwich beam is theoretically explored. A parametric study has revealed the effects of the parameters of NES on the vibration suppression performance. In summary, this paper gives a comprehensive theoretical, numerical, and experimental study of the dynamic performance of the sandwich beam with an hourglass truss core. Also, it provides a good exemplar of the application of 3D printing technology in the research of sandwich structures. Besides, the analytical method developed in this study could be adopted for analyzing a sandwich beam-based vibration energy harvester in the future.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.

Author Contributions

ZG: conceptualization, methodology, programming, experiment, result analysis, and draft manuscript writing. GH: conceptualization, experiment, result discussion, and manuscript writing polishing. JJ: 3D-printed prototype preparation and result discussion. LY: experiment and result discussion. XL: result discussion and proofreading. JL: conceptualization, result discussion, manuscript writing polishing, and supervision. All authors contributed to the article and approved the submitted version.

Funding

This research was financially supported by the scholarship from China Scholarship Council (No. 201806540003), the State Key Laboratory of Mechanical System and Vibration (No. MSV202108), National Natural Science Foundation of China (No. 61401277, 51775031), ShanghaiTech University (No. F-0203-13- 003), and Shanghai Key Laboratory of Mechanics in Energy Engineering (No. ORF202001).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Ahmed, K. M. (1972). Dynamic analysis of sandwich beams. J. Sound Vib. 21, 263–276. doi: 10.1016/0022-460X(72)90811-5

CrossRef Full Text | Google Scholar

Azzouz, L., Chen, Y., Zarrelli, M., Pearce, J. M., Mitchell, L., Ren, G. G., et al. (2019). Mechanical properties of 3-D printed truss-like lattice biopolymer non-stochastic structures for sandwich panels with natural fibre composite skins. Compos. Struct. 213, 220–230. doi: 10.1016/j.compstruct.2019.01.103

CrossRef Full Text | Google Scholar

Buannic, N., Cartraud, P., and Quesnel, T. (2003). Homogenization of corrugated core sandwich panels. Compos. Struct. 59, 299–312. doi: 10.1016/S0263-8223(02)00246-5

CrossRef Full Text | Google Scholar

Butt, J., Onimowo, D. A., Gohrabian, M., Sharma, T., and Shirvani, H. (2018). A desktop 3D printer with dual extruders to produce customised electronic circuitry. Front. Mech. Eng. 13, 528–534. doi: 10.1007/s11465-018-0502-1

CrossRef Full Text | Google Scholar

Chen, J. E., Zhang, W., Yao, M. H., and Liu, J. (2017). Vibration suppression for truss core sandwich beam based on principle of nonlinear targeted energy transfer. Compos. Struct. 171, 419–428. doi: 10.1016/j.compstruct.2017.03.030

CrossRef Full Text | Google Scholar

Chen, J. N., Zhang, W., Yao, M. H., Liu, J., and Sun, M. (2018). Vibration reduction in truss core sandwich plate with internal nonlinear energy sink. Compos. Struct. 193, 180–188. doi: 10.1016/j.compstruct.2018.03.048

CrossRef Full Text | Google Scholar

Cote, F., Biagi, R., Bart-Smith, H., and Deshpande, V. S. (2007). Structural response of pyramidal core sandwich columns. Int. J. Solids Struct. 44, 3533–3556. doi: 10.1016/j.ijsolstr.2006.10.004

CrossRef Full Text | Google Scholar

Decuir, F., Phelan, K., and Hollins, B. C. (2016). “Mechanical strength of 3-D printed filaments,” in 32nd Southern Biomedical Engineering Conference (SBEC) (Shreveport, LA: IEEE).

Google Scholar

Deng, S., and Suresh, K. (2016). Multi-constrained 3D topology optimization via augmented topological level-set. Comput. Struct. 170, 1–12. doi: 10.1016/j.compstruc.2016.02.009

CrossRef Full Text | Google Scholar

Deshpande, V. S., and Fleck, N. A. (2001). Collapse of truss core sandwich beams in 3-point bending. Int. J. Solids Struct. 38, 6275–6305. doi: 10.1016/S0020-7683(01)00103-2

CrossRef Full Text | Google Scholar

Elmadih, W., Syam, W. P., Maskery, I., Chronopoulos, D., and Leach, R. (2019). Mechanical vibration bandgaps in surface-based lattices. Addit. Manuf. 25, 421–429. doi: 10.1016/j.addma.2018.11.011

CrossRef Full Text | Google Scholar

Erturk, A., and Inman, D. J. (2008). A distributed parameter electromechanical model for cantilevered piezoelectric energy harvesters. J. Vib. Acoust. Trans. ASME 130:041002. doi: 10.1115/1.2890402

CrossRef Full Text | Google Scholar

Evans, A. G., Hutchinson, J. W., Fleck, N. A., Ashby, M. F., and Wadley, H. N. G. (2001). The topological design of multifunctional cellular metals. Prog. Mater. Sci. 46, 309–327. doi: 10.1016/S0079-6425(00)00016-5

CrossRef Full Text | Google Scholar

Fan, H. L., Jin, F. N., and Fang, D. N. (2008). Mechanical properties of hierarchical cellular materials. Part I: Analysis. Compos. Sci. Technol. 68, 3380–3387. doi: 10.1016/j.compscitech.2008.09.022

CrossRef Full Text | Google Scholar

Fan, H. L., Zeng, T., Fang, D. N., and Yang, W. (2010). Mechanics of advanced fiber reinforced lattice composites. Acta Mech. Sin. 26, 825–835. doi: 10.1007/s10409-010-0390-z

CrossRef Full Text | Google Scholar

Feng, L. J., Wu, L. Z., and Yu, G. C. (2016). An Hourglass truss lattice structure and its mechanical performances. Mater. Des. 99, 581–591. doi: 10.1016/j.matdes.2016.03.100

CrossRef Full Text | Google Scholar

Feng, L. J., Xiong, J., Yang, L. H., Yu, G. C., Yang, W., and Wu, L. Z. (2017). Shear and bending performance of new type enhanced lattice truss structures. Int. J. Mech. Sci. 134, 589–598. doi: 10.1016/j.ijmecsci.2017.10.045

CrossRef Full Text | Google Scholar

Guo, Z., Liu, C., and Li, F. (2017). Vibration analysis of sandwich plates with lattice truss core. Mech. Adv. Mater. Struct. 26, 1–6. doi: 10.1080/15376494.2017.1400616

CrossRef Full Text | Google Scholar

Guo, Z. K., Yang, X. D., and Zhang, W. (2020). Dynamic analysis, active, and passive vibration control of double-layer hourglass lattice truss structures. J. Sandw. Struct. Mater. 22, 1329–1356. doi: 10.1177/1099636218784339

CrossRef Full Text | Google Scholar

Hu, G., Tang, L., Liang, J., and Das, R. (2019). Modelling of a cantilevered energy harvester with partial piezoelectric coverage and shunted to practical interface circuits. J. Intell. Mater. Syst. Struct. 30:1045389X19849269. doi: 10.1177/1045389X.19849269

CrossRef Full Text | Google Scholar

Hwu, C. B., Chang, W. C., and Gal, H. S. (2004). Vibration suppression of composite sandwich beams. J. Sound Vib. 272, 1–20. doi: 10.1016/S.0022-460X.(03)00302-X

CrossRef Full Text | Google Scholar

IEEE Standard on piezoelectricity. IEEE Trans. Ultrason. Ferroelectr. Freq. Control (1996). 43, A1–A54. doi: 10.1109/TUFFC.1996.542065

CrossRef Full Text

Jiang, J., Lou, J., and Hu, G. (2019). Effect of support on printed properties in fused deposition modelling processes. Virtual Phys. Prototy. 14, 1–8. doi: 10.1080/17452759.2019.1568835

CrossRef Full Text

Kim, T., Hodson, H. P., and Lu, T. J. (2004). Fluid-flow and endwall heat-transfer characteristics of an ultralight lattice-frame material. Int. J. Heat Mass Transf. 47, 1129–1140. doi: 10.1016/j.ijheatmasstransfer.2003.10.012

CrossRef Full Text | Google Scholar

Li, F. M., and Lyu, X. X. (2014). Active vibration control of lattice sandwich beams using the piezoelectric actuator/sensor pairs. Compos. Part B Eng. 67, 571–578. doi: 10.1016/j.compositesb.2014.08.016

CrossRef Full Text | Google Scholar

Li, M., Li, F. M., and Jing, X. J. (2018). Active vibration control of composite pyramidal lattice truss core sandwich plates. J. Aerosp. Eng. 31:04017097. doi: 10.1061/(ASCE)AS.1943-5525.0000817

CrossRef Full Text | Google Scholar

Li, S., Yang, J. S., Wu, L. Z., Yu, G. C., and Feng, L. J. (2019). Vibration behavior of metallic sandwich panels with Hourglass truss cores. Mar. Struct. 63, 84–98. doi: 10.1016/j.marstruc.2018.09.004

CrossRef Full Text | Google Scholar

Liang, J., and Liao, W. (2012). Impedance modeling and analysis for piezoelectric energy harvesting systems. IEEE/ASME Trans. Mechatron. 17, 1145–1157. doi: 10.1109/TMECH.2011.2160275

CrossRef Full Text | Google Scholar

Lou, J., Ma, L., and Wu, L. Z. (2012). Free vibration analysis of simply supported sandwich beams with lattice truss core. Mater. Sci. Eng. B Adv. Funct. Solid State Mater. 177, 1712–1716. doi: 10.1016/j.mseb.2012.02.003

CrossRef Full Text | Google Scholar

Lou, J., Wang, B., Ma, L., and Wu, L. Z. (2013). Free vibration analysis of lattice sandwich beams under several typical boundary conditions. Acta Mech. Solida Sin. 26, 458–467. doi: 10.1016/S0894-9166(13)60041-5

CrossRef Full Text | Google Scholar

Mead, S. S. J. D. (1966). “The stodola method applied to sandwich beams vibration,” in Proceedings of the Symposium Numerical Methods for Vibration Problems (Crete).

Google Scholar

Nannan Guo, M. C. L. (2013). Additive manufacturing: technology, applications, and research needs. Front. Mech. Eng. 8, 215–243. doi: 10.1007/s11465-013-0248-8

CrossRef Full Text | Google Scholar

Queheillalt, D. T., Murty, Y., and Wadley, H. N. G. (2008). Mechanical properties of an extruded pyramidal lattice truss sandwich structure. Scr. Mater. 58, 76–79. doi: 10.1016/j.scriptamat.2007.08.041

CrossRef Full Text | Google Scholar

Rao, S. S., and Yap, F. F. (2011). Mechanical Vibrations, Vol. 4. Hoboken, NJ Prentice hall Upper Saddle River.

Roper, C. S. (2011). Multiobjective optimization for design of multifunctional sandwich panel heat pipes with micro-architected truss cores. Int. J. Heat Fluid Flow 32, 239–248. doi: 10.1016/j.ijheatfluidflow.2010.07.002

CrossRef Full Text | Google Scholar

Ruzzene, M. (2004). Vibration and sound radiation of sandwich beams with honeycomb truss core. J. Sound Vib. 277, 741–763. doi: 10.1016/j.jsv.2003.09.026

CrossRef Full Text | Google Scholar

Sypeck, D. J., and Wadley, H. N. G. (2002). Cellular metal truss core sandwich structures. Adv. Eng. Mater. 4, 759–764. doi: 10.1002/1527-2648(20021014)4:10%3C759::AID-ADEM759%3E3.0.CO;2-A

CrossRef Full Text | Google Scholar

Wadley, H. N. G., Fleck, N. A., and Evans, A. G. (2003). Fabrication and structural performance of periodic cellular metal sandwich structures. Compos. Sci. Technol. 63, 2331–2343. doi: 10.1016/S0266-3538(03)00266-5

CrossRef Full Text | Google Scholar

Wang, J., Evans, A. G., Dharmasena, K., and Wadley, H. N. G. (2003). On the performance of truss panels with Kagome cores. Int. J. Solids Struct. 40, 6981–6988. doi: 10.1016/S0020-7683(03)00349-4

CrossRef Full Text | Google Scholar

Wohlers, T., and Gornet, T. (2014). History of Additive Manufacturing. Wohlers Report. Wohlers Associates, Inc.

Google Scholar

Yang, X. D., Guo, Z. K., Zhang, W., Ren, Y., and Roderick, M. V. N. (2019). Substitution method: a technique to study dynamics of both non-gyroscopic and gyroscopic systems. J. Sound Vib. 458, 510–521. doi: 10.1016/j.jsv.2019.07.006

CrossRef Full Text | Google Scholar

Zhang, Y. W., Zhang, H., Hou, S., Xu, K. F., and Chen, L. Q. (2016). Vibration suppression of composite laminated plate with nonlinear energy sink. Acta Astronaut. 123, 109–115. doi: 10.1016/j.actaastro.2016.02.021

CrossRef Full Text | Google Scholar

Zhao, Z., Wen, S. R., and Li, F. M. (2018). Vibration analysis of multi-span lattice sandwich beams using the assumed mode method. Compos. Struct. 185, 716–727. doi: 10.1016/j.compstruct.2017.11.069

CrossRef Full Text | Google Scholar