Design and Shape Optimization of a Biodegradable Polymeric Stent for Curved Arteries Using FEM

Introduction

Coronary artery disease causes artery narrowing that can sometimes lead to complete blockage (stenosis). When this happens in coronary arteries, blood supply restricts and heart muscle cells die, which leads to heart attack. In general, stenosis is manageable by treatment with stents or with a bypass (Venkatraman et al., 2008). Stent treatment has revealed safe and efficient outcomes for straight arteries (Tambaca et al., 2011; Iqbal et al., 2015), while it is still challenging for curved coronary arteries. Stenosis typically occurs at the angled sections of the vascular pathway like arches and bifurcations (Tomita et al., 2015). The angular vessel gets straightened by stenting, and a hinge effect takes place at extremes of the stent. The maximum vessel stress is also exerted at hinge points (Ebrahimi et al., 2007; Wu et al., 2007). Restenosis (disease re-occurrence) may occur if the radial flexibility of the stent is too low (i.e., if the stent is too rigid). The stent should be flexible enough to take the curvature of the artery with less stress to the artery wall. It should also be flexible during the implant procedure. If the stent is not flexible, it could not track the catheter during the navigation inside a tortuous and curved blood vessel (Santos et al., 2020).

In 2020, Shen et al. worked on flexibility of a new self-expandable tapered stent. Their results revealed that the increase in the stent link space width can contribute to the reduction in the peak stress. Therefore, tapered stents with high link space width will improve the stent flexibility (Shen et al., 2020). Wei et al. investigated six stent structures into a curved stenotic coronary artery. Their results showed that the Palmaz-Schatz–shaped stent had the greatest maximum plastic strain and the largest diameter change but the highest maximum von Mises stress on plaque and arterial intima and media (Wei et al., 2019). Saito et al.’s investigation revealed that stent flexibility influences not only mechanical stress on the artery but also wall shear stress (WSS), which may induce local neointimal hyperplasia (Saito et al., 2020). Perrin et al.’s report revealed that increasing vessel curvature leads to stent graft kinks and inadequate apposition against the arterial wall (Perrin et al., 2015). Kasiri reported that a double segment stent provides higher flexibility, more conformity, and lower recoil (Kasiri and Kelly, 2011).

There is still lack of conformability to the vessel wall when deployed at curved lesions. The stent should also be sufficiently strong in order to prevent any artery diameter reduction after the implant, since the artery wall applies dynamic and static load to the stent. In practice, this load will change depending on the artery anatomy shape.

Thus, a designer should consider both flexibility and radial strength as the main properties of a stent that is intended to be implanted in a curved vessel. Since these two parameters are conflicting in a stent, a powerful method is required to find the optimum design that meets the essentials. By comparing the numerical results obtained from different design sets, the suggestion can be made to improve the existing design of a stent (Mortier et al., 2010; Wu et al., 2010; Pant et al., 2012). However, the questions are whether the findings are the best design and how to establish an optimal one in a systematic way instead of it being based on a few empirical designs.

Since the optimization theory is a powerful and practical mathematical technique for determining the most profitable or least disadvantageous choice, out of a set of alternatives (Mehne and Mirjalili, 2020; Mirjalili et al., 2020a; Mirjalili et al., 2020b), this paper attempts to explore the entire process for shape optimization of a stent and improve its mechanical properties by utilizing the multi-objective optimization.

In 2020, Torki et al. designed and optimized a stent with the optimization parameters including the longitudinal pattern (cell) number, circular–circumferential pattern (cell) number, connection of cells by an N, M, or W type flex connector, radius curve, thickness, and maximum and minimum width (Torki et al., 2020). In 2017, Vishwanathan optimized the structural shape of a stent, using NURBS for parameterization. Control point weights, strut thickness, and strut width were used as design variables for Latin hypercube sampling (LHS) in order to generate a dataset for stent deployment simulations (Chen et al., 2019). Alaimo et al. proposed an optimization framework through a local modification of the planar strut profile (Alaimo et al., 2017). Li et al. proposed a Kriging surrogate model to optimize the geometries of a stent and length of the stent dilatation balloon step by step (Li et al., 2017).

The finite element method is an excellent technique to test and improve stent designs and performance from biomechanical aspects. In comparison with experimental investigations, the FEM conveys data that are hard or impossible to be achieved in practice. It also brings about the opportunity to design and test different models with least cost and time spent until an optimal design is earned (Torki et al., 2020).

In this work, using the finite element method, a stent is designed to be implanted in a curved vessel. Its flexibility and radial strength are geometrically optimized by the GA multi-objective optimization method. Since a range of Pareto optimal design parameter values are obtained, which can be used in clinical design guides so as to accommodate variations observed across different patients, polylactic acid is chosen as the material for the stent. Indeed, the reasons include ease of production, control over properties of the polymer, ready availability, and versatility of manipulation (Venkatraman et al., 2008).

Stents can be made using additive manufacturing (AM) that builds models layer by layer from a computer-aided design (CAD) system and provides a fast and cost-effective process to develop more suitable biomedical products (Demir and Previtali, 2017; Guerra et al., 2017; Fathi et al., 2020). Various AM machines have been used in stent field processes, including fused deposition modeling (FDM). Specifically, FDM has been commonly used to fabricate stent scaffolds (Chung et al., 2018; Tabriz et al., 2019; Colpani et al., 2020). An FDM machine is composed basically of a double extruder head nozzle controlled by a CNC mechanism. FDM parts are produced by extruding filaments of thermoplastic materials layer by layer onto the build platform using a diameter extrusion head. The simplicity of the FDM process makes it suitable for the rapid development of molds (rapid tooling) (Hopkinson et al., 2006).

One of the innovations of this work is that flexibility is preferred rather than radial strength in distal and proximal parts of the stent, while radial strength is preferred to flexibility in its middle part. Subsequently, geometric parameters differ for extremes and middle section, but smoothness is considered to be kept all over the stent. In this way, the stent recoil and stress distribution in both the artery wall and the stent are expected to be improved simultaneously through the site.

The main models used in the analysis of stents and the description of the shape optimization problem will be shown in this work. After the optimization procedure, five different design sets are devised according to the optimization Pareto optimal solution. Their implementation in a curved artery is simulated, and the stresses and the recoil are compared among these stents. The discussion of the obtained results and the final conclusions are described at the end of this paper. The results of this study show the merits of the spline-based parameterization approach, which models a broader range of shapes than that was previously possible with traditional approaches.

Methodology

Finite Element Method

In this study, two FEM models were built to study the stent’s ABAQUS/Standard implicit solver. The radial strength after dilation and the bending flexibility of the PLLA stent were evaluated according to the American Society for Testing and Materials (ASTM) standard. The meshing method is very important, as it determines the total number of DOFs and the accuracy of calculation greatly. The element types of meshes decided for the stent were C3D20R, C3D15, and C3D10. The seed size was linearly proportional to the thickness of the stent, since thickness is one of the optimization variables. There are at least three meshes in the thickness of the stent. The structure with one ring for radial strength simulation was meshed to about 2,140 elements. The whole stent for bending simulation was meshed to about 24,060 elements.

The ordinary numerical simulation demands only an unalterable geometric model, whereas the optimization task requires a parameterized geometric model that is represented by a set of shape design variables rather than constant values. The geometric model has to be rebuilt and re-meshed according to the updated design variables at the beginning of each optimization loop. Thus, all simulations were parametrically coded in PYTHON, to be run in the ABAQUS/Standard implicit solver. In this way, not only was simple conformity with the optimization algorithm conducted in MATLAB obtained, but also some shortcomings of the ABAQUS/Standard implicit solver were overcome.

GA Multi-objective Optimization

A goal of this paper is to demonstrate a set of optimal stent designs for a range of curved arteries. The multi-objective genetic algorithm is conducted in MATLAB. The population size and the iteration number are 80 and 100, respectively. For each objective function calculation, the simulation is performed in the ABAQUS/Standard implicit solver, and the result is returned to MATLAB. We have tried to use shape optimization to optimize the strut structure of a stent, with the aim of increasing its flexibility and radial strength. The radial strength of the stent and its flexibility during the implant procedure will be optimized simultaneously.

Geometric Modeling

The spline curve is a sufficiently general mathematical method for defining arbitrarily smooth shaped curves and surfaces (Gordon and Riesenfeld, 1974). The spline function f is a piecewise polynomial function defined on an interval [x_min,x_max] (Hua et al., 2020) with specified continuity constraints, i.e., when the interval [x_min,x_max] is subdivided by control points ξ_i such that x_min = ξ₁ < …< ξ_q = x_max, then within each subinterval [ξ_j,ξ_j+1), the function is a polynomial P_j of specified degree (Bezhaev and Vasilenko, 2001). Control points are used to determine the shape of a spline curve.

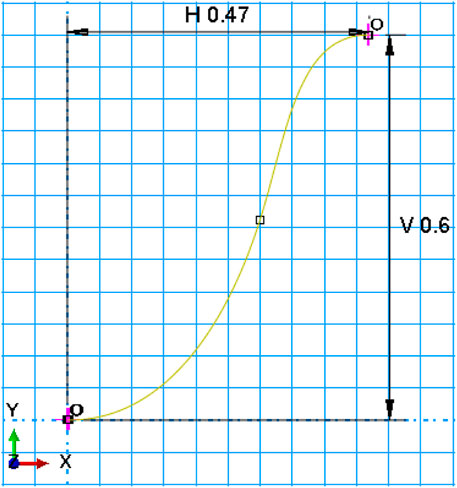
In this study, the spline curve is used to design the strut curvature since it provides a flexible shape design by handling control points while the curvature can retain its smoothness. The spline is first drawn in a two-dimensional plane and then rolled over a cylindrical surface. It is defined by seven control points, among which the fourth one’s Cartesian coordinates x and y are two of the optimization variables. Groups of three first and last control points are very close to each other and have the same highs (y). They are defined to make the beginning and the end of the curve tangent to the horizon, and thus, smoothness will be kept all over the structure and the curve will not be twisted (Figure 1).

FIGURE 1

FIGURE 1. Strut central line curvature, the middle point has variable x and y values (mm).

The stent is designed and optimized for a curved vessel with the curvature radius of 10 mm. The crimped diameter of the stent is 1.5 mm, while it is meant to be dilated up to 3.2 mm. The stent is constructed with 10 peak-to-valley struts (Figure 2) in the circular direction. The total length of the stent consisting of 28 rings is about 16.8 mm (which will be exactly determined after optimization) (Figure 2). The width and height of each peak-to-valley strut are 0.47 and 0.6, respectively.

FIGURE 2

FIGURE 2. Stent design.

Studies show that, in curved vessels, larger strain is observed around the center of stent than its two ends, while bending force is observed to be more in the ends (Wu et al., 2007; Zhao et al., 2014) (Figure 3). It can be concluded that more stiffness is required in the middle part of the stent where the plaque is concentrated and stiffer and more load will be applied when the vessel is narrower: in other words, its two ends should be more flexible. Subsequently, in post-processing, the objective function weights are managed to be different for 16 middle rings and 8 rings of each side. Therefore, their geometries and mechanical behavior will differ too.

FIGURE 3

FIGURE 3. Deformation of a straight stent in a curved vessel (Wu et al., 2007).

Clinical studies have noted a proportional relationship between strut thickness and angiographic restenosis (Pache et al., 2003). The increase in strut thickness is effective to improve the radial supporting ability of stents, but thicker struts will hamper the blood flow, delay full neointimal coverage, and increase the risk of subacute thrombosis (Hua et al., 2020). In this regard, thickness is the other optimization variable in this work.

Materials

Poly-L-lactide acid (PLLA) was chosen as the stent material. Wang et al. (2017) evaluated constitutive data of PLLA at exactly 37°C, which is the human body temperature. These data are used in this study for definition of material properties (Table 1).

TABLE 1

TABLE 1. Material properties of PLLA (Wang et al., 2017).

Radial Strength

The FE model for evaluating the radial strength 37° of the stent was set according to the ASTM standard (ASTM F3067-14, 2014). The test was driven in three static steps. In the first step, the balloon dilates the stent to the pre-defined inner diameter of 3.2 mm. In the second step, the stent is unloaded from the balloon pressure and has the chance to spring back. In the third step, a 0.7 displacement in the radial direction is exerted to the stent from an outer cylindrical displacement supplier with a low enough constant speed of 0.5 mm/s. In this step, the pressure applied by the displacement supplier is increasing by diameter decrease, until it reaches the constant amount per diameter displacement for a short distance, called collapse pressure. At this level, the constancy of the pressure demonstrates the stent’s buckling that can be interpreted as the stent’s failure (ASTM F3067-14, 2014).

The more the amount of collapse pressure, the more radial strength the stent enjoys. Thus, the goal of this optimization is to increase the collapse pressure. Because the aim of the optimization is to find the least amount of objective function, the reverse of collapse pressure is set as the objective function. In this model, the pressure in each frame is calculated by dividing the sum of all node forces by the current area of the displacement supplier. Only one ring of the whole stent is modeled on behalf of all the rings, in order to decrease the calculation cost.

Takashima et al. assumed a cylindrical surface as a balloon catheter to dilate the stent by applying radial direction displacement (step 1) and a cylindrical surface as a displacement supplier (step 3). In their study, the modeling results were validated both qualitatively and quantitatively (Takashima et al., 2007). Accordingly, in this simulation, the balloon and the displacement supplier were modeled as deformable cylindrical shells, whose diameter expanded to 3.2 mm and decreased to 2.5 mm, respectively. One end of the stent ring was fixed in the axial direction, and the other end was free. The assembly model including the stent ring, the balloon, and the displacement supplier is shown in Figure 4. One end of the stent ring was fixed in the axial direction. The interaction between the stent and both the balloon and the displacement supplier was assumed as isotropic with a friction coefficient of 0.1. The balloon and the displacement supplier were both modeled as an isotropic elastic material with extremely high elastic modulus.

FIGURE 4

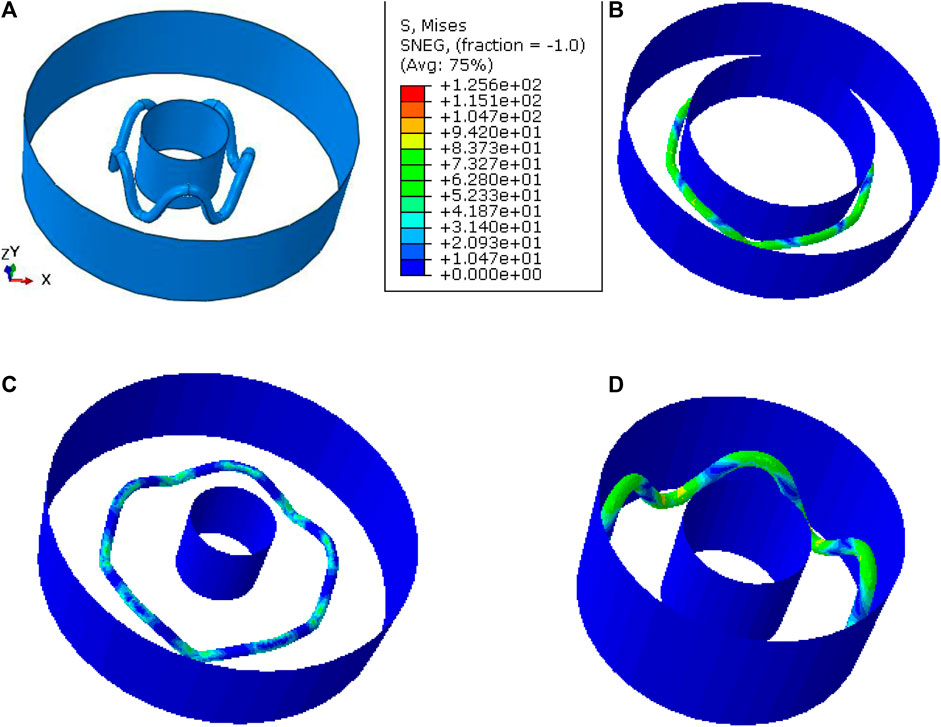
FIGURE 4. Radial strength test: (A) beginning of the test; (B) step 1: balloon dilation; (C) step 2: balloon contraction. (D) Displacement induced by the outer cylinder.

Bending Flexibility

There are different methods to quantify and assess a stent’s flexibility, among which the three-point bending test is opted in this work. Three-point bending of the stent was simulated according to the ASTM standard (ASTM F2606-08, 2014). The schematic of the three-point bending test is shown in Figure 5. Two lower static pins were set in a predefined center–center distance (span length) of 11 mm according to the stent’s length, based on ASTMF2606-08 (ASTM F2606-08, 2014). The upper pin was located in the middle of the span. A downward displacement 1.3 mm of the loading or upper pin was applied, which forced the tested stent to bend (Figure 5). This is the displacement both allowed in the ASTM standard and estimated for a vessel with a curvature radius of 10 mm.

FIGURE 5

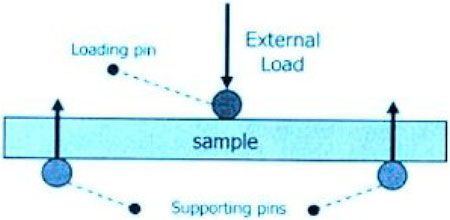
FIGURE 5. Schematic view of the three-point bending test (Nagler, 2019).

The reaction force and displacement of the upper pin were stated during simulation, creating a force–deflection curve. The less the force needed for bending, the more flexibility the stent benefits. Thus, the optimization goal is to reduce the force needed to bend the stent. The self-contact of the stent ring was defined, and the frictionless condition was supposed.

In the model of three-point bending, two lower static pins and the upper one that applies load were all modeled as the rigid cylinders with a diameter of 6.35 mm according to ASTMF2606-08 (ASTM F2606-08, 2014). As the total length of the stent is 32 mm, the span length of these parts is 11 mm. The model was symmetric; in order to reduce the calculation cost, half of the model was simulated. The displacement of the nodes on the plane passing through the diameter of the stent and parallel to the bending force (x direction) was set to zero in the z direction (Figure 6).

FIGURE 6

FIGURE 6. Three-point bending test simulation.

Optimization Results

The Pareto optimal solution, resulted from GA multi-objective optimization, is shown in Figure 7 and Table 2.

FIGURE 7

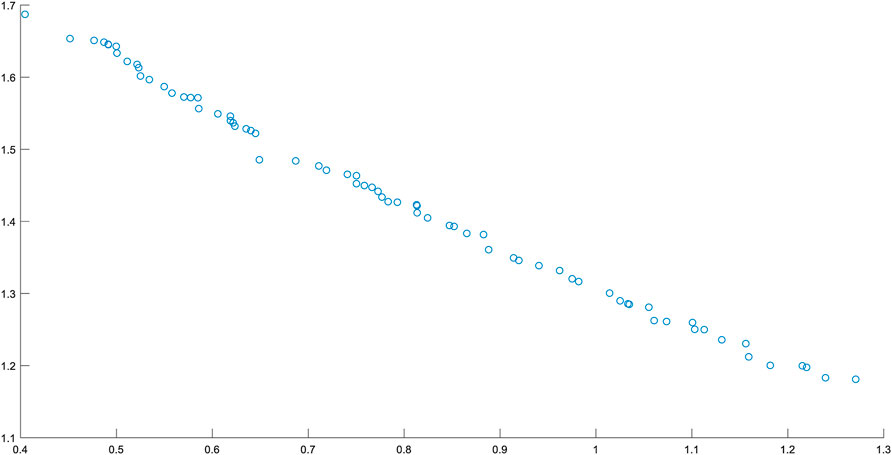
FIGURE 7. Pareto Front; vertical axis is the reverse of collapse pressure (1/MPa), horizontal axis is the 3point bending force (N).

TABLE 2

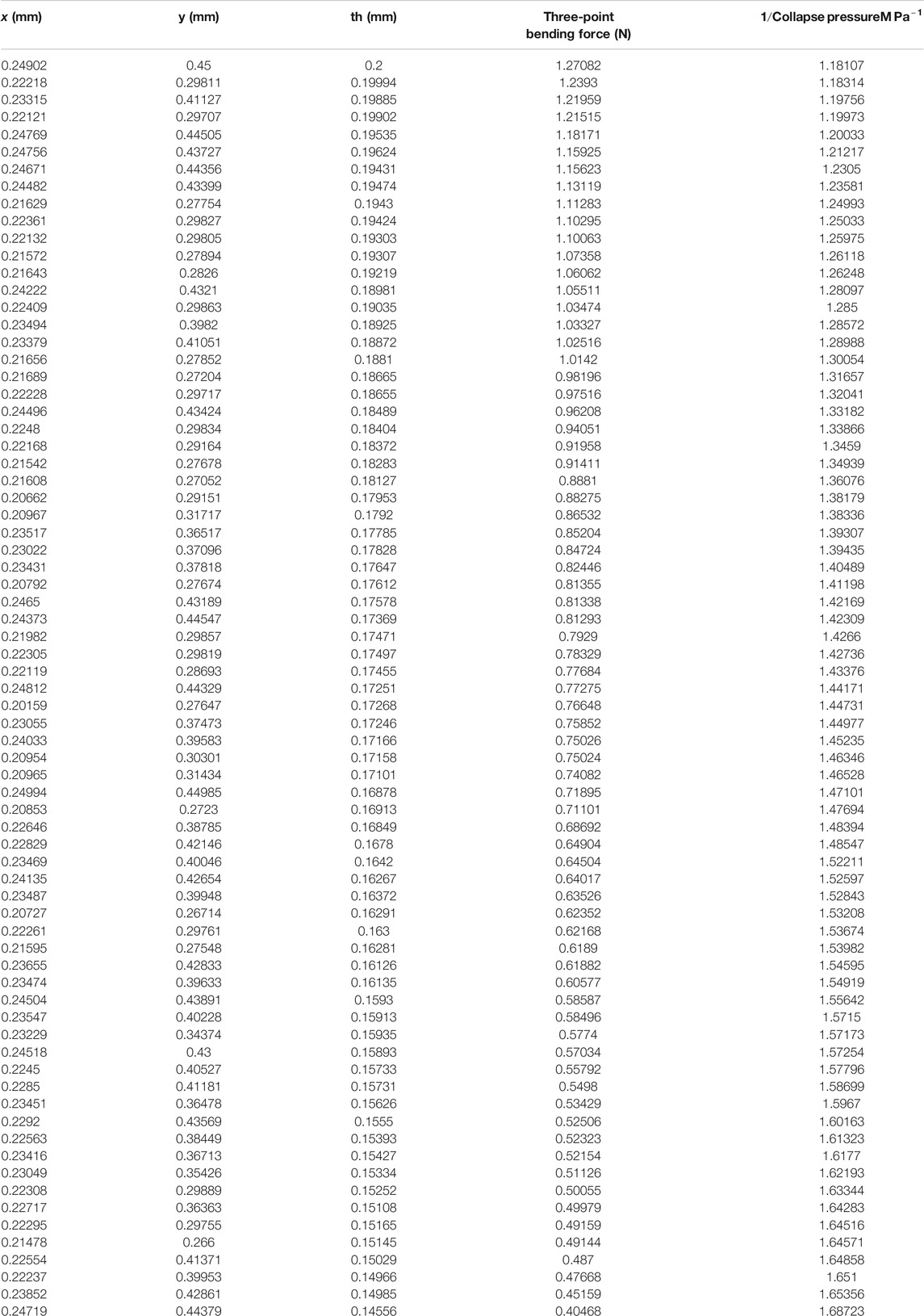
TABLE 2. Pareto front points—“x” and “y” are the spline middle point coordinates and “th” stands for the thickness.

Post-processing

The interest of the Pareto front approach in this context is, thus, to allow the designer to choose the appropriate stent design, depending on which criteria to enhance. Here, flexibility is preferred in the ends of the stent, while radial stiffness is preferred in the middle part. Accordingly, different weights are assigned to these objectives, in different parts of the stent. Five different sets are defined in Table 3. The fifth design is not defined by weighting. Here, maximum radial strength is associated with the middle part, and maximum flexibility is associated with the ends of the stent. These five sets are just the suggestions of the authors, while any other weight set based on the operator’s diagnosis is applicable to all the Pareto solution points.

TABLE 3

TABLE 3. Five sets for objective function weights.

For each set and each stent part, weight coefficients are multiplied in the normalized objective functions of the Pareto front and summed up together. The point of the minimum result is implemented for the design. The design parameters are listed in Table 4.

TABLE 4

TABLE 4. Design sets.

The outer diameter of the stent is equal all over the stent, while the thickness is different from middle parts to end parts. In order to avoid sharp edges caused by thickness difference in the intersection of these two parts, round fillets are applied (Figure 8). The thickness difference is too small to cause significant changes in the blood flow.

FIGURE 8

FIGURE 8. Fillet at the intersection of middle and end parts of the stent.

Each of the above stent implementation in a curved vessel was simulated in ABAQUS/CAE. The artery has the central curvature radius of 10 mm. Both the artery curvature and the stent structure are symmetric with respect to the plane passing through the middle section. In order to reduce the calculation costs, half of the artery, stent, and balloon was simulated and the symmetry boundary condition was applied.

The balloon was simulated as a cylindrical surface with the outer diameter of 1.3 mm. In the first step, the artery was avoided from dislocation by fixing the nodes on the symmetry plane. The assembly of the stent and the balloon was pushed to the vessel by a displacement. After the stent and the balloon completely reached the targeted lesion site, the balloon dilated the artery inner diameter to 3.2 mm. Thus, the stent was expanded to open the closed lumen. Then, the balloon shrinks to its initial diameter, letting the stent spring back. A friction coefficient of 0.1 was prescribed among all contact surfaces. The artery and plaque were meshed with about 4,170 quadratic tetrahedral elements of type C3D10. The stent was also discretized into about 34,660 quadratic tetrahedral elements of type C3D10, and the balloon was discretized into 988 elements. In the simulation, all the nodes on the symmetry plane passing through the length of the stent were close in the direction orthogonal to the plane.

The material properties of arterial tissue layers and plaque are stated in Table 5 (Karimi et al., 2014). Each layer was modeled as an incompressible isotropic hyperelastic material. The artery thickness was assumed to be 0.5 mm with a thickness ratio for Int:Med:Adv of 13:32:55 (Schulze-Bauer et al., 2003).

TABLE 5

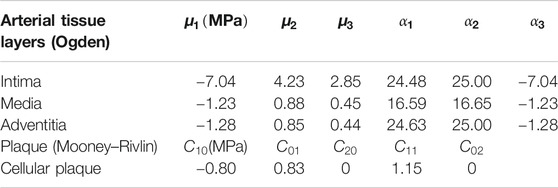
TABLE 5. Material coefficients of arterial tissue layers, plaque tissue, and balloon (Karimi et al., 2014).

Results and Discussion

Stress Distribution

Despite considering different objective function weights, design parameters were the same for the end part of the stent in all designs (Tables 3, 4). In this part, flexibility was weighted 1.5, 2, 4, and 5 times more than radial strength. In the middle part of the stent, radial strength was weighted more than flexibility. By increasing the radial strength weight, thickness increased relatively (Table 4).

We considered flexibility as an objective that allows the stent to take the curvature of the stent with lower force. The force deforming the stent causes stress distribution in the stent and the artery. In this regard, von Mises stress distribution after the first step of simulation is studied. The von Mises stress contour of the artery and the stent is shown in Figure 9.

FIGURE 9

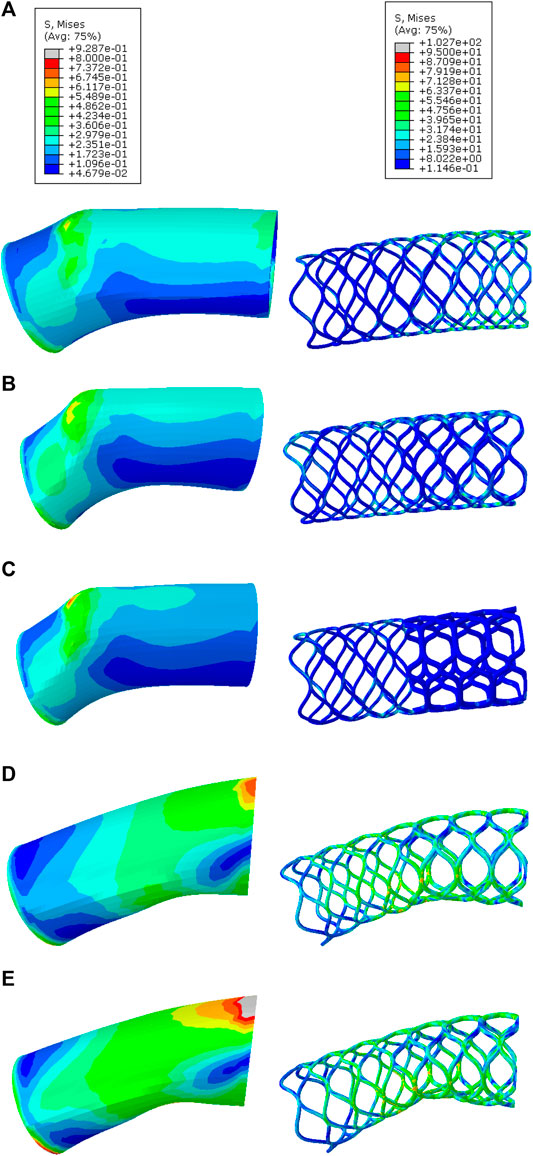
FIGURE 9. von Mises stress (MPa) distribution in the artery wall (left) and stent (right): (A) Design1, (B) Design2, (C) Design3, (D) Design4, and (E) Design5, after dilating the stent in the artery.

It can be seen that, by changing the radial strength and flexibility along the stent, the stress distribution changes in the artery wall (Figure 9). In the first three designs, the maximum stress is observed in the end part of the artery, while in the fourth and the fifth design, greater stresses are observed in the middle parts of the arteries. It is important to note that the maximum stress in the artery by the first three stents is less than the maximum stress by the last two designs (see Table 6). Since the artery stress instigates inflammation and restenosis, the first three designs are suitable for tortuous and highly curved arteries.

TABLE 6

TABLE 6. Maximum stress in the artery wall and the stent designs.

The artery straightening has occurred less in the fourth and the fifth design. Thus, it can be discussed that the comfortability of the stent to the artery curvature is easier when the radial strength is considerably different in the middle and end parts of the stent. In these five designs, as the mid-part radial strength weight increases, the stress gets distributed more evenly through the stent, which reduces the danger of stent breaking and restenosis. For curved arteries exposed to several external forces, the last two designs are suggested, since the risk of breaking gets reduced.

The thickness and strut curvature of the end part are the same for all designs, but stress amounts are different in these parts. This difference originates from the difference in the middle part. Indeed, the geometric parameters in the middle part affect the mechanical behavior of the whole stent. Despite having the mechanical properties of each part, the mechanical performance of the whole stent cannot be exactly predicted. But, by having the mechanical performance of these five designs, the mechanical performance of other combinations of the Pareto solution points can be almost estimated.

Radial Recoil

The radial recoil ratio after the expanding process, an important index characterizing the stent’s strength, was calculated in stent implementation steps. It is defined by the profile changes between two stages: In the first stage, the stent was expanded to a required inner diameter, 3.2 mm. In the second stage, the balloon shrinked to its initial diameter and the stent sprang back after expanding. The formula is stated as follows (Venkatraman et al., 2008):

$\text{Radial}\text{Recoil}=\frac{InnerDiamete{r}_{afterexpansion}-InnerDiamete{r}_{afterspringback}}{InnerDiamete{r}_{afterexpansion}}.(1)$

The radial recoil ratio after expanding determines the over-increment in the outer diameter of the stent applied in a particular vessel environment. Too much radial recoil causes large over-expanding and great strain generation in the arteries, leading to a great risk of mechanical injury and follow-up inflammation (Wang et al., 2017). Radial recoil ratios of the expanded stent in simulations were calculated at the middle of the stent length (Table 7). The results show that radial recoil decreases by radial strength decrease. It can also be interpreted that radial recoil has a direct relationship with stent thickness (Tables 4, 7).

TABLE 7

TABLE 7. Radial recoil ratios of the expanded stent in simulations.

Since its too high value can cause blockage and death, radial recoil is the most important criterion for the success of a stent implementation. Thus, in addition to stress distribution and maximum stress, radial recoil should be considered when opting for the right stent for a curved artery. Arteries with stiff plaque or those exposed to numeric loads should be healed with stents enjoying less rate of recoil.

The artery structure and properties differ person to person depending on age, gender, lifestyle, diet, and so forth. This is why physicians should be provided with a variety of stents with different characteristics to choose on a case-by-case basis. In other words, there is no ideal stent for all the arteries. Some arteries should be dilated by flexible stents because of their very short curvature radius or stiff structure, while other arteries should be dilated by radially strong stents because of their stiff plaque or presence of several dynamic loads in their location. Some arteries need both flexibility and radial strength at a moderate amount according to stenosis. Accordingly, in this work, a variety of optimized stents have been provided. Among these stents, five design sets, with different flexibilities and radial strength weights, have been simulated to be studied from a mechanical performance point of view.

All in all, one can choose a stent with a definite amount of radial strength considering a limit for flexibility, and vice versa. In order to utilize this design efficiently, physicians should provide a CT angiogram to assess the curvature and the plaque thickness. Considering the exposure level of the artery to external forces and its stiffness, physicians should give weight to each of the flexibility and radial strength for each section of the stent. Weight coefficients should be multiplied in the normalized objective functions of the Pareto front (Table 2) and get summed up together. The point of the minimum result should be implemented for the design. It is even possible to consider three different weight coefficient sets for the distal, middle, and proximal sections of the stent according to the geometry of the artery.

Conclusion

In this study, using the finite element method, a stent was designed to be implanted in a curved vessel. Rather than searching a single optimal design, the use of GA multi-objective optimization addresses the flexibility and radial strength variation in a stent. The resulting Pareto set forms the basis of a design guide from which physicians can select an appropriate flexible–radially strong design, depending on the characteristics of a particular patient’s diseased curved artery. The optimization methodology has proved that this technique can serve as a stent strut design tool. An optimization process seems to bring a real improvement compared to a less systematic approach that is currently used for the design of stents.

Since a range of Pareto optimal design parameter values were obtained, which can be used in clinical design guides so as to accommodate variations observed across different patients, polylactic acid was chosen as the material for the stent. In this way, the operator can opt for a desired stent from the Pareto front and produce or order it easily. The operator has also the option of joining two or more designs from the Pareto front, in order to have desired performance along the stent.

In this work, radial strength and flexibility are differently preferred in the middle section and extremes of the stent. Five different objective weight sets are allocated to the Pareto set, leading to five different stent designs, in the post-processing procedure. Using the finite element method, these stents are implemented in a curved vessel, and their stress distribution, maximum stress, and radial recoil are measured. The designs whose middle and end parts are more flexible are suitable for tortuous and highly curved arteries, since the maximum stress they exert to the artery wall is reduced. The designs with higher radial strength in the middle part are suggested for curved arteries exposed to several external forces, since the stress is distributed more evenly and, thus, the risk of breaking gets reduced.

One of this work’s main contributions is the use of spline curvature point coordinates and stent thickness to considerably expand the range of stent shapes that a single geometric modeler can produce. We proposed a method to use spline point coordinates and strut thickness as optimization design variables, achieving remarkable geometric variation compared to previous stent parameterizations. This spread variation ensures we are seeking a broad geometric design space during optimization.

The stenting modeling has revealed useful results that are hard or impossible to be caught by experimental approaches. The applicability of this modeling is not limited to von Mises stress and radial recoil measurement. There are other mechanical objectives that can be assessed through this modeling procedure, including principal stress and strain in both the artery and the stent, stent shortening, and energy magnitudes. This modeling can also be used to simulate stents with other elastic–plastic materials. Furthermore, it is applicable in other stent applications such as biliary stents, to simple plastic stents used to allow the flow of urine between the kidney and the bladder.

There were some limitations in this work. Struts were directly interconnected with each other, while they could be interconnected by links as a common way of increasing flexibility. The optimization procedure was time-consuming, which could take shorter time using other mathematical methods such as the Taguchi or neural network. In future works, other optimization variables such as the number of struts can be optimized. The shape difference can be applied to more than two parts of the stent. Biodegradable alloys might be used as the material of the stent.

Data Availability Statement

The original contributions presented in this study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.

Author Contributions

YB and MK designed the model and the computational framework and analyzed the data. MOB and MAB were involved in planning and supervised the work. SH and MOK aided in interpreting the results and worked on the manuscript. All authors contributed to manuscript writing and read and approved the submitted version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Alaimo, G., Auricchio, F., Conti, M., and Zingales, M. (2017). Multi-Objective Optimization of Nitinol Stent Design. Med. Eng. Phys. 47, 13–24. doi:10.1016/j.medengphy.2017.06.026

PubMed Abstract | CrossRef Full Text | Google Scholar

Bezhaev, A. Y., and Vasilenko, V. A. (2001). Variational Theory of Splines. New York: Springer.

Chen, C., Chen, J., Wu, W., Shi, Y., Jin, L., Petrini, L., et al. (2019). In vivo and in vitro Evaluation of a Biodegradable Magnesium Vascular Stent Designed by Shape Optimization Strategy. Biomaterials 221, 119414. doi:10.1016/j.biomaterials.2019.119414

PubMed Abstract | CrossRef Full Text | Google Scholar

Chung, M., Radacsi, N., Robert, C., McCarthy, E. D., Callanan, A., Conlisk, N., et al. (2018). On the Optimization of Low-Cost FDM 3D Printers for Accurate Replication of Patient-Specific Abdominal Aortic Aneurysm Geometry. 3D Print. Med. 4 (1), 1–10. doi:10.1186/s41205-017-0023-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Colpani, A., Fiorentino, A., and Ceretti, E. (2020). Design and Fabrication of Customized Tracheal Stents by Additive Manufacturing. Procedia Manufact. 47, 1029–1035. doi:10.1016/j.promfg.2020.04.318

CrossRef Full Text | Google Scholar

Demir, A. G., and Previtali, B. (2017). Additive Manufacturing of Cardiovascular CoCr Stents by Selective Laser Melting. Mater. Des. 119, 338–350. doi:10.1016/j.matdes.2017.01.091

CrossRef Full Text | Google Scholar

Ebrahimi, N., Claus, B., Lee, C. Y., Biondi, A., and Benndorf, G. (2007). Stent Conformity in Curved Vascular Models with Simulated Aneurysm Necks Using Flat-Panel CT: An In Vitro Study. AJNR Am. J. Neuroradiol 28 (5), 823–829.

PubMed Abstract | Google Scholar

Fathi, P., Capron, G., Tripathi, I., Misra, S., Ostadhossein, F., Selmic, L., et al. (2020). Computed Tomography-Guided Additive Manufacturing of Personalized Absorbable Gastrointestinal Stents for Intestinal Fistulae and Perforations. Biomaterials 228, 119542. doi:10.1016/j.biomaterials.2019.119542

PubMed Abstract | CrossRef Full Text | Google Scholar

Gordon, W. J., and Riesenfeld, R. F. (1974). “Computer Aided Geometric Design,” in Computer Aided Geometric Design. Editors R. Barnhill, and R. F. Riesenfeld (New York, NY: Academic Press), 95–126.

CrossRef Full Text | Google Scholar

Guerra, A., Roca, A., and de Ciurana, J. (2017). A Novel 3D Additive Manufacturing Machine to Biodegradable Stents. Procedia Manufact. 13, 718–723. doi:10.1016/j.promfg.2017.09.118

CrossRef Full Text | Google Scholar

Hopkinson, N., Hague, R., and Dickens, P. (2006). Rapid Manufacturing: An Industrial Revolution for the Digital Age. Chichister, United Kingdom: John Wiley & Sons.

Hua, R., Tian, Y., Cheng, J., Wu, G., Jiang, W., Ni, Z., et al. (2020). The Effect of Intrinsic Characteristics on Mechanical Properties of Poly (L-Lactic Acid) Bioresorbable Vascular Stents. Med. Eng. Phys. 81, 118–124. doi:10.1016/j.medengphy.2020.04.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Iqbal, J., Serruys, P. W., Silber, S., Kelbaek, H., Richardt, G., Morel, M-A., et al. (2015). Comparison of Zotarolimus- and Everolimus-Eluting Coronary Stents: Final 5-Year Report of the RESOLUTE All-Comers Trial. Circ. Cardiovasc. Interv. 8 (6), e002230. doi:10.1161/circinterventions.114.002230

PubMed Abstract | CrossRef Full Text | Google Scholar

Karimi, A., Navidbakhsh, M., Yamada, H., and Razaghi, R. (2014). A Nonlinear Finite Element Simulation of Balloon Expandable Stent for Assessment of Plaque Vulnerability Inside a Stenotic Artery. Med. Biol. Eng. Comput. 52 (7), 589–599. doi:10.1007/s11517-014-1163-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Kasiri, S., and Kelly, D. J. (2011). An Argument for the Use of Multiple Segment Stents in Curved Arteries. J. Biomech. Eng. 133 (8), 084501. doi:10.1115/1.4004863

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, H., Liu, T., Wang, M., Zhao, D., Qiao, A., Wang, X., et al. (2017). Design Optimization of Stent and its Dilatation Balloon Using Kriging Surrogate Model. Biomed. Eng. Online 16 (1), 1–17. doi:10.1186/s12938-016-0307-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Mehne, S. H. H., and Mirjalili, S. (2020). “Moth-Flame Optimization Algorithm: Theory, Literature Review, and Application in Optimal Nonlinear Feedback Control Design,” in Nature-Inspired Optimizers: Studies in Computational Intelligence. Editors S. Mirjalili, J. Song Dong, and A. Lewis (Basel, Switzerland: Springer, Cham), 811, 143–166.

CrossRef Full Text | Google Scholar

Mirjalili, S., Mirjalili, S. M., Saremi, S., and Mirjalili, S. (2020a). “Whale Optimization Algorithm: Theory, Literature Review, and Application in Designing Photonic Crystal Filters,” in Nature-Inspired Optimizers: Studies in Computational Intelligence. Editors S. Mirjalili, J. Song Dong, and A. Lewis (Basel, Switzerland: Springer, Cham), 811, 219–238.

CrossRef Full Text | Google Scholar

Mirjalili, S., Song Dong, J., Lewis, A., and Sadiq, A. S. (2020b). “Particle Swarm Optimization: Theory, Literature Review, and Application in Airfoil Design,” in Nature-Inspired Optimizers: Studies in Computational Intelligence. Editors S. Mirjalili, J. Song Dong, and A. Lewis (Basel, Switzerland: Springer, Cham), 811, 167–184. doi:10.1007/978-3-030-12127-3_10

CrossRef Full Text | Google Scholar

Mortier, P., Holzapfel, G. A., De Beule, M., Van Loo, D., Taeymans, Y., Segers, P., et al. (2010). A Novel Simulation Strategy for Stent Insertion and Deployment in Curved Coronary Bifurcations: Comparison of Three Drug-Eluting Stents. Ann. Biomed. Eng. 38 (1), 88–99. doi:10.1007/s10439-009-9836-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Nagler, J. (2019). Failure Mechanics of Multi Materials Laminated Systems Review Analysis-Based Project. Turin: School of Mechanical Engineering, University of Tel Aviv.

Pache, J., Kastrati, A., Mehilli, J., Schühlen, H., Dotzer, F., Hausleiter, J., et al. (2003). Intracoronary Stenting and Angiographic Results: Strut Thickness Effect on Restenosis Outcome (ISAR-STEREO-2) Trial. J. Am. Coll. Cardiol. 41 (8), 1283–1288. doi:10.1016/s0735-1097(03)00119-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Pant, S., Bressloff, N. W., and Limbert, G. (2012). Geometry Parameterization and Multidisciplinary Constrained Optimization of Coronary Stents. Biomech. Model. Mechanobiol. 11 (1–2), 61–82. doi:10.1007/s10237-011-0293-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Perrin, D., Demanget, N., Badel, P., Avril, S., Orgéas, L., Geindreau, C., et al. (2015). Deployment of Stent Grafts in Curved Aneurysmal Arteries: Toward a Predictive Numerical Tool. Int. J. Numer. Methods Biomed. Eng. 31 (1), e02698. doi:10.1002/cnm.2698

CrossRef Full Text | Google Scholar

Saito, N., Mori, Y., and Komatsu, T. (2020). Influence of Stent Flexibility on Artery Wall Stress and Wall Shear Stress in Bifurcation Lesions. Med. Devices (Auckl). 13, 365–375. doi:10.2147/MDER.S275883

PubMed Abstract | CrossRef Full Text | Google Scholar

Santos, J. D., Haig, C., and Schwartz, L. B. (2020). Radially Rigid and Longitudinally Flexible Multi-Element Intravascular Stent. Turin: Google Patents.

Schulze-Bauer, C. A. J., Mörth, C., and Holzapfel, G. A. (2003). Passive Biaxial Mechanical Response of Aged Human Iliac Arteries. J. Biomech. Eng. 125 (3), 395–406. doi:10.1115/1.1574331

PubMed Abstract | CrossRef Full Text | Google Scholar

Shen, X., Jiang, J. B., Zhu, H. F., Deng, Y. Q., and Ji, S. (2020). Numerical Investigation of the Flexibility of a New Self-Expandable Tapered Stent. J. Mech. 36 (4), 577–584. doi:10.1017/jmech.2020.11

CrossRef Full Text | Google Scholar

Tabriz, A. G., Douroumis, D., Okereke, M., and Khalaj, R. (2019). “3D Printing of Bioabsrorbable Polymeric Stents by Fused Deposition Modeling (FDM),”in ICS3M 2019: International Conference on Stents Materials, Mechanics and Manufacturing, London, United Kingdom, July 15–17, 2019.

Google Scholar

Takashima, K., Kitou, T., Mori, K., and Ikeuchi, K. (2007). Simulation and Experimental Observation of Contact Conditions Between Stents and Artery Models. Med. Eng. Phys. 29 (3), 326–335. doi:10.1016/j.medengphy.2006.04.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Tambaca, J., Canic, S., Kosor, M., Fish, R. D., and Paniagua, D. (2011). Mechanical Behavior of Fully Expanded Commercially Available Endovascular Coronary Stents. Tex. Heart Inst. J. 38 (5), 491–501.

PubMed Abstract | Google Scholar

Tomita, H., Higaki, T., Kobayashi, T., Fujii, T., and Fujimoto, K. (2015). Stenting for Curved Lesions Using a Novel Curved Balloon: Preliminary Experimental Study. J. Cardiol. 66 (2), 120–124. doi:10.1016/j.jjcc.2014.10.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Torki, M. M., Hassanajili, S., and Jalisi, M. M. (2020). Design Optimizations of PLA Stent Structure by FEM and Investigating its Function in a Simulated Plaque Artery. Math. Comput. Simul. 169, 103–116. doi:10.1016/j.matcom.2019.09.011

CrossRef Full Text | Google Scholar

Venkatraman, S., Boey, F., and Lao, L. L. (2008). Implanted Cardiovascular Polymers: Natural, Synthetic and Bio-Inspired. Prog. Polym. Sci. 33 (9), 853–874. doi:10.1016/j.progpolymsci.2008.07.001

CrossRef Full Text | Google Scholar

Wang, Q., Fang, G., Zhao, Y., Wang, G., and Cai, T. (2017). Computational and Experimental Investigation into Mechanical Performances of Poly-L-Lactide Acid (PLLA) Coronary Stents. J. Mech. Behav. Biomed. Mater. 65, 415–427. doi:10.1016/j.jmbbm.2016.08.033

PubMed Abstract | CrossRef Full Text | Google Scholar

Wei, L., Leo, H. L., Chen, Q., and Li, Z. (2019). Structural and Hemodynamic Analyses of Different Stent Structures in Curved and Stenotic Coronary Artery. Front. Bioeng. Biotechnol. 7, 366. doi:10.3389/fbioe.2019.00366

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, W., Petrini, L., Gastaldi, D., Villa, T., Vedani, M., Lesma, E., et al. (2010). Finite Element Shape Optimization for Biodegradable Magnesium Alloy Stents. Ann. Biomed. Eng. 38 (9), 2829–2840. doi:10.1007/s10439-010-0057-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, W., Wang, W.-Q., Yang, D.-Z., and Qi, M. (2007). Stent Expansion in Curved Vessel and Their Interactions: A Finite Element Analysis. J. Biomech. 40 (11), 2580–2585. doi:10.1016/j.jbiomech.2006.11.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, S., Lin, S., and Gu, L. (2014). “Stent Expansion in Curved Vessel and Their Interactions: An In Vitro Study,” in Proceedings of the ASME 2014 International Mechanical Engineering Congress and Exposition, Montreal, Canada, November 14–20, 2014 (New York, NY: American Society of Mechanical Engineers Digital Collection).

CrossRef Full Text | Google Scholar