Thermal Conductivity of Ti-6Al-4V in Laser Powder Bed Fusion

1 Introduction

Additive manufacturing (AM) of metals is today used in numerous applications e.g., in aerospace (Liu et al., 2017), industrial engineering (Galati et al., 2020) and tooling manufacture (Chantzis et al., 2020), to name a few only. Of all metal AM processes, powder bed fusion (PBF) is taking a share of 90% in terms of installed machines, with laser powder bed fusion (PBF-LB/M) being the most widely used technology within PBF (Herzog et al., 2021b).

While lightweight design is still among the key motivations for many AM applications (Plocher and Panesar, 2019), improving the functionality of a part is another important aspect (Barbieri et al., 2019). Depending on the function of the part, the design freedom of AM may be used to optimize e.g., the pressure drop of manifolds (Herzog et al., 2021a) or the heat transfer of structures in heat exchangers (Scheithauer et al., 2019). Such parts are often subject to a multiphysical optimization process, e.g., mechanical and thermal optimization. To effectively do so, understanding of the thermo-physical properties of the additively manufactured structures is needed in addition to the more often published mechanical data (Stautner et al., 2017).

Furthermore, AM may be used to manufacture functionally graded structures by either locally varying processing parameters, by controlling density or by using property differences between powder and bulk material (Loh et al., 2018). This could offer new opportunities in heat sensitive applications by locally tailoring the thermo-physical properties and directing heat flows. Here, parts of interest include for example cryogenic applications, such as heat switches investigated by Stautner et al. (Stautner et al., 2017) where local thermal conduction is a specific requirement. Another area of application are heat sinks (Wu et al., 2017) and heat dissipation in power electronics, where increasing cooling efficiency while locally separating cool and warm areas are of importance. Metamaterials with anisotropic thermal properties can be used to manipulate heat flux and design e.g. effective thermal shielding (Fan et al., 2008; Narayana and Sato, 2012) or local concentration (Vemuri et al., 2014). Hu et al. (Hu et al., 2016) have shown that using such metamaterials, heat flux can be directed in a 90° angle comparable to reflecting light on a mirror surface. Bandaru et al. (Bandaru et al., 2015) have shown that the manipulation of the heat flux could ultimately be used for thermal lenses and energy harvesting. The studies mentioned before typically use layered structures of dissimilar materials, such as copper and steel (Vemuri et al., 2014) or latex rubber and silicone elastomers with boron nitride particles (Narayana and Sato, 2012) to provide the difference in thermal conductivity.

This paper discusses the thermal conductivity of Ti-6Al-4V, a material widely used in PBF-LB/M, in bulk and powder state. In today’s state of the art, data regarding thermal conductivity of additively manufactured materials is sparse (Bartsch et al., 2021), thus design engineers often turn to values measured on material derived from other manufacturing processes, which may not be accurate. Also, the powder thermal conductivity is an important property when considering heat distribution within the PBF-LB/M process itself. Based on the findings, the possibility to manufacture metamaterials by alternating conductive bulk and less-conductive porous structures is investigated. This could highly facilitate the manufacture of heat flux directing structures without the necessity of dissimilar materials.

2 Thermal Conductivity of Bulk Ti-6Al-4V

In the literature, several studies have dealt with experimentally determining the thermal conductivity of bulk Ti-6Al-4V. They found it to be between 6.2 and 7.66 W/mK (Timmerhaus, 1963; Bolzoni et al., 2013; Gong et al., 2013; Bartsch et al., 2021). However, the data concerning thermal conductivity and other thermo-physical properties of Ti-6Al-4V is still sparse.

There is a variety of different methods for measuring thermal conductivity of bulk materials such as metals. One common technique is the steady state method using guarded parallel plates (Cha et al., 2012; Rausch et al., 2013). Here, a known heat flux ($\dot{Q}$) is applied to a sample, between two plates, with known surface area ($A$) and thickness ($t$), and the difference in temperature ($\Delta T$) is measured between the plates. The ideal, one-dimensional Fourier’s law can then be used to calculate the thermal conductivity at the respective ambient temperature $T_{amb}$ (Rausch et al., 2013). Note that $\text{Δ}T$ is significantly smaller than the ambient temperature.

$\dot{Q}= k\left(T_{amb}\right)\ast A\ast \frac{\mathrm{\Delta }T}{t}$

Additionally, transient techniques are available. Among others, transient methods include transient hot wire (Healy et al., 1976) or laser flash (Cha et al., 2012; Zajas and Heiselberg, 2013; Bartsch et al., 2021) techniques. In the transient plane source method (TPS), a thin disc sensor is placed between two identical samples. The disc sensor acts as a source of heat and a temperature sensor at the same time. During measurement, the disc sensor heats up and the heat dissipates into the material. The speed at which the heat dissipates can be measured by the temperature sensor. Thus, by recording temperature over time this technique can calculate the thermal conductivity of a given sample material (Gustafsson et al., 1974; Gustafsson, 1991). A rather novel method is the modified transient plane source technique (MTPS) which can measure thermal conductivity and effusivity of solids, liquids and powders (Emanuel, 2006; Emanuel et al., 2022). The MTPS sensor has a spiral heater that heats a sample with a unidirectional heat flux. The voltage drop on the sensors heater is measured before and during the heating. Emanuel et al. (Emanuel, 2006) showed that the voltage drop is directly correlated to the effusivity of a material. Since the effusivity is defined as

$e= \sqrt{k\ast \rho {\ast \text{c}}_{\text{p}}}$

with the density $\rho$ and specific heat capacity $c_p$, the thermal conductivity $k$ can be calculated directly. The advantage of the MTPS as a transient method is that it requires a single sample, while the TPS method requires two identical samples.

In the following a MTPS C-Therm TCi Analyzer (C-Therm Technologies Ltd., Fredericton, Canada) was used to determine the thermal conductivity of Ti-6Al-4V PBF-LB/M samples with varying relative density to analyze the influence of porosity in bulk material on the thermal conductivity.

2.1 Methods

Different test specimen are manufactured on a TruPrint 1000 (Trumpf GmbH & Co. KG, Ditzingen, Germany) with different process parameters with the goal to vary porosity between the samples. The sample geometry is chosen as cylindrical to fit the MTPS sensor probe with a height of 7 mm and a diameter of 18 mm seen in Figure 1. The process parameters used are shown in Table 1.

FIGURE 1

FIGURE 1. (A) Schematic drawing of MTPS sensor with liquid/powder cell (B) MTPS sensor without and (C) with bulk sample.

TABLE 1

TABLE 1. Process parameters for manufacturing density and MTPS samples.

Accompanying density cubes with the same parameters and an edge length of 10 mm are printed for density measurement via metallographic analysis. No separate contour parameters are used. After printing, all samples are removed manually from the build plate and the measurement surface of the cylindrical samples smoothed using grinding paper. The thermal conductivity is measured in as-built condition using distilled water as a contact agent. Last, a 500 g weight is put on top on the sample to enhance the contact further. Five individual measurements are averaged and the setup is repeated at least twice for each sample. Before each repeating measurement, the samples are dried to minimize the error due to potential water absorption into the porous samples. After the thermal conductivity measurement of the grinded samples, the surface was polished to further improve the contact between the sample and the sensor. The density cubes are metallographically prepared in XZ-plane according to ISO/ASTM 52900:2017 and the relative density is measured optically.

For application in part design or process simulation, material properties at temperatures up to 500 °C are of interest. The measurements are conducted at room temperatures, though, since the calibration of the available technical equipment does not allow for high temperature measurements.

2.2 Results and Discussion

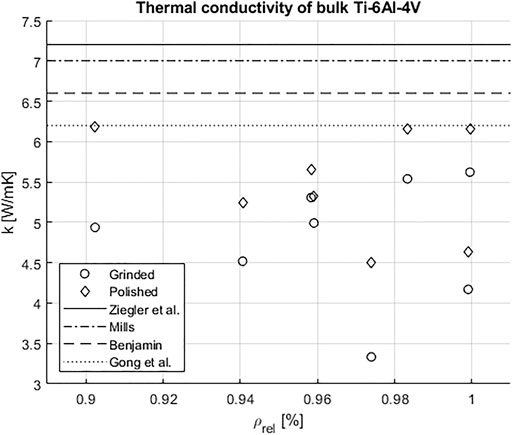
Different relative densities between 90.24 and 99.95% have been achieved with the proposed process parameters. The correlation with the thermal conductivity is shown in Figure 2.

FIGURE 2

FIGURE 2. Thermal conductivity against relative density of PBF-LB/M samples.

Initially as-printed samples were unsuitable for measurement with the MTPS method. After polishing one surface the resulting heat conductivities were between 4.00 and 6.18 W/mK for different samples, with an average of 5.4 W/mK. For comparison, the highest density samples were measured also with the TPS method according to ISO 22007-2, resulting in average thermal conductivity of 5.5 W/mK.

Partially the data points follow a trend that decreasing relative density results in lower thermal conductivity. However, samples at 99 and 97% rel. density have lower than expected thermal conductivity, respectively. Additionally, the most porous sample at 90% is measuring higher than expected values. Thus, contrary to the original hypothesis no clear correlation of thermal conductivity and density can be observed.

In Figure 3, four micrographs with varying densities and thermal conductivity are shown. It can be observed that for (a), (b) and (c) there is random porosity in varying degree in the sample. Sample (d) shows an ordered open porosity.

FIGURE 3

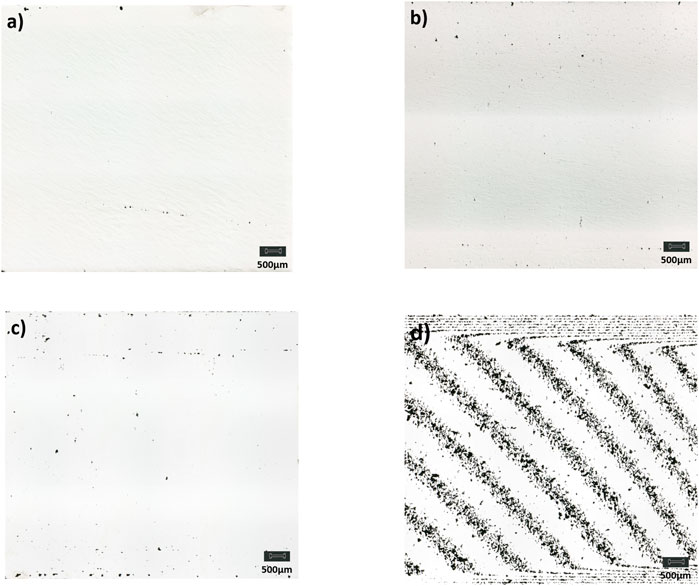
FIGURE 3. Micrographs for optical relative density measurements for different density cubes (A) $\mathit{\rho }$ = 99.95%, $\mathit{k}$ = 5.62 W/mK (B) $\mathit{\rho }$ = 99.90%, $\mathit{k}$ = 4.20 W/mK, (C) $\mathit{\rho }$ = 97.40%, $\mathit{k}$ = 3.33 W/mK, (D) $\mathit{\rho }$ = 90.24%, $\mathit{k}$ = 4.93 W/mK.

Since no clear correlation is present the thermal conductivity of polished samples is averaged to 5.47 W/mK and compared against literature also shown in Figure 2. Here, both the MTPS and TPS measurements show lower conductivity than that reported by (Ziegler et al., 1963; Benjamin and Kirkpatrick 1980; Mills, 2002; Gong et al., 2013), 6.6–7.2 W/mK, and by Bartsch et al. (2021), conducted on similar PBF-LB/M as-built Ti-6Al-4V samples with the LAF method (6.5 W/mK). The samples in this study are measured as-built with one surface polished and are predominantly in the martensitic (α’) phase. Contrary to expectation, no clear positive correlation of heat conductivity can be identified with relative density. The overall surface roughness has been ruled out as an explanation for the missing correlation. A possible solution for the underlying problem with porous bulk material and surfaces on the measurement should be negated in the future by using contour parameters to minimize surface porosity as well as prevent water absorption into the samples. Overall, it has been shown that it is possible to measure the thermal conductivity of Ti-6Al-4V by the MTPS method in a convenient measurement setup. However, for optimal measurement conditions the contact quality between samples and sensor needs to be improved by polishing the samples and the use of contour parameters in the PBF-LB/M process.

3 Thermal Conductivity of Powder Ti-6Al-4V

For powder material, typically the effective thermal conductivity (ETC) is of interest, because a volume filled with powder cannot be defined by the powders bulk thermal properties. While De Beer et al. (Beer et al., 2018) showed that there is extensive research on the ETC of packed powders in literature in general, there is only scarce experimental data available for the ETC of different PBF-LB/M feedstock. Comparing with bulk material the thermal properties of powder feedstock depend on additional powder specific properties, such as particle size distribution (PSD), particle shape, packing density or the surrounding medium (i.e., gas or liquid). This makes thermal characterization of powders challenging. Wei et al. (Wei et al., 2018) investigated the ETC of different feedstocks with the transient hot wire method. For Ti-6Al-4V the thermal conductivity is determined as approximately 0.2 W/mK at room temperature and ambient pressure. Gu et al. (Gu et al., 2014) used the steady-state method and found ETCs in the range of 20–60% of the bulk material. Lastly, Bartsch et al. (Bartsch et al., 2021) use the MTPS technique to measure Ti-6Al-4V feedstock at different temperatures and found thermal conductivities in the range of 0.17–0.19 W/mK at room temperature which is in good agreement with the measurements of (Wei et al., 2018). However, the effect of different powder properties on thermal conductivity is still unknown. Thus, this study aims to show the influence of particle size distribution as well as packing density on the thermal conductivity of Ti-6Al-4V powder feedstocks using the MTPS method.

3.1 Experiments

3.1.1 Methods

In this study, different Ti-6Al-4V feedstocks used in additive manufacturing are characterized with regard to their PSD, apparent and tap density, as well as thermal conductivity. PSD was determined by measuring d10, d50 and d90 with the laser diffraction method (LS 13 320, Beckmann Coulter, Brea, United States). Apparent density is measured by pouring powder feedstock into a pycnometer and taking the volume and weight. The tap density is determined thereafter by densifying the powder volume in a tap density tester and taking the tapped powder volume. The respective densities are related to the bulk density of Ti-6Al-4V of 4.43 g/cm³ resulting in a relative powder density. Furthermore, the morphology is confirmed to be mostly spherical by SEM shown exemplary in Figure 4.

FIGURE 4

FIGURE 4. SEM of 15–45 µm Ti-6Al-4V PBF-LB/M powder.

The ETC of the powder feedstocks is characterized by the MTPS method using a powder measurement cell shown in Figure 5. Each powder is measured in its apparent state by pouring the powder into the cell as well as in its densified state by tapping the powder until no further densification took place. The sensor is operated in its ‘liquids & powders’ mode which is optimized for low thermal conductivities. The sensor takes five different measurement points which then are averaged.

FIGURE 5

FIGURE 5. MTPS setup with powder measurement cell.

3.1.2 Results and Discussion

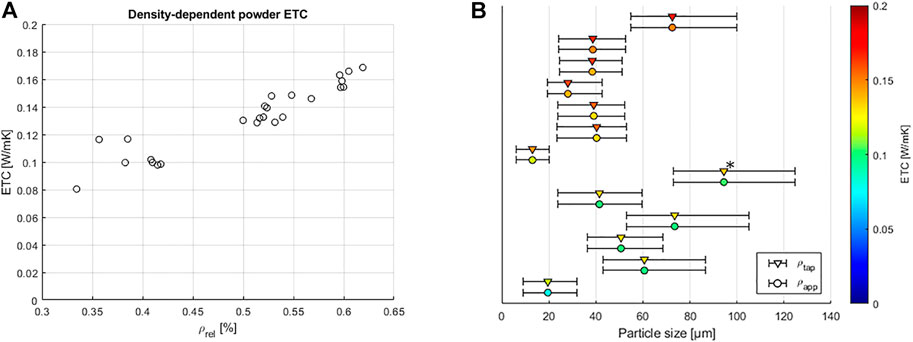
Figure 6 shows the correlations between the ETC and relative density. It includes the apparent as well as the tap density MTPS measurements. ETC ranges from 0.08 to 0.17 W/mK depending on the underlying relative density. A positive linear correlation can be observed between ETC and relative density with few outliers to higher ETCs especially in the lower density range. The experimental data is linearly fitted to:

$ETC=\mathrm{0,2994}\left[\frac{W}{mK}\right]\ast {\rho }_{rel}-0.0181\left[\frac{W}{mK}\right]$

FIGURE 6

FIGURE 6. Results of powder ETC measurements: (A) Density-dependent, (B) PSD-dependent.

Also shown is the effect of PSD on ETC. The diagram shows the powder feedstock PSDs from $d_{10}$ to $d_{90}$ with ETC being indicated by color mapping in apparent and tapped state. The powders are sorted by ETC in tapped state with one data point being estimated since it was not able to be densified in the measurement setup.

The ETC of Ti-6Al-4V powder feedstocks that are determined in this study are in good agreement with (Wei et al., 2018) and (Bartsch et al., 2021), but are significantly lower than shown in (Gu et al., 2014). The heat conductivity is largely governed by the relative density of the powder in the measurement cell leading to a positive correlation of those. One possible explanation is that with increasing rel. density the metal content in the powder volume increases. Since Ti-6Al-4V has a significantly larger heat conductivity than the surrounding air, this can lead to higher ETC in the powder volume. Additionally, a larger relative powder density increases the contact powders and potentially the contact area of the particles further increasing the heat conductivity between the particles. As expected, finding a clear correlation with PSD is more complex. However, powder feedstock that is typically used in PBF-LB/M with a PSD between 20 and 60 µm largely shows similar ETC. Finer and broader powder PSD on the other hand show lower ETC whereas there are contrary data points and no clear trend for coarser powders. It is plausible that finer powders show lower ETC due to lower packing density. However, there is no apparent explanation regarding the low ETC of powders with a broader PSD. Thus, other powder characteristics influencing packing behavior such as particle morphology, inter-particle friction and flowability have to be analyzed further. Overall, it was possible to show a clear correlation of ETC with relative density using the MTPS method. The influence of PSD on ETC could also be partially explained. This offers unique possibilities regarding powder quality control e.g., as an in-situ sensor in PBF-LB/M powder cycles to indicate powder degradation and changes in powder quality.

Additionally, it can be shown that a given powder volume regardless of densification is a poor conductor compared to bulk material. Relative powder bed density in the PBF-LB/M process is in the range of 50% (Rausch et al., 2013). According to Figure 6 the ETC of such powder beds are in the range of 0.13 W/mK. When relating this to bulk material, the powders thermal conductivity is roughly 50 times lower. Thus, it can be used in design to guide heat through optimized paths and shield temperature sensitive parts. Since the empirical effort to characterize different powder packings and materials at the complete temperature range of PBF-LB/M is very large, it can be beneficial to use numerical approaches to gauge the heat conductivity of different powders.

3.2 Modeling of the Powder Thermal Conductivity

The modeling of the ETC of a packed bed has been the scope of research for roughly a century today (Aberdeen and Laby, 1926; Kannuluik and Martin, 1933). A packed bed is defined as system of solid particles in contact, which are surrounded by a fluid phase, either liquid or gaseous (Tsotsas and Martin, 1987). This definition includes powder beds, although some authors (e.g., (S. C. Cheng and Vachon, 1969)) distinguish these two terms, because the particle size as well as particle shape may be significantly different. Currently, the main application of interest are pebble or packed bed gas-cooled reactors (van Antwerpen et al., 2010; Beer et al., 2018). This longtime interest leads to a variety of approaches, which may be categorized as analytical or numerical. Analytical approaches aim at either directly solving heat transfer equations or describing the thermal resistance of the packed bed. Both methods often consider a unit cell representation rather than the complete packed bed. This simplification restricts the analytical approaches to packed beds with only a few particle sizes and a defined packing structure. With increasing computational resources available, the numerical approaches developed to overcome the limitations of the analytical techniques. The network method represents the complete powder bed as a graph, where contact between particles is indicated. Then, the individual local thermal conductivity between two particles is modeled and the heat transfer equation is solved iteratively. A second numerical approach is the discrete element method (DEM). Here, the particles are physically modeled and their time-dependent interactions computed. DEM is often coupled with computational fluid dynamics (CFD) to incorporate the fluid phase in a packed bed. However, DEM is computationally demanding and therefore restricted in the applicable number of particles observed. Additionally, various heat transfer mechanisms within the packed bed can be distinguished (Yagi and Kunii 1957). Independent of the fluid flow in the packed bed are the thermal conduction through solid and contact surfaces of two particles, often referred to as particle-particle conduction, as well as the radiant heat transfer between two particle surfaces or adjacent gas voids. Fluid flow dependent heat transfer mechanisms include the thermal conduction through the fluid film near the contact surface of two particles, convection, and the heat transfer by lateral mixing of the fluid. In summary, various approaches to modeling the ETC of a packed bed exist, based on the packed bed representation, solution of heat transfer equation, and considered heat transfer mechanisms.

While there is a significant number of publications considering packed beds, only few publications deal with the powder bed as found in PBF-LB/M. On the one hand, this may be due to the complex geometrical situation created by a large PSD and the random packing due to the powder application process. On the other hand, the technical application of the powder bed’s ETC in part design or process simulation is rare.

Moser et al. (Moser et al., 2016) developed a DEM model to gain detailed insight regarding thermal conduction at the active, applied powder layer of various metal materials. They use Powell’s method (Powell, 1964) with Jacobians calculated by finite differencing to determine the particle temperatures in steady-state condition. Then, the heat fluxes from the walls are derived and from these the ETC is determined via Fourier’s law. They consider particle-particle conduction, particle-fluid-particle conduction as well as radiation. The investigation of various parameters led to the conclusion, that the powder bed temperature as well as the gas conductivity influence the ETC the most.

In (Chua et al., 2018), finite element analysis (FEA) is applied to determine the ETC of a Ti-6Al-4V PBF-LB/M powder bed near melting range. The FEA model consists of a unit cell representation of two particle halves. Particle-particle conduction as well as particle-fluid-particle conduction near the contact surface is modeled. Considering several contact geometries and ambient temperatures, data is collected to perform regression analysis for ETC estimation.

De Moraes and Czekanski (Moraes and Czekanski, 2018) investigated the effect of several parameters such as packing density on the ETC by implementing a thermal macro-scale PBF-LB/M FEA model. The ETC is represented by an analytical function (Wakao and Kato, 1969). In (Gusarov et al., 2003), the contact thermal conductivity between two particles is analytically evaluated. Wei et al. (Wei et al., 2018), Gu et al. (Gu et al., 2014), as well as Alkahari et al. (Alkahari et al., 2012) experimentally evaluated PBF-LB/M powder bed ETCs.

3.2.1 Methods

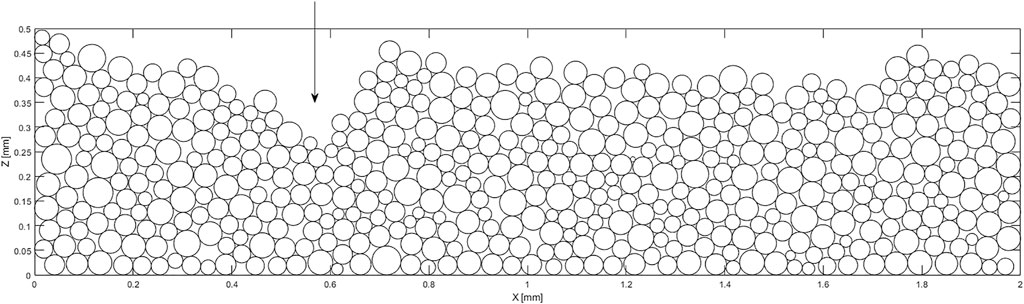
The sparse work on PBF-LB/M specific powder bed ETC calls for the setup of a new model. Because of the randomness involved due to PSD and the powder application procedure requires the use of statistics for the derivation of a general model, unit cell approaches and DEM are not suitable. The unit cell approach is not able to model the random geometries, whereas the computational resources necessary for DEM do not meet the goal of a large dataset. Therefore, the network approach is followed. Here, various powder bed configurations can be modeled and evaluated at several ambient temperatures to create a description of the temperature-dependent powder bed ETC. To reduce computational resources, the model is implemented for a 2D case. The Matlab 2021a software of Mathworks Inc. (Natick, United States) is used for programming.

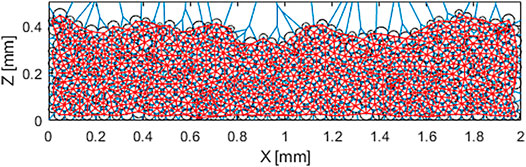
The described model is based on the assumption, that Ti-6Al-4V PBF-LB/M powder particles are spherical and have a smooth surface. Experimental investigations (e.g., (Seyda et al., 2017)) support this assumption. To generate powder bed configurations as found in PBF-LB/M, a three-step procedure is applied: First, the position and size of a specific number of particles in a defined space is determined. Here, the approach of a rain model with multiple restructuring, as described by Meakin & Jullien (Meakin and Jullien, 1987), is followed. A uniform random distribution of X,Z-coordinates in an area high above the powder bed ground ($Z=0$) is created. These coordinates denote the centers of the particles. Then, the center points are assigned a diameter, again randomly, but following a pre-defined PSD. Thus, the particles are assumed perfectly spherical. Having generated a particle cloud, the individual particles are moved to the ground in a drop-roll manner by simulating gravity. One by one, the particles are moved downwards until contact with the ground, the wall, or another particle is established. At contact, the stability of the particle’s position is checked: A stable position is existent when the particle either has reached the ground or has a point of contact on each side of its vertical axis. If the particle is not stable, it is rolled along the surface of its particle in contact (which is stable), until a new contact is achieved. This procedure of contact, stability check, and rotation is repeated until a stable position is reached. Following the approaches of (Sahimi and Tsotsis, 1997; Cheng et al., 1999; Cheng and Yu, 2013; Wu et al., 2016), the resulting powder bed configuration is converted into a Voronoi diagram in a second step. The last step consists of the calculation of the Voronoi network by Delaunay triangulation. Now, a network where the nodes represent the center of the particles and the edges denote particles in interaction is available. In Figure 7, such a powder bed configuration is depicted.

FIGURE 7

FIGURE 7. Powder bed configuration including voronoi tessellation (blue) and network (red).

The steady-state heat conduction through the powder bed in X-direction is computed to determine the ETC (Kanuparthi et al., 2008; Yun and Evans, 2010; Liang, 2015; Lee et al., 2017). To satisfy energy conservation, the sum of all heat flows towards or out of a particle $i$ needs to be in equilibrium:

${\displaystyle \sum q_i}=0$

The heat flow between the $i$ th and $j$ th particle is defined as

$q_{ij}=k_{ij}\left(T\right)\ast \left(T_i-T_j\right)$

where $k_{ij}$ is the temperature-dependent local coefficient of thermal conductivity between those two particles. For the local conductivity, the conductivity network modeling approach (Yun and Evans, 2010; Batchelor and O'Brien, 1977) is applied. Particle-particle as well as particle-fluid-particle conduction is considered, radiation effects are neglected. This is because the aim of the simulation is to model a point deep within the powder bed rather than the upper, freshly applied powder layer and the temperature difference between two adjacent particles is extremely small. Both types of conduction are modeled as a series of conductivities consisting of the solid particles conductivity and either the fluid or particle contact conductivity in-between.

$k_{ij}\left(T\right)=\{\begin{array}{cc}{\left[\frac{1}{k_i\left(T_i\right)}+\frac{1}{k_{ij}^{contact}\left(T\right)}+\frac{1}{k_j\left(T_j\right)}\right]}^{-1}& \text{particle}-\text{particle}\\ {\left[\frac{1}{k_i\left(T_i\right)}+\frac{1}{k_{fluid}^{contact}\left(T\right)}+\frac{1}{k_j\left(T_j\right)}\right]}^{-1}& \text{particle}-\text{fluid}-\text{particle}\end{array}$

The major assumption the model is based on is that the heat flux across the particle’s surface towards another particle is approximated by a cylindrical segment of equivalent radius $R_{ij}$ as proposed by Batchelor & O’Brien (Batchelor and O'Brien, 1977). $R_{ij}$ is defined by the respective particle radii $R_i$, $R_j$ as

$R_{ij}=\frac{2\ast R_i\ast R_j}{R_i+R_j}$

The particle conductivity is then formulated in relation to $R_{ij}$:

$k_n\left(T_n\right)=\pi \ast k_p\left(T_n\right)\ast \frac{{\left(\chi \ast R_{ij}\right)}^2}{R_n}, n=i\vee j$

Here, $k_p$ denotes the thermal conductivity of the powder material, i.e. the solid alloy. Furthermore, $\chi$ is an estimate of the fraction of the mean radius of curvature, which is set to $\chi =0.5$ according to (Yun and Evans, 2010). The contact conductivity of two particles in contact is further determined to be

$k_{ij}^{contact}\left(T\right)=\pi \ast k_f\left(T_{amb}\right)\ast R_{ij}\ast \left[K_c+\text{Δ}{K}_p+\ln \left(\alpha {\left(T\right)}^2\right)\right]$

where the auxiliary terms $K_c$ and $\text{Δ}{K}_p$ are defined as follows:

$\begin{array}{cc}\begin{array}{c}{K}_c=\frac{2\ast {\beta }_{ij}}{\pi }\\ \text{Δ}{K}_p=-2\ast \ln \left({\beta }_{ij}\right)\end{array}\}& \text{f}\text{o}\text{r} {\beta }_{ij}\to \infty \\ \begin{array}{c}{K}_c=0.22\ast {\beta }_{ij}^2\\ \text{Δ}{K}_p=-0.05\ast {\beta }_{ij}^2\end{array}\}& \text{f}\text{o}\text{r} {\beta }_{ij}<1\end{array}$

The thermal conductivity ratio between the powder and the fluid ($k_f$) is denoted by $\alpha$, while ${\beta }_{ij}$ is a parameter describing the overlap of two particles in contact:

${\beta }_{ij}=\frac{\alpha \left(T\right)\ast r_c}{R_{ij}}$

The contact radius $r_c$ is defined by

$\begin{array}{l}{r}_c=\sin \left({\theta }_i\right)\ast R_i\\ {\theta }_i={\cos }^{-1}\left(\frac{D_{ij}^2+R_i^2-R_j^2}{2\ast D_{ij}\ast R_i}\right)\end{array}$

Here, $D_{ij}$ is the distance between the particle’s centers. If the particles are not in contact, but separated by fluid, the contact thermal conductivity is determined as

$k_{fluid}^{contact}\left(T\right)=\{\begin{array}{cc}\pi \ast k_f\left(T_{amb}\right)\ast R_{ij}\ast \ln \left(\alpha {\left(T\right)}^2\right)& \text{f}\text{o}\text{r} {\lambda }_{ij}\left(T\right)\ll 1\\ \pi \ast k_f\left(T_{amb}\right)\ast R_{ij}\ast \ln \left(1+\frac{{\chi }^2\ast R_{ij}}{h_{ij}}\right)& \text{otherwise}\end{array}$

The particle separation parameter ${\lambda }_{ij}$, similar to the overlap parameter ${\beta }_{ij}$, is defined as follows:

${\lambda }_{ij}\left(T\right)=\frac{\alpha {\left(T\right)}^2\ast h_{ij}}{R_{ij}}$

Instead of the contact radius, the gap distance $h_{ij}$ is utilized as geometrical measure, which is determined via $D_{ij}$:

$h_{ij}=D_{ij}-\left(R_i+R_j\right)$

To determine the global ETC of the powder bed, the total heat flow out of the boundary wall ${\displaystyle \sum q_{ij,wall}}$ is used by applying Fourier’s law. Here, $l$ stands for the powder bed width in X-direction, e.g. the distance of conduction, and $\text{Δ}T$ denotes the temperature difference applied to the boundary walls.

$ETC={\displaystyle \sum q_{ij,wall}}\ast \frac{l}{\text{Δ}T}$

The algorithm is implemented in MATLAB 2021b (MathWorks Inc., Natick, United States). The material model presented in (Bartsch et al., 2021) is used. A total of 60 powder bed configurations with a width of 2 mm is created, which consist of 500 particles each. The PSD ranges from 20-60 µm with a normal distribution. A temperature difference of $\text{Δ}T$ = 60 K is imposed on the boundary walls, and the temperature range of 300–1600 K is investigated with a step size of 50 K. Note that thermo-physical phenomena such as sintering of the particles as well as the coexistence of the solid and liquid phase in the so-called ‘mushy zone’ are not considered.

3.2.2 Results and Discussion

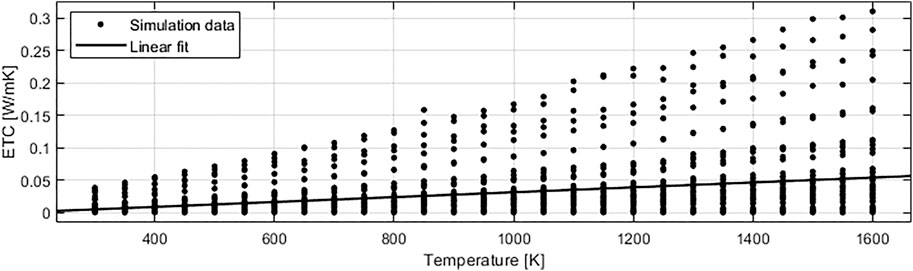
Figure 8 shows the computed ETC data as well as the linear fit, which is found to be

$ETC\left(T\right)=3.77\ast {10}^{-5}\ast T-0.0065$

FIGURE 8

FIGURE 8. ETC data from simulation.

The ETC data of the respective powder bed configurations is of linear nature. Powder beds differ in their individual slopes, though the majority tends towards a very flat slope. The observed variance is attributed to the geometrical powder bed configuration. As visualized in Figure 9, some powder bed configurations include notches, narrowing the cross section of heat flow.

FIGURE 9

FIGURE 9. Powder bed configuration with notch (arrow).

Compared to the experimental data of Section 3.1, the simulated ETC is significantly lower, e.g. ETC (300 K) = 0.00481 W/mK. This is attributed to the powder bed configuration, where no elastic particle deformation at the contact points is considered, i.e. point contact is modeled. This leads to local conductivities $k_{ij}^{contact}$ at the scale of ${10}^{-5}$ W/mK.

In summary, the network modeling approach in combination with the rain method is deemed suited to incorporate the uncertainties arising from the PSD and powder application process. It can therefore be used to extend experimental data to higher temperatures, as those are hard to measure, and to decrease experimental efforts in general. However, the presented model requires further work to be validated. This includes the extension to 3D spheres as well as the consideration of the mass and elastic deformation of the particles. Additionally, the influence of radiation at high temperatures may be investigated.

4 Designing Thermal Metamaterials by Using Bulk and Powder Material

To demonstrate the possibilities of including un-molten powder particles in PBF-LB/M part design, the study of (Narayana and Sato, 2012) is reproduced. Here, the engineering of an artificial material capable of controlling the path of energy transport via thermal conduction is shown. As use case, a hollow cylinder embedded in a block of a different material is used. On both sides of the setup a specific temperature is applied, 315 and 273 K respectively. Then the steady-state temperature profile is evaluated and the heat flow is visualized. The cylinder may be designed in different ways to achieve varying thermal behavior: either as homogeneous or metamaterial consisting of alternating sections of different materials.

Applying the methodology to PBF-LB/M, the two different materials are powder and bulk Ti-6Al-4V. In the first use case, the cylinder is designed as thermal barrier consisting of powder material only (see Figure 10A). The second use case, where the heat flux is to be concentrated in the middle of the cylinder, the cylinder consists of alternating, radial layers of powder and bulk material (see Figure 11A). The block the cylinder is embedded in consists of bulk Ti-6Al-4V. The model is implemented in COMSOL Multiphysics 5.2a (COMSOL Inc., Burlington, United States). The material data is based on (Bartsch et al., 2021), with the thermal conductivities of Section 2 and 3.1 added. Since the applied temperature difference is small, temperature-independent values at room temperature (293 K) are considered, see Table 2. The initial temperature is set to the minimum edge temperature of 273 K.

FIGURE 10

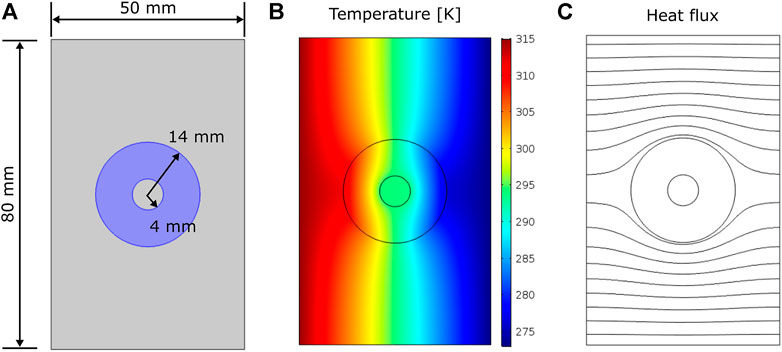
FIGURE 10. Thermal barrier simulation (A) Setup: blue–powder material, grey: solid material (B) Temperature distribution, (C) Heat flux lines.

FIGURE 11

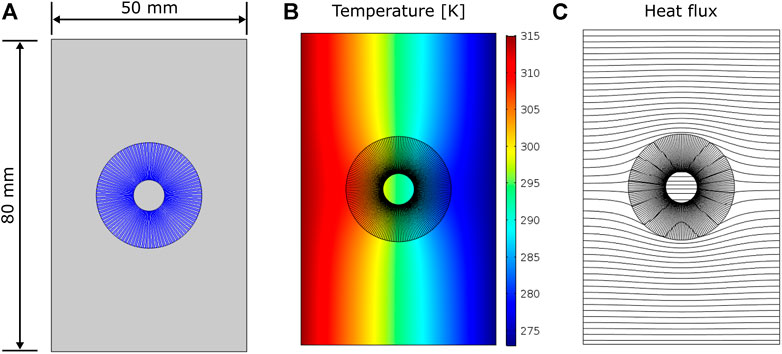
FIGURE 11. Thermal concentration simulation (A) Setup: blue–powder material, grey: solid material (B) Temperature distribution, (C) Heat flux lines.

TABLE 2

TABLE 2. Material model of Ti-6Al-4V used in demonstration.

The result of the thermal barrier simulation is shown in Figure 10. The overall temperature distribution is similar to the one presented in (Narayana and Sato 2012). The heat flux lines prove the effectiveness of the thermal barrier, as the heat flux lines avoid the powder cylinder. However, as the temperature within the cylinder has risen to 294 K, the thermal barrier is not perfect in its performance. Proper dimensioning of the cylinder’s thickness allows controlling the inner temperature, though.

The case of the thermal concentrator is shown in Figure 11. Here, it can be seen that the heat flux is directed towards the center of the cylinder. The center temperature is still 294 K, just as the first use case. This is on the one hand due to the steady-state study type, on the other hand the symmetrical design of the metamaterial facilitates both heat flow towards and from the center. As a result, the thermal gradient in the center area is greater than in the first use case (cf. Figure 10B and Figure 11B), where the temperature in the center is almost even.

Compared to (Narayana and Sato, 2012), it is concluded that the configuration of powder and bulk material is capable of reproducing the results and hence may be used to create thermal metamaterials. The corresponding designs can be complex and e.g. combine different aspects such as thermal barriers and concentration to not only direct heat towards a specific location, but also hold it there by shielding the colder side.

5 Conclusion

The thermal conductivity of grinded and polished Ti-6Al-4V PBF-LB/M samples has been measured using MTPS and TPS methods. Obtained values ranged from 4.00 to 6.18 W/mK for polished samples and thus are lower as those reported by Laser Flash Analysis (6.5 W/mK) for the same material but with different samples.

Measurements of the effective thermal conductivity of powder using MTPS resulted in ETC values correlating well with the tap and apparent density of the powder. For tap density values around 50% of bulk density, which is typical for PBF powder beds, ETC is within a close range around 0.13 W/mK. Measuring the ETC of a given powder using MTPS may therefore also allow to conclude on the powder’s tap density, which is a relevant property for powder quality in PBF processes. For different powder PSDs, no clear correlation with the ETC was found, however a tendency was observed that low particle sizes below 20 µm reduce the ETC.

While these values are valid at room temperature, a simulation of the steady-state heat conduction through a powder bed was set up to predict ETC values for higher temperatures up to 1600 K, which are not easy to obtain experimentally. It was found that the powder beds generated through a rain model vary significantly in their ETC, although the D10 and D90 values were kept constant. This can be attributed to the random local distribution of the particles as well as to differences in the actual individual powder particle sizes. This supports the observation from the experiments that the ETC of a powder may not be described by the PSD alone in a sufficient way. The model is able to show the linear increase in ETC with temperature. However, it underestimates the ETC by approx. two orders of magnitude compared to the experiments. One possible explanation is that elastic particle deformation has been neglected. Additionally, thermo-physical aspects such as sintering at high temperatures are not considered. Further work on incorporating the effect in the simulation is therefore planned.

It can be concluded that the thermal conductivity of the bulk material is approximately one order of magnitude higher than the ETC of the powder. This would allow for the design of thermal metamaterials by switching between densified and non-densified regions in a part, enabling the designer to manipulate heat flux as desired. To prove the concept, a study previously published by Narayana and Sato was partially reproduced using the values for thermal conductivity of bulk Ti-6Al-4V and powder Ti-6Al-4V, resulting in similar temperature distributions. Thus, it was shown that by Additive Manufacturing such metamaterials could easily be obtained and might be used for different applications in thermal shielding or concentration, e.g. to direct heat to the hot end of thermoelectric generators.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

Conception of the work: KB, BB, and DH; Data collection: KB, BB, and WC; Data analysis: KB, BB, ML, and DH; Drafting: KB, BB, and DH; Critical revision: KB, BB, and DH; Final approval: KB, BB, WC, ML, and DH.

Funding

This work was partially funded by the German Federal Ministry for Economic Affairs and Energy BMWi (grant number ZF4000519PO9).

Conflict of Interest

Author ML was employed by the company C-Therm Technologies Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors would like to thank C-Therm Technologies Ltd. (New Brunswick, Canada) for providing one of their MTPS sensor for the experimental measurements, and Florian Gerdts of Element 22 GmbH for the insightful discussions on powder properties.

References

Aberdeen, J., and Laby, T. H. (1926). Conduction of Heat through Powders and its Dependence on the Pressure and Conductivity of the Gaseous Phase. Proc. R. Soc. Lond. A 113 (764), 459–477. doi:10.1098/rspa.1926.0165

CrossRef Full Text | Google Scholar

Alkahari, M. R., Furumoto, T., Ueda, T., Hosokawa, A., Tanaka, R., Abdul Aziz, M. S., et al. (2012). Thermal Conductivity of Metal Powder and Consolidated Material Fabricated via Selective Laser Melting. Key Eng. Mater. 523-524, 244–249. doi:10.4028/www.scientific.net/kem.523-524.244

CrossRef Full Text | Google Scholar

Bandaru, P. R., Vemuri, K. P., Canbazoglu, F. M., and Kapadia, R. S. (2015). Layered Thermal Metamaterials for the Directing and Harvesting of Conductive Heat. AIP Adv. 5 (5), 053403. doi:10.1063/1.4916220

CrossRef Full Text | Google Scholar

Barbieri, L., Calzone, F., and Muzzupappa, M. (2019). “Form and Function: Functional Optimization and Additive Manufacturing,” in Advances on Mechanics, Design Engineering and Manufacturing II. Lecture Notes in Mechanical Engineering. Editors F. Cavas-Martínez, B. Eynard, F. J. Fernández Cañavate, D. G. Fernández-Pacheco, and P. M. Vincenzo Nigrelli (Cham: Springer International Publishing), 649–658. doi:10.1007/978-3-030-12346-8_63

CrossRef Full Text | Google Scholar

Bartsch, K., Herzog, D., Bossen, B., and Emmelmann, C. (2021). Material Modeling of Ti–6Al–4V Alloy Processed by Laser Powder Bed Fusion for Application in Macro-Scale Process Simulation. Mater. Sci. Eng. A 814, 141237. doi:10.1016/j.msea.2021.141237

CrossRef Full Text | Google Scholar

Batchelor, G. K., and O'Brien, R. W. (1977). Thermal or Electrical Conduction through a Granular Material. Proc. R. Soc. Lond. A 355 (1682), 313–333. doi:10.1098/rspa.1977.0100

CrossRef Full Text | Google Scholar

Benjamin, D., and Kirkpatrick, C. W. (1980). “Properties and Selection: Stainless Steels, Tool Material and Special-Pupose Metals,” in Metals Handbook (ASM International), 3.

Google Scholar

Bolzoni, L., Ruiz-Navas, E. M., and Gordo, E. (2013). Flexural Properties, Thermal Conductivity and Electrical Resistivity of Prealloyed and Master Alloy Addition Powder Metallurgy Ti–6Al–4V. Mater. Des. (1980-2015) 52, 888–895. doi:10.1016/j.matdes.2013.06.036

CrossRef Full Text | Google Scholar

Cha, J., Seo, J., and Kim, S. (2012). Building Materials Thermal Conductivity Measurement and Correlation with Heat Flow Meter, Laser Flash Analysis and TCi. J. Therm. Anal. Calorim. 109 (1), 295–300. doi:10.1007/s10973-011-1760-x

CrossRef Full Text | Google Scholar

Chantzis, D., Liu, X., Politis, D. J., El Fakir, O., Chua, T. Y., Shi, Z., et al. (2020). Review on Additive Manufacturing of Tooling for Hot Stamping. Int. J. Adv. Manuf. Technol. 109 (1-2), 87–107. doi:10.1007/s00170-020-05622-1

CrossRef Full Text | Google Scholar

Cheng, S. C., and Vachon, R. I. (1969). The Prediction of the Thermal Conductivity of Two and Three Phase Solid Heterogeneous Mixtures. Int. J. Heat Mass Transf. 12, 249–264. doi:10.1016/0017-9310(69)90009-x

CrossRef Full Text | Google Scholar

Cheng, G. J., and Yu, A. B. (2013). Particle Scale Evaluation of the Effective Thermal Conductivity from the Structure of a Packed Bed: Radiation Heat Transfer. Ind. Eng. Chem. Res. 52 (34), 12202–12211. doi:10.1021/ie3033137

CrossRef Full Text | Google Scholar

Cheng, G. J., Yu, A. B., and Zulli, P. (1999). Evaluation of Effective Thermal Conductivity from the Structure of a Packed Bed. Chem. Eng. Sci. 54, 4199–4209. doi:10.1016/s0009-2509(99)00125-6

CrossRef Full Text | Google Scholar

Chua, B.-L., Lee, H.-J., and Ahn, D.-G. (2018). Estimation of Effective Thermal Conductivity of Ti-6Al-4V Powders for a Powder Bed Fusion Process Using Finite Element Analysis. Int. J. Precis. Eng. Manuf. 19 (2), 257–264. doi:10.1007/s12541-018-0030-2

CrossRef Full Text | Google Scholar

De Beer, M., Rousseau, P. G., and Du Toit, C. G. (2018). A Review of Methods to Predict the Effective Thermal Conductivity of Packed Pebble Beds, with Emphasis on the Near-Wall Region. Nucl. Eng. Des. 331, 248–262. doi:10.1016/j.nucengdes.2018.02.029

CrossRef Full Text | Google Scholar

de Moraes, D., and Czekanski, A. (2018). Parametric Thermal FE Analysis on the Laser Power Input and Powder Effective Thermal Conductivity during Selective Laser Melting of SS304L. JMMP 2 (3), 47. doi:10.3390/jmmp2030047

CrossRef Full Text | Google Scholar

Emanuel, M., Brown, B. C., Ackermann, S. L. G., and Bateman, R. (2022). MTPS Analytical Temperature and Heat Flux Solution With Thermal Contact Resistance. ASME. J. Heat Transfer. 144 (7), 071401. doi:10.1115/1.4054383

CrossRef Full Text | Google Scholar

Emanuel, M. (2006). “Effusivity Sensor Package (ESP) System for Process Monitoring and Control,” in Proceedings of the 28th International Thermal Conductivity Conference, 256–268.

Google Scholar

Fan, C. Z., Gao, Y., and Huang, J. P. (2008). Shaped Graded Materials with an Apparent Negative Thermal Conductivity. Appl. Phys. Lett. 92 (25), 251907. doi:10.1063/1.2951600

CrossRef Full Text | Google Scholar

Galati, M., Calignano, F., Viccica, M., and Iuliano, L. (2020). Additive Manufacturing Redesigning of Metallic Parts for High Precision Machines. Crystals 10 (3), 161. doi:10.3390/cryst10030161

CrossRef Full Text | Google Scholar

Gong, X., Cheng, B., Price, S., and Chou, K. (2013). “Powder-Bed Electron-Beam-Melting Additive Manufacturing: Powder Characterization, Process Simulation and Metrology,” in ASME Early Career Technical Conference (ECTC), 59–64.

Google Scholar

Gu, H., Gong, H., Dilip, J. J. S., Pal, D., Hicks, A., Doak, H., et al. (2014). “Effects of Powder Variation on the Microstructure and Tensile Strength of Ti6Al4V Parts Fabricated by Selective Laser Melting,” in Proceedings of the 25th Annual International Solid Freeform Fabrication Symposium, 470–483.

Google Scholar

Gusarov, A. V., Laoui, T., Froyen, L., and Titov, V. I. (2003). Contact Thermal Conductivity of a Powder Bed in Selective Laser Sintering. Int. J. Heat Mass Transf. 46 (6), 1103–1109. doi:10.1016/S0017-9310(02)00370-8

CrossRef Full Text | Google Scholar

Gustafsson, S. E., Karawacki, E., and Khan, M. N. (1974). Transient Hot-Strip Method for Simultaneously Measuring Thermal Conductivity and Thermal Diffusivity of Solids and Fluids. J. Phys. D Appl. Phys. 12, 1411–1421.

Google Scholar

Gustafsson, S. E. (1991). Transient Plane Source Techniques for Thermal Conductivity and Thermal Diffusivity Measurements of Solid Materials. Rev. Sci. Instrum. 62 (3), 797–804. doi:10.1063/1.1142087

CrossRef Full Text | Google Scholar

Healy, J. J., de Groot, J. J., and Kestin, J. (1976). The Theory of the Transient Hot-Wire Method for Measuring Thermal Conductivity. Phys. B+C 82 (2), 392–408. doi:10.1016/0378-4363(76)90203-5

CrossRef Full Text | Google Scholar

Herzog, D., Asami, K., Scholl, C., Ohle, C., Emmelmann, C., Sharma, A., et al. (2021a). Design Guidelines for Laser Powder Bed Fusion in Inconel 718, (accepted paper): JLA21-CF-ICALEO2021-00164. J. Laser Appl. 34 (1), 012015. doi:10.2351/7.0000508

CrossRef Full Text | Google Scholar

Herzog, D., Bossen, B., and Bartsch, K. (2021b). “Hot Isostatic Pressing in Additive Manufacturing – a Costly Necessity or a Possibility to Add Value?,” paper EP215149292 in Proc. Of EuroPM 2021 (European Powder Metallurgy Association).

Google Scholar

Hu, R., Zhou, S., Shu, W., Xie, B., Ma, Y., and Luo, X. (2016). Directional Heat Transport through Thermal Reflection Meta-Device. AIP Adv. 6 (12), 125111. doi:10.1063/1.4973309

CrossRef Full Text | Google Scholar

Kannuluik, W. G., and Martin, L. H. (1933). Conduction of Heat in Powders. Proc. R. Soc. Lond. A 141 (843), 144–158. doi:10.1098/rspa.1933.0108

CrossRef Full Text | Google Scholar

Kanuparthi, S., Subbarayan, G., Siegmund, T., and Sammakia, B. (2008). An Efficient Network Model for Determining the Effective Thermal Conductivity of Particulate Thermal Interface Materials. IEEE Trans. Comp. Packag. Technol. 31 (3), 611–621. doi:10.1109/TCAPT.2008.2001839

CrossRef Full Text | Google Scholar

Lee, C., Zhuang, L., Lee, D., Lee, S., Lee, I.-M., and Choi, H. (2017). Evaluation of Effective Thermal Conductivity of Unsaturated Granular Materials Using Random Network Model. Geothermics 67 (9), 76–85. doi:10.1016/j.geothermics.2017.01.007

CrossRef Full Text | Google Scholar

Liang, Y. (2015). Expression for Effective Thermal Conductivity of Randomly Packed Granular Material. Int. J. Heat Mass Transf. 90 (7), 1105–1108. doi:10.1016/j.ijheatmasstransfer.2015.07.059

CrossRef Full Text | Google Scholar

Liu, R., Wang, Z., Sparks, T., Liou, F., and Newkirk, J. (2017). “Aerospace Applications of Laser Additive Manufacturing,” in Laser Additive Manufacturing (Elsevier), 351–371. doi:10.1016/b978-0-08-100433-3.00013-0

CrossRef Full Text | Google Scholar

Loh, G. H., Pei, E., Harrison, D., and Monzón, M. D. (2018). An Overview of Functionally Graded Additive Manufacturing. Addit. Manuf. 23, 34–44. doi:10.1016/j.addma.2018.06.023

CrossRef Full Text | Google Scholar

Meakin, P., and Jullien, R. (1987). Restructuring Effects in the Rain Model for Random Deposition. J. Phys. Fr. 48 (10), 1651–1662. doi:10.1051/jphys:0198700480100165100

CrossRef Full Text | Google Scholar

Mills, K. C. (2002). Recommended Values of Thermophysical Properties for Selected Commercial Alloys. Cambridge: Woodhead.

Google Scholar

Moser, D., Pannala, S., and Murthy, J. (2016). Computation of Effective Thermal Conductivity of Powders for Selective Laser Sintering Simulations. ASME. J. Heat Transfer. 138 (8), 082002. doi:10.1115/1.4033351

CrossRef Full Text | Google Scholar

Narayana, S., and Sato, Y. (2012). Heat Flux Manipulation with Engineered Thermal Materials. Phys. Rev. Lett. 108 (21), 214303. doi:10.1103/PhysRevLett.108.214303

PubMed Abstract | CrossRef Full Text | Google Scholar

Plocher, J., and Panesar, A. (2019). Review on Design and Structural Optimisation in Additive Manufacturing: Towards Next-Generation Lightweight Structures. Mater. Des. 183, 108164. doi:10.1016/j.matdes.2019.108164

CrossRef Full Text | Google Scholar

Powell, M. J. D. (1964). An Efficient Method for Finding the Minimum of a Function of Several Variables without Calculating Derivatives. Comput. J. 7 (2), 155–162. doi:10.1093/comjnl/7.2.155

CrossRef Full Text | Google Scholar

Rausch, M. H., Krzeminski, K., Leipertz, A., and Fröba, A. P. (2013). A New Guarded Parallel-Plate Instrument for the Measurement of the Thermal Conductivity of Fluids and Solids. Int. J. Heat Mass Transf. 58 (1-2), 610–618. doi:10.1016/j.ijheatmasstransfer.2012.11.069

CrossRef Full Text | Google Scholar

Sahimi, M., and Tsotsis, T. T. (1997). Transient Diffusion and Conduction in Heterogeneous Media: Beyond the Classical Effective-Medium Approximation. Ind. Eng. Chem. Res. 36 (8), 3043–3052. doi:10.1021/ie960602k

CrossRef Full Text | Google Scholar

Scheithauer, U., Kordaß, R., Kevin, N., Eichenauer, M. F., Hartmann, M., Abel, J., et al. (2019). “Potentials and Challenges of Additive Manufacturing Technologies for Heat Exchanger,” in Advances in Heat Exchangers. Editors L. C. Gómez, and V. M. Velázquez Flores (IntechOpen). doi:10.5772/intechopen.80010

CrossRef Full Text | Google Scholar

Seyda, V., Herzog, D., and Emmelmann, C. (2017). Relationship between Powder Characteristics and Part Properties in Laser Beam Melting of Ti-6Al-4V, and Implications on Quality. J. Laser Appl. 29 (2), 22311. doi:10.2351/1.4983240

CrossRef Full Text | Google Scholar

Stautner, W., Vanapalli, S., Weiss, K.-P., Chen, R., Amm, K., Budesheim, E., et al. (2017). The Scope of Additive Manufacturing in Cryogenics, Component Design, and Applications. IOP Conf. Ser. Mater. Sci. Eng. 278, 12134. doi:10.1088/1757-899X/278/1/012134

CrossRef Full Text | Google Scholar

K. D. Timmerhaus (Editor) (1963). Advances in Cryogenic Engineering (Boston, MA: Springer US).

Google Scholar

Tsotsas, E., and Martin, H. (1987). Thermal Conductivity of Packed Beds: A Review. Chem. Eng. Process. Process Intensif. 22 (1), 19–37. doi:10.1016/0255-2701(87)80025-9

CrossRef Full Text | Google Scholar

van Antwerpen, W., Du Toit, C. G., and Rousseau, P. G. (2010). A Review of Correlations to Model the Packing Structure and Effective Thermal Conductivity in Packed Beds of Mono-Sized Spherical Particles. Nucl. Eng. Des. 240 (7), 1803–1818. doi:10.1016/j.nucengdes.2010.03.009

CrossRef Full Text | Google Scholar

Vemuri, K. P., Canbazoglu, F. M., and Bandaru, P. R. (2014). Guiding Conductive Heat Flux through Thermal Metamaterials. Appl. Phys. Lett. 105 (19), 193904. doi:10.1063/1.4901885

CrossRef Full Text | Google Scholar

Wakao, N., and Kato, K. (1969). Effective Thermal Conductivity of Packed Beds. J. Chem. Eng. Jpn. 2 (1), 24–33. doi:10.1252/jcej.2.24

CrossRef Full Text | Google Scholar

Wei, L. C., Ehrlich, L. E., Powell-Palm, M. J., Montgomery, C., Beuth, J., and Malen, J. A. (2018). Thermal Conductivity of Metal Powders for Powder Bed Additive Manufacturing. Addit. Manuf. 21, 201–208. doi:10.1016/j.addma.2018.02.002

CrossRef Full Text | Google Scholar

Wu, H., Gui, N., Yang, X., Tu, J., and Jiang, S. (2016). Effect of Scale on the Modeling of Radiation Heat Transfer in Packed Pebble Beds. Int. J. Heat Mass Transf. 101, 562–569. doi:10.1016/j.ijheatmasstransfer.2016.05.090

CrossRef Full Text | Google Scholar

Wu, T., Ozpineci, B., Chinthavali, M., Wang, Z., Debnath, S., and Campbell, S. (2017). “Design and Optimization of 3D Printed Air-Cooled Heat Sinks Based on Genetic Algorithms,” in 2017 IEEE Transportation Electrification Conference and Expo (ITEC) (IEEE), 650–655. doi:10.1109/itec.2017.7993346

CrossRef Full Text | Google Scholar

Yagi, S., and Kunii, D. (1957). Studies on Effective Thermal Conductivities in Packed Beds. AIChE J. 3 (3), 373–381. doi:10.1002/aic.690030317

CrossRef Full Text | Google Scholar

Yun, T. S., and Evans, T. M. (2010). Three-Dimensional Random Network Model for Thermal Conductivity in Particulate Materials. Comput. Geotech. 37 (7-8), 991–998. doi:10.1016/j.compgeo.2010.08.007

CrossRef Full Text | Google Scholar

Zajas, J., and Heiselberg, P. (2013). Determination of the Local Thermal Conductivity of Functionally Graded Materials by a Laser Flash Method. Int. J. Heat Mass Transf. 60 (12), 542–548. doi:10.1016/j.ijheatmasstransfer.2013.01.030

CrossRef Full Text | Google Scholar

Ziegler, W. T., Mullins, J. C., and Hwa, S. C. P. (1963). “Specific Heat and Thermal Conductivity of Four Commercial Titanium Alloys from 20° to 300°K,” in Advances in Cryogenic Engineering. Editor K. D. Timmerhaus (Boston, MA: Springer US), 268–277. doi:10.1007/978-1-4757-0528-7_33

CrossRef Full Text | Google Scholar