- 1Center for 3D Medical Fabrication, Atlanta, GA, United States
- 2Coulter Department of Biomedical Engineering, Georgia Institute of Technology, Atlanta, GA, United States
3D-printed biomaterials have become ubiquitous for clinical applications including tissue-mimicking surgical/procedure planning models and implantable tissue engineering scaffolds. In each case, a fundamental hypothesis is that printed material mechanical properties should match those of the tissue being replaced or modeled as closely as possible. Evaluating these hypotheses requires 1) consistent nonlinear elastic/viscoelastic constitutive model fits of 3D-printed biomaterials and tissues and 2) metrics to determine how well 3D-printed biomaterial mechanical properties match a corresponding tissue. Here we utilize inverse finite element modeling to fit nonlinear viscoelastic models with Neo-Hookean kernels to 29 Polyjet 3D-printed tissue-mimicking materials. We demonstrate that the viscoelastic models fit well with R2 > 0.95. We also introduce three metrics ( least-squares difference, Kolmogorov–Smirnov statistics, and the area under stress/strain or load/displacement curve) to compare printed material properties to tissue properties. All metrics showed lower values for better matches between 3D-printed materials and tissues. These results provide a template for comparing 3D-printed material mechanical properties to tissue mechanical properties, and therefore, a basis for testing the fundamental hypotheses of 3D-printed tissue-mimicking materials.
Introduction
3D printing has become ubiquitous in clinical applications for a wide variety of disciplines. These clinical applications include 3D-printed implanted medical devices and tissue engineering scaffolds (Zopf et al., 2013; Di Prima et al., 2016; Ricles et al., 2018; Zhou et al., 2018) as well as models for surgical and procedure planning (Sommer et al., 2013; Pacione et al., 2016; Gocer et al., 2019; Chen et al., 2020a; Chen et al., 2020b; Bellia-Munzon et al., 2020; Capucha et al., 2020; Cho et al., 2020; Damon et al., 2020; Ghazi and Teplitz, 2020; Illmann et al., 2020; Javan et al., 2020; Kim et al., 2020; Levin et al., 2020; Liu et al., 2020; McMillan et al., 2020; Meglioli et al., 2020; Stramiello et al., 2020; Vannucci et al., 2020; Wang et al., 2020; Witowski et al., 2020; Ghazi et al., 2021). Although these applications may appear disparate at first glance, they are connected on two levels. First, tissue engineering scaffold development will benefit from simulating fixation and mechanical performance in tissue-mimicking materials 3D printed to simulate clinical defects. Second, both fields hypothesize that improving the match of the scaffold or model mechanical behavior to that of the tissue being replaced/simulated increases clinical benefit. For tissue engineering, this hypothesis states that a scaffold more closely matching the mechanics of the tissue to be replaced will produce better tissue regeneration (see for example Lin et al., 2004; Koh et al., 2019; Mardling et al., 2020; Chao et al., 2021; Ghorbani et al., 2021). For surgical planning, the hypothesis states that the closer a 3D-printed model matches tissue mechanics the better the clinical and training outcome. This is especially critical for example in haptic feedback for training (Grillo et al., 2018; Ratinam et al., 2019; Pietrabissa et al., 2020; Tejo-Otero et al., 2020), for practicing complex surgical procedures like transseptal puncture in cardiology (Bezek et al., 2020), and in developing cardiac valves tested in flow loops to achieve realistic hemodynamic and fluid–structure interaction (Vukicevic et al., 2017; Ferrari et al., 2019; Ferrari et al., 2020; Levin et al., 2020; Vukicevic et al., 2020).
Rigorously testing these hypotheses requires two fundamentals. First, the properties of the tissues of interest and the 3D-printed scaffolds and models must be characterized using the most appropriate and comparable constitutive models. Especially for the soft tissues, this would include nonlinear elastic and viscoelastic models. Second, there must be appropriate metrics that can be used to objectively compare constitutive properties for many different materials, even when these properties are very different. The goal of this study is to address both issues by 1) fitting nonlinear viscoelastic models to 3D-printed materials using an inverse finite element optimization approach by FEBio(Maas et al., 2012; Maas et al., 2017) and 2) developing metrics to compare the mechanical behavior tissue and 3D-printed materials using both nonlinear elastic and nonlinear viscoelastic constitutive models. We specifically focus in this study on using 3D-printed Polyjet materials.
Matching complex and varied tissue mechanical behavior has motivated the use of multi-material Polyjet 3D printers like the Stratasys Connex line and Stratasys J750/J850 Polyjet printers to create tissue-mimicking phantoms. Since detailed information on constitutive models for these materials is not readily available, recent studies have sought to characterize Polyjet material mechanical properties in relation to tissue properties. Cloonan et al. (2014) characterized the nonlinear elastic behavior of Connex 3D-printed Tango material using three to five term Ogden strain energy functions. They showed qualitative agreement with the nonlinear elastic Abdominal Aorta Aneurysm (AAA) tissue stress distributions (Raghavan and Vorp, 2000). Ruiz de Galarreta et al. (2017) used an exponential anisotropic strain energy function to compare Stratasys TangoPlus material stress distributions to those generated using the same strain energy function developed by Choi and Vito for canine pericardium (Choi and Vito, 1990). Finally, other studies have used simpler constitutive models like linear elastic modulus or Shore hardness values (Severseike et al., 2019; Bezek et al., 2020; Tejo-Otero et al., 2020), to relate Polyjet material to tissue mechanics.
While an important step, these studies do not provide the extensive constitutive modeling needed to completely characterize Polyjet materials in relation to tissue behavior for four reasons. First, Polyjet materials exhibit nonlinear viscoelastic behavior with stress relaxation, large deformation, and nonlinear stress-strain behavior. Second, tissues exhibit nonlinear anisotropic viscoelastic behavior with an extremely broad range of constitutive parameters, see for example (Puso and Weiss, 1998; Holzapfel et al., 2004; Motallebzadeh et al., 2013; Polzer et al., 2015; Chang et al., 2020). Since both J750 materials and tissues exhibit nonlinear viscoelastic behavior, it is necessary to characterize the Polyjet materials using nonlinear viscoelastic constitutive models to provide the most complete comparison of 3D-printed material to tissues. The nonlinear viscoelastic models can be used to compare with the tissue nonlinear elastic constitutive models as well. Finally, given that the Stratasys J750 with Digital Anatomy Printing (DAP) contains 96 distinct materials, a methodology to automatically determine the best-fit 3D-printed material from a large material database of nonlinear viscoelastic materials to a given tissue is needed. For these purposes, a complete constitutive characterization is needed for the printed materials to generate the needed force-displacement, force-time, stress-strain, and/or stress-time curves that can be used to compute metrics comparing 3D-printed behavior to tissue behavior.
In this study we present compressible and incompressible isotropic nonlinear viscoelastic constitutive models fit for the Stratasys J750 fundamental Shore, the DAP blood vessel materials, and the DAP structural heart materials. These are 29 of the 96 (at present) materials available in this system. We also present three metrics (least square difference, Kolmogorov–Smirnov statistics, and the area under force/stress-time/displacement/strain curves) computed in a MATLAB (MathWorks) program from a database of 3D-printed materials to find the best-matched material to mimic a given tissue mechanical behavior. Examples are shown for the tympanic membrane, the nasal cartilage, and the aortic wall tissue.
Materials and Methods
Test specimen geometry for both the 3D-printed specimens and finite element models for optimization was based on the ASTM D638 “Standard Test Method for Tensile Properties of Plastics” Type V specimen geometry (length: 63.5 mm, maximum width: 11 mm, thickness: 2 mm). Shore 30/35/40/50/60/70/85/95, DAP Blood Vessel materials, and DAP Structural Heart Materials (29 materials total) were printed and tested with n = 4-6 specimens per group.
3D Material Printing
The ASTM D638 dogbone STL file was loaded and duplicated into n = 6 per shore group using GrabCAD (Stratasys). The shore levels used were 30, 35, 40, 50, 60, 70, 85, and 95. Each comprises different mixed ratios of the Stratasys rigid Vero material and flexible Agilus material. For blood vessel specimens, the same dogbone STL file was loaded and duplicated into n = 6 specimens per group into GrabCAD and assigned the six different blood vessel wall anatomy function groups: compliant, moderately compliant, slightly compliant, low compliant, semi-rigid, and rigid. Structural heart specimens consisted of myocardium, leaflet, chordae, and vessel wall with n = 4 specimens per group.
Specimen Mechanical Testing
Printed dogbones were post-processed to remove all support structures. Each group (n = 4–6) was mechanically tested using an Instron 5,944 Single Column 2 kN universal Tensile Tester. Specimens were ramped in tension up to 10 mm displacement (1 mm for stiffer materials) over 60 s and then held at 10 mm displacement (1 mm for stiffer materials) for an additional 300 s with the resulting force, displacement, and time data exported to an Excel file. Once all specimens were printed and mechanically tested, they were fit using the constitutive models described in Nonlinear Viscoelastic Constitutive Model Theory using the methods described in Constitutive Model Parameter Fitting Using Inverse Finite Element Modeling.
Nonlinear Viscoelastic Constitutive Model Theory
The large deformation and nonlinear stress-strain relationship exhibited by the Stratasys J750 materials requires nonlinear constitutive models to account for this behavior. Adding rate-dependent and stress relaxation behavior additionally requires that we model J750 materials as viscoelastic. We sequentially describe the elastic and stress relaxation components of the resulting constitutive models.
A basic measure of deformation is the stretch ratio λ, a ratio of the specimen length after deformation l to the specimen before deformation l’. Furthermore, we have a stretch ratio in each of three directions, where we denote 1 as the x direction, 2 as the y direction, and 3 as the z direction:
where λi is the stretch ratio in the ith testing direction. For deformations in the principal directions (i.e., no shear deformation) the deformation gradient tensor Fij is defined in terms of the stretch ratios as:
The right Cauchy Deformation tensor Cij is defined in terms of the deformation gradient tensor Fij as:
The scalar volume change J is the determinant of Fij;
For materials that are nearly incompressible (nearly zero volume change), the deviatoric portion of the deformation measures are defined as:
Strain energy functions W are used to characterize nonlinear elastic behavior. We utilized the simplest isotropic nonlinear elastic constitutive models that would characterize the 3D-printed Stratasys behavior, compressible and incompressible Neo-Hookean strain energy functions. These are defined in FEBio (FEBio User Manual 3.3) as:
Compressible Neo-Hookean model:
Incompressible Neo-Hookean model:
where E denotes Young’s modulus and ν the Poisson’s ratio for the compressible Neo-Hookean material (Eq. (5a)) with stretch ratios λi (Eq. 1) and Jacobian (volume change) J (Eq. (4)). For the incompressible Neo-Hookean material often written with the coefficient c1 (Eq. (5b)) and(5μ) denotes a shear modulus (2*c1) and K is a bulk modulus chosen as 500–1,000*c1 to enforce the near incompressibility condition. Note that for the compressible material, the shear modulus, Young’s modulus, and Poisson’s ratio are related through the standard linear elastic relationship:
Thus, as the compressible material approaches incompressibility, Poisson’s ratio in the limit will reach 0.5 and Young’s modulus will be three times the shear modulus, six times c1. The second Piola–Kirchoff (second PK) elastic stress tensor
Compressible material:
Incompressible material:
where Dev indicates the deviatoric component defined as:
Accounting for the stress relaxation exhibited by the J750 materials requires a viscoelastic model. In this case, viscoelasticity was incorporated using a nonlinear stress-strain function to represent instantaneous elastic response coupled with stress relaxation through a reduced relaxation function that is independent of deformation. Thus, the nonlinear elastic kernels of Eq.(6a) and (6b) are modified by a reduced relaxation function that characterizes the relaxation behavior. Stress at a given time of loading is history-dependent, requiring integration of the strain history over the loading period together with a stress relaxation function that characterizes how stress relaxes overtime for a fixed displacement. We chose a 3-term Prony Series to model stress relaxation:
where γ1, γ2, and γ3 are model coefficients, τ1, τ2, and τ3 are model coefficients representing characteristic relaxation times, s is the current time in the loading history and t is the final loading time. The final loading time t for all tests was 360 s. The complete second Piola–Kirchoff (second PK) stress tensor as a function of time for a nonlinear compressible viscoelastic material can then be represented as:
where
where p is the hydrostatic pressure, J is the volume change, Cij is the right Cauchy Deformation tensor,
Constitutive Model Parameter Fitting Using Inverse Finite Element Modeling
For both nonlinear viscoelastic models, we fit not only the nonlinear elastic coefficients (c1 or E and ν) but also the stress relaxation coefficients γ1, γ2, γ3, τ1, τ2, and τ3 using inverse finite element modeling. This approach minimizes the difference in a least-squares sense over the entire 360 s loading period between the finite element model (Figure 1) reaction force at the rigid grips and the experimental force:
where Fe denotes the experimental reaction force and Fm denotes the model reaction force. We fit both the compressible and incompressible versions of the Neo-Hookean elastic kernel, as many investigators model soft tissues as incompressible.

FIGURE 1. (A) Finite element model of ASTM D638 dumbbell test specimen used to test J750 materials. (B) Actual 3D printed J750 Shore material undergoing tensile stress relaxation test in Instron. The finite element model was created using FEBio Preview 1.5. The model was analyzed using either FEBio 2.9.1 or FEBio 3.3.1 using the parameter optimization tool to fit the nonlinear viscoelastic model parameters. Rigid bodies at the end of the specimen allow for tension only contact mimic specimen gripping. The right platen was displaced to match the time-displacement curve from experimental tests.
All finite element modeling and parameter optimization fitting of constitutive model coefficients were performed using the FEBio software suite, versions 2.91 and 3.1.0 (Maas et al., 2012; Maas et al., 2017). Due to the long computing time (∼10–100 h) for nonlinear viscoelastic material coefficient fitting (resulting from nonlinear iterations for the optimization fit and iteratively solving a nonlinear finite element problem within each optimization iteration), all models were run on the Hive Cluster high performance computing cluster supported by the Partnership for Advanced Computing Environment (PACE) at Georgia Tech. FEBio PreView version 1.5 was used to generate a finite element model of the ASTM D638 dumbbell test specimen using the same STL file used for the J750 printing. The dumbbell finite element model consisted of 14,515 10-node tetrahedral elements with 28,303 nodes (Figure 1A). The parameter optimization module in FEBio uses the Levenberg–Marquardt algorithm to update material parameters that minimize the square difference between model and experimental reaction forces. The testing grips in this model were considered rigid materials under the FEBio sliding elastic tension contact algorithm with the J750 material dumbbell specimen. Default convergence parameters were chosen in FEBio for both the nonlinear optimization iteration in the Levenberg-Marquardt algorithm and the sub-optimization nonlinear stress equilibrium problem, with the exception that the displacement convergence tolerance for the stress equilibrium problem was set to 0.01.
The nonlinear viscoelastic constitutive models applied here contain either eight (compressible Neo-Hookean case) or seven (incompressible Neo-Hookean case) parameters to fit a single uniaxial test. Fitting complex constitutive models using least-squares optimization approaches often leads to non-unique material parameters, i.e. multiple parameter sets will give equivalent fits to experimental data, also known as coefficient identifiability issues (Safa et al., 2021). Safa et al. (2021) recommend using a randomized multi-start least-squares fitting approach. While this process is feasible if the objective for fitting can be analytically derived, it is not feasible to use when each optimization solution uses an inverse nonlinear finite element modeling method requiring significant computing time. Therefore, to address coefficient variability, we averaged initial optimization results for all materials, labeled as Coefficient Set 1 (Coeff Set 1), and used these average values as the initial guess for a second optimization run with a lower and upper bound on the parameters set to ±10% of the initial guess. This second optimization run was labeled Coefficient Set 2 (Coeff Set 2).
A coefficient of determination (R2 value) was calculated in MATLAB (Mathworks) for each fit between reaction forces from the constitutive model fit used for the finite element model (Figure 1) and experimental reaction force data. An R2 value greater than 0.95 is considered a good fit for the constitutive model of experimental data (Humphrey, 2002).
Metrics for Best Matched 3D-Printed Material to Tissue Mechanics
A prime motivation for characterizing 3D-printed materials is to determine which 3D-printed material best mimics a given tissue behavior. This motivation plays into the most basic hypotheses concerning clinical applications of 3D-printed models. In training, we hypothesize that the 3D-printed material which best mimics the target tissue mechanics will provide the most realistic haptic experience, where the training outcome is assessed by survey methods. In medical device development, we hypothesize that device performance is best assessed using 3D-printed tissue models where the 3D-printed material most closely mimics tissue mechanics. For nonlinear viscoelastic materials, it is not a straightforward task to pick the materials that best match or at least bound a given tissue mechanical response from a wide range of materials (29 fit in the current study, but up to 96 in the current DAP database).
We, therefore, propose three metrics for assessing the 3D-printed material that best mimics either the nonlinear elastic or viscoelastic behavior of a given tissue. The first method is the total least square difference between forces from the 3D-printed material compared to the forces (stresses can also be used) from a tissue under the same time-dependent deformation. Note that this parameter is used to drive the initial optimization fitting of Eq. (12). The second method is using a two-sample Kolmogorov–Smirnov test (Press and Teukolsky, 1988). We used the KStest2 Kolmogorov–Smirnov statistics test version in MATLAB which tests the null hypothesis that two data vectors come from the same populations. In our case, we test the null hypothesis that force vectors matched over time for the stress relaxation test come from the same material, i.e., the 3D-printed material has the same force vs. time distribution as the tissue of interest. Note that this can readily be applied to force-displacement curves, stress-strain curves, or stress-time curves. Our hypothesis is that lower KStest2 p values will delineate 3D-printed materials that better match target tissue mechanical behavior. The third parameter is the difference in the total area under the force-time curve for the experimental data versus model fit. This area was calculated using the trapz trapezoidal numerical integration function in MATLAB.
The tissue-mimicking 3D-printed fit metrics may be implemented in two ways. First, if constitutive parameters for a given tissue are reported, which may include nonlinear elastic or nonlinear viscoelastic, isotropic, or anisotropic, these properties may directly be input to the FEBio model of Figure 1. The resulting force-time curve under the ramp displacement curve described in the mechanical testing section can be computed in FEBio and saved in an Excel file. The force-time curve for all 3D-printed Stratasys materials from the mechanical test is also stored in an Excel file. Both datasets are read into a MATLAB code that calculates the summed least-square difference, the KStest2 p value, and the difference in the area under the force-time curve. The program then ranks how well the 3D-printed materials represent tissue behavior based on the three fit parameters. If the material is anisotropic, this matching procedure may be performed over all desired testing directions, and the ranking of 3D-printed materials performed for the aggregate of testing direction responses. We illustrate this approach for the human tympanic membrane (Motallebzadeh et al., 2013) and the human nasal cartilage (Chang et al., 2020) for published nonlinear viscoelastic constitutive parameters, searching the J750 standard and the DAP blood vessel data. Nonlinear elastic tissue data can be readily assessed using this approach as well.
Second, if either force-displacement or stress-strain data is reported or can be derived from published data, the experimental setup from the published tissue setup may be modeled with the Stratasys material parameters to generate a database to compare with tissue results. Polzer et al. (2015) performed biaxial testing of the porcine aortic wall, providing extensive raw first Piola-Kirchoff stress vs. stretch data for axial and circumferential directions. The first PK stresses were converted to Cauchy stress vs. stretch results. We modeled the biaxial test results for one specimen in FEBio using rigid tension contact (Figure 2) and computed axial and circumferential Cauchy stress vs. stretch results for all compressible Neo-Hookean models of the Stratasys materials. We then computed the least-square difference, Kolmogorov-Smirnov statistics, and the area under stress-strain curve to assess which 3D-printed material best matched the experimental porcine aorta wall mechanical behavior.

FIGURE 2. Finite element model was used to simulate biaxial testing of the porcine aorta wall tissue specimens reported by Polzer et al. Specimen dimensions matched those given by Polzer and displacements of rigid test grips were set to match the stretch ratios and loading rate. Cauchy stress versus stretch was calculated for all J750 constitutive models using the model. Model of aorta wall specimen contained 5,184 8-node hexahedral elements and 6,845 nodes. Sliding elastic tension contact was assumed between rigid grips and specimen.
Results
Complete Coeff Set 1 and Coeff Set 2 parameter fits and corresponding R2 values are presented for the following using Neo-Hookean Prony Series Viscoelastic models under a compressible or incompressible assumption as noted:
1) J750 Shore materials; compressible (Table 1)
2) J750 Shore materials; incompressible (Table 2)
3) J750 DAP Blood Vessel Wall materials; compressible (Table 3)
4) J750 DAP Blood Vessel Wall Materials; incompressible (Table 4)
5) J750 DAP Structural Heart materials; compressible (Table 5)
6) J750 DAP Structural Heart materials; incompressible (Table 6)
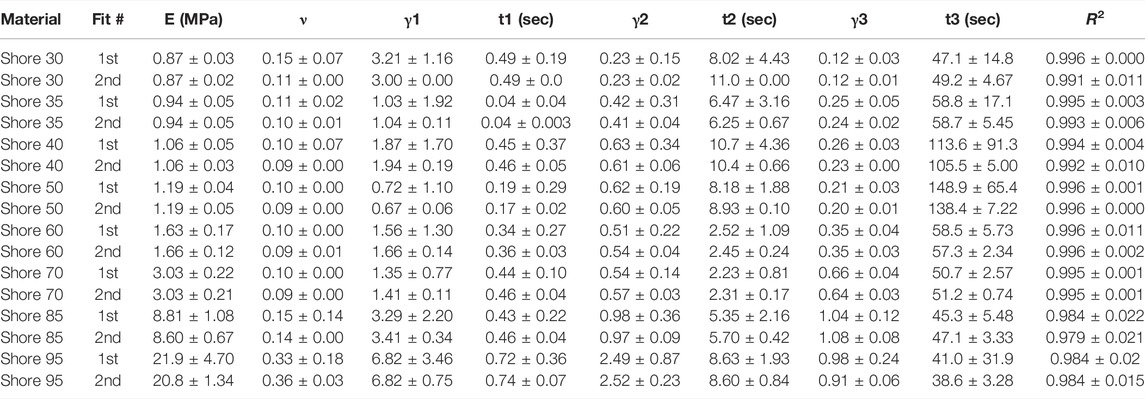
TABLE 1. Nonlinear viscoelastic compressible Neo-Hookean fit to J750 Shore materials. Table of compressible nonlinear viscoelastic compressible Neo-Hookean parameters for the J750 Shore materials along with the R2 values of the fit between the constitutive model and experimental data (n = 6 specimens per material except for Shore 30 with n = 5 specimens per material). Coefficient Set refers to the initial guess (first) with wide bounds on the parameters followed by a second optimization run with the bounds being the mean parameters from the first optimization run ±10% of the mean.
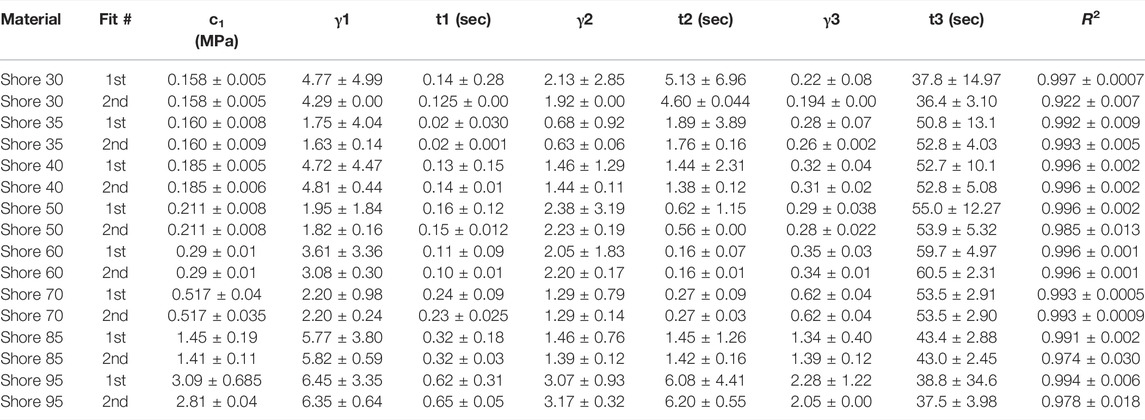
TABLE 2. Nonlinear viscoelastic incompressible Neo-Hookean fit to J750 Shore materials. Table of compressible nonlinear viscoelastic compressible Neo-Hookean parameters for the J750 Shore materials along with the R2 values of the fit between the constitutive model and experimental data (n = 6 specimens per material except for Shore 30 with n = 5 specimens per material). Coefficient Set refers to the initial guess (first) with wide bounds on the parameters followed by a second optimization run with the bounds being the mean parameters from the first optimization run ±10% of the mean.
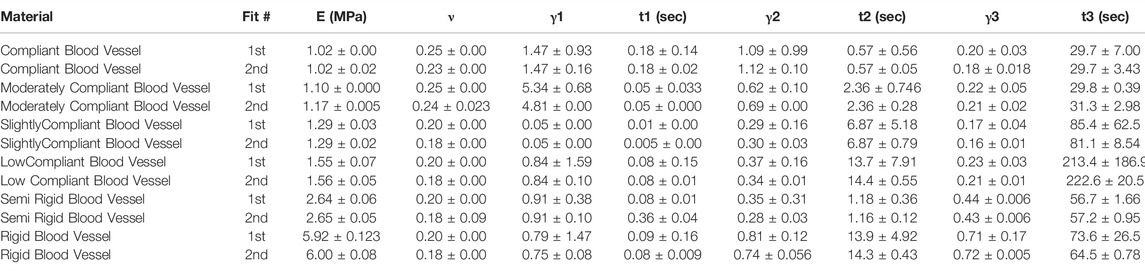
TABLE 3. Nonlinear viscoelastic compressible Neo-Hookean fit to J750 Digital Anatomy Printer (DAP) Blood Vessel Materials. Table of compressible nonlinear viscoelastic compressible Neo-Hookean parameters for the DAP, Blood Vessel materials along with the R2 values of the fit between the constitutive model and experimental data (n = 6 specimens per material except for Shore 30 with n = 5 specimens per material). Coefficient Set refers to the initial guess (first) with wide bounds on the parameters followed by a second optimization run with the bounds being the mean parameters from the first optimization run ±10% of the mean.
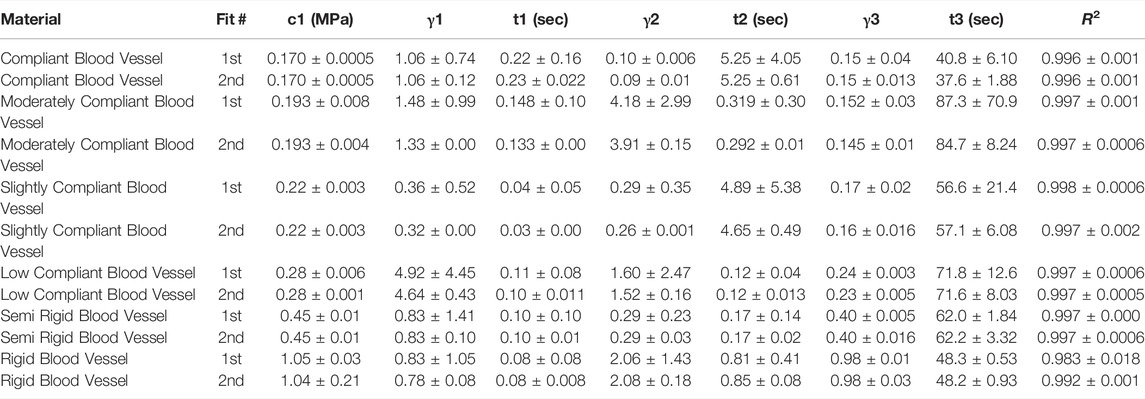
TABLE 4. Nonlinear viscoelastic incompressible Neo-Hookean fit to J750 Digital Anatomy Printer (DAP) Blood Vessel Materials. Table of compressible nonlinear viscoelastic compressible Neo-Hookean parameters for the DAP, Blood Vessel materials along with the R2 values of the fit between the constitutive model and experimental data (n = 6 specimens per material except for Shore 30 with n = 5 specimens per material). Coefficient Set refers to the initial guess (first) with wide bounds on the parameters followed by a second optimization run with the bounds being the mean parameters from the first optimization run ±10% of the mean.
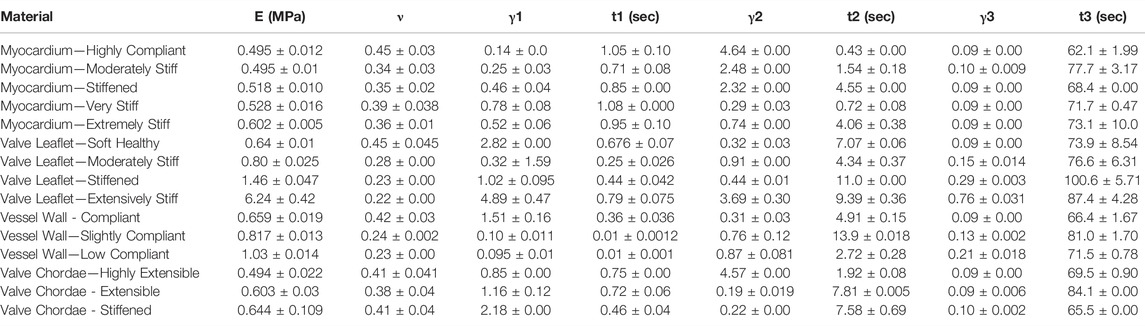
TABLE 5. Nonlinear viscoelastic compressible Neo-Hookean fit to J750 Digital Anatomy Printer (DAP) Structural Heart Materials. Table of compressible nonlinear viscoelastic compressible Neo-Hookean parameters for the Structural Heart materials along with the R2 values of the fit between the constitutive model and experimental data (n = 4 specimens per). Only the second optimization run with the bounds being the mean parameters from the first optimization run ±10% of the mean is presented.
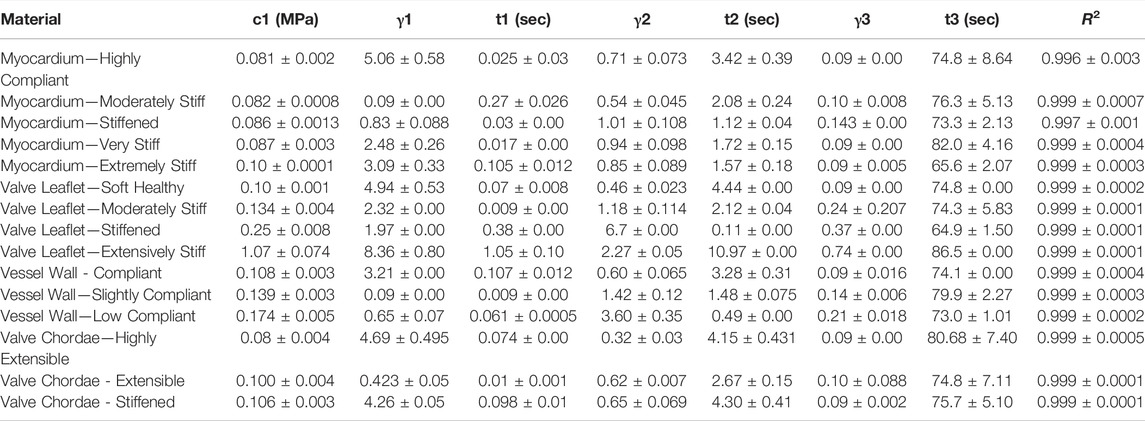
TABLE 6. Nonlinear viscoelastic incompressible Neo-Hookean fit to J750 Digital Anatomy Printer (DAP) Structural Heart Materials. Table of compressible nonlinear viscoelastic compressible Neo-Hookean parameters for the Structural Heart materials along with the R2 values of the fit between the constitutive model and experimental data (n = 4 specimens per material). Only the second optimization run with the bounds being the mean parameters from the first optimization run ±10% of the mean is presented.
All models fit the J750 Standard and DAP material behavior well with R2 > 0.95 (in most cases R2 > 0.99) except for the incompressible Neo-Hookean Coeff Set 2 for the Shore 30 material, with R2 = 0.922. As expected, Coeff Set 1 starting with a large parameter space fit the experimental data well, but exhibited a wide variation in coefficients with standard deviations up to 100% or greater of the mean values, demonstrating non-uniqueness, or equivalently coefficient identifiability issues. Coeff Set 2 using the average of Coeff Set 1 as the starting guess had much lower resulting variations due to the 10% fitting bound. Despite the narrower bound, R2 fits were equivalent for Coeff Set 2 as Coeff Set 1, except for the Shore 30 material. In this case, the Coeff Set 2 parameters tended towards the lower bound of the parameter space. Examples of fits for both compressible and incompressible nonlinear viscoelastic models are shown in Figure 3.
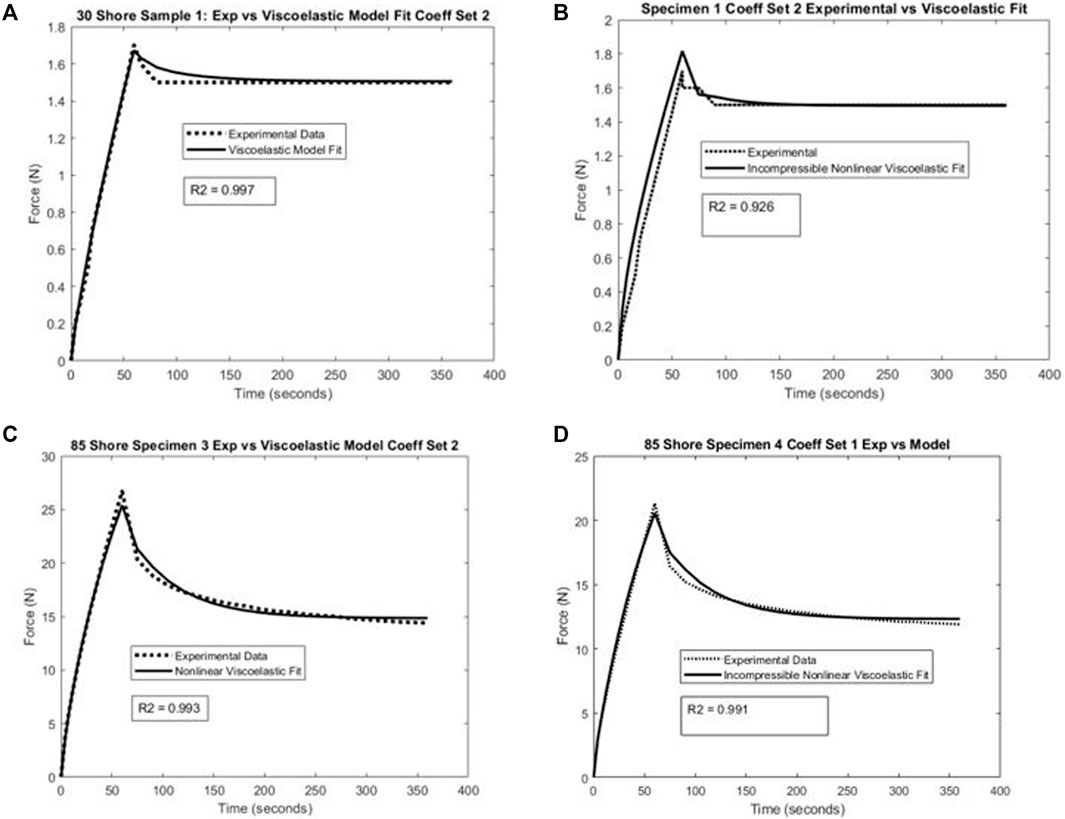
FIGURE 3. Example of nonlinear viscoelastic constitutive model fit and experimental uniaxial test data for (A) compressible model and Shore 30 material specimen, (B) incompressible model and Shore 30 material specimen, (C) compressible model and Shore 85 material specimen, and (D) incompressible model and Shore 85 material specimen.
Rankings of J750 standard Shore materials and Blood Vessel materials are shown for compressible nonlinear elastic modulus (Eq.(6a); see Figure 4), incompressible nonlinear elastic shear modulus (Eq. (6b); see Figure 5), and percent force relaxation (Figure 6). Note that many J750 materials exhibit significant stress relaxation, between 8 and 50% of peak force (Figure 6). As expected, the compressible nonlinear elastic modulus was nearly six times the incompressible c1 coefficient for all materials: 5.96 ± 0.46.
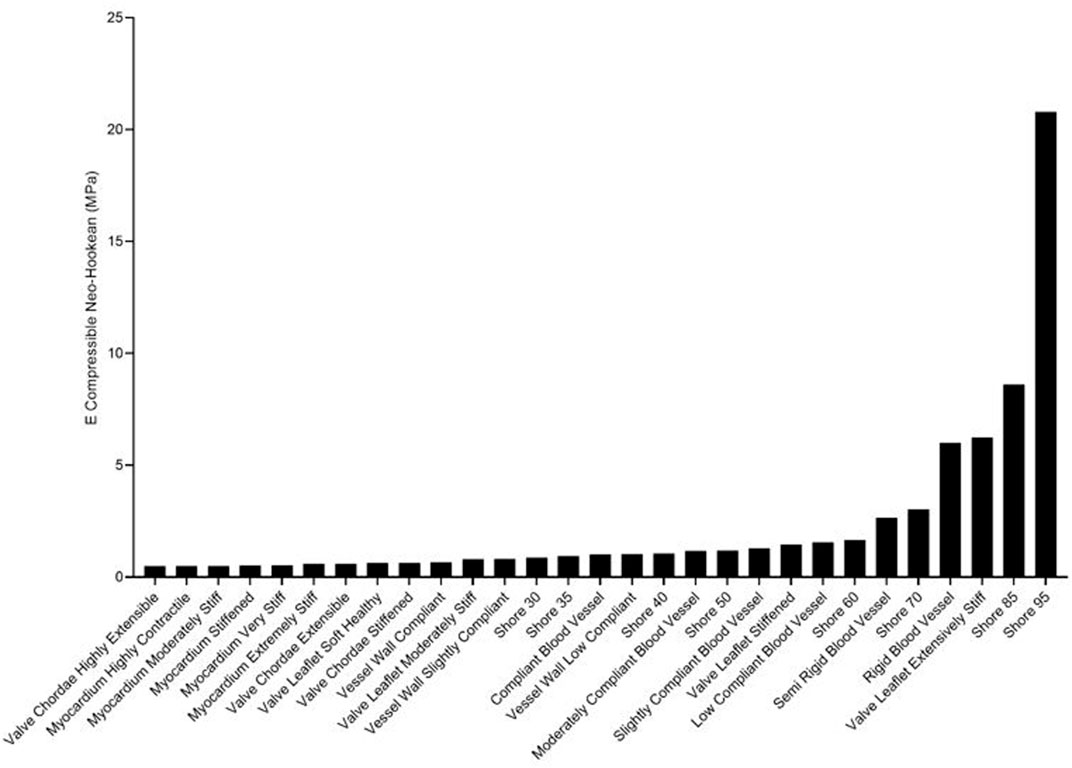
FIGURE 4. Ranking of J750 3D printed Shore, the DAP blood vessel materials, and the DAP structural heart materials for the elastic modulus of the compressible nonlinear strain energy function of Eq. 6a.
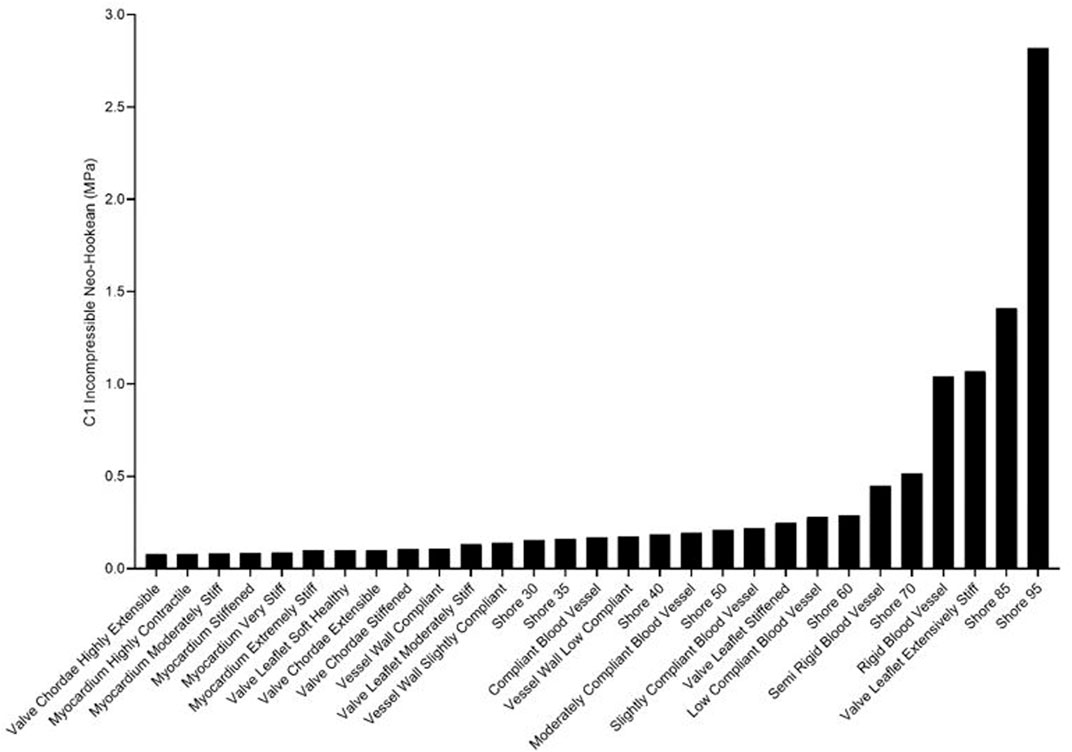
FIGURE 5. Ranking of J750 3D printed Shore, the DAP blood vessel materials, and the DAP structural heart materials for the c1 component of the incompressible Neo-Hookean strain energy function of Eq. 6b.
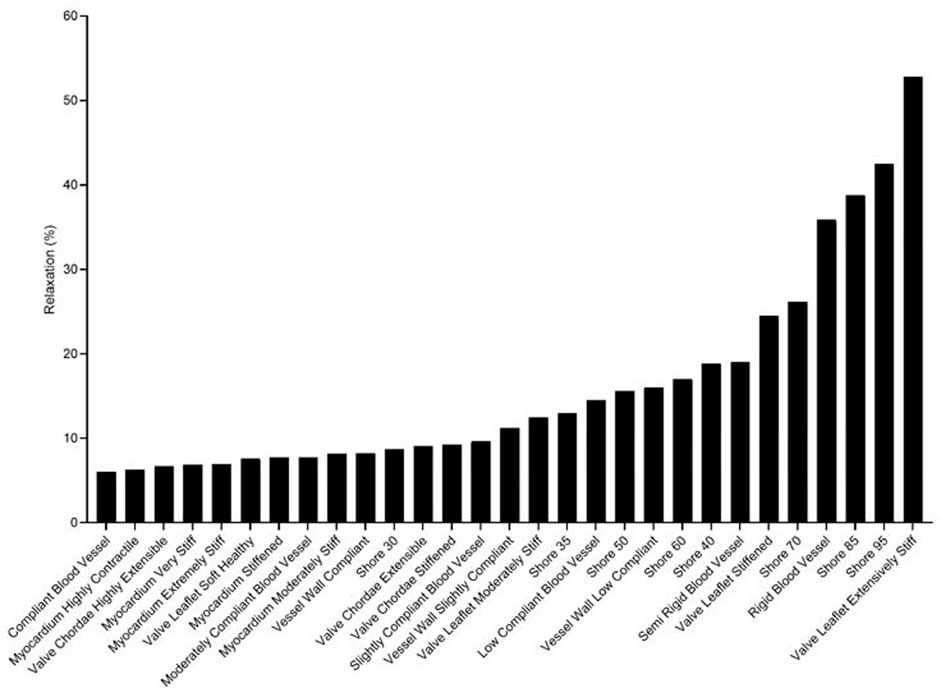
FIGURE 6. Ranking of J750 3D printed Shore, the DAP bloodvessel materials, and the DAP structural heart materials for the degree of force relaxation over time.
The use of least square differences, KStest2, and difference in total area under the force-time curves revealed similar trends in identifying J750 materials that best matched the nonlinear viscoelastic behavior of native tissues. Figure 5 shows the three best J750 material fit to the nonlinear viscoelastic behavior of the human tympanic membrane (Figure 7A) and the human nasal cartilage (Figure 7B) from published nonlinear viscoelastic constitutive data (Motallebzadeh et al., 2013; Chang et al., 2020) using the dumbbell model (Figure 1). In the case of the tympanic membrane, the metrics provide the best 3D-printed material choice that brackets the tympanic membrane mechanical response.
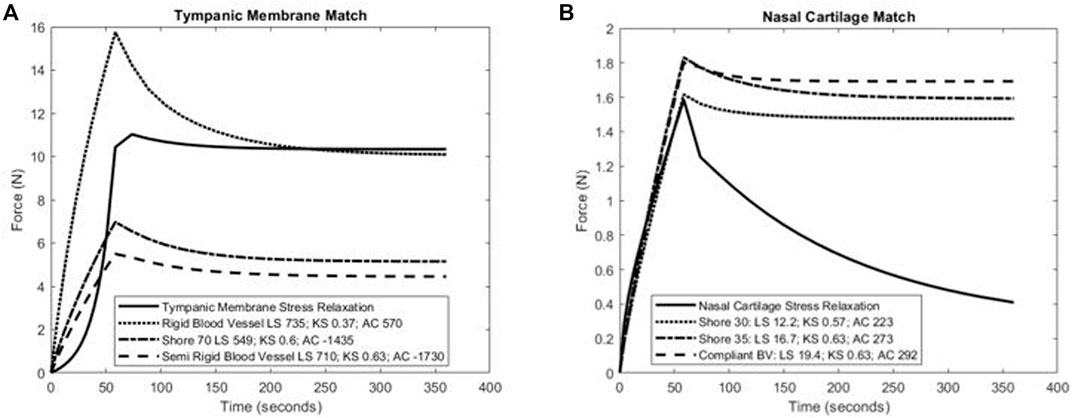
FIGURE 7. Calculation of least-square difference (LS), Kolmorogorov–Smirnov statistic (KS), and differences in area under the force-time curve between three closest J750 materials and (A) human tympanic membrane nonlinear viscoelastic properties (Motallebzadeh et al., 2013) and (B) human nasal cartilage nonlinear viscoelastic properties (Chang et al., 2020). Note that lower magnitude values of each parameter indicate a J750 parameter that more closely matches native tissue behavior. Results suggest that either the Shore 70 or Rigid Blood Vessel material best match the tympanic membrane (A), while the Shore 30 material best matches human nasal cartilage (B).
The material matching parameters were also calculated for one porcine aortic wall specimen under biaxial tension (Figure 2) (Polzer et al., 2015). Note that this was a ramp test to assess elastic response, not a stress relaxation test to assess viscoelastic response. However, the full viscoelastic 3D-printed material model was used and subject to the loading rate specified by Polzer et al. Parameters were calculated for Cauchy stress versus stretch results in both the axial and circumferential test directions, although plot results are only shown for the axial direction (Figure 8). In this case, the most compliant material tested (Shore 30) was chosen but was stiffer than the aorta wall.
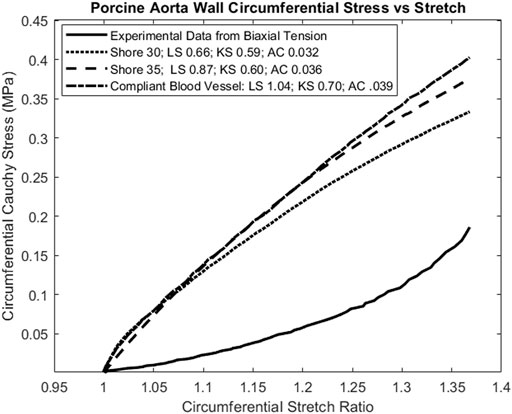
FIGURE 8. Calculation of tissue matching parameters for stress-strain elastic curve of porcine aortic wall specimen (Polzer et al., 2015). Again, the lowest magnitude values for all parameters agree, indicating that the Shore 30 J750 material is closest matched to this aortic wall specimen.
Discussion
We demonstrated that nonlinear three-term Prony series viscoelastic constitutive models, with either a compressible or incompressible Neo-Hookean strain energy kernel, fit the nonlinear stress relaxation behavior of Stratasys J750 materials well, with R2 values greater than 0.95 for 42 of 43 material fits (2 fits per material for J750 and DAP Blood Vessel and 1 for DAP Structural Heart). The remaining fit had an R2 value of 0.922. We also demonstrated that a two-step optimization approach, initially performing a fit with a broad parameter range, then averaging these parameters to use as the initial starting guess with a ±10% bound for a second optimization run, produced consistent, narrowly bound constitutive parameters that fit experimental data equally well. Although it cannot be proven that the second round fit coefficients are indeed unique, the results are likely to provide more rigorous results for comparing to native tissue properties or performing finite element simulations and subsequent experimental testing for procedure training or medical device development.
We presented new metrics to match 3D-printed material behavior against tissue properties by calculating least-squares differences, Kolmogorov–Smirnov statistics, and differences in curve areas that can be used for force-time curves, force-displacement curves, stress-time curves, or stress-strain data. All these metrics were consistently lower for materials that better-matched tissue mechanical behavior, and thus provide an automated way to choose the best material from a 3D printing database for matching a given tissue behavior. A weighted average of the three parameters may give the best prediction. Such an automated approach becomes more critical when the number of materials becomes exceedingly large, as the DAP catalog for the J750 Polyjet printer alone contains 96 different combinations.
Exactly matching tissue nonlinear viscoelastic properties remains a daunting challenge for a number of reasons. First, tissue properties are extremely varied and complex, exhibiting anisotropy due to embedded fibers with complicated orientation distributions (Holzapfel et al., 2004; Sommer et al., 2013; Limbert, 2017) which 3D-printed materials do not replicate. Tissues exhibit a classic strain stiffening response, with soft materials stiffening at higher strains due to these embedded fibers. In contrast, most synthetic biomaterial polymers for modeling or implantation (Mitsak et al., 2012; Ramaraju et al., 2020), including the J750 3D-printed materials, exhibit Neo-Hookean responses. These differences will clearly create a challenge in matching 3D-printed materials to tissue response. An interesting approach to address this mismatch has been put forward by Chen et al. (2018), who proposed printing stiffer sinusoidal fibers in softer matrices on Polyjet systems to mimic the embedded fibers of tissues.
A second challenge is the extremely varied models in the literature used to characterize tissue nonlinear elastic and viscoelastic properties which makes an “apples to apples” comparison to commonly used nonlinear viscoelastic constitutive models difficult. This widely varied data suggest the need for a standardized characterization of nonlinear elastic and viscoelastic constitutive models for 3D-printed materials, natural tissues, and engineered tissues to create a common database. In other words, common testing and constitutive modeling approaches including common nonlinear elastic strain energy and stress relaxation functions (like the Prony series) need to be applied to all these materials. Finally, although Polyjet and mulitjet printers like the Stratasys J750 have significantly advanced our capability to print and design a wide range of nonlinear material behaviors, printing extremely compliant materials to match tissues like esophagus and blood vessels remains a challenge.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
AV: 3D-printed samples, performed mechanical testing, prepared finite element files for the optimization, and wrote portions of the manuscript. ST: 3D-printed samples, performed mechanical testing, and wrote parts of the manuscript. YG: printed samples, performed mechanical testing, and prepared finite element files for the optimization. AP: 3D-printed samples and performed mechanical testing. SH: ran FEBio analyses, fit and interpreted data, wrote portions of the manuscript, and designed the study.
Funding
This study was supported by the Children’s Healthcare of Atlanta Pediatric Trust Fund.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
The cluster computing work used the Hive cluster, which is supported by the National Science Foundation under grant number 1828187. Cluster computing was also supported in part through research cyberinfrastructure resources and services provided by the Partnership for an Advanced Computing Environment (PACE) at the Georgia Institute of Technology, Atlanta, Georgia, USA.
References
Bellia-Munzon, G., Martinez, J., Toselli, L., Nazar Peirano, M., Sanjurjo, D., Vallee, M., et al. (2020). From Bench to Bedside: 3D Reconstruction and Printing as a Valuable Tool for the Chest wall Surgeon. J. Pediatr. Surg. 55 (12), 2703–2709. doi:10.1016/j.jpedsurg.2020.07.010
Bezek, L. B., Cauchi, M. P., De Vita, R., Foerst, J. R., and Williams, C. B. (2020). 3D Printing Tissue-Mimicking Materials for Realistic Transseptal Puncture Models. J. Mech. Behav. Biomed. Mater. 110, 103971. doi:10.1016/j.jmbbm.2020.103971
Capucha, T., Shilo, D., Blanc, O., Turgeman, S., Emodi, O., and Rachmiel, A. (2020). 3D Planning and Printing of Patient-Specific Implants for Reconstruction of Bony Defects. JoVE 162, e60929. doi:10.3791/60929
Chang, B., Reighard, C., Flanagan, C., Hollister, S., and Zopf, D. (2020). Evaluation of Human Nasal Cartilage Nonlinear and Rate Dependent Mechanical Properties. J. Biomech. 100, 109549. doi:10.1016/j.jbiomech.2019.109549
Chao, L., Jiao, C., Liang, H., Xie, D., Shen, L., and Liu, Z. (2021). Analysis of Mechanical Properties and Permeability of Trabecular-like Porous Scaffold by Additive Manufacturing. Front. Bioeng. Biotechnol. 9, 779854. doi:10.3389/fbioe.2021.779854
Chen, J., Wang, K., Zhang, C., and Wang, B. (2018). An Efficient Statistical Approach to Design 3D-Printed Metamaterials for Mimicking Mechanical Properties of Soft Biological Tissues. Additive Manufacturing 24, 341–352. doi:10.1016/j.addma.2018.10.007
Chen, M. Y., Skewes, J., Desselle, M., Wong, C., Woodruff, M. A., Dasgupta, P., et al. (2020a). Current Applications of Three‐dimensional Printing in Urology. BJU Int. 125 (1), 17–27. doi:10.1111/bju.14928
Chen, M. Y., Skewes, J., Woodruff, M. A., Dasgupta, P., and Rukin, N. J. (2020b). Multi-colour Extrusion Fused Deposition Modelling: a Low-Cost 3D Printing Method for Anatomical Prostate Cancer Models. Sci. Rep. 10 (1), 10004. doi:10.1038/s41598-020-67082-7
Cho, K.-H., Papay, F. A., Yanof, J., West, K., Bassiri Gharb, B., Rampazzo, A., et al. (2020). Mixed Reality and 3D Printed Models for Planning and Execution of Face Transplantation. Ann. Surg. 274, e1238–e1246. doi:10.1097/SLA.0000000000003794
Choi, H. S., and Vito, R. P. (1990). Two-dimensional Stress-Strain Relationship for Canine Pericardium. J. Biomech. Eng. 112 (2), 153–159. doi:10.1115/1.2891166
Cloonan, A. J., Shahmirzadi, D., Li, R. X., Doyle, B. J., Konofagou, E. E., and McGloughlin, T. M. (2014). 3D-Printed Tissue-Mimicking Phantoms for Medical Imaging and Computational Validation Applications. 3D Printing and Additive Manufacturing 1 (1), 14–23. doi:10.1089/3dp.2013.0010
Damon, A., Clifton, W., Valero-Moreno, F., and Quinones-Hinojosa, A. (2020). Cost-Effective Method for 3-Dimensional Printing Dynamic Multiobject and Patient-specific Brain Tumor Models: Technical Note. World Neurosurg. 140, 173–179. doi:10.1016/j.wneu.2020.04.184
Di Prima, M., Coburn, J., Hwang, D., Kelly, J., Khairuzzaman, A., and Ricles, L. (2016). Additively Manufactured Medical Products - the FDA Perspective. 3d Print Med. 2. doi:10.1186/s41205-016-0005-9
Ferrari, E., Gallo, M., Wang, C., Zhang, L., Taramasso, M., Maisano, F., et al. (2020). Three-dimensional Printing in Adult Cardiovascular Medicine for Surgical and Transcatheter Procedural Planning, Teaching and Technological Innovation. Interact Cardiovasc. Thorac. Surg. 30 (2), 203–214. doi:10.1093/icvts/ivz250
Ferrari, E., Piazza, G., Scoglio, M., Berdajs, D., Tozzi, P., Maisano, F., et al. (2019). Suitability of 3D-Printed Root Models for the Development of Transcatheter Aortic Root Repair Technologies. ASAIO J. 65 (8), 874–881. doi:10.1097/MAT.0000000000000903
Ghazi, A. E., and Teplitz, B. A. (2020). Role of 3D Printing in Surgical Education for Robotic Urology Procedures. Transl Androl. Urol. 9 (2), 931–941. doi:10.21037/tau.2020.01.03
Ghazi, A., Saba, P., Melnyk, R., and Joseph, J. (2021). Utilizing 3D Printing and Hydrogel Casting for the Development of Patient-specific Rehearsal Platforms for Robotic Assisted Partial Nephrectomies. Urology 147, 317. doi:10.1016/j.urology.2020.10.023
Ghorbani, F., Ghalandari, B., Sahranavard, M., Zamanian, A., and Collins, M. N. (2021). Tuning the Biomimetic Behavior of Hybrid Scaffolds for Bone Tissue Engineering through Surface Modifications and Drug Immobilization. Mater. Sci. Eng. C 130, 112434. doi:10.1016/j.msec.2021.112434
Göçer, H., Durukan, A. B., Tunc, O., Naseri, E., and Ercan, E. (2020). Evaluation of 3D Printed Carotid Anatomical Models in Planning Carotid Artery Stenting. Turk Gogus Kalp Dama 28 (2), 294–300. doi:10.5606/tgkdc.dergisi.2020.18939
Grillo, F. W., Souza, V. H., Matsuda, R. H., Rondinoni, C., Pavan, T. Z., Baffa, O., et al. (2018). Patient-specific Neurosurgical Phantom: Assessment of Visual Quality, Accuracy, and Scaling Effects. 3d Print Med. 4 (1), 3. doi:10.1186/s41205-018-0025-8
Holzapfel, G. A., Gasser, T. C., and Ogden, R. W. (2004). Comparison of a Multi-Layer Structural Model for Arterial walls with a Fung-type Model, and Issues of Material Stability. J. Biomech. Eng. 126 (2), 264–275. doi:10.1115/1.1695572
Humphrey, J. D. (2002). Cardiovascular Solid Mechanics: Cells, Tissues, and Organs. New York: Springer-Verlag.
Illmann, C. F., Hosking, M., and Harris, K. C. (2020). Utility and Access to 3-Dimensional Printing in the Context of Congenital Heart Disease: An International Physician Survey Study. CJC Open 2 (4), 207–213. doi:10.1016/j.cjco.2020.01.008
Javan, R., Schickel, M., Zhao, Y., Agbo, T., Fleming, C., Heidari, P., et al. (2020). Using 3D-Printed Mesh-like Brain Cortex with Deep Structures for Planning Intracranial EEG Electrode Placement. J. Digit Imaging 33 (2), 324–333. doi:10.1007/s10278-019-00275-3
Kim, M. J., Jeong, W. S., Jeon, D. N., Choi, J. W., and Kim, D. H. (2020). Comprehensive Three-Dimensional Technology Strategies for Autologous Free Fat Graft in Parry-Romberg Syndrome. J. Craniofac. Surg. 31 (1), 64–67. doi:10.1097/SCS.0000000000005855
Koh, Y.-G., Lee, J.-A., Kim, Y. S., Lee, H. Y., Kim, H. J., and Kang, K.-T. (2019). Optimal Mechanical Properties of a Scaffold for Cartilage Regeneration Using Finite Element Analysis. J. Tissue Eng. 10, 204173141983213. doi:10.1177/2041731419832133
Levin, D., Mackensen, G. B., Reisman, M., McCabe, J. M., Dvir, D., and Ripley, B. (2020). 3D Printing Applications for Transcatheter Aortic Valve Replacement. Curr. Cardiol. Rep. 22 (4), 23. doi:10.1007/s11886-020-1276-8
Limbert, G. (2017). Mathematical and Computational Modelling of Skin Biophysics: a Review. Proc. R. Soc. A. 473 (2203), 20170257. doi:10.1098/rspa.2017.0257
Lin, C. Y., Kikuchi, N., and Hollister, S. J. (2004). A Novel Method for Biomaterial Scaffold Internal Architecture Design to Match Bone Elastic Properties with Desired Porosity. J. Biomech. 37 (5), 623–636. doi:10.1016/j.jbiomech.2003.09.029
Liu, P., Hu, Z., Huang, S., Wang, P., Dong, Y., Cheng, P., et al. (2020). Application of 3D Printed Models of Complex Hypertrophic Scars for Preoperative Evaluation and Surgical Planning. Front. Bioeng. Biotechnol. 8, 115. doi:10.3389/fbioe.2020.00115
Maas, S. A., Ateshian, G. A., and Weiss, J. A. (2017). FEBio: History and Advances. Annu. Rev. Biomed. Eng. 19, 279–299. doi:10.1146/annurev-bioeng-071516-044738
Maas, S. A., Ellis, B. J., Ateshian, G. A., and Weiss, J. A. (2012). FEBio: Finite Elements for Biomechanics. J. Biomech. Eng. 134 (1), 011005. doi:10.1115/1.4005694
Mardling, P., Alderson, A., Jordan-Mahy, N., and Le Maitre, C. L. (2020). The Use of Auxetic Materials in Tissue Engineering. Biomater. Sci. 8 (8), 2074–2083. doi:10.1039/c9bm01928f
McMillan, A., Kocharyan, A., Dekker, S. E., Kikano, E. G., Garg, A., Huang, V. W., et al. (2020). Comparison of Materials Used for 3D-Printing Temporal Bone Models to Simulate Surgical Dissection. Ann. Otol Rhinol Laryngol. 129 (12), 1168–1173. doi:10.1177/0003489420918273
Meglioli, M., Naveau, A., Macaluso, G. M., and Catros, S. (2020). 3D Printed Bone Models in Oral and Cranio-Maxillofacial Surgery: a Systematic Review. 3d Print Med. 6 (1), 30. doi:10.1186/s41205-020-00082-5
Mitsak, A. G., Dunn, A. M., and Hollister, S. J. (2012). Mechanical Characterization and Non-linear Elastic Modeling of Poly(glycerol Sebacate) for Soft Tissue Engineering. J. Mech. Behav. Biomed. Mater. 11, 3–15. doi:10.1016/j.jmbbm.2011.11.003
Motallebzadeh, H., Charlebois, M., and Funnell, W. R. J. (2013). A Non-linear Viscoelastic Model for the Tympanic Membrane. The J. Acoust. Soc. America 134 (6), 4427–4434. doi:10.1121/1.4828831
Pacione, D., Tanweer, O., Berman, P., and Harter, D. H. (2016). The Utility of a Multimaterial 3D Printed Model for Surgical Planning of Complex Deformity of the Skull Base and Craniovertebral junction. Jns 125 (5), 1194–1197. doi:10.3171/2015.12.JNS151936
Pietrabissa, A., Marconi, S., Negrello, E., Mauri, V., Peri, A., Pugliese, L., et al. (2020). An Overview on 3D Printing for Abdominal Surgery. Surg. Endosc. 34 (1), 1–13. doi:10.1007/s00464-019-07155-5
Polzer, S., Gasser, T. C., Novak, K., Man, V., Tichy, M., Skacel, P., et al. (2015). Structure-based Constitutive Model Can Accurately Predict Planar Biaxial Properties of Aortic wall Tissue. Acta Biomater. 14, 133–145. doi:10.1016/j.actbio.2014.11.043
Press, W. H., and Teukolsky, S. A. (1988). Kolmogorov-Smirnov Test for Two-Dimensional Data. Comput. Phys. 2, 74–77. doi:10.1063/1.4822753
Puso, M. A., and Weiss, J. A. (1998). Finite Element Implementation of Anisotropic Quasi-Linear Viscoelasticity Using a Discrete Spectrum Approximation. J. Biomech. Eng. 120 (1), 62–70. doi:10.1115/1.2834308
Raghavan, M. L., and Vorp, D. A. (2000). Toward a Biomechanical Tool to Evaluate Rupture Potential of Abdominal Aortic Aneurysm: Identification of a Finite Strain Constitutive Model and Evaluation of its Applicability. J. Biomech. 33 (4), 475–482. doi:10.1016/s0021-9290(99)00201-8
Ramaraju, H., Ul-Haque, A., Verga, A. S., Bocks, M. L., and Hollister, S. J. (2020). Modulating Nonlinear Elastic Behavior of Biodegradable Shape Memory Elastomer and Small Intestinal Submucosa(SIS) Composites for Soft Tissue Repair. J. Mech. Behav. Biomed. Mater. 110, 103965. doi:10.1016/j.jmbbm.2020.103965
Ratinam, R., Quayle, M., Crock, J., Lazarus, M., Fogg, Q., and McMenamin, P. (2019). Challenges in Creating Dissectible Anatomical 3D Prints for Surgical Teaching. J. Anat. 234 (4), 419–437. doi:10.1111/joa.12934
Ricles, L. M., Coburn, J. C., Di Prima, M., and Oh, S. S. (2018). Regulating 3D-Printed Medical Products. Sci. Transl. Med. 10 (461), eaan6521. doi:10.1126/scitranslmed.aan6521
Ruiz de Galarreta, S., Antón, R., Cazón, A., and Finol, E. A. (2017). A Methodology for Developing Anisotropic AAA Phantoms via Additive Manufacturing. J. Biomech. 57, 161–166. doi:10.1016/j.jbiomech.2017.04.001
Safa, B. N., Santare, M. H., Ethier, C. R., and Elliott, D. M. (2021). Identifiability of Tissue Material Parameters from Uniaxial Tests Using Multi-Start Optimization. Acta Biomater. 123, 197–207. doi:10.1016/j.actbio.2021.01.006
Severseike, L., Lee, V., Brandon, T., Bakken, C., and Bhatia, V. (2019). Polyjet 3D Printing of Tissue-Mimicking Materials: How Well Can 3D Printed Synthetic Myocardium Replicate Mechanical Properties of Organic Myocardium? bioRxiv, 825794. doi:10.1101/825794
Sommer, G., Schriefl, A., Zeindlinger, G., Katzensteiner, A., Ainödhofer, H., Saxena, A., et al. (2013). Multiaxial Mechanical Response and Constitutive Modeling of Esophageal Tissues: Impact on Esophageal Tissue Engineering. Acta Biomater. 9 (12), 9379–9391. doi:10.1016/j.actbio.2013.07.041
Stramiello, J. A., Saddawi-Konefka, R., Ryan, J., and Brigger, M. T. (2020). The Role of 3D Printing in Pediatric Airway Obstruction: A Systematic Review. Int. J. Pediatr. Otorhinolaryngol. 132, 109923. doi:10.1016/j.ijporl.2020.109923
Tejo-Otero, A., Buj-Corral, I., and Fenollosa-Artés, F. (2020). 3D Printing in Medicine for Preoperative Surgical Planning: A Review. Ann. Biomed. Eng. 48 (2), 536–555. doi:10.1007/s10439-019-02411-0
Vannucci, J., Scarnecchia, E., Potenza, R., Ceccarelli, S., Monopoli, D., and Puma, F. (2020). Dynamic Titanium Prosthesis Based on 3D-Printed Replica for Chest wall Resection and Reconstruction. Transl Lung Cancer Res. 9 (5), 2027–2032. doi:10.21037/tlcr-20-699
Vukicevic, M., Faza, N. N., Avenatti, E., Durai, P. C., El-Tallawi, K. C., Filippini, S., et al. (2020). Patient-Specific 3-Dimensional Printed Modeling of the Tricuspid Valve for MitraClip Procedure Planning. Circ. Cardiovasc. Imaging 13 (7), e010376. doi:10.1161/CIRCIMAGING.119.010376
Vukicevic, M., Mosadegh, B., Min, J. K., and Little, S. H. (2017). Cardiac 3D Printing and its Future Directions. JACC: Cardiovasc. Imaging 10 (2), 171–184. doi:10.1016/j.jcmg.2016.12.001
Wang, S., Frisbie, J., Keepers, Z., Bolten, Z., Hevaganinge, A., Boctor, E., et al. (2021). The Use of Three-Dimensional Visualization Techniques for Prostate Procedures: A Systematic Review. Eur. Urol. Focus 7, 1274–1286. doi:10.1016/j.euf.2020.08.002
Witowski, J., Budzyński, A., Grochowska, A., Ballard, D. H., Major, P., Rubinkiewicz, M., et al. (2020). Decision-making Based on 3D Printed Models in Laparoscopic Liver Resections with Intraoperative Ultrasound: a Prospective Observational Study. Eur. Radiol. 30 (3), 1306–1312. doi:10.1007/s00330-019-06511-2
Zhou, G., Jiang, H., Yin, Z., Liu, Y., Zhang, Q., Zhang, C., et al. (2018). In Vitro Regeneration of Patient-specific Ear-Shaped Cartilage and its First Clinical Application for Auricular Reconstruction. EBioMedicine 28, 287–302. doi:10.1016/j.ebiom.2018.01.011
Keywords: 3D-printed biomaterials, tissue mimicking material, surgical planning models, scaffolds, nonlinear viscoelasticity, tissue matching metrics
Citation: Verga AS, Tucker SJ, Gao Y, Plaskett AM and Hollister SJ (2022) Nonlinear Viscoelastic Properties of 3D-Printed Tissue Mimicking Materials and Metrics to Determine the Best Printed Material Match to Tissue Mechanical Behavior. Front. Mech. Eng 8:862375. doi: 10.3389/fmech.2022.862375
Received: 25 January 2022; Accepted: 05 April 2022;
Published: 10 May 2022.
Edited by:
Feihu Zhao, Swansea University, United KingdomReviewed by:
Behrooz Fereidoonnezhad, National University of Ireland Galway, IrelandRui B. Ruben, Polytechnic Institute of Leiria, Portugal
Copyright © 2022 Verga, Tucker, Gao, Plaskett and Hollister. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Scott J. Hollister, c2NvdHQuaG9sbGlzdGVyQGJtZS5nYXRlY2guZWR1
†These authors share first authorship
 Adam S. Verga
Adam S. Verga Sarah Jo Tucker
Sarah Jo Tucker Yuming Gao2
Yuming Gao2 Scott J. Hollister
Scott J. Hollister