- 1Department of Mechanical Engineering, Islamic Azad University, South Tehran Branch, Tehran, Iran
- 2Department of Mechanical Engineering, Islamic Azad University, East Tehran Branch, Tehran, Iran
This analytical analysis examines the MHD micropolar fluid flow and mixed convection features using entropy production analysis of an inclined porous stretching sheet. Flow field and heat transfer analysis are presented to consider thermal radiation, heat source/sink, Lorentz, and buoyancy forces. The PDEs system is transformed by appropriate similarity variables, turned into a system of high non-linearity coupling ODEs, and then solved with the help of an analytical approach. An analytical approach can provide exact explicit solutions for the flow field, heat transport, entropy production, the local skin friction coefficient, the local couple stress coefficient, and the local Nusselt number. It is shown that the magnetic field, mixed convection, and sheet inclination effects can be incorporated together into a single parameter, which is called the magneto-buoyancy-inclination parameter here. In other words, this parameter controls the boundary layer flow. In addition, an experimental procedure called Box-Behnken design (BBD) was employed to analyze the influence of material (K), radiation (Rd), and buoyancy (Λ) parameters on entropy production in MHD micropolar fluid flow over the sheet. In order to estimate accurately the optimum entropy generation containing K, Rd, and Λ, we used a quadratic regression model. Based on the results of this investigation, the value of the entropy generation number became larger by decreasing the magneto-buoyancy-inclination parameter. Further, the magnitude of the local couple stress coefficient is reduced as the heat source parameter increases.
Introduction
In view of the fact that Navier-Stokes equations cannot be explained as non-Newtonian and Newtonian fluids theory, Eringen (1964); Eringen (1966) was the first to introduce the theory of micropolar fluids and developed it into thermomicropolar fluids. Micropolar fluid equations differ from Navier-Stokes equations due to the non-symmetry of the stress tensor and couple stress. Since then, a variety of investigations have been conducted based on micropolar fluids of animal blood, polymeric fluids, oils, paints, and ferrofluids (Ishak, 2010; Kumar and Gupta, 2012; Mahmoud and Waheed, 2012; Postelnicu, 2012; Cortell, 2013; Sajid et al., 2018; Abbas et al., 2020a; Rana et al., 2020; Shezad et al., 2020). Hashem Zadeh et al. (2020) have linked the change in Peclet number and bio-convection Lewis number directly to the coupled stress. Thermal radiation is a branch of heat transfer that generates electromagnetic radiation because of the thermal motion of particles. In industries, thermal radiation is essential in designing aircraft, astrophysical issues, satellites, solar power equipment, and gas turbine applications. A novel finding by Tiwari et al. (2020) is that Grashof number and radiation parameter strongly affect hematocrit and Fahraeus effects. It has been demonstrated that the local skin friction coefficient and the local Nusselt number are directly associated with the permeability parameter stated by Rosali et al. (2012). The decreased hydrodynamic permeability of the membrane can be attributed to the increased micro-rotation viscosity, according to Yu Khanukaeva et al. (2019). The thin film thickness parameter and the Soret number were explored by Ali et al. (2019), directly related to the concentration field. According to Hussanan et al. (2018), enhancing the conjugate parameter decreased the micro-rotation parameter. As Bhattacharjee et al. (2019) showed, the micropolar fluid has a greater stiffness coefficient and mass flow rate than a Newtonian fluid, resulting from the additional microstructural. The heat source/sink is significant in conduction or convection heat transfer. Manufacturing plastic film, wire coating, cooling of a machine tool, and condensers are the broad applications of the heat source/sink. It was found by Mishra et al. (2018) that the heat source has a considerable effect on the hydrodynamic boundary layer. In their study, Ramadevi et al. (2020) demonstrated that Dufour and Soret numbers increase and decrease temperature functions. Moreover, porous stretching sheets are also widely used in the industry. In addition to extrusion from dies, aerodynamic extrusion of plastic and drawing of plastic films and wires are some of the applications supported by technology. The effects of magneto-convection on a stretching sheet were probed by Eswaramoorti et al. (2020). The researchers determined that momentum and thermal boundary layer thicknesses are directly related to buoyancy ratio parameters. A radiative hybrid nanofluid that undergoes a chemical reaction on a stretching surface was researched by Santhi et al. (2020). Magnetic field parameters were inversely linked to skin friction coefficients, Nusselt, and Sherwood numbers. Researchers recently studied stretching sheets in 3-D (Anuar et al., 2020; Dinarvand and Rostami, 2020; Shankar et al., 2020; Shoaib et al., 2020; Thumma and Mishra, 2020). In a study by Hosseinzade et al. (2020), micropolar hybrid ferrofluid was perused in a vertical plane. Abbas et al. (2020b) showed that the reduction in heat transfer is caused by an increase in the Prandtl number and non-linearity parameter, as well as a decrease in heat flux constant. Patel et al. (2019) showed that the micro-rotation profiles increase with increasing volume fractions for stretching and shrinking sheets using a semi-analytical method. Khash’ie et al. (2019) found that temperature enhancement is provided by the thermal stratification parameter, while a reduction in concentration profiles is achieved by enhancing the solute stratification parameter. It was reported in a study by Lu et al. (2018) that the concentration profile is inversely related to the strength of homogeneous and heterogeneous reactions. As Lund et al. (2019) recognized, temperature and concentration profiles directly affect thermophoresis and concentration parameters. Shah et al. (2020) found that the velocity distribution increases as the electric field strength for the stretching sheet increases. On the other hand, when the sheet is shrunk, the micro-rotation parameter distribution decreases with an increase in the micro-rotation parameter. As the value of the solute stratification parameter (s) enhances, micro-rotation distributions decline and rise for opposing flow, as Ramzan et al. (2017) reported. A study by Jalili et al. (2021) used the finite element method and two semi-analytical methods (HPM and AGM) to solve the ODEs and showed that ferrofluid possesses more velocity without the magnetic parameter. It has been shown by Kumar et al. (2019) that the highest velocity is achieved by second-order velocity slip, whereas the highest temperature is achieved by first-order slip. A study conducted by Jalili et al. (2019) demonstrated that the highest temperature occurs when micro-rotation parameters are absent. Dawar et al. (2020) realized that concentration fields tended to increase with increasing Biot number, decreasing with increasing chemical reaction and Schmidt number. Rehman et al. (2021) demonstrated that buoyancy parameters affect velocity and angular velocity differently. Abdal et al. (2019) found that skin-friction coefficients are reduced when slip, magnetic, and unsteadiness parameters are increased. Mandal and Mukhopadhyay (2020) reported that the mixed convection parameter increased velocity, but the angular velocity and temperature declined with the mixed convection parameter. Khan et al. (2020) pointed out that the Nusselt number reduces due to the generation/absorption variable. In addition, the temperature increases with the Biot number. Chamkha (1999) stated that the Hartmann number lowered the wall heat transfer. The Nusselt number and skin friction coefficient increase with the magnetic parameter value and when the domain of dual solutions is widened, as stated by Mustafa et al. (2020). In addition, they concluded that the Schmidt number and slip parameter both boosted the Nusselt number. Other researchers have also studied the impact of many physical parameters on the analysis of entropy production (Jain S and Gupta, 2019; Rashid et al., 2019; Zaib et al., 2019; Sen et al., 2020; Hussain and Jamshed, 2021; Khan et al., 2022a; Khan et al., 2022b; Waini et al., 2022), Micropolar (Damseh et al., 2009; Khedr et al., 2009; Modather et al., 2009; Magyari and Chamkha, 2010), heat generation/absorption (Chamkha, 2000; Reddy and Chamkha, 2016; Krishna and Chamkha, 2019; Krishna et al., 2021), convection (Chamkha, 1997a; Krishna and Chamkha, 2020), MHD (Takhar et al., 1999; Takhar et al., 2002; Kumar et al., 2020; Wakif et al., 2020), radiation (Chamkha et al., 2011; Chamkha et al., 2019; Sreedevi et al., 2020), and inclined surface (Chamkha, 1997b; Krishna et al., 2020).
An extensive literature review indicated that numerous papers investigated MHD micropolar fluid flow using semi-analytical and numerical techniques. Nonetheless, no perusal has been presented on applying Lorentz and buoyancy forces, Rosseland thermal radiation, and heat source/sink using the varying wall temperature over an inclined porous stretching sheet to calculate the entropy production as well as experimental design. The current problem represents a film polymer on a heated/cooled inclined porous stretching sheet in the MHD micropolar fluid flow under the thermal radiation effect. Moreover, a new parameter is defined as a combination of the magnetic, buoyancy, and inclination of the porous stretching sheet. We present analytical solutions for non-Newtonian micropolar fluid flow with the abovementioned properties to fill the literature gap. After solving coupled PDEs by suitable similarity solutions, select exponential type solutions to solve highly nonlinear coupled ODEs.
Mathematical model
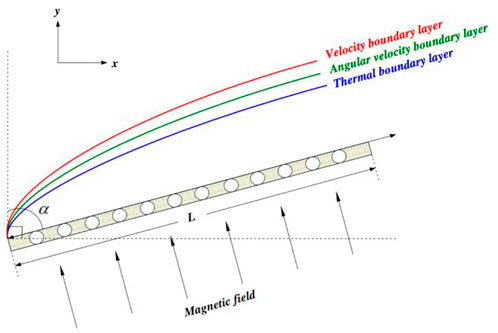
Assume a 2-D flow of a viscous, incompressible, laminar, and steady micropolar fluid over a stretching sheet continuously stretched in the x-direction. The x-component of the velocity varies linearly uw(x) = ax, where a is a positive constant and a variable surface temperature Tw(x) = T∞+bx, where b is also a positive constant. The sheet is presumed to be subjected to a vertical magnetic field. An illustration of the coordinate system and flow model can be seen in Figure 1.
In two dimensions, the simplified governing equations are (Turkyilmazoglu, 2017):
Based on Rosseland approximation, radiation heat flux is given by:
where
Substituting Eqs. 8 into Eqs. 2–4, we acquire the following ordinary differential equations:
Following the similarity transformation in Eqs. 5, 6 turn into
Here prime denotes differentiation with respect to the similarity variable
Exact analytic solutions
A Chakrabarti and Gupta (1979) figured out the exact solutions for stretching surfaces, and many researchers have worked in this field. It is important to remember that heat sources/sinks, non-Newtonian, mixed convection flow, sheet porosity, magnetic field, micropolar fluid, radiation, and inclined sheet characteristics all play a role in the process. We pick the exponential form of physical solutions to satisfy the boundary conditions as below:
The momentum, angular velocity, and energy equations produce relations:
We combine the mixed convection, magnetic field, and inclination parameters to define a new parameter called the magneto-buoyancy-inclination parameter
The parameter λ must be determined, and there are four negative and positive solutions. The negative solutions are mathematically and physically possible and impossible, respectively. On the other hand, the positive solutions are mathematically and physically conceivable. Therefore, the required solutions are positive ones. Solving Eq. 18 results in
where
Quantities of engineering interest
Among the most important engineering quantities are
Hence, we acquired reduced local skin friction, reduced local couple stress, and decreased local Nusselt number.
Entropy production analysis
The local volumetric rate of entropy production for the micropolar fluid flow is formulated as (Sayed and Abdel-wahed, 2020):
Here
Regression analysis
In this section, we conducted a quadratic regression to estimate the value of the entropy production number in a MHD micropolar fluid flow. To better understand the influences of K, Λ, and Rd, 3-D figures are presented. In accordance with the quadratic estimation equation, assuming
Seventeen different sets of values of the material parameter between [90, 100], buoyancy parameter between [60, 100], and thermal radiation parameter between (Mahmoud and Waheed, 2012; Abbas et al., 2020a) were computed using regression analysis. In Eq. 25, it can be seen that K, Λ, and Rd directly correlate with Ng.
Results and discussion
Here, the results are summarized in a tabular and graphical format based on the MHD mixed convection micropolar fluid flow with dual solutions. Additionally, the local couple stress was calculated. The dual exact explicit solutions are derived analytically. A comparison table supporting the validity of our current analytical solutions is also provided in Table 1, and this table shows perfect agreement with previous results.
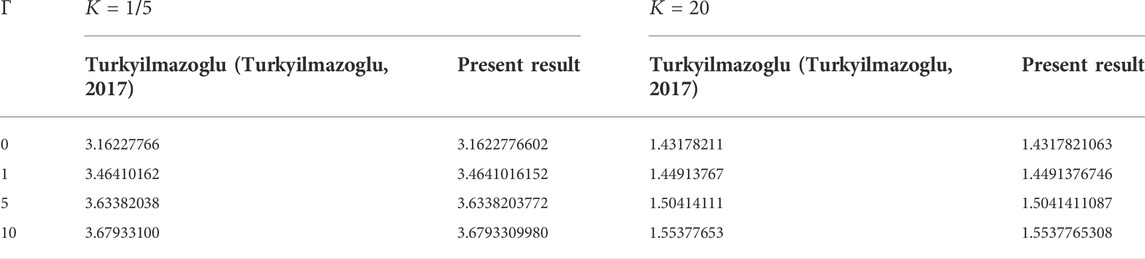
TABLE 1. Comparison of the present work with the published work (Turkyilmazoglu, 2017) on
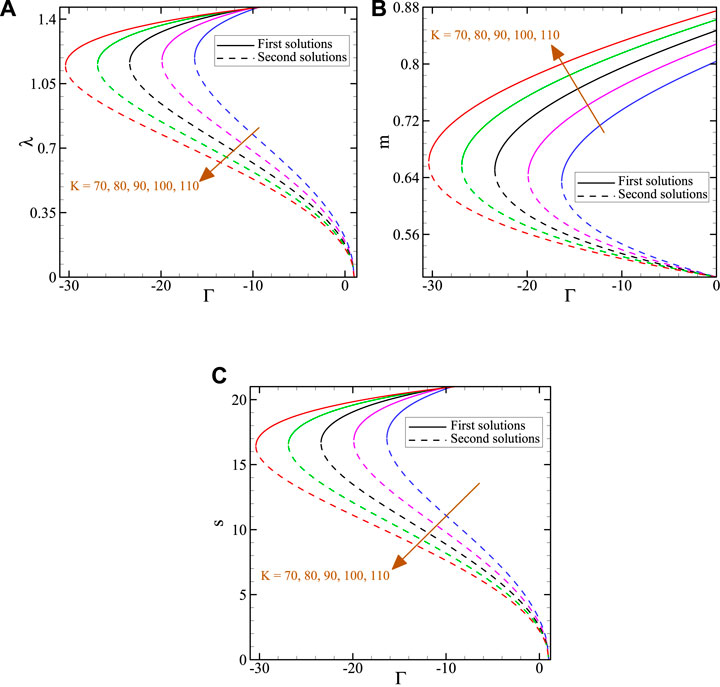
The following Figures 2A–C illustrates the existence domain of (λ, m, s) curves versus Γ for the various material parameters. The current analysis makes it possible to determine the overall trend based on the ranges displayed. Figure 2A indicates the changes in the heat transfer coefficient to the Γ with the increase of the material parameter. By fixing the Prandtl number, thermal radiation, and heat generation/absorption parameters, the range of the Γ parameter value expands with the increase of the material parameter. For example, for K = 70, the critical value of the Γ parameter is Γc = 16.4. The implication is that if Γc<16.4, there are dual solutions, and if Γc>16.4, there are no solutions. So, this is one of the necessary constraints for dual solutions. In this way, the justification of the choosing values for the physical parameters is based on this kind of calculation.
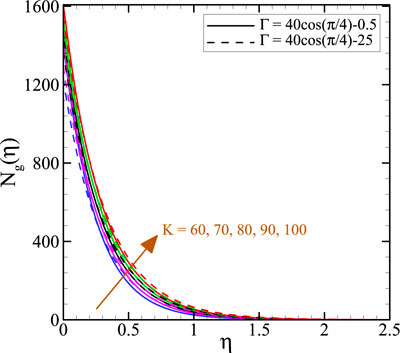
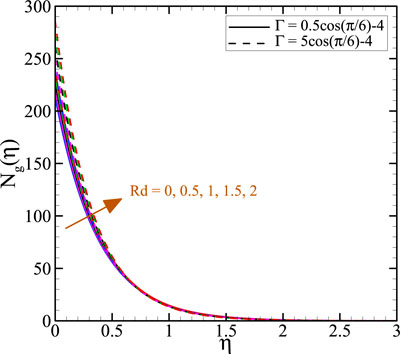
As shown in Figure 3, increased K is physically related to increasing vortex viscosity (micro-rotation motion) of the flow, which, in turn, boosts Ng(η). Also, by increasing the magnetic parameter 50 times, the generation of entropy is enhanced. Rising the magnetic field parameter boosted the resistant force against the fluid movement, so the heat transfer rate in the boundary layer was raised. When the buoyancy parameter is high, the heat is absorbed, and the stretching porous sheet inclination is
A simultaneous presentation of the effects of the magneto-buoyancy-inclination and thermal radiation parameters on entropy generation is shown in Figure 4. Entropy was raised by increasing the thermal radiation parameter and lowering the magneto-buoyancy-inclination parameter, which includes boosting Ha and Λ from 1 to 30 and the sheet orientation from horizontal to
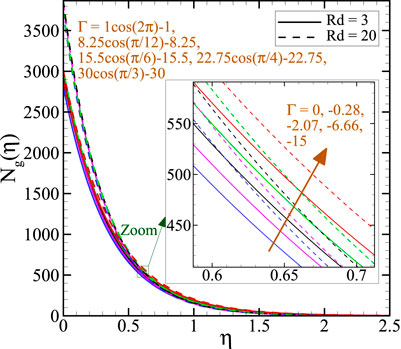
Figure 5 shows the effects of thermal radiation and buoyancy parameters on entropy generation under conditions of minor heat sources and
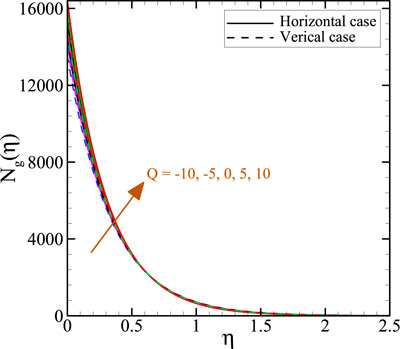
As shown in Figure 6, the heat source generates more entropy than the heat sinks due to the direct relationship between temperature and Ng(η). Under intense thermal radiation, by boosting Q from -10 to 10, the entropy generation over the horizontal and vertical sheets increased by 14.82% and 12.68%, respectively. Thus, the porous stretching sheet, that is, oriented horizontally causes more entropy.
In Figures 7A–C, you can observe how K, Λ, and Rd affect Ng in 3-D plots. The 3-D plots clarify the role of parameter coefficients in Eq. 25. For instance, since the Rd coefficient in Eq. 25 is greater than the Λ, in Figure 7C, the effect of Rd on the Ng is more than the Λ.
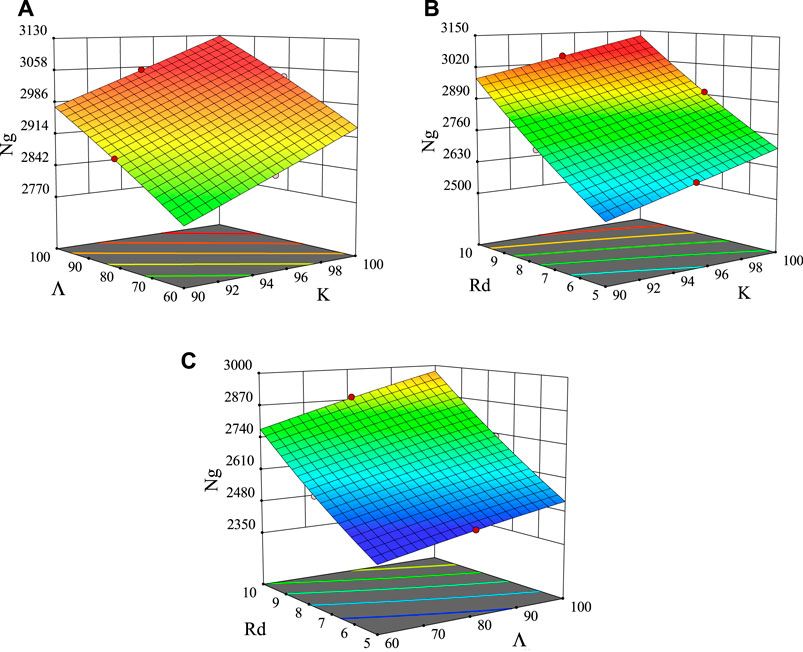
FIGURE 7. 3-D response surfaces: interactive influences of varied (A) buoyancy and material parameters at Rd = 10, (B) radiation and material parameters at Λ = 100, (C) radiation and buoyancy parameters at K = 90.
Figure 8 compares the analytical solutions (Actual) from Eq. 19 with the estimated entropy generation number (Predicted) from Eq. 25. The values of regression coefficients for Eq. 25 are quite suitable, and R2 = 0.9999 confirms this.
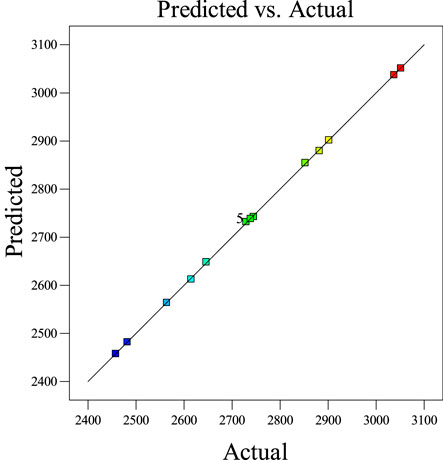
FIGURE 8. Comparative plot between the actual and predicted model Ng for the response surface quadratic model.
Table discussion
The numerical data have been set in Table 2 to illustrate the effect of K versus the heat source and sink for the

TABLE 2. Effects of the different material and heat source and sink parameters on the local couple stress coefficient with
According to the model summary statistics (Table 3), a quadratic model can be constructed based on the significant value of the adjusted R2 value. Calculating the quadratic model coefficients was done using the regression analysis method in the RSM.
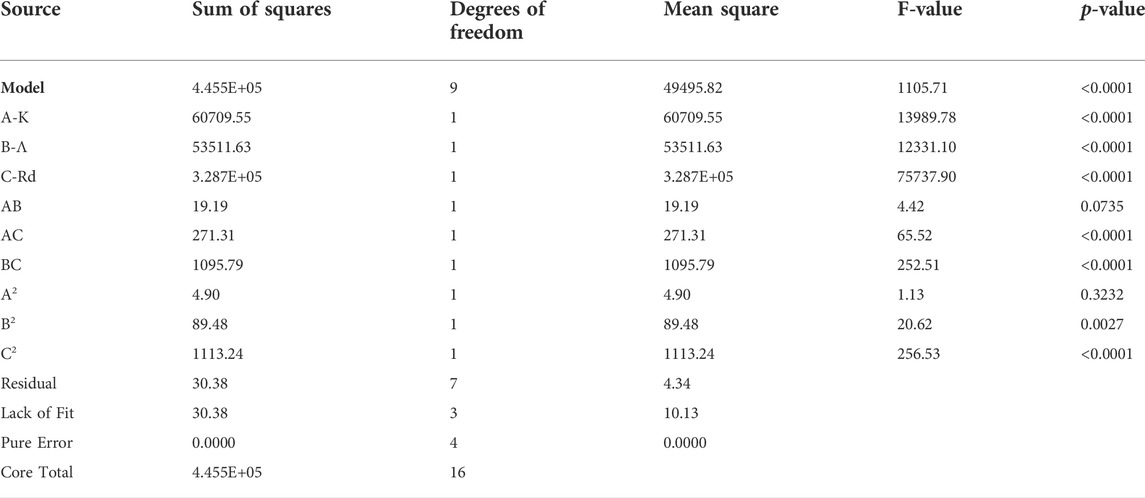
The following Table 4 is a statistical evaluation of the fit-response surface model based on the coefficient of determination (R2) and the results of an analysis of variance. The regression model is deemed highly significant when the p-value is low (less than 0.05). The F-value of 1,105.71 and the p-value of less than 0.0001 in Table 4 prove that the model achieved is reliable. There is only a 0.01% chance that this large F-value could happen due to noise.
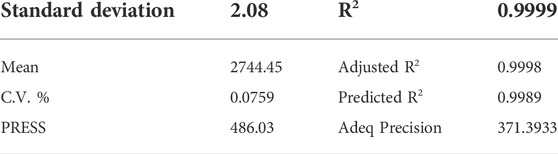
As shown in Table 5, the R2 value is 0.9999, which has in good agreement with the Predicted R2 of 0.9989. The adequate precision is 371.3933, which is quite good (since if it is greater than 4, the model has a powerful signal to be employed for optimization). By subtracting the Predicted R2 from the Adjusted R2, the difference is 0.000935, which is pretty decent (if the difference is less than 0.2, then the model matches the data and can confidently be applied to interpolate). Table 5 contains indicators proving that the model is effective in the experimental range.
Conclusion
All solutions to the dimensionless velocity, angular velocity, temperature, local skin friction coefficient, local couple stress coefficient, and local Nusselt number are explicitly derived. In addition to presenting analytical solutions, these solutions facilitate a deeper understanding of flow behavior, heat transfer, and entropy production. Additionally, the optimization process for entropy production was performed by experimental design (BBD) and yielded excellent results based on the predicted (analytical) values. The entropy production correlation on the sheet is estimated through a quadratic regression that involves three independent parameters. Among the key findings of this work are:
• Magnetic field, mixed convection, and inclination phenomena are governed by the magneto-buoyancy-inclination parameter.
• The Lorentz forces in the higher and lower values of the buoyancy forces inversely influence the entropy production number.
• Another way to reduce the entropy generation number is to reduce the magneto-buoyancy-inclination parameter, or, in other words, to simultaneously boost the Lorentz and buoyancy forces as well as the inclination of the stretching porous sheet.
• Due to the fact that the heat source raises the temperature more than the heat sink, the Ng(η) rises, and the local shear stress coefficient decreases. Meanwhile, Ng(η) also increases by changing the inclined sheet angle from vertical to horizontal.
• Another feasible way to reduce entropy generation is to decrease the buoyancy, thermal radiation, and material parameters.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
SS: Design of methodology, Analytical solution, Writing—Original Draft HA: Supervision and project administration, Resources, Investigation, Writing—Review and; Editing HADA: Supervision and project administration, Investigation MJ: Supervision, Review and; Editing.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abbas, N., Nadeem, S., and Malik, M. Y. (2020). On extended version of Yamada–Ota and Xue models in micropolar fluid flow under the region of stagnation point. Phys. A Stat. Mech. its Appl. 542, 123512. doi:10.1016/j.physa.2019.123512
Abbas, T., Rehman, S., Shah, R. A., Idrees, M., and Qayyum, M. (2020). Analysis of MHD Carreau fluid flow over a stretching permeable sheet with variable viscosity and thermal conductivity. Phys. A Stat. Mech. its Appl. 551, 124225. doi:10.1016/j.physa.2020.124225
Abdal, S., Ali, B., Younas, S., Ali, L., and Mariam, A. (2019). Thermo-Diffusion and multislip effects on MHD mixed convection unsteady flow of micropolar nanofluid over a shrinking/stretching sheet with radiation in the presence of heat source. Symmetry 12, 49. doi:10.3390/sym12010049
Ahmadi, G. (1976). Self-similar solution of imcompressible micropolar boundary layer flow over a semi-infinite plate. Int. J. Eng. Sci. 14, 639–646. doi:10.1016/0020-7225(76)90006-9
Ali, V., Gul, T., Afridi, Sh., Ali, F., Alharbi, S. O., and Khan, I. (2019). Thin film flow of micropolar fluid in a permeable medium. Coatings 9, 98. doi:10.3390/coatings9020098
Anuar, N. S., Bachok, N., and Pop, I. (2020). Radiative hybrid nanofluid flow past a rotating permeable stretching/shrinking sheet. Int. J. Numer. Methods Heat. Fluid Flow. 31, 914–932. doi:10.1108/hff-03-2020-0149
Bhattacharjee, B., Chakraborti, P., and Choudhuri, K. (2019). Evaluation of the performance characteristics of double-layered porous micropolar fluid lubricated journal bearing. Tribol. Int. 138, 415–423. doi:10.1016/j.triboint.2019.06.025
Chakrabarti, A., and Gupta, A. S. (1979). Hydromagnetic flow and heat transfer over a stretching sheet. Q. Appl. Math. 37, 73–78. doi:10.1090/qam/99636
Chamkha, A. J., Dogonchi, A. S., and Ganji, D. D. (2019). Magneto-hydrodynamic flow and heat transfer of a hybrid nanofluid in a rotating system among two surfaces in the presence of thermal radiation and Joule heating. AIP Adv. 9, 025103. doi:10.1063/1.5086247
Chamkha, A. J. (1997). Hydromagnetic natural convection from an isothermal inclined surface adjacent to a thermally stratified porous medium. Int. J. Eng. Sci. 35, 975–986. doi:10.1016/s0020-7225(96)00122-x
Chamkha, A. J. (1999). Hydromagnetic three-dimensional free convection on a vertical stretching surface with heat generation or absorption. Int. J. Heat. Fluid Flow. 20, 84–92. doi:10.1016/s0142-727x(98)10032-2
Chamkha, A. J. (1997). MHD-free convection from a vertical plate embedded in a thermally stratified porous medium with Hall effects. Appl. Math. Model. 21, 603–609. doi:10.1016/s0307-904x(97)00084-x
Chamkha, A. J., Mohamed, R. A., and Ahmed, S. E. (2011). Unsteady MHD natural convection from a heated vertical porous plate in a micropolar fluid with Joule heating, chemical reaction and radiation effects. Meccanica 46, 399–411. doi:10.1007/s11012-010-9321-0
Chamkha, A. J. (2000). Thermal radiation and buoyancy effects on hydromagnetic flow over an accelerating permeable surface with heat source or sink. Int. J. Eng. Sci. 38, 1699–1712. doi:10.1016/s0020-7225(99)00134-2
Cortell, R. (2013). A novel analytic solution of MHD flow for two classes of visco-elastic fluid over a sheet stretched with non-linearly (quadratic) velocity. Meccanica 48, 2299–2310. doi:10.1007/s11012-013-9749-0
Damseh, R. A., A-Odat, M. Q., Chamkha, A. J., and Shannak, B. A. (2009). Combined effect of heat generation or absorption and first-order chemical reaction on micropolar fluid flows over a uniformly stretched permeable surface. Int. J. Therm. Sci. 48, 1658–1663. doi:10.1016/j.ijthermalsci.2008.12.018
Dawar, A., Shah, Z., Kumam, P., Alrabaiah, H., Khan, W., Islam, S., et al. (2020). Chemically reactive MHD micropolar nanofluid flow with velocity slips and variable heat source/sink. Sci. Rep. 10, 20926. doi:10.1038/s41598-020-77615-9
Dinarvand, S., and Rostami, M. N. (2020). Rotating Al2O3-H2O nanofluid flow and heat transfer with internal heating, velocity slip and different shapes of nanoparticles. Multidiscip. Model. Mat. Struct. 17, 401–417. doi:10.1108/mmms-01-2020-0017
Eringen, A. C. (1964). Simple microfluids. Int. J. Eng. Sci. 2, 205–217. doi:10.1016/0020-7225(64)90005-9
Eringen, A. C. (1966). Theory of micropolar fluids. Indiana Univ. Math. J. 16, 1–18. doi:10.1512/iumj.1967.16.16001
Eswaramoorti, S., Bhuvaneswari, M., Sivasankaran, S., and Makinde, O. D. (2020). Analytical and numerical study on cross diffusion effects on magneto-convection of a chemically reacting fluid with suction/injection and convective boundary condition. Defect Diffusion Forum 401, 63–78. doi:10.4028/www.scientific.net/ddf.401.63
Hashem Zadeh, S. M., Mehryan, S. A. M., Sheremet, M. A., Izadi, M., and Ghodrat, M. (2020). Numerical study of mixed bio-convection associated with a micropolar fluid. Therm. Sci. Eng. Prog. 18, 100539. doi:10.1016/j.tsep.2020.100539
Hosseinzade, Kh., Roghani, So., Asadi, A., Mogharrebi, A., and Ganji, D. D. (2020). Investigation of micropolar hybrid ferrofluid flow over a vertical plate by considering various base fluid and nanoparticle shape factor. Int. J. Numer. Methods Heat. Fluid Flow. 31, 402–417. doi:10.1108/hff-02-2020-0095
Hussain, S. M., and Jamshed, W. (2021). A comparative entropy based analysis of tangent hyperbolic hybrid nanofluid flow: Implementing finite difference method. Int. Commun. Heat Mass Transf. 129, 105671. doi:10.1016/j.icheatmasstransfer.2021.105671
Hussanan, A., Salleh, M. Z., Khan, I., and Tahar, R. M. (2018). Heat and mass transfer in a micropolar fluid with Newtonian heating: An exact analysis. Neural comput. Appl. 29, 59–67. doi:10.1007/s00521-016-2516-0
Ishak, A. (2010). Thermal boundary layer flow over a stretching sheet in a micropolar fluid with radiation effect. Meccanica 45, 367–373. doi:10.1007/s11012-009-9257-4
Jain S, S., and Gupta, P. (2019). Entropy generation analysis of MHD viscoelasticity-based micropolar fluid flow past a stretching sheet with thermal slip and porous media. Int. J. Appl. Comput. Math. 5, 61. doi:10.1007/s40819-019-0643-x
Jalili, B., Jalili, P., Sadighi, S., and Ganji, D. D. (2021). Effect of magnetic and boundary parameters on flow characteristics analysis of micropolar ferrofluid through the shrinking sheet with effective thermal conductivity. Chin. J. Phys. 71, 136–150. doi:10.1016/j.cjph.2020.02.034
Jalili, B., Sadighi, S., Jalili, P., and Ganji, D. D. (2019). Characteristics of ferrofluid flow over a stretching sheet with suction and injection. Case Stud. Therm. Eng. 14, 100470. doi:10.1016/j.csite.2019.100470
Khan, M. I., Alzahrani, F., and Hobiny, A. (2020). Simulation and modeling of second order velocity slip flow of micropolar ferrofluid with Darcy–Forchheimer porous medium. J. Mat. Res. Technol. 9, 7335–7340. doi:10.1016/j.jmrt.2020.04.079
Khan, U., Zaib, A., Pop, I., Bakar, S. A., and Ishak, A. (2022). Stagnation point flow of a micropolar fluid filled with hybrid nanoparticles by considering various base fluids and nanoparticle shape factors. Int. J. Numer. Methods Heat. Fluid Flow. 32, 2320–2344. doi:10.1108/hff-07-2021-0445
Khan, U., Zaib, A., Pop, I., Bakar, S. A., and Ishak, A. (2022). Unsteady micropolar hybrid nanofluid flow past a permeable stretching/shrinking vertical plate. Alexandria Eng. J. 61, 11337–11349. doi:10.1016/j.aej.2022.05.011
Khash’ie, N. S., Arifin, N. M., Nazar, R., Hafidzuddin, E. H., Wahi, N., and Pop, I. (2019). Mixed convective flow and heat transfer of a dual stratified micropolar fluid induced by a permeable stretching/shrinking sheet. Entropy 21, 1162. doi:10.3390/e21121162
Khedr, M. -E. M., Chamkha, A. J., and Bayomi, M. (2009). MHD flow of a micropolar fluid past a stretched permeable surface with heat generation or absorption. Nonlinear Anal. Model. Control 14, 27–40. doi:10.15388/na.2009.14.1.14528
Krishna, M. V., Ahamad, N. A., and Chamkha, A. J. (2020). Hall and ion slip effects on unsteady MHD free convective rotating flow through a saturated porous medium over an exponential accelerated plate. Alexandria Eng. J. 59, 565–577. doi:10.1016/j.aej.2020.01.043
Krishna, M. V., Ahamad, N. A., and Chamkha, A. J. (2021). Hall and ion slip impacts on unsteady MHD convective rotating flow of heat generating/absorbing second grade fluid. Alexandria Eng. J. 60, 845–858. doi:10.1016/j.aej.2020.10.013
Krishna, M. V., and Chamkha, A. J. (2019). Hall and ion slip effects on MHD rotating boundary layer flow of nanofluid past an infinite vertical plate embedded in a porous medium. Results Phys. 15, 102652. doi:10.1016/j.rinp.2019.102652
Krishna, M. V., and Chamkha, A. J. (2020). Hall and ion slip effects on MHD rotating flow of elastico-viscous fluid through porous medium. Int. Commun. Heat Mass Transf. 113, 104494. doi:10.1016/j.icheatmasstransfer.2020.104494
Kumar, K. A., Sugunamma, V., Sandeep, N., and Mustafa, M. T. (2019). Simultaneous solutions for first order and second order slips on micropolar fluid flow across a convective surface in the presence of Lorentz force and variable heat source/sink. Sci. Rep. 9, 14706. doi:10.1038/s41598-019-51242-5
Kumar, K. G., Reddy, M. G., Sudharani, M. V. V. N. L., Shehzad, S. A., and Chamkha, A. J. (2020). Cattaneo-Christov heat diffusion phenomenon in Reiner-Philippoff fluid through a transverse magnetic field. Phys. A Stat. Mech. its Appl. 541, 123330. doi:10.1016/j.physa.2019.123330
Kumar, N., and Gupta, S. (2012). MHD free-convective flow of micropolar and Newtonian fluids through porous medium in a vertical channel. Meccanica 47, 277–291. doi:10.1007/s11012-011-9435-z
Lu, D., Ramzan, M., Ahmad, S., Chung, J. D., and Farooq, U. (2018). A numerical treatment of MHD radiative flow of Micropolar nanofluid with homogeneous-heterogeneous reactions past a nonlinear stretched surface. Sci. Rep. 8, 12431. doi:10.1038/s41598-018-30965-x
Lund, L. A., Omar, Z., and Khan, I. (2019). Mathematical analysis of magnetohydrodynamic (MHD) flow of micropolar nanofluid under buoyancy effects past a vertical shrinking surface: Dual solutions. Heliyon 5, e02432. doi:10.1016/j.heliyon.2019.e02432
Magyari, E., and Chamkha, A. J. (2010). Combined effect of heat generation or absorption and first-order chemical reaction on micropolar fluid flows over a uniformly stretched permeable surface: The full analytical solution. Int. J. Therm. Sci. 49, 1821–1828. doi:10.1016/j.ijthermalsci.2010.04.007
Mahmoud, M. A. A., and Waheed, S. E. (2012). MHD stagnation point flow of a micropolar fluid towards a moving surface with radiation. Meccanica 47, 1119–1130. doi:10.1007/s11012-011-9498-x
Mandal, I. C., and Mukhopadhyay, S. (2020). Nonlinear convection in micropolar fluid flow past a non-isothermal exponentially permeable stretching sheet in presence of heat source/sink. Therm. Eng. 67, 202–215. doi:10.1134/s0040601520040059
Mishra, S. R., Khan, I., Al-mdallal, Q. M., and Asifa, T. (2018). Free convective micropolar fluid flow and heat transfer over a shrinking sheet with heat source. Case Stud. Therm. Eng. 11, 113–119. doi:10.1016/j.csite.2018.01.005
Modather, M., Rashad, A. M., and Chamkha, A. J. (2009). An analytical study of MHD heat and mass transfer oscillatory flow of a micropolar fluid over a vertical permeable plate in a porous medium. Turk. J. Eng. Env. Sci. 33, 245–258.
Mustafa, I., Abbas, Z., Arif, A., Javed, T., and Ghaffari, A. (2020). Stability analysis for multiple solutions of boundary layer flow towards a shrinking sheet: Analytical solution by using least square method. Phys. A Stat. Mech. its Appl. 540, 123028. doi:10.1016/j.physa.2019.123028
Patel, H. R., Mittal, A. S., and Darji, R. R. (2019). MHD flow of micropolar nanofluid over a stretching/shrinking sheet considering radiation. Int. Commun. Heat Mass Transf. 108, 104322. doi:10.1016/j.icheatmasstransfer.2019.104322
Postelnicu, A. (2012). Free convection from a truncated cone subject to constant wall heat flux in a micropolar fluid. Meccanica 47, 1349–1357. doi:10.1007/s11012-011-9518-x
Ramadevi, B., Kumar, K. A., Sugunamma, V., Reddy, J. V. R., and Sandeep N, N. (2020). Magnetohydrodynamic mixed convective flow of micropolar fluid past a stretching surface using modified Fourier’s heat flux model. J. Therm. Anal. Calorim. 139, 1379–1393. doi:10.1007/s10973-019-08477-1
Ramzan, M., Ullah, N., Chung, J. D., Lu, D., and Farooq, U. (2017). Buoyancy effects on the radiative magneto Micropolar nanofluid flow with double stratification, activation energy and binary chemical reaction. Sci. Rep. 7, 12901. doi:10.1038/s41598-017-13140-6
Rana, Sh., Nawaz, M., Saleem, S., and Alharbi, S. O. (2020). Numerical study on enhancement of heat transfer in hybrid nano-micropolar fluid. Phys. Screen. 95, 045201. doi:10.1088/1402-4896/ab5a36
Rashid, I., Sagheer, M., and Hussain, S. (2019). Entropy formation analysis of MHD boundary layer flow of nanofluid over a porous shrinking wall. Phys. A Stat. Mech. its Appl. 536, 122608. doi:10.1016/j.physa.2019.122608
Reddy, P. S., and Chamkha, A. J. (2016). Soret and Dufour effects on MHD convective flow of Al2O3–water and TiO2–water nanofluids past a stretching sheet in porous media with heat generation/absorption. Adv. Powder Technol. 27, 1207–1218. doi:10.1016/j.apt.2016.04.005
Rehman, S. U., Mariam, A., Ullah, A., Asjad, M. I., Bajuri, M. Y., Pansera, B. A., et al. (2021). Numerical computation of buoyancy and radiation effects on MHD micropolar nanofluid flow over a stretching/shrinking sheet with heat source. Case Stud. Therm. Eng. 25, 100867. doi:10.1016/j.csite.2021.100867
Rosali, H., Ishak, A., and Pop, I. (2012). Micropolar fluid flow towards a stretching/shrinking sheet in a porous medium with suction. Int. Commun. Heat Mass Transf. 39, 826–829. doi:10.1016/j.icheatmasstransfer.2012.04.008
Sajid, M., Sadiq, M. N., Ali, N., and Javed, T. (2018). Numerical simulation for Homann flow of a micropolar fluid on a spiraling disk. Eur. J. Mech. - B/Fluids 72, 320–327. doi:10.1016/j.euromechflu.2018.06.008
Santhi, M., Rao, K. V. S., Reddy, P. S., and Sreedevi, P. (2020). Heat and mass transfer characteristics of radiative hybrid nanofluid flow over a stretching sheet with chemical reaction. Heat. Trans. 50, 2929–2949. doi:10.1002/htj.22012
Sayed, A. Y., and Abdel-wahed, M. S. (2020). Entropy analysis for an MHD nanofluid with a microrotation boundary layer over a moving permeable plate. Eur. Phys. J. Plus 135, 106. doi:10.1140/epjp/s13360-020-00181-6
Sen, S. S. S., Das, M., Mahato, R., and Shaw, S. (2020). Entropy analysis on nonlinear radiative MHD flow of Diamond-Co3O4/ethylene glycol hybrid nanofluid with catalytic effects. Int. Commun. Heat Mass Transf. 129, 105704. doi:10.1016/j.icheatmasstransfer.2021.105704
Shah, Z., Alzahrani, E. O., Dawar, A., Ullah, A., and Khan, I. (2020). Influence of Cattaneo-Christov model on Darcy-Forchheimer flow of Micropolar Ferrofluid over a stretching/shrinking sheet. Int. Commun. Heat Mass Transf. 110, 104385. doi:10.1016/j.icheatmasstransfer.2019.104385
Shankar, D. G., Raju, C. S. K., Kumar, M. S. J., and Makinde, O. D. (2020). Cattaneo-christov heat flux on an MHD 3D free convection casson fluid flow over a stretching sheet. Eng. Trans. 68, 223–238.
Shezad, S. A., Reddy, M. G., Vljayakumari, P., and Tlili, I. (2020). Behavior of ferromagnetic Fe2SO4 and titanium alloy Ti6Al4v nanoparticles in micropolar fluid flow. Int. Commun. Heat Mass Transf. 117, 104769. doi:10.1016/j.icheatmasstransfer.2020.104769
Shoaib, M., Raja, M. A. Z., Sabir, M. T., Islam, S., Shah, Z., Kumam, P., et al. (2020). Numerical investigation for rotating flow of MHD hybrid nanofluid with thermal radiation over a stretching sheet. Sci. Rep. 10, 18533. doi:10.1038/s41598-020-75254-8
Sreedevi, P., Reddy, P. S., and Chamkha, A. (2020). Heat and mass transfer analysis of unsteady hybrid nanofluid flow over a stretching sheet with thermal radiation. SN Appl. Sci. 2, 1222. doi:10.1007/s42452-020-3011-x
Takhar, H. S., Chamkha, A. J., and Nath, G. (2002). MHD flow over a moving plate in a rotating fluid with magnetic field, Hall currents and free stream velocity. Int. J. Eng. Sci. 40, 1511–1527. doi:10.1016/s0020-7225(02)00016-2
Takhar, H. S., Chamkha, A. J., and Nath, G. (1999). Unsteady flow and heat transfer on a semi-infinite flat plate with an aligned magnetic field. Int. J. Eng. Sci. 37, 1723–1736. doi:10.1016/s0020-7225(98)00144-x
Thumma, T., and Mishra, S. R. (2020). Effect of non-uniform heat source/sink, and viscous and Joule dissipation on 3D Eyring–Powell nanofluid flow over a stretching sheet. J. Comput. Des. Eng. 7, 412–426. doi:10.1093/jcde/qwaa034
Tiwari, A., Shah, P. D., and Chauhan, S. S. (2020). Analytical study of micropolar fluid flow through porous layered microvessels with heat transfer approach. Eur. Phys. J. Plus 135, 209. doi:10.1140/epjp/s13360-020-00128-x
Turkyilmazoglu, M. (2017). Mixed convection flow of magnetohydrodynamic micropolar fluid due to a porous heated cooled deformable plate: Exact solutions. Int. J. Heat. Mass Transf. 106, 127–134. doi:10.1016/j.ijheatmasstransfer.2016.10.056
Waini, I., Khan, U., Zaib, A., Ishak, I., and Pop, I. (2022). Inspection of TiO2-CoFe2O4 nanoparticles on MHD flow toward a shrinking cylinder with radiative heat transfer. J. Mol. Liq. 361, 119615. doi:10.1016/j.molliq.2022.119615
Wakif, A., Chamkha, A., Animasaun, I. L., Zaydan, M., Waqas, H., and Sehaqui, R. (2020). Novel physical insights into the thermodynamic irreversibilities within dissipative emhd fluid flows past over a moving horizontal riga plate in the coexistence of wall suction and joule heating effects: A comprehensive numerical investigation. Arab. J. Sci. Eng. 45, 9423–9438. doi:10.1007/s13369-020-04757-3
Yu Khanukaeva, D., Filippov, A. N., Yadav, P. K., and Tiwari, A. (2019). Creeping flow of micropolar fluid parallel to the axis of cylindrical cells with porous layer. Eur. J. Mech. - B/Fluids 76, 73–80. doi:10.1016/j.euromechflu.2019.01.012
Keywords: exact solution, MHD free convection flow, micropolar fluid, stretching sheet, entropy analysis, response surface methodology
Citation: Sadighi S, Afshar H, Jabbari M and Ahmadi Danesh Ashtiani H (2022) An analytical approach to entropy production in MHD mixed convection micropolar fluid flow over an inclined porous stretching sheet. Front. Mech. Eng 8:900316. doi: 10.3389/fmech.2022.900316
Received: 30 March 2022; Accepted: 01 August 2022;
Published: 14 September 2022.
Edited by:
Arash Shams Taleghani, Ministry of Science, Research and Technology, IranReviewed by:
Ali Chamkha, Kuwait College of Science and Technology, KuwaitAurang Zaib, Federal Urdu University of Arts, Sciences and Technology Islamabad, Pakistan
Copyright © 2022 Sadighi, Afshar, Jabbari and Ahmadi Danesh Ashtiani. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Hossein Afshar, aG9zc2Vpbi5hZnNoYXJAaWF1LmFjLmly
 Sina Sadighi
Sina Sadighi Hossein Afshar
Hossein Afshar Mohsen Jabbari1
Mohsen Jabbari1