On the adhesion between thin sheets and randomly rough surfaces

1 Introduction

Thin-film adhesion has gained much attention in the scientific community in recent years, in particular, in the context of biomimetic systems (Autumn et al., 2000, Autumn et al., 2002; Reddy et al., 2007; Boesel et al., 2010). Understanding what parameters control adhesion and thus traction can certainly aid the control of adhesive systems. Although Persson’s contact mechanics theory (Persson, 2001; Persson, 2002; Persson, 2003; Persson and Gorb, 2003) allows predictions on properties of adhesive systems to be made (Carbone et al., 2009; Wang and Müser, 2017; Joe et al., 2017; Joe et al., 2018; Joe et al., 2020), it does not provide any easy-to-evaluate guidelines. Nonetheless, achieving controllable adhesion in real systems can certainly be aided by an understanding of the basic detachment mechanism and the parameters controlling pull-off stresses or pull-off forces (Arzt et al., 2003; Persson, 2003; Kamperman et al., 2010).

Thin elastic layers generally stick better to nominally flat but microscopically rough surfaces compared to bulk solids. This is because thin sheets can accommodate the long-wavelength undulations of their counterfaces much more easily than thick solids do (Carbone et al., 2004). When thick elastomers comply with randomly rough surfaces, the required elastic energy resides predominantly in deformation modes near the roll-off wave vector q_r, at which the height spectrum C(q) transitions from being approximately constant to the self-affine scaling regime. In the latter domain, C(q) ∝ q^−2(1+H), where H is called the Hurst exponent, which typically takes values 0.8 ≲ H ≲ 1 (Majumdar and Tien, 1990; Palasantzas, 1993; Persson, 2014; Jacobs et al., 2017). In the rare cases, when H ≤ 0.5, the full-contact elastic energy, $v_{\text{ela}}^{\text{full}}$, would be dominated by contributions from short-wavelength undulations, in which case, thin sheets are not expected to adhere substantially better to counterfaces than semi-infinite solids do (Carbone et al., 2004; Violano et al., 2021). Interestingly, Menga et al. (2016) found the pull-off force of thin elastomers reduced compared to semi-infinite solids in a numerical study of one-dimensional, single-sinusoidal contacts. Local stickiness criteria (Pastewka and Robbins, 2014; Müser, 2016) are not in line with everyday experience either that thin sheets adhere well to counterfaces: their single-patch contact mechanics resembles that of semi-infinite solids, as long as the linear dimension of a patch is not similar to or greater than the sheet’s thickness t (Carbone et al., 2004). However, the importance of long-wavelength roughness for the suppression of apparent adhesion was clearly demonstrated in recent experiments: Tiwari et al. (2020) found that two surfaces with similar spectra, which differed mostly at long wavelengths led to similar local geometric properties but different root-mean-square (RMS) heights h_rms, and the surface with the smaller h_rms was sticky while the other showed no signs of adhesion.

Classical approaches to adhesion, most notably the one by Dahlquist (1966), assume that adhesion becomes macroscopically noticeable when the surface energy γ is greater than or similar to the elastic energy needed to fully conform two surfaces to each other. This explains why the more quantitative Persson theory also finds the effective surface energy to vanish when the surface spectrum of the rough surface has sufficient intensity at small wave vectors (Persson, 2002). Recent simulations by Wang and Müser (2022) identified a rather abrupt transition between high and low maximum tension at a reduced surface energy, or generalized Johnson parameter (Ciavarella and Papangelo, 2018), of $\tilde{\gamma }=\gamma /v_{\text{ela}}^{\text{full}}\approx 1/2$. Since the mechanics, in particular, the local detachment of thin sheets differs from that of semi-infinite solids, there is no a-priori reason that this simple stickiness criterion generalizes to thin sheets. Investigating to what extent the simple $\tilde{\gamma }=1/2$ criterion also applies to thin sheets is the content of this study.

In this study, we systematically study the effect of sheet thickness on the pull-off stress and other quantities defining the adhesive contact between elastic solids of varying thicknesses and a stiff counterface. The model and method used for our study are sketched in Sec 2, results are presented in Sec 3, and conclusions are drawn in Sec 4.

2 Model and method

2.1 Model

The definition of the model has three main aspects: the geometry of the rough substrate, which is fixed in space, the elastic properties of the flat elastic layer including the boundary conditions acting on it, and the interaction between substrate and layer.

2.1.1 Substrate geometry

In this study, the counterface topography is modeled in terms of either single- or multiscale-wavelength roughness. The profile of single-wavelength roughness is defined as a square-lattice pattern according to

$h\left(x,y\right)=\left\{2+\cos \left(2\pi x/\lambda \right)+\cos \left(2\pi y/\lambda \right)\right\}{h}_{\text{rms}},(1)$

where h_rms is the root-mean-square deviation of the height from its mean, while the wavelength λ is set equal to the linear dimension of the simulation L, which is periodically repeated, parallel to the interfacial directions x and y.

Randomly rough surfaces are modeled with a typical height spectrum of the form (Majumdar and Tien, 1990; Palasantzas, 1993; Persson, 2014; Jacobs et al., 2017)

$C\left(\mathbf{q}\right)=⟨|\tilde{h}\left(\mathbf{q}\right){|}^2⟩(2)$

$=\frac{C\left(0\right)\mathrm{\Theta }\left(q_{\mathrm{s}}-q\right)}{{\left\{1+{\left(q/q_{\mathrm{r}}\right)}^2\right\}}^{\left(1+H\right)}}.(3)$

Here, $\tilde{h}(\mathbf{q})$ is the Fourier transform of the (periodically repeated) height h(r), λ_r = 2π/q_r is the roll-off wavelength, and λ_s = 2π/q_s is the short-wavelength cutoff. The latter is used so that a well-defined continuum limit exists at small scales. The Hurst exponent H, which has already been introduced in Sec 1, is set to H = 0.8 throughout this work. The height topography is always normalized by selecting C (0) such that the root-mean-square height gradient of the surface satisfies $\bar{g}=1$.

For the sake of simplicity, we assume C(q) to depend only on q, which makes the surfaces statistically isotropic, and neglect any potential correlation between the phases of the complex $\tilde{h}(\mathbf{q})$, which leads to statistically homogeneous surfaces. While the random-phase approximation occasionally draws criticism, we see its use as the most meaningful default assumption as long as there is neither recipe nor reason for how to correlate the phases. See also the discussions by Persson (2014) and Müser (2018).

Our random topography is characterized by the ratios λ_r/λ_s = 64 and L/λ_r = 4, which results in a mean local radius of curvature of R_c ≈ 0.0057λ_r and $\bar{h}=3.27{\lambda }_{\mathrm{s}}$ for H = 0.8. A “typical” number to be used for λ_r could be a few dozen microns for a highly polished surface. By default, the surface is discretized into 2, 048 × 2, 048 identical square mesh points.

2.1.2 Properties of the elastic layer

The elastic layer is treated to have a finite thickness t. On the side opposite to the substrate, the stress is assumed to be constant and normal to the original, undeformed surface. The elastic energy as a function of the displacement field u(r), whose Fourier transform is $\tilde{u}(\mathbf{q})$, then reads

$v_{\text{ela}}=\frac{A}{4}\sum c\left(qt\right)q{E}^{\ast }|\tilde{u}\left(\mathbf{q}\right){|}^2,(4)$

in mechanical equilibrium. Here, E* is the contact modulus defined as E/(1 − ν²) with E being the Young’s modulus and ν the Poisson’s ratio. The thickness-dependent factor c (qt) is given by Carbone et al. (2009).

$c\left(qt\right)=\frac{\cosh \left(2qt\right)-2{\left(qt\right)}^2-1}{\sinh \left(2qt\right)+2qt}.(5)$

E* is used as unit for pressure, which corresponds to the usual choice of $[p]=E^{*}/\bar{g}$, since all surfaces are normalized such that $\bar{g}=1$. Figure 1 depicts a typical relaxed configuration of an adhesive, elastic layer of finite width in contact with a rigid, randomly rough substrate.

FIGURE 1

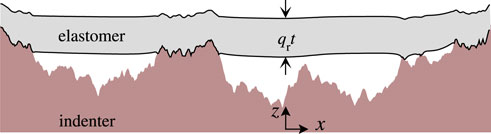
FIGURE 1. Cross-section of an adhesive, elastic layer of the finite thickness (q_rt = 0.5) in contact with a rigid, randomly rough substrate. The shown cross-section, which contains the highest point of our default topography, is not to scale.

2.1.3 Interactions between substrate and elastic layer

The local surface energy between elastic sheet and rigid substrate takes the recently suggested form of (Wang et al., 2021):

$v\left(\mathrm{\Delta }z\right)=-\gamma \times \left\{\begin{array}{cc}0\hfill & \mathrm{\Delta }z>g_{\mathrm{c}}\hfill \\ -1+{\left(\pi \mathrm{\Delta }z/g_{\mathrm{c}}\right)}^2/4\hfill & \mathrm{\Delta }z<0\hfill \\ \frac{1}{2}\left\{1+\cos \left(\pi \mathrm{\Delta }z/g_{\mathrm{c}}\right)\right\}\hfill & \mathrm{e}\mathrm{l}\mathrm{s}\mathrm{e},\hfill \end{array}\right.,(6)$

where γ is the surface energy that is gained per unit area when two parallel surfaces make contact, while g_c is the range of the interaction. This “cohesive-zone model” (CZM) is designed such that the interaction between elastomer and counterface is twice differentiable, which eases an efficient energy minimization. Typical values for γ with relevance to tribology range from O (10 mJ/m²) for chemically passivated solids, for example, those formed by many common polymers, to O (1 J/m²) for non-passivated metals or ceramics.

The specific choice for g_c depends on the investigated system, as explained next in Sec 2.1.4. However, we always ensured to increase the discretization with reference to the default to ensure smooth displacements near the contact lines. This was achieved by choosing the local elastic stiffness, defined as πE*/Δa to be at least 2.5 times the maximum curvature of the CZM, which is ${\pi }^2\gamma /(2g_{\mathrm{c}}^2)$. Herein, Δa is the linear size of a single mesh element.

2.1.4 Dimensionless parameters

Several dimensionless quantities characterizing the interface can be defined. One way of undimensionalizing the surface energy is to use $[\gamma ]=E^{*}{R}_{\mathrm{c}}{\bar{g}}^3$ as unit for the surface energy (Pastewka and Robbins, 2014; Müser, 2016), which will be marked with a prime, that is,

${\gamma }^{\prime }=\gamma /\left(E^{\ast }{R}_{\mathrm{c}}{\bar{g}}^3\right).(7)$

Individual contact patches are found to be locally sticky if γ′ ≳ 1. An advantage of this measure is that it does not depend on the sheet thickness. However, little is learned about the number of contact patches from γ′. The reduced surface energy,

$\tilde{\gamma }=\gamma /v_{\text{ela}}^{\text{full}},(8)$

introduced already in Sect. 1 holds promise to provide a more meaningful measure for the interfacial surface energy.

Another important quantity is the (local) Tabor parameter, defined as

${\mu }_{\mathrm{T}}=\frac{R_{\mathrm{c}}^{1/3}}{\rho }{\left(\frac{\gamma }{E^{\ast }}\right)}^{2/3},(9)$

which characterizes the range of the interaction. Large and small μ_T reflect short- and long-range adhesion, respectively. Throughout this article, μ_T = 4 is assumed. In single-asperity contact, this choice is sufficient to make the retraction curve be close to the continuum limit (Müser, 2014), while larger numbers are required in order to properly reflect the approach curve for short-range adhesion (Ciavarella et al., (2017); Wang et al., (2021)). However, the Tabor parameter is a scale-dependent quantity (Persson and Scaraggi, 2014) so that the Tabor parameter at coarse scales used here is clearly greater than its local default value. The only exceptions to this claim pertain to the hysteresis of the load-displacement curve in situations, where only the final maximum of the counterfaces touches the elastomer. Fortunately, this limit is well understood from the Johnson–Kendall–Roberts (JKR) theory (Johnson et al., 1971).

Finally, while the stress is usually defined in units of $E^{*}\bar{g}$, we will usually undimensionalize the pull-off stress σ_p with the maximum stress of the CZM, that is, according to

${\tilde{\sigma }}_{\mathrm{p}}={\sigma }_{\mathrm{p}}/{\sigma }_{\text{max}},(10)$

with σ_max = πγ/(2g_c).

2.2 Mass-weighted GFMD

Green’s function molecular dynamics (GFMD) (Campaná and Müser, 2006) is used, which has been discussed several times in the past. See in particular Appendix 2 in Prodanov et al. (2013). This is why we only provide a brief summary of the method. The main idea is to solve the equations of motion resulting from the total energy and, if present, constraints using the usual molecular-dynamics toolbox. Dynamics are formulated in terms of the Fourier representation of the displacements, which makes it possible to implement efficient methods for energy minimization, such as the mass-weighting (MW) algorithm (Zhou et al., 2019). MW-GFMD assigns less inertia to soft modes, which is utterly beneficial for the simulation of thin sheets, where long-wavelength modes are particularly soft compared to those at small scales.

In this work, we study quasi-static dynamics and thus disregard viscoelastic forces. To this end, we use a ramp as in Ref. (Wang et al., 2021). Specifically, we change the thin-sheet’s center of mass over Δτ = 50 time steps according to $\mathrm{\Delta }\tilde{u}(q)=\mathrm{\Delta }{\tilde{u}}_0\left\{2+2\cos [2\pi (t-t_0)/\mathrm{\Delta }\tau ]\right\}$ with ${\tilde{u}}_0=h_{\text{rms}}/200$ and then let the system relax toward its minimum over another 400 time steps. Figure 2 depicts the dynamics of a relaxation process that occurred for a sheet of thickness qt = 2 during the first approach-to-contact instability.

FIGURE 2

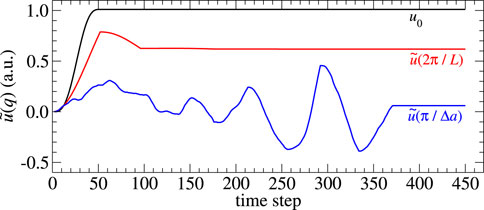
FIGURE 2. Displacement of selected modes, $\tilde{u}(\mathbf{q},\tau )$, as a function of time step τ during the first instability on approach for qt = 2, γ′ = 0.41 leading to $\tilde{\gamma }=0.32$. u₀ is the constrained center-of-mass mode, which is ramped to its new value over 50 time steps and then kept constant for another 400 time steps. Two additional modes are shown, that is, one with a small wave vector, q = 2π/L, and the other with a large wave vector, q = 2π/Δa. Displacements are rescaled for better visualization.

3 Results and discussion

3.1 Single-wavelength roughness

We first studied the load-displacement, or rather stress-displacement, dependence in the limiting case of single-wavelength roughness. In contrast to previous numerical studies by, for example, Zilberman and Persson (2002) or Menga et al. (2016), we investigate a two-dimensional (2D) rather than a one-dimensional (1D) interface so that our topography contains saddle points in addition to maxima and minima. Figure 3 shows the equilibrium relation between the mean interfacial stress σ₀ and the displacement d for a reduced surface energy $\tilde{\gamma }=1/4$, which is small enough for a semi-infinite solid to be on the low-traction branch, for which the ultimate failure of the contacts happens when only the highest peak is in contact.

FIGURE 3

FIGURE 3. Dimensionless interfacial stress σ₀/σ_max as a function of the dimensionless displacement d/d_p during approach and retraction for elastomers of different thicknesses t, that is, qt = ∞, 2, and 1, where q = 2π/λ. Here, d_p is the displacement required to break the contact in the JKR limit. The surface energy γ is kept constant at $v_{\text{ela}}^{\text{full}}(t=\infty )/4$ leading to the thickness-dependent reduced surface energies stated in the labels. The inset highlight the hysteresis associated with the height maxima.

The typical loading-unloading process of a semi-infinite body with short-ranged adhesion for single-sinusoidal, 2D roughness (Wang et al., 2021) is clearly revealed in Figure 3: a hysteresis related to the primary contact formation of the height maxima at negative stress (highlighted in the inset) and the later hysteresis at positive stresses associated with the coalescence of previously disconnected (but periodically repeated) contact patches, bringing the saddle points of the height profile in contact with the elastomer. Due to the small value of $\tilde{\gamma }$, the saddle-point hysteresis is located at compressive stresses in the semi-infinite case. When reducing the thickness of the elastomer, the saddle-point hysteresis moves to smaller stresses, however, the pertinent stresses near the saddle-point instability are still larger than those of the maxima as long as $\tilde{\gamma }\lesssim 0.4$. The respective load-displacement curves, highlighted in the inset of Figure 3, reveal that thinner sheets have smaller pull-off stress, as in the line contact discussed by Menga et al. (2016). However, once $\tilde{\gamma }\gtrsim 0.5$, the absolute stress minimum occurs when the saddle point loses contact and not when an isolated contact patch near the height maximum detaches. In this case, the thin-sheet pull-off stress exceeds that of the semi-infinite body.

The just-discussed simulations were repeated for a larger reduced surface energy, that is, for $\tilde{\gamma }=1$. Now, larger stress is required to break contact near the saddle points than of the height maxima, even for the semi-infinite sheet, as is revealed in Figure 4. Trends are similar as before in that reducing sheet thickness increases the pull-off stress needed to break contact of the saddle points. The thinner the sheet, the more closely the pull-off stress approaches its theoretical maximum σ_max.

FIGURE 4

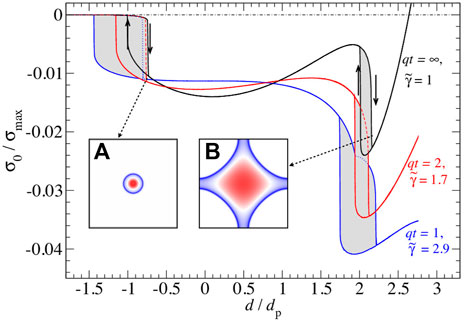
FIGURE 4. Stress-displacement dependence as in Figure 3, however, this time for $\tilde{\gamma }=1$. Inset depicts the stress field of the first JKR-like jump into contact (A) and the second saddle-point contact near the moment where two patches merge. (B) The color blue indicates tensile stress while red represents repulsive stress.

The results presented so far were obtained under displacement control of the layer facing the rigid counterface. Such boundary conditions would be difficult to establish experimentally. Instead, real systems can be assumed to be closer to a load-driven situation. For example, the back layer of an elastomer could be charged uniformly and exposed to an electric field, which would play the role of the external driving force. Under such load driving, it might be impossible to measure experimentally those portions of the σ₀(d) relation with a negative slope because the system would be mechanically unstable on those branches, yet not all of those branches are necessarily accessible. For example, the part of the σ₀(d) branch of the qt = ∞, $\tilde{\gamma }=1$ curve in Figure 4 located near d = 1, can be reached neither on approach, since the contact jumps right to d ≈ 2.1d_p on approach with σ = 0⁺, nor on retraction because contact is lost completely once the saddle point has detached under a sufficiently large, constant tensile stress.

Despite the difficulty to access experimentally all branches of the σ₀(d) curve, small parameter windows exist, in which the sheets can act like a pressure-sensitive adhesive. For example, for qt = 1 and $0.4\lesssim \tilde{\gamma }\lesssim 0.5$, the saddle-point detachment stress exceeds that associated with the height maxima while both detachment conditions are separated by a positive compressive stress. However, for most parameter choices, there is a unique (maximum) detachment stress. Very thin or very adhesive sheets can even jump into full contact without requiring a compressive stress. This behavior is summarized in Figure 5 for a few selected thicknesses, which shows that the range in which interfaces with single-wavelength roughness can be used as a pressure-sensitive adhesive is quite narrow.

FIGURE 5

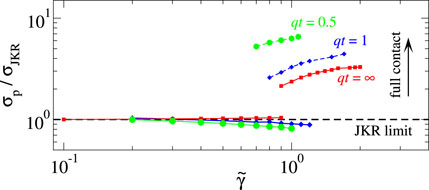
FIGURE 5. Pull-off stress normalized to that obtained in the JKR limit, σ_p/σ_JKR, as a function of the reduced surface energy $\tilde{\gamma }$ with the elastic layer thickness qt—0.5, 1, and ∞. The dashed black line indicates the JKR limit. The flat, low σ_p lines correspond to JKR-like snap-off, while the curved, high σ_p reflects saddle-point instabilities. Endpoints of qt = 0.5, 1, and ∞ are located at $\tilde{\gamma }=1.07,1.7$ and 2.0, at which point jump-into-full-contact instabilities are unavoidable even under displacement driving.

In the case of single-wavelength roughness, reaching a saddle-point contact for a thin sheet using constant-load driving will be generally difficult. For example, for qt = 1 and $\tilde{\gamma }=1$, a compressive load is required to reach contact in the saddle point, but this load is sufficient to make the system advance straight into the full-contact condition. Irrespective of this, the transition between high and low adhesion occurs near, actually slightly above, a value of $\tilde{\gamma }\gtrsim 0.5$.

3.2 Randomly rough surface with H = 0.8

Before presenting numerical results on a randomly rough surface, we find it instructive to study which wave numbers matter the most for the total elastic energy per unit area,

$v_{\text{ela}}^{\text{full}}\left(t\right)=\sum _{\mathbf{q}}\frac{c\left(qt\right)q{E}^{\ast }}{4}C\left(q\right)(11)$

required to bring the elastomer into conformal surface. When transitioning to a continuum description, the sum over wave vectors must be replaced with an appropriate integral. Individual summands or integrands are shown in Figure 6A for a ratio λ_r/λ_s = 1, 000. They reveal a maximum near a “representative” wave vector of $q_{\text{rep}}=\sqrt{4/{\lambda }_{\mathrm{r}}^2+9/t^2}$ for the investigated Hurst exponent of H = 0.8. The sum or integral over all wave vectors accumulates by more than 70% over a relatively narrow wave vector range, that is, a decade of wave vectors, as is revealed in panel (b) of Figure 6. This is why it may be legitimate to expect similar trends for randomly rough as for single-wavelength roughness.

FIGURE 6

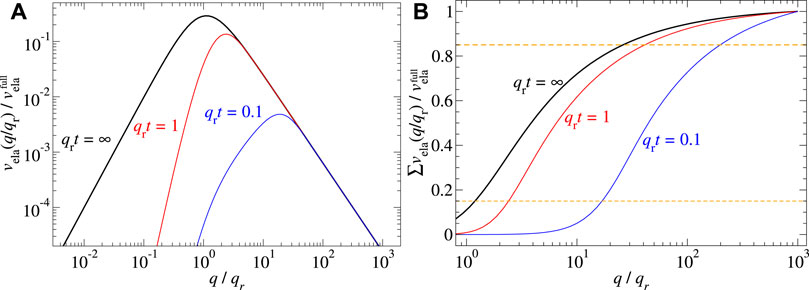
FIGURE 6. (A) Full-contact elastic energy per mode as a function of q/q_r. (B) Relative, cumulative full-contact elastic energy for thicknesses satisfying q_rt = ∞, 1, and 0.1.

Another way of rationalizing the enhanced adhesion of thin sheets to substrates is given by the concept of contact splitting (Kamperman et al., 2010). To this end, it is instructive to visualize the interfacial stress of different models at identical relative contact areas, as is done in Figure 7. Panel (a) shows the contact topography for a purely, repulsive, semi-infinite solid at a relative contact area of a_r ≈ 0.1, and panel (d) a zoom into a selected domain within that structure. If a similar contact area is induced by adhesion $(\tilde{\gamma }=0.526)$ rather than by load, see panel (b) and its zoom-in in panel (e), the contact zones densify although locations of high compressive remain in place. At finite thickness, depicted in panel (c) with a zoom-in in panel (f), the contact decomposes into smaller, yet compact contact patches, whereby the adhesive regions marked in blue color, are about to percolate across the entire domain. Here, the relative contact area was still kept near 10%, which was achieved by further reducing the load.

FIGURE 7

FIGURE 7. Stress distribution of an elastic sheet squeezed a rigid, randomly rough substrate: (A) thick slab without adhesion, (B) thick slab with adhesion, and (C) thin sheet with adhesion. All three configurations are simulated to obtain 10% relative contact area. Red and yellow mark compressive stress, while blue indicates attraction. Substrate specification: $p/E^{*}\bar{g}=0.05$ (A,D), 0.013 (B,E), and 0.001 (C,F) and γ′ = 0 (A,D) and 0.6 (B,E,C,F). The latter number becomes $\tilde{\gamma }=0$ (A,D), 0.205 (B,E), and 0.525 (C,F). The thickness of (C,F) gives q_rt = 0.5.

When changing $\tilde{\gamma }$ for our default system, a transition between a high-traction and a low-traction domain is found, which is located near $\tilde{\gamma }=0.5$, as can be seen Figure 8. This value is rather close to that of semi-infinite solids. Moreover, the dependence of quite a few quantities, that is, pull-off stress in panel (a), relative contact area in panel (b), work of adhesion, and energy hysteresis, both in panel (c), all reveal a strikingly similar dependence on the reduced surface energy for the sheet as for the semi-infinite solid. This is a non-trivial result since the full-contact elastic energy for the sheet was reduced by a factor of 50 compared to that of the semi-infinite case.

FIGURE 8

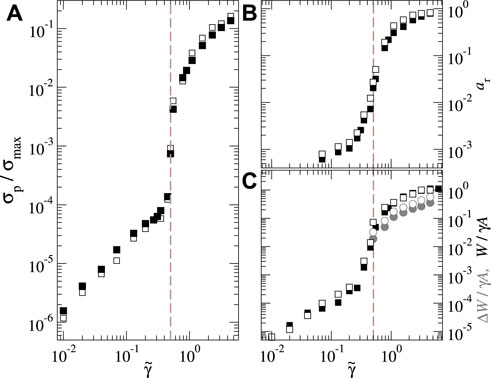
FIGURE 8. (A) Pull-off stress σ_p/σ_max, (B) relative contact area a_r, (C) work of adhesion W (black squares), and energy hysteresis ΔW (grey circles) for one realization of the default surface. Herein, solid symbols indicate the semi-infinite solid while open symbols refer to a thin sheet with a thickness of t = 1/(2q_r).

The just reported trends remain robust upon further lowering of the sheet thickness, as conveyed in Figure 9. For the smallest investigated thicknesses, the cross-over region moves to a slightly smaller $\tilde{\gamma }$, but shifts are small compared to the relative reduction of $v_{\text{ela}}^{\text{pro}}$ by a factor of 400 compared to the semi-infinite case.

FIGURE 9

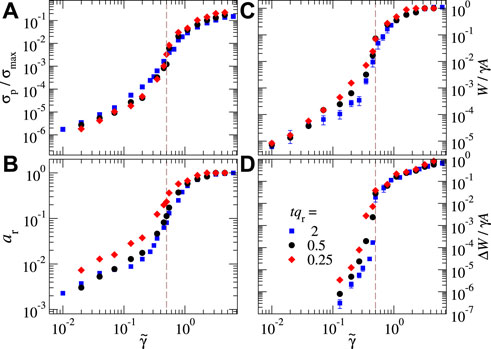
FIGURE 9. Normalied pull‐off force (A) relative contact area at zero load (B) work of separation (C) and energy loss (D) in a function of reduced surface energy for a broader range of sheet thicknesses from q_r = 2, 0.5 and 0.25.

3.3 Randomly rough surfaces with H = 0.3

The analysis shown in Figure 6 revealed that the main contributions to the full-contact elastic energy move to smaller wavelengths as the thickness is reduced. A similar effect occurs when using smaller H exponents. In fact, when using H < 0.5, the main contributions to v_ela come from the wavevectors near q_s. This is why thickness effects at q_rt = 0.1 are quite marginal in our random system for H = 0.3 but already substantial for H = 0.8 despite λ_r/λ_s being merely 128. Thus, for the study of adhesion with a H = 0.3 substrate, thickness effects are marginal, unless the thickness clearly falls below the inverse roll-off wavevector. Such thin layers, however, may rarely exist in applications.

For the just-mentioned reasons, we also investigated the dependence of the pull-off stress on the reduced surface energy for a semi-infinite solid in contact with an adhering H = 0.3 counterface. The results presented in Figure 10 reveal once more a transition near $\tilde{\gamma }=0.5$, which, however, differs in nature from the transitions observed so far, in that there is a cross-over in scaling rather than an almost discontinuous drop in the maximum tensile load.

FIGURE 10

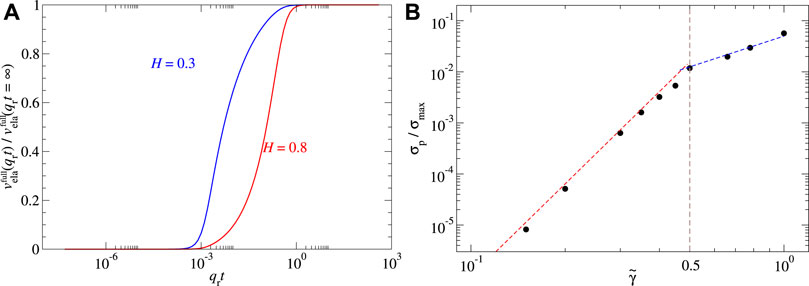
FIGURE 10. (A) Normalized full-contact elastic energy in a function of thickness with H = 0.3 and 0.8. (B) Normalized pull-off force in a function of normalized surface energy with H = 0.3. Here, q_rt = ∞ and same parameter setting as Figure 8.

4 Discussion and conclusions

In this work, we investigated the question to what extent thin elastic sheets—with a constant pressure condition on the back layer—adhere more strongly to rough counter faces than bulk elastomers. On one hand, thin sheets are readily separated from a substrate due to their large compliance, resulting in a process reminiscent of peeling. This explains why Menga et al. (2016) found smaller pull-off stresses for them than for semi-infinite solids. On the other hand, they accommodate long-wavelength undulations of their counterfaces quite easily, facilitating contact formation, which correlates with our experience that thin food wrap clings better to surfaces than thick sheets of the same material. Unsurprisingly, we find that the “peeling argument” keeps the upper hand at a small relative contact area, which, in the case of single-wavelength roughness, coincides with the situation that only the height maxima but not the saddle points are in contact. Once saddle points are in contact, peeling-like separation is strongly suppressed and the pull-off stress, the work of adhesion, and the adhesion hysteresis grow with decreasing thickness. For 2D, single-wavelength roughness, a narrow window of surface energies exists at which a pull-off instability can be associated with a saddle-point instability, irrespective of the sheet’s thickness. Trends for randomly rough surfaces were similar to those with single-wavelength roughness, which we rationalize with the observation that the elastic energy for conformal contact is located in a relatively narrow wave-number window. The pertinent wavelengths are located near the roll-off wavelength of the randomly rough surface for semi-infinite solid and move to smaller wavelengths having the order of magnitude of the sheet thickness t otherwise. Nonetheless, it seems somewhat easier to reach a state of saddle-point contact for randomly rough than for single-wavelength indenters, since the latter have an extreme propensity to form full contact, once the saddle points touch the elastomer.

This work, like our previous one (Wang and Müser, 2022), supports the idea of the possibility of energy loss due to contact hysteresis even without viscoelasticity (Dalvi et al., 2019; Li et al., 2019; Sanner and Pastewka, 2022). While these works were concerned with a semi-infinite elastomer interacting with a nominally flat Hertzian indenter, Li et al. (2019) found, as we did, a relative sharp transition between sticky and unsticky when a “Johnson adhesion parameter” α* took a value near 0.25. Their parameter correlates with but is not identical to our reduced surface energy $\tilde{\gamma }$. While both parameters show convincing correlation regarding the transition between large and small adhesion, $\tilde{\gamma }$ has already proven useful to determine the stickiness of thin sheets in addition to that of semi-infinite solids, while the Johnson adhesion parameter must most certainly be generalized to be applicable for finite thickness, since in its current form α* is insensitive to it.

Interestingly, we found $\tilde{\gamma }=0.5$ to also separate the high- and low-adhesion conditions for randomly rough surfaces with a Hurst exponent as small as H = 0.3. However, for the H = 0.3 surfaces, we did not observe a quasi-continuous drop in the pull-off force near $\tilde{\gamma }=0.5$ but rather a change in scaling, that is, a very quickly decaying pull-off force with decreasing γ. This qualitatively different behavior may be due to the fact that the full-contact elastic energy resides predominantly in short-wavelength undulations for H < 0.5 but in long-wavelength undulations for H > 0.5.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

MM designed the study, wrote the manuscript, and analyzed the results. AW ran the simulations, analyzed the results, and prepared the figures.

Funding

MM acknowledges receiving support from the Leibniz Foundation as an INM fellow.

Acknowledgments

Both authors thank Nicola Menga and Christian Müller for their helpful discussions.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Arzt, E., Gorb, S., and Spolenak, R. (2003). From micro to nano contacts in biological attachment devices. Proc. Natl. Acad. Sci. U.S.A. 100, 10603–10606. doi:10.1073/pnas.1534701100

PubMed Abstract | CrossRef Full Text | Google Scholar

Autumn, K., Liang, Y. A., Hsieh, S. T., Zesch, W., Chan, W. P., Kenny, T. W., et al. (2000). Adhesive force of a single gecko foot-hair. Nature 405, 681–685. doi:10.1038/35015073

PubMed Abstract | CrossRef Full Text | Google Scholar

Autumn, K., Sitti, M., Liang, Y. A., Peattie, A. M., Hansen, W. R., Sponberg, S., et al. (2002). Evidence for van der waals adhesion in gecko setae. Proc. Natl. Acad. Sci. U.S.A. 99, 12252–12256. doi:10.1073/pnas.192252799

PubMed Abstract | CrossRef Full Text | Google Scholar

Boesel, L. F., Greiner, C., Arzt, E., and del Campo, A. (2010). Gecko-inspired surfaces: A path to strong and reversible dry adhesives. Adv. Mat. 22, 2125–2137. doi:10.1002/adma.200903200

PubMed Abstract | CrossRef Full Text | Google Scholar

Campañá, C., and Müser, M. H. (2006). Practical Green’s function approach to the simulation of elastic semi-infinite solids. Phys. Rev. B 74, 075420. doi:10.1103/physrevb.74.075420

CrossRef Full Text | Google Scholar

Carbone, G., Lorenz, B., Persson, B. N., and Wohlers, A. (2009). Contact mechanics and rubber friction for randomly rough surfaces with anisotropic statistical properties. Eur. Phys. J. E 29, 275–284. doi:10.1140/epje/i2009-10484-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Carbone, G., Mangialardi, L., and Persson, B. (2004). Adhesion between a thin elastic plate and a hard randomly rough substrate. Phys. Rev. B 70, 125407. doi:10.1103/physrevb.70.125407

CrossRef Full Text | Google Scholar

Ciavarella, M., Greenwood, J., and Barber, J. (2017). Effect of tabor parameter on hysteresis losses during adhesive contact. J. Mech. Phys. Solids 98, 236–244. doi:10.1016/j.jmps.2016.10.005

CrossRef Full Text | Google Scholar

Ciavarella, M., and Papangelo, A. (2018). A generalized johnson parameter for pull-off decay in the adhesion of rough surfaces. Phys. Mesomech. 21, 67–75. doi:10.1134/s1029959918010095

CrossRef Full Text | Google Scholar

Dahlquist, C. A. (1966). Adhesion: Fundamentals and practice. Nottingham, United Kingdom: MacLaren.

Google Scholar

Dalvi, S., Gujrati, A., Khanal, S. R., Pastewka, L., Dhinojwala, A., Jacobs, T. D., et al. (2019). Linking energy loss in soft adhesion to surface roughness. Proc. Natl. Acad. Sci. U.S.A. 116, 25484–25490. doi:10.1073/pnas.1913126116

PubMed Abstract | CrossRef Full Text | Google Scholar

Jacobs, T. D. B., Junge, T., and Pastewka, L. (2017). Quantitative characterization of surface topography using spectral analysis. Surf. Topogr. Metrol. Prop. 5, 013001. doi:10.1088/2051-672x/aa51f8

CrossRef Full Text | Google Scholar

Joe, J., Scaraggi, M., and Barber, J. (2017). Effect of fine-scale roughness on the tractions between contacting bodies. Tribol. Int. 111, 52–56. doi:10.1016/j.triboint.2017.03.001

CrossRef Full Text | Google Scholar

Joe, J., Thouless, M., and Barber, J. (2018). Effect of roughness on the adhesive tractions between contacting bodies. J. Mech. Phys. Solids 118, 365–373. doi:10.1016/j.jmps.2018.06.005

CrossRef Full Text | Google Scholar

Joe, J., Thouless, M. D., and Barber, J. R. (2020). Effect of surface roughness on adhesive instabilities for the elastic layer. Front. Mech. Eng. 6. doi:10.3389/fmech.2020.00031

CrossRef Full Text | Google Scholar

Johnson, K. L., Kendall, K., and Roberts, A. (1971). Surface energy and the contact of elastic solids. Proc. R. Soc. Lond. A. Math. Phys. Sci. 324, 301–313. doi:10.1098/rspa.1971.0141

CrossRef Full Text | Google Scholar

Kamperman, M., Kroner, E., del Campo, A., McMeeking, R. M., and Arzt, E. (2010). Functional adhesive surfaces with “gecko” effect: The concept of contact splitting. Adv. Eng. Mat. 12, 335–348. doi:10.1002/adem.201000104

CrossRef Full Text | Google Scholar

Li, Q., Pohrt, R., and Popov, V. L. (2019). Adhesive strength of contacts of rough spheres. Front. Mech. Eng. 5, 7. doi:10.3389/fmech.2019.00007

CrossRef Full Text | Google Scholar

Majumdar, A., and Tien, C. (1990). Fractal characterization and simulation of rough surfaces. Wear 136, 313–327. doi:10.1016/0043-1648(90)90154-3

CrossRef Full Text | Google Scholar

Menga, N., Afferrante, L., and Carbone, G. (2016). Adhesive and adhesiveless contact mechanics of elastic layers on slightly wavy rigid substrates. Int. J. Solids Struct. 88-89, 101–109. doi:10.1016/j.ijsolstr.2016.03.016

CrossRef Full Text | Google Scholar

Müser, M. H. (2014). Single-asperity contact mechanics with positive and negative work of adhesion: Influence of finite-range interactions and a continuum description for the squeeze-out of wetting fluids. Beilstein J. Nanotechnol. 5, 419–437. doi:10.3762/bjnano.5.50

PubMed Abstract | CrossRef Full Text | Google Scholar

Müser, M. H. (2016). A dimensionless measure for adhesion and effects of the range of adhesion in contacts of nominally flat surfaces. Tribol. Int. 100, 41–47. doi:10.1016/j.triboint.2015.11.010

CrossRef Full Text | Google Scholar

Müser, M. H. (2018). Response to “A comment on meeting the contact-(mechanics) challenge”. Tribol. Lett. 66, 38. doi:10.1007/s11249-018-0986-1

CrossRef Full Text | Google Scholar

Palasantzas, G. (1993). Roughness spectrum and surface width of self-affine fractal surfaces via the k-correlation model. Phys. Rev. B 48, 14472–14478. doi:10.1103/physrevb.48.14472

PubMed Abstract | CrossRef Full Text | Google Scholar

Pastewka, L., and Robbins, M. O. (2014). Contact between rough surfaces and a criterion for macroscopic adhesion. Proc. Natl. Acad. Sci. U.S.A. 111, 3298–3303. doi:10.1073/pnas.1320846111

PubMed Abstract | CrossRef Full Text | Google Scholar

Persson, B. N. J., and Gorb, S. (2003). The effect of surface roughness on the adhesion of elastic plates with application to biological systems. J. Chem. Phys. 119, 11437–11444. doi:10.1063/1.1621854

CrossRef Full Text | Google Scholar

Persson, B. N. J., and Scaraggi, M. (2014). Theory of adhesion: Role of surface roughness. J. Chem. Phys. 141, 124701. doi:10.1063/1.4895789

PubMed Abstract | CrossRef Full Text | Google Scholar

Persson, B. N. J. (2001). Theory of rubber friction and contact mechanics. J. Chem. Phys. 115, 3840–3861. doi:10.1063/1.1388626

CrossRef Full Text | Google Scholar

Persson, B. (2002). Adhesion between an elastic body and a randomly rough hard surface. Eur. Phys. J. E 8, 385–401. doi:10.1140/epje/i2002-10025-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Persson, B. (2003). On the mechanism of adhesion in biological systems. J. Chem. Phys. 118, 7614. doi:10.1063/1.1562192

CrossRef Full Text | Google Scholar

Persson, B. (2014). On the fractal dimension of rough surfaces. Tribol. Lett. 54, 99–106. doi:10.1007/s11249-014-0313-4

CrossRef Full Text | Google Scholar

Prodanov, N., Dapp, W. B., and Müser, M. H. (2013). On the contact area and mean gap of rough, elastic contacts: Dimensional analysis, numerical corrections, and reference data. Tribol. Lett. 53, 433–448. doi:10.1007/s11249-013-0282-z

CrossRef Full Text | Google Scholar

Reddy, S., Arzt, E., and del Campo, A. (2007). Bioinspired surfaces with switchable adhesion. Adv. Mat. 19, 3833–3837. doi:10.1002/adma.200700733

CrossRef Full Text | Google Scholar

Sanner, A., and Pastewka, L. (2022). Crack-front model for adhesion of soft elastic spheres with chemical heterogeneity. J. Mech. Phys. Solids 160, 104781. doi:10.1016/j.jmps.2022.104781

CrossRef Full Text | Google Scholar

Tiwari, A., Wang, J., and Persson, B. (2020). Adhesion paradox: Why adhesion is usually not observed for macroscopic solids. Phys. Rev. E 102, 042803. doi:10.1103/physreve.102.042803

PubMed Abstract | CrossRef Full Text | Google Scholar

Violano, G., Papangelo, A., and Ciavarella, M. (2021). Stickiness of randomly rough surfaces with high fractal dimension: Is there a fractal limit? Tribol. Int. 159, 106971. doi:10.1016/j.triboint.2021.106971

CrossRef Full Text | Google Scholar

Wang, A., and Müser, M. H. (2017). Gauging erson theory on adhesion. Tribol. Lett. 65, 103. doi:10.1007/s11249-017-0886-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, A., and Müser, M. H. (2022). Is there more than one stickiness criterion? Friction. doi:10.1007/s40544-022-0644-3

CrossRef Full Text | Google Scholar

Wang, A., Zhou, Y., and Müser, M. H. (2021). Modeling adhesive hysteresis. Lubricants 9, 17. doi:10.3390/lubricants9020017

CrossRef Full Text | Google Scholar

Zhou, Y., Moseler, M., and Müser, M. H. (2019). Solution of boundary-element problems using the fast-inertial-relaxation-engine method. Phys. Rev. B 99, 144103. doi:10.1103/physrevb.99.144103

CrossRef Full Text | Google Scholar

Zilberman, S., and Persson, B. (2002). Adhesion between elastic bodies with rough surfaces. Solid State Commun. 123, 173–177. doi:10.1016/s0038-1098(02)00179-5

PubMed Abstract | CrossRef Full Text | Google Scholar