Binary liquid film condensation from water-ammonia vapors mixture flowing downward along a parallel plate condenser

The ammonia-water film condensation is used as an efficient working fluid in industrial applications such as refrigeration, plate condenser and evaporator, absorber/generator heat exchange, air-conditioning, heat pumps and separation processes. The present work focuses on a numerical investigation of water-ammonia condensation on a falling binary liquid film inside a parallel plate condenser by mixed convection. The parallel plate condenser is composed by two parallel vertical plates. One of the plates is wetted by liquidfilm and cooled by the thermal flux cooling while the other plate is isothermal and dry. Parametric computations were performed to investigate the effects of the inlet parameters of gas, the properties of the binary liquid film as well as the thermal flux cooling on the combined mass and heat transfer and on the efficiency of the parallel plate condenser. The results show that an increase in the inlet vapor of ammonia as well as of vapor water enhances the efficiency of the parallel plate condenser. It is shown also that an enhancement of efficiency of the parallel plate condenser has been recorded when the thermal flux cooling and inlet liquid flow rate is elevated. Whereas the increase of the inlet liquid concentration of ammonia inhibits the efficiency of the parallel plate condenser.

1 Introduction

The mixture vapors condensation is found in many industrial applications such as condenser, condensing devices, air-conditioning, refrigeration technology, absorber/generator heat exchange, nuclear technology and separation processes. The studies concern the case of mixture condensation are presented in (Akiyama et al., 2001; Kuchma et al., 2011; Kuchma et al., 2013; Zheng et al., 2019; Wang et al., 2020; George et al., 2022; Hughes and Chen, 2022). Akiyama et al. (2001) presented a numerical simulation of the water-ethanol condensation on a horizontal wall in a plane two-dimensional field. Hughes and Chen (2022) presented a machine learning regression models to predict the heat transfer coefficient and frictional pressure gradient during condensation of three zeotropic mixtures. Kuchma et al. (2011) studied the droplet composition and the droplet size as functions of time at small deviations from the stationary concentration in the growing droplet. (Kuchma et al. (2013) considered the transient stage of evolution in size, temperature and composition of a droplet, which non isothermaly condenses or evaporates in the diffusion or free-molecular regime in the atmosphere of two condensable vapors and neutral carrier gas. George et al. (2022) showed that the efficiency of heat transfer in DWC depends on the heat transfer rates of individual droplets and the droplet size distribution. Wang et al. (2020) presented an experimental system was designed and built to study the Marangoni condensation of ethanol–water mixtures on a horizontal surface, and the growth of condensate droplets during the time-series process. Zheng et al. (2019) proposed a distributed point sinks method (DPSM) for capturing the strong interaction during dropwise condensation because of a large number of the droplets and the closer inter-droplet spacing. A model of laminar pure film condensation from zeotropic binary mixtures in a vertical tube was developed by Le et al. (2022). It was found that the layer thickness and liquid thermal conductivity have an important effect on the local heat transfer coefficient. They showed that the local heat transfer coefficient increased with an increase in the mass fraction of the less condensable component.A numerical analysis of the laminar film condensation of vapor-gas mixtures in horizontal channels has been investigated by Siow et al. (2002). They examined how the film thickness and heat and mass transfers were affected by the gas concentration, Reynolds number, pressure, and the temperature difference from the intake to the wall. The pure liquid film condensation of vapor flowing in a vertical tube and between parallel plates has been treated by Panday (2003). They presented the heat transfer coefficient for the condensation of the R123/R134a vapour mixture as well as the heat flow rate for the condensation of R123. Li et al. (2022) presented a numerical model for the binary zeotropic mixture condensation. They presented a numerical model for the heat transfer coefficients from the experimental data. Wu et al. (2020) conducted a theoretical model of heat transfer during pure liquid film condensation inside the tube. They considered the effect of gravity, viscous force and centrifugal force on the film liquid condensation heat transfer. Liu et al. (2020) presented a theoretical study of laminar pure film condensation inside and outside vertical channels. They showed an enhancement of the condensation heat transfer coefficient on both inside and outside converging channels. However, they showed that the use of the diverging channels deteriorates the condensation heat transfer coefficient. Nasr (2018) numerically treated the pure liquid film condensation flowing down on a vertical channel coated with a porous layer. The author showed that the liquid film condensation is enhanced with the presence of the porous layer. Nasr and Al-Ghamdi (2017) presented a study of the pure film evaporation by natural convection in the presence of porous layer. They developed a heat transfer correlation of the experimental data during liquid film condensation under natural convection. They showed that the presence of the porous layer enhances the heat and mass transfer with liquid-film evaporation. Varier et al. (2022) presented an experimental work of multi-effect solar still and air gap distillation technologies. Berto et al. (2022) developed a several models during experimental study of pure liquid film condensation in microgravity. A numerical analysis of liquid film condensation on porous surface within ceramic membrane has been done by Yang et al. (2023). They showed that the numerical simulations have agreed with experimental results on a same size micro-porous ceramic membrane. Chang et al. (2021) conducted a film condensation heat transfer of low-mass-flux steam and high-pressure in inclined tube. They presented the effect of each parameter on the film condensation using the average heat transfer coefficients. Lee et al. (2022) presented a computational fluid dynamics (CFD) of the wall film condensation in the presence of non-condensable gases. Wang et al. (2018) presented a theoretical model of pure film condensation flow in oval microchannels. They presented the mean heat transfer coefficient and the local heat transfer coefficient along the flow direction. Turkyilmazoglu (2017) examined the liquid film condensation over curved vertical walls. It is shown that, in the presence of nanoparticles, the heat transfer is more enhanced in the two-phase model case compared to the one phase model case. A numerical and analytical analysis of the film condensation on the wall of an inclined porous plate was provided by Chaynane et al. (2004). The comparison of the Darcy-Brinkman-Forchheimer (DBF) model and the Darcy-Brinkman (DB) model has been treated. Additionally, they discussed the impact of the dimensionless thickness of porous coating, permeability and the effective viscosity on the heat and flow transfer. A numerical analysis of the laminar film condensation over an inclined channel with an insulated upper wall and an isothermal wall coated with a thin porous material was provided by Merouani et al. (1993). For various operating conditions, they displayed the axial evolution of the condensate flow rate and the wall heat flux. They provided that the porous layer properties have a negligible effects on the film condensation compared to the Reynolds number, the inclination angle and the relative humidity. Minkowycz and Sparrow’s study (Minkowycz and Sparrows, 1969) on the condensation of pure vapors on plates is one of the most significant studies. Theoretical research on falling film condensation caused by free convection on an isothermal vertical plate has been presented. They showed the significance of non-condensable gas impact at lower pressure levels. The experimental study of the liquid film and drop condensation has been presented by Chung et al. (2004). They reveals that the heat transfer rates of drop condensations are significantly higher than those of film condensations in the cases of pure steam. The liquid film condensation of a saturated vapor on an inclined plate embedded in a porous medium has been treated by Renken et al. (1993). They examined the effect of the presence of porous metallic coating on the film condensation.

This literature review shows that the problem of the numerical study of the water-ammonia binary liquid film condensation flowing downward along a parallel plate condenser has not been studied. The purpose of this paper is to discuss the effects of the inlet parameters of the gas mixture and of the liquid mixture film on the heat and mass transfer and on the total cumulated condensation rate of water-ammonia vapors mixture.

2 Analysis

The present work focus on a numerical investigation of water-ammonia condensation on a falling binary liquid film inside a parallel plate condenser by mixed convection. The parallel condenser is composed by two parallel vertical plates (Figure 1). One of the plates is wetted and cooled by the thermal flux cooling while the other plate is isothermal and dry. The falling mixture liquid enters the first plate with an inlet temperature T_0L, inlet mass flow rate m_0L and inlet liquid composition of ammonia c_{Liq, ammonia}. The air enters the channel with an inlet temperature T₀, water and ammonia vapour concentrations c₀₁ and c₀₂ and inlet velocity u₀.

FIGURE 1

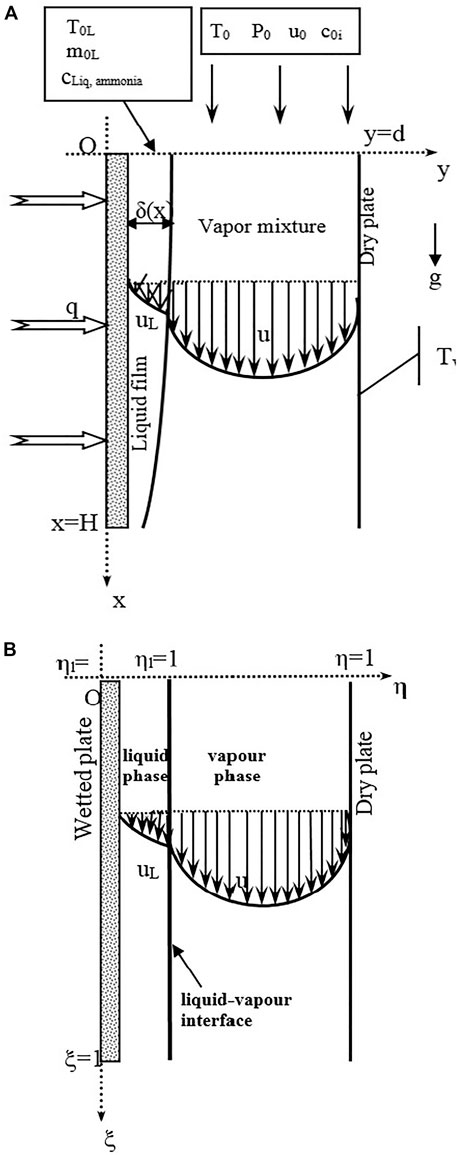
FIGURE 1. Schematic diagram of physical system of heat exchanger (A) and Domain of the physical system of heat exchanger (B).

2.1 Assumptions

For mathematical formulation of the problem, the following simplifying assumptions ar taken into consideration:

• Vapour mixture is ideal.

• The boundary layer approximation are valuables.

• Dufour and Soret effects are negligibles.

• Viscous dissipation and radiative heat transfer are negligibles.

• Liquid mixture is ideal.

• Flows and transfers in the two phases are steady, laminar and two-dimensional.

• The effect of the superficial tension is negligible. The gas-liquid interface is thermodynamic equilibrium.

2.2 Governing equations

The equations governing the flow and coupled mass and heat transfers in the liquid and in the gas phases are as follows (Siow et al., 2002; Le et al., 2022).

For the film condensate.

Continuity equation:

$\frac{\partial {\rho }_L{\mathrm{u}}_{\mathrm{L}}}{\partial \mathrm{x}}+\frac{\partial {\rho }_L{\mathrm{v}}_{\mathrm{L}}}{\partial \mathrm{y}}=0(1)$

x-momentum equation:

${\mathrm{\rho }}_{\mathrm{L}}\left({\mathrm{u}}_{\mathrm{L}}\frac{\partial {\mathrm{u}}_{\mathrm{L}}}{\partial \mathrm{x}}+{\mathrm{v}}_{\mathrm{L}}\frac{\partial {\mathrm{u}}_{\mathrm{L}}}{\partial \mathrm{y}}\right)={\mathrm{\rho }}_{\mathrm{L}}\mathrm{g}-\frac{\mathrm{d}\mathrm{p}}{\mathrm{d}\mathrm{x}}+\frac{\partial }{\partial }\left({\mathrm{\mu }}_{\mathrm{L}}\frac{\partial {\mathrm{u}}_{\mathrm{L}}}{\partial \mathrm{y}}\right)(2)$

Energy equation:

${\mathrm{\rho }}_{\mathrm{L}}{\mathrm{c}}_{\mathrm{p}\mathrm{L}}\left({\mathrm{u}}_{\mathrm{L}}\frac{\partial {\mathrm{T}}_{\mathrm{L}}}{\partial \mathrm{x}}+{\mathrm{v}}_{\mathrm{L}}\frac{\partial {\mathrm{T}}_{\mathrm{L}}}{\partial \mathrm{y}}\right)=\frac{\partial }{\partial \mathrm{y}}\left({\mathrm{\lambda }}_{\mathrm{L}}\frac{\partial {\mathrm{T}}_{\mathrm{L}}}{\partial \mathrm{y}}\right)+{\mathrm{\rho }}_{\mathrm{L}}{\mathrm{D}}_{\mathrm{L}}\left({\mathrm{c}}_{\mathrm{p}\mathrm{L},1}-{\mathrm{c}}_{\mathrm{p}\mathrm{L},2}\right)\frac{\partial {\mathrm{T}}_{\mathrm{L}}}{\partial \mathrm{y}}\frac{\partial {\mathrm{c}}_{\mathrm{L}1}}{\partial \mathrm{y}}(3)$

Species diffusion equation:

${\mathrm{u}}_{\mathrm{L}}\frac{\partial {\mathrm{c}}_{\mathrm{L}\mathrm{i}}}{\partial \mathrm{x}}+{\mathrm{v}}_{\mathrm{L}}\frac{\partial {\mathrm{c}}_{\mathrm{L}\mathrm{i}}}{\partial \mathrm{y}}=\frac{1}{{\mathrm{\rho }}_{\mathrm{L}}}\frac{\partial }{\partial \mathrm{y}}\left({\mathrm{\rho }}_{\mathrm{L}}{\mathrm{D}}_{\mathrm{L}}\frac{\partial {\mathrm{c}}_{\mathrm{L}\mathrm{i}}}{\partial \mathrm{y}}\right)\mathrm{i}=\mathrm{1,2}(4)$

Overall mass equation:

${\displaystyle \underset{0}{\overset{\delta }{\int }}}{\mathrm{\rho }}_{\mathrm{L}}{\mathrm{u}}_{\mathrm{L}}\mathrm{d}\mathrm{y}=m_{0\mathrm{L}}+{\displaystyle \underset{0}{\overset{\mathrm{x}}{\int }}}\mathrm{\rho }\mathrm{v}\left(\mathrm{x},0\right)\mathrm{d}\mathrm{x}(5)$

For the gaseous phase.

Continuity equation:

$\frac{\partial \rho \mathrm{u}}{\partial \mathrm{x}}+\frac{\partial \rho \mathrm{v}}{\partial \mathrm{y}}=0(6)$

x-momentum equation:

$\mathrm{u}\frac{\partial \mathrm{u}}{\partial \mathrm{x}}+\mathrm{v}\frac{\partial \mathrm{u}}{\partial \mathrm{y}}=-\frac{1}{\mathrm{\rho }}\frac{\mathrm{d}\mathrm{P}}{\mathrm{d}\mathrm{x}}-\mathrm{\beta }\mathrm{g}\left(\mathrm{T}-{\mathrm{T}}_0\right)-\mathrm{g}{\displaystyle \sum _{\mathrm{i}=1}^2}{\mathrm{\beta }}_{\mathrm{i}}^{*}\left({\mathrm{c}}_{\mathrm{i}}-{\mathrm{c}}_{\mathrm{i}0}\right)+\frac{1}{\mathrm{\rho }}\frac{\partial }{\partial }\left(\mathrm{\mu }\frac{\partial \mathrm{u}}{\partial \mathrm{y}}\right)(7)$

Energy equation:

$\mathrm{\rho }{\mathrm{c}}_{\mathrm{p}}\left(\mathrm{u}\frac{\partial \mathrm{T}}{\partial \mathrm{x}}+\mathrm{v}\frac{\partial \mathrm{T}}{\partial \mathrm{y}}\right)=\frac{\partial }{\partial \mathrm{y}}\left(\mathrm{\lambda }\frac{\partial \mathrm{T}}{\partial \mathrm{y}}\right)+\mathrm{\rho }{\displaystyle \sum _{\mathrm{i}=1}^2}\left({\mathrm{D}}_{\mathrm{g},\mathrm{i}\mathrm{m}}{\mathrm{c}}_{\mathrm{p}\mathrm{i}}-{\mathrm{D}}_{\mathrm{g},\mathrm{a}\mathrm{m}}{\mathrm{c}}_{\mathrm{p}\mathrm{a}}\right)\frac{\partial \mathrm{T}}{\partial \mathrm{y}}\frac{\partial {\mathrm{c}}_{\mathrm{i}}}{\partial \mathrm{y}}(8)$

Species diffusion equation:

$\mathrm{u}\frac{\partial {\mathrm{c}}_{\mathrm{i}}}{\partial \mathrm{x}}+\mathrm{v}\frac{\partial {\mathrm{c}}_{\mathrm{i}}}{\partial \mathrm{y}}=\frac{1}{\mathrm{\rho }}\frac{\partial }{\partial \mathrm{y}}\left(\mathrm{\rho }{\mathrm{D}}_{\mathrm{g},\mathrm{i}\mathrm{m}}\frac{\partial {\mathrm{c}}_{\mathrm{i}}}{\partial \mathrm{y}}\right)\mathrm{i}=\mathrm{1,2,3}(9)$

Where c₁+c₂+c₃ = 1.

Overall mass equation:

${\displaystyle \underset{\delta }{\overset{d}{\int }}}\mathrm{\rho }\mathrm{u}\mathrm{d}\mathrm{y}=\left(\mathrm{d}-\delta \right){\rho }_0{u}_0+{\displaystyle \underset{0}{\overset{\mathrm{x}}{\int }}}\mathrm{\rho }\mathrm{v}\left(\mathrm{x},0\right)\mathrm{d}\mathrm{x}(10)$

2.3 Boundary conditions

- At x = 0 (for the inlet conditions):

$\mathrm{u}={\mathrm{u}}_0;\mathrm{T}\left(0,\mathrm{y}\right)={\mathrm{T}}_0;\mathrm{P}={\mathrm{P}}_0;{\mathrm{c}}_{\mathrm{i}}\left(0.\mathrm{y}\right)={\mathrm{c}}_{0\mathrm{i}}(11)$

$\mathrm{u}={\mathrm{u}}_0;\mathrm{T}\left(0,\mathrm{y}\right)={\mathrm{T}}_0;\mathrm{P}={\mathrm{P}}_0\mathrm{a}\mathrm{n}\mathrm{d}{\mathrm{c}}_{\mathrm{i}}\left(0,\mathrm{y}\right)={\mathrm{c}}_{0\mathrm{i}}$

${\mathrm{T}}_{\mathrm{L}}\left(0,{\mathrm{y}}_{\mathrm{L}}\right)={\mathrm{T}}_{0\mathrm{L}}\mathrm{m}\left(0,{\mathrm{y}}_{\mathrm{L}}\right)={\mathrm{m}}_{0\mathrm{L}};{\mathrm{c}}_{\mathrm{L}\mathrm{i}\mathrm{q},\mathrm{a}\mathrm{m}\mathrm{m}\mathrm{o}\mathrm{n}\mathrm{i}\mathrm{a}=}{\mathrm{c}}_{\mathrm{L}}0(12)$

- At y = d (for the dry plate):

$\mathrm{v}\left(\mathrm{x}=\mathrm{d},\mathrm{y}\right)=0;\mathrm{u}(\mathrm{x}=\mathrm{d},\mathrm{y})=0;\frac{\partial {\mathrm{c}}_{\mathrm{i}}}{\partial \mathrm{y}}=0;\mathrm{T}\left(\mathrm{x}=\mathrm{d},\mathrm{y}\right)={\mathrm{T}}_{\mathrm{W}}(13)$

- At y_L = 0 (For the wet plate):

${\mathrm{u}}_{\mathrm{L}}\left(x,0\right)=\mathrm{v}\left(x,0\right)=0;{\mathrm{q}}_1=-{\mathrm{\lambda }}_{\mathrm{L}}\frac{\partial {\mathrm{T}}_{\mathrm{L}}}{\partial {\mathrm{y}}_{\mathrm{L}}};{\left.\frac{\partial c_{\mathrm{L}\mathrm{i}}}{\partial {\mathrm{y}}_{\mathrm{L}}}\right)}_{{\mathrm{y}}_{\mathrm{L}}=0}-0(14)$

- At y_L = δ and y = 0 (For the gas–liquid interface):

The continuities of velocities and temperatures are:

${\mathrm{u}}_{\mathrm{L}}\left(x,y_L=\delta \right)=\mathrm{u}\left(x,y=0\right);{\mathrm{T}}_{\mathrm{L}}\left(\mathrm{x},{\mathrm{y}}_{\mathrm{L}}=\delta \right)=\mathrm{T}\left(x,y=0\right)(15)$

The transversal velocity is:

$\mathrm{v}\left(x,\mathrm{y}=0\right)=\frac{{\displaystyle \sum _{\mathrm{i}=1}^2}{\mathrm{D}}_{\mathrm{g},\mathrm{i}\mathrm{m}}{\left.\frac{\partial {\mathrm{c}}_{\mathrm{i}}}{\partial y}\right)}_{\mathrm{y}=0}}{1-{\displaystyle \sum _{\mathrm{i}=1}^2}{\mathrm{c}}_{\mathrm{i}}\left(x,y=0\right)}(16)$

The continuities of shear stress and local condensation rate of species I give:

${\mathrm{\mu }}_{\mathrm{L}}{\left.\frac{\partial {\mathrm{u}}_{\mathrm{L}}}{\partial y_{\mathrm{L}}}\right)}_{{\mathrm{\eta }}_1=1}=\mathrm{\mu }{\left.\frac{\partial \mathrm{u}}{\partial y}\right)}_{\mathrm{y}=0};{\dot{\mathrm{m}}}_{\mathrm{i}}=\dot{\mathrm{m}}{\mathrm{c}}_{\mathrm{L}\mathrm{i}}-{\mathrm{\rho }}_{\mathrm{l}}{\mathrm{D}}_{\mathrm{L}}{\left.\frac{\partial {\mathrm{c}}_{\mathrm{L}\mathrm{i}}}{\partial y_{\mathrm{L}}}\right)}_{{\mathrm{y}}_{\mathrm{L}}=\delta }=\dot{\mathrm{m}}{\mathrm{c}}_{\mathrm{i}}-\mathrm{\rho }{\mathrm{D}}_{\mathrm{g},\mathrm{i}\mathrm{m}}{\left.\frac{\partial {\mathrm{c}}_{\mathrm{i}}}{\partial y}\right)}_{\mathrm{y}=0}(17)$

The heat balance at the interface implies:

${\left.-{\mathrm{\lambda }}_{\mathrm{L}}\frac{\partial {\mathrm{T}}_{\mathrm{L}}}{\partial y_{\mathrm{L}}}\right)}_{y_{\mathrm{L}}=\delta }{\left.=-\mathrm{\lambda }\frac{\partial \mathrm{T}}{\partial y}\right)}_{\mathrm{y}=0}-\dot{\mathrm{m}}{\mathrm{L}}_{\mathrm{v}}(18)$

2.4 Equation transformation

In order to fix the position of the liquid gas interface, we introduce the following transformations (Figure 1B):

In the gaseous phase:

$\eta$ = (y − δ((d − δ), ξ = x/H

$\frac{\partial }{\partial y}=\frac{1}{\mathrm{d}-\delta \left(x\right)}\frac{\partial }{\partial \eta }\mathrm{a}\mathrm{n}\mathrm{d}\frac{\partial }{\partial x}=\frac{1}{\mathrm{H}}\frac{\partial }{\partial \xi }+\frac{\eta -1}{\left(\mathrm{d}-\delta \left(x\right)\right)}\frac{1}{\mathrm{H}}\frac{\partial \delta }{\partial \xi }\frac{\partial }{\partial \eta }$

In the liquid phase:

${\eta }_L=\mathrm{y}/\mathrm{\delta },\mathrm{\xi }=\mathrm{x}/\mathrm{H}$

$\frac{\partial }{\partial \mathrm{y}}=\frac{1}{\mathrm{\delta }\left(\mathrm{x}\right)}\frac{\partial }{\partial {\mathrm{\eta }}_{\mathrm{L}}}$

and

$\frac{\partial }{\partial \mathrm{x}}=\frac{1}{\mathrm{H}}\frac{\partial }{\partial \mathrm{\xi }}-\frac{{\eta }_{\mathrm{L}}}{\mathrm{\delta }\left(\mathrm{x}\right)\mathrm{H}}\frac{\partial \mathrm{\delta }}{\partial \mathrm{\xi }}\frac{\partial }{\partial {\mathrm{\eta }}_{\mathrm{L}}}$

2.4.1 For the Liquid Phase

Continuity equation:

$\frac{\partial {\mathrm{\rho }}_{\mathrm{L}}{\mathrm{u}}_{\mathrm{L}}}{\partial \mathrm{\xi }}-\frac{{\mathrm{\eta }}_{\mathrm{L}}}{\mathrm{\delta }}\frac{\partial \mathrm{\delta }}{\partial \mathrm{\xi }}\frac{\partial {\mathrm{\rho }}_{\mathrm{L}}{\mathrm{u}}_{\mathrm{L}}}{\partial {\mathrm{\eta }}_{\mathrm{L}}}+\frac{\mathrm{H}}{\mathrm{\delta }}\frac{\partial {\mathrm{\rho }}_{\mathrm{L}}{\mathrm{v}}_{\mathrm{L}}}{\partial {\mathrm{\eta }}_{\mathrm{L}}}=0(19)$

x-momentum equation:

${\mathrm{u}}_{\mathrm{L}}\frac{\partial {\mathrm{u}}_{\mathrm{L}}}{\partial \mathrm{\xi }}+\left({\mathrm{v}}_{\mathrm{L}}\frac{\mathrm{H}}{\mathrm{\delta }}-{\mathrm{u}}_{\mathrm{L}}\frac{{\mathrm{\eta }}_{\mathrm{L}}}{\mathrm{\delta }}\frac{\partial \mathrm{\delta }}{\partial \mathrm{\xi }}\right)\frac{\partial {\mathrm{u}}_{\mathrm{L}}}{\partial {\mathrm{\eta }}_{\mathrm{L}}}=-\frac{1}{{\mathrm{\rho }}_{\mathrm{L}}}\frac{\mathrm{d}\mathrm{P}}{\mathrm{d}\mathrm{\xi }}-\frac{\mathrm{H}}{{\mathrm{\rho }}_{\mathrm{L}}{\mathrm{\delta }}^2}\frac{\partial }{\partial {\mathrm{\eta }}_{\mathrm{L}}}\left[{\mathrm{\mu }}_{\mathrm{L}}\frac{\partial {\mathrm{u}}_{\mathrm{L}}}{\partial {\mathrm{\eta }}_{\mathrm{L}}}\right]+\mathrm{g}\mathrm{H}(20)$

Energy equation:

$\begin{array}{l}{\mathrm{u}}_{\mathrm{L}}\frac{\partial {\mathrm{T}}_{\mathrm{L}}}{\partial \mathrm{\xi }}+\left({\mathrm{u}}_{\mathrm{L}}\frac{{\mathrm{\eta }}_{\mathrm{L}}-1}{\mathrm{\delta }}\frac{\partial \mathrm{\delta }}{\partial \mathrm{\xi }}+\frac{\mathrm{H}}{\mathrm{\delta }}{\mathrm{v}}_{\mathrm{L}}\right)\frac{\partial {\mathrm{T}}_{\mathrm{L}}}{\partial {\mathrm{\eta }}_{\mathrm{L}}}=\frac{1}{{\mathrm{\rho }}_{\mathrm{L}}{\mathrm{C}}_{\mathrm{p}\mathrm{L}}}\left\{\frac{\mathrm{H}}{{\left(\mathrm{\delta }\right)}^2}\frac{\partial }{\partial {\mathrm{\eta }}_{\mathrm{L}}}\left({\mathrm{\lambda }}_{\mathrm{L}}\frac{\partial {\mathrm{T}}_{\mathrm{L}}}{\partial {\mathrm{\eta }}_{\mathrm{L}}}\right)\right.\\ +\left.{\mathrm{\rho }}_{\mathrm{L}}{\mathrm{D}}_{\mathrm{L}}\left(C_{pL,1}-C_{pL,2}\right)\frac{\mathrm{H}}{{\left(\mathrm{\delta }\right)}^2}\frac{\partial {\mathrm{T}}_{\mathrm{L}}}{\partial {\mathrm{\eta }}_{\mathrm{L}}}\frac{\partial c_{\mathrm{L},1}}{\partial {\mathrm{\eta }}_{\mathrm{L}}}\right\}\end{array}(21)$

Species diffusion equation:

${\mathrm{u}}_{\mathrm{L}}\frac{\partial {\mathrm{c}}_{\mathrm{L}\mathrm{i}}}{\partial \mathrm{\xi }}+\left({\mathrm{u}}_{\mathrm{L}}\frac{{\mathrm{\eta }}_{\mathrm{L}}-1}{\mathrm{\delta }}\frac{\partial \mathrm{\delta }}{\partial \mathrm{\xi }}+\frac{\mathrm{H}}{\mathrm{\delta }}{\mathrm{v}}_{\mathrm{L}}\right)\frac{\partial {\mathrm{c}}_{\mathrm{L}\mathrm{i}}}{\partial {\mathrm{\eta }}_{\mathrm{L}}}=\frac{1}{{\mathrm{\rho }}_{\mathrm{L}}}\frac{\mathrm{H}}{{\mathrm{\delta }}^2}\frac{\partial }{\partial {\mathrm{\eta }}_{\mathrm{L}}}\left({\mathrm{\rho }}_{\mathrm{L}}{\mathrm{D}}_{\mathrm{L}\mathrm{i}}\frac{\partial {\mathrm{c}}_{\mathrm{L}\mathrm{i}}}{\partial {\mathrm{\eta }}_{\mathrm{L}}}\right);\mathrm{i}=\mathrm{1,2}(22)$

Overall mass balance:

${\displaystyle \underset{0}{\overset{1}{\int }}}\mathrm{\delta }{\mathrm{\rho }}_{\mathrm{L}}{\mathrm{u}}_{\mathrm{L}}\mathrm{d}{\mathrm{\eta }}_{\mathrm{L}}=\left[{\mathrm{m}}_{0\mathrm{L}}-\mathrm{H}{\displaystyle \underset{0}{\overset{\mathrm{\xi }}{\int }}}\mathrm{\rho }\mathrm{v}\left(\mathrm{\xi },\mathrm{\eta }=0\right)\mathrm{d}\mathrm{\xi }\right](23)$

2.4.2. For the gas phase

Continuity equation:

$\frac{\partial \rho u}{\partial \xi }+\frac{\eta -1}{d-\delta }\frac{\partial \delta }{\partial \xi }\frac{\partial \rho u}{\partial \eta }+\frac{H}{d-\delta }\frac{\partial \rho v}{\partial \eta }=0(24)$

x-momentum equation:

$\begin{array}{l}u\frac{\partial u}{\partial \xi }+\left(\frac{\eta -1}{d-\delta }\frac{\partial \delta }{\partial \xi }u+\frac{H}{d-\delta }v\right)\frac{\partial u}{\partial \eta }=-\frac{1}{\rho }\frac{dP}{d\xi }-g\beta H\left(T-T_0\right)-gH{\displaystyle \sum _{i=1}^2}{\beta }_i^{*}\left(c_i-c_{0i}\right)+\frac{1}{\rho }\frac{H}{{\left(d-\delta \right)}^2}\frac{\partial }{\partial \eta }\left(\mu \frac{\partial u}{\partial \eta }\right)\end{array}(25)$

Energy equation:

$\begin{array}{l}\mathrm{u}\frac{\partial \mathrm{T}}{\partial \mathrm{\xi }}+\left(\mathrm{u}\frac{\mathrm{\eta }-1}{\mathrm{d}-\mathrm{\delta }}\frac{\partial \mathrm{\delta }}{\partial \mathrm{\xi }}+\frac{\mathrm{H}}{\mathrm{d}-\mathrm{\delta }}\mathrm{v}\right)\frac{\partial \mathrm{T}}{\partial \mathrm{\eta }}=\frac{1}{\mathrm{\rho }{\mathrm{C}}_{\mathrm{p}}}\left\{\frac{\mathrm{H}}{{\left(\mathrm{d}-\mathrm{\delta }\right)}^2}\frac{\partial }{\partial \mathrm{\eta }}\left(\mathrm{\lambda }\frac{\partial \mathrm{T}}{\partial \mathrm{\eta }}\right)\right.\\ +\left.\mathrm{\rho }{\displaystyle \sum _{\mathrm{i}=1}^2}\left({\mathrm{D}}_{\mathrm{g},\mathrm{i}\mathrm{m}}{\mathrm{c}}_{\mathrm{p}\mathrm{i}}-{\mathrm{D}}_{\mathrm{g},\mathrm{a}\mathrm{m}}{\mathrm{c}}_{\mathrm{p}\mathrm{a}}\right)\frac{\mathrm{H}}{{\left(\mathrm{d}-\mathrm{\delta }\right)}^2}\frac{\partial \mathrm{T}}{\partial \mathrm{\eta }}\frac{\partial {\mathrm{c}}_{\mathrm{i}}}{\partial \mathrm{\eta }}\right\}\end{array}(26)$

Species diffusion equation:

$\mathrm{u}\frac{\partial {\mathrm{c}}_{\mathrm{i}}}{\partial \mathrm{\xi }}+\left(\mathrm{u}\frac{\mathrm{\eta }-1}{\mathrm{d}-\mathrm{\delta }}\frac{\partial \mathrm{\delta }}{\partial \mathrm{\xi }}+\frac{\mathrm{H}}{\mathrm{d}-\mathrm{\delta }}\mathrm{v}\right)\frac{\partial {\mathrm{c}}_{\mathrm{i}}}{\partial \mathrm{\eta }}=\frac{1}{\mathrm{\rho }}\frac{\mathrm{H}}{{\left(\mathrm{d}-\mathrm{\delta }\right)}^2}\frac{\partial }{\partial \mathrm{\eta }}\left(\mathrm{\rho }{\mathrm{D}}_{\mathrm{g},\mathrm{i}\mathrm{m}}\frac{\partial {\mathrm{c}}_{\mathrm{i}}}{\partial \mathrm{\eta }}\right);\mathrm{i}=\mathrm{1,2}(27)$

Overall mass balance:

${\displaystyle \underset{0}{\overset{1}{\int }}}\rho \left(d-\delta \right)u\left(\xi ,\eta \right)d\eta ==\left[\left(d-{\delta }_0\right){\rho }_0{u}_0+H{\displaystyle \underset{0}{\overset{\xi }{\int }}}\rho v\left(\xi ,\eta =0\right)d\xi \right](28)$

2.4.3. Boundary conditions

* For ξ = 0 (for the inlet conditions):

$\mathrm{T}\left(0,\mathrm{\eta }\right)={\mathrm{T}}_0;\mathrm{c}\mathrm{i}\left(0,\mathrm{\eta }\right)={\mathrm{c}}_{0\mathrm{i}};\mathrm{u}\left(0,\mathrm{\eta }\right)={\mathrm{u}}_0;\mathrm{p}\left(0,\mathrm{\eta }\right)={\mathrm{p}}_0(29)$

${\mathrm{T}}_{\mathrm{L}}\left(0,{\mathrm{\eta }}_{\mathrm{L}}\right)={\mathrm{T}}_{0\mathrm{L}};\mathrm{m}\left(0,{\eta }_{\mathrm{L}}\right)={\mathrm{m}}_{0\mathrm{L}};{\mathrm{c}}_{\mathrm{L}\mathrm{i}}\left(0,{\mathrm{\eta }}_{\mathrm{L}}\right)={\mathrm{c}}_{0\mathrm{L}}\mathrm{i}(30)$

* At η = 1(dry plate):

$\mathit{u}\left(\mathit{\xi },\mathbf{1}\right)=\mathbf{0}=\mathit{v}\left(\mathit{\xi },\mathbf{1}\right)=\mathbf{0};\mathit{T}\left(\mathit{\xi },\mathbf{1}\right)={\mathit{T}}_{\mathit{w}};{\left.\frac{\partial {\mathit{c}}_{\mathit{i}}}{\partial \mathit{\eta }}\right)}_{\mathrm{\eta }=1}=\mathbf{0}(31)$

* At η _L = 0 (wet plate):

${\mathrm{u}}_{\mathrm{L}}\left(\xi ,0\right)=0;{\mathrm{v}}_{\mathrm{L}}\left(\xi ,1\right)=0;{\mathrm{q}}_1=-{\mathrm{\lambda }}_{\mathrm{L}}\frac{1}{\mathrm{\delta }}{\left.\frac{\partial {\mathrm{T}}_{\mathrm{L}}}{\partial {\mathrm{\eta }}_{\mathrm{L}}}\right)}_{{\mathrm{\eta }}_1-0};{\left.\frac{\partial {\mathrm{c}}_{\mathrm{L}\mathrm{i}}}{\partial {\mathrm{\eta }}_{\mathrm{L}}}\right)}_{{\mathrm{\eta }}_L-0}=0(32)$

* At $\mathrm{\eta }=0$ (η _L = 1) (gas-liquid interface):

${\mathrm{u}}_{\mathrm{L}}\left(\xi ,{\mathrm{\eta }}_{\mathrm{L}}=1\right)=\mathrm{u}\left(\xi ,\mathrm{\eta }=0\right);{\mathrm{T}}_{\mathrm{L}}\left(\xi ,{\mathrm{\eta }}_{\mathrm{L}}=1\right)=\mathrm{T}\left(\xi ,\mathrm{\eta }=0\right)(33)$

$\mathrm{v}\left(\mathrm{\xi },\mathrm{\eta }=0\right)=-\frac{\frac{1}{\mathrm{d}-\mathrm{\delta }}{\displaystyle \sum _{\mathrm{i}=1}^2}{\mathrm{D}}_{\mathrm{g},\mathrm{i}\mathrm{m}}{\left.\frac{\partial {\mathrm{c}}_{\mathrm{i}}}{\partial \mathrm{\eta }}\right)}_{\mathrm{\eta }-0}}{1-{\displaystyle \sum _{\mathrm{i}=1}^2}{\mathrm{c}}_{\mathrm{i}}\left(\mathrm{\xi },\mathrm{\eta }=0\right)}(34)$

$\frac{1}{\mathrm{\delta }}{\mathrm{\mu }}_{\mathrm{L}}{\left.\frac{\partial {\mathrm{u}}_{\mathrm{L}}}{\partial {\mathrm{\eta }}_{\mathrm{L}}}\right)}_{{\mathrm{\eta }}_L=1}=\frac{1}{\mathrm{d}-\mathrm{\delta }}\mathrm{\mu }{\left.\frac{\partial \mathrm{u}}{\partial \mathrm{\eta }}\right)}_{\mathrm{\eta }=0};{\dot{\mathrm{m}}}_{\mathrm{i}}=\dot{\mathrm{m}}{\mathrm{c}}_{\mathrm{L}\mathrm{i}}-\frac{{\mathrm{\rho }}_{\mathrm{l}}{\mathrm{D}}_{\mathrm{L}}}{\mathrm{\delta }}{\left.\frac{\partial {\mathrm{c}}_{\mathrm{L}\mathrm{i}}}{\partial {\mathrm{\eta }}_{\mathrm{L}}}\right)}_{{\mathrm{\eta }}_1=0}=\dot{\mathrm{m}}{\mathrm{c}}_{\mathrm{i}}-\frac{\mathrm{\rho }{\mathrm{D}}_{\mathrm{g},\mathrm{i}\mathrm{m}}}{\mathrm{d}-\mathrm{\delta }}{\left.\frac{\partial {\mathrm{c}}_{\mathrm{i}}}{\partial \mathrm{\eta }}\right)}_{\mathrm{\eta }=0}(35)$

$-\frac{1}{\mathrm{\delta }}{\mathrm{\lambda }}_{\mathrm{L}}{\left.\frac{\partial {\mathrm{T}}_{\mathrm{L}}}{\partial {\mathrm{\eta }}_{\mathrm{L}}}\right)}_{{\mathrm{\eta }}_1=1}=-\frac{1}{\mathrm{d}-\mathrm{\delta }}\mathrm{\lambda }{\left.\frac{\partial \mathrm{T}}{\partial \mathrm{\eta }}\right)}_{\mathrm{\eta }-0}-\dot{\mathrm{m}}{\mathrm{L}}_{\mathrm{v}}with\dot{\mathrm{m}}=-\frac{\frac{1}{\mathrm{d}-\mathrm{\delta }}\rho {\displaystyle \sum _{\mathrm{i}=1}^2}{\mathrm{D}}_{\mathrm{g},\mathrm{i}\mathrm{m}}{\left.\frac{\partial {\mathrm{c}}_{\mathrm{i}}}{\partial \mathrm{\eta }}\right)}_{\mathrm{\eta }-0}}{1-{\displaystyle \sum _{\mathrm{i}=1}^2}{\mathrm{c}}_{\mathrm{i}}\left(\mathrm{\xi },\mathrm{\eta }=0\right)}(36)$

In order to evaluate the importance of the different processes of energy transfer, the following quantities are used:

- The cumulated condensation rate of species I vapor at the interface is given by:

${\mathrm{M}\mathrm{r}}_{\mathrm{i}}\left(x\right)={\displaystyle \underset{0}{\overset{\xi }{\int }}}{\stackrel{•}{\mathrm{m}}}_i\left(\xi \right)\mathrm{d}\xi where{\stackrel{•}{\mathrm{m}}}_i\left(\xi \right)=\dot{\mathrm{m}}{\mathrm{c}}_{\mathrm{i}}-\frac{\mathrm{\rho }{\mathrm{D}}_{\mathrm{g},\mathrm{i}\mathrm{m}}}{\mathrm{d}-\mathrm{\delta }}{\left.\frac{\partial {\mathrm{c}}_{\mathrm{i}}}{\partial \mathrm{\eta }}\right)}_{\eta =0}(37)$

- The cumulated condensation rate of vapor mixture at the interface is given by:

$\mathrm{M}\mathrm{r}={\displaystyle \underset{0}{\overset{\xi }{\int }}}{\stackrel{•}{\mathrm{m}}}_i\left(\xi \right)\mathrm{d}\xi =M{r}_1+M{r}_2(38)$

3 Solution method

The system of partial differential Equations and its boundary and interfacial conditions (1–19) was solved using FORTRAN code with the implicit finite difference method. The governing partial differential equations was transformed into finite difference equations by using a fully implicit marching scheme. The mesh is characterized by a longitudinal step $\Delta \xi =1/\left(N_{\xi }-1\right)$ and a transversal step $\Delta {\eta }_L=1/\left(N_{\eta L}-1\right)$ in liquid and $\Delta \eta =1/\left(N_{\eta }-1\right)$ in gas. The axial convection terms were approximated by the upstream difference and the transverse convection and diffusion terms by the central difference is employed to transform the governing equations into finite difference equations. The system of finite equations was solved by the Gaussian elimination method. To confirm that the results were grid-independent, we present in Table 1 the stability of calculation from the mesh variations local evaporation rate $\stackrel{•}{\mathrm{m}}\left(X\right)$. Table 1 shows that the difference in the local evaporation rate obtained using 51 × (51 + 31) and 151 × (51 + 51) grids was less than 1%.

TABLE 1

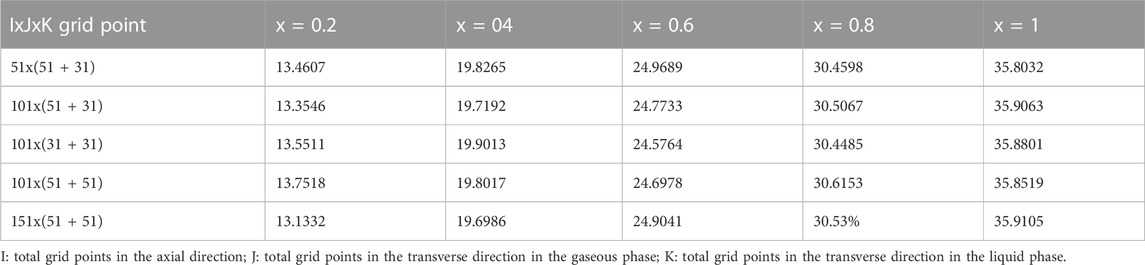
TABLE 1. Comparison of local evaporating rate (10⁵ Mr) (kg.s^-1.m^-2) for various grid arrangements for T₀ = 20°C, T_w = = 20°C, T_0L = 10°C, m_0L = 0.001 kg/m.s, q₁ = 0, p₀ = 9 atm, c₀₁ = 0, c₀₂ = 0 d/H = 0.015, u₀ = 0.75 m/s.

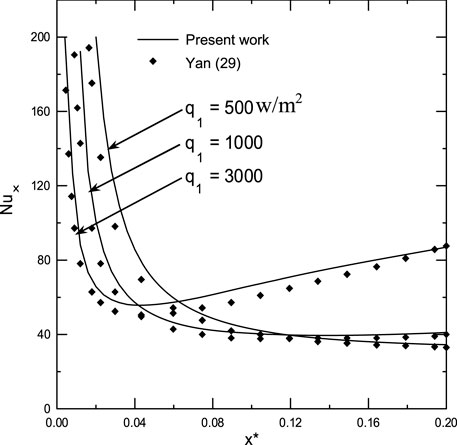
To check the adequacy of the numerical scheme adopted in the present study, the procedure has been tested by comparing the total evaporating rate (Mr), the interfacial temperature (T_p-T₀) and the concentration of ethylene glycol vapour calculated from the present code with the results of Ali Cherif (Ali and Daif, 1999) for the case of the evaporation of the binary (water-ethylene glycol) liquid film flowing down on one plate of the vertical channel (see Figures 2A–C). The first plate of a vertical channel is wetted by the binary liquid film and externally subjected to a uniform heated flux q₁ while the second (y = d) is dry and adiabatic. The comparison has been done for T₀ = 293.15K, c₀₁ = c₀₂ = 0, T_0L = 293.15K, q₂ = 0, $m_{0\mathrm{L}}=0.02Kg/m.s$ ,Re = 1,000, the geometrical ratio is d/H = 0.015, the imposed wall heat flux is q1 = 3000 W/m² and the inlet film composition of ethylene glycol is c_{Liq, ethylene glycol}. = 0.5 (50% water-ethylene glycol mixture). Figures 2A–C show a satisfactory conformity between our results and those obtained by Ali Cherif and Daif (Ali and Daif, 1999). The second validation of the numerical scheme adopted in the present study has been carried out in the case of evaporation of pure water liquid film under mixed convection. The water liquid film is falling down on one plate of a vertical channel. The first plate of a vertical channel is wetted by the liquid film and externally subjected to a uniform heated flux q₁ while the second (y = d) is dry and adiabatic. The comparison between our results and those obtained in the literature by Yan (1992) has been done for T₀ = 293.15K, c₀ = 0, ϕ₀ = 50%, T_0L = 293.15K, q₂ = 0, Re = 2000, d/H = 0.015, q₁ = 1000W/m². The procedure has been tested by comparing the local Nusselt number Nu_x at the interface to those of Yan (1992). Concerning the comparison of the local Nusselt number Nu_x, the inlet flow rate $m_{0\mathrm{L}}=0.02Kg/m.s$. Figure 3 shows a satisfactory conformity between our results and those obtained by Yan (Yan, 1992).

FIGURE 2

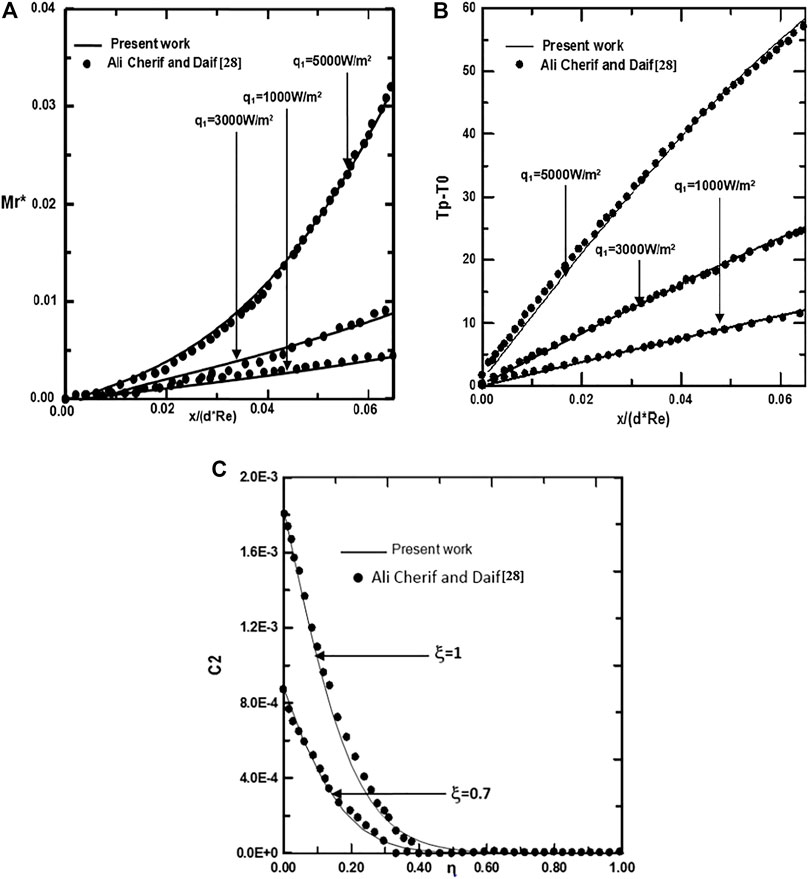
FIGURE 2. Validation of calculated total evaporating rate along the channel (A), interfacial temperature (B) and the concentration of ethylene glycol vapor along the channel (C): c_{Liq, ethylene glycol} = c_{Liq, water} = 0.5, (50% water-ethylene glycol mixture).

FIGURE 3

FIGURE 3. Validation of calculated local Nusselt number Nux at the interface liquid-gas.

4 Results and discussions

The study results were attained with the following values: d/H = 0.015, u₀ = 0.75 m/s, and P₀ = 9 bars. The saturation pressure of ammonia is more significant than that of water, as seen in Figures 4A, B and as a result, ammonia is more volatile than water. It is shown from Figure 3 A, B that the difference between the saturation pressures of ethylene-glycol and water is observed to grow increasingly significant as the wall temperature increases.

FIGURE 4

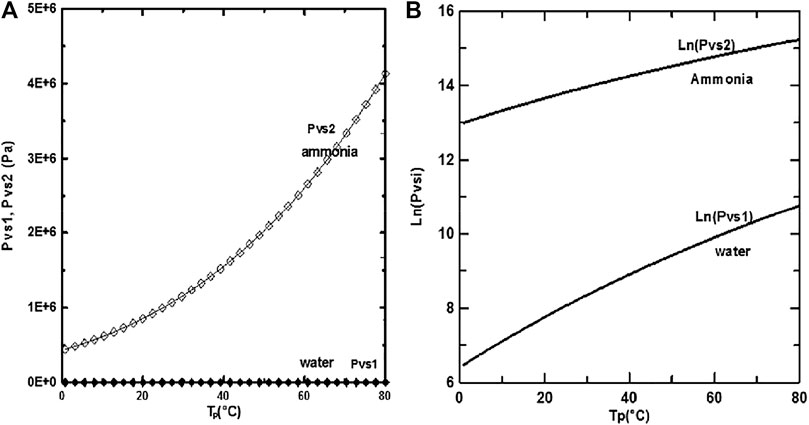
FIGURE 4. (A) and (B) corresponds to :Saturation pressure of water and ammonia but (B) is on logarithm scale.

4.1 Effects of the inlet parameters in the gas phase and the thermal flux cooling

Figure 5 illustrates the effect of the inlet ammonia vapor concentration on the vapors mixture condensation, the interfacial temperature, the ammonia vapor concentration at the interfacial and the Nusselt number. In fact, Figure 5A shows that the vapors mixture condensation is enhanced for higher inlet ammonia vapor concentration. This result is due to the fact that an augmentation of the inlet ammonia vapor concentration c₀₂ causes an intensification of the ammonia vapor amount in the gas witch will be condensable to the liquid film. As the inlet gas temperature T₀ rises, one can observe that the temperature at the liquid-gas interface also increase (Figure 5B). This results have been explained by the fact that an increasing of the mixture condensation is accompanied by an increase of temperature at the liquid-gas interface. It is obvious, from Figure 5C, that an augmentation of the ammonia vapour concentration at the channel entry increases its values at the liquid-gas interface. Figure 5D shows that the increase in the inlet vapor concentration of ammonia c₀₂ improves the heat transfer. This results is manifested by an increase in the Nusselt number Nu when we increase the inlet vapor concentration of ammonia c₀₂. Figure 6 illustrate the effect of inlet vapour concentration of water c₀₁ on the cumulated condensation rate of vapors mixture, the temperature at the liquid-gas interface, the ammonia vapor concentration at the liquid-gas Interface and the Nusselt number. Figure 6A shows that the mixture condensation is enhanced with an increase of inlet vapour concentration of water c₀₁ causing an increase in the temperature (Figure 6B) and vapor ammonia concentration (Figure 6C) at the liquid-gas interface. It is shown from Figure 6D that an increase in the inlet vapor concentration of water c₀₁ induces an increase of the Nusselt number Nu causing an enhancement in the heat transfer. Figure 7 give the evolution of the axial distribution of the cumulated condensation rates and the temperature, vapour ammonia concentration at the interface liquid-gas with different values of inlet gas temperature T₀ and on the Nusselt number. The observation of the curves of Figure 7A shows that a decrease of inlet gas temperature T₀ advantages the vapors mixture condensation causing an elevation in the temperature (Figure 7B) and vapor ammonia concentration (Figure 7C) the interface liquid-gas. It is shown from Figure 7D that the Nusselt number Nu is increased when the inlet gas temperature T₀ is elevated. The effect of the density of thermal flux cooling q₁ on the heat and mass transfer and on the vapors mixture condensation rate is given in the Figure 8. Figure 8A reveals a decrease of the interfacial temperature when the density of thermal flux cooling q₁ increases. The same behaviour has been observed in Figure 8B and it`s shown that the density of thermal flux cooling q₁ induces an increase in the vapor ammonia concentration at the liquid-gas interface. It is found from Figure 8C that the vapors mixture condensation is enhanced with an elevation of thermal flux cooling q₁. This results can be justified by the fact than an increase of q₁ ameliorates the cooling at the liquid-gas interface which causing an enhancement of vapors mixture condensation. It is found from Figure 8D that the Nusselt number Nu is decreased when the cooling heat flux q₁ is elevated.

FIGURE 5

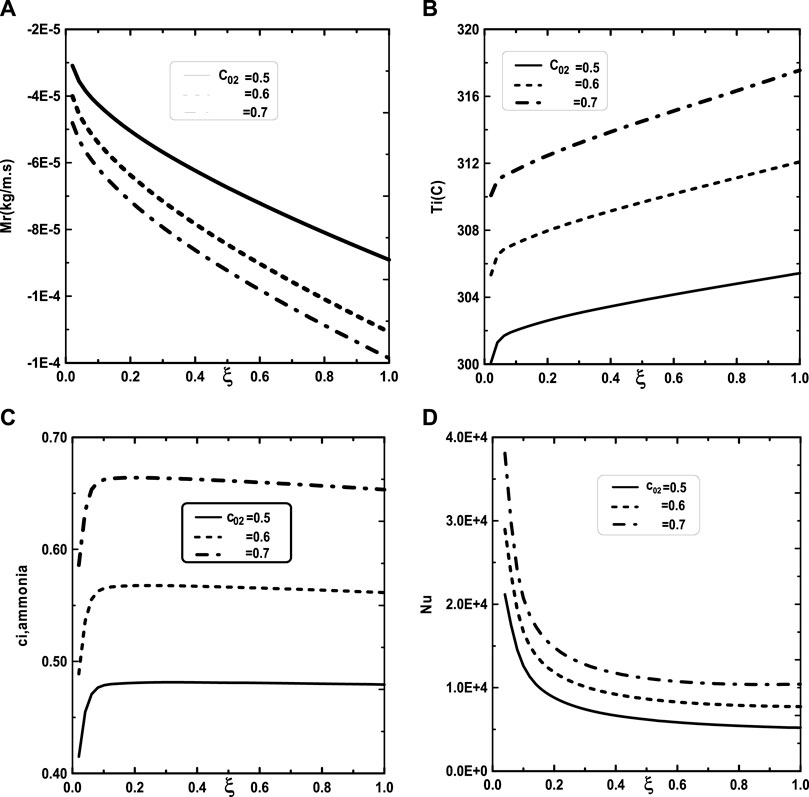
FIGURE 5. Effect of the inlet vapor concentration of ammonia c02 on the cumulated condensation rate of vapors mixture (A), the interfacial temperature (B), the ammonia vapor concentration (C) and the Nusselt number (D): c₀₁ = 0.3, T_0L = 10°C, T₀ = 20°C, T_w = 20°C, q₁ = 0, m_0L = 0.001 kg/m.s, c_{Liq, ammonia} = 0.5 (50% water-ammonia mixture).

FIGURE 6

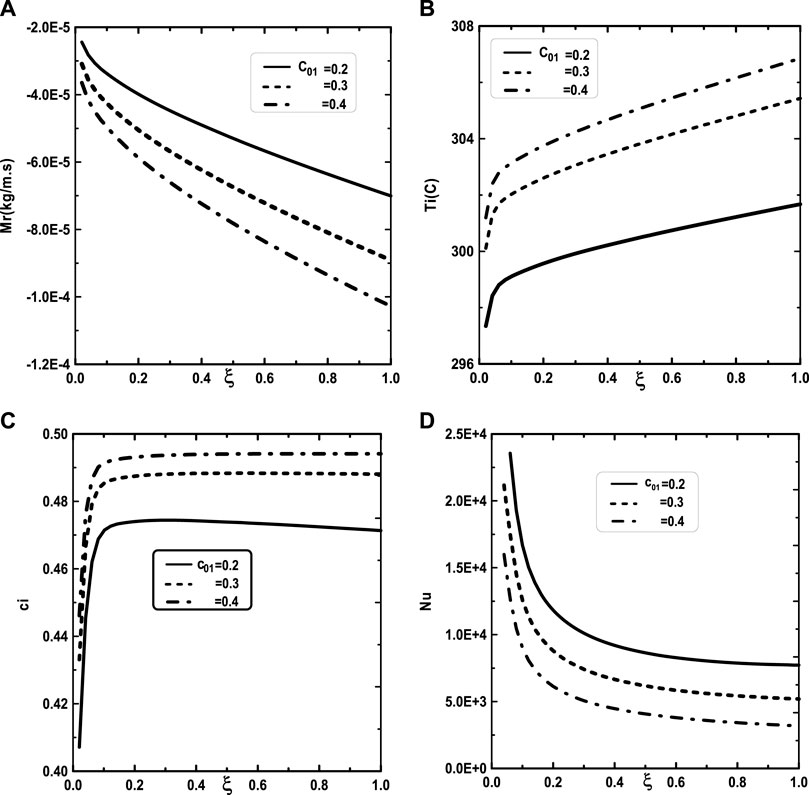
FIGURE 6. Effect of the inlet vapor concentration of water c₀₁ on the cumulated condensation rate of vapors mixture (A), the interfacial temperature (B), the ammonia vapor concentration (C) and the Nusselt number (D): c₀₂ = 0.5, T_0L = 10°C, T₀ = 20°C, T_w = 20°C, q₁ = 0, m_0L = 0.001 kg/m.s, c_{Liq, ammonia} = 0.5 (50% water-ammonia mixture).

FIGURE 7

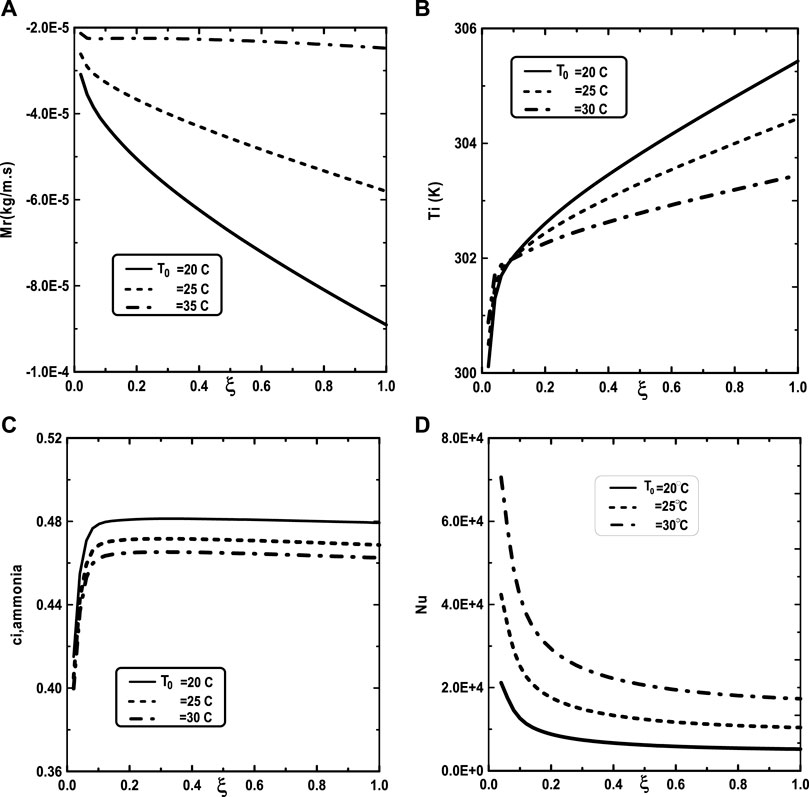
FIGURE 7. Effect of the inlet gas temperature T₀ on the cumulated condensation rate of vapors mixture (A), the interfacial temperature (B), the ammonia vapor concentration (C) and the Nusselt number (D): c₀₁ = 0.3, c₀₂ = 0.5, T_0L = 10°C, T_w = 20°C, q₁ = 0, m_0L = 0.001 kg/m.s, c_{Liq, ammonia} = 0.5 (50% water-ammonia mixture).

FIGURE 8

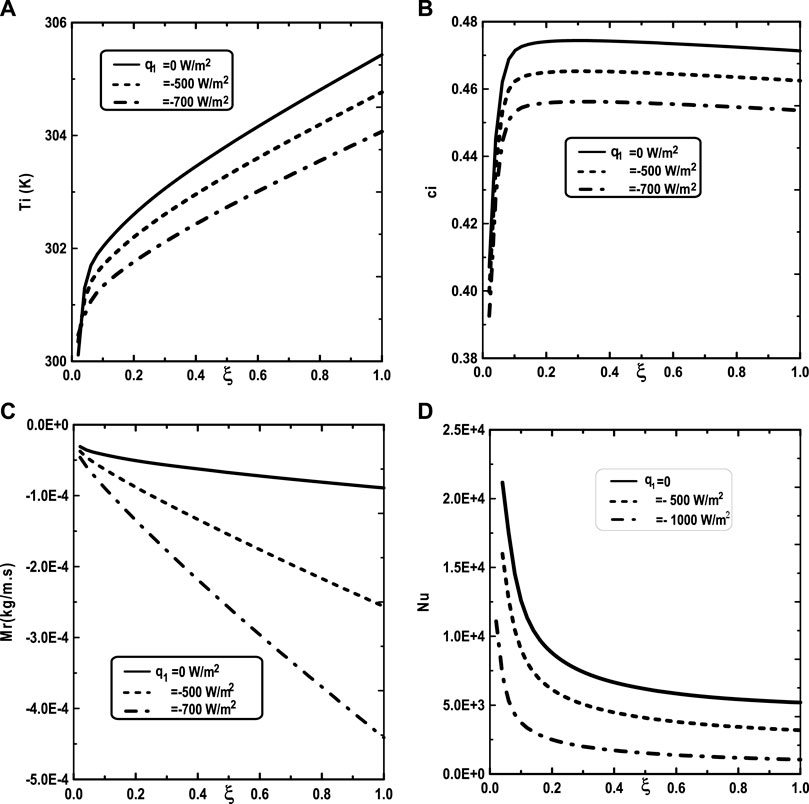
FIGURE 8. Effect of the heat flux q₁ on the cumulated condensation rate of vapors mixture (A), the interfacial temperature (B), the ammonia vapor concentration (C) and the Nusselt number (D): c₀₁ = 0.3, c₀₂ = 0.5, T_0L = 10°C, T_w = 20°C, T₀ = 20°C, m_0L = 0.001 kg/m.s, c_{Liq, ammonia} = 0.5 (50% water-ammonia mixture).

4.2 Effect of the inlet properties of the binary liquid film

In Figure 9, one presented the impact of binary liquid film composition on the temperature and vapor ammonia concentration, the vapors mixture condensation and on the Nusselt number. Figure 9A shows that when the inlet liquid concentration of ammonia c_{Liq, ammonia} increase, the interfacial temperature decrease causing a decrease in the vapor ammonia concentration at the liquid-gas interface. This results can be explained by the fact that an increase of inlet liquid concentration of ammonia c_{Liq, ammonia} causing an increase in the volatility of the binary liquid (the ammonia is more volatile than the water) and consequently enhances the interface liquid cooling. The decrease of the temperature at the interface liquid-gas causing a decrease in the vapor ammonia concentration at the interface liquid-gas (Figure 9B). It’s shown from Figure 9C that an augmentation in the inlet liquid concentration of ammonia c_{Liq, ammonia} improves the vapors mixture condensation. This result is due to the fact that an increase in the inlet liquid concentration of ammonia c_{Liq, ammonia} benefits the liquid-gas interface cooling causing an amelioration in the vapors mixture condensation. Figure 9D indicates that the Nusselt number Nu is decreased when the inlet liquid concentration of ammonia c_{Liq, ammonia} is elevated.

FIGURE 9

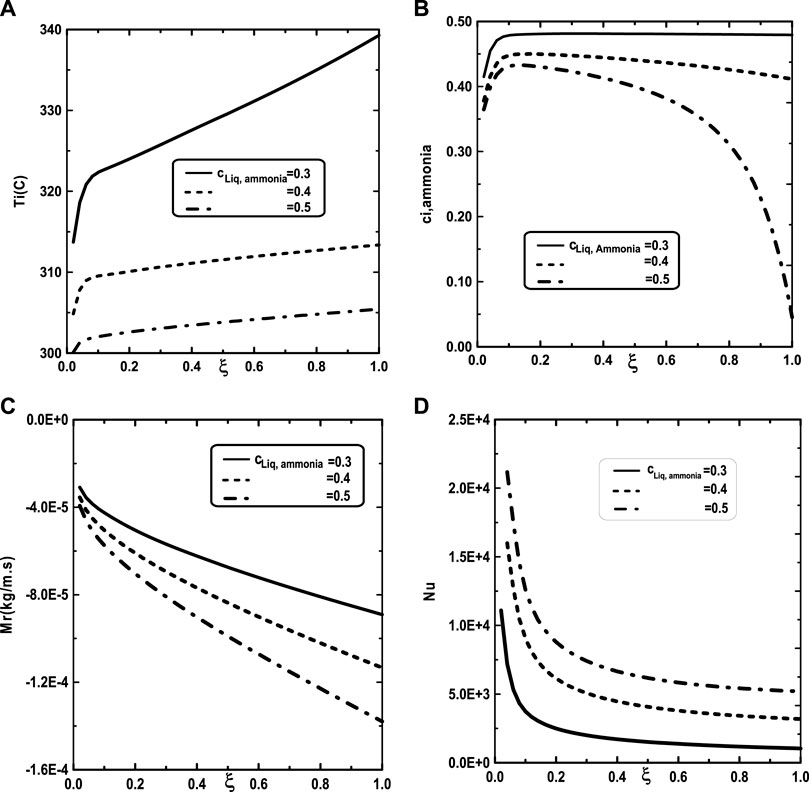
FIGURE 9. Effect of inlet liquid concentration of ammonia c_{1Liq, ammonia} on the interfacial temperature (A), the ammonia vapor concentration (B), the cumulated condensation rate of vapors mixture (C) and the Nusselt number (D): c₀₁ = 0.3, c₀₂ = 0.5, q₁ = 0, T_0L = 10°C, T_w = 20°C, T₀ = 20°C, m_0L = 0.001 kg/m.s.

We turn our attention now to the impact of the inlet flow rate m_0L of liquid film and the inlet liquid temperature T_0L on the temperature and vapor ammonia concentration at the interface liquid-gas, the vapors mixture condensation and on the Nusselt number. Figure 10A shows that the increase of the inlet flow rate m_0L of liquid film advantages the cooling at the interface liquid-gas. The observation of the curves of Figure 10B shows that the vapor ammonia concentration at the interface liquid-gas is elevated for the high value of inlet flow rate m_0L. Figure 10C reveals that a significant increase of the vapors mixture condensation when the inlet flow rate m_0L increases. This results have been explained by the fact that an increase in the inlet flow rate advantages the cooling at the interface liquid-gas causing an augmentation in the vapors mixture condensation. Figure 10D shows that the Nusselt number Nu is more important for the higher inlet flow rate m_0L. Figure 11 illustrates the influence of the inlet liquid temperature T_0L on the temperature at the interface liquid-gas, the vapor ammonia concentration at the liquid-gas interface and the vapors mixture condensation and the Nusselt number. As expected from Figure 11A, the interfacial temperature increase with an increase of inlet liquid temperature T_0L. It’s shown from Figure 11B that an increase of inlet liquid temperature T_0L induces an increase of the vapor ammonia concentration at the interface liquid-gas. Figure 11C indicates that a lower inlet liquid temperature T_0L results in a lower vapors mixture condensation. This result is explained by the fact that an increase in the inlet liquid temperature T_0L induces an increase in the temperature at the interface liquid-gas causing an augmentation in the vapor mixture condensation. Figure 11D indicates that an increase in the inlet liquid temperature T_0L causes a higher Nusselt number.

FIGURE 10

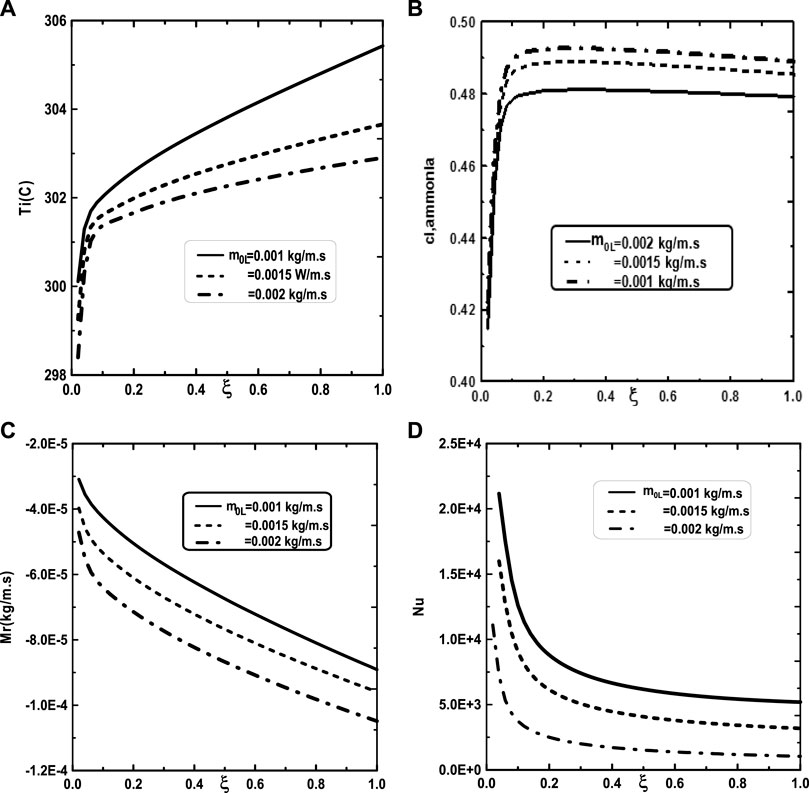
FIGURE 10. Effect of inlet liquid mass flow rate m_0L on the interfacial temperature (A), the ammonia vapor concentration (B), the cumulated condensation rate of vapors mixture (C) and the Nusselt number (D): c₀₁ = 0.3, c₀₂ = 0.5, q₁ = 0, T_0L = 10°C, T_w = 20°C, T₀ = 20°C, c_{Liq, ammonia} = 0.5 (50% water-ammonia mixture).

FIGURE 11

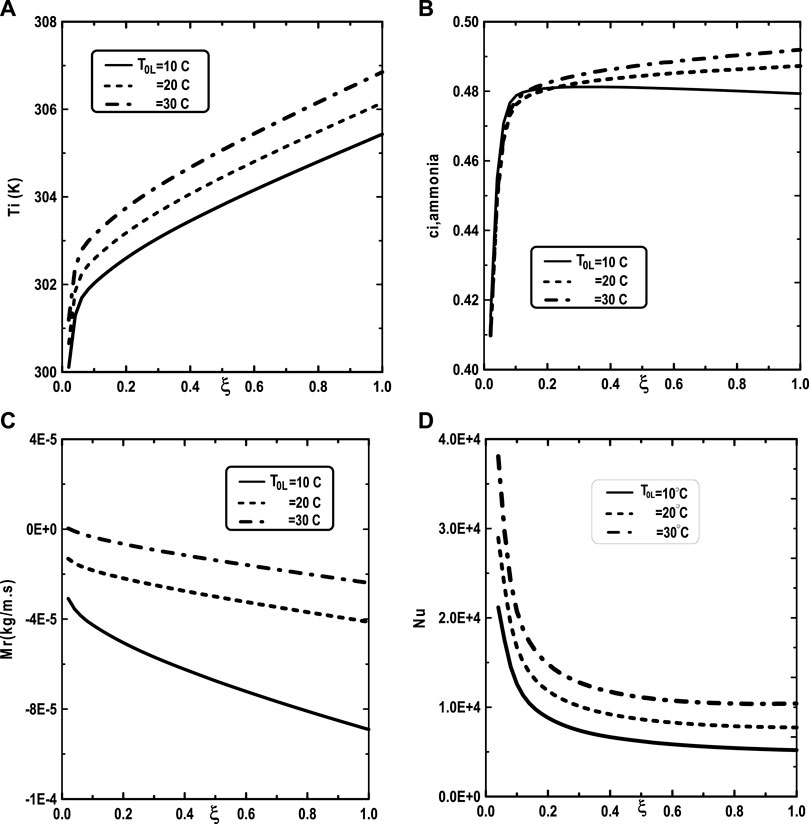
FIGURE 11. Effect of inlet liquid temperature T_0L on the interfacial temperature (A), the ammonia vapor concentration (B), the cumulated condensation rate of vapors mixture (C) and the Nusselt number (D): c₀₁ = 0.3, c₀₂ = 0.5, q₁ = 0, T_w = 20°C, T₀ = 20°C, c_{Liq, ammonia} = 0.5 (50% water-ammonia mixture), m_0L = 0.001 kg/m.s

5 Conclusion

The numerical investigation of binary liquid film condensation from water-ammonia vapors mixture flowing downward on a parallel plate condenser by mixed convection has been effected. The parallel plate condenser is composed by two parallel vertical plates (Figure 1). One of the plates is wetted by nanofilm liquid and cooled by the thermal flux cooling while the other plate is isothermal and dry. The influence of the inlet gas parameters, inlet liquid parameters and thermal flux cooling on the coupled heat and mass transfer and on on the efficiency of the parallel plate condenser has been studied. The finding of this study can be summarized as follows:

1) The increase in the inlet vapor of ammonia as well as of vapor water benefits the vapors mixture condensation.

2) The increase in the thermal flux cooling advantages the vapors mixture condensation.

3) The increase in the inlet liquid flow rate enhances the vapors mixture condensation.

4) The decrease of the inlet gas temperature improves the vapors mixture condensation.

5) A decrease in the inlet liquid temperature ameliorates the vapors mixture condensation.

6) The increase in the inlet liquid concentration of ammonia (or the increase of inlet liquid concentration of water) inhibits the vapors mixture condensation.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

Conceptualization, ABN; Data curation, ABN; Formal analysis, AA-G; Writing–original draft, ABN; Writing—review and editing, AA-G. All authors contributed to the article and approved the submitted version.

Acknowledgments

The authors would like to thank the Deanship of Scientific Research at Umm Al-Qura University for supporting this work by Grant Code: (23UQU4340531DSR001).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Akiyama, H., Nagasaki, T., and Ito, Y. (2001). “Numerical analysis on the dropwise condensation of a binary vapor mixture,” Proceedings of the ASME 2001 International Mechanical Engineering Congress and Exposition.

CrossRef Full Text | Google Scholar

Ali, C. A., and Daif, A. (1999). Numerical study of heat and mass transfer between two vertical flat plates in the presence of a binary liquid film flowing down on one of the heated plates. Int. J. Heat. Mass Transf. 42, 2399–2418.

Google Scholar

Yang, B., Sun, S., Fan, Y., Hu, N., and Chen, H., 2023, Numerical study of condensation film formation and transforming processes on porous surface within ceramic membrane, Int. J. Therm. Sci., 183, 107850, doi:10.1016/j.ijthermalsci.2022.107850

CrossRef Full Text | Google Scholar

Berto, A., Azzolin, M., Pascal, L., Glushchuk, A., Miscevic, M., Del Col, D., et al. (2022). Experimental investigation of liquid film thickness and heat transfer during condensation in microgravity. Int. J. Heat Mass Transf. 199, 123467. doi:10.1016/j.ijheatmasstransfer.2022.123467

CrossRef Full Text | Google Scholar

Chang, W., Yoo, J.-S., and Cho, H. K. (2021). Multi-scale simulation of wall film condensation in the presence of non-condensable gases using heat structure-coupled CFD and system analysis codes. Nucl. Eng. Technol. 53, 2488–2498. doi:10.1016/j.net.2021.03.001

CrossRef Full Text | Google Scholar

Chaynane, R., Mohamed, A., Boushaba, H., Zeghmati, B., and Khmou, A. (2004). Étude de la condensation en film laminaire d'une vapeur pure et saturée sur la paroi poreuse d'une plaque inclinée. Mech. Industry 5, 381–391. doi:10.1051/meca:2004038

CrossRef Full Text | Google Scholar

Chung, B. J., Kim, S., Kim, M. C., and Ahmadinejad, M. (2004). Experimental comparison of film-wise and drop-wise condensations of steam on vertical flat plates with the presence of air. Int. Commun. Heat Mass Transf. 31, 1067–1074. doi:10.1016/j.icheatmasstransfer.2004.08.004

CrossRef Full Text | Google Scholar

George, M., George, K., Constantoudis, V., Lam, C., Tripathy, A., Mitridis, E., et al. 2022, The role of shadowed droplets in condensation heat transfer, Int. J. Heat Mass Transf., 197, 123297, doi:10.1016/j.ijheatmasstransfer.2022.123297

CrossRef Full Text | Google Scholar

Hughes, M. T., and Chen, S. M. (2022). Srinivas Garimella, machine-learning-based heat transfer and pressure drop model for internal flow condensation of binary mixtures. Int. J. Heat Mass Transf. 194, 123109.

CrossRef Full Text | Google Scholar

Kuchma, A. E., Shchekin, A. K., and Kuni, F. M. (2011). Simultaneous establishing of stationary growth rate and composition of supercritical droplets at isothermal binary condensation in the diffusion-controlled regime. Phys. A Stat. Mech. its Appl. 390, 3308–3316. 20. doi:10.1016/j.physa.2011.05.028

CrossRef Full Text | Google Scholar

Kuchma, A. E., Martyukova, D. S., Lezova, A. A., and Shchekin, A. K. (2013). Size, temperature and composition of a spherical droplet as a function of time at the transient stage of nonisothermal binary condensation or evaporation. Colloids Surfaces A Physicochem. Eng. Aspects 432, 147–156. doi:10.1016/j.colsurfa.2013.04.023

CrossRef Full Text | Google Scholar

Lee, Y., Cha, M., Kim, H., and Jo, H. (2022). Film condensation heat transfer of high-pressure and low-mass-flux steam in inclined tube. Int. J. Heat Mass Transf. 189, 122714. doi:10.1016/j.ijheatmasstransfer.2022.122714

CrossRef Full Text | Google Scholar

Li, K., Liu, Y., Wen, J., Wang, S., and Tu, J. (2022). A numerical model for the flow condensation of the binary zeotropic mixture. Int. Commun. Heat Mass Transf. 130, 105767. doi:10.1016/j.icheatmasstransfer.2021.105767

CrossRef Full Text | Google Scholar

Liu, P., Ho, J. Y., Wong, T. N., and Toh, K. C. (2020). Laminar film condensation inside and outside vertical diverging/converging small channels: A theoretical study. Int. J. Heat Mass Transf. 149, 119193. doi:10.1016/j.ijheatmasstransfer.2019.119193

CrossRef Full Text | Google Scholar

Merouani, L., Zeghmati, B., Belhamri, A., Renken, K.-J., and Aboye, M. (1993). Experiments on film condensation promotion within thin inclined porous coatings. Int. J. Heat. Mass Transf. 36, 1347–1355. doi:10.1016/s0017-9310(05)80102-4

CrossRef Full Text | Google Scholar

Minkowycz, W. W. J., and Sparrows, E. M. (1969). The effect of superheating on condensation heat transfer in a forced convection boundary layer flow. Int. J. Heat Mass Transf. 12, 147–154. doi:10.1016/0017-9310(69)90058-1

CrossRef Full Text | Google Scholar

Nasr, A., and Al-Ghamdi, A. S. (2017). Numerical study of evaporation of falling liquid film on one of two vertical plates covered with a thin porous layer by free convection. Int. J. Therm. Sci. 112, 335–344. doi:10.1016/j.ijthermalsci.2016.10.018

CrossRef Full Text | Google Scholar

Nasr, A. (2018). Heat and mass transfer for liquid film condensation along a vertical channel covered with a thin porous layer. Int. J. Therm. Sci. 24, 288–299. doi:10.1016/j.ijthermalsci.2017.10.016

CrossRef Full Text | Google Scholar

Panday, P. K. (2003). Two-dimensional turbulent film condensation of vapours flowing inside a vertical tube and between parallel plates: A numerical approach. Int. J. Refrig. 26, 492–503. doi:10.1016/s0140-7007(02)00162-7

CrossRef Full Text | Google Scholar

Le, Q. T., Ormiston, S. J., and Soliman, H. M., 2022, Detailed modeling of laminar film condensation from zeotropic binary mixtures in a vertical tube, Int. J. Heat Mass Transf., 186, 122440, doi:10.1016/j.ijheatmasstransfer.2021.122440

CrossRef Full Text | Google Scholar

Renken, K. J., Aboye, M., Carneiro, M., and Meechan, K. (1993). Effect of vapor velocity on film condensation along a surface embedded in a porous medium. Int. Commun. Heat Mass Transf. 20, 1–13. doi:10.1016/0735-1933(93)90002-d

CrossRef Full Text | Google Scholar

Siow, E. C., Ormiston, S. J., and Soliman, H. M. (2002). Fully coupled solution of a two-phase model for laminar film condensation of vapor–gas mixtures in horizontal channels. Int. J. Heat Mass Transf. 45, 3689–3702. doi:10.1016/s0017-9310(02)00094-7

CrossRef Full Text | Google Scholar

Turkyilmazoglu, M. (2017). Condensation of laminar film over curved vertical walls using single and two-phase nanofluid models. Eur. J. Mech. - B/Fluids 65, 184–191. doi:10.1016/j.euromechflu.2017.04.007

CrossRef Full Text | Google Scholar

Varier, A. S., Joshi, M., and Swaminathan, J. (2022). Improved air gap distillation desalination through induced film condensation. Energy Convers. Manag. 258, 115545. doi:10.1016/j.enconman.2022.115545

CrossRef Full Text | Google Scholar

Wang, J., Li, J. M., and Hwang, Y. (2018). Modeling of film condensation flow in oval microchannels. Int. J. Heat Mass Transf. 126, 1194–1205. doi:10.1016/j.ijheatmasstransfer.2018.05.126

CrossRef Full Text | Google Scholar

Wang, J., Li, Y., Ma, Z., Chen, N., and Li, G. (2020). Condensate droplet growth characteristics of Marangoni condensation of ethanol–water mixtures on a horizontal surface. Int. J. Heat Mass Transf. 160, 120170. doi:10.1016/j.ijheatmasstransfer.2020.120170

CrossRef Full Text | Google Scholar

Wu, J., Sun, X., Xue, L., and Liu, Y. (2020). Research on film condensation heat transfer at the inside of spiral coil tube. Int. J. Heat Mass Transf. In press. doi:10.1016/j.ijheatmasstransfer.2019.118891

CrossRef Full Text | Google Scholar

Yan, W. M. (1992). Effects of film evaporation on laminar mixed convection heat and mass transfer in a vertical channel. Int. J. Heat. Mass Transf. 35, 3419–3429. doi:10.1016/0017-9310(92)90228-k

CrossRef Full Text | Google Scholar

Zheng, S., Eimann, F., Philipp, C., Tobias, F., and Gross, U. (2019). Dropwise condensation in the presence of non-condensable gas: Interaction effects of the droplet array using the distributed point sink method. Int. J. Heat Mass Transf. 141, 34–47. doi:10.1016/j.ijheatmasstransfer.2019.06.068

CrossRef Full Text | Google Scholar

Glossary