Background Adjusted Alignment-Free Dissimilarity Measures Improve the Detection of Horizontal Gene Transfer

Horizontal gene transfer (HGT) plays an important role in the evolution of microbial organisms including bacteria. Alignment-free methods based on single genome compositional information have been used to detect HGT. Currently, Manhattan and Euclidean distances based on tetranucleotide frequencies are the most commonly used alignment-free dissimilarity measures to detect HGT. By testing on simulated bacterial sequences and real data sets with known horizontal transferred genomic regions, we found that more advanced alignment-free dissimilarity measures such as CVTree and $d_2^{*}$ that take into account the background Markov sequences can solve HGT detection problems with significantly improved performance. We also studied the influence of different factors such as evolutionary distance between host and donor sequences, size of sliding window, and host genome composition on the performances of alignment-free methods to detect HGT. Our study showed that alignment-free methods can predict HGT accurately when host and donor genomes are in different order levels. Among all methods, CVTree with word length of 3, $d_2^{*}$ with word length 3, Markov order 1 and $d_2^{*}$ with word length 4, Markov order 1 outperform others in terms of their highest F₁-score and their robustness under the influence of different factors.

Introduction

As opposed to vertical transmission in which DNA is transferred from parent to offspring, horizontal gene transfer (HGT) or lateral gene transfer (LGT) is defined as the movement of genetic material between organisms that are not in a parent-offspring relationship. HGT plays an important role in bacterial evolution as it is the primary reason underlying the adaptation of bacteria such as metabolic adaptation (Pál et al., 2005) and antibiotic resistance (Gyles and Boerlin, 2014). Both alignment-based and alignment-free methods have been used to infer horizontal gene transfer (Karlin and Burge, 1995; Karlin, 2001; Tsirigos and Rigoutsos, 2005; Becq et al., 2010; Langille et al., 2010; Ravenhall et al., 2015; Cong et al., 2016a,b, 2017; Lu and Leong, 2016). Alignment-based, or phylogenetic methods, are often considered as the gold standard (Keeling and Palmer, 2008) for HGT detection because of their explicit model. Such methods detect horizontal gene transfer by integrating information from multiple organisms to find genes whose phylogenetic relationships among multiple organisms differ significantly from that of other genes (Ravenhall et al., 2015; Lu and Leong, 2016). Despite their extensive applications in horizontal gene transfer detection, finding topological incongruences is time-consuming, uses large memory, and requires that genomes of interest have to be annotated and their phylogenetic relationships are known. In addition, alignment-based methods can only be applied to gene or protein sequences and thus limit their ability to detect horizontal transfer in non-coding regions.

On the other hand, alignment-free, also called compositional parametric, methods detect horizontal gene transfer based on the detection of regions in a genome with atypical word pattern (kmer, ktuple, kgram, etc.) composition. These methods are based on the observation that different microbial species have their own genomic word pattern signatures (Karlin and Burge, 1995) so that sequences transferred from donor genome are likely to have different composition signatures from that of the host genome. DNA acquired via horizontal gene transfer will, over time, acquire the composition signatures of the host genome through a process called amelioration (Lawrence and Ochman, 1997). Recently, Cong et al. (2016a,b, 2017) introduced TF-IDF as a scalable alignment-free approach for HGT detection by combining multiple genomes and kmer occurrences. However, this method assumes that the donor genome is in the group of genomes under study and requires phylogenetic relationships among these genomes. More widely used alignment-free methods apply a sliding window to scan a single genome and calculate the distance between the composition of each window and the whole genome. Consecutive windows with distance from the whole genome higher than a threshold are inferred as HGT. The performances of alignment-free methods depend largely on the choice of genomic signatures. Commonly-used genomic signatures include, but are not limited to GC content (Karlin, 2001), codon usage (Karlin, 2001) and oligonucleotide (kmer) frequencies (Tsirigos and Rigoutsos, 2005). Becq et al. (2010) reviewed alignment-free methods on horizontal gene transfer detection and showed that kmer-based methods with a 5 kbp sliding window outperformed other alignment-free methods based on features such as GC content (Karlin, 2001), codon usage (Karlin, 2001) and dinucleotides (Karlin and Burge, 1995). However, they only tested Euclidean distance with kmer length 4 as genomic signature (Dufraigne et al., 2005) for kmer-based methods. In fact, the performances of kmer-based methods can vary largely depending on the choice of the value of k and dissimilarity measures between kmer vectors.

For kmer-based methods, Manhattan and Euclidean distances between the kmer frequency vector of a genomic region and that of the whole genome are the most frequently used measures for detecting HGTs because of their simplicity. For example, Dufraigne analyzed HGT regions of 22 genomes by using Euclidean distance with kmer length 4 (Dufraigne et al., 2005). In addition, they compared the genomic signatures of HGT regions with 12,000 species from GeneBank by Euclidean distance to find their potential donors. Rajan et al. used Manhattan distance with k-mer length 5 to detect HGT in 50 diverse bacterial genomes (Rajan et al., 2007). Tsirigos and Rigoutsos (2005) proposed to use relative kmer frequencies defined by the absolute kmer frequency over the expected frequency under the independent identically distributed (IID) model for HGT detection. They also investigated a few dissimilarity measures between the relative frequencies of a genomic region and the whole genome including correlation, covariance, Manhattan distance, Mahalanobis distance, and Kullback–Leibler (KL) distance for HTG detection. They showed that kmers of length 6–8 with covariance dissimilarity perform the best under their simulated situations. Several review papers on the use of kmers for the detection of HGT are available (Langille et al., 2010; Ravenhall et al., 2015; Lu and Leong, 2016). As in most studies of HGT, we concentrate on the use of kmers for HGT detection by using a single genome in this paper.

Recently, several new dissimilarity measures for sequence comparison based on kmer frequency vectors have been developed including CVTree (Qi et al., 2004), $d_2^{*}$ and $d_2^s$ (Reinert et al., 2009; Song et al., 2013; Lu et al., 2017). They have been shown to out-perform commonly used measures such as Manhattan and Euclidean distances for solving different problems including evolutionary distance estimation (Ren et al., 2016), virus-host interaction prediction (Ahlgren et al., 2017), and metagenome and metatranscriptome comparison (Jiang et al., 2012; Liao et al., 2016). However, these dissimilarity measures have not been used for HGT detection. It is important to know whether these new dissimilarity measures have better performance than available methods for detecting horizontal gene transfers. In addition, it is important to study the influence of evolutionary distance between host and donor genomes, sliding window size, and different host genome compositions on the performance of kmer-based alignment-free methods on HGT detection. In this study, we have addressed all these issues.

Materials and Methods

Artificial Genome Simulation

We chose Escherichia coli K12 (E. coli) as the host genome and Bacillus subtilis 168 (B. subtilis), Haemophilus influenzae Rd KW20 (H. influenzae), Helicobacter pylori 26695 (H. pylori), Mycobacterium tuberculosis H37RV (M. tuberculosis), and Streptococcus pneumoniae R6 (S. pneumoniae) as donor genomes. Each time, we picked a fragment randomly from the donor genome with length uniformly chosen from 8kbp to 40kbp and inserted it into a random position uniformly along the E. coli K12 genome until the simulated HGT consists of up to 10% of the artificial genome, since the HGT proportions in most bacteria genomes range from 2 to 15% (Garcia-Vallvé et al., 2000). We named the simulated genome as “E. coli_artificial.” To make our results more reliable, we did 10 simulations. Table S1 in the Supplementary Material shows the detailed composition of one of these 10 simulated genomes.

One of the challenges for evaluating HGT detection methods is the lack of a benchmark data. The host genome may contain genes historically transferred from other genomes, but they are not part of the simulated transferred regions. If a HGT detection method predicts such a gene as a HGT, although the prediction is correct, the prediction will be reported as a false positive since the gene is not transferred through the simulation. Therefore, the reported false positive rate maybe higher than the true false positive rate. On the other hand, such a problem is common to all the HGT detection methods and their relative performances are still valid. Therefore, we can still use artificial genomes to compare the relative performance of different methods.

Distance/Dissimilarity Measures Between Genomic Sequences

Given two genomic sequences i and j and a given word length k, we first count the number of occurrences of all kmers in sequence i and sequence j, respectively. The full set of kmers of length k is defined as ${{A}}^k$ where ${A}=(A,T,C,G)$ for nucleotide sequences. For a given kmer w, its occurrences in i is defined as $N_w^{(i)}$ and the frequency or the relative abundance of this kmer is defined as $f_w^{(i)}=\frac{N_w^{(i)}}{\sum _w{N}_w^{(i)}}$.

Some dissimilarity measures such as $d_2^{*}$ and $d_2^S$ need an m-th order Markov model for the background sequence. The expected number of occurrences of word w, $𝔼N_w^{(i)}$, can be calculated from the stationary probability of the first m-mer w[1 : m] and the transition probabilities from the n-th m-mer w[n : n + m − 1] to the (n + m)-th nucleotide w[n + m]:

$𝔼N_w^{(i)}=(L^{(i)}-k+1)\mu (w[1:m]){\displaystyle \prod _{n=1}^{k-m}\pi }(w[n:n+m-1],w[n+m])$

where L⁽ⁱ⁾ is the length of sequence i, μ is the stationary probability and π is the transition probability that can be estimated from the sequence data. The difference between the occurrences of kmer w and its expected occurrences is defined as ${Ñ}_w^{(i)}=N_w^{(i)}-𝔼N_w^{(i)}$.

Manhattan

The Manhattan distance (Ma) is defined as:

$Ma={\displaystyle \sum _{w\in {{A}}^k}|f_w^{(i)}-f_w^{(j)}|}$

Euclidean

The Euclidean distance (Eu) is defined as:

$Eu=\sqrt{{\displaystyle \sum _{w\in {{A}}^k}|f_w^{(i)}-f_w^{(j)}{|}^2}}$

d₂ (Torney et al., 1990)

The d₂ distance is defined as:

$d_2=\frac{1}{2}\left(1-\frac{{\displaystyle {\sum }_{w\in {{A}}^k}{f}_w^{(i)}{f}_w^{(j)}}}{\sqrt{{\displaystyle {\sum }_{w\in {{A}}^k}{(f_w^{(i)})}^2}}\sqrt{{\displaystyle {\sum }_{w\in {{A}}^k}{(f_w^{(j)})}^2}}}\right)$

CVTree (Qi et al., 2004)

The CVTree dissimilarity is defined as:

$CVTree=\frac{1}{2}\left(1-\frac{{\displaystyle {\sum }_{w\in {{A}}^k}{\widehat{f}}_w^{(i)}{\widehat{f}}_w^{(j)}}}{\sqrt{{\displaystyle {\sum }_{w\in {{A}}^k}{({\widehat{f}}_w^{(i)})}^2}}\sqrt{{\displaystyle {\sum }_{w\in {{A}}^k}{({\widehat{f}}_w^{(j)})}^2}}}\right)$

where ${\widehat{f}}_w^{(i)}=\frac{{Ñ}_w^{(i)}}{𝔼N_w^{(i)}}$. CVTree calculates $𝔼N_w^{(i)}$ by assuming a (k − 2)-th order Markov chain for genomic sequences.

$d_2^{*}$ (Reinert et al., 2009)

The $d_2^{*}$ dissimilarity is defined as:

$d_2^{\ast }=\frac{1}{2}\left(1-\frac{{\displaystyle {\sum }_{w\in {{A}}^k}{\overline{f}}_w^{(i)}{\overline{f}}_w^{(j)}}}{\sqrt{{\displaystyle {\sum }_{w\in {{A}}^k}{({\overline{f}}_w^{(i)})}^2}}\sqrt{{\displaystyle {\sum }_{w\in {{A}}^k}{({\overline{f}}_w^{(j)})}^2}}}\right)$

where ${\overline{f}}_w^{(i)}=\frac{{\tilde{N}}_w^{(i)}}{\sqrt{𝔼N_w^{(i)}}}$.

$d_2^s$ (Reinert et al., 2009)

The $d_2^s$ dissimilarity is defined as:

$d_2^s=\frac{1}{2}\left(1-\frac{{\displaystyle {\sum }_{w\in {{A}}^k}{\tilde{f}}_w^{(i)}{\tilde{f}}_w^{(j)}}}{\sqrt{{\displaystyle {\sum }_{w\in {{A}}^k}{({\tilde{f}}_w^{(i)})}^2}}\sqrt{{\displaystyle {\sum }_{w\in {{A}}^k}{({\tilde{f}}_w^{(j)})}^2}}}\right)$

where ${\tilde{f}}_w^{(i)}=\frac{{\tilde{N}}_w^{(i)}}{{({({\tilde{N}}_w^{(i)})}^2+{({\tilde{N}}_w^{(j)})}^2)}^{\frac{1}{4}}}$ and ${\tilde{f}}_w^{(j)}=\frac{{\tilde{N}}_w^{(j)}}{{({({\tilde{N}}_w^{(i)})}^2+{({\tilde{N}}_w^{(j)})}^2)}^{\frac{1}{4}}}$.

Distance Calculation

As in most studies (Dufraigne et al., 2005; Tsirigos and Rigoutsos, 2005), we used a sliding window approach for the detection of HGT. Starting from the 5′-end of the E. coli_artificial genome, we divided the genome into overlapped windows of size b with sliding step of 500 bps. As suggested by Dufraigne et al. (2005), we first used b = 5 kbp. We uesd CAFE (Lu et al., 2017), an accelerated alignment-free sequence analysis tool, to calculate different dissimilarity measures between each window and the whole genome by using the different alignment-free dissimilarity measures with different kmer lengths and Markov orders as needed. For measure d₂, Euclidean, and Manhattan, that do not require Markov order information, we used k = 3, 4, 5. For $d_2^{*}$ and $d_2^s$, we tested them with k = 3, 4, 5 and Markov order = 0, 1, 2, 3. For CVTree that assumes a Markov chain of order (k − 2), we tested it with k = 3, 4, 5. For all methods, a double-strand signature was used to remove strand compositional asymmetry (Karlin, 1999), which means we counted kmer occurrences in both the sequence and its reverse complementary sequence.

Predicting HGT Regions

Windows with high dissimilarity with the whole genome are more likely to be transferred from other genomes. Therefore, a window is predicted to be a HGT region if its dissimilarity with the whole genome D is above a certain threshold T. We used the same criterion as in Becq et al. (2010) to determine the threshold, that is,

$T=Q_3+r(Q_3-Q_1),$

where Q₁ and Q₃ are the first and third quartiles of the distribution of dissimilarity values between all the windows and the whole genome, and r is a parameter used to set the threshold that ranges from 0.25 to 10.00 with a step of 0.25. Therefore, for each alignment-free method with certain word length k and Markov order m, we could define 40 thresholds. Windows with distance from the whole genome above the threshold were defined as atypical windows. Overlapped atypical windows were then concatenated to form atypical regions, which were predicted as HGT regions.

Evaluation Criteria

By comparing the detected HGT and the real transferred fragments in E. coli_artificial, we calculated the recall (sensitivity) and precision. Recall is calculated as the length of the overlapped sequence between detected HGT and simulated HGT divided by the total length of simulated HGT fragments. Precision is calculated as the length of the overlapped sequence between detected HGT and simulated HGT divided by the total length of detected HGT. A commonly used measure that combines precision and recall is the harmonic mean of precision and recall, the traditional F₁-measure or balanced F₁-score, defined as

$F_1=2\times \frac{\text{precision}\times \text{recall}}{\text{precision}+\text{recall}}.$

Given an E. coli_artificial genome, for each threshold, we calculated the precision, recall and the F₁-score for each method. We then calculated the average precision, recall and the average F₁-score for each threshold over 10 simulated genomes and plotted the precision-recall curve. We report the optimal F₁-score for each dissimilarity measure.

Since most parts of the host genome are not transferred from other genomes, the receiver operating curve (ROC) showing the relationship between the false positive rate (FPR, 1 - specificity) and true positive rate (TPR, recall or sensitivity) is not optimal for comparing the different dissimilarity measures since the area under the ROC curve (AUC) and the specificity are generally very high. Therefore, we used the precision recall curve (PRC) and F₁-score as our criterion for comparing the different dissimilarity measures.

Investigating the Effect of Evolution Relationship Between the Host and Donor Genomes and Window Size on the Performance of Different Methods

In the simulated genome above, we assumed that all the donor genomes can contribute to the host genome through HGT. Since closely related genomes have similar kmer frequencies, it will be difficult to detect HGT from closely related genomes. On the other hand, if the donor genome has high evolutionary distance from the host genome, it will be relatively easy to identify HGT with any reasonable methods. Therefore, we next investigated how the evolutionary relationship between the the donor genome and the host genome affects the relative performance of the different HGT detection methods.

In our simulations, we still used E. coli K12 that is of the Proteobacteria phylum, Gammaproteobacteria class, Enterobacteriales order, Enterobacteriaceae family and Escherichia genus as host genome and chose 20 donor genomes having different evolutionary relationships with E. coli. Four of them are different species of the Escherichia genus [Escherichia albertii KF1 (E. albertii), Escherichia fergusonii ATCC 35469 (E. fergusonii), Escherichia hermannii NBRC 105704 (E. hermannii), Escherichia vulneris NBRC 102420 (E. vulneris)], four of them are in different genus of the Enterobacteriaceae family [Enterobacter cloacae ATCC 13047 (E. cloacae), Klebsiella pneumoniae HS11286 (K. pneumoniae), Salmonella typhimurium LT2 (S. typhimurium), Shigella sonnei 53G (S. sonnei)], four of them are in different families of the Enterobacteriales order [Yersinia pestis KIM 10+ (Y. pestis), Photorhabdus luminescens TT01 (P. luminescens), Pantoea ananatis LMG 20103 (P. ananatis), Brenneria goodwinii OBR1 (B. goodwinii)], four genomes are in different orders of the Gammaproteobacteria class [Legionella pneumophila Philadelphia 1 (L. pneumophila), Pseudomonas aeruginosa PA01 (P. aeruginosa), Vibrio parahaemolyticus RIMD 2210633 (V. parahaemolyticus), Xanthomonas axonopodis Xac29-1 (X. axonopodis)], and four genomes are in different classes of the Proteobacteria phylum [Burkholderia pseudomallei K96243 (B. pseudomallei), Brucella abortus 2308 (B. abortus), Campylobacter coli RM4661 (C. coli), Acidithiobacillus ferrooxidans ATCC 23270 (A. ferrooxidans)]. By transferring fragments between 8 and 40 kbp uniformly picked from these genomes into E. coli K12, we constructed 20 artificial genomes, each of them consists of 10% HGT from a certain single donor genome. We then detected the HGT using the different alignment-free methods and compared them using the same criteria as above.

In order to study the effect of window length, we continued to use the 20 artificial genomes generated above. Instead of using 5 kbp as the length of sliding window, we changed the window size to 3 and 8 kbp, respectively. Finally, we used the F₁-score to evaluate the different methods.

To see if our results are consistent for different host genomes, we changed the host genome from E. coli to B. abortus and K. pneumoniae, respectively. Then we did the same analyses as for E. coli.

Investigation of HGT Within 118 Genomes and E. faecalis V583

To evaluate the performances of alignment-free methods on HGT detection over real data, we used a data set constructed in Langille et al. (2008). In this study, the authors selected 118 genomes from 117 different strains and used a comparative genomics approach to detect genomic islands resulted from horizontal gene transfer. This benchmark data was constructed using alignments and did not use nucleotide composition information. Therefore, the data set can be used to evaluate different alignment-free HGT detection methods. For each genome, the authors provided positive and negative regions of HGT. As in Langille et al. (2008), we used precision, recall and overall accuracy to evaluate performances of alignment-free methods on HGT prediction over these 118 chromosomes, where the accuracy is calculated by the fraction of true positives and true negatives over all the predictions. In addition, we also used the optimal F₁-score and the precision-recall curve to compare the different methods.

We also used the different methods to identify HGT regions of Enterococcus faecalis V583 (E. faecalis) that contains seven known genes transferred from other genomes. Since we do not know the whole set of HGT genes, we just investigated if these seven genes are ranked higher than other genes. The higher these genes are ranked by a particular method, the better performance the method is in predicting HGT.

Results

Background Adjusted Dissimilarity Measures Outperform Non-background Adjusted Methods for HGT Detection Based on the E. coli_artificial Genome

Table 1 shows the precision and recall yielding the highest average F₁-score of the different alignment-free methods for different word size k and Markov order m when needed. The highest F₁-score of 0.88 is obtained for CVT(4), followed by CVT(3), $d_2^{*}(3,1)$ and $d_2^{*}(4,1)$ (the first number in the parenthesis is the word length and the second number is the order of MC) with average F₁-score at least 0.87. In comparison with background adusted dissimilarity measures, the widely-used Manhattan and Euclidean distances both have F₁-score at most 0.80.

TABLE 1

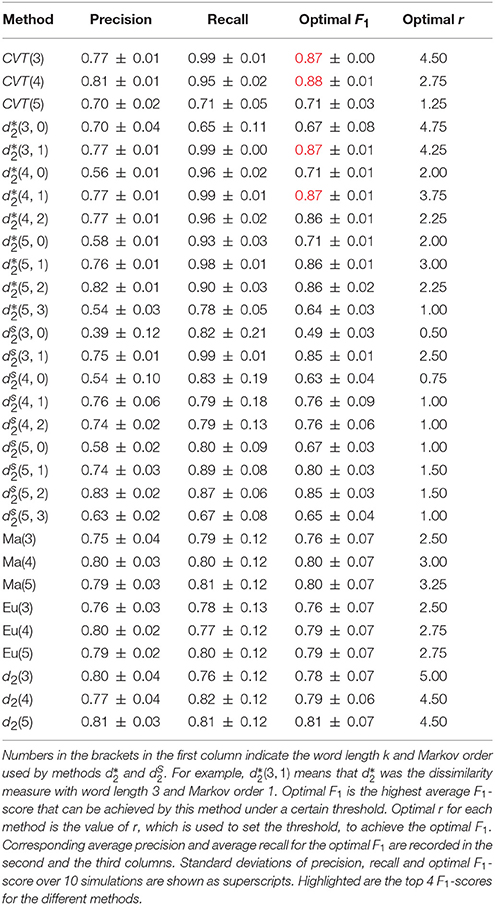
Table 1. Complete evaluation results for different dissimilarity measures with different word lengths k and Markov orders when needed.

In addition to comparing the different methods at the optimal F₁ level, we also plotted the precision-recall curves for the different methods shown in Figure 1. Figure 1D shows that non-background adjusted methods Ma, Eu and d₂ showed similar performace. Figures 1A–C show that background adjusted methods had better performance than non-background adjusted methods when k = 3 or k = 4. Among all methods, CVT(3), CVT(4), $d_2^{*}(3,1)$ and $d_2^{*}(4,1)$ had the best performace in terms of precision-recall curves. The conclusions about the relative performance of the different methods are the same based on either the F₁-score or the precision-recall curves.

FIGURE 1

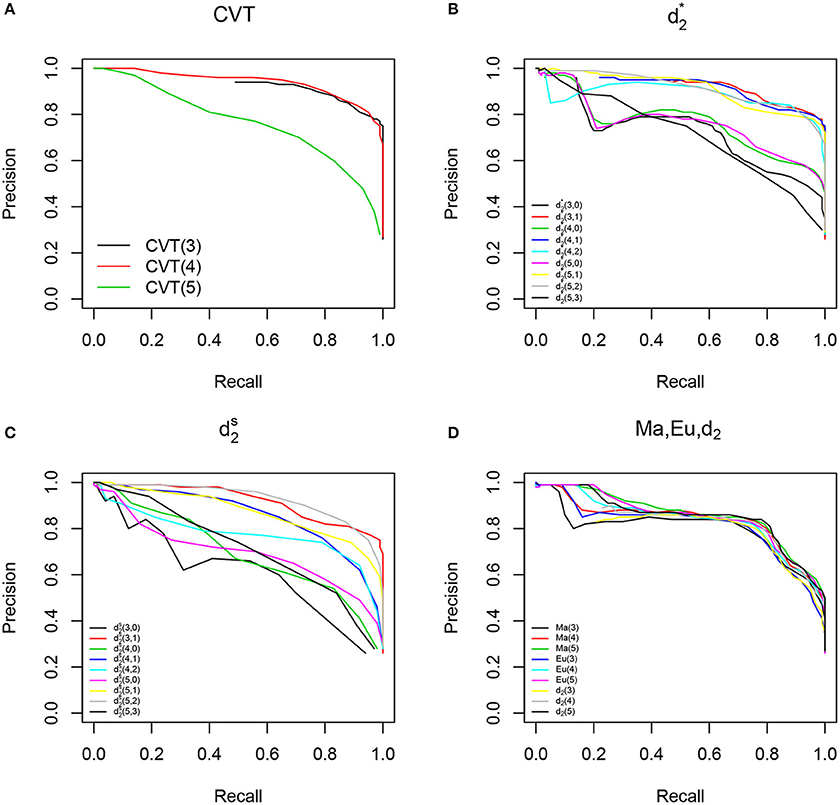
Figure 1. Precision-Recall Curves (PRC) for all the methods. (A) Shows PRC for CVTree with different word lengths. (B) Shows PRC for all the $d_2^{*}$ methods. (C) Shows PRC for all $d_2^s$ methods. (D) Shows PRC for Manhattan, Euclidean and d₂.

The better performance of the background adjusted methods (CVTree, $d_2^{*}$ and $d_2^S$) over the non-background adjusted methods (Manhattan, Euclidean, and d₂) can probably be explained by the following observations. By removing the background counts of the word patterns, the signals from the most relevant kmers representative of the host genome are amplified while the contributions of irrelevant kmers are mitigated. Therefore, the background adjusted dissimilarity measures perform well in HGT detection.

Based on the performances of the different methods shown in Table 1 and Figure 1, we only present our results for the top performing methods in the rest of the paper. We chose CVT(3), CVT(4), $d_2^{*}(3,1)$, and $d_2^{*}(4,1)$ to represent background adjusted methods and Ma(5), Eu(5), and d₂(5) to represent non-background adjusted methods as candidates for the following studies.

The Performance of the Alignment-Free Methods Increases With the Genetic Distance Between the Donor Genome and the Host Genome

We next investigated the influence of evolutionary distance between the donor genome and the host genome on the performance of the different methods CVT(3), CVT(4), $d_2^{*}(3,1)$, $d_2^{*}(4,1)$, Ma(5), Eu(5), and d₂(5) based on the 20 artificial genomes described in the “Materials and Methods” section and the results are given in Table 2. The 20 donor genomes were sorted by the Manhattan distance of the tetra-mer frequencies between the donor and E. coli K12.

TABLE 2

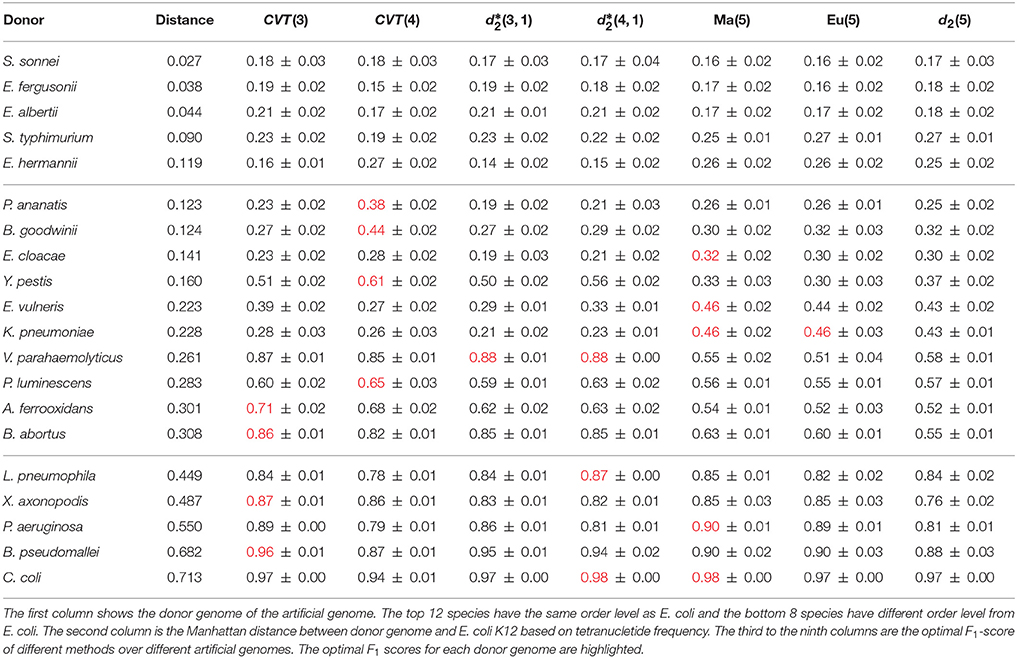
Table 2. Performance of different alignment-free HGT detection methods over 20 artificial genomes with different donor genomes.

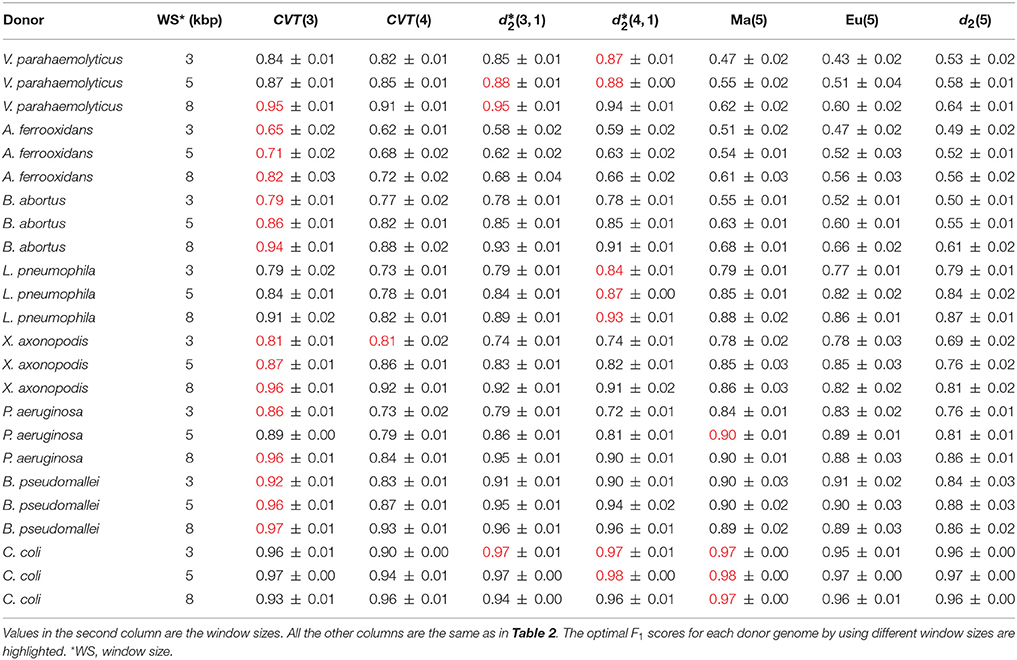
We divided the donor genomes into three groups separated by horizontal lines in Table 2. For the top group of donor genomes with Manhattan distance between the donor and host genomes less than 0.12, none of the methods have F₁ value greater than 0.30 indicating that none of them can successfully detect HGT when the donor genome and host genome are very close. For the second group of donor genomes with Manhattan distance between 0.12 to 0.31, for eight out of ten donor genomes except for V. parahaemolyticus and B. abortus, the optimal F₁ scores are moderate between 0.32 to 0.71. Except for E. cloacae, E. vulneris and K. pneumoniae, the background adjusted dissimilarity measures outperform the non-background adjusted measures, some times by a significant margin. For example, when the donor genome is V. parahaemolyticus, the F₁-scores for CVT(3), CVT(4), $d_2^{*}(3,1)$, and $d_2^{*}(4,1)$ are all at least 0.85, while the F₁-scores for Ma(5), Eu(5), and d₂(5) are at most 0.58. Within this group of donor genomes, CVT(4) seems to perform better than CVT(3) when the Manhattan distance between the donor and host genomes is between 0.12 and 0.22, while CVT(3) is slightly better than CVT(4) when the Manhattan distance is between 0.22 to 0.31. The results are reasonable since when the donor and host genomes are relatively close, relative long kmers are needed to separate the transferred fragments from the background. On the other hand, when the donor and host genomes are relatively far apart, relatively short-mers are more discriminative. For the last group of donor genomes with large distances between the donor and host genomes, all the seven methods perform decently well with CVT(3), $d_2^{*}(4,1)$ and Ma(5) generally as the best performers.

In addition to the comparison of the different methods based on the optimal F₁-score, we also plotted the precision-recall curves for three donor genomes S. sonnei, B. abortus, and C. coli in Figure 2 as examples for each group. Similar results for the relative performance of the different methods as based on F₁-scores were observed.

FIGURE 2

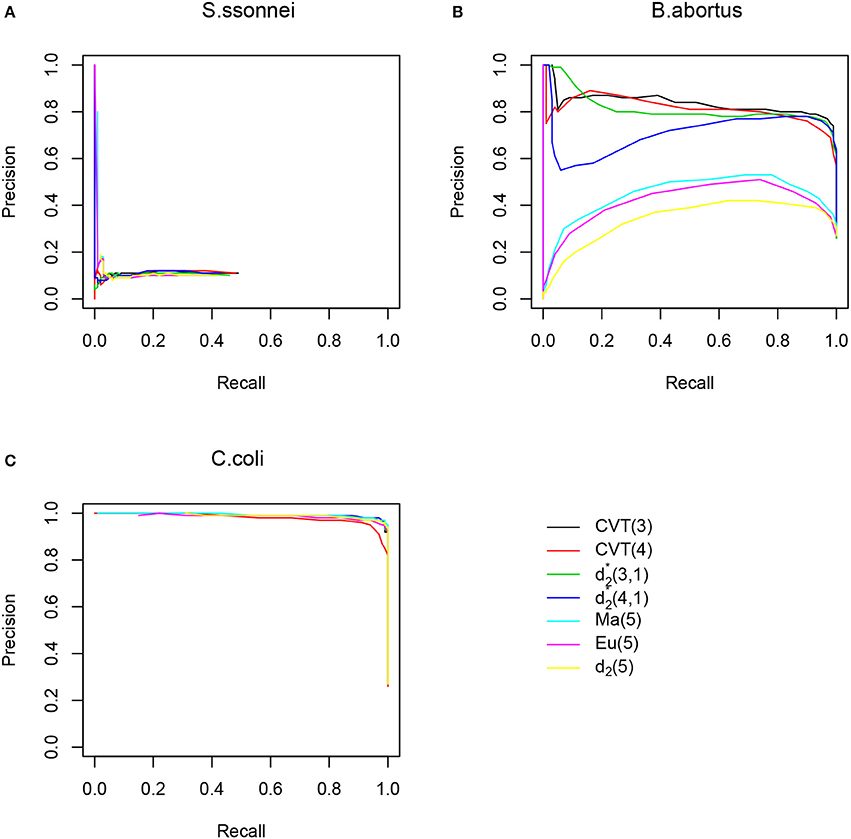
Figure 2. The Precision-Recall Curves (PRC) of different HGT detection methods along artificial genomes using E. coli as host genome. (A) PRC when using S.sonnei as donor genome, no methods performs well. (B) PRC when using B. abortus as donor genome, CVT(3), CVT(4),$d_2^{*}(3,1)$ and $d_2^{*}(4,1)$ outperform other methods. (C) PRC when using C.coli as donor genome, all methods perform reasonably well.

The Performance of the Alignment-Free Methods Increases With the Window Size Within the Range of 3–8 kbp

We further studied the influence of window size on different methods as the performances of alignment-free methods always reply on the sequence length that should be long enough to represent the genomic signature. Besides 5 kbp window size with 500 bp sliding step, we also checked the performance of different methods based on 3 kbp window size with 300 bp sliding step and 8kbp window size with 800 bp sliding step by using the same evaluation approach. Among the 20 artificial genomes that have been generated to study the influence of the genetic distance between the donor genome and host genome, we chose 8 of them in which donors have different order level from that of E. coli K12. Optimal F₁ score of different methods using different window sizes over these 8 genomes are shown in Table 3. All methods showed similar trend that their mean F₁ score increases as the window length increases from 3 to 8 kbp. But CVT(3) is the most robust with different window sizes and its performance suffers less with the decrease of window size compared with other methods.

TABLE 3

Table 3. Performance of different methods over artificial genomes by using different window sizes.

Robustness of the Relative Performance of the Different Methods With Respect to Different Host Genomes

To see the robustness of our results on the relative performance of the different alignment-free HGT detection methods with respect to host genomes, we changed the host genome from E. coli to B. abortus and K. pneumoniae, respectively. The complete results are given as Tables S2, S3 in Supplementary Material. From both tables, it can be seen that the conclusions about the relative performance of the different methods hold regardless of the host genome.

Applications to Real HGT Data Support the Good Performance of Background Adjusted Dissimilarity Measures

Evaluation of Different Methods Based on 118 Genomes With Known HGT Genomic Islands

We next applied the various dissimilarity measures to identify genomic islands generated from HGT for the 118 genomes described in the “Materials and Methods" section. We still chose 40 thresholds as in our simulation studies for each method, and calculated the optimal accuracy that is the highest accuracy one method can achieve under certain threshold. The results are shown in part (a) of Table 4. The values of the optimal accuracy for the different methods are not markedly different, but we can still see that the background adjusted dissimilarity measures CVT(3), CVT(4), $d_2^{*}(3,1)$, and $d_2^{*}(4,1)$ have slightly higher accuracy than the non-background adjusted dissimilarity measures Eu(5), Ma(5), and d₂(5). Similarly, we also evaluated the different methods based on the optimal F₁-score as shown in part (b) of Table 4. The conclusions on the relative performance of the methods based on F₁-score are essentially the same as that based on optimal accuracy. In addition, we also plotted the precision-recall curves of the different methods based on this data set and the resulting figures are shown in Figure 3. It is clear from the figure that CVT(3), $d_2^{*}(3,1)$ and $d_2^{*}(4,1)$ perform much better than the other methods. In Langille et al. (2008), SIGI-HMM and IslandPath/DIMOB showed the highest accuracy of 0.86. We did not include them in our comparison because they incorporate other information such as codon uasge, dinucleotide bias, gene expression and mobility that can only be used when the genome is annotated. However, in terms of accuracy, $d_2^{*}(4,1)$ can achieve the same performance as SIGI-HMM and IslandPath/DIMOB by detecting HGT purely based on the genomic composition.

TABLE 4

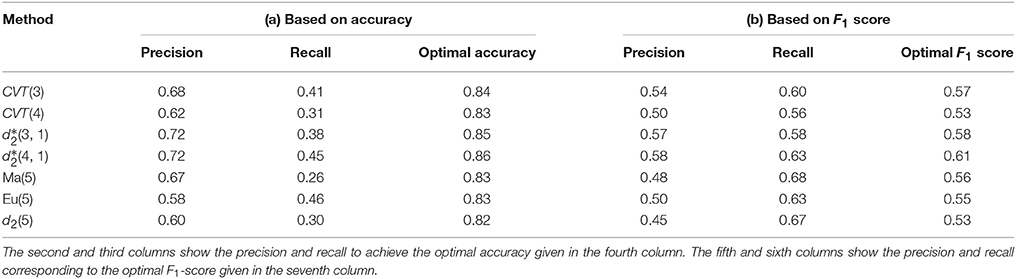
Table 4. Performance of different methods over 118 genomes with known HGT genomic islands in Langille et al. (2008) based on (a) optimal accuracy and (b) optimal F₁-score.

FIGURE 3

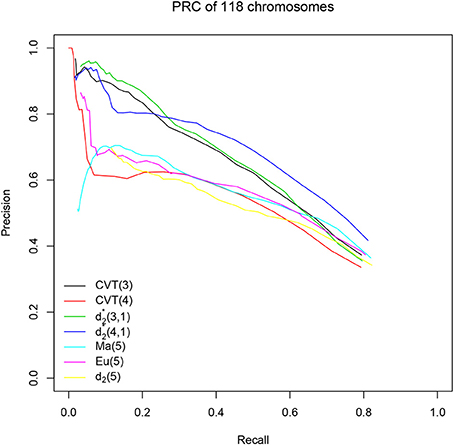
Figure 3. The Precision-Recall Curves (PRC) of the different methods based on 118 genomes with known HGT genomic islands.

Evaluation of Different Methods Based on E. faecalis V583 With Known Seven HGT Genes

In E. faecalis V583, a genomic region that contains 7 genes (EF2293-EF2299) conferring vancomycin resistance to E. faecalis has been known to have been horizontally transferred (Tsirigos and Rigoutsos, 2005). In this case, we calculated the distance between each gene and the E. faecalis V583 genome using different methods. We then ranked all 3112 E. faecalis V583 genes by the distance in descending order where the first gene has the largest distance to E. faecalis V583 genome. Better HGT detection methods should give EF2293-EF2299 lower ranks. Ranks of EF2293-EF2299 and the median and mean rank of these 7 genes for all the methods are shown in Table 5. $d_2^{*}(3,1)$ gives lower median and mean ranks for EF2293-EF2299 than other methods. In comparison with $d_2^{*}$, the median and mean ranks given by more commonly-used Manhanttan and Euclidean distances are larger than 1,000, which are unreasonably high considering the fact that the HGT proportions in most bacteria genomes range from only 2 to 15% (Garcia-Vallvé et al., 2000).

TABLE 5

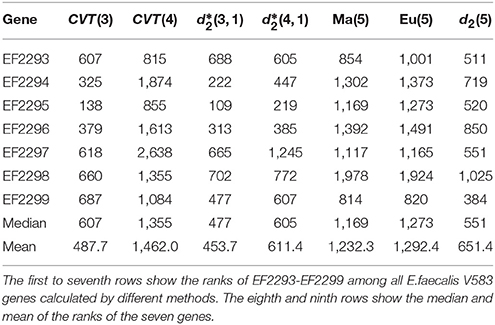
Table 5. The distances between each gene and E. faecalis V583 genome were calculated and genes were ranked by their distances.

Discussion

Kmer-based alignment-free methods have been used to detect horizontal gene transfers in bacterial genomes (Dufraigne et al., 2005; Tsirigos and Rigoutsos, 2005; Rajan et al., 2007). There are a number of advantages of kmer-based methods over other alignment-free methods or alignment-based methods. First of all, kmer-based methods are time efficient and memory friendly by avoiding alignment and topological data analysis. Secondly, kmer-based methods do not rely on phylogenetic relationships among multiple organisms, which enables them to detect HGTs from a single unannotated genome. In addition, kmer-based methods are able to detect HGTs in both coding and non-coding regions.

In this study, we investigated the potential of using recently developed alignment-free sequence comparison statistics, in particular, CVTree, $d_2^{*}$ and $d_2^S$, that adjust for the background word frequencies, for horizontal gene transfer detection. Although many composition based methods have been used for HGT detection, to the best of our knowledge, the background adjusted statistics have not been used for HGT detection.

We first generated simulated artificial genomes with HGT by using E. coli K12 as the host genome and inserted sequences uniformly chosen from other genomes into it. We then evaluated the performance of kmer-based alignment-free methods of different distance measures, kmer length and Markov order on HGT detection of artificial genomes. Based on the results, we reduced our set to CVTree(k = 3), CVTree(k = 4), $d_2^{*}(k=3,m=1)$, $d_2^{*}(k=4,m=1)$, Ma(k = 5), Eu(k = 5), and d₂(k = 5) for more detailed comparisons including influence of different factors and their performance on real data sets.

As a conclusion, we evaluated the performance of kmer-based alignment-free methods with different dissimilarity measures, kmer length and Markov order on both artificial genomes and real data sets. Our results suggest the background adjusted dissimilarity measures, CVTree, $d_2^{*}$ and $d_2^S$, generally perform better than the non-background adjusted measures based on Euclidean and Manhattan distances or d₂. In terms of word length, k = 3 or k = 4 seems to perform well in both our simulation and real data analysis.

Although kmer-based alignment-free methods for HGT detection are more time and memory efficient than alignment-based methods and they do not depend on genome annotation or evolutionary tree, they also have limits. First of all, their performances depend on the evolutionary distance between host and donor genomes. Our study showed alignment-free methods are suitable for HGT detection when host and donor genomes are in different order levels. In addition, the size of sliding window is the smallest length of HGT that can be detected by the kmer-based alignment-free methods, so they are not suitable for identifying HGT smaller than 5 kbp. Furthermore, they are not likely to detect HGT that occurred in the very distant past, as these sequences transferred from the donor genome will ameliorate to reflect the DNA composition of the host genome over time (Lawrence and Ochman, 1997). Finally, the detected atypical regions could be explained by some other reasons. For example, rRNA regions can have their own genomic signatures (Nicolas et al., 2002; Dufraigne et al., 2005), which differ from the host signature, but this does not imply that they are horizontally transferred.

Therefore, alignment-free methods are not aimed to replace alignment-based methods in all cases. Instead, they are complementary as each has unique advantages in different scenarios and they also tend to find complementary sets of HGT regions (Tamames and Moya, 2008). Alignment-free methods are preferred when no evolutionary trees are available or genomes are not annotated, which is common in many studies. The findings of our study suggest CVTree with word length of 3, $d_2^{*}$ with word length 3, Markov order 1 and $d_2^{*}$ with word length 4, Markov order 1 perform well in most situations.

Author Contributions

KT implemented and carried out the computational analyses and wrote the paper. YL provided software for calculating alignment-free dissimilarity measures. FS led the project and finalized the paper. All authors agree to the content of the final paper.

Funding

National Science Foundation (NSF) [DMS-1518001]; National Institutes of Health (NIH) [R01GM120624].

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This research utilized resources of HPC (High-Performance Computing), which is supported by the University of Southern California.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmicb.2018.00711/full#supplementary-material

References

Ahlgren, N. A., Ren, J., Lu, Y. Y., Fuhrman, J. A., and Sun, F. (2017). Alignment-free oligonucleotide frequency dissimilarity measure improves prediction of hosts from metagenomically-derived viral sequences. Nucl. Acids Res. 45, 39–53. doi: 10.1093/nar/gkw1002

PubMed Abstract | CrossRef Full Text | Google Scholar

Becq, J., Churlaud, C., and Deschavanne, P. (2010). A benchmark of parametric methods for horizontal transfers detection. PLoS ONE 5:e9989. doi: 10.1371/journal.pone.0009989

PubMed Abstract | CrossRef Full Text | Google Scholar

Cong, Y., Chan, Y. B., Phillips, C. A., Langston, M. A., and Ragan, M. A. (2017). Robust inference of genetic exchange communities from microbial genomes using TF-IDF. Front. Microbiol. 8:21. doi: 10.3389/fmicb.2017.00021

PubMed Abstract | CrossRef Full Text | Google Scholar

Cong, Y., Chan, Y. B., and Ragan, M. A. (2016a). Exploring lateral genetic transfer among microbial genomes using TF-IDF. Sci. Rep. 6:29319. doi: 10.1038/srep29319

PubMed Abstract | CrossRef Full Text | Google Scholar

Cong, Y., Chan, Y. B., and Ragan, M. A. (2016b). A novel alignment-free method for detection of lateral genetic transfer based on TF-IDF. Sci. Rep. 6:30308. doi: 10.1038/srep30308

PubMed Abstract | CrossRef Full Text | Google Scholar

Dufraigne, C., Fertil, B., Lespinats, S., Giron, A., and Deschavanne, P. (2005). Detection and characterization of horizontal transfers in prokaryotes using genomic signature. Nucl. Acids Res. 33:e6. doi: 10.1093/nar/gni004

PubMed Abstract | CrossRef Full Text | Google Scholar

Garcia-Vallvé, S., Romeu, A., and Palau, J. (2000). Horizontal gene transfer in bacterial and archaeal complete genomes. Genome Res. 10, 1719–1725. doi: 10.1101/gr.130000

PubMed Abstract | CrossRef Full Text | Google Scholar

Gyles, C., and Boerlin, P. (2014). Horizontally transferred genetic elements and their role in pathogenesis of bacterial disease. Veter. Pathol.gy 51, 328–340. doi: 10.1177/0300985813511131

PubMed Abstract | CrossRef Full Text | Google Scholar

Jiang, B., Song, K., Ren, J., Deng, M., Sun, F., and Zhang, X. (2012). Comparison of metagenomic samples using sequence signatures. BMC Genomics 13:730. doi: 10.1186/1471-2164-13-730

PubMed Abstract | CrossRef Full Text | Google Scholar

Karlin, S. (1999). Bacterial DNA strand compositional asymmetry. Trends Microbiol. 7, 305–308. doi: 10.1016/S0966-842X(99)01541-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Karlin, S. (2001). Detecting anomalous gene clusters and pathogenicity islands in diverse bacterial genomes. Trends Microbiol. 9, 335–343. doi: 10.1016/S0966-842X(01)02079-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Karlin, S., and Burge, C. (1995). Dinucleotide relative abundance extremes: a genomic signature. Trends Genet. 11, 283–290. doi: 10.1016/S0168-9525(00)89076-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Keeling, P. J., and Palmer, J. D. (2008). Horizontal gene transfer in eukaryotic evolution. Nat. Rev. Genet. 9:605. doi: 10.1038/nrg2386

PubMed Abstract | CrossRef Full Text | Google Scholar

Langille, M. G., Hsiao, W. W., and Brinkman, F. S. (2008). Evaluation of genomic island predictors using a comparative genomics approach. BMC Bioinformatics 9:329. doi: 10.1186/1471-2105-9-329

PubMed Abstract | CrossRef Full Text | Google Scholar

Langille, M. G., Hsiao, W. W., and Brinkman, F. S. (2010). Detecting genomic islands using bioinformatics approaches. Nat. Rev. Microbiol. 8:373. doi: 10.1038/nrmicro2350

PubMed Abstract | CrossRef Full Text | Google Scholar

Lawrence, J. G., and Ochman, H. (1997). Amelioration of bacterial genomes: rates of change and exchange. J. Mol. Evol. 44, 383–397. doi: 10.1007/PL00006158

PubMed Abstract | CrossRef Full Text | Google Scholar

Liao, W., Ren, J., Wang, K., Wang, S., Zeng, F., Wang, Y., et al. (2016). Alignment-free transcriptomic and metatranscriptomic comparison using sequencing signatures with variable length markov chains. Sci. Rep. 6:37243. doi: 10.1038/srep37243

PubMed Abstract | CrossRef Full Text | Google Scholar

Lu, B., and Leong, H. W. (2016). Computational methods for predicting genomic islands in microbial genomes. Comput. Struct. Biotechnol. J. 14, 200–206. doi: 10.1016/j.csbj.2016.05.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Lu, Y. Y., Tang, K., Ren, J., Fuhrman, J. A., Waterman, M. S., and Sun, F. (2017). CAFE: aCcelerated Alignment-FrEe sequence analysis. Nucl. Acids Res. 45, W554–W559. doi: 10.1093/nar/gkx351

PubMed Abstract | CrossRef Full Text | Google Scholar

Nicolas, P., Bize, L., Muri, F., Hoebeke, M., Rodolphe, F., Ehrlich, S. D., et al. (2002). Mining bacillus subtilis chromosome heterogeneities using hidden markov models. Nucl. Acids Res. 30, 1418–1426. doi: 10.1093/nar/30.6.1418

PubMed Abstract | CrossRef Full Text | Google Scholar

Pál, C., Papp, B., and Lercher, M. J. (2005). Adaptive evolution of bacterial metabolic networks by horizontal gene transfer. Nat. Genet. 37:1372. doi: 10.1038/ng1686

PubMed Abstract | CrossRef Full Text | Google Scholar

Qi, J., Luo, H., and Hao, B. (2004). CVTree: a phylogenetic tree reconstruction tool based on whole genomes. Nucl. Acids Res. 32(Suppl. 2):W45–W47. doi: 10.1093/nar/gkh362

PubMed Abstract | CrossRef Full Text | Google Scholar

Rajan, I., Aravamuthan, S., and Mande, S. S. (2007). Identification of compositionally distinct regions in genomes using the centroid method. Bioinformatics 23, 2672–2677. doi: 10.1093/bioinformatics/btm405

PubMed Abstract | CrossRef Full Text | Google Scholar

Ravenhall, M., Škunca, N., Lassalle, F., and Dessimoz, C. (2015). Inferring horizontal gene transfer. PLoS Comput. Biol. 11:e1004095. doi: 10.1371/journal.pcbi.1004095

PubMed Abstract | CrossRef Full Text | Google Scholar

Reinert, G., Chew, D., Sun, F., and Waterman, M. S. (2009). Alignment-free sequence comparison (i): statistics and power. J. Comput. Biol. 16, 1615–1634. doi: 10.1089/cmb.2009.0198

PubMed Abstract | CrossRef Full Text | Google Scholar

Ren, J., Song, K., Deng, M., Reinert, G., Cannon, C. H., and Sun, F. (2016). Inference of Markovian properties of molecular sequences from NGS data and applications to comparative genomics. Bioinformatics 32, 993–1000. doi: 10.1093/bioinformatics/btv395

PubMed Abstract | CrossRef Full Text | Google Scholar

Song, K., Ren, J., Reinert, G., Deng, M., Waterman, M. S., and Sun, F. (2013). New developments of alignment-free sequence comparison: measures, statistics and next-generation sequencing. Brief. Bioinform. 15, 343–353. doi: 10.1093/bib/bbt067

PubMed Abstract | CrossRef Full Text | Google Scholar

Tamames, J., and Moya, A. (2008). Estimating the extent of horizontal gene transfer in metagenomic sequences. BMC Genomics 9:136. doi: 10.1186/1471-2164-9-136

PubMed Abstract | CrossRef Full Text | Google Scholar

Torney, D. C., Burks, C., Davison, D., and Sirotkin, K. M. (1990). “Computation of d2: a measure of sequence dissimilarity,” in Computers and DNA: The Proceedings of the Interface between Computation Science and Nucleic Acid Sequencing Workshop, held December 12 to 16, 1988 in Santa Fe, New Mexico/edited by George I. Bell, Thomas G. Marr (Redwood City, CA: Addison-Wesley Pub. Co.).

Google Scholar

Tsirigos, A., and Rigoutsos, I. (2005). A new computational method for the detection of horizontal gene transfer events. Nucl. Acids Res. 33, 922–933. doi: 10.1093/nar/gki187

PubMed Abstract | CrossRef Full Text | Google Scholar