- School of Mathematics and Statistics, Qingdao University, Qingdao, China
Phages are viruses that infect bacteria. The phages can be classified into two different categories based on their lifestyles: temperate and lytic. Now, the metavirome can generate a large number of fragments from the viral genomic sequences of entire environmental community, which makes it impossible to determine their lifestyles through experiments. Thus, there is a need to development computational methods for annotating phage contigs and making prediction of their lifestyles. Alignment-based methods for classifying phage lifestyle are limited by incomplete assembled genomes and nucleotide databases. Alignment-free methods based on the frequencies of k-mers were widely used for genome and metagenome comparison which did not rely on the completeness of genome or nucleotide databases. To mimic fragmented metagenomic sequences, the temperate and lytic phages genomic sequences were split into non-overlapping fragments with different lengths, then, I comprehensively compared nine alignment-free dissimilarity measures with a wide range of choices of k-mer length and Markov orders for predicting the lifestyles of these phage contigs. The dissimilarity measure, , performed better than other dissimilarity measures for classifying the lifestyles of phages. Thus, I propose that the alignment-free method, , can be used for predicting the lifestyles of phages which derived from the metagenomic data.
Introduction
Viruses are distributed in every corner of the earth, and they play important roles in the ecosystem (Srinivasiah et al., 2008). A virus is a small individual with a simple structure, containing only one type of nucleic acid (DNA or RNA), and must parasitize and replicate in living cells (Whitman et al., 1998). Viruses can infect all kinds of organisms, from mammals to bacteria. An important class of viruses is bacteriophages, which can infect and kill bacterial cells.
The lifestyles of phages can be divided into two different types, temperate and lytic (Chopin et al., 2001; Knowles et al., 2016). Temperate phages can replicate and spread by integrating their genetic information into the bacterial genome. However, the lytic phages replicate themselves in bacterial cells and spread by killing the cells. Bacteriophages play important roles in microbial community, and identifying their lifestyles is the first step to understand their functions. Now, the metavirome can generate a large number of fragments from the viral genomic sequences of entire environmental community, which makes it impossible to determine their lifestyles through experiments. So, developing computational methods is necessary to predict the lifestyles of phages.
The previous studies of classifying phages using genomic data were mainly using alignment-based methods (Proux et al., 2002; Rohwer and Edwards, 2002; Lima-Mendez et al., 2008, 2011). However, very few studies focus on classifying the lifestyles of phages. McNair et al., 2012 utilizes a similarity algorithm and a supervised Random Forest classifier to predict the lifestyle of a phage (McNair et al., 2012). The similarity algorithm which creates a training set from phages with known lifestyles based on the alignment of protein sequences, is used to train a Random Forest to classify the lifestyle of a phage. Mavrich and Hatfull (2017) identified the temperate phages as those containing at least one temperate phage Pham (Mavrich and Hatfull, 2017). These two methods are based on protein sequence alignment, thus, the completely assembled phages sequences were needed before the usage of their methods. Nowadays, metavirome studies using high throughput sequencing technology can generate massive amounts of short read sequences from virus genomes (Lecuit and Eloit, 2013; Wylie et al., 2013; Brum et al., 2015). However, assembly of these short reads were difficulty for the highly mosaic organization of virus genomes (Hendrix et al., 1999). So, metavirome studies could produce large amount of incomplete of fragments from viral genome which made the previous alignment-based methods could not been used for predicting the lifestyles.
Alignment-free methods based on the frequencies of k-mers (k-words or k-tuples) were widely used for genome and metagenome comparison as recently reviewed (Song et al., 2014; Zielezinski et al., 2017; Ren et al., 2018). A k-tuple is a short base fragment of length k on genomic sequences. The alignment-free dissimilarity measures, and , were firstly developed for comparing two long DNA sequences, and then, successfully applied in many other fields, including phylogenetic tree construction (Song et al., 2013), the comparison of metagenomic samples (Jiang et al., 2012; Liao et al., 2016; Song et al., 2019) and gene regulatory regions (Song et al., 2013), identification of horizontal gene transfer (Tang et al., 2018) and virus-host interactions (Ahlgren et al., 2017), and improving contig binning for metagenomes (Wang et al., 2017). Also, many other alignment-free methods have been developed and applicated in many fields, see the reviews (Zielezinski et al., 2017, 2019; Ren et al., 2018).
In this study, I have conducted a comprehensive evaluation of nine alignment-free dissimilarity measures over various k-mer lengths for classifying the lifestyles of phages. To evaluate prediction accuracy, I used a benchmark dataset of 1,562 phages genomes available at the National Center for Biotechnology Information (NCBI) for which the lifestyles were reported. Then, the 1,225 of the phages identified before 31/12/2013 were used for constructing the training models. The 337 of the phages identified between 1/1/2014 and 31/12/2016 were used for testing different alignment-free methods. Overall, the dissimilarity measure performed better than other dissimilarity measures for classifying the lifestyles of phages. The software is available at https://github.com/songkai1987/PhagePred.
Materials and Methods
Virus Databases
RefSeq genomes of phages infecting bacteria or archaea were downloaded from NCBI on 20/10/2019. The lifestyles for the 1,562 phages identified before 31/12/2016 were predicted in Mavrich and Hatfull (2017) (Mavrich and Hatfull, 2017). In the set of phages with a known lifestyle, there were 463 temperate phages and 1,099 lytic phages. The 1,225 phages identified before 31/12/2013 were used for constructing the training models (Supplementary Table 1). The 337 of the phages identified between 1/1/2014 and 31/12/2016 were used for testing different alignment-free dissimilarity measures (Supplementary Table 2). The 325 phages identified after 1/1/2017 were used for novel phages for testing (Supplementary Table 3). The lifestyles of these phages were predicted using the same methods in (Mavrich and Hatfull, 2017).
To mimic the phage contigs assembly from metagenomic data sets, the temperate and lytic phages genomic sequences were split into non-overlapping fragments with length L = 500, 1000, 3000, 5000, and 10,000 bp. Fragments were generated for phage genomes identified between 1 January 2014 and 31 December 2016 were used as testing sets (Table 1). To generate the evaluation datasets with the same proportion of temperate and lytic phage contigs, the same number of contigs were randomly sampled from the genomic sequences of lytic phage as the number of contigs from temperate phages.
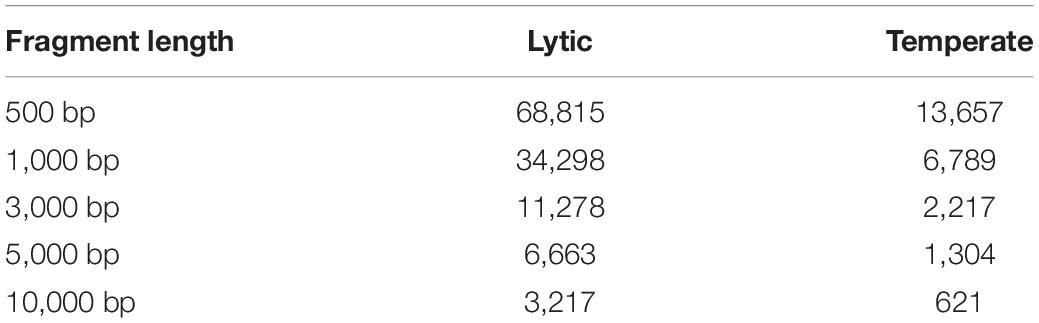
Table 1. The number of fragments generated from the lytic and temperate phage genomes discovered between 1 January 2014 and 31 December 2016.
Alignment-Free Dissimilarity Measures
Several alignment-free dissimilarity measures based on genomic oligonucleotide frequencies have been developed to infer the relationship between genomic sequences. Here, I studied nine alignment-free measures based on two different principles—those that consider background frequencies of k-mers and those that do not. First, the k-mer frequencies from the phage genomic sequences identified before 31 December 2013 were extracted and merged as two training sets for temperate and lytic phages, respectively. Then, for a contig, its k-mer frequencies were also extracted and used for calculating its distance to temperate and lytic k-mer frequencies for inferring its lifestyle. Several common methods are used to calculate the distance: Euclidean distance (Eu), Manhattan distance (Ma), Chebyshev distance (Ch), and d2 (Blaisdell, 1986). The background normalization methods, including , (Song et al., 2013), CVTree (Qi et al., 2004a,b), Teeling (Teeling et al., 2004), and EuF (Pride et al., 2006), which compute the expected k-mer frequencies to eliminate the effect of background and enhance the signal of differences between the viral sequences. These dissimilarity measures are described below.
Since a read could be from the forward or reverse strand of a genome, the read was considered together with its complement for calculating the occurrences of each k-mer. Thus, for a viral contig, all possible k-mers were calculated using a finite alphabet set S = {A,C,G,T}. For a given k-mer w, its occurrence in the contig is defined as Xw and the relative frequency of this k-mer is defined as . For a given k-mer w for temperate or lytic phages in training sets, its occurrence is defined as Yw.
Some dissimilarity measures, such as and , need an r-th order Markov model for the background sequence. The expected number of occurrences of word w = w1w2⋯wk, E(Xw), can be calculated using the Markov model. The transition probability matrix for the Markov model can be estimated based on the r-mers and (r-1)-mers, and the estimated probability of observing the k-mer w1w2⋯wr is PM(wr + 1|w1w2⋯wr) = Xw_1 w_2 ⋯w_r+1/Xw_1 w_2 ⋯w_r. Then, E(Xw) can be calculated as:
where L is the length of the contig. The difference between the occurrences of k-mer w and its expected occurrences is defined .
The Euclidean distance is defined as:
The Manhattan distance is defined as:
The Chebyshev distance is defined as:
The d2 dissimilarity measure is defined as:
The dissimilarity measure is defined as:
The dissimilarity measure is defined as:
The CVTree dissimilarity measure is defined as:
where , E(Xw) is estimated using a (k-2)-th order Markov model.
The Teeling dissimilarity measure is defined based on the (k-2)-th order Markov model:
where E(Xw) and var(Xw) for w = w1w2⋯wk can be calculated as:
The EuF dissimilarity measure is also defined based on the (k-2)-th order Markov model:
where , E(Xw) is estimated based on the (k-2)-th order Markov model as above.
Results
The framework of my method is given in Figure 1. To test the performance of different alignment-free dissimilarity measures, two separate sets of temperate and lytic phage sequences were used for training and testing: temperate and lytic phage genomes sequenced before 31 December 2013 for training (Supplementary Table 1), after 1 January 2014 and before 31 December 2016 for testing (Supplementary Table 2). In order to evaluate the ability of these measures for classifying novel viruses based on the previous sequenced phage genomes, date was used for parting the training and testing sequences. To mimic fragmented metagenomic sequences, phage genomes in testing sets were split into non-overlapping fragments of various lengths L = 500, 1000, 3000, 5000, and 10,000 bp (Table 1).
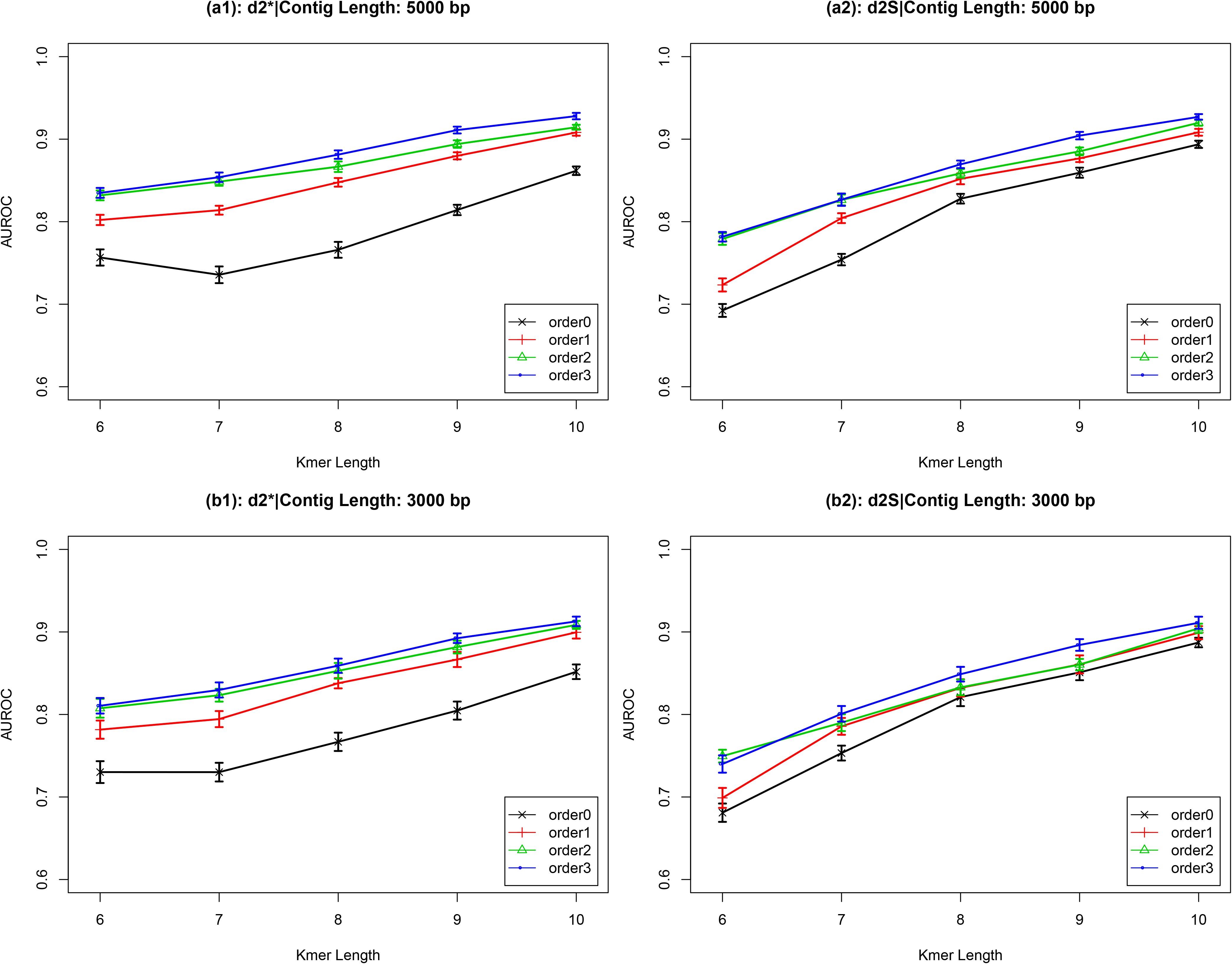
Figure 1. The work flow of my approach. First, the k-mer frequencies from two training sets of temperate and lytic phages were extracted, respectively. Then, the k-mer frequencies for a contig from new phage were extracted and used for calculating its distance to temperate and lytic k-mer frequencies for inferring its lifestyle.
The Effects of k-mer Length, Markov Order, and Contig Length
I used the temperate and lytic phages genomic sequences identified before 31 December 2013 to construct two k-mer frequency vectors, then calculated the distance (dissimilarity values) between a novel contig with these two k-mer frequency vectors. The ratio between the distance to temperate phages and to lytic phages which reflected the possibility of the contigs was temperate or not was calculated. The values lower than one indicated the contigs closer to the temperate phages and had higher possibility been from temperate phages. Then, the receiver operating characteristic (ROC) curves were used to evaluate and ’s performances for classification, while high values of the area under the ROC curves (AUROC) indicate good performance. For and , AUROC values increased as k-mer length increased (Figure 2 and Supplementary Figure 1). For contigs with length ≥1,000 bp, AUROC values also increased as the Markov order of background sequences increased. These two dissimilarity measures, and , had similar performance. For contigs with length ≥3,000 bp, the AUROC values were larger than 0.90 when the k-mer length was eight and Markov order was three. These high AUROC values demonstrate the strong ability of the and dissimilarity measures to correctly classifying newly obtained viral sequences. Based on these results, Markov order three was chosen for subsequent comparison with other alignment-free dissimilarity measures. To prove the validity of my proposed method, Supplementary Figure 2 showed that the distance of newly viral sequences to the temperate and lytic genomes.
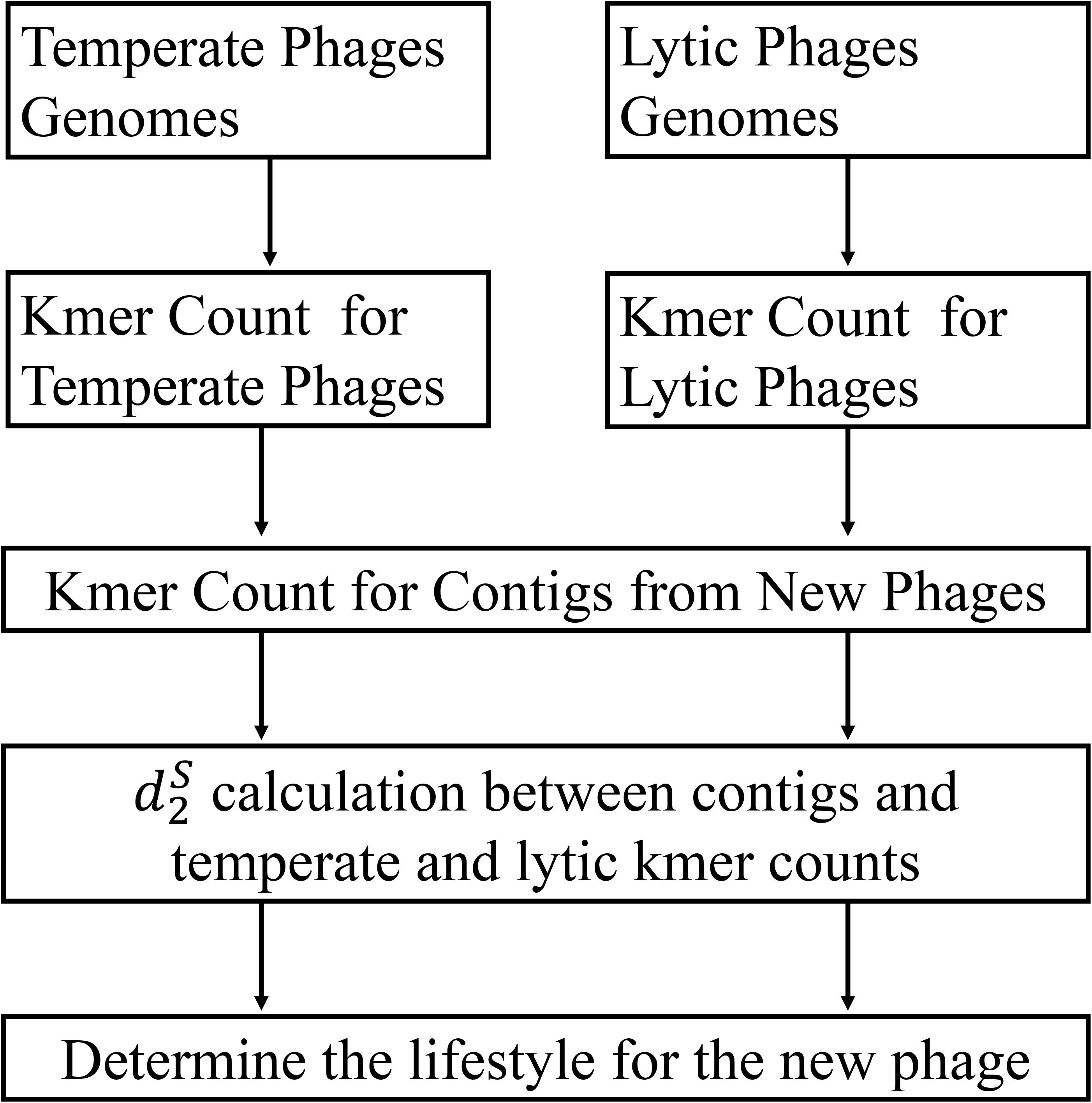
Figure 2. The AUROC values of and for classifying the lifestyles of phage contigs using k-mer lengths from 6 to 10, Markov order from 0 to 3, and contig lengths 5,000 bp (a) and 3,000 bp (b).
Comparison of These Alignment-Free Dissimilarity Measures’ Performance
I assessed the ability of the alignment-free dissimilarity measures, and , to correctly classify phage contigs in comparison to other alignment-free dissimilarity measures. All these measures were tested using the same set of evaluation contigs as above: equal numbers of contigs subsampled from temperate and lytic phage genomes identified after 1 January 2014 and before 31 December 2016. AUROC values were scored for each of these measures using k-mer lengths from 6 to 10 and contig lengths 500 – 10,000 bp (Table 2 and Supplementary Table 4). AUROC values generally increased for all the measures when k-mer length was increased from 6 to 10. For contigs with length ≥1,000 bp, both of and had highest AUROC values, thus, outperform other dissimilarity measures. For contigs with length = 500 bp, all these measures had much lower AUROC values. The measures, Manhatten, Euclidean and EuF, had similar or a little better AUROC values as and when the k-mer length 10 for contig length 500 bp.
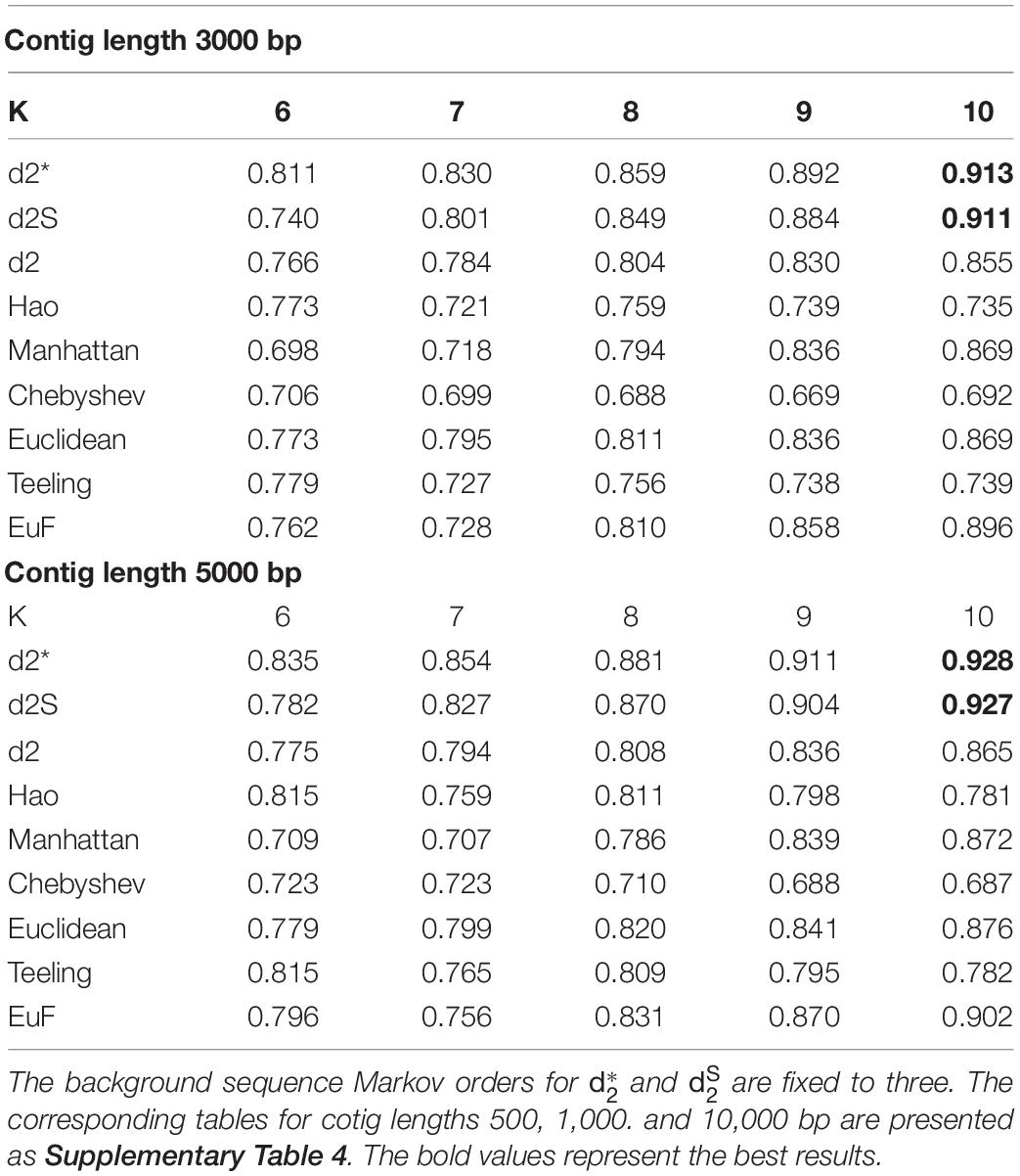
Table 2. The AUROC values of different dissimilarity measures for classifying the lifestyles of phage contigs using k-mer lengths from 6 to 10 and contig lengths 3,000 bp and 5,000 bp.
Sensitivity of and to Mutations
Because of the alignment-free dissimilarity measures relies on nucleotide k-mer frequency and there are errors in sequencing technologies, the sensitivity of our newly developed alignment-free dissimilarity measures, and , to mutations were tested. In Supplementary Figure 3, thirty replicates subsampled contigs with randomly inserted mutations at three different rates (0.001, 0.005, and 0.01) were used for comparing the performance with no mutations. The AUROC values were lower but not significantly for Markov order 0 and 1 at all the three different mutation rates. For Markov order 2 and 3, the AUROC values were only significantly lower at the highest rates of 0.01 mutations per bp (P-value < 0.01, t-test). As the sequencing error rates of Illumina and 454 platforms are ∼0.001 or 0.01, respectively (Glenn, 2011), sequencing errors only slightly impact the performance of the alignment-free dissimilarity measures for the NGS technologies.
Assessment of the Classification of Novel Phages
To assess the ability of these alignment-free dissimilarity measures to classify novel phages, the 136 phages (Supplementary Table 5) (18 temperate phages and 108 lytic phages, identified after 1 January 2014 and before 31 December 2016) that had no significant nucleotide similarity (blastn search, E-values < 10−5) to previously phages genome sequences were used for testing. I classify these novel phages according to their distance to the temperate and lytic trained k-mer frequencies. The True Positive Rates (TPR) for temperate and lytic phages and the accuracy of classification for these phages were scored for these alignment-free dissimilarity measures using k-mer lengths from 6 to 10. I only showed the results that the TPRs for temperate and lytic phages were both larger than 60%. Table 3 showed that the best classification result was obtained by using k-mer length of 10 and Markov order of three. could correctly predicted 12 (66.7%) of temperate phages and 95 (87.9%) of lytic phages. For other alignment-free dissimilarity measures, the best classification result was obtained by Euclidean (Eu) distance using k-mer length of 10. Euclidean distance correctly predicted 11 (61.1%) of temperate phages and 91 (84.3%) of lytic phages.
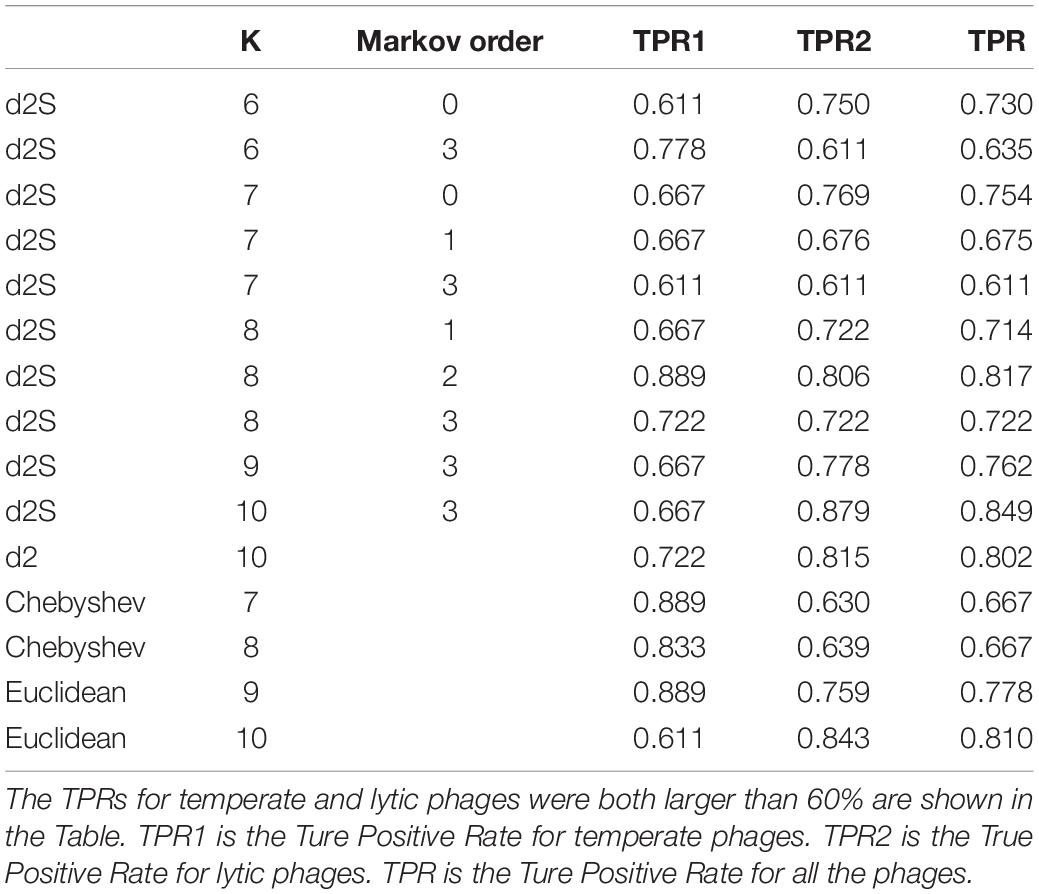
Table 3. The True Positive Rates (TPR) for classifying the lifestyles for the 108 phages without significant nucleotide similarity to previously phages genome sequences using different dissimilarity measures.
Application to Classification of Phages Identified After January 2017
The 325 phage genomes identified after 1 January 2017 were downloaded for analysis (Supplementary Table 3). The lifestyle of these phages were predicted used the same method in Mavrich and Hatfull, 2017 (Mavrich and Hatfull, 2017), then 72 temperate phages and 253 lytic phages were identified. These phages were used for assessing the classification accuracy of the alignment-free dissimilarity measures. Table 4 showed that the best classification result was obtained by using k-mer length of 10 and Markov order of three. could correctly predicted 64 (88.9%) of temperate phages and 197 (77.9%) of lytic phages. For other alignment-free dissimilarity measures, the best classification results were obtained by Teeling and Euclidean (Eu) using k-mer length of 10. The dissimilarity measure of Teeling correctly predicted 63 (87.5%) of temperate phages and 187 (73.9%) of lytic phages. Euclidean distance correctly predicted 63 (87.5%) of temperate phages and 186 (73.5%) of lytic phages.
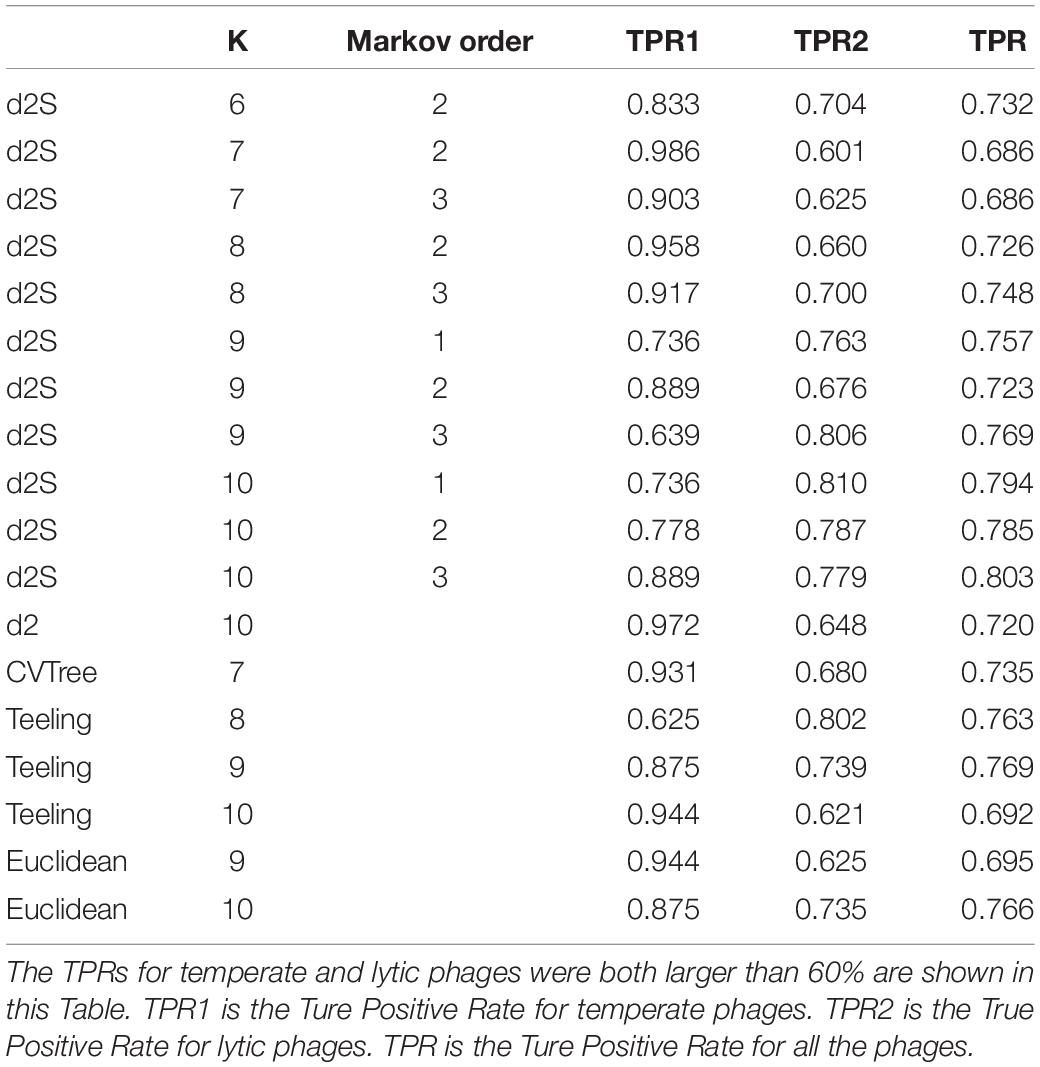
Table 4. The True Positive Rates (TPR) for classifying the lifestyles for the 325 phage genomes identified after 1 January 2017 using different dissimilarity measures.
To mimic fragmented metagenomic sequences, these virus genomes were split into non-overlapping fragments of various length L = 1000, 3000, and 5000 bp. Table 5 showed that the best classification result was also obtained by using k-mer length of 10 and Markov order of three for contigs with length = 5000 bp. could correctly predicted 665 (86.4%) contigs from temperate phages and 3441 (81.6%) contigs from lytic phages. For contigs with length = 1000 and 3000 bp, also got the best classification results using k-mer length of 10 and Markov order of 3 (Supplementary Tables 6,7).
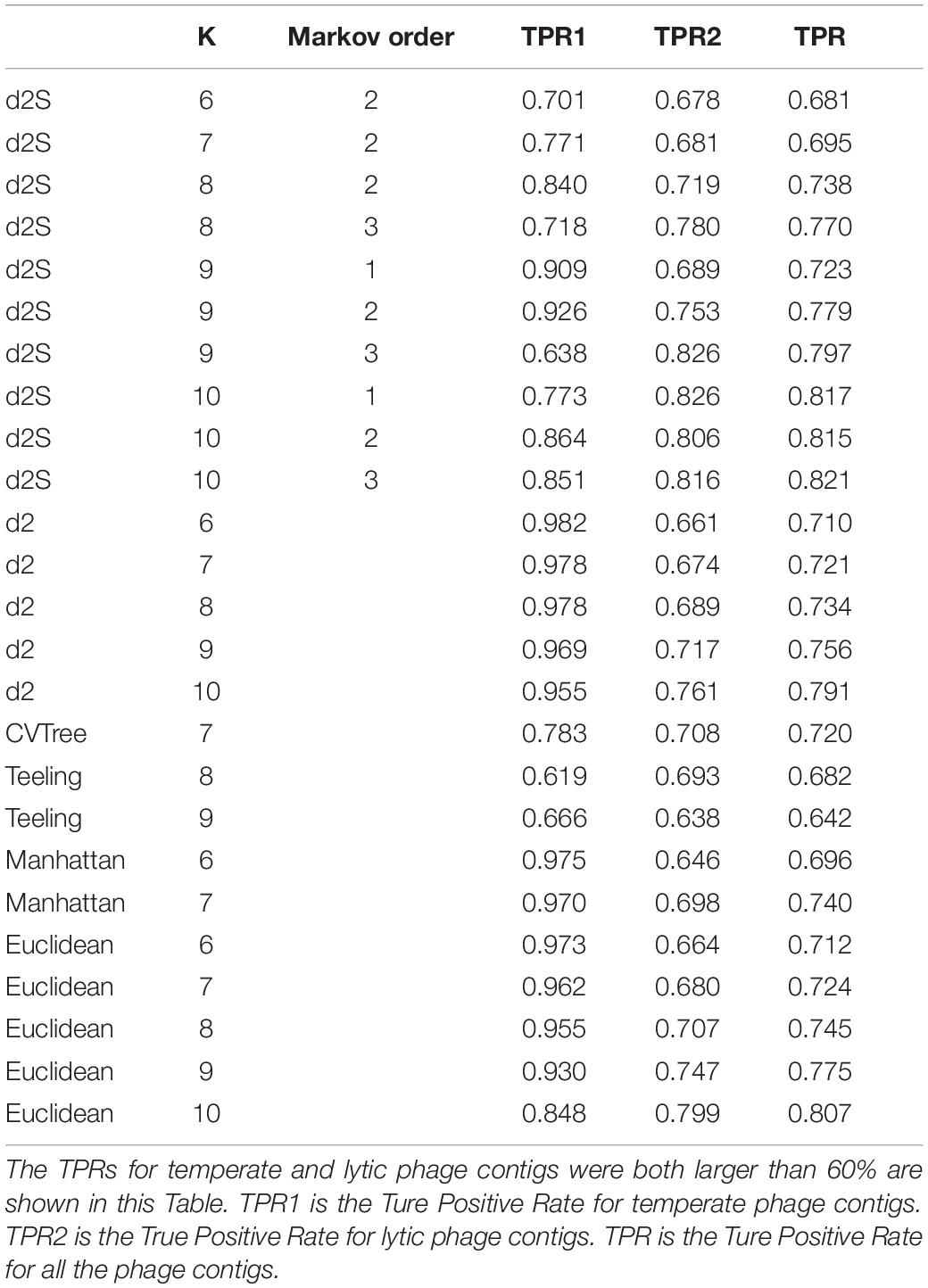
Table 5. The True Positive Rates (TPR) for classifying the lifestyles for contigs of 5,000 bp from the 325 phage genomes identified after 1 January 2017 using different dissimilarity measures.
Discussion
In this study, I have conducted a comprehensive evaluation of nine alignment-free dissimilarity measures over various k-mer lengths for classifying the lifestyles of phages. For these dissimilarity measures requiring a background model, different orders of Markov chains were used for estimating background k-mer frequencies. These alignment-free dissimilarity measures, with a wide range of choices of k-mer length and Markov orders, were compared using the simulated metagenomic fragments of different length. The dissimilarity measure, , could obtain the best performance for classifying the lifestyles of the phages contigs among these measures.
There are several limitations of the current study. First, for the dissimilarity measure, , could obtain well performance as using the evaluation of ROC values, however, the performance for to classify novel phage contigs according to the distance to the temperate and lytic k-mer frequencies was very bad. The distribution of ratios between the distance to temperate phages and the distance to lytic phages calculated by was skewed to larger than one which reflect the systematic deviation in predicting the lifestyles for this dissimilarity measure. The unequal number of temperate and lytic phage genomes used in training set maybe cause this deviation for . Second, the performance of these alignment-free dissimilarity measures depends on the phage genomes chosen in the training sets. In this study, I used the date as a criterion to split the phage genomes into training and testing sets. However, only less than two thousand phage genomes could be used in the study of these alignment-free measures which limits the accuracy of these methods. With the high-throughput sequencing technology widely used in viromics research, the assembled genomes for phages are becoming increasingly more available which would facilitate the development and application of these alignment-free dissimilarity measures. Third, the k-mer size k and orders of Markov models can markedly impact the performance of these alignment-free measures. In general, the k-mer size of 9 or 10 and Markov order of 2 or 3 for background sequences can give good performance. Since the viral genomes have great variability and highly mosaic organization, so longer length of k-mer and higher order of Markov chain can model the genomic sequences well. More studies are needed to see if this conclusion is robust for more phage genomes sequenced in the future.
In this study, I focused on classifying the lifestyles of phage contigs using alignment-free dissimilarity measures. Compared to alignment-based methods, the alignment-free methods can have better performance in classifying short contigs as a few kilobases without complete gene structure, however, alignment-free methods cannot give insights about the genome information responsible for the contigs. From this perspective, I can say that alignment-free and alignment-based methods for classifying phage contigs complement each other and should be used interactively for phage contigs classification.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
KS conceived of the project, developed the methods, performed the computations, and contributed to the final manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (grant number 11701546).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmicb.2020.567769/full#supplementary-material
References
Ahlgren, N. A., Ren, J., Lu, Y. Y., Fuhrman, J. A., and Sun, F. Z. (2017). Alignment-free d(2)(∗) oligonucleotide frequency dissimilarity measure improves prediction of hosts from metagenomically-derived viral sequences. Nucleic Acids Res. 45, 39–53. doi: 10.1093/nar/gkw1002
Blaisdell, B. E. (1986). A measure of the similarity of sets of sequences not requiring sequence alignment. Proc. Natl. Acad. Sci. U.S.A. 83, 5155–5159. doi: 10.1073/pnas.83.14.5155
Brum, J. R., Ignacio-Espinoza, J. C., Roux, S., Doulcier, G., Acinas, S. G., Alberti, A., et al. (2015). Patterns and ecological drivers of ocean viral communities. Science 348:1261498.
Chopin, A., Bolotin, A., Sorokin, A., Ehrlich, S. D., and Chopin, M. (2001). Analysis of six prophages in Lactococcus lactis IL1403: different genetic structure of temperate and virulent phage populations. Nucleic Acids Res. 29, 644–651. doi: 10.1093/nar/29.3.644
Glenn, T. C. (2011). Field guide to next-generation DNA sequencers. Mol. Ecol. Resour. 11, 759–769. doi: 10.1111/j.1755-0998.2011.03024.x
Hendrix, R. W., Smith, M. C. M., Burns, R. N., Ford, M. E., and Hatfull, G. F. (1999). Evolutionary relationships among diverse bacteriophages and prophages: all the world’s a phage. Proc. Natl. Acad. Sci. U.S. A. 96, 2192–2197. doi: 10.1073/pnas.96.5.2192
Jiang, B., Song, K., Ren, J., Deng, M. H., Sun, F. Z., and Zhang, X. G. (2012). Comparison of metagenomic samples using sequence signatures. BMC Genomics 13:730. doi: 10.1186/1471-2164-13-730
Knowles, B., Silveira, C. B., Bailey, B. A., Barott, K. L., Cantu, V. A., Cobianguemes, A. G., et al. (2016). Lytic to temperate switching of viral communities. Nature 531, 466–470.
Lecuit, M., and Eloit, M. (2013). The human virome: new tools and concepts. Trends Microbiol. 21, 510–515. doi: 10.1016/j.tim.2013.07.001
Liao, W., Ren, J., Wang, K., Wang, S., Zeng, F., Wang, Y., et al. (2016). Alignment-free transcriptomic and metatranscriptomic comparison using sequencing signatures with variable length markov chains. Sci. Rep. 6:37243.
Lima-Mendez, G., Toussaint, A., and Leplae, R. (2011). A modular view of the bacteriophage genomic space: identification of host and lifestyle marker modules. Res. Microbiol. 162, 737–746. doi: 10.1016/j.resmic.2011.06.006
Lima-Mendez, G., Van Helden, J., Toussaint, A., and Leplae, R. (2008). Reticulate representation of evolutionary and functional relationships between phage genomes. Mol. Biol. Evol. 25, 762–777. doi: 10.1093/molbev/msn023
Mavrich, T. N., and Hatfull, G. F. (2017). Bacteriophage evolution differs by host, lifestyle and genome. Nat. Microbiol. 2:17112.
McNair, K., Bailey, B. A., and Edwards, R. A. (2012). PHACTS, a computational approach to classifying the lifestyle of phages. Bioinformatics 28, 614–618. doi: 10.1093/bioinformatics/bts014
Pride, D. T., Wassenaar, T. M., Ghose, C., and Blaser, M. J. (2006). Evidence of host-virus co-evolution in tetranucleotide usage patterns of bacteriophages and eukaryotic viruses. BMC Genomics 7:8. doi: 10.1186/1471-2164-7-8
Proux, C., Van Sinderen, D., Suarez, J., Garcia, P., Ladero, V., Fitzgerald, G. F., et al. (2002). The dilemma of phage taxonomy illustrated by comparative genomics of Sfi21-like Siphoviridae in lactic acid bacteria. J. Bacteriol. 184, 6026–6036. doi: 10.1128/jb.184.21.6026-6036.2002
Qi, J., Luo, H., and Hao, B. L. (2004a). CVTree: a phylogenetic tree reconstruction tool based on whole genomes. Nucleic Acids Res. 32, W45–W47.
Qi, J., Wang, B., and Hao, B. L. (2004b). Whole proteome prokaryote phylogeny without sequence alignment: a K-string composition approach. J. Mol. Evol. 58, 1–11. doi: 10.1007/s00239-003-2493-7
Ren, J., Bai, X., Lu, Y. Y., Tang, K., Wang, Y., Reinert, G., et al. (2018). Alignment-free sequence analysis and applications. Annu. Rev. Biomed. Data Sci. 1, 93–114.
Rohwer, F., and Edwards, R. (2002). The phage proteomic tree: a genome-based taxonomy for phage. J. Bacteriol. 184, 4529–4535. doi: 10.1128/jb.184.16.4529-4535.2002
Song, K., Ren, J., Reinert, G., Deng, M. H., Waterman, M. S., and Sun, F. Z. (2014). New developments of alignment-free sequence comparison: measures, statistics and next-generation sequencing. Brief. Bioinform. 15, 343–353. doi: 10.1093/bib/bbt067
Song, K., Ren, J., and Sun, F. Z. (2019). Reads binning improves alignment-free metagenome comparison. Front. Genet. 10:1156. doi: 10.3389/fgene.2019.01156
Song, K., Ren, J., Zhai, Z. Y., Liu, X. M., Deng, M. H., and Sun, F. Z. (2013). Alignment-free sequence comparison based on next-generation sequencing reads. J. Comput. Biol. 20, 64–79. doi: 10.1089/cmb.2012.0228
Srinivasiah, S., Bhavsar, J., Thapar, K., Liles, M., Schoenfeld, T., and Wommack, K. E. (2008). Phages across the biosphere: contrasts of viruses in soil and aquatic environments. Res. Microbiol. 159, 349–357. doi: 10.1016/j.resmic.2008.04.010
Tang, K. J., Lu, Y. Y., and Sun, F. Z. (2018). Background adjusted alignment-free dissimilarity measures improve the detection of horizontal gene transfer. Front. Microbiol. 9:711. doi: 10.3389/fmicb.2018.00711
Teeling, H., Waldmann, J., Lombardot, T., Bauer, M., and Glöckner, F. O. (2004). TETRA: a web-service and a stand-alone program for the analysis and comparison of tetranucleotide usage patterns in DNA sequences. BMC Bioinformatics 5:163. doi: 10.1186/1471-2105-5-163
Wang, Y., Wang, K., Lu, Y. Y., and Sun, F. Z. (2017). Improving contig binning of metagenomic data using d(2)(S) oligonucleotide frequency dissimilarity. BMC Bioinformatics 18:425. doi: 10.1186/s12859-017-1835-1
Whitman, W. B., Coleman, D. C., and Wiebe, W. J. (1998). Prokaryotes: the unseen majority. Proc. Natl. Acad. Sci. U.S.A. 95, 6578–6583. doi: 10.1073/pnas.95.12.6578
Wylie, K. M., Weinstock, G. M., and Storch, G. A. (2013). Virome genomics: a tool for defining the human virome. Curr. Opin. Microbiol. 16, 479–484. doi: 10.1016/j.mib.2013.04.006
Zielezinski, A., Girgis, H. Z., Bernard, G., Leimeister, C.-A., Tang, K., Dencker, T., et al. (2019). Benchmarking of alignment-free sequence comparison methods. Genome Biol. 20:144.
Keywords: alignment-free dissimilarity measures, Markov model, lytic phages, contigs, temperate phages
Citation: Song K (2020) Classifying the Lifestyle of Metagenomically-Derived Phages Sequences Using Alignment-Free Methods. Front. Microbiol. 11:567769. doi: 10.3389/fmicb.2020.567769
Received: 30 May 2020; Accepted: 22 October 2020;
Published: 12 November 2020.
Edited by:
George Tsiamis, University of Patras, GreeceReviewed by:
Lin Wan, Academy of Mathematics and Systems Science (CAS), ChinaYing Wang, Xiamen University, China
Copyright © 2020 Song. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Kai Song, a3NvbmdAcWR1LmVkdS5jbg==; c29uZ2thaTE5ODdAMTI2LmNvbQ==
 Kai Song
Kai Song