- 1Natural Vision and Computation Team, Institut de la Vision, Paris, France
- 2Temasek Labs, National University of Singapore, Singapore
Pose estimation is a fundamental step in many artificial vision tasks. It consists of estimating the 3D pose of an object with respect to a camera from the object's 2D projection. Current state of the art implementations operate on images. These implementations are computationally expensive, especially for real-time applications. Scenes with fast dynamics exceeding 30–60 Hz can rarely be processed in real-time using conventional hardware. This paper presents a new method for event-based 3D object pose estimation, making full use of the high temporal resolution (1 μs) of asynchronous visual events output from a single neuromorphic camera. Given an initial estimate of the pose, each incoming event is used to update the pose by combining both 3D and 2D criteria. We show that the asynchronous high temporal resolution of the neuromorphic camera allows us to solve the problem in an incremental manner, achieving real-time performance at an update rate of several hundreds kHz on a conventional laptop. We show that the high temporal resolution of neuromorphic cameras is a key feature for performing accurate pose estimation. Experiments are provided showing the performance of the algorithm on real data, including fast moving objects, occlusions, and cases where the neuromorphic camera and the object are both in motion.
1. Introduction
This paper addresses the problem of 3D pose estimation of an object from the visual output of an asynchronous event-based camera if an approximate 3D model of the object is known (Lepetit and Fua, 2005). Current 3D pose estimation algorithms are designed to work on images acquired at a fixed rate by iteratively correcting errors in the focal plane until a correct estimate is found from a single image. Image acquisition is conventionally limited to the order of tens of milliseconds in real-time applications. Low frame rates usually restrict the ability to estimate robustly the pose of moving objects. Increasing the frame rate is often not a solution because the large amount of acquired data sets a limit to real-time computation. This real-time limitation is currently the bottleneck of several computer vision applications, where there is always a trade-off to find between frame rate and computational load.
A recent and evolving branch of artificial vision exploits the unique characteristics of a novel family of asynchronous frame-free vision sensors whose principle of operation is based on abstractions of the functioning of biological retinas (Delbrück et al., 2010). These event-based sensors acquire the content of scenes the changes in scenes asynchronously. Every pixel is independent and autonomously encodes visual information in its field of view into precisely timestamped events. As soon as change or motion is involved, which is the case for most machine vision applications, the universally accepted paradigm of visual frame acquisition becomes fundamentally flawed. If a camera observes a dynamic scene, no matter where the frame rate is set to, it will always be wrong. Because there is no relation whatsoever between dynamics present in a scene and the chosen frame rate controlling the pixel's data acquisition process, over-sampling or under-sampling will occur, and moreover both will usually happen at the same time. As different parts of a scene usually have different dynamic contents, a single sampling rate governing the exposure of all pixels in an imaging array will naturally fail to adequately acquire all these different simultaneously present dynamics.
Consider a natural scene with a fast moving object in front of static background, such as a pitcher throwing a baseball. When acquiring such a scene with a conventional video camera, motion blurring and displacement of the moving object between adjacent frames will result from under-sampling the fast motion of the ball, while repeatedly sampling and acquiring static background over and over again will lead to large amounts of redundant, previously known data that do not contain any new information. As a result, the scene is simultaneously under- and over-sampled. There is nothing that can be done about this sub-optimal sampling as long as all pixels of an image sensor share a common timing source that controls exposure intervals (such as a frame-clock).
Most vision algorithms, specially when dealing with dynamic input, have to deal with a mix of useless and bad quality data to deliver useful results, and continuously invest in power and resource-hungry complex processing to make up for the inadequate acquisition. This brute-force approach may however no longer be suitable in view of new vision tasks that ask for real-time scene understanding and visual processing in environments with limited power, bandwidth, and computing resources, such as mobile battery-powered devices, drones or robots.
The increasing availability and the improving quality of neuromorphic vision sensors open up the potential to introduce a shift in the methodology of acquiring and processing visual information in various demanding machine vision application (Benosman et al., 2011, 2012). As we will show, asynchronous acquisition allows us to introduce a novel computationally efficient and robust visual real-time 3D pose estimation method that relies on the accurate timing of individual pixels' response to visual stimuli. We will further show that asynchronous acquisition allows us to develop pose estimation techniques that can follow patterns at an equivalent frame rate of several kHz overcoming occlusions at the lowest computational cost. Processing can be performed on standard digital hardware and takes full advantage of the precise timing of the events.
Frame based stroboscopic acquisition induces massively redundant data and temporal gaps that make it difficult to estimate the pose of a 3D object without computationally expensive iterative optimization techniques (Chong and Zak, 2001). 3D pose estimation is a fundamental issue with various applications in machine vision and robotics such as Structure From Motion (SFM) (Snavely et al., 2007; Agarwal et al., 2011), object tracking (Drummond and Cipolla, 2002), augmented reality (Van Krevelen and Poelman, 2010) or visual servoing (Janabi-Sharifi, 2002; Janabi-Sharifi and Marey, 2010). Numerous authors have tackled finding a pose from 2D-3D correspondences. Methods range from simple approaches like DLT (Chong and Zak, 2001) to complex ones like PosIt (DeMenthon and Davis, 1995). There are two classes of techniques: iterative (DeMenthon and Davis, 1995; Kato and Billinghurst, 1999) or non-iterative (Chong and Zak, 2001; Lepetit et al., 2007). However, most techniques are based on a linear or non-linear system of equations that needs to be solved, differing mainly by the estimation techniques used to solve the pose equations and the number of parameters to be estimated.
Existing algorithms differ in speed and accuracy, some provide a fixed computation time independent of the number of points of the object (Lepetit et al., 2007). The DLT (Chong and Zak, 2001) is the simplest, slowest and weakest approach for estimating the 12 parameters in the projection matrix. However, it can be used to provide an initial estimate of the pose. PosIt (DeMenthon and Davis, 1995) is a fast method that does not use a perspective projection, but instead relies on an orthographic projection to estimate fewer parameters. The method was later extended (Oberkampf and DeMenthon, 1996) to take into account planar point clouds.
Recently, CamPoseCalib has been introduced (MIP, CAU Kiel, Germany, 2008), it is based on the Gauss-Newton method and non-linear least squares optimization (Araujo et al., 1996). Another way to solve the pose problem from point correspondences is known as the PnP (Perspective-n-Point) problem. It has been explored decades ago, readers can refer to Fischler and Bolles (1981), Lepetit et al. (2009). Other methods are based on edge correspondences (Harris, 1993; Drummond and Cipolla, 2002), or photometric information (Kollnig and Nagel, 1997).
This paper proceeds with an introduction to event-based vision sensors (Section 2.1), before describing our event-based 3D pose estimation algorithm (Section 2.2). In Section 3 we describe experiments and results obtained by our algorithm before concluding in Section 4.
2. Materials and Methods
2.1. Neuromorphic Silicon Retina
Event-based cameras are a new class of biomimetic vision sensors that, unlike conventional frame-based cameras, are not driven by artificially created clock signals. Instead, they transmit information about the visual scene in an asynchronous manner, just like their biological counterparts. One of the first attempts of incorporating the functionalities of the retina in a silicon chip is the work of Mahowald (1992) in the late eighties. Since then, the most interesting achievements in neuromorphic imagers has been the development of activity-driven sensing. Event-based vision sensors output compressed digital data in the form of events, removing redundancy, reducing latency, and increasing dynamic range when compared with conventional cameras. A complete review of the history and existing sensors can be found in Delbrück et al. (2010). The Asynchronous Time-based Image Sensor (ATIS; Posch et al., 2011) used in this work is an Address-Event Representation (AER; Boahen, 2000) silicon retina with 304 × 240 pixel resolution.
The ATIS output consists of asynchronous address-events that signal scene illuminance changes at the times they occur. Each pixel is independent and detects changes in log intensity larger than a threshold since the last emitted event (typically 15% contrast). As shown in Figure 1, when the change in log intensity exceeds a set threshold an ON or OFF event is generated by the pixel, depending on whether the log intensity increased or decreased. Immediately after, the measurement of an exposure/grayscale value is initiated, which encodes the absolute pixel illuminance into the timing of asynchronous event pulses, more precisely into inter-event intervals. The advantage of such a sensor over conventional clocked cameras is that only moving objects produce data. Thus, the amount of redundant information and the load of post-processing are reduced, making this technology particularly well-suited for high-speed tracking applications. Additionally, the timing of events can be conveyed with very low latency and accurate temporal resolution of 1 μ s. Consequently, the equivalent frame rate is typically several kHz. The encoding of log intensity of light change implements a form of local gain adaptation which allows them to work over scene illuminations that range from 2 lux to over 100 klux. When events are sent out, they are timestamped using off-chip digital components and then transmitted to a computer using a standard USB connection.
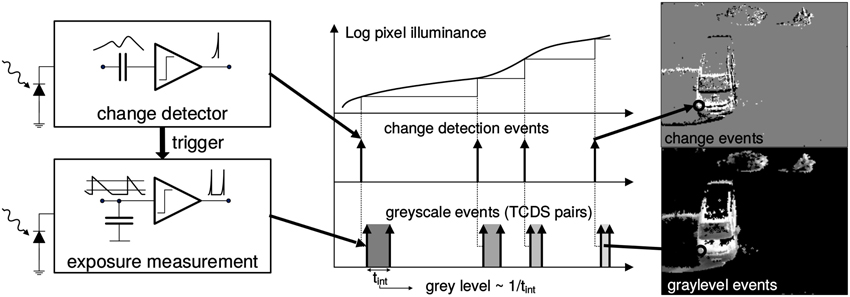
Figure 1. Functional diagram of an ATIS pixel (Posch et al., 2011). Two types of asynchronous events, encoding change (top) and illuminance (bottom) information, are generated and transmitted individually by each pixel in the imaging array when a change is detected in the scene. The bottom right image only shows grayscale of pixels for which illuminance has recently been measured. Black pixels indicate locations where illuminance has not been measured recently.
The present algorithm estimates 3D pose using only change detector events. The corresponding stream of events can be mathematically described in the following way: let be a quadruplet describing an event occurring at time tk at the position on the focal plane. The two possible values for the polarity, pk, are 1 or −1, depending on whether a positive or negative change of illuminance has been detected.
2.2. Event-Based 3D Pose Estimation
In the first two subsections below we formulate the 3D pose estimation problem and describe the notation we use for 3D rotations. In the subsequent two subsections we describe how we match incoming visual events to edge projections on the focal plane, and how we then match these events to the 3D locations of points on the object. Finally, in the fifth subsection below we describe how we update our model of the object's 3D pose using these event-based correspondences.
2.2.1. Problem Formulation
Let us consider a moving rigid object observed by a calibrated event-based camera. The movement of the object generates a stream of events on the focal plane of the camera. Attached to this object is a frame of reference, known as the object-centered reference frame, whose origin we denote as V0. The pinhole projection maps 3D points V expressed in the object-centered reference frame into υ on the camera's focal plane (see Figure 2), according to the relation:
Here, K is the 3 × 3 matrix defining the camera's intrinsic parameters—obtained through a prior calibration procedure— while T ∈ ℝ3 and R ∈ SO(3) are the extrinsic parameters. The sign ~ indicates that the equality is defined up to a scale (Hartley and Zisserman, 2003). (T, R) are also referred to as the relative pose between the object and the camera (Murray et al., 1994). As the object moves, it is only the pose which changes and needs to be estimated.

Figure 2. The object is described as a set of vertices {Vi}, whose corresponding projections on the focal plane are denoted as {vi}. An edge defined by vertices Vi, Vj is noted εij. If an event ek has been generated by a point Vi of the model, then Vi must lie on the line of sight of the event, which is the line passing through the camera center and the position of the event on the focal plane uk. When that happens, the projection of the point vi is guaranteed to be aligned with the event.
An estimation of the pose can be found by minimizing the orthogonal projection errors on the line of sight for each 3D point, as illustrated by Figure 2. Thus, we minimize a cost function directly on the 3D structure rather than computing it on the image plane (Lu et al., 2000). The advantage of this approach is that a correct match of the 3D points leads to a correct 2D projection on the focal plane, but the reverse is not necessarily true.
The high temporal resolution of the camera allows us to acquire a smooth trajectory of the moving object. We can then consider each event generated by the moving object as relatively close to the previous position of the object. Since the event-based camera detects temporal contours, all moving objects can be represented by a set of vertices and edges. We can then set the following convention: let {Vi} be the set of 3D points defining an object. These 3D points are vertices and their projections onto the retina focal plane are noted as υi. The edge defined by vertices Vi, Vj is noted as εij. Figure 2 shows a general illustration of the problem.
Using the usual computer graphics conventions (O'Rourke, 1998; Botsch et al., 2010), an object is described as a polygon mesh. This means that all the faces of the model are simple polygons, triangles being the standard choice. The boundaries of a face are defined by its edges.
2.2.2. Rotation Formalisms
A convenient parametrization for the rotation is to use unit quaternions (Murray et al., 1994). A quaternion is a 4-tuple, providing a more efficient and less memory intensive method of representing rotations compared to rotation matrices. It can be easily used to compose any arbitrary sequence of rotations. For example, a rotation of angle ϕ about rotation axis r is represented by a quaternion q satisfying:
where r is a unit vector. In what follows, we will use the quaternion parametrization for rotations.
When trying to visualize rotations, we will also use the axis-angle representation, defined as the rotation vector ϕr.
2.2.3. 2D Edge Selection
The model of the tracked object and its initial pose are assumed to be known. This allows us to virtually project the model onto the focal plane as a set of edges. For each incoming event ek occurring at position on the image plane, we are looking for the closest visible edge. Thus, for every visible edge εij, projected on the focal plane as the segment [υi, υj], we compute dij(uk), the euclidean distance from uk to [υi, υj] (see Figure 3). To compute this distance, uk is projected onto the line defined by [υi, υj]. If this projection falls inside of the segment [υi, υj], then the distance is given by the generic expression:
where × is the cross product. If the projection is not inside [υi, υj], then dij(uk) is set to be equal to the distance between uk and the closest endpoint.
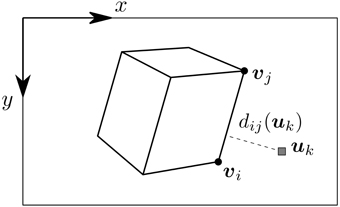
Figure 3. Edge selection for an event ek occurring at uk. The distance of uk to each visible edge εij is computed as dij(uk), the euclidean distance between uk and the segment defined by the projected edge [vi, vj].
We set a maximum allowed distance for the event to be assigned to an edge as dmax. The edge to which the event is assigned to is εnm such that:
assuming dnm(uk) ≤ dmax, otherwise the event is considered as noise and discarded.
Remark 1: In complex scenarios, the 2D matching step can be further strengthened by applying more refined criteria. We implement a 2D matching based on Gabor events, which are oriented events generated by events lying on a line (Orchard et al., 2015). When the 2D matching is performed using this technique, a Gabor event will only be assigned to a visible edge if the angle of the event and the angle formed by the edge are close enough. An example of application of this method will be shown in the experiments, where pose estimation is performed even with partial occlusions and egomotion of the camera.
Remark 2: This section assumes that the visibility of the edges is known. This is done via a Hidden Line Removal algorithm (Glaeser, 1994) applied for each new pose of the model.
2.2.4. 3D Matching
Once εnm is determined, we need to look for the point on the edge that has generated the event. The high temporal resolution of the sensor allows us to set this point as the closest to the line of sight of the incoming event. Performing this matching between an incoming event in the focal plane and a physical point on the object allows to overcome issues that appear when computation is performed directly in the focal plane. The perspective projection on the focal plane is neither preserving distances nor angles, i.e., the closest point on the edge in the focal plane is not necessarily the closest 3D point of the object.
The camera calibration parameters allow us to map each event at pixel uk to a line of sight passing through the camera's center. The 3D matching problem is then equivalent to a search for the smallest distance between any two points lying on the object's edge and the line of sight.
As shown in Figure 4, let Ak be a point on the line of sight of an incoming event ek located at uk in the focal plane. Let Bk be a point on the edge εnm that has been computed as being at a minimal distance from the line of sight passing through uk. We can assume ek to be generated by a 3D point on the moving object at the location Ak, that was at Bk before ek occurred. This hypothesis is reasonable as due to the high temporal resolution events are generated by small motions. Finding Ak and Bk is the scope of the 3D matching step.
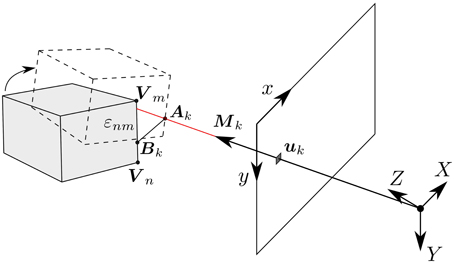
Figure 4. Geometry of the 3D matching problem: an event ek at position is generated by a change of luminosity in the line of sight passing through the event, defined by the vector Mk. Ak is a point on the line of sight and Bk a point on the edge εnm, such that the minimum distance between these two lines is reached. Finding Ak and Bk is the objective of the 3D matching step.
Let Mk be the vector defining the line of sight of ek, it can be obtained as:
Ak and Bk can therefore be expressed as:
where α1 and α2 are two real valued parameters.
Let εnm = Vm − Vn, we are looking for solutions such that (Ak − Bk) is perpendicular to both εnm and Mk. Hence, we obtain the following equation:
Solving this equation for α1 and α2 provides both Ak and Bk. The solution to this system is discussed in the Appendix.
We also set a maximum 3D distance between Ak and Bk, denoted Dmax. If the distance between Ak and Bk is larger than this value we discard the event.
2.2.5. Rigid Motion Estimation
Knowing Bk and Ak allows us to estimate the rigid motion that transforms Bk into Ak. We define two strategies: the direct estimation of the required transformation for every incoming event and the computation using an estimation of the velocity.
Direct Transformation
The rigid motion is composed of a translation ΔTk and a rotation Δqk around V0, the origin of the object-centered reference frame.
Let us define the scaling factor λT such that ΔTk is related to the vector Ak − Bk as:
where (Ak − Bk) is the translation that makes Bk coincide with Ak. Here, m is a multiplier that allows us to set the scaling factor independently for the Z axis. The need for this extra degree of freedom can be justified because changes in the depth of the object will only become apparent through changes in the x or y position of the events on the image plane. Consequently, the system does not react in the same way to changes in depth as it does to changes in the X or Y position, resulting in a different latency for the Z axis. m is then a tuning factor that will be set experimentally.
The rotation around V0 is given by a unit quaternion Δqk of the form:
where hk is a unit vector collinear to the axis of rotation and λθθk is equal to the rotation angle, that we conveniently define as a product between a scaling factor λθ and the angle θk defined below.
If πk is the plane passing through Bk, Ak and V0 (see Figure 5A) such that hk is the normal, then hk can be computed as:
We define θk as the angle between (Bk − V0) and (Ak − V0), as shown in Figure 5B.
In the case of Ak, Bk and V0 alignment If Ak, Bk and V0 are aligned, hk is undefined. This happens when no rotation is applied or when the rotation angle is equal to π. This last case is unlikely to occur because of the small motion assumption.
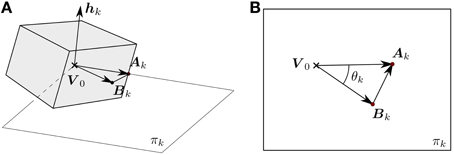
Figure 5. (A) πk represents the plane defined by Ak, Bk and the origin of the object-centered reference frame V0. The desired rotation is contained in this plane, and thus the rotation axis hk is normal to it. (B) Normal view to πk. Both (Bk − V0) and (Ak − V0) are contained in this plane, and thus their cross product gives us the axis of rotation. The angle θk between these two vectors is equal to the rotation angle that makes Bk and Ak coincide.
Finally, the pose of the model is updated incrementally according to:
For the rest of the paper, this described procedure will be referred to as the direct transformation strategy.
Remark 1: Once the pose is updated, the next step is to update the transformation between the object and the camera. This is a computationally expensive process that requires transforming the 3D points, projecting them onto the image plane and applying the hidden-line removal algorithm. Consequently, in order to increase the performance of the system, we do not apply the transformation for every incoming event, but every N events. N is experimentally chosen, and its effect on the algorithm discussed in the experiments section.
Remark 2: λT and λθ are set experimentally, and they should always be equal or smaller than one. When they are smaller than one, we do not fully transform the model so that Bk matches Ak for every event. Instead, we apply a small displacement for each incoming event. Here, it is important to keep in mind that a moving edge generates more than one event. This number and the frequency of events are proportional to the local contrast.
Velocity Estimation
We make an additional hypothesis on the motion smoothness which assumes the velocity of the object does not change abruptly. This hypothesis allows us to update the velocity only after every N events. Due to the high temporal resolution and the asynchronous nature of the neuromorphic camera, we consider this to be, in general, a reasonable assumption.
For an incoming event ek, let be the cumulative translation of the estimates from the last N events:
where ΔTi is equal to the translation for the ith event, computed using (9) with λT = 1. Let us note that here, ΔTi are not displacements to be applied to the model. Instead, we are using them to compute the cumulative translation for the last N events, that we will later use to estimate the mean linear velocity during that period. This fact justifies the choice of making λT = 1.
Analogously, let be the quaternion of the resulting rotation associated with the last N events:
where the quaternions Δqi are computed using (10) with λθ = 1, for the same reason as above.
From these cumulative translation and rotation, we define νk and ωk, the mean linear and angular velocities for the last N events:
and
where Δt = tk − tk − N.
Equations (17) and (18) have these forms because moving edges generate a certain number of events with the same timestamp, and the estimated pose is updated every N events. We can then consider the last N events to correspond to the same small motion. Consequently, the mean linear velocity is computed as the mean displacement over the corresponding time interval Δt. The same explanation holds for .
The velocities are finally updated every N events according to the following expressions:
where λν and λω are update factors, that will be set experimentally. Finally, the translation estimated for the model is computed as:
and the rotation is deduced from the angular velocity vector with the axis being ωk∕∥ωk∥ and the angle Δt∥ωk∥. This is represented by the unit quaternion Δqk:
Next, we update the pose of the model, which is only updated every N events when applying this strategy:
We will refer to this way of computing the transformation as the velocity estimation strategy. The general algorithm for both methods is given below (Algorithm 1).
3. Results
In this section we present experiments to test 3D pose estimation on real data1. The first two experiments estimate the pose of a moving icosahedron and house model while viewed by a static event-based sensor. In Section 3.3 we estimate the pose of the icosahedron from the view of a moving event-based sensor in a scene containing multiple moving objects. In Section 3.4 we estimate the pose of the icosahedron under high rotational velocity (mounted on a motor). Finally, in Section 3.5 and Section 3.6 we investigate how temporal resolution affects pose estimation accuracy, and how implementation parameters affect the time required for computation.
In what follows, we will denote the ground truth as {T, q} and the estimated pose as {T*, q*}.
The algorithm is implemented in C++ and tested in recordings of an icosahedron—shown in Figure 6A—and the model of a house—Figure 6B—freely evolving in the 3D space. We set the following metrics on ℝ3 and SO(3):
• The absolute error in linear translation is given by the norm of the difference between T* and T. For a given recording, let be the mean displacement of the object, where K is the total number of events. We define ξT the relative error as:
• For the rotation, the error is defined with the distance d between two unit quaternions q and q*:
which is proven to be a more suitable metric for SO(3), the space spanned by 3D rotations (Huynh, 2009). It takes values in the range . Thus, let ξq be the relative rotation error:
The algorithm provides an instantaneous value of the errors for each incoming event. In order to characterize its accuracy, we will consider and , the temporal mean of the errors for the whole duration of a given recording.

Figure 6. Real objects used in the experiments. (A) White icosahedron with black edges, used in the first experiment. (B) Non-convex model of a house with cross markers on its faces, used in the second experiment.
3.1. Icosahedron
The icosahedron shown in Figure 6A is recorded by an ATIS sensor for 25 s while freely rotating and moving. The 3D model is a mesh of 12 vertices and 20 triangular faces.
The ground truth is built from frames output from the event-based camera. We have manually selected the image position of the visible vertices every 100 ms and applied the OpenCV implementation of the EPnP (Efficient Perspective-n-Point) algorithm (Lepetit et al., 2009) to estimate the pose. In Lepetit et al. (2009), the authors test the robustness of their algorithm to gaussian noise perturbations on the focal plane. It is important to outline that this is a theoretical disturbance model. They are not assessing their algorithm's performance with real noisy data. Based on their noise model results, we can give an order of magnitude of the ground truth accuracy. Assuming that the manual annotation of the vertices of the icosahedron has at least 2 pixels precision, we can read the pose error from the error curves (Figure 5 in Lepetit et al., 2009), that is at most 2 %.
The intermediate positions are obtained by linear interpolation, and the intermediate rotations using Slerp (spherical linear interpolation Shoemake, 1985). From the ground truth we compute the model's linear velocity ν and the angular velocity ω. In this recording, the linear speed ∥ν∥ reaches a maximum of 644.5 mm/s, while the angular speed ∥ω∥ starts with a maximum of 2.18 revolutions per second at the beginning of the recording and then continuously decreases.
After several trials, the thresholds are set experimentally to values giving stable and repeatable pose estimations. These are: dmax = 20 pixels and Dmax = 10 mm. The remaining tuning parameters are experimentally chosen for each experiment as the ones giving the smallest sum of the mean relative estimation errors and . The update factors λT, λθ, λν, λω are always taken between 0.001 and 0.4, a large range in which the algorithm has proven to yield stable results.
Figure 7A shows the results when applying the direct transformation strategy with λT = 0.4, λθ = 0.2, N = 1 and m = 2. We show the translation vector T as well as the rotation vector ϕr. Plain curves, representing estimation results, are superimposed with dashed lines indicating the ground truth. Snapshots, showing the state of the system at interesting instants are shown. They provide the projection of the shape on the focal plane using the estimated pose.
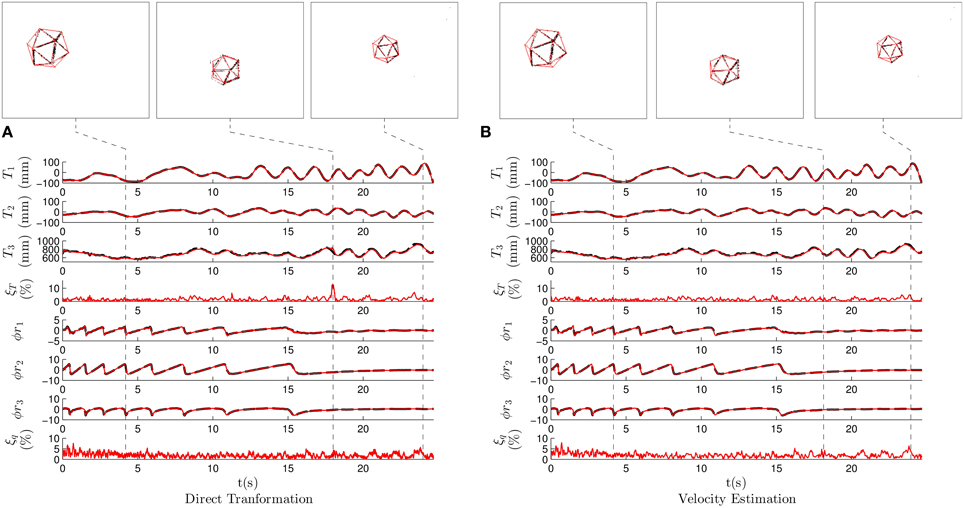
Figure 7. Results for the first experiment, where we recorded an icosahedron freely evolving in the 3D space. T1, T2, and T3 are the components of the translation vector T, and ϕr1, ϕr2, ϕr3 the components of the axis-angle representation of the rotation ϕr. The dashed lines represent ground truth, while the solid curves represent estimated pose. The snapshots on the top show the state of the system in some characteristic moments, with the estimation made by the algorithm printed over the events. (A) Results when applying the direct transformation strategy, with λT = 0.4, λθ = 0.2, N = 1 and m = 2. (B) Results when applying the velocity estimation strategy with λν = 0.05, λθ = 0.006, N = 5 and m = 10. We verify that the estimation and the ground truth are coincidental most of the time, allowing us to conclude that pose estimation is in general correctly performed.
We verify that plain and dashed lines (representing estimated and ground truth poses respectively) coincide most of the time, showing that the pose estimation is in general correctly performed. Experiments provide the following mean estimation errors: for the translation, and for the rotation. Instantaneous errors reach a local maximum, as a consequence of the large values chosen for λT and λθ. These parameters being gains, large values imply an oscillatory behavior around the correct pose parameters. We include in Figure 7A a snapshot showing the state of the system at this instant, where we observe that the estimation is slightly displaced from the true pose. However, even when considering this local maximum, the estimation errors remain below 15%. The system is always capable of recovering the correct pose.
Figure 7B shows the results when applying the velocity estimation strategy with λν = 0.05, λθ = 0.006, N = 5 and m = 10. The estimation of the pose is accurate: and 2.04%. The mean errors obtained are very similar to the ones produced in the case of the direct transformation strategy. However, when we analyze the instantaneous errors, we do not observe a large local maxima as in the previous case. The velocity estimation strategy assumes that the velocity of the object does not change abruptly, and consequently, the estimated motion is smoother. This constitutes the main advantage of the velocity strategy over the previous one. This will be further outlined in the following experiment.
The output of the algorithm for this experiment can be seen in Supplementary Video 1, where the results produced by both strategies are shown.
3.2. House
This experiment tests the accuracy of the algorithm using a more complex model of a house shown in Figure 6B. The object is recorded for 20 s while freely rotating and moving in front of the camera. The 3D model is composed of 12 vertices and 20 triangular faces. We compute velocities from the ground truth obtained from generated frames as was done with the icosahedron. In this case, the linear speed reaches a maximum of 537.4 mm/s, while the angular speed starts with a maximum of 1.24 revolutions per second at the beginning of the experiment and then continuously decreases.
As in the previous case, we experimentally choose the set of parameters that produces the minimum sum of errors. Figure 8A shows the results when applying the direct transformation strategy with λT = 0.2, λθ = 0.05, m = 1 and N = 10. We verify that there is a coherence between the ground truth and the estimated pose showing that the pose estimation is in general correctly estimated. However, in this case we observe a larger local maxima reaching values as high as 20%. These local maxima degrade the overall performance, they provide the following values for the mean estimation errors: for the translation and for the rotation, higher than in the previous case. Nevertheless, the system is always capable of recovering the correct pose after these maxima, and the mean estimation errors remain acceptable.
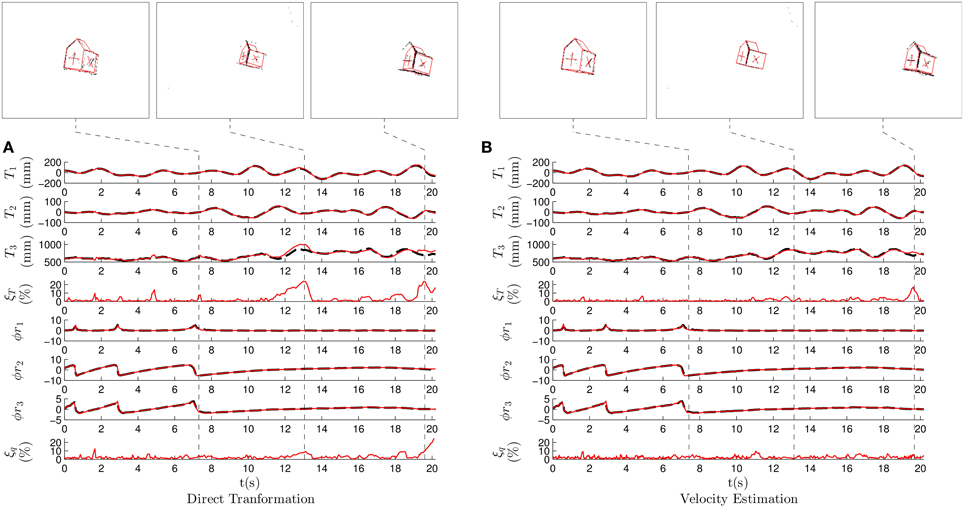
Figure 8. Results for the second experiment, where we recorded a non-convex model of a house freely evolving in the 3D space. (A) Translation and rotation results when applying the direct transformation strategy. (B) Translation and rotation results when applying the velocity estimation strategy.
In this recording, local maxima mostly occur because of the algorithm mistakenly interpreting the cross markers as edges or viceversa. This usually happens when a given face is almost lateral with respect to the camera. In that case, it provides the projection of these lines very close to each other. The negative effect of these ambiguous poses is difficult to mitigate when applying this strategy.
Figure 8B shows the results when the velocity estimation strategy is applied with λν = 0.4, λω = 0.0125, m = 4 and N = 5. As in the previous experiment, we verify that the effect of the local maxima is reduced when applying this strategy. This results in the following errors: and , clearly outperforming the direct transformation strategy. We verify that in the case of complex objects and ambiguous poses, using an estimation of the velocity provides more robust results. In this case, the small value for λω makes the angular velocity very stable, preventing the estimation from rapidly switching from one pose to another. It also reduces the negative effect of the ambiguous poses.
Pose estimation is accurate in both the presented cases, but the velocity estimation strategy provides more stable results. Results produced by both strategies when treating this recording are shown in Supplementary Video 2.
3.3. 2D Matching Using Gabor Events
In this experiment we test pose estimation in a more complex scenario, with egomotion of the camera and partial occlusions of the object, using Gabor events for the 2D matching step. A hand-held icosahedron is recorded for 20 s while the camera moves. Ground truth is obtained from reconstructed frames as in the previous experiments.
The parameters for the Gabor events' generation process are set as in Orchard et al. (2015), and the maximum angular distance for an event to be assigned to an edge is set as 0.174 rad (obtained as , where 12 is the number of different orientations that the Gabor events can take). The tuning parameters are experimentally chosen as in previous experiments.
Figure 9A shows the evolution of the errors when applying the direct transformation strategy, with λT = 0.4, λθ = 0.2, N = 5 and m = 4 (we do not show T or ϕr in order to lighten the figures). We verify that the estimation errors remain low for the whole recording, always below 10%.
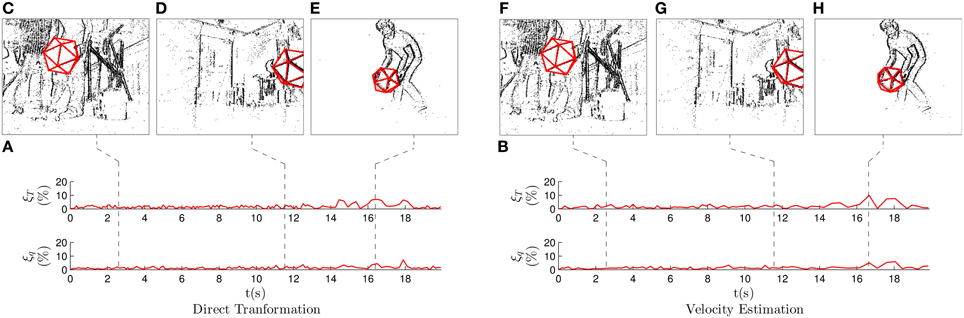
Figure 9. Results for the third experiment, where we recorded a hand-held icosahedron while the camera moved to follow it. Snapshots show the state of the system at some characteristic moments. (A) Translation and rotation errors when applying the direct transformation strategy. The errors remain low, always below 10%. (B) Translation and rotation errors when applying the velocity estimation strategy. (C–H) Snapshots showing the state of the system. We observe a large number of events produced by the egomotion of the camera. However, pose estimation is correctly performed.
Figure 9C shows the state of the system while the camera is moving: as we can see, the number of events is much higher in this case, as a result of the camera not being static. Consequently, most of these events are not generated by the tracked object, but rather by other visible edges in the scene. However, we verify that pose estimation is correctly performed, since the errors remain low and the projection of the estimation is coincidental with the position of the events. In Figure 9D we can see how pose estimation is performed even when a fraction of the icosahedron has left the field of view of the camera. Figure 9E shows one of the instants in which the errors reach their highest values. This happens when the object is at its furthest position from the camera, and thus when we are less precise (a pixel will represent a larger 3D distance when points are further away from the camera). However, even at this moment errors remain below 10% and the projection of the estimation is almost coincidental with the events. We conclude that pose estimation is correctly performed even in this complex scenario, providing the following mean values for the estimation errors: and .
Figure 9B shows the evolution of the errors for the whole experiment when applying the velocity estimation strategy, with λν = 0.2, λω = 0.4, N = 10 and m = 8. The obtained results are very similar to those of the direct transformation, and the mean errors take the following values: and . Figures 9F–H display the output of the system at the same instants as for the previous strategy, showing very similar results. As in the first experiment, we verify that in the case of simple objects without ambiguous positions, keeping an estimation of the velocity does not provide any advantage.
This experiment shows how the method can perform pose estimation even in complex scenarios, by simply adding some additional criteria for the matching of events. The corresponding results are displayed in Supplementary Video 3. In this case, the video depicts the whole 3D scene, showing the motion of both the camera and the tracked object.
3.4. Fast Spinning Object
In order to test the accuracy of the algorithm with fast moving objects, we attached the icosahedron to an electric brushless motor and recorded it at increasing angular speeds. As shown in Figure 10, the icosahedron is mounted on a plane with four dots, used for ground truth. These four points are tracked using the Spring-Linked Tracker Set described in Reverter Valeiras et al. (2015).

Figure 10. Experimental set-up for the fast spinning experiment. An icosahedron is attached to a brushless motor and recorded by the event-based camera. The four dots on the plane are used for ground truth.
Through electronic control of the motor, we created four sections during which the angular speed is approximately constant. From the obtained ground truth, we can estimate the corresponding velocities ν and ω. We obtain a maximum angular speed of 26.4 rps.
The estimation errors are, for an experimentally selected optimal set of parameters: , for the direct transformation strategy, and , for the velocity estimation strategy. The velocity estimation strategy provides in this case provides less accurate results. This is due to the large angular acceleration (even if the angular speed remains approximately constant, the object is not perfectly aligned with the axis of the motor, and thus the rotation axis changes constantly). However, the mean values for the errors are low enough to conclude that, in general, the pose is correctly estimated even for objects moving at high velocity.
The results produced by the algorithm when tracking the fast spinning icosahedron are shown in Supplementary Video 4. In the video, we gradually slow down the display, allowing us to appreciate the true motion of the icosahedron. Let us note that this video was created at 25 fps, causing what is known as the wagon-wheel illusion. Thus, until the video is played 8 times slower than real time we do not appreciate the true direction of the rotation.
3.5. Degraded Temporal Resolution
In order to test the impact of the acquisition rate and to emphasize the importance of the high temporal resolution on the accuracy of our algorithm, we repeated the previous experiment progressively degrading the temporal resolution of recorded events. To degrade the temporal resolution, we select all the events occurring within a given time window of size dt and assign the same timestamp to all of them. If several events occur at the same spatial location inside of this time window, we only keep a single one. We also shuffle the events randomly, since the order of the events contains implicit high temporal resolution information. Figure 11A shows, in semi-logarithmic scale, the evolution of both the mean relative translation error and the mean relative rotation error with the size of the time window when tracking the fast spinning icosahedron applying the direct transformation strategy, with a fixed set of tuning parameters taken from the previous step. We only plot errors between 0 and 20%, since we consider the estimation to be unsuccessful for errors above 20%. The errors remain approximately stable until the time window reaches 1 ms. This can be explained because the small motion assumption is experimentally satisfied for time windows of 1 ms for the typical velocity in this recording. From this point on the errors start growing, until the tracker gets completely lost for values above 10 ms.
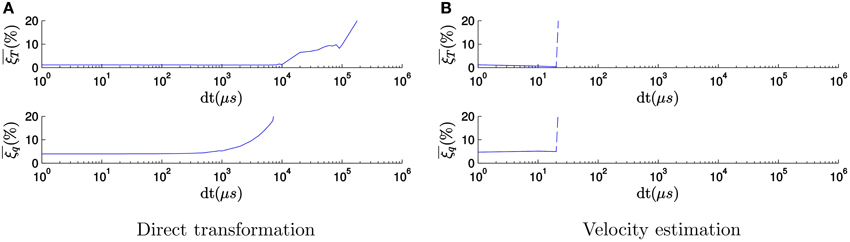
Figure 11. Evolution of the errors with the size of the binning window dt (in μ s), when tracking the fast spinning icosahedron applying the direct transformation strategy. As the time resolution is degraded, the errors start growing, until the tracker gets completely lost for values above 10 ms. (A) Evolution of the errors when applying the direct transformation strategy. (B) Evolution of the errors when applying the velocity estimation strategy.
When applying the velocity estimation strategy, if the temporal resolution is degraded we lose track of the object very rapidly. This happens because the estimation of the velocity is based on the precise timing between events. When this information is lost, Δt in Equations (17) and (18) becomes 0, which makes the estimated velocity infinite. As a result, the tracking gets lost. For the current set of parameters, this occurs for values of dt above 30 μ s, as one can see in Figure 11B.
We conclude from this experiment that the high temporal resolution of the neuromorphic camera output is a key feature to the successful performance of the 3D pose estimation algorithm. Beyond 10 ms pose estimation becomes a difficult problem. 10 ms is already smaller than the frame interval used by conventional computer vision algorithms.
3.6. Computation Time
The presented experiments were carried out using a conventional laptop, equipped with an Intel Core i7 processor and running Debian Linux, while the algorithm was implemented in C++. The code was not parallelized, and just one core was used.
Let t10 be the time required to process 10 ms of events (10 ms is a pure technical choice, due to the software architecture used). Consequently, if t10 is below 10 ms, we consider the computation to be performed in real-time. Figure 12A shows the computational time required for processing the icosahedron sequence, when applying the velocity estimation strategy with the experimentally selected optimal set of parameters. The horizontal line indicates the real-time threshold. This threshold is never exceeded by the implementation. We will characterize the performance of the algorithm by the mean value of the computational time , equal in this case to 4.99 ms.
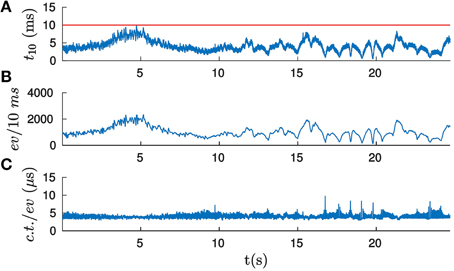
Figure 12. (A) Computational time (in ms) required for processing 10 ms of events when computing the pose of the icosahedron, applying the velocity estimation strategy with the experimentally selected optimal set of parameters. If t10 is below 10 ms (indicated here by the horizontal line), then the computation is carried out in real-time. (B) Number of incoming events per 10 ms. As we can observe, the number of events and t10 has a similar form, suggesting that the computational time per event remains approximately constant. (C) Computational time required per event (in μs). As we can see, it remains almost constant for the whole experiment, its mean value being equal to 5.11 μ s.
The variability in t10 can be explained by the variations in the rate of incoming events. Figure 12B shows the number of incoming events per 10 ms for the corresponding recording. This curve has a similar shape to the t10 one, suggesting that the computational time per event is stable through the whole recording. Dividing t10 by the number of incoming events gives us the computational time per event, as shown in Figure 12C. We verify that it remains approximately constant. Its mean value is equal to 5.11 μ s, which imposes a maximum rate of events that can be treated in real time equal to 195 events/ms.
We next study the effect of the parameter N in the computational time and the estimation errors. Figure 13 shows the corresponding results when tracking the icosahedron, with N taking values between 1 and 500. Here, the mean computational time is obtained as the mean value for 10 simulations.
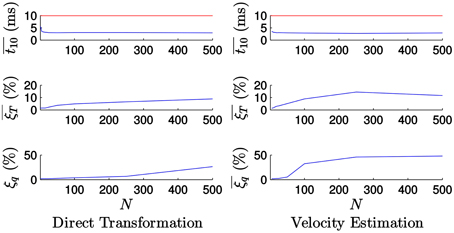
Figure 13. Evolution of the errors and the computational time with the value of N when tracking the icosahedron. is the mean computational time required for processing 10 ms of events. Left: Results when applying the direct transformation strategy. The computational time decreases with the value of N until it reaches a plateau, while the errors increases with the value of N. Right: Results when applying the velocity estimation strategy. The computational time decreases and the errors increases with the value of N.
Figure 13 (left) shows the results when applying the direct transformation strategy. For small values of N the computational time decreases as the value of N increases, but then it reaches a plateau. In order to illustrate this behavior more clearly, let us examine the evolution of for small values of N (between 1 and 25), as shown in Figure 14. In this cases, the computational time is largely reduced for the first values of N, but then it is almost insensitive to its value. This can be explained if we consider that the computational time consists of the time required to update the estimation with each incoming event—which does not vary with the value of N—and the time required for actually applying the transformation to the model, which is a computationally expensive process, only applied every N events. For small values of N, the relative importance of the time required for transforming the model is large. Consequently, increasing the value of N will have a strong impact on the computational time. As N gets larger, the relative importance of this process is smaller, and increasing N will have a weaker effect.
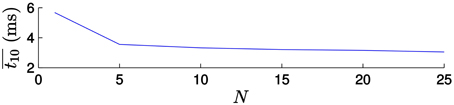
Figure 14. Evolution of the computational time for the first values of N. We can clearly see how the computational time is largely reduced for small values of N, but then it reaches a plateau.
We verify as well that the tracking errors grow with N. This occurs because for large values of N the small motion assumption is not true anymore, and thus the algorithm fails to yield correct results. In other words, when we accumulate too many events we are losing the high temporal resolution of the data, and the accuracy of the pose estimation will therefore degrade.
Figure 13 (right) shows the results when applying the velocity estimation strategy. For values of N below 5 the method is unstable, losing track of the object and producing errors that tend to infinity. As in the case of the degraded temporal resolution, this happens because Δt in Equations (17) and (18) can be equal to 0. Above this value, the computational time soon reaches its plateau and is not too affected by the value of N. We verify that the computational time required for applying the direct transformation and the velocity estimation strategies are very similar. The errors grow with the value of N as well, but in this case they do it faster. We conclude that we need a higher temporal resolution to correctly estimate the velocity of the object.
Figure 15 shows the evolution of the computational time and the tracking errors with the value of N when tracking the house. Figure 15 (left) shows the corresponding results when applying the direct transformation strategy: as one can see, the results are similar to the ones obtained when tracking the icosahedron, but the computational time is much higher in this case. This is mainly due to the higher complexity of the hidden line removal algorithm. As we can see, for small values of N we cannot guarantee real-time performance. However, as the value of N grows, the computational time is reduced.
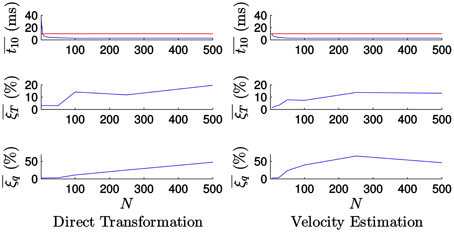
Figure 15. Evolution of the errors and the computational time with the value of N when tracking the house. For small values of N we cannot guarantee real-time performance. However, slightly increasing the value of N the computational time is reduced, with small effect on the accuracy.
We verify as well that the errors grow with the value of N. Nevertheless, for small values of N there is a plateau in which they are very slightly affected by its value. For example, for N = 25 we get and , while the mean computational time is = 4.123 ms. Therefore, we get low values for the estimation errors while keeping the computational time below the real-time threshold. We conclude that it is possible to guarantee real-time performance even for this more complex object by slightly increasing the value of N, with small effect on the accuracy. The same considerations apply in the case of the velocity estimation strategy, shown in Figure 15 (right).
4. Discussion
This paper introduces a new method for 3D pose estimation from the output of a neuromorphic event based camera. To our knowledge, this is the first 3D pose estimation algorithm developed using this technology. The method is truly event-driven, as every incoming event updates the estimation of the pose. The transformation applied with each event is intuitively simple and uses the distance to the line of sight of pixels.
We showed that the method is able to estimate and track 3D moving objects at high accuracy and low computational costs by exploiting the high temporal resolution of the event-based sensor. Depending on the recording and the method chosen, we get translation errors ranging from 1.06 to 3.12% and rotation errors from 1.29 to 4.71%. These values are reasonably low for us to conclude that pose estimation is correctly performed.
We have also shown that when the temporal resolution of the events is degraded to simulate frame based conditions, a point is reached after which the pose cannot be accurately estimated. In the studied recording, this happens when the temporal resolution is 10 ms in the case of the direct estimation strategy, or 30 μs when the velocity estimation strategy is applied. We conclude that the high temporal resolution of the neuromorphic camera is a key feature to the accuracy of our algorithm.
Compared to frame-based methods, we consider our approach to be conceptually simpler. Instead of redundantly processing all pixels, as it is usually done in the frame based approach, the event-based philosophy is to minimize the computational resources applied to each event. Once we are close to the solution, the event-based approach allows us to continuously track the correct pose, thanks to the high temporal precision of the sensor. As a canonical example, we are able to accurately estimate the pose of an object spinning at angular speeds up to 26.4 rps. To achieve equivalent accuracy with a frame-based camera, high frame rates would be required, and consequently the number of frames to process will increase.
The method can also be used in mobile scenarios by applying more robust matching algorithms relying on additional matching criteria, such as the local orientation of edges. The method is robust to partial occlusions and does not impose any limitation on the type of model that can be used. The only constraint is given by the increase in computational time associated with the complexity of the object specially in computing hidden surfaces. Other models, including parametric curves or point clouds, could be used with very small modifications to the algorithm. In the case of real-time requirements, we show that the tuning of the parameter N provides lower computational times with little impact on the accuracy of the pose estimation.
We have also shown how an assumption of velocity smoothness can improve pose estimation results when an expected rate of change of velocity is known for the object. This being a reasonable hypothesis, the velocity estimation strategy is in most cases the standard choice. The direct transformation strategy should be chosen when high values for the acceleration are expected.
Author Contributions
DR: Main contributor. Formalized the theory, implemented the experiments and evaluated the results. GO: Provided support for the experimental setup and participated in the experiments. SI: Co-supervisor. RB: thesis director and main instigator of the work.
Funding
This work received financial support from the LABEX LIFESENSES [ANR-10-LABX-65] which is managed by the French state funds (ANR) within the Investissements d'Avenir program [ANR-11-IDEX-0004-02].
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Supplementary Material
The Supplementary Material for this article can be found online at: http://journal.frontiersin.org/article/10.3389/fnins.2015.00522
Footnotes
1 ^All recordings and the corresponding ground truth data are publicly available at https://drive.google.com/folderview?id=0B5gzfP0R1VEFNS1PZ0xKU3F5dG8&usp=sharing.
References
Agarwal, S., Furukawa, Y., Snavely, N., Simon, I., Curless, B., Seitz, S., et al. (2011). Building rome in a day. Commun. ACM 54, 105–112. doi: 10.1145/2001269.2001293
Araujo, H., Carceroni, R. L., and Brown, C. M. (1996). A Fully Projective Formulation for Lowe's Tracking Algorithm. Technical Report, Department of Computer Science, University of Rochester.
Benosman, R., Ieng, S.-H., Clercq, C., Bartolozzi, C., and Srinivasan, M. (2012). Asynchronous frameless event-based optical flow. Neural Netw. 27, 32–37. doi: 10.1016/j.neunet.2011.11.001
Benosman, R., Ieng, S.-H., Rogister, P., and Posch, C. (2011). Asynchronous event-based hebbian epipolar geometry. IEEE Trans. Neural Netw. 22, 1723–1734. doi: 10.1109/TNN.2011.2167239
Boahen, K. A. (2000). Point-to-point connectivity between neuromorphic chips using address-events. IEEE Trans. Circ. Syst. II 47, 416–434. doi: 10.1109/82.842110
Botsch, M., Kobbelt, L., Pauly, M., Alliez, P., and Lévy, B. (2010). Polygon Mesh Processing. Natick, MA: A K Peters, Ltd.
Chong, E. K. P., and Zak, S. H. (2001). An Introduction to Optimization. New York, NY: John Wiley and Sons.
Delbrück, T., Linares-Barranco, B., Culurciello, E., and Posch, C. (2010). “Activity-driven, event-based vision sensors,” in Proceedings of 2010 IEEE International Symposium on Circuits and Systems (ISCAS) (Paris: IEEE), 2426–2429.
DeMenthon, D. F., and Davis, L. S. (1995). Model-based object pose in 25 lines of code. Int. J. Comput. Vis. 15, 123–141. doi: 10.1007/BF01450852
Drummond, T., and Cipolla, R. (2002). Real-time visual tracking of complex structures. IEEE Trans. Pattern Anal. Mach. Intell. 24, 932–946. doi: 10.1109/TPAMI.2002.1017620
Fischler, M. A., and Bolles, R. C. (1981). Random sample consensus: a paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 24, 381–395. doi: 10.1145/358669.358692
Glaeser, G. (1994). “Hidden-line removal,” in Fast Algorithms for 3D-Graphics (New York, NY: Springer), 185–200.
Harris, C. (1993). “Tracking with rigid models,” in Active Vision (Cambridge, MA: MIT Press), 59–73.
Hartley, R., and Zisserman, A. (2003). Multiple View Geometry in Computer Vision. Cambridge, UK: Cambridge University Press.
Huynh, D. Q. (2009). Metrics for 3d rotations: Comparison and analysis. J. Math. Imaging Vis. 35, 155–164. doi: 10.1007/s10851-009-0161-2
Janabi-Sharifi, F. (2002). “Visual servoing: theory and applications,” in Opto-Mechatronic Systems Handbook ed H. Cho (Boca Raton, FL: CRC Press), 15-1–15-24.
Janabi-Sharifi, F., and Marey, M. (2010). A kalman-filter-based method for pose estimation in visual servoing. IEEE Trans. Robot. 26, 939–947. doi: 10.1109/TRO.2010.2061290
Kato, H., and Billinghurst, M. (1999). “Marker tracking and hmd calibration for a video-based augmented reality conferencing system,” in Proceedings of the 2nd IEEE and ACM International Workshop on Augmented Reality, 1999 (IWAR'99) (San Francisco, CA: IEEE), 85–94.
Kollnig, H., and Nagel, H.-H. (1997). 3d pose estimation by directly matching polyhedral models to gray value gradients. Int. J. Comput. Vis. 23, 283–302. doi: 10.1023/A:1007927317325
Lepetit, V., and Fua, P. (2005). Monocular model-based 3d tracking of rigid objects: A survey. Found. Trends Comput. Graph. Vis. 1, 1–89. doi: 10.1561/0600000001
Lepetit, V., Fua, P., and Moreno-Noguer, F. (2007). “Accurate non-iterative O(n) solution to the PnP problem” in IEEE International Conference on Computer Vision (Rio de Janeiro: IEEE), 1–8. doi: 10.1109/ICCV.2007.4409116
Lepetit, V., Moreno-Noguer, F., and Fua, P. (2009). EPnP: an accurate O(n) solution to the PnP problem. Int. J. Comput. Vis. 81, 155–166. doi: 10.1007/s11263-008-0152-6
Lu, C.-P., Hager, G., and Mjolsness, E. (2000). Fast and globally convergent pose estimation from video images. IEEE Trans. Pattern Anal. Mach. Intell. 22, 610–622. doi: 10.1109/34.862199
Mahowald, M. (1992). VLSI Analogs of Neuronal Visual Processing: A Synthesis of Form and Function. PhD thesis, California Institute of Technology.
MIP, CAU Kiel, Germany (2008). BIAS: Basic Image AlgorithmS Library. Available online at: http://www.mip.informatik.uni-kiel.de/BIAS
Murray, R. M., Li, Z., and Sastry, S. S. (1994). A Mathematical Introduction to Robotic Manipulation. Boca Raton, FL: CRC Press.
Oberkampf, D., and DeMenthon, L. S. D. D. (1996). Iterative pose estimation using coplanar feature points. Comput. Vis. Image Underst. 63, 495–511. doi: 10.1006/cviu.1996.0037
Orchard, G., Meyer, C., Etienne-Cummings, R., Posch, C., Thakor, N., and Benosman, R. (2015). Hfirst: a temporal approach to object recognition. IEEE Trans. Pattern Anal. Mach. Intell. 37, 2028–2040. doi: 10.1109/tpami.2015.2392947
Posch, C., Matolin, D., and Wohlgenannt, R. (2011). A QVGA 143 dB dynamic range frame-free PWM image sensor with lossless pixel-level video compression and time-domain CDS. IEEE J. Solid-State Circ. 46, 259–275. doi: 10.1109/JSSC.2010.2085952
Reverter Valeiras, D., Lagorce, X., Clady, X., Bartolozzi, C., Ieng, S.-H., and Benosman, R. (2015). An asynchronous neuromorphic event-driven visual part-based shape tracking. IEEE Trans. Neural Netw. Learn. Syst. 26, 3045–3059. doi: 10.1109/TNNLS.2015.2401834
Shoemake, K. (1985). Animating rotation with quaternion curves. Comput. Graph. 19, 245–254. doi: 10.1145/325165.325242
Snavely, N., Seitz, S. M., and Szelisk, R. (2007). Modeling the world from internet photo collections. Int. J. Comput. Vis. 80, 189–210. doi: 10.1007/s11263-007-0107-3
Van Krevelen, D., and Poelman, R. (2010). A survey of augmented reality technologies, applications and limitations. Int. J. Virt. Real. 9:1.
Appendix
In this section, we discuss the solutions to the system of equations defined in Equation (8). Let S be the system matrix, that has the form:
Next, we discuss the solutions to this system, both in the singular and in the general case.
Singular Case
The system matrix S is singular when det(S) = 0, where the determinant takes the following value:
Developing the dot products in this equation, we get:
where γ is the angle between Mk and εnm.
Consequently, S will be singular if γ = 0 or γ = π, this is equivalent to have Mk collinear to εnm. In this case, Bk is chosen between Vn and Vm by taking the one with smaller Z coordinate. We then compute α1 from the perpendicularity constraint between Mk and (Ak − Bk), getting the following result:
and insert this value in Equation (6) to obtain Ak.
General Case
In the general case, S will be invertible. Since S is a 2 × 2 matrix, we can analytically precompute its inverse, saving computational power. In order to solve the system, we define the following dot products
Thus, the inverse will have the following expression:
where det(S) = −ab + c2. This allows us to solve the system for α1 and α2. As a final observation, we need to take into account that εnm is a segment, which means that α2 has to be contained in the interval [0, 1]. Thus, the final values for α1 and α2 are:
and
Inserting these values in Equations (6) and (7) provides Ak and Bk.
Keywords: neuromorphic vision, event-based imaging, 3D pose estimation, event-based computation, tracking
Citation: Reverter Valeiras D, Orchard G, Ieng S-H and Benosman RB (2016) Neuromorphic Event-Based 3D Pose Estimation. Front. Neurosci. 9:522. doi: 10.3389/fnins.2015.00522
Received: 13 November 2015; Accepted: 24 December 2015;
Published: 22 January 2016.
Edited by:
Themis Prodromakis, University of Southampton, UKReviewed by:
Omid Kavehei, Royal Melbourne Institute of Technology, AustraliaChristoph Richter, Technische Universität München, Germany
Copyright © 2016 Reverter Valeiras, Orchard, Ieng and Benosman. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ryad B. Benosman, cnlhZC5iZW5vc21hbkB1cG1jLmZy
 David Reverter Valeiras
David Reverter Valeiras Garrick Orchard
Garrick Orchard Sio-Hoi Ieng
Sio-Hoi Ieng Ryad B. Benosman
Ryad B. Benosman