- 1Department of Neurosurgery, Second Affiliated Hospital of Zhejiang University School of Medicine, Hangzhou, China
- 2Department of Neurology, Second Affiliated Hospital of Zhejiang University School of Medicine, Hangzhou, China
- 3Department of Radiology, Second Affiliated Hospital of Zhejiang University School of Medicine, Hangzhou, China
Purpose: To present a new modified tri-exponential model for diffusion-weighted imaging (DWI) to detect the strictly diffusion-limited compartment, and to compare it with the conventional bi- and tri-exponential models.
Methods: Multi-b-value diffusion-weighted imaging (DWI) with 17 b-values up to 8,000 s/mm2 were performed on six volunteers. The corrected Akaike information criterions (AICc) and squared predicted errors (SPE) were calculated to compare these three models.
Results: The mean f0 values were ranging 11.9–18.7% in white matter ROIs and 1.2–2.7% in gray matter ROIs. In all white matter ROIs: the AICcs of the modified tri-exponential model were the lowest (p < 0.05 for five ROIs), indicating the new model has the best fit among these models; the SPEs of the bi-exponential model were the highest (p < 0.05), suggesting the bi-exponential model is unable to predict the signal intensity at ultra-high b-value. The mean ADCvery−slow values were extremely low in white matter (1–7 × 10−6 mm2/s), but not in gray matter (251–445 × 10−6 mm2/s), indicating that the conventional tri-exponential model fails to represent a special compartment.
Conclusions: The strictly diffusion-limited compartment may be an important component in white matter. The new model fits better than the other two models, and may provide additional information.
Introduction
Diffusion-weighted imaging (DWI) is the only noninvasive method for detecting the diffusion motion of water molecules in tissues. Currently, in clinical practice, apparent diffusion coefficient (ADC) maps are typically calculated with the mono-exponential model. However, it has been well established that the attenuation of the DWI signal does not follow the mono-exponential model in many tissues (Clark and Le Bihan, 2000; Koh et al., 2011). It is believed that more than one proton pool exists inside each voxel (Bennett et al., 2003, 2006). Therefore, many models have been developed in order to accurately reflect the diffusion motion of water molecules in vivo (Le Bihan et al., 1988; Bennett et al., 2003; Jensen et al., 2005), such as the bi-exponential model.
However, the bi-exponential model is being challenged for the heterogeneity of its results across studies and its lack of reproducibility (Müller et al., 1998; Grant et al., 2001; Schwarcz et al., 2004; Koh et al., 2011; Steier et al., 2012; Hu et al., 2014; Lin et al., 2015). This model is considered oversimplified (Bisdas et al., 2013), and some researchers even speculate that there are continuous distributions of diffusion coefficients inside each voxel (Bennett et al., 2003, 2006). Recent studies have demonstrated that the three-pool model can perform a better fitting and may provide more detailed information than the bi-exponential model in many tissues (Hayashi et al., 2013, 2014; Cercueil et al., 2015; Ohno et al., 2016; Ueda et al., 2016; van Baalen et al., 2017). However, it is well known that a highly parameterized model can always fit a given data set better than a model with fewer parameters. Whether or not a model can provide more information should be well verified to avoid over-fitting.
Recently, ultra-high b-value DWI has been studied more frequently in recent years because of the popularization of 3.0-Tesla MR systems (Ling et al., 2015; Hu et al., 2017). Several studies using DWI with ultra-high b-value have found that the signal curves of DWI decrease very slowly and tend to be stability at ultra-high b-values in some tissues (Grant et al., 2001; Ling et al., 2015). This phenomenon can be hardly explained by the existing models. Many studies have suggested the existence of the strictly diffusion-limited compartment with extremely low ADC in tissues and even cells (Niendorf et al., 1996; Grant et al., 2001; Sen and Basser, 2005; Baxter and Frank, 2013; Ling et al., 2015). The ADC of water molecules, which are strictly limited in microstructures with extremely small space (such as intracellular organelles), might be extremely low. Because of the very low signal attenuation of this compartment at normal b-values, the ADC of this compartment can be set as zero mathematically. Accordingly, by setting one ADC value of the conventional tri-exponential model as zero, we developed a new modified tri-exponential model.
The purpose of this study was to present the new modified tri-exponential model to detect the strictly diffusion-limited compartment, and to compare it with the conventional bi- and tri-exponential models. Previously, stationary water molecules have been suspected to be exist in white matter (Alexander et al., 2010), and three compartment models with a “dot” compartment (zero radius sphere) have been found to produce a better fitting for diffusion MRI in white matter (Ferizi et al., 2014). Accordingly, we hypothesized that the modified tri-exponential model with a “zero-ADC” compartment might also produce a better fitting for DWI in white matter. Hence, we performed this preliminary study in brain. To indicate the existence of the strictly diffusion-limited compartment, a multi-b-value DWI sequence with b-values range from 0 to 8,000 s/mm2 was used in this study.
Materials and Methods
Participants
This study was approved by the institutional review board at the Second Affiliated Hospital of Zhejiang University. Six young healthy volunteers (four males and two females, age range 24–27 years) were enrolled in this study, without any previous history of central nervous system diseases. Written informed consents were obtained from all participants. This study was conducted according to the principles expressed in the Declaration of Helsinki.
DWI Parameters
The volunteers were imaged on a 3.0-Tesla MR system (Discovery MR750, GE Healthcare Systems, Milwaukee, WI) with a gradient strength of 50 mT/m using an eight-channel high-resolution receiver head coil. A single-shot echo planer imaging sequence was used for the imaging with the following parameters: number of sections, 24; section thickness, 4 mm; field of view, 240 × 240 mm; matrix, 256 × 256; in-plane resolution, 0.94 × 0.94 mm; repetition time/echo time, 3,000/107.7 ms; phase FOV, 1.00; flip angle, 90; and pixel bandwidth, 1953.1 Hz/pixel. The sequence was performed with 17 b-values (0, 10, 20, 30, 50, 70, 100, 150, 200, 300, 500, 700, 1,000, 2,000, 3,000, 5,000, and 8,000 s/mm2) in three orthogonal directions, and the signals were averaged over three directions by the imaging system automatically. The numbers of scan averages (NSAs) for b = 0 to 8,000 s/mm2 were 1, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 5, 5, 5, 5, 9, and 12, respectively. Magnitude reconstruction was applied by the imaging system automatically. The total scan time was 21 min 30 s.
Models
The potential biological interpretations for the three compartments of the modified tri-exponential model are shown in Figure 1A. The strictly diffusion-limited compartment is suspected to represent water molecules strictly limited in microstructures with extremely small space, such as intracellular organelles. The signal attenuation curves for three different ADC values are shown in Figure 1B. For normal ADC values, the remaining signal ratio will be very low at b = 8,000 s/mm2 (1.8% for ADC = 500 mm2/s and 0.0% for ADC = 2,000 mm2/s). However, the signal ratio will still remain high at b = 8,000 s/mm2 for an extremely low ADC value (92.3% for ADC = 10 mm2/s).
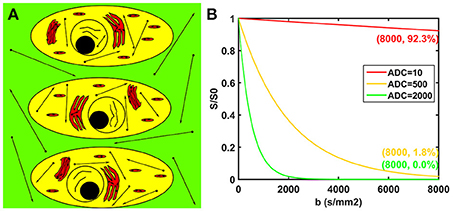
Figure 1. Potential biological interpretations for the three compartments of the modified tri-exponential model (A). The red regions represent the strictly diffusion-limited compartment, the yellow regions represent the slow diffusion compartment, and the green regions represent the fast diffusion compartment. Signal attenuation curves of three ADC values (B). The unit of the ADC values was mm2/s.
The signal attenuation of the bi-exponential model, the conventional tri-exponential model and the modified tri-exponential model as a function of b is expressed by Equations (1–3), respectively.
In these equations, S represents the signal intensity at corresponding b, and S0 represents the signal intensity at b = 0 s/mm2. The fvery−slow, fslow, and ffast, respectively represent the fractions of corresponding diffusion compartments, with corresponding ADC marked as ADCvery−slow, ADCslow, and ADCfast. The f0 represents the fraction of the strictly diffusion-limited compartment.
Model Ranking
For model selection, the small-sample corrected Akaike information criterion (AICc) has been widely used in previous studies (Bourne et al., 2014; Jambor et al., 2015). The akaike information criterion (AIC) was first proposed by Akaike for determining the best model among models and avoiding over-fitting (Akaike, 1974). Hurvich and Tsai improved this method and proposed AICc to compensate for the number of data points, and this improved method has been tested valuable in small samples (Hurvich and Tsai, 1989). The equation for calculating the AICc is as listed below:
where k is the number of free parameters of models, N is the number of points used for fitting, and RSS is the RSS from fitting (Hurvich and Tsai, 1989; Jambor et al., 2015).
Besides, we also compared the models with a leave-one-out test, in order to confirm that the models were correctly ranked by the AICc (Bourne et al., 2014). The predicted residual sum of squares (PRESS) is an index of this method first proposed by Allen for model selection (Allen, 1974).
Image Processing and Analysis
The DWI images were realigned by using SPM12 (available at: www.fil.ion.ucl.ac.uk/spm). Then, these images were analyzed by using programs written in MatLab (MatLab 2009b; MathWorks, Natick, MA). The conventional bi- and tri-exponential models and the modified tri-exponential model were all used for curve fitting.
Curve fittings of these three models were performed using DWI maps obtained with the first 16 b-values (excluding b = 8,000 s/mm2), and were implemented voxel-by-voxel using the steepest descent algorithm (Lenglet et al., 2009). Signal values were all normalized to corresponding signal value S0 prior to model fitting. The initial values of parameters were set empirically. For these three models, the initial value of fslow was set to 0.50, with ADCslow set to 600 × 10−6 mm2/s and ADCfast set to 2,000 × 10−6 mm2/s. For the modified tri-exponential model, the initial value of f0 was set to 0.10, while for the conventional tri-exponential model, the initial value of fvery−slow was set to 0.10, with ADCvery−slow set to 100 × 10−6 mm2/s. The detail description of the programmed algorithm of model fit is shown in Supplement Figure S1. Thus, the parametric maps and the maps of residual sums of squares (RSS) were derived. Subsequently, the AICc maps of these three models were calculated from the RSS maps. Besides, the PRESS maps were also obtained.
After the curve fitting, the signal intensities at b = 8,000 s/mm2 were predicted, and the error of the prediction was squared to form the squared prediction error (SPE) by Equation (5). Thus, the SPE maps were derived. The SPE was a new index presented in the current study to evaluate the ability of models in predicting DWI signals at ultra-high b-values.
where Sm and Sp represent the measured signal intensity and the predicted signal intensity at b = 8,000 s/mm2, respectively.
The regions of interest (ROIs) were drawn by an experienced neuroradiologist. Each ROI was drawn to include corresponding zones as much as possible at one section. Two ROIs were drawn in the cingulate gyrus and supramarginal gyrus, representing gray matter. Six ROIs were drawn in the genu of the corpus callosum, splenium of the corpus callosum, posterior limbs of the internal capsule, centrum semiovale, forceps minor and forceps major, representing white matter. Average values of the parameters and indexes were calculated within each ROI. Besides, the signal-to-noise ratios (SNR) of DWI maps were determined by using a “difference method,” which is based on the evaluation of a difference image of two repeated acquisitions on a single volunteer (Dietrich et al., 2007). ROIs were placed on centrum semiovale and cingulate gyrus, representing for white matter and gray matter, respectively.
In addition, we also performed a stability experiment to investigate the fitting stability of the modified tri-exponential model toward initial conditions. We set random values between 0.05 and 0.10 to initial f0 values, random values between 0.50 and 0.60 to initial fslow values, random values between 500 and 800 mm2/s to initial ADCslow values and random values between 1,900 and 2,200 mm2/s to initial ADCfast values. Thus, we totally generated 20 random initial value sets for the modified tri-exponential model. For each initial value set, curve fitting of the modified tri-exponential model was performed, and the mean values of the parameters were calculated over the ROI on the genu of the corpus callosum (CCG) for one volunteer.
Statistical Analysis
All statistical analyses were performed using SPSS version 22 (SPSS Inc, Chicago, IL, USA). The median values and quartile ranges of the RSS, SPE, and AICc were calculated. Wilcoxon signed-rank test were used to compare these three indexes between any pair of the models. A value of p < 0.05 was regarded as statistically significant.
Results
The mean DWI signal intensity over an ROI decayed much more slowly in white matter than in gray matter, shown in Figure 2. In particular, the remaining signal intensity ratio at b = 8,000 s/mm2 was as high as 18.7% in the white matter ROI, while only 2.4% in the gray matter ROI. In white matter, the SNRs of the DWI image at b = 0, 5,000, and 8,000 s/mm2 were 28.2, 27.8, and 23.7, respectively. In gray matter, those were 31.2, 9.8, and 6.5, respectively. For the modified tri-exponential model, the stability experiment showed that the distributions (mean ± SD) of the mean f0, fslow, ffast, ADCslow, and ADCfast values on CCG over the initial value sets were 18.2 ± 0.6, 58.4 ± 1.2, 23.6 ± 1.2%, 816 ± 7 and 4,525 ± 88 mm2/s, respectively.
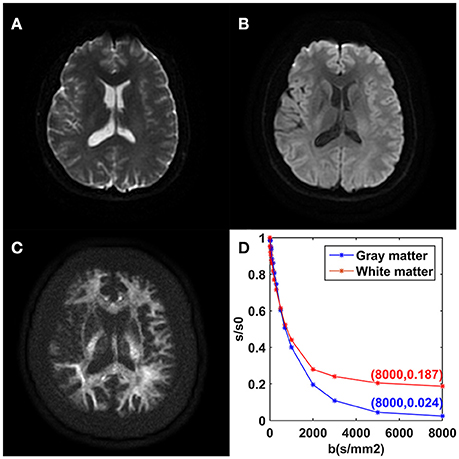
Figure 2. DWI images achieved with b = 0 (A), b = 1,000 (B), and b = 8,000 s/mm2 (C) from one volunteer. Plots of the average signal-intensity decay of two ROIs as a function of b (D). CG, cingulate gyrus; CCg, genu of the corpus callosum.
For the white matter ROIs, the RSSs of the modified tri-exponential model were lower than those of the other two models (p < 0.05). Besides, the RSSs of the conventional tri-exponential model were lower than those of the bi-exponential model (p < 0.05), shown in Table 1. For the gray matter ROIs, the RSSs of the conventional tri-exponential model were lower than those of the other two models, and there were no significant differences in RSSs between the modified tri-exponential model and the bi-exponential model.
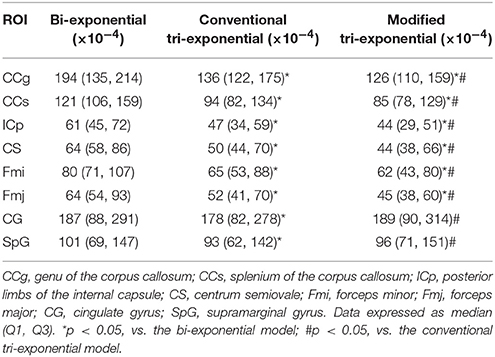
Table 1. Residual sums of squares (RSSs) of the bi-exponential, conventional tri-exponential, and modified tri-exponential models in ROIs.
The AICcs of the conventional tri-exponential model were significantly larger than those of the other two models in all ROIs (p < 0.05), shown in Table 2. The AICcs of the modified tri-exponential model were lower than those of the bi-exponential model in the white matter ROIs (p < 0.05, except for the genu of the corpus callosum), while were higher than those of the bi-exponential model in the gray matter ROIs (p < 0.05).
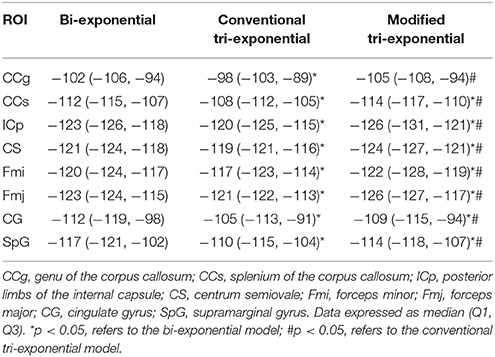
Table 2. Small-sample corrected Akaike information criterions (AICcs) of the bi-exponential, conventional tri-exponential and modified tri-exponential models in ROIs.
The PRESSs of the modified tri-exponential model were significantly lower than those of the other two models in all white matter ROIs (p < 0.05), while those of the conventional tri-exponential model were significantly lower than those of the other two models in two gray matter ROIs (p < 05), shown in Table 3.
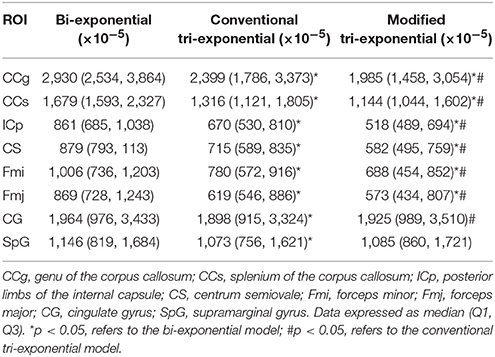
Table 3. Predicted error sums of squares (PRESS) of the bi-exponential, conventional tri-exponential and modified tri-exponential models in ROIs.
The bi-exponential model was unable to predict the DWI signal at b = 8,000 s/mm2 as accurately as the other two models, shown in Figure 3. The SPEs of the bi-exponential model were significantly higher than those of the other two models in all white matter ROIs (p < 0.05), shown in Table 4.
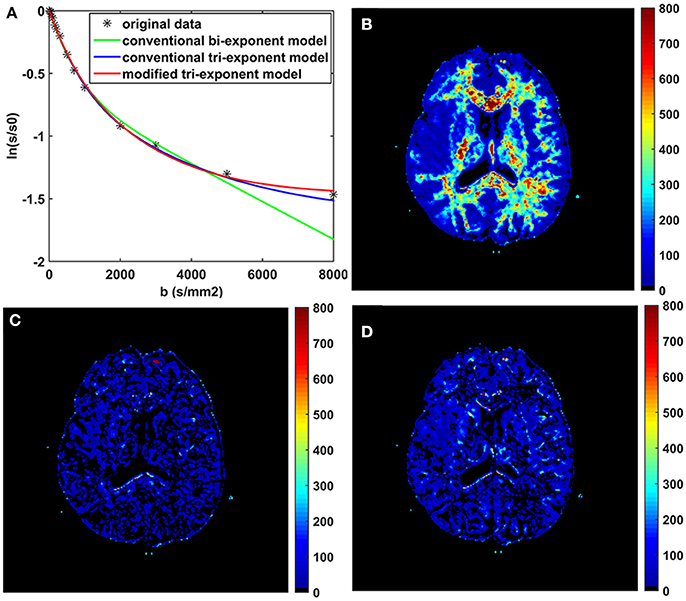
Figure 3. The fitting curves of the three models with the first 16 b-values in a typical voxel of white matter (A). The maps of the squared prediction errors (SPE) calculated by the bi-exponential model (B), the conventional tri-exponential model (C), and the modified tri-exponential model (D). The unit for SPE is ×10−5.
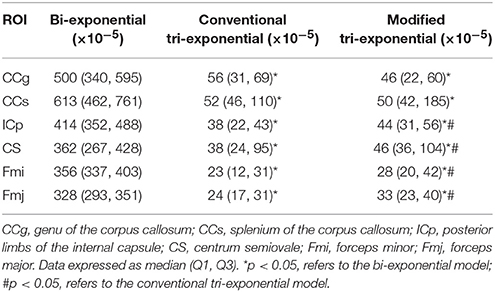
Table 4. Squared prediction errors (SPEs) of the bi-exponential, conventional tri-exponential and modified tri-exponential models in ROIs of white matter.
Representative parameter maps derived from the modified tri-exponential model and the conventional tri-exponential model are shown in Figure 4. In the white matter ROIs, the mean ADCvery−slow values (1–7 × 10−6 mm2/s) were extremely low, and the mean fvery−slow values (11.8–18.3%) were similar to the mean f0 values (11.9–18.7%). However, in the gray matter ROIs, the mean ADCvery−slow values (251–445 × 10−6 mm2/s) were not extremely low and the mean fvery−slow values (11.9–15.7%) were much higher than the mean f0 values (1.2–2.7%), shown in Table 5.
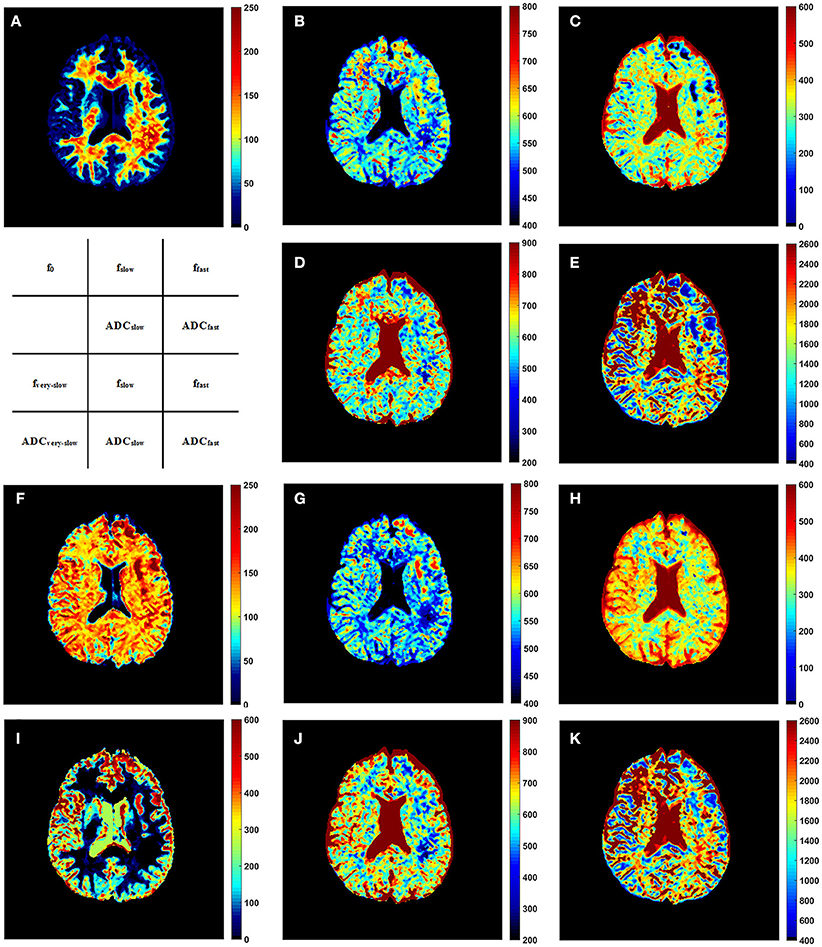
Figure 4. The f0 map (A), fslow map (B), ffast map (C), ADCslow map (D), and ADCfast map (E) derived from the modified tri-exponential model. The fvery−slow map (F), fslow map (G), ffast map (H), ADCvery−slow map (I), ADCslow map (J), and ADCfast map (K) derived from the conventional tri-exponential model. The unit for f maps is ‰, and the unit for ADC maps is ×10−6 mm2/s.
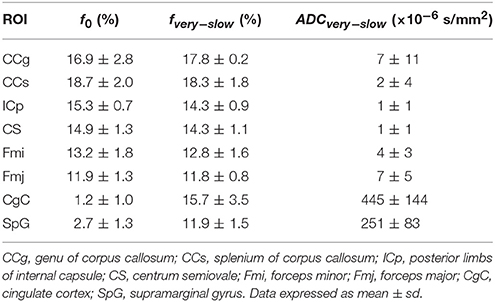
Table 5. The f0 derived from the modified tri-exponential models, and the fvery−slow and the ADCvery−slow derived from the conventional tri-exponential in ROIs.
Figure 5 presents the whole brain f0 maps of one volunteer. The f0 is high in white matter, but very low in gray matter. These images show good resolution and good definition at white-gray matter interfaces.
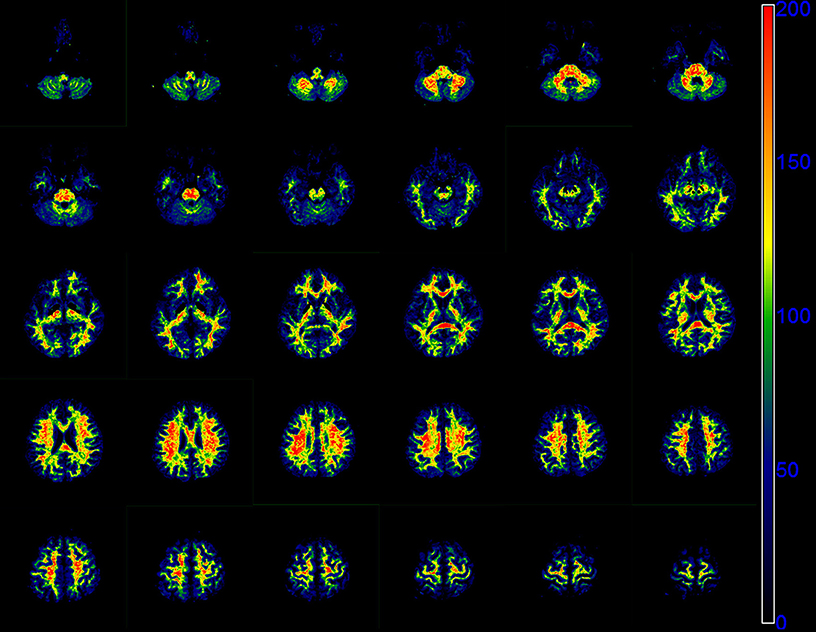
Figure 5. Sequential 30 slices of the f0 maps of one volunteer derived by the modified tri-exponential model. The f0 maps are displayed from the top left. The unit is ‰.
Discussion
In our study, the AICcs and PRESSs of the new model were found to be the lowest in white matter, suggesting that this new model fit better than the conventional bi-exponential and tri-exponential models and may provide more detailed information. The f0 values were found to be very small in gray matter but ranging 10–20% in white matter. This result indicates that the strictly diffusion-limited compartment may be an important component in white matter and may need to be considered when we develop models for multi-b-value DWI.
First of all, we certified that the fraction of the strictly diffusion-limited compartment (f0) in white matter cannot be explained only by noise. In white matter, the remaining signal intensity ratio was as high as 18.7% at b = 8,000 s/mm2, while the SNR was 23.7. Thus, the ratio of noise at b = 8,000 s/mm2 to signal at b = 0 s/mm2 was only 0.79%. This ratio is much lower than the fractions of the strictly diffusion-compartment in white matter which were ranging from 11.8 to 18.7%. Thus, the existence of the strictly diffusion-limited compartment in white matter is not only a result of noise.
In the present study, the bi-exponential model was found to be an over-simplified model. According to the intravoxel incoherent motion (IVIM) theory, the fast ADC is thought to be linked to the microcirculatory perfusion of blood within the capillaries, while the slow ADC is related to diffusion of water molecules in the tissues (Le Bihan and Turner, 1992; Koh et al., 2011; Cercueil et al., 2015). This theory is not suitable when b > 1,000 s/mm2. Another explanation for this model is that two components represent intra- and extra-cellular compartments, respectively (Niendorf et al., 1996; Steier et al., 2012). However, researchers have found that the attenuation of DWI signal does not obey the mono-exponential model even without extra-cellular compartment or even in a single cell (Grant et al., 2001; Schwarcz et al., 2004; Steier et al., 2012). These findings of previous studies also indicate that the bi-exponential model may not be a satisfying model for explaining the attenuation of DWI signal. Models with more pools might be preferable to accurately reflect the diffusion motion of water molecules in tissues.
In the present study, we also found that the SPEs of the bi-exponential model were much higher than the other two models in white matter. As we know, the remaining signal intensity ratio will be very low at ultra-high b-value for compartments with a normal ADC, while this ratio will still remain high for the compartment with an extremely low ADC. Hence, as the bi-exponential model does not contain the compartment with extremely low ADC, it is conceivable that the predicted signal at b = 8,000 s/mm2 would be much lower than the measured value, resulting in high SPE.
When compared with the modified tri-exponential model, the conventional tri-exponential model had significantly higher AICcs in all ROIs and was considered as an over-fitting model. More importantly, the biological implications of the ADCvery−slow compartment differed between white matter and gray matter. In the white matter ROIs, ADCvery−slow values were extremely small, and the fvery−slow values were found to be similar to the f0 values. Thus, f0 and fvery−slow represent the fraction of the same compartment with extremely small ADC in white matter. However, when f0 values were negligible in the gray matter ROIs, the fvery−slow values were still as high as in white matter, while the ADCvery−slow values were not extremely small. This finding suggests that the ADCvery−slow compartment no longer represents the compartment with extremely small ADC in gray matter. In our view, the three compartments of the conventional tri-exponential model may represent three major proton pools in tissues, while the major proton pools may differ among tissues. Hence, the parameters derived from this model may have no specific biological implications. This might be an important limitation for the application of the conventional tri-exponential model. Generally, models with more pools may also suffer from this fatal limitation.
On the contrary, by directly setting the ADCvery−slow to zero, the modified tri-exponential model is able to detect the volume fraction of the extremely-low ADC compartment. In the present study, the mean f0 values were found to be non-ignorable in white matter, ranging from 11.9 to 18.7%. Ferizi et al. also found that three compartment models with a “dot” compartment (zero radius sphere) can produce better fit for diffusion MRI in white matter, suggesting the existence of the extremely-low ADC compartment (Ferizi et al., 2014). In white matter, it has been suspected that there are stationary water molecules trapped in glial cells and other small compartments or bound to membranes and other subcellular structures (Alexander et al., 2010). However, Dhita et al. recently showed that still water compartment was absent in white matte by using isotropic diffusion measurement (Dhital et al., 2017). A similar conclusion was also made by Veraart el al. using single-direction measurements (Veraart et al., 2016). Although Dhital et al. found that the slowly diffusing water pools existed in all directions, these pools were suspected to reside in separate micro-environments (Dhital et al., 2017). It is recommended that orientation dispersion of axons and glial processes should be taken into account when developing models for fitting isotropic diffusion measurement (Dhital et al., 2017). Thus, the exact biological interpretation for the strictly diffusion-limited compartment in white matter needs to be investigated further. Besides, the existence of this compartment in other normal or pathological tissue also needs to be investigated.
One limitation of the application of ultra-high b-value DWI is low SNR. To ensure high SNRs, the NSAs were designed very large in this study, especially for DWI images with ultra-high b-values. Our result showed that the SNRs of DWI maps with ultra-high b-values were comparable with that of DWI maps with b = 0 s/mm2. However, traditional magnitude reconstruction which is used in this study, may lead to an accumulation of noise (Eichner et al., 2015). Averaging the repeat measurements in complex domain is recommend to further improve the SNR, while it requires complex phase navigation and is not normally provided by hardware vendors (Jones et al., 2013; Eichner et al., 2015).
Anisotropic resolution with a high in-plant resolution and a large slice thickness was applied in this study. Clinically, a high in-plant resolution is required to distinguish fine structure in brain. SNR has a linear relationship with voxel volume, thus a relative large slice thickness can improve the SNR. Besides, a large slice thickness can also shorten the scan time. However, anisotropic resolution can lead to differential averaging of fiber orientations (Jones et al., 2013). This effect is not accounted for in this study because the DWI images used for model fitting do not contain direction information.
There are still several limitations in this study. First, the total scan time of this sequence is too long for clinical practice. Hence, the multi-b-value DWI sequence should be optimized, including the selection of b-values and NSAs. Second, in gray matter, the SNRs of DWI maps at ultra-high b-values were low, which reduced the reliability of some results. However, the main focus of the study was on white matter, and the SNR still remained high at ultra-high b-values in white matter. Third, the impact of T2 values of different compartments were not evaluated in our study, and need further research.
In conclusion, the bi-exponential model is an over-simplified model and unable to predict the signal intensity at ultra-high b-values in white matter, while the conventional tri-exponential model is an over-fitting model and has no specific biological implication for each compartment. The new model fits better than the other two models, and may provide additional information.
Author Contributions
QZ: Conceived the idea; BJ: Supervised the work; CL and FD: Collected the data; JZ, FD, and FS: Analyzed the data; QZ, FS, and CL: Wrote the main manuscript text. All authors reviewed the manuscript.
Funding
This study was supported by Zhejiang Provincial Natural Science Foundation of China (Grant number, LY13H180006).
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fnins.2018.00102/full#supplementary-material
References
Akaike, H. (1974). A new look at the statistical model identification. IEEE Trans. Autom. Control 9, 716–723. doi: 10.1109/TAC.1974.1100705
Alexander, D. C., Hubbard, P. L., Hall, M. G., Moore, E. A., Ptito, M., Parker, G. J. M., et al. (2010). Orientationally invariant indices of axon diameter and density from diffusion MRI. Neuroimage 52, 1374–1389. doi: 10.1016/j.neuroimage.2010.05.043
Allen, D. M. (1974). The relationship between variable selection and data agumentation and a method for prediction. Technometrics 16, 125–127. doi: 10.1080/00401706.1974.10489157
Baxter, G. T., and Frank, L. R. (2013). A computational model for diffusion weighted imaging of myelinated white matter. Neuroimage 75, 204–212. doi: 10.1016/j.neuroimage.2013.02.076
Bennett, K. M., Hyde, J. S., and Schmainda, K. M. (2006). Water diffusion heterogeneity index in the human brain is insensitive to the orientation of applied magnetic field gradients. Magn. Reson. Med. 56, 235–239. doi: 10.1002/mrm.20960
Bennett, K. M., Schmainda, K. M., Bennett Tong, R., Rowe, D. B., Lu, H., and Hyde, J. S. (2003). Characterization of continuously distributed cortical water diffusion rates with a stretched-exponential model. Magn. Reson. Med. 50, 727–734. doi: 10.1002/mrm.10581
Bisdas, S., Koh, T. S., Roder, C., Braun, C., Schittenhelm, J., Ernemann, U., et al. (2013). Intravoxel incoherent motion diffusion-weighted MR imaging of gliomas: feasibility of the method and initial results. Neuroradiology 55, 1189–1196. doi: 10.1007/s00234-013-1229-7
Bourne, R. M., Panagiotaki, E., Bongers, A., Sved, P., Watson, G., and Alexander, D. C. (2014). Information theoretic ranking of four models of diffusion attenuation in fresh and fixed prostate tissue ex vivo. Magn. Reson. Med. 72, 1418–1426. doi: 10.1002/mrm.25032
Cercueil, J. P., Petit, J. M., Nougaret, S., Soyer, P., Fohlen, A., Pierredon-Foulongne, M. A., et al. (2015). Intravoxel incoherent motion diffusion-weighted imaging in the liver: comparison of mono-, bi- and tri-exponential modelling at 3.0-T. Eur. Radiol. 25, 1541–1550. doi: 10.1007/s00330-014-3554-6
Clark, C. A., and Le Bihan, D. (2000). Water diffusion compartmentation and anisotropy at high b values in the human brain. Magn. Reson. Med. 44, 852–859. doi: 10.1002/1522-2594(200012)44:6<852::AID-MRM5>3.0.CO;2-A
Dhital, B., Kellner, E., Kiselev, V. G., and Reisert, M. (2017). The absence of restricted water pool in brain white matter. Neuroimage. doi: 10.1016/j.neuroimage.2017.10.051. [Epub ahead of print].
Dietrich, O., Raya, J. G., Reeder, S. B., Reiser, M. F., and Schoenberg, S. O. (2007). Measurement of signal-to-noise ratios in MR images: influence of multichannel coils, parallel imaging, and reconstruction filters. J. Magn. Reson. Imaging 26, 375–385. doi: 10.1002/jmri.20969
Eichner, C., Cauley, S. F., Cohen-Adad, J., Moller, H. E., Turner, R., Setsompop, K., et al. (2015). Real diffusion-weighted MRI enabling true signal averaging and increased diffusion contrast. Neuroimage 122, 373–384. doi: 10.1016/j.neuroimage.2015.07.074
Ferizi, U., Schneider, T., Panagiotaki, E., Nedjati-Gilani, G., Zhang, H., Wheeler-Kingshott, C. A. M., et al. (2014). A ranking of diffusion MRI compartment models with in vivo human brain data. Magn. Reson. Med. 72, 1785–1792. doi: 10.1002/mrm.25080
Grant, S. C., Buckley, D. L., Gibbs, S., Webb, A. G., and Blackband, S. J. (2001). MR microscopy of multicomponent diffusion in single neurons. Magn. Reson. Med. 46, 1107–1112. doi: 10.1002/mrm.1306
Hayashi, T., Miyati, T., and Takahashi, J. (2013). Diffusion analysis with triexponential function in liver cirrhosis. J. Magn. Reson. Imaging 38, 148–153. doi: 10.1002/jmri.23966
Hayashi, T., Miyati, T., Takahashi, J., Tsuji, Y., Suzuki, H., Tagaya, N., et al. (2014). Diffusion analysis with triexponential function in hepatic steatosis. Radiol. Phys. Technol. 7, 89–94. doi: 10.1007/s12194-013-0235-0
Hu, Y. C., Yan, L. F., Sun, Q., Liu, Z. C., Wang, S. M., Han, Y., et al. (2017). Comparison between ultra-high and conventional mono b-value DWI for preoperative glioma grading. Oncotarget 8, 37884–37895. doi: 10.18632/oncotarget.14180
Hu, Y. C., Yan, L. F., Wu, L., Du, P., Chen, B. Y., Wang, L., et al. (2014). Intravoxel incoherent motion diffusion-weighted MR imaging of gliomas: efficacy in preoperative grading. Sci. Rep. 4:7208. doi: 10.1038/srep.07208
Hurvich, C. M., and Tsai, C. L. (1989). Regression and time series model selection in small samples. Biometrika 76, 297–307. doi: 10.1093/biomet/76.2.297
Jambor, I., Merisaari, H., Taimen, P., Boström, P., Minn, H., Pesola, M., et al. (2015). Evaluation of different mathematical models for diffusion-weighted imaging of normal prostate and prostate cancer using high b-values: a repeatability study. Magn. Reson. Med. 73, 1988–1998. doi: 10.1002/mrm.25323
Jensen, J. H., Helpern, J. A., Ramani, A., Lu, H., and Kaczynski, K. (2005). Diffusional kurtosis imaging: the quantification of non-gaussian water diffusion by means of magnetic resonance imaging. Magn. Reson. Med. 53, 1432–1440. doi: 10.1002/mrm.20508
Jones, D. K., Knosche, T. R., and Turner, R. (2013). White matter integrity, fiber count, and other fallacies: the do“s and don”ts of diffusion MRI. Neuroimage 73, 239–254. doi: 10.1016/j.neuroimage.2012.06.081
Koh, D. M., Collins, D. J., and Orton, M. R. (2011). Intravoxel incoherent motion in body diffusion-weighted MRI: reality and challenges. Am. J. Roentgenol. 196, 1351–1361. doi: 10.2214/AJR.10.5515
Le Bihan, D., Breton, E., Lallemand, D., Aubin, M. L., Vignaud, J., and Laval-Jeantet, M. (1988). Separation of diffusion and perfusion in intravoxel incoherent motion MR imaging. Radiology 168, 497–505. doi: 10.1148/radiology.168.2.3393671
Le Bihan, D., and Turner, R. (1992). The capillary network: a link between IVIM and classical perfusion. Magn. Reson. Med. 27, 171–178. doi: 10.1002/mrm.1910270116
Lenglet, C., Campbell, J. S. W., Descoteaux, M., Haro, G., Savadjiev, P., Wassermann, D., et al. (2009). Mathematical methods for diffusion MRI processing. Neuroimage 45, S111–S122. doi: 10.1016/j.neuroimage.2008.10.054
Lin, Y., Li, J., Zhang, Z., Xu, Q., Zhou, Z., Zhang, Z., et al. (2015). Comparison of intravoxel incoherent motion diffusion-weighted MR imaging and arterial spin labeling MR imaging in gliomas. Biomed. Res. Int. 2015, 234245–234210. doi: 10.1155/2015/234245
Ling, X., Zhang, Z., Zhao, Z., Guo, L., Tang, Y., Shi, C., et al. (2015). Investigation of apparent diffusion coefficient from ultra-high b-values in Parkinson's disease. Eur. Radiol. 25, 2593–2600. doi: 10.1007/s00330-015-3678-3
Müller, M. F., Prasad, P. V., and Edelman, R. R. (1998). Can the IVIM model be used for renal perfusion imaging? Eur. J. Radiol. 26, 297–303. doi: 10.1016/S0720-048X(97)01161-3
Niendorf, T., Dijkhuizen, R. M., Norris, D. G., van Lookeren Campagne, M., and Nicolay, K. (1996). Biexponential diffusion attenuation in various states of brain tissue: implications for diffusion-weighted imaging. Magn. Reson. Med. 36, 847–857. doi: 10.1002/mrm.1910360607
Ohno, N., Miyati, T., Kobayashi, S., and Gabata, T. (2016). Modified triexponential analysis of intravoxel incoherent motion for brain perfusion and diffusion. J. Magn. Reson. Imaging 43, 818–823. doi: 10.1002/jmri.25048
Schwarcz, A., Bogner, P., Meric, P., Correze, J. L., Berente, Z., Pál, J., et al. (2004). The existence of biexponential signal decay in magnetic resonance diffusion-weighted imaging appears to be independent of compartmentalization. Magn. Reson. Med. 51, 278–285. doi: 10.1002/mrm.10702
Sen, P. N., and Basser, P. J. (2005). A model for diffusion in white matter in the brain. Biophys. J. 89, 2927–2938. doi: 10.1529/biophysj.105.063016
Steier, R., Aradi, M., Pál, J., Perlaki, G., Orsi, G., Bogner, P., et al. (2012). A biexponential DWI study in rat brain intracellular oedema. Eur. J. Radiol. 81, 1758–1765. doi: 10.1016/j.ejrad.2011.03.058
Ueda, Y., Takahashi, S., Ohno, N., Kyotani, K., Kawamitu, H., Miyati, T., et al. (2016). Triexponential function analysis of diffusion-weighted MRI for diagnosing prostate cancer. J. Magn. Reson. Imaging 43, 138–148. doi: 10.1002/jmri.24974
van Baalen, S., Leemans, A., Dik, P., Lilien, M. R., Ten Haken, B., and Froeling, M. (2017). Intravoxel incoherent motion modeling in the kidneys: comparison of mono-, bi-, and triexponential fit. J. Magn. Reson. Imaging 46, 228–239. doi: 10.1002/jmri.25519
Keywords: diffusion magnetic resonance imaging, brain, white matter, computer-assisted image processing, theoretical models
Citation: Zeng Q, Shi F, Zhang J, Ling C, Dong F and Jiang B (2018) A Modified Tri-Exponential Model for Multi-b-value Diffusion-Weighted Imaging: A Method to Detect the Strictly Diffusion-Limited Compartment in Brain. Front. Neurosci. 12:102. doi: 10.3389/fnins.2018.00102
Received: 07 November 2017; Accepted: 12 February 2018;
Published: 26 February 2018.
Edited by:
Sune Nørhøj Jespersen, Aarhus University, DenmarkReviewed by:
Chantal M. W. Tax, Cardiff University, United KingdomLipeng Ning, Brigham and Women's Hospital, United States
Copyright © 2018 Zeng, Shi, Zhang, Ling, Dong and Jiang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Biao Jiang, amlhbmdiaWFvQHpqdS5lZHUuY24=
 Qiang Zeng
Qiang Zeng Feina Shi
Feina Shi Jianmin Zhang
Jianmin Zhang Chenhan Ling1
Chenhan Ling1 Biao Jiang
Biao Jiang