- 1 Equipe de Chimie et Biochimie Théoriques, UMR Synthèse et Réactivité de Systèmes Moléculaires Complexes, Centre National de la Recherche Scientifique Université de Lorraine, Nancy, France
- 2 Institute for Computational Molecular Science, Temple University, Philadelphia, PA, USA
Since their discovery in the 1950s, the structure and function of voltage-gated cation channels (VGCC) has been largely understood thanks to results stemming from electrophysiology, pharmacology, spectroscopy, and structural biology. Over the past decade, computational methods such as molecular dynamics (MD) simulations have also contributed, providing molecular level information that can be tested against experimental results, thereby allowing the validation of the models and protocols. Importantly, MD can shed light on elements of VGCC function that cannot be easily accessed through “classical” experiments. Here, we review the results of recent MD simulations addressing key questions that pertain to the function and modulation of the VGCC’s voltage-sensor domain (VSD) highlighting: (1) the movement of the S4-helix basic residues during channel activation, articulating how the electrical driving force acts upon them; (2) the nature of the VSD intermediate states on transitioning between open and closed states of the VGCC; and (3) the molecular level effects on the VSD arising from mutations of specific S4 positively charged residues involved in certain genetic diseases.
Introduction
Voltage-gated cation channels (VGCCs) are transmembrane (TM) proteins ubiquitous to excitable cells of superior organisms. Their role is to transport ions across the cell membrane in a manner that depends on its polarization state. Being implicated in a wide variety of biological functions such as the transmission of the nervous impulse, mutations in genes encoding them may give rise to inherited genetic diseases such as long and short QT syndrome of the heart, epilepsies, periodic paralyses, deafness, diabetes, etc. The physiological role of VGCCs has made them objects of interest since their discovery in the 1950s and understanding their function at a molecular level has benefited greatly from results from a large number of experimental techniques, especially structural biology, electrophysiology, and pharmacology, as well as spectroscopies of various kinds.
Among the body of discoveries that have contributed to increase our knowledge of VGCC structure and function, three of them were recognized to have a remarkable impact: the first was the recording of transient currents of very low amplitude (∼200 times lower than ionic currents). These currents, called today “gating currents,” initially measured in the 1970s (Armstrong and Bezanilla, 1973; Schneider and Chandler, 1973; Keynes and Rojas, 1974) follow from the reorganization of charged residues of the protein in response to a change in the TM voltage. Their integral, i.e., the gating charge, Q, represent the total charge that is transported through the membrane capacitance during gating (opening or closing) of the channel and is a characteristic feature of VGCC function. The second came from the sequencing of VGCCs (Noda et al., 1984; Tempel et al., 1987), which revealed that they were made of either homo- or hetero-tetramers of 6 TM segments (S1–S6). The segment S4 contains a number of positively charged residues (mostly arginines) and was as such recognized to constitute the “voltage-sensor.” Following from this, it was hypothesized that it is the movement of S4 across the membrane capacitance in response to changes in the TM potential that gives rise to the gating currents aforementioned. The third discovery was the X-ray crystal structure of a mammalian member of the VGCC family, the Shaker-like (potassium) Kv1.2 channel (Long et al., 2005b). Indeed, while a previous structure had captured an archeal voltage gated K+ channel, the KvAP from Aeropyrum pernix, in a non-native conformation 2 years prior (Jiang et al., 2003a), the Kv1.2 structure revealed for the first time the native 3-D arrangement of the channel: a homo tetramer of S5 and S6 segments forms the central pore (homologous to all K+ channels) and four separate bundles made of segments S1–S4 each form an auxiliary “voltage-sensor” domain (VSD) on the periphery. In this particular Kv1.2 crystallized structure, S4, which contains six positively charged residues, is located in an “up” position, indicating that the VSD was captured in its “activated” conformation. While leaving open the question of the resting/closed state VSD conformation and the channel’s deactivation mechanism, this structure enabled one to start envisioning the molecular level operation mechanism of the VSD. In particular, it allowed computational approaches such as molecular dynamics (MD) simulations to step in and contribute to answering questions concerning the functional mechanism.
In this review, we will provide the reader with our perspective on the results obtained so far using an MD approach. After describing the technique and depicting the protocols designed to specifically address questions that are peculiar to the study of VGCCs (e.g., how to reproduce voltage clamp conditions in silico, and how to estimate the gating charge, etc.), we will review the main molecular insights gleaned on VSD operation. In particular, we will show how the protocols devised have enabled construction of models of the resting/closed state as well as being able to access the conformations of kinetic intermediate states. We also show how MD simulation results have been used to tackle questions of biological and pharmacological interest, namely how mutations of the S4 positively charged residues are involved in genetic diseases.
Methods in Molecular Dynamics Simulations
As already mentioned, the field of VGCC research has benefited from a large number of experimental techniques ranging from pharmacology to structural biology (Hille, 2001). Computational methods such as MD simulations contributed only later as high-resolution structures have become available. When performed under conditions corresponding to laboratory scenarios, MD simulations can provide a detailed view of the structure and dynamics of a macromolecular system. They can also be used to perform “computer experiments” that cannot be carried out in the laboratory, either because they do not represent a physical behavior, or because the necessary controls cannot be achieved in the lab. Additionally, information from MD simulations like positions and velocities of atoms can also enable to calculate quantities that can be tested against experimental results to ensure the validity of the protocols employed. As an illustration, voltage clamp electrophysiology measurements record currents flowing through the external clamp circuit, giving indirect access to the currents moving across the membrane, whereas in MD simulations, it is possible to follow directly ionic charge displacement at an atomic level (Aksimentiev and Schulten, 2005; Jensen et al., 2010; Kutzner et al., 2011) and use this information to estimate currents from a statistical sampling (repetition) of such events. A comparison of the simulation results with experiments enables one to validate (or invalidate) the theoretical models and ensures that molecular scale dynamics embodied in the MD simulation are reliable.
In this section, we offer a brief description of the general principles of MD simulations, and present the protocols developed specifically to address questions concerning VGCC structure and function.
General Considerations
MD simulations refer to a family of computational methods aimed at simulating macroscopic behaviors of a microscopic many-body system through the numerical integration of the classical equations of motion. In this review, we report mainly results from atomistic simulations, in which each atom of the system (particle) is represented by a single interaction center with its net charge, mass and specific interaction characteristics. The macroscopic properties of the whole simulation system are expressed as functions of the particle coordinates and momenta, which are computed along a phase space trajectory generated by classical dynamics (Allen and Tildesley, 1987; Leach, 2001; Frenkel and Smit, 2002). The time evolution of the system trajectories are driven by the forces between particles, which in turn derive from a potential energy function U, also called a force field. The force fields in common use in biophysics, which include GROMOS (Schuler et al., 2001), CHARMM (MacKerell et al., 1998) and AMBER (Case et al., 1999), are based on a classical treatment of particle–particle interactions that does not allow chemical bond dissociation: Specifically, the function U is written in terms of interactions between pairs of atoms and is typically divided into “bonded” and “non-bonded” contributions. Typically, the bonded interactions consist of intramolecular harmonic bond stretching (Ebond), angle bending (Eangle), and dihedral angle deformation (Etorsion). Non-bonded interactions include electrostatic (Eel) and van der Waals terms (Evdw). The former are calculated from the Coulomb interaction between partial charges assigned to each atom, whereas the latter describe the short-range repulsion and long-range attraction between pairs of atoms.
Recently, other types of force field have emerged, where a single interaction site encompasses several atoms (Bond et al., 2007; Marrink et al., 2007; Devane et al., 2009; Khalfa et al., 2009). These so-called coarse-grained (CG) models have the advantage of reducing by almost an order of magnitude the number of particles, enabling to increase the size of the system and reach a much longer simulation time. For instance, they were used to investigate biologically interesting processes such as the interaction of VGCCs with lipids (Bond and Sansom, 2007; Mokrab and Sansom, 2011) or with toxins (Wee et al., 2008). On the other hand, as the resolution of the system is reduced, details that may be important are lost. For example, a single water bead often represents several (3–4) water molecules, i.e., 9–12 atoms. In most CG force fields, its molecular polarizability is lost and several of its properties cannot be modeled, limiting therefore the number of applications that can be studied with these force fields.
The number of atoms considered in an MD simulation is typically of the order of 105–106. To minimize surface effects, and thereby simulate more closely the expected behavior of a macroscopic system, it is customary to use 3-D periodic boundary conditions (PBCs). The system as a whole is divided into cells. Each cell is surrounded on all sides by periodic images of itself. Hence, in the case of a VGCC in its membrane environment, what is usually modeled is in fact a multilamellar lipid bilayer stack with a high density of channels. This setup mimics therefore conditions close to the ones in crystallography or neutron- or x-ray reflectivity studies rather than the ones in physiology experiments.
MD simulations generate a set of atomic positions and velocities as a function of time that evolve deterministically from an initial configuration according to the interaction potential U. Information (positions, velocities or momenta, and forces) at a given instant in time, t, is used to predict the positions and momenta at a later time, t + δt, by numerically integrating the classical equations of motion. The timestep δt should be typically of the order of a few femtoseconds (fs = 10−15 s) for all-atom simulations in order to ensure energy conservation. Accordingly, the time range that can be reached nowadays by this technique on large systems like ions channels or membrane proteins in their host environment is of the order of microseconds (millisecond in very rare occurrences; Shaw et al., 2009).
In general, the MD technique is a scheme for studying the natural time evolution of a classical system of fixed number of particles N in a volume V. In MD simulations using the Newton equations of motion, the total energy E is conserved and along the trajectory, the system samples the micro-canonical ensemble (NVE). Modified algorithms have been devised to perform simulations in conditions that mimic the laboratory conditions. Temperature (T) and pressure (P) control can then be achieved to simulate the isothermal (NVT) or isothermal-isobaric (NPT) ensembles (Martyna et al., 1992).
Evaluation of the Local Electrostatic and TM Potential
The function of VGCCs is to transport ions through the membrane in a manner that depends on the polarization state of the latter. The main force that drives their opening/closing is the action of TM potentials on their charged residues. In general, the TM potential is defined as the difference between the electrostatic potential (EP) in the cytoplasm and in the cell exterior. In MD simulations, as a convention, the bottom bath represents the cell’s inside while the top bath represents its outside. Estimating the TM potential then requires evaluating the difference between the EP in the two baths. The EP may be linked (ignoring electronic polarization) to the charge density distribution through Poisson’s equation. This EP can be computed at a location r of the system, provided an MD trajectory, by solving (for instance on a 3-D grid):
where the sum runs over all atoms i bearing a partial charge ρi in the system. The local electric field at a position r may be obtained as the derivative of the EP. Note that access to such a quantity enables one to verify whether or not and how much the electric field is focused within the VSD, which in turn has been crucial for the proper estimation of the gating charge resulting from a conformational change of the channel (see details below).
Applying a TM Voltage
A central question in the study of the VSD operation using MD is the correct modeling of the applied TM potential in a way that complies with experiments. When a cell membrane is subjected to an electrical stress, either naturally, or during a patch clamp experiment, the TM potential arises from a local ionic charge imbalance, i.e., from an excess of charges on one side of the membrane with respect to the other. The correct handling of such an effect in MD simulations is challenging because of the use of 3-D PBCs. Thus, an ionic imbalance along the membrane normal cannot be applied directly, due to the communication of the top of the simulation system with the bottom of its image and vice versa. Two major methods have been proposed to circumvent this technical problem.
Electric field method
In experiments, a charge imbalance gives rise to a TM potential and therefore to an electric field along the membrane normal, z. In MD simulations, the first strategy developed to apply a TM potential, which is also the simplest to implement technically, was to apply a constant electric field E perpendicular to the membrane (Suenaga et al., 1998; Zhong et al., 1998; Crozier et al., 2001; Tieleman et al., 2001). In practice, this is done by applying a force F = qi.E to all the atoms bearing a charge qi. Reorganization of the molecules and most particularly of the water dipoles then induces a voltage difference across the bilayer. In experiments, the potential difference arising from the application of an electric field to a capacitor (e.g., a lipid membrane) amounts to ΔV = E.d, d being the thickness of the capacitor. In MD simulations, due to the use of PBCs, evaluation of the TM potential by the Poisson equation shows that ΔV is rather a function of Lz, the box size along z (Tieleman, 2004; Tarek, 2005; Gumbart et al., 2012) resulting in ΔV = E.Lz. Due to this property, it is important to stress here that the quantity that is the most appropriate to consider when comparing simulations with electrophysiology experiments is the TM potential rather than the electric field (Delemotte and Tarek, 2012).
Charge imbalance method
In patch clamp experiments, electrodes are inserted on both sides of the membrane and the TM voltage pulse is long enough (milliseconds, i.e., above the membrane charging time) to generate an ionic reorganization within the solution and subsequent charge of the membrane. To mimic such conditions in MD simulations, another class of methods was proposed, where an explicit ionic charge imbalance is considered. Note that to ensure such an imbalance, communication between the system and periodic images of the solution baths on either side of the membrane needs to be avoided. To do so, a system consisting of three salt-water baths separated by two bilayers was proposed (Sachs et al., 2004; Gurtovenko and Vattulainen, 2005; Kandasamy and Larson, 2006).
A variant of this method consists of using a single bilayer between two independent electrolyte baths, each terminated by an air (vacuum)/water interface (Delemotte et al., 2008). The vacuum slab prevents ionic diffusion from one side of the membrane to the other via the PBC (Bostick and Berkowitz, 2003) and maintains constant the charge imbalance imposed between the two baths. For large enough electrolyte baths (>30 Å) the lipid bilayer behaves as if it was in contact with an infinite solution. In both of these setups, it was shown that the bilayer behaves as a capacitor, and that separation of the charges by a low dielectric medium gives rise to a TM potential ΔV = Qs/C, when a charge imbalance per surface area Qs is imposed, C being the capacitance of the membrane.
Such a method has an important drawback for applications where the TM voltage should remain constant, namely due to the relatively small size of the system, reorganization of the charges within the membrane in response to an applied voltage (ion conduction, reorganization of charged residues of a protein, etc.) leads to a drop in the TM voltage. Whereas this may be a desired effect in some applications (see next paragraph for the computation of gating charges), a method that enables one to maintain ΔV roughly constant was recently proposed (Kutzner et al., 2011).
Gating Charge Calculations
Gating currents arise from the movements of charged groups (ions or charged residues, dipoles…) within the lipid dielectric in response to the application of a TM voltage. In the case of VGCCs submitted to an activating voltage, the displacements of the charges tethered to the VSD give rise to tiny transient “gating” currents. The time integral of the latter, Q, corresponds to the amount of electric charge translocated across the membrane capacitor, and is characteristic of a specific conformational change. In voltage clamp experiments, when current through the main pore is blocked [using for instance a non-conductive mutant such as the W434F Shaker mutant (Perozo et al., 1993)], the current measured through the external circuit can be related directly to the “gating” current within the protein, the integral of which is Q. Q may also be formally related to the excess free energy due to the applied TM voltage. It is then expressed as the product of the channel’s charges by the fraction of the electric field that they traverse during the conformational change that the TM voltage induces (Nonner et al., 2004). Accordingly, in MD simulations, two independent routes can be used to estimate, Q.
Direct measurement or Q-route
Both the charge imbalance and the electric field MD setups enable one to monitor the gating charge, Q mimicking what is done in patch clamp experiments. With the charge imbalance method, if ionic conduction through the channel’s pore is prevented, the movement of protein charges across the membrane capacitor is reflected directly by a change in the measured TM potential ΔV (Treptow et al., 2009). In practice, the gating charge, Q associated with the conformational change from state λ1 to λ2 can be written as:
The TM voltage is related to the charge imbalance q0 between the electrolytes through:
in which q0 arises from the contribution of both ions and of the protein A is the membrane area and C the membrane capacitance. As C is constant for a channel/membrane system in the TM voltage range considered (Stefani et al., 1994; Treptow et al., 2009), this allows one to combine Eqs. 2 and 3 to express as
As is maintained fixed, variations in ΔV are then directly linked to the expression of the protein gating charge.
With the electric field method ensuring a constant ΔV value, it was shown that it is possible to monitor the capacitive charge flowing through the external circuit as in voltage clamp setups (Roux, 2008). To do so, one considers ensemble averages of the displacement charge, Q in conformational state λ under a TM voltage ΔV as:
where Lz is the size of the simulation box along the normal to the bilayer, qi the partial charge of atom i, and the unwrapped coordinate of atom i along the z axis.
Energetic formalism or W-route
In general, the total free energy of a system comprises an intrinsic contribution arising from the molecular environment, and another reflecting the coupling of the system to the applied TM potential ΔV. This second contribution may be linked to the gating charge, Q through:
where ΔG(λ) is the excess free energy of the channel (in its conformation λ) due to ΔV. ΔG(λ) may be evaluated directly by summing over all charges the finite difference between two free energy perturbation calculations performed at two different TM voltages (Roux, 2008). However, such time-costly calculation may be avoided sinceΔG(λ) can also be directly linked to the “electrical” distance (Sigworth, 1994; Lecar et al., 2003; Jogini and Roux, 2007) by:
where the sum runs over all charges qi of the channel and the “electrical distance” is given by:
with the local EP at the charge location (Roux, 1997; Islas and Sigworth, 2001; Grabe et al., 2004). Here, in contrast to experiments, the contributions of individual residues of the protein to the total gating charge, and therefore their role in the voltage-sensing mechanism may be directly evaluated.
Molecular Insight into the Function of Kv Channels
The Kv1.2 X-ray crystal structure provided the MD community with a robust starting conformation to investigate, for the first time, the structural and dynamical properties of a mammalian K+ selective VGCC (Long et al., 2005b), while previous investigations had relied on approximate homology models (Ranatunga et al., 2001; Capener and Sansom, 2002; Eriksson and Roux, 2002; Guy, 2002; Durell et al., 2004; Treptow et al., 2004). Naturally, the first studies have focused on elucidating the properties of the activated/open state derived from the crystal structure embedded in a model lipid bilayer mimicking the cell membrane. Such simulations have made it possible to describe in detail the environment of the positive charges of S4, with the goal to gain understanding in the voltage-sensing mechanism (Treptow and Tarek, 2006a; Jogini and Roux, 2007). Others studied the permeation mechanism and the origin of selectivity at the level of the pore. Such investigations were recently reviewed in (Jensen et al., 2010) and will not be discussed here.
Later, efforts were devoted to uncover the resting/closed state and ultimately, the mechanism of VSD deactivation linking the two states. To do so, two different strategies were adopted. The first consisted in building ab initio models of the closed/resting state of Kv1.2 by introducing constraints derived from experiments. After relaxation of this structure in a membrane/solution environment, the transition pathway was then deduced by comparing the resting state conformation with the initial activated one. The second strategy has been to “follow” the deactivation of the channel submitted to a hyperpolarized (closing) TM potential. Such a brute force approach required reaching time scales well above those accessible to standard simulations and was made possible only with the advent of large high performance computing (HPC) resources. Importantly, we will show that such an approach enabled the discovery of the early steps of the deactivation mechanism.
Molecular Description of Kv1.2 the Activated State
Details of the crystal structure
Preceding the first TM segment (S1), the N-terminus from each of the four subunits of the Kv1.2 channel come together to form an intracellular tetramerization (T1) domain. It is believed that this auxiliary subunit is very important as it enables contacts between the proteins of different cells. The T1 domain, of dimension ∼135 Å × 95 Å × 95 Å has an I4 symmetry, the four-fold symmetry axis running through the center of the main pore, and extends by ∼30 Å in the direction perpendicular to the membrane.
As expected, the Kv1.2 pore domain is quite similar to the pore of the bacterial potassium channel KscA (Doyle et al., 1998). The tetrameric assembly of S5 and S6 forms an inverted teepee. As in other K channels, the pore domain is divided into two major regions: at the extracellular side, the selectivity filter (formed by the P-loop linking S5 and S6) controls the passage of ions and favors the transport of K+ with respect to other ions whereas at the intracellular side, the gate defines the open and closed states of the channel. The inner helix of the pore (S6) contains the amino-acid sequence PVP at which the helix is kinked. This kink is thought to be important for coupling of the VSD to the gate and for the channel gating (del Camino et al., 2000; Beckstein et al., 2003; Domene et al., 2003). Based on the diameter of the pore at the bundle crossing (∼12 Å), the pore was hypothesized to be in an open state.
The S1–S4 bundles form the VSDs and are organized in a manner that agree with previous experimental results (Broomand et al., 2003; Neale, 2003): the VSD of one subunit sits next to the pore domain of the adjacent subunit and the connection between the VSD and the pore of the same subunit is insured by an S4–S5 helical linker (Figure 1). The VSD, of which all the segments are oriented roughly perpendicular to the membrane plane, shows rather tight packing. As electron densities are weak in the VSD region, the backbones were easily identified as TM alpha helices but the side chains were not all resolved: most side chains are present in the model on S2, S4, and the S4–S5 linker but S1 and S3 were built as polyalanine helices. The loops connecting the helices were also omitted in the original structure model.
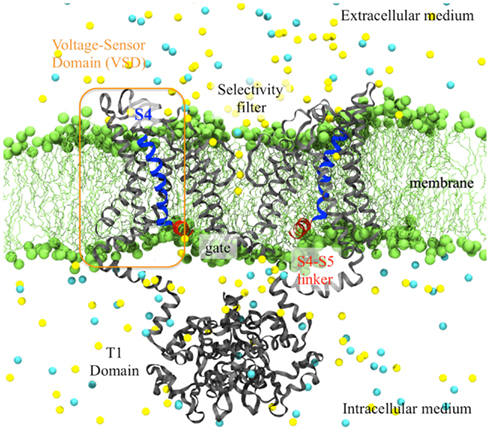
Figure 1. Side view of the activated Kv1.2 (derived from the X-ray crystal structure) embedded in its membrane environment. The entire channel is represented as gray ribbons while the highly charged S4-helix is highlighted in blue and the S4–S5 linker in red. The lipid head groups of the membrane (green) and the ions (K+ in yellow and Cl− in cyan) of the solution are represented as spheres. The water molecules are not shown for clarity.
In Kv1.2, S4 bears six positively charged residues (R294, R297, R300, R303, K306, and R309, referred to hereafter as R1, R2, R3, R4, K5, and R6) and four negative charges are lining the interior of the VSD (E183 on S1, E226 and E236 and S2 and D259 on S3). In a refined structure (Chen et al., 2010), as well as in a chimera (a Kv1.2 structure in which the S3b/S4 paddle was replaced by its equivalent in Kv2.1; Long et al., 2007), the conformations of side chains and the loops were later uncovered, enabling a better characterization of the VSD and of the salt bridge network stabilizing S4 in a TM orientation. In the refined structure, R3 is engaged in a salt bridge with E183, R4 with E226, K5 with D259 and R6 with E236, while R1 and R2 face the lipid head groups of the top bilayer. This conformation was recognized to correspond to an activated state of the VSD, in agreement with the open pore state.
The coupling between the VSD and the pore is posited to occur through the amphiphatic α-helix bridging between S4 of the VSD and S5 of the pore (S4–S5 linker). This linker is located along the pore, with its hydrophilic face facing the solution and hydrophobic face facing the hydrophobic core of the membrane. It crosses over the top of the S6 inner helix from the same subunit and makes many amino-acid contacts with it. The kink in the S6 helix makes the bottom half of S6 a “receptor” for this linker, which is thought to be involved mechanically in the channel closure mechanism.
MD simulations of the activated Kv1.2 structure
The first studies carried out by the modeling community following publication of the Kv1.2 activated structure were limited to the structural characterization of the channel relaxed in a model membrane/solution environment for a few nanoseconds. MD simulations of Kv1.2 in its membrane environment has indicated that the channel’s gate (pore) at the motif is indeed large enough (pore radius >4.5 Å) to let ions through and that the conduction pathway seems to involve passing through the S1–T1 linkers. Along the S6 segment, MD simulations have enabled the identification of V478 of the PVP motif as the residue constituting the main gate (Treptow and Tarek, 2006b).
At the level of the VSD domain, much effort was dedicated to the elucidation of the environment of the S4 basic residues. Indeed, the location of the S4-helix in a TM environment originally had been challenged because it required setting charges in a hydrophobic, energetically unfavorable environment. Several groups reconstructed the missing side chain residues of the original structure and observed the following properties: in the activated state, the two outermost positive charges of S4, R1, and R2, are turned toward the lipid head groups and seem to interact with them through an electrostatic interaction (Sands and Sansom, 2007). The remaining four charges, R3, R4, K5, and R6 are engaged in salt bridges with negative residues of the remainder of the VSD. Because water crevices protrude into the VSD from the intra- and the extracellular media, all the S4 basic residues lie in a solution environment, rationalizing the stability of S4 in a TM orientation (Freites et al., 2006; Treptow and Tarek, 2006a; Jogini and Roux, 2007; Nishizawa and Nishizawa, 2008; Krepkiy et al., 2009). Such a property also accounts for the focused electric field necessary to transport 12–14e during activation while the vertical translation of S4 remains of intermediate magnitude. Using continuum electrostatic computations, Jogini and Roux (2007) determined that the TM potential sensed by the S4 basic residues varies mostly over the outer part of the membrane (“focused electric field”) while others find that the electric field is most focused in the inner region of the membrane (Treptow and Tarek, 2006a); a discrepancy that remains to be explained. Looking further at the interaction of a single VSD with the membrane using a CG model, Bond and Sansom (2007) found that the insertion of the protein leads to considerable local membrane deformation, mainly due to the interaction of S4 with the surrounding lipids. Such a property is proposed to participate to the focusing of the electric field. These results were later confirmed by neutron diffraction, solid-state nuclear magnetic resonance (NMR) spectroscopy and all-atom MD simulations (Krepkiy et al., 2009).
Ab initio Molecular Models of the Kv1.2 Closed State
After the activated Kv1.2 structure was resolved, protocols were designed to develop a model of the resting state and to gain a complete view of the process associated with the response of the channel to depolarization. The first resting state model to be proposed was built on the basis of the ROSETTA Membrane ab initio structural modeling program (Yarov-Yarovoy et al., 2006). A candidate was selected using as constraints the experimentally probed distances between E226 (S2) and R1 and the exposure of two of the four potential gating charge-carrying arginines in S4 to the intracellular water-accessible environment, supposed to account for the 12–14e gating charge. In the gating mechanism derived from the comparison between this closed state model and the activated structure, S4 moves outwards by ∼3 Å and rotates clockwise ∼180° about its axis while the extracellular part of S4 changes its tilt angle from ∼10° to ∼45° relative to the membrane normal vector. The same modeling method was used by a different group, only introducing new experimental constraints derived from fluorescence scan data (Pathak et al., 2007). While the coarse features were similar, the models differ in that the activation now involves a vertical translation of S4 by 6–8 Å. Independently, Grabe et al. (2007) constructed a down state model of the channel using homology modeling with six pairs of interacting residues as structural constraints and verified this model by engineering suppressor mutations on the basis of spatial considerations. Tombola et al. (2006a) proposed yet another model of the resting conformation of the VSD of Kv1.2 that they tested using leak current measurements concomitant with S4 mutations (see next paragraph).
Recently, Clayton et al. (2008) solved the structure of MlotiK in its closed state. In this non-voltage-gated potassium-selective channel, uncharged residues replace the first four basic residues of S4, and two of the acidic countercharges are absent. The packing of the VSD domain as well as the interaction between the VSD and the pore seem to be quite different than the ones in VGCCs. Yet, this structure provides us with a good idea of what a closed Kv channel looks like, mostly in the pore region. Hence, models of the resting states of other channels (Hv1, NaChBac, and the plant KAT channel) have been derived from homology modeling methods, using among others, the MlotiK structure as templates (Shafrir et al., 2008; Schow et al., 2010; DeCaen et al., 2011; Wood et al., 2012). All these models bear similarities, as they place S4 inwards. The deactivation mechanisms derived involve a sliding helix motion for S4 while the bundle made of S1–S3 remains static. The details of the process, however, depend on the particular channel, with the S4 vertical translation ranging from 3 to 15 Å and its tilt from a few degrees to a much larger angle.
Han and Zhang (2008) were the first to relax the closed state model by Pathak et al. (2007) in a membrane environment using MD simulations. They observed differences in a variety of properties between the open and closed state channel (stability, environment of the S4 basic residues, salt bridge arrangements, and further interactions between the VSD and the pore), concluding that only the sliding helix model could enable going from one to the other state. Khalili-Araghi et al. (2010) then pushed the MD simulations further and measured the total gating charge associated with the activation of the channel. They revealed that in the down state, S4 had to be placed in a slightly lower position than originally proposed by Pathak et al. to reach a total Q = 12–14e transported across the membrane capacitor. As the applied electric field varies rapidly over a narrow region of 10–15 Å in the outer leaflet of the membrane, they confirmed that the gating charge could reach 12–14e without full translocation of S4 across the membrane.
In silico VSD Deactivation by the Application of a TM Potential
Interestingly, even without applying a TM voltage, an early study using a coarse grained (CG) representation of the Kv1.2 (Treptow et al., 2008) revealed the first computationally induced conformational change of Kv1.2. Such a representation, in which few atoms are regrouped into one interaction center, allowed the simulation to reach time scales where large conformational changes could be sampled. The gating mechanism revealed suggested a downward movement of S4 combined with a lateral displacement of the S4–S5 linker acts on the gate to induce closure of the channel. Because of the low resolution of the method, results obtained with CG force fields are only qualitative but they nevertheless gave first indications on the route followed by Kv1.2 to deactivate.
Fully atomistic MD simulations applying membrane hyperpolarization have been conducted recently mainly by three groups in order to observe directly the deactivation of the channel by “brute force.” Two groups followed the protocol employed by Treptow et al. (2004) in a pioneering study of a homology model of Shaker. By submitting the system to an electric field, this simulation triggered a conformational response, including displacement of the S4-charges in response to a change in the TM voltage. Applying a strong electric field (0.1 V/nm) to an isolated Kv1.2 VSD (for 30 ns), Nishizawa and Nishizawa (2008) sampled a 6.7 Å displacement of S4 in a screw-like axial rotation, in which the S4 basic residues formed serial interactions with E183 (E0) and E226 (E1). The authors identified two intermediate states, which they found to be in good agreement with kinetic models such as the ZHA (Zagotta et al., 1994a) one. Their subsequent work brought more information on the coupling mechanism between VSD operation and gate closure/opening: this mechanism involves the S4–S5 linker, which brings S6 in its open/closed position through salt bridges between a positive charge at the end of S4 and a negative charge at the end of S6 (Nishizawa and Nishizawa, 2009).
The group of Lindahl carried out a long MD simulation (1 μs) of an entire Kv1.2 channel (Bjelkmar et al., 2009) submitted to a hyperpolarized potential. The response they described involved a large rotation of S4 (120°), changes in hydrogen bonding patterns and an extension of the 310 helical stretch but almost no translation of S4. They implied that the final downwards translation that is necessary to complete the deactivation process is partly entropic explaining the slow nature of the process. The same authors continued by investigating the energetic cost of dragging S4 basic residues downwards when S4 is in a 310 helical conformation compared to a α-helical one (Schwaiger et al., 2011). For the first transition toward the resting state, i.e., when R4 passes through the hydrophobic seal at the center of the VSD, the free energy is lower by about a factor of two with the 310 helix conformation and leads to less distortion of the rest of the VSD; a finding that supports the hypothesis that S4 adopts a 310 helix conformation during activation/deactivation (see next paragraph for more discussion).
Others have adopted the charge imbalance setup (see Methods in Molecular Dynamics Simulations; Denning et al., 2009; Treptow et al., 2009; Delemotte et al., 2011). Delemotte et al. (2011) have used an extensive 2.2 μs MD simulation of the membrane-bound Kv1.2 channel subject to a hyperpolarized potential to reveal the VSD response and reorganization during the initial steps of the channel deactivation. The conformational changes taking place within the VSD involved a zipper-like motion of the S4 basic residues in sequential ion pairing with nearby counter charges and lipid head groups from both the upper and lower membrane leaflets (Figure 2). This essential feature is in agreement with early mutagenesis experiments (Papazian et al., 1995; Tiwari-Woodruff et al., 2000; Zhang et al., 2005) and with the recent hypotheses from the groups of Cui and Catterall. The former probed the salt bridge interactions in the different states of Kv7.1 by charge reversal mutagenesis (Wu et al., 2010). The latter probed these interactions in NaChBac, a bacterial Nav channel, whose VSD is very similar to that of Kv, by disulfide locking (DeCaen et al., 2009) and showed indeed that, during activation, the S4 segment moves from an inward position to an outward position by forming sequentially state-dependent salt bridges (c.f. also Catterall, 2010).
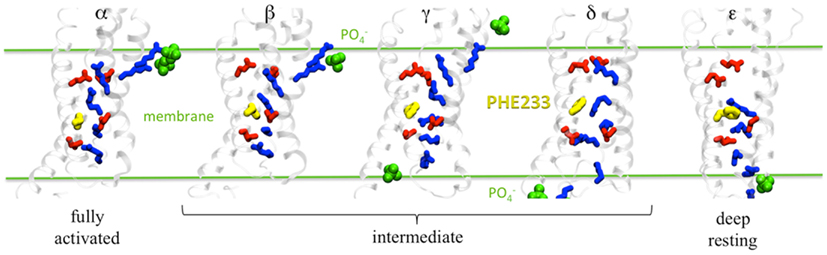
Figure 2. Salt bridge network in each Kv1.2 conformation (α to ε). Basic residues are in blue and acidic residues in red. F233 is represented as yellow spheres and lipid groups within 6 Å of the basic residues are shown in green. Adapted from Delemotte et al. (2011).
Overall, the Delemotte et al. (2011) study has uncovered five states of the channel. In addition to the α (open) state and the two intermediate states (β, γ) arising from the unbiased MD trajectory, one more (δ) was identified resorting to biased MD simulations using so-called steered MD simulations (thus using additional forces to pull certain atoms in the desired direction) in which the imposed “reaction” pathway was consistent with the zipper-like motion (Figure 2). To further validate their resting state model of the VSD, the authors evaluated the gating charge associated with the transition from α to ε. The latter, computed using the direct measurement, is most appropriate to compare with electrophysiology measurements of the gating charge. It is associated with the whole channel deactivation. For the entire system, it amounts to 12.8 ± 0.3e which is in good agreement with values obtained for Shaker-like channels (12–14e) in the 1990s (Schoppa et al., 1992; Aggarwal and MacKinnon, 1996; Seoh et al., 1996). Also, the position of S4 basic residues in the ε-state was checked by probing the effect of mutations of the arginines, R1 and R2 (see next paragraph). Importantly, the final down state (ε) arising from the biased MD bears similarities with the ones generated by de novo (ab initio) modeling (Tombola et al., 2005a; Pathak et al., 2007) or by further using restrained all-atom MD simulation of the channel embedded in a membrane environment to bias the conformation toward the hypothetical resting state (Khalili-Araghi et al., 2010; Vargas et al., 2011). Note however there is a difference between the resting state models proposed by the two groups concerning the position and orientation of R1, which is slightly different. The Delemotte et al. model places R1 in a lower position, i.e., close to D2 (D259), in agreement with recent (Tao et al., 2010) and subsequent work (Lin et al., 2011) placing R1 in the so-called catalytic center (c.f. below). The probable discrepancy from these two models comes from the fact that there are multiple closed, non-conductive states, as proposed in various kinetic models. The relative population of these states depends on the length and the magnitude of the hyperpolarizing pulse. The Khalili-Araghi model then likely represents the closed state that is most populated at a slightly less negative voltage, which may be referred to as a “penultimate closed state” as proposed by (Lin et al., 2011), while the Delemotte et al. (2011) model is reached only at more negative TM voltages, and in that sense is possibly a candidate for the “deep resting state.”
The overall VSD activation mechanism proposed by Delemotte et al. (2011) is consistent with experiments and kinetic models devised to fit the curves of the gating current, which assume that activation of each of the VSDs proceeded in multiple sequential steps. Interestingly, the gating charge measured for each transition (∼0.45–1.2e per subunit) is of the same order of magnitude as the elementary charge movements estimated from measurements of gating current fluctuations (Sigworth, 1994) and as the “loose” charges, an early component of the gating current in Shaker channels (∼1e per VSD unit; Sigg et al., 2003), indicating that the intermediate states uncovered are of functional significance. Naturally, early models, e.g., the Zagotta–Hoshi–Aldrich model (Zagotta et al., 1994a) have considered a small number of states (a minimum of three was required for proper fitting). Later, other groups, extending the study to a broader voltage range, have proposed the same types of models, but introducing additional states (Baker et al., 1998; Schoppa and Sigworth, 1998; Zheng and Sigworth, 1998; Kanevsky and Aldrich, 1999; Loboda and Armstrong, 2001; Sigg et al., 2003). One of the most recent proposals suggested that the VSD can adopt five conformational states (Tao et al., 2010). This last investigation by Mackinnon and co-workers demonstrated indeed that the VSD transitions involve sequential passage of the S4 basic residues through a catalytic center involving the conserved F233 residue. This feature is captured in the five states (α to ε), in each of which a different basic residue occupies the gating charge transfer center. Furthermore, the unbiased MD simulation have clearly indicated the response of the four VSDs of the channel and particularly the intermediate transitions are not occurring simultaneously for all VSDs, in agreement with electrophysiology experiments that all indicate that only the final opening transition is concerted (Zagotta et al., 1994b).
Concerning the overall displacement of S4 which was subject to much debate in the literature, the overall conformational change from the active to the resting states of the VSD is shown in the Delemotte et al. (2011) study to necessitate a large displacement of the S4 backbone amounting to 10–15 Å, which is in closer agreement with estimates from avidin binding experiments (Ruta et al., 2005) than previous models (Catterall, 2010). Up to 2005, two main contradictory models were competing to describe VSD activation (Börjesson and Elinder, 2008): (1) the helical screw model, in which S4 moves independently from the rest of the VSD in a screw-like motion, involving a large translation of the latter by ∼10–20 Å while rotating about its own axis by 180°, advocated mostly by cysteine accessibility studies and disulfide scanning experiments and (2) the transporter model involving instead a large reorganization of the electric field in the vicinity of S4 with only a small overall displacement of S4, which had been put forward mostly to rationalize fluorescence measurements. Since then however, several attempts have been undertaken at reconciling these various views (Tombola et al., 2006b; Jogini and Roux, 2007; Pathak et al., 2007). It was claimed that all the experiments involving mutagenesis introduce an alteration of the structure, of the function and probably of the dynamics of the channel (Durell et al., 2004), and that all the fluorescence studies have a tendency to underestimate measured distances (Selvin, 2002). Also, avidin binding may lock the channel in extreme positions, which are scarcely visited otherwise, leading to overestimation of measured distances (Jiang et al., 2003b). Taking this into account, the molecular conformations of the transition states identified by the computational study of Delemotte et al. (2011) appear to be not only consistent with the sliding helix model, but also complying with most experiments, and thus likely provide a picture of the complete operation of the VSD.
In order to satisfy the charge pairing of the basic and acidic residues, some studies have suggested that the movement of S4 and particularly the passage of S4 through the catalytic center require the transitory switch of a stretch of S4 into a 310 helix (DeCaen et al., 2009). Recent simulations have found results pointing toward this direction: Khalili-Araghi et al. (2010) found a spontaneous conversion of the 10 residue stretch of S4 located in the catalytic center into a 310 helix in their Rosetta model of the resting state. The group of Lindahl (Bjelkmar et al., 2009) found an extension of 310 helix stretch when submitting the open Kv1.2/2.1 paddle chimera channel to a hyperpolarized electric field. They further showed that the free energy of dragging S4 downward is much lower for the 310 helix conformation (Schwaiger et al., 2011). Interestingly, Delemotte et al. (2011) simulations have shown that for one subunit, the short stretch around the residue transferring through the gating charge transfer center takes the form of a 310 helix, for each of the four transitions. In contrast, all the other subunits underwent the four transitions without such secondary structure change. From this data, it is not clear therefore which mechanism would be most favorable from an energetic point of view and further investigations are needed before drawing firm conclusions. In addition, it is important to stress here that secondary structure stability and conformational changes are likely to be dependent on the force field used and interpretation of related data should be with caution (Yoda et al., 2004; Matthes and de Groot, 2009).
Perhaps the most interesting feature revealed by MD simulations and the analysis of the electrical activity of the channel is the finding that the cumulative gating charge transported by the S4 basic residues can be described by a unique sigmoidal function, which defines the electromechanical coupling mechanism that the VSD charges undergo (Delemotte et al., 2011). As inferred by early MD studies, because water crevices protrude into the VSD from the intra- and the extracellular media, all the S4 basic residues lie in a solution environment. Such a shape ensures the presence of a focused electric field, which is required to transport 12–14e during activation without having to translate S4 vertically in an excessive manner (Freites et al., 2006; Treptow and Tarek, 2006a; Jogini and Roux, 2007; Nishizawa and Nishizawa, 2008; Krepkiy et al., 2009). However, while Jogini and Roux determined using continuum electrostatic computations that the TM potential sensed by the S4 basic residues varies mostly over the outer half of the membrane, Delemotte et al. (2011) found that such a variation is maximal at the level of the gating charge transfer center, just under the middle of the VSD. As mentioned earlier, the origin of this discrepancy is not yet understood. The former model agrees better with the fluorescence measurements from the Bezanilla lab (Asamoah et al., 2003), while the latter agrees better with the hypothesis of a charge transfer center within the hydrophobic plug (Tao et al., 2010). Note that in addition, and as importantly, Delemotte et al. (2011) show that the shape and intensity of the focused electric field is hardly modified during deactivation, thus invalidating the transporter model.
Though the ensemble of these results is specific to the VSD of the Kv1.2 channel, the coarse features can likely be generalized to other VGCCs. Also, when combined with electrophysiology measurements, they may allow a better characterization of the molecular mechanisms implicated in the modulation of these channels. Among others, for instance, one finds those implicating the interaction of VGCCs with their lipidic environment. Indeed, recent studies have shown that the presence or absence of the phosphate groups has a dramatic influence on VGCCs function: the activation of K+ channels may indeed be suppressed when they are embedded in bilayers formed by cationic lipids (Schmidt et al., 2006). Removal of the lipid head groups by enzymes also results in an immobilization of the VSD motion, thereby inhibiting function (Ramu et al., 2006; Xu et al., 2008; Zheng et al., 2011). As inferred from electrophysiology experiments, MD simulations confirmed that lipids, and in particular their negatively charged phosphate head group moieties provide counter charges for the S4 basic residues, during the gating process. While earlier molecular models of the VSD (Bjelkmar et al., 2009; Treptow et al., 2009; Khalili-Araghi et al., 2010) have shown that lipids from the upper and lower bilayer leaflets stabilize, respectively the activated and resting states of the VSD, Delemotte et al. (2011) provided evidence that lipids are also crucial in stabilizing conformations of the intermediate states (Figure 2).
Channelopathies Arising from VSD Mutations
Due to their ubiquity, genetic mutations in VGCCs give rise to a variety of inherited diseases, called channelopathies. Neuromuscular disorders were the first to be described but we now know that they can affect tissues of any excitable cell such as the heart. Moreover, one gene encoding a particular ion channel can suffer from various mutations, causing either the same disease, or a different one. For example, Kv7.1, encoded by the KCNQ1 gene and found in heart cells, has a total of 49 mutations that lead to 5 different phenotypes: long QT syndrome types 1 and 2, short QT syndrome, Jervell and Lange-Nielsen syndrome 1 or atrial fibrillation (listed in the Online Mendelian Inheritance in Man (OMIM) database). Usually these mutations can be spread throughout the ion channel sequence, in the VSD, the pore, or in the N- and C-termini domains, leading to molecular scale effects that should in principle be drastically different.
Here, we focus particularly on the mutations within the VSD, especially those affecting the S4 basic residues. Mutations of the charged residues of S4 in K+, Na+, or Ca2+ VGCCs have been shown to impair cellular function and have been linked to a number of inherited channelopathies leading to epilepsy, long QT syndrome, and paralyses (Lehmann-Horn and Jurkat-Rott, 1999). Most of these mutations modify the physical properties of VGCCs, e.g., sensitivity to voltage changes, which in turn alters conduction through the central (alpha) pore (Bao et al., 1999; Jurkat-Rott et al., 2000; Soldovieri et al., 2007). Recently, however, specific mutations have been identified that lead to the appearance of another current component aside from the alpha conduction. In Shaker for instance, such so-called “omega” or gating-pore current was attributed to a non-specific leakage of cations through a conduction pathway within the VSD, indicating that R1 in the S4 segment sterically hinders ion passage through the gating-pore (Tombola et al., 2005b). Substitution of the latter in the VSD by histidine, R1H, allows a H+ current to flow at hyperpolarized potentials (Starace and Bezanilla, 2004), while a R4H mutant allows a proton flux at depolarized potentials (Starace and Bezanilla, 2001). Moreover, mutations of R1 into smaller, uncharged residues give rise to an influx of a non-selective cation current, called “omega current,” through an unidentified pathway through the VSD (Tombola et al., 2006a). Interestingly, it seems that such mutants may have also evolved into “useful” channels: A member of the Kv3 family was identified in a flatworm, N.at-Kv3.2, which has an inward rectifier phenotype, and in which two S4 basic residues are replaced by neutral amino-acids. It was shown that this channel mediates ion permeation through the modified gating (omega) pore, yielding qualitatively different ion permeability when compared to all other members of this gene family (Klassen et al., 2008).
In Na+ VGCCs, omega currents were correlated with mutations that cause normo- and hypo-kalemic periodic paralysis (Sokolov et al., 2005, 2007, 2008; Struyk and Cannon, 2007). Interestingly, in such a channel, it was shown that the mutation of residues R2 or R3 in one of the four S4 helices allows an influx of cations through the omega pore in a state-dependent manner: the omega current is observed only when the channel is in its hyperpolarized conformation. Under depolarization, the omega pore closes and the canonical ion-selective pore opens.
In the following, we show how the study of mutations via MD simulations performed both for the open and closed conformations of Kv1.2, which serves as a prototype for the entire Kv family, can unveil the elementary molecular processes involved in the omega currents detected by electrophysiology.
MD Simulations of the Effects of VSD S4 Mutations
In Kv1.2, no “natural” mutations of S4 basic residues were shown to give rise to channelopathies. To take advantage of the molecular conformations at hand, Delemotte et al. (2010) designed artificial mutants (double and single mutants) that enabled them to use Kv1.2 as a prototype to study the effect of S4 basic mutations. Two key conformations of the channel were considered: the first corresponds to the X-ray crystal structure of the open channel, the aforementioned α state (Long et al., 2005a), while the other corresponds to the closed state, in which the VSD has the resting conformation (conformation ε). Interestingly, in both conformations, the topology of the VSD has shared characteristics: whereas the salt bridge network between the basic residues of S4 and acidic residues of the S1–S3 bundle is state-dependent, the solvent-accessible volume has the shape of an hourglass. The constriction, i.e., the region of lowest diameter, where diffusion of water is shown to be hampered, is located around the salt bridge that involves D259 (and R1 in the closed and K5 in the open state). Such a shape was described also in independent work (Bezanilla, 2005; Sokolov et al., 2005; Treptow and Tarek, 2006a; Krepkiy et al., 2009).
Accordingly, to investigate leak currents through the VSD, Delemotte et al. (2010) chose to mutate one or two residues around the constriction. Mutants away from the constriction were used as controls. As expected, several MD simulations showed that the mutation of the residues (to their uncharged homolog) not involved in the water constriction does not change the overall topology of the VSD. The salt bridge in which the residue is involved is indeed broken, but the interaction being away from the constriction, the VSD retains its hourglass like shape. In contrast, mutation of residues involved in the constriction, i.e., that of K5 in the open structure and that of R1 in the closed one opens up in each case a hydrophilic path (omega pore), drastically changing the topology of the VSD (Figure 3).

Figure 3. VSD topologies of the activated (A,B) and resting (C,D) states of the Kv1.2 VSDs before mutation, i.e., in the wild-type channel (A,C) and after mutation of a single residue, i.e., K5 in the activated (B) and R1 in the resting (D) state. Representations and colors are the same as in Figure 2. The water is represented as a continuous surface (yellow) and highlights the presence of a constriction in the WT VSDs and not in the mutants.
Submitting each of these mutants to TM potentials using explicit ion dynamics showed that the hydrophilic pathway within the VSD of the closed state is permeable to K+cations. In agreement with experiments on the other hand, in the open state K5 mutant, only a partial conduction event was witnessed. Due to the neutralization of basic residues, the resulting omega pore contains an excess of negative charge (one or more glutamates). Accordingly, the K+ diffusion followed a jump diffusion model in which the acidic residues serve as binding sites, and in agreement with experiments (Gamal El-Din et al., 2010), despite the presence of chloride ions in the electrolyte baths, the omega pores were selective to cations. Repetition of permeation events and transposition to physiological conditions (TM voltage ∼100 mV and ionic concentration ∼100 mM) enabled evaluation of the leak conductance ∼106 ions/s, which is over one order of magnitude below the alpha currents (∼ 107 ions/s).
Recently, Khalili-Araghi et al. (2012) studied the same type of mutations in their model of the resting state of Kv1.2, where R1 is in interaction with E1 of S2. Simulation of four mutants (R1S, R1N, E1D-R1N, and E1D-R1S) under a depolarized TM voltage indicates a similar process: K+ ions are transported stochastically, more favorably than Cl− ions, due to the presence of a negatively charged constriction in the mutated VSD. The need to resort to double mutants to achieve more conduction than in the WT VSD, however, is in disagreement with experimental data (Tombola et al., 2005b; Gamal El-Din et al., 2010) and may indicate (as also discussed in In silico VSD Deactivation by the Application of a TM Potential) that the Khalili-Araghi et al. resting state model is a “penultimate” closed state rather than a fully resting closed state (Lin et al., 2011).
Relationship to Diseases
The results from MD simulations may be summarized as follows: at rest, VGCCs are in a closed non-conducting conformation and S4 is in the so-called “down” state. Within the VSD, the salt bridges that maintain the constriction between the intra- and extracellular water crevices involve the top S4 residues and only their mutation leads to omega currents (Figure 4, top). Under depolarized TM potentials, S4 positive residues are dragged upwards (S4 moves to the “up” state) and the VGCCs adopt the open conformation. Within the VSD, the bottom S4 basic residues become critical in maintaining the constriction (Tombola et al., 2005b; Nishizawa and Nishizawa, 2008). Accordingly, mutations of the latter destabilize the VSDs and lead to omega currents (Figure 4, bottom). Hence, mutations of the S4 basic residues give rise to state-dependent omega currents. Overall, these results are consistent with experiments showing that (1) mutations (synthetic or genetic) of the S4 top basic residues of the Na+ VGCCs Nav1.2a (Sokolov et al., 2005) and Nav1.4 (Sokolov et al., 2007) and of Shaker channels (Tombola et al., 2005b) lead to inward omega currents under hyperpolarized potentials and (2) mutations of the S4 bottom basic residues of Nav1.2a (Sokolov et al., 2005) and Nav1.4 (Sokolov et al., 2008) lead to outward omega currents under depolarized potentials.
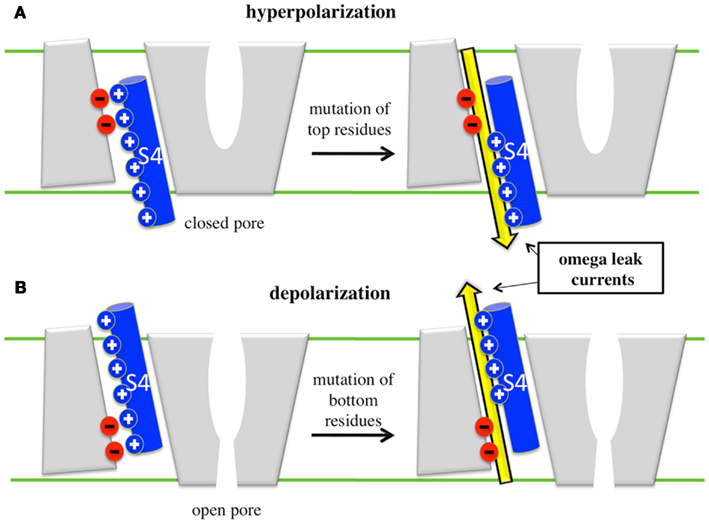
Figure 4. Cartoon representation of the appearance of omega leaks. (A) Under hyperpolarized potentials, when the VSD is in its resting position, mutation of top residues give rise to omega currents, which then represent an inward cation leak (yellow arrow). (B) Under depolarized potentials, when the VSD is activated, mutation of bottom residues gives rise to outward omega currents.
In VGCCs, the positive residues of S4 are the main sensors of the TM voltage and are directly implicated in the conformational changes of the VSD, which control switching (gating) of the channels from open to closed conformations (Schoppa et al., 1992; Seoh et al., 1996). A mutation of any S4 basic residue alters the sensitivity of the channels and modifies their gating kinetics as shown for several VGCCs. In Kv1.2. Delemotte et al. (2010) have identified the mutations that are critical for the stability of α and ε VSD conformations, and determined in which conformational state these mutations give rise to omega currents. Under hyperpolarized TM potentials, omega currents affect directly the channel’s function since they constitute a leak through a closed channel supposedly impermeable to ions. Quite interestingly, most mutations associated with genetic diseases, e.g., epilepsy, hypo- or hyper-kalemic periodic paralysis, or long QT syndrome fall in this category. Under depolarized TM potentials, VGCCs are open and omega currents are a mere modulation of the main alpha current (the omega pore conductance is ∼2 orders of magnitude lower than the alpha pore conductance (Sokolov et al., 2005, 2007, 2008). Such small conductance must however have a more dramatic consequence on VGCCs that undergo N-type inactivation – i.e., become non-conductive under extended depolarized potentials – as shown for Nav1.4, for which omega leak currents were implicated in NormoPP symptoms (Sokolov et al., 2008).
To generalize these results to other members of the large VGCC family (Nav, Cav, and Kv), however, more structural data is required. Indeed, whereas the general characteristics of omega conduction should be similar in other more or less homologous channels, a more precise knowledge of the salt bridge network within each conformation of the VSD, and therefore of the location of the constriction, is necessary to enable identification of the mutations that would give rise to omega currents. Finally, although the appearance of an omega current is the easiest effect of S4 mutations to characterize using MD simulations, one should recall that it is most likely not the only effect of such mutations. Indeed, mutating such charges probably results in the alteration of the response of the VSD to TM voltage change, as manifested by shifts in G/V and Q/V curves and modified kinetics of ON and OFF currents (Miceli et al., 2008). To explain the molecular origin of such experimental observations, it would be most insightful to compare the free energy surface of activation/deactivation of the WT and of the mutants, which requires sophisticated MD simulations protocols (Hénin and Chipot, 2004; Maragliano et al., 2006; Laio and Gervasio, 2008).
Conclusion
Since the release of the first crystal structure of a mammalian voltage gated K+ channel, Kv1.2 in 2005, theoretical and computational methods have been used to gain insights into the molecular level function of these ubiquitous proteins. The focus of this review has been directed at the specific contribution from MD simulations to advance our understanding of the function and modulation of the VSD.
Starting from the open/activated state crystal structure, we have presented different protocols that have been devised to uncover the resting/closed state structure and, in some occurrences, the conformation of kinetic intermediate states. We have shown how these models may be tested and validated against experimental data such as the gating charge value, molecular contacts, etc. and how such molecular level insights may help reconcile diverging views derived from different sets of experimental data. We have then shown how the availability of these computational-based models has enable done to tackle questions with direct biological or pharmacological implication, i.e., to look into the molecular details of the appearance of leak currents, which follow from genetic mutations involved in inherited diseases.
Since it seems unlikely that a crystal structure of the closed state will be resolved in the near future, results from computational methods, in combination with the ones from all other experimental techniques, are crucial to gain a molecular level picture of the entire activation/deactivation cycle. As ever, larger computer resources become available, the accessible time scale will exceed the millisecond domain. Thus the day where a complete brute force MD calculation will uncover the entire deactivation/activation pathway is not so far away; an event that will finally bridge the gaps between the results from the different studies described in this review.
Finally, as a crystal structure of the first bacterial voltage-gated Na+ channel was released last year (Payandeh et al., 2011), modelers have already started to take a serious interest in unraveling the structure/function behavior of Na+ selective channels (Carnevale et al., 2011; Corry and Thomas, 2011). Such an achievement opens up a whole new world that should enable, together with the results on voltage-gated K+ channels, to explain the basis of cellular excitability at a molecular level.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank Werner Treptow for his collaboration and input on the ion channels studies we carried out. This work was performed using HPC resources from GENCI-CINES (grant No. c2010075137, c2011075137, c2011076742).
Note Added in Proof
A recent paper by Jensen et al. (2012) reports on an impressive over 200 μs MD simulation of Kv1.2 channel switching between deactivated and activated states, that quite interestingly confirms essentially all the findings of Delemotte et al. (2010, 2011).
References
Aggarwal, S. K., and MacKinnon, R. (1996). Contribution of the S4 segment to gating charge in the Shaker K+ channel. Neuron 16, 1169–1177.
Aksimentiev, A., and Schulten, K. (2005). Imaging a-hemolysin with molecular dynamics: ionic conductance, osmotic permeability, and the electrostatic potential map. Biophys. J. 88, 3745–3761.
Armstrong, C. M., and Bezanilla, F. (1973). Currents related to movement of the gating particles of the sodium channels. Nature 242, 459–461.
Asamoah, O. K., Wuskell, J. P., Loew, L. M., and Bezanilla, F. (2003). A fluorometric approach to local electric field measurements in a voltage-gated ion channel. Neuron 37, 85–97.
Baker, O., Larsson, H., Mannuzzu, L., and Isacoff, E. (1998). Three transmembrane conformations and sequence-dependent displacement of the S4 domain in Shaker K channel gating. Neuron 20, 1283–1294.
Bao, H., Hakeem, A., Henteleff, M., Starkus, J. G., and Rayner, M. D. (1999). Voltage-insensitive gating after charge-neutralizing mutations in the S4 segment of Shaker channels. J. Gen. Physiol. 113, 139–151.
Beckstein, O., Biggin, P. C., Bond, P., Bright, J. N., Domene, C., Grottesi, A., Holyoake, J., and Sansom, M. S. P. (2003). Ion channel gating: insights via molecular dynamics. FEBS Lett. 555, 85–90.
Bezanilla, F. (2005). The voltage-sensor structure in a voltage-gated ion channel. Trends Biochem. Sci. 30, 166–168.
Bjelkmar, P., Niemelä, P. S., Vattulainen, I., and Lindahl, E. (2009). Conformational changes and slow dynamics through microsecond polarized atomistic molecular simulation of an integral Kv1.2 ion channel. PLoS Comput. Biol. 5, e1000289.
Bond, P. J., Holyoake, J., Ivetac, A., Khalid, S., and Sansom, M. S. (2007). Coarse-grained molecular dynamics simulations of membrane proteins and peptides. J. Struct. Biol. 157, 593–605.
Bond, P. J., and Sansom, M. S. P. (2007). Bilayer deformation by the Kv channel voltage sensor domain revealed by self-assembly simulations. Proc. Natl. Acad. Sci. U.S.A. 104, 2631–2636.
Börjesson, S. I., and Elinder, F. (2008). Structure, function, and modification of the voltage sensor in voltage-gated ion channels. Cell Biochem. Biophys. 52, 149–174.
Bostick, D., and Berkowitz, M. L. (2003). The implementation of slab geometry for membrane-channel molecular dynamics simulations. Biophys. J. 85, 97–107.
Broomand, A., Männikkö, R., Larsson, P., and Elinder, F. (2003). Molecular movement of the voltage sensor in a K channel. J. Gen. Physiol. 122, 741–748.
Capener, C. E., and Sansom, M. S. P. (2002). Molecular dynamics simulations of a K+ channel model: sensitivity to changes in ions, waters, and membrane environment. J. Phys. Chem. 106, 4543–4551.
Carnevale, V., Treptow, W., and Klein, M. L. (2011). Sodium ion binding sites and hydration in the lumen of a bacterial ion channel from molecular dynamics simulations. J. Phys. Chem. Lett. 2, 2504–2508.
Case, D. A., Pearlman, D. A., Caldwell, J. W., Cheatham, T. E. III, Ross, W. S., Simmerling, C. L., Darden, T. A., Merz, K. M., Stanton, R. V., and Cheng, A. L. (1999). AMBER6. San Francisco: University of California.
Catterall, W. A. (2010). Ion channel voltage sensors: structure, function, and pathophysiology. Neuron 67, 915–928.
Chen, X., Wang, Q., Ni, F., and Ma, J. (2010). Structure of the full-length Shaker potassium channel Kv1. 2 by normal-mode-based X-ray crystallographic refinement. Proc. Natl. Acad. Sci. U.S.A. 107, 11352.
Clayton, G., Altieri, S., Heginbotham, L., Unger, V., and Morais-Cabral, J. (2008). Structure of the transmembrane regions of a bacterial cyclic nucleotide-regulated channel. Proc. Natl. Acad. Sci. U.S.A. 105, 1511–1515.
Corry, B., and Thomas, M. (2011). Mechanism of ion permeation and selectivity in a voltage gated sodium channel. J. Am. Chem. Soc. 134, 1840–1846.
Crozier, P. S., Henderson, D., Rowley, R. L., and Busath, D. D. (2001). Model channel ion currents in NaCl extended simple point charge water solution with applied-field molecualr dynamics. Biophys. J. 81, 3077–3089.
DeCaen, P. G., Yarov-Yarovoy, V., Scheuer, T., and Catterall, W. A. (2011). Gating charge interactions with the S1 segment during activation of a Na+ channel voltage sensor. Proc. Natl. Acad. Sci. U.S.A. 108, 18825–18830.
DeCaen, P. G., Yarov-Yarovoy, V., Sharp, E. M., Scheuer, T., and Catterall, W. A. (2009). Sequential formation of ion pairs during activation of a sodium channel voltage sensor. Proc. Natl. Acad. Sci. U.S.A. 106, 22498.
del Camino, D., Holmgren, M., Liu, Y., and Yellen, G. (2000). Blocker protection in the pore of a voltage-gated K+ channel and its structural implications. Nature 403, 321–325.
Delemotte, L., Dehez, F., Treptow, W., and Tarek, M. (2008). Modeling membranes under a transmembrane potential. J. Phys. Chem. B 112, 5547–5550.
Delemotte, L., and Tarek, M. (2012). Molecular dynamics simulations of lipid membranes electroporation. J. Memb. Biol.
Delemotte, L., Tarek, M., Klein, M. L., Amaral, C., and Treptow, W. (2011). Intermediate states of the Kv1.2 voltage sensor from atomistic molecular dynamics simulations. Proc. Natl. Acad. Sci. U.S.A. 108, 6109–6114.
Delemotte, L., Treptow, W., Klein, M. L., and Tarek, M. (2010). Effect of sensor domain mutations on the properties of voltage-gated ion channels: molecular dynamics studies of the potassium channel Kv1.2. Biophys. J. 99, L72–L74.
Denning, E. J., Crozier, P. S., Sachs, J. N., and Woolf, T. B. (2009). From the gating charge response to pore domain movement: initial motions of Kv1.2 dynamics under physiological voltage changes. Mol. Membr. Biol. 26, 397–421.
Devane, R., Shinoda, W., Moore, P. B., and Klein, M. L. (2009). A transferable coarse grain non-bonded interaction model for amino acids. J. Chem. Theory. Comput. 5, 2115–2124.
Domene, C., Haider, S., and Sansom, M. S. P. (2003). Ion channel structures: a review of recent progress. Curr. Opin. Drug Discov. Devel. 6, 611–619.
Doyle, D. A., Cabral, J. M., Pfuetzner, R. A., Kuo, A., Gulbis, J. M., Cohen, S. L., Chait, B. T., and MacKinnon, R. (1998). The structure of the potassium channel: molecular basis of K+ conduction and selectivity. Science 280, 69–77.
Durell, S. R., Shrivastava, I. H., and Guy, H. R. (2004). Models of the structure and voltage-gating mechanism of the Shaker K+ channel. Biophys. J. 87, 2116–2130.
Eriksson, M. A. L., and Roux, B. (2002). Modeling the structure of Agitoxin in complex with the Shaker K+ channel: a computational approach based on experimental distance restraints extracted from thermodynamic mutant cycles. Biophys. J. 83, 2595–2609.
Freites, J. A., Tobias, D. J., and White, S. H. (2006). A voltage-sensor water pore. Biophys. J. 91, L90–L92.
Frenkel, D., and Smit, B. (2002). Molecular Simulations – From Algorithms to Applications, 2nd Edn. Salt Lake City: Academic Press.
Gamal El-Din, T. M., Heldstab, H., Lehmann, C., and Greeff, N. G. (2010). Double gaps along Shaker S4 demonstrate omega currents at three different closed states. Channels (Austin) 4, 93–100.
Grabe, M., Lai, H. C., Jain, M., Jan, Y. N., and Jan, L. Y. (2007). Structure prediction for the down state of a potassium channel voltage sensor. Nature 445, 550–553.
Grabe, M., Lecar, H., Jan, Y. N., and Jan, L. Y. (2004). A quantitative assessment of models for voltage-dependent gating ion channels. Proc. Natl. Acad. Sci. U.S.A. 101, 17640–17645.
Gumbart, J., Khalili-Araghi, F., Sotomayor, M., and Roux, B. (2012). Constant electric field simulations of the membrane potential illustrated with simple systems. Biochim. Biophys. Acta 1818, 294–302.
Gurtovenko, A. A., and Vattulainen, I. (2005). Pore formation coupled to ion transport through lipid membranes as induced by transmembrane ionic charge imbalance: atomistic molecular dynamics study. J. Am. Chem. Soc. 127, 17570–17571.
Guy, H. R. (2002). Computational simulations of peptide binding to proteins: how scorpions sting K+ channels. Biophys. J. 83, 2325–2326.
Han, M., and Zhang, J. Z. H. (2008). Molecular dynamic simulation of the Kv1.2 voltage-gated potassium channel in open and closed state conformations. J. Phys. Chem. B 112, 6966–16974.
Hénin, J., and Chipot, C. (2004). Overcoming free energy barriers using unconstrained molecular dynamics simulations. J. Chem. Phys. 121, 2904–2914.
Islas, L. D., and Sigworth, F. J. (2001). Electrostatic and the gating pore of Shaker potassium channels. J. Gen. Physiol. 117, 69–89.
Jensen, M. Ø., Borhani, D. W., Lindorff-Larsen, K., Maragakis, P., Jogini, V., Eastwood, M. P., Dror, R. O., and Shaw, D. E. (2010). Principles of conduction and hydrophobic gating in K+ channels. Proc. Natl. Acad. Sci. U.S.A. 107, 5833–5838.
Jensen, M. Ø., Jogini, V., Borhani, D. W., Leffler, A. E., Dror, R. O., and Shaw, D. E. (2012). Mechanism of voltage gating in potassium channels. Science 336, 229–233.
Jiang, Y., Lee, A., Chen, J., Ruta, V., Cadene, M., Chait, B. T., and MacKinnon, R. (2003a). X-ray structure of a voltage-dependent K+ channel. Nature 423, 33–41.
Jiang, Y., Ruta, V., Chen, J., Lee, A., and MacKinnon, R. (2003b). The principle of gating charge movement in a voltage-dependent K+ channel. Nature 423, 42–48.
Jogini, V., and Roux, B. (2007). Dynamics of the Kv1. 2 voltage-gated K+ channel in a membrane environment. Biophys. J. 93, 3070–3082.
Jurkat-Rott, K., Mitrovic, N., Hang, C., Kouzmekine, A., Iaizzo, P., Herzog, J., Lerche, H., Nicole, S., Vale-Santos, J., Chauveau, D., Fontaine, B., and Lehmann-Horn, F. (2000). Voltage-sensor sodium channel mutations cause hypokalemic periodic paralysis type 2 by enhanced inactivation and reduced current. Proc. Natl. Acad. Sci. U.S.A. 97, 9549–9554.
Kandasamy, S. K., and Larson, R. G. (2006). Cation and anion transport through hydrophilic pores in lipid bilayers. J. Chem. Phys. 125, 074901.
Kanevsky, M., and Aldrich, R. W. (1999). Determinants of voltage-dependent gating and open-state stability in the S5 segment of Shaker potassium channels. J. Gen. Physiol. 114, 215–242.
Keynes, R. D., and Rojas, E. (1974). Kinetics and steady-state properties of the charged system controlling sodium conductance in the squid giant axon. J. Gen. Physiol. 239, 393–434.
Khalfa, A., Treptow, W., Maigret, B., and Tarek, M. (2009). Self assembly of peptides near or within membranes using coarse grained MD simulations. Chem. Phys. 358, 161–170.
Khalili-Araghi, F., Jogini, V., Yarov-Yarovoy, V., Tajkhorshid, E., Roux, B., and Schulten, K. (2010). Calculation of the gating charge for the Kv1.2 voltage-activated potassium channel. Biophys. J. 98, 2189–2198.
Khalili-Araghi, F., Tajkhorshid, E., Roux, B., and Schulten, K. (2012). Molecular dynamics investigation of the ω-current in the Kv1.2 voltage sensor domains. Biophys. J. 102, 258–267.
Klassen, T. L., Spencer, A. N., and Gallin, W. J. (2008). A naturally occurring omega current in a Kv3 family potasium channel from a platyhelminth. BMC Neurosci. 9, 52–64.
Krepkiy, D., Mihailescu, M., Freites, J. A., Schow, E. V., Worcester, D. L., Gawrisch, K., Tobias, D. J., White, S. H., and Swartz, K. J. (2009). Structure and hydration of membranes embedded with voltage-sensing domains. Nature 462, 473–479.
Kutzner, C., Grubmüller, H., de Groot, B. L., and Zachariae, U. (2011). Computational electrophysiology: the molecular dynamics of ion channel permeation and selectivity in atomistic detail. Biophys. J. 101, 809–817.
Laio, A., and Gervasio, F. L. (2008). Metadynamics: a method to simulate rare events and reconstruct the free energy in biophysics, chemistry and material science. Rep. Prog. Phys. 71, 126601.
Leach, A. R. (2001). Molecular Modeling – Principles and Applications, 2nd Edn. Upper Saddle River: Pearson Education Limited.
Lecar, H., Larsson, H. P., and Grabe, M. (2003). Electrostatic model of S4 motion in voltage-gated ion channels. Biophys. J. 85, 2854–2864.
Lehmann-Horn, F., and Jurkat-Rott, K. (1999). Voltage-gated ion channels and hereditary disease. Physiol. Rev. 79, 1517.
Lin, M. A., Hsieh, J.-Y., Mock, A. F., and Papazian, D. M. (2011). R1 in the Shaker S4 occupies the gating charge transfer center in the resting state. J. Gen. Physiol. 138, 155–163.
Loboda, A., and Armstrong, C. M. (2001). Resolving the gating charge movement associated with late transitions in K channel activation. Biophys. J. 81, 905–916.
Long, B. S., Campbell, E. B., and Mackinnon, R. (2005a). Voltage sensor of Kv1.2: Structural basis of electromechanical coupling. Science 309, 903–908.
Long, B. S., Campbell, E. B., and MacKinnon, R. (2005b). Crystal structure of a mammalian voltage-dependent Shaker family K+ channel. Science 309, 897–903.
Long, S. B., Tao, X., Campbell, E. B., and MacKinnon, R. (2007). Atomic structure of a voltage-dependent K+ channel in a lipid membrane-like environment. Nature 450, 376–382.
MacKerell, J. A. D., Bashford, D., Bellott, M., Dunbrack, R. L., Evanseck, J. D., Field, M. J., Fischer, S., Gao, J., Guo, H., Ha, S., Joseph-McCarthy, D., Kuchnir, L., Kuczera, K., Lau, F. T. K., Mattos, C., Michnick, S., Ngo, T., Nguyen, D. T., Prodhom, B., Reiher, W. E., Roux, B., Schlenkrich, M., Smith, J. C., Stote, R., Straub, J., Watanabe, M., Wiorkiewicz-Kuczera, J., Yin, D., and Karplus, M. (1998). All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B 102, 3586–3616.
Maragliano, L., Fischer, A., Vanden-Eijnden, E., and Ciccotti, G. (2006). String method in collective variables: minimum free energy paths and isocommittor surfaces. J. Chem. Phys. 125, 024106–24115.
Marrink, S. J., Risselda, H. J., Yelfinov, S., Tieleman, D. P., and de Vries, A. H. (2007). The MARTINI force field: coarse grained model for biomolecular simulations. J. Phys. Chem. B 111, 7812–7824.
Martyna, G. J., Tuckerman, M. E., and Klein, M. L. (1992). Nosé-hoover chains: the canonical ensemble via continuous dynamics. J. Chem. Phys. 97, 2635–2643.
Matthes, D., and de Groot, B. L. (2009). Secondary structure propensities in peptide folding simulations: a systematic comparison of molecular mechanics interaction schemes. Biophys. J. 97, 599–608.
Miceli, F., Soldovieri, M. V., Hernandez, C. C., Shapiro, M. S., Annunziato, L., and Taglialatela, M. (2008). Gating consequences of charge neutralization of arginine residues in the S4 segment of Kv7.2, an epilepsy-linked K+ channel subunit. Biophys. J. 95, 2254–2264.
Mokrab, Y., and Sansom, M. S. P. (2011). Interaction of diverse voltage sensor homologs with lipid bilayers revealed by self-assembly simulations. Biophys. J. 100, 875–884.
Neale, E. J. (2003). Evidence for intersubunit interactions between S4 and S5 transmembrane segments of the Shaker potassium channel. J. Biol. Chem. 278, 29079–29085.
Nishizawa, M., and Nishizawa, K. (2008). Molecular dynamics simulation of Kv channel voltage sensor helix in a lipid membrane with applied electric field. Biophys. J. 95, 1729–1744.
Nishizawa, M., and Nishizawa, K. (2009). Coupling of S4 helix translocation and S6 gating analyzed by molecular-dynamics simulations of mutated Kv channels. Biophys. J. 97, 90–100.
Noda, M., Shimizu, S., Tanabe, T., Takai, T., Kayano, T., Ikeda, T., Takahashi, H., Nakayama, H., Kanaoka, Y., and Minamino, N. (1984). Primary structure of electrophorus electricus sodium channel deduced from cDNA sequence. Nature 312, 121–127.
Nonner, W., Peyser, A., Gillespie, D., and Eisenberg, B. (2004). Relating microscopic charge movement to macroscopic currents: the Ramo-Schockley theorem applied to ion channels. Biophys. J. 87, 3716–3722.
Papazian, D. M., Shao, X. M., Seoh, S., Mock, A. F., Huang, Y., and Wainstock, D. H. (1995). Electrostatis interactions of S4 voltage sensor in Shaker K+ channel. Neuron 14, 1293–1301.
Pathak, M. M., Yarov-Yarovoy, V., Agarwal, G., Roux, B., Barth, P., Kohout, S., Tombola, F., and Isaccoff, E. Y. (2007). Closing in on the resting state of the Shaker K+ channel. Neuron 56, 124–140.
Payandeh, J., Scheuer, T., Zheng, N., and Catterall, W. A. (2011). The crystal structure of a voltage-gated sodium channel. Nature 475, 353–358.
Perozo, E., MacKinnon, R., Bezanilla, F., and Stefani, E. (1993). Gating currents from a nonconducting mutant reveal open-closed conformations in Shaker K+ channels. Neuron 11, 353–358.
Ramu, Y., Xu, Y., and Lu, Z. (2006). Enzymatic activation of voltage-gated potassium channels. Nature 442, 696–699.
Ranatunga, K. M., Law, R. J., Smith, G. R., and Sansom, M. S. (2001). Eletrostatics studies and molecular dynamics simulations of a homology model of the Shaker K+ channel pore. Eur. Biophys. J. 30, 295–303.
Roux, B. (2008). The membrane potential and its representation by a constant electric field in computer simulations. Biophys. J. 95, 4205–4216.
Roux, B. T. (1997). Influence of the membrane potential on the free energy of an intrinsic protein. Biophys. J. 73, 2980–2989.
Ruta, V., Chen, J., and Mackinnon, R. (2005). Calibrated measurement of gating-charge arginine displacement in the KvAP voltage-dependent K+ channel. Cell 123, 463–475.
Sachs, J. N., Crozier, P. S., and Woolf, T. B. (2004). Atomistic simulations of biologically realistic transmembrane potential gradients. J. Chem. Phys. 121, 10847–10851.
Sands, Z. A., and Sansom, M. S. P. (2007). How does a voltage sensor interact with a lipid bilayer? Simulations of a potassium channel domain. Structure 15, 235–244.
Schmidt, D., Jiang, Q., and MacKinnon, R. (2006). Phospholipids and the origin of cationic gating charges in voltage sensors. Nature 444, 775–779.
Schneider, M. F., and Chandler, W. K. (1973). Voltage dependent charge movement in skeletal muscle: a possible step in excitation-contraction coupling. Nature 242, 244–246.
Schoppa, N. E., McCormack, K., Tanouye, M. A., and sigworth, F. J. (1992). The size of gating charge in wild-type and mutant Shaker potassium channels. Science 255, 1712–1715.
Schoppa, N. E., and Sigworth, F. J. (1998). Activation of Shaker potassium channels. III. An activation gating model for wild-type and V2 mutant channel. J. Gen. Physiol. 111, 313–342.
Schow, E. V., Freites, J. A., Gogna, K., White, S. H., and Tobias, D. J. (2010). Down-state model of the voltage-sensing domain of a potassium channel. Biophys. J. 98, 2857–2866.
Schuler, L. D., Daura, X., and van Gunsteren, W. F. (2001). An improved GROMOS96 force field for aliphatic hydrocarbons in the condensed phase. J. Comput. Chem. 22, 1205–1218.
Schwaiger, C. S., Bjelkmar, P., Hess, B., and Lindahl, E. (2011). 310-helix conformation facilitates the transition of a voltage sensor S4 segment toward the down state. Biophys. J. 100, 1446–1454.
Selvin, P. R. (2002). Principles and biophysical applications of lanthanide-based probes. Annu. Rev. Biophys. Biomol. Struct. 31, 275–302.
Seoh, S. A., Sigg, D., Papazian, D. M., and Bezanilla, F. (1996). Voltage-sensing residues in the S2 and S4 segments of the Shaker K+ channel. Neuron 16, 1159–1167.
Shafrir, Y., Durell, S. R., and Guy, H. R. (2008). Models of voltage-dependent conformational changes in NaChBac channels. Biophys. J. 95, 3663–3676.
Shaw, D., Dror, R., Salmon, J., Grossman, J., Mackenzie, K., Bank, J., Young, C., Deneroff, M., Batson, B., Bowers, K., Chow, E., Eastwood, M. P., Ierardi, D. J., Klepeis, J. L., Kuskin, J. S., Larson, R. H., Larsen, K. L., Maragakis, P., Moraes, M. A., Piana, S., Shan, Y., and Towles, B. (2009). “Millisecond-scale molecular dynamics simulations on Anton,” in SC ’09: Proceedings of the Conference on High Performance Computing Networking, Storage and Analysis (Portland, OR: ACM), 1–11.
Sigg, D., Bezanilla, F., and Stefani, E. (2003). Fast gating in the Shaker K+ channel and the energy landscape of activation. Proc. Natl. Acad. Sci. U.S.A. 100, 7611–7615.
Sokolov, S., Scheuer, T., and Catterall, W. A. (2005). Ion permeation through a voltage-sensitive gating pore in brain sodium channels having voltage sensor mutations. Neuron 47, 183–189.
Sokolov, S., Scheuer, T., and Catterall, W. A. (2007). Gating pore current in an inherited ion channelopathy. Nature 446, 76–78.
Sokolov, S., Scheuer, T., and Catterall, W. A. (2008). Depolarization-activated gating pore current conducted by mutant sodium channels in potassium-sensitive normokalemic periodic paralysis. Proc. Natl. Acad. Sci. U.S.A. 105, 19980–19985.
Soldovieri, M. V., Miceli, F., Bellini, G., Coppola, G., Pascotto, A., and Tagliatela, M. (2007). Correlating the clinical and genetic features of benign familial neonatal seizures (BFNS) with the functional consequences of underlying mutations. Channels (Austin) 1, 228–233.
Starace, D. M., and Bezanilla, F. (2001). Histidine scanning mutagenesis of basic residues of the S4 segment of the Shaker potassium channel. J. Gen. Physiol. 117, 469–490.
Starace, D. M., and Bezanilla, F. (2004). A proton pore in a potassium channel voltage sensor reveals a focused electric field. Nature 427, 548–553.
Stefani, E., Toro, L., Perozo, E., and Bezanilla, F. (1994). Gating of Shaker K+ channels: I. Ionic and gating currents. Biophys. J. 66, 996–1010.
Struyk, A. F., and Cannon, S. C. (2007). A Na+ channel mutation linked to hypokalemic periodic paralysis exposes a proton selective gating Pore. J. Gen. Physiol. 130, 11–20.
Suenaga, A., Komeiji, Y., Uebayasi, M., Meguro, T., Saito, M., and Yamato, I. (1998). Computational observation of an ion permeation through a channel protein. Biosci. Rep. 18, 39–48.
Tao, X., Lee, A., Limapichat, W., Dougherty, D. A., and MacKinnon, R. (2010). A gating charge transfer center in voltage sensors. Science 328, 67–73.
Tarek, M. (2005). Membrane electroporation: a molecular dynamics simulation. Biophys. J. 88, 4045–4053.
Tempel, B. L., Papazian, D. M., Schwarz, T. L., Jan, Y. N., and Jan, L. Y. (1987). Sequence of a probable potassium channel component encoded at Shaker locus of Drosophila. Science 237, 770–775.
Tieleman, D. P., Biggin, P. C., Smith, G. R., and Sansom, M. S. P. (2001). Simulation approaches to ion channel structure-function relationships. Q. Rev. Biophys. 34, 473–561.
Tiwari-Woodruff, S. K., Lin, M. A., Schulteis, C. T., and Papazian, D. M. (2000). Voltage-dependent structural interactions in the Shaker K+ channel. J. Gen. Physiol. 115, 123–138.
Tombola, F., Pathak, M. M., Gorostiza, P., and Isacoff, E. Y. (2006a). The twisted ion-permeation pathway of a resting voltage-sensing domain. Nature 445, 546–549.
Tombola, F., Pathak, M. M., and Isacoff, E. Y. (2006b). How does voltage open an ion channel? Annu. Rev. Cell Dev. Biol. 22, 23–52.
Tombola, F., Pathak, M. M., and Isacoff, E. Y. (2005a). How far will you go to sense voltage? Neuron 48, 719–725.
Tombola, F., Pathak, M. M., and Isacoff, E. Y. (2005b). Voltage-sensing arginines in a potassium channel permeate and occlude cation-selective pores. Neuron 45, 379–388.
Treptow, W., Maigret, B., Chipot, C., and Tarek, M. (2004). Coupled motions between pore and voltage-sensor domains: a model for Shaker B, a voltage-gated potassium channel. Biophys. J. 87, 2365–2379.
Treptow, W., Marrink, S. J., and Tarek, M. (2008). Gating motions in voltage-gated potassium channels revealed by coarse-grained molecular dynamics simulations. J. Phys. Chem. B 112, 3277–3282.
Treptow, W., and Tarek, M. (2006a). Environment of the gating charges in the Kv1.2 Shaker potassium channel. Biophys. J. 90, L64–L66.
Treptow, W., and Tarek, M. (2006b). K+ conduction in the selectivity filter of potassium channels is monitored by the charge distribution along their sequence. Biophys. J. 91, L81–L83.
Treptow, W., Tarek, M., and Klein, M. L. (2009). Initial response of the potassium channel voltage sensor to a transmembrane potential. J. Am. Chem. Soc. 131, 2107–2110.
Vargas, E., Bezanilla, F., and Roux, B. (2011). In search of a consensus model of the resting state of a voltage-sensing domain. Neuron 72, 713–720.
Wee, C. L., Gavaghan, D., and Sansom, M. S. P. (2008). Lipid bilayer deformation and the free energy of interaction of a Kv channel gating-modifier toxin. Biophys. J. 95, 3816–3826.
Wood, M. L., Schow, E. V., Freites, J. A., White, S. H., Tombola, F., and Tobias, D. J. (2012). Water wires in atomistic models of the Hv1 proton channel. Biochim. Biophys. Acta 1818, 286–293.
Wu, D., Delaloye, K., Zaydman, M. A., Nekouzadeh, A., Rudy, Y., and Cui, J. (2010). State-dependent electrostatic interactions of S4 arginines with E1 in S2 during Kv7.1 activation. J. Gen. Physiol. 135, 595–606.
Xu, Y., Ramu, Y., and Lu, Z. (2008). Removal of phospho-head groups of membrane lipids immobilizes voltage sensors of K+ channels. Nature 451, 826–829.
Yarov-Yarovoy, V., Baker, D., and Catterall, W. A. (2006). Voltage sensor conformations in the open and closed states in Rosetta structural models of K+ channels. Proc. Natl. Acad. Sci. U.S.A. 103, 7292–7297.
Yoda, T., Sugita, Y., and Okamoto, Y. (2004). Secondary-structure preferences of force fields for proteins evaluated by generalized-ensemble simulations. Chem. Phys. 307, 269–283.
Zagotta, W. N., Hoshi, T., and Aldrich, R. W. (1994a). Shaker potassium channel gating. III: Evaluation of kinetic models for activation. J. Gen. Physiol. 103, 321.
Zagotta, W. N., Hoshi, T., Dittman, J., and Aldrich, R. W. (1994b). Shaker potassium channel gating. II: Transitions in the activation pathway. J. Gen. Physiol. 103, 279–319.
Zhang, M., Liu, J., Jiang, M., Wu, D.-M., Sonawane, K., Guy, H. R., and Tseng, G.-N. (2005). Interactions between charged residues in the transmembrane segments of the voltage-sensing domain in the hERG channel. J. Membr. Biol. 207, 169–181.
Zheng, H., Liu, W., Anderson, L. Y., and Jiang, Q.-X. (2011). Lipid-dependent gating of a voltage-gated potassium channel. Nat. Commun. 2, 250.
Zheng, J., and Sigworth, F. J. (1998). Intermediate conductances during deactivation of heteromultimeric Shaker potassium channels. J. Gen. Physiol. 112, 457–474.
Keywords: Kv1.2, gating charges, VSD intermediate states, molecular models, channelopathies, mutations, omega currents
Citation: Delemotte L, Klein ML and Tarek M (2012) Molecular dynamics simulations of voltage-gated cation channels: insights on voltage-sensor domain function and modulation. Front. Pharmacol. 3:97. doi: 10.3389/fphar.2012.00097
Received: 21 March 2012; Accepted: 01 May 2012;
Published online: 28 May 2012.
Edited by:
Gildas Loussouarn, University of Nantes, FranceCopyright: © 2012 Delemotte, Klein and Tarek. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: Mounir Tarek, UMR Synthèse et Réactivité de Systèmes Moléculaires Complexes, Faculté des Sciences et Techniques, Université de Lorraine, B.P. 70239, 54506 Vandoeuvre les Nancy Cedex, France. e-mail:bW91bmlyLnRhcmVrQHVuaXYtbG9ycmFpbmUuZnI=

 Michael L. Klein2
Michael L. Klein2